Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T12:09:01.375Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of a susceptible–infected–susceptible epidemic reaction–diffusion model

Part of: Applications - Dynamical systems and ergodic theory Mathematical sociology Partial differential equations Parabolic equations and systems

Published online by Cambridge University Press:  19 July 2016

Keng Deng  and
Yixiang Wu
Keng Deng
Affiliation:
Department of Mathematics, University of Louisiana at Lafayette, Lafayette, LA 70504, USA (deng@louisiana.edu)
Yixiang Wu
Affiliation:
Department of Mathematics, University of Louisiana at Lafayette, Lafayette, LA 70504, USA (deng@louisiana.edu)
Get access Rights & Permissions [Opens in a new window]

Extract

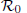We study a susceptible–infected–susceptible reaction–diffusion model with spatially heterogeneous disease transmission and recovery rates. A basic reproduction number is defined for the model. We first prove that there exists a unique endemic equilibrium if 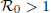. We then consider the global attractivity of the disease-free equilibrium and the endemic equilibrium for two cases. If the disease transmission and recovery rates are constants or the diffusion rate of the susceptible individuals is equal to the diffusion rate of the infected individuals, we show that the disease-free equilibrium is globally attractive if 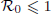, while the endemic equilibrium is globally attractive if .

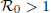Keywords

SIS epidemic reaction–diffusion modelspatial heterogeneitydisease-free equilibriumendemic equilibriumglobal attractivity

MSC classification

Secondary: 92D30: Epidemiology 91D25: Spatial models 35K57: Reaction-diffusion equations 37N25: Dynamical systems in biology 35B35: Stability
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 146 , Issue 5 , October 2016 , pp. 929 - 946
Copyright
Copyright © Royal Society of Edinburgh 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)