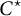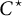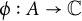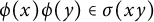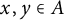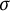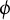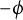A multiplicative Kowalski–Słodkowski theorem for $C^\star $-algebras

Abstract

We present here a multiplicative version of the classical Kowalski–Słodkowski theorem, which identifies the characters among the collection of all functionals on a complex and unital Banach algebra A. In particular, we show that, if A is a $C^\star $-algebra, and if $\phi :A\to \mathbb C $ is a continuous function satisfying $ \phi (x)\phi (y) \in \sigma (xy) $ for all $x,y\in A$ (where $\sigma $ denotes the spectrum), then either $\phi $ is a character of A or $-\phi $ is a character of A.

1 Introduction

Over the past two decades, there has been considerable interest in the area of nonlinear preserver problems (see a detailed introduction in [1] and the references therein). Loosely speaking, these problems deal with characterizing maps between algebras that preserve a certain (given) algebraic aspect of the spectrum, but without assuming any algebraic conditions, like linearity or multiplicativity, of the map itself. One of the earliest results in this direction is a theorem of Kowalski and Słodkowski [7]; they discovered a nonlinear version of the renowned Gleason–Kahane–Żelazko theorem [3, 6, 17], which states that every unital, invertibility-preserving, linear functional on a Banach algebra is necessarily multiplicative, and hence a character of A. The Gleason–Kahane–Żelazko theorem continues to attract attention, and some recent papers of Mashreghi, Ransford, and Ransford include [9, 10]. The main result of the current paper simultaneously improves the main result of [16] and the main result of [2], thereby settling the problem for general $C^\star $ -algebras. We start with the statement of the Kowalski–Słodkowski theorem.

Theorem 1.1 (Kowalski–Słodkowski [7])

Let B be a complex Banach algebra. Then a function $\phi :B\to \mathbb C$ is linear and multiplicative if and only if $\phi $ satisfies:

1. (i) $\phi (\mathbf 0)=0$ ,

2. (ii) $\phi (x)-\phi (y)\in \sigma (x-y)$ for every $x,y\in B$ .

One may observe that the hypothesis of Theorem 1.1 can be stated more economically by requiring only the condition $\phi (x)+\phi (y)\in \sigma (x+y)$ for every pair $x,y\in B$ . Furthermore, as a consequence of the Kowalski–Słodkowski theorem, one can prove, in a few lines, the following generalization due to Hatori et al.

Theorem 1.2 [5, Theorem 3.1]

Let B be a unital Banach algebra, and let $B'$ be a unital, semisimple, commutative Banach algebra. Suppose that T is a map from B into $B'$ such that $\sigma (T(a)+T(b))\subseteq \sigma (a+b)$ holds for every pair a and b in B. Then T is linear and multiplicative.

Very close to the current paper are the results that appear in [4, 5, 11–13]: In [11], Molnár studied multiplicatively spectrum-preserving maps $T:B(H)\to B(H)$ where H is an infinite-dimensional Hilbert space, as well as for maps $T:C(X)\to C(X)$ where X is a first countable compact Hausdorff space. Specifically, he proved that surjective maps T on the aforementioned Banach algebras B satisfying

$$ \begin{align*}\sigma(T(a)T(b))= \sigma(ab),\quad \mbox{ for all } a,b\in B,\end{align*} $$

are “almost” automorphisms. In particular, if T preserves the unit, then T is an automorphism. His results were extended, in several directions, for uniform algebras and semisimple commutative Banach algebras by, among others, Hatori et al. in [4], and by Rao and Roy in [12, 13]. Hatori et al., in [5], proposed that if the Kowalski–Słodkowski theorem could be modified (multiplicatively) so that a map $\phi $ from a Banach algebra B (with unit $\mathbf {1}$ ) into $\mathbb {C}$ satisfying

(1.1) $$ \begin{align} \phi(\mathbf{1}) = 1 \mbox{ and } \phi(a)\phi(b)\in\sigma(ab),\quad \mbox{ for all } a,b\in B, \end{align} $$

was always linear and multiplicative, then some theorems of Molnár and their generalizations could be proved in a way similar to the proof of Theorem 1.2. However, as one sees in [8, pp. 44–45] and [15, p. 56], a raw multiplicative version of the Kowalski–Słodkowski theorem does not even hold for commutative $C^\star $ -algebras. However, one should observe that in these examples, the map $\phi $ is not continuous, and hence any hope of proving the multiplicative result would require continuity to be added as an assumption. What we will show here, at least for the case where A is a $C^\star $ -algebra, is that continuity is the only problem which needs to be addressed. To formalize our main result:

Main Result If A is a unital $C^\star $ -algebra, and if $\phi :A\to \mathbb C$ is a continuous function that satisfies

(1.2) $$ \begin{align} \phi(\mathbf{1}) = 1 \mbox{ and } \phi(a)\phi(b)\in\sigma(ab),\mbox{ for all } a,b\in A, \end{align} $$

then $\phi $ must be a character of A.

As an easy corollary of our main result, we can then obtain a multiplicative version of Hatori et al.’ s Theorem 1.2 (stated above).

Corollary Let A be a unital $C^\star $ -algebra, and let $B'$ be a unital, semisimple, commutative Banach algebra. Suppose that T is a continuous map from A into $B'$ such that $\sigma (T(a)T(b))\subseteq \sigma (a+b)$ holds for every pair a and b in A. Then T is linear and multiplicative.

2 Preliminaries

Throughout the remainder of this paper, A denotes a complex and unital $C^\star $ -algebra with unit $\mathbf {1}$ and additive identity $\mathbf {0}.$ Since our proofs are elementary (but far from trivial), it suffices to consult a standard reference, such as [14], for the basics of $C^\star $ -algebras. We denote by ${\mathcal S}_A $ the set of self-adjoint elements of A, and by $G(A)$ the set of invertible elements of A. Furthermore, we write $G_{\mathbf 1}(A)$ for the connected component of the group $G(A)$ containing the unit. It is well known that

$$ \begin{align*}G_{\mathbf 1}(A):=\{ e^{x_1}e^{x_2}\cdots e^{x_n}: n \in \mathbb{N} \mbox{ and } x_i \in A \}.\end{align*} $$

For any x in $A $ , we shall use $\sigma $ and $\rho $ to denote, respectively, the spectrum $ \sigma (x) := \{ \lambda \in \mathbb {C} : \lambda \mathbf {1} -x \notin G(A) \},$ and the spectral radius $ \rho (x) := \sup \{ \vert \lambda \vert : \lambda \in \sigma (x) \}$ of x. For every $x\in A$ , $|x|$ denotes the positive square root of $x^\star x$ . By a functional on A, we shall mean any function that maps A to $\mathbb {C}$ ; specifically, for the purpose of this paper, a functional is not necessarily linear. A character of A is a linear functional $\chi :A\to \mathbb {C}$ which is simultaneously multiplicative, i.e., $\chi (ab)=\chi (a)\chi (b)$ for every $a,b\in A$ . To shorten the statements of some results, we also introduce the following general terminology.

Definition 2.1 (Multiplicatively spectral functional)

Let B be a unital complex Banach algebra. Then a functional $\phi :B\to \mathbb C$ is said to be a multiplicatively spectral functional on B whenever $\phi $ satisfies the following two conditions:

1. (P1) $\phi (x)\phi (y) \in \sigma (xy)$ , for all $x,y\in B$ .

2. (P2) $\phi (\mathbf 1)=1$ .

Definition 2.2 (Spectrally multiplicative functional)

Let B be a unital complex Banach algebra. Then a functional $\phi :B\to \mathbb C$ is said to be a spectrally multiplicative functional on B whenever $\phi $ satisfies the following condition:

1. (P1) $\phi (x)\phi (y) \in \sigma (xy)$ , for all $x,y\in B$ .

Our motivation for this terminology follows from the observation that if $\phi $ satisfies (P1) and (P2), then $\phi $ takes values in the spectrum; if $\phi $ satisfies only (P1), then either $\phi $ or $-\phi $ takes values in the spectrum. So, if $\phi $ is a spectrally multiplicative functional, then either $\phi $ or $-\phi $ is a multiplicatively spectral functional. For $x\in A$ , we will denote the real and imaginary parts of x by, respectively, $R_x$ and $I_x$ , that is,

$$ \begin{align*}x= R_x+i I_x \mbox{ where } R_x=\frac{x+x^\star}{2} \in {\mathcal S}_A \mbox{ and } I_x=\frac{x-x^\star}{2i}\in {\mathcal S}_A .\end{align*} $$

If there is no danger of confusion, we will simply write

$$ \begin{align*}x=R+iI .\end{align*} $$

In [16], the authors showed that if $\phi :A\to \mathbb {C}$ is continuous and satisfies (P1) and (P2), then $\phi $ generates a character $\psi _\phi $ of A, and, moreover, $\psi _\phi $ and $\phi $ agree on certain subsets of A; the precise statement, which will be the starting point of the proof of our main result, is as follows.

Theorem 2.1 [16, Theorems 3.7 and 3.9]

Let $\phi $ be a continuous multiplicatively spectral functional on a $C^\star $ -algebra A. Then the formula

$$ \begin{align*}\psi_\phi(x) := \phi(R_x) + i \phi(I_x)\end{align*} $$

defines a character on A. Furthermore, $ \phi (x) = \psi _\phi (x) $ whenever x belongs to $G_{\mathbf 1}(A)\cup {\mathcal S}_A $ .

3 Proof of the main result

Proceeding through a series of lemmas, we show that any continuous multiplicatively spectral functional on a $C^\star $ -algebra is a character. Our first three results are rather easy, and we give the short proofs for the sake of completeness. Furthermore, throughout this section, the function $\psi _\phi $ refers to the character in Theorem 2.1.

Lemma 3.1 Let $a, b $ be positive elements of a $C^\star $ -algebra A such that $a^2\leq b^2$ , and let $(v_n)$ be a sequence in A such that $ \lim _n b v_n= \mathbf {0}$ . Then $\lim _n a v_n= \mathbf {0} $ .

Proof It suffices to show that $\Vert av_n\Vert ^2 \leq \Vert b v_n \Vert ^2$ for every n. Observe first that

$$ \begin{align*}\Vert a v_n \Vert^2 =\Vert (a v_n)^\star(a v_n)\Vert=\Vert ( v_n^\star a)(a v_n)\Vert=\Vert v_n^\star a^2 v_n\Vert .\end{align*} $$

Since $ a^2\leq b^2$ , we have $v_n^\star a^2 v_n\leq v_n^\star b^2 v_n$ and hence $ \Vert v_n^\star a^2 v_n \Vert \leq \Vert v_n^\star b^2 v_n \Vert =\Vert b v_n \Vert ^2 $ . Consequently, we get $ \Vert a v_n \Vert ^2 \leq \Vert b v_n \Vert ^2$ .

Corollary 3.2 Let A be a $C^\star $ -algebra, $a\in {\mathcal S}_A$ , and let $(v_n)$ be a sequence in A such that $\lim _n \vert a \vert v_n =\mathbf {0}$ . Then $\lim _n a v_n =\mathbf {0} .$

Proof Clearly, $\mathbf {0} \leq (\vert a \vert -a)^2 \leq (2\vert a \vert )^2$ . Invoking Lemma 3.1, we infer that $\lim _n (\vert a \vert -a)v_n= \mathbf {0} \implies \lim _n a v_n= \mathbf {0} $ .

Lemma 3.3 Let x be an element of ${\mathcal S}_A$ . Then

$$ \begin{align*}\lim_n \vert x \vert e^{ -n\vert x \vert}=\mathbf{0}\quad \mbox{ and }\quad \lim_n \vert x \vert \left(\mathbf{1}+in\vert x\vert\right)^{ -1}=\mathbf{0}.\end{align*} $$

Proof We shall prove the result where a is any positive element of A: by the Gelfand–Naimark theorem, we can assume, without loss of generality, that A is commutative so that $A=C(X)$ for some compact set X. For each $n\in \mathbb N$ , define $b_n=a e^{-na} $ and $c_n=a \left (\mathbf {1}+in a\right )^{-1}$ . Then

$$ \begin{align*} \Vert b_n \Vert=\sup_{}\left\{ a(x)e^{-na(x)}: x \in X \right\}\leq \sup_{}\left\{ te^{-nt} : t \geq 0 \right\} \leq \frac{e^{-1}}{n}, \end{align*} $$

and hence $\lim _n b_n=\mathbf {0}.$ Similarly,

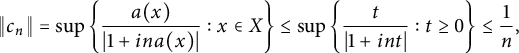$$ \begin{align*} \Vert c_n \Vert=\sup_{}\left\{ \frac{a(x)}{ \vert 1 +i na(x) \vert } : x \in X\right\} \leq \sup_{ }\left\{ \frac{t}{ \vert 1 +i n t \vert }: t \geq 0 \right\} \leq \frac{1}{n}, \end{align*} $$

so that $\lim _n c_n=\mathbf {0}.$ Since $\vert x \vert $ is positive, we have the result.

The next three lemmas progressively narrow down the connection between $\phi $ and $\psi _\phi $ : the idea is to construct two sequences (from the sequences $b_n$ and $c_n$ which were defined in the proof of Lemma 3.3) and then to filter them through the spectrum while simultaneously keeping track of $\phi $ and $\psi _\phi $ via the condition (P1) and Theorem 2.1. The main result then follows from a compactness argument using the results obtained in the preceding lemmas.

Lemma 3.4 Let $\phi $ be a continuous multiplicatively spectral functional on a $C^\star $ -algebra A, and suppose that $x\in A$ satisfies $\psi _\phi (x) = 0$ . Then $\phi (x)=0$ .

Proof We know that $\psi _\phi (x) = 0=\psi _\phi \left ( R+i I\right)\hspace{-1.2pt}{,}$ which implies that $\psi _\phi \left ( R\right )=\psi _\phi \left ( I\right )=0.$ For each $n\in \mathbb N$ , let $W_n:=e^{-n \sqrt {\vert R \vert ^2+\vert I \vert ^2} }$ and observe, using Theorem 2.1, that $\phi \left ( W_n\right )=\psi _\phi \left ( W_n\right )=1$ . From (P1), it follows that

(3.1) $$ \begin{align} \phi(x)=\phi(x)\phi\left( W_n\right)\in \sigma\left( xW_n\right)=\sigma\left(RW_n +iIW_n\right)\hspace{-1pt}. \end{align} $$

Using Lemmas 3.1 and 3.3 and Corollary 3.2, we deduce that

$$ \begin{align*}\lim_n \sqrt{\vert R \vert^2+\vert I \vert^2}\,W_n=\mathbf{0}\implies \lim_n \vert R \vert W_n=\mathbf 0\implies \lim_n R W_n=\mathbf 0,\end{align*} $$

and similarly, $\lim _n I W_n= \mathbf {0}.$ Thus,

$$ \begin{align*}\lim_n xW_n= \lim_n \left(RW_n +iIW_n\right)= \mathbf{0}.\end{align*} $$

Using (3.1), we have that $\vert \phi (x)\vert \leq \|xW_n\|$ and so, by taking the limit as $n\to \infty $ , we get $\phi (x)=0$ .

Lemma 3.5 Let $\phi $ be a continuous multiplicatively spectral functional on a $C^\star $ -algebra A, $\alpha \in \mathbb {C} $ , and suppose that $x\in A$ satisfies $\psi _\phi (x)=0 $ . Then $\phi (\alpha \mathbf {1}+ x) =c_\alpha \alpha $ , for some $c_\alpha \in [0,1]$ .

Proof Let $\alpha $ be an arbitrary nonzero complex number. With $W_n$ defined as in the proof of Lemma 3.4, let $Y_n:=\frac {1}{ \alpha }xW_n$ , and set $c_\alpha :=\frac {1}{ \alpha }\phi (\alpha \mathbf {1}+x)$ . Then, using (P1) together with $\phi \left (W_n \right )=1$ , for each $n\in \mathbb N$ ,

(3.2) $$ \begin{align} c_\alpha= \frac{1}{ \alpha }\phi(\alpha\mathbf{1}+x)\phi\left(W_n \right) \in \sigma\left( W_n+ Y_n \right)\hspace{-1.5pt}. \end{align} $$

Observe, from the proof of Lemma 3.4, that $\lim _n Y_n = \mathbf {0}$ . To show that $c_\alpha \in [0,1],$ assume, to the contrary, that $c_\alpha \notin [0, 1].$ For each n, we have that $W_n\in {\mathcal S}_A$ and $\sigma (W_n ) \subseteq [0,1] $ . From (3.2), we see that

$$ \begin{align*}c_\alpha\mathbf{1} -W_n -Y_n \notin G(A) \;\mbox{ implying that } \;\mathbf{1} -Y_n( c_\alpha\mathbf{1} -W_n)^{-1} \notin G(A).\end{align*} $$

Since $( c_\alpha \mathbf {1} -W_n)^{-1}$ is normal for each $n,$ we have the estimation

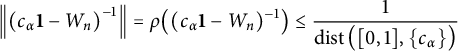$$ \begin{align*}\left\Vert\left( c_\alpha\mathbf{1} -W_n\right)^{-1} \right\Vert=\rho\big( ( c_\alpha\mathbf{1} -W_n)^{-1} \big) \leq \frac{1}{\operatorname{\mathrm{dist}}\big([0,1] , \{c_\alpha\}\big) }\end{align*} $$

from which it follows that $\lim _n Y_n( c_\alpha \mathbf {1} -W_n)^{-1} =\mathbf {0}$ , hence contradicting the fact that $ G(A) $ is open. Therefore, $c_\alpha \in [0,1]$ , and thus $\phi (\alpha \mathbf {1}+x)=c_\alpha \alpha .$

The final lemma shows that the value of $c_\alpha $ in Lemma 3.5 can be narrowed down to one of two possibilities.

Lemma 3.6 Let $\phi $ be a continuous multiplicatively spectral functional on a $C^\star $ -algebra A. If $\alpha \in \mathbb {C} $ and $x\in A$ satisfies $\psi _\phi (x)=0 $ , then $\phi (\alpha \mathbf {1}+ x)\in \{ 0,\alpha \} .$

Proof For each $n\in \mathbb N$ , let $V_n:=\left (\mathbf {1}+in\sqrt {\vert R \vert ^2+\vert I \vert ^2} \right )^{-1}\hspace{-2pt}.$ Again, using Lemmas 3.1 and 3.3 and Corollary 3.2, we have that

$$ \begin{align*}\lim_n\sqrt{\vert R \vert^2+\vert I \vert^2}\, V_n=\mathbf{0} \implies \lim_n \vert R \vert V_n=\mathbf{0}\implies \lim_n R V_n=\mathbf{0}.\end{align*} $$

Similarly, $\lim _n I V_n=\mathbf {0} $ . Observe that each $V_n$ belongs to $ G_{\mathbf 1}(A)$ , whence it follows that $\phi (V_n) = \psi _\phi (V_n)=1 $ . Let $\alpha \neq 0 $ . From Lemma 3.5, we have that $\phi (\alpha \mathbf {1}+x)=c_\alpha \alpha $ , with $c_\alpha \in [0,1]$ . To obtain the result, we have to show that $c_\alpha \in \{0,1\}$ : For the sake of a contradiction, assume that $ 0< c_\alpha <1$ . If we set $Z_n:=\frac {1}{\alpha }xV_n=\frac {1}{\alpha }(R+iI) V_n$ , then

(3.3) $$ \begin{align} c_\alpha=\frac{1}{\alpha}\phi(\alpha\mathbf{1}+x)\phi(V_n)\in \sigma\left(V_n+Z_n\right). \end{align} $$

The first paragraph of the proof shows that $\lim _n Z_n=\mathbf {0}$ , and (3.3) shows that $c_\alpha \mathbf {1}-V_n-Z_n \notin G(A) $ . From the definition of $V_n$ , we have that $\sigma \left (V_n\right ) \subseteq C_r $ , where $C_r$ is the circle in $\mathbb C$ with center $\frac {1}{2}$ and radius $\frac {1}{2}$ : indeed, if $\theta \in \sigma \left (V_n\right )$ , then $\theta =\frac {1}{1+v^2} +i\frac {-v}{1+v^2}$ , for some $v \geq 0$ , and so $\left ( \operatorname {\mathrm {Re}}(\theta )-\frac {1}{2}\right )^2+\left ( \operatorname {\mathrm {Im}}(\theta )\right )^2=\frac {1}{4} $ . Owing to the fact that $C_r \cap \mathbb {R} =\{ 0,1\} $ , we infer that $c_\alpha \notin \sigma \left (V_n\right )$ . Thus,

$$ \begin{align*}c_\alpha\mathbf{1} -V_n-Z_n \notin G(A) \mbox{ and } c_\alpha\mathbf{1} -V_n \in G(A) ,\end{align*} $$

which together implies that $ \mathbf {1}-Z_n\left ( c_\alpha \mathbf {1} -V_n\right )^{-1} \notin G(A) .$ Since $V_n$ is normal, we obtain the estimate

$$ \begin{align*}\left\Vert \left( c_\alpha\mathbf{1} -V_n\right)^{-1}\right\Vert =\rho\left( \left( c_\alpha\mathbf{1} -V_n\right)^{-1} \right) \leq \frac{1}{\operatorname{\mathrm{dist}}(C_r,\{ c_\alpha \} ) }\end{align*} $$

from which it follows that $\lim _n Z_n\left ( c_\alpha \mathbf {1} -V_n\right )^{-1}= \mathbf {0}$ , contradicting the fact that $G(A)$ is open. Subsequently, $c_\alpha \in \{0,1\}$ , and $\phi (\alpha \mathbf {1}+x)\in \{0, \alpha \}$ follows as advertised.

We are now in a position to prove the main result.

Theorem 3.7 Let $\phi $ be a continuous multiplicatively spectral functional on a $C^\star $ -algebra A. Then $\phi (x) = \psi _\phi (x)$ for all x in A, and hence $\phi $ is a character of A.

Proof For $x\in A$ , define $K_x:=\{\alpha \in \mathbb {C} : \phi (\alpha \mathbf {1}+x)=0\}$ , and assume first that $\psi _\phi (x)=0$ . Our aim is to prove that $K_x=\{0\}$ . Observe that $0 \in K_x$ (by Lemma 3.4), $K_x \subseteq \sigma (-x)$ (by P(1) and P(2)), and $K_x$ is closed (since $\phi $ is continuous). Thus, $K_x$ is nonempty and compact. Let m be a maximum modulus element of $K_x$ . From the definition of m, there is a sequence $(k_n) \subset \mathbb C\setminus K_x$ which converges to m. Therefore, by Lemma 3.6, $\lim _n\phi \big (k_n\mathbf {1}+x \big )=\lim _n k_n =m $ , and by continuity of $\phi $ , $\lim _n\phi \big (k_n\mathbf {1}+x \big )=\phi \big (m\mathbf {1}+x \big )=0 $ . Thus, $m=0$ from which it follows that $K_x=\{0\}$ . Invoking Lemma 3.6 again, we then obtain $\phi (\alpha \mathbf {1}+x)=\alpha $ for each $\alpha \in \mathbb C$ . For any value of $ \psi _\phi (x) $ , we use the first part of the proof to deduce that

$$ \begin{align*}\phi(x)=\phi\left( \psi_\phi(x)\mathbf{1}+\left[x-\psi_\phi(x)\mathbf{1}\right] \right)= \psi_\phi(x).\\[-36pt]\end{align*} $$

As a direct consequence of Theorem 3.7, one also has the following.

Corollary 3.8 Let $\phi $ be a continuous spectrally multiplicative functional on a $C^\star $ -algebra A. Then either $\phi $ is a character of A or $-\phi $ is a character of A.

Proof If $\phi $ is spectrally multiplicative, then either $\phi $ or $-\phi $ is multiplicatively spectral. The result then follows from Theorem 3.7.

As a further consequence of Theorem 3.7, we can now address a problem raised by Hatori et al. [5, p. 286] in the case where A is a $C^\star $ -algebra.

Corollary 3.9 Let A be a $C^\star $ -algebra, let B be a semisimple commutative Banach algebra, and suppose $\phi :A\to B$ is a function that satisfies:

1. (1) $\sigma \left (\phi (x)\phi (y)\right ) \subseteq \sigma (xy)$ , for all $x,y\in A$ ,

2. (2) $\phi (\mathbf 1)=\mathbf 1$ ,

3. (3) $\phi $ is continuous on A.

Then $\phi $ is a homomorphism.

Proof Let $\chi $ be an arbitrary character of B. Then $\chi \circ \phi $ is a continuous multiplicatively spectral functional on A. Hence, by Theorem 3.7, $\chi \circ \phi $ is a character. The result then follows from the semisimplicity of B.