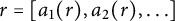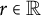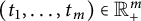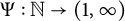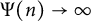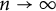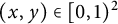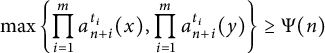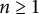1 Introduction
The theory of continued fractions is simple yet extremely useful in characterizing irrational numbers. It is well known that every irrational
![]() $x\in [ 0,1)$
can be uniquely expressed as a simple infinite continued fraction expansion of the form
$x\in [ 0,1)$
can be uniquely expressed as a simple infinite continued fraction expansion of the form
where
![]() $a_{n}(x)\in \mathbb {N}, n\geq 1$
, are known as the partial quotients of
$a_{n}(x)\in \mathbb {N}, n\geq 1$
, are known as the partial quotients of
![]() $x.$
The theory of continued fractions plays a pivotal role in giving quantitative information on how well a real number can be approximated by rationals. The main connection is that the nth convergents of a real number x are good rational approximates for
$x.$
The theory of continued fractions plays a pivotal role in giving quantitative information on how well a real number can be approximated by rationals. The main connection is that the nth convergents of a real number x are good rational approximates for
![]() $x, $
summarized as
$x, $
summarized as
 $$ \begin{align*} \frac{1}{(2+a_{n+1}(x))q^2_{n}(x)}\leq \,\Big|x-\frac{p_{n}(x)}{q_{n}(x)}\Big|\leq\,\frac{1}{a_{n+1}(x)q^2_{n}(x)}. \end{align*} $$
$$ \begin{align*} \frac{1}{(2+a_{n+1}(x))q^2_{n}(x)}\leq \,\Big|x-\frac{p_{n}(x)}{q_{n}(x)}\Big|\leq\,\frac{1}{a_{n+1}(x)q^2_{n}(x)}. \end{align*} $$
The nth convergent of x,
![]() $\frac {p_n(x)}{q_n(x)}$
, is a rational number obtained by truncating the continued fraction expansion of x at the
$\frac {p_n(x)}{q_n(x)}$
, is a rational number obtained by truncating the continued fraction expansion of x at the
![]() $n\textrm{th}$
term, that is,
$n\textrm{th}$
term, that is,
![]() $ \frac {p_n(x)}{q_n(x)}:= [a_{1}(x), a_{2}(x),\ldots , a_n(x)]$
. This, in turn, gives an alternative form of the famous Jarník–Besicovitch set; for any
$ \frac {p_n(x)}{q_n(x)}:= [a_{1}(x), a_{2}(x),\ldots , a_n(x)]$
. This, in turn, gives an alternative form of the famous Jarník–Besicovitch set; for any
![]() $\tau>0$
,
$\tau>0$
,
The Hausdorff dimension, denoted by
![]() $\dim _{\mathcal H}$
, of this set is
$\dim _{\mathcal H}$
, of this set is
![]() $\frac 2{2+\tau }$
(see [Reference Wang and Wu16] for more details). There have been plenty of work regarding the metrical properties of the growth of partial quotients, for instance, the classical Borel–Bernstein theorem states that the Lebesgue measure of the set
$\frac 2{2+\tau }$
(see [Reference Wang and Wu16] for more details). There have been plenty of work regarding the metrical properties of the growth of partial quotients, for instance, the classical Borel–Bernstein theorem states that the Lebesgue measure of the set
is either zero or full according to the convergence or divergence of the series
![]() $\sum _n1/\Psi (n)$
. For rapidly increasing functions,
$\sum _n1/\Psi (n)$
. For rapidly increasing functions,
![]() $\Psi $
gives no information regarding the size of this set other than that its Lebesgue measure zero. One of the most appropriate tools to distinguish between Lebesgue zero sets is the notion of Hausdorff dimension. Good [Reference Good6] proved the Hausdorff dimension for the set
$\Psi $
gives no information regarding the size of this set other than that its Lebesgue measure zero. One of the most appropriate tools to distinguish between Lebesgue zero sets is the notion of Hausdorff dimension. Good [Reference Good6] proved the Hausdorff dimension for the set
![]() $\{x\in [0, 1): a_n(x)\to \infty \ \text {as} n\to \infty \}$
to be
$\{x\in [0, 1): a_n(x)\to \infty \ \text {as} n\to \infty \}$
to be
![]() $1/2$
. Later, Łuczak [Reference Łuczak14] extended Good’s result to the functions of the type
$1/2$
. Later, Łuczak [Reference Łuczak14] extended Good’s result to the functions of the type
![]() $\Psi (n)=c^{b^n}$
, where
$\Psi (n)=c^{b^n}$
, where
![]() $b, c>1$
. The Hausdorff dimension for an arbitrary function
$b, c>1$
. The Hausdorff dimension for an arbitrary function
![]() $\Psi $
was comprehensively established by Wang and Wu in [Reference Wang and Wu16].
$\Psi $
was comprehensively established by Wang and Wu in [Reference Wang and Wu16].
Since the nth convergents are the best approximations, the continued fractions approach has proved to be extremely useful in analyzing the approximation properties of real numbers by rational numbers. However, this “standard approach” is not applicable in higher dimensions. There are various alternative tools proposed to replace the continued fraction approach to tackle the higher-dimensional approximation properties of real points by rational points. The dynamics on the space of lattices, for example, has proved to be useful, but the efficacy of continued fractions is yet to be matched. There have been many attempts to construct higher-dimensional analogue of the Gauss map, so that it captures all the features of simultaneous approximation. The theory is not well developed yet.
Lü and Zhang [Reference Lü and Zhang13] used the Continued Fraction algorithm to compute the Hausdorff dimension of a set of points in the plane with certain growth conditions on the partial quotients in their continued fraction expansion. To be precise, they considered the following set:
and calculated its Hausdorff dimension to be
![]() $\frac {3}{2}$
. As stated above, this set is a generalization to the plane of a classical result of Good [Reference Good6].
$\frac {3}{2}$
. As stated above, this set is a generalization to the plane of a classical result of Good [Reference Good6].
Recently, it has been shown that the products of the consecutive partial quotients are associated with the improvements to Dirichlet’s theorem (uniform approximation). To be precise, building on a work of Davenport and Schmidt [Reference Davenport and Schmidt4], Kleinbock and Wadleigh [Reference Kleinbock and Wadleigh12] considered the set
 $$ \begin{align*} D(\psi):=\left\{x\in\mathbb R: \begin{array}{ll}\exists\, N \ \mathrm{such\ that\ the\ system}\ |qx-p|\, <\, \psi(t), \ |q|<t\ \\[2ex] \text{has a nontrivial integer solution for all }t>N\quad \end{array} \!\!\!\right\}, \end{align*} $$
$$ \begin{align*} D(\psi):=\left\{x\in\mathbb R: \begin{array}{ll}\exists\, N \ \mathrm{such\ that\ the\ system}\ |qx-p|\, <\, \psi(t), \ |q|<t\ \\[2ex] \text{has a nontrivial integer solution for all }t>N\quad \end{array} \!\!\!\right\}, \end{align*} $$
calling it a set of
![]() $\psi $
-Dirichlet improvable numbers, where
$\psi $
-Dirichlet improvable numbers, where
![]() $\psi $
is a nonincreasing function. A simple calculation shows the following simple yet extremely important criterion:
$\psi $
is a nonincreasing function. A simple calculation shows the following simple yet extremely important criterion:
One of the consequences of this observation is the following inclusion of sets:
where
and
![]() $ \Phi (t):=\frac {t\psi (t)}{1-t\psi (t)}$
. We refer the reader to [Reference Bakhtawar, Bos and Hussain1–Reference Bos, Hussain and Simmons3, Reference Feng and Xu5, Reference Huang and Wu7–Reference Hussain, Kleinbock, Wadleigh and Wang9, Reference Zhang17] for the background and the metrical results related to
$ \Phi (t):=\frac {t\psi (t)}{1-t\psi (t)}$
. We refer the reader to [Reference Bakhtawar, Bos and Hussain1–Reference Bos, Hussain and Simmons3, Reference Feng and Xu5, Reference Huang and Wu7–Reference Hussain, Kleinbock, Wadleigh and Wang9, Reference Zhang17] for the background and the metrical results related to
![]() $G(\Phi )$
.
$G(\Phi )$
.
In this article, we expand on the work of Lü and Zhang [Reference Lü and Zhang13] by considering the relative growth properties of the products of consecutive partial quotients whose exponents are not necessarily units. Let
![]() $\Psi :\mathbb {N}\rightarrow (1,\infty )$
be a function such that
$\Psi :\mathbb {N}\rightarrow (1,\infty )$
be a function such that
![]() $\Psi (n)\to \infty $
as
$\Psi (n)\to \infty $
as
![]() $n\to \infty $
. Let
$n\to \infty $
. Let
![]() $(t_1, \ldots , t_m)\in \mathbb R_{+}^m$
. Define the set
$(t_1, \ldots , t_m)\in \mathbb R_{+}^m$
. Define the set
 $$ \begin{align*} \Lambda(\Psi):=\left\{(x, y)\in[0,1]^2:\max\left\{\prod_{i=1}^ma_{n+i}^{t_i}(x), \prod_{i=1}^ma_{n+i}^{t_i}(y)\right\} \geq \Psi(n) \ \text{for all} \ n\geq 1\right\}. \end{align*} $$
$$ \begin{align*} \Lambda(\Psi):=\left\{(x, y)\in[0,1]^2:\max\left\{\prod_{i=1}^ma_{n+i}^{t_i}(x), \prod_{i=1}^ma_{n+i}^{t_i}(y)\right\} \geq \Psi(n) \ \text{for all} \ n\geq 1\right\}. \end{align*} $$
We prove the following result.
Theorem 1.1 Let
![]() $\Psi $
be a positive function. Then,
$\Psi $
be a positive function. Then,
2 Preliminaries
2.1 Hausdorff measure and dimension
Let
![]() $s>0$
, and let
$s>0$
, and let
![]() $E\subset \mathbb R^n$
. Then, for any
$E\subset \mathbb R^n$
. Then, for any
![]() $\rho>0$
, a countable collection
$\rho>0$
, a countable collection
![]() $\{B_i\}$
of balls in
$\{B_i\}$
of balls in
![]() $\mathbb R^n$
with diameters
$\mathbb R^n$
with diameters
![]() $\mathrm {diam} (B_i)\le \rho $
such that
$\mathrm {diam} (B_i)\le \rho $
such that
![]() $E\subset \bigcup _i B_i$
is called a
$E\subset \bigcup _i B_i$
is called a
![]() $\rho $
-cover of E. Let
$\rho $
-cover of E. Let
where the infimum is taken over all possible
![]() $\rho $
-covers
$\rho $
-covers
![]() $\{B_i\}$
of E. Note that
$\{B_i\}$
of E. Note that
![]() $\mathcal H_\rho ^s(E)$
increases as
$\mathcal H_\rho ^s(E)$
increases as
![]() $\rho $
decreases and so approaches a limit as
$\rho $
decreases and so approaches a limit as
![]() $\rho \rightarrow 0$
. This limit could be zero or infinity, or take a finite positive value. Accordingly, the s-Hausdorff measure
$\rho \rightarrow 0$
. This limit could be zero or infinity, or take a finite positive value. Accordingly, the s-Hausdorff measure
![]() $\mathcal H^s$
of E is defined to be
$\mathcal H^s$
of E is defined to be
It is easily verified that the Hausdorff measure is monotonic, countably subadditive, and
![]() $\mathcal H^s(\varnothing )=0$
. Thus, it is an outer measure on
$\mathcal H^s(\varnothing )=0$
. Thus, it is an outer measure on
![]() $\mathbb R^n$
.
$\mathbb R^n$
.
For any subset E, one can verify that there exists a unique critical value of s at which
![]() $\mathcal H^s(E)$
“jumps” from infinity to zero. The value taken by s at this discontinuity is referred to as the Hausdorff dimension of E and is denoted by
$\mathcal H^s(E)$
“jumps” from infinity to zero. The value taken by s at this discontinuity is referred to as the Hausdorff dimension of E and is denoted by
![]() $\dim _{\mathcal H} E $
;
$\dim _{\mathcal H} E $
;
When
![]() $s=n$
,
$s=n$
,
![]() $\mathcal H^n$
coincides with standard Lebesgue measure on
$\mathcal H^n$
coincides with standard Lebesgue measure on
![]() $\mathbb R^n$
.
$\mathbb R^n$
.
2.2 Continued fractions and Diophantine approximation
The Gauss transformation
![]() $T:[0,1)\to [0,1)$
is defined as
$T:[0,1)\to [0,1)$
is defined as
For
![]() $x \in [0,1)\smallsetminus \mathbb Q$
with continued fraction expansion
$x \in [0,1)\smallsetminus \mathbb Q$
with continued fraction expansion
![]() $x= [a_1, a_2,\dots ]$
, as in Section, we have
$x= [a_1, a_2,\dots ]$
, as in Section, we have
![]() $a_n(x)=[1/T^{n-1}(x)]$
for each
$a_n(x)=[1/T^{n-1}(x)]$
for each
![]() $n\ge 1.$
Recall the sequences
$n\ge 1.$
Recall the sequences
![]() $p_n:= p_n(x)$
,
$p_n:= p_n(x)$
,
![]() $q_n:= q_n(x)$
has the recursive relation
$q_n:= q_n(x)$
has the recursive relation
Thus,
![]() $p_n, q_n$
are determined by the partial quotients
$p_n, q_n$
are determined by the partial quotients
![]() $a_1,\dots ,a_n$
which we may write
$a_1,\dots ,a_n$
which we may write
![]() $p_n=p_n(a_1,\dots , a_n), q_n=q_n(a_1,\dots ,a_n)$
. When it is clear which partial quotients are involved, we denote them by
$p_n=p_n(a_1,\dots , a_n), q_n=q_n(a_1,\dots ,a_n)$
. When it is clear which partial quotients are involved, we denote them by
![]() $p_n, q_n$
for simplicity.
$p_n, q_n$
for simplicity.
For any integer vector
![]() $(a_1,\dots ,a_n)\in \mathbb N^n$
with
$(a_1,\dots ,a_n)\in \mathbb N^n$
with
![]() $n\geq 1$
, write
$n\geq 1$
, write
for the corresponding “cylinder of order n,” i.e., the set of all real numbers in
![]() $[0,1)$
whose continued fraction expansions begin with
$[0,1)$
whose continued fraction expansions begin with
![]() $(a_1, \dots , a_n).$
$(a_1, \dots , a_n).$
We will frequently use the following well-known properties of continued fraction expansions. They are explained in the standard texts [Reference Iosifescu and Kraaikamp10, Reference Khintchine11].
Proposition 2.1 For any positive integers
![]() $a_1,\dots ,a_n$
, let
$a_1,\dots ,a_n$
, let
![]() $p_n=p_n(a_1,\dots ,a_n)$
and
$p_n=p_n(a_1,\dots ,a_n)$
and
![]() $q_n=q_n(a_1,\dots ,a_n)$
be defined recursively by (2.1). Then,
$q_n=q_n(a_1,\dots ,a_n)$
be defined recursively by (2.1). Then,
 $$ \begin{align*} I_n= \left\{ \begin{array}{ll} \left[\frac{p_n}{q_n}, \frac{p_n+p_{n-1}}{q_n+q_{n-1}}\right) & \mathrm{if }\ \ n\ \mathrm{{is\ even}},\\[3pt] \left(\frac{p_n+p_{n-1}}{q_n+q_{n-1}}, \frac{p_n}{q_n}\right] & \mathrm{if }\ \ n\ \mathrm{{is\ odd}}. \end{array} \right. \end{align*} $$
$$ \begin{align*} I_n= \left\{ \begin{array}{ll} \left[\frac{p_n}{q_n}, \frac{p_n+p_{n-1}}{q_n+q_{n-1}}\right) & \mathrm{if }\ \ n\ \mathrm{{is\ even}},\\[3pt] \left(\frac{p_n+p_{n-1}}{q_n+q_{n-1}}, \frac{p_n}{q_n}\right] & \mathrm{if }\ \ n\ \mathrm{{is\ odd}}. \end{array} \right. \end{align*} $$
Thus, its length is given by
 $$ \begin{align*} \frac{1}{2q_n^2}\leq |I_n|=\frac{1}{q_n(q_n+q_{n-1})}\leq \frac1{q_n^2}\leq \left(\prod_{i=1}^na_i\right)^{-2}, \end{align*} $$
$$ \begin{align*} \frac{1}{2q_n^2}\leq |I_n|=\frac{1}{q_n(q_n+q_{n-1})}\leq \frac1{q_n^2}\leq \left(\prod_{i=1}^na_i\right)^{-2}, \end{align*} $$
since
The following result is due to Łuczak [Reference Łuczak14].
Lemma 2.2 (Łuczak [Reference Łuczak14])
For any
![]() $b, c>1$
, the sets
$b, c>1$
, the sets
 $$ \begin{align*} &\left\{x\in[0, 1): a_{n}(x)\ge c^{b^n}\ {\text{for infinitely many}} \ n\in \mathbb N \right\},\\ &\left\{x\in[0, 1): a_{n}(x)\ge c^{b^n}\ {\text{for all }} \ n\geq 1 \right\} \end{align*} $$
$$ \begin{align*} &\left\{x\in[0, 1): a_{n}(x)\ge c^{b^n}\ {\text{for infinitely many}} \ n\in \mathbb N \right\},\\ &\left\{x\in[0, 1): a_{n}(x)\ge c^{b^n}\ {\text{for all }} \ n\geq 1 \right\} \end{align*} $$
have the same Hausdorff dimension
![]() $\frac 1{b+1}$
.
$\frac 1{b+1}$
.
Lemma 2.3 (Good [Reference Good6])
The following lemma proved by Marstrand [Reference Marstrand15] is well known.
Lemma 2.4 For any measurable sets A and B,
3 Proof of Theorem 1.1
To prove Theorem 1.1, we first prove the following proposition for the set
 $$ \begin{align*} \Lambda:=\left\{(x, y)\in[0,1]^2:\max\left\{\prod_{i=1}^ma_{n+i}^{t_i}(x), \prod_{i=1}^ma_{n+i}^{t_i}(y)\right\} \to\infty\ \text{as} \ n\to\infty \right\}. \end{align*} $$
$$ \begin{align*} \Lambda:=\left\{(x, y)\in[0,1]^2:\max\left\{\prod_{i=1}^ma_{n+i}^{t_i}(x), \prod_{i=1}^ma_{n+i}^{t_i}(y)\right\} \to\infty\ \text{as} \ n\to\infty \right\}. \end{align*} $$
Proposition 3.1
Proof. It is trivial that
 $$ \begin{align*} \Lambda&\supset\left\{x\in[0,1]:\prod_{i=1}^ma_{n+i}^{t_i}(x) \to\infty\ \text{as} \ n\to\infty \right\}\times [0, 1)\\ &\supset\left\{x\in[0,1]:a_{n+1}^{t_1}(x) \to\infty\ \text{as} \ n\to\infty \right\}\times [0, 1). \end{align*} $$
$$ \begin{align*} \Lambda&\supset\left\{x\in[0,1]:\prod_{i=1}^ma_{n+i}^{t_i}(x) \to\infty\ \text{as} \ n\to\infty \right\}\times [0, 1)\\ &\supset\left\{x\in[0,1]:a_{n+1}^{t_1}(x) \to\infty\ \text{as} \ n\to\infty \right\}\times [0, 1). \end{align*} $$
From Lemmas 2.3 and 2.4, it follows that
![]() $\dim _{\mathcal H}\Lambda \geq 3/2.$
For the upper bound, we proceed as follows. Let
$\dim _{\mathcal H}\Lambda \geq 3/2.$
For the upper bound, we proceed as follows. Let
![]() $M\in \mathbb R$
be fixed. It is clear that
$M\in \mathbb R$
be fixed. It is clear that
 $$ \begin{align*}\Lambda\subseteq \bigcup_{N=1}^\infty\left\{(x, y)\in[0,1]^2:\max\left\{\prod_{i=1}^ma_{n+i}^{t_i}(x), \prod_{i=1}^ma_{n+i}^{t_i}(y)\right\}\geq M \ \text{for all} \ n\geq N \right\}\end{align*} $$
$$ \begin{align*}\Lambda\subseteq \bigcup_{N=1}^\infty\left\{(x, y)\in[0,1]^2:\max\left\{\prod_{i=1}^ma_{n+i}^{t_i}(x), \prod_{i=1}^ma_{n+i}^{t_i}(y)\right\}\geq M \ \text{for all} \ n\geq N \right\}\end{align*} $$
and the Hausdorff dimension of every set on the right-hand side is the same. Therefore, we only need to consider one of the sets,
 $$ \begin{align*}\Lambda(M):=\left\{(x, y)\in[0,1]^2:\max\left\{\prod_{i=1}^ma_{n+i}^{t_i}(x), \prod_{i=1}^ma_{n+i}^{t_i}(y)\right\}\geq M \ \text{for all} \ n\geq 1 \right\}.\end{align*} $$
$$ \begin{align*}\Lambda(M):=\left\{(x, y)\in[0,1]^2:\max\left\{\prod_{i=1}^ma_{n+i}^{t_i}(x), \prod_{i=1}^ma_{n+i}^{t_i}(y)\right\}\geq M \ \text{for all} \ n\geq 1 \right\}.\end{align*} $$
Let
![]() $(x, y)$
be an element in
$(x, y)$
be an element in
![]() $\Lambda (M)$
. Then, for any integer N and any
$\Lambda (M)$
. Then, for any integer N and any
![]() $1\leq n\leq N$
, either
$1\leq n\leq N$
, either
![]() $\prod _{i=1}^ma_{n+i}^{t_i}(x)\geq M$
or
$\prod _{i=1}^ma_{n+i}^{t_i}(x)\geq M$
or
![]() $\prod _{i=1}^ma_{n+i}^{t_i}(y)\geq M$
. For this reason, either
$\prod _{i=1}^ma_{n+i}^{t_i}(y)\geq M$
. For this reason, either
 $$ \begin{align*}\#\left\{1\leq n\leq N: \prod_{i=1}^ma_{n+i}^{t_i}(x)\geq M\right\}\geq \left[\frac{N}{2}\right]\end{align*} $$
$$ \begin{align*}\#\left\{1\leq n\leq N: \prod_{i=1}^ma_{n+i}^{t_i}(x)\geq M\right\}\geq \left[\frac{N}{2}\right]\end{align*} $$
or
 $$ \begin{align*}\#\left\{1\leq n\leq N: \prod_{i=1}^ma_{n+i}^{t_i}(y)\geq M\right\}\geq \left[\frac{N}{2}\right],\end{align*} $$
$$ \begin{align*}\#\left\{1\leq n\leq N: \prod_{i=1}^ma_{n+i}^{t_i}(y)\geq M\right\}\geq \left[\frac{N}{2}\right],\end{align*} $$
where the notation
![]() $\left [x\right ]$
denotes the largest integer not greater than x. Thus, if we write
$\left [x\right ]$
denotes the largest integer not greater than x. Thus, if we write
 $$ \begin{align*}\Lambda_N(M):=\left\{x\in[0,1]:\#\left\{1\leq n\leq N: \prod_{i=1}^ma_{n+i}^{t_i}(x)\geq M\right\}\geq \left[\frac{N}{2}\right]\right\},\end{align*} $$
$$ \begin{align*}\Lambda_N(M):=\left\{x\in[0,1]:\#\left\{1\leq n\leq N: \prod_{i=1}^ma_{n+i}^{t_i}(x)\geq M\right\}\geq \left[\frac{N}{2}\right]\right\},\end{align*} $$
then it is straightforward to see that
Next, we find a cover for
![]() $\Lambda _N(M)\times [0, 1)$
. The cover for
$\Lambda _N(M)\times [0, 1)$
. The cover for
![]() $[0,1)\times \Lambda _N(M))$
can be estimated similarly.
$[0,1)\times \Lambda _N(M))$
can be estimated similarly.
Let
![]() $l=\left [\frac {N}{2}\right ]$
and
$l=\left [\frac {N}{2}\right ]$
and
![]() $\mathcal A$
be all the possible choices
$\mathcal A$
be all the possible choices
![]() $\omega =\{n_1<n_2<\cdots <n_l\}$
, then the cardinality of
$\omega =\{n_1<n_2<\cdots <n_l\}$
, then the cardinality of
![]() $\mathcal A$
is bounded from above by
$\mathcal A$
is bounded from above by
![]() $2^N$
. Denote the integers in
$2^N$
. Denote the integers in
![]() $[2, N]\setminus \omega $
by
$[2, N]\setminus \omega $
by
![]() $\omega ^c$
. For any
$\omega ^c$
. For any
![]() $n\geq 1$
, set
$n\geq 1$
, set
 $$ \begin{align*} D_n(\omega):=\left\{(a_1, \ldots, a_n, \ldots a_{n+m})\in\mathbb N^{n+m}: \begin{array}{l} \prod\limits_{i=1}^ma_{r+i}^{t_i}(x)\geq M \ \text{for} \ r\in\omega \\[1ex] \prod\limits_{i=1}^ma_{r+i}^{t_i}(y)\geq M \ \text{for} \ r\in\omega^c \end{array} \right\}. \end{align*} $$
$$ \begin{align*} D_n(\omega):=\left\{(a_1, \ldots, a_n, \ldots a_{n+m})\in\mathbb N^{n+m}: \begin{array}{l} \prod\limits_{i=1}^ma_{r+i}^{t_i}(x)\geq M \ \text{for} \ r\in\omega \\[1ex] \prod\limits_{i=1}^ma_{r+i}^{t_i}(y)\geq M \ \text{for} \ r\in\omega^c \end{array} \right\}. \end{align*} $$
By the definition of
![]() $\Lambda _N(M)$
, we see that
$\Lambda _N(M)$
, we see that
 $$ \begin{align*} \Lambda_N(M)\times [0, 1)&\subseteq \bigcup_{\omega\in \mathcal A} \left\{x\in [0, 1): \prod_{i=1}^ma_{r+i}^{t_i}(x)\geq M \ \text{for} \ r\in\omega \right\}\times[0, 1)\\ &=\bigcup_{\omega\in \mathcal A} \ \bigcup_{(a_1, \ldots, a_{N+m})\in D_N(\omega)} I_{N+m}(a_1, \ldots, a_{N+m})\times[0, 1). \end{align*} $$
$$ \begin{align*} \Lambda_N(M)\times [0, 1)&\subseteq \bigcup_{\omega\in \mathcal A} \left\{x\in [0, 1): \prod_{i=1}^ma_{r+i}^{t_i}(x)\geq M \ \text{for} \ r\in\omega \right\}\times[0, 1)\\ &=\bigcup_{\omega\in \mathcal A} \ \bigcup_{(a_1, \ldots, a_{N+m})\in D_N(\omega)} I_{N+m}(a_1, \ldots, a_{N+m})\times[0, 1). \end{align*} $$
For each
![]() $(a_1, \ldots , a_{N+m})\in D_N(\omega )$
, the set
$(a_1, \ldots , a_{N+m})\in D_N(\omega )$
, the set
![]() $I_{N+m}(a_1, \ldots , a_{N+m})\times [0, 1)$
can be covered by
$I_{N+m}(a_1, \ldots , a_{N+m})\times [0, 1)$
can be covered by
many cubes of side length
![]() $|I_{N+m}(a_1, \ldots , a_{N+m})|$
. Furthermore, for each
$|I_{N+m}(a_1, \ldots , a_{N+m})|$
. Furthermore, for each
![]() $(a_1, \ldots , a_{N+m})\in D_N(\omega ), \prod \limits _{i=1}^ma_{r+i}^{t_i}(x)\geq M$
for each
$(a_1, \ldots , a_{N+m})\in D_N(\omega ), \prod \limits _{i=1}^ma_{r+i}^{t_i}(x)\geq M$
for each
![]() $ r\in \{n_1, \ldots , n_l\}$
. Then we have
$ r\in \{n_1, \ldots , n_l\}$
. Then we have
 $$ \begin{align}mt_{\max}\sum_{k=1}^{N+m} \log a_k \geq \left[\frac{N}{2}\right]\log M.\end{align} $$
$$ \begin{align}mt_{\max}\sum_{k=1}^{N+m} \log a_k \geq \left[\frac{N}{2}\right]\log M.\end{align} $$
Define a family of probability measures
![]() $\{\mu _h\}_{h>1}$
on the unit interval
$\{\mu _h\}_{h>1}$
on the unit interval
![]() $[0, 1]$
. For each
$[0, 1]$
. For each
![]() $h>1$
and any
$h>1$
and any
![]() $(a_1, \ldots , a_{N+m})\in \mathbb N^{n+m}$
, define
$(a_1, \ldots , a_{N+m})\in \mathbb N^{n+m}$
, define
where
![]() $P(h)=\log \sum _{j=1}^\infty \frac 1{j^h}<\infty $
.
$P(h)=\log \sum _{j=1}^\infty \frac 1{j^h}<\infty $
.
Fix
![]() $s>\tfrac 32$
and let
$s>\tfrac 32$
and let
![]() $h=s-\tfrac 12>1$
. Choose M sufficiently large such that
$h=s-\tfrac 12>1$
. Choose M sufficiently large such that
Then the s-dimensional Hausdorff measure of this cover can be estimated as
 $$ \begin{align*} \mathcal H^s(\Lambda(M))&\ll \liminf_{n\to\infty} \sum_{\omega\in\mathcal A}\sum_{(a_1,\ldots, a_{N+m})\in D_N(\omega)} | I_{N+m}(a_1,\ldots, a_{N+m})|^{-1} |I_{N+m}(a_1,\ldots, a_{N+m})|^{s}\\ &\leq \liminf_{n\to\infty} \sum_{\omega\in\mathcal A}\sum_{(a_1,\ldots,a_{N+m})\in D_N(\omega)} \prod_{k=1}^{N+m} (a_k)^{-2(s-1)} \\ &\leq \liminf_{n\to\infty} \sum_{\omega\in\mathcal A}\sum_{(a_1,\ldots, a_{N+m})\in D_N(\omega)} e^{-2(s-1)\sum\limits_{k=1}^{N+m}\log a_k} \\ &\leq \liminf_{n\to\infty} 2^{-N}\sum_{\omega\in\mathcal A}\sum_{(a_1,\ldots, a_{N+m})\in D_N(\omega)} e^{-(s-\frac{3}{2})\sum\limits_{k=1}^{N+m}\log a_k-(s-\frac12) \sum\limits_{k=1}^{N+m}\log a_k+N\log2} \\ &\overset{(3.1), (3.2)}{\leq} \liminf_{n\to\infty} 2^{-N}\sum_{\omega\in\mathcal A}\sum_{(a_1,\ldots, a_{N+m})\in D_N(\omega)} e^{-(N+m)p(h)-h\sum\limits_{k=1}^{N+m}\log a_k} \\ & \ll\liminf_{n\to\infty}\sum_{(a_1,\ldots, a_{N+m})\in\mathbb N^{N+m}} e^{-(N+m)p(h)-h\sum\limits_{k=1}^{N+m}\log a_k}=1. \end{align*} $$
$$ \begin{align*} \mathcal H^s(\Lambda(M))&\ll \liminf_{n\to\infty} \sum_{\omega\in\mathcal A}\sum_{(a_1,\ldots, a_{N+m})\in D_N(\omega)} | I_{N+m}(a_1,\ldots, a_{N+m})|^{-1} |I_{N+m}(a_1,\ldots, a_{N+m})|^{s}\\ &\leq \liminf_{n\to\infty} \sum_{\omega\in\mathcal A}\sum_{(a_1,\ldots,a_{N+m})\in D_N(\omega)} \prod_{k=1}^{N+m} (a_k)^{-2(s-1)} \\ &\leq \liminf_{n\to\infty} \sum_{\omega\in\mathcal A}\sum_{(a_1,\ldots, a_{N+m})\in D_N(\omega)} e^{-2(s-1)\sum\limits_{k=1}^{N+m}\log a_k} \\ &\leq \liminf_{n\to\infty} 2^{-N}\sum_{\omega\in\mathcal A}\sum_{(a_1,\ldots, a_{N+m})\in D_N(\omega)} e^{-(s-\frac{3}{2})\sum\limits_{k=1}^{N+m}\log a_k-(s-\frac12) \sum\limits_{k=1}^{N+m}\log a_k+N\log2} \\ &\overset{(3.1), (3.2)}{\leq} \liminf_{n\to\infty} 2^{-N}\sum_{\omega\in\mathcal A}\sum_{(a_1,\ldots, a_{N+m})\in D_N(\omega)} e^{-(N+m)p(h)-h\sum\limits_{k=1}^{N+m}\log a_k} \\ & \ll\liminf_{n\to\infty}\sum_{(a_1,\ldots, a_{N+m})\in\mathbb N^{N+m}} e^{-(N+m)p(h)-h\sum\limits_{k=1}^{N+m}\log a_k}=1. \end{align*} $$
In some of the estimates, every term has been evaluated over
![]() $\prod _{i=1}^{m}a_{r+i}^{t_{i}}(x) \geq M$
, for
$\prod _{i=1}^{m}a_{r+i}^{t_{i}}(x) \geq M$
, for
![]() $r\in \omega $
, and
$r\in \omega $
, and
![]() $t_{\max }=\max \{t_1,t_2,\ldots ,t_{m}\}$
.
$t_{\max }=\max \{t_1,t_2,\ldots ,t_{m}\}$
.
Thus, by the definition of Hausdorff measure,
![]() $\dim _{\mathcal H}\Lambda (M)\leq 3/2$
and consequently
$\dim _{\mathcal H}\Lambda (M)\leq 3/2$
and consequently
![]() $\dim _{\mathcal H}\Lambda \leq 3/2$
.
$\dim _{\mathcal H}\Lambda \leq 3/2$
.
![]() $\blacksquare $
$\blacksquare $
To complete the proof of Theorem 1.1, we consider three cases for
![]() $\tau $
.
$\tau $
.
3.1
 $1<\tau <\infty .$
$1<\tau <\infty .$
Let
![]() $1<c<\tau $
. By the definition of
$1<c<\tau $
. By the definition of
![]() $\tau $
, there exist infinitely many n in an infinite subset
$\tau $
, there exist infinitely many n in an infinite subset
![]() $\Omega \subset \mathbb N$
such that
$\Omega \subset \mathbb N$
such that
Thus, for every
![]() $n\in \Omega $
, either
$n\in \Omega $
, either
![]() $\prod \limits _{i=1}^ma_{n+i}^{t_i}(x)\geq e^{c^n}$
or
$\prod \limits _{i=1}^ma_{n+i}^{t_i}(x)\geq e^{c^n}$
or
![]() $\prod \limits _{i=1}^ma_{n+i}^{t_i}(y)\geq e^{c^n}$
. Then, for at least one index
$\prod \limits _{i=1}^ma_{n+i}^{t_i}(y)\geq e^{c^n}$
. Then, for at least one index
![]() $1\leq i\leq m$
, we have either
$1\leq i\leq m$
, we have either
![]() $a_{n+i}^{t_i}(x)\geq e^{\frac {c^n}{m}}$
or
$a_{n+i}^{t_i}(x)\geq e^{\frac {c^n}{m}}$
or
![]() $a_{n+i}^{t_i}(x)\geq e^{\frac {c^n}{m}}$
. Hence,
$a_{n+i}^{t_i}(x)\geq e^{\frac {c^n}{m}}$
. Hence,
where
and
Therefore, by Lemma 2.2, we have
The lower bound is given by a similar argument as above. For this, fix
![]() $c>\tau $
, then
$c>\tau $
, then
![]() $\Psi (n)\leq e^{c^n}$
holds for all
$\Psi (n)\leq e^{c^n}$
holds for all
![]() $n\geq n_0$
. Therefore, we have the inclusion
$n\geq n_0$
. Therefore, we have the inclusion
 $$ \begin{align*} \Lambda (\Psi)&\supseteq \left\{x\in[0,1]: \prod_{i=1}^ma_{n+i}^{t_i}(x)\geq e^{c^n} \ \text{for all} \ n\geq n_0 \right\}\times[0, 1] \\ &\supseteq\left\{x\in[0,1]: a_{n+1}^{t_1}(x)\geq e^{c^n} \ \text{for all} \ n\geq n_0 \right\}\times[0, 1]. \end{align*} $$
$$ \begin{align*} \Lambda (\Psi)&\supseteq \left\{x\in[0,1]: \prod_{i=1}^ma_{n+i}^{t_i}(x)\geq e^{c^n} \ \text{for all} \ n\geq n_0 \right\}\times[0, 1] \\ &\supseteq\left\{x\in[0,1]: a_{n+1}^{t_1}(x)\geq e^{c^n} \ \text{for all} \ n\geq n_0 \right\}\times[0, 1]. \end{align*} $$
Hence, by Lemmas 2.2 and 2.4, we get that
3.1.1
 $\tau =\infty .$
$\tau =\infty .$
This case readily follows from the upper bound argument above, that is,
3.1.2
 $\tau =1.$
$\tau =1.$
In this case, for any
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $n_0\in \mathbb N$
such that for all
$n_0\in \mathbb N$
such that for all
![]() $n\geq n_0$
, we have
$n\geq n_0$
, we have
![]() $\Psi (n)\leq e^{(1+\epsilon )^n}$
. Then,
$\Psi (n)\leq e^{(1+\epsilon )^n}$
. Then,
 $$ \begin{align*} \Lambda(\Psi)&\supset \left\{x\in[0, 1): \prod_{i=1}^{m} a^{t_i}_{n+i}\ge \Psi(n)\ {\text{for all}} \ n\geq n_0 \right\}\times [0, 1]\\ & \supset \left\{x\in[0, 1): a^{t_1}_{n+1}(x)\ge e^{(1+\epsilon)^n}\ {\text{for all }} \ n \geq n_0 \right\}\times [0, 1).\end{align*} $$
$$ \begin{align*} \Lambda(\Psi)&\supset \left\{x\in[0, 1): \prod_{i=1}^{m} a^{t_i}_{n+i}\ge \Psi(n)\ {\text{for all}} \ n\geq n_0 \right\}\times [0, 1]\\ & \supset \left\{x\in[0, 1): a^{t_1}_{n+1}(x)\ge e^{(1+\epsilon)^n}\ {\text{for all }} \ n \geq n_0 \right\}\times [0, 1).\end{align*} $$
Hence, by using Lemmas 2.2 and 2.4, we have
The upper bound follows from Proposition 3.1 as
![]() $\Lambda (\Psi )\subseteq \Lambda $
.
$\Lambda (\Psi )\subseteq \Lambda $
.
![]() $\blacksquare $
$\blacksquare $
Acknowledgment
We thank the anonymous referee for the careful reading of the paper and helpful suggestions for improvement.