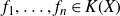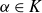1. Introduction
1.1. Motivation
Given non-zero complex numbers
![]() $\alpha_1, \ldots, \alpha_n \in {\mathbb{C}}^*$
, we say that they are multiplicatively dependent if there exist integers
$\alpha_1, \ldots, \alpha_n \in {\mathbb{C}}^*$
, we say that they are multiplicatively dependent if there exist integers
![]() $k_1,\ldots,k_n \in {\mathbb{Z}}$
, not all zero, such that
$k_1,\ldots,k_n \in {\mathbb{Z}}$
, not all zero, such that
and we say that they are multiplicatively dependent modulo G, where G is a subset of
![]() ${\mathbb{C}}^*$
, if there exist integers
${\mathbb{C}}^*$
, if there exist integers
![]() $k_1,\ldots,k_n \in {\mathbb{Z}}$
, not all zero, such that
$k_1,\ldots,k_n \in {\mathbb{Z}}$
, not all zero, such that
Multiplicative dependence of algebraic numbers has been studied for a long time and still very actively; see, for instance, [Reference Barroero, Capuano, Mérai, Ostafe and Sha4, Reference Barroero and Sha5, Reference Bombieri, Masser and Zannier12, Reference Dubickas and Sha14, Reference Konyagin, Sha, Shparlinski and Stewart19, Reference Loxton and van der Poorten22, Reference Ostafe, Sha, Shparlinski and Zannier27, Reference Ostafe, Sha, Shparlinski and Zannier28, Reference Pappalardi, Sha, Shparlinski and Stewart31, Reference van der Poorten and Loxton35, Reference Stewart41] and the references therein. The authors in [Reference Ostafe, Sha, Shparlinski and Zannier28] have studied the multiplicative dependenc of elements in an orbit of an algebraic dynamical system, and recently in [Reference Bérczes, Ostafe, Shparlinski and Silverman9] this has been extended to the more general setting of multiplicative dependence modulo a finitely generated multiplicative group.
In this paper, we want to study multiplicative dependence among values of rational functions modulo sets which can be roughly described as approximate division groups of finitely generated groups
![]() $\Gamma$
, denoted by
$\Gamma$
, denoted by
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
(which is defined in the next section), that is, sets which are not far with respect to the Weil height from the division group of a finitely generated multiplicative group of a number field.
$\Gamma^{{\textrm{div}}}_\varepsilon$
(which is defined in the next section), that is, sets which are not far with respect to the Weil height from the division group of a finitely generated multiplicative group of a number field.
The motivation also partly comes from the study of points on subvarieties of tori. Let
![]() ${\mathbb{G}_{\textrm{m}}}$
be the multiplicative algebraic group over the complex numbers
${\mathbb{G}_{\textrm{m}}}$
be the multiplicative algebraic group over the complex numbers
![]() ${\mathbb{C}}$
, that is
${\mathbb{C}}$
, that is
![]() ${\mathbb{G}_{\textrm{m}}} = {\mathbb{C}}^*$
endowed with the multiplicative group law. Intersection of varieties in
${\mathbb{G}_{\textrm{m}}} = {\mathbb{C}}^*$
endowed with the multiplicative group law. Intersection of varieties in
![]() ${\mathbb{G}_{\textrm{m}}}^n$
with sets of the type
${\mathbb{G}_{\textrm{m}}}^n$
with sets of the type
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
falls within two conjectures, the Mordell–Lang conjecture on intersection of varieties with finitely generated subgroups and the Bogomolov conjecture which is about the discreteness of the set of points of bounded height in a variety. This direction has been extensively studied over several decades, see [Reference Aliev and Smyth1, Reference Amoroso and Viada3, Reference Bérczes, Evertse, Győry and Pontreau8, Reference Beukers and Smyth10, Reference Bombieri and Zannier13, Reference Evertse16, Reference Laurent20, Reference Liardet21, Reference Martinez23, Reference Mazur26, Reference Pontreau32, Reference Poonen33, Reference Rémond36, Reference Schmidt39] and references therein, which in particular give precise quantitative results about the intersection of varieties with
$\Gamma^{{\textrm{div}}}_\varepsilon$
falls within two conjectures, the Mordell–Lang conjecture on intersection of varieties with finitely generated subgroups and the Bogomolov conjecture which is about the discreteness of the set of points of bounded height in a variety. This direction has been extensively studied over several decades, see [Reference Aliev and Smyth1, Reference Amoroso and Viada3, Reference Bérczes, Evertse, Győry and Pontreau8, Reference Beukers and Smyth10, Reference Bombieri and Zannier13, Reference Evertse16, Reference Laurent20, Reference Liardet21, Reference Martinez23, Reference Mazur26, Reference Pontreau32, Reference Poonen33, Reference Rémond36, Reference Schmidt39] and references therein, which in particular give precise quantitative results about the intersection of varieties with
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
.
$\Gamma^{{\textrm{div}}}_\varepsilon$
.
Here, in some sense, instead of assuming each coordinate of a point is from
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
, we impose that the coordinates of a point multiplicatively generate an element in
$\Gamma^{{\textrm{div}}}_\varepsilon$
, we impose that the coordinates of a point multiplicatively generate an element in
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
.
$\Gamma^{{\textrm{div}}}_\varepsilon$
.
1.2. Notation
Throughout the paper, we use the following notation:
-
(i) K is a number field;
-
(ii)
 $\overline{K}$
is an algebraic closure of K;
$\overline{K}$
is an algebraic closure of K; -
(iii) S is a finite set of places of K containing all the infinite places;
-
(iv)
 $O_S$
is the ring of S-integers of K;
$O_S$
is the ring of S-integers of K; -
(v)
 $R^*$
is the unit group of a ring R;
$R^*$
is the unit group of a ring R; -
(vi)
 $\Gamma$
is a finitely generated subgroup of
$\Gamma$
is a finitely generated subgroup of
 $K^*$
;
$K^*$
; -
(vii) For
 $A \subseteq K^*$
,
$A \subseteq K^*$
,  $$A^{{\textrm{div}}}\,:\!=\,\{\alpha \in \overline{K} \,:\, \alpha^m \in A \text{ for some integer } m \ge 1\}.$$
$$A^{{\textrm{div}}}\,:\!=\,\{\alpha \in \overline{K} \,:\, \alpha^m \in A \text{ for some integer } m \ge 1\}.$$
For
![]() $\varepsilon \gt 0$
,
$\varepsilon \gt 0$
,
Here
![]() ${\textrm{h}}(\cdot)$
stands for the absolute logarithmic Weil height function. The set
${\textrm{h}}(\cdot)$
stands for the absolute logarithmic Weil height function. The set
![]() $\Gamma^{\textrm{div}}$
is called the division group of
$\Gamma^{\textrm{div}}$
is called the division group of
![]() $\Gamma$
.
$\Gamma$
.
In addition, let
![]() $M_K$
be the set of places of K,
$M_K$
be the set of places of K,
![]() $M_K^\infty$
the set of infinite places of K, and
$M_K^\infty$
the set of infinite places of K, and
![]() $M_K^0 = M_K \setminus M_K^\infty$
.
$M_K^0 = M_K \setminus M_K^\infty$
.
1.3. Main results
In this section we state the main results proved in this paper. Informally, our results can be summarised as follows: given
![]() $f_1, f_2, \ldots, f_n \in K[X]$
satisfying some natural conditions (some results hold for rational functions as well), we prove finiteness of the sets of:
$f_1, f_2, \ldots, f_n \in K[X]$
satisfying some natural conditions (some results hold for rational functions as well), we prove finiteness of the sets of:
-
•
 $\alpha\in K$
such that
$\alpha\in K$
such that
 $f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
$f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
 $\Gamma^{{\textrm{div}}}_\varepsilon$
;
$\Gamma^{{\textrm{div}}}_\varepsilon$
; -
•
 $\alpha\in\Gamma^{{\textrm{div}}}_\varepsilon$
such that
$\alpha\in\Gamma^{{\textrm{div}}}_\varepsilon$
such that
 $f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
$f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
 $\Gamma^{{\textrm{div}}}_\varepsilon$
.
$\Gamma^{{\textrm{div}}}_\varepsilon$
.
We would like to unify these results and have a finiteness result for the set of
![]() $\alpha\in K(\Gamma^{\textrm{div}})$
satisfying the conclusion above, and thus we conclude this section with an open problem in this direction.
$\alpha\in K(\Gamma^{\textrm{div}})$
satisfying the conclusion above, and thus we conclude this section with an open problem in this direction.
We now formally state our results.
Theorem 1·1.
Let
![]() $f_1, f_2, \ldots, f_n \in K[X]$
be pairwise coprime polynomials. Assume that each of them has at least two distinct roots. Then, for every
$f_1, f_2, \ldots, f_n \in K[X]$
be pairwise coprime polynomials. Assume that each of them has at least two distinct roots. Then, for every
![]() $\varepsilon \gt 0$
there are only finitely many elements
$\varepsilon \gt 0$
there are only finitely many elements
![]() $\alpha \in K$
such that
$\alpha \in K$
such that
![]() $f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
$f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
.
$\Gamma^{{\textrm{div}}}_\varepsilon$
.
We first remark that in Theorem 1·1, since
![]() $\alpha \in K$
and the polynomials
$\alpha \in K$
and the polynomials
![]() $f_1, \ldots, f_n$
are in K[X], by Lemma 2·1 below we know that “modulo
$f_1, \ldots, f_n$
are in K[X], by Lemma 2·1 below we know that “modulo
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
” can be reduced to modulo a subset of
$\Gamma^{{\textrm{div}}}_\varepsilon$
” can be reduced to modulo a subset of
![]() $K^*$
which is somehow “close” to
$K^*$
which is somehow “close” to
![]() $\Gamma$
.
$\Gamma$
.
We also remark that in Theorem 1·1 the two conditions of the polynomials being “pairwise coprime” and “each of them has at least two distinct roots” somehow cannot be removed. For example, choosing
![]() $f_1 = X(X+2)$
,
$f_1 = X(X+2)$
,
![]() $f_2 = (X+1)(X+2)$
, and
$f_2 = (X+1)(X+2)$
, and
![]() $f_3,\ldots,f_n$
arbitrary, for any
$f_3,\ldots,f_n$
arbitrary, for any
![]() $\alpha = 1/(\beta -1)$
with
$\alpha = 1/(\beta -1)$
with
![]() $\beta \in \Gamma$
and
$\beta \in \Gamma$
and
![]() $\beta \ne 1, 1/2$
and
$\beta \ne 1, 1/2$
and
![]() $f_3(\alpha) \cdots f_n(\alpha) \ne 0$
, we have
$f_3(\alpha) \cdots f_n(\alpha) \ne 0$
, we have
In addition, choosing pairwise coprime polynomials
![]() $f_1, f_2, \ldots, f_n \in K[X]$
with
$f_1, f_2, \ldots, f_n \in K[X]$
with
![]() $f_1=X - a$
for some
$f_1=X - a$
for some
![]() $a \in K$
, for any
$a \in K$
, for any
![]() $\alpha \in \Gamma$
satisfying
$\alpha \in \Gamma$
satisfying
![]() $f_2(\alpha+a) \cdots f_n(\alpha+a) \ne 0$
, we have
$f_2(\alpha+a) \cdots f_n(\alpha+a) \ne 0$
, we have
Using Theorem 1·1, we establish the following result, which holds for rational functions. For this, we say that non-zero rational functions
![]() $f_1,\ldots, f_n \in K(X)$
are multiplicatively independent modulo constants if they are multiplicatively independent modulo
$f_1,\ldots, f_n \in K(X)$
are multiplicatively independent modulo constants if they are multiplicatively independent modulo
![]() $K^*$
, that is, there is no non-zero integer vector
$K^*$
, that is, there is no non-zero integer vector
![]() $(k_1,\ldots,k_n)$
such that
$(k_1,\ldots,k_n)$
such that
In addition, for any rational function
![]() $f \in K(X)$
, the numerator and denominator of f are meant to be two polynomials
$f \in K(X)$
, the numerator and denominator of f are meant to be two polynomials
![]() $g, h \in K[X]$
, respectively, such that
$g, h \in K[X]$
, respectively, such that
![]() $f= g / h$
and
$f= g / h$
and
![]() $\gcd(g,h)=1$
.
$\gcd(g,h)=1$
.
Theorem 1·2.
Let
![]() $f_1, f_2, \ldots, f_n \in K(X)$
be non-constant rational functions such that they are multiplicatively independent modulo constants. Assume that for each
$f_1, f_2, \ldots, f_n \in K(X)$
be non-constant rational functions such that they are multiplicatively independent modulo constants. Assume that for each
![]() $f_i, i =1, 2, \ldots, n$
, its numerator either has no linear factor or has at least two distinct linear factors over K, and so does its denominator. Assume further that
$f_i, i =1, 2, \ldots, n$
, its numerator either has no linear factor or has at least two distinct linear factors over K, and so does its denominator. Assume further that
![]() $f_1, f_2, \ldots, f_n$
have distinct linear factors over K (if they have). Then, for every
$f_1, f_2, \ldots, f_n$
have distinct linear factors over K (if they have). Then, for every
![]() $\varepsilon \gt 0$
there are only finitely many elements
$\varepsilon \gt 0$
there are only finitely many elements
![]() $\alpha \in K$
such that
$\alpha \in K$
such that
![]() $f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
$f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
.
$\Gamma^{{\textrm{div}}}_\varepsilon$
.
Remark 1·3. If
![]() $f_1, f_2, \ldots, f_n \in K(X)$
in Theorem 1·2 are all monic (that is, both numerator and denominator are monic), then the assumption “they are multiplicatively independent modulo constants” can be replaced by “they are multiplicatively independent”.
$f_1, f_2, \ldots, f_n \in K(X)$
in Theorem 1·2 are all monic (that is, both numerator and denominator are monic), then the assumption “they are multiplicatively independent modulo constants” can be replaced by “they are multiplicatively independent”.
The following corollary is about multiplicative dependence in orbits of a rational function, which somehow can be viewed as an extension of [Reference Bérczes, Ostafe, Shparlinski and Silverman9, theorem 1·7]. For a rational function
![]() $f \in K(X)$
and a positive integer
$f \in K(X)$
and a positive integer
![]() $n \ge 1$
, let
$n \ge 1$
, let
![]() $f^{(n)}$
be the nth compositional iterate of f. In addition, for any rational function
$f^{(n)}$
be the nth compositional iterate of f. In addition, for any rational function
![]() $f \in K(X)$
, if both its numerator and denominator have no linear factor over K, we say that f has no linear factor.
$f \in K(X)$
, if both its numerator and denominator have no linear factor over K, we say that f has no linear factor.
Corollary 1·4.
Let
![]() $f \in K(X)$
be a non-constant rational function satisfying one of the following two conditions:
$f \in K(X)$
be a non-constant rational function satisfying one of the following two conditions:
-
(i)
 $f \in K[X]$
, f has at least two distinct roots, and 0 is not a periodic point of f;
$f \in K[X]$
, f has at least two distinct roots, and 0 is not a periodic point of f; -
(ii) f has no linear factor.
Then, for any
![]() $\varepsilon\gt0$
and any integer
$\varepsilon\gt0$
and any integer
![]() $n \ge 1$
, there are only finitely many elements
$n \ge 1$
, there are only finitely many elements
![]() $\alpha \in K$
such that
$\alpha \in K$
such that
![]() $f^{(m+1)}(\alpha)$
,
$f^{(m+1)}(\alpha)$
,
![]() $\ldots, f^{(m+n)}(\alpha)$
are multiplicatively dependent modulo
$\ldots, f^{(m+n)}(\alpha)$
are multiplicatively dependent modulo
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
for some integer
$\Gamma^{{\textrm{div}}}_\varepsilon$
for some integer
![]() $m \ge 0$
.
$m \ge 0$
.
When
![]() $n=2$
in Theorem 1·1, we can relax the condition of coprimality on the polynomials
$n=2$
in Theorem 1·1, we can relax the condition of coprimality on the polynomials
![]() $f_1$
and
$f_1$
and
![]() $f_2$
.
$f_2$
.
We say that
![]() $f_1,\ldots,f_n\in{\mathbb{C}}(X)$
multiplicatively generate a rational function g if there exist integers
$f_1,\ldots,f_n\in{\mathbb{C}}(X)$
multiplicatively generate a rational function g if there exist integers
![]() $k_1,\ldots,k_n \in {\mathbb{Z}}$
, not all zero, such that
$k_1,\ldots,k_n \in {\mathbb{Z}}$
, not all zero, such that
We have the following result:
Theorem 1·5.
Let
![]() $f_1,f_2 \in K[X]$
be polynomials of degree at least 2, each having at least two distinct roots. Assume that they cannot multiplicatively generate a power of a linear fractional function. Then, for any
$f_1,f_2 \in K[X]$
be polynomials of degree at least 2, each having at least two distinct roots. Assume that they cannot multiplicatively generate a power of a linear fractional function. Then, for any
![]() $\varepsilon\gt0$
there are only finitely many elements
$\varepsilon\gt0$
there are only finitely many elements
![]() $\alpha \in K$
such that
$\alpha \in K$
such that
![]() $f_1(\alpha)$
and
$f_1(\alpha)$
and
![]() $f_2(\alpha)$
are multiplicatively dependent modulo
$f_2(\alpha)$
are multiplicatively dependent modulo
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
.
$\Gamma^{{\textrm{div}}}_\varepsilon$
.
In Theorem 1·5, the condition related to linear fractional function cannot be removed. See the example below Theorem 1·1. Here, we view non-zero constants as linear fractional functions.
We remark that in Theorem 1·5 we can replace the condition related to linear fractional function with the total number of distinct roots of
![]() $f_1$
and
$f_1$
and
![]() $f_2$
which are not common roots being at least three.
$f_2$
which are not common roots being at least three.
We also remark that the results in Theorems 1·1 and 1·5 are both not effective, due to Lemma 2·2.
As a direct consequence of Maurin’s theorem [Reference Maurin24, théorème 1·2] (see [Reference Bombieri, Habegger, Masser and Zannier11] for an effective version), if
![]() $f_1, f_2, \ldots, f_n \in K(X)$
are such that
$f_1, f_2, \ldots, f_n \in K(X)$
are such that
![]() $X,f_1,\ldots, f_n$
are multiplicatively independent modulo
$X,f_1,\ldots, f_n$
are multiplicatively independent modulo
![]() $\Gamma$
, then the set
$\Gamma$
, then the set
is finite (see [Reference Ostafe and Shparlinski30, lemma 3·2] for more details). This is an effective generalisation of Liardet’s theorem [Reference Liardet21, théorème 1] on division points on curves; see also [Reference Bérczes, Evertse, Győry and Pontreau8, theorem 2·2] for an effective version of Liardet’s result.
We remark that by definition, multiplicative dependence modulo
![]() $\Gamma$
is equivalent to multiplicative dependence modulo
$\Gamma$
is equivalent to multiplicative dependence modulo
![]() $\Gamma^{\textrm{div}}$
.
$\Gamma^{\textrm{div}}$
.
Using [Reference Maurin25, théorème 1·10], which improves [Reference Maurin24, théorème 1·7], we are able to extend this conclusion by enlarging
![]() $\Gamma^{\textrm{div}}$
to
$\Gamma^{\textrm{div}}$
to
![]() $\Gamma^{\textrm{div}}_\varepsilon$
for certain
$\Gamma^{\textrm{div}}_\varepsilon$
for certain
![]() $\varepsilon \gt0$
(but in a non-effective manner).
$\varepsilon \gt0$
(but in a non-effective manner).
Theorem 1·6.
Let
![]() $f_1, f_2, \ldots, f_n \in K(X)$
be such that
$f_1, f_2, \ldots, f_n \in K(X)$
be such that
![]() $X,f_1, \ldots, f_n$
are multiplicatively independent modulo
$X,f_1, \ldots, f_n$
are multiplicatively independent modulo
![]() $\Gamma$
. Then, there exists a real number
$\Gamma$
. Then, there exists a real number
![]() $\varepsilon \gt0$
for which there are only finitely many elements
$\varepsilon \gt0$
for which there are only finitely many elements
![]() $\alpha \in \Gamma^{\textrm{div}}_\varepsilon$
such that
$\alpha \in \Gamma^{\textrm{div}}_\varepsilon$
such that
![]() $f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
$f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
![]() $\Gamma^{\textrm{div}}_\varepsilon$
.
$\Gamma^{\textrm{div}}_\varepsilon$
.
We end this section with an open problem. We would like to combine Theorem 1·1 with the finiteness of the set (1·1), and ask the following question:
Problem 1·7. Let
![]() $f_1,\ldots,f_n \in K(X)$
be non-zero rational functions. Under what conditions is the following set
$f_1,\ldots,f_n \in K(X)$
be non-zero rational functions. Under what conditions is the following set
finite?
When
![]() $\Gamma=\{1\}$
, then
$\Gamma=\{1\}$
, then
![]() $\Gamma^{\textrm{div}}$
is the set of all roots of unity, and
$\Gamma^{\textrm{div}}$
is the set of all roots of unity, and
![]() $K(\Gamma^{\textrm{div}})$
is the cyclotomic closure of K. In this case, it has been proven in [Reference Ostafe, Sha, Shparlinski and Zannier28, theorem 4·2] that if
$K(\Gamma^{\textrm{div}})$
is the cyclotomic closure of K. In this case, it has been proven in [Reference Ostafe, Sha, Shparlinski and Zannier28, theorem 4·2] that if
![]() $f_1,\ldots,f_n$
do not multiplicatively generate a power of a linear fractional function, then the set (1·2) is finite (in fact, the result holds more generally for the abelian closure of K).
$f_1,\ldots,f_n$
do not multiplicatively generate a power of a linear fractional function, then the set (1·2) is finite (in fact, the result holds more generally for the abelian closure of K).
When
![]() $n=1$
, Problem 1·7 becomes that for a non-zero rational function
$n=1$
, Problem 1·7 becomes that for a non-zero rational function
![]() $f \in K(X)$
, under which condition the set
$f \in K(X)$
, under which condition the set
![]() $\{\alpha \in K(\Gamma^{\textrm{div}}) \,:\, \ f(\alpha) \in \Gamma^{\textrm{div}}\}$
is finite. This would extend the cyclotomic version of the Hilbert Irreducibility Theorem proved by Dvornicich and Zannier [Reference Dvornicich and Zannier15, corollary 1] in the case when
$\{\alpha \in K(\Gamma^{\textrm{div}}) \,:\, \ f(\alpha) \in \Gamma^{\textrm{div}}\}$
is finite. This would extend the cyclotomic version of the Hilbert Irreducibility Theorem proved by Dvornicich and Zannier [Reference Dvornicich and Zannier15, corollary 1] in the case when
![]() $\Gamma=\{1\}$
. Recall also that a special case of a general conjecture of Rémond (see [Reference Rémond37, conjecture 3·4]) asserts that there exists a constant
$\Gamma=\{1\}$
. Recall also that a special case of a general conjecture of Rémond (see [Reference Rémond37, conjecture 3·4]) asserts that there exists a constant
![]() $c_\Gamma$
such that for any
$c_\Gamma$
such that for any
![]() $\alpha \in K(\Gamma^{\textrm{div}}) \setminus \Gamma^{\textrm{div}}$
,
$\alpha \in K(\Gamma^{\textrm{div}}) \setminus \Gamma^{\textrm{div}}$
,
![]() ${\textrm{h}}(\alpha) \ge c_\Gamma$
(see [Reference Pottmeyer34, conjecture 1·1 (c)], and see [Reference Amoroso2, theorem 1·3] for a non-trivial example). Clearly, under this conjecture, the finiteness of the set
${\textrm{h}}(\alpha) \ge c_\Gamma$
(see [Reference Pottmeyer34, conjecture 1·1 (c)], and see [Reference Amoroso2, theorem 1·3] for a non-trivial example). Clearly, under this conjecture, the finiteness of the set
![]() $\{\alpha \in K(\Gamma^{\textrm{div}}) \,:\, \ f(\alpha) \in \Gamma^{\textrm{div}}\}$
implies the finiteness of the set
$\{\alpha \in K(\Gamma^{\textrm{div}}) \,:\, \ f(\alpha) \in \Gamma^{\textrm{div}}\}$
implies the finiteness of the set
![]() $\{\alpha \in K(\Gamma^{\textrm{div}}) \,:\, \ {\textrm{h}}(f(\alpha)) \lt \varepsilon\}$
for any
$\{\alpha \in K(\Gamma^{\textrm{div}}) \,:\, \ {\textrm{h}}(f(\alpha)) \lt \varepsilon\}$
for any
![]() $\varepsilon \lt c_\Gamma$
.
$\varepsilon \lt c_\Gamma$
.
2. Preliminaries
2.1. On some intersections with approximate groups and algebraic subgroups
We define the set
![]() ${\mathscr{A}}(K,H)$
as the set of nonzero elements in the algebraic number field K of height at most H, that is,
${\mathscr{A}}(K,H)$
as the set of nonzero elements in the algebraic number field K of height at most H, that is,
We note that by Northcott’s Theorem the set
![]() $ {\mathscr{A}}(K, H)$
is a finite set.
$ {\mathscr{A}}(K, H)$
is a finite set.
We need the following result from [Reference Ostafe, Shparlinski, Elsholtz and Grabner29, theorem 2·1].
Lemma 2·1.
Let
![]() $\{g_1, \ldots, g_r\}$
be a set of generators of
$\{g_1, \ldots, g_r\}$
be a set of generators of
![]() $\Gamma$
, which minimises
$\Gamma$
, which minimises
![]() $H = \max_{i=1, \ldots, r} {\textrm{h}}( g_i)$
. Then, for every
$H = \max_{i=1, \ldots, r} {\textrm{h}}( g_i)$
. Then, for every
![]() $\varepsilon\gt 0$
, we have
$\varepsilon\gt 0$
, we have
As usual, for any non-constant rational function
![]() $f \in K(X)$
, the degree of f is defined to be the maximum of the degrees of its numerator and denominator.
$f \in K(X)$
, the degree of f is defined to be the maximum of the degrees of its numerator and denominator.
The following result is [Reference Bérczes, Ostafe, Shparlinski and Silverman9, theorem 1·2 (a)].
Lemma 2·2.
Let
![]() $f \in K(X)$
be a rational function of degree
$f \in K(X)$
be a rational function of degree
![]() $d \ge 2$
. Assume that f is not of the form
$d \ge 2$
. Assume that f is not of the form
![]() $a(X-b)^d$
or
$a(X-b)^d$
or
![]() $a(X-b)^d / (X-c)^d$
with
$a(X-b)^d / (X-c)^d$
with
![]() $a,b,c \in K$
,
$a,b,c \in K$
,
![]() $a(b-c)\ne0$
, and
$a(b-c)\ne0$
, and
![]() $d \in {\mathbb{Z}}$
. Then, the set
$d \in {\mathbb{Z}}$
. Then, the set
![]() $\{\alpha \in K\,:\, f(\alpha) \in \Gamma \}$
is finite.
$\{\alpha \in K\,:\, f(\alpha) \in \Gamma \}$
is finite.
We remark that the result in Lemma 2·2 is not effective, due to the use of the Faltings theorem [Reference Faltings17] about finiteness of rational points on a curve. See also [Reference Ostafe, Shparlinski, Elsholtz and Grabner29, corollary 2·2] and references therein.
We conclude this section with a result of Maurin [Reference Maurin25, théorème 1·10], which we present in our setting of parametric curves by noticing [Reference Maurin25, remarque 1·3].
For this we introduce the following notation: we define
![]() ${\mathcal{H}}^{[2]}$
to be the union of all algebraic subgroups in
${\mathcal{H}}^{[2]}$
to be the union of all algebraic subgroups in
![]() ${\mathbb{G}_{\textrm{m}}}^n$
of codimension at least 2. For
${\mathbb{G}_{\textrm{m}}}^n$
of codimension at least 2. For
![]() $\varepsilon\gt0$
, we let
$\varepsilon\gt0$
, we let
![]() ${\mathcal{H}}^{[2]}_\varepsilon$
be defined similarly as in Section 1.2, that is,
${\mathcal{H}}^{[2]}_\varepsilon$
be defined similarly as in Section 1.2, that is,
We have the following result, which is a special case of [Reference Maurin25, thàreme 1·10].
Lemma 2·3.
Let
![]() $g_1,\ldots,g_r\in K^*$
and
$g_1,\ldots,g_r\in K^*$
and
![]() $f_1,\ldots,f_n\in K(X)$
be such that
$f_1,\ldots,f_n\in K(X)$
be such that
![]() $f_1,\ldots,f_n,g_1,\ldots,g_r$
are multiplicatively independent. Let
$f_1,\ldots,f_n,g_1,\ldots,g_r$
are multiplicatively independent. Let
Then there exists a real number
![]() $\varepsilon\gt0$
such that
$\varepsilon\gt0$
such that
![]() ${\mathcal{C}}\cap {\mathcal{H}}^{[2]}_\varepsilon$
is finite.
${\mathcal{C}}\cap {\mathcal{H}}^{[2]}_\varepsilon$
is finite.
2.2. On some functional properties of rational functions
We need the following special case of the result of Young [Reference Young42, corollary 1·2], which generalises the previous result of Gao [Reference Gao18, theorem 1·4] to multiplicative independence of consecutive iterations of rational functions over fields of characteristic zero.
Lemma 2·4.
Let F be an arbitrary field of characteristic zero, and let
![]() $f \in F(X)$
be a rational function of degree
$f \in F(X)$
be a rational function of degree
![]() $d \ge 2$
which is not of the form
$d \ge 2$
which is not of the form
![]() $aX^{\pm d}$
. Then, for any integer
$aX^{\pm d}$
. Then, for any integer
![]() $n\ge 1$
, the iterates
$n\ge 1$
, the iterates
![]() $f^{(1)}(X), \ldots,f^{(n)}(X)$
are multiplicatively independent modulo constants.
$f^{(1)}(X), \ldots,f^{(n)}(X)$
are multiplicatively independent modulo constants.
We also need the following simple lemma.
Lemma 2·5.
Let
![]() $f \in K(X)$
be a rational function such that it has no linear factor. Then, for any non-constant rational function
$f \in K(X)$
be a rational function such that it has no linear factor. Then, for any non-constant rational function
![]() $g \in K(X)$
, the rational function
$g \in K(X)$
, the rational function
![]() $f \circ g$
has no linear factor.
$f \circ g$
has no linear factor.
Proof. First, we note that it suffices to prove that for any monic irreducible factor, say p(X), of either the numerator or the denominator of f, the rational function
![]() $p \circ g$
has no linear factor.
$p \circ g$
has no linear factor.
By contradiction, suppose that the rational function
![]() $p \circ g$
has a linear factor. Then, there is an element, say
$p \circ g$
has a linear factor. Then, there is an element, say
![]() $\alpha$
, in K such that
$\alpha$
, in K such that
![]() $p \circ g (\alpha) = 0$
.
$p \circ g (\alpha) = 0$
.
If
![]() $g(\alpha)$
is well-defined, then
$g(\alpha)$
is well-defined, then
![]() $g(\alpha) \in K$
, which means that the polynomial p has a root (that is,
$g(\alpha) \in K$
, which means that the polynomial p has a root (that is,
![]() $g(\alpha)$
) in K. However, by assumption p is an irreducible polynomial over K of degree at least 2. So, we get a contradiction.
$g(\alpha)$
) in K. However, by assumption p is an irreducible polynomial over K of degree at least 2. So, we get a contradiction.
Now, if
![]() $g(\alpha)$
is not well-defined, then
$g(\alpha)$
is not well-defined, then
![]() $\alpha$
is a pole of g. Write
$\alpha$
is a pole of g. Write
![]() $p = X^d + a_{1}X^{d-1} + \cdots + a_{d-1} X + a_d$
and
$p = X^d + a_{1}X^{d-1} + \cdots + a_{d-1} X + a_d$
and
![]() $g = u/w$
with
$g = u/w$
with
![]() $u, w \in K[X]$
and
$u, w \in K[X]$
and
![]() $\gcd(u,w)=1$
. Since
$\gcd(u,w)=1$
. Since
![]() $\alpha$
is a pole of g, we have
$\alpha$
is a pole of g, we have
![]() $w(\alpha) = 0$
. Note that
$w(\alpha) = 0$
. Note that
![]() $p \circ g = p(u/w) = {1}/{w^d}(u^d + a_1 u^{d-1}w + \cdots + a_{d-1}uw^{d-1} + a_d w^d)$
. Then, since
$p \circ g = p(u/w) = {1}/{w^d}(u^d + a_1 u^{d-1}w + \cdots + a_{d-1}uw^{d-1} + a_d w^d)$
. Then, since
![]() $p \circ g (\alpha) = 0$
and
$p \circ g (\alpha) = 0$
and
![]() $w(\alpha)=0$
, we obtain
$w(\alpha)=0$
, we obtain
![]() $u(\alpha) = 0$
. So,
$u(\alpha) = 0$
. So,
![]() $\alpha$
is a common root of u and w, which contradicts with
$\alpha$
is a common root of u and w, which contradicts with
![]() $\gcd(u, w)=1$
.
$\gcd(u, w)=1$
.
Therefore, the rational function
![]() $f \circ g$
has no linear factor.
$f \circ g$
has no linear factor.
2.3. Generalised Schinzel–Tijdeman theorem
Another important tool for our results is the following general version, established in [Reference Bérczes, Bugeaud, Győry, Mello, Ostafe and Sha6], of the Schinzel–Tijdeman theorem [Reference Schinzel and Tijdeman38], which extends [Reference Bérczes, Evertse and Győry7, theorem 2·3] and [Reference Bérczes, Ostafe, Shparlinski and Silverman9, lemma 2·8]. We present it in a simplified form, which is sufficient for our purposes.
Let K be a number field and S a finite subset of
![]() $M_K$
containing all the infinite places. The following theorem is proved in [Reference Bérczes, Bugeaud, Győry, Mello, Ostafe and Sha6, theorem 2·2].
$M_K$
containing all the infinite places. The following theorem is proved in [Reference Bérczes, Bugeaud, Győry, Mello, Ostafe and Sha6, theorem 2·2].
Lemma 2·6.
Let
![]() $f(X)=a_0X^n + \cdots +a_n\in O_S[X]$
be a polynomial of degree n and with at least two distinct roots. There is an effectively computable constant C(f,K,S), depending only on f, K and S, so that the following holds: if
$f(X)=a_0X^n + \cdots +a_n\in O_S[X]$
be a polynomial of degree n and with at least two distinct roots. There is an effectively computable constant C(f,K,S), depending only on f, K and S, so that the following holds: if
![]() $b\in O_S^*$
and if the equation
$b\in O_S^*$
and if the equation
has a solution (x, y) with
![]() $y\ne 0$
and
$y\ne 0$
and
![]() $y \notin O_S^*$
, then
$y \notin O_S^*$
, then
We remark that, when f has only simple roots, the result in Lemma 2·6 has been established in [Reference Bérczes, Ostafe, Shparlinski and Silverman9, lemma 2·8], In addition, when S only consists of infinite places, the result in Lemma 2·6 has been given in [Reference Shorey and Tijdeman40, theorem 10·3] (choosing
![]() $\tau = 0, z=1, \gamma =1, \varepsilon=b$
there).
$\tau = 0, z=1, \gamma =1, \varepsilon=b$
there).
3. Proofs of the main results
3.1 Preliminary discussion
Let
![]() $S_\Gamma$
be the following set of places of K:
$S_\Gamma$
be the following set of places of K:
where, as usual,
![]() $v(\gamma)$
means the additive valuation of v at
$v(\gamma)$
means the additive valuation of v at
![]() $\gamma$
. Note that the set
$\gamma$
. Note that the set
![]() $S_\Gamma$
is finite, since
$S_\Gamma$
is finite, since
![]() $\Gamma$
is finitely generated.
$\Gamma$
is finitely generated.
As usual, we say that a polynomial
has bad reduction at
![]() $v\in M_{K}^0$
if either
$v\in M_{K}^0$
if either
![]() $v(a_i)\lt0$
for some
$v(a_i)\lt0$
for some
![]() $i \ge 1$
or
$i \ge 1$
or
![]() $v(a_0)\ne0$
; otherwise we say it has good reduction at v.
$v(a_0)\ne0$
; otherwise we say it has good reduction at v.
Let
be a vector of non-constant polynomials
and we define
Note that
![]() $S_{{\textbf{f}},\Gamma}$
is a finite set. Moreover, each
$S_{{\textbf{f}},\Gamma}$
is a finite set. Moreover, each
![]() $f_i \in O_{S_{{\textbf{f}},\Gamma}}[X]$
, and in fact for any
$f_i \in O_{S_{{\textbf{f}},\Gamma}}[X]$
, and in fact for any
![]() $v\not\in S_{{\textbf{f}},\Gamma}$
we have
$v\not\in S_{{\textbf{f}},\Gamma}$
we have
If
is a vector of non-constant rational functions, we will use the same notation
![]() $S_{{\textbf{f}},\Gamma}$
for the set including
$S_{{\textbf{f}},\Gamma}$
for the set including
![]() $S_\Gamma$
and all the places
$S_\Gamma$
and all the places
![]() $v\in M_K^0$
such that at least one of the numerators or denominators of
$v\in M_K^0$
such that at least one of the numerators or denominators of
![]() $f_1,\ldots,f_n$
has bad reduction at v.
$f_1,\ldots,f_n$
has bad reduction at v.
By definition, we have
Note that
![]() $O_{S_{{\textbf{f}},\Gamma}}^*$
is also a finitely generated subgroup of
$O_{S_{{\textbf{f}},\Gamma}}^*$
is also a finitely generated subgroup of
![]() $K^*$
. Hence, it suffices to prove the main results by replacing
$K^*$
. Hence, it suffices to prove the main results by replacing
![]() $\Gamma$
with
$\Gamma$
with
![]() $O_{S_{{\textbf{f}},\Gamma}}^*$
. Then, in the sequel we will prove the main results by replacing
$O_{S_{{\textbf{f}},\Gamma}}^*$
. Then, in the sequel we will prove the main results by replacing
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
with
$\Gamma^{{\textrm{div}}}_\varepsilon$
with
![]() $O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
, where
$O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
, where
![]() $S_{{\textbf{f}},\Gamma,\varepsilon}$
is some finite set of places containing
$S_{{\textbf{f}},\Gamma,\varepsilon}$
is some finite set of places containing
![]() $S_{{\textbf{f}},\Gamma}$
and depending also on
$S_{{\textbf{f}},\Gamma}$
and depending also on
![]() $\varepsilon$
.
$\varepsilon$
.
3.2. Proof of Theorem 1·1
Let
![]() $\alpha \in K$
be such that there exist integers
$\alpha \in K$
be such that there exist integers
![]() $k_1,\ldots, k_n$
, not all zero such that
$k_1,\ldots, k_n$
, not all zero such that
By Lemma 2·1 there exists
![]() $\beta \in O_{S_{{\textbf{f}},\Gamma}}^*$
and
$\beta \in O_{S_{{\textbf{f}},\Gamma}}^*$
and
![]() $\eta \in K^*$
with
$\eta \in K^*$
with
![]() ${\textrm{h}}(\eta)\ll_{\varepsilon,\Gamma} 1$
such that
${\textrm{h}}(\eta)\ll_{\varepsilon,\Gamma} 1$
such that
Since
![]() $\eta \in K^*$
is of bounded height depending only on
$\eta \in K^*$
is of bounded height depending only on
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $\Gamma$
, by Northcott’s theorem there are only finitely many such
$\Gamma$
, by Northcott’s theorem there are only finitely many such
![]() $\eta$
. Thus we can enlarge the set
$\eta$
. Thus we can enlarge the set
![]() $S_{{\textbf{f}},\Gamma}$
to include all prime ideals that divide the finitely many elements
$S_{{\textbf{f}},\Gamma}$
to include all prime ideals that divide the finitely many elements
![]() $\eta$
. We also include in this larger set the prime ideals outside
$\eta$
. We also include in this larger set the prime ideals outside
![]() $S_{{\textbf{f}},\Gamma}$
that divide the product
$S_{{\textbf{f}},\Gamma}$
that divide the product
![]() $\displaystyle\prod_{1\le i \neq j\le n}$
Res
$\displaystyle\prod_{1\le i \neq j\le n}$
Res
![]() $(f_i,f_j)$
of all the resultants of
$(f_i,f_j)$
of all the resultants of
![]() $f_i$
and
$f_i$
and
![]() $f_j$
for
$f_j$
for
![]() $i\ne j$
(we recall that all
$i\ne j$
(we recall that all
![]() ${\textrm{Res}} (f_i,f_j)$
are
${\textrm{Res}} (f_i,f_j)$
are
![]() $S_{{\textbf{f}},\Gamma}$
-integers), which are only finitely many. We denote the new set by
$S_{{\textbf{f}},\Gamma}$
-integers), which are only finitely many. We denote the new set by
![]() $S_{{\textbf{f}},\Gamma,\varepsilon}$
and we note that
$S_{{\textbf{f}},\Gamma,\varepsilon}$
and we note that
![]() $S_{{\textbf{f}},\Gamma,\varepsilon}$
is still a finite set.
$S_{{\textbf{f}},\Gamma,\varepsilon}$
is still a finite set.
By the construction of the set
![]() $S_{{\textbf{f}},\Gamma, \varepsilon}$
, we have
$S_{{\textbf{f}},\Gamma, \varepsilon}$
, we have
Thus, it suffices to prove the desired result by replacing
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
with
$\Gamma^{{\textrm{div}}}_\varepsilon$
with
![]() $O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
.
$O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
.
Now, we write
If
![]() $n = 1$
, since
$n = 1$
, since
![]() $f_1$
is a polynomial having at least two distinct roots and
$f_1$
is a polynomial having at least two distinct roots and
![]() $O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
is a finitely generated subgroup, we see that applying Lemma 2·2 to
$O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
is a finitely generated subgroup, we see that applying Lemma 2·2 to
![]() $f_1$
and
$f_1$
and
![]() $O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
gives the desired finiteness result. We thus suppose that
$O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
gives the desired finiteness result. We thus suppose that
![]() $n \geq 2$
, and that the result is valid for
$n \geq 2$
, and that the result is valid for
![]() $n-1$
, in order to apply an induction.
$n-1$
, in order to apply an induction.
We note that if some
![]() $k_i=0$
, then the desired finiteness of
$k_i=0$
, then the desired finiteness of
![]() $\alpha \in K$
satisfying (3·2) follows directly from the induction hypothesis. Hence, we can assume from now on that
$\alpha \in K$
satisfying (3·2) follows directly from the induction hypothesis. Hence, we can assume from now on that
![]() $k_1 \cdots$
$k_1 \cdots$
![]() $k_n \ne 0$
.
$k_n \ne 0$
.
We now complete the proof case by case.
Case I:
![]() $\alpha \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
.
$\alpha \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
.
In this case, since
![]() $\alpha \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
and
$\alpha \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
and
![]() $f_i\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}[X]$
for any
$f_i\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}[X]$
for any
![]() $i=1,\ldots,n$
, we have
$i=1,\ldots,n$
, we have
We note that if
![]() $f_i(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
for some
$f_i(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
for some
![]() $i \in \{1,\ldots,n\}$
, then Lemma 2·2 implies the finiteness of such
$i \in \{1,\ldots,n\}$
, then Lemma 2·2 implies the finiteness of such
![]() $\alpha \in K$
satisfying (3·2).
$\alpha \in K$
satisfying (3·2).
Thus, we now assume that
![]() $f_1(\alpha),\ldots, f_n(\alpha)\not\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
. This implies that there exists a prime ideal
$f_1(\alpha),\ldots, f_n(\alpha)\not\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
. This implies that there exists a prime ideal
![]() ${\mathfrak{p}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
in K such that
${\mathfrak{p}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
in K such that
![]() $v_{\mathfrak{p}}(f_1(\alpha))\gt0$
. Moreover, since
$v_{\mathfrak{p}}(f_1(\alpha))\gt0$
. Moreover, since
![]() $f_i(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
, we have
$f_i(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
, we have
![]() $v_{\mathfrak{p}}(f_i(\alpha))\ge 0$
for each
$v_{\mathfrak{p}}(f_i(\alpha))\ge 0$
for each
![]() $i=2, \ldots, n$
.
$i=2, \ldots, n$
.
If
![]() $k_1k_i \gt 0$
for each
$k_1k_i \gt 0$
for each
![]() $i =2,\ldots, n$
, without loss of generality we can assume that
$i =2,\ldots, n$
, without loss of generality we can assume that
![]() $k_1,k_2,\ldots, k_n \gt 0$
. Then, equation (3·2) implies
$k_1,k_2,\ldots, k_n \gt 0$
. Then, equation (3·2) implies
Since
![]() $v_{\mathfrak{p}}(f_1(\alpha))\gt0$
and
$v_{\mathfrak{p}}(f_1(\alpha))\gt0$
and
![]() $v_{\mathfrak{p}}(f_i(\alpha))\ge 0$
for each
$v_{\mathfrak{p}}(f_i(\alpha))\ge 0$
for each
![]() $i =2, \ldots, n$
, we obtain a contradiction.
$i =2, \ldots, n$
, we obtain a contradiction.
We now assume
![]() $k_1k_i \lt 0$
for some
$k_1k_i \lt 0$
for some
![]() $i \in \{2,\ldots, n\}$
. In this case, without loss of generality, we assume
$i \in \{2,\ldots, n\}$
. In this case, without loss of generality, we assume
![]() $k_1\gt0, \ldots, k_m \gt0$
and
$k_1\gt0, \ldots, k_m \gt0$
and
![]() $k_{m+1} \lt0 , \ldots, k_n \lt 0$
for some positive integer m. So, equation (3·2) becomes
$k_{m+1} \lt0 , \ldots, k_n \lt 0$
for some positive integer m. So, equation (3·2) becomes
Then, since
![]() $v_{\mathfrak{p}}(f_1(\alpha)) \gt 0$
and
$v_{\mathfrak{p}}(f_1(\alpha)) \gt 0$
and
![]() $v_{\mathfrak{p}}(f_i(\alpha))\ge 0$
for each
$v_{\mathfrak{p}}(f_i(\alpha))\ge 0$
for each
![]() $i=2,\ldots, n$
, there must exist some
$i=2,\ldots, n$
, there must exist some
![]() $j \in \{m+1, \ldots, n\}$
such that
$j \in \{m+1, \ldots, n\}$
such that
![]() $v_{\mathfrak{p}}(f_j(\alpha)) \gt 0$
. In other words, we have
$v_{\mathfrak{p}}(f_j(\alpha)) \gt 0$
. In other words, we have
This allows us to conclude that
![]() $v_{\mathfrak{p}}({\textrm{Res}} (f_1,f_j))\gt0$
(notice that, since
$v_{\mathfrak{p}}({\textrm{Res}} (f_1,f_j))\gt0$
(notice that, since
![]() $f_1,f_{j} \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}[X]$
and
$f_1,f_{j} \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}[X]$
and
![]() $f_1$
and
$f_1$
and
![]() $f_j$
do not have common roots, we have
$f_j$
do not have common roots, we have
![]() ${\textrm{Res}} (f_1,f_j)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
and
${\textrm{Res}} (f_1,f_j)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
and
![]() ${\textrm{Res}} (f_1,f_j) \ne 0$
). By our construction of the set
${\textrm{Res}} (f_1,f_j) \ne 0$
). By our construction of the set
![]() $S_{{\textbf{f}},\Gamma,\varepsilon}$
, this implies that
$S_{{\textbf{f}},\Gamma,\varepsilon}$
, this implies that
![]() ${\mathfrak{p}} \in S_{{\textbf{f}},\Gamma,\varepsilon}$
, which is a contradiction with the choice of
${\mathfrak{p}} \in S_{{\textbf{f}},\Gamma,\varepsilon}$
, which is a contradiction with the choice of
![]() ${\mathfrak{p}}$
above. This completes the proof of Case I.
${\mathfrak{p}}$
above. This completes the proof of Case I.
Case II:
![]() $\alpha \not\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
.
$\alpha \not\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
.
In this case, there exists a prime ideal
![]() ${\mathfrak{p}}$
of the ring of integers of K such that
${\mathfrak{p}}$
of the ring of integers of K such that
Let
![]() $d_i = \deg f_i, i =1, \ldots,n$
. Then, using the ultrametric inequality of non-Archimedean valuations and noticing (3.1), we directly have
$d_i = \deg f_i, i =1, \ldots,n$
. Then, using the ultrametric inequality of non-Archimedean valuations and noticing (3.1), we directly have
Considering valuations in (3·2) and using (3·3) we obtain (since
![]() $v_{\mathfrak{p}}(\gamma)=0$
due to
$v_{\mathfrak{p}}(\gamma)=0$
due to
![]() $\gamma\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
)
$\gamma\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
)
We view the above identity as a linear Diophantine equation with unknowns
![]() $k_1, \ldots, k_n$
in
$k_1, \ldots, k_n$
in
![]() ${\mathbb{Z}}$
. Then, we have a basis of the integer solutions
${\mathbb{Z}}$
. Then, we have a basis of the integer solutions
![]() $(k_1, k_2, \ldots, k_n)$
of the equation (3·4), say,
$(k_1, k_2, \ldots, k_n)$
of the equation (3·4), say,
Therefore,
![]() $k_1, k_2, \ldots, k_n$
can be expressed as
$k_1, k_2, \ldots, k_n$
can be expressed as
 $$k_j = \sum_{i=1}^{n-1} s_i t_{i,j}, \quad j=1,\ldots,n,$$
$$k_j = \sum_{i=1}^{n-1} s_i t_{i,j}, \quad j=1,\ldots,n,$$
for some integers
![]() $s_1, \ldots, s_{n-1}$
. Substituting this into the equation (3·2), we obtain
$s_1, \ldots, s_{n-1}$
. Substituting this into the equation (3·2), we obtain
 \begin{equation} \left( \prod_{j=1}^{n} f_j(\alpha)^{t_{1,j}} \right)^{s_1} \cdots \left( \prod_{j=1}^{n} f_j(\alpha)^{t_{n-1, j}} \right)^{s_{n-1}}= \gamma.\end{equation}
\begin{equation} \left( \prod_{j=1}^{n} f_j(\alpha)^{t_{1,j}} \right)^{s_1} \cdots \left( \prod_{j=1}^{n} f_j(\alpha)^{t_{n-1, j}} \right)^{s_{n-1}}= \gamma.\end{equation}
Now, we let
 $$F(X) = \prod_{j=1}^{n} f_j(X)^{t_{1,j}},$$
$$F(X) = \prod_{j=1}^{n} f_j(X)^{t_{1,j}},$$
where the exponent vector
![]() $(t_{1,1}, \ldots, t_{1,n})$
is non-zero by its choice above.
$(t_{1,1}, \ldots, t_{1,n})$
is non-zero by its choice above.
For any prime
![]() ${\mathfrak{q}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
, if
${\mathfrak{q}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
, if
![]() $v_{\mathfrak{q}}(\alpha) \lt 0$
, then (3·3) holds and we have
$v_{\mathfrak{q}}(\alpha) \lt 0$
, then (3·3) holds and we have
 \begin{equation}\begin{split}v_{\mathfrak{q}}(F(\alpha)) & = \sum_{j=1}^{n} t_{1,j}v_{\mathfrak{q}}(f_j(\alpha)) \\& =(t_{1,1}d_1 + t_{1,2}d_2 + \cdots + t_{1,n} d_n) v_{\mathfrak{q}}(\alpha) = 0,\end{split}\end{equation}
\begin{equation}\begin{split}v_{\mathfrak{q}}(F(\alpha)) & = \sum_{j=1}^{n} t_{1,j}v_{\mathfrak{q}}(f_j(\alpha)) \\& =(t_{1,1}d_1 + t_{1,2}d_2 + \cdots + t_{1,n} d_n) v_{\mathfrak{q}}(\alpha) = 0,\end{split}\end{equation}
since
![]() $(t_{1,1}, t_{1,2}, \ldots, t_{1,n})$
is a solution to (3·4).
$(t_{1,1}, t_{1,2}, \ldots, t_{1,n})$
is a solution to (3·4).
For any prime
![]() ${\mathfrak{q}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
, if
${\mathfrak{q}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
, if
![]() $v_{\mathfrak{q}}(\alpha) \ge 0$
, then by (3·1) we have
$v_{\mathfrak{q}}(\alpha) \ge 0$
, then by (3·1) we have
![]() $v_{\mathfrak{q}}(f_i(\alpha)) \ge 0$
for each
$v_{\mathfrak{q}}(f_i(\alpha)) \ge 0$
for each
![]() $i = 1, \ldots, n$
.
$i = 1, \ldots, n$
.
If there exists some prime
![]() ${\mathfrak{q}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
such that
${\mathfrak{q}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
such that
![]() $v_{\mathfrak{q}}(\alpha) \ge 0$
and moreover
$v_{\mathfrak{q}}(\alpha) \ge 0$
and moreover
![]() $v_{\mathfrak{q}}(f_i(\alpha)) \gt 0$
,
$v_{\mathfrak{q}}(f_i(\alpha)) \gt 0$
,
![]() $v_{\mathfrak{q}}(f_j(\alpha)) \gt 0$
for some
$v_{\mathfrak{q}}(f_j(\alpha)) \gt 0$
for some
![]() $i \ne j$
, then by the same discussion as in the last part of Case I we arrive to a contradiction.
$i \ne j$
, then by the same discussion as in the last part of Case I we arrive to a contradiction.
If there exists some prime
![]() ${\mathfrak{q}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
such that
${\mathfrak{q}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
such that
![]() $v_{\mathfrak{q}}(\alpha) \ge 0$
and moreover
$v_{\mathfrak{q}}(\alpha) \ge 0$
and moreover
![]() $v_{\mathfrak{q}}(f_i(\alpha)) \gt 0$
for exactly one i for
$v_{\mathfrak{q}}(f_i(\alpha)) \gt 0$
for exactly one i for
![]() $i=1, \ldots, n$
, say
$i=1, \ldots, n$
, say
![]() $v_{\mathfrak{q}}(f_1(\alpha)) \gt 0$
and
$v_{\mathfrak{q}}(f_1(\alpha)) \gt 0$
and
![]() $v_{\mathfrak{q}}(f_i(\alpha)) = 0$
for each
$v_{\mathfrak{q}}(f_i(\alpha)) = 0$
for each
![]() $i = 2, \ldots, n$
, then by (3·5) we obtain
$i = 2, \ldots, n$
, then by (3·5) we obtain
which however contradicts with
![]() $k_1 \ne 0$
because
$k_1 \ne 0$
because
![]() $k_1 = s_1 t_{1,1} + \cdots + s_{n-1} t_{n-1, 1}$
.
$k_1 = s_1 t_{1,1} + \cdots + s_{n-1} t_{n-1, 1}$
.
Hence, we may assume that for any prime
![]() ${\mathfrak{q}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
, if
${\mathfrak{q}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
, if
![]() $v_{\mathfrak{q}}(\alpha) \ge 0$
, then
$v_{\mathfrak{q}}(\alpha) \ge 0$
, then
![]() $v_{\mathfrak{q}}(f_i(\alpha)) = 0$
for each
$v_{\mathfrak{q}}(f_i(\alpha)) = 0$
for each
![]() $i = 1, \ldots, n$
. In this case, we have
$i = 1, \ldots, n$
. In this case, we have
![]() $v_{\mathfrak{q}}(F(\alpha)) = 0$
. Combining this with (3·6), we have
$v_{\mathfrak{q}}(F(\alpha)) = 0$
. Combining this with (3·6), we have
![]() $v_{\mathfrak{q}}(F(\alpha)) = 0$
for any prime
$v_{\mathfrak{q}}(F(\alpha)) = 0$
for any prime
![]() ${\mathfrak{q}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
, and thus
${\mathfrak{q}} \not\in S_{{\textbf{f}},\Gamma,\varepsilon}$
, and thus
![]() $F(\alpha) \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
. Now, the desired result follows directly from Lemma 2·2 (which we can apply, since
$F(\alpha) \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
. Now, the desired result follows directly from Lemma 2·2 (which we can apply, since
![]() $f_i$
,
$f_i$
,
![]() $i=1,\ldots,n$
, has at least two distinct roots and they are pairwise coprime, and therefore, F has at least two distinct roots or two distinct poles). This completes the proof.
$i=1,\ldots,n$
, has at least two distinct roots and they are pairwise coprime, and therefore, F has at least two distinct roots or two distinct poles). This completes the proof.
3.3. Proof of Theorem 1·2
First, we assume that the rational functions
![]() $f_1, f_2, \ldots, f_n$
all have no linear factor.
$f_1, f_2, \ldots, f_n$
all have no linear factor.
Let
![]() $g_1, \ldots, g_m$
be all the distinct monic irreducible factors (over K) in the numerators and denominators of the rational functions
$g_1, \ldots, g_m$
be all the distinct monic irreducible factors (over K) in the numerators and denominators of the rational functions
![]() $f_{1}, f_{2}, \ldots, f_{n}$
. So, by assumption, the irreducible polynomials
$f_{1}, f_{2}, \ldots, f_{n}$
. So, by assumption, the irreducible polynomials
![]() $g_1, \ldots, g_m$
are all of degree at least two. Then, for each
$g_1, \ldots, g_m$
are all of degree at least two. Then, for each
![]() $f_i, 1\le i \le n$
, we can write
$f_i, 1\le i \le n$
, we can write
 \begin{equation} f_i = a_i \prod_{j=1}^{m} g_j^{e_{ij}},\quad a_i\in K^*,\end{equation}
\begin{equation} f_i = a_i \prod_{j=1}^{m} g_j^{e_{ij}},\quad a_i\in K^*,\end{equation}
for some integers
![]() $e_{i1}, \ldots, e_{im}$
.
$e_{i1}, \ldots, e_{im}$
.
Let
![]() $\alpha \in K$
be such that there exist integers
$\alpha \in K$
be such that there exist integers
![]() $k_1,\ldots, k_n$
, not all zero such that
$k_1,\ldots, k_n$
, not all zero such that
As in (3·2), we can write
where the set
![]() $S_{{\textbf{f}},\Gamma,\varepsilon}$
is defined as in the proof of Theorem 1·1, however without including the prime ideals outside
$S_{{\textbf{f}},\Gamma,\varepsilon}$
is defined as in the proof of Theorem 1·1, however without including the prime ideals outside
![]() $S_{{\textbf{f}},\Gamma}$
that divide the product
$S_{{\textbf{f}},\Gamma}$
that divide the product
![]() $\displaystyle\prod_{1\le i \neq j\le n}$
Res
$\displaystyle\prod_{1\le i \neq j\le n}$
Res
![]() $(f_i,f_j)$
of all the resultants of
$(f_i,f_j)$
of all the resultants of
![]() $f_i$
and
$f_i$
and
![]() $f_j$
for
$f_j$
for
![]() $i\ne j$
, because
$i\ne j$
, because
![]() $f_i$
and
$f_i$
and
![]() $f_j$
might not be polynomials.
$f_j$
might not be polynomials.
By the discussion in Section 3.1, we know that
![]() $a_i \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
for each
$a_i \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
for each
![]() $i=1,\ldots,n$
. Hence, combining (3·8) with (3·7), we get that for some
$i=1,\ldots,n$
. Hence, combining (3·8) with (3·7), we get that for some
![]() $\gamma^{\prime} \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
,
$\gamma^{\prime} \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
,
If for each
![]() $1\le j \le m$
,
$1\le j \le m$
,
![]() $k_1e_{1j} + \cdots + k_ne_{nj} = 0$
, then this means that
$k_1e_{1j} + \cdots + k_ne_{nj} = 0$
, then this means that
![]() $f_1^{k_1} \cdots f_n^{k_n}$
is a constant, which contradicts with the assumption that
$f_1^{k_1} \cdots f_n^{k_n}$
is a constant, which contradicts with the assumption that
![]() $f_1, \ldots, f_n$
are multiplicatively independent modulo constants.
$f_1, \ldots, f_n$
are multiplicatively independent modulo constants.
So, we must have that
![]() $k_1e_{1j} + \cdots + k_ne_{nj} \ne 0$
for some
$k_1e_{1j} + \cdots + k_ne_{nj} \ne 0$
for some
![]() $1 \le j \le m$
. Then, in view of (3·9) and noticing that
$1 \le j \le m$
. Then, in view of (3·9) and noticing that
![]() $g_1, \ldots, g_m$
are pairwise distinct irreducible polynomials of degree at least 2, we obtain directly the desired finiteness result by applying Theorem 1·1 to the polynomials
$g_1, \ldots, g_m$
are pairwise distinct irreducible polynomials of degree at least 2, we obtain directly the desired finiteness result by applying Theorem 1·1 to the polynomials
![]() $g_1, \ldots, g_m$
. This completes the proof of the case when
$g_1, \ldots, g_m$
. This completes the proof of the case when
![]() $f_1, f_2, \ldots, f_n$
all have no linear factor.
$f_1, f_2, \ldots, f_n$
all have no linear factor.
Now, without loss of generality, we assume that for each
![]() $f_i, i =1, 2, \ldots, n$
, both its numerator and denominator have linear factors.
$f_i, i =1, 2, \ldots, n$
, both its numerator and denominator have linear factors.
Then, for each
![]() $f_i, i=1,2,\ldots, n$
, we write
$f_i, i=1,2,\ldots, n$
, we write
where
![]() $f_{i1} \in K(X)$
is monic and only has linear factors, and
$f_{i1} \in K(X)$
is monic and only has linear factors, and
![]() $f_{i2} \in K(X)$
is monic and only has irredicible factors of degree at least two; and moreover, we write
$f_{i2} \in K(X)$
is monic and only has irredicible factors of degree at least two; and moreover, we write
By assumption, for each
![]() $i=1,2, \ldots, n$
, both
$i=1,2, \ldots, n$
, both
![]() $h_{i1}$
and
$h_{i1}$
and
![]() $h_{i2}$
have at least two distinct linear factors and they only have linear factors. Moreover, since we have assumed that
$h_{i2}$
have at least two distinct linear factors and they only have linear factors. Moreover, since we have assumed that
![]() $f_1, f_2, \ldots, f_n$
have distinct linear factors, we know that
$f_1, f_2, \ldots, f_n$
have distinct linear factors, we know that
![]() $h_{11}, h_{12}, \ldots, h_{n1}, h_{n2}$
are pairwise coprime.
$h_{11}, h_{12}, \ldots, h_{n1}, h_{n2}$
are pairwise coprime.
Let
![]() $g_1, \ldots, g_m$
(assume
$g_1, \ldots, g_m$
(assume
![]() $m \ge 1$
) be all the distinct monic irreducible factors (over K) in the numerators and denominators of the rational functions
$m \ge 1$
) be all the distinct monic irreducible factors (over K) in the numerators and denominators of the rational functions
![]() $f_{12}, \ldots, f_{n2}$
.
$f_{12}, \ldots, f_{n2}$
.
By assumption, the irreducible polynomials
![]() $g_1, \ldots, g_m$
are all of degree at least two. So, the polynomials
$g_1, \ldots, g_m$
are all of degree at least two. So, the polynomials
![]() $h_{11}, h_{12}, \ldots, h_{n1}, h_{n2}$
,
$h_{11}, h_{12}, \ldots, h_{n1}, h_{n2}$
,
![]() $g_1, \ldots, g_m$
are pairwise coprime.
$g_1, \ldots, g_m$
are pairwise coprime.
Then, for each
![]() $f_i, 1\le i \le n$
, we can write
$f_i, 1\le i \le n$
, we can write
 \begin{equation} f_i = a_i h_{i1} h_{i2}^{-1}\prod_{j=1}^{m} g_j^{e_{ij}},\quad a_i\in K^*,\end{equation}
\begin{equation} f_i = a_i h_{i1} h_{i2}^{-1}\prod_{j=1}^{m} g_j^{e_{ij}},\quad a_i\in K^*,\end{equation}
for some integers
![]() $e_{i1}, \ldots, e_{im}$
.
$e_{i1}, \ldots, e_{im}$
.
As in (3·9), combining (3·8) with (3·10) we can get that for some
![]() $\gamma^{\prime} \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
,
$\gamma^{\prime} \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
,
 \begin{equation} \prod_{i=1}^{n} h_{i1}(\alpha)^{k_i} h_{i2}(\alpha)^{-k_i} \cdot \prod_{j=1}^{m}g_j(\alpha)^{k_1e_{1j} + \cdots + k_ne_{nj}}= \gamma^{\prime}.\end{equation}
\begin{equation} \prod_{i=1}^{n} h_{i1}(\alpha)^{k_i} h_{i2}(\alpha)^{-k_i} \cdot \prod_{j=1}^{m}g_j(\alpha)^{k_1e_{1j} + \cdots + k_ne_{nj}}= \gamma^{\prime}.\end{equation}
Then, in view of (3·11) and noticing that the integers
![]() $k_1, \ldots, k_n$
are not all zero, we obtain directly the desired finiteness result by applying Theorem 1·1 to the polynomials
$k_1, \ldots, k_n$
are not all zero, we obtain directly the desired finiteness result by applying Theorem 1·1 to the polynomials
![]() $h_{11}, h_{12}, \ldots, h_{n1}, h_{n2}$
,
$h_{11}, h_{12}, \ldots, h_{n1}, h_{n2}$
,
![]() $g_1, \ldots, g_m$
. This completes the proof.
$g_1, \ldots, g_m$
. This completes the proof.
3.4. Proof of Corollary 1·4
First, we assume that
![]() $f \in K[X]$
and 0 is not a periodic point of f. Since 0 is not a periodic point of f, we have that for any integer
$f \in K[X]$
and 0 is not a periodic point of f. Since 0 is not a periodic point of f, we have that for any integer
![]() $n \ge 1$
,
$n \ge 1$
,
![]() $f^{(n)}(0) \ne 0$
, which means that
$f^{(n)}(0) \ne 0$
, which means that
![]() $f^{(n)}$
has non-zero constant term. So, all the iterates of f are pairwise coprime. In addition, since f has at least two distinct roots, it is easy to see that each iterate of f also has at least two distinct roots. Hence, by Theorem 1·1 we know that there are only finitely many elements
$f^{(n)}$
has non-zero constant term. So, all the iterates of f are pairwise coprime. In addition, since f has at least two distinct roots, it is easy to see that each iterate of f also has at least two distinct roots. Hence, by Theorem 1·1 we know that there are only finitely many elements
![]() $\beta \in K$
such that
$\beta \in K$
such that
![]() $f^{(1)}(\beta), \ldots, f^{(n)}(\beta)$
are multiplicatively dependent modulo
$f^{(1)}(\beta), \ldots, f^{(n)}(\beta)$
are multiplicatively dependent modulo
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
.
$\Gamma^{{\textrm{div}}}_\varepsilon$
.
Now, we assume that f has no linear factor. Then, by Lemma 2·5, the iterates
![]() $f^{(1)}, \ldots, f^{(n)}$
all have no linear factor. Moreover, it follows directly from Lemma 2·4 that the iterates
$f^{(1)}, \ldots, f^{(n)}$
all have no linear factor. Moreover, it follows directly from Lemma 2·4 that the iterates
![]() $f^{(1)}, \ldots, f^{(n)}$
are multiplicatively independent modulo constants. So, using Theorem 1·2 we get that there are only finitely many elements
$f^{(1)}, \ldots, f^{(n)}$
are multiplicatively independent modulo constants. So, using Theorem 1·2 we get that there are only finitely many elements
![]() $\beta \in K$
such that
$\beta \in K$
such that
![]() $f^{(1)}(\beta), \ldots, f^{(n)}(\beta)$
are multiplicatively dependent modulo
$f^{(1)}(\beta), \ldots, f^{(n)}(\beta)$
are multiplicatively dependent modulo
![]() $\Gamma^{{\textrm{div}}}_\varepsilon$
.
$\Gamma^{{\textrm{div}}}_\varepsilon$
.
So, for proving the desired result, it suffices to fix such an element
![]() $\beta$
and show that there are only finitely many
$\beta$
and show that there are only finitely many
![]() $\alpha \in K$
such that
$\alpha \in K$
such that
![]() $f^{(m)}(\alpha) = \beta$
for some integer
$f^{(m)}(\alpha) = \beta$
for some integer
![]() $m \ge 0$
. Indeed, this follows directly from [Reference Bérczes, Ostafe, Shparlinski and Silverman9, lemma 2·3] and the well-known fact that f has only finitely many preperiodic points lying in K.
$m \ge 0$
. Indeed, this follows directly from [Reference Bérczes, Ostafe, Shparlinski and Silverman9, lemma 2·3] and the well-known fact that f has only finitely many preperiodic points lying in K.
3.5 Proof of Theorem 1·5
The proof follows similar ideas as in the proof of [Reference Bérczes, Ostafe, Shparlinski and Silverman9, theorem 1·7].
Let
![]() $\alpha \in K$
be such that there exist integers
$\alpha \in K$
be such that there exist integers
![]() $k_1,k_2$
, not both zero, such that
$k_1,k_2$
, not both zero, such that
As in the proof of Theorem 1·1, we enlarge the set
![]() $S_{{\textbf{f}},\Gamma}$
(in this case
$S_{{\textbf{f}},\Gamma}$
(in this case
![]() ${\textbf{f}}=(f_1,f_2)$
) to a larger set
${\textbf{f}}=(f_1,f_2)$
) to a larger set
![]() $S_{{\textbf{f}},\Gamma,\varepsilon}$
such that
$S_{{\textbf{f}},\Gamma,\varepsilon}$
such that
Also, as in the proof of Theorem 1·1 we can assume that
![]() $k_1 k_2 \ne 0$
. From (3·12) and the power saturation of
$k_1 k_2 \ne 0$
. From (3·12) and the power saturation of
![]() $O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
in
$O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
in
![]() $K^*$
, we see that
$K^*$
, we see that
This allows us to take the
![]() $\gcd(k_1, k_2)$
-root of (3·12), so without loss of generality we can assume that
$\gcd(k_1, k_2)$
-root of (3·12), so without loss of generality we can assume that
We now complete the proof case by case.
Case I:
![]() $\alpha \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
.
$\alpha \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
.
In this case, we have
![]() $f_1(\alpha),f_2(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
. We note that if
$f_1(\alpha),f_2(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
. We note that if
![]() $f_1(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
or
$f_1(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
or
![]() $f_2(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
, then Lemma 2·2 implies the finiteness of such
$f_2(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
, then Lemma 2·2 implies the finiteness of such
![]() $\alpha \in K$
satisfying (3·12).
$\alpha \in K$
satisfying (3·12).
Thus, we can assume that
![]() $f_1(\alpha),f_2(\alpha)\not\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
. This implies that there exists a prime ideal
$f_1(\alpha),f_2(\alpha)\not\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
. This implies that there exists a prime ideal
![]() ${\mathfrak{p}}$
of K such that the additive valuation
${\mathfrak{p}}$
of K such that the additive valuation
![]() $v_{\mathfrak{p}}(f_1(\alpha))\gt0$
. Moreover, since
$v_{\mathfrak{p}}(f_1(\alpha))\gt0$
. Moreover, since
![]() $f_2(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
, we have
$f_2(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
, we have
![]() $v_{\mathfrak{p}}(f_2(\alpha))\ge 0$
.
$v_{\mathfrak{p}}(f_2(\alpha))\ge 0$
.
If
![]() $k_1k_2 \gt 0$
, then we can assume that
$k_1k_2 \gt 0$
, then we can assume that
![]() $k_1, k_2 \gt 0$
. In this case, since equation (3·12) implies
$k_1, k_2 \gt 0$
. In this case, since equation (3·12) implies
we obtain a contradiction by noticing
![]() $v_{\mathfrak{p}}(f_1(\alpha)) \gt 0$
and
$v_{\mathfrak{p}}(f_1(\alpha)) \gt 0$
and
![]() $v_{\mathfrak{p}}(f_2(\alpha)) \ge 0$
.
$v_{\mathfrak{p}}(f_2(\alpha)) \ge 0$
.
We now assume
![]() $k_1k_2\lt0$
. Moreover, we can assume
$k_1k_2\lt0$
. Moreover, we can assume
![]() $k_1\gt0$
and
$k_1\gt0$
and
![]() $k_2\lt0$
(similar discussion applies for
$k_2\lt0$
(similar discussion applies for
![]() $k_1\lt0$
and
$k_1\lt0$
and
![]() $k_2\gt0$
). Since
$k_2\gt0$
). Since
![]() $\gcd(k_1,k_2)=1$
, there exist integers s, t such that
$\gcd(k_1,k_2)=1$
, there exist integers s, t such that
Then, using (3·12), we have
 \begin{equation}\begin{split}& f_1(\alpha) = f_1(\alpha)^{sk_1 + tk_2} = \gamma^s (f_1(\alpha)^{-t}f_2(\alpha)^s)^{-k_2}, \\& f_2(\alpha) = f_2(\alpha)^{sk_1 + tk_2} = \gamma^t (f_1(\alpha)^{-t}f_2(\alpha)^s)^{k_1}.\end{split}\end{equation}
\begin{equation}\begin{split}& f_1(\alpha) = f_1(\alpha)^{sk_1 + tk_2} = \gamma^s (f_1(\alpha)^{-t}f_2(\alpha)^s)^{-k_2}, \\& f_2(\alpha) = f_2(\alpha)^{sk_1 + tk_2} = \gamma^t (f_1(\alpha)^{-t}f_2(\alpha)^s)^{k_1}.\end{split}\end{equation}
We note that, since
![]() $f_1(\alpha) \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}, \gamma \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
and
$f_1(\alpha) \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}, \gamma \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
and
![]() $-k_2\gt0$
, we have
$-k_2\gt0$
, we have
![]() $f_1(\alpha)^{-t}f_2(\alpha)^s \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
.
$f_1(\alpha)^{-t}f_2(\alpha)^s \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
.
If
![]() $f_1(\alpha)^{-t}f_2(\alpha)^s \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
, then by (3·13) we obtain that
$f_1(\alpha)^{-t}f_2(\alpha)^s \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
, then by (3·13) we obtain that
![]() $f_1(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
, which contradicts our assumption above. Thus,
$f_1(\alpha)\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
, which contradicts our assumption above. Thus,
![]() $f_1(\alpha)^{-t}f_2(\alpha)^s \not\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
. Then, by Lemma 2·6 (with
$f_1(\alpha)^{-t}f_2(\alpha)^s \not\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
. Then, by Lemma 2·6 (with
![]() $y=f_1(\alpha)^{-t}f_2(\alpha)^s$
and noticing
$y=f_1(\alpha)^{-t}f_2(\alpha)^s$
and noticing
![]() $\gamma \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
), the exponent
$\gamma \in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
), the exponent
![]() $-k_2$
is bounded above only in terms of
$-k_2$
is bounded above only in terms of
![]() $f_1, f_2, K, \Gamma$
and
$f_1, f_2, K, \Gamma$
and
![]() $\varepsilon$
. Similarly, we obtain that the exponent
$\varepsilon$
. Similarly, we obtain that the exponent
![]() $k_1$
is also bounded above only in terms of
$k_1$
is also bounded above only in terms of
![]() $f_1, f_2, K, \Gamma$
and
$f_1, f_2, K, \Gamma$
and
![]() $\varepsilon$
. Hence, in (3·12) there are only finitely many choices of the two exponents
$\varepsilon$
. Hence, in (3·12) there are only finitely many choices of the two exponents
![]() $k_1, k_2$
. Then, fixing
$k_1, k_2$
. Then, fixing
![]() $k_1, k_2$
and applying Lemma 2·2 to the rational function
$k_1, k_2$
and applying Lemma 2·2 to the rational function
![]() $f_1^{k_1}f_2^{k_2}$
, we obtain the desired finiteness result, where we need to use the assumption on
$f_1^{k_1}f_2^{k_2}$
, we obtain the desired finiteness result, where we need to use the assumption on
![]() $f_1$
and
$f_1$
and
![]() $f_2$
that they can not multiplicatively generate a power of a linear fractional function. This completes the proof of Case I.
$f_2$
that they can not multiplicatively generate a power of a linear fractional function. This completes the proof of Case I.
Case II:
![]() $\alpha \not\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
.
$\alpha \not\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}$
.
In this case, as in the proof of Theorem 1·1, we can choose a prime ideal
![]() ${\mathfrak{p}}$
of the ring of integers of K such that
${\mathfrak{p}}$
of the ring of integers of K such that
Let
![]() $d_i = \deg f_i, i =1, 2$
. Then, using the ultrametric inequality of non-Archimedean valuations and noticing (3·1), we directly have
$d_i = \deg f_i, i =1, 2$
. Then, using the ultrametric inequality of non-Archimedean valuations and noticing (3·1), we directly have
Considering valuations in (3·12) and using (3.14) we obtain (since
![]() $v_{\mathfrak{p}}(\gamma)=0$
due to
$v_{\mathfrak{p}}(\gamma)=0$
due to
![]() $\gamma\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
)
$\gamma\in O_{S_{{\textbf{f}},\Gamma,\varepsilon}}^*$
)
Since
![]() $\gcd(k_1,k_2)=1$
, this implies that
$\gcd(k_1,k_2)=1$
, this implies that
![]() $k_1 \mid d_2$
and
$k_1 \mid d_2$
and
![]() $k_2 \mid d_1$
. Thus we can assume that both
$k_2 \mid d_1$
. Thus we can assume that both
![]() $k_1$
and
$k_1$
and
![]() $k_2$
are fixed. Then, as in Case I, the desired finiteness result follows from Lemma 2·2. This completes the proof.
$k_2$
are fixed. Then, as in Case I, the desired finiteness result follows from Lemma 2·2. This completes the proof.
3.6. Proof of Theorem 1·6
The proof follows directly from Maurin’s result (that is, Lemma 2·3). Indeed, let r be the rank of
![]() $\Gamma$
modulo torsion and let
$\Gamma$
modulo torsion and let
![]() $g_1,\ldots,g_r \in \Gamma$
be its generators, and thus, they are multiplicatively independent elements. We define the parametric curve
$g_1,\ldots,g_r \in \Gamma$
be its generators, and thus, they are multiplicatively independent elements. We define the parametric curve
We choose
![]() $\varepsilon$
to be half of the size of the real
$\varepsilon$
to be half of the size of the real
![]() $\varepsilon$
from Lemma 2·3.
$\varepsilon$
from Lemma 2·3.
For an element
![]() $\alpha \in \Gamma^{\textrm{div}}_\varepsilon$
, assume that
$\alpha \in \Gamma^{\textrm{div}}_\varepsilon$
, assume that
![]() $f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
$f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
![]() $\Gamma^{\textrm{div}}_\varepsilon$
. Since
$\Gamma^{\textrm{div}}_\varepsilon$
. Since
![]() $\alpha \in \Gamma^{\textrm{div}}_\varepsilon$
, there exist a non-zero vector
$\alpha \in \Gamma^{\textrm{div}}_\varepsilon$
, there exist a non-zero vector
![]() $(k_0,\ldots,k_r)\in{\mathbb{Z}}^{r+1}$
,
$(k_0,\ldots,k_r)\in{\mathbb{Z}}^{r+1}$
,
![]() $k_0 \ne 0$
, such that
$k_0 \ne 0$
, such that
for some
![]() $\beta \in \overline{K}^*$
with
$\beta \in \overline{K}^*$
with
![]() $ {\textrm{h}}(\beta) \leq \varepsilon$
, implying that
$ {\textrm{h}}(\beta) \leq \varepsilon$
, implying that
Moreover, since
![]() $f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
$f_1(\alpha), \ldots, f_n(\alpha)$
are multiplicatively dependent modulo
![]() $\Gamma^{\textrm{div}}_\varepsilon$
, there exist some positive integer t and a non-zero vector
$\Gamma^{\textrm{div}}_\varepsilon$
, there exist some positive integer t and a non-zero vector
![]() $(\ell_1,\ldots,\ell_{n+r})\in{\mathbb{Z}}^{n+r}$
such that
$(\ell_1,\ldots,\ell_{n+r})\in{\mathbb{Z}}^{n+r}$
such that
for some
![]() $\gamma \in \overline{K}^*$
with
$\gamma \in \overline{K}^*$
with
![]() ${\textrm{h}}(\gamma) \leq \varepsilon$
, implying that (without loss of generality, we assume
${\textrm{h}}(\gamma) \leq \varepsilon$
, implying that (without loss of generality, we assume
![]() $\ell_1 \cdots \ell_n \ne 0$
)
$\ell_1 \cdots \ell_n \ne 0$
)
Therefore, the point
satisfies the multiplicative dependence relations (3.15) and (3.16), which have linearly independent vectors of exponents. Moreover,
 \begin{align*}&\left(\alpha,f_1(\alpha),\ldots,f_n(\alpha),g_1,\ldots,g_r\right)\\&=\left(\dfrac{\alpha}{\beta},\frac{f_1(\alpha)}{\gamma^{1/n\ell_1}},\ldots,\frac{f_n(\alpha)}{\gamma^{1/n\ell_n}},g_1,\ldots,g_r\right) \cdot (\beta,\gamma^{1/n\ell_1},\ldots ,\gamma^{1/n\ell_n},1,\ldots,1)\end{align*}
\begin{align*}&\left(\alpha,f_1(\alpha),\ldots,f_n(\alpha),g_1,\ldots,g_r\right)\\&=\left(\dfrac{\alpha}{\beta},\frac{f_1(\alpha)}{\gamma^{1/n\ell_1}},\ldots,\frac{f_n(\alpha)}{\gamma^{1/n\ell_n}},g_1,\ldots,g_r\right) \cdot (\beta,\gamma^{1/n\ell_1},\ldots ,\gamma^{1/n\ell_n},1,\ldots,1)\end{align*}
is a point on
![]() $\mathcal{C}$
with
$\mathcal{C}$
with
We also note that by assumption, the functions
![]() $X, f_1,\ldots,f_n,g_1,\ldots,g_r$
are multiplicatively independent. Hence, the desired result follows directly from Lemma 2·3.
$X, f_1,\ldots,f_n,g_1,\ldots,g_r$
are multiplicatively independent. Hence, the desired result follows directly from Lemma 2·3.
Acknowledgements
The authors are grateful to the referee for a careful reading of the manuscript and valuable comments. The research of Attila Bérczes was supported in part by grants K128088 and ANN130909 of the Hungarian National Foundation for Scientific Research and by the project EFOP-3.6.1-16-2016-00022 co-financed by the European Union and the European Social Fund. Kálmán Győry was supported in part by grants K128088 and ANN130909 of the Hungarian National Foundation for Scientific Research. Jorge Mello and Alina Ostafe were partially supported by the Australian Research Council Grants DP180100201 and DP200100355. Min Sha was supported by the Guangdong Basic and Applied Basic Research Foundation (No. 2022A1515012032) and also by the Australian Research Council Grant DE190100888. Alina Ostafe also gratefully acknowledges the generosity and hospitality of the Max Planck Institute for Mathematics where parts of her work on this project were developed.