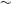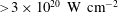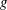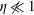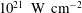1 Introduction
Radiation reaction is the effective recoil force on an accelerating charged particle caused by the particle emitting electromagnetic radiation. This effect will play an important role in laser–matter interactions at the intensities set to be reached by next generation high-intensity laser facilities (
![]() ${\gtrsim}10^{23}~\text{W}~\text{cm}^{-2}$
), where radiation reaction can lead to almost complete absorption of the laser pulse: Bashinov & Kim (Reference Bashinov and Kim2013) (using a classical theory) and Zhang, Ridgers & Thomas (Reference Zhang, Ridgers and Thomas2015) (including quantum corrections), have shown that radiation reaction gives an imaginary part in the dispersion relation for waves in a plasma. At intensities
${\gtrsim}10^{23}~\text{W}~\text{cm}^{-2}$
), where radiation reaction can lead to almost complete absorption of the laser pulse: Bashinov & Kim (Reference Bashinov and Kim2013) (using a classical theory) and Zhang, Ridgers & Thomas (Reference Zhang, Ridgers and Thomas2015) (including quantum corrections), have shown that radiation reaction gives an imaginary part in the dispersion relation for waves in a plasma. At intensities
![]() ${\gtrsim}10^{23}~\text{W}~\text{cm}^{-2}$
, plasma electrons will become sufficiently energetic that in their individual rest frames the electric field
${\gtrsim}10^{23}~\text{W}~\text{cm}^{-2}$
, plasma electrons will become sufficiently energetic that in their individual rest frames the electric field
![]() $E_{\text{RF}}$
approaches the critical field for quantum electrodynamics
$E_{\text{RF}}$
approaches the critical field for quantum electrodynamics
![]() $E_{\text{crit}}=1.38\times 10^{18}~\text{V}~\text{m}^{-1}$
(Heisenberg & Euler Reference Heisenberg and Euler1936). In this case, the emission of radiation by the electrons must be described in the framework of strong-field quantum electrodynamics (QED), using the Furry (Reference Furry1951) picture. Specifically, when the quantum efficiency parameter
$E_{\text{crit}}=1.38\times 10^{18}~\text{V}~\text{m}^{-1}$
(Heisenberg & Euler Reference Heisenberg and Euler1936). In this case, the emission of radiation by the electrons must be described in the framework of strong-field quantum electrodynamics (QED), using the Furry (Reference Furry1951) picture. Specifically, when the quantum efficiency parameter
![]() $\unicode[STIX]{x1D702}=E_{\text{RF}}/E_{\text{crit}}\gtrsim 0.1$
the radiation reaction force becomes stochastic (Duclous, Kirk & Bell Reference Duclous, Kirk and Bell2011) and electron’s dynamics is no longer well approximated by deterministic motion along a classical worldline (Shen & White Reference Shen and White1972).
$\unicode[STIX]{x1D702}=E_{\text{RF}}/E_{\text{crit}}\gtrsim 0.1$
the radiation reaction force becomes stochastic (Duclous, Kirk & Bell Reference Duclous, Kirk and Bell2011) and electron’s dynamics is no longer well approximated by deterministic motion along a classical worldline (Shen & White Reference Shen and White1972).
This quantum regime has been reached in experiments on the Super Proton Synchrotron at CERN in the interaction of
![]() ${\sim}$
100 GeV electrons with the strong fields of atoms in a crystal lattice, as described by Andersen et al. (Reference Andersen, Esberg, Knudsen, Thomsen, Uggerhøj, Sona, Mangiarotti, Ketel, Dizdar and Ballestrero2012), where the Gaunt factor for synchrotron emission was measured. The analogous process of nonlinear Compton scattering was studied experimentally at the Stanford Linear Accelerator (SLAC) in the interaction between an electron beam of energy
${\sim}$
100 GeV electrons with the strong fields of atoms in a crystal lattice, as described by Andersen et al. (Reference Andersen, Esberg, Knudsen, Thomsen, Uggerhøj, Sona, Mangiarotti, Ketel, Dizdar and Ballestrero2012), where the Gaunt factor for synchrotron emission was measured. The analogous process of nonlinear Compton scattering was studied experimentally at the Stanford Linear Accelerator (SLAC) in the interaction between an electron beam of energy
![]() $E=46.6$
GeV and a counter-propagating high intensity (
$E=46.6$
GeV and a counter-propagating high intensity (
![]() $10^{18}{-}10^{19}~\text{W}~\text{cm}^{-2}$
) laser pulse, as reported by Bula et al. (Reference Bula, McDonald, Prebys, Bamber, Boege, Kotseroglou, Melissinos, Meyerhofer, Ragg and Burke1996) (positron generation was also observed in this experiment – see Burke et al.
Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann and Bula1997). In this experiment the laser intensity was too low to access the very nonlinear regime of relevance to next generation laser–matter interactions, where
$10^{18}{-}10^{19}~\text{W}~\text{cm}^{-2}$
) laser pulse, as reported by Bula et al. (Reference Bula, McDonald, Prebys, Bamber, Boege, Kotseroglou, Melissinos, Meyerhofer, Ragg and Burke1996) (positron generation was also observed in this experiment – see Burke et al.
Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann and Bula1997). In this experiment the laser intensity was too low to access the very nonlinear regime of relevance to next generation laser–matter interactions, where
![]() $a_{0}\approx \sqrt{I\unicode[STIX]{x1D706}^{2}/10^{18}~\text{W}~\text{cm}^{-2}~\unicode[STIX]{x03BC}\text{m}^{2}}\gg 1$
(
$a_{0}\approx \sqrt{I\unicode[STIX]{x1D706}^{2}/10^{18}~\text{W}~\text{cm}^{-2}~\unicode[STIX]{x03BC}\text{m}^{2}}\gg 1$
(
![]() $\unicode[STIX]{x1D706}$
is the laser wavelength). This is now possible with current Petawatt laser systems, which can achieve focused intensities of
$\unicode[STIX]{x1D706}$
is the laser wavelength). This is now possible with current Petawatt laser systems, which can achieve focused intensities of
![]() $I>10^{21}~\text{W}~\text{cm}^{-2}$
. In the interaction of an electron beam with energy
$I>10^{21}~\text{W}~\text{cm}^{-2}$
. In the interaction of an electron beam with energy
![]() ${\mathcal{E}}$
with a counter-propagating laser pulse of intensity
${\mathcal{E}}$
with a counter-propagating laser pulse of intensity
![]() $I$
,
$I$
,
![]() $\unicode[STIX]{x1D702}$
can be estimated as
$\unicode[STIX]{x1D702}$
can be estimated as
![]() $\unicode[STIX]{x1D702}\sim 0.1({\mathcal{E}}/500~\text{MeV})\sqrt{I/10^{21}~\text{W}~\text{cm}^{-2}}$
. The quantum, nonlinear regime of Compton scattering and the resultant radiation reaction can therefore be studied by accelerating the electrons to energies greater than 500 MeV. Laser wakefield acceleration (Tajima & Dawson Reference Tajima and Dawson1979) is a technique that can generate monoenergetic, well collimated and ultra-relativistic electron beams (Faure et al.
Reference Faure, Glinec, Pukhov, Kiselev, Gordienko, Lefebvre, Rousseau, Burgy and Malka2004; Geddes et al.
Reference Geddes, Toth, van Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans2004; Mangles et al.
Reference Mangles, Murphy, Najmudin, Thomas, Collier, Dangor, Divall, Foster, Gallacher and Hooker2004). Recent experiments have now demonstrated energies approaching 5 GeV (Leemans et al.
Reference Leemans, Gonsalves, Mao, Nakamura, Benedetti, Schroeder, Tóth, Daniels, Mittelberger and Bulanov2014). Laser wakefield accelerators are ideal for studying electron-beam collisions with the tightly focused lasers required for studies of nonlinear Compton scattering due to the inherent synchronicity of the generated electron beam and the laser which allows precise overlap in space and time. Therefore, all-optical equivalents of the SLAC experiment are possible using PW lasers (Sokolov et al.
Reference Sokolov, Naumova, Nees and Mourou2010; Bulanov et al.
Reference Bulanov, Chen, Schroeder, Esarey, Leemans, Bulanov, Esirkepov, Kando, Koga and Zhidkov2012; Thomas et al.
Reference Thomas, Ridgers, Bulanov, Griffin and Mangles2012; Neitz & Di Piazza Reference Neitz and Di Piazza2013; Blackburn et al.
Reference Blackburn, Ridgers, Kirk and Bell2014; Vranic et al.
Reference Vranic, Martins, Vieira, Fonseca and Silva2014; Blackburn Reference Blackburn2015). Nonlinear Compton scattering at
$\unicode[STIX]{x1D702}\sim 0.1({\mathcal{E}}/500~\text{MeV})\sqrt{I/10^{21}~\text{W}~\text{cm}^{-2}}$
. The quantum, nonlinear regime of Compton scattering and the resultant radiation reaction can therefore be studied by accelerating the electrons to energies greater than 500 MeV. Laser wakefield acceleration (Tajima & Dawson Reference Tajima and Dawson1979) is a technique that can generate monoenergetic, well collimated and ultra-relativistic electron beams (Faure et al.
Reference Faure, Glinec, Pukhov, Kiselev, Gordienko, Lefebvre, Rousseau, Burgy and Malka2004; Geddes et al.
Reference Geddes, Toth, van Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans2004; Mangles et al.
Reference Mangles, Murphy, Najmudin, Thomas, Collier, Dangor, Divall, Foster, Gallacher and Hooker2004). Recent experiments have now demonstrated energies approaching 5 GeV (Leemans et al.
Reference Leemans, Gonsalves, Mao, Nakamura, Benedetti, Schroeder, Tóth, Daniels, Mittelberger and Bulanov2014). Laser wakefield accelerators are ideal for studying electron-beam collisions with the tightly focused lasers required for studies of nonlinear Compton scattering due to the inherent synchronicity of the generated electron beam and the laser which allows precise overlap in space and time. Therefore, all-optical equivalents of the SLAC experiment are possible using PW lasers (Sokolov et al.
Reference Sokolov, Naumova, Nees and Mourou2010; Bulanov et al.
Reference Bulanov, Chen, Schroeder, Esarey, Leemans, Bulanov, Esirkepov, Kando, Koga and Zhidkov2012; Thomas et al.
Reference Thomas, Ridgers, Bulanov, Griffin and Mangles2012; Neitz & Di Piazza Reference Neitz and Di Piazza2013; Blackburn et al.
Reference Blackburn, Ridgers, Kirk and Bell2014; Vranic et al.
Reference Vranic, Martins, Vieira, Fonseca and Silva2014; Blackburn Reference Blackburn2015). Nonlinear Compton scattering at
![]() $a_{0}\simeq 2$
(but not radiation reaction) was recently observed in such a set-up by Sarri et al. (Reference Sarri, Corvan, Schumaker, Cole, Di Piazza, Ahmed, Harvey, Keitel, Krushelnick and Mangles2014). Devising ways in which quantum effects on radiation reaction can be distinguished is therefore timely, as has been considered by Di Piazza, Hatsagortsyan & Keitel (Reference Di Piazza, Hatsagortsyan and Keitel2010), Neitz & Di Piazza (Reference Neitz and Di Piazza2013), Blackburn et al. (Reference Blackburn, Ridgers, Kirk and Bell2014), Vranic et al. (Reference Vranic, Grismayer, Fonseca and Silva2015), Wang, Yan & Zepf (Reference Wang, Yan and Zepf2015) and Harvey et al. (Reference Harvey, Gonoskov, Ilderton and Marklund2017).
$a_{0}\simeq 2$
(but not radiation reaction) was recently observed in such a set-up by Sarri et al. (Reference Sarri, Corvan, Schumaker, Cole, Di Piazza, Ahmed, Harvey, Keitel, Krushelnick and Mangles2014). Devising ways in which quantum effects on radiation reaction can be distinguished is therefore timely, as has been considered by Di Piazza, Hatsagortsyan & Keitel (Reference Di Piazza, Hatsagortsyan and Keitel2010), Neitz & Di Piazza (Reference Neitz and Di Piazza2013), Blackburn et al. (Reference Blackburn, Ridgers, Kirk and Bell2014), Vranic et al. (Reference Vranic, Grismayer, Fonseca and Silva2015), Wang, Yan & Zepf (Reference Wang, Yan and Zepf2015) and Harvey et al. (Reference Harvey, Gonoskov, Ilderton and Marklund2017).
To simplify the treatment of quantum radiation reaction, we use the quasi-classical approach described by Baĭer & Katkov (Reference Baĭer and Katkov1968). Here, we assume that the electromagnetic fields may be split into two types depending on their frequency scale. Fields varying on the scale of the laser frequency are treated as classical background fields. The photons emitted by the electrons on acceleration by these background fields, i.e. those responsible for the radiation reaction force, are treated in the framework of strong-field QED. These photons are of much higher energy (typically
![]() $h\unicode[STIX]{x1D708}\gtrsim$
MeV) than the laser photons (
$h\unicode[STIX]{x1D708}\gtrsim$
MeV) than the laser photons (
![]() $h\unicode[STIX]{x1D708}\sim$
eV). Two further simplifying approximations are made (see Kirk, Bell & Arka Reference Kirk, Bell and Arka2009). By making the quasi-static approximation we assume that the formation length of the hard photons is much smaller than the scale over which the background fields vary and thus the background fields may thus be treated as constant over the space–time interval during which the emission occurs. This approximation is valid for
$h\unicode[STIX]{x1D708}\sim$
eV). Two further simplifying approximations are made (see Kirk, Bell & Arka Reference Kirk, Bell and Arka2009). By making the quasi-static approximation we assume that the formation length of the hard photons is much smaller than the scale over which the background fields vary and thus the background fields may thus be treated as constant over the space–time interval during which the emission occurs. This approximation is valid for
![]() $a_{0}\gg 1$
, which is the case in high-intensity laser–matter interactions (Di Piazza et al.
Reference Di Piazza, Hatsagortsyan and Keitel2010 has shown that
$a_{0}\gg 1$
, which is the case in high-intensity laser–matter interactions (Di Piazza et al.
Reference Di Piazza, Hatsagortsyan and Keitel2010 has shown that
![]() $a_{0}\gtrsim 10$
is sufficient). By making the weak-field approximation, we assume that the emission rate of photons depends entirely on
$a_{0}\gtrsim 10$
is sufficient). By making the weak-field approximation, we assume that the emission rate of photons depends entirely on
![]() $\unicode[STIX]{x1D702}$
and not the field invariants
$\unicode[STIX]{x1D702}$
and not the field invariants
![]() ${\mathcal{F}}=(E^{2}-c^{2}B^{2})/E_{\text{crit}}^{2}$
and
${\mathcal{F}}=(E^{2}-c^{2}B^{2})/E_{\text{crit}}^{2}$
and
![]() ${\mathcal{G}}=c\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}/E_{\text{crit}}^{2}$
. This is valid if these invariants are much smaller than
${\mathcal{G}}=c\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}/E_{\text{crit}}^{2}$
. This is valid if these invariants are much smaller than
![]() $\unicode[STIX]{x1D702}$
. For next generation laser–matter interactions
$\unicode[STIX]{x1D702}$
. For next generation laser–matter interactions
![]() $E,cB\lesssim 10^{-3}E_{\text{crit}}$
, so this approximation is also reasonable. The weak-field approximation allows us to assume that the rate of photon emission (and the energy spectrum of the emitted photons) is well described by the well-known rate in an equivalent set of constant fields as given in Ritus (Reference Ritus1985) (for constant crossed electric and magnetic fields) and Erber (Reference Erber1966) (for a constant magnetic field). The accuracy of this quasi-classical approach has recently been demonstrated by comparison to full QED calculations for the electron energies and laser intensities considered here by Dinu et al. (Reference Dinu, Harvey, Ilderton, Marklund and Torgrimsson2016).
$E,cB\lesssim 10^{-3}E_{\text{crit}}$
, so this approximation is also reasonable. The weak-field approximation allows us to assume that the rate of photon emission (and the energy spectrum of the emitted photons) is well described by the well-known rate in an equivalent set of constant fields as given in Ritus (Reference Ritus1985) (for constant crossed electric and magnetic fields) and Erber (Reference Erber1966) (for a constant magnetic field). The accuracy of this quasi-classical approach has recently been demonstrated by comparison to full QED calculations for the electron energies and laser intensities considered here by Dinu et al. (Reference Dinu, Harvey, Ilderton, Marklund and Torgrimsson2016).
Using this quasi-classical model (making the quasi-static and weak-field approximations), it is possible to include the quantum radiation reaction force in a kinetic equation describing the evolution of the electron distribution, as given by Shen & White (Reference Shen and White1972), Sokolov et al. (Reference Sokolov, Naumova, Nees and Mourou2010), Elkina et al. (Reference Elkina, Fedotov, Kostyukov, Legkov, Narozhny, Nerush and Ruhl2011), Neitz & Di Piazza (Reference Neitz and Di Piazza2013) and Ridgers et al. (Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell2014). Although this equation has been solved numerically using a Monte Carlo algorithm (see Duclous et al.
Reference Duclous, Kirk and Bell2011; Elkina et al.
Reference Elkina, Fedotov, Kostyukov, Legkov, Narozhny, Nerush and Ruhl2011; Ridgers et al.
Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell2014; Gonoskov et al.
Reference Gonoskov, Bastrakov, Efimenko, Ilderton, Marklund, Meyerov, Muraviev, Sergeev, Surmin and Wallin2015) it has not been solved analytically for even the simplest configuration of electromagnetic fields (for example a uniform, static magnetic field as in Shen & White Reference Shen and White1972). On the other hand, the electron equation of motion containing a classical model of radiation reaction, using the prescription of Landau & Lifshitz (Landau & Lifshitz (Reference Landau and Lifshitz1987) – shown to be consistent with the classical limit of strong-field QED by Krivitskii & Tsytovich (Reference Krivitskii and Tsytovich1991), Ilderton & Torgrimsson (Reference Ilderton and Torgrimsson2013)), has been solved analytically in several cases for example: for electron motion in a rotating electric field (by Bell & Kirk Reference Bell and Kirk2008) and a plane electromagnetic wave (by DiPiazza Reference DiPiazza2008). A modified classical model, where the radiated power is reduced by the Gaunt factor, has been used to derive the dispersion relation for an electromagnetic wave moving through a plasma where the electrons experience significant radiation reaction by Zhang et al. (Reference Zhang, Ridgers and Thomas2015) (and the equivalent classical result by Bashinov & Kim Reference Bashinov and Kim2013). The kinetic equation can be used to show that the modified classical model of radiation reaction is sufficient to describe the average energy loss of the electrons (Ridgers et al.
Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell2014). In addition, the kinetic equation can give insight into which observables can be used to measure various aspects of quantum radiation reaction. Here we show that the measurements of the average energy loss can be used to measure the Gaunt factor associated with the emission and that the evolution of the variance of the electron energy distribution can be used to measure the degree of stochasticity of the emission. To do the latter, we derive an equation of motion for the variance, which extends the results of Vranic et al. (Reference Vranic, Grismayer, Fonseca and Silva2015) to arbitrary
![]() $\unicode[STIX]{x1D702}$
.
$\unicode[STIX]{x1D702}$
.
2 Radiation reaction models
In this section we describe the radiation reaction models considered here: (i) classical – using the ultra-relativistic form of the Landau and Lifshitz prescription; (ii) modified classical – as the classical model but including a function describing the reduction in the power radiated due to quantum effects, the Gaunt factor
![]() $g$
(Baier, Katkov & Strakhovenko Reference Baier, Katkov and Strakhovenko1991); (iii) stochastic – a probabilistic treatment of the emission consistent with the approximations made in the quantum emission model described above and in more detail by Ridgers et al. (Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell2014). The stochastic model is the most physical as it includes both the important quantum effects (the Gaunt factor and quantum stochasticity).
$g$
(Baier, Katkov & Strakhovenko Reference Baier, Katkov and Strakhovenko1991); (iii) stochastic – a probabilistic treatment of the emission consistent with the approximations made in the quantum emission model described above and in more detail by Ridgers et al. (Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell2014). The stochastic model is the most physical as it includes both the important quantum effects (the Gaunt factor and quantum stochasticity).
Using the quasi-classical approach we may write the evolution of the electron distribution function, including the radiation reaction force, as
![]() $fd^{3}\boldsymbol{x}d^{3}\boldsymbol{p}$
is the number of electrons at position
$fd^{3}\boldsymbol{x}d^{3}\boldsymbol{p}$
is the number of electrons at position
![]() $\boldsymbol{x}$
with momentum
$\boldsymbol{x}$
with momentum
![]() $\boldsymbol{p}$
(velocity
$\boldsymbol{p}$
(velocity
![]() $\boldsymbol{v}$
).
$\boldsymbol{v}$
).
![]() $\boldsymbol{E}$
and
$\boldsymbol{E}$
and
![]() $\boldsymbol{B}$
are the low frequency classical background electromagnetic fields.
$\boldsymbol{B}$
are the low frequency classical background electromagnetic fields.
![]() $(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}t)_{\text{em}}^{X}$
is an operator describing how recoil from photon emission affects the electron distribution function – we will refer to this as the emission operator. The superscript
$(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}t)_{\text{em}}^{X}$
is an operator describing how recoil from photon emission affects the electron distribution function – we will refer to this as the emission operator. The superscript
![]() $X$
denotes which of the classical (
$X$
denotes which of the classical (
![]() $cl$
), modified classical (
$cl$
), modified classical (
![]() $\mathit{mod}~cl$
) and stochastic (
$\mathit{mod}~cl$
) and stochastic (
![]() $st$
) models is under consideration.
$st$
) models is under consideration.
Note that we are neglecting pair production by the emitted gamma-ray photons in the background electromagnetic fields. This is reasonable in the moderately quantum regime described by Di Piazza et al. (Reference Di Piazza, Hatsagortsyan and Keitel2010), i.e. where
![]() $\unicode[STIX]{x1D702}\sim 0.1$
.
$\unicode[STIX]{x1D702}\sim 0.1$
.
2.1 Classical and modified classical emission operators
If the radiating electron is ultra-relativistic with
![]() $\unicode[STIX]{x1D6FE}\gg 1$
, we may assume that all photons are emitted in the direction of the electron’s instantaneous velocity (Duclous et al.
Reference Duclous, Kirk and Bell2011). Using the Landau and Lifshitz prescription for radiation reaction (in the ultra-relativistic limit – Landau & Lifshitz Reference Landau and Lifshitz1987) the classical and modified classical emission operators should describe radiation reaction forces of the form
$\unicode[STIX]{x1D6FE}\gg 1$
, we may assume that all photons are emitted in the direction of the electron’s instantaneous velocity (Duclous et al.
Reference Duclous, Kirk and Bell2011). Using the Landau and Lifshitz prescription for radiation reaction (in the ultra-relativistic limit – Landau & Lifshitz Reference Landau and Lifshitz1987) the classical and modified classical emission operators should describe radiation reaction forces of the form
respectively. Here
![]() $g(\unicode[STIX]{x1D702})$
is the Gaunt factor for synchrotron emission, i.e. a function that gives the reduction in the radiated power
$g(\unicode[STIX]{x1D702})$
is the Gaunt factor for synchrotron emission, i.e. a function that gives the reduction in the radiated power
![]() $P_{\text{cl}}$
due to quantum modifications to the synchrotron spectrum.
$P_{\text{cl}}$
due to quantum modifications to the synchrotron spectrum.
![]() $P_{\text{cl}}$
is parameterised in terms of
$P_{\text{cl}}$
is parameterised in terms of
![]() $\unicode[STIX]{x1D702}$
as
$\unicode[STIX]{x1D702}$
as
where
![]() $\unicode[STIX]{x1D6FC}_{f}$
is the fine-structure constant,
$\unicode[STIX]{x1D6FC}_{f}$
is the fine-structure constant,
![]() $\unicode[STIX]{x1D706}_{c}$
is the reduced Compton wavelength and
$\unicode[STIX]{x1D706}_{c}$
is the reduced Compton wavelength and
![]() $g(\unicode[STIX]{x1D702})$
is defined as
$g(\unicode[STIX]{x1D702})$
is defined as
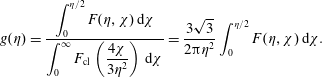 $$\begin{eqnarray}g(\unicode[STIX]{x1D702})=\frac{\displaystyle \int _{0}^{\unicode[STIX]{x1D702}/2}F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})\,\text{d}\unicode[STIX]{x1D712}}{\displaystyle \int _{0}^{\infty }F_{\text{cl}}\left({\displaystyle \frac{4\unicode[STIX]{x1D712}}{3\unicode[STIX]{x1D702}^{2}}}\right)\,\text{d}\unicode[STIX]{x1D712}}=\frac{3\sqrt{3}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D702}^{2}}\int _{0}^{\unicode[STIX]{x1D702}/2}F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})\,\text{d}\unicode[STIX]{x1D712}.\end{eqnarray}$$
$$\begin{eqnarray}g(\unicode[STIX]{x1D702})=\frac{\displaystyle \int _{0}^{\unicode[STIX]{x1D702}/2}F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})\,\text{d}\unicode[STIX]{x1D712}}{\displaystyle \int _{0}^{\infty }F_{\text{cl}}\left({\displaystyle \frac{4\unicode[STIX]{x1D712}}{3\unicode[STIX]{x1D702}^{2}}}\right)\,\text{d}\unicode[STIX]{x1D712}}=\frac{3\sqrt{3}}{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D702}^{2}}\int _{0}^{\unicode[STIX]{x1D702}/2}F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})\,\text{d}\unicode[STIX]{x1D712}.\end{eqnarray}$$
![]() $F_{\text{cl}}$
and
$F_{\text{cl}}$
and
![]() $F$
are the classical and quantum synchrotron spectra respectively. For completeness their forms are given in appendix A. An accurate fit to this function is
$F$
are the classical and quantum synchrotron spectra respectively. For completeness their forms are given in appendix A. An accurate fit to this function is
![]() $g(\unicode[STIX]{x1D702})\approx [1+4.8(1+\unicode[STIX]{x1D702})\ln (1+1.7\unicode[STIX]{x1D702})+2.44\unicode[STIX]{x1D702}^{2}]^{-2/3}$
(Baier et al.
Reference Baier, Katkov and Strakhovenko1991).
$g(\unicode[STIX]{x1D702})\approx [1+4.8(1+\unicode[STIX]{x1D702})\ln (1+1.7\unicode[STIX]{x1D702})+2.44\unicode[STIX]{x1D702}^{2}]^{-2/3}$
(Baier et al.
Reference Baier, Katkov and Strakhovenko1991).
The emission operators which yield radiation reaction forces as given in (2.2), as shown in § 3, are
2.2 Stochastic emission operator
The stochastic emission operator should consist of two terms: a term describing the movement of electrons out of a given region of phase space due to emission and a term describing electrons moving into the region under consideration by leaving regions of higher energy as they emit. Assuming the electrons are ultra-relativistic and so photon emission is in the direction of propagation of the electron, we may formulate this as
We define
![]() $\unicode[STIX]{x1D702}\equiv \unicode[STIX]{x1D6FE}b$
. For
$\unicode[STIX]{x1D702}\equiv \unicode[STIX]{x1D6FE}b$
. For
![]() $\unicode[STIX]{x1D6FE}\gg 1$
, we may take
$\unicode[STIX]{x1D6FE}\gg 1$
, we may take
![]() $b=|\boldsymbol{E}_{\bot }+\boldsymbol{v}\times \boldsymbol{B}|/E_{s}$
.
$b=|\boldsymbol{E}_{\bot }+\boldsymbol{v}\times \boldsymbol{B}|/E_{s}$
.
![]() $\unicode[STIX]{x1D712}=(h\unicode[STIX]{x1D708}b)/(2m_{e}c^{2})$
is the quantum efficiency parameter for an emitted photon (with energy
$\unicode[STIX]{x1D712}=(h\unicode[STIX]{x1D708}b)/(2m_{e}c^{2})$
is the quantum efficiency parameter for an emitted photon (with energy
![]() $h\unicode[STIX]{x1D708}$
). The explicit form of the photon emission rate
$h\unicode[STIX]{x1D708}$
). The explicit form of the photon emission rate
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}$
and the probability
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}$
and the probability
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712}}\,\text{d}\unicode[STIX]{x1D712}$
that an electron with energy parameterised by
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712}}\,\text{d}\unicode[STIX]{x1D712}$
that an electron with energy parameterised by
![]() $\unicode[STIX]{x1D702}$
emits a gamma-ray photon with energy parameterised by
$\unicode[STIX]{x1D702}$
emits a gamma-ray photon with energy parameterised by
![]() $\unicode[STIX]{x1D712}$
are given in appendix A.
$\unicode[STIX]{x1D712}$
are given in appendix A.
3 Moment equations
The average over the distribution function
![]() $f$
of a momentum dependent quantity
$f$
of a momentum dependent quantity
![]() $\unicode[STIX]{x1D713}(\boldsymbol{p})$
is defined as
$\unicode[STIX]{x1D713}(\boldsymbol{p})$
is defined as
where
![]() $n_{e}$
is the electron number density.
$n_{e}$
is the electron number density.
3.1 The temporal evolution of
 $\langle \,\boldsymbol{p}\rangle$
$\langle \,\boldsymbol{p}\rangle$
The equation for the evolution of the expectation value of the momentum of the electron population
![]() $\langle \,\boldsymbol{p}\rangle$
has been derived previously by Elkina et al. (Reference Elkina, Fedotov, Kostyukov, Legkov, Narozhny, Nerush and Ruhl2011). The equation for the evolution of the average energy
$\langle \,\boldsymbol{p}\rangle$
has been derived previously by Elkina et al. (Reference Elkina, Fedotov, Kostyukov, Legkov, Narozhny, Nerush and Ruhl2011). The equation for the evolution of the average energy
![]() $\langle \unicode[STIX]{x1D6FE}\rangle$
of the population has been derived by Ridgers et al. (Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell2014):
$\langle \unicode[STIX]{x1D6FE}\rangle$
of the population has been derived by Ridgers et al. (Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell2014):
In appendix B we show how this equation can be derived by taking the first moment of the stochastic emission operator in (2.6).
Taking the first moment of the classical and modified classical emission operators given in (2.5), as detailed in appendix B, yields
3.2 The temporal evolution of
 $\unicode[STIX]{x1D70E}^{2}$
$\unicode[STIX]{x1D70E}^{2}$
Following the derivation in appendix B we can obtain the following equation for the evolution of the variance
![]() $\unicode[STIX]{x1D70E}^{2}$
in the Lorentz factor
$\unicode[STIX]{x1D70E}^{2}$
in the Lorentz factor
![]() $\unicode[STIX]{x1D6FE}$
of the electron distribution:
$\unicode[STIX]{x1D6FE}$
of the electron distribution:
![]() $\unicode[STIX]{x1D70E}^{2}=\langle \unicode[STIX]{x1D6FE}^{2}\rangle -\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
and
$\unicode[STIX]{x1D70E}^{2}=\langle \unicode[STIX]{x1D6FE}^{2}\rangle -\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}-\langle \unicode[STIX]{x1D6FE}\rangle$
. The first term in (3.4), which we label
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}-\langle \unicode[STIX]{x1D6FE}\rangle$
. The first term in (3.4), which we label
![]() $T_{-}$
, always acts to reduce the variance. It arises because higher energy electrons radiate more energy than those at lower energy. This term can be written
$T_{-}$
, always acts to reduce the variance. It arises because higher energy electrons radiate more energy than those at lower energy. This term can be written
![]() $T_{-}=(2/m_{e}c^{2})[\langle \unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}P_{\text{cl}}\rangle -\langle (1-g)\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}P_{\text{cl}}\rangle ]$
, where the first term is purely classical and the second shows that quantum effects reduce the rate of decrease of the variance by reducing the power radiated below the classical prediction (
$T_{-}=(2/m_{e}c^{2})[\langle \unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}P_{\text{cl}}\rangle -\langle (1-g)\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}P_{\text{cl}}\rangle ]$
, where the first term is purely classical and the second shows that quantum effects reduce the rate of decrease of the variance by reducing the power radiated below the classical prediction (
![]() $g\leqslant 1$
). The second term in (3.4)
$g\leqslant 1$
). The second term in (3.4)
![]() $T_{+}$
represents stochastic effects, is positive and so tends to increase the variance. The competition between these two terms determines whether the emission operator causes
$T_{+}$
represents stochastic effects, is positive and so tends to increase the variance. The competition between these two terms determines whether the emission operator causes
![]() $\unicode[STIX]{x1D70E}^{2}(t)$
to increase or decrease.
$\unicode[STIX]{x1D70E}^{2}(t)$
to increase or decrease.
The function
![]() $S(\unicode[STIX]{x1D702})$
is given by
$S(\unicode[STIX]{x1D702})$
is given by
![]() $g_{2}(\unicode[STIX]{x1D702})$
, which is analogous to
$g_{2}(\unicode[STIX]{x1D702})$
, which is analogous to
![]() $g(\unicode[STIX]{x1D702})$
, is defined as
$g(\unicode[STIX]{x1D702})$
, is defined as
 $$\begin{eqnarray}g_{2}(\unicode[STIX]{x1D702})=\frac{\displaystyle \int _{0}^{\unicode[STIX]{x1D702}/2}\unicode[STIX]{x1D712}F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})\,\text{d}\unicode[STIX]{x1D712}}{\displaystyle \int _{0}^{\infty }\unicode[STIX]{x1D712}F_{\text{cl}}\left({\displaystyle \frac{4\unicode[STIX]{x1D712}}{3\unicode[STIX]{x1D702}^{2}}}\right)\text{d}\unicode[STIX]{x1D712}}=\frac{144}{55\unicode[STIX]{x03C0}\unicode[STIX]{x1D702}^{4}}\int _{0}^{\unicode[STIX]{x1D702}/2}\unicode[STIX]{x1D712}F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})\,\text{d}\unicode[STIX]{x1D712}.\end{eqnarray}$$
$$\begin{eqnarray}g_{2}(\unicode[STIX]{x1D702})=\frac{\displaystyle \int _{0}^{\unicode[STIX]{x1D702}/2}\unicode[STIX]{x1D712}F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})\,\text{d}\unicode[STIX]{x1D712}}{\displaystyle \int _{0}^{\infty }\unicode[STIX]{x1D712}F_{\text{cl}}\left({\displaystyle \frac{4\unicode[STIX]{x1D712}}{3\unicode[STIX]{x1D702}^{2}}}\right)\text{d}\unicode[STIX]{x1D712}}=\frac{144}{55\unicode[STIX]{x03C0}\unicode[STIX]{x1D702}^{4}}\int _{0}^{\unicode[STIX]{x1D702}/2}\unicode[STIX]{x1D712}F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})\,\text{d}\unicode[STIX]{x1D712}.\end{eqnarray}$$
As for
![]() $g$
, it is useful to find an accurate fit to
$g$
, it is useful to find an accurate fit to
![]() $g_{2}$
. We find the following
$g_{2}$
. We find the following
![]() $g_{2}(\unicode[STIX]{x1D702})\approx [1+(1+4.528\unicode[STIX]{x1D702})\ln (1+12.29\unicode[STIX]{x1D702})+4.632\unicode[STIX]{x1D702}^{2}]^{-7/6}$
. This gives the correct limits for
$g_{2}(\unicode[STIX]{x1D702})\approx [1+(1+4.528\unicode[STIX]{x1D702})\ln (1+12.29\unicode[STIX]{x1D702})+4.632\unicode[STIX]{x1D702}^{2}]^{-7/6}$
. This gives the correct limits for
![]() $\unicode[STIX]{x1D702}\ll 1$
and
$\unicode[STIX]{x1D702}\ll 1$
and
![]() $\unicode[STIX]{x1D702}\gg 1$
(
$\unicode[STIX]{x1D702}\gg 1$
(
![]() $g_{2}\approx 1$
and
$g_{2}\approx 1$
and
![]() $g_{2}\approx 0.167\unicode[STIX]{x1D702}^{-7/3}$
respectively).
$g_{2}\approx 0.167\unicode[STIX]{x1D702}^{-7/3}$
respectively).
![]() $g_{2}$
, as a function of
$g_{2}$
, as a function of
![]() $\unicode[STIX]{x1D702}$
, along with the fit are shown in figure 1.
$\unicode[STIX]{x1D702}$
, along with the fit are shown in figure 1.

Figure 1.
![]() $g_{2}(\unicode[STIX]{x1D702})$
(solid line) and the fit used here (dashed line).
$g_{2}(\unicode[STIX]{x1D702})$
(solid line) and the fit used here (dashed line).
We may also derive the corresponding expressions for
![]() $\text{d}\unicode[STIX]{x1D70E}^{2}/\text{d}t$
from the classical and modified classical emission operators in (2.5) (the derivation is given in appendix B).
$\text{d}\unicode[STIX]{x1D70E}^{2}/\text{d}t$
from the classical and modified classical emission operators in (2.5) (the derivation is given in appendix B).
We now consider the specific case where a high energy electron beam with Gaussian energy distribution collides with a plane electromagnetic wave. In the limit where
![]() $\unicode[STIX]{x1D702}\ll 1$
and the energy distribution is Gaussian with
$\unicode[STIX]{x1D702}\ll 1$
and the energy distribution is Gaussian with
![]() $\unicode[STIX]{x1D70E}\ll \langle \unicode[STIX]{x1D6FE}\rangle$
(and assumed to be a Gaussian at all times), equation (3.4) reduces to
$\unicode[STIX]{x1D70E}\ll \langle \unicode[STIX]{x1D6FE}\rangle$
(and assumed to be a Gaussian at all times), equation (3.4) reduces to
which reproduces Vranic et al. (Reference Vranic, Grismayer, Fonseca and Silva2015, equation (14)).
4 Comparison to QED-PIC simulations
To test the validity of the expression for the evolution of
![]() $\unicode[STIX]{x1D70E}^{2}$
given above we have simulated the interaction of an electron beam with a counter-propagating circularly polarised plane wave using the QED-Particle-in-Cell (PIC) code EPOCH (Arber et al.
Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz and Bell2015). EPOCH includes the stochastic emission model using a Monte Carlo algorithm (described in detail by Ridgers et al.
Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell2014). For this work we have extended the code to include the classical and modified classical emission operators by directly solving (2.2) using first-order Eulerian integration.
$\unicode[STIX]{x1D70E}^{2}$
given above we have simulated the interaction of an electron beam with a counter-propagating circularly polarised plane wave using the QED-Particle-in-Cell (PIC) code EPOCH (Arber et al.
Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz and Bell2015). EPOCH includes the stochastic emission model using a Monte Carlo algorithm (described in detail by Ridgers et al.
Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell2014). For this work we have extended the code to include the classical and modified classical emission operators by directly solving (2.2) using first-order Eulerian integration.

Figure 2. Electron energy distribution, 10.5 fs after collision of the electron bunch with the laser pulse, compared to initial distribution using the stochastic, modified classical and classical emission operators.
The simulation parameters were as follows. The laser pulse had peak intensity
![]() $10^{21}~\text{W}~\text{cm}^{-2}$
, wavelength
$10^{21}~\text{W}~\text{cm}^{-2}$
, wavelength
![]() $1~\unicode[STIX]{x03BC}\text{m}$
and a half-Gaussian temporal profile (rise time 1 fs). Four thousand grid cells were used to discretise a spatial domain extending from
$1~\unicode[STIX]{x03BC}\text{m}$
and a half-Gaussian temporal profile (rise time 1 fs). Four thousand grid cells were used to discretise a spatial domain extending from
![]() $-40~\unicode[STIX]{x03BC}\text{m}$
to
$-40~\unicode[STIX]{x03BC}\text{m}$
to
![]() $40~\unicode[STIX]{x03BC}\text{m}$
and
$40~\unicode[STIX]{x03BC}\text{m}$
and
![]() $10^{5}$
macroparticles were used to represent an electron bunch consisting of
$10^{5}$
macroparticles were used to represent an electron bunch consisting of
![]() $10^{9}$
electrons. The electron bunch had a Gaussian spatial profile, centred on
$10^{9}$
electrons. The electron bunch had a Gaussian spatial profile, centred on
![]() $39.7~\unicode[STIX]{x03BC}\text{m}$
, with a full width at half maximum (FWHM) of
$39.7~\unicode[STIX]{x03BC}\text{m}$
, with a full width at half maximum (FWHM) of
![]() $0.17~\unicode[STIX]{x03BC}\text{m}$
and had initial distribution
$0.17~\unicode[STIX]{x03BC}\text{m}$
and had initial distribution
![]() $f(\boldsymbol{x},\boldsymbol{p},t=0)=[n_{e}(\boldsymbol{x})/(\sqrt{2\unicode[STIX]{x03C0}}\unicode[STIX]{x1D70E})]\unicode[STIX]{x1D6FF}(p_{y})\unicode[STIX]{x1D6FF}(p_{z})\exp [-(p_{x}+\unicode[STIX]{x1D6FE}_{0}m_{e}c)^{2}/(2\unicode[STIX]{x1D70E}^{2})]$
where
$f(\boldsymbol{x},\boldsymbol{p},t=0)=[n_{e}(\boldsymbol{x})/(\sqrt{2\unicode[STIX]{x03C0}}\unicode[STIX]{x1D70E})]\unicode[STIX]{x1D6FF}(p_{y})\unicode[STIX]{x1D6FF}(p_{z})\exp [-(p_{x}+\unicode[STIX]{x1D6FE}_{0}m_{e}c)^{2}/(2\unicode[STIX]{x1D70E}^{2})]$
where
![]() $\boldsymbol{p}=(p_{x},p_{y},p_{z})$
is the momentum coordinate in phase space and
$\boldsymbol{p}=(p_{x},p_{y},p_{z})$
is the momentum coordinate in phase space and
![]() $n_{e}$
the number density of electrons in the beam.
$n_{e}$
the number density of electrons in the beam.
![]() $\unicode[STIX]{x1D6FE}_{0}$
was the initial average energy of the bunch.
$\unicode[STIX]{x1D6FE}_{0}$
was the initial average energy of the bunch.
Figure 2 shows a comparison of the spatially integrated electron energy distribution using classical, modified classical and stochastic emission operators with the initial spectrum
![]() $t=10.5$
fs after the collision. We see that the modified classical and classical emission operators both give a decrease in the variance of the electron distribution whereas the stochastic emission operator gives an increase in the variance. Figure 3 shows the temporal evolution of the mean Lorentz factor
$t=10.5$
fs after the collision. We see that the modified classical and classical emission operators both give a decrease in the variance of the electron distribution whereas the stochastic emission operator gives an increase in the variance. Figure 3 shows the temporal evolution of the mean Lorentz factor
![]() $\langle \unicode[STIX]{x1D6FE}\rangle$
and the standard deviation of the Lorentz factor
$\langle \unicode[STIX]{x1D6FE}\rangle$
and the standard deviation of the Lorentz factor
![]() $\unicode[STIX]{x1D70E}$
. The QED-PIC simulations demonstrate the validity of (3.2)–(3.7).
$\unicode[STIX]{x1D70E}$
. The QED-PIC simulations demonstrate the validity of (3.2)–(3.7).
We saw earlier in (3.4) that the evolution of the variance is governed by the competition between
![]() $T_{-}$
and
$T_{-}$
and
![]() $T_{+}$
. To characterise which of these terms is dominant (in a similar way to Vranic et al.
Reference Vranic, Grismayer, Fonseca and Silva2015), and thereby how stochastic quantum effects (prevalent when
$T_{+}$
. To characterise which of these terms is dominant (in a similar way to Vranic et al.
Reference Vranic, Grismayer, Fonseca and Silva2015), and thereby how stochastic quantum effects (prevalent when
![]() $T_{+}$
dominates), may be measured in a colliding beams experiment, we derive an analytical expression their ratio
$T_{+}$
dominates), may be measured in a colliding beams experiment, we derive an analytical expression their ratio
![]() $\unicode[STIX]{x1D709}$
:
$\unicode[STIX]{x1D709}$
:
Considering an electron bunch whose initial distribution is
![]() $f(\boldsymbol{x},p_{x},t=0)=n_{e}(\boldsymbol{x})/(2W\unicode[STIX]{x1D6FE}_{0}m_{e}c)\unicode[STIX]{x1D6FF}(p_{y})\unicode[STIX]{x1D6FF}(p_{z})$
for
$f(\boldsymbol{x},p_{x},t=0)=n_{e}(\boldsymbol{x})/(2W\unicode[STIX]{x1D6FE}_{0}m_{e}c)\unicode[STIX]{x1D6FF}(p_{y})\unicode[STIX]{x1D6FF}(p_{z})$
for
![]() $\unicode[STIX]{x1D6FE}_{0}m_{e}c(1-W)<|p_{x}|<\unicode[STIX]{x1D6FE}_{0}m_{e}c(1+W)$
and assuming
$\unicode[STIX]{x1D6FE}_{0}m_{e}c(1-W)<|p_{x}|<\unicode[STIX]{x1D6FE}_{0}m_{e}c(1+W)$
and assuming
![]() $g=g_{2}=1$
, we obtain (as outlined in appendix C)
$g=g_{2}=1$
, we obtain (as outlined in appendix C)
where
![]() $\unicode[STIX]{x1D709}$
is the ratio
$\unicode[STIX]{x1D709}$
is the ratio
![]() $T_{+}/T_{-}$
when the electron bunch first collides with the laser pulse (i.e. before the distribution
$T_{+}/T_{-}$
when the electron bunch first collides with the laser pulse (i.e. before the distribution
![]() $f$
has evolved under the action of radiation reaction) and
$f$
has evolved under the action of radiation reaction) and
![]() $\unicode[STIX]{x1D702}_{0}=\unicode[STIX]{x1D6FE}_{0}b$
. As the variance increases and the expectation value of the
$\unicode[STIX]{x1D702}_{0}=\unicode[STIX]{x1D6FE}_{0}b$
. As the variance increases and the expectation value of the
![]() $\unicode[STIX]{x1D6FE}$
decreases we expect
$\unicode[STIX]{x1D6FE}$
decreases we expect
![]() $T_{-}$
to eventually become dominant and so we would expect the variance to peak and then decrease after some time. This behaviour is clearly seen in the results from the simulation using the stochastic emission operator shown in figure 3. Therefore, we define
$T_{-}$
to eventually become dominant and so we would expect the variance to peak and then decrease after some time. This behaviour is clearly seen in the results from the simulation using the stochastic emission operator shown in figure 3. Therefore, we define
![]() $T_{+}$
as being important for
$T_{+}$
as being important for
![]() $\unicode[STIX]{x1D709}>2$
initially in order to compensate for the increased importance of
$\unicode[STIX]{x1D709}>2$
initially in order to compensate for the increased importance of
![]() $T_{-}$
at later times. In the case where the width of the electron distribution is equal to the mean,
$T_{-}$
at later times. In the case where the width of the electron distribution is equal to the mean,
![]() $W=0.5$
, equation (4.2) shows that
$W=0.5$
, equation (4.2) shows that
![]() $\unicode[STIX]{x1D702}_{0}>0.2$
is required for
$\unicode[STIX]{x1D702}_{0}>0.2$
is required for
![]() $\unicode[STIX]{x1D709}>2$
. For a narrow electron distribution,
$\unicode[STIX]{x1D709}>2$
. For a narrow electron distribution,
![]() $W\ll 1$
,
$W\ll 1$
,
![]() $\unicode[STIX]{x1D702}_{0}>1.3W^{2}$
is required and so
$\unicode[STIX]{x1D702}_{0}>1.3W^{2}$
is required and so
![]() $T_{+}$
can be important at lower
$T_{+}$
can be important at lower
![]() $\unicode[STIX]{x1D702}_{0}$
.
$\unicode[STIX]{x1D702}_{0}$
.

Figure 4.
![]() $\unicode[STIX]{x1D709}$
as a function of: laser intensity and average Lorentz factor of the electron bunch (a); laser intensity and width of the electron energy distribution (b). The solid white lines show
$\unicode[STIX]{x1D709}$
as a function of: laser intensity and average Lorentz factor of the electron bunch (a); laser intensity and width of the electron energy distribution (b). The solid white lines show
![]() $\unicode[STIX]{x1D709}=2$
and the dashed white lines show the prediction of where
$\unicode[STIX]{x1D709}=2$
and the dashed white lines show the prediction of where
![]() $\unicode[STIX]{x1D709}=2$
from (4.2).
$\unicode[STIX]{x1D709}=2$
from (4.2).
From (4.2) we see that
![]() $\unicode[STIX]{x1D709}$
depends on three variables: the average Lorentz factor of the electron bunch
$\unicode[STIX]{x1D709}$
depends on three variables: the average Lorentz factor of the electron bunch
![]() $\unicode[STIX]{x1D6FE}_{0}$
; the width of the electron energy distribution
$\unicode[STIX]{x1D6FE}_{0}$
; the width of the electron energy distribution
![]() $W$
and the laser intensity
$W$
and the laser intensity
![]() $I$
(which determines
$I$
(which determines
![]() $b$
). Figure 4 shows
$b$
). Figure 4 shows
![]() $\unicode[STIX]{x1D709}$
(including
$\unicode[STIX]{x1D709}$
(including
![]() $g$
and
$g$
and
![]() $g_{2}$
) as a function of
$g_{2}$
) as a function of
![]() $I$
and
$I$
and
![]() $\unicode[STIX]{x1D6FE}_{0}$
(for
$\unicode[STIX]{x1D6FE}_{0}$
(for
![]() $W=0.2$
) and
$W=0.2$
) and
![]() $W$
and
$W$
and
![]() $I$
(for
$I$
(for
![]() $\unicode[STIX]{x1D6FE}_{0}m_{e}c^{2}=1.5$
GeV). The prediction of
$\unicode[STIX]{x1D6FE}_{0}m_{e}c^{2}=1.5$
GeV). The prediction of
![]() $\unicode[STIX]{x1D709}=2$
from (4.2), i.e. making the assumption
$\unicode[STIX]{x1D709}=2$
from (4.2), i.e. making the assumption
![]() $g=g_{2}=1$
, is shown to be reasonably accurate for
$g=g_{2}=1$
, is shown to be reasonably accurate for
![]() $I\lesssim 10^{21}~\text{W}~\text{cm}^{-2}$
.
$I\lesssim 10^{21}~\text{W}~\text{cm}^{-2}$
.
To investigate whether the expression for
![]() $\unicode[STIX]{x1D709}$
in (4.2) predicts whether
$\unicode[STIX]{x1D709}$
in (4.2) predicts whether
![]() $T_{+}$
or
$T_{+}$
or
![]() $T_{-}$
dominates the evolution of the variance we performed further EPOCH simulations of the interaction of an electron beam (again with initial distribution
$T_{-}$
dominates the evolution of the variance we performed further EPOCH simulations of the interaction of an electron beam (again with initial distribution
![]() $f(\boldsymbol{x},\boldsymbol{p},t=0)=[n_{e}/(\sqrt{2\unicode[STIX]{x03C0}}\unicode[STIX]{x1D70E})]\unicode[STIX]{x1D6FF}(p_{y})\unicode[STIX]{x1D6FF}(p_{z})\exp [-(p_{x}+\unicode[STIX]{x1D6FE}_{0}m_{e}c)^{2}/(2\unicode[STIX]{x1D70E})^{2}]$
) and a counter-propagating plane wave of intensity
$f(\boldsymbol{x},\boldsymbol{p},t=0)=[n_{e}/(\sqrt{2\unicode[STIX]{x03C0}}\unicode[STIX]{x1D70E})]\unicode[STIX]{x1D6FF}(p_{y})\unicode[STIX]{x1D6FF}(p_{z})\exp [-(p_{x}+\unicode[STIX]{x1D6FE}_{0}m_{e}c)^{2}/(2\unicode[STIX]{x1D70E})^{2}]$
) and a counter-propagating plane wave of intensity
![]() $I$
. The following parameters were chosen:
$I$
. The following parameters were chosen:
We have shown where these simulations lie in the parameter space shown in figure 4 according to the symbols given in the table 1 and assuming
![]() $W=\sqrt{2}\unicode[STIX]{x1D70E}$
. The time evolution of the change in the standard deviation of the electron energy distribution in these simulations is shown in figure 5. We see that only those simulations where (4.2) predicts that
$W=\sqrt{2}\unicode[STIX]{x1D70E}$
. The time evolution of the change in the standard deviation of the electron energy distribution in these simulations is shown in figure 5. We see that only those simulations where (4.2) predicts that
![]() $T_{+}$
is dominant show an increase in the variance.
$T_{+}$
is dominant show an increase in the variance.

Figure 5. Temporal evolution of the change in standard deviation in the electron energy distribution in simulations 1–4.
Table 1. Simulation parameters used to investigate the dominance of
![]() $T_{+}$
over
$T_{+}$
over
![]() $T_{-}$
and vice versa
$T_{-}$
and vice versa
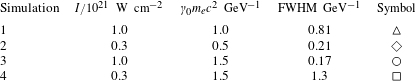
5 Discussion
The results of this investigation can be summarised as follows:
-
(i)
 $\langle \,\boldsymbol{p}\rangle$
evolves in the same way for the stochastic and modified classical emission operators and differently for the classical emission operator.
$\langle \,\boldsymbol{p}\rangle$
evolves in the same way for the stochastic and modified classical emission operators and differently for the classical emission operator. -
(ii)
 $\unicode[STIX]{x1D70E}^{2}$
evolves differently for all operators. In particular, the stochastic emission operator can result in an increase in
$\unicode[STIX]{x1D70E}^{2}$
evolves differently for all operators. In particular, the stochastic emission operator can result in an increase in
 $\unicode[STIX]{x1D70E}^{2}$
whereas the classical and modified classical operators can only cause a decrease in
$\unicode[STIX]{x1D70E}^{2}$
whereas the classical and modified classical operators can only cause a decrease in
 $\unicode[STIX]{x1D70E}^{2}$
(as seen by Vranic et al. (Reference Vranic, Grismayer, Fonseca and Silva2015) for
$\unicode[STIX]{x1D70E}^{2}$
(as seen by Vranic et al. (Reference Vranic, Grismayer, Fonseca and Silva2015) for
 $\unicode[STIX]{x1D702}\ll 1$
).
$\unicode[STIX]{x1D702}\ll 1$
).
Result (i) requires further explanation. Although we have shown that
![]() $(\text{d}\langle \,\boldsymbol{p}\rangle /\text{d}t)_{st}$
and
$(\text{d}\langle \,\boldsymbol{p}\rangle /\text{d}t)_{st}$
and
![]() $(\text{d}\langle \,\boldsymbol{p}\rangle /\text{d}t)_{\text{mod}\,\text{cl}}$
evolve according to the same equation, it does not necessarily follow that the expectation values themselves are the same for these two emission models (as noted by Elkina et al.
Reference Elkina, Fedotov, Kostyukov, Legkov, Narozhny, Nerush and Ruhl2011). We have previously shown in Ridgers et al. (Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell2014) that, in fact, the expectation values of the energy using these two models do agree to a high degree of accuracy and this was shown again for the parameters considered here in figure 3. We would expect this in the classical limit where
$(\text{d}\langle \,\boldsymbol{p}\rangle /\text{d}t)_{\text{mod}\,\text{cl}}$
evolve according to the same equation, it does not necessarily follow that the expectation values themselves are the same for these two emission models (as noted by Elkina et al.
Reference Elkina, Fedotov, Kostyukov, Legkov, Narozhny, Nerush and Ruhl2011). We have previously shown in Ridgers et al. (Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell2014) that, in fact, the expectation values of the energy using these two models do agree to a high degree of accuracy and this was shown again for the parameters considered here in figure 3. We would expect this in the classical limit where
![]() $\unicode[STIX]{x1D702}\ll 1$
. In this case
$\unicode[STIX]{x1D702}\ll 1$
. In this case
![]() $T_{-}$
in (3.4) dominates (from (4.2) we see that
$T_{-}$
in (3.4) dominates (from (4.2) we see that
![]() $\unicode[STIX]{x1D709}\propto \unicode[STIX]{x1D702}_{0}$
) and rapidly reduces the variance of the electron bunch; the electron distribution in both the modified classical and stochastic models approaches a delta function
$\unicode[STIX]{x1D709}\propto \unicode[STIX]{x1D702}_{0}$
) and rapidly reduces the variance of the electron bunch; the electron distribution in both the modified classical and stochastic models approaches a delta function
![]() $\unicode[STIX]{x1D6FF}(\boldsymbol{p}-\langle \,\boldsymbol{p}\rangle )$
. The time evolution of
$\unicode[STIX]{x1D6FF}(\boldsymbol{p}-\langle \,\boldsymbol{p}\rangle )$
. The time evolution of
![]() $\langle \,\boldsymbol{p}\rangle$
depends on
$\langle \,\boldsymbol{p}\rangle$
depends on
![]() $\langle P_{\text{cl}}\rangle$
(
$\langle P_{\text{cl}}\rangle$
(
![]() $g\approx 1$
in the classical limit) which is equal to
$g\approx 1$
in the classical limit) which is equal to
![]() $(\langle \unicode[STIX]{x1D702}\rangle )P_{\text{cl}}(\langle \unicode[STIX]{x1D702}\rangle )$
for both the stochastic and modified classical models when
$(\langle \unicode[STIX]{x1D702}\rangle )P_{\text{cl}}(\langle \unicode[STIX]{x1D702}\rangle )$
for both the stochastic and modified classical models when
![]() $f$
is narrow in momentum space. However, in the simulation whose results are shown in figure 3
$f$
is narrow in momentum space. However, in the simulation whose results are shown in figure 3
![]() $\unicode[STIX]{x1D702}>0.1$
. From figure 2 we see that in this case the electron energy distribution is very different when the stochastic emission operator is used compared to when the modified classical emission operator is used and in the former case is certainly not narrow. Despite this the evolution of
$\unicode[STIX]{x1D702}>0.1$
. From figure 2 we see that in this case the electron energy distribution is very different when the stochastic emission operator is used compared to when the modified classical emission operator is used and in the former case is certainly not narrow. Despite this the evolution of
![]() $\langle \,\boldsymbol{p}\rangle$
is the same due to the functional form of
$\langle \,\boldsymbol{p}\rangle$
is the same due to the functional form of
![]() $gP_{\text{cl}}$
. When
$gP_{\text{cl}}$
. When
![]() $\unicode[STIX]{x1D702}\gg 1$
,
$\unicode[STIX]{x1D702}\gg 1$
,
![]() $gP_{\text{cl}}\propto \unicode[STIX]{x1D702}^{2/3}$
. This almost linear dependence on
$gP_{\text{cl}}\propto \unicode[STIX]{x1D702}^{2/3}$
. This almost linear dependence on
![]() $\unicode[STIX]{x1D702}$
means that the difference in the evolution of
$\unicode[STIX]{x1D702}$
means that the difference in the evolution of
![]() $\langle \,\boldsymbol{p}\rangle$
between the models should be small. Finally we note that, as shown in figure 3,
$\langle \,\boldsymbol{p}\rangle$
between the models should be small. Finally we note that, as shown in figure 3,
![]() $\langle \,\boldsymbol{p}\rangle$
predicted by the classical emission model differs markedly from that predicted by the modified classical and stochastic models due to the neglect of the Gaunt factor
$\langle \,\boldsymbol{p}\rangle$
predicted by the classical emission model differs markedly from that predicted by the modified classical and stochastic models due to the neglect of the Gaunt factor
![]() $g$
in the classical model.
$g$
in the classical model.
![]() $\text{d}\unicode[STIX]{x1D70E}^{2}/\text{d}t$
is always negative for both the classical and modified classical emission operators. Physically, this is because electrons at higher energy radiate more energy than those at lower energy, causing a decrease in the width of the energy distribution. The classical operator predicts a more rapid decrease than the modified classical operator due to the assumption that
$\text{d}\unicode[STIX]{x1D70E}^{2}/\text{d}t$
is always negative for both the classical and modified classical emission operators. Physically, this is because electrons at higher energy radiate more energy than those at lower energy, causing a decrease in the width of the energy distribution. The classical operator predicts a more rapid decrease than the modified classical operator due to the assumption that
![]() $g=1$
and the consequent overestimate of the scaling of the power radiated by the electrons with increasing
$g=1$
and the consequent overestimate of the scaling of the power radiated by the electrons with increasing
![]() $\unicode[STIX]{x1D702}$
. For the stochastic emission operator
$\unicode[STIX]{x1D702}$
. For the stochastic emission operator
![]() $\text{d}\unicode[STIX]{x1D70E}^{2}/\text{d}t$
can be either positive or negative and so
$\text{d}\unicode[STIX]{x1D70E}^{2}/\text{d}t$
can be either positive or negative and so
![]() $\unicode[STIX]{x1D70E}^{2}$
can increase or decrease. The evolution of
$\unicode[STIX]{x1D70E}^{2}$
can increase or decrease. The evolution of
![]() $\unicode[STIX]{x1D70E}^{2}$
is determined by the balance between
$\unicode[STIX]{x1D70E}^{2}$
is determined by the balance between
![]() $T_{+}$
(which causes
$T_{+}$
(which causes
![]() $\unicode[STIX]{x1D70E}^{2}$
to increase due the probabilistic nature of the emission) and
$\unicode[STIX]{x1D70E}^{2}$
to increase due the probabilistic nature of the emission) and
![]() $T_{-}$
(which, as just described, causes
$T_{-}$
(which, as just described, causes
![]() $\unicode[STIX]{x1D70E}^{2}$
to decrease as higher energy electrons radiate more energy). We have shown (as did Vranic et al.
Reference Vranic, Grismayer, Fonseca and Silva2015) that which of these terms dominates depends on the width of the energy distribution and
$\unicode[STIX]{x1D70E}^{2}$
to decrease as higher energy electrons radiate more energy). We have shown (as did Vranic et al.
Reference Vranic, Grismayer, Fonseca and Silva2015) that which of these terms dominates depends on the width of the energy distribution and
![]() $\unicode[STIX]{x1D702}$
. For large width
$\unicode[STIX]{x1D702}$
. For large width
![]() $T_{-}$
increases in importance as it depends on
$T_{-}$
increases in importance as it depends on
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}-\langle \unicode[STIX]{x1D6FE}\rangle$
. For high
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}-\langle \unicode[STIX]{x1D6FE}\rangle$
. For high
![]() $\unicode[STIX]{x1D702}$
$\unicode[STIX]{x1D702}$
![]() $T_{+}$
becomes more important due to its scaling with
$T_{+}$
becomes more important due to its scaling with
![]() $\unicode[STIX]{x1D702}^{4}$
compared to at most
$\unicode[STIX]{x1D702}^{4}$
compared to at most
![]() $\unicode[STIX]{x1D702}^{3}$
for
$\unicode[STIX]{x1D702}^{3}$
for
![]() $T_{-}$
(assuming
$T_{-}$
(assuming
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}\sim \unicode[STIX]{x1D6FE}$
). In (4.2) we have provided a formula for the determination of which term is dominant.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}\sim \unicode[STIX]{x1D6FE}$
). In (4.2) we have provided a formula for the determination of which term is dominant.
The first of these results, i.e. that the evolution of the expectation value is the same for the modified classical and stochastic (but not classical) models, is useful in two ways. Firstly it shows that measuring the expectation value of an electron bunch after interaction with a high-intensity laser pulse can give information about one quantum effect: the reduction of the total power emitted as expressed by
![]() $g$
. It cannot, however, give information about the probabilistic nature of the emission. Secondly, this result suggests that the modified classical model of radiation reaction is sufficient for the calculation of laser absorption in high-intensity laser–plasma interactions (Brady et al.
Reference Brady, Ridgers, Arber, Bell and Kirk2012; Zhang et al.
Reference Zhang, Ridgers and Thomas2015). Laser absorption in this context depends on the average energy loss by the electrons (and positrons) in the plasma due to radiation reaction. The second result, i.e. the evolution of the variance differs between the models, can be used to measure the stochasticity of the radiation reaction. An increase in the variance of the energy distribution of electrons must be due to the probabilistic nature of the emission. As further work we propose a comparison of QED-PIC simulations of laser absorption in laser–plasma interactions using the different emission models and an investigation of the use of the variance to observe stochasticity in three-dimensional simulations of the interaction of a focusing laser pulse with a counter-propagating electron bunch produced by laser wakefield acceleration (with a realistic energy spectrum).
$g$
. It cannot, however, give information about the probabilistic nature of the emission. Secondly, this result suggests that the modified classical model of radiation reaction is sufficient for the calculation of laser absorption in high-intensity laser–plasma interactions (Brady et al.
Reference Brady, Ridgers, Arber, Bell and Kirk2012; Zhang et al.
Reference Zhang, Ridgers and Thomas2015). Laser absorption in this context depends on the average energy loss by the electrons (and positrons) in the plasma due to radiation reaction. The second result, i.e. the evolution of the variance differs between the models, can be used to measure the stochasticity of the radiation reaction. An increase in the variance of the energy distribution of electrons must be due to the probabilistic nature of the emission. As further work we propose a comparison of QED-PIC simulations of laser absorption in laser–plasma interactions using the different emission models and an investigation of the use of the variance to observe stochasticity in three-dimensional simulations of the interaction of a focusing laser pulse with a counter-propagating electron bunch produced by laser wakefield acceleration (with a realistic energy spectrum).
6 Conclusions
We have derived equations for the evolution of the expectation value of the momentum and variance in the energy of an electron population subject to three different radiation reaction models. We have considered classical and modified classical models, where the radiation reaction is deterministic and the power emitted is the classical synchrotron power in the former case and in the latter case accounts for reduction to the power emitted by quantum effects (the Gaunt factor
![]() $g$
). We have also considered a stochastic model which calculates the emission using a more physically correct probabilistic treatment. We have shown that the expectation value of the energy evolves in almost the same way for the stochastic and modified classical models but differently for the classical model. The variance of the energy distribution evolves differently for all the models. This suggests that measuring the decrease in the expectation value of the energy is sufficient to measure the Gaunt factor but that a measurement of the variance is required to distinguish quantum stochastic effects.
$g$
). We have also considered a stochastic model which calculates the emission using a more physically correct probabilistic treatment. We have shown that the expectation value of the energy evolves in almost the same way for the stochastic and modified classical models but differently for the classical model. The variance of the energy distribution evolves differently for all the models. This suggests that measuring the decrease in the expectation value of the energy is sufficient to measure the Gaunt factor but that a measurement of the variance is required to distinguish quantum stochastic effects.
Acknowledgements
This work was funded by Engineering and Physical Science Research Council grants EP/M018156/1, EP/M018091/1 and EP/M018555/1 and partially by the Knut and Alice Wallenberg Foundation (T.G.B., M.M.). Data access: the data required to reproduce the simulation results presented here are available at doi: 10.15124/ 332b52e8-7687-4c74-899b-eec1ecb46875. The derivation of the analytical results presented here is given in appendix B.
Appendix A. Functions describing synchrotron emission
The rate of photon emission (making the quasi-static and weak-field approximations) is
The quantum synchrotron function is given in Sokolov & Ternov (Reference Sokolov and Ternov1968, equation (6.5)). In our notation it is, for
![]() $\unicode[STIX]{x1D712}<\unicode[STIX]{x1D702}/2$
,
$\unicode[STIX]{x1D712}<\unicode[STIX]{x1D702}/2$
,
where
![]() $y=4\unicode[STIX]{x1D712}/[3\unicode[STIX]{x1D702}(\unicode[STIX]{x1D702}-2\unicode[STIX]{x1D712})]$
and
$y=4\unicode[STIX]{x1D712}/[3\unicode[STIX]{x1D702}(\unicode[STIX]{x1D702}-2\unicode[STIX]{x1D712})]$
and
![]() $\text{K}_{n}$
are modified Bessel functions of the second kind. For
$\text{K}_{n}$
are modified Bessel functions of the second kind. For
![]() $\unicode[STIX]{x1D712}\geqslant \unicode[STIX]{x1D702}/2$
,
$\unicode[STIX]{x1D712}\geqslant \unicode[STIX]{x1D702}/2$
,
![]() $F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})=0$
. In the classical limit
$F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})=0$
. In the classical limit
![]() $\hbar \rightarrow 0$
the quantum synchrotron spectrum reduces to the classical synchrotron spectrum
$\hbar \rightarrow 0$
the quantum synchrotron spectrum reduces to the classical synchrotron spectrum
![]() $F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})\rightarrow F_{\text{cl}}(y_{c})=y_{c}\int _{y_{c}}^{\infty }\,\text{d}uK_{5/3}(u)$
;
$F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})\rightarrow F_{\text{cl}}(y_{c})=y_{c}\int _{y_{c}}^{\infty }\,\text{d}uK_{5/3}(u)$
;
![]() $y_{c}=4\unicode[STIX]{x1D712}/3\unicode[STIX]{x1D702}^{2}$
. The probability that a photon is emitted with a given
$y_{c}=4\unicode[STIX]{x1D712}/3\unicode[STIX]{x1D702}^{2}$
. The probability that a photon is emitted with a given
![]() $\unicode[STIX]{x1D712}$
(by an electron with a given
$\unicode[STIX]{x1D712}$
(by an electron with a given
![]() $\unicode[STIX]{x1D702}$
) is
$\unicode[STIX]{x1D702}$
) is
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})\,\text{d}\unicode[STIX]{x1D712}=[1/h(\unicode[STIX]{x1D702})][F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})/\unicode[STIX]{x1D712}]\,\text{d}\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})\,\text{d}\unicode[STIX]{x1D712}=[1/h(\unicode[STIX]{x1D702})][F(\unicode[STIX]{x1D702},\unicode[STIX]{x1D712})/\unicode[STIX]{x1D712}]\,\text{d}\unicode[STIX]{x1D712}$
.
Appendix B. Derivation of the moment equations
We obtain an equation for the evolution of the expectation value of the electron momentum by multiplying (2.6) by
![]() $\boldsymbol{p}$
and integrating over momentum.
$\boldsymbol{p}$
and integrating over momentum.
In spherical polars
![]() $d^{3}\boldsymbol{p}=p^{2}\,\text{d}pd^{2}\unicode[STIX]{x1D6FA}$
. We also write
$d^{3}\boldsymbol{p}=p^{2}\,\text{d}pd^{2}\unicode[STIX]{x1D6FA}$
. We also write
![]() $\boldsymbol{p}=p\hat{\boldsymbol{p}}$
. Therefore,
$\boldsymbol{p}=p\hat{\boldsymbol{p}}$
. Therefore,
We may exchange the order of integration over
![]() $p$
and
$p$
and
![]() $p^{\prime }$
in the second term on the right-hand side
$p^{\prime }$
in the second term on the right-hand side
Here the
![]() $p$
dependence of
$p$
dependence of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712}}$
is in
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712}}$
is in
![]() $\unicode[STIX]{x1D712}=[(p^{\prime }-p)b]/(2m_{e}c)$
(where we have assumed the electrons are ultra-relativistic). To simplify the identification of
$\unicode[STIX]{x1D712}=[(p^{\prime }-p)b]/(2m_{e}c)$
(where we have assumed the electrons are ultra-relativistic). To simplify the identification of
![]() $gP_{\text{cl}}$
we define
$gP_{\text{cl}}$
we define
![]() $\unicode[STIX]{x1D70C}_{h\unicode[STIX]{x1D708}}\,\text{d}h\unicode[STIX]{x1D708}$
as the probability that an electron with energy parameterised by
$\unicode[STIX]{x1D70C}_{h\unicode[STIX]{x1D708}}\,\text{d}h\unicode[STIX]{x1D708}$
as the probability that an electron with energy parameterised by
![]() $\unicode[STIX]{x1D702}$
emits a photon with energy
$\unicode[STIX]{x1D702}$
emits a photon with energy
![]() $h\unicode[STIX]{x1D708}$
.
$h\unicode[STIX]{x1D708}$
.
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D70C}_{h\unicode[STIX]{x1D708}}(\text{d}h\unicode[STIX]{x1D708}/\text{d}\unicode[STIX]{x1D712})=\unicode[STIX]{x1D70C}_{h\unicode[STIX]{x1D708}}(2mc^{2})/b$
. We may therefore write
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D70C}_{h\unicode[STIX]{x1D708}}(\text{d}h\unicode[STIX]{x1D708}/\text{d}\unicode[STIX]{x1D712})=\unicode[STIX]{x1D70C}_{h\unicode[STIX]{x1D708}}(2mc^{2})/b$
. We may therefore write
 $$\begin{eqnarray}\displaystyle n_{e}\left(\frac{\text{d}\langle \,\boldsymbol{p}\rangle }{\text{d}t}\right)_{st} & = & \displaystyle -\!\int d^{3}\boldsymbol{p}\boldsymbol{p}\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D702})f+\int d^{2}\unicode[STIX]{x1D6FA}\hat{\boldsymbol{p}}\int _{0}^{\infty }\,\text{d}p^{\prime }\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D702}^{\prime })f(\boldsymbol{p}^{\prime })p^{\prime 2}\int _{0}^{p^{\prime }c}\,\text{d}h\unicode[STIX]{x1D708}\nonumber\\ \displaystyle & & \displaystyle \times \,\left(p^{\prime }-\frac{h\unicode[STIX]{x1D708}}{c}\right)\unicode[STIX]{x1D70C}_{h\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D702}^{\prime },h\unicode[STIX]{x1D708}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{e}\left(\frac{\text{d}\langle \,\boldsymbol{p}\rangle }{\text{d}t}\right)_{st} & = & \displaystyle -\!\int d^{3}\boldsymbol{p}\boldsymbol{p}\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D702})f+\int d^{2}\unicode[STIX]{x1D6FA}\hat{\boldsymbol{p}}\int _{0}^{\infty }\,\text{d}p^{\prime }\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D702}^{\prime })f(\boldsymbol{p}^{\prime })p^{\prime 2}\int _{0}^{p^{\prime }c}\,\text{d}h\unicode[STIX]{x1D708}\nonumber\\ \displaystyle & & \displaystyle \times \,\left(p^{\prime }-\frac{h\unicode[STIX]{x1D708}}{c}\right)\unicode[STIX]{x1D70C}_{h\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D702}^{\prime },h\unicode[STIX]{x1D708}).\end{eqnarray}$$
Now we use
to get
Cancelling the appropriate terms and identifying
![]() $gP_{\text{cl}}=\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}(h\unicode[STIX]{x1D708})_{\text{av}}$
yields (3.2),
$gP_{\text{cl}}=\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}(h\unicode[STIX]{x1D708})_{\text{av}}$
yields (3.2),
The equation for the evolution of
![]() $\unicode[STIX]{x1D70E}^{2}$
(3.4) is obtained by using the same procedure to obtain an equation for
$\unicode[STIX]{x1D70E}^{2}$
(3.4) is obtained by using the same procedure to obtain an equation for
![]() $(\text{d}\langle \unicode[STIX]{x1D6FE}^{2}\rangle /\text{d}t)_{st}$
, i.e. we multiply (2.6) by
$(\text{d}\langle \unicode[STIX]{x1D6FE}^{2}\rangle /\text{d}t)_{st}$
, i.e. we multiply (2.6) by
![]() $\unicode[STIX]{x1D6FE}^{2}$
and integrate over momentum,
$\unicode[STIX]{x1D6FE}^{2}$
and integrate over momentum,
which can be written as
 $$\begin{eqnarray}\displaystyle n_{e}\left(\frac{\text{d}\langle \unicode[STIX]{x1D6FE}^{2}\rangle }{\text{d}t}\right)_{st} & = & \displaystyle -\!\int d^{3}\boldsymbol{p}\unicode[STIX]{x1D6FE}^{2}\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D702})f+\int d^{2}\unicode[STIX]{x1D6FA}\int _{0}^{\infty }\,\text{d}p^{\prime }\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D702}^{\prime })f(\boldsymbol{p}^{\prime })p^{\prime 2}\int _{0}^{p^{\prime }c}\,\text{d}h\unicode[STIX]{x1D708}\nonumber\\ \displaystyle & & \displaystyle \times \,\left(\unicode[STIX]{x1D6FE}^{\prime }-\frac{h\unicode[STIX]{x1D708}}{m_{e}c^{2}}\right)^{2}\unicode[STIX]{x1D70C}_{h\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D702}^{\prime },h\unicode[STIX]{x1D708}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{e}\left(\frac{\text{d}\langle \unicode[STIX]{x1D6FE}^{2}\rangle }{\text{d}t}\right)_{st} & = & \displaystyle -\!\int d^{3}\boldsymbol{p}\unicode[STIX]{x1D6FE}^{2}\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D702})f+\int d^{2}\unicode[STIX]{x1D6FA}\int _{0}^{\infty }\,\text{d}p^{\prime }\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D702}^{\prime })f(\boldsymbol{p}^{\prime })p^{\prime 2}\int _{0}^{p^{\prime }c}\,\text{d}h\unicode[STIX]{x1D708}\nonumber\\ \displaystyle & & \displaystyle \times \,\left(\unicode[STIX]{x1D6FE}^{\prime }-\frac{h\unicode[STIX]{x1D708}}{m_{e}c^{2}}\right)^{2}\unicode[STIX]{x1D70C}_{h\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D702}^{\prime },h\unicode[STIX]{x1D708}),\end{eqnarray}$$
where we have assumed
![]() $\unicode[STIX]{x1D6FE}^{\prime }=p^{\prime }/m_{e}c$
. Defining
$\unicode[STIX]{x1D6FE}^{\prime }=p^{\prime }/m_{e}c$
. Defining
gives
We again cancel the appropriate terms and this time identify
![]() $S=\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}[(h\unicode[STIX]{x1D708})^{2}]_{\text{av}}$
as well as
$S=\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}[(h\unicode[STIX]{x1D708})^{2}]_{\text{av}}$
as well as
![]() $gP_{\text{cl}}=\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}(h\unicode[STIX]{x1D708})_{\text{av}}$
to get
$gP_{\text{cl}}=\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6FE}}(h\unicode[STIX]{x1D708})_{\text{av}}$
to get
To get an equation for
![]() $(\text{d}\unicode[STIX]{x1D70E}^{2}/\text{d}t)_{st}$
we identify
$(\text{d}\unicode[STIX]{x1D70E}^{2}/\text{d}t)_{st}$
we identify
![]() $\unicode[STIX]{x1D70E}^{2}=\langle \unicode[STIX]{x1D6FE}^{2}\rangle -\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
. Therefore,
$\unicode[STIX]{x1D70E}^{2}=\langle \unicode[STIX]{x1D6FE}^{2}\rangle -\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
. Therefore,
Substituting the results for
![]() $(\text{d}\langle \unicode[STIX]{x1D6FE}^{2}\rangle /\text{d}t)_{st}$
and
$(\text{d}\langle \unicode[STIX]{x1D6FE}^{2}\rangle /\text{d}t)_{st}$
and
![]() $(\text{d}\langle \unicode[STIX]{x1D6FE}\rangle /\text{d}t)_{st}=\langle gP_{\text{cl}}\rangle /(m_{e}c^{2})$
(the latter is obtained by taking the dot product of (3.2) with
$(\text{d}\langle \unicode[STIX]{x1D6FE}\rangle /\text{d}t)_{st}=\langle gP_{\text{cl}}\rangle /(m_{e}c^{2})$
(the latter is obtained by taking the dot product of (3.2) with
![]() $\hat{\boldsymbol{p}}$
and assuming
$\hat{\boldsymbol{p}}$
and assuming
![]() $p=\unicode[STIX]{x1D6FE}m_{e}c$
) gives the result in (3.4):
$p=\unicode[STIX]{x1D6FE}m_{e}c$
) gives the result in (3.4):
Here we have used
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}-\langle \unicode[STIX]{x1D6FE}\rangle$
.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}-\langle \unicode[STIX]{x1D6FE}\rangle$
.
The moments of the classical and modified classical emission operators are straightforwardly obtained by integration by parts. To obtain (3.3) for
![]() $(\text{d}\langle \,\boldsymbol{p}\rangle /\text{d}t)_{\text{mod}\,\text{cl}}$
we multiply the emission operator
$(\text{d}\langle \,\boldsymbol{p}\rangle /\text{d}t)_{\text{mod}\,\text{cl}}$
we multiply the emission operator
![]() $(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}t)_{\text{em}}^{\text{mod}\,\text{cl}}$
in (2.5) by
$(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}t)_{\text{em}}^{\text{mod}\,\text{cl}}$
in (2.5) by
![]() $\boldsymbol{p}$
and integrate over momentum
$\boldsymbol{p}$
and integrate over momentum
Substituting
![]() $d^{3}\boldsymbol{p}=p^{2}\,\text{d}pd^{2}\unicode[STIX]{x1D6FA}$
and
$d^{3}\boldsymbol{p}=p^{2}\,\text{d}pd^{2}\unicode[STIX]{x1D6FA}$
and
![]() $\boldsymbol{p}=p\hat{\boldsymbol{p}}$
and integrating by parts yields
$\boldsymbol{p}=p\hat{\boldsymbol{p}}$
and integrating by parts yields
 $$\begin{eqnarray}\displaystyle n_{e}\left(\frac{\text{d}\langle \,\boldsymbol{p}\rangle }{\text{d}t}\right)_{\text{mod}\,\text{cl}} & = & \displaystyle \int d^{2}\unicode[STIX]{x1D6FA}\hat{\boldsymbol{p}}\left(\left[p^{3}g\frac{P_{\text{cl}}}{c}f\right]_{0}^{\infty }-\int _{0}^{\infty }\,\text{d}pp^{2}g\frac{P_{\text{cl}}}{c}f\right)\nonumber\\ \displaystyle & = & \displaystyle -\!\int d^{2}\unicode[STIX]{x1D6FA}\hat{\boldsymbol{p}}\int _{0}^{\infty }\,\text{d}pp^{2}g\frac{P_{\text{cl}}}{c}f.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{e}\left(\frac{\text{d}\langle \,\boldsymbol{p}\rangle }{\text{d}t}\right)_{\text{mod}\,\text{cl}} & = & \displaystyle \int d^{2}\unicode[STIX]{x1D6FA}\hat{\boldsymbol{p}}\left(\left[p^{3}g\frac{P_{\text{cl}}}{c}f\right]_{0}^{\infty }-\int _{0}^{\infty }\,\text{d}pp^{2}g\frac{P_{\text{cl}}}{c}f\right)\nonumber\\ \displaystyle & = & \displaystyle -\!\int d^{2}\unicode[STIX]{x1D6FA}\hat{\boldsymbol{p}}\int _{0}^{\infty }\,\text{d}pp^{2}g\frac{P_{\text{cl}}}{c}f.\end{eqnarray}$$
We have used the fact that
![]() $f\rightarrow 0$
as
$f\rightarrow 0$
as
![]() $p\rightarrow \infty$
(faster than
$p\rightarrow \infty$
(faster than
![]() $p^{5}$
diverges) to get the last result. We have now derived (3.3)
$p^{5}$
diverges) to get the last result. We have now derived (3.3)
To derive (3.7) for
![]() $(\text{d}\unicode[STIX]{x1D70E}^{2}/\text{d}t)_{\text{mod}\,\text{cl}}$
we first multiply the emission operator
$(\text{d}\unicode[STIX]{x1D70E}^{2}/\text{d}t)_{\text{mod}\,\text{cl}}$
we first multiply the emission operator
![]() $(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}t)_{\text{em}}^{\text{mod}\,\text{cl}}$
in (2.5) by
$(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}t)_{\text{em}}^{\text{mod}\,\text{cl}}$
in (2.5) by
![]() $\unicode[STIX]{x1D6FE}^{2}$
and integrate over momentum
$\unicode[STIX]{x1D6FE}^{2}$
and integrate over momentum
Substituting
![]() $d^{3}\boldsymbol{p}=p^{2}\,\text{d}pd^{2}\unicode[STIX]{x1D6FA}$
,
$d^{3}\boldsymbol{p}=p^{2}\,\text{d}pd^{2}\unicode[STIX]{x1D6FA}$
,
![]() $\unicode[STIX]{x1D6FE}=p/(m_{e}c)$
and integrating by parts yields
$\unicode[STIX]{x1D6FE}=p/(m_{e}c)$
and integrating by parts yields
 $$\begin{eqnarray}\displaystyle n_{e}\left(\frac{\text{d}\langle \unicode[STIX]{x1D6FE}^{2}\rangle }{\text{d}t}\right)_{\text{mod}\,\text{cl}} & = & \displaystyle \int d^{2}\unicode[STIX]{x1D6FA}\left(\left[\frac{p^{4}}{m_{e}^{2}c^{2}}g\frac{P_{\text{cl}}}{c}f\right]_{0}^{\infty }-2\int _{0}^{\infty }\,\text{d}p\frac{p^{3}}{m_{e}^{2}c^{2}}g\frac{P_{\text{cl}}}{c}f\right)\nonumber\\ \displaystyle & = & \displaystyle -\!\int d^{2}\unicode[STIX]{x1D6FA}\hat{\boldsymbol{p}}\int _{0}^{\infty }\,\text{d}pp^{2}\unicode[STIX]{x1D6FE}g\frac{P_{\text{cl}}}{m_{e}c^{2}}f.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n_{e}\left(\frac{\text{d}\langle \unicode[STIX]{x1D6FE}^{2}\rangle }{\text{d}t}\right)_{\text{mod}\,\text{cl}} & = & \displaystyle \int d^{2}\unicode[STIX]{x1D6FA}\left(\left[\frac{p^{4}}{m_{e}^{2}c^{2}}g\frac{P_{\text{cl}}}{c}f\right]_{0}^{\infty }-2\int _{0}^{\infty }\,\text{d}p\frac{p^{3}}{m_{e}^{2}c^{2}}g\frac{P_{\text{cl}}}{c}f\right)\nonumber\\ \displaystyle & = & \displaystyle -\!\int d^{2}\unicode[STIX]{x1D6FA}\hat{\boldsymbol{p}}\int _{0}^{\infty }\,\text{d}pp^{2}\unicode[STIX]{x1D6FE}g\frac{P_{\text{cl}}}{m_{e}c^{2}}f.\end{eqnarray}$$
Again, we have used the fact that
![]() $f\rightarrow 0$
as
$f\rightarrow 0$
as
![]() $p\rightarrow \infty$
(this time faster than
$p\rightarrow \infty$
(this time faster than
![]() $p^{6}$
diverges) to get the final result. We may write this more compactly as
$p^{6}$
diverges) to get the final result. We may write this more compactly as
We get (3.7) by identifying
![]() $\unicode[STIX]{x1D70E}^{2}=\langle \unicode[STIX]{x1D6FE}^{2}\rangle -\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
and
$\unicode[STIX]{x1D70E}^{2}=\langle \unicode[STIX]{x1D6FE}^{2}\rangle -\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}-\langle \unicode[STIX]{x1D6FE}\rangle$
,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}-\langle \unicode[STIX]{x1D6FE}\rangle$
,
Appendix C. Derivation of
 $\unicode[STIX]{x1D709}$
$\unicode[STIX]{x1D709}$
For simplicity in what follows we define
![]() $\unicode[STIX]{x1D70F}_{S}$
and
$\unicode[STIX]{x1D70F}_{S}$
and
![]() $\unicode[STIX]{x1D70F}_{R}$
as
$\unicode[STIX]{x1D70F}_{R}$
as
Then we may write
![]() $\unicode[STIX]{x1D709}$
as
$\unicode[STIX]{x1D709}$
as
where we have set
![]() $g_{2}=g=1$
. We may evaluate the averages by substituting
$g_{2}=g=1$
. We may evaluate the averages by substituting
![]() $f=[1/(2W\unicode[STIX]{x1D6FE}_{0}m_{e}c)]\unicode[STIX]{x1D6FF}(p_{y})\unicode[STIX]{x1D6FF}(p_{z})$
for
$f=[1/(2W\unicode[STIX]{x1D6FE}_{0}m_{e}c)]\unicode[STIX]{x1D6FF}(p_{y})\unicode[STIX]{x1D6FF}(p_{z})$
for
![]() $\unicode[STIX]{x1D6FE}_{0}m_{e}c(1-W)<p_{x}<\unicode[STIX]{x1D6FE}_{0}m_{e}c(1+W)$
.
$\unicode[STIX]{x1D6FE}_{0}m_{e}c(1-W)<p_{x}<\unicode[STIX]{x1D6FE}_{0}m_{e}c(1+W)$
.
 $$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D6FE}^{4}\rangle & = & \displaystyle \frac{1}{2W\unicode[STIX]{x1D6FE}_{0}m_{e}c}\int _{\unicode[STIX]{x1D6FE}_{0}m_{e}c(1-W)}^{\unicode[STIX]{x1D6FE}_{0}m_{e}c(1+W)}\unicode[STIX]{x1D6FE}^{4}\,\text{d}p_{x}=\frac{\unicode[STIX]{x1D6FE}_{0}^{4}}{10W}[(1+W)^{5}-(1-W)^{5}]\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D6FE}_{0}^{4}}{5W}(10W^{3}+5W+W^{5})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D6FE}^{4}\rangle & = & \displaystyle \frac{1}{2W\unicode[STIX]{x1D6FE}_{0}m_{e}c}\int _{\unicode[STIX]{x1D6FE}_{0}m_{e}c(1-W)}^{\unicode[STIX]{x1D6FE}_{0}m_{e}c(1+W)}\unicode[STIX]{x1D6FE}^{4}\,\text{d}p_{x}=\frac{\unicode[STIX]{x1D6FE}_{0}^{4}}{10W}[(1+W)^{5}-(1-W)^{5}]\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D6FE}_{0}^{4}}{5W}(10W^{3}+5W+W^{5})\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FE}^{2}\rangle & = & \displaystyle \frac{1}{2W\unicode[STIX]{x1D6FE}_{0}m_{e}c}\int _{\unicode[STIX]{x1D6FE}_{0}m_{e}c(1-W)}^{\unicode[STIX]{x1D6FE}_{0}m_{e}c(1+W)}(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FE}_{0})\unicode[STIX]{x1D6FE}^{2}\,\text{d}p_{x}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D6FE}_{0}^{3}}{24W}[(1-W)^{3}(1+3W)-(1+W)^{3}(1-3W)]=\frac{2\unicode[STIX]{x1D6FE}_{0}^{3}}{3}W^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FE}^{2}\rangle & = & \displaystyle \frac{1}{2W\unicode[STIX]{x1D6FE}_{0}m_{e}c}\int _{\unicode[STIX]{x1D6FE}_{0}m_{e}c(1-W)}^{\unicode[STIX]{x1D6FE}_{0}m_{e}c(1+W)}(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FE}_{0})\unicode[STIX]{x1D6FE}^{2}\,\text{d}p_{x}\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D6FE}_{0}^{3}}{24W}[(1-W)^{3}(1+3W)-(1+W)^{3}(1-3W)]=\frac{2\unicode[STIX]{x1D6FE}_{0}^{3}}{3}W^{2}.\end{eqnarray}$$
Substituting these results into (C 2) yields (4.2)
where we have used
![]() $\unicode[STIX]{x1D70F}_{S}/\unicode[STIX]{x1D70F}_{R}=(55b)/(16\sqrt{3})$
and
$\unicode[STIX]{x1D70F}_{S}/\unicode[STIX]{x1D70F}_{R}=(55b)/(16\sqrt{3})$
and
![]() $\unicode[STIX]{x1D702}_{0}=\unicode[STIX]{x1D6FE}_{0}b$
.
$\unicode[STIX]{x1D702}_{0}=\unicode[STIX]{x1D6FE}_{0}b$
.