Pair production by Schwinger and Breit–Wheeler processes in bi-frequent fields

Abstract

Counter-propagating and suitably polarized light (laser) beams can provide conditions for pair production. Here, we consider in more detail the following two situations: (i) in the homogeneity regions of anti-nodes of linearly polarized ultra-high intensity laser beams, the Schwinger process is dynamically assisted by a second high-frequency field, e.g. by an XFEL beam; and (ii) a high-energy probe photon beam colliding with a superposition of co-propagating intense laser and XFEL beams gives rise to the laser-assisted Breit–Wheeler process. The prospects of such bi-frequent field constellations with respect to the feasibility of conversion of light into matter are discussed.

1 Introduction

The Schwinger effect (Sauter 1931; Schwinger 1951) refers to the instability of a spatially homogeneous, purely electric field with respect to the decay into a state with pairs, e.g. electrons ( $e^{-}$ ) and positrons ( $e^{+}$ ), and a screened electric field, symbolically $|\boldsymbol{E}\rangle \rightarrow |\boldsymbol{E}^{\prime }e^{+}e^{-}\rangle$ (cf. Gelis & Tanji (2016) for a recent review). The pair creation rate $w\propto \exp \{-{\rm\pi}E_{c}/|\boldsymbol{E}|\}$ for fields attainable presently in mesoscopic laboratory installations is exceedingly small since the Sauter–Schwinger (critical) field strength $E_{c}=m^{2}/|e|=1.3\times 10^{18}~\text{V}~\text{m}^{-1}$ is so large for electrons/positrons with mass $m$ and charge $\pm e$ (we employ here natural units with $c=\hbar =1$ ). The notion of the dynamical Schwinger process refers to a situation where the spatially homogeneous electric field has a time dependence, $\boldsymbol{E}(t)$ . The particular case of a periodic field is dealt with in Brezin & Itzykson (1970) with the motivation that tightly focused laser beams can provide high field strengths, e.g. in the anti-nodes of pair-wise counter propagating, linearly polarized beams. The superposition of many laser beams, as considered, for instance, in Narozhny et al. (2004), can enlarge the pair yield noticeably. A particular variant is the superposition of strong laser beams and weaker but high-frequency beams which may be idealized as a common classical background field $\boldsymbol{E}(t)=\boldsymbol{E}_{1}({\it\omega}t)+\boldsymbol{E}_{2}(N{\it\omega}t)$ . If the frequency of the second field, $N{\it\omega}$ , is sufficiently large, the tunnelling path through the positron–electron gap is shortened by the assistance of the multi-photon effect (Schützhold, Gies & Dunne 2008; Dunne, Gies & Schützhold 2009) and, as a consequence, the pair production is enhanced. This dynamically assisted Schwinger process supposes a Keldysh parameter ${\it\gamma}_{1}=(E_{c}/E_{1})({\it\omega}/m)\ll 1$ to stay in the tunnelling regime ¹ . The combination ${\it\gamma}_{1}<1$ and ${\it\gamma}_{2}=(E_{c}/E_{2})(N{\it\omega}/m)>1$ is dubbed the assisted dynamical Schwinger effect, since the field ‘1’ with parameters $E_{1}$ , ${\it\omega}$ refers to the dynamical Schwinger effect in the nomenclature of Brezin & Itzykson (1970), and the field ‘2’ with parameters $E_{2}$ , $N{\it\omega}$ is assisting. Various pulse shapes for $E_{1,2}$ have been studied with the goal of finding the optimal combinations (Kohlfürst et al. 2013; Akal, Villalba-Chávez & Müller 2014; Hebenstreit & Fillion-Gourdeau 2014). Current lasers reach intensities of $2\times 10^{22}~\text{W}~\text{cm}^{-2}$ (cf. Di Piazza et al. (2012) for an overview) corresponding to an inverse Keldysh parameter of ${\it\gamma}^{-1}=10$ . Planned facilities are, for example, ELI-NP (ELI 2015) and Apollon (Zou et al. 2015) (10 PW, $10^{22}~\text{W}~\text{cm}^{-2}$ ) or HiPER (HiPER 2015) (100 PW, $10^{26}~\text{W}~\text{cm}^{-2}$ ). (The Sauter–Schwinger field strength requires an intensity of $4\times 10^{29}~\text{W}~\text{cm}^{-2}$ .)

All these investigations aim to verify the decay of the vacuum. Besides the mentioned strong (but presently not strong enough) fields, the Coulomb fields accompanying heavy and super-heavy atomic nuclei have also been considered as an option to study the vacuum break down (Rafelski, Fulcher & Greiner 1971; Müller et al. 1972; Müller, Rafelski & Greiner 1973; Rafelski, Müller & Greiner 1978; Bialynicki-Birula, Gornicki & Rafelski 1991). Previous experiments, however, have not been conclusive (Heinz et al. 2000).

Another avenue for pair creation is the conversion of light into matter in the collision of photon beams. The Breit–Wheeler process (Breit & Wheeler 1934) refers to the reaction ${\it\gamma}^{\prime }+{\it\gamma}\rightarrow e^{+}+e^{-}$ which is a crossing channel of the Compton process or the time-reversed annihilation. The famous experiment E-144 at SLAC (Burke et al. 1997) can be interpreted as a two-step process with Compton backscattering of a laser beam and subsequent reaction of the Compton backscattered photons with the laser beam in nonlinear Breit–Wheeler pair production (Burke et al. 1997; Bamber et al. 1999). The nonlinear Breit–Wheeler process means that there is an instantaneous reaction with multiple laser beam photons, i.e. ${\it\gamma}^{\prime }+n{\it\omega}_{L}\rightarrow e^{+}+e^{-}$ . Also here one can ask whether the laser-assisted nonlinear Breit–Wheeler process ${\it\gamma}^{\prime }+{\it\omega}_{XFEL}+n{\it\omega}_{L}\rightarrow e^{+}+e^{-}$ shows peculiarities due to the superposition of the co-propagating XFEL and laser beams.

Other field combinations, such as the nuclear Coulomb field and XFEL/laser beams, are also conceivable (Di Piazza et al. 2010; Augustin & Müller 2014) (cf. Di Piazza et al. (2012) for a recent review and further references), but will not be addressed here.

Our paper is organized as follows. In § 2 we consider the reasoning for forming resonance-type structures in the phase space distribution of pairs created in the assisted dynamical Schwinger process. The considered classical background field configuration has been characterized above: the superposition of two spatially homogeneous fields of different strengths and frequencies with a common envelope, as investigated in Otto et al. (2015a , b ), Panferov et al. (2015). Examples are given for clarification, and some glimpses of the time evolution in simple pulses are provided too. Section 3 deals with the laser-assisted Breit–Wheeler process, where spectral caustics have been identified already in Nousch et al. (2016). Specifically, we show here the sensitivity of the spectral caustics to the laser beam intensity, which is important for multi-shot experiments with intensity parameters that are not perfectly tuneable. Our approach here utilizes the common XFEL + laser field again as a classical background field to be dealt with in the Furry picture, while the probe photon ${\it\gamma}^{\prime }$ refers to a quantized radiation field. We briefly summarize in § 4.

2 Assisted dynamical Schwinger process

In this section we consider pair production in the spirit of the Schwinger process, i.e. the creation of $e^{\pm }$ pairs by a purely electric background field which is assumed to be spatially homogeneous. In the following, we use the notation and formalism as introduced in Otto et al. (2015a ). The quantum kinetic equation (Schmidt et al. 1998)

(2.1) $$\begin{eqnarray}{\dot{f}}(\boldsymbol{p},t)=\frac{{\it\lambda}(\boldsymbol{p},t)}{2}\int _{-\infty }^{t}\,\text{d}t^{\prime }{\it\lambda}(\boldsymbol{p},t^{\prime })(1-2f(\boldsymbol{p},t^{\prime }))\cos {\it\theta}(\boldsymbol{p},t,t^{\prime })\end{eqnarray}$$

determines the time $(t)$ evolution of the dimensionless phase space distribution function per spin projection degree of freedom ²   $f(\boldsymbol{p},t)=\text{d}N(\boldsymbol{p},t)/\text{d}^{3}p\,\text{d}^{3}x$ , where $N$ refers to the particle number and $\text{d}^{3}p$ and $\text{d}^{3}x$ are the three-dimensional volume elements in momentum ( $p$ ) and configuration ( $x$ ) spaces. We emphasize that only $f(\boldsymbol{p},t\rightarrow +\infty )$ can be considered as single particle distribution which may represent the source term of a subsequent time evolution of the emerging $e^{+}e^{-}$ plasma. The initial condition for solving (2.1) is $f(\boldsymbol{p},t\rightarrow -\infty )=0$ . Screening and back-reaction are not included by virtue of the small values of $f$ in subcritical fields (cf. Gelis & Tanji (2013) for recent work on that issue). The quantity ${\it\lambda}(\boldsymbol{p},t)=(eE(t)\,{\it\varepsilon}_{\bot }(p_{\bot }))/{\it\varepsilon}^{2}(\boldsymbol{p},t)$ stands for the amplitude of the vacuum transition, and ${\it\theta}(\boldsymbol{p},t,t^{\prime })=2\int _{t^{\prime }}^{t}\,\text{d}{\it\tau}\,{\it\varepsilon}(\boldsymbol{p},{\it\tau})$ stands for the dynamical phase, describing the vacuum oscillations modulated by the external field; the quasi-energy ${\it\varepsilon}$ , the transverse energy ${\it\varepsilon}_{\bot }$ and the longitudinal quasi-momentum $P$ are defined as ${\it\varepsilon}(\boldsymbol{p},t)=\sqrt{{\it\varepsilon}_{\bot }^{2}(p_{\bot })+P^{2}(p_{\Vert },t)}$ and ${\it\varepsilon}_{\bot }(p_{\bot })=\sqrt{m^{2}+p_{\bot }^{2}},$ $P(p_{\Vert },t)=p_{\Vert }-eA(t),$ where $p_{\bot }=|\boldsymbol{p}_{\bot }|$ is the modulus of the kinetic momentum ( $\boldsymbol{p}$ ) component of positrons (electrons) perpendicular to the electric field and $p_{\Vert }$ denotes the $E$ -parallel kinetic momentum component. The electric field follows from the potential

(2.2) $$\begin{eqnarray}A=K({\it\omega}t)\left(\frac{E_{1}}{{\it\omega}}\cos ({\it\omega}t)+\frac{E_{2}}{N{\it\omega}}\cos (N{\it\omega}t)\right)\end{eqnarray}$$

by $E=-{\dot{A}}$ in the Hamilton gauge. Equation (2.2) describes a bi-frequent field with frequency ratio $N$ (integer) and field strengths $E_{1}$ (the strong field ‘1’) and $E_{2}$ (the weak field ‘2’). The quantity $K$ is the common envelope function with the properties (i) absolutely flat in the flat-top time interval $-t_{\mathit{f.t.}}/2<t<+t_{\mathit{f.t.}}/2$ ; (ii) absolutely zero for $t<-t_{\mathit{f.t.}}/2-t_{\mathit{ramp}}$ and $t>t_{\mathit{f.t.}}/2+t_{\mathit{ramp}}$ ; and (iii) absolutely smooth everywhere, i.e. $K$ belongs to the $C^{\infty }$ class; $t_{\mathit{ramp}}$ is the ramping duration characterizing the switching on/off time intervals.

Figure 1. (a–c) Asymptotic transverse momentum ( $p_{\bot }$ ) spectrum at $p_{\Vert }=0$ for the bi-frequent field (2.2) (b) and the field components ‘1’ (a), ( $E_{1}=0.1E_{c}$ , ${\it\omega}=0.02m$ ) and ‘2’ (c), ( $E_{2}=0.05E_{c}$ , $N=25$ ) alone. (d–f): Fourier zero-modes $2{\it\Omega}(p_{\bot },p_{\Vert }=0)$ scaled by ${\it\omega}$ (d,e) and $N{\it\omega}$ (f) for the fields in (a–c) with resonance conditions (horizontal dashed lines for $\ell =341$ and $343$ (a,d; higher- $\ell$ resonances are not depicted since the peaks are underneath the scale displayed in (a)), $\ell =341,\ldots ,373$ (b,e) and $\ell =5$ (c,f); vertical dashed lines are for the resonance positions; peaks for even $\ell$ appear only for $p_{\Vert }\neq 0$ but get a zero amplitude at $p_{\Vert }=0$ , and thus their positions are not depicted).

Figure 1(a) exhibits three examples for the transverse phase space distribution $f(p_{\bot },p_{\Vert }=0,t\rightarrow \infty )$ for $E_{1}=0.1E_{c}$ , $E_{2}=0.05E_{c}$ , ${\it\omega}=0.02m$ , $N=25$ , $t_{\mathit{ramp}}=5{\it\omega}^{-1}$ and $t_{\mathit{f.t.}}=25{\it\omega}^{-1}$ obtained by numerically solving (2.1). The chosen parameters are still far from reach at present or near-future facilities. Due to the periodicity of the involved fields and their finite duration a pronounced peak structure emerges (the peaks become sharp, elliptically bent ridges with deep notches when continuing the spectrum to finite values of $p_{\Vert }$ ). The peak heights scale with $t_{\mathit{f.t.}}^{2}$ where the pulse duration is not too long. The peak positions are determined by the resonance condition (Otto et al. 2015a )

(2.3) $$\begin{eqnarray}2{\it\Omega}(p_{\bot },p_{\Vert })-\ell {\it\omega}=0,\end{eqnarray}$$

where

(2.4) $$\begin{eqnarray}{\it\Omega}=\frac{m}{2{\rm\pi}}\int _{0}^{2{\rm\pi}}\,\text{d}x\sqrt{1+(p_{\bot }/m)^{2}+[(p_{\Vert }/m)-{\it\gamma}_{1}^{-1}\cos x-{\it\gamma}_{2}^{-1}\cos Nx]^{2}}\end{eqnarray}$$

is the Fourier zero-mode of ${\it\varepsilon}$ . The values of $\ell$ (integer) where the resonance condition (2.3) is fulfilled can be used to label the peaks. The quantity ${\it\Omega}(p_{\bot }=p_{\Vert }=0)$ may be interpreted as effective mass $m^{\ast }$ (Kohlfürst, Gies & Alkofer 2014) which determines $\ell _{\mathit{min}}=\text{int}(1+2m^{\ast }/{\it\omega})$ . The Fourier zero-modes as functions of $p_{\bot }$ at $p_{\Vert }=0$ are displayed in the bottom row in figure 1 together with the resonance positions. For the field ‘1’ alone (d) one has to take the limit ${\it\gamma}_{2}\rightarrow \infty$ in the Fourier zero-mode, while field ‘2’ alone (f) corresponds to ${\it\gamma}_{1}\rightarrow \infty$ and the replacement ${\it\omega}\rightarrow N{\it\omega}$ in (2.3).

Figure 2. Time evolution of $f(p_{\bot }=p_{\Vert }=0,t)$ in the adiabatic basis for the Sauter pulse (2.5) for ${\it\tau}=1~\text{m}^{-1}$ (blue), ${\it\tau}=2~\text{m}^{-1}$ (green), ${\it\tau}=5~\text{m}^{-1}$ (red), ${\it\tau}=10~\text{m}^{-1}$ (cyan), ${\it\tau}=20~\text{m}^{-1}$ (purple) and ${\it\tau}=50~\text{m}^{-1}$ (yellow), where $E_{0}=0.2E_{c}$ (a) and $E_{0}=0.15E_{c}$ (b). The dashed black curves depict the Schwinger case as the limit of large values of ${\it\tau}$ . Note the vast drop of the residual phase space occupancy for larger values of ${\it\tau}$ when changing $E_{0}$ from $0.2E_{c}$ to $0.15E_{c}$ .

The striking feature in figure 1 (cf. Otto et al. (2015a , b ) for other examples with different parameters, in particular $t_{\mathit{f.t.}}$ , and Hähnel (2015) for a wider range of field strengths) is the lifting of the spectrum related to field ‘1’ by the assistance of field ‘2’. While the amplification of the created pair distribution by the assistance field can be huge, for sub-critical fields the frequency $N{\it\omega}$ must be $O(m)$ to overcome the exponential suppression. This implies that the intensities envisaged in ELI pillar IV (ELI 2015) must be at our disposal in conjunction with much higher frequencies to arrive at measurable pair numbers enhanced further by an assistant field (Otto et al. 2015b ).

Even with low pair creation probability, a once produced pair may seed a further avalanche evolution (Bell & Kirk 2008; Elkina et al. 2011; King, Elkina & Ruhl 2013) toward an electron–positron plasma. In this respect one may ask for the time scales to approach the asymptotic out-state. A unique answer seems not to be achievable within the present framework due to the unavoidable ambiguity of the particle definition (see e.g. Dabrowski & Dunne (2014) for examples of changing the time evolution of $f$ at intermediate times when changing the basis). Having this disclaimer in mind one can nevertheless inspect graphs of $f(t)$ . Figure 2 exhibits the time evolution in the adiabatic basis for the Sauter pulse

(2.5) $$\begin{eqnarray}\displaystyle E(t)=\frac{E_{0}}{\cosh ^{2}(t/{\it\tau})} & & \displaystyle\end{eqnarray}$$

which is fairly different from (2.2). The analytical solution (Narozhny & Nikishov 1970; Hebenstreit 2011) of (2.1) is useful for checking numerical codes which are challenged by dealing with rapidly changing functions over many orders of magnitude. For large values of the pulse duration parameter ${\it\tau}$ the Schwinger case is recovered, see Hebenstreit (2011):

(2.6) $$\begin{eqnarray}f=\frac{1}{8}\left(1+\frac{u}{\sqrt{2\hat{{\it\eta}}+u^{2}}}\right)\text{e}^{-({\rm\pi}\hat{{\it\eta}})/4}|X+Y|^{2},\end{eqnarray}$$

with

(2.7a,b ) $$\begin{eqnarray}\displaystyle X=\left(\sqrt{2\hat{{\it\eta}}+u^{2}}-u\right)D_{-1+(\text{i}\hat{{\it\eta}})/2}(-u\text{e}^{-(\text{i}{\rm\pi})/4}),\quad Y=-2\text{e}^{(\text{i}{\rm\pi})/4}D_{(\text{i}\hat{{\it\eta}})/2}(-u\text{e}^{-(\text{i}{\rm\pi})/4}), & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

where $D$ is the parabolic cylinder function,

(2.8a,b ) $$\begin{eqnarray}\displaystyle u=\sqrt{\frac{2}{|e|E_{0}}}(p_{\Vert }+eE_{0}t)\quad \text{and}\quad \hat{{\it\eta}}=\frac{m^{2}+p_{\bot }^{2}}{|e|E_{0}}. & & \displaystyle\end{eqnarray}$$

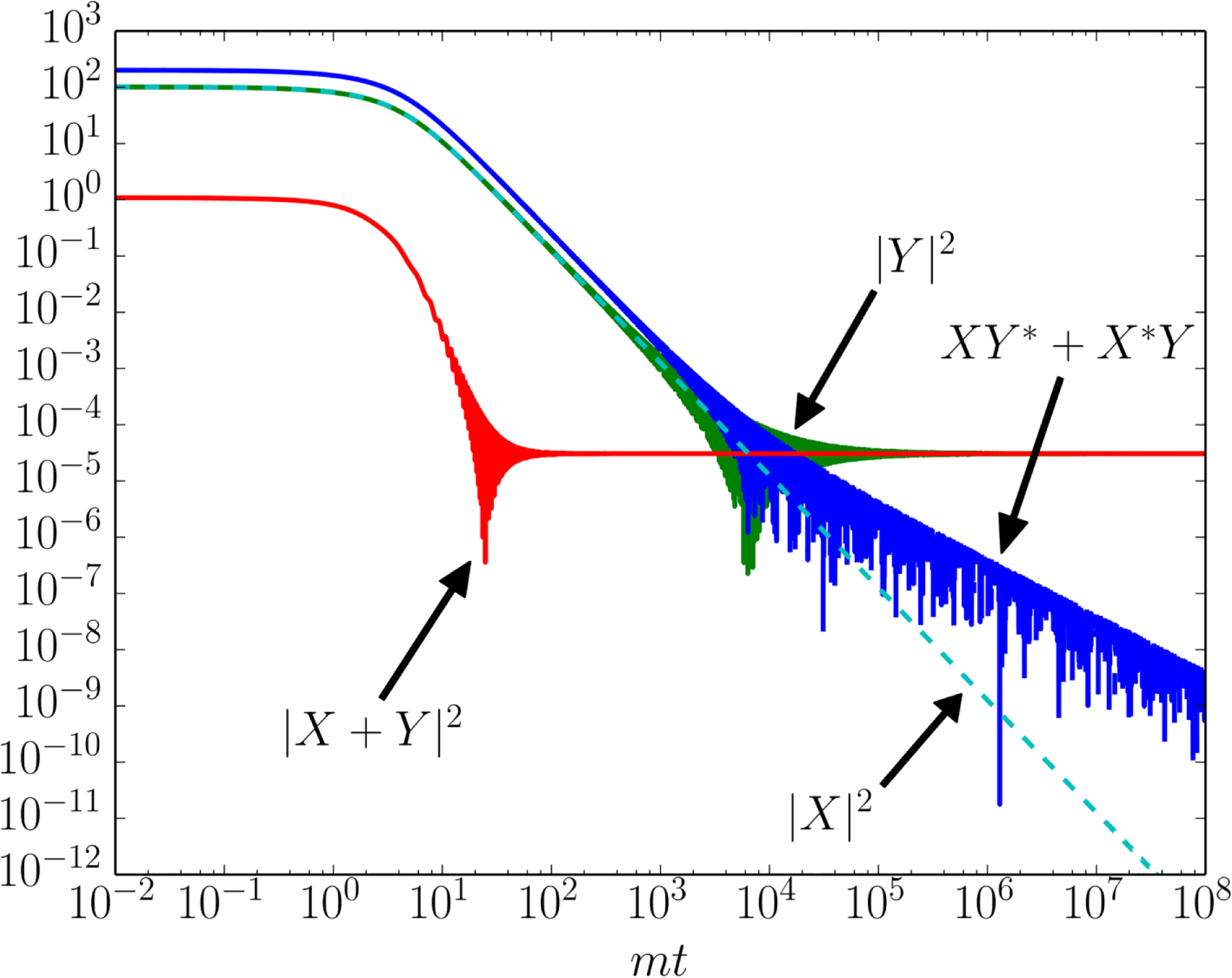
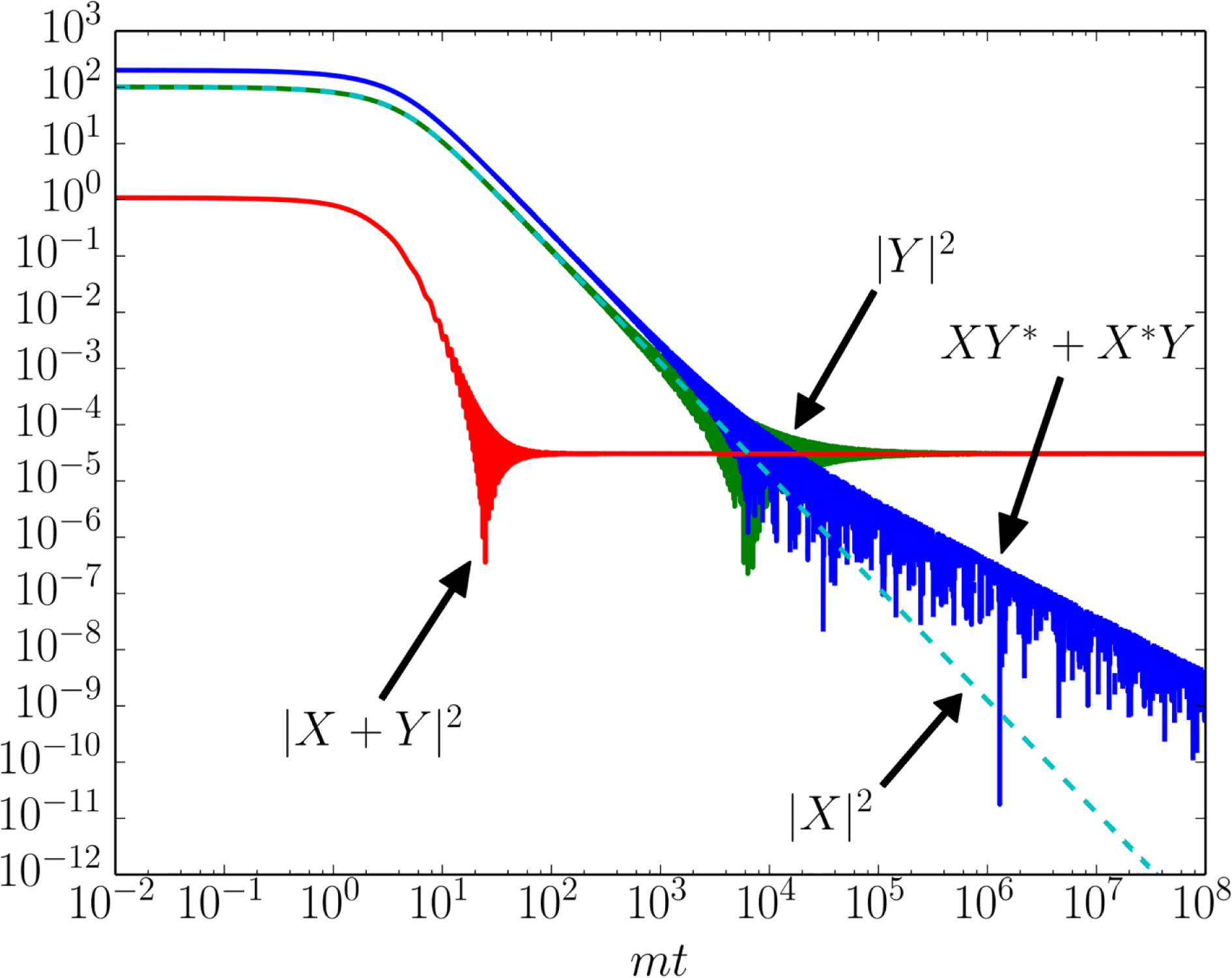
While for $E=0.2E_{c}$ the net function $\propto |X+Y|^{2}$ has already reached its asymptotic value at $tm\approx 20$ (see figure 3), the individual components $|X|^{2}$ , $|Y|^{2}$ and $XY^{\ast }+X^{\ast }Y$ display a violent time dependence on much longer times. Note also the subtle cancellations.

In the case of the Sauter pulse, see figure 2, the asymptotic values of $f$ are reached at shorter times with decreasing values of ${\it\tau}$ . The relatively large values of $f\;(t\approx 0)$ have sometimes tempted researchers to relate them to particular effects caused by the transient state. Clearly, only observables, e.g. those provided by probe beams, at asymptotic times are reliable. It is questionable, however, whether such probes can disentangle transient state contributions and asymptotic state contributions in a unique manner.

Figure 3. Time evolution of the components defined in (2.7) of the analytical solution (2.6) of the Schwinger case depicted for $E_{0}=0.2E_{c}$ . Cyan dashed curve: $|X|^{2}$ , green curve: $|Y|^{2}$ , blue curve: interference term $XY^{\ast }+X^{\ast }Y$ , red curve: $|X+Y|^{2}$ .

3 Laser-assisted Breit–Wheeler process

The laser-assisted, nonlinear Breit–Wheeler process (cf. Jansen & Müller 2013, 2016; Krajewska & Kaminski 2014; Wu & Xue 2014; Meuren et al. 2015) is dealt with within the strong-field QED (Furry picture) as reaction ${\it\gamma}^{\prime }\rightarrow e_{A}^{+}+e_{A}^{-}$ where $e_{A}^{\pm }$ denote dressed electron/positron states as Volkov solutions of the Dirac equation in a plane wave model with vector potential of the common classical background field

(3.1) $$\begin{eqnarray}A^{{\it\mu}}({\it\phi})={\it\gamma}_{X}^{-1}f_{X}({\it\phi}){\it\varepsilon}_{X}^{{\it\mu}}\cos {\it\phi}+{\it\gamma}_{L}^{-1}f_{L}({\it\eta}{\it\phi}){\it\varepsilon}_{L}^{{\it\mu}}\cos {\it\eta}{\it\phi},\end{eqnarray}$$

where the polarization four-vectors are ${\it\varepsilon}_{X,L}^{{\it\mu}}$ and the above-defined Keldysh parameters ${\it\gamma}_{1,2}$ have been transposed to ${\it\gamma}_{X,L}$ ; ${\it\gamma}^{\prime }$ denotes the high-energy probe photon traversing the field (3.1). The XFEL (frequency ${\it\omega}$ ) and laser (frequency ${\it\eta}{\it\omega}$ , we assume in the following ${\it\eta}\ll 1$ ) beams are co-propagating and their linear polarizations are set perpendicular to each other to simplify the cumbersome numerical evaluation. Both are pulsed as described, for the sake of computational convenience, by the envelope functions $f_{X}=\exp \{-{\it\phi}^{2}/(2{\it\tau}_{X}^{2})\}$ and $f_{L}=\cos ^{2}({\rm\pi}{\it\phi}/(2{\it\tau}_{L}))$ for $-{\it\tau}_{L}\leqslant {\it\phi}\leqslant +{\it\tau}_{L}$ and zero elsewhere for the latter pulse shape. In contrast to (2.2) we treat here a somewhat more realistic case with different pulse durations ${\it\tau}_{X}$ and ${\it\tau}_{L}$ . The invariant phase is ${\it\phi}=k\cdot x$ with the dot indicating the scalar product of the four-wave vector $k$ and the space–time coordinate $x$ . It is convenient to parameterize the produced positron’s phase space by the following three variables: (i) the momentum exchange parameter $\ell$ , (ii) the azimuthal angle ${\it\varphi}$ with respect to the polarization direction of the assisting laser field; and (iii) the shifted rapidity $z=\log (p_{+}^{+}/p_{+}^{-})/2+\log ((1+{\it\eta}\ell ){\it\omega}_{X}/{\it\omega}_{X^{\prime }})/2$ . The energy-momentum balance for laser-assisted pair production can be put into the form $k_{X^{\prime }}^{{\it\mu}}+k_{X}^{{\it\mu}}+\ell k_{L}^{{\it\mu}}=p_{+}^{{\it\mu}}+p_{-}^{{\it\mu}}$ ( ${\it\mu}$ is a Lorentz index, as above), where $\ell$ represents here a hitherto unspecified momentum exchange between the assisting laser field $L$ and the produced pair. We define light-front coordinates, e.g. $x^{\pm }=x^{0}\pm x^{3}$ and $\boldsymbol{x}_{\bot }=(x_{1},x_{2})$ and analogously the light front components of four-momenta of the probe photon $X^{\prime }$ , the XFEL photon $X$ , the laser beam photons $L$ and the positron (subscript $+$ ) and electron (subscript $-$ ). They become handy because the laser four-momentum vectors only have one non-vanishing light-front component $k_{X,L}^{-}=2{\it\omega}_{X,L}$ . In particular, the energy-momentum balance contains the three conservation equations in light-front coordinates $k_{X^{\prime }}^{+}=p_{+}^{+}+p_{-}^{+}$ and $\boldsymbol{p}_{+}^{\bot }=-\boldsymbol{p}_{-}^{\bot }$ . Moreover, the knowledge of all particle momenta makes it possible to calculate $\ell$ via the fourth equation $\ell =((p_{+}^{-}+p_{-}^{-}-k_{X^{\prime }}^{-})/(k_{X}^{-}-1)/{\it\eta})$ . Treating $(\ell ,z,{\it\varphi})$ as independent variables the positron’s four-momenta are completely determined by the above energy-momentum balance equations (see Nousch et al. (2016) for details, in particular for expressing the positron and electron momenta $p_{\pm }$ by $(\ell ,z,{\it\varphi})$ ).

Figure 4. Spectra for the laser-assisted Breit–Wheeler process for a probe photon of energy 60 MeV colliding head-on with an XFEL photon (energy 6 keV) and a co-propagating laser beam (frequency 10 eV). Further parameters are ${\it\eta}=1/600$ , ${\it\gamma}_{X}=10^{5}$ , ${\it\tau}_{X}=7{\it\tau}/(4{\rm\pi}{\it\eta})$ , ${\it\gamma}_{L}=2$ and ${\it\tau}_{L}=8{\rm\pi}$ in the field (3.1). These parameters translate into intensities of $6.2\times 10^{15}~\text{W}~\text{cm}^{-2}$ and $4.3\times 10^{19}~\text{W}~\text{cm}^{-2}$ for the XFEL and the laser, respectively. (a) Values of $\text{d}{\it\sigma}/\text{d}\ell \,\text{d}z\,\text{d}{\it\varphi}$ at $z=0$ and ${\it\varphi}={\rm\pi}$ as a function of $\ell$ (lower axis; the corresponding values of $p_{\bot }$ are given on the upper axis). The calculated spectrum is smoothed by a Gaussian window function with width ${\it\delta}=1.3$ to get the red curve. (b) Smoothed spectrum separately. (c) Phase ${\it\phi}$ as a function of $\ell$ (see Nousch et al. (2016) for details). The vertical dotted lines depict the positions of diverging $\text{d}{\it\phi}/\text{d}\ell$ , where two branches of ${\it\phi}(\ell )$ merge.

Figure 5. As in figure 4(b) but for ${\it\gamma}_{L}=10$ , laser intensity $1.7\times 10^{18}~\text{W}~\text{cm}^{-2}$ (a) and ${\it\gamma}_{L}=1$ , laser intensity $1.7\times 10^{20}~\text{W}~\text{cm}^{-2}$ (b).

The theoretical basis for formulating and evaluating the cross-section is outlined in Nousch et al. (2016). An example is displayed in figure 4(a) for ${\it\eta}=1/600$ , ${\it\gamma}_{X}=10^{5}$ , ${\it\tau}_{X}=7{\it\tau}/(4{\rm\pi}{\it\eta})$ , ${\it\gamma}_{L}=2$ and ${\it\tau}_{L}=8{\rm\pi}$ (examples for other parameters are exhibited in Nousch et al. (2016)) for kinematical conditions, where the linear Breit–Wheeler effect for $X^{\prime }+X$ is just above the threshold. The involved spectral distribution (note that without the laser assistance only the Breit–Wheeler peak centred at $\ell =0$ corresponding to $p_{\bot }=0.62~\text{m}$ would appear with a finite width as a consequence of the finite x-ray pulse duration; cf. Titov et al. (2012, 2013) and Nousch et al. (2012) for an enhancement of pair production in short laser pulses). The spectrum can be smoothed by a window function with a resolution scale of ${\it\delta}=1.3$ (which is an ad hoc choice to better show the strength distribution and which may be considered as a simple account for finite energy resolution respective $p_{\bot }$ distribution) resulting in the red curve which is exhibited separately in (b). In line with the interpretation in Seipt et al. (2016) and Nousch et al. (2016) the prominent peaks are caustics related to stationary phase points determined by the turning points of the invariant phase ${\it\phi}$ as a function of the variable $\ell$ , see figure 4(c). This interpretation implies that the total cross-section may be approximately factorized into a plain Breit–Wheeler production part and a final-state interaction part, where the latter means the redistribution of the produced particles by the impact of the laser field. An analogue interpretation of particle production in constant cross-field approximation in very strong fields has been put forward in Meuren, Keitel & Di Piazza (2016). Figure 5 demonstrates the strong impact of the laser field intensity. For smaller values of ${\it\gamma}_{L}$ , the transverse momentum spectrum becomes more stretched and its shape is changed. This challenges the observability of the peaks related to caustics in multi-shot experiments with fluctuating laser intensities. In fact, for the unfavourable case of equally weighted deviations, a window of less than 20 % is required to keep the peak structures, see figure 6. A truncated Gaussian distribution with $1{\it\sigma}$ width in the same interval is, of course, much more favourable for keeping the peaks, in particular for larger $p_{\bot }$ . We consider here only one particular case of the laser-assisted, linear Breit–Wheeler process which turns into the textbook Breit–Wheeler process upon switching off the laser. Nonlinearities with reference to the XFEL beam, subthreshold (with reference to the $X^{\prime }$ + XFEL kinematics) effects combined with larger laser intensities, carrier envelope phase effects and a wider range of kinematical parameters (e.g. ${\it\omega}_{L}=O$ (1 eV)) need to be explored as well to arrive at a complete picture. Among the yet to be analysed issues in terms of an experimental proposal are non-monochromaticity and misalignment disturbances.

Figure 6. As in figure 4(b) but variation of ${\it\gamma}_{L}$ around ${\it\gamma}_{L}=2$ . (a) ${\it\gamma}_{L}=2.22$ , (b) ${\it\gamma}_{L}=1.82$ , (c) superposition of smoothed spectra for ${\it\gamma}_{L}=1.88\ldots 2.12$ corresponding to the laser intensity parameter $a_{0}={\it\gamma}_{L}^{-1}=0.5\pm 0.03$ .

4 Summary

In summary we have supplied further important details of (i) the amplification effect of the assisted dynamical Schwinger effect, and (ii) the phase space redistribution in the laser-assisted Breit–Wheeler process. Both topics are motivated by the availability of x-rays by XFELs and upcoming ultra-high intensity laser beams. We consider the perspectives offered by the combination of both beam types resulting in bi-frequent fields. Concerning the Schwinger-related investigations we find that significant pair production by the dynamical assistance requires much higher frequencies than those provided by XFEL beams in conjunction with future ELI-IV field intensities. The crucial challenge for the laser-assisted Breit–Wheeler process and an access to the predicted caustic structures is the high-energy probe photon beam in combination with dedicated phase space selective detector set-ups. The bi-frequent fields are dealt with as a classical background. An avenue for further work is the proper account of quantum fluctuations and a unifying description of counter- and co-propagating fields.