1. Introduction
Markov Chain Monte Carlo (MCMC) is the most common method for inference, and for sampling multi-modal probability distributions (Hastings Reference Hastings1970; Gelfand & Smith Reference Gelfand and Smith1990; Sharma Reference Sharma2017; Hogg & Foreman-Mackey Reference Hogg and Foreman-Mackey2018; Speagle Reference Speagle2019). Following the rapid rise in the usage of Bayesian analysis in astronomy, MCMC (and nested sampling) techniques are now widely used (starting with Saha & Williams Reference Saha and Williams1994) for a variety of problems ranging from parameter estimation, model comparison, evaluating model goodness-of-fit, to forecasting for future experiments. This is because it is usually not possible to analytically calculate the multi-dimensional integrals needed for computing the Bayesian posteriors or evidence, and the numerical evaluation of these integrals can easily get intractable. Also, almost all numerical optimisation techniques run into problems while maximising the Bayesian posterior, when the total number of free parameters gets large. For this reason, there has been an unprecedented surge in the usage of Monte Carlo techniques in astrophysics. However, MCMC techniques are not tied only to Bayesian methods. They have also been used in frequentist analysis, for sampling complex multi-dimensional likelihood needed for parameter estimation (Wei et al. Reference Wei, Zhang, Shao, Wu and MÉszáros2017). That said, the ubiquity of MCMC methods in astronomy has been driven by the increasing usage of Bayesian methods. Applications of MCMC to a whole slew of astrophysical problems have been recently reviewed in (Sharma Reference Sharma2017). Although a large number of MCMC sampling methods have been used, the most widely used MCMC sampler in astrophysics is Emcee (Foreman-Mackey et al. Reference Foreman-Mackey, Hogg, Lang and Goodman2013). Bayesian model comparison is usually done using Nested sampling (Skilling et al. Reference Skilling2006), which is also a Monte Carlo-based technique. A large number of packages have been used in astrophysics for carrying out Bayesian model comparison using Nested Sampling techniques, such as MultiNest (Feroz, Hobson, & Bridges Reference Feroz, Hobson and Bridges2009), Nestle,Footnote a dynesty (Speagle Reference Speagle2020) etc. These techniques are however computationally expensive.
Although, MCMC has evolved into one of the most important tools for Bayesian inference (Robert & Casella Reference Robert and Casella2011), there are problems for which we cannot easily use this approach, especially in the case of large datasets or models with high dimensionality. Variational inference (Jordan et al. Reference Jordan, Ghahramani, Jaakkola and Saul1999) provides a good alternative approach for approximate Bayesian inference and has been the subject of considerable research recently (Blei, Kucukelbir, & McAuliffe Reference Blei, Kucukelbir and McAuliffe2017). It provides an approximate posterior for Bayesian inference faster than simple MCMC by solving an optimisation problem. Ranganath, Gerrish, & Blei (Reference Ranganath, Gerrish, Blei, Kaski and J. Corander2014) and Kucukelbir et al. (Reference Kucukelbir, Tran, Ranganath, Gelman and Blei2016) compare the convergence rates for variational inference against other sampling algorithms. They both show that variational inference convergences much faster in lesser number of iterations, even when the Metropolis–Hastings algorithm does not converge for the same problem.
The use of variational inference with deep learning is becoming more widespread in Astrophysics, especially in the areas of image generation and classification. Generating reliable synthetic data that can be used as calibration data for future surveys is an important task, which otherwise is a expensive task. Ravanbakhsh et al. (Reference Ravanbakhsh, Lanusse, Mandelbaum, Schneider and Poczos2016), Spindler, Geach, & Smith (Reference Spindler, Geach and Smith2020), Bastien et al. (Reference Bastien, Scaife, Tang, Bowles and Porter2021) have used conditional variational auto encoder (cVAE) for the task of image generation. Ravanbakhsh et al. (Reference Ravanbakhsh, Lanusse, Mandelbaum, Schneider and Poczos2016) used cVAE with convolutional layers and adversarial loss to generate galaxy images using galaxy zoo dataset, Bastien et al. (Reference Bastien, Scaife, Tang, Bowles and Porter2021) used cVAE with fully connected layers for the task of generating synthetic images from radio galaxies. Walmsley et al. (Reference Walmsley2019) used Bayesian neural networks (BNNs) for calculating posterior over image labels, which can provide uncertainties for each label for a given image. This can be converted to traditional deterministic classification by collapsing posterior to corresponding point estimates.
Jiang et al. (Reference Jiang, Jing, Wang, Liu, Li, Xu, Wang and Wang2021) used BNN for tracing fibrils in the
![]() $\mathrm{H}\alpha$
images of the sun. A specific BNN dubbed FibrilNet was used for the segmentation task, i.e., the probability of each pixel being a fibril is predicted with a uncertainty, then a fibril fitting algorithm is used on this mask to trace firbils and identify their orientation. A significant number of confirmed exoplanets (about 4 000 which is 30% of all identified exoplanets) have been identified through the validation of false positive cases from non-planet scenarios. Armstrong, Gamper, & Damoulas (Reference Armstrong, Gamper and Damoulas2020) used Gaussian process classifier (GPC) for this validation task and showed that their method is much faster than the competing algorithm vespa with comparable results. Lin & Wu (Reference Lin and Wu2021) combined deterministic deep learning classifier CLDNN (it combines CNN and a LSTM) with variational inference to detect events of binary coalescence in observation data of gravitational waves along with uncertainty estimates. This can be used in real-time detection of events and the events with high uncertainty can be pushed for further examination rather than accepting or discarding event. Morales-Álvarez et al. (Reference Morales-álvarez, Ruiz, Coughlin, Molina and Katsaggelos2019) used variational gaussian processes for tackling the problem of crowdsourcing in Glitch detection in LIGO. They show that variational gaussian processes very well compared to other traditional deep learning techniques and also take less time to train.
$\mathrm{H}\alpha$
images of the sun. A specific BNN dubbed FibrilNet was used for the segmentation task, i.e., the probability of each pixel being a fibril is predicted with a uncertainty, then a fibril fitting algorithm is used on this mask to trace firbils and identify their orientation. A significant number of confirmed exoplanets (about 4 000 which is 30% of all identified exoplanets) have been identified through the validation of false positive cases from non-planet scenarios. Armstrong, Gamper, & Damoulas (Reference Armstrong, Gamper and Damoulas2020) used Gaussian process classifier (GPC) for this validation task and showed that their method is much faster than the competing algorithm vespa with comparable results. Lin & Wu (Reference Lin and Wu2021) combined deterministic deep learning classifier CLDNN (it combines CNN and a LSTM) with variational inference to detect events of binary coalescence in observation data of gravitational waves along with uncertainty estimates. This can be used in real-time detection of events and the events with high uncertainty can be pushed for further examination rather than accepting or discarding event. Morales-Álvarez et al. (Reference Morales-álvarez, Ruiz, Coughlin, Molina and Katsaggelos2019) used variational gaussian processes for tackling the problem of crowdsourcing in Glitch detection in LIGO. They show that variational gaussian processes very well compared to other traditional deep learning techniques and also take less time to train.
VI has also been used in the task of parameter estimation. (Hortúa, Malagò, & Volpi Reference Hortúa, Malagò and Volpi2020a) combined BNN with normalising flows (NFs) for estimating astronomical and cosmological parameters from 21 cm surveys. Gabbard et al. (Reference Gabbard, Messenger, Heng, Tonolini and Murray-Smith2020) use cVAE for estimating the source parameters for gravitational wave detection. They show that the estimated parameters are close to the parameters from traditional MCMC algorithms. The significant amount of time taken in this process is training of the cVAE network; it takes about
![]() $\mathcal{O}(1)$
day. Once trained the network need not be trained again, and the GW detection parameters can be obtained six orders of magnitude faster, when compared to existing techniques.
$\mathcal{O}(1)$
day. Once trained the network need not be trained again, and the GW detection parameters can be obtained six orders of magnitude faster, when compared to existing techniques.
Few works were done comparing MCMC and VI approached. In the work done by Regier et al. (Reference Regier, Miller, Schlegel, Adams and McAuliffe2018), a generative model for constructing astronomical catalogs using telescope image datasets was developed using Bayesian inference. They developed two approximate inference procedures using MCMC and variational inference for their statistical model and compared the effectiveness of the methods. The aforementioned paper found that for the synthetic data generated from their model, MCMC was better in estimating uncertainties, but it was about three orders slower compared when compared to the competing variational inference procedure. Whereas on real data taken from SDSS, the uncertainty estimates in both the procedures were far from perfect. In that work, they were successful in applying variational inference to the entire SDSS data, thus demonstrating its feasibility on very large datasets. This technique has also been used in lensing for estimating the uncertainties in parameters through BNNs (Blundell et al. Reference Blundell, Cornebise, Kavukcuoglu and Wierstra2015) for the problem of Singular Isothermal Ellipsoid plus external shear and total flux magnification (Perreault Levasseur, Hezaveh, & Wechsler Reference Perreault Levasseur, Hezaveh and Wechsler2017). Recently, Hortúa et al. (Reference Hortúa, Volpi, Marinelli and Malagò2020b) used BNN for estimating parameters for cosmic microwave background. They found that VI was four orders faster when compared to MCMC with slight compromise in accuracy. They also showed that using output from BNN as initial proposal for Markov chain resulted in higher acceptance rate for Metropolis–Hasting algorithm.
For the purpose of computing Bayesian evidence, needed for model comparison, Bernardo et al. (Reference Bernardo2003) have compared Variational Bayes and Annealed importance sampling (AIS) (Neal Reference Neal2001) for the task of evidence estimation and posterior evaluation. Their results show that Variational Bayes is about 100 times faster when compared to AIS without any significant loss in accuracy.
In this study, we shall explain how a particular adaptation of variational inference (dubbed ADVI) can supersede Monte Carlo techniques such as MCMC and nested sampling for parameter estimation and Bayesian model comparison and apply these techniques to five different problems in astrophysics and compare the results to Monte Carlo methods. The outline of this paper is as follows. In Section 2, we introduce the idea of Bayesian modeling and provide an introduction to MCMC. In Section 3, we present an overview of the variational inference method. In Section 4, we discuss a specific implementation of variational inference called Automatic differentiation variational inference (ADVI). In Section 5, we explain how variational inference can be used for parameter estimation and model comparison. Applications to ancillary problems in astronomy are outlined in Section 6. We conclude in Section 7. The code for all the analyses in this study can also be found on a github link provided at the end of this study.
2. Overview of Bayesian modeling and MCMC
We first start with a very brief primer on Bayesian modeling and parameter inference, and then explain how Monte Carlo methods are applied to these problems. More details on Bayesian methods and their applications in astrophysics are reviewed in Trotta (Reference Trotta2017), Sharma (Reference Sharma2017), Kerscher & Weller (Reference Kerscher and Weller2019) and references therein. Bayes Theorem in general terms is given as
where
![]() $p(\theta)$
is the prior belief on the parameter
$p(\theta)$
is the prior belief on the parameter
![]() $\theta$
,
$\theta$
,
![]() $p(\textbf{D} |\theta)$
is known as the likelihood, which models the probability of observing the data
$p(\textbf{D} |\theta)$
is known as the likelihood, which models the probability of observing the data
![]() $\textbf{D}$
given parameter
$\textbf{D}$
given parameter
![]() $\theta$
.
$\theta$
.
![]() $p(\theta|\textbf{D})$
called posterior probability, is the conditional probability of
$p(\theta|\textbf{D})$
called posterior probability, is the conditional probability of
![]() $\theta$
given
$\theta$
given
![]() $\textbf{D}$
, which can be interpreted as the posterior belief over the parameters after evidence or data
$\textbf{D}$
, which can be interpreted as the posterior belief over the parameters after evidence or data
![]() $\textbf{D}$
is observed.
$\textbf{D}$
is observed.
![]() $p(\textbf{D})$
is termed as the marginal likelihood or model evidence, which is obtained by integrating out
$p(\textbf{D})$
is termed as the marginal likelihood or model evidence, which is obtained by integrating out
![]() $\theta$
from the joint probability distribution
$\theta$
from the joint probability distribution
![]() $p(\textbf{D}, \theta) $
, the numerator term in Equation (1). All the conditional probabilities in Equation (1) are implicitly conditioned on the model m. Hence, the marginal likelihood
$p(\textbf{D}, \theta) $
, the numerator term in Equation (1). All the conditional probabilities in Equation (1) are implicitly conditioned on the model m. Hence, the marginal likelihood
![]() $p(\textbf{D})$
provides the probability that the model m will generate the data irrespective of its parameter values and is a useful quantity for model selection.
$p(\textbf{D})$
provides the probability that the model m will generate the data irrespective of its parameter values and is a useful quantity for model selection.
Bayesian models treat the parameters as a random variable and impose preliminary knowledge about the parameter through the prior. Inference in the Bayesian model amounts to conditioning on the data and computing the posterior
![]() $P(\theta|\textbf{D})$
. This computation is intractable for models where the prior and likelihood take different functional forms (non-conjugates). In these cases, analytical closed form estimation of the marginal likelihood is also intractable. This has led to the usage of sampling methods to solve for such intractable distributions.
$P(\theta|\textbf{D})$
. This computation is intractable for models where the prior and likelihood take different functional forms (non-conjugates). In these cases, analytical closed form estimation of the marginal likelihood is also intractable. This has led to the usage of sampling methods to solve for such intractable distributions.
MCMC methods are sampling techniques, which enable us to sample for any unnormalised distribution (Hastings Reference Hastings1970; Gelfand & Smith Reference Gelfand and Smith1990; Sharma Reference Sharma2017; Hogg & Foreman-Mackey Reference Hogg and Foreman-Mackey2018; Speagle Reference Speagle2019). The idea of MCMC algorithms is to construct and sample from a Markov chain whose stationary distribution is the same as the desired distribution, and use those samples to compute expectations and integrals of required quantities using Monte Carlo integration techniques. We will briefly introduce the Metropolis–Hastings algorithm (M–H) (Metropolis et al. Reference Metropolis, Rosenbluth, Rosenbluth, Teller and Teller1953; Hastings Reference Hastings1970), which is the simplest MCMC algorithm. Although the M–H algorithm is simple, it shares many of the same principles with the newer and more complex MCMC algorithms. M–H algorithm requires a proposal distribution
![]() $q(\theta'|\theta)$
, which is used to generate parameter samples. Assume the unnormalised posterior distribution over the parameters
$q(\theta'|\theta)$
, which is used to generate parameter samples. Assume the unnormalised posterior distribution over the parameters
![]() $\theta$
to be represented as the function
$\theta$
to be represented as the function
![]() $f(\theta)$
, i.e.
$f(\theta)$
, i.e.
![]() $f(\theta) \propto p(\textbf{D} |\theta)p(\theta)$
. The M–H algorithm works as follows.
$f(\theta) \propto p(\textbf{D} |\theta)p(\theta)$
. The M–H algorithm works as follows.
-
• Assume that
 $\theta_k$
is the previous sampled point, draw the next sample
$\theta_k$
is the previous sampled point, draw the next sample
 $\theta'$
from the proposal distribution
$\theta'$
from the proposal distribution
 $q(\theta'|\theta_k)$
$q(\theta'|\theta_k)$
-
• Draw a random number r from a uniform distribution between 0 and 1
-
• Accept the sample if
 $\frac{f(\theta')q(\theta_t|\theta')}{f(\theta_k)q(\theta'|\theta_t)} > r$
$\frac{f(\theta')q(\theta_t|\theta')}{f(\theta_k)q(\theta'|\theta_t)} > r$
 $(\theta_{k+1}\leftarrow\theta')$
else reject the sample
$(\theta_{k+1}\leftarrow\theta')$
else reject the sample
 $(\theta_{k+1}\leftarrow\theta_k)$
$(\theta_{k+1}\leftarrow\theta_k)$
When run long enough, the M–H algorithm produces samples from the desired posterior distribution. Although the algorithm is simple, there are many different parameters in the algorithm that are to be tuned to achieve ideal results. One of the important parameters for the algorithm is the number of samples that the algorithm has to run for achieving reliable results. There is nothing called absolute convergence for a MCMC algorithm and one can only rely on heuristics. We can run multiple chains with different initial points and can compare posterior inferences like the mean and variance from both the chains. There are other metrics like autocorrelation time (Sokal Reference Sokal1997) and Gelman–Rubin diagnostic (Gelman & Rubin Reference Gelman and Rubin1992) which can be used to check for pseudo-convergence of MCMC algorithms.
Choosing a proposal distribution also plays a vital role in the quality of samples that are produced. A proposal distribution that is too narrow can result in accepting all the samples and will take a lot of time covering the entire parameter space, while a proposal distribution that is too wide can result in taking large steps and rejecting most of the samples. For example, consider a Gaussian distribution
![]() $\mathcal{N}(0,\sigma)$
as the proposal distribution and
$\mathcal{N}(0,\sigma)$
as the proposal distribution and
![]() $\theta_k$
is the current sample, then the next sample
$\theta_k$
is the current sample, then the next sample
![]() $\theta'$
is calculated as
$\theta'$
is calculated as
![]() $\theta' \leftarrow \theta_k + \mathcal{N}(0,\sigma)$
. The value of
$\theta' \leftarrow \theta_k + \mathcal{N}(0,\sigma)$
. The value of
![]() $\sigma$
dictates the distance between the two proposal and it is the step size in this case. One can use a simple heuristic like the acceptance ratio for tuning the step size, high acceptance ratio means that you are accepting all the generated samples and hence has to reduce the step size and vice-versa. The choice of proposal distribution is not problem independent and finding efficient proposal distribution can become increasingly difficult with increase in dimensions of parameter space.
$\sigma$
dictates the distance between the two proposal and it is the step size in this case. One can use a simple heuristic like the acceptance ratio for tuning the step size, high acceptance ratio means that you are accepting all the generated samples and hence has to reduce the step size and vice-versa. The choice of proposal distribution is not problem independent and finding efficient proposal distribution can become increasingly difficult with increase in dimensions of parameter space.
Initialisation like proposal distribution is an input parameter to most of the MCMC algorithms. A badly initialised chain can spend a lot of time in regions of low probability, which can result in a large number iterations for the MCMC algorithm to reach a stationary condition. In such cases, we discard a certain number of initial samples from the chain before the stationary condition is reached. This idea is called as burn-in and the length of burn-in depends on each individual problem and initialisation. If the proposal distribution is multi-modal, then starting multiple chains with different initialisations and comparing the samples will help in identifying if chains have covered all the modes. If different initialisations result in different chains, then there is no straight forward method of combining the samples from multiple chains. One has to run a MCMC algorithm for a long time so that each chain can cover all the modes, and produce a representative sample or resort to Nested sampling techniques.
There are many advanced methods like tempering (Vousden, Farr, & Mandel Reference Vousden, Farr and Mandel2015), which help the MCMC samplers from being stuck at one mode in multi-modal distributions. Hamiltonian Monte Carlo (HMC) (Betancourt Reference Betancourt2018) which uses the gradients of the function
![]() $f(\theta)$
for efficient generation of proposals. HMC avoids the random walk sampling approach and hence can be efficient in exploring parameter space even for high dimensional cases. HMC’s performance is sensitive to two tunable parameters: the step size
$f(\theta)$
for efficient generation of proposals. HMC avoids the random walk sampling approach and hence can be efficient in exploring parameter space even for high dimensional cases. HMC’s performance is sensitive to two tunable parameters: the step size
![]() $\epsilon$
and the desired number of steps L. If L is too small then HMC ends up exhibiting random walk behaviour which is undesirable, and if L is too high the algorithm can waste a lot of computational power. No-U-Turn Sampler (NUTS) (Hoffman & Gelman Reference Hoffman and Gelman2011) is an extension to HMC which eliminates the manual tuning of L and calculates the number of steps through a recursive algorithm. Therefore, NUTS is as efficient as HMC if not better in most of the cases and eliminates the need for manual tuning.
$\epsilon$
and the desired number of steps L. If L is too small then HMC ends up exhibiting random walk behaviour which is undesirable, and if L is too high the algorithm can waste a lot of computational power. No-U-Turn Sampler (NUTS) (Hoffman & Gelman Reference Hoffman and Gelman2011) is an extension to HMC which eliminates the manual tuning of L and calculates the number of steps through a recursive algorithm. Therefore, NUTS is as efficient as HMC if not better in most of the cases and eliminates the need for manual tuning.
Affine invariant ensemble sampling uses multiple random walkers for drawing proposal samples and it significantly outperforms the standard M–H algorithm in drawing independent samples with much lesser autocorrelation time (Goodman & Weare Reference Goodman and Weare2010; Foreman-Mackey et al. Reference Foreman-Mackey, Hogg, Lang and Goodman2013). Nested sampling (Feroz et al. Reference Feroz, Hobson, Cameron and Pettitt2019) converts the multi-dimensional integration of evidence D into a 1D integration by mapping likelihood to the corresponding prior volume in the corresponding iso-likelihood contours on a 2D curve. This 1D curve integration can be evaluated using trapezoid rule. MCMC methods as seen, may require a lot of tuning and in most cases this tuning can require a deeper mathematical understanding of algorithm being used for achieving desirable results.
Therefore in this study, we study a alternative method for performing Bayesian inference called as variational inference, which is considerably faster than MCMC techniques and does not suffer from any convergence issues.
3. Variational inference
The central idea behind variational inference is to solve an optimisation problem by approximating the target probability density. The target probability density could be the Bayesian posterior or the likelihood from frequentist analysis. The first step is to propose a family of densities and then to find the member of that family, which is closest to the target probability density. Kullback–Leibler (KL) divergence (Kullback & Leibler Reference Kullback and Leibler1951) is used as a measure of such proximity.
For this purpose, we then posit a family of approximate densities (variational distribution)
![]() $\mathcal{Q}$
. This is a set of densities over the parameters. It is important to choose an complex enough variational family such that the target distribution lies in it, otherwise the solution obtained will not be close to the target probability distribution. Then, we try to find the member of that family
$\mathcal{Q}$
. This is a set of densities over the parameters. It is important to choose an complex enough variational family such that the target distribution lies in it, otherwise the solution obtained will not be close to the target probability distribution. Then, we try to find the member of that family
![]() $q(\theta) \in \mathcal{Q}$
, known as the variational posterior that minimises the KL divergence to the exact posterior,
$q(\theta) \in \mathcal{Q}$
, known as the variational posterior that minimises the KL divergence to the exact posterior,
The KL divergence is defined as
where all the expectations are with respect to
![]() $q(\theta)$
. We shall see in Equation (4) that KL divergence depends on the posterior
$q(\theta)$
. We shall see in Equation (4) that KL divergence depends on the posterior
![]() $\log p(\theta | \textbf{D})$
, which is usually intractable to compute. We can expand the conditional using (1) and re-write KL divergence as
$\log p(\theta | \textbf{D})$
, which is usually intractable to compute. We can expand the conditional using (1) and re-write KL divergence as
 \begin{align} \mathrm{KL} (q(\theta) | | p(\theta | \textbf{D})) & = \mathbb{E}_{q(\theta)}\left[\log q(\theta)\right] + \mathbb{E}_{q(\theta)}\left[\log p(\textbf{D})\right] \nonumber \\[3pt]& \quad -\mathbb{E}_{q(\theta)}\left[\log p(\textbf{D}, \theta)\right] \nonumber \\[3pt]& = \log p(\textbf{D}) + \mathbb{E}_{q(\theta)}\left[\log q(\theta)\right] \nonumber \\[3pt]&\quad -\mathbb{E}_{q(\theta)}\left[\log p(\textbf{D}, \theta)\right] .\end{align}
\begin{align} \mathrm{KL} (q(\theta) | | p(\theta | \textbf{D})) & = \mathbb{E}_{q(\theta)}\left[\log q(\theta)\right] + \mathbb{E}_{q(\theta)}\left[\log p(\textbf{D})\right] \nonumber \\[3pt]& \quad -\mathbb{E}_{q(\theta)}\left[\log p(\textbf{D}, \theta)\right] \nonumber \\[3pt]& = \log p(\textbf{D}) + \mathbb{E}_{q(\theta)}\left[\log q(\theta)\right] \nonumber \\[3pt]&\quad -\mathbb{E}_{q(\theta)}\left[\log p(\textbf{D}, \theta)\right] .\end{align}
The expected value of the log evidence with respect to the variational posterior is the log evidence term itself, and is independent of the variational distribution. Hence, minimising the KL divergence term is equivalent to minimising the second and third terms in Equation (4). Equivalently, one could estimate the variational posterior by maximising the variational lower bound (also known as evidence lower bound or ELBO Blei et al. Reference Blei, Kucukelbir and McAuliffe2017) with respect to
![]() $q(\theta)$
.
$q(\theta)$
.
ELBO can be viewed as a lower bound to the evidence term by rearranging the terms in Equation (4).
The KL divergence between any two distributions is a non-negative quantity and hence,
![]() $\log p(\textbf{D}) \geq \mathrm{ELBO}(q(\theta))$
. Again, we can see that as the evidence term is independent of the variational distribution, maximising ELBO will result in minimising the KL divergence between the variational posterior and the actual posterior.
$\log p(\textbf{D}) \geq \mathrm{ELBO}(q(\theta))$
. Again, we can see that as the evidence term is independent of the variational distribution, maximising ELBO will result in minimising the KL divergence between the variational posterior and the actual posterior.
Expanding the joint likelihood in Equation (5), the variational lower bound can be rewritten as
 \begin{align} \mathrm{ELBO}(q(\theta)) &= \mathbb{E}_{q(\theta)}\left[\log p(\textbf{D}| \theta)\right] - \mathbb{E}_{q(\theta)}\left[\log q(\theta)\right]\nonumber \\[3pt]&\quad + \mathbb{E}_{q(\theta)}\left[\log p(\theta)\right] \nonumber \\[3pt]& = \mathbb{E}_{q(\theta)}\left[\log p(\textbf{D}| \theta)\right] - \mathrm{KL} (q(\theta) | | p(\theta)).\end{align}
\begin{align} \mathrm{ELBO}(q(\theta)) &= \mathbb{E}_{q(\theta)}\left[\log p(\textbf{D}| \theta)\right] - \mathbb{E}_{q(\theta)}\left[\log q(\theta)\right]\nonumber \\[3pt]&\quad + \mathbb{E}_{q(\theta)}\left[\log p(\theta)\right] \nonumber \\[3pt]& = \mathbb{E}_{q(\theta)}\left[\log p(\textbf{D}| \theta)\right] - \mathrm{KL} (q(\theta) | | p(\theta)).\end{align}
The first term in Equation (7), which can be interpreted as the data fit term, will result in selecting a variational posterior, which maximises the likelihood of observing the data. While the second term can be seen as the regularisation term, which minimises the KL divergence between the variational posterior and the prior. Thus, ELBO implicitly regularises the selection of the variational posterior and trades-off likelihood and prior in arriving at a proper choice for the variational posterior. The log evidence term in Equation (6) and hence the variational lower bound (ELBO) are implicitly conditioned on the hyper-parameters of the model. The hyper-parameters can be learned by maximising the variational lower bound. Typically, the variational parameters and the hyper-parameters are learned alternatively by maximising the variational lower bound.
Variational inference converts the Bayesian parameter estimation into an optimisation problem through the maximisation of the variational lower bound. Hence, convergence is guaranteed in variational inference, as is the case of any optimisation problem, to a local optimum and if the likelihood is log-concave then to a global optimum. Another important feature of variational inference is that it is trivial to parallelise. It can handle large datasets with ease without compromising on the model complexity with the use of stochastic variational inference (Hoffman et al. Reference Hoffman, Blei, Wang and Paisley2013). In the case of some specific likelihoods and variational families, ELBO cannot be computed in closed form as the computations of required expectations are intractable. In these settings, either one resorts to model specific algorithms (Jaakkola & Jordan Reference Jaakkola and Jordan1996; Blei & Lafferty Reference Blei and Lafferty2007; Braun & McAuliffe Reference Braun and McAuliffe2010) or generic algorithms that require model specific calculations (Knowles & Minka Reference Knowles and Minka2011; Wang & Blei Reference Wang and Blei2013; Paisley, Blei, & Jordan Reference Paisley, Blei and Jordan2012).
Recent advances in variational inference use ‘black box’ techniques to avoid model specific lower bound calculations (Ranganath et al. Reference Ranganath, Gerrish, Blei, Kaski and J. Corander2014; Kingma & Welling Reference Kingma and Welling2013; Jimenez Rezende, Mohamed, & Wierstra Reference Jimenez Rezende, Mohamed and Wierstra2014; Salimans & Knowles Reference Salimans and Knowles2014; Titsias & Lázaro-Gredilla Reference Titsias and Lázaro-Gredilla2014). These ideas were leveraged to develop automatic differentiation variational inference techniques (ADVI) (Kucukelbir et al. Reference Kucukelbir, Tran, Ranganath, Gelman and Blei2016) that works on any model written in the probabilistic programming systems such as Stan (Carpenter et al. Reference Carpenter2016)Footnote b or PyMC3 (Salvatier, Wiecki, & Fonnesbeck Reference Salvatier, Wiecki and Fonnesbeck2016).
4. Automatic differentiation variational inference
Variational inference algorithm requires model specific computations to obtain the variational lower bound. Typically, variational inference requires the manual calculation of a custom optimisation objective function by choosing a variational family relevant to the model, computing the objective function and its derivative, and running a gradient-based optimisation.
Automatic differentiation variational inference (ADVI) (Kucukelbir et al. Reference Kucukelbir, Tran, Ranganath, Gelman and Blei2016) automates this by building a ‘black-box’ variational inference technique, which takes a probabilistic model and a dataset as inputs and returns posterior inferences about the model’s latent variables. ADVI achieves the results by performing the following sequence of steps.
-
• ADVI applies a transformation on the latent variables
 $\theta$
to obtain real-valued latent variables
$\theta$
to obtain real-valued latent variables
 $\zeta$
, where
$\zeta$
, where
 $\zeta = T(\theta)$
and
$\zeta = T(\theta)$
and
 $\zeta \in \mathbb{R}^{{\rm dim}(\theta)}$
. The transformation T ensures that all the latent variables lie on a real co-ordinate space, and allows ADVI to use the same variational family
$\zeta \in \mathbb{R}^{{\rm dim}(\theta)}$
. The transformation T ensures that all the latent variables lie on a real co-ordinate space, and allows ADVI to use the same variational family
 $q(\zeta; \phi)$
(e.g. Gaussian where
$q(\zeta; \phi)$
(e.g. Gaussian where
 $q(\zeta; \phi) = \mathcal{N}(\zeta;\mu,\Sigma))$
on all the models. This transformation changes the variational lower bound and the joint likelihood
$q(\zeta; \phi) = \mathcal{N}(\zeta;\mu,\Sigma))$
on all the models. This transformation changes the variational lower bound and the joint likelihood
 $p(\textbf{D}, \theta)$
is written in terms of
$p(\textbf{D}, \theta)$
is written in terms of
 $\zeta$
as
$\zeta$
as
 $p(\textbf{D}, \zeta) = p(\textbf{D}, T^{-1}(\zeta)) |J_{T^{-1}}(\zeta)|$
, where
$p(\textbf{D}, \zeta) = p(\textbf{D}, T^{-1}(\zeta)) |J_{T^{-1}}(\zeta)|$
, where
 $|\cdot|$
represents the determinant. Here,
$|\cdot|$
represents the determinant. Here,
 $J_{T^{-1}}(\zeta)$
is the Jacobian of the inverse of the transformation T. The variational lower bound takes the following form under this transformation.
(8)
$J_{T^{-1}}(\zeta)$
is the Jacobian of the inverse of the transformation T. The variational lower bound takes the following form under this transformation.
(8) \begin{align} \!\!\!\!\!\!\!\!\! ELBO\left(q\left(\zeta; \phi\right)\right)=\, &\mathbb{E}_{q\left(\zeta; \phi\right)} \left[\log p\left(\textbf{D}, T^{-1}\left(\zeta\right)\right) +log |J_{T^{-1}}\left(\zeta\right)|\right] \nonumber \\[3pt] &-\mathbb{E}_{q\left(\zeta; \phi\right)} \left(\log q\left(\zeta; \phi\right)\right).\end{align}
\begin{align} \!\!\!\!\!\!\!\!\! ELBO\left(q\left(\zeta; \phi\right)\right)=\, &\mathbb{E}_{q\left(\zeta; \phi\right)} \left[\log p\left(\textbf{D}, T^{-1}\left(\zeta\right)\right) +log |J_{T^{-1}}\left(\zeta\right)|\right] \nonumber \\[3pt] &-\mathbb{E}_{q\left(\zeta; \phi\right)} \left(\log q\left(\zeta; \phi\right)\right).\end{align}
-
• The variational objective (ELBO) as a function of the variational parameters
 $\phi$
(for instance mean
$\phi$
(for instance mean
 $\mu$
and covariance
$\mu$
and covariance
 $\Sigma$
of a Gaussian) can be optimised using gradient ascent.
$\Sigma$
of a Gaussian) can be optimised using gradient ascent.However, the calculation of gradients of ELBO with respect to the variational parameters is generally intractable. To push the gradients inside the expectation, ADVI applies elliptical standardisation. Consider a transformation
 $S_{\phi}$
, which absorbs the variational parameters
$S_{\phi}$
, which absorbs the variational parameters
 $\phi$
and converts the non-standard Gaussian
$\phi$
and converts the non-standard Gaussian
 $\zeta$
into a standard Gaussian
$\zeta$
into a standard Gaussian
 $\eta$
,
$\eta$
,
 $\eta = S_{\phi} (\zeta)$
. For instance,
$\eta = S_{\phi} (\zeta)$
. For instance,
 $\eta = L^{-1}(\zeta - \mu)$
, where L is the Cholesky factor for the covariance
$\eta = L^{-1}(\zeta - \mu)$
, where L is the Cholesky factor for the covariance
 $\Sigma$
. The expectation in the variational lower bound can be written in terms of the standard Gaussian
$\Sigma$
. The expectation in the variational lower bound can be written in terms of the standard Gaussian
 $\displaystyle q(\eta) = \mathcal{N}(\eta;0,I)$
and the variational lower bound becomes
(9)
$\displaystyle q(\eta) = \mathcal{N}(\eta;0,I)$
and the variational lower bound becomes
(9) \begin{align}ELBO\left(q\left(\zeta; \phi\right)\right) =\,& \mathbb{E}_{\mathcal{N}\left(\eta;0,I\right)} \left[\log p\!\left(\textbf{D}, T^{-1}\left(S_{\phi}^{-1}\left(\eta\right)\right)\right)\right. \nonumber \\[4pt]&\!\left.+ \log |J_{T^{-1}}\left(S_{\phi}^{-1}\left(\eta\right)\right)|\right] + \mathbb{H}\left(q\left(\zeta; \phi\right)\right).\end{align}
\begin{align}ELBO\left(q\left(\zeta; \phi\right)\right) =\,& \mathbb{E}_{\mathcal{N}\left(\eta;0,I\right)} \left[\log p\!\left(\textbf{D}, T^{-1}\left(S_{\phi}^{-1}\left(\eta\right)\right)\right)\right. \nonumber \\[4pt]&\!\left.+ \log |J_{T^{-1}}\left(S_{\phi}^{-1}\left(\eta\right)\right)|\right] + \mathbb{H}\left(q\left(\zeta; \phi\right)\right).\end{align}
-
• The entropy term in Equation (9) is problem independent and its gradient can be evaluated in closed form for a Gaussian distribution. Therefore, its gradients are evaluated before hand and are used for all the problems. The variational lower bound Equation (9) has expectations independent of
 $\zeta$
, and hence the gradient of ELBO with respect to
$\zeta$
, and hence the gradient of ELBO with respect to
 $\phi$
can be calculated by pushing the gradient inside the expectations.
(10)The gradients inside the expectations are computed using automatic differentiation, while the expectation with respect to the standard Gaussian is computed using Monte Carlo sampling. The values of
$\phi$
can be calculated by pushing the gradient inside the expectations.
(10)The gradients inside the expectations are computed using automatic differentiation, while the expectation with respect to the standard Gaussian is computed using Monte Carlo sampling. The values of \begin{align}\nabla_{\phi} ELBO\left(q\left(\zeta; \phi\right)\right) =\ & \mathbb{E}_{\mathcal{N}\left(\eta;0,I\right)} \left[\left\{\nabla_{\theta} \log p\!\left(\textbf{D},\theta\right) \nabla_{\zeta} T^{-1}\right.\right. \nonumber \\[4pt]&\!+ \left.\left. \nabla_{\zeta} \log |J_{T^{-1}}\left(\zeta\right)\right\}\nabla_{\phi}S_{\phi}^{-1}\left(\eta\right)\right] \nonumber \\[4pt]&\!+\nabla_{\phi}\mathbb{H}\left(q\left(\zeta; \phi\right)\right) .\end{align}
\begin{align}\nabla_{\phi} ELBO\left(q\left(\zeta; \phi\right)\right) =\ & \mathbb{E}_{\mathcal{N}\left(\eta;0,I\right)} \left[\left\{\nabla_{\theta} \log p\!\left(\textbf{D},\theta\right) \nabla_{\zeta} T^{-1}\right.\right. \nonumber \\[4pt]&\!+ \left.\left. \nabla_{\zeta} \log |J_{T^{-1}}\left(\zeta\right)\right\}\nabla_{\phi}S_{\phi}^{-1}\left(\eta\right)\right] \nonumber \\[4pt]&\!+\nabla_{\phi}\mathbb{H}\left(q\left(\zeta; \phi\right)\right) .\end{align}
 $\zeta = S_{\phi}^{-1}(\eta)$
and
$\zeta = S_{\phi}^{-1}(\eta)$
and
 $\theta = T^{-1}(S_{\phi}^{-1}(\eta))$
at corresponding
$\theta = T^{-1}(S_{\phi}^{-1}(\eta))$
at corresponding
 $\eta$
are calculated and substituted while evaluating the expectation.
$\eta$
are calculated and substituted while evaluating the expectation.
5. Parameter estimation and Bayesian model selection
Once we have the approximate posterior, we can draw samples from the variational posterior over the parameters. Unlike in MCMC, the number of samples required is not an input to the optimisation and it does not affect the training time of variational inference. We can find a point estimate of the parameters using the mean (or median) of the samples from the variational posterior. In certain cases, we consider the variational distribution family to be parameterised by the mean, and we learn the variational posterior by maximising the variational lower bound with respect to the mean. In these cases, we can directly make use of the mean rather than sampling from the variational posterior. The errors and marginalised credible intervals for the parameters can be obtained by passing the samples from ADVI (similar to MCMC) to the corner module (Foreman-Mackey Reference Foreman-Mackey2016) or similar packages such as ChainConsumer (Hinton Reference Hinton2016) or GetDist (Lewis Reference Lewis2019).
A major challenge in statistical modeling is choosing a proper model, which generates the observations. In a Bayesian setting, one could use a posterior probability over the models in choosing the right model. Consider two models
![]() $M_1$
and
$M_1$
and
![]() $M_2$
with a prior probability over them denoted by
$M_2$
with a prior probability over them denoted by
![]() $p(M_1)$
and
$p(M_1)$
and
![]() $p(M_2)$
. The probability of these models generating the observations irrespective of the parameter values is given by the evidence (marginal likelihood)
$p(M_2)$
. The probability of these models generating the observations irrespective of the parameter values is given by the evidence (marginal likelihood)
![]() $p(\textbf{D} | M_1)$
and
$p(\textbf{D} | M_1)$
and
![]() $p(\textbf{D} | M_2)$
. Combining the prior and the likelihood, one could obtain the posterior over the models
$p(\textbf{D} | M_2)$
. Combining the prior and the likelihood, one could obtain the posterior over the models
![]() $p(M_1 | \textbf{D})$
and
$p(M_1 | \textbf{D})$
and
![]() $p(M_2 | \textbf{D})$
.
$p(M_2 | \textbf{D})$
.
As discussed earlier, the evidence term is computed by evaluating the integral over the parameter likelihood and prior
This is independent of
![]() $\theta$
and represents a normalisation constant associated with the posterior. The evidence term provides the probability of generating the data by some model M. It implicitly penalises models with high complexity through the Bayesian Occam’s Razor (MacKay Reference MacKay1992; Murphy Reference Murphy2013). Complex models (models with large number of parameters) will be able to generate a wider set of observations but with a lower probability for each set of observation, since
$\theta$
and represents a normalisation constant associated with the posterior. The evidence term provides the probability of generating the data by some model M. It implicitly penalises models with high complexity through the Bayesian Occam’s Razor (MacKay Reference MacKay1992; Murphy Reference Murphy2013). Complex models (models with large number of parameters) will be able to generate a wider set of observations but with a lower probability for each set of observation, since
![]() $p(\textbf{D} | M)$
over observation sets should sum to unity. While simpler models will be able to generate only a fewer set of observations with a higher probability to each set of observations. For given set of observations
$p(\textbf{D} | M)$
over observation sets should sum to unity. While simpler models will be able to generate only a fewer set of observations with a higher probability to each set of observations. For given set of observations
![]() $\textbf{D}$
, one could choose an appropriate model based on the complexity involved in generating
$\textbf{D}$
, one could choose an appropriate model based on the complexity involved in generating
![]() $\textbf{D}$
. If
$\textbf{D}$
. If
![]() $\textbf{D}$
is simple, we will choose a simple model. Simple models will be able to provide high likelihood values
$\textbf{D}$
is simple, we will choose a simple model. Simple models will be able to provide high likelihood values
![]() $p(\textbf{D} | \theta, M)$
for a large number of parameter values
$p(\textbf{D} | \theta, M)$
for a large number of parameter values
![]() $\theta$
, and the prior value
$\theta$
, and the prior value
![]() $p(\theta | M)$
also takes higher values as the parameter space is small. When the model complexity increases, the prior over the parameters
$p(\theta | M)$
also takes higher values as the parameter space is small. When the model complexity increases, the prior over the parameters
![]() $p(\theta | M)$
takes a lower value. Also, a complex model will give a high likelihood value only for a small number of parameters. For a large number of parameter values, it will not be able to model simple data sets.
$p(\theta | M)$
takes a lower value. Also, a complex model will give a high likelihood value only for a small number of parameters. For a large number of parameter values, it will not be able to model simple data sets.
5.1. Posterior-weighted importance sampling for evidence
The evidence term
![]() $p(\textbf{D} | M)$
is intractable for non-conjugate cases, and variational inference provides a lower bound to the evidence term (ELBO), which acts as a proxy to the evidence. The tightness of the ELBO bound depends on how close the approximate posterior is to the actual posterior. ELBO provides a good proxy for the evidence only when the variational posterior is the same as the actual posterior. If the variational approximation assumed is not close to the actual posterior, the bound can be very large and hence using ELBO for model comparison might not be always correct. In this study, we derive an approximation to Bayesian evidence based on the variational posterior and the importance sampling technique.
$p(\textbf{D} | M)$
is intractable for non-conjugate cases, and variational inference provides a lower bound to the evidence term (ELBO), which acts as a proxy to the evidence. The tightness of the ELBO bound depends on how close the approximate posterior is to the actual posterior. ELBO provides a good proxy for the evidence only when the variational posterior is the same as the actual posterior. If the variational approximation assumed is not close to the actual posterior, the bound can be very large and hence using ELBO for model comparison might not be always correct. In this study, we derive an approximation to Bayesian evidence based on the variational posterior and the importance sampling technique.
Monte Carlo integration technique allows us to approximate Equation (11) by replacing the integral with a sum over samples taken from
![]() $p(\theta)$
.
$p(\theta)$
.
This approximation generally results in a good estimate for the expectation but can require a large number of samples in some cases. Consider a scenario where the likelihood is small in regions where
![]() $p(\theta)$
is large, and the likelihood is large where
$p(\theta)$
is large, and the likelihood is large where
![]() $p(\theta)$
is small. In such a scenario, the approximation is dominated by regions of low likelihood and can require large number of samples from
$p(\theta)$
is small. In such a scenario, the approximation is dominated by regions of low likelihood and can require large number of samples from
![]() $p(\theta)$
to achieve the desired estimate. Importance sampling provides a methodology for efficient sampling for such scenarios. In importance sampling, we choose a proposal distribution and use the samples from the proposal distribution for evaluating the expectation in Equation (11).
$p(\theta)$
to achieve the desired estimate. Importance sampling provides a methodology for efficient sampling for such scenarios. In importance sampling, we choose a proposal distribution and use the samples from the proposal distribution for evaluating the expectation in Equation (11).
where
![]() ${\theta}_i$
denotes the samples from the proposal distribution. The quantities
${\theta}_i$
denotes the samples from the proposal distribution. The quantities
![]() $\frac{p({\theta}_i)}{q({\theta}_i)}$
are known as importance weights and these importance weights compensate for the bias introduced because of sampling from
$\frac{p({\theta}_i)}{q({\theta}_i)}$
are known as importance weights and these importance weights compensate for the bias introduced because of sampling from
![]() $q(\theta)$
instead of
$q(\theta)$
instead of
![]() $p(\theta)$
. It can be easily seen that a proposal distribution should have a large value whenever the product of the likelihood and the prior is large and a small value whenever the product is small. From Equation (1), we can see that the posterior is equal to the product of likelihood and prior divided by a normalising constant and hence is a perfect choice for a proposal distribution. Since the posterior distribution is unknown and is approximated by the variational distribution, we can use the variational distribution as the proposal distribution. We propose to use Equation (14) to compute the approximate evidence term with
$p(\theta)$
. It can be easily seen that a proposal distribution should have a large value whenever the product of the likelihood and the prior is large and a small value whenever the product is small. From Equation (1), we can see that the posterior is equal to the product of likelihood and prior divided by a normalising constant and hence is a perfect choice for a proposal distribution. Since the posterior distribution is unknown and is approximated by the variational distribution, we can use the variational distribution as the proposal distribution. We propose to use Equation (14) to compute the approximate evidence term with
![]() $q(\theta)$
as the variational approximation to the posterior learnt by maximising ELBO. We call this approximate quantity as posterior weighted importance sampling for evidence (PWISE) and this will be used as a proxy to the evidence (or marginal likelihood) for performing Bayesian model comparison.
$q(\theta)$
as the variational approximation to the posterior learnt by maximising ELBO. We call this approximate quantity as posterior weighted importance sampling for evidence (PWISE) and this will be used as a proxy to the evidence (or marginal likelihood) for performing Bayesian model comparison.
6. Applications to astrophysical problems
As a proof of principle, we now apply ADVI to five different problems from astronomy, particle astrophysics, and gravitation, where MCMC and nested sampling techniques were previously used for parameter estimation and model comparison. We discuss in detail the ELBO derivation for one of these problems, namely the COSINE-100 dark matter experiment, in Section 6.1. We also compare the computational costs using ADVI over MCMC and nested sampling techniques. In this study, we use the PyMC3 python package for all our ADVI experiments and PyMC3 or emcee python packages for our MCMC experiments. We also use nestle or dynesty packages to calculate evidence and compare with our approximate evidence calculation using PWISE.
Previously, Cameron, Eggers, & Kroon (Reference Cameron, Eggers and Kroon2019) had compared AIS and nested sampling and showed that nested sampling outperforms AIS in many cases with much shorter run time. Although other sampling techniques such as Gaussianized Bridge Sampling (Jia & Seljak Reference Jia and Seljak2019), proximal nested sampling (Cai, McEwen, & Pereyra Reference Cai, McEwen and Pereyra2021), stepping stone algorithm (Maturana-Russel et al. Reference Maturana-Russel, Meyer, Veitch and Christensen2019), diffuse nested sampling (Brewer Reference Brewer2014), adaptive annealed importance sampling (Liu Reference Liu2014) have been investigated. Nested sampling is most widely used because of the ready availability of packages such as Dynesty and Nestle. Hence for model selection problems, we check if Nested samling and approximate evidence lead to the same qualitative conclusion using Jeffreys scale.
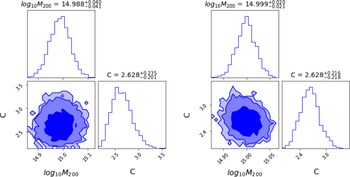
6.1. Assessment of significance of annual modulation in cosine-100 data
Weakly interacting massive particles (WIMP) are elementary particles beyond the standard model of particle physics that are hypothesised as dark matter candidates (Desai et al. Reference Desai2004). Over the past few decades, many experiments have been carried out to detect WIMPs, and out of all of these, only DAMA/LIBRA has identified annual modulations, which show all the correct characteristics of being generated by WIMP particle interactions (Bernabei et al. Reference Bernabei2018). This result however has been ruled out by many other direct detection experiments. However, all these experiements used a target material different than DAMA/LIBRA. The COSINE-100 experiment dark matter experiment (Adhikari et al. Reference Adhikari2019) is the first experiment with target material, which is a replica of the DAMA/LIBRA target, and therefore can be used to verify the claims of annual modulation of DAMA/LIBRA using an independent detector target. This experiment has recently started taking data and released its first results about 2 years ago (Adhikari et al. Reference Adhikari2019). An independent analysis of this data using Bayesian model comparison methods was carried out in Krishak & Desai (Reference Krishak and Desai2019). The COSINE-100 experiment uses data from five different crystals. The event rate for each of these crystals is given by
The last term in Equation (15) corresponds to the annual modulation caused by the WIMP particle interactions (Freese, Frieman, & Gould Reference Freese, Frieman and Gould1988). We do a model selection between two hypothesis: viz., that the data from the crystals consist of the cosine term (H1), versus without the cosine term (H2). For this purpose, the data of all the five crystals are fit simultaneously using the same values for the cosine parameters across all crystals, and crystal-specific values for the remaining background-only parameters.
Before we move on to model comparison, we explain the process involved in variational inference and the lower bound derivation for this problem. This will provide a deeper theoretical understanding of variational inference and also serve as a motivation for using automatic differentiation variational inference. As discussed in Section 3, we first need to posit a family of variational distributions
![]() $\mathcal{Q}$
that approximate the posterior distribution. Let us approximate the variational family as a Gaussian distribution with diagonal variance, i.e.
$\mathcal{Q}$
that approximate the posterior distribution. Let us approximate the variational family as a Gaussian distribution with diagonal variance, i.e.
![]() $q_{\phi}(\theta) = \mathcal{N}(\mu,\Sigma)$
. For this particular problem, the likelihood
$q_{\phi}(\theta) = \mathcal{N}(\mu,\Sigma)$
. For this particular problem, the likelihood
![]() $P(D|\theta)$
is a Gaussian with mean given by the event rate described in Equation (15) and standard deviation given by the errors in the data. The priors
$P(D|\theta)$
is a Gaussian with mean given by the event rate described in Equation (15) and standard deviation given by the errors in the data. The priors
![]() $P(\theta)$
used for all the parameters are uniformly distributed. More details of the analysis and choice of priors can be found in Krishak & Desai (Reference Krishak and Desai2019).
$P(\theta)$
used for all the parameters are uniformly distributed. More details of the analysis and choice of priors can be found in Krishak & Desai (Reference Krishak and Desai2019).
 \begin{align*}q(\theta) & = \prod_{i \in {\left(C,p_0,p_1,A,\omega,t_0\right)}} \frac{1}{\sqrt{2\pi\sigma_{i}^2}} \exp\left(-\frac{(\theta_i-\mu_i)^2}{2\sigma_{i}^2}\right). \\[3pt]p(\theta) & = \prod_{i \in {\left(C,p_0,p_1,A,\omega,t_0\right)}} \frac{1}{\max_i - \min_i}. \\[3pt]p(D|\theta) & = \prod_{i} \frac{1}{\sqrt{2\pi\sigma_{i}^2}} \exp\left(-\frac{(r-R_i)^2}{2\sigma_{i}^2}\right) ,\end{align*}
\begin{align*}q(\theta) & = \prod_{i \in {\left(C,p_0,p_1,A,\omega,t_0\right)}} \frac{1}{\sqrt{2\pi\sigma_{i}^2}} \exp\left(-\frac{(\theta_i-\mu_i)^2}{2\sigma_{i}^2}\right). \\[3pt]p(\theta) & = \prod_{i \in {\left(C,p_0,p_1,A,\omega,t_0\right)}} \frac{1}{\max_i - \min_i}. \\[3pt]p(D|\theta) & = \prod_{i} \frac{1}{\sqrt{2\pi\sigma_{i}^2}} \exp\left(-\frac{(r-R_i)^2}{2\sigma_{i}^2}\right) ,\end{align*}
where
![]() $\mu_i$
and
$\mu_i$
and
![]() $\sigma_i$
are the variational parameters (denoted by
$\sigma_i$
are the variational parameters (denoted by
![]() $\phi)$
and
$\phi)$
and
![]() $T_i = p_0\exp{(\frac{-\ln{2} \cdot t_i}{p_1})}+A\cos{\omega(t_i-t_0)}$
. The variational parameters
$T_i = p_0\exp{(\frac{-\ln{2} \cdot t_i}{p_1})}+A\cos{\omega(t_i-t_0)}$
. The variational parameters
![]() $(\phi)$
are then estimated through ELBO maximisation. The ELBO for the cosine problem is given in Equation (16), and we will simplify the equation for one chosen latent variable ‘C’ for brevity.
$(\phi)$
are then estimated through ELBO maximisation. The ELBO for the cosine problem is given in Equation (16), and we will simplify the equation for one chosen latent variable ‘C’ for brevity.
 \begin{align}\mathrm{ELBO} =\,& \mathbb{E}_{q\left(C,p_0,p_1,A,\omega,t_0\right)}\left[\log p\left(\textbf{D}| C,p_0,p_1,A,\omega,t_0\right)\right] \nonumber \\[3pt]&- \mathrm{KL} \left(q\left(C,p_0,p_1,A,\omega,t_0\right) | | p\left(C,p_0,p_1,A,\omega,t_0\right)\right) \nonumber \\[3pt]=\,& \mathbb{E}_{q(\theta)}\bigg[ \mathbb{E}_{q(C)}\bigg[\log p(\textbf{D}|\theta)] \log\frac{p(C)}{q(C)}\bigg]\bigg] \nonumber \\[3pt]&-\mathrm{KL}\big(q(\theta) | | p(\theta)\big) ,\end{align}
\begin{align}\mathrm{ELBO} =\,& \mathbb{E}_{q\left(C,p_0,p_1,A,\omega,t_0\right)}\left[\log p\left(\textbf{D}| C,p_0,p_1,A,\omega,t_0\right)\right] \nonumber \\[3pt]&- \mathrm{KL} \left(q\left(C,p_0,p_1,A,\omega,t_0\right) | | p\left(C,p_0,p_1,A,\omega,t_0\right)\right) \nonumber \\[3pt]=\,& \mathbb{E}_{q(\theta)}\bigg[ \mathbb{E}_{q(C)}\bigg[\log p(\textbf{D}|\theta)] \log\frac{p(C)}{q(C)}\bigg]\bigg] \nonumber \\[3pt]&-\mathrm{KL}\big(q(\theta) | | p(\theta)\big) ,\end{align}
where
![]() $(p_0,p_1,A,\omega,t_0)$
are the latent variables
$(p_0,p_1,A,\omega,t_0)$
are the latent variables
![]() $\theta$
. Equation (17) shows the final equation for ELBO for the latent variable ‘C’ after substituting for the aforementioned likelihood, prior, and variational distribution. For a detailed derivation of Equation (17), please refer to Appendix.
$\theta$
. Equation (17) shows the final equation for ELBO for the latent variable ‘C’ after substituting for the aforementioned likelihood, prior, and variational distribution. For a detailed derivation of Equation (17), please refer to Appendix.
 \begin{align}\mathrm{ELBO} =& \frac{1}{2} + \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}} \nonumber \\[4pt]&-\sum_i \frac{1}{2\sigma_i^2}\left(\mathbb{E}_{q\left(p_0,p_1,A,\omega,t_0\right)}\left[(r_i-T_i-\mu_C)^2 \right]+ \sigma_C^2\right)\nonumber \\[4pt]&-\mathrm{KL}\left(q\left(p_0,p_1,A,\omega,t_0\right) | | p\left(p_0,p_1,A,\omega,t_0\right)\right),\end{align}
\begin{align}\mathrm{ELBO} =& \frac{1}{2} + \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}} \nonumber \\[4pt]&-\sum_i \frac{1}{2\sigma_i^2}\left(\mathbb{E}_{q\left(p_0,p_1,A,\omega,t_0\right)}\left[(r_i-T_i-\mu_C)^2 \right]+ \sigma_C^2\right)\nonumber \\[4pt]&-\mathrm{KL}\left(q\left(p_0,p_1,A,\omega,t_0\right) | | p\left(p_0,p_1,A,\omega,t_0\right)\right),\end{align}
where
![]() $\mu_C$
and
$\mu_C$
and
![]() $\sigma_C$
are the variational parameters describing the posterior over ‘C’. The log term (second term) in Equation (17) is the result of KL divergence between the variational distribution and the prior distribution. This acts as a regularisation term, which will prevent
$\sigma_C$
are the variational parameters describing the posterior over ‘C’. The log term (second term) in Equation (17) is the result of KL divergence between the variational distribution and the prior distribution. This acts as a regularisation term, which will prevent
![]() $\sigma_C$
(variance of variational posterior) from going to zero during the maximisation of ELBO (due to the third term, which is negative). Consequently, the variational posterior learnt by maximising ELBO will be a well formed distribution, with probability density not only around the mean but also over a larger region covering the posterior. We can calculate the gradients of the ELBO with respect to the variational parameters
$\sigma_C$
(variance of variational posterior) from going to zero during the maximisation of ELBO (due to the third term, which is negative). Consequently, the variational posterior learnt by maximising ELBO will be a well formed distribution, with probability density not only around the mean but also over a larger region covering the posterior. We can calculate the gradients of the ELBO with respect to the variational parameters
![]() $(\phi)$
and use stochastic gradient decent for estimating
$(\phi)$
and use stochastic gradient decent for estimating
![]() $\phi$
.
$\phi$
.
The problem of choosing a suitable variational family
![]() $\mathcal{Q}$
is not always easy. Consider the above case where the variational distribution is the Gaussian distribution. The prior for ‘C’ is a uniform distribution between 0 and 400, which implies that the mean of the posterior distribution
$\mathcal{Q}$
is not always easy. Consider the above case where the variational distribution is the Gaussian distribution. The prior for ‘C’ is a uniform distribution between 0 and 400, which implies that the mean of the posterior distribution
![]() $\mu$
should be a positive value. But there is no explicit condition present in Equation (17) that constrains the
$\mu$
should be a positive value. But there is no explicit condition present in Equation (17) that constrains the
![]() $\mu$
to take only positive values after optimisation. Therefore, the choice of the variational family
$\mu$
to take only positive values after optimisation. Therefore, the choice of the variational family
![]() $\mathcal{Q}$
depends on each individual problem and involves solving a complex constrained optimisation problem.
$\mathcal{Q}$
depends on each individual problem and involves solving a complex constrained optimisation problem.
ADVI mitigates the above problems by using a clever transformation on the latent variables, by converting the constrained latent space to unconstrained space as discussed in Section 4. ADVI models the variational distribution in the unconstrained space as a Gaussian distribution and the transformations applied on the latent variables will satisfy the required constraints on the posterior distribution. The transformation into unconstrained space also mitigates the constraints of support matching that are essential, when choosing a variational distribution in constraint space, making ADVI a desirable choice for performing variational inference.
For doing the Bayesian model comparison, Krishak & Desai (Reference Krishak and Desai2019) used nested sampling with the dynesty (Speagle Reference Speagle2020) package for model comparison, as the nestle package was not converging while calculating Bayesian evidence for this problem. To perform model comparison, we calculate PWISE as discussed in Section 5.1, using samples from the posterior approximation obtained through ADVI. Table 1 shows a comparison of the results between the proposed approximation to evidence (PWISE) and Nestled Sampling (computed using dynesty) for the same sets of priors. We can see that the Bayes factor in both the cases is approximately the same and leads to the same qualitative evidence using Jeffreys scale (Trotta Reference Trotta2017). Of course, one caveat in directly applying the Jeffreys scale is that in case the priors for an alternate model are not theoretically motivated, the Jeffreys scale needs to be revised and calibrated to the specific model used Gordon & Trotta (Reference Gordon and Trotta2007). The Bayes factor calculated for H2 compared to H1 with PWISE is
![]() $e^{11.2}$
. Hence, we conclude that H2 is favoured over H1, which agrees with the result from Krishak & Desai (Reference Krishak and Desai2019). For assessing the relative computational cost between both the methods, we executed the nested sampling code given in Krishak & Desai (Reference Krishak and Desai2019). The dynesty sampling code took about 13 h (using a single core), whereas ADVI took only 5 min, which is two orders smaller than nested sampling.
$e^{11.2}$
. Hence, we conclude that H2 is favoured over H1, which agrees with the result from Krishak & Desai (Reference Krishak and Desai2019). For assessing the relative computational cost between both the methods, we executed the nested sampling code given in Krishak & Desai (Reference Krishak and Desai2019). The dynesty sampling code took about 13 h (using a single core), whereas ADVI took only 5 min, which is two orders smaller than nested sampling.
Table 1. Log evidence values and Bayes factor for the two hypotheses computed using PWISE, and dynesty packages. This result favours
![]() $H_2$
that there is no annual modulation in COSINE-100 data.
$H_2$
that there is no annual modulation in COSINE-100 data.

6.2. Exoplanet discovery using radial velocity data
The presence of a planet or a companion star results in temporal variations in the radial velocity of the host star. By analysing the radial velocity data, one can draw inferences about the ratio of masses between the host planet and the companion, and orbital parameters like the period and eccentricity. For this purpose, a MCMC package has been designed called Exofit (Balan & Lahav Reference Balan and Lahav2009), which enables the retrieval of the orbital parameters of exoplanets from radial velocity measurements. We shall determine the orbital parameters using both MCMC and ADVI techniques and compare the results.
The first step involves defining a model and imposing priors on the latent variables. We follow the model defined in Section 2.2 of Balan & Lahav (Reference Balan and Lahav2009). The equations used for the analysis are now discussed. The radial velocity of a star of mass M in a binary system with companion of mass m in an orbit with time period T, inclination I and eccentricity e is given by:
where
In Equations (18) and (19),
![]() $v_0$
is the mean velocity of the center of mass of the binary system, T is the orbital period of the planet, and
$v_0$
is the mean velocity of the center of mass of the binary system, T is the orbital period of the planet, and
![]() $\omega$
is the angle of the pericenter measured from the ascending point.
$\omega$
is the angle of the pericenter measured from the ascending point.
If
![]() $d_i$
is the observed radial velocity data, the likelihood function is given by Balan & Lahav (Reference Balan and Lahav2009):
$d_i$
is the observed radial velocity data, the likelihood function is given by Balan & Lahav (Reference Balan and Lahav2009):
 \begin{equation}P(D|\theta, M)= A \exp - \left(\sum_{i=1}^N \left[\frac{(d_i-v_i)^2}{2(\sigma_i^2+s^2)}\right]\right),\end{equation}
\begin{equation}P(D|\theta, M)= A \exp - \left(\sum_{i=1}^N \left[\frac{(d_i-v_i)^2}{2(\sigma_i^2+s^2)}\right]\right),\end{equation}
where
![]() $A = (2\pi)^{-N/2}\left[ \prod \limits_{i=1}^N (\sigma_i^2+s^2)^{-1/2}\right]$
. Here, s is an additional systematic term, which is estimated by maximising the likelihood of Equation (20). The choice of priors for each of the above parameters can be found in Table 2. PyMC3 allows us to easily place these priors on model variables and define our model.
$A = (2\pi)^{-N/2}\left[ \prod \limits_{i=1}^N (\sigma_i^2+s^2)^{-1/2}\right]$
. Here, s is an additional systematic term, which is estimated by maximising the likelihood of Equation (20). The choice of priors for each of the above parameters can be found in Table 2. PyMC3 allows us to easily place these priors on model variables and define our model.
Table 2. The assumed prior distribution of various parameters and their boundaries. It is similar to choice of priors given by Balan & Lahav (Reference Balan and Lahav2009). For the parameters marked as Jeffreys prior, the prior used is equal to the reciprocal of the parameter. We note that modified Jeffreys refers to a slight modification of the standard Jeffreys prior, in which additive constants are added, since the lower limits are zero (Gregory Reference Gregory2005)

The data for this purpose have been obtained from Sharma (Reference Sharma2017) and the parameter values obtained from both the procedures are shown in Table 3. We find that ADVI converges to a solution in 10 s with a mean error of
![]() $1.83 \times 10^{-5}$
whereas MCMC took 31 s to converge with a mean error of
$1.83 \times 10^{-5}$
whereas MCMC took 31 s to converge with a mean error of
![]() $1.98\times 10^{-5}$
. The results and Bayesian credible intervals are shown in Figure 1 and agree with the corresponding results from Sharma (Reference Sharma2017). (cf. Figure 8 of Sharma Reference Sharma2017.)
$1.98\times 10^{-5}$
. The results and Bayesian credible intervals are shown in Figure 1 and agree with the corresponding results from Sharma (Reference Sharma2017). (cf. Figure 8 of Sharma Reference Sharma2017.)
Table 3. The parameter values from both MCMC (computing using PyMC3) and ADVI for determination of exoplanet parameters from radial velocity data. Both of these are comparable to the actual values obtained from (Sharma Reference Sharma2017), which are used to generate the synthetic data used for this analysis.


Figure 1. Left: Radial velocity as a function of time for a star in a binary system. The orange line is the best fit obtained using ADVI and the green line is obtained from NUTS MCMC. Right: 68%, 90% and 95% credible intervals of parameters obtained using ADVI. The corresponding plots for the same data using MCMC can be found in Figure 8 of Sharma (Reference Sharma2017).
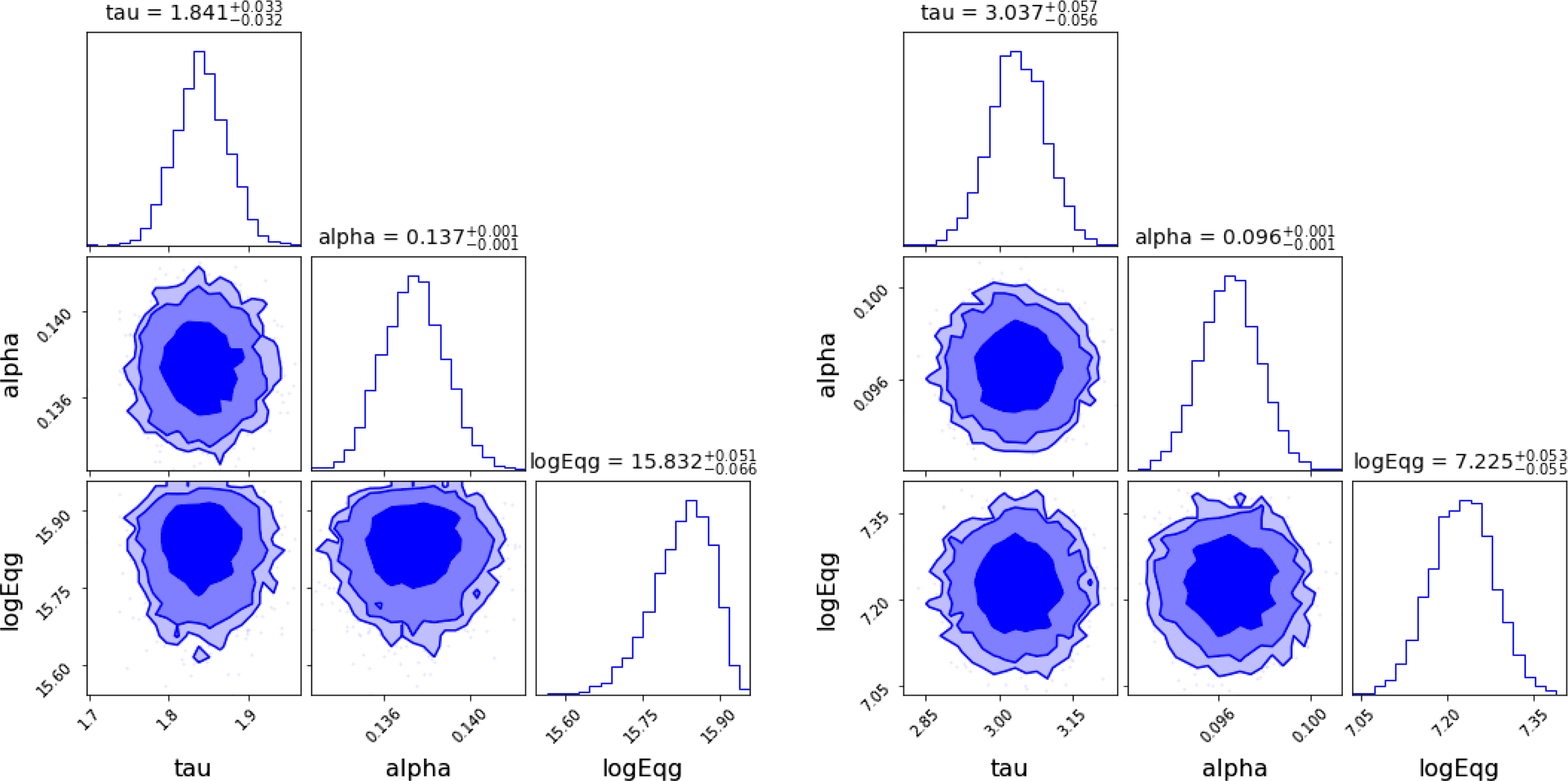
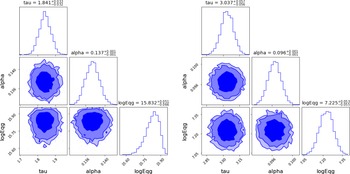
Figure 2. Left: ADVI based marginalised credible intervals of the linear
![]() $(n=1)$
LIV fit for the spectral lag energy data. Right: ADVI based Marginalized parameter constraints of the linear
$(n=1)$
LIV fit for the spectral lag energy data. Right: ADVI based Marginalized parameter constraints of the linear
![]() $(n=2)$
LIV fit for the spectral lag energy data. Both the plots were generated using the corner.py module (Foreman-Mackey Reference Foreman-Mackey2016). The corresponding parameter constraints obtained using MCMC can be found in Figures 3 and 4 from Wei et al. (Reference Wei, Zhang, Shao, Wu and MÉszáros2017), and they agree with these contours.
$(n=2)$
LIV fit for the spectral lag energy data. Both the plots were generated using the corner.py module (Foreman-Mackey Reference Foreman-Mackey2016). The corresponding parameter constraints obtained using MCMC can be found in Figures 3 and 4 from Wei et al. (Reference Wei, Zhang, Shao, Wu and MÉszáros2017), and they agree with these contours.
6.3. Testing the periodic G claim
Anderson et al. (Reference Anderson, Schubert, Trimble and Feldman2015) have argued for a periodicity of 5.9 yr in the CODATA measurements of Newton’s gravitational constant G, which also show strong correlations with similar variations in the length of the day. These results have been disputed by Pitkin (Reference Pitkin2015) using Bayesian inference as well as by Desai (Reference Desai2016) using frequentist analysis, both of which argued that the data for G can be explained without invoking any sinusoidal modulations. Pitkin (Reference Pitkin2015) tested this claim by performing Bayesian model selection using samples generated from MCMC and found from the Bayesian Odds ratio that the data favoured a constant value of G with some extra noise over a periodic modulation of G by a factor of
![]() $e^{30}$
. We performed model selection using ADVI and nestle on the data provided by Pitkin (Reference Pitkin2015) to compare the accuracy of variational inference approach.
$e^{30}$
. We performed model selection using ADVI and nestle on the data provided by Pitkin (Reference Pitkin2015) to compare the accuracy of variational inference approach.
We compute the Bayesian evidence for all the four hypotheses considered by Pitkin using the same notation as in Pitkin (Reference Pitkin2015) and compare them as follows:
-
1.
 $H_1$
—the data variation can be described by Gaussian noise given by the experimental errors and an unknown offset;
$H_1$
—the data variation can be described by Gaussian noise given by the experimental errors and an unknown offset; -
2.
 $H_2$
—the data variation can be described by Gaussian noise given by the experimental errors, an unknown offset and an unknown systematic noise term;
$H_2$
—the data variation can be described by Gaussian noise given by the experimental errors, an unknown offset and an unknown systematic noise term; -
3.
 $H_3$
—the data variation can be described by Gaussian noise given by the experimental errors, and unknown offset, and a sinusoid with unknown period, phase and amplitude;
$H_3$
—the data variation can be described by Gaussian noise given by the experimental errors, and unknown offset, and a sinusoid with unknown period, phase and amplitude; -
4.
 $H_4$
—the data variation can be described by Gaussian noise given by the experimental errors, an unknown offset, an unknown systematic noise term, and a sinusoid with unknown period, phase and amplitude;
$H_4$
—the data variation can be described by Gaussian noise given by the experimental errors, an unknown offset, an unknown systematic noise term, and a sinusoid with unknown period, phase and amplitude;
The general model used is
where A is the sinusoid amplitude, P is the period,
![]() $\phi_0$
is the initial phase,
$\phi_0$
is the initial phase,
![]() $t_0$
is the initial epoch, and
$t_0$
is the initial epoch, and
![]() $\mu_G$
is an overall offset. The details of the model and assumptions can be found in Pitkin (Reference Pitkin2015). We have assumed a Gaussian likelihood and uniform prior for all the parameters. Following the model defined by Pitkin (Reference Pitkin2015), we perform model selection using the approximate evidence calculated using the PWISE. Our results computed using PWISE and nestle can be found in Table 4. The log evidence for all the hypotheses are comparable, except for
$\mu_G$
is an overall offset. The details of the model and assumptions can be found in Pitkin (Reference Pitkin2015). We have assumed a Gaussian likelihood and uniform prior for all the parameters. Following the model defined by Pitkin (Reference Pitkin2015), we perform model selection using the approximate evidence calculated using the PWISE. Our results computed using PWISE and nestle can be found in Table 4. The log evidence for all the hypotheses are comparable, except for
![]() $H_3$
. However, even for
$H_3$
. However, even for
![]() $H_3$
, the Bayes factor (compared to H1) using both the methods qualitatively lead to the same conclusion using Jeffreys scale, viz.
$H_3$
, the Bayes factor (compared to H1) using both the methods qualitatively lead to the same conclusion using Jeffreys scale, viz.
![]() $H_3$
been decisively favoured over
$H_3$
been decisively favoured over
![]() $H_1$
. All the experiments were completed under a minute and the time taken by both ADVI and nested sampling are similar.
$H_1$
. All the experiments were completed under a minute and the time taken by both ADVI and nested sampling are similar.
Table 4. Log evidence values for the four hypotheses and Bayes factor computed with respect to
![]() $H_1$
calculated using both PWISE and nestle package. The log evidence for all hypotheses are comparable, except for
$H_1$
calculated using both PWISE and nestle package. The log evidence for all hypotheses are comparable, except for
![]() $H_3$
. However, even for
$H_3$
. However, even for
![]() $H_3$
, the Bayes factor using both the methods qualitatively leads to the same conclusion using Jeffreys scale of
$H_3$
, the Bayes factor using both the methods qualitatively leads to the same conclusion using Jeffreys scale of
![]() $H_3$
been decisively favoured over
$H_3$
been decisively favoured over
![]() $H_1$
.
$H_1$
.

6.4. Statistical significance of spectral lag transition in GRB 160625B
Wei et al. (Reference Wei, Zhang, Shao, Wu and MÉszáros2017) have detected a spectral lag transition in the spectral lag data of GRB 1606025B, which they have argued could be a signature of the violation of Lorentz invariance (LIV). Ganguly & Desai (Reference Ganguly and Desai2017) perform a frequentist model comparison test to ascertain the statistical significance of this claim for a transition from positive to negative time lags, and showed the significance of this detection is about
![]() $3-4\sigma$
, depending on the specific model used for LIV.
$3-4\sigma$
, depending on the specific model used for LIV.
For this analysis, Wei et al. (Reference Wei, Zhang, Shao, Wu and MÉszáros2017) have fit these observed lags to a sum of two components: an assumed functional form for the intrinsic time lag due to astrophysical mechanisms and an energy-dependent speed of light due to quadratic and linear LIV models (See Equations (2) and (5) of Wei et al. Reference Wei, Zhang, Shao, Wu and MÉszáros2017). Using the same equations, we first carry out parameter estimation using ADVI and our best-fit model can be found in Figure 2. Again, a Gaussian likelihood and uniform prior was used for this analysis.
Furthermore, we supplement the studies in Ganguly & Desai (Reference Ganguly and Desai2017) by performing Bayesian model selection using ADVI by fitting a variational family on each of the three models, consisting of the null hypothesis and two Lorentz violation models. We then calculate the approximate evidence using PWISE to perform model selection as defined in Section 5.1. The credible intervals for our parameters can be found in Figure 2. The log evidence values and the Bayes factors compared to the null hypothesis are shown in Table 5 for both Nested sampling (using nestle) and PWISE. We see that they are comparable in both the cases and would lead to the same conclusion using Jeffreys scale. For this example, all the experiments were completed under a minute and the time taken by both ADVI and nested sampling are similar. Using Jeffery’s scale, we can say that
![]() $n=2$
(quadratic) LIV model is significantly favoured by the data over the other two models, which is in agreement with the information theory based model comparisons carried out in Ganguly & Desai (Reference Ganguly and Desai2017).
$n=2$
(quadratic) LIV model is significantly favoured by the data over the other two models, which is in agreement with the information theory based model comparisons carried out in Ganguly & Desai (Reference Ganguly and Desai2017).
Table 5. Log Evidence values computed using PWISE and nestle package and Bayes factor for hypothesis
![]() $n=1$
and
$n=1$
and
![]() $n=2$
LIV, when compared to the null hypothesis are shown.
$n=2$
LIV, when compared to the null hypothesis are shown.
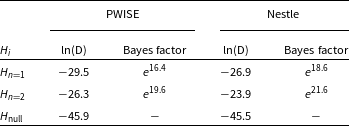
6.5. Estimating the mass of a galaxy cluster with weak lensing
The propagation of light is affected by the gravitational field it passes through along its way from the observer. This effect is called gravitational lensing (Schneider, Ehlers, & Falco Reference Schneider, Ehlers and Falco1992). The distortion in the image of an object compared to its true intrinsic shape is usually known as weak lensing. Hoekstra et al. (Reference Hoekstra, Bartelmann, Dahle, Israel, Limousin and Meneghetti2013) outline how the mass of galaxy clusters and mass–concentration relation can be obtained using weak lensing. Here, we use MCMC to estimate the logarithm of the virial mass
![]() $(\log_{10} M_{200})$
and the concentration parameter c from synthetic lensing observations.
$(\log_{10} M_{200})$
and the concentration parameter c from synthetic lensing observations.
Variational inference and Metropolis–Hastings MCMC were used to calculate the aforementioned lensing parameters. The dataset used for this analysis was downloaded from this url. This lensing catalogue has been randomly sampled from the shear map of a simulated galaxy cluster using simulations done in Becker & Kravtsov (Reference Becker and Kravtsov2011), who used mock galaxy clusters from cosmological simulations to study the bias and scatter in mass measurements of clusters. These simulations were created using an Adaptive Refinement Tree (Kravtsov, Klypin, & Khokhlov Reference Kravtsov, Klypin and Khokhlov1997) based on the cosmological parameters from WMAP7 analysis (Komatsu et al. Reference Komatsu2011). More details on these simulations and the identification of galaxy cluster halos can be found in Becker & Kravtsov (Reference Becker and Kravtsov2011). A corresponding cookbook for computing the cluster masses using MCMC has also been made available here, wherein more details of the equations used can be found, and which we use for reconstructing the mass and concentration parameter. We have used a Gaussian likelihood and uniform priors for the concentration and logarithm of the mass.
For this example, we have used used pymc3 to run ADVI and emcee to run MCMC experiments. MCMC took about 313 min of clock time running in multi-threaded mode on 25 cores (corresponding to a total CPU time of
![]() $25 \times 313\ \mathrm{min}$
or about 5 d), whereas ADVI took only 40 min running on a single core. We also note that for this dataset we were unable to run MCMC using PyMC3, as it ran out of memory because of the large datasize. The credible intervals for the parameters for both MCMC and ADVI can be found in Figure 3. The credible intervals using both the techniques are in agreement with each other.
$25 \times 313\ \mathrm{min}$
or about 5 d), whereas ADVI took only 40 min running on a single core. We also note that for this dataset we were unable to run MCMC using PyMC3, as it ran out of memory because of the large datasize. The credible intervals for the parameters for both MCMC and ADVI can be found in Figure 3. The credible intervals using both the techniques are in agreement with each other.
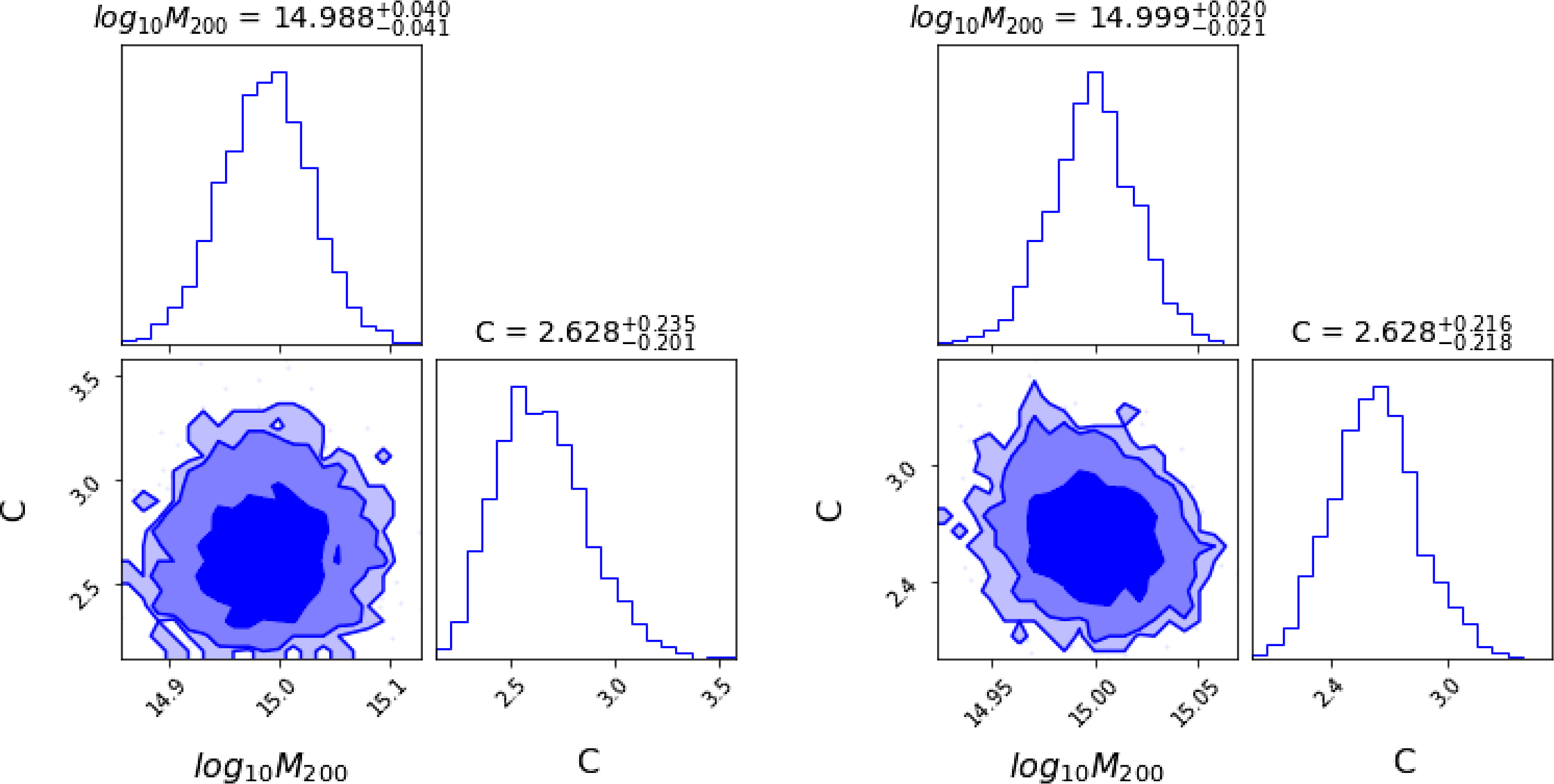
Figure 3. Left : Credible intervals for parameter estimates using ADVI. Right: Credible intervals for parameter estimates using emcee MCMC sampler. The credible intervals were plotted using Corner python module. Note that
![]() $M_{200}$
is expressed in terms of
$M_{200}$
is expressed in terms of
![]() ${\rm M}_{\odot}$
.
${\rm M}_{\odot}$
.
7. Conclusions
In this study, we have introduced variational inference, and outlined how it can be used for Bayesian and frequentist parameter estimation by maximising the posterior/frequentist likelihood. We have also explained how this method can be used to compute the Bayesian evidence (or marginal likelihood), which is needed for Bayesian model comparison. Variational inference has a strong theoretical foundation and with the rise of probabilistic programming frameworks such as PyMC3, and the development of generic Variational Inference methods such as ADVI, it presents a viable alternative to sampling based approaches such as MCMC. We have also introduced a approximation to evidence, called posterior weighted importance sampling for evidence (PWISE) which is used as a proxy for Bayesian evidence (or Marginal likelihood).
ADVI is a ‘black-box’ approach which automates the manual steps required for traditional VI using variable transformation and automatic differentiation techniques. As a proof of principle, we apply ADVI to five problems in astrophysics and gravitation from literature involving parameter estimation or model comparison. These include assessment of significance of annual modulation in COSINE-100 determination of orbital parameters from exoplanet radial velocity data, tests of periodicities in the measurements of G, looking for a turnover in spectral lag data from GRB 160625B, and determination of galaxy cluster mass using synthetic weak lensing observations.
The results obtained for both the parameter estimation problem problem were in agreement with the MCMC results. For model comparison, both the methods point to the same qualitative conclusion using Jeffreys scale. Furthermore, in many cases, we obtained significant speedup when compared with MCMC methods. This is especially important when dealing with large datasets and highly complex models as the time required for MCMC approach grows exponentially. On the other hand, variational inference reduces the problem to an optimisation problem, which performs very well in these conditions, and hence the computational cost does not scale with data size. The Markov Chains guarantee producing (asymptotically) exact samples from the target density, but they do not scale very well with large datasets. Variational inference therefore provides a viable alternative to MCMC sampling by being significantly faster and given the proper choice of variational distribution, only sacrificing slightly in accuracy. The variational inference algorithm is sensitive to the choice of priors and they can be treated like another hyperparameter.
These five examples of parameter estimation/model comparison from different domains of astrophysics provide proof of principles demonstration of application of variational inference to astrophysical problems, for which MCMC and nested sampling techniques were previously used. The codes for all the examples given here is available at https://github.com/geetakrishna1994/varational-inference.
Acknowledgements
Geetakrishnasai Gunapati was supported by DST-ICPS grant. Anirudh Jain was supported by the Microsoft summer internship program at IIT Hyderabad. We would like to thank Daniel Gruen, Soumya Mohanty, Sanjib Sharma, and Jochen Weller for useful correspondence and making available to us some of the datasets used in this work.
A. Appendix
We derive the ELBO equation for the cosine-100 problem wrt one parameter ‘C’. The variational distribution is isometric Gaussian distribution and uniform priors on all the parameters. The likelihood is Gaussian with a mean given by Equation (15).
 \begin{align*}\mathrm{ELBO} &= \mathbb{E}_{q\left(C,p_0,p_1,A,\omega,t_0\right)}\left[\log p\left(\textbf{D}| C,p_0,p_1,A,\omega,t_0\right)\right]\\[4pt]& \quad - \mathrm{KL} \left(q\left(C,p_0,p_1,A,\omega,t_0\right) | | p\left(C,p_0,p_1,A,\omega,t_0\right)\right) \\[4pt]&= \mathbb{E}_{q\left(p_0,p_1,A,\omega,t_0\right)}\Big[ \mathbb{E}_{q\left(C\right)}\Big[\log p\left(\textbf{D}| C,p_0,p_1,A,\omega,t_0\right)]\\[4pt]& \quad \left.\left.+ \log\frac{p\left(C\right)}{q\left(C\right)}\right]\right]\\[4pt]& \quad - \mathrm{KL}\left(q\left(p_0,p_1,A,\omega,t_0\right) | | p\left(p_0,p_1,A,\omega,t_0\right)\right).\end{align*}
\begin{align*}\mathrm{ELBO} &= \mathbb{E}_{q\left(C,p_0,p_1,A,\omega,t_0\right)}\left[\log p\left(\textbf{D}| C,p_0,p_1,A,\omega,t_0\right)\right]\\[4pt]& \quad - \mathrm{KL} \left(q\left(C,p_0,p_1,A,\omega,t_0\right) | | p\left(C,p_0,p_1,A,\omega,t_0\right)\right) \\[4pt]&= \mathbb{E}_{q\left(p_0,p_1,A,\omega,t_0\right)}\Big[ \mathbb{E}_{q\left(C\right)}\Big[\log p\left(\textbf{D}| C,p_0,p_1,A,\omega,t_0\right)]\\[4pt]& \quad \left.\left.+ \log\frac{p\left(C\right)}{q\left(C\right)}\right]\right]\\[4pt]& \quad - \mathrm{KL}\left(q\left(p_0,p_1,A,\omega,t_0\right) | | p\left(p_0,p_1,A,\omega,t_0\right)\right).\end{align*}
Gaussian likelihood:
 \begin{align*} & \log p\left(\textbf{D}| C,p_0,p_1,A,\omega,t_0\right)\\ &= \log B - \sum_{i}\left(\frac{\left(r_i - \left(C + p_0\exp{\left(\frac{-\ln{2} \cdot t_i}{p_1}\right)}+A\cos{\omega\left(t_i-t_0\right)}\right) \right)^{2}}{2 \sigma_{i}^{2}}\right) \end{align*}
\begin{align*} & \log p\left(\textbf{D}| C,p_0,p_1,A,\omega,t_0\right)\\ &= \log B - \sum_{i}\left(\frac{\left(r_i - \left(C + p_0\exp{\left(\frac{-\ln{2} \cdot t_i}{p_1}\right)}+A\cos{\omega\left(t_i-t_0\right)}\right) \right)^{2}}{2 \sigma_{i}^{2}}\right) \end{align*}
 \begin{align*}&\!\!\!\!\!\!\!\!\!=\, \log B - \sum_{i}\left(\frac{\left(\left(r_i - T_i\right) - C \right)^{2}}{2 \sigma_{i}^{2}}\right)\qquad\qquad \\&\!\!\!\!\!\!\!\!\!=\, \log B - \sum_{i}\left(\frac{\left(r_i - T_i\right)^{2}+C^2-2 C\left(r_i-T_i\right)}{2 \sigma_{i}^{2}}\right) ,\qquad\qquad\end{align*}
\begin{align*}&\!\!\!\!\!\!\!\!\!=\, \log B - \sum_{i}\left(\frac{\left(\left(r_i - T_i\right) - C \right)^{2}}{2 \sigma_{i}^{2}}\right)\qquad\qquad \\&\!\!\!\!\!\!\!\!\!=\, \log B - \sum_{i}\left(\frac{\left(r_i - T_i\right)^{2}+C^2-2 C\left(r_i-T_i\right)}{2 \sigma_{i}^{2}}\right) ,\qquad\qquad\end{align*}
where B is a normalising constant for the Gaussian distribution and
![]() $T_i = p_0\exp{(\frac{-\ln{2} \cdot t_i}{p_1})}+A\cos{\omega(t_i-t_0)}$
.
$T_i = p_0\exp{(\frac{-\ln{2} \cdot t_i}{p_1})}+A\cos{\omega(t_i-t_0)}$
.
Prior on C:
Variational Distribution of C (Gaussian):
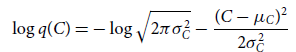 \begin{align*} \log q(C) = - \log \sqrt{2\pi\sigma_{C}^{2}} - \frac{(C - \mu_{C})^{2}}{2\sigma_{C}^{2}} \end{align*}
\begin{align*} \log q(C) = - \log \sqrt{2\pi\sigma_{C}^{2}} - \frac{(C - \mu_{C})^{2}}{2\sigma_{C}^{2}} \end{align*}
 \begin{align*} & \log p\left(\textbf{D}| C,p_0,p_1,A,\omega,t_0\right) + \log p\left(C\right) - \log q\left(C\right)\\& \quad = \log B - \sum_{i}\left(\frac{\left(r_{i}-T_i\right)^{2}+C^2-2 C\left(r_i-T_i\right)}{2 \sigma_{i}^{2}}\right) \\&\qquad - \log \left(C_{\max} - C_{\min}\right) + \log \sqrt{2\pi\sigma_{C}^{2}} + \frac{\left(C - \mu_{C}\right)^{2}}{2\sigma_{C}^{2}} \\&\quad = \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}} + C^{2}\left(\frac{1}{2\sigma_{C}^{2}} - \sum_i\frac{1}{2\sigma_{i}^{2}} \right)\\&\qquad + C\left(\sum_{i}\frac{r_i-T_i}{\sigma_i^2} - \frac{\mu_C}{\sigma_C^2}\right) +\left(\frac{\mu_C^2}{2\sigma_C^2} - \sum_{i}\frac{\left(r_i-T_i\right)^2}{2\sigma_i^2}\right).\end{align*}
\begin{align*} & \log p\left(\textbf{D}| C,p_0,p_1,A,\omega,t_0\right) + \log p\left(C\right) - \log q\left(C\right)\\& \quad = \log B - \sum_{i}\left(\frac{\left(r_{i}-T_i\right)^{2}+C^2-2 C\left(r_i-T_i\right)}{2 \sigma_{i}^{2}}\right) \\&\qquad - \log \left(C_{\max} - C_{\min}\right) + \log \sqrt{2\pi\sigma_{C}^{2}} + \frac{\left(C - \mu_{C}\right)^{2}}{2\sigma_{C}^{2}} \\&\quad = \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}} + C^{2}\left(\frac{1}{2\sigma_{C}^{2}} - \sum_i\frac{1}{2\sigma_{i}^{2}} \right)\\&\qquad + C\left(\sum_{i}\frac{r_i-T_i}{\sigma_i^2} - \frac{\mu_C}{\sigma_C^2}\right) +\left(\frac{\mu_C^2}{2\sigma_C^2} - \sum_{i}\frac{\left(r_i-T_i\right)^2}{2\sigma_i^2}\right).\end{align*}
We can evaluate the expectation of the above term wrt q(C).
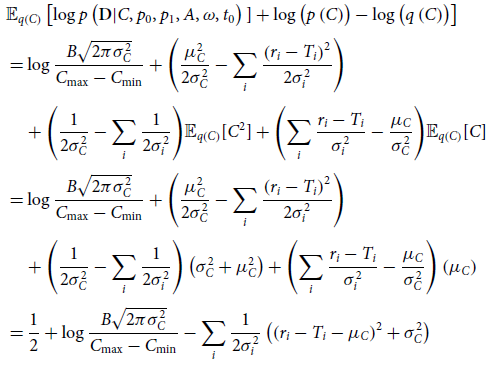 \begin{align*}& \mathbb{E}_{q\left(C\right)}\left[\log p\left(\textbf{D}| C,p_0,p_1,A,\omega,t_0\right)] + \log\left(p\left(C\right)\right) - \log\left(q\left(C\right)\right)\right]\\[3pt]& = \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}} +\left(\frac{\mu_C^2}{2\sigma_C^2} - \sum_{i}\frac{\left(r_i-T_i\right)^2}{2\sigma_i^2}\right) \\[3pt]& \quad + \left(\frac{1}{2\sigma_{C}^{2}} - \sum_i\frac{1}{2\sigma_{i}^{2}} \right)\! \mathbb{E}_{q\left(C\right)}[C^2] + \left(\sum_{i}\frac{r_i-T_i}{\sigma_i^2} - \frac{\mu_C}{\sigma_C^2}\right)\! \mathbb{E}_{q\left(C\right)}[C] \\[3pt]&= \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}} +\left(\frac{\mu_C^2}{2\sigma_C^2} - \sum_{i}\frac{\left(r_i-T_i\right)^2}{2\sigma_i^2}\right) \\[3pt]& \quad + \left(\frac{1}{2\sigma_{C}^{2}} - \sum_i\frac{1}{2\sigma_{i}^{2}} \right)\left(\sigma_C^2+\mu_C^2\right) + \left(\sum_{i}\frac{r_i-T_i}{\sigma_i^2} - \frac{\mu_C}{\sigma_C^2}\right)\left(\mu_C\right) \\[3pt]&= \frac{1}{2} + \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}}-\sum_i \frac{1}{2\sigma_i^2}\left(\left(r_i-T_i-\mu_C\right)^2 + \sigma_C^2\right)\end{align*}
\begin{align*}& \mathbb{E}_{q\left(C\right)}\left[\log p\left(\textbf{D}| C,p_0,p_1,A,\omega,t_0\right)] + \log\left(p\left(C\right)\right) - \log\left(q\left(C\right)\right)\right]\\[3pt]& = \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}} +\left(\frac{\mu_C^2}{2\sigma_C^2} - \sum_{i}\frac{\left(r_i-T_i\right)^2}{2\sigma_i^2}\right) \\[3pt]& \quad + \left(\frac{1}{2\sigma_{C}^{2}} - \sum_i\frac{1}{2\sigma_{i}^{2}} \right)\! \mathbb{E}_{q\left(C\right)}[C^2] + \left(\sum_{i}\frac{r_i-T_i}{\sigma_i^2} - \frac{\mu_C}{\sigma_C^2}\right)\! \mathbb{E}_{q\left(C\right)}[C] \\[3pt]&= \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}} +\left(\frac{\mu_C^2}{2\sigma_C^2} - \sum_{i}\frac{\left(r_i-T_i\right)^2}{2\sigma_i^2}\right) \\[3pt]& \quad + \left(\frac{1}{2\sigma_{C}^{2}} - \sum_i\frac{1}{2\sigma_{i}^{2}} \right)\left(\sigma_C^2+\mu_C^2\right) + \left(\sum_{i}\frac{r_i-T_i}{\sigma_i^2} - \frac{\mu_C}{\sigma_C^2}\right)\left(\mu_C\right) \\[3pt]&= \frac{1}{2} + \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}}-\sum_i \frac{1}{2\sigma_i^2}\left(\left(r_i-T_i-\mu_C\right)^2 + \sigma_C^2\right)\end{align*}
 \begin{align*}\mathrm{ELBO} &= \mathbb{E}_{q(p_0,p_1,A,\omega,t_0)}\bigg[\frac{1}{2} + \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}}\\[3pt]& \quad -\sum_i \frac{1}{2\sigma_i^2}\bigg((r_i-T_i-\mu_C)^2 + \sigma_C^2\bigg) \bigg]\\[3pt]& \quad - \mathrm{KL}\big(q(p_0,p_1,A,\omega,t_0) | | p(p_0,p_1,A,\omega,t_0)\big) \\[3pt]&= \frac{1}{2} + \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}}\\[3pt]& \quad -\sum_i \frac{1}{2\sigma_i^2}\bigg(\mathbb{E}_{q(p_0,p_1,A,\omega,t_0)}\bigg[(r_i-T_i-\mu_C)^2\bigg]+ \sigma_C^2\bigg)\\[3pt]& \quad - \mathrm{KL}\big(q(p_0,p_1,A,\omega,t_0) | | p(p_0,p_1,A,\omega,t_0)\big)\end{align*}
\begin{align*}\mathrm{ELBO} &= \mathbb{E}_{q(p_0,p_1,A,\omega,t_0)}\bigg[\frac{1}{2} + \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}}\\[3pt]& \quad -\sum_i \frac{1}{2\sigma_i^2}\bigg((r_i-T_i-\mu_C)^2 + \sigma_C^2\bigg) \bigg]\\[3pt]& \quad - \mathrm{KL}\big(q(p_0,p_1,A,\omega,t_0) | | p(p_0,p_1,A,\omega,t_0)\big) \\[3pt]&= \frac{1}{2} + \log \frac{B\sqrt{2\pi\sigma_{C}^{2}}}{C_{\max}-C_{\min}}\\[3pt]& \quad -\sum_i \frac{1}{2\sigma_i^2}\bigg(\mathbb{E}_{q(p_0,p_1,A,\omega,t_0)}\bigg[(r_i-T_i-\mu_C)^2\bigg]+ \sigma_C^2\bigg)\\[3pt]& \quad - \mathrm{KL}\big(q(p_0,p_1,A,\omega,t_0) | | p(p_0,p_1,A,\omega,t_0)\big)\end{align*}