SHCal20 Southern Hemisphere Calibration, 0–55,000 Years cal BP

Abstract

Early researchers of radiocarbon levels in Southern Hemisphere tree rings identified a variable North-South hemispheric offset, necessitating construction of a separate radiocarbon calibration curve for the South. We present here SHCal20, a revised calibration curve from 0–55,000 cal BP, based upon SHCal13 and fortified by the addition of 14 new tree-ring data sets in the 2140–0, 3520–3453, 3608–3590 and 13,140–11,375 cal BP time intervals. We detail the statistical approaches used for curve construction and present recommendations for the use of the Northern Hemisphere curve (IntCal20), the Southern Hemisphere curve (SHCal20) and suggest where application of an equal mixture of the curves might be more appropriate. Using our Bayesian spline with errors-in-variables methodology, and based upon a comparison of Southern Hemisphere tree-ring data compared with contemporaneous Northern Hemisphere data, we estimate the mean Southern Hemisphere offset to be 36 ± 27 ¹⁴C yrs older.

1. HISTORY OF SOUTHERN HEMISPHERE CALIBRATION

The conversion of terrestrial radiocarbon (¹⁴C) ages into calendar time requires a calibration curve that accurately reflects past atmospheric ¹⁴C levels. Tree rings offer unsurpassed accuracy and resolution if derived from a replicated tree-ring chronology and if adequately pretreated, so that the dated fraction faithfully captures atmospheric ¹⁴C concentrations at the time of growth, unaffected by variable lignin contents or species-specific differences (McCormac et al. 1998a).

Whilst a major focus of the radiocarbon community has been the calibration of the timescale, early work soon demonstrated there was an offset in atmospheric ¹⁴C concentrations between the hemispheres. Some of the earliest measurements of Southern Hemisphere (SH) tree rings indicated depleted ¹⁴C levels with SH tree rings giving older values compared to contemporaneous tree rings from the Northern Hemisphere (NH). This was probably a result of higher sea-air ¹⁴CO₂ flux from the larger expanse of SH oceans (Lerman et al. 1970; Rodgers et al. 2011). Lerman et al. (1969, 1970) measured a North-South (N-S) hemispheric offset of ~ 36–42 ¹⁴C yrs and Vogel et al. (1986, 1993) measured additional Netherlands/South Africa sample pairs and obtained a value of 41 ± 5 ¹⁴C yrs^†. Vogel et al. (1993) recommended using this constant to create a calibration curve for SH mid-latitudes, based upon the data of Stuiver and Pearson (1993) for the NH.

Subsequently, paired decadal measurements made from contemporaneous British oak (Quercus petraea) and New Zealand (NZ) cedar (Libocedrus bidwillii) or silver pine (Manoao colensoi) tree rings from 1000–0 cal BP by Queen’s University Belfast (identifier UB) and Waikato University (identifier Wk), showed there were differences between the structural forms of the radiocarbon calibration curves for each hemisphere. They demonstrated that the N-S offset was not constant but varied with time, with a periodicity of approximately 130 cal yrs, and amplitudes ranging from 8–80 ¹⁴C yrs (McCormac et al. 1998a, 1998b; Hogg et al. 2002). Building on this work, McCormac et al. (2002) published the first iteration of SHCal (SHCal02) covering the interval 1000–100 cal BP, compiled from data sets derived from NZ (Wk, UB; McCormac et al. 1998a, 1998b; Hogg et al. 2002), Chile (Quaternary Isotope Lab, identifier QL; Stuiver and Braziunus 1998), Tasmania (QL; Stuiver and Braziunus 1998) and South Africa (Pretoria, identifier Pta; Vogel et al. 1993). The combined SH data sets showed a mean offset of 41 ± 14 ¹⁴C yrs for the interval 1000–100 cal BP and in the absence of additional measured SH data, the authors recommended this value be applied to IntCal98 (Stuiver et al. 1998) for the period outside this range. The SH calibration was extended to 11,000 cal BP by McCormac et al. (2004) using the same random walk model and parameters as for IntCal04 (Reimer et al. 2004, Buck and Blackwell 2004). SHCal04 contained the SHCal02 data sets and IntCal04 data with a modeled offset beyond the range of the SH measurements. The modeled offset ranged from 55 to 58 ¹⁴C yrs with uncertainties increasing from ±7.9 ¹⁴C yrs at 1000 cal BP to ±25 ¹⁴C yrs at 11,000 cal BP.

In parallel with the above studies, Hua et al. (2004a) obtained 16 decadal sample pairs (Australian Nuclear Science & Technology Organisation, identifier OZ) from Tasmania (Huon pine, Lagarostrobos franklinii) and Thailand (Pinus merkusii) for the interval 325–175 cal BP to investigate the ¹⁴C content of the atmosphere sampled by tropical trees. The mean offset between Tasmania (older) and Thailand was 30 ± 8 ¹⁴C yrs. Further back in time, Hua et al. (2009) analysed 134 tree-ring samples (OZ) from four Younger Dryas (YD)-age Tasmanian Huon pine subfossil logs (SRT-779, -781, -782, -783) extracted from alluvial sediments along Stanley River in Northwest Tasmania (Australia). Ring-width measurements, supplemented by ¹⁴C wiggle-matching against IntCal04 data (utilizing a 40 ¹⁴C-yrs constant N-S offset) produced a 617-yrs-long floating chronology, spanning the calendar age interval of 12,679–12,072 (± 11) cal BP. Zimmerman et al. (2010) obtained new decadal measurements (Center for AMS, identifier CAMS) from a Huon pine tree-ring series for the interval 2115–855 cal BP. However, Hogg et al. (2011) obtained data (Wk) for a similar interval from NZ kauri (Agathis australis: 2145–955 cal BP) tree-ring series (Boswijk et al. 2014) and suggested some of the equivalent Huon pine data had underestimated uncertainties, with some data points (1205–1075 cal BP) that could be too young. This was confirmed by re-measurement of nine Huon pine decadal samples (Wk) from the interval 1175–1095 cal BP (Hogg et al. 2013a).

Building on the above studies and new datasets from the NH, the 2013 iteration of the SH curve was extended from 0 to 50,000 cal BP (Hogg et al. 2013b). The resulting SHCal13 was a compilation of the SH data sets described above, and based upon IntCal13 data (Reimer et al. 2013), corrected for a N-S offset, beyond the range of the measured data sets. The calibration curve was constructed using a Markov Chain Monte Carlo (MCMC) implementation of the random walk model, with transitional regions where the variance depends upon the measured (SH data) and modeled (IntCal13 data adjusted by the N-S offset) data sets (Heaton et al. 2009; Niu et al. 2013).

There are some aspects of SHCal13 that have potentially important implications for SHCal20:

1. 1. The value of 129 ± 14 BP from Pretoria (identifier Pta) for 100 cal BP (1850 CE) that was used in SHCal04 and SHCal13 is incorrect. The correct value of 155 ± 11 BP (Hogg et al. 2019) is used in SHCal20.

2. 2. Of the four YD-age subfossil Huon pine ¹⁴C data sets in Hua et al. (2009), only SRT-779 agreed closely with contemporaneous YD-age subfossil New Zealand kauri (see further details below). For this reason, the other three Huon pine data sets (SRT-781, -782, and -783) have been omitted from SHCal20.

2. NEW SOUTHERN HEMISPHERE DATA SETS

2.1 High-resolution data relating to the 774 and 993 CE cosmic events

Miyake et al. (2012, 2013) discovered two large and rapid increases in atmospheric ¹⁴C concentration (Δ¹⁴C) from Japanese tree rings dated to 1176/5 cal BP (774/5 CE) and 957/6 cal BP (993/4 CE). Corresponding anomalous ¹⁰Be and ³⁶Cl events recorded in ice cores (Mekhaldi et al. 2015) suggest extreme fluxes from high-energy solar particles were responsible. The NH expression of these events has been detailed in several studies (see Büntgen et al. 2018 and references therein). Güttler et al. (2015) measured Δ¹⁴C levels in NZ kauri, showing their global nature. Annual or biennial SH Δ¹⁴C data from seven tree-ring series, six relating to the 774 CE event (four from NZ and one each from Chile and Tasmania) and one to the 993 CE event (NZ)—Table 1 are available from the Büntgen et al. (2018) study (ETH/AMS facility, identifier ETH, alpha-cellulose). They calculated offsets to contemporaneous NH data of ~30 ¹⁴C yrs (in terms of Δ¹⁴C, these offsets equate to 4.0 ± 0.4‰ in 774 CE and 3.5 ± 0.7‰ in 993 CE). These data are available from the SHCal database (http://intcal.org/shcal20/— datasets 9-1, 9-2, 9-3, 9-4, 9-5, 9-6). The high-resolution SH data compare well with existing SH decadal data (Figures 1A and 1B).

Table 1 Summary of new high-resolution SH tree-ring chronologies/data sets including the time span, block interval (number of yrs [i.e. rings] per analysis) and total number of analyses (N). From Büntgen et al. (2018).

^a Series numbers 9-1 to 9-6 correspond with “Set No.” and “Division” in SHCal database (http://intcal.org/shcal20).

Figure 1A Southern Hemisphere tree-ring ¹⁴C data relating to the 774 CE event. Tree-ring series include: 3-1 (Wk, Manoao colensoi, Oroko Swamp, NZ and Libocedrus bidwillii, Takapari Forest Park, NZ); 3-6 (Wk, Lagarostrobos franklinii, Stanley River, Tasmania, Australia); 9-1, 9-2, 9-3 (ETH, Agathis australis, Dargaville, NZ); 9-4 (ETH, Manoao colensoi, Moana, NZ); 9-5 (ETH, Austrocedrus chilensis, El Asiento, Chile); 9-6 (ETH, Lagarostrobos franklinii, Stanley River, Tasmania, Australia).

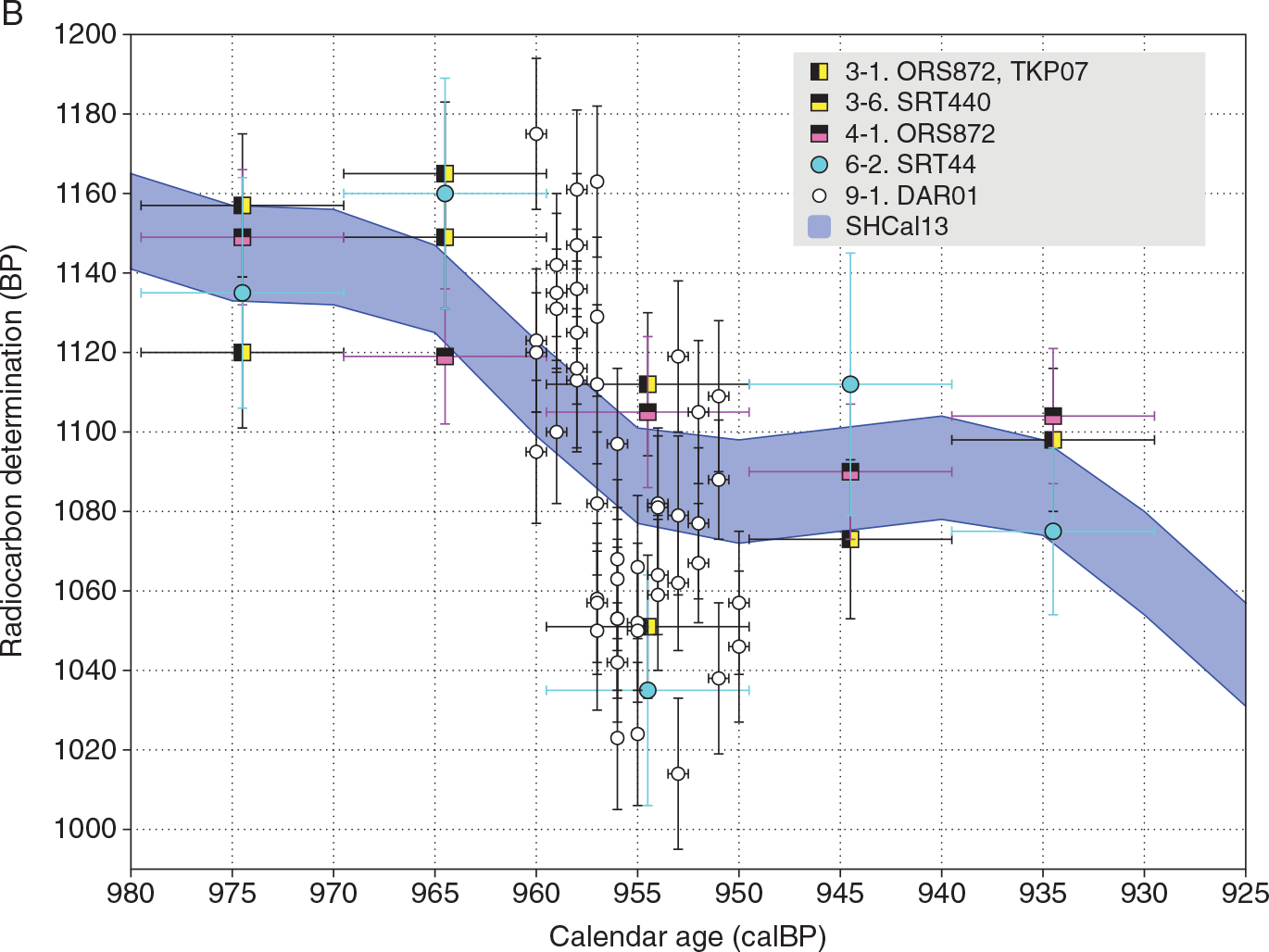
Figure 1B Southern Hemisphere tree-ring ¹⁴C data relating to the 993 CE event. Tree-ring series include: 3-1 (Wk, Manoao colensoi, Oroko Swamp, NZ and Libocedrus bidwillii, Takapari Forest Park, NZ); 3-6 (Wk, Lagarostrobos franklinii, Stanley River, Tasmania, Australia); 4-1 (UB, Manoao colensoi, Oroko Swamp, NZ); 6-2 (CAMS, Lagarostrobos franklinii, Stanley River, Tasmania, Australia); 9-1 (ETH, Agathis australis, Dargaville, NZ).

2.2 New 450–0 cal BP data sets

Four new data sets in the interval 450–0 cal BP have been included in SHCal20 (see Table 2). Data set 3-7 contains 22 Wk decadal solvent-extracted alpha-cellulose high precision radiometric analyses spanning the interval 1725–1935 CE and first given in McCormac et al. (1998a). This group of analyses was accidentally omitted from SHCal04 and SHCal13 but is included in SHCal20.

Table 2 Summary of new 450–0 cal BP SH tree-ring chronologies/data sets showing the time span, block interval (number of yrs [i.e. rings] per analysis) and total number of analyses (N). Dating methods: HPLSC—high precision liquid scintillation counting; AMS—accelerator mass spectrometry.

^ 1915–1945 decades given preliminary multiple solvent (acetone) extractions.

¶ duplicate analyses.

# 1931–1950 decades from Takapari FP (40°04’S, 175°59’E).

+ solv. extr. = solvent (acetone) extracted.

^‡ kauri derived from the upper North Island of NZ but exact geographic location unknown.

Data sets 3-8 and 3-9 are composed from Wk decadal alpha-cellulose AMS analyses spanning the interval 1705–1945 CE and published in Turney et al. (2016). This publication also contained complementary data from Lake Tay (Western Australia) and Campbell Island (NZ). The Lake Tay data set was not considered for SHCal20 because of suspicions that the very high resin content characteristic of the Callitris columellaris trees may have resulted in translocation of ¹⁴C across ring boundaries. The Campbell Island Dracophyllum longifolium data, also omitted, was systematically older than contemporaneous measurements from mid-latitude SH locations, probably as a result of its high latitude Southern Ocean location. See Hogg et al. (2019) for a discussion of both the Lake Tay and Campbell Island data sets. Data set 3-10 contains duplicated Wk five-ring alpha-cellulose AMS analyses spanning the interval 1652–1827 CE and published in Hogg et al. (2019).

Hogg et al. (2019) presented a new Bayesian spline method for calibration curve construction (see below) and tested it on 11 SH data sets. The four new data sets presented here had relative offsets from the mean of ~ +6 to –6 ¹⁴C yrs indicating their suitability for inclusion in SHCal20.

2.3 New 3608–3453 cal BP data sets

Two new single tree ring data sets in the interval 3608–3453 cal BP have been included in SHCal20 (see Table 3). Data set 7-1 contains 16 University of Arizona AMS Facility analyses (identifier AA) spanning the interval 3608–3590 cal BP and 65 AA analyses spanning 3520–3453 cal BP. Pearson et al. (2020 in this issue) compare a sub-set of these data with single year measurements (AA) from Irish oak and North American bristlecone pine, and provide additional fine scale information on the N-S offset during this period.

The two new AA data sets are plotted with SHCal13 in Figure 2.

Table 3 Summary of new 3608–3453 cal BP SH tree-ring chronologies/data sets showing the time span, block interval (number of yrs [i.e. rings] per analysis) and total number of analyses (N).

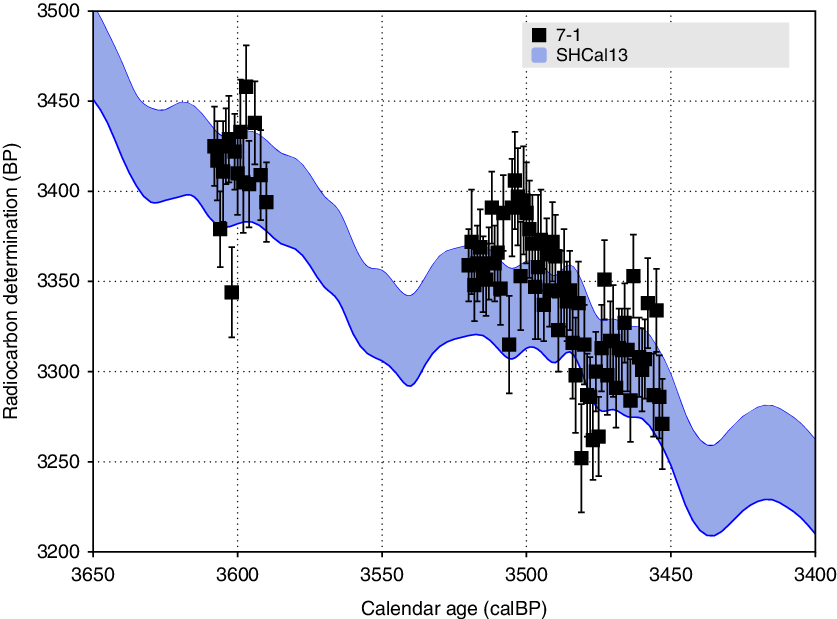
Figure 2 New single-ring ¹⁴C data sets (7-1) in the interval 3608–3453 cal BP. Series 7-1 (AA, Agathis australis, Dargaville NZ).

2.4 New Younger Dryas-age measurements

Hogg et al. (2016a, 2016b) presented a floating ¹⁴C chronology containing 1022 measurements from NZ kauri trees spanning the interval ~11,285–9990 ¹⁴C yrs BP (mean 1σ uncertainty = ±28 ¹⁴C yrs). The kauri trees were located in Northland, at Towai (series name 8-1, CRW003) and Dargaville (series name 8-2, FIN11). The Towai decadal samples (~11,285–10,070 ¹⁴C BP) were derived from a well replicated and securely cross-matched tree-ring chronology (1451 rings, 91 radial strips derived from 37 trees with an average cross-correlation coefficient between all series of 0.71, Palmer et al. 2016). The 778 analyses were determined principally by University of California, Irvine (identifier UCI, holo-cellulose, AMS), Wk (alpha-cellulose, high precision liquid scintillation spectroscopy) and Oxford University (identifier OxA, alpha-cellulose, AMS) with a few additional analyses by ETH (alpha-cellulose, AMS) and University of Heidelberg (identifier Hd, holo-cellulose, Gas Proportional Counting - GPC).

The Dargaville decadal samples (~10,305–9990 ¹⁴C yrs BP) were obtained from a single tree (FIN11, two measured radii, estimated 533 rings), with the 244 analyses undertaken by UCI (holo-cellulose, AMS) and Wk (alpha-cellulose, predominantly high precision liquid scintillation spectroscopy).

The Towai and Dargaville ¹⁴C data sets were wiggle-matched against contemporaneous NH data contained within IntCal13, being careful to avoid aberrant sections of the curve (see Hogg et al. 2016a for details), returning calendar age estimates of ~13,134–11,695 cal BP (Towai) and ~11,870–11,367 cal BP (Dargaville). More recent unpublished higher resolution NH pine (Pinus sylvestris) and NZ kauri measurements by ETH have indicated that the Towai kauri YD ¹⁴C data set should be shifted towards older ages by 10 ± 3 cal yrs resulting in a final calendar age range of ~13,144–11,705 ± 3 cal BP (Sookdeo et al. 2019 in this issue, 2020). This shift also affects the Dargaville series, with an adjusted calendar age range of ~11,880–11,377 ± 5 cal BP. Both Towai and Dargaville data sets have been included in SHCal20 on the basis of a recent decision made by the IntCal Working Group to accept wiggle-matched data from pre-Holocene floating trees.

The four YD-age Huon pine samples analysed by Hua et al. (2009) were compared with the Towai kauri series by Hogg et al. (2016a). The four trees could not be cross-matched by dendrochronology alone and required additional linking by ¹⁴C wiggle-matching (Hua et al., 2009); of the four, only SRT-779 agreed closely with the well-replicated Towai chronology (n = 24; Acomb = 126.4%; An = 14.4%. ${\chi ^2}$-test: df = 23 T = 15.018 (5% 35.173) - see Hogg et al. 2016a for model details) and is retained for SHCal20. For more information on the chronological issues associated with some of the YD-age Huon pine ¹⁴C series and ultimately their exclusion from SHCal20, please refer to Hogg et al. (2016a, 2016b).

The YD-age data sets included in SHCal20 are shown graphically in Figure 3. The new YD measurements refine the shape of the SH atmospheric curve from ~13,100–11,400 cal BP.

Figure 3 Southern Hemisphere YD-age tree-ring ¹⁴C data sets. Tree-ring series include: 8-1 (UCI, Wk and OxA, Agathis australis, Towai, NZ; 8-2 (UCI and Wk, Agathis australis, Dargaville NZ); 5-1 (OZ, Lagarostrobos franklinii, Stanley River, Tasmania, Australia).

Hogg et al. (2016a) showed that the ¹⁴C calibration curve IntCal13, and as a consequence SHCal13, was clearly too young from ~12,200–11,900 cal BP. This time interval had previously been occupied by an incorrectly linked larch tree-ring series from Ollon, Switzerland (Ollon505, also termed VOD505, Hogg et al. 2013c). They also showed that the YD-B chronology was incorrectly linked by dendrochronology to NH Holocene data and this caused the ~10,400 BP ¹⁴C plateau in IntCal13 and SHCal13 to be ~5 decades too short, thus shifting the two ¹⁴C peaks seen at around 12,500 cal BP towards older calendar ages by about 50 cal yrs. This finding has recently been confirmed with new dendrochronological and ¹⁴C measurements on NH trees (Sookdeo et al. 2019, 2020).

3. CALIBRATION CURVE CONSTRUCTION

We would ideally wish to create a complete, annually resolved, SHCal20 calibration curve based solely upon direct SH observations and without requiring any modeling assumptions about the nature of the N-S hemispheric offset to be made. Such a curve would be entirely independent from the NH IntCal20 curve (Reimer et al. 2020 in this issue). With our new and existing datasets this is achievable in four distinct time periods: those covering the SH trees dated by dendrochronology of approximately 2140–0, 3520–3453, and 3608–3590 cal BP; and that covering the floating SH trees of approximately 13,140–11,375 cal BP. However outside these time periods we are lacking direct SH observations, and so in order to create the SHCal curve, we will need to include information from the corresponding NH IntCal20 curve. This requires us to make a simple statistical model of the N-S atmospheric radiocarbon offset to transfer information from the NH data.

We aim to provide a construction method where, for the four time periods listed above with dense SH data, the SHCal20 curve is the exact curve one would obtain using only that SH data. These SH-data-based sections of curve are then used to learn about the nature of the N-S hemispheric offset and extrapolate to extend SHCal20 over the complete 0–55 cal kBP (thousands of calibrated years before present) time range. The construction process is shown in Figure 4. The concept is similar to that used for SHCal13 although the new SHCal20 methodology incorporates and estimates the N-S offset, and hence the final SH calibration curve, more rigorously.

Figure 4 A step-by-step illustration of SHCal20 curve construction. Panel A: The SH ¹⁴C observations covering the four distinct time periods where direct measurements are available. We initially fit a Bayesian spline to this observed SH ¹⁴C data. In the periods where we have sufficient direct SH observations, this spline fit is SHCal20; outside these times, in periods where we not have direct SH observations and this initial spline is not informative, we instead base SHCal20 on importing information from the NH by modeling the N-S hemispheric offset. Panel B: A zoomed-in section with a posterior realization of the initial spline fitted to the SH ¹⁴C observations, the rug indicates the knot locations. Where we do not have direct SH observations this initial fitted spline is deleted (red dashed line) leaving an incomplete part SH-realization (red solid line). Panel C: The incomplete part SH-realization (red solid line) is paired with a complete 0–55 cal kBP NH IntCal20 spline realization (blue solid line). Panel D: In periods where we have direct SH data the offset between the selected part SH- and complete NH- spline realizations is calculated (black solid line) and extended to the missing periods (green solid line) by modeling, conditional on the black calculated values, as an AR(1) process. Panel E: The completed, AR(1)-simulated, offset is added back to the NH-realization providing a completed 0–55 cal kBP SH-realization (red solid line). Due to construction, in periods where SH data is available this completed SH-realization will be identical to the initial part SH-realization. Panel F: This process is repeated with multiple (part SH- and complete NH-) spline realizations to provide an ensemble of AR(1)-completed SH-realizations which are summarized to provide the SHCal20 curve. (Please see electronic version for color figures.)

3.1 Creating a curve where we have SH observations

We commence by creating a preliminary SH calibration curve based only on the available SH data using the same Bayesian spline with errors-in-variables methodology of IntCal20; see Heaton et al. (2020 in this issue) for further details. For the three distinct time periods covered by the observed SH trees dated by dendrochronology (approximately 2140–0, 3520–3453, 3608–3590 cal BP) we select the same knots for our spline, both in terms of number and location, as used in IntCal20. This includes the specific, additional knots placed around 774/5 CE and 993/4 CE used to enable representation of the rapid Miyake “cosmic” events (Miyake et al. 2012, 2013). This matched knot selection with the NH IntCal20 curve enables equitable comparisons on the N-S hemispheric offset to be made and, since the density of the SH data is lower than the density of the data from the NH, is sufficient for us to capture the detail within the available SH ¹⁴C observations. For the floating SH tree rings (approximately 13,140–11,375 cal BP) we use the same number of knots as in the corresponding section of the IntCal20 curve but space them evenly over the interval. Such a placement allows the Bayesian method to explore the exact calendar location of these floating trees equitably—an uneven knot spacing introduces bias as the method will tend to align the trees so that wiggles in the underlying levels of ¹⁴C fit with higher knot density (Heaton et al. 2020 in this issue). Outside these time periods, where no SH data are present, we reduce the number of knots in our spline.

Repeat observations on same-sample material are combined as for IntCal20. We also place the same prior on the additive over-dispersion, obtained from the Sixth International Radiocarbon Intercomparison (SIRI, Scott et al. 2017), as used for IntCal20 (see Heaton et al. 2020 in this issue, for details on how this prior was constructed). This over-dispersion attempts to identify and quantify any potential additional variability in ¹⁴C determinations beyond the laboratory-quoted uncertainty (e.g. growing season, intra-hemispheric regional effects, species) to ensure we do not obtain an over-precise calibration curve. Our SIRI-based prior, together with the posterior we obtain from the SHCal20 data, are shown in Figure 5.

Figure 5 Histogram of the posterior for $\tau $, the level of over-dispersion in the SHCal20 data. We model ${F_i}$, the observed value of F¹⁴C in (annual) datum $i$ with calendar age ${\theta _i}$, as ${F_i} = f\left( {{\theta _i}} \right) + ϵ{_i} + {\eta _i}$. Here $f\left( {{\theta _i}} \right)$ is the underlying atmospheric F¹⁴C level at ${\theta _i}$ cal BP in the SH; $ϵ{_i} \sim N\left( {0,\sigma _i^2} \right)$ the laboratory reported uncertainty; and ${\eta _i} \sim N\left( {0,{\tau ^2}f\left( {{\theta _i}} \right)} \right)$ the over-dispersion used to model any potential further additional variability seen in the SHCal20 data. Note that, as for IntCal20, our model for this over-dispersion/additional variability scales with $\surd f\left( {{\theta _i}} \right)$, the square root of F¹⁴C. We also show the SIRI-based prior in red. As expected, this SIRI-based prior on the level of over-dispersion is larger than our posterior due to the screening criteria for SHCal20 data. The posterior estimate is dominated by the SHCal20 data rather than the prior.

The MCMC Bayesian spline curve fitting process was run for 50,000 iterations with the first 25,000 discarded as “burn-in” (for an introduction to Bayesian analysis and MCMC, see Gelman et al. 2013). Due to the predominantly Gibbs update steps, and after a visual assessment of various individual parameters, this length of run was felt to be sufficient to achieve convergence. The output was then thinned, saving only every 10th iteration, to reduce auto-correlation in the fitted location of the floating trees.

The described approach provides curve estimates in these four time intervals based only upon the SH data in such a way that still allows us to share information on ¹⁴C variability over time (as represented by the spline’s smoothing parameter) between the disjoint intervals and jointly estimate the level of over-dispersion. After thinning, we obtain from this MCMC 2500 posterior part-realizations (so called since they only cover these four disjoint time intervals) of the SH atmosphere (Figure 4B) together with corresponding posterior estimates for the over-dispersion in ¹⁴C within the SH. We call these sections of the curve SH-data-based.

Outside of these four time intervals however, the above approach does not work since we do not have SH data on which to base an estimate. To create a complete SH curve from 0–55 cal kBP we need to rely upon importing information from the NH curve based upon a model for the N-S offset. However, we wish to do this in such a way that ensures that, in these four specific intervals, our final SHCal20 curve still corresponds to these SH-data-based estimates.

3.2 Extending the SH curve by modeling

We model the evolution of the N-S offset over time as a first-order autoregressive (AR(1)) process. This time-varying process models ${X_t}$, the N-S offset at calendar age $t$, as linearly dependent upon the size of the offset in the previous year, with the addition of a stochastic/random component. Specifically,

${X_t} = μ + \phi \left( {{X_{t - 1}} - μ } \right) + {ϵ_t},$

where the $ϵ{_t}$ are considered independent and identically distributed from a $N\left( {0,\sigma _e^2} \right)$ distribution. Here $μ $ denotes the mean N-S offset and the parameter $\phi $ encapsulates the N-S offset’s dependence over time. We aim to learn about this offset based upon both our SH-data-based curve and our corresponding IntCal20 curve. We can then extrapolate the NH curve accordingly in the time periods where SH data are lacking.

Each of the 2500 SH-data-based part-realizations is paired with a randomly drawn NH curve realization from the IntCal20 posterior (Figure 4C). Unlike the SH part-realizations, each of these NH realizations extend from 0–55 cal kBP. In the SH-data sections, the offset between the NH and SH realization is calculated and an AR(1) process is fitted to these observed values using maximum likelihood. We then form, conditional on the observed offset in the SH-data sections, predictions for the N-S offset for the calendar ages outside the range of the SH-data covering the complete 0–55 cal kBP period (Figure 4D). To create a full SH-realization this offset is then added to the NH realization (Figure 4E).

This approach provides 2500 complete SH-realizations (Figure 4F) which, in the SH-data-based regions, are identical to their corresponding part SH-realization. Outside they transition smoothly to an offset version of their paired NH realization, with the size of that offset realization dependent and determined according to our best, maximum likelihood, estimate.

3.3 Adding in over-dispersion and creating predictive intervals

Finally we add back in our SH-data-based measure of over-dispersion to these 2500 complete SH-realizations to create predictive intervals for the complete SHCal20 curve. This over-dispersion aims to assess any potential additional ¹⁴C variability, seen within observed SH tree-ring determinations with identical calendar ages, beyond that quoted by the laboratories. Such additional ¹⁴C variability is to be expected since laboratories are only able to quantify those elements within their control and could occur as a consequence of intra-hemispheric regional differences in ¹⁴C levels; between-tree, species or growing season differences; or inter-laboratory differences. By incorporating this additional variability into predictive intervals on the calibration curve we aim to ensure we do not provide overly precise calendar age estimates. For more details see Heaton et al. (2020 in this issue).

We note that the level of over-dispersion estimated from the SHCal20 data (shown in Figure 5) is smaller than that within the NH (Heaton et al. 2020 in this issue: Figure 5). This could be due to the smaller range of potential sources of additional variability within the collated SHCal20 tree rings when compared to the NH IntCal20 data. The SH ¹⁴C tree-ring measurements generally have fewer overlapping trees in any time period, come from a smaller number of laboratories, cover a smaller number of tree species, and arise from a smaller set of locations. However, alternatively it might be that there is less additional variation in ¹⁴C levels within the SH, perhaps due to reduced regional effects. As a consequence of this reduced over-dispersion with the SH tree rings, as we extend past ~40 cal kBP the published SHCal20 curve has slightly narrower predictive intervals than IntCal20.

3.4 Model robustness: An alternative approach with sampling importance resampling (SIR)

The above approach of randomly pairing NH and SH curve realizations does not fully incorporate all the information one could extract from the offset model, as it does not take into account possible dependence between the uncertainties in the two curves. Specifically, we may end up with pairings whereby the calculated offset does not agree well with an AR(1) process in which case we have the potential to overestimate the uncertainty in the predicted offset and consequently the final SHCal20 curve.

To investigate if this was a genuine concern, we therefore also considered an alternative, more statistically rigorous sampling importance resampling (SIR) approach, whereby each SH part-realization was compared to all of the 2500 NH realizations stored for IntCal20. The maximised likelihood of the observed offset between the SH part-realization and each of these NH realizations was calculated under the AR(1) model to provide an importance weight for each match of the SH part-realization to all the NH realizations. The specific NH realization with which to pair the SH part-realization was then randomly chosen according to these importance weights. The offset was then extrapolated as for the random pairing but now with a pair that best approximates an AR(1) process. As for the random pairing, this SIR approach ensures that the complete SHCal20 realizations agree with their corresponding part-realization.

This SIR approach was however extremely slow to run since, unlike the random pairing, it required calculation of the maximised likelihood for all possible combinations of SH and NH realizations. Further, and more significantly, this SIR approach gave a very small effective sample size with the same few NH realizations being chosen repeatedly. In the older pre-Holocene time periods where the underlying NH data have considerable calendar age uncertainty and a large posterior sample is required to accurately represent the curve, the SIR approach consequently failed. The value of the NH calibration curve in these older time periods is almost independent of its value in the calendar periods (e.g. 2000–0 cal BP) where the weighting was performed, and the offset observed. As a result of this independence, during these older periods where we have no direct SH data, the SH curve should simply be a constant offset from IntCal20 since for these older times we are reliant upon the NH curve and our offset model to provide the SH estimate. This was not the case for the SIR based estimate. The random pairing approach did however create an SH curve estimate with a constant offset from IntCal20 as we extend back beyond our observed SH data and towards 55 cal kBP indicating that random pairing worked appropriately for these older time periods.

Further, in regions where the underlying NH curve is based on trees dated by dendrochronology and a small posterior sample is sufficient to reliably summarize the curve, the SIR approach was indistinguishable from the random pairing method. This suggests the random pairing approach is robust and does not introduce additional uncertainty, providing confidence in the reconstruction.

Finally, we note that it would be possible to construct both the NH and SH curves simultaneously, combining data from both hemispheres and a model for the offset into a joint curve creation. This is a consideration for future curve updates although it would raise the issue of potential asymmetry (which hemisphere should be considered offset?) and that, even in regions where SH data were dense, the SH curve would be influenced by the NH data. Such an integrated MCMC approach may also re-introduce some of the mixing difficulties seen in the random walk approach of IntCal13 making curve estimation much more computationally intensive.

3.5 Value of the N-S offset

Each of the 2500 pairings of NH and SH curve realizations provides a slightly different estimate of the N-S offset. This will result in us estimating 2500 different AR(1) processes each with its own mean and standard deviations. In Figure 6, we present the estimated mean offsets and standard deviation over time for all these 2500 realized offsets. Based upon these 2500 paired curves we estimate the mean N-S offset to be 36 ¹⁴C yrs with a standard deviation of 27 ¹⁴C yrs (i.e. 36 ± 27 ¹⁴C yrs).

Figure 6 Histograms of the estimated means and standard deviations (sd) of the AR(1) processes used to model the N-S hemispheric offset.

For time intervals based upon IntCal20 data adjusted for the N-S hemispheric offset, we recommend that readers also consult the complementary IntCal20 paper (Reimer et al. 2020 in this issue) which details the differences between IntCal20 and IntCal13.

A comparison of the SHCal13 and SHCal20 curves without the underlying data for clarity is given in Supplementary Material (Figure S1).

4. ShCal20 CALIBRATION FOR TROPICAL AND SUBTROPICAL REGIONS

4.1 The Inter-Tropical Convergence Zone (ITCZ) and inter-hemispheric air mass mixing

The youngest portions of IntCal20 and SHCal20 curves are based on tree rings from temperate latitudes of each hemisphere. An obvious question is which calibration curve should be used in the tropics and subtropics given no long tree-ring ¹⁴C records for these regions are currently available.

Several studies suggest that atmospheric ¹⁴C over tropical and subtropical regions could be influenced by north-south air-mass mixing as a result of monsoon circulation. Hua et al. (2004a, 2004b) and Hua and Barbetti (2007) discussed influences of SH air masses on atmospheric ¹⁴C over northern tropical and subtropical regions during the pre-bomb and post-bomb periods. Similarly, Hua et al. (2012) reported monsoonal influences of NH air masses on atmospheric ¹⁴C over a southern tropical island (latitude 5°S) in Indonesia during the post-bomb period. The use of either IntCal20 or SHCal20 curve for regions which are influenced by monsoon circulation, might be therefore inappropriate, and a mixed curve accounting for north-south air-mass mixing can be used for these regions. This approach is similar to that for tropical South America proposed by Marsh et al. (2018).

Monsoon circulation can result in air-mass mixing and high precipitation (McGregor and Nieuwolt 1998; Zhang and Wang 2008), and in several monsoon regions the bands of highest summer precipitation approximately follow the position of the ITCZ (Figure 7). However, climate model simulations and reanalysis data indicate that not all areas experiencing high precipitation are strongly influenced by air masses from the opposing hemisphere. In particular, reanalysis data for the past 3 decades (Figure 7) shows that the intrusion of NH air into the southeast trending South Pacific Convergence Zone (SPCZ) is sharply truncated (but see Section 4.2). We therefore consider it more prudent to use wind data and the seasonal ITCZ positions rather than precipitation to estimate the zonal boundaries of the areas in which IntCal20, SHCal20 and a mixed curve are used.

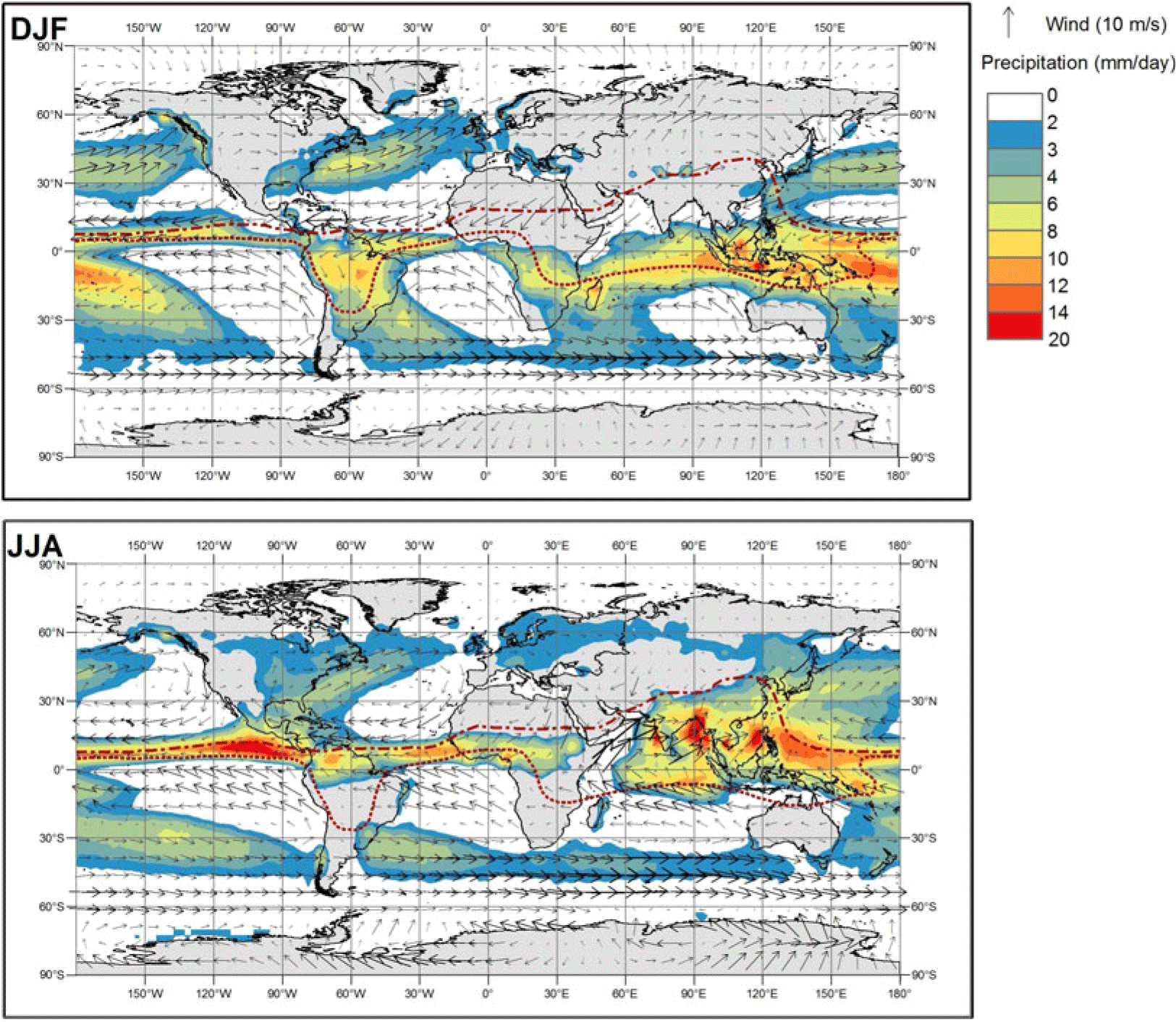
Figure 7 World map showing means of winds (1981–2010) and precipitation (1979–2018) at 925 hPa for two different periods: December–February (top panel) and June–August (bottom panel). These data are derived from the NCEP reanalysis wind (https://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis.derived.pressure.html) and the CMAP precipitation (Xie and Arkin 1997), respectively. Dotted and dashed lines represent the ITCZ during December–February and June–August, respectively.

We therefore recommend the use of (i) IntCal20 for areas north of the ITCZ in June–August (dashed lines in Figure 7) which receive NH air masses all year round, (ii) SHCal20 for areas south of ITCZ in December–February (dotted lines in Figure 7) which see SH air masses all year round, and (iii) a mixed curve for areas between the two seasonal ITCZ positions shown in Figure 7, which receive northern air masses in December–February and southern air masses in June–August.

The degree of north-south air-mass mixing for the mixed curve is another issue. For vegetation, which grows almost all year round, the degree of air-mass mixing should be 50%:50% (northern:southern air masses). For seasonal vegetation, the degree of air-mass mixing might be different than the above value. However, Hua and Barbetti (2007) estimated a 52 ± 13% contribution of southern air masses to northern tropical and subtropical regions influenced by monsoons during the boreal summer months, which was based on atmospheric and tree-ring ¹⁴C data during the bomb-peak period. We thus recommend a simple approach with 50%:50% of north-south air-mass mixing for the mixed curve, and age calibration using that curve can be easily carried out using the “Mix_curve” command in OxCal program (Bronk Ramsey, 2009) or selected as a curve option in CALIB 8.2 (Stuiver et al. 2020).

4.2 Past ITCZ variations

As the mean seasonal positions of the ITCZ and the strength of monsoon circulation change at different timescales (inter-annual, decadal, centennial, etc.; e.g., Haug et al. 2001), the boundaries of the mixed-curved areas in the past can be different from those shown in Figure 7, which are based on the modern meteorological data. At least for the remote past, the use of IntCal, SHCal or a mixed curve for a particular region in the tropics and subtropics becomes less critical for many studies when the maximum ¹⁴C offsets of these curves, which are the N-S offsets of 36 ± 27 ¹⁴C yrs (based upon our estimates in Section 3.5) are negligible compared to the ages of the events to be dated.

However, this may not be the case for researchers studying human expansion over short time scales. For example, Goodwin et al. (2014) have reconstructed Pacific climate and in particular wind field patterns associated with changing El Niño and La Niña events, over the last ~1000 yrs, using a general circulation climate model extensively calibrated with paleoclimate data. Their model showed large variations on decadal and longer timescales in the mixing of NH air into the South Pacific via the SPCZ, dependent on the state of the Pacific Decadal Oscillation and the decadal-scale predominance of El Niño vs La Niña events, with minimal mixing in some bi-decades and a mixed region extending as far as 30°S across most of the Pacific in others.

It seems highly likely that similarly detailed wind field reconstructions in other areas will also show significant variations in the past boundaries of the zone covered by the movement of the ITCZ. Until new tree-ring ¹⁴C data sets are created from within the tropics and subtropics, only approximations for the boundaries of the mixed region and the regional balance of northern and southern air masses within it are possible, and researchers wishing to calibrate radiocarbon data from these regions should be mindful of these limitations. Future research efforts should focus on ¹⁴C measurement on tree rings from these areas in order to construct proper calibration curves for these regions, and to gain a better understanding of regional ¹⁴C offsets and their temporal variations.

5. HIGH SOUTHERN LATITUDES

De Pol-Holz et al. (2017) have suggested that an additional high latitude SH region should be distinguished, as the region south of the peak intensity of the Southern Westerly Winds (~50°S) is influenced by the release of old carbon from the Southern Ocean due to upwelling and air-sea gas exchange. Turney et al. (2016) and Hogg et al. (2019) also found lower ¹⁴C levels from Campbell Island (53°S) tree rings, supporting this finding. We have not implemented such a feature in this version of SHCal, but researchers calibrating measurements from the subantarctic SH should be aware of the likelihood that a small and likely time-varying offset exists. As more calibration data from southern South America and subantarctic islands in the Southern Ocean become available, we anticipate that a separate high latitude Region 1 will likely be incorporated into future versions of SHCal.