Introduction
Surges are common on most of the larger ice caps in Iceland. A thorough account of glacier surges in Iceland is given by Reference Björnsson, Sigurðsson and FlowersBjörnsson and others (2003). All the broad, large outlet glaciers of Vatnajökull ice cap, on the southeast coast of Iceland, have a history of regular surges. These surges contribute significantly to the total mass transport of the outlet glaciers and affect their size, morphology and flow regime. In this paper, the surge of Dyngjujökull, an outlet glacier on the northwestern side of Vatnajökull, is described and computations with a numerical model are conducted to cast light on the effect of the surge on the flow regime of the glacier.
Dyngjujökull has all the characteristics of a surging glacier as listed by Reference RaymondRaymond (1987) and described by Reference Meier and PostMeier and Post (1969). The surges occur repeatedly, with a relatively constant quiescent interval of 20-30years between surges. Documented surges on Dyngjujökull occurred in ∼1900, 1934, 1951, 1977 and 1999; the intervals between the surges were thus ∼34, 17, 26 and 22 years. The area affected by surges is 400-800 km2, and generally the terminus advance is about 1.5 km (Reference Björnsson, Sigurðsson and FlowersBjörnsson and others, 2003). The surge phase is 1-2 years in duration, which is short relative to the quiescent interval. During a surge the surface velocities increase 100-200-fold, and mass is rapidly transported from the up-glacier reservoir area to the down-glacier receiving area. During the quiescent period, the surface velocity is lower than the velocity required to maintain the size of the glacier, causing a build-up in the reservoir area and ice loss in the receiving area. Thickness changes during this period gradually return the surface to the pre-surge state.
Study Area and Measurements
Dyngjujökull is a north-facing, gently sloping outlet glacier of Vatnajökull ice cap (Fig. 1). It is about 40 km long, 20 km wide and has an area of 1040 km2. The surface elevation range is 700–1650m, with an average surface slope of about 1.6˚ (Reference Björnsson, Sigurðsson and FlowersBjörnsson and others, 2003). The surface and bedrock geometry was surveyed with radio-echo sounding methods in 1989, resulting in a digital elevation model (DEM) with a 200m resolution and 2–5 m accuracy for the surface and 10–30 m accuracy for the bedrock geometry (Reference Björnsson, Pálsson and GuðmundssonBjörnsson and others, 1992). The measured surface thus shows the glacier in the middle of a quiescent phase and can be expected to have the relatively flat surface of a retreating glacier.
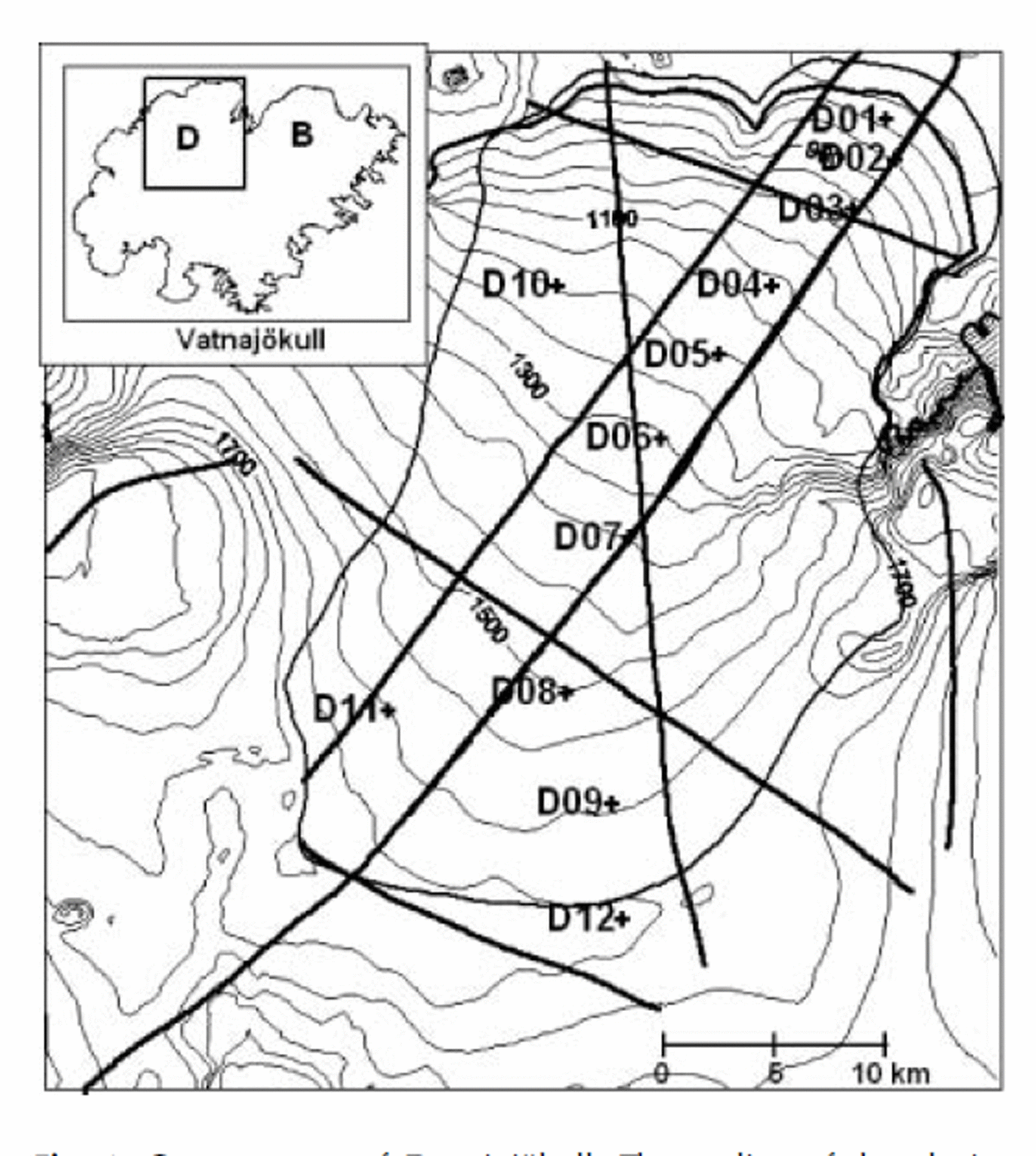
Fig. 1. Contour map of Dyngjujökull. The outline of the glacier which is also the numerical model boundary is delineated. The paths of the airborne radar elevation surveys are shown with thick lines. The path of the January 2000 flight falls onto the September 2000 flight along the measurement sites. The sites of mass-balance and surface velocity measurements are shown with crosses and labeled with corresponding names. The inset map shows Vatnajökull and the outline of the contour map. D and B refer to Dyngjujökull and Brúarjökull, respectively.
In a gravity survey effort in the summers of 1997 and 1998, surface elevation measurements were conducted on 40–50 sites on the glacier (Guðmundsson and Högnadóttir, 2001), allowing a new surface map to be created. The change in surface elevation from 1989 to 1998 is shown in Figure 2. During this period the glacier surface lowered considerably in the ablation area, up to 60–70 m close to the margin, but rose slightly in the accumulation area.
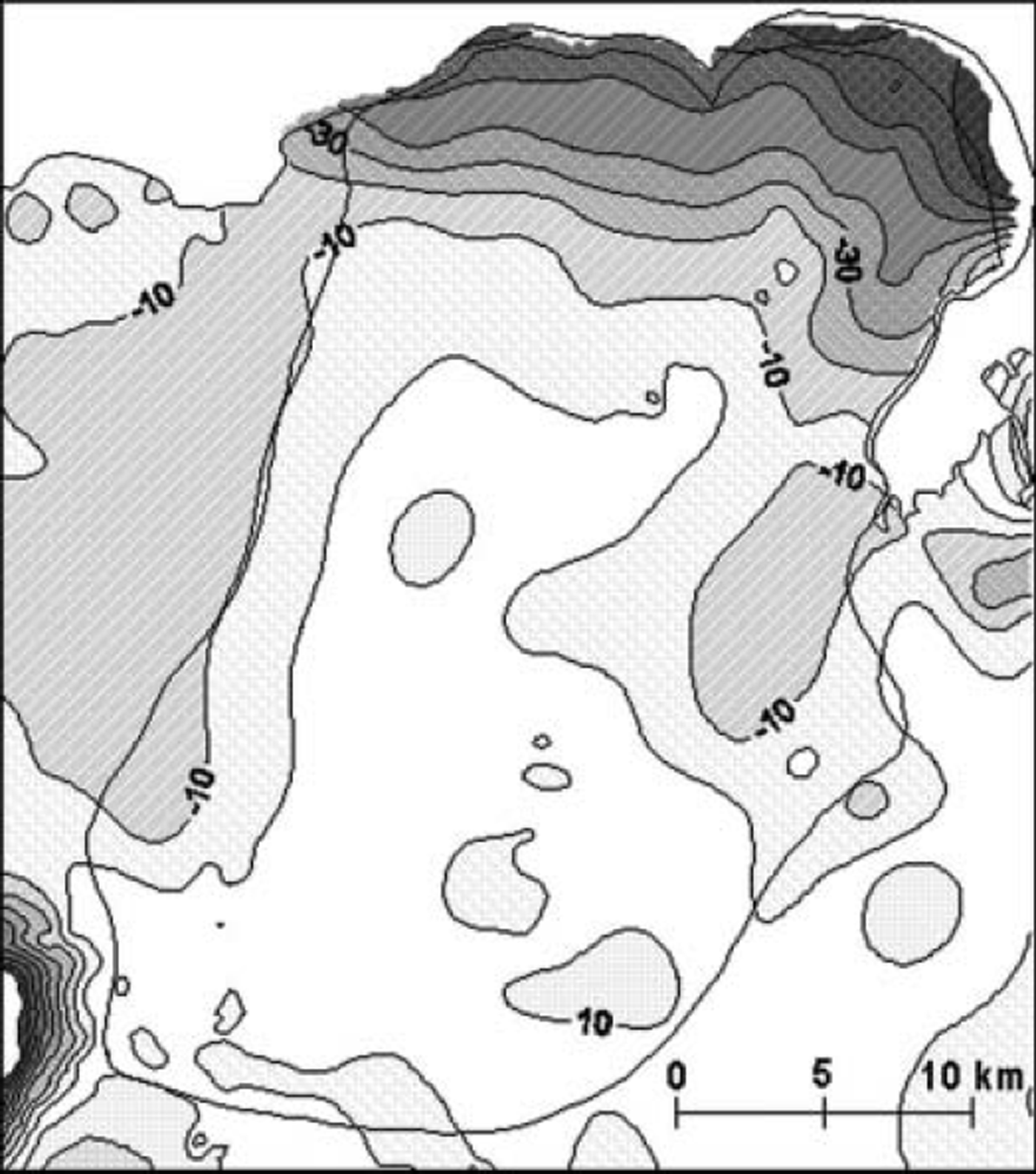
Fig. 2. Difference in surface elevation (m) from the time of the radio-echo sounding survey in 1989 to the gravity survey in 1998, at the beginning of the surge. The surface lowered by up to 70m close to the terminus, but rose slightly in the accumulation area.
Mass balance and surface velocity have been measured on 10–15 sites on Dyngjujökull since 1993, but during the 1998–2004 period it was not possible to access the survey sites due to the heavily crevassed surface. The location of the sites is shown in Figure 1 , and the profile along the glacier length through the survey points together with the mass-balance and surface velocity measurements are shown in Figure 3. The equilibrium-line altitude (ELA) varied between 1100 and 1385 ma.s.l. during the measurement period, 1993–98 (Reference Björnsson, Pálsson, Guðmundsson and HaraldssonBjörnsson and others, 1998). Prior to the surge, the measured surface velocities were only about 25–70% of the balance velocities (Reference Björnsson, Pálsson and GuðmundssonBjörnsson and others, 1995a, Reference Björnsson, Pálsson and Guðmundssonb, Reference Björnsson, Pálsson, Guðmundsson and Haraldsson1997). Meltwater from Dyngjujökull is the largest source for the river Jökulsá á Fjöllum which has a discharge of about 50 m3 s–1 in winter, increasing to 200-300 m3 s–1 in summer (personal communication from H. Haraldsson, 2000). Reference SigurðssonSigurðsson (1990) showed with chemical analysis of the groundwater that water originating from glaciers is present in shallow aquifers, bordering on or extending under the glaciers. He also notes that the drainage basin of Jökulsá á Fjöllum is situated on a permeable young rock formation (mostly Late Quaternary to Recent) and has considerably higher winter discharge than the neighboring river Jökulsá á Bru (∼5-10m3 s–1), which drains Brúarjökull, the northeast outlet of Vatnajökull, and is situated on an impermeable formation (mostly Tertiary and Early Quaternary), while the summer discharge of these two rivers is similar. This difference indicates an active groundwater system in the drainage basin of Jökulsá á Fjöllum and the possibility of groundwater infiltration beneath Dyngjujokull. Reference Flowers, Björnsson and PálssonFlowers and others (2003) showed with a numerical glacio-hydraulic model that, of all the outlet glaciers of Vatnajökull, Dyngjujökull exhibits the highest sensitivities to geothermally derived meltwater, subsurface groundwater loss and surface snowmelt routing.
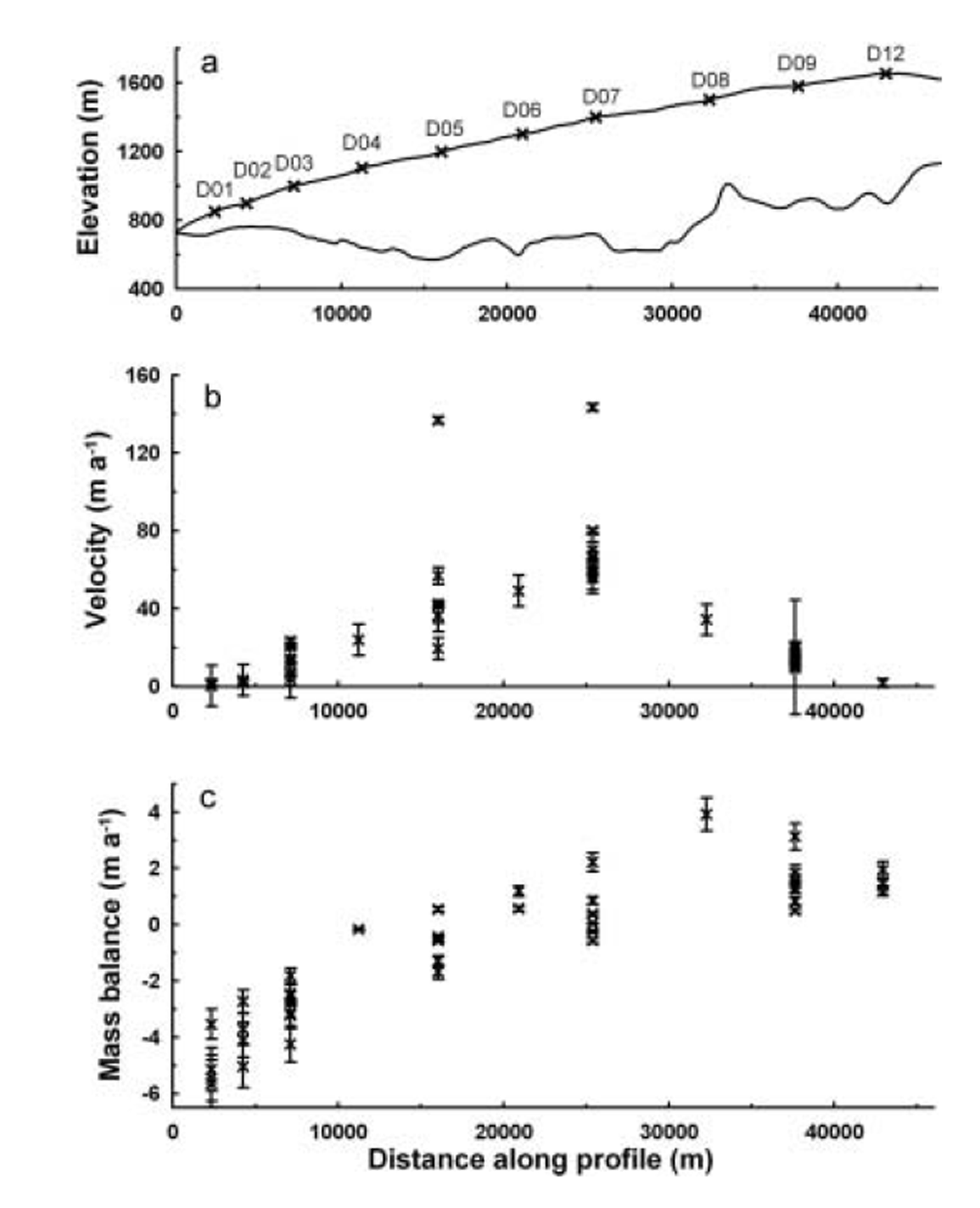
Fig. 3. Profile along the measurement sites shown in Figure 1. (a) Surface and bedrock elevation, along with the location of mass-balance and surface velocity measurements; (b) surface velocity measurements at each site, 1993–98; and (c) the mass-balance measurements at the same sites.
Surge in Dyngjujökull, 1998–2000
The first indicator of the surge was increased sliding velocity at sites D05, D07 and D09 during summer 1996. A year later, a significant velocity increase was measured at sites D03 and D07 (no data for D05). In the autumn, unusual crevasses were observed between sites D07 and D05. In summer 1998, the velocity increased considerably at D03 (from about 10 m a–1 to 23 m a–1) and tripled at sites D05 (from about 40–50ma–1 to 137 ma–1) and D07 (from about 50–70ma–1 to 143 ma–1), between which the ELA normally lies (Fig. 3). In the autumn, long crevasses, following altitude contours (tens of cm up to 1.5 m wide), were observed in a 1 km wide area around site D07, and new crevasses were open close to site D05. In spring 1999, the crevassed belt had extended much higher up-glacier and open and clearly active crevasses were spotted 2.5 km south of D09. During the period 1998–2004 no direct velocity or mass-balance measurements were carried out on the glacier due to the heavily crevassed surface after the surge. In a reconnaissance flight on 18 August 1999 the outline of the surge-affected area was located. A visible bulge on the surface was clearly observed at an elevation of about 1000–1100 m. On 20 September 1999, when site D11 was measured, extension crevasses were clearly seen in its neighborhood. In a flight over the glacier on 8 November 1999 the visibility was poor, but it seemed that the surge front had only reached the glacier margin on the western side of the surge area. In another flight on 15 November 1999 it was seen that the surge wave had reached the margin everywhere. On 27 January 2000 an airborne radar elevation survey was conducted along a line that approximately follows sites D01, D02, D03, D05 and D07. Another, more extensive radar elevation survey was carried out on 14 September 2000, when five survey lines across the surge area, one following the survey line from January, were flown. These survey data allowed a difference map between the data and the surface map from 1998 to be created. This difference map (Fig. 4) provides a fair estimate for the surface of Dyngjujökull at the end of 2000. It appears that during the surge an elevation drop of up to 70m occurred in the reservoir area and the surface rose by up to 100 m near the glacier margin. No attempt was made to estimate the surface changes outside the surge area. Therefore the surface maps from 1998 and 2000 are the same outside that area.
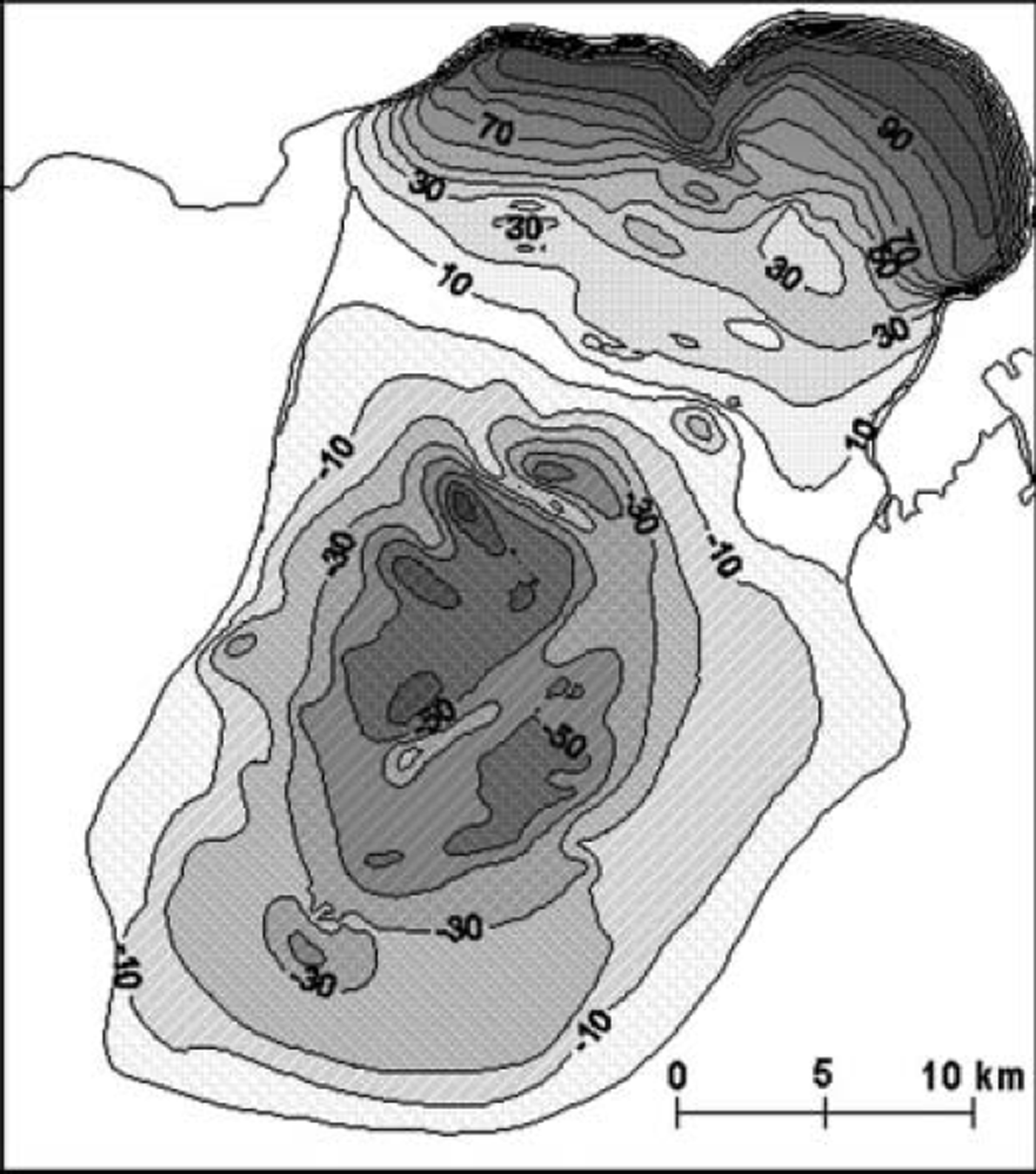
Fig. 4. Difference in surface elevation (m) from 1998 to September 2000. The reservoir area lowered by up to 70m and the receiving area rose by up to 100 m near the margin.
This surge was also observed using European Remote-sensing Satellite (ERS) synthetic aperture radar (SAR) tandem interferograms (Reference Fischer, Rott and BjörnssonFischer and others, 2003). There are interferograms available from before the surge start and three during the surge. Between March 1996 and January 1997, surface velocity acceleration was observed in an area of 200 km2 near the ELA. In an interferogram from 6/7 January 1999 a well-developed 210 km2 surge area is observed, which increased to 250km2 by 10/11 February 1999. The third interferogram, from 26/27 January 2000, shows an area of 550 km2 affected by the surge. In the interferograms of January and February 1999 the maximum velocity is located near the ELA, but in the January 2000 interferogram it is located near the snout. In this sequence of interferograms, a southward migration of the area with very low or no flow at the head of the glacier, indicating the location of the ice divide, is observed. The location of the ice divide cannot be determined from these images, but the southward migration of the no-flow area during the surge would increase the accumulation area (Reference Fischer, Rott and BjörnssonFischer and others, 2003).
An attempt was made to retrieve the surface velocity with a speckle-tracking method. In the surging area, this was not possible due to decorrelation caused by high deformation rates, but surface velocities of up to 7 m d–1 were measured outside the highly deformed areas (Reference Fischer, Rott and BjörnssonFischer and others, 2003). By using mass continuity to provide the connection between the displacement and the ice-thickness change, an estimate for the displacement during the surge, the mass transport and velocity was made by comparing the surface maps from 1998 and 2000 (Reference Pálsson, Magnusson and BjörnssonPálsson and others, 2002). The glacier is assumed to move as a block, which is reasonable in a surge. The horizontal displacement along the profile from September 1998 to September 2000 increases from the head of the glacier to approximately the ELA at 20 km down-glacier, where it reaches a value of approximately 1800 m. The displacement is close to this value until 30 km down-glacier, at the boundary between the reservoir and receiving area, and then increases towards the margin to 2600 m. At the margin the accumulated displacement is close to 2 km. This is in agreement with an independent estimate of 1.9 km made by assuming that the shape of the margin is similar to 1989 and examining margin surface slopes and surface–bed crossover points from the airborne radar survey in 2000 (Reference Pálsson, Magnusson and BjörnssonPálsson and others, 2002). This displacement estimate gives an average velocity of 2.7–3.5md–1 for the period 1998– 2000, which includes a period when the glacier was not surging. The flights in August and November 1999 that located the surge wave, and the radar surveys in January and September 2000 allow the maximum velocity in the surge to be estimated as at least 42 md–1. This is thought to be a conservative estimate since it is an average over an elevation contour and the timing of the surge termination is not well constrained.
By integrating the difference map shown in Figure 4, the volume change of the surging area within the glacier can be estimated. A mass loss of 13.0 km3 in the reservoir area, but a gain of 9.8 km3 in the receiving area, is computed. Uncertainty in these volume estimates, due to possible bias in the radar data of ± 2 m, is 1.6 km3. The difference is due to enhanced melt rates during the surge period as discussed below. An estimate for the mass transport from January to September 2000 finds that 1.5 km3 of ice was transported through the surge equilibrium-line cross-section. This is about 10% of the total mass transport, indicating that the surge was nearly finished before January 2000.
Numerical Flow Model
A numerical flow model is applied to the outlet glacier Dyngjujökull to analyze the effect of the surge on the flow regime and the size of the glacier. This is a two-dimensional, standard shallow-ice approximation (SIA) model (Reference HutterHutter, 1983). The constitutive equation for the ice is Glen’s flow law (Reference GlenGlen, 1955), and sliding at the bed is approximated using a Weertman-type sliding law (Reference PatersonPaterson, 1994). This model uses the alternating direction semi-implicit (ADS-I) finite-difference scheme (Reference HuybrechtsHuybrechts, 1986) to solve the continuity equation on a 1 km grid, and has been adapted for use on Vatnajökull (Reference AðalgeirsdόttirAðalgeirsdόttir, 2003). The mass-balance distribution is computed from a parameterization of the available mass-balance measurements that uses the ELA as an independent variable to determine the net balance (Reference Aðalgeirsdόttir, Guðmundsson and BjörnssonAðalgeirsdόttir and others, 2003). Dyngjujökull is separated from the rest of the ice cap by applying a no-flow boundary condition at the ice divide, thus fixing the ice divide at the same location, but allowing the surface elevation to change freely. This may not be a realistic boundary condition during a surge; it has been observed that the ice divide migrated during the surge in 1999 (Reference Fischer, Rott and BjörnssonFischer and others, 2003). It is, however, not thought to have a significant effect on the modeling results presented here as the lowering of the surface during the surge will counteract the increased accumulation area.
The rate factor in Glen’s flow law in all the model experiments is the value recommended for temperate ice (A = 6.8 × 10–15s–1 kPa–3; Reference PatersonPaterson, 1994). Sliding at the bed and the ELA are the two model parameters that are adjusted until the corresponding steady-state geometry leads to a good fit to the measured surface geometry. The resulting sliding parameter is C = 58 × 10–15ma−1 Pa-3, similar to the value obtained in a study for the whole ice cap (Reference AðalgeirsdόttirAðalgeirsdόttir, 2003), and the resulting ELA will hereafter be referred to as the reference ELA (ΔELA = 0). The resulting steady-state surface profile, at the same location as the profile in Figure 3, is shown in Figure 5, as well as the modeled deformation velocity, the total velocity (deformation plus sliding) and the mass balance. A comparison with the measured surface profile (dashed line in Fig. 5a) shows that the modeled profile is slightly thicker in the lower part, thinner in the upper part and the terminus of the modeled glacier is steeper. This indicates that the mass transport from the upper to the lower part is more efficient in the model than for the measured glacier. The comparison of the modeled velocity with the measurements confirms this. The modeled velocity, which is the balance velocity for the corresponding surface geometry, is about three times higher than the measured velocity before the onset of the surge. The velocities measured at D05 and D07 in summer 1998, at the beginning of the surge, are similar to the modeled velocity. The modeled deformation velocity is within the range given by the velocity measurements. The modeled mass balance is similar to the measured mass balance.
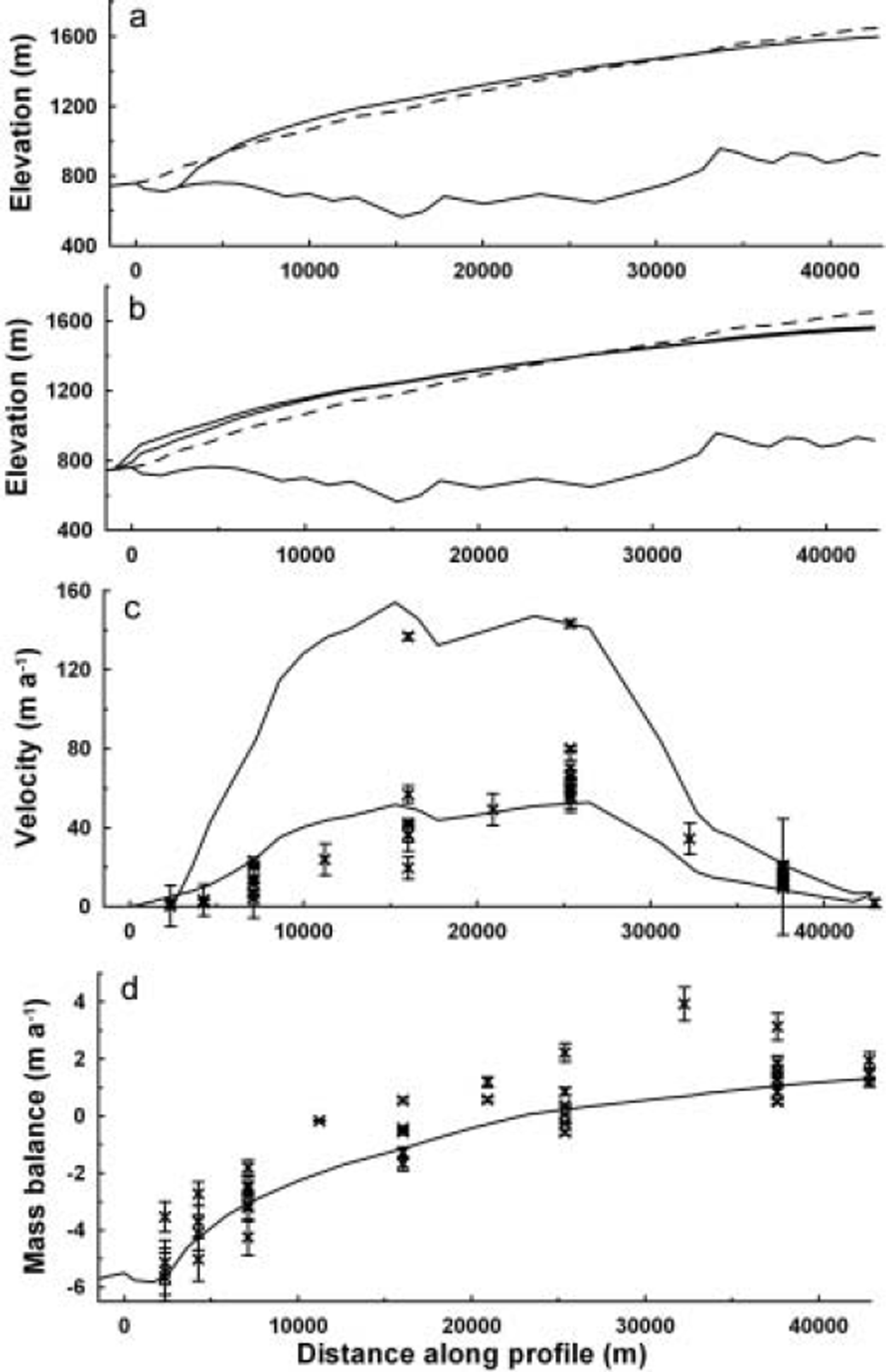
Fig. 5. Model results. (a) The steady-state numerical glacier which is similar in size to the measured glacier, shown with a dotted line. (b) The profile of the surging glacier just before a surge and just after a surge. The measured surface is shown with a dotted line. (c) The modeled deformation velocity and the balance velocity (deformation plus sliding velocity) for the steady-state glacier. Measured surface velocity is shown for comparison. (d) The modeled mass balance for the reference ELA; the measured mass balance is shown for comparison.
Sensitivity tests show that small changes in the ELA, that are within the elevation range given by the measurements, cause the glacier to start to advance northwards and thicken, or retreat and thin. The volume evolution of the ice cap for the sensitivity tests is shown in Figure 6a. Thickening or thinning of this outlet glacier would influence the whole ice cap, but because of the fixed ice divide in the model this influence is not taken into account. This model cannot therefore produce other realistic steady states within the measured mass-balance regime.
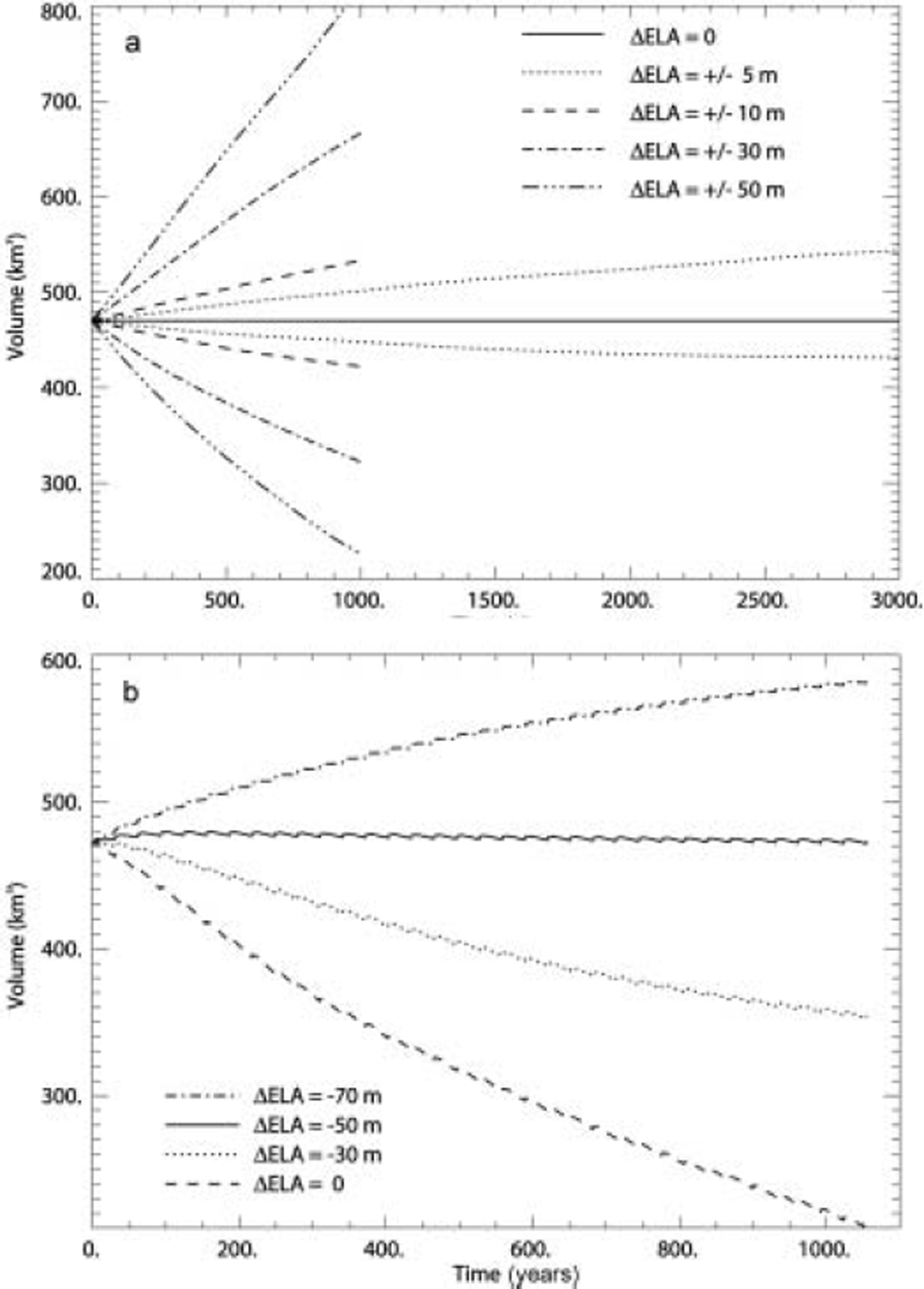
Fig. 6. Volume evolution during the model experiments. (a) Sensitivity to the ELA. Small changes in the ELA cause the glacier volume to increase or decrease. (b) Volume evolution during the surge experiment. Model run with the reference ELA and periodic surges shows a vanishing glacier. By lowering the ELA by 50m, the modeled glacier oscillates around a volume similar to the steady-state volume.
Model runs that imitate surges were conducted. No sliding was allowed in the quiescent phase, so the modeled velocity was similar to the measured velocity. Then repeatedly, every 30 years, for a period of one model year the model was run with a 100-fold sliding parameter from the previous model experiment, representing surge cycles. The resulting volume evolution during the model runs with different values for the ELA is shown in Figure 6b. With the same value of the ELA as before (ΔELA = 0), the volume of the surging outlet glacier reduces by more than half within 1000 years. If the ELA is lowered, and thereby the accumulation area increased, the retreat is slowed. With a 50 m lower ELA than in the no-surge experiment, the outlet glacier oscillates around a volume similar to that of the present glacier. The surface profiles of this surging glacier, just before and just after a surge, are shown in Figure 5b. The surging outlet glacier is thicker than the measured glacier in the ablation area and thinner in the accumulation area. This indicates more mass transport than observed. In each modeled surge, the volume of ice transported is about 21 km3. This is more than observed in the 1999 surge. In the model the sliding is increased over the whole area simultaneously, while in reality the area affected by the surge gradually increases, so the difference is not unexpected. The effect of the surge is, however, the same. By lowering the ELA further, the surging outlet glacier grows, but approaches a steady state. The repeated surges shrink the glacier and decrease the sensitivity to perturbations in the ELA. This is analogous to the result obtained with a flowline model, which showed that surges cause glaciers, subject to the same accumulation as non-surging glaciers, to be smaller on average (Reference Gudmundsson, Aðalgeirsðóttir and BjörnssonGudmundsson and others, 2003). The redistribution of the mass from the accumulation area to the ablation area during surges is more efficient in promoting ablation than the effect of the lowered ELA that causes the glacier to grow when no surges occur.
Discussion and Conclusion
The 1998-2000 surge of Dyngjujökull caused a drop of up to 70 m in elevation in the reservoir area and a thickening of up to 100 m close to the margin. The terminus advanced up to 1.9 km in the eastern part but less in the western part. The total volume of ice transported from the reservoir area to the receiving area, through the surge equilibrium line, was about 13 km3. This caused >1.5km average horizontal displacement. The velocity of the glacier probably exceeded 40md−1 at the surge wave front in autumn 1999. The ice volume transported to the receiving area is only about three-quarters of the mass lost in the reservoir area, according to the integration over the difference map from 1998-2000 (Fig. 4). Possible reasons for this difference could be:
1. additional melt due to friction at the bed during the surge;
2. enhanced melt rates due to changed elevation distribution;
3. increased surface area subject to melt after the surface was broken up with crevasses, and
4. enhanced turbulent fluxes over the rougher surface, causing increased melting.
Reasons (3) and (4) are difficult to quantify, but we can estimate the effect of (1) and (2). The amount of additional melt due to change in elevation distribution is estimated to be 0.15 km3 (Reference Pálsson, Magnusson and BjörnssonPálsson and others, 2002). The elevation distribution will gradually change and be similar to that of 1998 in two to three decades. Assuming that all the change in potential energy during the surge is used to melt ice at the bed, this would give ice loss of about 0.2 km3. No direct mass-balance measurements are available, but an estimate for normal surface conditions of -0.5 km3 for the total mass balance this year was made by comparing the neighboring glaciers and the relation between the glaciers in previous years (Reference Pálsson, Magnusson and BjörnssonPálsson and others, 2002). The remaining volume of ice, 2.3 ± 1.6 km3, that is not accounted for in the difference between the ice lost in the reservoir area and gained in the receiving area, is probably due to enhanced melting of the crevassed surface. On a hydrograph provided by the Icelandic National Power Company (personal communication from H. Haraldsson, 2000), an increase of about 30% in the annual runoff in the river Jökulsá á Fjöllum is observed. The summer average discharge originating from the glacier increased from approximately 120 m3 s–1 to270m3s–1 in the year 2000. This increase amounts to roughly 1.5 km3 over the summer. The drainage basin is situated on a permeable rock formation, so some of the additional meltwater may have filtered to the groundwater and therefore not be visible in the hydrograph. Groundwater of glacial origin has been found in the groundwater system stretching more than 10 km away from the glacier (Reference SigurðssonSigurðsson, 1990).
The model experiments show that a glacier similar in size, and subject to similar mass balance, flows about three times faster than the measured surface velocity of Dyngjujökull during the quiescent phase. This difference clearly expresses the surge nature of Dyngjujokull.
Surges were forced in the model by periodically increasing the sliding parameter during one model year. The result of this model experiment shows that repeated surges are efficient in displacing mass to the ablation area, causing surging glaciers to be smaller than non-surging glaciers subject to the same mass-balance distribution.
Acknowledgements
We thank M.T. Guðmundsson, þ. Högnadόttir and H.Gíslason for the global positioning system survey points on Dyngjujökull in 1998. M.T. Guðmundsson carried out the airborne radar elevation survey in January and September 2000. This work was supported by the National Power Company (Landsvirkjun), the National Research Council of Iceland, the Nordic Energy Research of the Nordic Council of Ministers, and the National Energy Fund of Iceland. Comments by T. Jόhannesson and two anonymous reviewers are gratefully acknowledged.







