1. INTRODUCTION
Design activities, of which music composition is one example, can be categorized as either routine or nonroutine (Gero & Maher, Reference Gero and Maher1993). Routine design activities are ones in which the “functions (i.e., goals or requirements) are known as are the available structures and the processes which map function to structure” (Gero & Maher, Reference Gero and Maher1993, p. v), whereas in nonroutine design activities, there is incomplete knowledge regarding one or more of function, structure, or mapping. According to Gero and Maher (Reference Gero and Maher1993), artificial intelligence has generally been concerned with addressing routine design activities, whereas the field of computational creativity has emerged more recently, out of a need to study nonroutine design activities. These sentiments are echoed by an observation that although artificial intelligence algorithms “are able to produce remarkable results (Spector, Reference Spector2008), it appears unlikely they will tell us much about creativity” (Brown, Reference Brown2013, p. 52).
The topic of this article is the generation of music in the style of an existing corpus. It falls under the heading of a nonroutine design activity and within the remit of computational creativity, because the functions (requirements or goals) involved in generating a stylistically successful passage of music are difficult to specify, as are the processes mapping function to structure. Our structure here will be musical notes, or more precisely, triples consisting of when a note (sound) begins, at what pitch height, and for what duration.
The computational system toward which the current paper drives is called random constrained chain of Markovian nodes with inheritance of form (Racchmaninof). At a high level, Racchmaninof can be described as a within-domain analogy-based design system (Vattam et al., Reference Vattam, Helms, Goel, Gero and Goel2008; Goel et al., Reference Goel, Rugaber and Vattam2009). It consists of a target design (the new passage of music to be generated) and a source design (an excerpt of human-composed music in the intended style). The large-scale structure of the source design (e.g., bars 1–4 repeat at 13–16, and bars 3–4 occur transposed at 5–6) “establishes a platform for the exploration of a new solution” (Qian & Gero, Reference Qian and Gero1996, p. 289). Attention to large-scale repetitive structure is the most important contribution of the current work, because “[i]n music, what happens in measure 5 may directly influence what happens in measure 55, without necessarily affecting any of the intervening material” (Cope, Reference Cope2005, p. 98). While acknowledging the existence of large-scale temporal dependencies in music, almost all current approaches to music generation are focused on small-scale relationships, such as how to get from one melody note or chord to the next, or how to create a sense of local phrasing (exceptions are Cope, Reference Cope2005; Shan & Chiu, Reference Shan and Chiu2010).
In addition to our balancing of small- and large-scale concerns when generating new designs, those working in the wider field of engineering design might also be interested in how we achieve plausible small-scale relationships between musical events and evaluate our systems.
1. Plausible small-scale relationships are achieved by a constrained Markov model calculated over a database of pieces in the intended style. Checks concerning the range (is it too high or too low?), likelihood (will a generated event sound too surprising or too quotidian in the current context?), and sources (have too many consecutive events been sampled from the same database piece?) act as critics, recognizing potential mistakes and controlling the number of candidate passages generated (Thurston, Reference Thurston1991; Minsky, Reference Minsky2006; Brown, Reference Brown2013).
2. Final evaluation of our systems' designs consists of a listening study that uses Amabile's (Reference Amabile1996) consensual assessment technique (CAT), adapted to assessment of music-stylistic success. There are a number of alternatives for evaluating the extent to which a system is creative (Shah et al., Reference Shah, Vargas-Hernandez and Smith2003; Boden, Reference Boden2004; Besemer, Reference Besemer2006; Wiggins, Reference Wiggins2006; Ritchie, Reference Ritchie2007; Nelson & Yen, Reference Nelson and Yen2009), but we favored Amabile's (Reference Amabile1996) CAT for its similarity to how a student-composed passage of music would be assessed by an expert, and because it enables us to regress stylistic success ratings on quantitative properties of our systems' designs in order to generate some suggestions for musical aspects requiring attention in future work (see also Pearce & Wiggins, Reference Pearce, Wiggins, Cardoso and Wiggins2007).
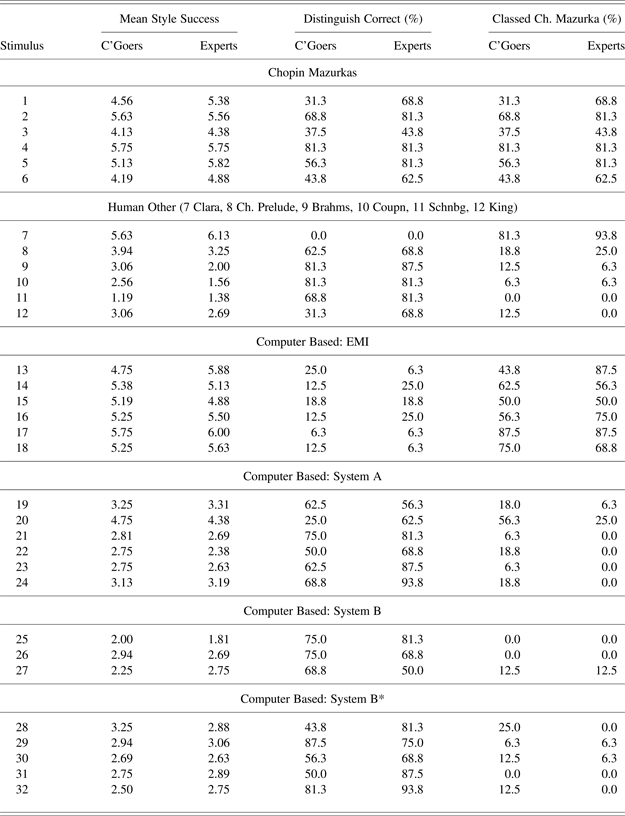
The focus moves now from setting the current work in the context of computational design creativity to an early but highly illustrative example of modeling musical style. The model appeared in the Age of Reason (ca. 1650–1800), a period of flourishing scientific investigation. The musical dice game, or Musikalisches Würfespiel, has been peddled as an example many times (Schwanauer & Levitt, Reference Schwanauer and Levitt1993; Cope, Reference Cope1996; Nierhaus, Reference Nierhaus2009), despite its attribution to Wolfgang Amadeus Mozart (1756–1791) being most likely false (Hedges, Reference Hedges1978). We use the example again, however, because its principles underpin several more recent models of musical style that will be reviewed and developed below. Segments from a simplified version of the game attributed to Mozart are shown in Figure 1. To generate the first bar of a new waltz, the game's player rolls a die. The segment in Figure 1 with label v m,1, corresponding to the observed roll 1 ≤ m ≤ 6, becomes the first bar of the new waltz. To generate the second bar, the player rolls the die again, observes the outcome 1 ≤ m′ ≤ 6, and the corresponding segment v m′,2 from Figure 1 becomes the second bar of the new waltz. The process continues until eight bars have been generated. The dice game is represented as a graph in Figure 2. Each vertex represents a segment of music, and an arc from vertex v i,j to v k,l indicates that segment v i,j can be followed by v k,l when the dice game is played. A walk from left to right in Figure 2 corresponds to an outcome of the dice game. One possible outcome is shown in black.

Fig. 1. Bar-length segments of music adapted from a musical dice game attributed to Mozart, k294d. In the original game, the segments are arranged in a different order, so that the equivalent harmonic function of segments in the same column and the equality of segments in the eighth column are disguised.
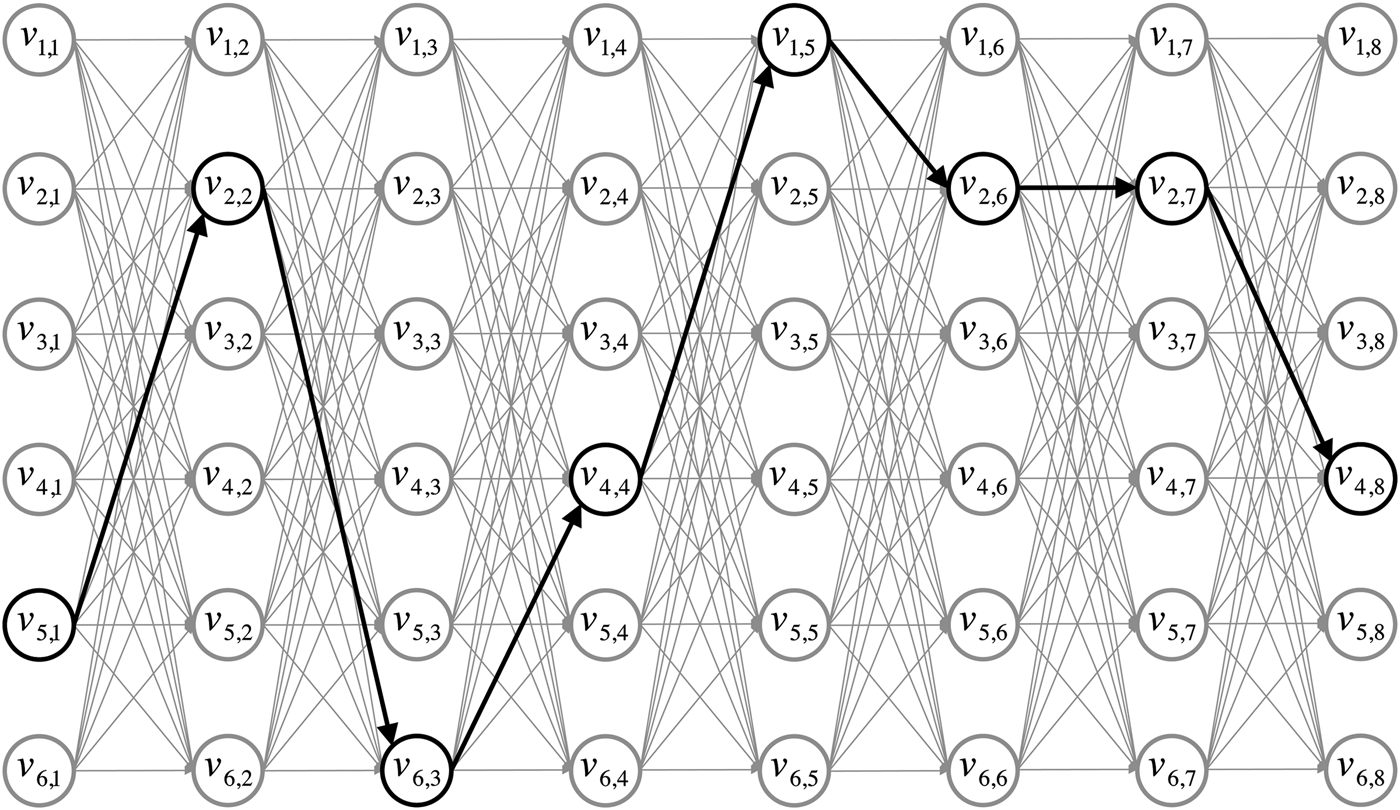
Fig. 2. A graph with vertices that represent bar-length segments of music from Figure 1. An arc from vertex v i,j to v k,l indicates that segment v i,j can be followed by v k,l when the dice game is played. A walk from left to right is shown in black, corresponding to one possible outcome of the dice game.
As we move on to more recent models of musical style, two relevant aspects of the dice game are database construction (compiling the segments and graph) and generating mechanism (rolling of the die). In some models below, existing music is segmented to form a database. The segments may vary in size (beat and subbeat) and texture (monophonic and polyphonic), but the principle is the same.Footnote 1 In the dice game, database construction was done by hand, but in recent models it is totally or partially algorithmic, and also determines which segments can be recombined with which. In the dice game, the generating mechanism is random but algorithmic, and this also tends to be the case for recent models, which use pseudorandom numbers to make choices between alternative musical continuations.
In the spirit of the Age of Reason, our aim in this paper is to take a more rigorous and scientific approach to modeling of music style than has been adopted previously. We will describe and evaluate two new computational models of musical style (Racchman-Oct2010 and Racchmaninof-Oct2010), with the objective of determining how close an algorithm can get to Experiments in Musical Intelligence's (EMI; Cope, Reference Cope1996, Reference Cope2001, Reference Cope2005) standard based on available explanations and code. A description of the new algorithms is offered here, with full details and more discussion available in Collins (Reference Collins2011). The source code for the algorithms has also been made freely available (http://www.tomcollinsresearch.net) to encourage researchers to engage in the challenging and open problem of modeling musical style. The review (Section 2) begins with example briefs in stylistic composition, leading to a discussion of existing algorithmic approaches. For the new models developed in Section 3, we select and discuss the brief of composing the opening section of a mazurka in the style of Chopin. An evaluation of the models is reported in Section 4, using an adapted version of the CAT (Amabile, Reference Amabile1996; Pearce & Wiggins, Reference Pearce and Wiggins2001, Reference Pearce, Wiggins, Cardoso and Wiggins2007). Judges listened to music excerpts (including genuine Chopin mazurkas and computer-generated passages from Racchman-Oct2010, Racchmaninof-Oct2010, and EMI), gave ratings of stylistic success on a scale of 1 to 7, and placed each excerpt in one of three categories (Chopin mazurka, human-composed but not a Chopin mazurka, or computer-based). The evaluation sheds light on the creativity of our models, in the sense of behavior “which would be deemed creative if exhibited by humans” (Wiggins, Reference Wiggins2006, p. 451).
2. REVIEW OF COMPUTATIONAL MODELS OF MUSICAL STYLE
To help frame the review of existing algorithms for stylistic composition, at the outset we state four important, recurring issues:
1. Avoidance of replication: Is the model's output ever too similar to works from the intended style? Does the model include any steps to avoid replicating substantial parts of existing work?
2. Database construction: How are the stylistic aim and corpus of music selected (for instance, Classical string quartets and Chopin mazurkas)? If the model is database driven, are both database construction and generating mechanism algorithmic, or is only the generating mechanism algorithmic?
3. Level of disclosure: To what extent is it possible to reproduce somebody else's model, based on either their description or published source code?
4. Rigor and extent of evaluation: How has the computational model of musical style been evaluated? For which different corpora (different composers, periods, or compositional strategies) has the model been evaluated?
Algorithmic composition is a field of great variety and antiquity, which is perhaps unsurprising given the broadness of the terms “algorithm” and “composition.” Some aspects of composition that can be described as a process are eminently suited to being turned into algorithms. In a recent summary of algorithmic composition organized by algorithm class, Nierhaus (Reference Nierhaus2009) gives examples ranging from hidden Markov models (Allan, Reference Allan2002) to genetic algorithms (Gartland-Jones & Copley, Reference Gartland-Jones and Copley2003). His introductory historical overview credits Guido of Arezzo (ca. 991–1033) with devising the first system for algorithmic composition (see also the recent review of Fernández & Vico, Reference Fernández and Vico2013).
This paper focuses on algorithms for stylistic composition (or pastiche), that is, works in the style of another composer or period. Free composition, in contrast, is something of a catchall term for any work that is not a pastiche. Reich (Reference Reich, Sadie and Tyrrell2001) suggests, for instance, that Clara Schuman's (née Wieck; 1819–1896) Mazurka in G minor from Soirées musicales opus 6 number 3 is a stylistic composition, inspired by Chopin's mazurkas. Clara Schumann was among the first pianists to perform the mazurkas, which began to appear a decade before Soirées musicales was published. The mazurka is a “Polish folk dance from the Mazovia region [where Chopin spent his childhood]. … In his [fifty-plus] examples the dance became a highly stylized piece for the fashionable salon of the 19th century” (Downes, Reference Downes, Sadie and Tyrrell2001, p. 189). As an example of a free composition, we might cite “Moro, lasso” from Madrigals book 6 by Carlo Gesualdo (ca. 1561–1613). The opening chord sequence (C♯ major, A minor, B major, G major) is so distinctive that it would be surprising to find instances of other composers using this sequence in the next three hundred or so years. Distinctiveness then, formalized to a degree by Conklin (Reference Conklin2010), ought to be added to the definition of free composition. Often the line separating stylistic composition (or pastiche) and free composition is blurred. A more credible stance is that most pieces are neither entirely free nor entirely stylistic, but somewhere in between. At the former extreme, a work is so highly original and lacking in references to existing work that listeners remain perplexed, long after the premiere. At the latter extreme, a piece that is entirely stylistic merely replicates existing work, perhaps even note for note.
Some example briefs within stylistic composition are listed in Table 1. These briefs are in the order of most (1) to least (6) constrained. In chorale harmonization (AQA, 2009), a relatively large number of conditions help the composer respond to the brief: the soprano part is already written, and the number of remaining parts to be composed is specified. A composer who only wrote one note per part per beat might do well enough to pass an exam on chorale harmonization. This task is the most studied by far in music computing, and it is also one of the most straightforward. An important contribution of this paper is to highlight some alternative briefs from undergraduate and A-level music courses, and to develop algorithms for one of the least constrained tasks.
Table 1. Six briefs in stylistic composition

Note: For musical examples, see Collins (Reference Collins2011), section 5.2.
The briefs of ground bass and fugal exposition (Cambridge University Faculty of Music, 2010b) involve different compositional strategies, compared to each other and chorale harmonization. For example, in harmonizing the soprano part of a chorale, the concern for harmony (the identity of vertical sonorities) dominates the concern for counterpoint (the combination of independent melodic voices). Inherent in the name “ground bass” is a different compositional strategy of beginning with the bass (bottom) part, and supplying the upper parts. We are not aware of any existing systems for automated generation of material on a ground bass. Although a system proposed by Eigenfeldt and Pasquier (Reference Eigenfeldt, Pasquier, Ventura, Pease, Péréz y Péréz, Ritchie and Veale2010) does allow the user to specify a bass line, it is not intended to model a particular musical style. In ground bass and fugal exposition, the concern for counterpoint dominates the concern for harmony. A system for generating fugal expositions is outlined by Craft and Cross (Reference Craft and Cross2003), and the selected output of a second system is available (Cope, Reference Cope2002). Stylistic composition briefs such as the Classical string quartet or Romantic song cycle are relatively unconstrained. A composer responding to the brief of the Classical string quartet (AQA, 2007) will hopefully produce material that is stylistically similar to the quartets of Haydn or Mozart, say, but there would appear to be less guidance in terms of provided parts or explicit rules.
For the sake of completeness, and without further explanation, some tasks that might be classed as free composition include the following: a soundtrack to accompany a promotional video for a low-cost airline (Edexcel, 2009, p. 4); a competition test piece exploiting a melody instrument's playing techniques (Edexcel, 2009, p. 3); and a portfolio of free compositions, in which candidates are encouraged “to develop the ability to compose in a manner and style of their own choice” (Cambridge University Faculty of Music, 2010a, p. 26).
Sections 3 and 4 of this paper are concerned with the fifth stylistic composition brief in Table 1 (Chopin mazurka). The larger hypothesis, of which this compositional brief is one test, concerns whether a random generation Markov chain can be applied successfully to music from multiple composers/periods. Therefore, it does not make sense to go into detail about the mazurka style (or to try to encode this knowledge), although detailed accounts of mazurkas are available (Rink, Reference Rink and Samson1992; Rosen, Reference Rosen1995). We chose Chopin's mazurkas as a corpus because there are enough pieces (~50) to display characteristic features in the frequency required to build a representative database. They also provide the opportunity for comparison with EMI's mazurkas (Cope, Reference Cope1997a).
2.1. Existing algorithms for stylistic composition
Allan (Reference Allan2002) uses hidden Markov models (HMMs) to harmonize chorale melodies (for a general guide to HMMs, please see Rabiner, Reference Rabiner1989). Treating a chorale melody as the observed sequence, the Viterbi algorithm is used to determine which hidden sequence of harmonic symbols is most likely to underlie this melody. The information about melody notes and harmonic symbols (initial distribution, transition, and emission probabilities) is determined empirically by analyzing other chorales, referred to as the training set. In a second HMM, “the harmonic symbols decided by the previous subtask [were] treated as an observation sequence, and [used to] generate chords as a sequence of hidden states. This model [aimed] to ‘recover' the fully filled-out chords for which the harmonic symbols are a shorthand” (Allan, Reference Allan2002, p. 45). A final step introduces decoration (e.g., passing notes) to what would otherwise be a one note/voice/beat harmonization. HMMs are appropriate for tasks within stylistic composition if an entire part is provided (such as the soprano part in a chorale harmonization), which is then used to generate hidden states such as harmonic symbols. If a melody or some other part is not provided, however, then Markov models of the nonhidden variety are more appropriate.
A Markov model consists of a state space (e.g., the set of pitch classes), a transition matrix describing the probability that one state is followed by another (in our example, the probability that pitch class X is followed by pitch class Y), and an initial distribution for generating the first state. The use of Markov models in music computing is well established. The Musikalisches Würfespiel from the Introduction can be described as a Markov model with bar-length states and uniform transition matrix and initial distribution. Hiller and Isaacson (Reference Hiller and Isaacson1959) repopularized the use, and Ames (Reference Ames1989) gives an overview. Cope's (Reference Cope1996, Reference Cope2005, p. 89) method for chorale harmonization is akin to a Markov model with extra features, and Ponsford et al. (Reference Ponsford, Wiggins and Mellish1999) use n-gram models (similar to Markov models) to imitate the harmonic style of 17th-century dance forms. In addition, the use of Markov models for music generation has continued throughout the last decade (e.g., Pachet, Reference Pachet, Anagnostopoulou, Ferrand and Smaill2002; Roy & Pachet, Reference Roy and Pachet2013).
An n-gram model also underpins Conklin and Witten's (Reference Conklin and Witten1995) Stochastically Oriented Note Generator (SONG/3), a system that can be used to predict attributes of the next note in a composition based on contextual information. Prediction may seem unrelated to algorithmic composition at first glance, but Conklin and Witten (Reference Conklin and Witten1995) conclude with an application to composition, and this paper forms the theoretical framework for much subsequent research (Conklin, Reference Conklin2003; Pearce, Reference Pearce2005; Pearce & Wiggins, Reference Pearce, Wiggins, Cardoso and Wiggins2007; Whorley et al., Reference Whorley, Wiggins, Rhodes, Pearce, Ventura, Pease, Péréz y Péréz, Ritchie and Veale2010). An example input to SONG/3 might consist of a chorale melody in G minor, say, up to and including a B♭4 in bar 3; a collection of other chorale melodies; and an attribute that the user is interested in predicting, such as duration. Given this input, the output of SONG/3 would be a prediction for the duration of the note following the aforementioned B♭4. This prediction and the input can be used to elicit successive predictions from SONG/3 if desired. Systems A–D described by Pearce (Reference Pearce2005) have the same framework for calculating probability distributions as SONG/3, but use the Metropolis–Hastings algorithm to generate melodies, as suggested by Conklin (Reference Conklin2003). Instead of generating pitches successively (Conklin & Witten, Reference Conklin and Witten1995), the Metropolis–Hastings algorithm alters an existing melody one randomly selected note at a time. It could be argued, therefore, that this method is more appropriate for generating a variation on a theme than for generating a new melody.
Although Cope (Reference Cope1996, Reference Cope2001, Reference Cope2005) has not published details of EMI to the extent that some would like (Pearce et al., Reference Pearce, Meredith and Wiggins2002; Pedersen, Reference Pedersen2008; Wiggins, Reference Wiggins2008), he has proposed key ideas that have influenced several threads of research based on EMI. A summary of the databases and programs referred to collectively as EMI is given by Hofstadter (writing in Cope Reference Cope2001, pp. 44–51), who identifies recombinancy (segmenting and reassembling existing pieces of music) as the main underlying principle, as well as four related principles: syntactic meshing, semantic meshing, signatures, and templagiarism. Each of the four principles is addressed in Collins (Reference Collins2011, their section 5.6), but we mention just a few points here. The principle of recombinancy is a starting point for our systems, and we adhere reasonably closely to available descriptions of syntactic meshing and templagiarism. However, our systems should not be seen as an “open-source EMI,” because we do not attempt to implement descriptions of semantic meshing or signatures.
EMI uses statement, preparation, extension, antecedent, and consequent (SPEAC) analysis (Cope, Reference Cope2005, pp. 221–243), to try to ensure that recombined music does not contain semantic violations. Inspired by the work of Schenker (1935/Reference Schenker and Oster1979), SPEAC analysis begins by selecting a so-called framework piece (or excerpt thereof). Each beat is given a label (“S,” “P,” “E,” “A,” or ‘“C”), and then these are combined to form labels at successively higher levels, corresponding roughly to bar, phrase, and section, until a whole piece (or excerpt) is represented by a single letter. Recombined music, selected from a database that has also been SPEAC analyzed, must conform to the framework labels as closely as possible. A particularly important question is whether the piece being used as a framework is omitted from the database. Suppose the corpus comprises four Chopin mazurkas, opus 68 numbers 1–4, and one piece, opus 68 number 4, is to be used as a framework. Is the database stipulating which segments can follow which constructed over all four pieces, or just opus 68 numbers 1–3? If the framework piece is not omitted, then the likelihood that the generated passage replicates the framework piece note for note is increased. An example is given in Figure 3a and b. The black noteheads in these figures indicate pairs of ontimes and MIDI note numbers (MNN) that the EMI mazurka and Chopin mazurka have in common. Furthermore, bars 25–26 of Figure 3a are an exact copy of bars 41–42 of the Mazurka in F minor opus 7 number 3 by Chopin. Existing essays on EMI (contributors to Cope, Reference Cope2001) are of a general nature and claim, rather than demonstrate, deep engagement with EMI's output and corresponding original corpus: “I know all of the Chopin mazurkas well, and yet in many cases, I cannot pinpoint where the fragments of Emmy's mazurkas are coming from. It is too blurry, because the breakdown is too fine to allow easy traceability” (Hofstadter writing in Cope Reference Cope2001, pp. 297–298).

Fig. 3. (a) Bars 1–28 of the Mazurka number 4 in E minor by David Cope with Experiments in Musical Intelligence. Transposed up a minor second to F minor to aid comparison with (b). The black noteheads indicate that a note with the same ontime and pitch occurs in Chopin's Mazurka in F minor opus 68 number 4. (b) Bars 1–28 of the Mazurka in F minor opus 68 number 4 by Chopin. Dynamic and other expressive markings have been removed from this figure to aid clarity. The black noteheads indicate that a note with the same ontime and pitch occurs in Experiments in Musical Intelligence's Mazurka number 4 in E minor (a).
Templagiarism is a term coined by Hofstadter (writing in Cope Reference Cope2001, p. 49) to describe borrowing from an existing piece/excerpt on an abstract or template level. Suppose that in the piece selected for use as a framework, bars 1–4 repeat at bars 9–12, and again at bars 63–66. There may be further elements of repetition in the framework piece (including transposed or inexact repetition of bars 1–4 and repetition of other motives), but for the sake of simplicity, focus is restricted to bars 1–4, labeled A 1, and the two subsequent occurrences of A 1, labeled A 2 and A 3, respectively. The positions (but not the actual notes) of these occurrences, in terms of temporal and pitch displacement relative to the first note of A 1, are recorded and used to guide EMI's generating mechanism. For instance, material is generated for bars 1–4 first, and then “copied and pasted” to bars 9–12 and bars 63–66. Now material for intervening bars, bars 5–8 and 13–62, is generated, as well as for bar 67 to the end of the framework piece. Thus, the generated passage contains a collection of notes in bars 1–4, which we label B 1, and this collection repeats at bars 9–12 (label B 2) and 63–66 (label B 3). The collections A 1 and B 1 may not share a note in common, but on the more abstract level of relative temporal and pitch displacement, the sets {A 1, A 2, A 3} and {B 1, B 2, B 3} are equivalent (see Czerny, Reference Czerny1848).
“In order to quote the template, you need to supplement it with a new ‘low-level’ ingredient—a new motive—and so the quotation, though exact on the template level, sounds truly novel on the note level, even if one is intimately familiar with the input piece from which the template was drawn” (Hofstadter writing in Cope, Reference Cope2001, p. 50). An explanation of templagiarism is conspicuous by its absence in Cope (Reference Cope1996, Reference Cope2001, Reference Cope2005), although there are passing references (Cope, Reference Cope2001, p. 175, 2005, p. 245). With only Hofstadter's description (cited above) on which to rely, our own explanation may be inaccurate. While critical of the type of borrowing shown between Figures 3a and b, we see templagiarism as an important component of stylistic composition. The caveats are that a slightly more flexible approach would be preferable (e.g., do the temporal and pitch displacements retained have to be exact?), that borrowed patterns ought to be over one bar, say, in duration, and that the framework piece ought to be omitted from the database to reduce the probability of note-for-note replication.
In summary, Cope's (Reference Cope1996, Reference Cope2005) work on EMI represents the most ambitious and, in our opinion, most successful attempt to model musical style. However, it is not presented in sufficient detail to replicate, nor has it been evaluated rigorously in listening experiments: the latter criticism applies equally to the other research reviewed above, with the exception of Pearce (Reference Pearce2005). Although the above criticisms remain valid, we see the successful modeling of musical style as an open, unsolved, scientific problem.
Markov-type models are the focus of the above review, in part because existing algorithms with the goal of pastiche often adopt this approach. Alternative computational approaches to stylistic composition exist, however. Ebciǒglu (Reference Ebciǒglu, Balaban, Ebciǒglu and Laske1994) describes a system called CHORAL for the task of chorale harmonization. A logic programming language called Backtracking Specification Language is used to encode some 350 musical “rules” that the author and other theorists observe in J.S. Bach's chorale harmonizations, for example, “rules that enumerate the possible ways of modulating to a new key, the constraints about the preparation and resolution of a seventh in a seventh chord, … a constraint about consecutive octaves and fifths” (Ebciǒglu, Reference Ebciǒglu, Balaban, Ebciǒglu and Laske1994, pp. 310–311). Like the HMM of Allan (Reference Allan2002), there are separate chord-skeleton and chord-filling steps. Unlike the HMM of Allan (Reference Allan2002), which consists of probability distributions learned from a training set of chorale harmonizations, CHORAL is based on the programmer's hand-coded rules. While use of hand-coded rules persists (Phon-Amnuaisuk et al., Reference Phon-Amnuaisuk, Smaill and Wiggins2006; Anders & Miranda, Reference Anders and Miranda2010), we suggest that reliance on music theorists' observations is not ideal, because the quality and quantity of observations varies across composers and periods. With Markov-type models, however, the same training process has the potential to generalize to music databases from different composers/periods.
3. TWO NEW MARKOV MODELS OF STYLISTIC COMPOSITION
This section develops two models for stylistic composition, Racchman-Oct2010 and Racchmaninof-Oct2010. In the former model, repetitive structure can only occur by chance, but the latter model incorporates the results of a pattern discovery algorithm called structure induction algorithm and compactness trawler (Meredith et al., Reference Meredith, Lemström and Wiggins2002; Collins et al., Reference Collins, Thurlow, Laney, Willis, Garthwaite, Downie and Veltkamp2010), thus ensuring that generated passages contain certain types of repeated pattern. The development of the models addresses general issues in stylistic composition, such as how to generate a passage without replicating too much of an existing piece.
3.1. Definition and example of a Markov model for melody
As a first example, pitch classes could form the state space of the Markov chain, while the relative frequencies with which one pitch class leads to the following pitch class could form the matrix of transition probabilities. We will illustrate this using the melody in Figure 4. The piece of music contains all of the natural pitch classes as well as B♭, so the obvious choice for the state space (I) is the set of pitch classes

Fig. 4. Bars 3–10 of the melody from “Lydia” opus 4 number 2 by Gabriel Fauré (1845–1924).
To obtain the transition matrix, for each i, j in I, we count the number of transitions from i to j in Figure 4 and record this number, divided by the total number of transitions from state i. The resulting transition matrix is
 $$\matrix{\matrix{\hbox{F} & \hbox{G} & \hbox{A} & \hbox{B}\flat & \hbox{B} & \hbox{C} & \hbox{D}\hfill & \hbox{E}}\hfill \cr \matrix{\hbox{F} \cr \hbox{G} \cr \hbox{A} \cr \hbox{B}\flat \cr \hbox{B} \cr \hbox{C} \cr \hbox{D} \cr \hbox{E}} \left\vert \matrix{0 &3/4 & 1/4 & 0 & 0 & 0 & 0 & 0 \cr 2/7 & 0 & 4/7 & 1/7 & 0 & 0 & 0 & 0 \cr 1/8 & 1/2 & 0 & 0 & 1/4 & 1/8 & 0 & 0 \cr 0 & 0 & 2/3 & 1/3 & 0 & 0 & 0 & 0 \cr 0 & 1/3 & 0 & 0 & 0 & 1/3 & 1/3 & 0 \cr 0 & 0 & 1/3 & 1/3 & 0 & 0 & 1/3 & 0 \cr 0 & 0 & 0 & 0 & 0 & 1/2 & 0 & 1/2 \cr 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0} \right\vert} = {\bf P}{\bf.} $$
$$\matrix{\matrix{\hbox{F} & \hbox{G} & \hbox{A} & \hbox{B}\flat & \hbox{B} & \hbox{C} & \hbox{D}\hfill & \hbox{E}}\hfill \cr \matrix{\hbox{F} \cr \hbox{G} \cr \hbox{A} \cr \hbox{B}\flat \cr \hbox{B} \cr \hbox{C} \cr \hbox{D} \cr \hbox{E}} \left\vert \matrix{0 &3/4 & 1/4 & 0 & 0 & 0 & 0 & 0 \cr 2/7 & 0 & 4/7 & 1/7 & 0 & 0 & 0 & 0 \cr 1/8 & 1/2 & 0 & 0 & 1/4 & 1/8 & 0 & 0 \cr 0 & 0 & 2/3 & 1/3 & 0 & 0 & 0 & 0 \cr 0 & 1/3 & 0 & 0 & 0 & 1/3 & 1/3 & 0 \cr 0 & 0 & 1/3 & 1/3 & 0 & 0 & 1/3 & 0 \cr 0 & 0 & 0 & 0 & 0 & 1/2 & 0 & 1/2 \cr 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0} \right\vert} = {\bf P}{\bf.} $$For example, there are four transitions from F: three are to G and one to A. Because F is the first element of the state space, this gives the first row of the table: for F to G the probability is 3/4, for F to A it is 1/4, and 0 otherwise. Transitions from each pitch class are recorded in subsequent rows of the matrix.Footnote 2 It can be seen that most transitions are from one pitch class to an adjacent one.
An initial state is required to use this matrix to generate a melody. For instance,
means that the initial pitch class of a generated melody will be F with probability 1/2, and A with probability 1/2. (These probabilities need not be drawn empirically from the data, though often they are.) We use uppercase notation (X n)n≥0 = X 0, X 1, … for a sequence of random variables, and lowercase notation (i n)n≥0 to denote values taken by the variables. Suppose i 0 = A, then we look along the third row of P (because A is the third element of the state space) and randomly choose between X 1 = F, X 1 = G, X 1 = B, X 1 = C, with respective probabilities 1/8, 1/2, 1/4, 1/8, and so on. Below are two pitch sequences generated from the Markov model using random numbers (we have imposed the same number of notes and phrase lengths as in Fig. 4).
Here are formal definitions of a Markov model and a Markov chain (Norris, Reference Norris1997).
Definition 1:Markov Model. A Markov model of a piece (possibly many pieces) of music consists of
1. a countable set I called the state space, with a well-defined onto mapping from the score of the piece to elements of I;
2. a transition matrix P such that for i, j ∈ I, p i,j is the number of transitions in the music from i to j, divided by the total number of transitions from state i; and
3. an initial distribution a = (a i : i ∈ I), enabling the generation of an initial state.■
Definition 2:Markov Chain. Let (X n)n≥0 be a sequence of random variables, and I, P, a be as in Definition 1. Then (X n)n≥0 is a Markov chain if
1. a is the distribution of X 0;
2. for n ≥ 0, given X n = i, X n+1 is independent of X 0, X 1, … , X n−1, with distribution (p i,j : j ∈ I).
Writing these conditions as equations, for n ≥ 0 and i 0, i 1, … , i n+1 ∈ I,
1.
 ${\opf P}\lpar X_{0} = i_{0}\rpar= a_{i_{0}} $;
${\opf P}\lpar X_{0} = i_{0}\rpar= a_{i_{0}} $;2.
 ${\opf P}\lpar X_{n + 1} = i_{n + 1} \vert X_{0} = i_{0}\comma \; X_{1} = i_{1}\comma \; \ldots\comma \; X_{n} = i_{n}\rpar $
${\opf P}\lpar X_{n + 1} = i_{n + 1} \vert X_{0} = i_{0}\comma \; X_{1} = i_{1}\comma \; \ldots\comma \; X_{n} = i_{n}\rpar $ $= {\opf P}\lpar X_{n + 1} = i_{n+1} \vert X_{n} = i_{n}\rpar = p_{{i_n}\comma i_{n+1}}.$
$= {\opf P}\lpar X_{n + 1} = i_{n+1} \vert X_{n} = i_{n}\rpar = p_{{i_n}\comma i_{n+1}}.$
Conditions (1) and (2) apply to a finite sequence of random variables as well. It is also possible to model dependence in the opposite direction. That is, for n ≥ 1, given X n = i, X n−1 is independent of X n+1, X n+2, … .■
Definition 3:Realization. Sometimes the output generated by formation of a Markov model does not consist of ontime–pitch–duration triples, which might be considered the bare minimum for having generated a passage of music. The term realization refers to the process of converting output that lacks one or more of the dimensions of ontime, pitch, duration, into ontime–pitch–duration triples.■
Loy (Reference Loy2005) discusses higher order Markov chains in the context of monophonic music, which take into account more temporal context. In a second-order Markov chain, given X n = i n and X n−1 = i n−1, X n+1 is independent of X 0, X 1, … , X n−2. The disadvantage of more temporal context is an increased probability of replicating original material (Loy, Reference Loy2005).
3.2. A beat/spacing state space
The previous section was limited to consideration of melody, which is useful for exemplifying the definitions of Markov model, Markov chain, and the concept of realization, but monophony constitutes a very small proportion of textures in Western classical music. That is not to say models for generation of melodies contribute little to an understanding of musical style. Because a common compositional strategy is to begin by composing a melody (followed by harmonic or contrapuntal development), models that generate stylistically successful melodies are useful for modeling the first step of this particular strategy. Our proposed model assumes a different compositional strategy; one that begins with the full texture, predominantly harmonic (or vertical), but with scope for generated passages to contain contrapuntal (or horizontal) elements.
Figure 5 will be used to demonstrate the state space of our proposed Markov model. A state in the state space consists of two elements: the beat of the bar on which a particular minimal segment begins; and the spacing in semitone intervals of the sounding set of pitches.
Definition 4: Partition point and minimal segment. A partition point occurs where the set of pitches currently sounding in the music changes due to the ontime or offtime of one or more notes, and a minimal segment is the set of notes that sound between two consecutive partition points (Pardo & Birmingham, Reference Pardo and Birmingham2002, pp. 28–29).■

Fig. 5. Bars 1–13 (without lyrics) of “If ye love me,” by Thomas Tallis (ca.1505–1585), annotated with partition points and minimal segments (cf. Definition 4). The partition points are shown beneath the stave. The units are crotchet beats, starting from zero.
The partition points for the excerpt from Figure 5 are shown beneath the stave. The units are crotchet beats, starting from zero. Therefore, the first partition point is t 0 = 0, the second is t 1 = 3, and the third is t 2 = 4, coinciding with the beginning of bar 2, and so on. The first minimal segment S 0 consists of the notes sounding in the top-left box in Figure 5. Representing these notes as ontime–pitch–duration triples, we have
the second minimal segment
and so on. Beats of the bar are conventionally counted from 1, not 0. Therefore, the first minimal segment S 0 has ontime 0, and begins on beat 1 of the bar. The next segment S 1 begins on beat 4.
The second element of a state, which is the chord expressed as a set of intervals above its bass note, is considered now. Each pitch s in a sounding set of pitches S can be mapped to a MNN y.
Definition 5: Semitone spacing. Let y 1 < y 2 < · · · < y m be MNNs. The spacing in semitone intervals is the vector (y 2 − y 1, y 3 − y 2, … , y m − y m−1). For m = 1, the spacing of the chord is the empty set. For m = 0, a symbol for “rest” is used.■
The first minimal segment S 0 contains the pitches F3, A3, C4, F4, mapping to MNNs 53, 57, 60, 65, and a semitone spacing of (4, 3, 5). The next segment S 1 has spacing (3, 9, 3), and so on.
Definition 6: Beat/spacing state space. Let I denote a state space where each state is a pair: the first element of the pair is the beat of the bar on which a minimal segment begins (cf. Definition 4); the second element of the pair is the semitone spacing of that minimal segment (cf. Definition 5).■
If we construct a Markov model over the excerpt in Figure 5, using the beat/spacing state space I, then the first state encountered is
Is the inclusion of beat of the bar in the state space justified? When Tallas (1505–1585) was writing, for instance, barlines were not in widespread use. Still the piece has a metric hierarchy, and points of arrival, such as the last beat of bar 12 into bar 13, coincide with strong pulses in the hierarchy. As an example, the chord F3, C4, F4, A4 occurs in bar 2 and again in bar 3, with the first occurrence on beat 3 of the bar, and the second on beat 2. Being relatively strong and weak beats, respectively, this is likely to influence what happens next, so representing the two occurrences as different states is justified (Huron, Reference Huron2006).
3.3. Details of musical context to be retained
When analyzing transitions between states, we retain information about the musical context of the transitions, to help with realization (cf. Definition 3). It is more convenient to store this information in a transition list L than in a transition matrix P (2), although sampling uniformly from L is equivalent to sampling from P. The transition list, containing all instances of transitions, is similar to what Cope (Reference Cope1996, Reference Cope2005) calls a lexicon, but below we give a more explicit description of the information stored and how it is utilized. In general, for a state space I with n elements, the form of the transition list is
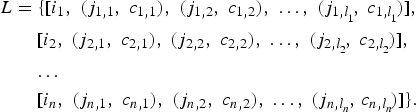 $$\eqalign{L &= \lcub [ i_{1}\comma \; \lpar j_{1\comma 1}\comma \; c_{1\comma 1}\rpar \comma \; \lpar j_{1\comma 2}\comma \; c_{1\comma 2}\rpar \comma \; \ldots \comma \; \lpar j_{1\comma l_{_{1}}}\!\comma \; c_{1\comma l_{_{1}}}\!\rpar ] \comma \; \cr & \quad\ [ i_{2}\comma \; \lpar j_{2\comma 1}\comma \; c_{2\comma 1}\rpar \comma \; \lpar j_{2\comma 2}\comma \; c_{2\comma 2}\rpar \comma \; \ldots \comma \; \lpar j_{2\comma l_{_{2}}}\!\comma \; c_{2\comma l_{_{2}}}\!\rpar ] \comma \; \cr &\quad\ \!\ldots \cr &\quad\ [ i_{n}\comma \; \lpar j_{n\comma 1}\comma \; c_{n\comma 1}\rpar \comma \; \lpar j_{n\comma 2}\comma \; c_{n\comma 2}\rpar \comma \; \ldots\comma \; \lpar j_{n\comma l_{_{n}}}\!\comma \, c_{n\comma l_{_{n}}}\!\rpar ] \rcub.}$$
$$\eqalign{L &= \lcub [ i_{1}\comma \; \lpar j_{1\comma 1}\comma \; c_{1\comma 1}\rpar \comma \; \lpar j_{1\comma 2}\comma \; c_{1\comma 2}\rpar \comma \; \ldots \comma \; \lpar j_{1\comma l_{_{1}}}\!\comma \; c_{1\comma l_{_{1}}}\!\rpar ] \comma \; \cr & \quad\ [ i_{2}\comma \; \lpar j_{2\comma 1}\comma \; c_{2\comma 1}\rpar \comma \; \lpar j_{2\comma 2}\comma \; c_{2\comma 2}\rpar \comma \; \ldots \comma \; \lpar j_{2\comma l_{_{2}}}\!\comma \; c_{2\comma l_{_{2}}}\!\rpar ] \comma \; \cr &\quad\ \!\ldots \cr &\quad\ [ i_{n}\comma \; \lpar j_{n\comma 1}\comma \; c_{n\comma 1}\rpar \comma \; \lpar j_{n\comma 2}\comma \; c_{n\comma 2}\rpar \comma \; \ldots\comma \; \lpar j_{n\comma l_{_{n}}}\!\comma \, c_{n\comma l_{_{n}}}\!\rpar ] \rcub.}$$Fixing k ∈ {1, 2, … , n}, let us look at an arbitrary element of this transition list,
The first element i k is a state in the state space I. In the example from Section 3.1, i k would be a pitch class. In the current model, i k ∈ I is a beat/spacing state as discussed above. Each of j k,1, j k,2, … , j k,l k is an element of the state space (and not necessarily distinct). In Section 3.1, these were other pitch classes; in the current model, they are the beat/spacing states for which there exists a transition from i k, over one or more pieces of music. Each of j k,1, j k,2, … , j k, l k has a corresponding musical context c k,1, c k,2, … , c k, l k, which is considered now in more detail. To avoid introducing further subscripts, attention is restricted to the first context c k,1, which is itself a list,
where γ1 and γ2 are integers, s is a string, and D is a set of ontime–pitch–duration triples (data set; Meredith et al., Reference Meredith, Lemström and Wiggins2002). The data set D ∈ c k,1 contains data points that determine the beat/spacing state j k,1. In the original piece, the state j k,1 will be preceded by the state i k,1, which was determined by some set D′ of data points. For the lowest sounding note in each data set D and D′, γ1 gives the interval in semitones and γ2 the interval in scale steps. For example, the interval in semitones between bass notes of the asterisked chords shown in Figure 6 is γ1 = −5, and the interval in scale steps is γ2 = −3. If either of the data sets is empty, because it represents a “rest” state, then the interval between their lowest sounding notes is defined as Ø. The string s is a piece identifier. For instance, s = “C-56-3” means that the beat/spacing state j k,1 was observed in Chopin's opus 56 number 3. Reasons for retaining this particular information in the format c k,1 will become apparent in a worked example following Definition 8.

Fig. 6. Bars 115–120 of the Mazurka in C major opus 24 number 2 by Chopin.
We close this subsection by justifying three design decisions. All decisions are based on trying to decrease the sparsity of the transition list (sparse transition lists make replication of original material more likely). First, why use beat position and vertical interval set as the state variables (cf. Section 3.2)? Cope (Reference Cope2005, p. 89) describes a method for syntactic meshing where each database piece is transposed to C major or A minor and then uses beat/pitch states (as opposed to our not transposing and using beat/spacing states). We chose to use spacing (interval sets) because the transition list is less sparse than the corresponding list using pitches. Second, why use the context in realization, but not in calculating outgoing transition probabilities (earlier in this subsection)? Similar to our first question, separation of state and context increases the number of coincident states, which decreases the sparsity of the transition list. Third, why use the lowest sounding note in the realization of a generated passage (immediately above)? The use of some reference point is a consequence of including spacing in the state variable. Inter-onset intervals tend to be longer for lower notes (Broze & Huron, Reference Broze, Huron, Cambouropoulos, Tsougras, Mavromatis and Pastiadis2012), and so lowest sounding notes are more stable and therefore preferable to using highest sounding notes, say.
3.4. Random generation Markov chain (RGMC)
Definition 7: RGMC. Let (I, L, A) be an mth-order Markov chain, where I is the state space, L is the transition list of the form (9), and A is a list containing possible initial state-context pairs. An RGMC means that
1. a random number is used to select an element of the initial distribution list A;
2. more random numbers (N − 1 in total) are used to select elements of the transition list L, dependent on the previous selections;
3. the result is a list of state-context pairs H = {(i 0, c 0), (i 1, c 1), … , (i N−1, c N−1)}, referred to as the generated output.■
Definition 8: Markov model for Chopin mazurkas. Let I denote the state space for a first-order Markov model, containing all beat/spacing states (cf. Section 3.2) found over 39 Chopin mazurkas.Footnote 3 Let the model have a transition list L with the same structure as L in (9), and let it retain musical context as in (11). The model's initial distribution list A contains the first beat/spacing state and musical context for each of the 39 mazurkas, and selections made from A are equiprobable.■
An RGMC for the model (I, L, A) generated the output
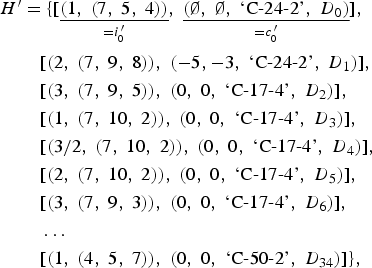 $$\eqalign{{ H}^{\prime} & = \lcub [ \mathop{\underline{\lpar 1\comma \; \lpar 7\comma \; 5\comma \; 4\rpar \rpar }}\limits_{=i^{\, \prime}_{0}}\comma \; \mathop{\underline{\lpar \emptyset\comma \; \emptyset\comma \; \hbox{`C-24-2'}\comma \; D_{0}\rpar }}\limits_{= c^{\, \prime}_{0}}] \comma \; \cr & \quad [ \lpar 2\comma \; \lpar 7\comma \; 9\comma \; 8\rpar \rpar \comma \; \lpar - 5\comma - 3\comma \; \hbox{`C-24-2'}\comma \; D_{1}\rpar ] \comma \; \cr & \quad [ \lpar 3\comma \; \lpar 7\comma \; 9\comma \; 5\rpar \rpar \comma \; \lpar 0\comma \; 0\comma \; \hbox{`C-17-4'}\comma \; D_{2}\rpar ] \comma \; \cr & \quad [ \lpar 1\comma \; \lpar 7\comma \; 10\comma \; 2\rpar \rpar \comma \; \lpar 0\comma \; 0\comma \; \hbox{`C-17-4'}\comma \; D_{3}\rpar ] \comma \; \cr & \quad [ \lpar 3/2\comma \; \lpar 7\comma \; 10\comma \; 2\rpar \rpar \comma \; \lpar 0\comma \; 0\comma \; \hbox{`C-17-4'}\comma \; D_{4}\rpar ] \comma \; \cr & \quad [ \lpar 2\comma \; \lpar 7\comma \; 10\comma \; 2\rpar \rpar \comma \; \lpar 0\comma \; 0\comma \; \hbox{`C-17-4'}\comma \; D_{5}\rpar ] \comma \; \cr & \quad [ \lpar 3\comma \; \lpar 7\comma \; 9\comma \; 3\rpar \rpar \comma \; \lpar 0\comma \; 0\comma \; \hbox{`C-17-4'}\comma \; D_{6}\rpar ] \comma \; \cr & \quad \ldots \cr & \quad [ \lpar 1\comma \; \lpar 4\comma \; 5\comma \; 7\rpar \rpar \comma \; \lpar 0\comma \; 0\comma \; \hbox{`C-50-2'}\comma \; D_{34}\rpar ] \rcub \comma }$$
$$\eqalign{{ H}^{\prime} & = \lcub [ \mathop{\underline{\lpar 1\comma \; \lpar 7\comma \; 5\comma \; 4\rpar \rpar }}\limits_{=i^{\, \prime}_{0}}\comma \; \mathop{\underline{\lpar \emptyset\comma \; \emptyset\comma \; \hbox{`C-24-2'}\comma \; D_{0}\rpar }}\limits_{= c^{\, \prime}_{0}}] \comma \; \cr & \quad [ \lpar 2\comma \; \lpar 7\comma \; 9\comma \; 8\rpar \rpar \comma \; \lpar - 5\comma - 3\comma \; \hbox{`C-24-2'}\comma \; D_{1}\rpar ] \comma \; \cr & \quad [ \lpar 3\comma \; \lpar 7\comma \; 9\comma \; 5\rpar \rpar \comma \; \lpar 0\comma \; 0\comma \; \hbox{`C-17-4'}\comma \; D_{2}\rpar ] \comma \; \cr & \quad [ \lpar 1\comma \; \lpar 7\comma \; 10\comma \; 2\rpar \rpar \comma \; \lpar 0\comma \; 0\comma \; \hbox{`C-17-4'}\comma \; D_{3}\rpar ] \comma \; \cr & \quad [ \lpar 3/2\comma \; \lpar 7\comma \; 10\comma \; 2\rpar \rpar \comma \; \lpar 0\comma \; 0\comma \; \hbox{`C-17-4'}\comma \; D_{4}\rpar ] \comma \; \cr & \quad [ \lpar 2\comma \; \lpar 7\comma \; 10\comma \; 2\rpar \rpar \comma \; \lpar 0\comma \; 0\comma \; \hbox{`C-17-4'}\comma \; D_{5}\rpar ] \comma \; \cr & \quad [ \lpar 3\comma \; \lpar 7\comma \; 9\comma \; 3\rpar \rpar \comma \; \lpar 0\comma \; 0\comma \; \hbox{`C-17-4'}\comma \; D_{6}\rpar ] \comma \; \cr & \quad \ldots \cr & \quad [ \lpar 1\comma \; \lpar 4\comma \; 5\comma \; 7\rpar \rpar \comma \; \lpar 0\comma \; 0\comma \; \hbox{`C-50-2'}\comma \; D_{34}\rpar ] \rcub \comma }$$giving N = 34 state-context pairs in total. We have tried to make the format clear by underlining the first pair H ′0 = (i ′0, c′0) in (12). The formats of i′0 and c ′0 are analogous to (8) and (11), respectively. By definition, different random numbers would have given rise to a different, perhaps more stylistically successful, passage of music, but the output in (12) and the corresponding passage in Figure 7 have been chosen as a representative example of RGMC for the model (I, L, A). The steps involved in realizing the generated output H of an RGMC (cf. Definition 3), to form a data set D consisting of ontime–pitch–duration triples (considered the bare minimum for having generated a passage of music) are addressed now.
To convert the first element H′0 = (i′0, c′0) of the list H′ into ontime–pitch–duration triples, an initial bass pitch is stipulated, say, E4, having MNN 64 and morphetic pitch number (MPN) 62. MPNs are required for correct pitch spelling (see Meredith, Reference Meredith2006). The chord spacing (7, 5, 4) determines the other MNNs, 64 + 7 = 71, 64 + 7 + 5 = 76, and 64 + 7 + 5 + 4 = 80. The corresponding MPNs are found by combining the initial bass MPN, 62, with the data set from the musical context,
Due to a bijection between pitch and MNN–MPN representations, the pitch material of the first element H′0 of the list H′ is determined as E4, B4, E5, and G♯5 (see the first chord in Fig. 7).
To calculate an ontime for the first element H′0, we use the state i′0, coming from beat 1, indicating that the mazurka chosen to provide the initial state (opus 24 number 2) begins on the first beat of the bar. Adhering to the convention that the first full bar of a piece begins with ontime zero, the ontime for each triple being realized from H′0 will be zero.Footnote 4 It can be seen in the data set from the musical context (13) that each data point has the same duration, 1 crotchet beat. This duration becomes the duration of each of the realized triples for H′0. The realization of durations is always done with reference to the data sets D 0, D 1, … , D 34, but it is not always so straightforward due to notes belonging to more than one minimal segment (cf. Definition 4 and see bars 4–5 of Fig. 5). For more information on this topic, including how polyphonic textures arise from generated output, see section 8.4 of Collins (Reference Collins2011). The second element
of the list H′ is converted into ontime–pitch–duration triples in much the same way as the first element H′0. One difference is the use of contextual information (in particular the intervals between bass notes of consecutive minimal segments). For example, the interval in semitones between bass notes of the asterisked chords shown in Figure 6 is γ1 = −5, and the interval in scale steps is γ2 = −3. This is the origin of the two asterisked numbers in (14). The interval between bass notes is retained in the passage being realized, giving the MNN–MPN pairs (59, 59), (66, 63), (75, 68), and (83, 73). By virtue of the bijection between pitch and MNN–MPN representations, these pairs map to the pitches B3, F♯4, D♯5, and B5 (see the second chord in Fig. 7). The realization of H′ continues, mapping H′2, H′3, … , H′34 to ontime–pitch–duration triples.
The key signature, time signature, tempo, and initial bass note of the passage shown in Figure 7 are borrowed from Chopin's opus 56 number 1. Information from the chosen initial state could have been used instead, but further information from opus 56 number 1 will be used in Section 3.6.

Fig. 7. Realized generated output of a random generating Markov chain for the model (I, L, A). This passage of music is derived from H′ in (12). The numbers written above the stave give the opus/number and bar of the source. Only when a source changes is a new opus–number–bar written. The box in bars 5–6 is for a later discussion.
3.5. Stylistic shortcomings of RGMC
First-order Markov modeling is a common and promising approach for algorithmic stylistic composition, because it “ensures beat-to-beat logic in new compositions” (Cope, Reference Cope2005, p. 91). Unfortunately, “it does not guarantee the same logic at higher levels … phrases simply string together without direction or any large-scale structure” (Cope, Reference Cope2005, p. 91). The passage shown in Figure 7 is arguably too short to be criticized for lacking global structure, but there are other shortcomings:
Sources: Too many consecutive states come from the same original source. Numbers above each state in Figure 7 are the opus, number within that opus, and the bar number in which the state occurs. The boxed material contains four consecutive states from opus 50 number 2, for instance. Having criticized the output of EMI for bearing too much resemblance to original Chopin (Fig. 3), steps should be taken to avoid the current model being susceptible to the same criticism.
Range: The passage in Figure 7 begins in the top half of the piano's range, due to stipulating the initial bass note as E4. However, this is from opus 56 number 1, so some mazurkas do begin this high. A four-note chord built on top of this bass note contributes to the sense of an unusually high opening. Therefore, a solution to this shortcoming ought to be sensitive to positions of both lowest and highest sounding notes in a chord. An awareness of the distribution of notes within that chord, for instance, spread evenly or skewed toward the top, may also be useful.
Likelihood: Monitoring the probability of new pitch material is one way of quantifying and controlling what may be perceived as a lack of tonal direction. For example, MNNs corresponding to the pitches B♯4, E♯4, and A♯4 appear in bar 5 of Figure 7 for the first time. Using a local empirical distribution, formed over the current ontime and a number of preceding beats, it is possible to calculate the likelihood of the chords that appear in bar 5. If the empirical likelihood of any chord is too low, then this could identify a stylistic shortcoming. Low likelihood alone may not be the problem, because a Chopin mazurka may well contain several such chords: the temporal position of these chords within an excerpt will be appropriate to altering or obscuring the tonal direction, however.
Departure and arrival: The passage in Figure 7 outlines a IV–I progression in bars 1–4; thus, the first half of the passage conveys a sense of departure and arrival, albeit serendipitously. The move toward D minor in bars 7 and 8, by contrast, does not convey the same sense of arrival. Stipulating a final bass note (in addition to stipulating the initial bass note of E4) would have increased the chance of the passage ending in a certain way. Students of chorale harmonization are sometimes encouraged to compose the end of the current phrase first, and then to attempt a merging of the forward and backward processes. Cope (Reference Cope2005, p. 241) has also found the concept of composing backward useful.
The use of hand-coded rules (or constraints) to guide the generation of a passage of music was mentioned in Section 2.1 (Ebciǒglu, Reference Ebciǒglu, Balaban, Ebciǒglu and Laske1994; Phon-Amnuaisuk et al., Reference Phon-Amnuaisuk, Smaill and Wiggins2006; Anders & Miranda, Reference Anders and Miranda2010; Elowsson & Friberg, Reference Elowsson, Friberg, Cambouropoulos, Tsougras, Mavromatis and Pastiadis2012). We questioned whether such systems alone are viable beyond relatively restricted tasks in stylistic composition. RGMCs, in contrast, seem to be appropriate for modeling open-ended stylistic composition briefs. There is a role for constraints to play, however, in addressing the shortcomings outlined above. For a so-called template piece (Fig. 8a), we monitor the range (Fig. 8b) and likelihood profile (Fig. 8c, dashed line).Footnote 5 At each step of the RGMC (cf. Definition 7), the generated passage must not have sampled too many consecutive states from the same source (parameter c src), and it must have a range (parameters c min, c max, and c¯) and likelihood profile (parameters c prob and c beat) that fall within specifiable distances of the template piece. If any of the constraints cannot be met at Step k, the selected state is revised by resampling from the transition list L. After c term revisions, the process backtracks and revises Step k − 1. The passage shown in Figure 8d satisfies the constraints without replicating the template piece (Fig. 8a).Footnote 6 The effect of the constraints is evident on comparing Figure 8d to Figure 7. A template is defined formally as follows.
Definition 9: Template. For an existing excerpt of music, a template consists of the tempo instruction; key signature; time signature; pitch of the first minimal segment's lowest sounding note; partition points (cf. Definition 4); lowest and highest sounding, and mean MNNs at each partition point; and geometric mean likelihood at each partition point (likelihood profile).■
The use of a template as a basis for composition is discussed by Collins (Reference Collins2009, p. 108) and Hofstader (writing in Cope, Reference Cope2001), who coins the verb to “templagiarise” (p. 49). We argue that the term plagiarize is too negative, except when the composer (or algorithm for music generation) uses: a particularly well-known piece as a template and does little to mask the relationship; or too explicit a template (even if the piece is not well known), the result being obvious quotations from the musical surface.
To impart generated passages with a sense of departure and arrival, we return to the idea of a backward Markov process that was mentioned at the bottom of Definition 2. Up to this point, a list of states A from the beginning of each mazurka in the database has been used to generate an initial state. This list is referred to as the external initial states, now denoted A ←. When generating backward, a list A → of external final states (i.e., a list of states from the end of each mazurka in the database) may be appropriate. However, if the brief were to generate a passage from bar 1 up to the downbeat of bar 9, then states from the very end of each mazurka are unlikely to provide stylistically suitable material for bar 9 of a generated passage. Another list A ← of internal final states is required. This list contains three beat/spacing states from each mazurka in the database (three is an arbitrary choice), taken from the time points at which the first three phrases are marked as ending in the score (Paderewski, Reference Paderewski1953). For bar 9, say, of a generated passage, the internal final states would probably provide more stylistically suitable material than the external final states. The list A → of internal initial states is defined similarly: it is a list consisting of three beat/spacing states (where these exist) from each database mazurka, taken from time points corresponding to the beginning of phrases two, three, and four. The internal initial states would be appropriate if the brief was to generate a passage from bar 9 onward, for instance.
Our four-step process for trying to ensure that a generated passage imparts a sense of departure and arrival is as follows. Let us assume the brief is to generate a passage from ontime x 1 to ontime x 2, and let x 1|2 = ⌈(x 1 + x 2)/2⌉.
• Use a forward RGMC process with a template and constraints to generate c for lots of output, realized as the data sets D →1, D →2, … , D →c for, all of which are candidates for occupying the time interval [x 1, x 1|2].
• Use a backward RGMC process with a template and constraints to generate c back lots of output, realized as the data sets D ←1, D ←2, … , D ←c back, all of which are candidates for occupying the time interval [x 1|2, x 2,].
• Consider all possible combinations of passages constructed by appending D →i and D ←j, where 1 ≤ i ≤ c for and 1 ≤ i ≤ c back, and then removing the data points of D ←j at ontime x 1|2, removing the data points of D →i at ontime x 1|2, or superposing the data points of D →i, D ←j. Therefore, there will be 3 × c for × c back candidate passages in total.
• Of the 3c forc back candidate passages, select the passage whose states are all members of the transition list and whose likelihood profile is, on average, closest to that of the template piece.

Fig. 8. (a) Bars 1–9 of the Mazurka in B major opus 56 number 1 by Chopin. (b) Plots of lowest and highest sounding, and mean MIDI note numbers against ontime are indicated by black lines passing through grey noteheads. (c) Two likelihood profiles, for the excerpt in (a) and the passage in (d). (d) Realized generated output of a random generation Markov chain for the model (I, L, A), with constraints applied to sources, range, and likelihood.
This approach should be contrasted with Pachet and Roy's (Reference Pachet and Roy2011) attempt to steer Markov sequences to achieve certain musical aims, which involves recasting sequence generation as a constraint satisfaction problem. The algorithms generate chord sequences and melodies, however, rather than the full textures studied here.
Bringing together several definitions, we define Racchman-Oct2010 as random constrained chain of Markovian nodes.Footnote 7 A date stamp is appended, so it can be clearly differentiated in future work. Racchman-Oct2010 is one of the models evaluated in Section 4.
Definition 10: The Racchman. Racchman-Oct2010 is an RGMC with the state space I and transition list L from Definition 8. It has four lists, A ↪, A →, A ←, and A ↩, for generating internal or external initial states as appropriate. At each stage 0 ≤ n ≤ N − 1 of the RGMC, the generated output is realized and tested for the constraints pertaining to sources, range, and low-likelihood chords. If at an arbitrary stage 0 ≤ k ≤ N − 1 any of these constraints are not satisfied, the RGMC is said to have reached a terminal state, and an alternative continuation based on stage k − 1 is selected and retested, and so on. If the constraints are not satisfied more than c term times at stage k, the state at stage k − 1 is revised and retested, and so forth. The RGMC continues until either the generated output consists of a specified number of beats, in which case the generated output is realized and stored as one of the candidate passages (see above list); or the constraints are not satisfied more than c term times at stage k = 0, in which case the RGMC is restarted.■
An example output of Racchman-Oct2010 is given in Figure 9.Footnote 8Figure 9a and b are realized output of a forward RGMC process, and are candidates for occupying a time interval [0, 12]. Figure 9c and d are realized output of a backward RGMC process and are candidates for occupying a time interval [12, 24]. For the backward process, the template contains the pitch of the last minimal segment's lowest sounding note, as opposed to the first. Definitions of the transition list and the likelihood profile are also reversed appropriately. With two candidates for each time interval (c for = c back = 2), and three ways of combining each pair of candidates (as described in the penultimate point above), there are 12 = 3c forc back candidate passages in total. Of these 12, it is the passage shown in Figure 9e whose states are all members of the transition list and whose likelihood profile is, on average, closest to that of the template.

Fig. 9. (a, b) Passages generated by forward random generating Markov chain. (c, d) Passages generated by backward random generating Markov chain. (e) One solution for combining passages generated by forward and backwars random generating Markov chain.
The difference between Figures 8d and 9e is a degree of control in the latter case over the sense of departure and arrival, due to the combination of forward and backward processes, and the extra pitch constraint for the last lowest sounding note. The excerpt used as a template for both Figures 8d and 9e is bars 1–9 of opus 56 number 1, as shown in Figure 8a. At the end of this excerpt, there is a pedal consisting of G2 and D2, which in the full piece persists for a further three bars, followed by chord V7 in bars 13–15 and chord I in bar 16. Arguably, therefore, the template itself lacks a sense of arrival in bar 9, and this is reflected better in Figure 9e, ending with chord ivb, than in Figure 8d, which cadences on to chord v.
3.6. Pattern inheritance
One of the criticisms of RGMC is that the resultant music lacks large-scale structure: as observed in the Introduction, “[i]n music, what happens in measure 5 may directly influence what happens in measure 55, without necessarily affecting any of the intervening material” (Cope, Reference Cope2005, p. 98). When developing the model Racchman-Oct2010, no attempt was made to address this criticism: local or global structures that the listener hears in the passages of Figures 7, 8d, and 9 have occurred by serendipity. This model is not alone in ignoring matters of structure, for “[t]he formalization of music has not always covered so readily the form of music, particularly from a psychological angle that takes the listener into account” (Collins, Reference Collins2009, p. 103).
In this section, the matter of structure is addressed by a second model, Racchmaninof-Oct2010.Footnote 9 This model tries to ensure that discovered patterns from the template piece are inherited by the generated passage. The pattern discovery algorithm SIACT (Collins et al., Reference Collins, Thurlow, Laney, Willis, Garthwaite, Downie and Veltkamp2010) is applied to a projection (ontime, MNN, and MPN) of the excerpt being used as a template. SIACT is intended for intra-opus pattern discovery (i.e., discovering repeated patterns within a piece of music). It uses a geometric representation of a piece (Meredith et al., Reference Meredith, Lemström and Wiggins2002) in which notes are converted to points in pitch-time space (e.g., a dimension for ontime, another for MNN, and another for MPN). First SIACT calculates and sorts the difference between each pair of points, to find point collections that are all translatable by some fixed amount in the point set. One such collection, for instance, might correspond to all and only those notes that are repeated six beats later and one pitch step lower. The collections are called maximal translatable patterns (Meredith et al., Reference Meredith, Lemström and Wiggins2002). A potential problem with maximal translatable patterns, which is called the problem of isolated membership (Collins et al., Reference Collins, Thurlow, Laney, Willis, Garthwaite, Downie and Veltkamp2010), is that sometimes they contain a perceptually salient pattern as well as temporally isolated notes that also satisfy the mathematical condition. The second part of SIACT is responsible for removing these temporally isolated members, and returning only the perceptually salient patterns. SIACT is sufficiently flexible to find short motifs, medium-length themes, as well as longer repeated sections.
The resulting patterns are filtered and rated by a perceptually validated formula (Collins et al., Reference Collins, Laney, Willis and Garthwaite2011). Collins et al. asked music undergraduates to rate the musical importance of already discovered repeated patterns. Variable selection techniques were used to relate observed ratings to quantifiable properties of the patterns (such as the number of notes contained in one occurrence). Ratings of a pattern's musical importance could be predicted by a linear combination of three factors: compactness, compression ratio, and the pattern's expected number of occurrences. While a pattern occurs, some notes that are not part of the pattern may be played, and compactness measures the proportion of contemporaneous notes that are in the pattern (Meredith et al., Reference Meredith, Lemström and Wiggins2003). The compression ratio is approximately the harmonic mean of the number of notes in a pattern and the pattern's number of occurrences (Meredith et al., Reference Meredith, Lemström and Wiggins2003). A pattern's perceived importance seemed to be increased by having high compactness and compression ratio, while unexpected patterns (Conklin & Bergeron, Reference Conklin and Bergeron2008) were also perceived as more important.
The rated patterns are labeled in order of rank, so that pattern P i,j rates higher than P k,l if and only if i < k. The second subscript denotes occurrences of the same pattern in lexicographic order. That is, pattern P i,j occurs before P i,l if and only if j < l. An example of the output of the discovery process is shown in Figure 10. Pattern P 1,1 (indicated by the solid line) is rated higher than pattern P 2,1 (indicated by the dashed line), which in turn is rated higher than P 3,1 (indicated by the dotted line). The second model for generating stylistic compositions, Racchmaninof-Oct2010, attempts to ensure that the same type of patterns discovered in the template excerpt occur in a generated passage. The location but not the content of each discovered pattern is retained, as indicated in Figure 11.
Definition 11: Template with patterns. The term template was the subject of Definition 9. Template with patterns refers to the following supplementary information being retained when patterns P 1,1, P 2,1, … , P M,1 have been discovered in an excerpt. For each discovered pattern P i,1, retain the following:
• The ontimes of the first and last data points. For the sake of simplicity, these are rounded down and up, respectively, to the nearest integer.
• Its translators vi,2, vi,3, … , vi,m i in D, which bring P i,1 to the other occurrences P i,2, P i,3, … , P i,m i.
• The lowest sounding pitch of the first and last minimal segments of the region in which the discovered pattern P i,j occurs (j ≠ 1 if the algorithm discovered an occurrence other than the first).
• The number of other discovered patterns of which P i,1 is a subset, called the subset score and denoted §(P i,1). The scores §(P i,2), §(P i,3), … , §(P i,m i) are retained also. ■

Fig. 10. SIACT was applied to a representation of bars 1–16 of the Mazurka in B major opus 56 number 1 by Chopin, and the results were filtered and rated. Occurrences of the top three patterns are shown.

Fig. 11. A representation of the supplementary information retained in a template with patterns. For comparison, an ordinary template (cf. Definition 9) is represented in Figure 8. Most of the content of the excerpt from opus 56 number 1 has been removed, but the location of the discovered patterns remains.
It is demonstrated with reference to Figure 12 how this supplementary information is employed in the generation of a passage. The passage to be generated can be thought of as an open interval of ontimes [a, b] = [0, 45], the same length as the excerpt chosen for the template (opus 56 number 1). When the set of intervals U for which material has been generated covers the interval [a, b], the process is complete. At the moment this set is empty, U = Ø.
1. Generation begins with the pattern P i,j that has maximum subset score §(P i,j). Tied scores between §(P i,j) and §(P k,l) are broken by highest rating (min{i, k}) and then by lexicographic order (min{j, l}). It is evident from Figure 10 that P 3,3 has the maximum subset score. The ontimes of the first and last data point have been retained in the template with patterns, so it is known that material for the ontime interval [a 1, b 1] = [12, 15] must be generated. This is done using the first model Racchman-Oct2010, with internal initial and final states, and the lowest sounding pitches retained in the template with patterns. The resulting music is contained in box 1 in Figure 12. The set of intervals for which material has been generated becomes U = {[12, 15]}.
2. Having retained the nonzero translators of P i,1 = P 3,1 in D in the template with patterns, translated copies of the material generated in Step 1 are placed appropriately, giving the music contained in boxes labeled 2 in Figure 12. Now U = {[0, 3], [6, 9], [12, 15], [24, 27]}. It is said that P 3,1, P 3,2, P 3,3, P 3,4 have been addressed.
3. Generation continues for the pattern with the next highest subset score, in this example P 2,2. This pattern has corresponding ontime interval [a 2, b 2] = [12, 15]. Because this interval is contained in U, no material is generated. (Had [a 2, b 2] = [12, 17], say, then material would have been generated for [15, 17] and connected to that already generated for [12, 15]. Had [a 2, b 2] = [9, 17], say, then material for [9, 12] and [15, 17] would have been generated and connected either side of that for [15, 17].) Ontime intervals for patterns P 2,1 and P 2,3 have also been covered, so generation continues with the pattern P 1,1, because this is the remaining unaddressed pattern. Pattern P 1,1 has an ontime interval of [a 3, b 3] = [12, 24]. Now [12, 15] ∈ U, meaning that material must be generated for the remainder of this interval, [15, 24]. Again, the model Racchman-Oct2010 is used, and the resulting music is contained in box 3 in Figure 12. Because [12, 15], [24, 27] ∈ U, initial and final states for the material to fill [15, 24] have been generated already. This ensures continuity of the music between the three time intervals, as illustrated by the overlapping of box 3 by surrounding boxes in Figure 12. Now U = {[0, 3], [6, 9], [12, 15], [15, 24], [24, 27]}.
4. Having retained the nonzero translator of P 1,1 in D in the template with patterns, a translated copy of the material generated in Step 3 is placed appropriately, giving the music contained in box 4 in Figure 12. Now U = {[0, 3], [6, 9], [12, 15], [15, 24], [24, 27], [27, 36]}.
5. All patterns contained in the template have been addressed, but still U does not cover the passage's ontime interval [a, b] = [0, 45]. Material for the remaining intervals, [a 4, b 4] = [3, 6], [a 5, b 5] = [9, 12], and [a 6, b 6] = [36, 45] is generated in this final step. The model Racchman-Oct2010 is used three times (once for each interval), and the resulting music appears in boxes labeled 5 in Figure 12. These intervals are included in U and the process is complete.

Fig. 12. Passage generated by the random constrained chain of Markovian nodes with inheritance of form model, October 2010 (Racchmaninof-Oct 2010). The numbered boxes indicate the order in which different parts of the passage are generated, and correspond to the numbered list after Definition 11. This passage is used in the evaluation in Section 4, as Stimulus 29.
The above list outlines an example run of the model that we call Racchmaninof-Oct2010.Footnote 10 This description of an example run, with the resulting passage in Figure 12, is intended to provide a better impression of the workings of Racchmaninof-Oct2010 than would a more abstract definition. Racchmaninof-Oct2010 comprises several runs of the simpler model Racchman-Oct2010, runs that generate material for ontime intervals, according to the order of subset scores and until the ontime interval for the entire passage is covered. The result is a Markov model where, in Cope's (Reference Cope2005) terms, it is possible for what happens at bar 5 to influence bar 55. For instance, comparing Figures 10 and 12, it is evident that the locations, but not the content, of the discovered patterns have been inherited by the generated passage.
4. EVALUATION
This section consists of an evaluation of our models Racchman-Oct2010 and Racchmaninof-Oct2010, and Cope's (Reference Cope1996, Reference Cope2005) EMI. The chosen stylistic composition brief is to compose the opening section (~16 bars) of a Chopin-style mazurka, and the evaluation addresses the following questions:
1. Success: How do mazurkas generated by our models compare in terms of stylistic success to original Chopin mazurkas; Mazurkas, after Chopin (Cope, Reference Cope1997b) attributed to EMI; and mazurkas by other human composers?
2. Distinguishing: Are judges able to distinguish between the different categories of music stimulus (e.g., humancomposed/computer based)? Are judges better than chance at distinguishing between human-composed stimuli and those based on computer programs that learn from Chopin's mazurkas?
3. Reliability: In terms of the stylistic success ratings for each stimulus, is there a significant level of interjudge reliability? What about interjudge reliability for aesthetic pleasure?
4. Correlations: For a given judge, is there significant correlation between any pair of the following: ratings of stylistic success; ratings of aesthetic pleasure; or categorization of stimuli as computer based?
5. Attributes: Are there particular aspects of a stimulus that lead to its stylistic success rating (high or low)? Are certain musical attributes useful predictors of stylistic success?
The general framework for the evaluation is Amabile's (Reference Amabile1996) CAT. In our particular version of the CAT, a judge's task involves giving ratings of stylistic success (Pearce & Wiggins, Reference Pearce, Wiggins, Cardoso and Wiggins2007) and aesthetic pleasure, and distinguishing between different categories of music stimulus (Pearce & Wiggins, Reference Pearce and Wiggins2001). Each of the evaluation questions can be cast as quantitative, testable hypotheses, apart from the first part of Question 5, which was assessed using judges' open-ended textual responses.
4.1. Judges and instructions
The first group of judges (eight males, eight females), referred to here as concertgoers, were recruited at a concert containing music by Camille Saint-Saëns (1835–1921) and Marcel Tournier (1879–1951) for violin and harp, which took place in St. Michael's Church, the Open University. The second group of judges (seven males, nine females), referred to here as experts, were recruited from various e-mail lists, were pursuing or had obtained a master's degree or a PhD, and played/sang 19th-century music or considered it to be one of their research interests.
Both the concertgoers (mean age = 59.65 years, SD = 5.51) and the experts (mean age = 31.25 years, SD = 11.89) were paid £10 for an hour of their time, during which they were asked to listen to excerpts of music and answer corresponding multiple-choice and open-ended questions. Judges participated one at a time, and were seated at a computer on which instructions and tasks appeared in a graphical user interface. The instructions, which were the same for concertgoer and expert judges, began by introducing Chopin's mazurkas. Judges listened to two Chopin mazurka excerpts (opus 24 number 1 and opus 41 number 4, approximately the first 16 bars) and were asked by the first author to comment verbally on musical characteristics that the excerpts had in common. Judges received these instructions for the main task:
You will be asked to listen to and answer questions about short excerpts of music. Some of these excerpts will be from Chopin mazurkas. Some excerpts will be from the work of human composers, but not Chopin mazurkas (e.g., a fantasia by Mozart would fit into this category, as would an impromptu by Chopin, as would a mazurka by Grieg). Some excerpts will be based on computer programs that learn from Chopin's mazurkas.
The last category, including output of the models described in Section 3 and EMI (Cope, Reference Cope1997b), is referred to here as computer based. Judges were warned that some of the computer-based stimuli were more obvious than others. The instructions then described distinguishing between the three different categories above, rating of a stimulus's stylistic success, and rating of the aesthetic pleasure conferred by a stimulus. Working definitions of stylistic success and aesthetic pleasure were provided:
Stylistic success: An excerpt of music is stylistically successful as a Chopin mazurka if, in your judgment, its musical characteristics are in keeping with those of Chopin's mazurkas. Use the introductory examples as a means of comparison, and/or any prior knowledge about this genre of music.
Aesthetic pleasure: How likely would you be to add a recording of this piece to your music collection?
Ratings of stylistic success and aesthetic pleasure were elicited using a 7-point scale (1 = low, 7 = high). For each stimulus, the three questions (distinguish, style, and aesthetic) were framed above by the embedded sound file and a question that checked whether the judge had heard an excerpt before, and below by a textbox for any other comments. There was also a textbox for comments specific to the rating of stylistic success. The main task consisted of 32 stimuli, with order of presentation randomized for each judge, and three different question orders employed (distinguish, style, aesthetic; style, distinguish, aesthetic; aesthetic, distinguish, style) to mitigate ordering effects. Prior to the main task each judge completed the same short warm-up task, responding to the questions for two excerpts. A judge's answers to the warm-up task were reviewed before the main task, and it was disclosed that one of the warm-up excerpts was a Chopin mazurka (opus 6 number 2). The three Chopin mazurkas (two from the introductory instructions and one from the warm-up task) were embedded in a menu to one side of the interface, so that judges could remind themselves of the examples at any point.
4.2. Selection and presentation of stimuli
Stimuli were prepared as MIDI files with a synthesized piano sound. Each stimulus was the first 45 beats from the selected piece, which is approximately 15 bars in triple time. To avoid abrupt endings, a gradual fade was applied to the last nine beats. Depending on a judge's preference and the listening environment (we traveled to expert judges, rather than vice versa), stimuli were presented via external speakers (RT Works 2.0) or headphones (Performance Plus II ADD-800, noise canceling). The MIDI files were metronomically exact and dynamically uniform. We considered that the alternatives (MIDI with expressive timing and dynamic variation, or audio recorded by a professional pianist) would introduce uncontrollable sources of variation. However, rubato is a prominent feature in professional recordings of Chopin's mazurkas (Spiro et al., Reference Spiro, Gold, Rink, Miyazaki, Hiraga, Adachi, Nakajima and Tsuzaki2008), so it would be worth manipulating metronomic rendering versus expressive rendering in the future. The stimuli are available from the website mentioned previously, which are as follows:
Chopin mazurka: Mazurkas by Chopin in
1. B♭ minor opus 24 number 4.
2. G major opus 67 number 1.
3. A♭ major opus 7 number 4.
4. F♯ minor opus 59 number 3.
5. C♯ minor opus 63 number 3.
6. B minor opus 33 number 4.
Human other
7. Mazurka in G minor from Soirées musicales opus 6 number 3 by Clara Schumann.
8. Prelude in B major from Twenty-Four Preludes opus 28 number 11 by Chopin.
9. Romance in F major from Six Piano Pieces opus 118 number 5 by Johannes Brahms.
10. Rondeau, “Les baricades mistérieuses,” from Ordre number 6 by François Couperin (1668–1733).
11. Number 5 (Etwas rasch) from Six Little Piano Pieces opus 19 by Arnold Schoenberg (1874–1951).
12. Mazurka in F major, “Michaela's mazurka,” by David A. King.Footnote 11
Computer based
EMI: Mazurkas, after Chopin (Cope, Reference Cope1997b) attributed to EMI. Mazurkas in
13. A minor number 1.
14. C major number 2.
15. B♭ major number 3.
16. E minor number 4.
17. B♭ major number 5.
18. D major number 6.
System A: Passages generated by the model Racchman-Oct2010, with parameter values for number of terminations permitted (c term = 10), for consecutive states from the same source (c src = 4), for constraining range (c min = c max = c¯ = 19), for constraining low-likelihood chords (c prob = .2, and c beat = 12), and for a sense of departure/arrival (c for = c back = 3). The Chopin mazurka used as a template is in brackets. Mazurkas in
19. C major (opus 56 number 2).
20. E♭ minor (opus 6 number 4).
21. E minor (opus 41 number 2).
22. C minor (opus 56 number 3).
23. A minor (opus 17 number 4).
24. F minor (opus 63 number 2).
System B: Passages generated by the model Racchmaninof-Oct2010, with parameter values less than or equal to c term = 10, c src = 4, c min = c max = c¯ = 31, c prob = 1, c beat = 12, and c for = c back = 3. The Chopin mazurka used as a template is in brackets. Mazurkas in
25. C♯ minor (opus 50 number 3).
26. C major (opus 67 number 3).
27. B major (opus 41 number 3).
System B*: Passages generated by the model Racchmaninof-Oct2010, with parameter values less than or equal to c term = 10, c src = 4, c min = c max = c¯ = 24, c prob = .2, c beat = 12, and c for = c back = 3. Again, the Chopin mazurka used as a template is in brackets. Mazurkas in
28. C major (opus 68 number 1).
29. B major (opus 56 number 1).
30. F major (opus 68 number 3).
31. A minor (opus 7 number 2).
32. A♭ major (opus 24 number 3).
The main difference between Systems A, B, and B* is that Systems B and B* use pattern inheritance. The difference between Systems B and B* is that the parameter values of the latter are tighter, meaning one would expect stylistic success ratings for System B* to be greater on average than for System B. Consequently, Systems A and B* have comparable parameter values, whereas Systems A and B do not. Different numbers of stimuli per category for Systems B and B* are permissible for the chosen analytical methods. A mazurka section generated by System B* appears in Figure 12 (and is Stimulus 29). Collins (Reference Collins2011, his appendix E) provides notated versions of stimuli from Systems A, B, and B*.
The Chopin mazurkas (Stimuli 1–6) were selected to be representative of the corpus. The database used by Systems A, B, and B* to generate passages did not contain any of these mazurkas, to remove the possibility of between-stimuli references. Template pieces were selected at random from the remaining mazurkas. For Systems A, B, and B*, the database used to generate a passage did not contain the template mazurka selected for that stimulus, to reduce the probability of replication. The first successfully generated passage was used for each stimulus: we did not choose what “sounded best” from a pool of generated passages. Human other is a catchall category, with two mazurkas by composers other than Chopin and a piece by Chopin that is not a mazurka. Nonmazurka music from a range of musical periods is also represented: Baroque (Couperin), Romantic (Brahms), and 20th century (Schoenberg).
4.3. Results
4.3.1 Answer to evaluation Question 3 (reliability)
The analysis begins by answering Question 3 (reliability) because this determines how Question 1 (success) is approached. For the time being, the concertgoers (judges 1–16) and experts (judges 17–32) will be kept separate. Considering ratings of stylistic success, the Kendall coefficient of concordance is significant for both the concertgoers [W = 0.52, χ2 (31) = 258, p < 0.001] and the experts [W = 0.61, χ2 (31) = 301, p < 0.001]. Turning to simulated pairwise correlations for judges' ratings of stylistic success, 102 of the 120 (=16 × 15/2) interjudge correlations were significant at the 0.05 level for concertgoers. For the experts, 116 of the 120 interjudge correlations were significant at the 0.05 level. One expert judge appeared in all four of the nonsignificant correlations. A higher proportion of expert judges' ratings are significantly correlated, compared to the proportion for the concertgoer judges, suggesting that it is appropriate to continue considering the two groups separately. The reliability of aesthetic pleasure ratings were analyzed in the same way as stylistic success ratings and were also significant. Of note, whereas expert stylistic success ratings showed more concordance than those of concertgoers, it was the other way around for ratings of aesthetic pleasure. The large age gap between the two groups of judges should also be noted, because this could be influencing between-group differences in performance. However, by keeping data from the two groups separate, we mitigate problems that could arise from the age gap.
4.3.2 Answer to evaluation question 1 (success)
Because the ratings of stylistic success are mainly significantly positively correlated, it is reasonable to take the mean rating of stylistic success for each excerpt. These are shown in Table 2, along with the percentage of judges who classified each excerpt correctly, and the percentage of judges who classified each excerpt as a Chopin mazurka. The first column of Table 2 gives the stimulus number (details in Section 4.2).
Table 2. Mean stylistic success ratings, percentage of judges distinguishing correctly, and percentage of judges classing a stimulus as a Chopin mazurka

Note: The stimulus number corresponds to the list given in Section 4.2. C'Goers, Concertgoers.
It is possible to make general observations about the stylistic success ratings in Table 2. For instance, Clara Schumann's mazurka (stimulus 7) is rated by the expert judges as more stylistically successful than any of Chopin's mazurkas, and more successful than any of those from EMI. All but one of the excerpts from System B* (stimuli 28–32) are rated by the expert judges as more stylistically successful than the amateur mazurka (stimulus 12). Both Chopin's mazurkas and those from EMI appear to be rated as more stylistically successful than those of Systems A, B, and B*. To formally test for differences in stylistic success, we conducted an analysis of variance (ANOVA) using indicator variables for mazurka-generating systems. One ANOVA was conducted for concertgoer judges, and another for experts. The contrasts for the ANOVAs are given in Table 3, and they should be interpreted as follows. If the number in the ith row, jth column of the table is positive (negative), then the jth source produces excerpts that are rated as more (less) stylistically successful than those of the ith source. The magnitude of the number indicates the significance of this difference in stylistic success. For instance, the concertgoers judged mazurkas from EMI as more stylistically successful than those of System B* (as 4.88 > 0).
Table 3. Contrasts for two ANOVAs, using concertgoer ratings of stylistic success or expert ratings as the response variables

Note: The significance of the regression is reported in the bottom row of each table; s is the error standard deviation.
*p = 0.001.
Table 3 suggests that Chopin's mazurkas are more stylistically successful than those of Systems A, B, and B*. Mazurkas from EMI rate significantly higher for stylistic success than Systems A, B, and B* as well. The excerpts from EMI are not rated significantly different from the Chopin mazurkas. It would have been encouraging to see the contrasts between System B* and System A, and between System B* and System B, emerge as statistically significant, but they did not. A significant contrast between System B* and System A would constitute evidence that pattern inheritance leads to a significant increase in stylistic success. A significance contrast between System B* and System B would constitute evidence that tightening the parameters leads to a significant increase in stylistic success. This contrast shows an increase (of 0.429 for the concertgoers and 0.421 for the experts), but it is not significant at the 0.05 level.
To check for ordering effects, we investigated the proportion of times that a stimulus from EMI was misclassified when it followed a stimulus from Systems A, B, or B* (p 1 = 0.89), compared to the proportion of times that an EMI stimulus was misclassified following a Chopin mazurka (p 2 = 0.84). The difference between p 1 and p 2 was not significant (z = 0.67, p = 0.51), allaying our concerns about ordering effects.
4.3.3. Answer to evaluation Question 2 (distinguishing)
If a judge guesses when distinguishing between Chopin mazurka, human other, and computer based, the probability of distinguishing 16 or more of the 32 excerpts correctly is less than 0.05: binomial, B(32, 1/3). Eight out of 16 concertgoer judges scored better than chance, and 15 out of 16 expert judges.Footnote 12 Low percentages in columns 4 and 5 of Table 2 indicate that judges had trouble distinguishing an excerpt correctly as Chopin mazurka, human other, or computer based. EMI excerpts do particularly well, with none of excerpts 13–18 being classified as computer based by judges more than 25% of the time.
4.3.4. Answer to evaluation Question 4 (correlations)
For the majority of judges, a judge's ratings of stylistic success and aesthetic pleasure are significantly positively correlated. This does not necessarily imply that judges failed to understand the nuanced difference between stylistic success and aesthetic pleasure. More likely, this correlation is due to there being only a couple of excerpts (Couperin Rondeau and Brahms Romance) that one would expect to receive low stylistic success ratings but that are eminently aesthetically pleasing. If the analysis is limited to stylistic success and aesthetic pleasure ratings for the Couperin Rondeau and the Brahms Romance, correlation between stylistic success and aesthetic pleasure is not significant at the 0.05 level.
To investigate whether judges appear to be biased in favor or against what they perceive as computer-based stimuli, but which are genuine Chopin mazurkas, a two-sample t test was conducted. The data consist of judges' stylistic success ratings, restricted to Stimuli 1–6 (Chopin mazurkas). The first sample contains ratings where judges misclassified stimuli as computer based. The data associated with participant 4 were removed from this analysis, because they revealed a strong bias against all stimuli perceived as computer based. Even after this removal, the result of the test suggests judges do appear to be biased against genuine Chopin mazurkas that they perceive as computer-based stimuli [t (184) = −3.11, p < 0.01].
4.3.5. Answer to evaluation Question 5 (attributes)
For stimuli from Systems A, B, and B*, the experts made a total of 65 negative textual comments, which were assigned to six categories, first used by Pearce and Wiggins (Reference Pearce, Wiggins, Cardoso and Wiggins2007): 12% pitch range, 11% melody, 43% harmony, 3% phrasing, and 6% rhythm, leaving 25% categorized as “other.” Among the “other” category were some comments on texture and repetition, but not enough to warrant extra categories. Of 27 positive comments, the most highly represented of the categories was rhythm. The concertgoer comments on stylistic success ratings exhibited similar profiles for positive and negative categories. The results suggest harmonic aspects of Racchman-Oct2010 and Racchmaninof-Oct2010 require most attention.
Are certain musical attributes of an excerpt useful predictors of its stylistic success? A model for relating judges' ratings of stylistic success to musical attributes was determined using stepwise selection (as in Pearce & Wiggins, Reference Pearce, Wiggins, Cardoso and Wiggins2007).Footnote 13 Explanatory variables consisted of pitch center, signed pitch range, unsigned pitch range, small intervals, intervallic leaps, chromatic, cadential, rhythmic density, rhythmic variability, and metric syncopation (Pearce & Wiggins, Reference Pearce, Wiggins, Cardoso and Wiggins2007), as well as eight new attributes based on a chord labeling algorithm called HarmAn (Pardo & Birmingham, Reference Pardo and Birmingham2002), keyscapes that display the output of a key finding algorithm (Sapp, Reference Sapp2005), and general metric weights (Volk, Reference Volk2008). Definitions of the variables appear in Collins (Reference Collins2011, his appendix C). The model that resulted from stepwise selection was
 $$\eqalign{\hbox{rating} & = 0.56-6.92 \times \hbox{rel}\_\hbox{metric}\_ \hbox{weight}\_ \hbox{entropy}\cr & \quad -0.05 \times \hbox{unsigned}\_ \hbox{pitch}\_ \hbox{range} \cr & \quad -0.88 \times \hbox{metric}\_ \hbox{syncopation} \cr & \quad + 4.97 \times \hbox{max}\_ \hbox{metric}\_ \hbox{weight}\_ \hbox{entropy} \cr & \quad - 1.05 \times \hbox{keyscape}\_ \hbox{entropy} - 0.11 \times \hbox{pitch}\_ \hbox{center} \cr & \quad - 1.50 \times \hbox{mean}\_ \hbox{metric}\_\hbox{weight}\_ \hbox{entropy}\comma \;}$$
$$\eqalign{\hbox{rating} & = 0.56-6.92 \times \hbox{rel}\_\hbox{metric}\_ \hbox{weight}\_ \hbox{entropy}\cr & \quad -0.05 \times \hbox{unsigned}\_ \hbox{pitch}\_ \hbox{range} \cr & \quad -0.88 \times \hbox{metric}\_ \hbox{syncopation} \cr & \quad + 4.97 \times \hbox{max}\_ \hbox{metric}\_ \hbox{weight}\_ \hbox{entropy} \cr & \quad - 1.05 \times \hbox{keyscape}\_ \hbox{entropy} - 0.11 \times \hbox{pitch}\_ \hbox{center} \cr & \quad - 1.50 \times \hbox{mean}\_ \hbox{metric}\_\hbox{weight}\_ \hbox{entropy}\comma \;}$$with test statistic F (7, 24) = 17.34, p < 0.001, and s = 0.70 as the error standard deviation. The stepwise model has a value of R 2 = 0.83, meaning that it explains 83% of the variation in ratings of stylistic success. This model was built in order to suggest specific variables for new constraints in future work, so it is discussed again in the next section. It is worth saying here that the metric variables in (15) may be doing more to differentiate human-composed music of other periods from Chopin mazurkas than to differentiate the output of Racchman-Oct2010 or Racchmaninof-Oct2010 from Chopin mazurkas: a coefficient value of −6.92 for relative metric weight entropy (RMWE), for instance, means that excerpts with either unusually high or low syncopation (compared to the mean syncopation level of the stimulus set) tend to receive lower (minus sign) ratings of stylistic success. This applies to highly syncopated excerpts such as the Schoenberg (RMWE = 0.505) or unsycnopated excerpts such as the Couperin (RMWE = 1.081) but less so to Racchman-Oct2010 or Racchmaninof-Oct2010 output (e.g., RMWE for Stimuli 20 and 29 are 0.096 and 0.012, respectively). Keyscape entropy, which quantifies the extent to which an excerpt establishes a sense of key, is probably the first variable of interest in (15).
5. DISCUSSION
Of perennial interest to researchers within computational creativity is how cultural artifacts are conceived and constructed. Music compositions, an example of such artifacts, are particularly intriguing because, as Cook (Reference Cook1987) remarks, they can move “people involuntarily, even subliminally, and yet all this is done by means of the most apparently precise and rational techniques … a few combinations of pitches, durations, timbres and dynamic values can unlock the most hidden contents of man's spiritual and emotional being” (p. 1). It is fair to say that these precise and rational techniques (these combinations) are not yet fully understood, but that the field of computational creativity may shed some light on them in due course.
In this respect, the present paper's main contribution has been to specify how to extract repetitive structure from an existing composition (source design), and transfer that repetitive structure to a new composition (target design). Most often, repetitive structure in music is hierarchical. Figure 10, for instance, shows a source design in which pattern P 2,2 nests within P 1,1. This hierarchical structure is maintained in the target design, shown in Figure 12 (bar 5, labeled 1, is nested within a segment in bars 5–8 that repeats in bars 9–12). More generally, motifs may nest within themes, which themselves may nest within repeated sections. Although inheritance of patterns has been mentioned before as a concept (Hofstadter writing in Cope Reference Cope2001, p. 49) and applied to some extent to melodic material (Shan & Chiu, Reference Shan and Chiu2010), the current work achieves new standards in terms of application to full textures, detailed description of the method, and releasing the source code.Footnote 14 We hope that these steps encourage other researchers from engineering, engineering education, and design to engage in the open, challenging problem of modeling musical creativity.
Our system Racchmaninof-Oct2010, which we cast as a within-domain analogy-based design system (Vattam et al., Reference Vattam, Helms, Goel, Gero and Goel2008; Goel et al., Reference Goel, Rugaber and Vattam2009), begins by borrowing abstract information about the most nested repetitive element in the source design, and generating material for the target design that is consistent with this information. The next most nested element in the source design is then addressed, causing more material to be generated for the target design while respecting any material that is already in place. Generation of this small-scale or local material is achieved using a Markov chain constrained by critics, and the process continues until the large-scale structure of the target design is complete. Because the borrowing is on an abstract structural level, our “analogous designs do not share superficial commonalities … [rather] the causal relations provide the deep understanding of the design and provide a platform for analogical reasoning” (Qian & Gero, Reference Qian and Gero1996, p. 311). As such, researchers in engineering and/or computational creativity whose designs exhibit hierarchical structure may benefit from reflecting upon the current approach. Qian and Gero (Reference Qian and Gero1996) were concerned primarily with cross-domain knowledge, so it would seem appropriate to investigate whether a general description of hierarchical repetitions could be applied beyond the domain of music, to the design of machines, architecture, poetry, narrative, and visual art.
5.1. OUTCOMES OF THE LISTENING STUDY
Two new models of musical style, Racchman-Oct2010 and Racchmaninof-Oct2010, were described and evaluated alongside EMI (Cope, Reference Cope1996, Reference Cope2005), which was evaluated rigorously here for the first time. The evaluation produced some encouraging results. As shown in Table 2, all but one of the excerpts from System B* (Racchmaninof-Oct2010, Stimuli 28–32) are rated by the expert judges as more stylistically successful than the amateur mazurka (Stimulus 12). Stimulus 20 (Racchman-Oct2010, System A) was miscategorized as a Chopin mazurka by 56% of concertgoer judges and 25% of expert judges, and stimulus 28 (System B*) was miscategorized similarly by 25% of concertgoer judges. Together, these results suggest that some aspects of musical style are being modeled well by Racchman-Oct2010 and Racchmaninof-Oct2010, and that some of the generated passages can be considered on a par with human-composed music. Analysis of open-ended textual responses suggests phrasing and rhythm are aspects of the mazurka style that are well modeled by our system.
The results also indicate potential for future improvements. Chopin mazurkas are rated significantly higher in terms of stylistic success than those of Systems A (Racchman-Oct2010), B, and B* (both Racchmaninof-Oct2010). The mazurkas from EMI rate significantly higher for stylistic success than Systems A, B, and B* as well. This result indicates that we were unable to replicate the stylistic success of EMI's output, based on available descriptions and related code. This was an ambitious aim (excerpts from EMI were not rated significantly different from the Chopin mazurkas), but the comparative evaluation and analysis of results has enabled us to identify specific areas for future improvements (in particular, the tracking and control of tonal harmony). Identification of this area arose from analysis of judges' open-ended textual responses, and from keyscape entropy (measuring the extent to which an excerpt establishes a key center) being one of the variables to enter the stepwise regression (15). In terms of features of EMI that lead to its output receiving higher ratings, it should be possible to implement a version of the signatures component described by Cope (Reference Cope2005), using more up-to-date algorithms (Collins et al., Reference Collins, Thurlow, Laney, Willis, Garthwaite, Downie and Veltkamp2010), and this may help to bridge the gap. The SPEAC component is more difficult to implement, because accounts of labeling assignments differ between Cope (Reference Cope1996, p. 68) and Cope (Reference Cope2005, pp. 227–237).
The results showed no statistically significant difference between stylistic success ratings for patterned computer-generated stimuli (from Systems B and B*, Racchmaninof-Oct2010) versus nonpatterned (System A, Racchman-Oct2010). However, this does not mean that repeated patterns are unimportant for modeling musical style. Some judges were sensitive to repetition: “It sounds like a human composer in that it is unified” (expert judge 3 on Stimulus 28 from System B*); “First half appears to be repeated” (concertgoer judge 16 on the amateur mazurka, Stimulus 12). A de facto argument can be made that inheritance of form leads to stylistically superior output (because such output is closer in structure to that of Chopin's mazurkas), but perhaps other aspects of style (e.g., harmony or melody) need to be better modeled in the first place, before judges use the presence or absence of repeated patterns as a basis for rating stylistic success. Perception of repeated patterns may also require deeper engagement with a piece. Judges had an hour to rate 32 excerpts of music, and perhaps a listener is unlikely to gain an appreciation of an excerpt's repeated patterns when only a couple of minutes will be spent listening to and thinking about it. Another possible reason why there was no significant difference due to pattern inheritance is that System B* involves generating music over several time intervals, trying to stitch an imperceptible seam between forward and backward processes for each interval. Each excerpt from System A had only one seam. It would be worth examining whether seams are perceived by judges as stylistic shortcomings, because if so, ratings for System B* could suffer more than ratings for System A.
In terms of distinguishing between human-composed and computer-generated music, what do the judges' comments tell us about listening strategies? Similar comments from judges sometimes lead to different decisions, perhaps reflecting the difficulty of articulating listening strategies that were used to make distinctions: Stimulus 1 (Chopin opus 24 number 4) was categorized by concertgoer judge 5 as human other, observing that “the intro seemed not in character”; in contrast, the same stimulus was categorized correctly as Chopin mazurka by expert judge 6, observing that the stimulus is “harmonically … complex but also goes where one hopes it will. Slightly unusual opening (solo right hand), but seems to get going after this.” There was also a mixture of holistic and instantaneous listening strategies used: a holistic remark from expert judge 7 on Stimulus 27 from Racchmaninof-Oct2010 was that “all the gestures in themselves work, but the way they are put together certainly does not”; an instantaneous decision was made by expert judge 3 for the same stimulus, remarking that “I thought it was Chopin at first, but there is a rhythm that leads me to believe it isn't. Between bars 7–8.”
Some comments revealed lack of familiarity with the mazurka style. For instance, parallel fifths are more common in Chopin mazurkas (see Fig. 6) than in J.S. Bach's chorale harmonizations, but one judge observed “dissonant downbeats, parallel fifths—eek!” in Stimulus 32 from Racchmaninof-Oct2010. As another example, the third beat of the bar in a Chopin mazurka might not contain any new notes, because some mazurkas emphasize the second beat. However, one judge categorized Stimulus 28 from Racchmaninof-Oct2010 as human other, perhaps because “the missing third beat in bars one and three sound[s] untypical.” It is interesting that perceived randomness of a stimulus was a feature on which judges commented, but they were unsure whether or not it indicated a computer-based excerpt: one judge observed, “it sounds too random to be computer generated,” of Stimulus 19 from Racchman-Oct2010, whereas another judge said of the same stimulus that the “rhythm [was] mostly OK but the random melodic line seems computerish.” Overall, the above quotations suggest that sometimes judges come to the correct decision for the wrong reasons. These situations highlight the importance of eliciting stylistic success ratings and categorization decisions separately, as well as open-ended comments that justify the responses.
6. LIMITATIONS AND FUTURE WORK
One clear candidate for future work is to use the models Racchman-Oct2010 and Racchmaninof-Oct2010 with different music databases (e.g., Haydn minuets). It is an open question as to whether the same model can generate stylistically successful passages for different databases. Transition list sparsity is another topic worthy of further investigation. For instance, we will compare state spaces over pitch collections and chord spacings (so far only the latter has been implemented), and quantify the sparsity in each case. The sparser a transition list, the more likely it is that a generated sequence will replicate original data. If replication–avoidance strategies are being used, then these will be employed more often for sparser lists, and so the runtime for an algorithm associated with a sparse transition list will typically be longer.
Judges' ratings of stimuli were used to build a model (15), in order to suggest specific variables for new constraints in future versions of Racchman and Racchmaninof (as in Pearce & Wiggins, Reference Pearce, Wiggins, Cardoso and Wiggins2007). The variable keyscape entropy emerged as a candidate for a new constraint that monitors the establishment of key. Because constraints for pitch range and mean pitch already exist in Systems A, B, and B*, the presence of the variables unsigned pitch range and pitch center in (15) suggests that parameters for these constraints were too relaxed. Further work is required in order to investigate whether such constraints can be tightened (and new constraints added), and still have the models produce output within several hours.
Using an existing music database, will an algorithm ever be capable of generating compositions that are judged as stylistically successful compared to pieces from the intended style? With a success rate dependent on the difficulty of the composition brief, our answer is a tentative “yes.” What are the implications for human musical creativity? A revised version of the algorithm could potentially be added to standard notation software, allowing users to request novel fragments or continuations from diverse styles (Cope, Reference Cope1997a; Ju & Leifer, Reference Ju and Leifer2008; Collins & Coulon, Reference Collins and Coulon2012; Keller et al., Reference Keller, Toman-Yih, Schofield, Merritt, Maher, Hammond, Pease, Péréz y Péréz, Ventura and Wiggins2012; Maxwell et al., Reference Maxwell, Eigenfeldt, Pasquier and Gonzalez Thomas2012). The way in which humans create music can be enhanced, not inhibited, by the capability of automatically generating stylistic compositions, perhaps in a more iterative or implicit fashion compared to how current software such as PG Music's Band in a Box or Microsoft's Songsmith enable nonexperts to compose. For humans learning the art of music creation, we see exciting possibilities involving algorithms for automated stylistic composition.
ACKNOWLEDGMENTS
This research was undertaken during the first author's EPSRC-funded studentship at the Open University, United Kingdom. We are grateful to those who took part in the study described here, as well as the pilot study. Thank you to Germa Adan for recruiting so many participants. We thank three anonymous reviewers for their insightful comments, which have helped us to improve the manuscript.
Tom Collins is a Researcher in the Faculty of Technology at De Montfort University, United Kingdom. He worked as a postdoctoral scholar at the Department for Computational Perception, Johannes Kepler University Linz, Austria, and the Center for Mind and Brain, University of California, Davis. He undertook his PhD research at the Faculty of Mathematics, Computing and Technology, the Open University, and holds BA degrees in music, and mathematics and statistics. Tom's main research areas are music psychology and cognitive psychology more generally, music informatics research, and computational creativity.
Robin Laney is a Senior Lecturer at the Open University, United Kingdom. He has a background in software engineering and research interests in computational musicology and music computing more generally.
Alistair Willis is a Senior Lecturer in computing at the Open University, United Kingdom. His main research interests are in computational linguistics and wider questions in artificial intelligence. Before joining the Open University, he worked in automated software engineering at Philips Research.
Paul Garthwaite is a Professor of statistics at the Open University, United Kingdom. He has a long-standing interest in subjective probability assessment: the theoretical development of elicitation methods, experimental work with substantive experts to improve methods, and their application in practice. Other research areas include Bayesian methods, Monte Carlo and bootstrap methods, and interdisciplinary research, notably in animal and human nutrition, medicine, and psychology.