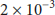1. Introduction
The influence of chain reactions on the rate R1 of p-11B fusion reaction
is discussed since 1973 [Reference Weaver, Zimmerman and Wood1–Reference Gruenwald12]. One of the chain reactions consists of the scattering of at least one of the three alpha particles, generated by reaction (1), on proton(s) with acceleration of the proton(s) to kinetic energies, corresponding to a relatively high cross-section σ1 for reaction (1) and the subsequent participation of the accelerated proton(s) in this reaction [Reference Weaver, Zimmerman and Wood1, Reference Eliezer, Hora, Korn, Nissim and Martinez Val4, Reference Shmatov6–Reference Gruenwald12]. According to [Reference Weaver, Zimmerman and Wood1], at the temperature of 150–350 keV and the density of 1016–1026 cm−3, this chain reaction and other “nonthermal” effects result in an increase in R 1 on 5–15%. The type of particles with such densities was not mentioned [Reference Weaver, Zimmerman and Wood1], but this detail is not essential because in plasma under consideration, the densities of all particles are comparable [Reference Shmatov8]. According to [Reference Belyaev, Krainov, Zagreev and Matafonov2–Reference Eliezer, Hora, Korn, Nissim and Martinez Val4, Reference Eliezer, Hora, Korn, Nissim and Martinez Val7, Reference Eliezer and Martinez-Val9, Reference Eliezer, Schweitzer, Nissim and Martinez Val10, Reference Gruenwald12], at least if special measures are taken, the increase in R 1 due to the chain reactions can be so high that it will provide the possibility of the use of reaction (1) for power production. The negative results of analysis of such assumptions from [Reference Belyaev, Krainov, Zagreev and Matafonov2–Reference Eliezer, Hora, Korn, Nissim and Martinez Val4] are presented in [Reference Shmatov5, Reference Shmatov6, Reference Shmatov8, Reference Belloni11].
In 2020, Eliezer and Martinez-Val [Reference Eliezer and Martinez-Val9] and Eliezer et al. [Reference Eliezer, Schweitzer, Nissim and Martinez Val10] proposed p-11B fusion scenarios with the influence of electric and magnetic fields on protons and alpha particles in the gas medium. The main idea of the proposal is that during some time periods, time-dependent electric field should compensate approximately for the transfer of kinetic energy εp of a proton with
![]() , where
, where
![]() is εp corresponding to the largest value of σ1 for the collision of proton with the nucleus of 11B in the rest, to the medium and for transfer of the kinetic energy of the alpha particle to the medium [Reference Eliezer and Martinez-Val9, Reference Eliezer, Schweitzer, Nissim and Martinez Val10]. This compensation should increase the probability of participation of the protons in reaction (1) and that of “useful” acceleration of protons due to the scattering of alpha particles on them. The magnetic field should provide the realization of these scenarios in reactors with acceptable sizes [Reference Eliezer and Martinez-Val9, Reference Eliezer, Schweitzer, Nissim and Martinez Val10]. Below, it is shown that in the scenario proposed in [Reference Eliezer, Schweitzer, Nissim and Martinez Val10], the ratio g of energy release of reaction (1) to the average value
is εp corresponding to the largest value of σ1 for the collision of proton with the nucleus of 11B in the rest, to the medium and for transfer of the kinetic energy of the alpha particle to the medium [Reference Eliezer and Martinez-Val9, Reference Eliezer, Schweitzer, Nissim and Martinez Val10]. This compensation should increase the probability of participation of the protons in reaction (1) and that of “useful” acceleration of protons due to the scattering of alpha particles on them. The magnetic field should provide the realization of these scenarios in reactors with acceptable sizes [Reference Eliezer and Martinez-Val9, Reference Eliezer, Schweitzer, Nissim and Martinez Val10]. Below, it is shown that in the scenario proposed in [Reference Eliezer, Schweitzer, Nissim and Martinez Val10], the ratio g of energy release of reaction (1) to the average value
![]() of the energy spent for the initiation of one reaction (1) will be unacceptably low for power production.
of the energy spent for the initiation of one reaction (1) will be unacceptably low for power production.
2. The Upper Boundary of g
Eliezer et al. [Reference Eliezer, Schweitzer, Nissim and Martinez Val10] analyzed the situations when reaction (1) occurs in gaseous H3
11B or other hydride of 11B with a density of 1019 cm−3 or of the order of 1019 cm−3 and temperature of about 1 eV or few eV. Ionization of this gas is supposed negligible [Reference Eliezer, Schweitzer, Nissim and Martinez Val10]. Since a free molecule of H3B does not exist and at the temperature above 700°C all hydrides of boron dissociate into boron and hydrogen [Reference Vasilevskiy13], we will estimate the lowest boundary
![]() of
of
![]() in gas medium consisting of atoms of 11B with the density
in gas medium consisting of atoms of 11B with the density
and molecules of H2 with the density
At the conditions described in [Reference Eliezer, Schweitzer, Nissim and Martinez Val10], the medium containing atoms of boron and molecules of hydrogen will also contain atoms of hydrogen and ions, but this is not essential for the analysis of the acceptability of attainable values of g for power production. The ratio
![]() corresponds to the ratio of the numbers of nuclei of 11B and protons in the nonexisting free molecule of H3
11B discussed in [Reference Eliezer, Schweitzer, Nissim and Martinez Val10]. The choice of
corresponds to the ratio of the numbers of nuclei of 11B and protons in the nonexisting free molecule of H3
11B discussed in [Reference Eliezer, Schweitzer, Nissim and Martinez Val10]. The choice of
![]() corresponds to an example presented on page 5 of Reference [Reference Eliezer, Schweitzer, Nissim and Martinez Val10] and is mainly important for an estimate of the typical proton path
corresponds to an example presented on page 5 of Reference [Reference Eliezer, Schweitzer, Nissim and Martinez Val10] and is mainly important for an estimate of the typical proton path
![]() , corresponding to one reaction (1). The estimate of
, corresponding to one reaction (1). The estimate of
![]() presented below yields that this parameter is independent of
presented below yields that this parameter is independent of
![]() .
.
In the situation under consideration, the change
![]() of εp on proton path dx is given approximately by
of εp on proton path dx is given approximately by
where e is the proton charge, E is the strength of the electric field, and
![]() and
and
![]() are the parameters describing the transfer of εp to molecules of hydrogen and atoms of boron, respectively. The parameter
are the parameters describing the transfer of εp to molecules of hydrogen and atoms of boron, respectively. The parameter
![]() was calculated as
was calculated as
where A H is the atomic mass of hydrogen, mu is the atomic mass unit, and
![]() is the stopping power of molecular hydrogen for proton. The parameter
is the stopping power of molecular hydrogen for proton. The parameter
![]() was calculated as
was calculated as
where A Be is the atomic mass of beryllium,
![]() is its stopping power for proton, A C is the atomic mass of carbon, and
is its stopping power for proton, A C is the atomic mass of carbon, and
![]() is the stopping power of amorphous carbon with the density of 2 g/cm3 for proton. The values of
is the stopping power of amorphous carbon with the density of 2 g/cm3 for proton. The values of
![]() ,
,
![]() , and
, and
![]() from [Reference Berger, Coursey, Zuker and Chang14] were used.
from [Reference Berger, Coursey, Zuker and Chang14] were used.
The parameter
![]() was approximated by (6) due to the absence of data on the stopping power of boron for proton in [Reference Berger, Coursey, Zuker and Chang14]. This equation corresponds to the assumption that the product P of the stopping power of the medium, consisting of atoms or molecules of one chemical element with atomic number Z, on the atomic mass of this element depends on Z approximately linearly and, therefore,
was approximated by (6) due to the absence of data on the stopping power of boron for proton in [Reference Berger, Coursey, Zuker and Chang14]. This equation corresponds to the assumption that the product P of the stopping power of the medium, consisting of atoms or molecules of one chemical element with atomic number Z, on the atomic mass of this element depends on Z approximately linearly and, therefore,
where ΔZ is a small natural number, for example, unity or two. In order to demonstrate that at least in some situations, the accuracy of (7) is rather high, let us compare
![]() MeV cm2 g−1 and
MeV cm2 g−1 and
![]() MeV cm2 g−1, calculated using
MeV cm2 g−1, calculated using
![]() from [Reference Berger, Coursey, Zuker and Chang14], with the same parameters, calculated using (7) and
from [Reference Berger, Coursey, Zuker and Chang14], with the same parameters, calculated using (7) and
![]() . Substituting
. Substituting
![]() and the stopping power of molecular oxygen for proton from [Reference Berger, Coursey, Zuker and Chang14] into (7), we obtain
and the stopping power of molecular oxygen for proton from [Reference Berger, Coursey, Zuker and Chang14] into (7), we obtain
![]() MeV cm2 g−1 and
MeV cm2 g−1 and
![]() MeV cm2 g−1. Thus, in these cases, the relative accuracy of (7) is better than 1%. This allows us to assume that at 600 keV
MeV cm2 g−1. Thus, in these cases, the relative accuracy of (7) is better than 1%. This allows us to assume that at 600 keV
![]() keV (see below), the relative accuracy of (6) is of the order of 1% or even better.
keV (see below), the relative accuracy of (6) is of the order of 1% or even better.
According to [Reference Nevins and Swain15],
![]() keV and
keV and
Let us denote the value of E corresponding to the condition
![]() , i.e., to the almost exact compensation of the transfer of kinetic energy of protons to the gas medium by the electric field, as E 0. This value depends on εp ((4)). Equations (2)–(6) and (8)) yield that at
, i.e., to the almost exact compensation of the transfer of kinetic energy of protons to the gas medium by the electric field, as E 0. This value depends on εp ((4)). Equations (2)–(6) and (8)) yield that at
![]() ,
,
![]() cm,
cm,
![]() kV/cm,
kV/cm,
![]() , and
, and
![]() .
.
At
![]() ,
,
![]() and
and
![]() decrease with increasing εp ((5) and (6) and [Reference Eliezer, Schweitzer, Nissim and Martinez Val10, Reference Berger, Coursey, Zuker and Chang14]). This results, in particular, in the impossibility to provide a stable motion of proton with such kinetic energy at constant E [Reference Eliezer, Schweitzer, Nissim and Martinez Val10]. The highest value of
decrease with increasing εp ((5) and (6) and [Reference Eliezer, Schweitzer, Nissim and Martinez Val10, Reference Berger, Coursey, Zuker and Chang14]). This results, in particular, in the impossibility to provide a stable motion of proton with such kinetic energy at constant E [Reference Eliezer, Schweitzer, Nissim and Martinez Val10]. The highest value of
![]() corresponds to
corresponds to
![]() keV,
keV,
![]() kV/cm,
kV/cm,
![]() cm,
cm,
![]() GeV, and
GeV, and
![]() . These values of
. These values of
![]() and
and
![]() can serve as
can serve as
![]() and the upper boundary of g, respectively. It should be emphasized that the real value of
and the upper boundary of g, respectively. It should be emphasized that the real value of
![]() can be much greater than
can be much greater than
![]() due to acceleration of secondary charged particles, i.e., molecular ions of hydrogen, protons, ions of 11B, and electrons created by the fast protons considered above and alpha particles, etc. [Reference Nagy and Végh16–Reference Raizer18]. At sufficiently high temperature, the acceleration of electrons and ions arising due to thermal ionization can also be important. The problem of the possibility of electric breakdown in the gas medium under consideration can probably be solved only experimentally. The presented estimate of
due to acceleration of secondary charged particles, i.e., molecular ions of hydrogen, protons, ions of 11B, and electrons created by the fast protons considered above and alpha particles, etc. [Reference Nagy and Végh16–Reference Raizer18]. At sufficiently high temperature, the acceleration of electrons and ions arising due to thermal ionization can also be important. The problem of the possibility of electric breakdown in the gas medium under consideration can probably be solved only experimentally. The presented estimate of
![]() corresponds to the assumption that the magnetic field prevents the acceleration of electrons and relatively slow molecular ions of hydrogen, protons, and ions of 11B by the electric field. However, the accuracy of this estimate is sufficient for the reliable qualitative conclusion about the unacceptability of the scenario proposed in [Reference Eliezer, Schweitzer, Nissim and Martinez Val10] for power production: in any case,
corresponds to the assumption that the magnetic field prevents the acceleration of electrons and relatively slow molecular ions of hydrogen, protons, and ions of 11B by the electric field. However, the accuracy of this estimate is sufficient for the reliable qualitative conclusion about the unacceptability of the scenario proposed in [Reference Eliezer, Schweitzer, Nissim and Martinez Val10] for power production: in any case,
![]() will include
will include
![]() and, therefore, g will be too low. The reason is that the efficiency of the use of any fusion reaction for power production will be determined, in particular, by the cost of electricity [Reference Teller19, Reference Smirnov, Subbotin and Sharkov20]. According to [Reference Smirnov, Subbotin and Sharkov20], for the inertial fusion energy power plant with conversion of fusion energy into thermal energy and subsequent conversion of 30–35% of the latter into electricity, the cost of electricity will be acceptable when the product of the target gain on the driver efficiency ηd exceeds ten. The target gain is the ratio of fusion energy release of one microexplosion to the energy delivered to the target for ignition of the microexplosion [Reference Smirnov, Subbotin and Sharkov20]. This parameter should exceed ten even if ηd is close to unity and is an analog of the parameter g. Thus, g of the order of 10−3 and less is not sufficient for power production involving conversion of fusion energy into thermal energy. Note that Weaver et al. [Reference Weaver, Zimmerman and Wood1] discussed briefly the potential feasibility of power production in the regime of subignition operation corresponding to
and, therefore, g will be too low. The reason is that the efficiency of the use of any fusion reaction for power production will be determined, in particular, by the cost of electricity [Reference Teller19, Reference Smirnov, Subbotin and Sharkov20]. According to [Reference Smirnov, Subbotin and Sharkov20], for the inertial fusion energy power plant with conversion of fusion energy into thermal energy and subsequent conversion of 30–35% of the latter into electricity, the cost of electricity will be acceptable when the product of the target gain on the driver efficiency ηd exceeds ten. The target gain is the ratio of fusion energy release of one microexplosion to the energy delivered to the target for ignition of the microexplosion [Reference Smirnov, Subbotin and Sharkov20]. This parameter should exceed ten even if ηd is close to unity and is an analog of the parameter g. Thus, g of the order of 10−3 and less is not sufficient for power production involving conversion of fusion energy into thermal energy. Note that Weaver et al. [Reference Weaver, Zimmerman and Wood1] discussed briefly the potential feasibility of power production in the regime of subignition operation corresponding to
![]() . In any case, g of the order of 10−3 and less seems to be too low even for this regime.
. In any case, g of the order of 10−3 and less seems to be too low even for this regime.
Note also that in the scenario proposed in [Reference Eliezer, Schweitzer, Nissim and Martinez Val10], the acceleration of alpha particles, if it is not suppressed by the magnetic field, will not provide the effective acceleration of protons and, therefore, will serve mainly as a process increasing
![]() . This can be shown using equations, similar to (4)–(6), and the data from [Reference Eliezer, Schweitzer, Nissim and Martinez Val10, Reference Belloni11, Reference Berger, Coursey, Zuker and Chang14, Reference Landau and Lifshitz21] for the analysis of the motion of alpha particles and the transfer of their kinetic energy to protons. The compensation of deceleration of protons in the gas medium consisting mainly of atoms of 11B will also not provide sufficiently high values of g: at
. This can be shown using equations, similar to (4)–(6), and the data from [Reference Eliezer, Schweitzer, Nissim and Martinez Val10, Reference Belloni11, Reference Berger, Coursey, Zuker and Chang14, Reference Landau and Lifshitz21] for the analysis of the motion of alpha particles and the transfer of their kinetic energy to protons. The compensation of deceleration of protons in the gas medium consisting mainly of atoms of 11B will also not provide sufficiently high values of g: at
![]() , the highest value of
, the highest value of
![]() corresponds to
corresponds to
![]() keV,
keV,
![]() GeV, and
GeV, and
![]() .
.
3. Conclusion
The scenario proposed in [Reference Eliezer, Schweitzer, Nissim and Martinez Val10] cannot be used for effective power production due to the very low attainable g, the upper boundary of which is about 10−3. A decrease in
![]() down to zero can result only in an approximately two-fold increase in the upper boundary of g. The real value of g can be much less than its upper boundary.
down to zero can result only in an approximately two-fold increase in the upper boundary of g. The real value of g can be much less than its upper boundary.
Data Availability
The data used to support the findings of this study are included within the article.
Conflicts of Interest
The author declares that there are no conflicts of interest.
Acknowledgments
The author would like to thank the company HB11 Energy Pty Ltd. for the payment of APC for the publication of this manuscript.