A short history of scientific investigations on glaciers

Abstract

Scientific investigations on valley glaciers engaged some of the greatest natural philosophers of the nineteenth century. Among these, Louis Agassiz has unique importance for he personifies the transition from the protoscientific period of de Saussure and Scheuchzer to the scientific one of Forbes and his successors. In this brief history I have attempted to connect the achievements of the past 50 years with the aspirations of our predecessors.

“The air immediately above me seemed filled with rainbow-dust, for the ice-needles glittered with a thousand hues under the decomposition of light upon them, while the dark storm in the valley below offered a strange contrast to the brilliancy of the upper region in which I stood”.

–Louis Agassiz

“To myself, I confess that this now appears the strongest argument of all for considering the glacier as a united mass like a river, in which there is a nice equilibrium between the force of gravitation, acting by hydrostatic pressure, and the molecular resistance of the semi-solid; the degree of regularity of the law which connects the partial movements is wonderful, and I maintain that it is inexplicable except upon the viscous theory”.

–James D. Forbes

Introduction

The tradition of glacier studies that we inherit draws upon two great legacies of the eighteenth and nineteenth centuries: classical physics and romantic enthusiasm for Nature. This compelling mixture of the classical and romantic has drawn many of us to glaciology and brings both substance and vitality to the science. It is easy to undervalue the romantic contribution, but in glaciology it would be a mistake to do so. Love of the mountains drew great scientists like Agassiz, Forbes, Huxley, and Tyndall to the study of glaciers and remains a potent force attracting newcomers to our field and creating an audience for our work.

The main concerns of Alpine glaciologists seem to have changed remarkably little since the work of Agassiz in the 1840s and one is left with the unsettling feeling that, equipped with a few modern tools, much of the progress of the past few decades could have been gained a century earlier by Agassiz and other pioneers. This observation suggests that technological advances rather than revolutions in thinking have often been the spurs to progress in our discipline. Many of the measurements still routinely taken differ only in the speed and accuracy with which they can now be made.

Glacier Flow

The most interesting property of glaciers is that they flow. This fact intrigued the earliest scientific investigators and today flow mechanics has become one of the best developed areas of glaciology.

Early measurements of flow and ideas concerning the flow mechanism

Evidence of glacier flow was recognized by Agassiz's predecessors Scheuchzer, Gruner, and de Saussure but the first actual measurements seem to have been taken by Franz Josef Hugi, a professor of physics and natural history at Solothurn. In 1827, he established a field station beneath a large boulder on the medial moraine of Unteraargletscher, Switzerland, and by visual alignment using fixed geographical references he measured the progressive displacement of the roof boulder. From 1827 to 1836, the block moved 1315 m (Hugi, 1842, p. 79).* To modern readers, Hugi's results would be accepted as clear evidence of glacier flow, but to sceptical contemporaries it seemed possible that the boulder was sliding along the glacier surface and the ice beneath was motionless (Agassiz, 1866, p. 295–96).

Louis Agassiz, of Neuchatel, first visited Unteraargletscher in 1839 and began his historic investigations of that glacier in the following year. For his 1840 field base he had hoped to occupy Hugi's cabin but, finding it in ruins, he established a similar dwelling, whimsically named the “Hôtel de Neuchâtelois”, on the same moraine but farther up-glacier (Marcou, 1896, p. 163–64). The 1840 field season was an ambitious one for Agassiz and his companions. A number of shallow holes were drilled into the glacier using a long metal rod with a cutting tip. The deepest hole did not exceed 7 m but the experience gained would prove useful (Desor, 1844, p. 159; Mercanton, 1905, p. 374). A transverse line of six flow markers was set into shallower holes and Agassiz intended to measure their down-glacier displacement the following year.

When Agassiz began his research on Unteraargletscher he subscribed to the dilatation theory of glacier motion, proposed by Scheuchzer, polished by Charpentier, and restated by Agassiz (1840, p. 163; 1967, p. 90). The essence of this theory is that ice is relatively permeable to water flow and that melt water can flow readily to the interior of a glacier and freeze there; the volume expansion that accompanies freezing was believed to result in a progressive down-glacier transport of ice. Some implications of the dilatation theory are that flow rate should increase monotonically from the headwall to the terminus and that dilatation would be greatest in regions where water was introduced and at times when water input was greatest. Because Agassiz believed that water input was greatest at the edge and base of glaciers, he expected to find that flow velocity increased toward the edges and with depth.

Shortly after returning from the field, Agassiz set off for Glasgow to attend a scientific conference and win new converts to the ice-age theory. In Glasgow he met the Edinburgh physicist James D. Forbes and, finding common interest, invited him to visit the “Hôtel” the following summer. Forbes accepted with enthusiasm. In August 1841, Forbes and a companion from Cambridge joined Agassiz's party on Unteraargletscher and remained with them for 3 weeks. Forbes cannot have been a rewarding guest: “[He] was as silent as a sphinx; it was impossible to draw from him a single remark or hint …” (Marcou, 1896, p. 188). Meanwhile, Agassiz and his crew were hard at work. Unfortunately, the flow markers emplaced in 1840 had completely melted out so that no trustworthy measurement of flow could be derived. A new set of holes 3–5 m deep was drilled and flow markers were re-positioned (Agassiz, 1866, p. 296–97). A more ambitious drilling program was launched and holes 10 m and 46 m deep were completed. The deeper hole drained so that temperatures could be measured in it.

That winter, Agassiz and Forbes fell out with each other (Desor, 1844, p. 434–47). Despite Forbes' sphinx-like silence, he was a keen observer and, without informing Agassiz, he published some findings of the 1841 field work (Forbes, 1842[b]). Agassiz regarded this as a breach of trust and wrote Forbes to this effect (Desor, 1844, p. 438–43). No reconciliation was possible and in 1842 Agassiz returned to Unteraargletscher and Forbes began his own investigations on Mer de Glace in France. Forbes had studied the drilling efforts on Unteraargletscher and employed the same methods to establish measurement points on Mer de Glace (Forbes, 1846[b], p. 164). He could not have failed to appreciate that Agassiz's plan to measure the pattern of surface flow on Unteraargletscher would bear fruit in the summer of 1842. By the time Agassiz and his party had reached Unteraargletscher to resume their flow measurements, Forbes had communicated his findings to the Edinburgh New Philosophical Journal (Forbes, 1842[a]). With a theodolite, Forbes was able to accomplish in several days what Agassiz had waited a year to achieve. In a few short weeks, Forbes (1842[c]) reached the following conclusions: “(1) The continuous imperceptible motion of glaciers is entirely confirmed … (2) This motion is not by any means the same, however, from day to day and from week to week … (3) This variation of motion appears to be common to every part of the glacier, as well where compact and completely even, as where most fissured … (4) From numerous observations, made in all parts of the glacier, it invariably results as before, that the centre moves faster than the sides of the ice-stream … (5) The variations of glacier motion affect the central parts most sensibly. (6) The greatest daily motion which I have observed, nearly opposite the Montanvert, amounts to 27.1 inches … .” The theory that was to emerge from these observations became known as the viscous flow theory. Abbé Rendu, a cleric from Annecy, first proposed the idea in 1841 in his little read memoire “Théorie des glaciers de la Savoie” (Rendu, 1841) but Forbes was its principal architect and most zealous defender.

A contending theory at this time was the “sliding theory”, attributed by Agassiz (1840, p. 152–54; 1967, p. 85–86) to his predecessors Gottlieb Sigmund Gruner and Horace-Benedict de Saussure. William Hopkins, a Cambridge mathematician, was undeterred by Forbes' strongly held convictions and argued in favour of the sliding theory. Debate was protracted and the issue proved difficult to resolve because each side had good points to make and skillfully misrepresented the other's position. A deep-seated problem was that ice had confusing material properties; it was both brittle and viscous. Forbes at first claimed that the intense friction between a glacier and its bed would all but prevent sliding and, should sliding start, it would be accelerated like an avalanche (Forbes, 1845[b], p. 132). This gave Hopkins a position that could be defended. The most useful result of this debate was that Hopkins performed experiments to demonstrate that ice could slide over rough rock (Hopkins, 1845[b], 1849).

Without rejecting any of Forbes' conclusions, the London physicist John Tyndall concerned himself with what, to him, were important points of detail: “The question then occurs, is the viscosity real or apparent? Does any property equivalent to viscosity exist, in virtue of which ice can move and mould itself in the manner indicated, and which is still in harmony with our own experience of the nonviscous character of the substance?” (Tyndall and Huxley, 1857, p. 327). Tyndall concluded that the viscosity of ice was apparent, not real, and that “regelation” was the property equivalent to viscosity.

Regelation was a new idea at the time. William Thompson, later Lord Kelvin, had observed the phenomenon of pressure melting in ice and his older brother James then demonstrated, using a thermodynamic analysis, that pressure melting implies that melting temperature is lowered by pressure (Thompson, 1849), a prediction that was experimentally confirmed by brother William (Thompson, 1850). In 1850, the physicist Michael Faraday lectured on the subject of regelation (Forbes, 1859, p. 228–31). The potential relevance to glacier flow was not lost on Tyndall and Huxley (1857), and J. Thompson (1857) who, independently it seems, proposed that regelation was the process that allowed glacier ice to deform as if it were a viscous fluid. Forbes was sufficiently disconcerted by the rise of the “regelation theory” of flow and by the danger that it might be seen to supplant rather than confirm his viscous theory that he arranged to have his collected papers published as a special volume (Forbes, 1859, p. xviii).

Tyndall's field work on Mer de Glace led him to propose a new law of glacier motion: “When a glacier moves through a sinuous valley, the locus of the point of maximum motion does not coincide with a line drawn along the centre of the glacier, but always lies on the convex side of the central line. It is therefore a curve more deeply sinuous than the valley itself, and crosses the axis of the glacier at each point of contrary flexure” (Tyndall, 1859, p. 267–68). Why this law seemed significant to him is unclear. Tyndall's scientific career ended suddenly in 1893 when his wife unwittingly administered a lethal dose of chloral; the regelation theory did not outlive him by many years, for it was wrong. If regelation was the process that allowed ice to deform viscously, then cold glaciers would not flow.

Although Forbes underestimated the importance of glacier sliding, he was essentially correct on other matters. His viscous theory prevailed and this had a healthy effect on the youthful science of glacier mechanics for it established a firm connection to fluid mechanics. The viscous theory also motivated laboratory measurements of the deformation properties of ice (Reusch, 1864; McConnel and Kidd, 1888; McConnel, 1891; Hess, 1902; Weinberg, 1905) and efforts to use glacier-flow measurements for estimating ice viscosity (Marchi, 1897; Weinberg, 1907; Deeley and Parr, 1913). Harry F. Reid, a mathematically skilled geologist from Johns Hopkins University, used the theory qualitatively in his classic paper “The mechanics of glaciers” (Reid, 1896) to predict the pattern of flow lines and age stratification in glaciers. One of his most interesting conclusions was that the surface-ice velocity need not be tangential to the free surface, but may have a submergent or emergent component – an observational truth that seemed paradoxical to many of his contemporaries. Odin (1888), Marchi (1897), Weinberg (1907), Deeley and Parr (1913), Somigliana (1921), and Lagally (1930) showed, with varying degrees of success, that standard equations from fluid mechanics could be used to describe many aspects of glacier flow. The Russian physicist, Boris Weinberg, treated ice as a linear viscous fluid and solved the equations for fluid flow down an inclined semi-elliptical channel as well as for other channel cross-sections. By adjusting the magnitude of the viscosity coefficient to match the observed surface flow pattern for Hintereisferner (Blümcke and Hess, 1899), he estimated the apparent viscosity of ice. Richard M. Deeley and P.H. Parr repeated this analysis and found flow solutions for more general (including asymmetric) channel cross-sections. Carlo Somigliana, professor of mathematical physics at Turin, and M. Lagally reversed this point of view and attempted to demonstrate that if the viscosity of ice was known then surface-flow measurements could be used to find the channel cross-section.

The viscous theory does not explain the existence of shear planes in glaciers. Discussion continued as to whether viscous flow or internal slippage along thrust faults was the dominant flow mechanism, geologists tending to favour the second view. Rollin T. Chamberlin, of the University of Chicago, set out to measure internal slippage using a clockwork device (Chamberlin, 1928). Measurements from four North American glaciers yielded disappointing results, but on Glacier de la Brenva, Mont Blanc, he recorded small but distinct slippage events, and concluded that “the common conception of viscous liquid flow has to be eliminated from the picture before any real understanding of glacier motion is possible”. This advice was too strong and fortunately it was not universally accepted.

The past 50 years

Given the progress that had been achieved, it is curious that the unsound extrusion-flow theory, the notion that glaciers flow more rapidly at depth than at the surface, was to receive serious consideration in the twentieth century. The pressure influence on melting temperature appears to have led to the mistaken view that pressure itself, rather than deviatoric stress, could drive glacier flow. In his discussion of the flow of the Greenland ice sheet, the young American, Max Demorest (1937, p. 47), distinguished between two different flow mechanisms, one applying to the interior regions where “ice is thick and the movement is by hydrostatic pressure” and the other to the border regions where “deep valleys … allow outlet glaciers to move down slope under the direct influence of gravity”. A more systematic elaboration of the idea was presented by Demorest (1942, 1943). At the same time, Roland Streiff-Becker (1938) found that extrusion flow could explain some puzzling results of his work on Claridenfirn in Austria. From measurements of surface accumulation and flow rate, he concluded that ice flux from Claridenfern was greater than the flux indicated by surface measurements. Thus, he reasoned, the flow rate at depth must exceed that at the surface.

The extrusion-flow idea was greeted with polite scepticism by the more physically oriented glaciologists and it was recognized that measurements of the depth variation of glacier flow rate could prove decisive. Such measurements had previously been made on the terminal face of Glacier des Bois, Mer de Glace (Forbes, 1846[a]), and on exposed sidewalls of Unteraargletscher (Martins, 1846), and Glacier du Geant, Mer de Glace (Tyndall, 1859[a], p. 270). For a definitive result, the observations must be taken near the glacier centre line, not at the edges where special arguments might be invoked. Thus, it was necessary to measure the deformation of a vertical bore hole to discover the nature of glacier flow. This was not a new idea but it had not previously been attempted. Forbes (1844), thinking of the deep hole drilled by Agassiz into Unteraargletscher, commented: “In the first place the fact of verticality requires confirmation; for it is difficult to understand how, by means of a plummet, a hole 140 feet, and only 3 or 4 inches in diameter, could have its verticality tested.” In 1949, a 137 m cased hole was drilled to the bed of Jungfraufirn (part of the accumulation region for Grosser Aletschgletscher, Switzerland); by repeated use of inclinometer measurements, the progressive deformation of the bore hole was measured over the interval from August 1948 to October 1949 (Perutz, 1950) and from August 1948 to September 1950 (Gerrard and others, 1952). No evidence for extrusion flow was found in this experiment nor in subsequent ones on Malaspina Glacier in Alaska (Sharp, 1953), Salmon Glacier (Mathews, 1959), and Saskatchewan Glacier in Canada (Meier, 1960). The most complete measurements to date are those of Charles Raymond (1971 [a], [b]), who drilled nine holes through Athabasca Glacier in Canada and measured bore-hole deformation. He observed that, although “extrusion flow has been discredited as a mechanism for the longitudinal component of flow, it may represent the normal pattern of transverse flow”.

The Jungfrau bore-hole results did not persuade Streiff-Becker, who argued that the drilling site was located too far up-glacier to reveal extrusion flow (Streiff-Becker, 1953). This style of defence could have forestalled a resolution for decades and it was theory, not measurement, that laid the question to rest. John Nye, our foremost contributor on the subject of glacier-flow mechanics, showed that not only did extrusion flow not occur at the Jungfrau drill site, it was unlikely to occur anywhere because it was a mechanical absurdity. To illustrate this claim, he showed that, if extrusion flow was occurring in the Greenland ice sheet, the flow velocity would reach nearly one-fifth the speed of light in 100 years (Nye, 1952[b]). As Stan Paterson (1981, p. 3) stated in the introduction to his book The physics of glaciers:

“In the author's opinion, a mere handful of mathematical physicists, who may seldom set foot on a glacier, have contributed far more to the understanding of the subject than have a hundred measurers of ablation stakes or recorders of advances and retreats of glacier termini.”

None can doubt that Nye was one of these mathematical physicists.

Nye, like Forbes a century earlier, viewed “glacier theory as a branch of mechanical physics” (Forbes, 1842[c], p. 341–42). Unlike Forbes and disciples of the viscous theory, Nye knew that ice does not flow according to a linear viscous law. A joint meeting of the British Glaciological Society, the British Rheologists' Club, and the Institute of Metals, held in London in 1948, was to set the stage for Nye's enduring contributions on flow mechanics. The key speaker, Egon Orowan the materials physicist, explained that ice and other crystalline solids deform plastically, not viscously, and he discussed in a clear simple way the mechanics of perfectly plastic glaciers (British Glaciological Society, 1949). Nye, a graduate student at the time, reported this meeting (Nye, 1948) and proceeded to develop Orowan's ideas.

By assuming that ice was a perfectly plastic solid, Nye showed that extending and compressive flow in glaciers and ice sheets could be described mathematically and that the calculated slip-line fields give insight into the observed geometry of thrust planes in glaciers (Nye, 1951). Deformation experiments performed by John Glen (1952, 1955) established that ice was neither a linear viscous nor a perfectly plastic material and his laboratory determination of the flow law was a turning point in the science of glacier mechanics. In his classic paper “The mechanics of glacier flow”, Nye (1952[c]) used Glen's flow law to calculate the velocity distribution in idealized valley glaciers. The solutions presented were for an inclined slab (a very wide glacier), a vertical slot (a deep narrow glacier), and an inclined semi-cylindrical trough. Nye (1953) was the first attempt to match laboratory determinations of the flow law with the in situ behaviour of glacier ice as revealed by measurements of tunnel closure and bore-hole deformation. It also gave the first statement of a tensor flow law; previous to this, the flow law was expressed as a scalar relationship between uniaxial strain-rate and uniaxial stress, or between shear strain-rate and shear stress. The scalar law can only be applied to very simple stress systems, so that there is a limit to what it can reveal about glacier behaviour. From the generalized law, it was possible to reexamine the cases of extending and compressive flow and replace the assumption of perfect plasticity with something more realistic (Nye, 1957). A justification of the generalized law was given by Glen (1958).

Adoption of the generalized flow law allowed major advances in glacier mechanics to occur, but the generalized law greatly simplifies the potential complexity of real glacier ice. A key assumption is that the third invariant of deviatoric stress does not affect deformation rate. Experiments by Steinemann (1958) suggested that the third invariant does influence deformation, but more recent work by Duval (1976) supported the opposite conclusion. The generalized law applies to isotropic ice but, in fact, deformed glacier ice acquires a complex fabric (Shumskiy, 1955; Kamb, 1959; Rigsby, 1960) that renders it anisotropic. Increased water content also affects creep rate (Duval, 1977). These and other complexities led Lliboutry and Duval (1985) to conclude in a recent review that “any attempt to determine the creep law of ice is illusory.”

Although the generalized law provides a better constitutive description of glacier ice than the linear viscous law used by Weinberg and his successors, the penalty for introducing a more complicated law is that the flow equations become far more complicated. In consequence, the inclined semi-cylindrical channel is the most realistic geometry that can be readily solved. For a semi-elliptical channel, a simple problem if linear viscous rheology is assumed, no exact solution is known. Progress in glacier-flow mechanics might well have come to a complete stop had it not been for the advent of high-speed computers. In what appears to be the first example of what is now called “glacier modelling”, Nye (1965[b]) used a computer to obtain finite-difference solutions for flow in inclined rectangular, semi-elliptical, and parabolic channels. Nye's computations were performed on an IBM 1620 computer and his table I shows that calculations for one of his models required 53 h of computing time. Since 1965, computers have grown far more powerful and many glaciologists have become skilled at numerical analysis. Representative examples of glacier modelling can be found in papers by Campbell and Rasmussen (1969), Budd and Jenssen (1971), Rasmussen and Campbell (1973), Budd (1975), Jenssen (1977), Hooke and others (1979), and Bindschadler (1982).

Early research on glacier sliding

Horace-Bénédict de Saussure, a naturalist from a distinguished Geneva family, was an early proponent of the sliding theory of glacier motion. “When one sees walls of ice more than one hundred feet in height terminating at the edge of an escarpment, when one sees at each moment masses of ice detaching from these walls, & this ice, accumulated by these repeated falls, forming substantial piles at the foot of these escarpments, can one doubt that this ice slides perpetually from high to low, & consequently has progressive movement” (de Saussure, 1779–96, torn. 4, §2284, p. 449“50). A problem with early thinking on glacier sliding was that sliding was presented as the single explanation of glacier flow. Forbes believed that his flow measurements on Mer de Glace ruled against the sliding theory and argued that for many reasons block sliding of glaciers was impossible. If ice was essentially rigid (as the advocates of sliding tended to emphasize), then it could not mould itself around subglacial asperities and could not flow from a broad catchment basin through a narrow outlet (Forbes, 1845[a], p. 414–15). When a rigid block slides down a rough surface, the observed motion is accelerated; the same should hold for glaciers if they move by sliding (Forbes, 1845[b], p. 132).

Hopkins set out to demonstrate that Forbes' viscous theory was incorrect and that the Mer de Glace observations could as easily be explained by sliding. He performed experiments involving the sliding down an inclined rock slab of a frame containing lumps of ice (Hopkins, 1845[b], p. 4–5; 1849, p. 53–55) and discovered that ice slid at a steady unaccelerated rate except when the inclination angle was great. He noted that the lower surface of the ice mass was in a state of disintegration, thus explaining how moulding could occur. He therefore rejected Forbes' claim that sliding must be accelerated and showed that this was only true if the friction between ice and rock was assumed to be constant, that is, independent of sliding velocity (Hopkins, 1845[b], p. 3). From his experiments, he found that frictional resistance increased with the sliding rate and thus, in a sense, the sliding rate is like a terminal velocity (Hopkins, 1845[b], p. 5). The problem of explaining why glaciers were observed to flow most rapidly near the centre line and less rapidly near the channel margins, and how glaciers could flow through channel constrictions was ingeniously dismissed by invoking en échelon faulting along internal discontinuity surfaces (Hopkins, 1845[a], p. 160–61).

As the mathematical tutor of James Clark Maxwell, George Stokes, and William Thompson (Lord Kelvin), Hopkins' historical place is secure. To modern eyes, his publications seem marred by wordiness and cluttered with monotonous algebra, but he must be recognized as the first substantial contributor to scientific discussions of glacier sliding. He performed the first sliding experiments, proposed the first sliding law (in effect v _s = Aτ where v _s is sliding velocity, τ is shear stress, and A is a constant of proportionality), and he understood the importance of the regelation process to sliding (Hopkins, 1862).

Weinberg (1907), and later Deeley and Parr (1913), used measurements of the flow and subglacial geometry of Hintereisferner (Blümcke and Hess, 1899) to calculate a “viscosity” for glacier ice. From this, they evaluated the deformational contribution to flow and attributed the difference between theory and observation to slip at the boundaries. Without attempting to describe the slip mechanism, Deeley and Parr (1913, p. 98) proposed a sliding law identical to that of Hopkins: “the slip may reasonably be expected to be directly proportional to the force f producing it, and inversely proportional to the frictional resistance”, adding the stipulation that resistance was directly proportional to ice-overburden pressure.

Their subsequent paper “The Hintereis Glacier” (Deeley and Parr, 1914) was a scientific landmark and foresaw many “modern” ideas on sliding. They performed two experiments to gain insight into the sliding process. In the first, the rate of penetration of a glass rod forced into a block of ice was measured and from this the drag between an obstacle and flowing ice was calculated. The second was a sliding experiment of ice over rock. Deeley and Parr identified two mechanisms that are important to sliding: “Against the up-stream sides of these projections the pressure of the ice is greatest, whilst on the downstream sides it is least. On the up-stream sides melting, therefore, takes place, the water produced passing round the projections and freezing again on their lower sides. In this way the mass of ice is allowed to move slowly forwards over the somewhat rough surface” (Deeley and Parr, 1914, p. 156). The second mechanism was described as follows: “the very small irregularities of the glacier-bed are not, of course, the only hindrances to motion. The glacier has to change its form to accommodate itself to the bends and larger irregularities of its channel” (Deeley and Parr, 1914, p. 159).

As well as identifying the mechanisms of regelation and creep around obstacles, Deeley and Parr took a major conceptual step by introducing an idealized roughness asperity and analyzing its contribution to sliding resistance. They took as their roughness element a pyramid with base length 2l and base angle θ. They assumed that sliding resistance was proportional to the resisting area, l ² tan θ, and imagined an idealized glacier bed completely tiled with these roughness elements. From their penetration experiments, they obtained an empirical coefficient relating the resisting area to the penetration rate and combined the results of theory and experiment to produce a sliding law, in effect v _s = Cτ/tan θ where C is a constant. The pyramid slope tan θ serves as a dimensionless measure of bed roughness r = h/l where h is obstacle height (i.e. pyramid height); thus the Deeley-Parr sliding law is v _s = Cτ/r. By adjusting the slope angle, bed roughness could be varied and observed sliding rates matched to theory.

Rene Koechlin (1944, p. 95–116) also introduced a measure of bed roughness in his analysis of sliding. The roughness elements that he considered resemble thin walllike obstacles of height h, separated by a distance l. The ratio r = h/l defined his roughness coefficient, essentially the same as that used by Deeley and Parr (1914). Koechlin's analysis was nevertheless peculiar. The fracture strength of ice plays a role and the central idea seems to be that sliding cannot occur until the bottom shear stress is sufficiently high that bottom ice can crumble around obstacles.

Contemporary research on the sliding problem

The paper “On the sliding of glaciers” by Hans Weertman (1957) opened the recent era. Weertman analyzed the roughness contribution of cube-shaped asperities protruding from a perfectly smooth bed. Like Deeley and Parr (1914), Weertman considered that regelation and ice flow around obstacles were the key processes that allowed sliding. He used Glen's power law to describe ice rheology rather than a linear viscous law, and the resulting sliding law has the form v _s = D(l/r) ⁿ⁺¹τ^(n+1)/2 where D is a proportionality constant. For n = 1 (linear viscous fluid), the Weertman law is v _s = Dτ/r ², differing from the Deeley–Parr law. What distinguishes Weertman's contribution from earlier work is that the constant D is not an empirically determined fitting factor but is explicitly related to the physical properties of ice and rock. Thus Weertman's theory is the first complete theory of glacier sliding (complete in the sense that if it is correct there are no loose threads). In subsequent papers, Weertman modified and improved his theory by considering how the presence of a basal water layer might influence sliding (Weertman, 1962) and by introducing more complicated obstacle geometry and the possibility of cavitation in the lee of obstacles (Weertman, 1964).

Soon after Weertman's sliding theory appeared in the Journal of Glaciology, Louis Lliboutry published two short papers on sliding in Comptes Rendus (Lliboutry, 1958[a], [b]); of these, the paper 1968[a] is especially significant. Instead of adopting Weertman's “tombstone” bed, he introduced the aesthetically superior sinusoidal “washboard” bed, but the major step taken by Lliboutry was to identify a third important sliding process, subglacial cavitation. If cavities are water-filled, then water pressure p can help support the ice-overburden pressure p _i and reduce frictional contact between a glacier and its bed; thus effective pressure p′ = p _i − p plays an important role in his theory. Lliboutry's proposal that water pressure could be an independent variable proved to be contentious but has since been confirmed. Over the past decades, Lliboutry has had the satisfaction of seeing his once revolutionary ideas gain acceptance and has continued to refine his original theory (e.g. Lliboutry, 1959, 1968, 1979).

The sliding theory of Nye (1969, 1970) and, independently, of Barclay Kamb (1970) has a different aim from those of Weertman and Lliboutry. So far as it goes, the Nye-Kamb theory is exact. In certain areas, the theory is more realistic than either the Weertman or Lliboutry theory, but in others it is less so. Ice is assumed to be a linear viscous fluid; the glacier bed is taken to be a plane surface with small random topographic fluctuations superimposed upon it; ice is assumed to be in close contact with the bed so that the effects of cavitation can be ignored. The resulting sliding law has the form v _s = Aτ where the proportionality constant A depends on the physical properties of rock and ice as well as a bed-roughness measure. The great achievement of this theory is that it shows exactly how bed roughness contributes to sliding resistance. Apart from the oversimplified ice rheology and restriction to beds having low roughness, the main shortcoming of the Nye–Kamb theory is that it fails to give an exact treatment when cavitation is important. Recently, Andrew Fowler (1986) has extended the Nye–Kamb sliding theory to obtain an exact solution for flow with cavitation. In order to wrest a solution, he was forced to dispense with the regelation process and to assume a simple periodically repeating bed geometry. A similar problem was examined by Almut Iken (1981), who used a finite-element computer model to examine the effect of pressurized subglacial water cavities on glacier sliding. She assumed linear viscous rheology and a periodically repeating bed. Regelation plays no role in her analysis because only large smooth bed undulations are considered.

The foregoing sliding theories build from highly simplified assumptions. Ice is taken to be clean, the bed is rigid and impermeable, water or vapour cavities may or may not be present, and the glacier/bed contact is sharply defined. Such sliding models start by eliminating virtually everything that glacial geologists find interesting about glaciers. The past decade has seen a serious effort to expand sliding theories so that they can help shed light on a complex range of interactions between glaciers and their beds. Examination of deglaciated beds (Hallet, 1976[a]) and of the chemical composition of basal ice (Souchez and Lorrain, 1978) have revealed that there can be a chemical interaction between a glacier and its bed. Dissolved solutes lower the freezing temperature of subglacial water and therefore interfere with the regelation process and inhibit sliding (Hallet, 1976[b]). Processes of erosion and sedimentation are also excluded from conventional sliding theories but these shortcomings are being addressed. Theories of glacial abrasion have been constructed (Boulton, 1979; Hallet, 1979) and, in the face of compelling field evidence (Engelhardt and others, 1978; Boulton, 1979), theories that assume deformable subglacial sediments are being developed (e.g. Boulton and Jones, 1979).

Fluctuations and surging

Forbes (on Mer de Glace) and Agassiz (on Unteraargletscher) measured seasonal and shorter-term variations in glacier flow rate. Measurements were taken at approximately monthly intervals for a period of 1 year (Forbes, 1846[b], p. 183–84; Agassiz, 1847, p. 475–76) and revealed a strong seasonal variation. Minimum flow occurred in late fall or early winter and maximum flow was in spring or early summer. That summer rates exceed the annually averaged rate has been confirmed by many subsequent investigators (e.g. Blümcke and Finsterwalder, 1905) but few have attempted to follow the changes throughout a complete year. The measurements of Hodge (1974) on Nisqually Glacier, Washington, offer a modern counterpart to those of Forbes and Agassiz. Hodge's measurements were continued for 2 years and repeated more frequently.

As survey equipment has improved, it has become possible to measure finer and finer details of the variability of glacier flow (Washburn and Goldthwait, 1937; Millecamps, 1956; Meier, 1960; Iken, 1978; Kamb and others, 1985). However, Reynaud (1975) has cast doubt on some of this work by his discovery that lateral atmospheric refraction can account for much of the apparent jerkiness in flow rate. Both Forbes and Agassiz recognized that water somehow influenced flow rate but only recently has this become understood. Forbes (1843) concluded that flow “is more rapid in summer than in winter, in hot than in cold weather, and especially more rapid after rain, and less rapid in sudden frosts”. Agassiz noted that flow rate increased in the spring and took this as supporting the dilatation theory: “It is without doubt to this dilation that the accelerated glacier flow in spring must be attributed” (Agassiz, 1847, p. 538).

The discovery that subglacial water pressure can vary over a wide range (Mathews, 1964) and the subsequent association of high subglacial water pressure with increased flow rate (Iken, 1972, 1978), surface uplift (Iken and Bindschadler, 1986; Iken and others, 1983), and surging (Kamb and others, 1985) has done much to clarify the cause of glacier-flow variations.

The phenomenon of surging was noted by Ralph S. Tarr and Lawrence Martin (1914) in their historic research on the glaciers of Yakutat Bay, Alaska. A surprising proportion of the glaciers that had been inactive in 1905 were surging when Tarr returned in 1906. A major earthquake had occurred in Yakutat Bay in 1899 and Tarr and Martin suggested that the surges had been triggered by this earthquake (Tarr, 1910; Tarr and Martin, 1914, p. 168-97). Marchi (1911) proposed that earthquake-triggered avalanches had disturbed the balance of the Yakutat Bay glaciers and that the resulting advances were a natural consequence of the mathematical theory of glacier waves that he had already developed (Marchi, 1895). Austin Post (1965) demonstrated that an earthquake trigger was unlikely and went on to show that the geographical distribution of surging glaciers is itself a puzzle (Post, 1969). His influential paper “What are glacier surges?” with Mark Meier (Meier and Post, 1969) has shaped much of the subsequent research on the cause and mechanics of surging. To date, these studies seem to illustrate Robert Louis Stevenson's adage that “to travel hopefully is a better thing than to arrive, and the true success is to labour”. The existence of this surprising phenomenon has stimulated thinking about a wide range of potential instabilities that could beset glacier flow (Robin, 1955; Weertman, 1962; Robin and Weertman, 1973; Clarke, 1976; Clarke and others, 1977; Boulton and Jones, 1979; Kamb and others, 1985). The result has been to enrich our appreciation of the complexity of glaciers and their astonishing catalogue of processes and interactions. Despite the comparative rarity of surge-type glaciers, several of these, Medvezhiy Glacier (Dolgushin and Osipova, 1975, 1978), Trapridge Glacier (Clarke and others, 1984), and Variegated Glacier (Kamb and others, 1985) are among the most thoroughly studied of any glaciers in the world.

Mass Balance and Length Variations

The reality of glacier advances was well recognized by Agassiz and his contemporaries. Unteraargletscher was probably near its Little Ice Age maximum in 1842 when M.J. Wild, Agassiz's topographical engineer, prepared a superb map of the glacier (see Swiss National Tourist Office (1981, p. 66-67) for a colour reproduction). Against this reference, the subsequent thinning and terminus retreat of Unteraargletscher can be compared (Haefeli, 1970). According to Herfried Hoinkes (1968), routinely repeated observations of glacier terminal position were not seriously undertaken until after 1894 when the Commission Internationale des Glaciers was formed. One aim of the Commission was to use glaciers as indicators of climate change, but it was not until the contributions of Hans Wilhelmsson Ahlmann, professor of physical geography at Stockholm, that a systematic approach was established (Ahlmann, 1927). Ahlmann emphasized the importance of consistent methodology and made the first major intercomparison over a large geographical area (Ahlmann, 1948). Since the time that the Commission was founded, measuring changes in glacier length and budget have become a timehonoured commitment of field glaciologists. Such studies are too numerous to list but the continuing series Fluctuations of glaciers initiated by Peter Kasser (1967) and the impressive compilation Mountain glaciers of the Northern Hemisphere by William O. Field (1975) give data and references. Although long-term mass-balance studies are unglamorous and uncelebrated, collectively they have great value. Glacier variations reflect changes in weather and climate (Hoinkes, [^c1964]) and contribute substantially to variations in sea-level (Thorarinsson, 1940; Meier, 1984).

Excerpts from the publications of de Saussure, Agassiz, and Forbes suggest that they had a correct but incomplete conception of how the principle of mass balance applied to glaciers: “Glaciers contained within defined limits by evaporation, by external & internal [i.e. geothermal] heat, & by the slope of their beds that drive them to the lower valleys, therefore furnish a new proof of these admirable proportions that Nature has established between the generative forces & the destructive forces, wherever she has wished to maintain some uniformity” (de Saussure, 1779-96, torn. 1, §539, p. 384-85). “[A] glacier is always descending; if the extremity at any time seems to retire, this implies nothing more than that the portion of ice, melted by the heat of summer, is more considerable than that which the glacier brings along with it in its progress” (Agassiz, 1839, p. 383). “A glacier is a mass of ice … which makes its way down towards the lower valleys, where it gradually melts, and it terminates exactly where the melting … compensates for the bodily descent of the ice from the snow reservoirs of the higher mountains … The snow line is a fact as definite on the surface of a glacier as on that of a mountain, only in the former case it occurs at a somewhat lower level. It cannot be too distinctly understood that the fresh snow annually disappears from the glacier proper. Where it ceases entirely to melt, it of course becomes incorporated with the glacier. We have therefore arrived at the region where the glacier forms; everywhere below it only wastes. This snowy region of the glacier is called in French névé; in German, firn. As we ascend the glacier it passes gradually from the state of ice to the state of snow“ (Forbes, 1859, p. 234-44).

The foundations of present understanding of glacier variations and waves were established in remarkable papers by Marchi (1895, 1911), Reid (1896, 1905), and Finsterwalder (1907). Luigi de Marchi was professor of physical geography at Padua; his 1895 paper “Le variazioni periodiche dei ghiacciai” seems to have escaped the notice of his contemporaries but is impressively comprehensive. He introduced a continuity equation of the form ∂Q/∂x + ∂S/∂t = B where Q is the ice-volume flux integrated over the channel cross-section, x is down-stream distance, S is the cross-sectional area of the channel, t is time, and B is obtained from the surface accumulation or ablation of ice volume (the notation is mine) and he showed that mass-balance perturbations propagate down-glacier as waves. Marchi avoided any rheological assumptions and arrived at the general result that waves travel at a velocity u = dQ/dS that exceeds the average flow velocity v = Q/S. It seems that Marchi's paper is the first theoretical paper in which time appears as a variable. His 1911 paper is an elaboration (in French) of the 1895 paper with added discussion of the connection between waves and the reported advance of Alaskan glaciers.

Reid's 1896 paper was non-mathematical but his diagrams and discussion show that he understood the steady-state mass-balance relation dQ/dx = B. He clearly defined the accumulation and ablation regions (termed the “accumulator“ and “dissipator“) and his statement: “the general law that the flow is less below, than at, the névé-line must hold; this flow equals the product of the average velocity by the sectional area by the effective density” shows that he understood the relationship of mass flux to the equilibrium line. He appreciated that this truth depended only on the “law of indestructibility of matter” and was unrelated to ice rheology. The 1905 paper was a mathematical extension of these ideas and introduced time dependence so that glacier variations could be studied. Reid considered the response at the equilibrium line to a step increase in accumulation rate. His calculations led to the conclusion “that the advance of a glacier not only lags behind the increase in snowfall on account of the time necessary for the increased thickness to travel down that glacier, but that this increased thickness in the reservoir itself lags nearly a quarter of a period behind the increase in snowfall which produces it” (Reid, 1905, p. 488).*

Sebastian Finsterwalder, a professor of mathematics at Munich, developed a theory of glacier variations that appears to have circulated for several years before his 1907 paper was published, for it is outlined in Die Gletscher by Hess (1904, p. 349-52). A continuity equation of the form dq/dx + dh/dt = b was used where q is volume flux of ice, h is thickness, and b is the surface accumulation/ablation rate.

The continuity equation and its connection to glacier waves was somehow forgotten until Bodvarsson (1955) reintroduced the equation in the more general form ∇ · q + ∂h/∂t = b where q is the volume-flux vector (in two dimensions). This was a very ambitious paper but so many simplifying assumptions were necessary that when the final result was gained, the wave-like response of glaciers to mass-balance perturbations had been lost. Papers by Nye and Weertman marked the re-discovery by glaciologists of what are now called kinematic waves. In the note “Surges in glaciers”, Nye (1958) drew attention to the work of Finsterwalder (1907) and suggested a connection between waves and surging, a point previously made by Marchi (1911). Both Nye and Weertman (1958) in his paper “Traveling waves on glaciers” combined Glen's creep law with Weertman's sliding law to reach the conclusion that waves travel at least several times faster than the ice-flow rate. Weertman used a linear perturbation analysis to show that waves are attenuated as they propagate down-glacier. In a fine series of papers, Nye (1960, 1963[a], [b], 1965[a], [c]), explored these ideas and showed how they could be applied to real glaciers subjected to realistic mass-balance disturbances. He showed that, for small balance perturbations, glaciers can be approximated as linear dynamic systems and that it is helpful to view the glacier as a filter having a transfer function that relates balance fluctuations to the glacier response. In recent years, work on this subject has split into two distinct efforts. Those like Shumskiy (1975), Landon and Raymond (1978), Hutter (1980), and Fowler (1982) are extending our understanding of glacier waves and their mathematical description. Those like Budd (1975) and Bindschadler (1982) are using the mass-balance equation as the basis for modelling glacier flow on the computer.

Glacier Hydrology

Internal and subglacial water channels

A possible relationship between subglacial water and glacier flow was suspected early in the history of scientific glaciology. In his Voyages dans les Alpes, de Saussure (1779-96, torn. 1, §535, p. 378-79) asserted that geothermal melting was appreciable and that the resulting melt water was necessary for sliding en masse to occur.

“Almost all glaciers … rest on inclined beds; & all of them, of any appreciable size, have beneath them, even in winter, streams of water that flow between the ice & the bed that supports it.

One therefore understands that these ice masses, driven by the loss of contact with the bed on which they rest, freed by the loss of contact with the bed on which they rest, freed by water from contact that ice could make with that same bed, sometimes even lifted by this water, must little-by-little, slide & descend following the valley slope or ridge that they cover.“

Agassiz was doubtful about the significance of geothermal melting and decided to test the idea by seeing whether water flowed from beneath glaciers in winter as well as summer. In March 1841, he visited Unteraargletscher and to his satisfaction, for he disbelieved the sliding theory, only a trickle of water was flowing from the terminus (Agassiz, 1847, p. 373-76).

Questions about subglacial and englacial water have remained with us to the present day but, until sliding theories had reached a certain level of maturity, it was hard to define what questions to ask. Lliboutry's sliding theory was the first in which water played an explicit part and Weertman's theory soon reached this point. The observation of very high and rapidly changing water pressure beneath South Leduc Glacier (Mathews, 1964) confirmed Lliboutry's claim that water pressure should be treated as a free independent variable in sliding theories. Subsequent measurements of water-level variations in moulins and bore holes have emphatically confirmed this fact (Iken, 1972; Hodge, 1976; Engelhardt, 1978) and have led to greatly improved understanding of the subglacial water system. A less direct approach that has also proved useful is to analyze the chemistry and sediment load of water flowing out from beneath glaciers (Østrem, 1975; Collins, 1978, 1979; Humphrey and others, 1986).

Once it became apparent that subglacial water could affect glacier sliding, it was inevitable that studies of the geometry and physics of the subglacial water system should become important. Weertman (1962) analyzed the physics of thin subglacial water sheets and showed that there are many similarities to the mass-balance problem for glaciers, for example, that kinematic waves are a possibility. One of the main results of Weertman's research on water sheets is that thick subglacial water layers are difficult to establish.

Nye, Röthlisberger, and Shreve considered the physics of water flowing in discrete subglacial channels. The kind of channels envisaged by Nye (1973), now called “Nye channels” or “N channels” are cut downward into bedrock and are therefore spatially fixed, not mobile. The existence of large subglacially excavated channels has long been recognized by geologists (see Charlesworth (1957, p. 238-45) for discussion and references); on a smaller scale, subglacial drainage traces on deglaciated bedrock have been carefully examined and mapped (e.g. Walder and Hallet, 1979). The channels analyzed by Röthlisberger (1972) and Shreve (1972), now called “Röthlisberger channels” or “R channels”, are melted upward into glacier ice and are potentially mobile and ephemeral features. N and R channels maintain themselves in similar ways, by melting ice at a rate that compensates for creep closure, but they may differ in their ability to collect water. According to Weertman (1972), R channels are poor collectors of water because the pressure gradient in basal water near such channels may direct flow away from rather than toward the channel. (This collection problem only applies to R channels that are fed by basal water, not to R channels fed from the glacier surface.) N channels, on the other hand, are shown to be efficient collectors of basal water. Discussion of the efficiency and stability of subglacial water channels is by no means completed. Walder (1982) analyzed the stability of water sheets and found that there is a strong tendency for sheet flow to evolve into R channels. Weertman and Birchfield (1983) reversed the argument and demonstrated (again theoretically) that R channels are unable to collect water efficiently so that they would have difficulty tapping a water source necessary to maintain themselves. Thus R channels, though they exist, may not be stable features.

Röthlisberger channels can grow unstably but only in the special case when they are connected to a water reservoir, for example, to an ice-marginal lake. The rapid growth of R channels can result in the catastrophic release of water through subglacial (or englacial) tunnels. Such a flood is called a glacier outburst of “jokulhlaup”. In the twentieth century, the most violent outburst floods have been those from Grimsv8tn in Iceland (Thorarinsson, 1953) and the most closely studied are those from Gornersee (Bezinge and others, 1973) in Switzerland, Summit Lake (Mathews, 1973) in Canada, and “Hazard Lake” (Clarke, 1982) in Canada. The physics of outburst flooding seems to be quite well understood. Mathews (1973) and Björnsson (1975) correctly identified the essential physical processes and Nye (1976) synthesized these ideas to produce a theory that has been extended by Spring (1979), Spring and Hutter (1981), and Clarke (1982).

The subglacial drainage networks described above are located at the contact between glacier ice and impermeable bedrock. In a significant departure from this viewpoint, Boulton and others (1974) considered the flow of water through a permeable subglacial aquifer.

Much of the water that flows beneath valley glaciers derives from the glacier surface and flows to the bed through an englacial channel system. Thus, subglacial water pressure, and hence sliding rate, can respond sensitively to surface melting and rainfall (Mathews, 1964; Iken, 1972). Dye tracing has proved a useful technique for studying,how the englacial and subglacial systems are connected. This line of research appears to have been started by Francois-Alphonse Forel (1898), a Swiss limnologist, who released fluorescein dye into moulins on Glacier du Rhdne and measured the average transport velocity of water as it passed through the glacier. Subsequent contributors to this subject include Vallot and Vallot (1900), Stenborg (1969), Krimmel and others (1973), Behrens and others (1975), and Kamb and others (1985).

Ice permeability

The question of whether ice is permeable or impermeable to water flow has commanded attention for well over a century. If anything, the question had greater significance in the 1840s than today because the credibility of the dilatation theory rested on the belief that ice was permeable. According to Forel (1887, p. 7), Hugi set out in 1842 to determine whether or not ice on Lower Grindelwald, in Switzerland, was permeable. He used indigo-coloured dye as a tracer and concluded that ice was essentially impermeable. In the same year, Agassiz used a potassium chromate tracer to perform similar experiments on Unteraargletscher and reached the opposite conclusion (Agassiz, 1847, p. 170-79). Such contradictory results kept the question of ice permeability unsettled. Repeated failures to duplicate Agassiz's result (e.g. Huxley, 1857; Forel, 1887) eventually led to the consensus that, large-scale structures excepted, ice is essentially impermeable.

The permeability debate was re-kindled a century later when at a conference in 1969 Nye and Frank (1973) presented evidence suggesting that a connected network of intergranular veins might exist within temperate glaciers. Lliboutry (1971 [a]) was quick to take issue and argued that much of the intergranular water is immobilized, for example, by air bubbles blocking veins. Further investigations led to more pessimistic estimates of permeability (Nye and Mae, 1972; Raymond and Harrison, 1975) but it is now accepted that some degree of permeability exists in temperate ice (Nye, 1976; Hantz and Lliboutry, 1983). Berner and others (1978) used a subtle analysis to estimate water flux through the vein system of Griesgletscher, in Switzerland, and concluded that it is of the order 0.02-0.04 m a^-1. Needless to add, the volume dilatation that would result by freezing so small a quantity of water is negligible.

Thermal Regime

In 1842, Agassiz (1847, p. 423) measured ice temperature in Unteraargletscher to a depth of 60 m and concluded that “the interior of the glacier, with the exception of near-surface layers, in summer has an invariable temperature, which is zero”. Today, we would refer to Unteraargletscher as temperate, following Ahlmann's (1935) geophysical classification of glaciers as temperate or polar. Many valley glaciers are temperate and their temperature distributions are controlled by the various factors that influence melting temperature: stress, concentration of water-soluble impurities, interfacial free energies, and the micro-structure of the liquid phase (Lliboutry, 1971 [a]; Harrison, 1972; Harrison and Raymond, 1976). In temperate glaciers, water and ice coexist and water content has an important influence on ice rheology (Duval, 1977). Measurement on cores from Mer de Glace show water content varying from 0.0% to 3.0% (Vallon and others, 1976; Lliboutry and Duval, 1985).

Hopkins (1845[b]) appears to have been the first to apply a mathematical analysis to a problem involving glacier temperature. In an attempt to promote his theory of sliding and to defend it from Forbes’ criticisms, he cited Poisson's theory of heat transfer and reproduced the now familiar solution for the penetration of a sinusoidal time variation of boundary temperature into a conducting half space. Forbes (1845[a], p. 407), who took a dim view of mathematical glaciology, especially when it was used to shore up weak ideas, described this as “a ponderous display of dexterity, where the physical conditions of the problem are so entirely left out of sight that it conveys no positive information whatever on the subject.“

For the mathematically inclined, polar glaciers present some intriguing challenges. Lagally's theoretical paper “Zur Thermodynamic der Gletscher” (Lagally, 1932) appears to be the first attempt at simultaneous consideration of the dynamics and thermodynamics of such glaciers. By treating ice as a linear viscous fluid and applying standard results from classical hydrodynamics he calculated the effect of viscous heating on the temperature profile. A subsequent paper (Lagally, 1933) is wide-ranging, but includes an independent re-statement of the solution that Hopkins had presented in 1845. A major improvement was added by Benfield (1951) who introduced the effects of steady surface accumulation in his analysis of the near-surface temperature of a snow field. Gordon Robin (1955) recognized the relevance of these calculations to the interesting question of the distribution of temperature within cold glaciers and ice sheets, and also speculated on a thermal trigger for glacier surges. This idea was explored by others (Schytt, 1969; Clarke, 1976; Clarke and others, 1977) but has now fallen from favour. Robin's (1955) analysis is attractive in its simplicity, but complexity can also be attractive. “Polythermal glaciers”, a mathematical abstraction that includes both temperate and polar glaciers as special cases, have received the careful attention of Fowler and Larson (1978) and of Hutter (1982).

Glacier Drilling

Before glacier mechanics could become a quantitative science, it was necessary to complete the three-dimensional picture of glaciers. Geophysical measurements were unknown to early glaciologists, thus by default drilling became the standard approach to measuring ice thickness (Fig. 1). In 1841, Agassiz made his first attempt to drill to the bed of Unteraargletscher. He transported iron rods totalling 50 m in length to the glacier and assembled a solid lance with which he attempted to penetrate the glacier. According to de Saussure (1779-96, torn. 1, §523, p. 367),

Fig. 1. A history of glacier drilling, (a) A cable tool drill as used by Agassiz in 1842 in his unsuccessful attempts to drill through Unteraargletscher. After 6 weeks of effort, holes 16, 32.5, and 60 m had been completed. For the first 3 days of drilling each hole, the typical drilling rate was 13 m d^-1 (with four men); this decreased to 3-4 m d^-1 (with eight men) as hole depth increased. This drawing is based on written descriptions (Desor, 1844, p. 294-96, 491-94; Mercanton, 1905, p. 374-76), an 1844 portrait of Agassiz (Lurie, 1960), and illustrations of the Unteraargletscher landscape near Agassiz's camp (Agassiz, 1866). (b) The hand-powered rotary drill used by Blümcke and Hess to drill through Hintereisferner (after Blümcke and Hess, 1899, fig. 13). In the period from 1895 to 1909 they completed 11 holes to the glacier bed; depths ranged from 38 to 224 m and a typical drilling rate was 4–5 m h^-1. (c) Electrothermal drilling 137 m to the bed of Jungfraufirn in 1947 (after Gerrard and others (1952, fig. 2)); the inset shows the construction of the hot-point element (Gerrard and others, 1952, fig. 3). (d) A rotary diamond-drill rig used to drill 91 m into upper Taku Glacier, Alaska (after Miller, 1951, figs 1, 2, and 5). (e) A coring electrothermal drill used by Shreve and Kamb (1964) to extract cores from Blue Glacier. Holes as deep as 137 m were drilled, (f) A hot-water drill used in 1986 to drill through Trapridge Glacier, Yukon Territory, at rates of 100 m h^-1 the inset is after Gillet (1975, fig. 2).

“The thickness or depth of these ice masses is different in different places. In the Glacier des Bois at Chamouni, I found it commonly from 80 to 100 feet [24-30 m]; but one understands that wherever hollows or depressions occur this depth must be much greater: it is said that ice thicknesses greater than 100 Wise [195 m] have been found; & although I have not seen it, I have, however, no trouble believing it.“

Agassiz used all his extension rods without attaining the bed of Unteraargletscher. The following year he brought with him a few hundred metres of cable from which the iron lance could be suspended, rigging in effect a rudimentary cable tool (Fig. 1a). On a good day, the drilling rate was 5-6 m d“1. After 6 weeks of tedious effort involving as many as eight men, the attempt was abandoned after a depth of 60 m was reached.

“When I first began my investigations upon the glacier, now more than twenty-five years ago, scarcely any measurements of their size or their motion had been made. One of my principal objects, therefore, was to ascertain the thickness of the mass of ice, generally supposed to be from eighty to a hundred feet, and even less. The first year I took with me a hundred feet of iron rods (no easy matter, where it had to be transported to the upper part of a glacier on men's backs), thinking to bore the glacier through and through. As well might I have tried to sound the ocean with a ten-fathom line. The following year I took two hundred feet of rods with me, and again I was foiled.“

Discouraged, Agassiz made no further attempts to drill through glaciers but remained interested in measuring their thickness. By sounding moulins with a weighted line, he showed that near the “H6tel” ice was at least 260 m thick (Agassiz, 1847, p. 345). Using a simple mass-balance argument, he estimated that slightly up-glacier from the “Hôtel“ ice thickness exceeded 570 m (Agassiz, 1847, p. 88-89).

Adolf Blümcke and Hans Hess were the first to drill successfully through a glacier and between 1895 and 1909 they drilled 11 holes through Hintereisferner and many others that were stopped before the bed was reached (Blümcke and Hess, 1909; Hess, [1924]). The maximum depth attained was 224 m in a hole that was not completed. Drilling rates were typically 4-5 m h^-1, quite respectable by modern standards and impressive considering that their rotary drill was hand-powered (Fig. 1b).

In later years, the advent of geophysical sounding methods shifted the primary purpose of glacier drilling from its original one. Holes were seldom drilled to measure ice thickness but instead were for implanting sensors or extracting ice cores. The first reported use of a machine-driven rotary diamond drill to extract a long ice core from an alpine glacier was by Maynard M. Miller (1951) on upper Taku Glacier, Alaska (Fig. 1d). A depth of 91 m was reached but the equipment weighed in excess of 7 tons (6000 kg) and it is not surprising that this approach was not followed by others. In recent years, rotary drills have been designed for comparative portability (Rufli and others, 1976) but rotary drilling is not widely used to drill through glaciers.

Although early rotary drilling yielded acceptable drilling rates, it was heavy work and unpleasant to do. For this reason, the electro-thermal drill proved an attractive alternative and enjoyed several decades of popularity. The first use of electro-thermal drilling was in connection with the Jungfraufirn drilling project of Gerrard and others (1952; Fig. 1c). The drilling party faced more than the usual range of difficulties (Perutz, unpublished). Between Calais and Boulogne a package containing all the electrical heating elements fell from the window of their speeding train, and despite “magnificent local efforts” involving police, boy scouts, and school children it was never recovered. Substitute elements were urgently sought and found in Zurich. The historic Jungfrau bore hole was drilled using a commercially manufactured beer-barrel tapper as the heating element. Drilling began in July 1948 and after 2 weeks the bed was reached at a depth of 137 m. Proximity of the drilling site to the Jungfraujoch Research Station allowed the drillers the unusual luxury of a nearby and reliable electrical supply. The maximum drilling rate was only 1.5 m h^-1.

Numerous papers devoted to improving the design and efficiency of electro-thermal drills were to follow (e.g. Stacey, 1960; Shreve, 1962; LaChapelle, 1963). Upgraded versions attained drilling rates of 11.6 m h^-1 or more, but electro-thermal drilling, at best, was beset by troublesome problems such as probe burn-out and the inability to drill through debris-rich ice. A design variation allowed ice cores to be extracted (Fig. 1e; Shreve and Kamb, 1964), but coring of glaciers is uncommon because cores from valley glaciers tend to be less interesting than those taken from ice sheets. The usual ice-residence time for glaciers is hundreds rather than thousands of years, and if the glacier happens to be temperate or near-temperate, isotopic and chemical stratification of the ice is not preserved. Notable exceptions are the cores that have been extracted at 4450 m a.s.l. on Colle Gnifetti, Switzerland, by Oeschger and others (1978), and at 5340 m a.s.l. on Mount Logan, Yukon Territory, by Holdsworth (1984).

One of the most decisive improvements in drilling technology has been the development of the hot-water drill (Fig. 1f; Kasser, 1960; Gillet, 1975; Iken and others, 1977; Taylor, 1984). With this equipment, drilling rates of 100 m h^-1 are typical and debris-laden ice presents less of a problem. The advent of the hot-water drill is surely one of the most significant advances of the past decade for it has shifted thinking away from the problem of drilling to the problem of designing good down-hole instruments. It is now possible to drill many holes through a glacier in a rather short time and the present challenge is to make the most of this new freedom.

Geophysical Measurements

Drilling is a brutish approach to measuring ice thickness and as a mapping technique it is completely unsatisfactory, being limited in application to very thin glaciers. The admirable efforts of Blumcke and Hess from 1895 to 1909 yielded only 11 holes to the bed of Hintereisferner (Blumcke and Hess, 1909). When geophysical methods became available, they completely replaced drilling as the favoured approach to mapping glacier thickness (Fig. 2).

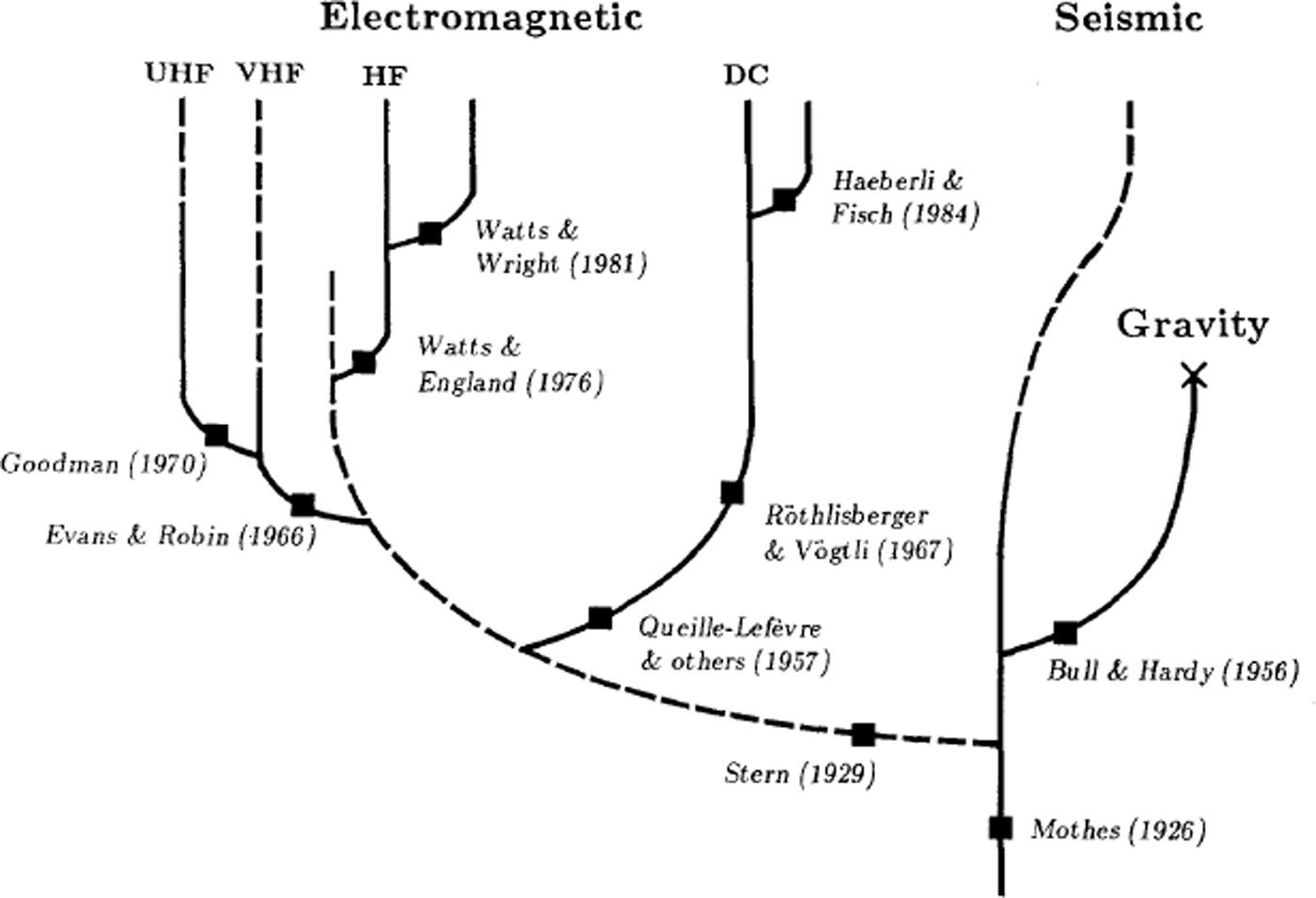
Fig. 2. Milestones in the application of geophysical methods to the depth sounding of glaciers. Thriving branches are indicated by solid lines, non-thriving branches by dashed lines. The symbol × denotes an apparent “extinction event”. Ground-based impulse radars (Watts and England, 1976) have proved so successful that the gravity method has been rendered obsolete and the seismic and VHF radar-sounding methods have lost popularity.

Seismic method

The earliest use of geophysical measurements to determine valley-glacier thickness was by Hans Mothes (1926, 1927, 1929), first on Hintereisferner and later on Grosser Aletschgletscher. Using a rudimentary seismograph and dynamite charges, he measured the P-wave and S-wave velocity of glacier ice and made many depth soundings. On Hintereisferner, he sounded ice as thick as 293 m, and at Konkordia Platz on Grosser Aletschgletscher, he found ice as thick as 792 m. For five decades, seismic sounding remained the preferred method for measuring ice thickness. Glaciers that have been seismically mapped include Rhonegletscher (Gerecke and M¨ller, 1932), and Unteraargletscher (Mercanton, 1936) in Switzerland, South Crillon and Klooch Glaciers in Alaska (Goldthwait, 1936), Highway Glacier in the Canadian Arctic (Röthlisberger, 1955), and Athabasca Glacier in the Canadian Rockies (Paterson and Savage, 1963).

Relative to drilling, seismic sounding is fast and straightforward. Relative to almost anything else, it can be a slow and troublesome business. Richard Goldthwait's (1936, p. 498) unaffectionate description gives a fine sense of what early seismic work was like:

“This seismograph had many drawbacks compared with the modern oil exploration equipment, as follows: its geophones were only moderately sensitive; the amplifier radio tubes deteriorated very rapidly (although they remained good enough for radio uses); the galvanometers leaked damping oil constantly and were extremely difficult to focus; each light source required 11 amperes of current, which is unreasonably great; photographic developing on ice is very slow and impractical; and since the whole apparatus was designed originally for automobile use it weighed nearly 200 lb. (not including dynamite and cables).“

Seismic equipment is also used to detect icequakes and monitor other forms of glacier seismicity. To my knowledge, the first scientific description of icequakes is that of Hugi (1831):

“One day being on the inferior glacier of the Aar, during an intense heat, at three o'clock P.M., I heard a very peculiar noise. I advanced rapidly from 30 or 40 paces, from the side where the noise was heard; I felt the mass of the glacier shake by jolts under my feet, and I soon discovered the cause. A fissure was formed in an instant, the aperture was elongated from 12 to 20 feet, so that I was unable to follow its formation. Sometimes the operation seemed about to cease, and the mass separated itself very slowly; then again the fissure continued to open quickly, and by jolts … During the whole period of my stay on the inferior glacier of the Aar, we were awoke every night, twice or thrice, by the subterranean noises which proceeded from the interior of the glacier. Twice the bed itself which we had dug in the glacier, and which was lined with slates and moss, was violently shaken by jolts analogous to those which I had observed during the formation of fissures; but the shaking appeared so deeply seated, that we could not for a moment entertain the idea that any rent or crevice would open at the surface.“

Neave and Savage (1970) set out to record such icequakes on Athabasca Glacier and found that seismic sources were near the surface and associated with crevasse opening. Hydraulic transients may also contribute to glacier seismicity (St. Lawrence and Qamar, 1979) and it has been discovered that changes in flow rate are associated with the changes in the level of seismicity (Deichmann and others, 1979; Kamb and others, 1985; Raymond and Malone, 1986).

By the 1980s, radar sounding had replaced seismic sounding as the routine method for measuring glacier thickness. A virtue of the seismic method is that it can yield more complete information about the glacier substrate than radar can. Thus, it is unlikely that radar sounding will completely replace seismic methods.

Gravity method

An alternative geophysical tool, the gravimeter, was first used to measure valley-glacier thickness by Bull and Hardy (1956) on Austerdalsbre in Norway. The gravity method works from the fact that ice is substantially less dense than rock and thus, over glaciers, there is a mass deficit that reduces the strength of the Earth's gravitational pull. The main advantage of the gravity method is that the instrument is relatively light and portable, and that measurements can be taken rapidly. The main shortcoming is that it is not a true sounding measurement but rather a measurement of the cumulative gravity effect for the glacier and its surroundings. Thus, interpreting gravity data and estimating ice thickness involves lengthy computations that commonly yield inaccurate estimates of ice thickness. Topographic relief produces a gravity disturbance that can be large and this must be corrected for. For this reason alone, mountainous terrain where valley glaciers are situated is practically the worst possible environment for conducting gravity surveys. An impressive (but virtually solitary) example of the successful application of the gravity method to mapping subglacial geometry is that of Kanasewich (1963) on Athabasca Glacier.

Electromagnetic methods

Interferometry. The first attempt to use electrical methods to measure ice thickness was by Walter Stern (1929, 1930) on the lower part of Vernagtferner in Austria. As a doctoral thesis project, he developed and tested an interferometric apparatus for measuring ice thickness. A continuous oscillating signal was transmitted from a dipole antenna and received by a second antenna placed at some distance from the transmitting antenna. The interference between the direct wave and that passing through ice was observed and from this measurement the ice thickness was calculated. An alternative approach that also proved successful was to measure the capacitative influence of the glacier on his transmitting antenna. Depths in the range 10–40 m were found. Stern (1930) was satisfied that his measurements were successful but he did not attempt to verify his depth interpretations by drilling through the glacier. In recent years, the terminus position of Vernagtferner has retreated so that the bed sounded by Stern is exposed. It can now be confirmed that Stern's pioneering effort was indeed successful (personal communication from Heinz Miller).

To date, the interferometric approach has not received much favour and, compared to radar sounding, it does not seem to be a particularly good method of measuring ice thickness. Rossiter and others (1973) and Strangway and others (1974), without apparently knowing of Stern's work, revived the method in an interesting application. A multi-frequency interferometer (1-32 MHz) was developed for studying the lunar surface and field tested on Athabasca Glacier and Gornergletscher. On Earth, ice is one of the few surface materials that is as resistive as the dry lunar surface.

Pulsed radar. Papers by Waite and Schmidt (1961), Evans (1963), Walford (1964), and Bailey and others (1964) heralded the modern era of glacier-depth sounding (see Bogorodskiy and others (1985) for a review). Amory (Bud) Waite and Stanley Schmidt confirmed that the standard SCR 718 (440 MHz) pulsed radar aircraft altimeter was subject to dangerously large errors when used over ice sheets, and they demonstrated the radio transparency of ice by using this radar to take depth soundings in Greenland and Antarctica. Subsequently, a system operating at 35 MHz was specially designed for ice sounding (Evans, 1963) and successfully tested in Antarctica (Walford, 1964) and Greenland (Bailey and others, 1964). The first application to valley glaciers was by Stan Evans and Gordon Robin (1966) who used a 35 MHz radar for airborne sounding of glaciers in Ellesmere Island. The Ellesmere Island glaciers are a special case in that they are very cold and, in this respect, well suited to VHF equipment. UHF radars were also successfully employed on valley glaciers, at first for ground-based surveys and later from the air. A standard SCR 718 aircraft altimeter, converted to an ice-sounding radar, was used for a ground-based survey of Roslingletscher in East Greenland (Davis and others, 1973). A highly sophisticated 620 MHz radar designed specifically for glacier sounding was developed by Goodman (1970, 1975). The system was mounted in a tracked vehicle and employed digital recording, an on-board computer, and navigation system. Not surprisingly, the equipment was unwieldy and had to be transported by a tracked vehicle. Though complicated, the system unquestionably worked but Athabasca Glacier and Wapta Icefield, the glaciers chosen to test the radar, are temperate and proved difficult to sound. Airborne UHF systems were also successfully employed to measure the thickness of cold, but not temperate, valley glaciers (Narod and Clarke, 1980, 1983; Macheret and Zhuravlev, 1982).

The major break-through in sounding temperate glaciers was the development of impulse radar systems by the United States Geological Survey (Watts and England, 1976). The idea of using impulse radars to sound ice thickness had been proposed by Cook (1960) but more than a decade passed before it was successfully demonstrated on South Cascade Glacier. Sverrison and others (1980) made further improvements and devised a continuous profiling ground-based instrument that they used to survey glaciers in Iceland. Subsequently, an airborne version was developed (Watts and Wright, 1981) and tested on Columbia Glacier, but there is much room for improving airborne impulse radar systems.

Promising but incompletely realized lines of research are the use of radar to measure glacier motion and basal changes (Walford, 1972; Doake, 1975) and to monitor englacial changes (Goodman, 1973, 1975). Goodman interpreted temporal changes in radar returns from Athabasca Glacier as being related to the intraglacial water system, a plausible but as yet unsubstantiated claim. Recently, Jacobel and Raymond (1984) used radar to measure changes in Variegated Glacier that they attributed to internal water movement, and Walford and others (1986) detected englacial radar targets and attempted to deduce some statistical properties of these scattering objects.

Radar sounding has not completely replaced seismic sounding because radar has the disturbing tendency to sound false bottoms, presumed to result from internal debris horizons. With the advent of impulse radars, gravity measurements ceased to be the simplest way to estimate ice thickness. It therefore proved to be the extinction event for the gravity method.

Other electrical methods. The d.c. resistivity method has also been used to sound glacier thickness (Queille-Lefevre and others, 1959; Röthlisberger and Vögtli, 1967). The method is unsatisfactory for ice-thickness mapping but may nevertheless have a bright future as Haeberli and Fisch (1984) have illustrated. In a novel application, they drilled through Grubengletscher, Switzerland, and placed electrodes at the ice-bed interface. From these measurements, they determined that the glacier was resting on thick unconsolidated sediments, not bedrock. As drilling through glaciers becomes simpler and interest in glacier substrates continues to grow, measurements of this type may well become commonplace.

The Frontier

The present frontier of our knowledge of glaciers can be very precisely located - it is the lower boundary between a glacier and its substrate. Here is where water flows, ice slides, and a host of complex interactions between ice, water, rock, and sediment can occur. For obvious reasons, exploration of this frontier is difficult.

Natural and Man-made tunnels have allowed bottom-side viewing of glaciers and permitted imaginative experiments to be conducted. An early study involving Man-made tunnels was that of Haefeli (1951), who carried out scientific investigations in two tunnels beneath Mount Collon glacier, Switzerland, in connection with the Grande Dixence hydro-electric project. McCall (1952) excavated a tunnel to the bed of Skauthoebreen, a thin cirque glacier in Norway, and made direct measurements of the sliding rate, finding that it was steady. Both studies were completed at a time when no worthwhile sliding theories were in place. In contrast, observations by Kamb and LaChapelle (1964) in the Blue Glacier tunnel, Washington, were regarded from the outset as an opportunity to test theory. Weertman's sliding law was found to be qualitatively acceptable but quantitatively lacking.

Permanent tunnels through rock have been driven beneath Glacier d'Argentiere (Vivian and Bocquet, 1973; Vivian, 1980) in France, and Bondhusbreen (Wold and Østrem, 1979) in Norway. In both cases, the tunnels are part of schemes to divert subglacial water to hydro-electric stations. The Glacier d'Argentiere tunnel provides ready access to four subglacial cavities that have become a virtual subglacial laboratory. Sliding variations have been reported (Vivian and Bocquet, 1973; Bocquet and Ricq, 1977; Vivian, 1980), basal stress and glacial abrasion have been directly measured (Boulton and others, 1979), and curious subglacial strain events have been recorded (Goodman and others, 1979).

A tunnel excavated into the margin of Breidamerkur-j¨okull (Boulton, 1979) in Iceland has special significance because it is the only tunnel that reveals a glacier resting on soft deformable material. Observations in that tunnel have disclosed a fourth important sliding mechanism, bed deformation.

Trends in Scientific Style

One way to discover trends in glacier studies is to examine the Journal of Glaciology. Figure 3 shows that glacier studies have remained an important and relatively stable component of Journal content. Roughly 30% of the Journal is devoted to reporting valley-glacier research and this component has not changed significantly over the life of the International Glaciological Society. It is also evident that glacier studies have kept pace with the development of the science of glaciology as a whole. As the Journal of Glaciology has grown, so too have new journals appeared: Zeitschrift fur Gletscherkunde und Glazialgeologie (revived and re-named in 1949) from Austria, Jokull (started in 1951) from Iceland, Materialy Glyatsiologicheskikh Fssledovaniy, Khronika, Obsuzhdeniya from the U.S.S.R., Cold Regions Science and Technology (started in 1979) from The Netherlands, Journal of Glaciology and Cryopedology (started in 1979) from China, and Annals of Glaciology (started in 1980) from the United Kingdom.

Fig. 3. Valley glacier content of the Journal of Glaciology.

Although glacier studies are a stable component of scientific glaciology, the style has evolved significantly since the early days of the International Glaciological Society. All of us can discern the co-existence of several distinct schools within the science of glacier studies. One of these schools is largely comprised of geologists and physical geographers, and a second by physicists. As a rough indicator of trends in scientific style, I have counted the number of maps and the number of equations in articles written on valley glaciers in the Journal of Glaciology. The results are interesting (Fig. 4). In 1947, when the Journal first began publication, I calculate that 21.8 pages were devoted to reporting valley-glacier work. One equation appeared (Perutz, 1947) and one map (Seligman, 1947). Thus, the rate of equations equalled the rate of maps per page. Over the years, the map rate (which I think tends to reflect contributions from the geology/geography school) has remained reasonably constant. The equation rate, however, reveals pronounced peaks superimposed upon a strong upward trend. The peaks can often be labelled. The first peak (B) can be attributed to Henri Bader (1950), the second (Nl) to John Nye (1952[a], [c]), the third (RR) to Gordon Robin (1955) and Hans Röthlisberger (1955), and the fourth (N2) to Nye (1959[a], [b]) again. I have skipped the years 1962-79, and the final peak (HL) is attributed to Kolumban Hutter and others (1981), and to Lliboutry and Reynaud (1981). Whatever one makes of this analysis, it is apparent the style of our science has changed enormously since the Journal began publication.

Fig. 4. Maps and equations in the Journal of Glaciology. The peaks are labelled to indicate the main contributors to each peak: B (Bader, 1950), Nl (Nye, 1952[a], [c]), RR (Robin, 1955; Röthlisbergei; 1955), N2 (Nye, 1959[a], [b]), and HL (Hutter and others, 1981; Lliboutry and Reynaud, 1981).

Examination of the Journal also reveals that, in early issues, maps and equations never appeared in the same article (Fig. 5). The first Journal contributor to hit on the idea of combining maps and equations in a single article was Haefeli (1952), followed by Röthlisberger (1955). This approach to glaciology has continued to gain favour and over the period 1980-83 more than 25% of the Journal articles on valley-glacier research contained both maps and equations (Fig. 5). I suggest that three different schools can now be identified and propose to name these, after their exemplars: the “Lewis school” (a physical geography/geology emphasis (e.g. Lewis, 1938)), the “Nye school” (a mathematical physics emphasis (e.g. Nye, 1951, 1957, 1960, 1970)), and the “Röthlisberger school” (a geophysical emphasis (e.g. Röthlisberger, 1955)). It is pointless to reflect on the observation that subglacially we have Nye and Röthlisberger channels, while supraglacially we have Nye and Röthlisberger schools.

Fig. 5. Evidence for the existence of the “Lewis school” (maps and no equations), the “Nye school” (equations and no maps), and for the emergence of the “Röthlisberger school” (maps and equations).

The differences between the geography and physics schools are substantial. Geographers tend to view glaciers as either a collection of geomorphological features or an intricate network of interacting processes. Physicists, on the other hand, tend to strip away detail. As Nye (1972, p. 265-66) put it:

“One of the most important tasks of the physicist is to examine the phenomena and to identify those situations that are essentially simple, or better, simplifiable … In this I have come to believe that the physicist parts company in a fundamental way from the geographer and the geologist. The exact recording of the complexity of nature is a necessary early state in any science, but a delight in complexity of this sort is no part of the physicist's outlook.“

A reason that mathematical physicists seek simplicity is that only the simplest problems yield closed-form mathematical solutions. Non-linearity and coupling, two essential features of realistic glacier models, tend to rule against simple solutions. Here, I think, high-speed computers are coming to the rescue and exerting a counter-influence on the reductive eye of the mathematical physicist. Using the mathematical physicists’ results as building blocks, the computer modellers are constructing models of increasing complexity and perhaps of increasing realism as well. In their delight in complexity, the modellers share something with the geologists and geographers and, in the end, may be the agents for joining the two main streams of glacier studies.

Final Remarks

The foregoing historical account contains distortions that must be confessed. One that I regret is (hat I have relied largely on English-language sources and most of my entry points to the substantial European literature have been through what traces of it protrude into English-language sources, primarily the Journal of Glaciology. As a weak justification of what was for me a necessary choice, this history was written to mark the occasion of the fiftieth anniversary of the International Glaciological Society, and the Journal is the Society's major publication. A second distortion was intentional. I have employed a kind of reversed perspective that enlarges the past, starting from the time of Agassiz and Forbes, and shrinks as the present is approached. Lastly, this is not a comprehensive scientific review. Some valuable ones that together span the history of Alpine glaciology include Agassiz (1840, 1967), Forbes (1842[d]), Heim (1855), Hess (1904), Evans (1913), Matthes (1942), Koechlin (1944), Klebelsberg (1948-49), Charlesworth (1957), Lliboutry (1964-65, 1971[b]), Shumskiy (1978), Raymond (1980), Paterson (1981), and Hutter ([c1983]).