Although sex differences in psychosocial and behavioural aspects of weight gain and weight loss have been described( Reference Sarlio-Lähteenkorva, Rissanen and Kaprio 1 – Reference Parmenter, Waller and Wardle 6 ), very little attention has been paid to sex differences in potential physiological factors. One such factor is the composition of weight change in terms of fat-free mass (FFM) and fat mass (FM). FFM and FM differ by 9-fold in their energy content/kg, and a lower percentage of FFM (%FFM) and 37 % higher energy content of weight gain have been reported in obese women, compared with men, by Pietrobelli et al. ( Reference Pietrobelli, Allison and Heshka 7 ). According to these authors, this implies more weight change in men than in women for a unit energy imbalance. However, some years ago, a dynamic model of human body weight regulation was proposed by Payne & Dugdale( Reference Dugdale and Payne 8 – Reference Payne and Dugdale 10 ), which predicted the opposite influence, i.e. less weight change and a lower equilibrium body weight for subjects who partitioned a higher proportion of their energy intake into protein and FFM than into FM. The reason for this was that, compared with that of FM, the deposition of dietary energy as protein and FFM was identified as much less energetically efficient and the metabolic rate of the deposited FFM was much higher than that of FM. This reduced the magnitude of positive energy balance when FFM was deposited and more than compensated for the lower tissue energy density of FFM. Within this model( Reference Dugdale and Payne 8 – Reference Payne and Dugdale 10 ), the %FFM of weight gains or losses is defined as a phenotypic energy-partitioning P-ratio (protein energy as a fraction of total energy gained or lost). Thus, men who have a higher P-ratio should exhibit less weight change and achieve a lower equilibrium weight than women with the same energy imbalance. Subsequent models of weight regulation modelling the relative FFM and FM contents have used different assumptions and approaches related to the determination of FFM change relative to FM( Reference Forbes 11 – Reference Thomas, Das and Levine 17 ), and the main assumptions of the Payne and Dugdale model have been criticised( Reference Dulloo and Jacquet 14 , Reference Hansen and Lambert 18 – Reference Millward and Wijesinghe 20 ). It is also not clear whether the observed sex dimorphism in the %FFM of weight gain( Reference Pietrobelli, Allison and Heshka 7 ) is generalisable to weight loss, especially given the potential influence of time-dependent protein-sparing adaptive changes( Reference Elia and Parkinson 13 , Reference Wijesinghe, Millward and Rivers 19 , Reference Elia 21 , Reference Cahill 22 ) and external factors such as dietary protein content( Reference Krieger, Sitren and Daniels 23 ). Taken together, these raise several questions about the predictability of any sex dimorphism in the %FFM of weight loss as a potential influence on the extent of weight loss.
Diet Trials, a multi-centred, large-scale, UK randomised controlled study, was designed to examine the efficacy of four popular commercially available weight loss programmes( Reference Truby, Baic and deLooy 24 ). It involved measurements of initial body composition by dual-energy X-ray absorptiometry (DEXA) and of anthropometry in 300 overweight and obese adults before and at 2 and 6 months during weight loss on four different dietary regimens and in a no-diet control group. Sex was not taken into account in the study design, and more women than men were recruited. Nevertheless, the relative number of men and women studied does allow the effects of sex on the P-ratio of excess weight at baseline to be determined from a cross-sectional analysis and the P-ratio of weight loss to be determined from the longitudinal measurements. The results obtained from these investigations allow the hypothesis to be tested that contrary to the Payne and Dugdale prediction( Reference Dugdale and Payne 8 – Reference Payne and Dugdale 10 ), men with a higher P-ratio (lower energy density) of their excess weight exhibit greater weight loss than women with a lower P-ratio (higher energy density) during similar, albeit unsupervised, dieting regimens. The results also allow the effects of dietary composition and duration of the dieting regimen on the relationship between the extent of weight loss and its P-ratio to be examined, albeit to a very limited extent, since the study was not powered to examine any diet and sex interactions.
Methods
The present study was conducted according to the guidelines laid down in the Declaration of Helsinki.
Participants
The study design has been described in detail elsewhere( Reference Truby, Baic and deLooy 24 , Reference Morgan, Griffin and Millward 25 ), where the effect of dietary regimen on weight and fat loss and cardiac risk factors has been described on an intention-to-treat basis and for completers. The study was a multi-centred, randomised controlled trial of four diets: Dr Atkins' New Diet Revolution; The Slim-Fast Plan; Weight-Watchers Pure Points programme; Rosemary Conley's ‘Eat yourself Slim’ Diet and Fitness Plan, against a control diet, in parallel for 6 months. From five regional UK university centres, Surrey (Guildford), Nottingham, Ulster (Coleraine), Bristol and Edinburgh (sixty participants per centre), 300 overweight and obese men and women, aged 21–60 years with a BMI between >25 and < 40 kg/m2, were recruited. Exclusion criteria for potential participants were prior histories of CHD, known type 1 or 2 diabetes, liver or respiratory failure, gout, use of lipid-lowering or antihypertensive drugs, history of obesity with known cause (i.e. Cushing's disease and hypothyroidism), previous gastric or weight loss surgery, use of any weight loss drug (including Orlistat or Sibutramine), clinical depression, eating disorders, drug or alcohol abuse, any malabsorptive state (including lactose intolerance), treatment for a malignancy, pregnancy or breast-feeding. The participants gave written informed consent for participation in the study. Ethical approval for the study was obtained from the South East Multi-centre Research Ethics Committee: approval number MREC 01/01/44. Local ethics committee approval was also obtained at each centre.
Study design
The participants visited the test centres at the start of the study and 12 and 24 weeks after the commencement of the study. They were weighed in light clothing, blood pressure and waist circumference were measured, and fasting venous blood samples were collected for the measurement of insulin, glucose and lipid concentrations. Waist circumference was measured at the midpoint between the iliac crest and the lower ribs.
Body composition in terms of FM, FFM and bone mineral content (BMC) was measured by DEXA. The instruments used were Hologic QDR 4500 fan beam (two centres), Lunar Prodigy fan beam (two centres) (GE Healthcare) and a Lunar DPX-1 pencil beam (one centre) (GE Healthcare). A single phantom was used to assess the varying characteristics of the five instruments with respect to a sixth reference centre on two occasions. Because systematic variation in the absolute estimates of body composition determined by DEXA can arise from different hardware and software combinations( Reference Tothill, Avenell and Love 26 – Reference Schoeller, Tylavsky and Baer 29 ), the performance of individual instruments was assessed in terms of z-scores (difference between each instrument and the mean value for all the six instruments expressed as a fraction of the overall standard deviations (n 12)). In addition, the characteristic relationships between body weight and body FM and FFM recorded at each centre were also examined. These investigations indicated between-instrument variations in FM and FFM measurements. In the absence of any absolute independent measure of FM and FFM, a body weight-dependent adjustment algorithm was constructed. This involved initially generating sex-specific regressions of FM and FFM on body weight for the entire cohort and for each centre. Data obtained from centres with similar instrument performances were combined, resulting in two groups, namely centres 1 and 2 (Hologic QDR 4500 fan beam) and centres 3 and 4 (Lunar Prodigy fan beam) and 5 (Lunar DPX-1 pencil beam). Sex-specific regressions of FM and FFM on body weight were derived from the data obtained for the two instrument groups and from those obtained for the entire cohort. Each of the two combined regressions was then used to predict FM and FFM for body weights ranging from the minimum to the maximum for the entire cohort. These values were compared with FM and FFM values predicted by the overall cohort regression, enabling the calculation of body weight-dependent error values for FM and FFM for the two instrument groups. The slopes and intercepts of the regression of these error terms on body weight were then used to adjust (increase or decrease) the original values of FM and FFM as a function of body weight and centre. In this way, the measured values were adjusted for average instrument differences while retaining any other variance in the measurements. This adjustment, by its nature, will not influence the overall mean values of FM or FFM as a function of sex, time of measurement or diet, but will influence the magnitude of the variance.
It should be noted that because of the cross-sectional nature of the measurements at baseline, the interrelationships between FM, FFM and body weight, which indicate the sex-specific FM and FFM contents of excess body weight, are not strictly the same as might be obtained from the longitudinal measurements of weight gain if such studies could be carried out. However, the study at baseline did include BMI values that varied over a wide range (from 26·4 to 39·1 in women and 26·6 to 37·7 in men) so that the relationships between increasing FM and FFM and body weight can reasonably be assumed to be similar to the actual longitudinal changes during weight gain.
Statistical analysis
The analysis of the effect of dietary regimen on weight and fat loss and cardiac risk factors on an intention-to-treat basis and for completers has been reported previously( Reference Truby, Baic and deLooy 24 ). Herein, the main focus of the analysis was to (1) establish the magnitude of the P-ratio for men and women during weight gain and weight loss and (2) test whether any sex differences in the P-ratio influenced sex differences in weight loss in terms of a direct relationship as commonly assumed( Reference Pietrobelli, Allison and Heshka 7 ) or inversely as predicted by the Payne and Dugdale model. The effect of diet and sex on the composition of weight loss was also examined recognising that the study was insufficiently powered to examine diet–sex interactions securely. No attempt was made to examine the results in relation to any other models of weight regulation( Reference Forbes 11 – Reference Thomas, Das and Levine 17 ). This will be done in a separate report.
The composition of increasing body weight for the entire cohort was examined as the non-standardised multiple regression coefficients of unadjusted FM, FFM and BMC on weight and height. This assumes linear relationships within the range of body weights represented by this cohort (BMI from 26·4 to 39·1). The validity of the assumption was examined by visual inspection of the linear regressions of height-adjusted FM and FFM with body weight. It was clear that the assumption of linearity was reasonable with no indication of more complex relationships. The slopes of the linear regressions of FM and FFM on weight after height adjustment should be similar to the non-standardised multiple regression coefficients of FM and FFM on weight and height. The adjustment of height to the sex-specific average height of the cohort, 1·63 m for women and 1·78 m for men, involved multiplying individual values of FFM and FM by 1·632/H 2 for women and by 1·782/H 2 for men. In this analysis, body weight was the value derived from the DEXA (i.e. FM+FFM+BMC).
The influence of the four intervention diets on the composition of weight loss in terms of FM and FFM was examined by an analysis of all the subjects scanned at least twice, i.e. at baseline and 2 months, baseline and 6 months, and at both 2 and 6 months. As a result of this, the 0–2-month population group was slightly larger than the 0–6-month group owing to some dropouts after the 2-month scan. The control non-intervention group was not included in the analysis because weight change in this group was generally small and involved highly variable amounts of gains and losses. FM loss was analysed by a factorial ANCOVA of sex and diet with FM0 as a covariate. For FFM loss, ANOVA of sex and diet was used without a covariate, because baseline FFM was not correlated with FFM loss within each sex. Contrast analysis was used to test the significance of the group differences.
The composition of weight gain and weight loss was calculated in terms of an energy-partitioning parameter, the P-ratio, which is protein energy (gained or lost) as a fraction of total tissue energy (protein+fat) gained or lost. This can be expressed in terms of changes in FM and FFM by the following equations:
where 9·05 is the ratio of energy equivalents for FM (38·9 MJ/kg) and FFM (4·3 MJ/kg)( Reference Dulloo and Jacquet 14 ). For P-ratiogain, the cross-sectional analysis at baseline only allowed calculation of the mean values from the multiple regression coefficients for FM and FFM against weight at baseline. For P-ratioloss, because calculations of the ratios of losses of FFM and FM as the difference between successive scans can result in spurious values when such differences are small and may include some gains as well as losses, for the entire cohort, the best estimates of mean sex and dietary treatment-specific P-ratioloss were calculated from the observed mean values of ΔFM and ΔFFM of all the subjects between baseline and 2 months, 2 and 6 months, and baseline and 6 months. Because no statistical analysis was possible for this set of mean P-ratio values, individual values of P-ratioloss were also calculated after trimming to remove spurious values. The trimming approach involved cut-off levels that were based on the magnitude of smallest detectable values of ΔFM and ΔFFM by the DEXA scanners calculated from the CV of repeat measurements of the phantom at each centre (FM: 2·25 % and FFM: 2·47 %). These were 0·8 kg FM (men and women) and 1·67 kg FFM (men) and 1·1 kg FFM (women). The subjects were excluded from the analysis if FM or FFM losses were less than these values. Such trimming should not, by its nature, influence sex differences, but will allow the analysis of the characteristics of the P-ratios in relation to the extent of weight loss within a secure set of values. However, because the trimming will remove unsecure P-ratios unpredictably, the sex- and diet-specific means of this subsample cannot be assumed to be the same as the overall population group means. Trimming was not attempted for FM and FFM losses after 2 months, because FFM loss decreased to levels below the detection threshold for most subjects and only a very small number of subjects fulfilled the selection criteria (fourteen women and five men).
For this trimmed subset, FM and FFM losses and P-ratios were analysed by ANOVA of sex and diet, because neither baseline FM or FFM correlated with FM or FFM loss within each sex. Contrast analysis was used to test the significance of the differences.
Data are reported as means with standard deviations or 95 % CI, and P values < 0·05 were considered statistically significant. Data were analysed using the Statistica statistical package v6 (Statsoft).
Results
Dual-energy X-ray absorptiometry instrument characteristics
ANOVA showed no effect of test centre on weight, height or BMI, but it did show differences in FM and FFM as a function of the different DEXA instruments. This was apparent on comparing the measured FM or FFM values at each centre with the values predicted from body weight by means of the sex-specific regression equations of measured FM or FFM on body weight derived from the overall dataset. This indicated that in men and women examined at centres 1 and 2 the measured amounts of FM were lower (2·3–2·6 kg) and FFM higher (2·3–2·7 kg), while at centres 3, 4 and 5, those of FM were higher (1·5–1·8 kg) and FFM lower (1·6–1·9 kg). The adjustment algorithm removed any significant between-centre differences in FM and FFM and reduced the variance in the cohort mean values of FM and FFM by up to 15 % for women and 10 % for men, but did not change those of FM, FFM or total DEXA-measured body weight. The minor corrections did not influence any conclusion reported herein about the interrelationships between FFM and FM at baseline or P-ratios for tissue loss. The sum of the adjusted DEXA-derived values for men and women together (i.e. FM+FFM+BMC) was 98·7 % of weight (sd= 1·6, maximum = 107·7 and minimum = 93·3), with the linear regression indicating DEXA total = 1·66+0·968 × weight, r 0·99.
Anthropometry and body composition of the cohort
For subjects for whom a complete set of measurements was taken at baseline (n 287), BMI, FM, FFM and BMC (data not shown) were independent of age. As shown in Table 1, mean BMI was slightly higher for men than for women (32·0 (sd 2·7) v. 31·0 (sd 2·5) kg/m2, P ≤0·005), with fewer men with BMI values in the overweight range (between >25 and < 30 kg/m2) than women (28 v. 41 %). Waist circumference was higher in men than in women (111 (sd 8·3) v. 97 (sd 8·6) cm, P ≤0·0001), as was the waist circumference:height ratio (men: 0·62 (sd 0·04); women: 0·59 (sd 0·05); P< 0·0001). Although women were, on average, lighter and shorter, FM was higher in absolute terms, more so after correction for height. FFM was higher in men, a difference that persisted after correcting for height.
Table 1 Characteristics of the study population of overweight and obese men and women (Mean values and standard deviations; minimum and maximum values)

FM, fat mass; FFM, fat-free mass.
Interrelationships between fat-free mass and fat mass at baseline
The multiple regression results are given in Table 2. Within the age range studied (20–61 years), there were no significant effects of age for either sex. FM was significantly predicted by weight and height (inversely) in women and by weight in men. FFM was significantly predicted by weight and height (positively) in women and by weight in men. BMC was significantly predicted by height in women and by weight in men. The coefficients for weight and their 95 % CI indicate that at the same height for each sex, FM and FFM comprise 73 (67–78) and 27 (22–33) % of increasing weight for women and 58 (47–68) and 40 (30–51) % for men. These values were very similar to the slopes of the linear regressions shown in Fig. 1. For these data, linear relationships of FM and FFM with body weight, each adjusted to the sex-specific mean height, best explained the variance in FM (61–78 %) and FFM (33–46 %) within this weight range. Thus, the data are explained by a simple model in which increasing weight involves the sex-specific fixed ratios of increases in FFM and FM. For men, the regressions for FFM and FM have heights and slopes, which ensure that FFM exceeds FM up to (and beyond) the highest weights examined: i.e. at any level of obesity. In contrast to women, the much steeper slope for FM than for FFM (0·73 v. 0·27) indicates that at weight values in excess of 105 kg (BMI values in excess of 36), FM may exceed FFM.
Table 2 Multiple linear regression of fat mass (FM), fat-free mass (FFM) and bone mineral content (BMC) on weight and height in subjects at baseline (Regression coefficients, 95% confidence intervals and P-ratios)
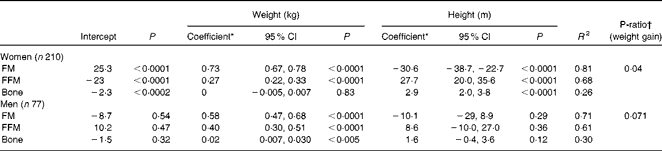
* Non-standardised regression coefficient (weights) in multiple regressions of FM, FFM and BMC on weight and height.
† P-ratio, protein energy as a fraction of total energy of increasing weight: i.e. FFMcoefficient/(FFMcoefficient+9·05 × FMcoefficient).
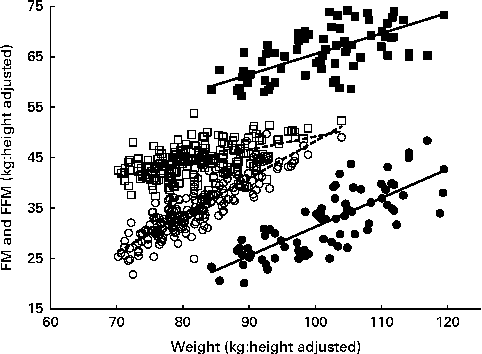
Fig. 1 Relationship of height-adjusted fat-free mass (FFM, □, ■) and fat mass (FM, ○, ●) with weight in overweight and obese men (■, ●) and women (□, ○). Regression equations: men – FM = − 25·9+0·57 × weight (r 2 0·61, P≤ 0·0001), FFM = 24·8+0·41 × weight (r 2 0·46, P≤ 0·0001); women – FM = − 25·1+0·73 × weight (r 2 0·77, P≤ 0·0001), FFM = 22·72+0·26 × weight (r 2 0·32, P≤ 0·0001).
The slopes of the regressions shown in Fig. 1 are reasonably accurate estimates of the proportions of weight gain accounted for by FM and FFM and are similar to the values obtained by the multiple regressions of FM, FFM and BMC on weight and height (Table 2). This indicates P-ratios for the increasing weight of 0·040 for women compared with 0·071 for men. Some of the subjects included in the regression given in Table 2 did not lose weight or were not scanned at 2 months and so represent a population group that is slightly different from those for whom the %FFM and P-ratios of weight loss at 2 months were measured. For this population, baseline regression coefficients and 95 % CI were not substantially different from the values given in Table 2: i.e. women (n 143): FM = 0·71 (0·64–0·77) and FFM = 0·29 (0·23–0·36); men (n 56): FM = 0·54 (0·40–0·68) and FFM = 0·44 (0·30–0·58). The overall body composition as indicated by these regressions at baseline was not altered by weight loss over the 6-month study period: i.e. the regression coefficients for FM and FFM were not significantly different at baseline and 6 months for the subgroup of women and men who lost some weight at 6 months (data not shown).
Weight loss
As has been described previously(24), when analysed on an intention-to-treat basis with no sex separation, there were no between-intervention diet differences in loss of body fat and weight over the 6-month trial. For the present analysis of sex-separated completers, weight loss (which can be inferred from the values for FM and FFM losses in Table 3) was significantly higher for men than for women at 2 months (7·34 v. 3·80 kg) and at 6 months (10·3 v. 6·27 kg). Dietary treatment was not a significant factor either at 2 or 6 months. The distribution of men and women between dietary groups did not differ markedly, ranging from 23·3 % (RC, Rosemary Conley's Diet and Fitness Plan) to 31·4 % (WW, Weight-Watchers programme), and did not appear to be a confounding factor in the analysis of dietary effects. Thus, the Atkins group, which exhibited the highest mean value for weight loss, had a proportion of men (28·3 %) that was similar to the mean proportion in the entire cohort (28·2 %). For diet–sex interactions on weight loss, at 2 months, there were no dietary effects for women, but for men, the effects were greater for the Atkins group than for the WW group, although these groups did not differ from the RC or SF (The Slim-Fast Plan) group. At 6 months, there were no diet–sex interactions.
Table 3 Fat mass (FM) and fat-free mass (FFM) loss and P-ratios of weight loss for all subjects (Mean values, 95 % confidence intervals and P-ratios)

A, Atkins Diet; RC, Rosemary Conley's Diet and Fitness Plan; SF, The Slim-Fast Plan; WW, Weight-Watchers programme.
* P-ratios (P = (ΔFFM)/(ΔFFM+9·05 × ΔFM)) calculated from weighted mean values for loss of FFM and FM for all groups at the stated time periods apart from for the two groups shown where the average change in FFM was a gain (ΔFFM = negative): i.e. diet group A, 2–6 months; and subgroup men, A, 2–6 months.
† Values are weighted means from factorial ANCOVA for all subjects with 95 % CI with baseline FM as covariate. Where ANCOVA indicates a significant effect, homogeneous groups are shown with the same superscript.
‡ Values are weighted means from factorial ANOVA for all subjects with 95 % CI. Where ANOVA indicates a significant effect, homogeneous groups are shown with the same superscript.
Fat mass loss: all subjects on intervention diets
Those allocated to the intervention diets lost, on average, 3·5 and 6·1 kg FM at 2 and 6 months, respectively; weight loss was more in men at 2 and 6 months (4·99 and 7·68 kg) than in women (2·95 and 5·38 kg). FM loss varied with initial FM in women and men (P ≤0·03) and was analysed by ANCOVA with baseline FM as a covariate. Weighted means for FMloss (Table 3) indicate that FM loss was significantly higher in men at all time intervals (0–2 months, 2–6 months and 0–6 months), although post hoc testing at 2–6 months showed no difference. The significant dietary effect at 0–2 months (P< 0·0001) reflected the greater loss for male subjects in the Atkins group, compared with all the other intervention subjects. After 2 months, subjects in the Atkins and SF groups did less well and those in the RC group did better, so that by 6 months there were no significant differences between the intervention groups. Overall, these responses indicate that there were only minor differences in the effectiveness of the intervention groups in achieving FM loss, apart from an initial, but not sustained, better response among men in the Atkins group. There was a similar pattern of FM losses between those who lost weight (data not shown), except that no dietary effects were observed for FM loss between 2 and 6 months.
Fat-free mass loss: all subjects on intervention diets
As shown in Table 3, FFM loss at 2 months was much more marked than that between 2 and 6 months. Men lost three times more FFM than women (P ≤0·0001) at 2 months and over the entire 6-month study period, and there were no dietary effects. As indicated by the higher P-ratio at 2 months for men, the FFM content of weight loss was also almost twice that for women. After 2 months, FFM loss was markedly reduced over the remaining 4 months, and because of the continued FM loss during this period, FFM accounted for only a very small proportion of weight loss during this period: i.e. P-ratios of only 0·009 and 0·006 for men and women with no sex effects. Because of this, the pattern of absolute FFM losses calculated over the entire 6-month study period was similar to that observed at 2 months, i.e. a marked sex effect but no dietary effect. However, FFM loss as a proportion of weight loss over the 6 months was much lower than that in the 2-month period, i.e. P-ratios of 0·037 and 0·018 for men and women, respectively. This indicates a change in the composition of weight loss with time in both men and women involving some protein conservation. For those who lost weight (data not shown), there were no dietary effects for FFM loss at 0–2, 2–6 or 0–6 months. Overall, these responses indicate an obvious effect of sex on both absolute and relative amounts of FFM loss, with higher values for men than for women being observed for all the diets, a difference that was reduced over time. However, all the intervention diets appeared to be similar in terms of FFM loss over the 6 months.
Fat mass and fat-free mass losses and P-ratios of the selected subset at 2 months
A total of seventy-eight subjects fulfilled the selection criteria for smallest detectable values of ΔFM and ΔFFM at 2 months (Table 4). The individual P-ratios are shown in Fig. 2, plotted as a function of weight loss. Although the weight loss threshold for inclusion was set higher for men, 2·47 kg, than for women, 1·9 kg, a higher proportion of women than men were excluded, with the subset representing 33 % of the women and 62 % of the men. This indicates that more women exhibited only very small amounts of weight loss than men. The cut-off levels for FM and FFM losses would correspond to P-ratios of 0·13 (women) and 0·19 (men), but did not preclude subjects with P-ratios greater than these values, as indicated in Fig. 2 for one woman. However, it is clear that the selected subjects mainly had P-ratios less than these values. The characteristics of the subset reflect those of the entire cohort, a significant sex dimorphism, with greater losses of FM and FFM and overall weight in men than in women and a higher %FFM loss as indicated by the higher P-ratio for men. The mean values for P-ratiosloss at 0–2 and 2–6 months for men and women for the whole cohort are also shown in Fig. 2.
Table 4 Fat mass (FM) and fat-free mass (FFM) losses at 2 months for the selected subset of subjects* (Mean values and 95 % confidence intervals)

A, Atkins Diet; RC, Rosemary Conley's Diet and Fitness Plan; SF, The Slim-Fast Plan; WW, Weight-Watchers programme.
* Subjects selected fulfilled the selection criteria for the smallest detectable values of ΔFM and ΔFFM: i.e. 0·8 kg FM (men and women) and 1·67 kg FFM (men) and 1·1 kg FFM (women).
† Values are weighted means from factorial ANOVA for all the subjects with 95 % CI. ANCOVA for FM loss indicated that baseline FM was not a significant predictor. Where ANOVA indicates a significant effect, homogeneous groups are shown with the same superscript.
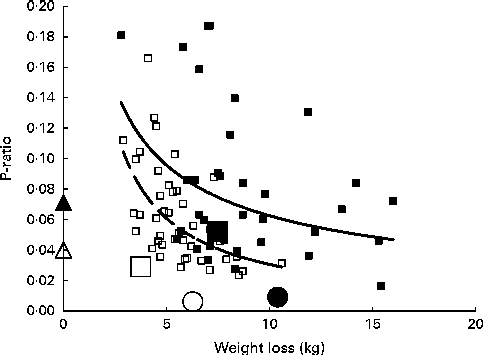
Fig. 2 Relationship between the energy-partitioning parameter (P-ratio) and the extent of weight loss. Individual P-ratios for weight loss at 2 months calculated for a subset of subjects fulfilling the selection criteria for minimum detectable differences in loss of fat mass (FM) and fat-free mass (FFM) (see text), plotted against weight loss: ■, men; □, women. The lines shown are power curves fitted separately to male (![]() ) and female (
) and female (![]() ) values; i.e. men (
) values; i.e. men (![]() ): P = 0·257 × weight loss− 0·61 (R
2 0·14), women (
): P = 0·257 × weight loss− 0·61 (R
2 0·14), women (![]() ): P = 0·301 × weight loss− 0·993 (R
2 0·38). Mean P-ratios v. weight loss for all subjects calculated from (a) baseline regressions given in Table 2, i.e. mean P-ratios of gain, men (▲), women (△); or from mean values for loss of FFM and FM shown in Table 3 at 2 months, men (■), women (□): or between 2 and 6 months – men (●); women (○), plotted against weight loss at either 2 or 6 months.
): P = 0·301 × weight loss− 0·993 (R
2 0·38). Mean P-ratios v. weight loss for all subjects calculated from (a) baseline regressions given in Table 2, i.e. mean P-ratios of gain, men (▲), women (△); or from mean values for loss of FFM and FM shown in Table 3 at 2 months, men (■), women (□): or between 2 and 6 months – men (●); women (○), plotted against weight loss at either 2 or 6 months.
Within each sex, there was a significant inverse relationship between P-ratio and weight loss best fit by inverse power curves explaining 14 and 38 % of the variance for men and women, respectively. These relationships indicate that P-ratio0–2 months is lower over the observed range of weight loss levels at any weight loss level for women compared with men, although at the subthreshold weight loss level, the predicted sex differences become less. For the entire cohort, the sex-specific mean P-ratio0–2 months values were below the sex-specific regressions for the subset, but for this larger population group, their values in relation to weight loss, higher for men than for women, were nevertheless consistent with comparable sex-specific regressions. Fig. 2 also shows that after 2 months with further weight loss, the cohort mean values for P-ratio2–6 months were lower than those at 2 months, especially for men, so that the values were no longer related to weight loss or sex.
Comparison of P-ratiosloss and P-ratiosgain
The present study does not indicate the magnitude of the P-ratio of initial weight loss. Compared with the P-ratios for weight gain (Table 2, 0·040 for women and 0·071 for men), the mean P-ratios for weight loss at 2 months for all the subjects on the intervention diets were slightly lower (Table 3, 0·029 for women and 0·052 for men). This comparison is made in Fig. 2, with P-ratiosgain for women and men being indicated on the Y-axis (i.e. corresponding to zero weight loss). However, the implication of the relationship between weight loss and P-ratio in Fig. 2 is that for small amounts of weight loss, the P-ratioloss is much higher than the P-ratiogain. At body weight losses of 2·47 and 1·9 kg for men and women (the cut-off levels for minimum detectable FM and FFM losses), the inverse power curves predict P-ratios of 0·148 (men) and 0·159 (women).
Discussion
Although the multi-centre design of Diet Trials enabled a larger cohort to be tested than could be managed by a single centre, it does require protocols to be followed strictly at each centre. In fact, the only identifiable effect of centre on the results was the small differences associated with the different types of DXA instruments, which were accounted for by the adjustment algorithm described above. However, the present study has several obvious limitations. First, sex was not a consideration in the study plan and more women than men were recruited, although randomisation was stratified by sex to account for this. For the baseline cross-sectional analysis, the numbers, age and size characteristics of men and women were such that the analysis could be assumed to be robust. This can also be assumed for the analysis of weight loss for sex. However, for the diet–sex interactions, the study was clearly underpowered, especially for the subset analysis summarised in Table 4, and we have, therefore, limited the discussion of these results below. Second, the analysis of the effects of sex on weight and FFM loss could not exclude differential compliance to the regimens, because Diet Trials did not involve any attempt to control compliance. However, we believe this to be unlikely since (1) a detailed analysis of dietary change showed that macronutrient intake altered in the expected direction of the programme to which the participants were randomised( Reference Truby, Hiscutt and Herriot 30 ) and we observed no indication of differences between men and women in terms of the degree of energy restriction; (2) the overall ranges of responses in terms of weight loss over the 6 months were similar: i.e. − 2·4–20·0 kg for women and 2·1–24·0 kg for men; and (c) the effect of sex on weight and FFM loss was observed in the subset selected after trimming for minimum detectable differences. This trimming would have removed non-compliant male and female subjects.
The present study shows that the well-known sex dimorphism in relative FM and FFM for adults of normal body weight is also observed for the composition of excess weight in obesity and that of weight loss occurring in response to weight-reducing regimens. Thus, the %FFM and P-ratios of both excess weight and initial weight loss in the overweight/obese are lower for women than for men. For excess weight, the lower %FFM for women (27 %, P-ratio = 0·040), compared with men (40 %, P-ratio = 0·071), is consistent with the sex dimorphism indicated by the regression analysis of in vivo neutron-activation body composition measurements( Reference Pietrobelli, Allison and Heshka 7 ). In the latter studies, the energy values assigned to FM and FFM were 39·3 and 3·8 kJ/kg, and the overall energy content calculated for a healthy normal-weight woman or man gaining 20 kg was 28·5 MJ/kg for women and 20·9 MJ/kg for men. Our regression coefficients correspond to energy values for weight gain of 29·7 MJ/kg for women and 24·3 MJ/kg for men, i.e. values that are not dissimilar. The magnitude of the additional FFM in weight gain in men is consistent with overfeeding studies, mainly in men, which have indicated FFM to comprise 42( Reference Diaz, Prentice and Goldberg 31 ), 38( Reference Norgan and Durnin 32 ) and 33 %( Reference Bouchard, Tremblay and Despres 33 ) of weight gains. Fewer studies have been reported in women, and surprisingly in one overfeeding study, mainly in women, the %FFM of weight gain was, on average, 50 %( Reference Forbes, Brown and Welle 34 ), although the wide range of reported values (0–108 %FFM) indicated low precision in the measurements.
A higher %FFM loss in obese men than in women might reasonably be expected given the greater accumulation of FFM in them during weight gain. However, there is no obvious physiological explanation for the greater FFM content of the excess weight in men in the first instance. The distribution pattern of the FM component of excess weight shows a clear sex dimorphism (e.g. bust and hips in women and waist in men( Reference Wells, Treleaven and Cole 35 )), but this is unrelated to the additional FFM in the cohort of the present study. WC had no effect as an additional independent variable in the multiple regression of FM and FFM on weight and height for women, but it did capture a significant fraction of the variation in FM and exerted a negative effect on FFM in men (data not shown). Thus, the ‘male’ FM distribution pattern of central obesity is not associated with increased FFM elsewhere in the body. Increased skeletal muscle mass is likely to be part of the additional FFM with weight gain, given that increased creatinine excretion is an early observation in obese women( Reference Tager and Kirsch 36 ). A greater expansion of the skeletal muscle mass with obesity in men than in women might be expected, given their greater skeletal muscle mass/lower FM at healthy weights( Reference Forbes, Shils and Young 37 ), but it is not obvious why this would occur. Clearly, this is an important research question that remains to be answered.
The main characteristic of the %FFM or P-ratio of weight loss observed in the present study is its reduction with the extent of weight loss and with time in both men and women. Given the low P-ratios after 2 months with no sex difference, with the continuing weight loss comprising mainly FM loss, this implies a greater overall protein-conserving reduction in FFM loss in men than in women, and there is no obvious explanation for this. Indeed, although the preservation of FFM is often an objective of weight-reducing strategies for the obese, the question can be posed as to why protein conservation occurs at all if restoration of ‘ideal’ body FFM and FM stores is a regulatory target. Protein conservation in terms of the reduction of P-ratio to the same low value, if it was sustained, would mean that an ‘ideal’ body weight would comprise excess FFM, especially for men. In fact, female subjects who had dieted below a BMI of 25 kg/m2 by various conventional self-selected diets exhibited, at BMI values of 21–22 kg/m2, body FM and FFM contents that were the same as those of normal lean women( Reference Kreitzman, Coxon and Brodie 38 ). This is a puzzle.
Much of the literature on body composition during weight loss assumes that the extent of FFM loss can be influenced by dietary composition. Thus, low-carbohydrate, high-protein diets such as the Atkins diet are assumed to limit FFM loss. Such an effect has been reported in a meta-regression of the impact of carbohydrate and protein intakes on body composition during weight loss( Reference Krieger, Sitren and Daniels 23 ), with higher protein intakes (>1·05 g/kg per d: mean = 1·27 g/kg) being reported to be associated with less FFM loss compared with lower intakes ( ≤ 1·05 g/kg per d: mean = 0·74 g/kg), especially in studies with a duration of more than 3 months. Food intake measurements in the studies carried out by us( Reference Truby, Baic and deLooy 24 ) indicated that at baseline protein intakes were, on average, 1·28 g/kg (16 % energy) and changed little in absolute terms for the Atkins diet (1·3 g/kg at 2 months), but increased as a proportion of energy to 28 % at 2 months because of the decrease in carbohydrate intake. In contrast, for the other three intervention diets, protein intakes decreased in absolute terms (to 0·9 g/kg at 2 and 6 months) and increased slightly to 19–20 % energy intake at 2 months. Thus, a lower FFM loss or a lower P-ratio for weight loss might have been expected with the Atkins diet. However, this was not observed in the present study with no significant dietary effects on FFM loss and no difference between dietary group means for P-ratio0–2 months. However, a lower P-ratio0–2 months was observed for the Atkins diet among the men, consistent with the meta-regression discussed above, but given that this was not observed for the women and that the diet–sex interactions were underpowered, it seems to us unlikely that there is an effect of sex on the response to the Atkins diet. Thus, in the studies carried out by us where compliance to the regimens was not supervised by the investigators, there is no firm evidence that dietary composition had an effect on the overall tissue pattern of weight loss or contributed to the variance in P-ratio0–2 months.
In the context of the autoregulatory Payne and Dugdale dynamic model of body weight regulation( Reference Dugdale and Payne 8 – Reference Payne and Dugdale 10 ), which proposes a fixed phenotypic P-ratio during daily cycles of energy gain or loss, while our data do not identify the P-ratio for the initial weight loss at the beginning of the dietary intervention period, our findings suggest that this equivalence is unlikely. Thus, it is quite clear that the P-ratio for weight loss decreases with the extent of weight loss (Fig. 2) and with time (P-ratio2–6 months is lower than P-ratio0–2 months; Table 3). This suggests that for small amounts of weight loss, P-ratioloss at an early time point is higher than the P-ratiogain. As discussed previously( Reference Millward and Wijesinghe 20 ), our own animal work and human work and work carried out by others have indicated examples of changes in the P-ratio inconsistent with the Payne and Dugdale model of a fixed phenotypic value. Our animal work with fasting lean and obese Zucker rats( Reference Hansen and Lambert 18 ) showed the phenotypic P-ratioloss to decrease with time.
The other aspect of the Payne and Dugdale model examined in the present study is that the extent of weight gains or losses with a specified energy imbalance is inversely related to the phenotypic P-ratio for weight change: i.e. those with a low P-ratio (metabolically fat) exhibit more weight change than those with a high P-ratio (metabolically lean). The reason for this is that the model assumes that the negative influence on weight gain of a greater energy density of weight change for the metabolically fat to be more than offset in the metabolically lean by the negative influence of greater heat production associated with weight change. Although the studies carried out by us were not specifically powered to assess sex differences in weight loss for each of the four diets, they did show that at 2 months, weight loss for all women was only half that for all men, a difference observed in each dietary group. This is the opposite of that predicted by the Payne and Dugdale model and is more consistent with most other models in which weight change mainly reflects tissue energy density: i.e. the lower energy density in men (higher P-ratio) results in a greater weight loss for a fixed energy imbalance than for women. However, this is not a complete explanation because the greater weight loss in men than in women at 2 months in the present study was more than would have been expected from their respective P-ratios0–2 months. Values of 0·029 for women and 0·052 for men imply only a 15 % higher energy density of weight loss or 13 % less weight loss for women than for men for the same dietary energy deficit. Indeed, the men lost not only more weight and FFM than women but also more FM. The implication of this is that the greater weight loss for men within community-based weight management regimens as in Diet Trials reflects physiological factors that we have not identified and/or non-physiological factors such as greater dietary compliance/energy deficit or more exercise, which are more important than physiological factors such as a genotypic P-ratio in influencing weight loss.
In conclusion, we have demonstrated clear sex differences in the composition of weight gain and initial weight loss in an overweight and obese population, with greater changes in FFM than in FM for men than for women, as well as greater overall weight loss for men than for women on similar weight loss regimens. There is no obvious physiological or anatomical explanation for the sex difference in the FFM content of increasing body weight with increasing adiposity. However, if it is assumed that the greater FFM content of excess body weight in obese men indicates a higher mobilisable protein reserve relative to fat, then the greater FFM content of weight loss during energy restriction in men is consistent with this. Protein-conserving adaptations occur with increasing weight loss and over time, more extensively in men, which were independent of dietary protein intake in the studies carried out by us.
Acknowledgements
The authors thank Linda Morgan, Manana Stanley, Rebecca Hiscutt, Anne Herriot, Kathryn Hart, Rachel Barratt, Monique Raats, Richard Shepherd, Anne deLooy, Sue Baic, Catherine M. Logan, Moira A. Taylor, Karen Sargent, Sarah Jones, Julie Littlewood, Sujata Dissanayake, Elizabeth Simpson, Michelle Hazell, Mark Davis, Katherine Collings, Paula J. Robson, Julie M. W. Wallace, Maxine P. Bonham and Laura Nichol, who were all involved in the Diet Trials project.
The present study was funded by the BBC. The BBC had no role in the study design; data collection, analysis or interpretation; or report writing.
The authors' contributions were as follows: D. J. M. conducted the analysis and wrote the first draft of the paper and this was reviewed and amended by the other authors.
K. R. F. received consulting fees for serving on the scientific advisory panel of Slimming World, a company that offers a support service for weight loss, but it was not involved in the trial.








