CROSS HEDGING WINTER CANOLA

Abstract

The growth in winter canola acreage in the southern Great Plains has led to questions about the best way to reduce price risk because there is no U.S. canola futures market. Cross-hedge ratios and hedging effectiveness are calculated, and encompassing tests are conducted for short-horizon hedging. Possible cross-hedge markets considered are U.S. soybeans, soybean oil, soybean meal, hard red winter wheat, and Canadian canola. The selected cross hedge is a combination of soybean oil and meal futures, but its hedging effectiveness is substantially less than what is typically provided by a direct hedge.

1. Introduction

In the early 2000s, new varieties of winter hardy canola, including Roundup-Ready varieties, were introduced, and since then canola acreage has dramatically increased in the southern Great Plains. Winter canola provides many advantages for wheat growers. First, the yield and quality of wheat increases by planting canola because cultivation of canola interrupts the cycle of diseases and stops the growth of grassy winter weeds, especially ryegrass (Boyles, Peeper, and Medlin, 2004). Moreover, a winter canola–winter wheat crop rotation is more profitable than continuous winter wheat (Bushong et al., 2012; DeVuyst et al., 2009). In addition, winter canola varieties suitable for the southern Great Plains are continually being developed by various programs such as those at the Kansas Agriculture Experiment Station and at private seed companies. Oklahoma canola production has increased from 89.6 million pounds in 2010 to 161 million pounds in 2012, making Oklahoma the second-largest canola-producing state in the United States (U.S. Department of Agriculture [USDA], National Agricultural Statistics Service [NASS], 2013). Figure 1 illustrates the major producing counties for winter canola in Oklahoma (USDA, Risk Management Agency [RMA], 2014).

Figure 1. The Major Producing Counties for Winter Canola in Oklahoma (source: USDA-RMA [2014]; star indicates location of region's major processor)

The increase in canola production is also in response to increasing demand. The increased demand for canola originates from canola oil being considered healthy because of its lower levels of saturated fatty acids and low-density lipoprotein cholesterol (Eskin and McDonald, 1991). The increased demand for canola oil in the United States has been met by an increase in imports. The quantity of canola oil imported into the United States has steadily increased from 1,108 million pounds in 2002 to 3,289 million pounds in 2012 (USDA, Economic Research Service [ERS], 2015).

The winter canola market has shown relatively high price volatility. For example, Oklahoma canola annualized price volatilities in 2011 and 2012 were 26.4% and 32.4%, respectively¹ (USDA-NASS, 2014). Because of the risk created by price volatility, canola producers and processors need price risk management tools.

Futures are an efficient way to reduce price risk (Kolb and Overdahl, 2007). However, it is impossible to use a direct hedge for winter canola because it is not traded in any U.S. futures market. To deal with this issue, a cross hedge, which means a spot price is hedged by using another futures market not its own, can be used, and two alternatives are available. One is to cross hedge by using other U.S. futures contracts, and the second is using canola futures traded in the Intercontinental Exchange (ICE) Futures Canada, which reflects largely spring canola. In the latter case, the exchange rate between the United States and Canada needs to be taken into account. The purpose of this study is to determine the optimal futures contracts to cross hedge winter canola.

Because of the short time series available, the focus is on short-horizon hedging, and thus the findings might be most relevant to a processor or elevator. Also, producers typically hedge less than processors, and producers now have the alternative of revenue insurance. However, the winter canola insurance² available in Oklahoma, Texas, and Kansas covers only from 50% to 75% of loss, which is relatively lower than that of North Dakota, which provides a coverage level ranging from 50% to 85% (USDA-RMA, 2013, 2014). In addition, the percentage of insured canola acres is estimated to be less than 70% in Oklahoma, Kansas, and Texas, which is significantly lower than the 98% insured rate seen in North Dakota (USDA-RMA, 2015). Because the large price fluctuation of canola is a challenge not only to the farm sector but also to the processor, an effective method to reduce price risk would help to expand winter canola supply in the southern Great Plains.

Anderson and Danthine (1981) suggest a theoretical cross-hedging model. Cross-hedging strategies for various oilseed crops have been proposed (Rahman, Dorfman, and Turner, 2004; Rahman, Turner, and Costa, 2001; Tejeda and Goodwin, 2014; Wilson, 1989). Wilson (1989) considers soybean complex futures as a tool to cross hedge sunflowers and shows that sunflowers can be hedged using soybean oil futures. Rahman, Turner, and Costa (2001) argue that simple cross hedging using soybean meal futures is effective for reducing price risk of cottonseed meal producers. Rahman, Dorfman, and Turner (2004) use a Bayesian approach for examining the feasibility that soybean, soybean meal, and soybean oil futures can be used as cross-hedging vehicles for cottonseed, cottonseed meal, and cottonseed oil. They conclude that soybean complex futures can be useful as a hedging instrument. Optimal hedging has been studied with models that have an increasingly large number of parameters. For example, Tejeda and Goodwin (2014) examine optimal multiproduct time-varying hedge ratios for a soybean complex using a regime-switching dynamic correlation model. The relatively short time period available here precludes considering models with many parameters.

Research on hedging spring canola by Flaskerud, Wilson, and Dahl (2002) suggests that canola futures at the Winnipeg Commodity Exchange (WCE) can be the most effective market to manage price risk for North Dakota spring canola compared with using a futures market not its own, such as the soybean complex futures markets. They also find that the effective hedge is not a 1 to 1, traditional hedge ratio, but an approximately 0.8 to 0.9 ratio to reduce price risk, when based on 1993–2000 data. Mann (2010) finds canola contracts traded in ICE Futures Canada are effective to manage price risk for Canadian canola based on direct hedging. However, no similar research has been conducted related to managing the price risk of winter canola by using cross hedging because the cultivation of winter canola in the southern Great Plains is a relatively new venture.

To achieve the research objective, hedge ratios and hedging effectiveness of the potential contracts are estimated for four different hedging horizons: 1 day, 1 week (5 trading days), 1 month (20 trading days), and 2 months (40 trading days). The focus is on hedging over short periods because winter canola has not been produced long enough to provide data for a study of longer hedging periods. The hedging effectiveness of using a single futures market, as well as multiple futures markets, is considered. An encompassing test for selecting the optimal futures contract with which to cross hedge is carried out. Futures contracts considered are U.S. soybean complex, Kansas City wheat, and Canadian canola. Estimation methods are developed that provide asymptotically efficient estimates in the presence of overlapping data. The use of overlapping data is especially important given the relatively short time series and frequent missing observations.

2. Procedures

The theory of optimal cross hedging is based on the same theory as the optimal hedge ratios of Johnson (1960), Stein (1961), and Ederington (1979). To estimate the simple hedge ratio, the conventional method involves estimating the following linear regression model:

(1)$$\begin{equation} s_t = {\rm \alpha } + {\rm \beta }f_t + u_t,\end{equation}$$

where s_t and f_t are the spot and futures returns, and u_t is a normally distributed error term for period t. Some of the literature has used price levels and some of it has used price changes, but the more recent literature has generally used continuous-time returns (changes in natural logarithms) as we do. The ordinary least squares (OLS) estimator of β provides an estimate of the minimum-variance (risk minimizing) hedge ratio. The hedging effectiveness (HE) indicates the proportion of the reduction in variance of the hedged portfolio over an unhedged portfolio, which is calculated by

(2)$$\begin{equation} HE = 1 - \frac{{{\rm Var}\left( H \right)}}{{{\rm Var}\left( {UH} \right)}},\end{equation}$$

where Var(H) is the variance of the hedged portfolio, and Var(UH) is the variance of the unhedged portfolio. The measure of hedging effectiveness for the minimum variance hedge model is equal to R ² from the linear regression model (equation 1). Since Ederington (1979), this approach has been extensively applied in the voluminous literature. Even though a variety of alternative procedures to the conventional method exist, most of the empirical research indicates only weak evidence of significant improvements in hedging effectiveness compared with the conventional method (Casillo, 2004; Collins, 1997; Cotter and Hanly, 2006; Garcia, Roh, and Leuthold, 1995; Lien, 2005).

As Lence (1996) discusses, the minimum variance hedge ratio does not consider the effects of costs such as commissions, liquidity costs, or the costs of margin calls. As a result, minimum variance hedge ratios may overestimate optimal hedge ratios. Commissions have dropped substantially with electronic trading, and liquidity costs have also dropped with the advent of electronic trading (Shah and Brorsen, 2011). So these costs are small. McKenzie and Kunda (2009) discuss a possible derivative to mitigate the effects of margin calls. Hedging costs are not likely to affect the choice between single futures contracts, but they might make a multivariate hedge less desirable even if it reduced risk.

2.1. Overlapping Data Problem and Missing Value Problem

To estimate multiple-period returns, overlapping data can be used to achieve higher efficiency because of the fact that nonoverlapping data do not use all information in the time series. For instance, when 1-year daily returns consisting of 252 observations are available, up to 248 weekly returns would be obtained using overlapping data, whereas 52 weekly returns would be considered using nonoverlapping data. As a result of using overlapping data when calculating the spot and futures returns for period t, OLS is no longer appropriate except for the 1-day hedge ratio. Using overlapping time periods creates a moving average process with order equal to the length of the hedge period (Harri and Brorsen, 2009). To account for the overlapping data issue, equation (1) is modified.

The regression equation for aggregated price returns for k days becomes

(3)$$\begin{equation} S_t = {\rm \gamma } + {\rm \beta }F_t + e_t,\end{equation}$$

where the overlapping observations are calculated by summing the original observations:

(4)$$\begin{equation} S_t = \mathop \sum \limits_{j = t - k + 1}^t s_j,\end{equation}$$

(5)$$\begin{equation} F_t = \mathop \sum \limits_{j = t - k + 1}^t f_j,\end{equation}$$

(6)$$\begin{equation} e_t = \mathop \sum \limits_{j = t - k + {\rm }1}^t u_j.\end{equation}$$

When multiple cross hedging is considered, F_t becomes a vector of futures returns. In equation (6), the aggregated error term, e_t, is not independently distributed because e_t and e _{t + s} have k − s common original error terms, u_t. In this case, OLS is inefficient and hypothesis tests will be biased because of autocorrelation in the estimated residual. Moreover, daily log return data of Oklahoma canola include missing values in the early period because Oklahoma winter canola was a new venture at that time. To deal with these overlapping data and missing value problems, this study uses two alternative methods to estimate the hedge ratio: generalized least squares (GLS) and maximum likelihood estimation (MLE).

2.2. GLS Method

If the only source of autocorrelation comes from overlapping data in the aggregated error term, e_t, the GLS estimator of the aggregate model will be best linear unbiased and asymptotically efficient (Gilbert, 1986; Harri and Brorsen, 2009). To solve the missing data problem, the correlation matrix can be calculated as if all winter canola price data exist and then deleting the respective row and column of any missing observations. To use GLS, a correlation matrix is needed. Because u_t is a normally distributed error term, the mean and variance of e_t are as follows:

(7)$$\begin{equation} E\left[ {e_t } \right] = E\left[ {\mathop \sum \limits_{j = t}^{t + k - 1} u_j } \right] = \mathop \sum \limits_{j = t}^{t + k - 1} E[u_j ] = 0\end{equation}$$

(8)$$\begin{equation} {\rm var}\left[ {e_t } \right] = E\left[ {e_t^2 } \right] - E\left[ {e_t } \right]^2 = E\left[ {e_t^2 } \right] = k{\rm \sigma }_u^2.\end{equation}$$

With the condition k > s, the covariance and correlation between the error terms, e_t and e _{t + s}, are the following:

(9)$$\begin{equation} {\rm cov}\left[ {e_t ,{\rm }e_{t + s} } \right] = \left( {k - s} \right){\rm \sigma }_u^2\end{equation}$$

(10)$$\begin{equation} {\rm corr}\left[ {e_t ,e_{t + s} } \right] = \frac{{k - s}}{k}.\end{equation}$$

From equations (9) and (10), the correlation matrix, Ω, is calculated as the following matrix (Gilbert, 1986):

(11)\begin{equation} {\rm \Omega } = \left[ {\begin{array}{*{20}c} {\frac{k}{k}} &\quad {\frac{{k - 1}}{k}} &\quad \cdots &\quad {\frac{1}{k}} &\quad 0 &\quad \cdots &\quad 0 \\[6pt] {\frac{{k - 1}}{k}} &\quad {\frac{k}{k}} &\quad {\frac{{k - 1}}{k}} &\quad \cdots &\quad {\frac{1}{k}} &\quad 0 &\quad 0 \\[6pt] \cdots &\quad \cdots &\quad \cdots &\quad \cdots &\quad \cdots &\quad \cdots &\quad \cdots \\[6pt] \cdots &\quad \cdots &\quad \cdots &\quad \cdots &\quad \cdots &\quad \cdots &\quad \cdots \\[6pt] 0 &\quad 0 &\quad {\frac{1}{k}} &\quad \cdots &\quad {\frac{{k - 1}}{k}} &\quad {\frac{k}{k}} &\quad {\frac{{k - 1}}{k}} \\[6pt] 0 &\quad \cdots &\quad 0 &\quad {\frac{1}{k}} &\quad \cdots &\quad {\frac{{k - 1}}{k}} &\quad {\frac{k}{k}} \\ \end{array}} \right].\end{equation}

The coefficient and variance of the aggregated model to handle the overlapping data problem and missing value problems can be obtained as

(12)$$\begin{equation} {\rm \hat{\beta} } = \left( {F_{it}^\prime {\rm \Omega }^{ - 1} F_{it} } \right)^{ - 1} F_{it}^\prime {\rm \Omega }^{ - 1} S_t\end{equation}$$

(13)$$\begin{equation} {\rm var}[{\rm \hat \beta }] = {\rm \sigma }_e^2 \left( {F_{it}^\prime {\rm \Omega }^{ - 1} F_{it} } \right)^{ - 1},\end{equation}$$

where σ²_e is the variance of the error term, e_t, in the aggregated model. To obtain hedging effectiveness following equation (2), the variance of the hedged portfolio is calculated using the hedge ratio, ${\rm \hat \beta }$, in equation (12).

2.3. MLE Method

To use MLE, the moving average process is approximated by using a higher-order autoregressive process. Using an autoregressive process has some advantages. Not only is it easier to estimate than the moving average process, but it can potentially capture autocorrelation from sources other than overlapping data (Brorsen, Buck, and Koontz, 1998). In this case, maximum likelihood methods for estimating a regression with autoregressive errors can be used, and the error term in equation (3) is redefined as

(14)$$\begin{equation} e_t = - \mathop \sum \limits_{j = 1}^n {\rm \varphi }_j e_{t - j} + v_t,\end{equation}$$

where φ_j indicates the coefficient, and v_t is the white-noise error term, which is normally and independently distributed with zero mean and constant variance. The length of autoregressive error, n, is chosen based on the 5% significance level and is longer than the hedge period in every case.

2.4. Forecast Encompassing Test

The alternative models are not nested, and so forecast encompassing tests (Diebold, 2007, p. 264; Harvey, Leybourne, and Newbold, 1998) are used to test hypotheses. Sanders and Manfredo (2004) consider the null hypothesis that $\hat P_{0,t} $ provides the best cross hedge versus the nonnested alternative hypothesis that $\hat P_{1,t} $ provides the best cross hedge. By assuming only two competing futures contracts for hedging a spot position, forecast encompassing can be examined following Harvey, Leybourne, and Newbold (1998) as

(15)$$\begin{equation} \varepsilon _{0,t - h} = \phi + {\rm \lambda }_{t - h} ( {{\rm \varepsilon }_{0,t - h} - {\rm \varepsilon }_{1,t - h} } ) + {\rm \tau }_t,\end{equation}$$

(16)$$\begin{equation} {\rm \varepsilon }_{0,t - h} = P_t - \hat P_{0,t - h},\end{equation}$$

(17)$$\begin{equation} {\rm \varepsilon }_{1,t - h} = P_t - \hat P_{1,t - h},\end{equation}$$

where ε_{0, t − h} and ε_{1, t − h} are the forecast error terms of the hypothesized model and the competing one with hedge horizon h. P_t, $\hat P_{0,t - h} $, and $\hat P_{1,t - h} $ indicate the actual price and forecasted prices of the hypothesized model and the competing one, respectively. The value of λ_{t − h} indicates the weight, which the alternative should hold in constructing a composite forecast and minimizes the mean squared forecast error and vice versa for 1 − λ_{t − h} (Sanders and Manfredo, 2004). A failure to reject the null hypothesis (λ_{t − h} = 0) implies the hypothesized futures contract encompasses the competing one. As defined by Maddala (2001, p. 504), the value of λ_{t − h} in equation (15), which brings about the minimum forecast error, can be expressed as

(18)\begin{equation} \displaystyle\begin{array}{l} {\rm \lambda }_{t - h} = \displaystyle\frac{{{\rm \sigma }_{{\rm \varepsilon }_{0,t - h} }^2 - {\rm \rho }_{{\rm \varepsilon }_{0,t - h} {\rm \varepsilon }_{1,t - h} } {\rm \sigma }_{{\rm \varepsilon }_{0,t - h} } {\rm \sigma }_{{\rm \varepsilon }_{1,t - h} } }}{{{\rm \sigma }_{{\rm \varepsilon }_{0,t - h} }^2 + {\rm \sigma }_{{\rm \varepsilon }_{1,t - h} }^2 - 2{\rm \rho }_{{\rm \varepsilon }_{0,t - h} {\rm \varepsilon }_{1,t - h} } {\rm \sigma }_{{\rm \varepsilon }_{0,t - h} } {\rm \sigma }_{{\rm \varepsilon }_{1,t - h} } }} \ \hbox{and} \ {\rm \lambda }_{t - h} \frac{>}{<} 0 \\[16pt] {\rm if\ and\ only\ if}\; \displaystyle\frac{{{\rm \sigma }_{{\rm \varepsilon }_{0,t - h} } }}{{{\rm \sigma }_{{\rm \varepsilon }_{1,t - h} } }}\frac{1}{{{\rm \rho }_{{\rm \varepsilon }_{0,t - h} {\rm \varepsilon }_{1,t - h} } }} \frac{>}{<} 1, \\ \end{array}\end{equation}

where σ²_{ε0, t − h} and σ²_{ε1, t − h} are the variance of ε_{0, t − h} and ε_{1, t − h}, and ρ_{ε0, t − hε1, t − h} is the correlation between these forecast errors.

3. Data

The futures contracts of Chicago soybean, soybean meal, soybean oil, Kansas City wheat, and Canada canola were selected as the potential contracts for cross hedging winter canola (see Figure 2). Oklahoma canola spot prices were obtained from the USDA's “Market News” (USDA, Agricultural Marketing Service [AMS], 2015) and directly from Equity Marketing Alliance (EMA).³ The prices of Chicago soybean, soybean meal, soybean oil, Kansas City wheat, and Canadian dollar futures were gathered from Price-Data.com. The Canada canola futures were obtained from the Commodity Research Bureau.

Figure 2. Price Index for Oklahoma Canola Spot, Domestic, and Canola Futures (source: USDA-AMS [2015]; price index calculated based on price on September 19, 2009)

To test for unit roots in price levels and daily log return of all futures and canola spot, the augmented Dickey-Fuller (ADF) test is used. The ADF test failed to reject the null hypothesis of a unit root at the 5% significance level for all price-level data.⁴ However, the null hypothesis of a unit root is strongly rejected at the 1% level for the daily log returns.

Daily log returns of Oklahoma canola spot price and futures price are used from September 19, 2009, when Oklahoma canola price data started to be listed on the USDA's “Market News” (USDA-AMS, 2015), to January 14, 2013. Oklahoma City canola prices only exist for the period of September 19, 2009, through March 7, 2012. In this study, the canola price of Dacoma, a town in Woods County, Oklahoma, is substituted⁵ for the Oklahoma canola price starting from July 26, 2011, because the Dacoma region canola price has the largest number of observations. Price from the nearby futures contract month is used until the 19th of the month preceding the futures contract month. After the 19th of the preceding month, the price for the next nearby futures contract month is used. Differences are taken before splicing to avoid outliers on the rollover day. To calculate the daily log returns of Canada canola futures, the Canada canola futures price is converted into U.S. dollars by multiplying the Canada canola futures price by the Canadian dollar futures price. The hedge ratios and hedging effectiveness are calculated for 1, 5, 20, and 40 market-day hedge periods, which correspond to 1 day, 1 week, 1 month, and 2 months approximately. Longer hedging horizons were not considered because of the limited data available. The short hedging horizons might be more appropriate for an elevator or processor than for a producer.

Daily log returns of the Oklahoma canola spot price, domestic futures, and Canada canola futures include 682, 838, and 816 observations, respectively. Most of the missing values (18.7%) in Oklahoma canola exist in the early years of production.⁶ When available, linear regression is used to impute a small number of missing values using canola prices in the neighboring areas.

4. Results

Table 1 shows the estimated Pearson correlation coefficients of the daily returns of Oklahoma canola spot, domestic futures, and Canada canola futures. The results indicate high correlation between the returns of Oklahoma canola spot and those of soybean oil futures with a correlation coefficient of 0.773. This result is consistent with canola oil being more valuable than canola meal.⁷ On the other hand, the correlation between Oklahoma canola and Kansas City wheat futures is low, with a correlation coefficient of 0.405, which suggests that Kansas City wheat futures is a poor choice for cross hedging Oklahoma canola.

Table 1. Pearson Correlation Coefficients

Note: Correlation coefficients are all significant at the 1% level.

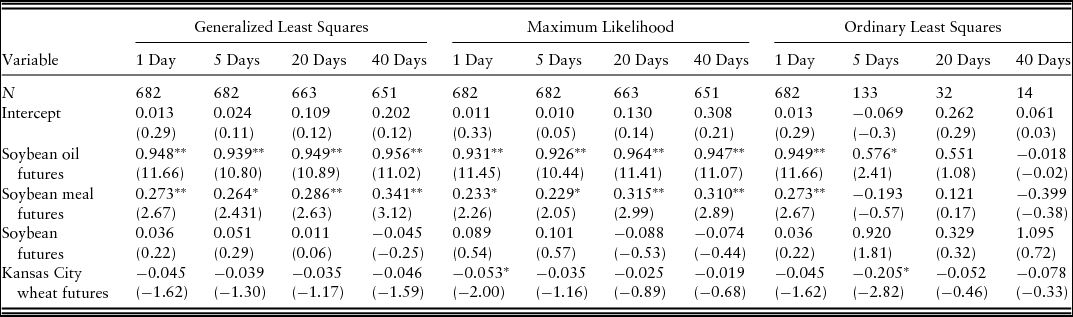
Table 2 shows multivariate hedge ratios using domestic futures to cross hedge Oklahoma canola for hedging periods of 1 day, 5 days, 20 days, and 40 days. The hedge ratios using GLS and MLE are only slightly different. The parameter estimates of soybean oil and meal futures are significant at the 5% level in all hedge periods based on GLS and MLE. The OLS hedge ratios are not significantly different from zero at horizons greater than 5 days, and hedge ratios shrink as the horizon increases. The noticeably different results of OLS to GLS and MLE for hedging periods greater than 1 day are because of the OLS hedge ratio being estimated using nonoverlapping data with fewer observations. The reduced number of observations leads to OLS parameter estimates being inefficient. The results from the Pearson correlation coefficients in Table 1 and GLS and MLE in Table 2 imply that soybean and Kansas City wheat futures contracts are not good candidates and soybean oil futures is the optimal futures contract for univariate cross hedging winter canola, with soybean meal being the second-best alternative in the domestic market.

Table 2. Multiple Hedge Ratios Using Domestic Futures and Oklahoma Canola

Notes: The t values for the test statistics are presented in parentheses. Asterisks, * and **, indicate statistical significance at the 5% and 1% levels, respectively.

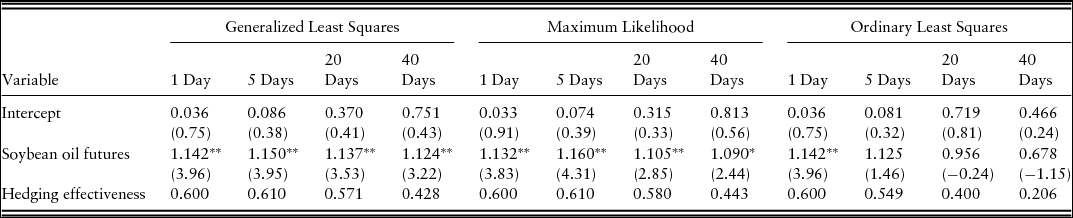
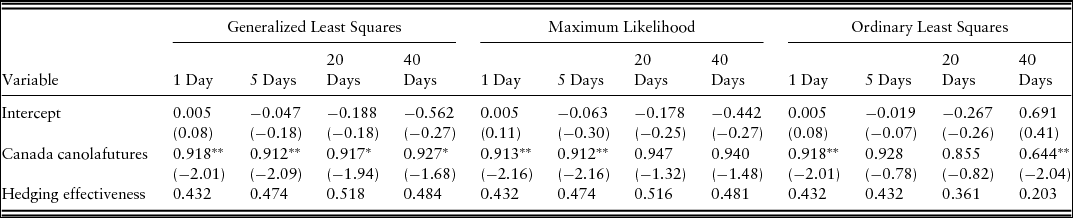
Tables 3 and 4 report the hedge ratios and hedging effectiveness of soybean oil and Canada canola futures contracts. Based on GLS and MLE, soybean oil futures hedge ratios are significantly greater than 1, which is a result of canola prices being more volatile than soybean oil. Most of the hedge ratios using Canada canola futures are significantly less than 1, but there are cases in which they are not significantly different from 1 (Table 4). Because of a relatively small sample size, OLS estimates are inefficient, resulting in considerably different results than the alternative estimation methods. The hedge ratio of 1.142, using soybean oil futures for 1-day hedging horizon can be interpreted as 1.142 dollars of soybean oil futures are needed for each dollar of winter canola to achieve the risk-minimizing hedge.⁸ Soybean oil futures have a higher hedging effectiveness than Canada canola futures except when considering a 2-month hedging period. Because this is a cross hedge, the hedging effectiveness does not match what would be achieved with a direct hedge. For instance, if Oklahoma canola processors use soybean oil futures for 5 days to hedge their crop, the price risk can be reduced by as much as 61%. In contrast, the direct hedging effectiveness of Canadian canola using canola futures traded in the ICE Futures Canada is roughly 90% (Mann, 2010). A direct hedge typically shows a substantially higher hedging effectiveness over a cross hedge (Dahlgran, 2009). A winter canola futures market⁹ with a delivery point in the U.S. southern plains could reduce the basis risk, but production would likely need to grow considerably to support a winter canola futures market. This imperfect cross hedge suggests the potential to introduce a futures market for winter canola with a delivery point in the southern plains if production continues to expand.

Table 3. Hedge Ratios and Hedging Effectiveness Using Soybean Oil Futures and Oklahoma Canola

Notes: The t values for the test statistics are presented in parentheses. The hedging effectiveness measures are calculated using the Buse (1973) R-squared measure. Asterisks, * and **, indicate statistical significance at the 5% and 1% level, respectively.

Table 4. Hedge Ratios and Hedging Effectiveness Using Canada Canola Futures and Oklahoma Canola

Notes: The t values for the test statistics are presented in parentheses. Asterisks, *and **, indicate statistical significance at the 10% and 5% level, respectively.

The forecast encompassing tests (Table 5) show significant estimated hedging weight for both Canada canola and soybean oil futures indicating that neither forecast encompasses the other and each contains unique information. The results imply that market participants can reduce canola price risk better by using both soybean oil and Canada canola futures rather than either alone. For example, the hedging weight of 0.803 for 5-day periods means that hedging using 80.3% soybean oil and 19.7% of soybean meal futures has the minimum forecast error for a 5-day hedging period.

Table 5. Encompassing Regression (preferred futures are soybean oil futures to Canada canola futures)

Notes: The t values for the test statistics are presented in parentheses. All correlation coefficients are statistically significant at the 1% level. Asterisks, **, indicate statistical significance at the 1% level.

Table 6 reports the encompassing regression in the multiple hedge case using soybean oil and meal futures as preferred futures contracts to soybean oil and Canada canola futures for Oklahoma canola. All estimated hedging weights (λ_t) for the preferred model are significant, but the weights (1 − λ_t) for the alternative model are not significant in all hedging horizons at the 1% level. Thus, the cross hedge with soybean oil and meal encompasses the cross hedge with soybean oil and Canadian canola.

Table 6. Encompassing Regression (preferred futures are soybean oil and meal futures to soybean oil and Canada canola futures)

Notes: The t values for the test statistics are presented in parentheses. All correlation coefficients are statistically significant at the 1% level. Asterisks, **, indicates statistical significance at the 1% level.

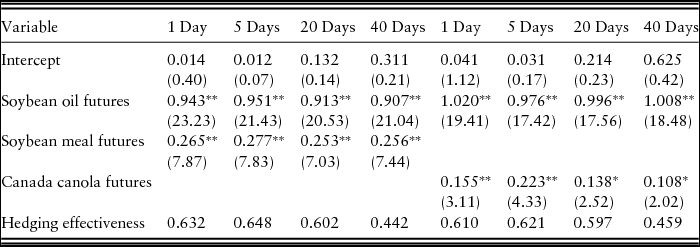
Table 7 indicates hedge ratios and hedging effectiveness with soybean oil and meal futures in the domestic market and soybean oil and Canada canola futures in the intercountry market based on maximum likelihood. All parameter estimates are significant at the 5% level. In all hedging horizons, the proportions of soybean oil futures (~0.780) and soybean meal futures (~0.220¹⁰) are similar to those of the 2009–2013 U.S. revenues for canola oil (0.714) and canola meal (0.286¹¹) (USDA-ERS, 2015). Domestic multiple hedges show slightly higher hedging effectiveness than those with soybean oil and Canada canola, except for the 40-day horizon. As Sephton (1993) points out, the variance of a portfolio constructed with multiple markets will always be lower than that with only one market as can be seen in Tables 3, 4, and 7.

Table 7. Hedge Ratios and Hedging Effectiveness Using Soybean Oil and Meal Futures and Soybean Oil and Canadian Canola Futures Based on Maximum Likelihood

Notes: The t values for the test statistics are presented in parentheses. Asterisks, * and **, indicate statistical significance at the 5% and 1% level, respectively.

5. Summary and Conclusion

This article seeks to determine the risk-minimizing cross-hedging strategy for winter canola in the U.S. southern plains. Among domestic futures contracts, soybean oil shows the highest correlation with Oklahoma canola prices. Even though soybean oil futures shows higher hedging effectiveness than Canada canola futures, they do not encompass each other and contain unique information. In the comparison between multiple hedges, using soybean oil and meal futures encompasses using soybean oil and Canada canola futures. This result suggests that soybean oil and soybean meal futures are the optimal multiple cross-hedging vehicles to reduce Oklahoma canola spot price risk. However, the hedging effectiveness for Oklahoma canola using soybean oil and meal futures is lower than what is usually expected with direct hedging.

This study indicates a different result than Flaskerud, Wilson, and Dahl (2002). They find that changes of canola cash prices in Velva, North Dakota, are most closely correlated with canola futures in the WCE¹² in Canada, while soybean oil futures at Chicago are only second best when using 1993–2000 data. The differing results might originate from differences in winter canola and spring canola markets as well as Oklahoma being further from Canada than North Dakota. In addition, the exchange rate volatility between U.S. and Canadian dollars from 2009 to 2012 is higher than that from 1993 to 2000.¹³ As production in Oklahoma and Kansas continues to expand, the winter canola and spring canola markets may become more integrated, so the optimal cross-hedge strategy could change in future years. As of now, our results favor the hedgers of winter canola using soybean oil and meal futures in the domestic futures market.