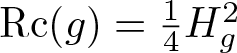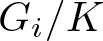1. Introduction
In the context of generalized Riemannian geometry has arisen an extension of the Ricci flow equation called generalized Ricci flow. Given a manifold M and a generalized metric encoded in the pair (g, H), where g is a Riemannian metric and H a closed 3-form on M, this flow studied in [Reference Garcia-Fernandez and Streets5] is given by
 \begin{equation}
\left\{\begin{array}{l}
\frac{\partial}{\partial t} g(t) = -2\operatorname{Rc}(g(t)) +\tfrac{1}{2} (H(t))_{g(t)}^2, \\ \\
\frac{\partial}{\partial t} H(t) = -dd_{g(t)}^*H(t),
\end{array}\right.
\end{equation}
\begin{equation}
\left\{\begin{array}{l}
\frac{\partial}{\partial t} g(t) = -2\operatorname{Rc}(g(t)) +\tfrac{1}{2} (H(t))_{g(t)}^2, \\ \\
\frac{\partial}{\partial t} H(t) = -dd_{g(t)}^*H(t),
\end{array}\right.
\end{equation} where  $H_g^2:=g(\iota_\cdot H,\iota_\cdot H)$ and
$H_g^2:=g(\iota_\cdot H,\iota_\cdot H)$ and ![]() $d_g^*$ is the adjoint of d with respect to g.
$d_g^*$ is the adjoint of d with respect to g.
A pair (g, H) is naturally associated with Bismut connections, i.e., the unique metric connection on the Riemannian manifold (M, g) with torsion equal to H, in this sense the generalized Ricci flow is the natural evolution in the direction of the Ricci tensor of this connection.
In search of canonical generalized geometry, García-Fernandez and Streets in [Reference Garcia-Fernandez and Streets5] proposed to look for the fixed points of this flow, the so-called Bismut Ricci flat (BRF for short) generalized metrics or generalized Einstein metrics, i.e., (g, H) such that
 \begin{equation*}
\operatorname{Rc}(g)=\tfrac{1}{4} H_g^2 \quad\mbox{and}\quad H\mbox{ is }g\mbox{-harmonic}.
\end{equation*}
\begin{equation*}
\operatorname{Rc}(g)=\tfrac{1}{4} H_g^2 \quad\mbox{and}\quad H\mbox{ is }g\mbox{-harmonic}.
\end{equation*} Let ![]() $G_1, G_2$ be compact, connected, simple Lie groups and
$G_1, G_2$ be compact, connected, simple Lie groups and ![]() $K\subset G_1,G_2$ a closed Lie subgroup. Suppose that for
$K\subset G_1,G_2$ a closed Lie subgroup. Suppose that for ![]() $i=1,2$, there exist constants
$i=1,2$, there exist constants ![]() $0 \lt a_1\leq a_2 \lt 1$ such that
$0 \lt a_1\leq a_2 \lt 1$ such that ![]() $\operatorname{B}_{\mathfrak{k} }=a_i\operatorname{B}_{\mathfrak{g} _i}|_{\mathfrak{k} }$, where
$\operatorname{B}_{\mathfrak{k} }=a_i\operatorname{B}_{\mathfrak{g} _i}|_{\mathfrak{k} }$, where ![]() $\mathfrak{k}, \mathfrak{g} _i$ are the Lie algebras of K and Gi, respectively, and
$\mathfrak{k}, \mathfrak{g} _i$ are the Lie algebras of K and Gi, respectively, and ![]() $\operatorname{B}_{\mathfrak{h} }$ is the Killing form of the Lie algebra
$\operatorname{B}_{\mathfrak{h} }$ is the Killing form of the Lie algebra ![]() $\mathfrak{h} $. The homogeneous space defined by
$\mathfrak{h} $. The homogeneous space defined by ![]() $M = G_1 \times G_2/\Delta K$ is aligned with
$M = G_1 \times G_2/\Delta K$ is aligned with  $(c_1,c_2)=(\tfrac{a_1+a_2}{a_2},\tfrac{a_1+a_2}{a_1})$ and
$(c_1,c_2)=(\tfrac{a_1+a_2}{a_2},\tfrac{a_1+a_2}{a_1})$ and  $\lambda_1=\dots=\lambda_t=\tfrac{a_1a_2}{a_1+a_2}$, as defined in [Reference Lauret and Will8], and so its third Betti number is one. Recently in [Reference Lauret and Will7], Lauret and Will found a BRF G-invariant generalized metric on any aligned homogeneous space
$\lambda_1=\dots=\lambda_t=\tfrac{a_1a_2}{a_1+a_2}$, as defined in [Reference Lauret and Will8], and so its third Betti number is one. Recently in [Reference Lauret and Will7], Lauret and Will found a BRF G-invariant generalized metric on any aligned homogeneous space ![]() $M = G/K$, where G is a compact semisimple Lie group with two simple factors generalizing results obtained in [Reference Podestà and Raffero13, Reference Podestà and Raffero14].
$M = G/K$, where G is a compact semisimple Lie group with two simple factors generalizing results obtained in [Reference Podestà and Raffero13, Reference Podestà and Raffero14].
If ![]() $G:=G_1 \times G_2$, then we consider its Killing metric given by
$G:=G_1 \times G_2$, then we consider its Killing metric given by
and let ![]() $\mathfrak{g} =\mathfrak{k} \oplus\mathfrak{p} $ be the
$\mathfrak{g} =\mathfrak{k} \oplus\mathfrak{p} $ be the ![]() $g_{\operatorname{B}}$-orthogonal reductive decomposition of
$g_{\operatorname{B}}$-orthogonal reductive decomposition of ![]() $\mathfrak{g} $. We fix the standard metric of
$\mathfrak{g} $. We fix the standard metric of ![]() $M = G_1 \times G_2/\Delta K$ determined by
$M = G_1 \times G_2/\Delta K$ determined by ![]() $g_{\operatorname{B}}|_{\mathfrak{p} \times \mathfrak{p} }$ as a background metric and consider the
$g_{\operatorname{B}}|_{\mathfrak{p} \times \mathfrak{p} }$ as a background metric and consider the ![]() $g_{\operatorname{B}}$-orthogonal Ad(K)-invariant decomposition
$g_{\operatorname{B}}$-orthogonal Ad(K)-invariant decomposition
where each ![]() ${\mathfrak{p}}_i$ is equivalent to the isotropy representation of the homogeneous space
${\mathfrak{p}}_i$ is equivalent to the isotropy representation of the homogeneous space ![]() $M_i=G_i/K$ for
$M_i=G_i/K$ for ![]() $i=1,2$ and
$i=1,2$ and ![]() ${\mathfrak{p}}_3$ is equivalent to the adjoint representation
${\mathfrak{p}}_3$ is equivalent to the adjoint representation ![]() $\mathfrak{k} $ (see [Reference Lauret and Will8, Proposition 5.1]).
$\mathfrak{k} $ (see [Reference Lauret and Will8, Proposition 5.1]).
Following [Reference Lauret and Will8], the closed 3-form H 0 on M given by
 \begin{align*}
H_0(X,Y,Z) & := Q([X,Y],Z) + Q([X,Y]_\mathfrak{k}, Z) - Q([X,Z]_\mathfrak{k}, Y) + Q([Y,Z]_\mathfrak{k}, X) \\ &\quad \text{for all\ } X,Y,Z \in \mathfrak{p},
\end{align*}
\begin{align*}
H_0(X,Y,Z) & := Q([X,Y],Z) + Q([X,Y]_\mathfrak{k}, Z) - Q([X,Z]_\mathfrak{k}, Y) + Q([Y,Z]_\mathfrak{k}, X) \\ &\quad \text{for all\ } X,Y,Z \in \mathfrak{p},
\end{align*} where  $Q=\operatorname{B}_{\mathfrak{g} _1}-\tfrac{a_2}{a_1}\operatorname{B}_{\mathfrak{g} _2}$, is g-harmonic for any G-invariant metric
$Q=\operatorname{B}_{\mathfrak{g} _1}-\tfrac{a_2}{a_1}\operatorname{B}_{\mathfrak{g} _2}$, is g-harmonic for any G-invariant metric ![]() $g=(x_1,x_2,x_3)_{g_{\operatorname{B}}}$ of the form:
$g=(x_1,x_2,x_3)_{g_{\operatorname{B}}}$ of the form:
these metrics will be called diagonal.
The G-invariant BRF generalized metric found in [Reference Lauret and Will7] is given, up to scaling, by ![]() $(g_0,H_0)$ (see [Reference Lauret and Will10, Remark A.3]), where
$(g_0,H_0)$ (see [Reference Lauret and Will10, Remark A.3]), where
 \begin{equation}
g_0:={\left(1,\tfrac{a_2}{a_1},\tfrac{a_1+a_2}{a_1}\right)}_{g_{\operatorname{B}}}.
\end{equation}
\begin{equation}
g_0:={\left(1,\tfrac{a_2}{a_1},\tfrac{a_1+a_2}{a_1}\right)}_{g_{\operatorname{B}}}.
\end{equation} In this paper, we study the dynamical stability of this generalized metric as a fixed point of the generalized Ricci flow given in Equation 1 on homogeneous spaces of the form ![]() $M = G_1 \times G_2/\Delta K$ as above, such that the standard metric on
$M = G_1 \times G_2/\Delta K$ as above, such that the standard metric on ![]() $M_i=G_i/K$ is Einstein for
$M_i=G_i/K$ is Einstein for ![]() $i=1,2$. Note that since each Gi is simple, the spaces Mi are given in [Reference Besse1] (see also [Reference Lauret and Lauret6] and [Reference Lauret and Will9]), there are 17 families and 50 isolated examples among irreducible symmetric, isotropy irreducible and non-isotropy irreducible homogeneous spaces. Note that we can consider
$i=1,2$. Note that since each Gi is simple, the spaces Mi are given in [Reference Besse1] (see also [Reference Lauret and Lauret6] and [Reference Lauret and Will9]), there are 17 families and 50 isolated examples among irreducible symmetric, isotropy irreducible and non-isotropy irreducible homogeneous spaces. Note that we can consider ![]() $G_1=G_2=H$, in this case
$G_1=G_2=H$, in this case ![]() $a_1=a_2$. Our main result is the following.
$a_1=a_2$. Our main result is the following.
Theorem 1.1. Let ![]() $M = G_1 \times G_2/\Delta K$ be a homogeneous space as above such that
$M = G_1 \times G_2/\Delta K$ be a homogeneous space as above such that ![]() $\operatorname{B}_{\mathfrak{k} }=a_i \operatorname{B}_{\mathfrak{g} _i}|_{\mathfrak{k} }$ and
$\operatorname{B}_{\mathfrak{k} }=a_i \operatorname{B}_{\mathfrak{g} _i}|_{\mathfrak{k} }$ and ![]() $(M_i=G_i/K, g_{\operatorname{B}}^i)$ is Einstein, where
$(M_i=G_i/K, g_{\operatorname{B}}^i)$ is Einstein, where ![]() $g_{\operatorname{B}}^i$ is the standard metric on each Mi for
$g_{\operatorname{B}}^i$ is the standard metric on each Mi for ![]() $i=1,2$, then
$i=1,2$, then
(i) There exists a neighbourhood U of the metric
 $g_0=(1,\tfrac{a_2}{a_1},\tfrac{a_1+a_2}{a_1})_{g_{\operatorname{B}}}$ in the space of all diagonal metrics, such that the generalized Ricci flow converges to
$g_0=(1,\tfrac{a_2}{a_1},\tfrac{a_1+a_2}{a_1})_{g_{\operatorname{B}}}$ in the space of all diagonal metrics, such that the generalized Ricci flow converges to  $(g_0,H_0)$ starting at any generalized metric
$(g_0,H_0)$ starting at any generalized metric  $(g,H_0)$ with g in U (see Theorem 3.5 and Proposition 3.2).
$(g,H_0)$ with g in U (see Theorem 3.5 and Proposition 3.2).(ii) Let
 $M=H\times H/\Delta K$ (i.e.,
$M=H\times H/\Delta K$ (i.e.,  $a_1=a_2$) be a homogeneous space such that
$a_1=a_2$) be a homogeneous space such that  $(H/K, g_{\operatorname{B}})$ is Einstein and
$(H/K, g_{\operatorname{B}})$ is Einstein and  $\operatorname{B}_{\mathfrak{k} }=a\operatorname{B}_{\mathfrak{h} }|_{\mathfrak{k} }$, then any diagonal generalized Ricci flow solution converges to the BRF metric
$\operatorname{B}_{\mathfrak{k} }=a\operatorname{B}_{\mathfrak{h} }|_{\mathfrak{k} }$, then any diagonal generalized Ricci flow solution converges to the BRF metric  $(g_0,H_0)$, where
$(g_0,H_0)$, where  $g_0=(1,1,2)_{g_{\operatorname{B}}}$ (see Theorem 4.3).
$g_0=(1,1,2)_{g_{\operatorname{B}}}$ (see Theorem 4.3).
Remark 1.2. If ![]() $M = G_1 \times G_2/\Delta K$ is multiplicity-free, i.e.,
$M = G_1 \times G_2/\Delta K$ is multiplicity-free, i.e., ![]() $M_1,M_2$ are both isotropy irreducible, K is simple, the Ad(K)-representations
$M_1,M_2$ are both isotropy irreducible, K is simple, the Ad(K)-representations ![]() ${\mathfrak{p}}_1$,
${\mathfrak{p}}_1$, ![]() ${\mathfrak{p}}_2$ are inequivalent and neither of them is equivalent to the adjoint representation
${\mathfrak{p}}_2$ are inequivalent and neither of them is equivalent to the adjoint representation ![]() $\mathfrak{k} $, then the metrics of the form given in Equation 3 are all the G-invariant metrics on the homogeneous space M.
$\mathfrak{k} $, then the metrics of the form given in Equation 3 are all the G-invariant metrics on the homogeneous space M.
Finally, in ![]() $\S$ 5, we give an overview of the generalized Ricci flow and its fixed points on simple compact Lie groups and an analysis of the stability on
$\S$ 5, we give an overview of the generalized Ricci flow and its fixed points on simple compact Lie groups and an analysis of the stability on ![]() $\mathrm{SO}(n)$, the only known simple Lie group admitting a nice basis. Our result is the following.
$\mathrm{SO}(n)$, the only known simple Lie group admitting a nice basis. Our result is the following.
Theorem 1.3. There exists a neighbourhood U of the Killing metric ![]() $g_{\operatorname{B}}$ on the compact Lie group
$g_{\operatorname{B}}$ on the compact Lie group ![]() $\mathrm{SO}(n)$, such that any generalized Ricci flow solution starting at a diagonal metric in U converges to
$\mathrm{SO}(n)$, such that any generalized Ricci flow solution starting at a diagonal metric in U converges to ![]() $g_{\operatorname{B}}$.
$g_{\operatorname{B}}$.
This implies that near the Killing metric of ![]() $\mathrm{SO}(n)$, the conjecture given in [Reference Garcia-Fernandez and Streets5, Conjecture 4.14] holds, i.e., for any initial condition
$\mathrm{SO}(n)$, the conjecture given in [Reference Garcia-Fernandez and Streets5, Conjecture 4.14] holds, i.e., for any initial condition ![]() $(g,H_0)$ close enough to
$(g,H_0)$ close enough to ![]() $(g_{\operatorname{B}},H_0)$, where g is a left-invariant metric on
$(g_{\operatorname{B}},H_0)$, where g is a left-invariant metric on ![]() $\mathrm{SO}(n)$ diagonal with respect to
$\mathrm{SO}(n)$ diagonal with respect to ![]() $g_{\operatorname{B}}$ and H 0 is the Cartan 3-form, the generalized Ricci flow exists on
$g_{\operatorname{B}}$ and H 0 is the Cartan 3-form, the generalized Ricci flow exists on ![]() $[0,\infty)$ and converges to the BRF structure
$[0,\infty)$ and converges to the BRF structure ![]() $(g_{\operatorname{B}},H_0)$.
$(g_{\operatorname{B}},H_0)$.
2. Preliminaries
2.1. Aligned homogeneous spaces
The known results on compact homogeneous spaces ![]() $G/K$ differs substantially between the cases of G simple and non-simple. One potential reason for this could be that the isotropy representation of
$G/K$ differs substantially between the cases of G simple and non-simple. One potential reason for this could be that the isotropy representation of ![]() $G/K$ is rarely multiplicity-free when G is non-simple. The class of homogeneous spaces with the richest third cohomology was studied in [Reference Lauret and Will8], and they are called aligned due to their special properties concerning the decomposition in irreducibles of G and K and their Killing constants. We provide an overview of this definition and properties when G has only two simple factors (s = 2 in [Reference Lauret and Will7]).
$G/K$ is rarely multiplicity-free when G is non-simple. The class of homogeneous spaces with the richest third cohomology was studied in [Reference Lauret and Will8], and they are called aligned due to their special properties concerning the decomposition in irreducibles of G and K and their Killing constants. We provide an overview of this definition and properties when G has only two simple factors (s = 2 in [Reference Lauret and Will7]).
Let ![]() $M=G/K$ be a homogeneous space, where G is a compact, connected, semisimple with two simple factors Lie group and K is a connected closed subgroup. We fix the following decomposition for the Lie algebra of G and K:
$M=G/K$ be a homogeneous space, where G is a compact, connected, semisimple with two simple factors Lie group and K is a connected closed subgroup. We fix the following decomposition for the Lie algebra of G and K:
where ![]() $\mathfrak{g} _i$'s and
$\mathfrak{g} _i$'s and ![]() $\mathfrak{k} _j$'s are simple ideals of
$\mathfrak{k} _j$'s are simple ideals of ![]() $\mathfrak{g} $ and
$\mathfrak{g} $ and ![]() $\mathfrak{k} $, respectively, and
$\mathfrak{k} $, respectively, and ![]() $\mathfrak{k} _0$ is the center of
$\mathfrak{k} _0$ is the center of ![]() $\mathfrak{k} $. We call
$\mathfrak{k} $. We call ![]() $\pi_i:\mathfrak{g} \rightarrow\mathfrak{g} _i$ the usual projections and we set
$\pi_i:\mathfrak{g} \rightarrow\mathfrak{g} _i$ the usual projections and we set ![]() $Z_i:=\pi_i(Z)$ for any
$Z_i:=\pi_i(Z)$ for any ![]() $Z\in\mathfrak{g} $,
$Z\in\mathfrak{g} $, ![]() $i=1,2$. The Killing form of any Lie algebra
$i=1,2$. The Killing form of any Lie algebra ![]() $\mathfrak{h} $ will always be denoted by
$\mathfrak{h} $ will always be denoted by ![]() $\operatorname{B}_\mathfrak{h} $.
$\operatorname{B}_\mathfrak{h} $.
Definition 2.1. A homogeneous space ![]() $G/K$ as above is said to be aligned if there exist
$G/K$ as above is said to be aligned if there exist ![]() $c_1,c_2 \gt 0$ such that:
$c_1,c_2 \gt 0$ such that:
(i) The Killing constants, defined by
 \begin{equation*}
\operatorname{B}_{\pi_i(\mathfrak{k} _j)} = a_{ij}\operatorname{B}_{\mathfrak{g} _i}|_{\pi_i(\mathfrak{k} _j)\times\pi_i(\mathfrak{k} _j)},
\end{equation*}
\begin{equation*}
\operatorname{B}_{\pi_i(\mathfrak{k} _j)} = a_{ij}\operatorname{B}_{\mathfrak{g} _i}|_{\pi_i(\mathfrak{k} _j)\times\pi_i(\mathfrak{k} _j)},
\end{equation*}satisfy the following alignment property:
 \begin{align*}
(a_{1j},a_{2j}) = \lambda_j(c_1,c_2) \quad\mbox{for some}\quad \lambda_j \gt 0, \qquad\forall j=1,\dots,t.
\end{align*}
\begin{align*}
(a_{1j},a_{2j}) = \lambda_j(c_1,c_2) \quad\mbox{for some}\quad \lambda_j \gt 0, \qquad\forall j=1,\dots,t.
\end{align*}(ii) There exists an inner product
 $\langle\cdot,\cdot\rangle$ on
$\langle\cdot,\cdot\rangle$ on  $\mathfrak{k} _0$ such that
(6)
$\mathfrak{k} _0$ such that
(6) \begin{equation}
\operatorname{B}_{\mathfrak{g} _i}(Z_i,W_i) = -\tfrac{1}{c_i}\langle Z,W\rangle, \qquad\forall Z,W\in\mathfrak{k} _0, \quad i=1,2.
\end{equation}
\begin{equation}
\operatorname{B}_{\mathfrak{g} _i}(Z_i,W_i) = -\tfrac{1}{c_i}\langle Z,W\rangle, \qquad\forall Z,W\in\mathfrak{k} _0, \quad i=1,2.
\end{equation}(iii)
 $\frac{1}{c_1}+\frac{1}{c_2}=1$.
$\frac{1}{c_1}+\frac{1}{c_2}=1$.
The ideals ![]() $\mathfrak{k} _j$'s are therefore uniformly embedded on each
$\mathfrak{k} _j$'s are therefore uniformly embedded on each ![]() $\mathfrak{g} _i$ in some sense. From the definition,
$\mathfrak{g} _i$ in some sense. From the definition, ![]() $G/K$ is automatically aligned if
$G/K$ is automatically aligned if ![]() $\mathfrak{k} $ is simple or one-dimensional and the following properties hold:
$\mathfrak{k} $ is simple or one-dimensional and the following properties hold:
(i)
 $\pi_i(\mathfrak{k} )\simeq\mathfrak{k} $ for
$\pi_i(\mathfrak{k} )\simeq\mathfrak{k} $ for  $i=1,2$.
$i=1,2$.(ii) The Killing form of
 $\mathfrak{k} _j$ is given by
$\mathfrak{k} _j$ is given by  $\operatorname{B}_{\mathfrak{k} _j}=\lambda_j\operatorname{B}_{\mathfrak{g} }|_{\mathfrak{k} _j\times\mathfrak{k} _j}, \qquad\forall j=1,\dots,t.$
$\operatorname{B}_{\mathfrak{k} _j}=\lambda_j\operatorname{B}_{\mathfrak{g} }|_{\mathfrak{k} _j\times\mathfrak{k} _j}, \qquad\forall j=1,\dots,t.$
From now on, given homogeneous spaces ![]() $M_i=G_i/K$,
$M_i=G_i/K$, ![]() $i=1,2$, such that each Gi is simple and their Killing constants satisfy
$i=1,2$, such that each Gi is simple and their Killing constants satisfy ![]() $\operatorname{B}_{\mathfrak{k} }=a_i\operatorname{B}_{\mathfrak{g} _i}|_{\mathfrak{k} }$ for
$\operatorname{B}_{\mathfrak{k} }=a_i\operatorname{B}_{\mathfrak{g} _i}|_{\mathfrak{k} }$ for ![]() $i=1,2$, we consider the homogeneous space
$i=1,2$, we consider the homogeneous space ![]() $M=G_1\times G_2 / \Delta K$, which is an aligned homogeneous space with
$M=G_1\times G_2 / \Delta K$, which is an aligned homogeneous space with
 \begin{equation}
c_1=\tfrac{a_1+a_2}{a_2}\text{,} \quad c_2=\tfrac{a_1+a_2}{a_1} \quad \text{and } \quad \lambda:=\lambda_1=\dots=\lambda_t=\tfrac{a_1a_2}{a_1+a_2}.
\end{equation}
\begin{equation}
c_1=\tfrac{a_1+a_2}{a_2}\text{,} \quad c_2=\tfrac{a_1+a_2}{a_1} \quad \text{and } \quad \lambda:=\lambda_1=\dots=\lambda_t=\tfrac{a_1a_2}{a_1+a_2}.
\end{equation} If ![]() $a_1\leq a_2$, then
$a_1\leq a_2$, then ![]() $ 1 \lt c_1 \leq 2 \leq c_2$.
$ 1 \lt c_1 \leq 2 \leq c_2$.
Let ![]() $G:=G_1\times G_2$ and consider the reductive decomposition
$G:=G_1\times G_2$ and consider the reductive decomposition ![]() $\mathfrak{g} =\mathfrak{k} \oplus\mathfrak{p} $, which is orthogonal with respect to
$\mathfrak{g} =\mathfrak{k} \oplus\mathfrak{p} $, which is orthogonal with respect to ![]() $g_{\operatorname{B}}$, the Killing metric of G. We fix the G-invariant metric on M called standard given by
$g_{\operatorname{B}}$, the Killing metric of G. We fix the G-invariant metric on M called standard given by
as a background metric. Note that we denote by ![]() $g_{\operatorname{B}}$ both, the bi-invariant metric on the Lie group G and the G-invariant metric on M.
$g_{\operatorname{B}}$ both, the bi-invariant metric on the Lie group G and the G-invariant metric on M.
Consider the ![]() $g_{\operatorname{B}}$-orthogonal Ad(K)-invariant decomposition
$g_{\operatorname{B}}$-orthogonal Ad(K)-invariant decomposition
where ![]() ${\mathfrak{p}}_i$ is equivalent to the isotropy representation of the homogeneous space
${\mathfrak{p}}_i$ is equivalent to the isotropy representation of the homogeneous space ![]() $M_i=G_i/\pi_i(K)$ for
$M_i=G_i/\pi_i(K)$ for ![]() $i=1,2$ and
$i=1,2$ and
 \begin{equation}
{\mathfrak{p}}_3:=\left\{\bar{Z}=\left(Z_1,-\tfrac{c_2}{c_1}Z_2\right) : Z\in \mathfrak{k} \right\}
\end{equation}
\begin{equation}
{\mathfrak{p}}_3:=\left\{\bar{Z}=\left(Z_1,-\tfrac{c_2}{c_1}Z_2\right) : Z\in \mathfrak{k} \right\}
\end{equation} is equivalent to the adjoint representation ![]() $\mathfrak{k} $ (see [Reference Lauret and Will8, Proposition 5.1]).
$\mathfrak{k} $ (see [Reference Lauret and Will8, Proposition 5.1]).
In order to use some known results assume the following technical property:
Assumption 2.2. None of the irreducible components of ![]() ${\mathfrak{p}}_1,{\mathfrak{p}}_2$ is equivalent to any of the simple factors of
${\mathfrak{p}}_1,{\mathfrak{p}}_2$ is equivalent to any of the simple factors of ![]() $\mathfrak{k} $ as
$\mathfrak{k} $ as ![]() $\operatorname{Ad}(K)$-representations and either
$\operatorname{Ad}(K)$-representations and either ![]() $\mathfrak{z} (\mathfrak{k} )=0$ or the trivial representation is not contained in any of
$\mathfrak{z} (\mathfrak{k} )=0$ or the trivial representation is not contained in any of ![]() ${\mathfrak{p}}_1,{\mathfrak{p}}_2$ (see [Reference Lauret and Will8, Section 6] for more details on this assumption).
${\mathfrak{p}}_1,{\mathfrak{p}}_2$ (see [Reference Lauret and Will8, Section 6] for more details on this assumption).
2.2. Bismut connection and generalized Ricci flow
For further information on the subject of this subsection, we refer to the recent book [Reference Garcia-Fernandez and Streets5] and the articles [Reference Cortes and Krusche3, Reference Garcia-Fernandez4, Reference Lee11, Reference Podestà and Raffero13–Reference Streets17].
Given a compact Riemannian manifold (M, g) and a 3-form H on M, we call Bismut the unique metric connection on M with torsion T such that it satisfies the 3-covariant tensor
is the 3-form H on M. When it holds, this connection ![]() $\nabla^B$ is given by
$\nabla^B$ is given by
 \begin{align*}
g(\nabla^B_XY,Z)=g(\nabla^g_XY,Z)+\tfrac{1}{2} H(X,Y,Z), \qquad\forall X,Y,Z\in\chi(M),
\end{align*}
\begin{align*}
g(\nabla^B_XY,Z)=g(\nabla^g_XY,Z)+\tfrac{1}{2} H(X,Y,Z), \qquad\forall X,Y,Z\in\chi(M),
\end{align*} where ![]() $\nabla^g$ is the Levi Civita connection of (M, g).
$\nabla^g$ is the Levi Civita connection of (M, g).
If H is closed then the pair (g, H) is called a generalized metric. A way to make these structures evolve naturally is provided by the Ricci tensor of the Bismut connection giving rise to the evolution Equation 1 called generalized Ricci flow (see [Reference Garcia-Fernandez and Streets5, Reference Lee11] and references therein).
The fixed points of this flow are the BRF generalized metrics, also called generalized Einstein metrics, i.e., (g, H) such that
 \begin{equation}
\operatorname{Rc}(g)=\tfrac{1}{4} H_g^2 \quad\mbox{and} \quad H\mbox{ is }g\mbox{-harmonic}.
\end{equation}
\begin{equation}
\operatorname{Rc}(g)=\tfrac{1}{4} H_g^2 \quad\mbox{and} \quad H\mbox{ is }g\mbox{-harmonic}.
\end{equation}2.3. BRF metrics on aligned homogeneous spaces
We review in this section the homogeneous BRF generalized metrics recently found in [Reference Lauret and Will10], which is a new version of [Reference Lauret and Will7] including a Corrigendum.
According to [Reference Lauret and Will8], a bi-invariant symmetric bilinear form Q 0 on ![]() $\mathfrak{g} $ defined by
$\mathfrak{g} $ defined by
 \begin{align*}
Q_0={\operatorname{B}}_{{\mathfrak{g}} _1}-(\tfrac{1}{c_1-1}){\operatorname{B}}_{{\mathfrak{g}} _2},
\end{align*}
\begin{align*}
Q_0={\operatorname{B}}_{{\mathfrak{g}} _1}-(\tfrac{1}{c_1-1}){\operatorname{B}}_{{\mathfrak{g}} _2},
\end{align*}defines a G-invariant closed 3-form on M denoted H 0 and given by
 \begin{align*}
H_0(X,Y,Z) &:= Q_0([X,Y],Z) + Q_0([X,Y]_\mathfrak{k}, Z) - Q_0([X,Z]_\mathfrak{k}, Y) + Q_0([Y,Z]_\mathfrak{k}, X)\\ & \quad \text{for all\ } X,Y,Z \in \mathfrak{p},
\end{align*}
\begin{align*}
H_0(X,Y,Z) &:= Q_0([X,Y],Z) + Q_0([X,Y]_\mathfrak{k}, Z) - Q_0([X,Z]_\mathfrak{k}, Y) + Q_0([Y,Z]_\mathfrak{k}, X)\\ & \quad \text{for all\ } X,Y,Z \in \mathfrak{p},
\end{align*} which is g-harmonic for any diagonal G-invariant metric ![]() $g=(x_1,x_2,x_3)_{g_{\operatorname{B}}}$ of the form:
$g=(x_1,x_2,x_3)_{g_{\operatorname{B}}}$ of the form:
Recently in [Reference Lauret and Will10, Theorem A.2], it was proved the existence of a G-invariant BRF generalized metric on any homogeneous space ![]() $M=G/K$ where G has two simple factors and the Assumption 2.2 holds. Expressed in terms of the standard metric as a background the result is as follows (see [Reference Lauret and Will10, Remark A.3]).
$M=G/K$ where G has two simple factors and the Assumption 2.2 holds. Expressed in terms of the standard metric as a background the result is as follows (see [Reference Lauret and Will10, Remark A.3]).
Theorem 2.3. (Lauret and Will [Reference Lauret and Will10, Theorem A.2]) Let ![]() $M=G/K$ be an aligned homogeneous space with s = 2 such that Assumption 2.2 holds.
$M=G/K$ be an aligned homogeneous space with s = 2 such that Assumption 2.2 holds.
(i) The G-invariant generalized metric
 $(g_0,H_{0})$ defined by
(10)
$(g_0,H_{0})$ defined by
(10) \begin{align}
g_0:=\left(1,\tfrac{1}{c_1-1},\tfrac{c_1}{c_1-1}\right)_{g_{\operatorname{B}}}
\end{align}
\begin{align}
g_0:=\left(1,\tfrac{1}{c_1-1},\tfrac{c_1}{c_1-1}\right)_{g_{\operatorname{B}}}
\end{align}is BRF.
(ii) This is the only G-invariant BRF generalized metric on
 $M=G/K$ up to scaling of the form
$M=G/K$ up to scaling of the form  $(g=(x_1,x_2,x_3)_{g_{\operatorname{B}}},H_0)$.
$(g=(x_1,x_2,x_3)_{g_{\operatorname{B}}},H_0)$.
As these metrics are precisely the fixed points of the generalized Ricci flow, we will utilize the elements involved in the proof of their main theorem. We consider the homogeneous space ![]() $M_i=G_i/K$ for
$M_i=G_i/K$ for ![]() $i=1,2$, and its
$i=1,2$, and its ![]() $\operatorname{B}_{\mathfrak{g} _i}$-orthogonal reductive decomposition
$\operatorname{B}_{\mathfrak{g} _i}$-orthogonal reductive decomposition ![]() $\mathfrak{g} _i=\mathfrak{k} \oplus {\mathfrak{p}}_i$. For each
$\mathfrak{g} _i=\mathfrak{k} \oplus {\mathfrak{p}}_i$. For each ![]() $i=1,2$, we endowed it with the standard metric, which we denote by
$i=1,2$, we endowed it with the standard metric, which we denote by ![]() $g_{\operatorname{B}}^i$ (i.e.,
$g_{\operatorname{B}}^i$ (i.e.,  $g_{\operatorname{B}}^i=-\operatorname{B}_{\mathfrak{g} _i}|_{{\mathfrak{p}}_i\times{\mathfrak{p}}_i}$). For what follows, we called
$g_{\operatorname{B}}^i=-\operatorname{B}_{\mathfrak{g} _i}|_{{\mathfrak{p}}_i\times{\mathfrak{p}}_i}$). For what follows, we called ![]() $\operatorname{C}_{\chi_{i}}:{\mathfrak{p}}_i\rightarrow {\mathfrak{p}}_i$, the Casimir operator of the isotropy representation
$\operatorname{C}_{\chi_{i}}:{\mathfrak{p}}_i\rightarrow {\mathfrak{p}}_i$, the Casimir operator of the isotropy representation
of Mi with respect to ![]() $-\operatorname{B}_{\mathfrak{g} _i}|_{\mathfrak{k} \times\mathfrak{k} }$, and we fix this notation:
$-\operatorname{B}_{\mathfrak{g} _i}|_{\mathfrak{k} \times\mathfrak{k} }$, and we fix this notation:
 \begin{align*}
A_3:=-\tfrac{c_2}{c_1}, \qquad B_3:=\tfrac{1}{c_1}+A_3^2\tfrac{1}{c_2}, \qquad
B_4:=\tfrac{1}{c_1}+\tfrac{1}{c_2}=1.
\end{align*}
\begin{align*}
A_3:=-\tfrac{c_2}{c_1}, \qquad B_3:=\tfrac{1}{c_1}+A_3^2\tfrac{1}{c_2}, \qquad
B_4:=\tfrac{1}{c_1}+\tfrac{1}{c_2}=1.
\end{align*} The following proposition is demonstrated in [Reference Lauret and Will7, Proposition 3.2] and gives the formula for the Ricci operator when condition Equation 7 holds (![]() $\lambda:=\lambda_1=\dots=\lambda_t$). Note that the added hypothesis only changes (iii) from the original proposition.
$\lambda:=\lambda_1=\dots=\lambda_t$). Note that the added hypothesis only changes (iii) from the original proposition.
Proposition 2.4. (Lauret and Will [Reference Lauret and Will7, Proposition 3.2]) If s = 2 and Equation 7 holds, then the Ricci operator of the metric ![]() $g=(x_1,x_2,x_3)_{g_{\operatorname{B}}}$ is given as follows:
$g=(x_1,x_2,x_3)_{g_{\operatorname{B}}}$ is given as follows:
(i)
 $\operatorname{Ric}(g)|_{{\mathfrak{p}}_1} = \tfrac{1}{4x_1}I_{{\mathfrak{p}}_1}
+ \tfrac{1}{2x_1} \left(1 - \tfrac{x_{3}}{x_1c_1B_{3}}\right) \operatorname{C}_{\chi_{1}}$.
$\operatorname{Ric}(g)|_{{\mathfrak{p}}_1} = \tfrac{1}{4x_1}I_{{\mathfrak{p}}_1}
+ \tfrac{1}{2x_1} \left(1 - \tfrac{x_{3}}{x_1c_1B_{3}}\right) \operatorname{C}_{\chi_{1}}$.(ii)
 $\operatorname{Ric}(g)|_{{\mathfrak{p}}_2} = \tfrac{1}{4x_2}I_{{\mathfrak{p}}_2}
+ \tfrac{1}{2x_2}\left(1 - \tfrac{x_{3}}{x_2c_2B_{3}} A_{3}^2\right) \operatorname{C}_{\chi_{2}} $.
$\operatorname{Ric}(g)|_{{\mathfrak{p}}_2} = \tfrac{1}{4x_2}I_{{\mathfrak{p}}_2}
+ \tfrac{1}{2x_2}\left(1 - \tfrac{x_{3}}{x_2c_2B_{3}} A_{3}^2\right) \operatorname{C}_{\chi_{2}} $.(iii)
 $\operatorname{Ric}(g)|_{{\mathfrak{p}}_3}= rI_{{\mathfrak{p}}_3}$, where
$\operatorname{Ric}(g)|_{{\mathfrak{p}}_3}= rI_{{\mathfrak{p}}_3}$, where
 \begin{align*}
r :=& \tfrac{\lambda}{4x_{3}B_3}\left(\tfrac{2x_1^2-x_{3}^2}{x_1^2}
+\tfrac{(2x_2^2-x_{3}^2)A_3^2}{x_2^2}
-\tfrac{1+A_3}{B_3}\left(\tfrac{1}{c_1}+\tfrac{1}{c_2}A_3^3\right)\right) \\
&+\tfrac{1}{4x_{3}B_3}\left(2\left(\tfrac{1}{c_1}+\tfrac{1}{c_2}A_3^2\right)
-\tfrac{2x_1^2-x_{3}^2}{x_1^2c_1}
- \tfrac{(2x_2^2-x_{3}^2)A_3^2}{x_2^2c_2}\right).
\end{align*}
\begin{align*}
r :=& \tfrac{\lambda}{4x_{3}B_3}\left(\tfrac{2x_1^2-x_{3}^2}{x_1^2}
+\tfrac{(2x_2^2-x_{3}^2)A_3^2}{x_2^2}
-\tfrac{1+A_3}{B_3}\left(\tfrac{1}{c_1}+\tfrac{1}{c_2}A_3^3\right)\right) \\
&+\tfrac{1}{4x_{3}B_3}\left(2\left(\tfrac{1}{c_1}+\tfrac{1}{c_2}A_3^2\right)
-\tfrac{2x_1^2-x_{3}^2}{x_1^2c_1}
- \tfrac{(2x_2^2-x_{3}^2)A_3^2}{x_2^2c_2}\right).
\end{align*}(iv)
 $g(\operatorname{Ric}(g){\mathfrak{p}}_i,{\mathfrak{p}}_j)=0 \quad \text{for all } i\neq j$.
$g(\operatorname{Ric}(g){\mathfrak{p}}_i,{\mathfrak{p}}_j)=0 \quad \text{for all } i\neq j$.
The formula of the symmetric bilinear form  $(H_0)_g^2$ used in the definition of the generalized Ricci flow is provided in the following results. In general, a bi-invariant symmetric bilinear form Q on
$(H_0)_g^2$ used in the definition of the generalized Ricci flow is provided in the following results. In general, a bi-invariant symmetric bilinear form Q on ![]() $\mathfrak{g} $,
$\mathfrak{g} $,
 \begin{align*}
Q=y_1\operatorname{B}_{\mathfrak{g} _1}+y_2\operatorname{B}_{\mathfrak{g} _2} \text{such that } \tfrac{y_1}{c_1}+\tfrac{y_2}{c_2}=0,
\end{align*}
\begin{align*}
Q=y_1\operatorname{B}_{\mathfrak{g} _1}+y_2\operatorname{B}_{\mathfrak{g} _2} \text{such that } \tfrac{y_1}{c_1}+\tfrac{y_2}{c_2}=0,
\end{align*}defines a G-invariant closed 3-form on M given by
 \begin{align*}
H_Q(X,Y,Z) &:= Q([X,Y],Z) + Q([X,Y]_\mathfrak{k}, Z) - Q([X,Z]_\mathfrak{k}, Y) + Q([Y,Z]_\mathfrak{k}, X), \\ &\quad \text{for all\ } X,Y,Z \in \mathfrak{p}.
\end{align*}
\begin{align*}
H_Q(X,Y,Z) &:= Q([X,Y],Z) + Q([X,Y]_\mathfrak{k}, Z) - Q([X,Z]_\mathfrak{k}, Y) + Q([Y,Z]_\mathfrak{k}, X), \\ &\quad \text{for all\ } X,Y,Z \in \mathfrak{p}.
\end{align*}Proposition 2.5. (Lauret and Will [Reference Lauret and Will7, Proposition 4.2]) For any ![]() $X\in{\mathfrak{p}}_k$,
$X\in{\mathfrak{p}}_k$, ![]() $k=1,2$,
$k=1,2$,
 \begin{align*}
(H_Q)_g^2(X,X) = g_{\operatorname{B}}\left(\left(\left(\tfrac{2S_k}{x_kc_k}-\tfrac{2y_k^2}{x_k^2}\right)\operatorname{C}_{\chi_k}+\tfrac{y_k^2}{x_k^2}I_{{\mathfrak{p}}_k}\right)X,X\right),
\end{align*}
\begin{align*}
(H_Q)_g^2(X,X) = g_{\operatorname{B}}\left(\left(\left(\tfrac{2S_k}{x_kc_k}-\tfrac{2y_k^2}{x_k^2}\right)\operatorname{C}_{\chi_k}+\tfrac{y_k^2}{x_k^2}I_{{\mathfrak{p}}_k}\right)X,X\right),
\end{align*}where
 \begin{align*}
C_3=\tfrac{y_1}{c_1}+A_3\tfrac{y_2}{c_2},\qquad
S_1= \tfrac{1}{x_3B_3}\left(y_1 + \tfrac{C_3}{B_4}\right)^2, \qquad
S_2 = \tfrac{1}{x_3B_3}\left(A_3y_2+ \tfrac{C_3}{B_4}\right)^2.
\end{align*}
\begin{align*}
C_3=\tfrac{y_1}{c_1}+A_3\tfrac{y_2}{c_2},\qquad
S_1= \tfrac{1}{x_3B_3}\left(y_1 + \tfrac{C_3}{B_4}\right)^2, \qquad
S_2 = \tfrac{1}{x_3B_3}\left(A_3y_2+ \tfrac{C_3}{B_4}\right)^2.
\end{align*}Proposition 2.6. (Lauret and Will [Reference Lauret and Will10, Proposition A.1]) If ![]() $\bar{Z}\in{\mathfrak{p}}_3$ (see Equation 8), with
$\bar{Z}\in{\mathfrak{p}}_3$ (see Equation 8), with ![]() $g_{\operatorname{B}}(\bar{Z},\bar{Z})=1$, then
$g_{\operatorname{B}}(\bar{Z},\bar{Z})=1$, then
 \begin{align*}
(H_Q)_{g}^2(\bar{Z},\bar{Z})
= & \tfrac{1}{x_1^2B_3} \left(y_1 + \tfrac{C_3}{B_{4}} \right)^2 \tfrac{1-c_1\lambda}{c_1}
+\tfrac{1}{x_2^2B_3} \left(y_2A_3 + \tfrac{C_3}{B_{4}}\right)^2 \tfrac{1-c_2\lambda}{c_2} \\
& +\tfrac{\lambda}{x_3^2B_3^3}\left(\tfrac{y_1}{c_1}+A_3^3\tfrac{y_2}{c_2} + \tfrac{3C_3}{B_{4}} \left(\tfrac{1}{c_1}+A_3^2\tfrac{1}{c_2}\right)\right)^2.
\end{align*}
\begin{align*}
(H_Q)_{g}^2(\bar{Z},\bar{Z})
= & \tfrac{1}{x_1^2B_3} \left(y_1 + \tfrac{C_3}{B_{4}} \right)^2 \tfrac{1-c_1\lambda}{c_1}
+\tfrac{1}{x_2^2B_3} \left(y_2A_3 + \tfrac{C_3}{B_{4}}\right)^2 \tfrac{1-c_2\lambda}{c_2} \\
& +\tfrac{\lambda}{x_3^2B_3^3}\left(\tfrac{y_1}{c_1}+A_3^3\tfrac{y_2}{c_2} + \tfrac{3C_3}{B_{4}} \left(\tfrac{1}{c_1}+A_3^2\tfrac{1}{c_2}\right)\right)^2.
\end{align*}3. Generalized Ricci flow on aligned spaces
The aim of this paper is to study the generalized Ricci flow on homogeneous spaces of the form ![]() $M=G_1\times G_2 / K$, such that each Gi is a simple Lie group, K is a closed subgroup of them and their Killing constants satisfy
$M=G_1\times G_2 / K$, such that each Gi is a simple Lie group, K is a closed subgroup of them and their Killing constants satisfy ![]() $\operatorname{B}_{\mathfrak{k} }=a_i\operatorname{B}_{\mathfrak{g} _i}|_{\mathfrak{k} }$ for
$\operatorname{B}_{\mathfrak{k} }=a_i\operatorname{B}_{\mathfrak{g} _i}|_{\mathfrak{k} }$ for ![]() $i=1,2$. As in
$i=1,2$. As in ![]() $\S$ 2.1, M is an aligned homogeneous space satisfying Equation 7, note that
$\S$ 2.1, M is an aligned homogeneous space satisfying Equation 7, note that ![]() $a_i=\lambda c_i$, for
$a_i=\lambda c_i$, for ![]() $i=1,2$. We assume that the standard metric
$i=1,2$. We assume that the standard metric ![]() $g_{\operatorname{B}}^i$ on each homogeneous space
$g_{\operatorname{B}}^i$ on each homogeneous space ![]() $M_i:=G_i/K$ is Einstein for
$M_i:=G_i/K$ is Einstein for ![]() $i=1,2$. In that sense, we look for invariant solutions
$i=1,2$. In that sense, we look for invariant solutions ![]() $(g(t),H(t))$ to the equations given in Equation 1.
$(g(t),H(t))$ to the equations given in Equation 1.
We set ![]() $x_1:=x_1(t)$,
$x_1:=x_1(t)$, ![]() $x_2:=x_2(t)$,
$x_2:=x_2(t)$, ![]() $x_3:=x_3(t)$ smooth positive functions and define
$x_3:=x_3(t)$ smooth positive functions and define
As every scalar multiple of H 0 is g(t)-harmonic for every ![]() $t\geq0$, the second equation of the flow in Equation 1 vanishes and
$t\geq0$, the second equation of the flow in Equation 1 vanishes and ![]() $H(t)\equiv H_0$; therefore, we only need to focus on the first one, starting from some generalized metric of the form
$H(t)\equiv H_0$; therefore, we only need to focus on the first one, starting from some generalized metric of the form ![]() $(g(0),H_0)$, that is
$(g(0),H_0)$, that is
 \begin{equation}
\tfrac{\partial}{\partial t}g(t)=-2\operatorname{Ric}(g(t))+\tfrac{1}{2}(H_0)^2_{g(t)}.
\end{equation}
\begin{equation}
\tfrac{\partial}{\partial t}g(t)=-2\operatorname{Ric}(g(t))+\tfrac{1}{2}(H_0)^2_{g(t)}.
\end{equation} Note that by definition, g(t) is diagonal for all ![]() $t \geq 0$. In the next lemma we see that, under certain conditions, the set of diagonal metrics is invariant under the flow.
$t \geq 0$. In the next lemma we see that, under certain conditions, the set of diagonal metrics is invariant under the flow.
Lemma 3.1. Let ![]() $M=G_1\times G_2 / K$ be an aligned homogeneous space satisfying Equation 7 and assume that
$M=G_1\times G_2 / K$ be an aligned homogeneous space satisfying Equation 7 and assume that ![]() $(M_i =G_i/K, g_{\operatorname{B}}^i)$ is Einstein, where
$(M_i =G_i/K, g_{\operatorname{B}}^i)$ is Einstein, where ![]() $g_{\operatorname{B}}^i$ is the standard metric on Mi, then the set of diagonal metrics with respect to the decomposition
$g_{\operatorname{B}}^i$ is the standard metric on Mi, then the set of diagonal metrics with respect to the decomposition ![]() $\mathfrak{p} ={\mathfrak{p}}_1\oplus{\mathfrak{p}}_2\oplus{\mathfrak{p}}_3$ is invariant under the generalized Ricci flow.
$\mathfrak{p} ={\mathfrak{p}}_1\oplus{\mathfrak{p}}_2\oplus{\mathfrak{p}}_3$ is invariant under the generalized Ricci flow.
Proof. As ![]() $(M_i, g_{\operatorname{B}}^i)$ is Einstein, there exist constants
$(M_i, g_{\operatorname{B}}^i)$ is Einstein, there exist constants  $ \kappa_i \in (0,\tfrac{1}{2}]$ such that
$ \kappa_i \in (0,\tfrac{1}{2}]$ such that ![]() $\operatorname{C}_{\chi_{i}} = \kappa_i \operatorname{Id}_{{\mathfrak{p}}_i}$ for
$\operatorname{C}_{\chi_{i}} = \kappa_i \operatorname{Id}_{{\mathfrak{p}}_i}$ for ![]() $i=1,2$. Therefore, from Propositions 2.4, 2.5 and 2.6, we see that
$i=1,2$. Therefore, from Propositions 2.4, 2.5 and 2.6, we see that  $\tfrac{d}{dt}g(t)$ is tangent to the space of diagonal metrics, because all the operators involved are multiples of the identity in each
$\tfrac{d}{dt}g(t)$ is tangent to the space of diagonal metrics, because all the operators involved are multiples of the identity in each ![]() ${\mathfrak{p}}_j$ for
${\mathfrak{p}}_j$ for ![]() $j=1,2,3$.
$j=1,2,3$.
Proposition 3.2. Let ![]() $M=G_1\times G_2/ K$ be as in Lemma 3.1 such that
$M=G_1\times G_2/ K$ be as in Lemma 3.1 such that ![]() $\operatorname{C}_{\chi_{i}} = \kappa_i \operatorname{Id}_{{\mathfrak{p}}_i}$ for
$\operatorname{C}_{\chi_{i}} = \kappa_i \operatorname{Id}_{{\mathfrak{p}}_i}$ for ![]() $i=1,2$. Fix the standard metric of M,
$i=1,2$. Fix the standard metric of M, ![]() $g_{\operatorname{B}}$, as a background metric, then the generalized Ricci flow for metrics of the form
$g_{\operatorname{B}}$, as a background metric, then the generalized Ricci flow for metrics of the form ![]() $g=(x_1,x_2,x_3)_{g_{\operatorname{B}}}$ is given by the following system of ordinary differential equations :
$g=(x_1,x_2,x_3)_{g_{\operatorname{B}}}$ is given by the following system of ordinary differential equations :
 \begin{align}
\left\{\begin{aligned}
x_1'(t)= &\tfrac{2 \kappa_1 x_1 x_3^2 + c_1 x_3 \left(-1 + x_1^2 + 2 \kappa_1 (1 + x_1^2 - 2 x_1 x_3)\right) + c_1^2 \left(x_3 - x_1^2 x_3 - 2 \kappa_1 \left(x_3 + x_1^2 x_3 - x_1 (1 + x_3^2)\right)\right)}{2 (c_1-1) c_1 x_1^2 x_3},\\
x_2'(t)= &-\tfrac{c_1^3 (1 + 2 \kappa_2) x_2^2 x_3 - 2 \kappa_2 x_2 x_3^2 +
c_1 x_3 \left(\!-1 + x_2^2 + 2 \kappa_2 (1 + x_2^2 + 2 x_2 x_3)\!\right) -
2 c_1^2 x_2 \left(\!x_2 x_3 + \kappa_2 (1 + 2 x_2 x_3 + x_3^2)\!\right)}{2 (c_1-1)^2 c_1 x_2^2 x_3},\\
x_3'(t)=&\tfrac{\left(x_3^2 - 2 c_1 x_3^2 + c_1^2 (x_3^2-1)\right)\left(\!-c_1^2 (1 + 2\lambda) x_2^2 x_3^2 + (x_1^2 - x_2^2) x_3^2 + c_1 \left(\!(\lambda-1) x_1^2 + (2 +\lambda) x_2^2\right) x_3^2 + c_1^3\lambda x_2^2 (x_3^2-x_1^2)\right)}{2 (c_1-1)^3 c_1 x_1^2 x_2^2 x_3^2}.\\
\end{aligned}
\right.
\end{align}
\begin{align}
\left\{\begin{aligned}
x_1'(t)= &\tfrac{2 \kappa_1 x_1 x_3^2 + c_1 x_3 \left(-1 + x_1^2 + 2 \kappa_1 (1 + x_1^2 - 2 x_1 x_3)\right) + c_1^2 \left(x_3 - x_1^2 x_3 - 2 \kappa_1 \left(x_3 + x_1^2 x_3 - x_1 (1 + x_3^2)\right)\right)}{2 (c_1-1) c_1 x_1^2 x_3},\\
x_2'(t)= &-\tfrac{c_1^3 (1 + 2 \kappa_2) x_2^2 x_3 - 2 \kappa_2 x_2 x_3^2 +
c_1 x_3 \left(\!-1 + x_2^2 + 2 \kappa_2 (1 + x_2^2 + 2 x_2 x_3)\!\right) -
2 c_1^2 x_2 \left(\!x_2 x_3 + \kappa_2 (1 + 2 x_2 x_3 + x_3^2)\!\right)}{2 (c_1-1)^2 c_1 x_2^2 x_3},\\
x_3'(t)=&\tfrac{\left(x_3^2 - 2 c_1 x_3^2 + c_1^2 (x_3^2-1)\right)\left(\!-c_1^2 (1 + 2\lambda) x_2^2 x_3^2 + (x_1^2 - x_2^2) x_3^2 + c_1 \left(\!(\lambda-1) x_1^2 + (2 +\lambda) x_2^2\right) x_3^2 + c_1^3\lambda x_2^2 (x_3^2-x_1^2)\right)}{2 (c_1-1)^3 c_1 x_1^2 x_2^2 x_3^2}.\\
\end{aligned}
\right.
\end{align}Proof. From Definition 2.1 (iii),  $c_2=\tfrac{c_1}{c_1-1}$. Hence, as in [Reference Lauret and Will7, Section 5], we have that
$c_2=\tfrac{c_1}{c_1-1}$. Hence, as in [Reference Lauret and Will7, Section 5], we have that  $A_3=-\tfrac{1}{c_1-1}\text{and } B_3=\tfrac{1}{c_1-1}$. Note that for
$A_3=-\tfrac{1}{c_1-1}\text{and } B_3=\tfrac{1}{c_1-1}$. Note that for ![]() $j=1,2,3$,
$j=1,2,3$,
and  $\operatorname{Ric}(g)|_{{\mathfrak{p}}_j}$ is a multiple of the identity in
$\operatorname{Ric}(g)|_{{\mathfrak{p}}_j}$ is a multiple of the identity in ![]() ${\mathfrak{p}}_j$ given by Proposition 2.4.
${\mathfrak{p}}_j$ given by Proposition 2.4.
Given Q 0 with ![]() $y_1=1$ and
$y_1=1$ and  $y_2=-\tfrac{1}{c_1-1}$, the formula of
$y_2=-\tfrac{1}{c_1-1}$, the formula of  $(H_0)^2_{g}$ follows from Propositions 2.5 and 2.6 with
$(H_0)^2_{g}$ follows from Propositions 2.5 and 2.6 with
 \begin{align*}
C_3=\tfrac{1}{c_1-1}, \quad S_1=\tfrac{c_1^2}{(c_1-1)x_3}, \text{and } \ S_2=\tfrac{c_1^2}{(c_1-1)^3x_3}.
\end{align*}
\begin{align*}
C_3=\tfrac{1}{c_1-1}, \quad S_1=\tfrac{c_1^2}{(c_1-1)x_3}, \text{and } \ S_2=\tfrac{c_1^2}{(c_1-1)^3x_3}.
\end{align*}Therefore, replacing these on Equation 11, the proposition holds.
Note that we can write these equations using the usual notation of nonlinear systems of differential equations
where ![]() $x:=(x_1,x_2,x_3)$ and
$x:=(x_1,x_2,x_3)$ and ![]() $f: {\Bbb R}^3_{ \gt 0}\rightarrow {\Bbb R}^3$ is given by the equations in Equation 12.
$f: {\Bbb R}^3_{ \gt 0}\rightarrow {\Bbb R}^3$ is given by the equations in Equation 12.
According to Theorem 2.3, ![]() $(g_0,H_0)$ defined by Equation 10 is a BRF generalized metric, which means a fix or an equilibrium point of the flow. If we set
$(g_0,H_0)$ defined by Equation 10 is a BRF generalized metric, which means a fix or an equilibrium point of the flow. If we set  $x_0:=(1,\tfrac{1}{c_1-1},\tfrac{c_1}{c_1-1})$ then
$x_0:=(1,\tfrac{1}{c_1-1},\tfrac{c_1}{c_1-1})$ then ![]() $f(x_0)=0$ and the local behaviour of Equation 12 is qualitatively determined by the behaviour of the linear system
$f(x_0)=0$ and the local behaviour of Equation 12 is qualitatively determined by the behaviour of the linear system ![]() $x'=Ax$ near the origin, where
$x'=Ax$ near the origin, where ![]() $A=Df(x_0)$, the derivative of f at x 0.
$A=Df(x_0)$, the derivative of f at x 0.
To initiate our study of the generalized Ricci flow on this class of aligned homogeneous spaces, we define some invariant subspaces and show some plots. Regardless of whether K is abelian ![]() $(\lambda=0)$ or not, we see that:
$(\lambda=0)$ or not, we see that:
• The plane given by
 $x_3=\tfrac{c_1}{c_1-1}$ is invariant by the flow.
$x_3=\tfrac{c_1}{c_1-1}$ is invariant by the flow.• Within the plane, the lines defined by
 $x_1=1$ and
$x_1=1$ and  $x_2=\tfrac{1}{c_1-1}$ are invariant, and
$x_2=\tfrac{1}{c_1-1}$ are invariant, and• when
 $\kappa_1=\kappa_2$, the plane
$\kappa_1=\kappa_2$, the plane  $x_1=(c_1-1)x_2$ and the line in it given by
$x_1=(c_1-1)x_2$ and the line in it given by  $x_3=\tfrac{c_1}{c_1-1}$ are also invariant.
$x_3=\tfrac{c_1}{c_1-1}$ are also invariant.
Just to illustrate the flow in those invariant planes we consider ![]() $M=\mathrm{SU}(7)\times\mathrm{SO}(8)/\mathrm{SO}(7)$, a homogeneous space of dimension 55 such that
$M=\mathrm{SU}(7)\times\mathrm{SO}(8)/\mathrm{SO}(7)$, a homogeneous space of dimension 55 such that  $c_1=\tfrac{10}{7}$,
$c_1=\tfrac{10}{7}$,  $\kappa_1=\kappa_2=\tfrac{1}{2}$ and
$\kappa_1=\kappa_2=\tfrac{1}{2}$ and  $\lambda=\tfrac{1}{4}$. In this case, the BRF metric is
$\lambda=\tfrac{1}{4}$. In this case, the BRF metric is  $x_0=(1,\tfrac{7}{3},\tfrac{10}{3})$ and the plots of the invariant planes of the flow are shown in Figure 1 and Figure 2.
$x_0=(1,\tfrac{7}{3},\tfrac{10}{3})$ and the plots of the invariant planes of the flow are shown in Figure 1 and Figure 2.

Figure 1. Flow in the invariant plane  $x_3=\tfrac{10}{3}$.
$x_3=\tfrac{10}{3}$.

Figure 2. Flow in the invariant plane  $x_1=\tfrac{3}{7}x_2$.
$x_1=\tfrac{3}{7}x_2$.
For the remainder of this section, we recall some definitions of the local theory of nonlinear systems. Consider the system given in Equation 13,
Definition 3.3. An equilibrium point x 0 (i.e., ![]() $f(x_0)=0$) is called hyperbolic if none of the eigenvalues of the matrix
$f(x_0)=0$) is called hyperbolic if none of the eigenvalues of the matrix ![]() $Df(x_0)$ have zero real part.
$Df(x_0)$ have zero real part.
Definition 3.4. Let ϕt denote the flow of the differential equation in Equation 13 defined for all ![]() $t\in {\Bbb R}$. An equilibrium point x 0 is stable if for all ɛ > 0 there exists a δ > 0 such that for all
$t\in {\Bbb R}$. An equilibrium point x 0 is stable if for all ɛ > 0 there exists a δ > 0 such that for all ![]() $x\in N_{\delta}(x_0)$ and
$x\in N_{\delta}(x_0)$ and ![]() $t\geq 0$ we have
$t\geq 0$ we have
where ![]() $N_{\alpha}(x_0)$ is the open ball of positive radius α centred at x 0.
$N_{\alpha}(x_0)$ is the open ball of positive radius α centred at x 0.
x 0 is asymptotically stable if it is stable and there exists δ > 0 such that for all ![]() $x \in N_{\delta}(x_0)$ we have
$x \in N_{\delta}(x_0)$ we have
 \begin{align*}
\lim_{t\rightarrow \infty}\phi_t(x)=x_0.
\end{align*}
\begin{align*}
\lim_{t\rightarrow \infty}\phi_t(x)=x_0.
\end{align*} Since the stability of an equilibrium point is a local property it is reasonable to expect that it would be the same as the stability at the origin of the linear system ![]() $x'(t) = Df(x_0)x$. This expectation is not always met, but it holds for hyperbolic equilibrium points.
$x'(t) = Df(x_0)x$. This expectation is not always met, but it holds for hyperbolic equilibrium points.
The next result gives us a better understanding of the local behaviour of the flow near the BRF generalized metric.
Theorem 3.5. The metric  $g_0=(1,\tfrac{1}{c_1-1},\tfrac{c_1}{c_1-1})_{g_{\operatorname{B}}}$ is asymptotically stable for the dynamical system Equation 12.
$g_0=(1,\tfrac{1}{c_1-1},\tfrac{c_1}{c_1-1})_{g_{\operatorname{B}}}$ is asymptotically stable for the dynamical system Equation 12.
Proof. From Theorem 2.3, ![]() $(g_0,H_0)$ is a BRF generalized metric, which means an equilibrium point of the generalized Ricci flow.
$(g_0,H_0)$ is a BRF generalized metric, which means an equilibrium point of the generalized Ricci flow.
If ![]() $f:=\left(f_1(x_1,x_2,x_3),f_2(x_1,x_2,x_3),f_3(x_1,x_2,x_3)\right)$ satisfies
$f:=\left(f_1(x_1,x_2,x_3),f_2(x_1,x_2,x_3),f_3(x_1,x_2,x_3)\right)$ satisfies
 \begin{align*}
\left\{\begin{aligned}
x_1'(t) &= f_1(x_1,x_2,x_3), \\
x_2'(t) &= f_2(x_1,x_2,x_3),\\
x_3'(t) &= f_3(x_1,x_2,x_3),
\end{aligned}
\right.
\end{align*}
\begin{align*}
\left\{\begin{aligned}
x_1'(t) &= f_1(x_1,x_2,x_3), \\
x_2'(t) &= f_2(x_1,x_2,x_3),\\
x_3'(t) &= f_3(x_1,x_2,x_3),
\end{aligned}
\right.
\end{align*} as in Equation 12, then ![]() $f(g_0)=0$ and its differential at g 0 is given by:
$f(g_0)=0$ and its differential at g 0 is given by:
 \begin{align*}
Df(g_0)=\begin{pmatrix}
-1 & 0 & 0 \\
0 & 1-c_1 & 0 \\
0 & 0 & c_1 (-1 + \lambda)
\end{pmatrix}.
\end{align*}
\begin{align*}
Df(g_0)=\begin{pmatrix}
-1 & 0 & 0 \\
0 & 1-c_1 & 0 \\
0 & 0 & c_1 (-1 + \lambda)
\end{pmatrix}.
\end{align*} As all the eigenvalues of the matrix are real and negative, the equilibrium point  $g_0=(1,\tfrac{1}{c_1-1},\tfrac{c_1}{c_1-1})_{g_{\operatorname{B}}}$ is asymptotically stable by [Reference Perko12, Section 2.9].
$g_0=(1,\tfrac{1}{c_1-1},\tfrac{c_1}{c_1-1})_{g_{\operatorname{B}}}$ is asymptotically stable by [Reference Perko12, Section 2.9].
4. Global stability
In the previous section, we study the local behaviour of the nonlinear dynamical system given in Equation 12, the study of its global behaviour is substantially harder due to the possibility of chaos.
Definition 4.1. An equilibrium point x 0 of a nonlinear system of differential equations ![]() $x'(t) = f(x)$ is globally stable if it is stable and globally attractive, which means
$x'(t) = f(x)$ is globally stable if it is stable and globally attractive, which means
 \begin{align*}
\lim_{t\rightarrow \infty}\phi_t(x)=x_0 \text{ for all } x \in D,
\end{align*}
\begin{align*}
\lim_{t\rightarrow \infty}\phi_t(x)=x_0 \text{ for all } x \in D,
\end{align*}where D is the domain of f.
This definition says that an equilibrium point is globally stable if the set of points in the space that are asymptotic to it is the whole space. The Lyapunov stability theorems provide sufficient conditions for this type of stability as well as asymptotic stability, this approach is based on finding a scalar function of a state that satisfies certain properties. Namely, this function has to be continuously differentiable and positive definite. Besides, if the first derivative of this function with respect to time is negative semidefinite along the state trajectories, then we can conclude that the equilibrium point is stable. Further, if the first derivative along every state trajectories is negative definite then we can conclude that the equilibrium point is globally stable.
As there is no universal method for creating Lyapunov functions for ordinary differential equations, this problem is far from trivial.
Theorem 4.2. [Reference Perko12, Section 2.9] Let E be an open subset of ![]() ${\Bbb R}^n$ containing x 0, the equilibrium point. Suppose that
${\Bbb R}^n$ containing x 0, the equilibrium point. Suppose that ![]() $f\in C^1(E)$ and that
$f\in C^1(E)$ and that ![]() $f(x_0)=0$. Suppose further that there exists a real-valued function
$f(x_0)=0$. Suppose further that there exists a real-valued function ![]() $V \in C^1(E)$ (called Lyapunov function) satisfying
$V \in C^1(E)$ (called Lyapunov function) satisfying ![]() $V(x_0)=0$ and
$V(x_0)=0$ and ![]() $V(x) \gt 0$ if
$V(x) \gt 0$ if ![]() $x\neq x_0$. Then,
$x\neq x_0$. Then,
(a) if
 $V'(x)\leq 0$ for all
$V'(x)\leq 0$ for all  $x\in E$, x 0 is stable.
$x\in E$, x 0 is stable.(b) If
 $V'(x) \lt 0$ for all
$V'(x) \lt 0$ for all  $x\in E \setminus \{x_0\}$, x 0 is asymptotically stable.
$x\in E \setminus \{x_0\}$, x 0 is asymptotically stable.(c) If
 $V'(x) \gt 0$ for all
$V'(x) \gt 0$ for all  $x\in E \setminus \{x_0\}$, x 0 is unstable.
$x\in E \setminus \{x_0\}$, x 0 is unstable.
Given the space ![]() $H/K$, where H is a simple Lie group and
$H/K$, where H is a simple Lie group and ![]() $K\subseteq H$, we consider the homogeneous space
$K\subseteq H$, we consider the homogeneous space ![]() $M = H\times H/\Delta K$, such that
$M = H\times H/\Delta K$, such that ![]() $G_1 = G_2 = H$ and
$G_1 = G_2 = H$ and ![]() $c_1 = 2$. We aim to establish global stability for this specific case, when hypothesis used before hold.
$c_1 = 2$. We aim to establish global stability for this specific case, when hypothesis used before hold.
Theorem 4.3. Let ![]() $M=H\times H/\Delta K$, (
$M=H\times H/\Delta K$, (![]() $c_1=2$) a homogeneous space such that
$c_1=2$) a homogeneous space such that ![]() $(H/K, g_{\operatorname{B}})$ is Einstein (i.e.,
$(H/K, g_{\operatorname{B}})$ is Einstein (i.e., ![]() $\operatorname{C}_{\chi} = \kappa \operatorname{Id}_{\mathfrak{p} }$ for a constant
$\operatorname{C}_{\chi} = \kappa \operatorname{Id}_{\mathfrak{p} }$ for a constant  $\kappa \in (0,\tfrac{1}{2}]$) and
$\kappa \in (0,\tfrac{1}{2}]$) and ![]() $\operatorname{B}_{\mathfrak{k} }=2\lambda\operatorname{B}_{\mathfrak{h} }|_{\mathfrak{k} }$. Then the BRF metric
$\operatorname{B}_{\mathfrak{k} }=2\lambda\operatorname{B}_{\mathfrak{h} }|_{\mathfrak{k} }$. Then the BRF metric ![]() $g_0:=(1,1,2)_{g_{\operatorname{B}}}$ is globally stable.
$g_0:=(1,1,2)_{g_{\operatorname{B}}}$ is globally stable.
Proof. Consider the function,
 \begin{align*}
V(x_1,x_2,x_3):= \frac{\tfrac{\lambda}{10}(x_1-1)^2+\tfrac{\lambda}{10}(x_2-1)^2+(x_3-2)^2}{2},
\end{align*}
\begin{align*}
V(x_1,x_2,x_3):= \frac{\tfrac{\lambda}{10}(x_1-1)^2+\tfrac{\lambda}{10}(x_2-1)^2+(x_3-2)^2}{2},
\end{align*} we will prove that this is a Lyapunov function for the dynamical system given in Equation 12 taking ![]() $c_1=2$ and
$c_1=2$ and ![]() $\kappa:=\kappa_1=\kappa_2$, i.e.,
$\kappa:=\kappa_1=\kappa_2$, i.e.,
 \begin{align}
\left\{\begin{aligned}
x_1'(t)= &\tfrac{x_3 - x_1^2 x_3 + \kappa \left(-2 x_3 - 2 x_1^2 x_3 + x_1 (4 + x_3^2)\right)}{2 x_1^2 x_3},\\
x_2'(t)= &\tfrac{x_3 - x_2^2 x_3 + \kappa \left(-2 x_3 - 2 x_2^2 x_3 + x_2 (4 + x_3^2)\right)}{2 x_2^2 x_3},\\
x_3'(t)=&-\tfrac{(x_3^2-4) \left((x_1^2 + x_2^2) x_3^2 -
2 \lambda \left(x_2^2 x_3^2 + x_1^2 (-4 x_2^2 + x_3^2)\right)\right)}{4 x1^2 x2^2 x3^2}.\\
\end{aligned}
\right.
\end{align}
\begin{align}
\left\{\begin{aligned}
x_1'(t)= &\tfrac{x_3 - x_1^2 x_3 + \kappa \left(-2 x_3 - 2 x_1^2 x_3 + x_1 (4 + x_3^2)\right)}{2 x_1^2 x_3},\\
x_2'(t)= &\tfrac{x_3 - x_2^2 x_3 + \kappa \left(-2 x_3 - 2 x_2^2 x_3 + x_2 (4 + x_3^2)\right)}{2 x_2^2 x_3},\\
x_3'(t)=&-\tfrac{(x_3^2-4) \left((x_1^2 + x_2^2) x_3^2 -
2 \lambda \left(x_2^2 x_3^2 + x_1^2 (-4 x_2^2 + x_3^2)\right)\right)}{4 x1^2 x2^2 x3^2}.\\
\end{aligned}
\right.
\end{align} Set ![]() $E:=\{(x_1,x_2,x_3)\in {\Bbb R}^3 \ / \ x_1,x_2,x_3 \gt 0\}$, it is evident that
$E:=\{(x_1,x_2,x_3)\in {\Bbb R}^3 \ / \ x_1,x_2,x_3 \gt 0\}$, it is evident that ![]() $V(1,1,2)=0$ and V is clearly positive for all other
$V(1,1,2)=0$ and V is clearly positive for all other ![]() $(x_1,x_2,x_3)\in E$, and thus V is a Lyapunov function for the dynamical system Equation 14 if its derivative F is negative definite on
$(x_1,x_2,x_3)\in E$, and thus V is a Lyapunov function for the dynamical system Equation 14 if its derivative F is negative definite on ![]() $E \setminus \{(1,1,2)\}$, where
$E \setminus \{(1,1,2)\}$, where
 \begin{align*}
\begin{aligned}
F(x_1,x_2, x_3):= & \frac{\lambda}{10}(x_1-1)x_1'+\frac{\lambda}{10}(x_2-1)x_2'+(x_3-2)x_3'= \\
= &-\frac{1}{4 x_1^2 x_2^2 x_3^2}\left(64 \lambda x_1^2 x_2^2 \right.\\
&+ \tfrac{8}{10}\lambda \kappa x_1^2 x_2 x_3 + \tfrac{8}{10} \lambda\kappa x_1 x_2^2 x_3 - \tfrac{8}{10}\lambda \kappa x_1^2 x_2^2 x_3 - \tfrac{8}{10}\lambda \kappa x_1^2 x_2^2 x_3 - 32 \lambda x_1^2 x_2^2 x_3 \\
&+ \tfrac{2}{10}\lambda x_1^2 x_3^2 + 8 x_1^2 x_3^2 - \tfrac{4}{10}\lambda \kappa x_1^2 x_3^2 - 16 \lambda x_1^2 x_3^2 - \tfrac{2}{10}\lambda x_1^2 x_2 x_3^2 + \tfrac{4}{10}\lambda \kappa x_1^2 x_2 x_3^2 \\
&+ \tfrac{2}{10}\lambda x_2^2 x_3^2 + 8 x_2^2 x_3^2 - \tfrac{4}{10}\lambda \kappa x_2^2 x_3^2 - 16\lambda x_2^2 x_3^2 - \tfrac{2}{10}\lambda x_1 x_2^2 x_3^2 + \tfrac{4}{10}\lambda \kappa x_1 x_2^2 x_3^2 \\
&- \tfrac{2}{10}\lambda x_1^2 x_2^2 x_3^2 - \tfrac{2}{10}\lambda x_1^2 x_2^2 x_3^2 -
\tfrac{4}{10}\lambda \kappa x_1^2 x_2^2 x_3^2 - \tfrac{4}{10}\lambda \kappa x_1^2 x_2^2 x_3^2 - 16 \lambda x_1^2 x_2^2 x_3^2 \\
&+ \tfrac{2}{10}\lambda x_1^3 x_2^2 x_3^2 +
\tfrac{4}{10}\lambda \kappa x_1^3 x_2^2 x_3^2 + \tfrac{2}{10}\lambda x_1^2 x_2^3 x_3^2 +
\tfrac{4}{10}\lambda \kappa x_1^2 x_2^3 x_3^2 \\
& - 4 x_1^2 x_3^3 + 8 \lambda x_1^2 x_3^3 +
\tfrac{2}{10}\lambda \kappa x_1^2 x_2 x_3^3 - 4 x_2^2 x_3^3 + 8 \lambda x_2^2 x_3^3 +
\tfrac{2}{10}\lambda \kappa x_1 x_2^2 x_3^3 \\
&- \tfrac{2}{10}\lambda \kappa x_1^2 x_2^2 x_3^3 - \tfrac{2}{10}\lambda \kappa x_1^2 x_2^2 x_3^3 + 8 \lambda x_1^2 x_2^2 x_3^3\\
& - 2 x_1^2 x_3^4 + 4 \lambda x_1^2 x_3^4 - 2 x_2^2 x_3^4 + 4 \lambda x_2^2 x_3^4 +
\left. x_1^2 x_3^5 - 2 \lambda x_1^2 x_3^5 + x_2^2 x_3^5 - 2 \lambda x_2^2 x_3^5\right).
\end{aligned}
\end{align*}
\begin{align*}
\begin{aligned}
F(x_1,x_2, x_3):= & \frac{\lambda}{10}(x_1-1)x_1'+\frac{\lambda}{10}(x_2-1)x_2'+(x_3-2)x_3'= \\
= &-\frac{1}{4 x_1^2 x_2^2 x_3^2}\left(64 \lambda x_1^2 x_2^2 \right.\\
&+ \tfrac{8}{10}\lambda \kappa x_1^2 x_2 x_3 + \tfrac{8}{10} \lambda\kappa x_1 x_2^2 x_3 - \tfrac{8}{10}\lambda \kappa x_1^2 x_2^2 x_3 - \tfrac{8}{10}\lambda \kappa x_1^2 x_2^2 x_3 - 32 \lambda x_1^2 x_2^2 x_3 \\
&+ \tfrac{2}{10}\lambda x_1^2 x_3^2 + 8 x_1^2 x_3^2 - \tfrac{4}{10}\lambda \kappa x_1^2 x_3^2 - 16 \lambda x_1^2 x_3^2 - \tfrac{2}{10}\lambda x_1^2 x_2 x_3^2 + \tfrac{4}{10}\lambda \kappa x_1^2 x_2 x_3^2 \\
&+ \tfrac{2}{10}\lambda x_2^2 x_3^2 + 8 x_2^2 x_3^2 - \tfrac{4}{10}\lambda \kappa x_2^2 x_3^2 - 16\lambda x_2^2 x_3^2 - \tfrac{2}{10}\lambda x_1 x_2^2 x_3^2 + \tfrac{4}{10}\lambda \kappa x_1 x_2^2 x_3^2 \\
&- \tfrac{2}{10}\lambda x_1^2 x_2^2 x_3^2 - \tfrac{2}{10}\lambda x_1^2 x_2^2 x_3^2 -
\tfrac{4}{10}\lambda \kappa x_1^2 x_2^2 x_3^2 - \tfrac{4}{10}\lambda \kappa x_1^2 x_2^2 x_3^2 - 16 \lambda x_1^2 x_2^2 x_3^2 \\
&+ \tfrac{2}{10}\lambda x_1^3 x_2^2 x_3^2 +
\tfrac{4}{10}\lambda \kappa x_1^3 x_2^2 x_3^2 + \tfrac{2}{10}\lambda x_1^2 x_2^3 x_3^2 +
\tfrac{4}{10}\lambda \kappa x_1^2 x_2^3 x_3^2 \\
& - 4 x_1^2 x_3^3 + 8 \lambda x_1^2 x_3^3 +
\tfrac{2}{10}\lambda \kappa x_1^2 x_2 x_3^3 - 4 x_2^2 x_3^3 + 8 \lambda x_2^2 x_3^3 +
\tfrac{2}{10}\lambda \kappa x_1 x_2^2 x_3^3 \\
&- \tfrac{2}{10}\lambda \kappa x_1^2 x_2^2 x_3^3 - \tfrac{2}{10}\lambda \kappa x_1^2 x_2^2 x_3^3 + 8 \lambda x_1^2 x_2^2 x_3^3\\
& - 2 x_1^2 x_3^4 + 4 \lambda x_1^2 x_3^4 - 2 x_2^2 x_3^4 + 4 \lambda x_2^2 x_3^4 +
\left. x_1^2 x_3^5 - 2 \lambda x_1^2 x_3^5 + x_2^2 x_3^5 - 2 \lambda x_2^2 x_3^5\right).
\end{aligned}
\end{align*}Given the symmetries of x 1 and x 2, to establish the negative condition of F, we define a function g as follows,
 \begin{align*}
F(x_1,x_2,x_3)=-\tfrac{1}{4 x_1^2 x_2^2 x_3^2}\left(x_1^2 g(x_2,x_3)+x_2^2 g(x_1,x_3)\right),
\end{align*}
\begin{align*}
F(x_1,x_2,x_3)=-\tfrac{1}{4 x_1^2 x_2^2 x_3^2}\left(x_1^2 g(x_2,x_3)+x_2^2 g(x_1,x_3)\right),
\end{align*}where
 \begin{align*}
\begin{aligned}
g(x,y)&:= 32\lambda x^2 + \tfrac{8}{10}\lambda \kappa x y - \tfrac{8}{10}\lambda \kappa x^2 y - 16 \lambda x^2 y + \tfrac{2}{10} \lambda y^2 + 8 y^2 - \tfrac{4}{10}\lambda \kappa y^2 - 16 \lambda y^2\\
&\quad - \tfrac{2}{10}\lambda x y^2 + \tfrac{4}{10}\lambda \kappa x y^2 - \tfrac{2}{10}\lambda x^2 y^2 - \tfrac{4}{10}\lambda \kappa x^2 y^2 - 8 \lambda x^2 y^2 + \tfrac{2}{10}\lambda x^3 y^2 + \tfrac{4}{10} \lambda \kappa x^3 y^2 \\
&\quad - 4y^3 + 8\lambda y^3 + \tfrac{2}{10}\lambda \kappa x y^3 -
\tfrac{2}{10}\lambda \kappa x^2 y^3 + 4 \lambda x^2 y^3 - 2 y^4 + 4 \lambda y^4 + y^5 - 2 \lambda y^5.
\end{aligned}
\end{align*}
\begin{align*}
\begin{aligned}
g(x,y)&:= 32\lambda x^2 + \tfrac{8}{10}\lambda \kappa x y - \tfrac{8}{10}\lambda \kappa x^2 y - 16 \lambda x^2 y + \tfrac{2}{10} \lambda y^2 + 8 y^2 - \tfrac{4}{10}\lambda \kappa y^2 - 16 \lambda y^2\\
&\quad - \tfrac{2}{10}\lambda x y^2 + \tfrac{4}{10}\lambda \kappa x y^2 - \tfrac{2}{10}\lambda x^2 y^2 - \tfrac{4}{10}\lambda \kappa x^2 y^2 - 8 \lambda x^2 y^2 + \tfrac{2}{10}\lambda x^3 y^2 + \tfrac{4}{10} \lambda \kappa x^3 y^2 \\
&\quad - 4y^3 + 8\lambda y^3 + \tfrac{2}{10}\lambda \kappa x y^3 -
\tfrac{2}{10}\lambda \kappa x^2 y^3 + 4 \lambda x^2 y^3 - 2 y^4 + 4 \lambda y^4 + y^5 - 2 \lambda y^5.
\end{aligned}
\end{align*} Hence, it is enough to prove that ![]() $g(x,y)\geq0$ on
$g(x,y)\geq0$ on ![]() $\tilde{E}$, where
$\tilde{E}$, where ![]() $\tilde{E}:=\{(x,y)\in {\Bbb R}^2 \ / \ x,y \gt 0\}$, and equality is only attained at
$\tilde{E}:=\{(x,y)\in {\Bbb R}^2 \ / \ x,y \gt 0\}$, and equality is only attained at ![]() $(x,y)=(1,2)$. We split the function g considering the terms where λ or κ is involved,
$(x,y)=(1,2)$. We split the function g considering the terms where λ or κ is involved,
 \begin{align*}
g(x,y):=\frac{1}{10}\lambda h_1(x,y) +h_2(x,y)+\frac{2}{10}\lambda\kappa h_3(x,y) + 2 \lambda h_4(x,y),
\end{align*}
\begin{align*}
g(x,y):=\frac{1}{10}\lambda h_1(x,y) +h_2(x,y)+\frac{2}{10}\lambda\kappa h_3(x,y) + 2 \lambda h_4(x,y),
\end{align*}where
 \begin{equation*}
\begin{aligned}
h_1(x,y) &:=2 y^2 - 2 x y^2 - 2 x^2 y^2 + 2 x^3 y^2,\\
h_2(x,y) &:= 8 y^2 - 4 y^3 - 2 y^4 + y^5,\\
h_3(x,y) &:= 4 x y - 4 x^2 y - 2 y^2 + 2 x y^2 - 2 x^2 y^2 + 2 x^3 y^2 + x y^3 - x^2 y^3,\\
h_4(x,y) &:= 16 x^2 - 8 x^2 y - 8 y^2 - 4 x^2 y^2 + 4 y^3 + 2 x^2 y^3 +
2 y^4 - y^5.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
h_1(x,y) &:=2 y^2 - 2 x y^2 - 2 x^2 y^2 + 2 x^3 y^2,\\
h_2(x,y) &:= 8 y^2 - 4 y^3 - 2 y^4 + y^5,\\
h_3(x,y) &:= 4 x y - 4 x^2 y - 2 y^2 + 2 x y^2 - 2 x^2 y^2 + 2 x^3 y^2 + x y^3 - x^2 y^3,\\
h_4(x,y) &:= 16 x^2 - 8 x^2 y - 8 y^2 - 4 x^2 y^2 + 4 y^3 + 2 x^2 y^3 +
2 y^4 - y^5.
\end{aligned}
\end{equation*} Now, from its factorization, it is clear that h 1 and h 2 are greater than zero on ![]() $\tilde{E} \setminus \{(1,2)\}$,
$\tilde{E} \setminus \{(1,2)\}$,
 \begin{align*}
\begin{aligned}
h_1(x,y) &:=2 (x-1)^2 (1 + x) y^2,\\
h_2(x,y) &:= (y-2)^2 y^2 (2 + y).\\
\end{aligned}
\end{align*}
\begin{align*}
\begin{aligned}
h_1(x,y) &:=2 (x-1)^2 (1 + x) y^2,\\
h_2(x,y) &:= (y-2)^2 y^2 (2 + y).\\
\end{aligned}
\end{align*} We now define the functions ![]() $g_1,g_2$ as follows:
$g_1,g_2$ as follows:
 \begin{align*}
\begin{aligned}
g_1(x,y) &:=h_4(x,y)+\tfrac{1}{20}h_1(x,y),\\
g_2(x,y) &:= \tfrac{1}{20}h_3(x,y),\\
\end{aligned}
\end{align*}
\begin{align*}
\begin{aligned}
g_1(x,y) &:=h_4(x,y)+\tfrac{1}{20}h_1(x,y),\\
g_2(x,y) &:= \tfrac{1}{20}h_3(x,y),\\
\end{aligned}
\end{align*}such that
The proof that ![]() $g(x,y) \gt 0$ on
$g(x,y) \gt 0$ on ![]() $\tilde{E} \setminus \{(1,2)\}$ is going to be by cases, as h 2 is already positive, we have to differenciate if g 1 and g 2 are positive or not on
$\tilde{E} \setminus \{(1,2)\}$ is going to be by cases, as h 2 is already positive, we have to differenciate if g 1 and g 2 are positive or not on ![]() $\tilde{E} \setminus \{(1,2)\}$.
$\tilde{E} \setminus \{(1,2)\}$.
• Case 1:
 $g_1 \lt 0$ and
$g_1 \lt 0$ and  $g_2 \lt 0$, The
$g_2 \lt 0$, The  $(x,y) \in \tilde{E}$ satisfying these conditions are represented in Figure 3. Note that
$(x,y) \in \tilde{E}$ satisfying these conditions are represented in Figure 3. Note that  $g_1 \lt 0$ if and only if
$g_1 \lt 0$ if and only if  $h_4 \lt 0$.
$h_4 \lt 0$.
Figure 3. Region of Case 1:
 $g_1 \lt 0$ and
$g_1 \lt 0$ and  $g_2 \lt 0$.
$g_2 \lt 0$.Since
 $g_1 \lt 0$ and
$g_1 \lt 0$ and  $2\lambda \lt 1$, we have that
$2\lambda \lt 1$, we have that  $g_1 \lt 2\lambda g_1$. In the same way,
$g_1 \lt 2\lambda g_1$. In the same way,  $g_2 \lt 4\lambda\kappa g_2$ and the following inequality hold for all
$g_2 \lt 4\lambda\kappa g_2$ and the following inequality hold for all  $(x,y) \in \tilde{E}$,
$(x,y) \in \tilde{E}$,
 \begin{align*}
h_2 +g_1+ g_2 \ \lt \ h_2 +2\lambda g_1+ 4 \lambda \kappa g_2.
\end{align*}
\begin{align*}
h_2 +g_1+ g_2 \ \lt \ h_2 +2\lambda g_1+ 4 \lambda \kappa g_2.
\end{align*}Our aim now is to demonstrate that the function
 $h_2 +g_1+ g_2$ is greater than zero on
$h_2 +g_1+ g_2$ is greater than zero on  $\tilde{E}$. It is a cubic function on x such that p(x) defined below is quadratic,
$\tilde{E}$. It is a cubic function on x such that p(x) defined below is quadratic,
 \begin{align*}
(h_2+g_1+g_2)(x,y)&=x\left(\tfrac{1}{20} y (4 + y^2) +
x \tfrac{1}{20} (320 - 164 y - 84 y^2 + 39 y^3) + x^2 \tfrac{y^2}{5} \right)\\
&:=xp(x).
\end{align*}
\begin{align*}
(h_2+g_1+g_2)(x,y)&=x\left(\tfrac{1}{20} y (4 + y^2) +
x \tfrac{1}{20} (320 - 164 y - 84 y^2 + 39 y^3) + x^2 \tfrac{y^2}{5} \right)\\
&:=xp(x).
\end{align*}To understand
 $p(x) \in {\Bbb R}[y][x]$, we look for its critical point, which is always a minimum given that the quadratic coefficient
$p(x) \in {\Bbb R}[y][x]$, we look for its critical point, which is always a minimum given that the quadratic coefficient  $\tfrac{y^2}{5}$ is always positive.
$\tfrac{y^2}{5}$ is always positive. \begin{align*}
p'(x)=0\,\text{ if and only if } x=\bar{x}:=\tfrac{1}{y^2}\left(\tfrac{21}{2}y^2-40+\tfrac{41}{2}y-\tfrac{39}{8}y^3\right).
\end{align*}
\begin{align*}
p'(x)=0\,\text{ if and only if } x=\bar{x}:=\tfrac{1}{y^2}\left(\tfrac{21}{2}y^2-40+\tfrac{41}{2}y-\tfrac{39}{8}y^3\right).
\end{align*}Since
 $p(0)=\tfrac{1}{20} y (4 + y^2)$ is positive for y > 0, and due to the continuity of p(x), we conclude that if
$p(0)=\tfrac{1}{20} y (4 + y^2)$ is positive for y > 0, and due to the continuity of p(x), we conclude that if  $\bar{x} \lt 0$ then
$\bar{x} \lt 0$ then  $p(x)\geq 0$ for all
$p(x)\geq 0$ for all  $x,y \gt 0$ and hence
$x,y \gt 0$ and hence  $h_1+g_1+g_2\geq 0$ for all
$h_1+g_1+g_2\geq 0$ for all  $x,y \gt 0$, with equality only occurring a
$x,y \gt 0$, with equality only occurring a  $(x,y)=(1,2)$.
$(x,y)=(1,2)$.Thus, the values of y we have to study are those that lead to
 $\bar{x} \gt 0$, signifying
$\bar{x} \gt 0$, signifying  $y \in I:=\left(\frac{1}{39}\left(81-\sqrt{321}\right),\tfrac{1}{39}\left(81+\sqrt{321}\right)\right)$. For this interval, we want that
$y \in I:=\left(\frac{1}{39}\left(81-\sqrt{321}\right),\tfrac{1}{39}\left(81+\sqrt{321}\right)\right)$. For this interval, we want that  $p(\bar{x}) \gt 0$, as the positivity of the minimum implies the positivity of the entire function.
$p(\bar{x}) \gt 0$, as the positivity of the minimum implies the positivity of the entire function.
 \begin{align*}
p(\bar{x}):=-\tfrac{(y-2)^2 (25600 - 640 y - 13756 y^2 - 484 y^3 + 1521 y^4)}{320 y^2},
\end{align*}
\begin{align*}
p(\bar{x}):=-\tfrac{(y-2)^2 (25600 - 640 y - 13756 y^2 - 484 y^3 + 1521 y^4)}{320 y^2},
\end{align*}and this is positive in the interval we are interested in if and only if
 $q(y):=(25600 - 640 y - 13756 y^2 - 484 y^3 + 1521 y^4)$ is negative for all
$q(y):=(25600 - 640 y - 13756 y^2 - 484 y^3 + 1521 y^4)$ is negative for all  $y \in I$. Note that as
$y \in I$. Note that as  $q(\tfrac{7}{5}) \gt 0, \ q(\tfrac{3}{2}) \lt 0 $ and
$q(\tfrac{7}{5}) \gt 0, \ q(\tfrac{3}{2}) \lt 0 $ and  $q(\tfrac{13}{5}) \lt 0, \ q(3) \gt 0$ we can localize the positive roots of q and conclude that there are no roots of q in I (see Figure 6), besides
$q(\tfrac{13}{5}) \lt 0, \ q(3) \gt 0$ we can localize the positive roots of q and conclude that there are no roots of q in I (see Figure 6), besides  $q(2)=-10240 \lt 0$.
$q(2)=-10240 \lt 0$.This implies that
 $p(\bar{x}) \gt 0$ for all
$p(\bar{x}) \gt 0$ for all  $y \in I$ and therefore,
$y \in I$ and therefore,  $h_2+g_1+g_2 \gt 0$ on
$h_2+g_1+g_2 \gt 0$ on  $\tilde{E} \setminus \{(1,2)\}$ as desired.
$\tilde{E} \setminus \{(1,2)\}$ as desired.
• Case 2:
 $g_1 \lt 0$ and
$g_1 \lt 0$ and  $g_2 \gt 0$,
$g_2 \gt 0$,The
 $x,y \gt 0$ satisfying these conditions are plotted in Figure 4. As in Case 1,
$x,y \gt 0$ satisfying these conditions are plotted in Figure 4. As in Case 1,  $g_1 \lt 0$ implies that
$g_1 \lt 0$ implies that  $h_4 \lt 0$ and therefore
$h_4 \lt 0$ and therefore  $h_4 \lt 2\lambda h_4$. It is easy to see that
$h_4 \lt 2\lambda h_4$. It is easy to see that
 \begin{align*}
(h_2+h_4)(x,y)=2 x^2 (y-2)^2 (2 + y),
\end{align*}
\begin{align*}
(h_2+h_4)(x,y)=2 x^2 (y-2)^2 (2 + y),
\end{align*}
Figure 4. Region of Case 2:
 $g_1 \lt 0$ and
$g_1 \lt 0$ and  $g_2 \gt 0$.
$g_2 \gt 0$.and hence,
 \begin{align*}
0 \lt h_2+h_4 \lt h_2 + 2\lambda h_4 \lt h_2 + 2\lambda h_4 + 2 \lambda \tfrac{1}{20}h_1,
\end{align*}
\begin{align*}
0 \lt h_2+h_4 \lt h_2 + 2\lambda h_4 \lt h_2 + 2\lambda h_4 + 2 \lambda \tfrac{1}{20}h_1,
\end{align*}proving that
 $g(x,y) \gt 0$ for all
$g(x,y) \gt 0$ for all  $(x,y)\in \tilde{E} \setminus \{(1,2)\}$ in this case.
$(x,y)\in \tilde{E} \setminus \{(1,2)\}$ in this case.• Case 3:
 $g_1 \gt 0$ and
$g_1 \gt 0$ and  $g_2 \lt 0$,
$g_2 \lt 0$,This represents the last case for our analysis, it includes the cases when x tends to infinity and y tends to 0, as illustrated in Figure 5.

Figure 5. Region of Case 3:
 $g_1 \gt 0$ and
$g_1 \gt 0$ and  $g_2 \lt 0$.
$g_2 \lt 0$.
Figure 6. q(y).
Consider g factorized as follows:
 \begin{align*}
g (x,y)=h_2+2\lambda(g_1+2\kappa g_2).
\end{align*}
\begin{align*}
g (x,y)=h_2+2\lambda(g_1+2\kappa g_2).
\end{align*}Since
 $g_2 \lt 0$ in this case,
$g_2 \lt 0$ in this case,  $g_2 \lt 2\kappa g_2$, therefore if
$g_2 \lt 2\kappa g_2$, therefore if  $g_1+g_2$ is positive this case is proved.
$g_1+g_2$ is positive this case is proved.On the other hand, if
 $g_1+g_2 \lt 0$, since
$g_1+g_2 \lt 0$, since  $g_1 \gt 0$, we have the following inequalities
$g_1 \gt 0$, we have the following inequalities
 \begin{align*}
g_1+g_2 \lt 2\kappa (g_1 + g_2) \lt 2\kappa g_1 + 2\kappa g_2 \lt g_1+ 2\kappa g_2.
\end{align*}
\begin{align*}
g_1+g_2 \lt 2\kappa (g_1 + g_2) \lt 2\kappa g_1 + 2\kappa g_2 \lt g_1+ 2\kappa g_2.
\end{align*}If the last expression is still negative for some
 $x,y \gt 0$ satisfying the hypothesis of this case, one obtains that:
$x,y \gt 0$ satisfying the hypothesis of this case, one obtains that:
 \begin{align*}
& h_2+g_1+g_2 \lt h_2 + 2\kappa(g_1+g_2) \lt h_2 + (g_1+2\kappa g_2) \lt h_2+2\lambda ((g_1+2\kappa g_2)\\ &\quad = g(x,y),
\end{align*}
\begin{align*}
& h_2+g_1+g_2 \lt h_2 + 2\kappa(g_1+g_2) \lt h_2 + (g_1+2\kappa g_2) \lt h_2+2\lambda ((g_1+2\kappa g_2)\\ &\quad = g(x,y),
\end{align*}
and the proof is complete due to the proof of Case 1.
5. Generalized Ricci flow on the Lie group  $\mathrm{SO}(n)$
$\mathrm{SO}(n)$
5.1. Setup for any compact Lie group
Before presenting the main problem in this section, we review some known facts for compact Lie groups, see [Reference Lauret and Will7, Section 6].
Let ![]() $M^d=G$ be a compact, semisimple, connected Lie group and
$M^d=G$ be a compact, semisimple, connected Lie group and ![]() $\mathfrak{g} $ its Lie algebra. By [Reference Bredon2, Chapter V], we know that every class in the set of all closed 3-forms of G,
$\mathfrak{g} $ its Lie algebra. By [Reference Bredon2, Chapter V], we know that every class in the set of all closed 3-forms of G, ![]() $H^3(G)$ has a unique bi-invariant representative called Cartan 3-forms of the form:
$H^3(G)$ has a unique bi-invariant representative called Cartan 3-forms of the form:
We note that if G is simple, then ![]() $H^3(G)={\Bbb R}\left[H_{\operatorname{B}}\right]$ where
$H^3(G)={\Bbb R}\left[H_{\operatorname{B}}\right]$ where ![]() $H_{\operatorname{B}}:=\overline{\operatorname{B}_{\mathfrak{g} }}$, and
$H_{\operatorname{B}}:=\overline{\operatorname{B}_{\mathfrak{g} }}$, and ![]() $\operatorname{B}_{\mathfrak{g} }$ is the Killing form of
$\operatorname{B}_{\mathfrak{g} }$ is the Killing form of ![]() $\mathfrak{g} $. It is well-known that Cartan 3-forms are harmonic with respect to any bi-invariant metric on G.
$\mathfrak{g} $. It is well-known that Cartan 3-forms are harmonic with respect to any bi-invariant metric on G.
Following [Reference Lauret and Will8, Section 3], we consider a bi-invariant metric gb on G, a gb-orthonormal basis ![]() $\left\{e_1, \dots e_d\right\}$ and a left-invariant metric
$\left\{e_1, \dots e_d\right\}$ and a left-invariant metric ![]() $g=(x_1,\dots,x_d)$ on G, such that
$g=(x_1,\dots,x_d)$ on G, such that ![]() $g(e_i,e_j)=x_i\delta_{ij}$. The ordered basis
$g(e_i,e_j)=x_i\delta_{ij}$. The ordered basis ![]() $\left\{e_1, \dots e_d\right\}$ determines structural constants given by
$\left\{e_1, \dots e_d\right\}$ determines structural constants given by
 \begin{align*}
c_{ij}^{k}:=g_b([e_i,e_j],e_k),
\end{align*}
\begin{align*}
c_{ij}^{k}:=g_b([e_i,e_j],e_k),
\end{align*}and by [Reference Lauret and Will8, Corollary 3.2 (ii)]:
 \begin{equation}
H_{\operatorname{B}} \text{ is } g\text{-harmonic if and only if,} \sum_{1\leq i,j \leq n}\frac{c_{ij}^kc_{ij}^l}{x_ix_j}=0 \quad \forall k,l \text{ such that } x_k\neq x_l.
\end{equation}
\begin{equation}
H_{\operatorname{B}} \text{ is } g\text{-harmonic if and only if,} \sum_{1\leq i,j \leq n}\frac{c_{ij}^kc_{ij}^l}{x_ix_j}=0 \quad \forall k,l \text{ such that } x_k\neq x_l.
\end{equation}Therefore, within the context of the generalized Ricci flow, if Equation 15 holds, then H will remain constant along any solution and the flow will be governed by the equation
 \begin{equation}
\tfrac{\partial}{\partial t}g(t)=-2\operatorname{Ric}(g(t))+\tfrac{1}{2}(H(t))^2_{g(t)}.
\end{equation}
\begin{equation}
\tfrac{\partial}{\partial t}g(t)=-2\operatorname{Ric}(g(t))+\tfrac{1}{2}(H(t))^2_{g(t)}.
\end{equation} We will use the formulas derived in [Reference Lauret and Will7, Section 6], which are as follows for ![]() $H_b:=g_b([\cdot,\cdot],\cdot)$:
$H_b:=g_b([\cdot,\cdot],\cdot)$:
 \begin{equation}
(H_b)_g^2(e_k,e_l) = \sum_{i,j} \tfrac{1}{x_ix_j} g_b([e_k,e_i],e_j)g_b([e_l,e_i],e_j)
= \sum_{i,j} \tfrac{c_{ij}^kc_{ij}^l}{x_ix_j}, \qquad\forall k,l.
\end{equation}
\begin{equation}
(H_b)_g^2(e_k,e_l) = \sum_{i,j} \tfrac{1}{x_ix_j} g_b([e_k,e_i],e_j)g_b([e_l,e_i],e_j)
= \sum_{i,j} \tfrac{c_{ij}^kc_{ij}^l}{x_ix_j}, \qquad\forall k,l.
\end{equation}Concerning the Ricci curvature, it is well-known that
 \begin{equation}
\operatorname{Rc}(g)(e_k,e_l) = \tfrac{1}{2}\sum_{i,j} c_{ij}^kc_{ij}^l-\tfrac{1}{4}\sum_{i,j} c_{ij}^kc_{ij}^l\tfrac{x_i^2+x_j^2-x_kx_l}{x_ix_j}, \qquad\forall k, l.
\end{equation}
\begin{equation}
\operatorname{Rc}(g)(e_k,e_l) = \tfrac{1}{2}\sum_{i,j} c_{ij}^kc_{ij}^l-\tfrac{1}{4}\sum_{i,j} c_{ij}^kc_{ij}^l\tfrac{x_i^2+x_j^2-x_kx_l}{x_ix_j}, \qquad\forall k, l.
\end{equation}5.2. Case  $\mathrm{SO}(n)$
$\mathrm{SO}(n)$
For this section, we consider ![]() $G=\mathrm{SO}(n)$, the usual basis of its Lie algebra is
$G=\mathrm{SO}(n)$, the usual basis of its Lie algebra is ![]() $\beta=\{e_{rs}:=E_{rs}-E_{sr}\}$, which is nice as it satisfies
$\beta=\{e_{rs}:=E_{rs}-E_{sr}\}$, which is nice as it satisfies  $c_{ij}^kc_{ij}^l=0$ for all k ≠ l.
$c_{ij}^kc_{ij}^l=0$ for all k ≠ l.
For computational purposes, we label the elements of the basis as  $\beta:=\{e_1,e_2,\dots, e_{\tfrac{n(n-1)}{2}}\}$. This basis is orthogonal with respect to
$\beta:=\{e_1,e_2,\dots, e_{\tfrac{n(n-1)}{2}}\}$. This basis is orthogonal with respect to ![]() $g_{\operatorname{B}}$, the Killing metric of
$g_{\operatorname{B}}$, the Killing metric of ![]() $\mathrm{SO}(n)$, and any diagonal left-invariant metric can be expressed as
$\mathrm{SO}(n)$, and any diagonal left-invariant metric can be expressed as  $g=(x_1,\dots,x_{\tfrac{n(n-1)}{2}})_{g_{\operatorname{B}}}$.
$g=(x_1,\dots,x_{\tfrac{n(n-1)}{2}})_{g_{\operatorname{B}}}$.
Proposition 5.1. Consider ![]() $G=\mathrm{SO}(n)$ and fix the Killing metric
$G=\mathrm{SO}(n)$ and fix the Killing metric ![]() $g_{\operatorname{B}}$ as a background metric. For
$g_{\operatorname{B}}$ as a background metric. For  $\left(g(t)=(x_1(t),\dots,x_{\tfrac{n(n-1)}{2}}(t))_{g_{\operatorname{B}}},H_{\operatorname{B}}\right)$, the generalized Ricci flow is given by
$\left(g(t)=(x_1(t),\dots,x_{\tfrac{n(n-1)}{2}}(t))_{g_{\operatorname{B}}},H_{\operatorname{B}}\right)$, the generalized Ricci flow is given by
 \begin{equation}
x_k'(t)=- \sum_{i,j}(c_{ij}^k)^2+\frac{1}{2}\sum_{i,j}(c_{ij}^k)^2\frac{x_i^2+x_j^2-x_k^2}{x_ix_j}+\frac{1}{2}\sum_{i,j}\frac{(c_{ij}^k)^2}{x_ix_j} \quad \forall k= 1, \dots, \tfrac{n(n-1)}{2}.
\end{equation}
\begin{equation}
x_k'(t)=- \sum_{i,j}(c_{ij}^k)^2+\frac{1}{2}\sum_{i,j}(c_{ij}^k)^2\frac{x_i^2+x_j^2-x_k^2}{x_ix_j}+\frac{1}{2}\sum_{i,j}\frac{(c_{ij}^k)^2}{x_ix_j} \quad \forall k= 1, \dots, \tfrac{n(n-1)}{2}.
\end{equation}Proof. Replacing Equation 17 and (Equation 18) in Equation 16, the proposition follows as the basis β is nice.
It is clear that ![]() $g_{\operatorname{B}}=(1,1,\dots,1)_{g_{\operatorname{B}}}$ is a BRF generalized metric, which means a fix point of the above system. To study the dynamical stability of this point, we examine the linearization of the provided nonlinear system.
$g_{\operatorname{B}}=(1,1,\dots,1)_{g_{\operatorname{B}}}$ is a BRF generalized metric, which means a fix point of the above system. To study the dynamical stability of this point, we examine the linearization of the provided nonlinear system.
Theorem 5.2. The Killing metric ![]() $g_{\operatorname{B}}$ on the compact Lie group
$g_{\operatorname{B}}$ on the compact Lie group ![]() $\mathrm{SO}(n)$ is asymptotically stable for the dynamical system given in Equation 19.
$\mathrm{SO}(n)$ is asymptotically stable for the dynamical system given in Equation 19.
Proof. We define functions
 \begin{align*}
f_k(x_1,\dots,x_{\tfrac{n(n-1)}{2}}):=-\sum_{i,j}(c_{ij}^k)^2+\frac{1}{2}\sum_{i,j}(c_{ij}^k)^2\frac{x_i^2+x_j^2-x_k^2+1}{x_ix_j}, \quad \text{for } k= 1, \dots, \tfrac{n(n-1)}{2},
\end{align*}
\begin{align*}
f_k(x_1,\dots,x_{\tfrac{n(n-1)}{2}}):=-\sum_{i,j}(c_{ij}^k)^2+\frac{1}{2}\sum_{i,j}(c_{ij}^k)^2\frac{x_i^2+x_j^2-x_k^2+1}{x_ix_j}, \quad \text{for } k= 1, \dots, \tfrac{n(n-1)}{2},
\end{align*} such that ![]() $x'(t)=f(x)$. Therefore, the differential of f is given by:
$x'(t)=f(x)$. Therefore, the differential of f is given by:
 \begin{align*}
\left\{\begin{aligned}
\frac{\partial f_k}{\partial x_k}=& \frac{1}{2}\sum_{i,j}\frac{(c_{ij}^k)^2}{x_ix_j}(-2x_k) \qquad \forall k= 1, \dots, \tfrac{n(n-1)}{2},\\
\frac{\partial f_k}{\partial x_i}=& \frac{1}{2}\sum_{i,j}(c_{ij}^k)^2\frac{x_i^2-x_j^2+x_k^2-1}{x_i^2x_j} \qquad \forall k\neq i. \\
\end{aligned}
\right.
\end{align*}
\begin{align*}
\left\{\begin{aligned}
\frac{\partial f_k}{\partial x_k}=& \frac{1}{2}\sum_{i,j}\frac{(c_{ij}^k)^2}{x_ix_j}(-2x_k) \qquad \forall k= 1, \dots, \tfrac{n(n-1)}{2},\\
\frac{\partial f_k}{\partial x_i}=& \frac{1}{2}\sum_{i,j}(c_{ij}^k)^2\frac{x_i^2-x_j^2+x_k^2-1}{x_i^2x_j} \qquad \forall k\neq i. \\
\end{aligned}
\right.
\end{align*} Hence, on the Killing metric ![]() $g_{\operatorname{B}}$,
$g_{\operatorname{B}}$,
 \begin{align*}
Df(1,1,\dots,1)=\begin{pmatrix}
-\sum_{i,j}(c_{ij}^k)^2 & 0 & \dots& \dots & 0 \\
0 & -\sum_{i,j}(c_{ij}^k)^2& \dots& \dots& 0 \\
0 & 0 & \ddots & \dots & 0 \\
0 & \dots& \dots& 0 & -\sum_{i,j}(c_{ij}^k)^2
\end{pmatrix}.
\end{align*}
\begin{align*}
Df(1,1,\dots,1)=\begin{pmatrix}
-\sum_{i,j}(c_{ij}^k)^2 & 0 & \dots& \dots & 0 \\
0 & -\sum_{i,j}(c_{ij}^k)^2& \dots& \dots& 0 \\
0 & 0 & \ddots & \dots & 0 \\
0 & \dots& \dots& 0 & -\sum_{i,j}(c_{ij}^k)^2
\end{pmatrix}.
\end{align*}As all its eigenvalues are reals and negative the proof is complete.
Acknowledgements
I wish to express my deep gratitude to my Ph.D. advisor Dr. Jorge Lauret for his continued guidance and to the ICTP support during my research visit to Trieste. Also, I would like to thank to Dr. Damián Fernández for very helpful conversations.
Funding statement
This research was partially supported by a CONICET doctoral fellowship.