Introduction
The development of new engineering materials closely mirrored the ages of human development, with the particular periods of history labeled by the materials used in those eras. For example, the tools and weapons of prehistory, 300,000 or more years ago, were bone and stone; that period is referred to as the Stone Age. The discovery of ways to reduce ferrous oxides to make iron, a material with greater stiffness, strength, and hardness than any other then available, occurred around 1450 bc. However, two millennia passed before the blast furnace was developed in 1500 ad, enabling the widespread use of cast iron in the Iron Age. The development of new materials significantly accelerated the industrial revolution, and with the addition of polymers to the suite of materials available to engineers, enabled developments in multiple technologies.
One way to examine the availability of engineering materials to possess a given set of properties is via material property charts or so-called “Ashby charts.”Reference Ashby1 Material property charts display materials on axes based typically on two of their properties. Materials have many properties of course—mechanical, thermal, electrical, optical, and many more—so the number of such pair-wise combinations is large. Each chart can thus be thought of as a slice through “material property space”—a multidimensional space with material properties as its axes. Figure 1 shows one such multidimensional chart displaying the relation between strength, modulus, and density of engineering materials. There are many obvious incentives for seeking materials with greater strength: more durable and effective tools; faster, more economical transport; and larger, more daring structures. In recent times, it has been high strength at low weight that is frequently sought, with transport and aerospace as the direct drivers.
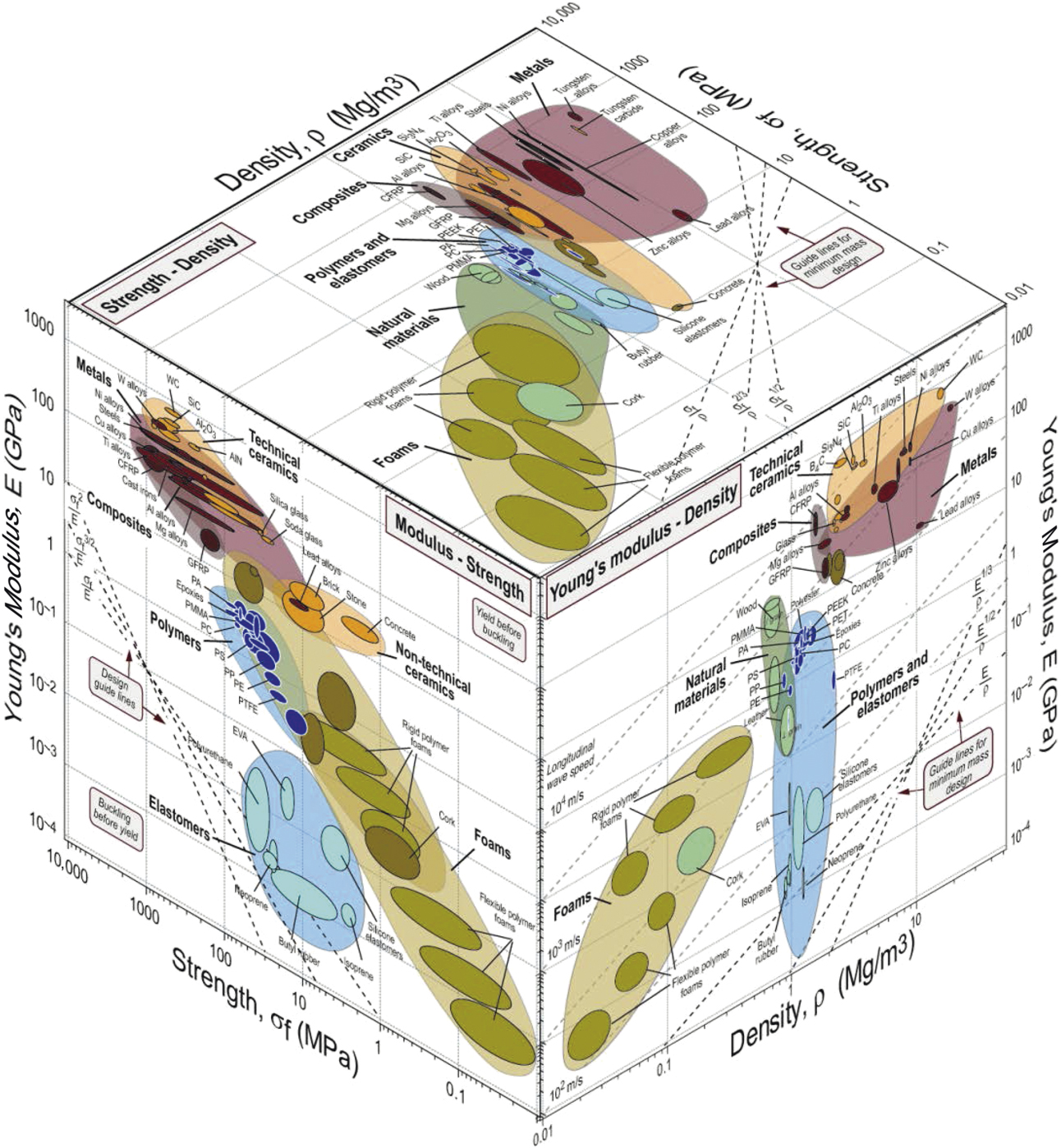
Figure 1. An Ashby plot of engineering materials showing the relation of strength, modulus, and density. The white spaces on these plots represent opportunities for the development of new materials, although some of these white spaces are inaccessible for fundamental reasons related to the size of atoms and the nature of the forces that bind them together.Reference Ashby1
All such material property charts contain regions that are densely populated with materials, and other parts that are not populated—in the so-called “white spaces.” Some regions are inaccessible for fundamental reasons related to the size of atoms and the nature of the forces that bind them together. Other parts are empty even though, in principle, they could be filled. One approach to filling holes in material property space is by manipulating chemistry, developing new metal alloys, new polymer formulations, and new compositions of glass and ceramic that extend the populated areas of the property charts. A second is by manipulating microstructure, using thermomechanical or thermochemical processing to control the distribution of phases and defects within materials. Both have been exploited systematically for many decades, leaving little room for further gains. A third approach is that of controlling architecture to create hybrid materials—combinations of materials or of materials and space in configurations that offer enhanced performance. A relatively well-known example of such an architecture is carbon fiber-reinforced composites, which have been highly successful in replacing structural metals for lightweight applications (e.g., the Airbus A350-XWB aircraft airframe has 50% carbon fiber composite by weight). A key feature of hybridization and architecting is that synergistic effects can be exploited to achieve more than the “sum of the parts” (glass fiber-reinforced epoxy is much tougher than either constituent due to the synergistic effect of distributed cracking).
Recent major technological advances have opened pathways to create architected “metamaterials” that have the potential to solve key challenges in our society. These include development of (1) nano- and microscale fabrication processes with precise control of material chemical composition, morphology, and topology; (2) mathematical tools for the construction of material property bounds; (3) computational capabilities that permit accurate simulation and prediction of effective materials properties as a function of constituent phases, and the arrangement of microstructural features at various length scales; and (4) experimental characterization methods with resolutions capable of quantifying and measuring the chemical and morphological constructs of architected features. For example, we can envisage devices and materials generated by nanoscale additive manufacturing that can fundamentally change conventional technologies in the realms of electronics, optoelectronics, energy storage and harvesting, biochemical sensors, and many others. One could also imagine that these devices—powered, actuated, and controlled remotely—could be freely dispersed in foreign environments for ubiquitous sensing, injected into the blood stream for whole body imaging, or integrated with molecules for designed drug delivery.
Architected materials
The term “architected material” first used in an overview paper by Ashby and BréchetReference Ashby and Bréchet2 was coined to make a link between the practice in architecture and structural engineering of topology optimization that has been employed to produce reliable, light, and elegant constructions. An architected material is a combination of several simple materials, possibly involving open space, configured to reach performances not offered by any individual material. Hence, there is a clear target in terms of a set of properties and performance to optimize at the onset, which motivates and guides its development. To focus the scope of this issue of MRS Bulletin, we limit attention to the extreme case of porous solids (a hybrid of solid and air), and explore the effects of micro-architecture, length scale, and constituent solid material on properties. Some representative examples of nano- and micro-architected materials that are created using various additive manufacturing and three-dimensional (3D) printing techniques are shown in Figure 2.Reference Meza, Zelhofer, Clarke, Mateos, Kochmann and Greer3–Reference Eckel, Zhou, Martin, Jacobsen, Carter and Schaedler6
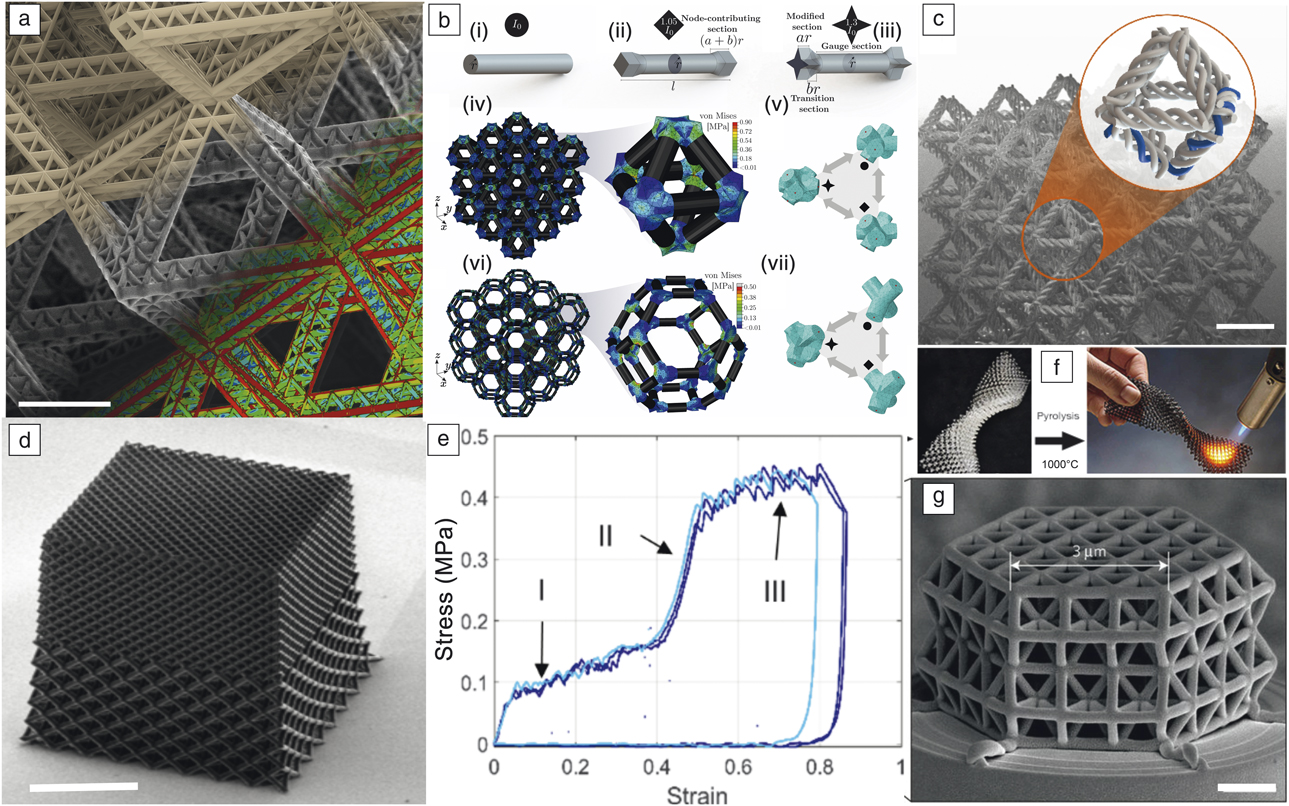
Figure 2. (a) A scanning electron microscope (SEM) image of the second-order octahedron of an octahedral lattice showing the first-order repeating units that make up the structure.Reference Meza, Zelhofer, Clarke, Mateos, Kochmann and Greer3 Scale bar = 10 μm. (b) Truss architecture and geometry definitions: (i) unmodified circular strut of radius, r, and length, l; (ii) square-modified strut; (iii) star-modified strut; (iv) uniaxial compression of a 3 × 3 × 3 reduced-order octahedron model; (v) octahedron node substructures depicting the tetrahedral mesh and the retained degrees of freedom (DOF) points in red; (vi) uniaxial compression of a 3 × 3 × 3 reduced-order tetrakaidecahedron model; and (vii) tetrakaidecahedron node substructures depicting the tetrahedral mesh and the retained DOF points in red. (c) SEM image of a “woven” octahedron nanolattice where each beam is composed of three woven beams woven into a spiral. Scale bar = 20 μm. Image and sample produced by W. Moestopo and C.M. Portela, California Institute of Technology. (d) SEM image of a bi-phase hollow alumina nanolattice with 10-nm-thick walls that shows two distinct relative densities, of 0.87% in the top half and 0.43% in the bottom half. Scale bar = 50 μm. Image and sample produced by M. Lifson, California Institute of Technology. (e) Uniaxial compression data for the nanolattice shown in (d).Reference Lifson4 (f) Additive manufacturing of polymer-derived ceramics using polymer waveguide technique followed by pyrolysis. Reprinted with permission from Reference 6. © 2016 AAAS. (g) Solid-beam glassy carbon lattice made by direct laser writing and subsequent pyrolysis. Scale bar = 1 μm. Reprinted with permission from Reference 5. © 2016 Nature Publishing Group.
Topological design
Fleck et al.Reference Fleck, Deshpande and Ashby7 defined a general lattice material as a cellular, reticulated, truss, or lattice structure made up of a large number of uniform lattice elements (e.g., slender beams or rods) and generated by tesselating a unit cell, comprised of just a few lattice elements, throughout two- (2D) or three-dimensional (3D) space. This shall serve as our working definition of an architected material.
Classically, periodic planar (i.e., 2D) lattices are classified as regular, semi-regular, or other. Regular lattices are generated by tessellating a regular polygon to fill the entire plane.Reference Frederickson8 Only a few regular polygons produce such a lattice—these are the triangle, square, and hexagon. Semi-regular lattices are generated by tessellating two or more different kinds of regular polygons to fill the entire plane; only eight independent semi-regular lattices exist, for example, the triangular-hexagonal lattice, also known as the kagome lattice.Reference Syozi, Domb and Green9,Reference Hyun and Torquato10 Additional plane-filling lattices can be constructed from two or more polygons of different sizes, or by relaxing the restriction that each joint have the same connectivity. Spatial or 3D lattices can be generated by filling space with polyhedra. Of the regular polyhedra with a small number of faces only the cube and the rhombic dodecahedra can be tessellated to fill all space.Reference Gibson and Ashby11 Typically, spatial lattices are constructed using combinations of different polygonal structures. For example, tetrahedra and octahedra may be packed to form the octet-truss lattice.Reference Deshpande, Ashby and Fleck12
The relative density ![]() ${\rm{\bar{\rho }}}$ of a lattice material is defined as the ratio of the unit cell solid fill fraction in the unit cell to the density of the solid. Lattice materials resemble frameworks when
${\rm{\bar{\rho }}}$ of a lattice material is defined as the ratio of the unit cell solid fill fraction in the unit cell to the density of the solid. Lattice materials resemble frameworks when ![]() ${\rm{\bar{\rho }}}$ is less than about 0.2, and in this regime
${\rm{\bar{\rho }}}$ is less than about 0.2, and in this regime ![]() ${\rm{\bar{\rho }}}$ is directly related to the thickness t and length l of a slender strut according to
${\rm{\bar{\rho }}}$ is directly related to the thickness t and length l of a slender strut according to ![]() ${\rm{\bar{\rho }}} \propto (t/\ell )$ and
${\rm{\bar{\rho }}} \propto (t/\ell )$ and ![]() ${\rm{\bar{\rho }}} \propto {(t/\ell )^2}$ in two dimensions and three dimensions, respectively. In the classical limit of slender-beam architectures, there are two distinct species of cellular solids. The first, typified by foams, are bending-dominated structures; the second, typified by triangulated micro-architected solids structures, are stretching-dominated—a distinction most evident in their mechanical properties.Reference Deshpande, Ashby and Fleck13 To give an idea of the difference, a foam with a relative density of 0.1 (meaning that the solid cell walls occupy 10% of the volume) is a factor of three less stiff than a triangulated lattice of the same relative density. The distinction between a bending-dominated and a stretching-dominated structure is largely dictated by the connectivity of joints rather than by the regularity of the microstructure, and is closely linked to the collapse response of a pin-jointed structure of the same morphology. If the parent, pin-jointed lattice exhibits collapse mechanisms that generate macroscopic strain, then the welded-joint version relies upon the rotational stiffness and strength of the nodes and struts for its macroscopic behavior. Consequently, the parent lattice is bending-dominated. In contrast, when the parent lattice has either only periodic or no collapse mechanisms, the welded-joint version is stretching-governed. The necessary, but not sufficient, condition for rigidity is Z = 4 in two dimensions and Z = 6 in three dimensions, where Z is nodal connectivity.Reference Deshpande, Ashby and Fleck13
${\rm{\bar{\rho }}} \propto {(t/\ell )^2}$ in two dimensions and three dimensions, respectively. In the classical limit of slender-beam architectures, there are two distinct species of cellular solids. The first, typified by foams, are bending-dominated structures; the second, typified by triangulated micro-architected solids structures, are stretching-dominated—a distinction most evident in their mechanical properties.Reference Deshpande, Ashby and Fleck13 To give an idea of the difference, a foam with a relative density of 0.1 (meaning that the solid cell walls occupy 10% of the volume) is a factor of three less stiff than a triangulated lattice of the same relative density. The distinction between a bending-dominated and a stretching-dominated structure is largely dictated by the connectivity of joints rather than by the regularity of the microstructure, and is closely linked to the collapse response of a pin-jointed structure of the same morphology. If the parent, pin-jointed lattice exhibits collapse mechanisms that generate macroscopic strain, then the welded-joint version relies upon the rotational stiffness and strength of the nodes and struts for its macroscopic behavior. Consequently, the parent lattice is bending-dominated. In contrast, when the parent lattice has either only periodic or no collapse mechanisms, the welded-joint version is stretching-governed. The necessary, but not sufficient, condition for rigidity is Z = 4 in two dimensions and Z = 6 in three dimensions, where Z is nodal connectivity.Reference Deshpande, Ashby and Fleck13
Fleck et al.Reference Fleck, Deshpande and Ashby7 used this idea to construct a Venn diagram to illustrate the various types of mechanisms exhibited by classes of 2D periodic pin-jointed trusses, as shown in Figure 3. Consider a fully triangulated structure, comprising equilateral triangles with a nodal connectivity of Z = 6; it is highly redundant and possesses no collapse mechanisms. In contrast, a triangular-triangular lattice collapses by a mechanism that leads to a macroscopic hydrostatic strain. Thus, this structure has zero macroscopic stiffness against this collapse mode. The kagome microstructure has a connectivity of Z = 4 and has no strain-producing collapse mechanisms; it can only collapse by periodic mechanisms, which do not produce a macroscopic strain. Consequently, it is rigid in all directions. The cases of the square lattice and hexagonal lattice, with Z = 4 and Z = 3, respectively, are different. Each of these structures can collapse by macroscopic strain-producing mechanisms and by periodic collapse mechanisms. The main conclusion to draw from Figure 3 is that the fully triangulated structure is macroscopically stiff because it possesses no collapse mechanisms, while the kagome structure is macroscopically stiff because it has only periodic collapse mechanisms, which generate no macroscopic strain.

Figure 3. Venn diagram for the classification of the deformation mechanisms of selected 2D lattices.Reference Fleck, Deshpande and Ashby7
Since nodal connectivity controls whether the deformation of a lattice is stretch or bend-dominated, this is directly reflected in the scaling expressions of their strength and stiffness with relative density. Simple beam theory dictates that the Young’s modulus and strength of lattice materials, made from a solid material of Young’s modulus E S (where the subscript S stands for solid), and yield strength σYS (where the subscript YS stands for yield strength), are related to their relative density via scaling laws of the form:
 $${E \over {{E_s}}} = A{{\rm{\bar{\rho }}}^n},$$
$${E \over {{E_s}}} = A{{\rm{\bar{\rho }}}^n},$$and
 $${{{{\rm{\sigma }}_Y}} \over {{{\rm{\sigma }}_{YS}}}} = B{{\rm{\bar{\rho }}}^m},$$
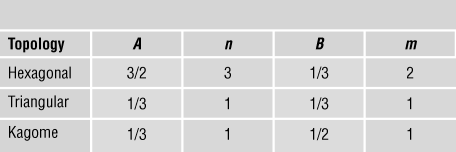
$${{{{\rm{\sigma }}_Y}} \over {{{\rm{\sigma }}_{YS}}}} = B{{\rm{\bar{\rho }}}^m},$$respectively. The coefficients (A, B, n, m) for some common 2D lattices are listed in Table I.
Table I. Coefficients for scaling laws.Reference Fleck, Deshpande and Ashby7
See Equation 1 in the text.
First, consider the case of stiffness. The hexagonal lattice is bending-dominated, with n = 3. In contrast, the kagome and fully triangulated lattices are stretching-dominated with n = 1. Remarkably, the coefficient A is identical for the triangulated and kagome lattices. These lattices have identical effective properties, and each achieves the Hashin–ShtrikmanReference Hashin and Shtrikman14 upper bound—the tightest possible bound for a bi-material composite with two different moduli. The differences between the two lattices, however, show up when imperfections are introduced. For example, by randomly perturbing the location of the nodes at fixed relative density, there is a large drop in the modulus of the kagome lattice, but a much smaller drop in modulus of the triangulated lattice.Reference Romijn and Fleck15 This is because the triangulated lattice has a higher nodal connectivity of Z = 6 than the kagome lattice (Z = 4) and is a much more redundant structure when the struts are assumed to be pin-jointed at the nodes.
The main conclusions for stiffness carry over to strength with m = 1 for the triangular and kagome structures that deform by bar stretching, while the hexagonal honeycomb deforms by bar bending, leading to m = 2. Similarly, scaling laws have been developed for a host of 3D lattice materials, with the primary conclusions carrying over from the 2D case. For example, the octet truss, identical in crystal structure to face-centered cubic (fcc), has a nodal connectivity (coordination number) of 12 and is a stretching-dominated structure. The Young’s modulus E and yield strength σYS scale linearly with relative density such that ![]() $E \approx 0.3{\rm{\bar{\rho }}}{E_S}$ and
$E \approx 0.3{\rm{\bar{\rho }}}{E_S}$ and ![]() ${{\rm{\sigma }}_YS} \approx 0.3{\rm{\bar{\rho }}}{{\rm{\sigma }}_{YS}}$. These values are close but not equal to the Hashin–Shtrikman upper bound for an isotropic solid. Such lattice materials have their stiffness and strength scale linearly with the relative density and outperform not only metallic foams, but also other 3D lattice materials such as low density gyroidsReference Khaderi, Deshpande and Fleck16 and topologies reminiscent of body-centered-cubic (bcc) structures; see Schaedler et al.Reference Schaedler, Jacobsen, Torrents, Sorensen, Lian, Greer, Valdevit and Carter17 and Zok et al.Reference Zok, Latture and Begley18 for a geometric classification of 3D lattice topologies.
${{\rm{\sigma }}_YS} \approx 0.3{\rm{\bar{\rho }}}{{\rm{\sigma }}_{YS}}$. These values are close but not equal to the Hashin–Shtrikman upper bound for an isotropic solid. Such lattice materials have their stiffness and strength scale linearly with the relative density and outperform not only metallic foams, but also other 3D lattice materials such as low density gyroidsReference Khaderi, Deshpande and Fleck16 and topologies reminiscent of body-centered-cubic (bcc) structures; see Schaedler et al.Reference Schaedler, Jacobsen, Torrents, Sorensen, Lian, Greer, Valdevit and Carter17 and Zok et al.Reference Zok, Latture and Begley18 for a geometric classification of 3D lattice topologies.
Length scale and effects of nano-architecting
In the last 15 years, it was ubiquitously demonstrated that at the micron- and submicron scales, the sample size dramatically affects crystalline strength, as revealed by room-temperature uniaxial compression and tension experiments on a wide range of single-crystalline metallic nanopillars.Reference Greer and De Hosson19,Reference Uchic, Shade and Dimiduk20 To date, these micro- and nanodeformation studies (both compression and tension) include (but are not limited to) fcc metals (Ni and Ni-based superalloys), Au, Cu, Al (as-fabricated and intentionally passivated), bcc metals (Mo, Ta, W, V, Nb), hexagonal close-packed metals (Ti and Mg), tetragonal low-temperature metals, Gum metal, nanocrystalline metals (Ni, Pt, and Cu), shape-memory alloys, and a variety of metallic glasses.Reference Greer and De Hosson19 Most of these experiments, where the initial microstructure contained dislocations or other defects, revealed a remarkable dependence of the attained flow strength on sample diameter due to the presence of unique defect-driven deformation mechanisms in nanoscale plasticity, often characterized by discrete strain bursts and size-dependent stress–strain relationships. These findings suggest that when the extrinsic sample size is reduced to that on the order of or below the characteristic microstructural length scale of the material, size reduction has a significant effect on material strength and susceptibility to failure through the activation of unique deformation mechanisms, pertinent to surface-dominated nano- and micron-sized materials. Nearly all classes of materials—ceramics, glasses, metals, and semiconductors—exhibit size effects when their dimensions are reduced to the nanometer and submicron scales. These size effects manifest themselves in a range of mechanical properties; for example, smaller can be stronger (single crystalline metals) or weaker (nanocrystalline metals). Reducing structures to nano- or micron levels can suppress failure in intrinsically brittle materials (glasses and ceramics) and can toughen the material (ceramics and composites). Nano-architected solids with engineered features on the nano- and micron scale represent a unique platform to exploit these size effects, allowing for the creation of “designed materials.” They enable decoupling of historically co-dependent properties such as strength and weight through architectural control and have the potential to push the envelope of existing materials.
Nanoarchitected solids can harness the beneficial properties offered by nanoscale material properties and proliferate them onto the macroscale while maintaining full control of stiffness, material, and geometry. For example, methods existReference Meza, Das and Greer21 that allow the creation of virtually any geometry with nano- and micron dimensions (Figure 2) that can mimic natural structures (i.e., hard biological shells and bone) and can engineer devices and materials, such as ultra-lightweight batteries and damage-tolerant foams. Such architected 3D metamaterials have profound implications not only in fundamental materials science, but also for proliferating material size effects onto the macroscale.
Combining architecture, atomic-level microstructure, and nanoscale dimensions could fundamentally change the way we design materials. Such a “materials by design” approach shifts the paradigm of material creation away from relying on classical processing routes, notorious for coupling properties such as strength and density, toward smart design. The development of hierarchical, 3D nano-architected platforms will provide insights into amplified damage tolerance, resilience, thermal, electronic, and photonic properties of ultra-lightweight nano-architected metamaterials. By utilizing clever syntheses routes in 3D printable resins, it is becoming possible to form metallic, semiconducting, ceramic, and otherwise multifunctional architected metamaterials where the dimensions of the individual building blocks are at the nanoscale, a regime where nearly all materials exhibit size effects.
For example, smaller can be stronger,Reference Greer, Oliver and Nix22–Reference Greer, Jang, Kim and Burek24 weaker,Reference Kiener, Motz, Dehm and Pippan25,Reference Gu, Loynachan, Wu, Zhang, Srolovitz and Greer26 suppress brittle failure and induce ductility,Reference Chen, Jang, Guan, An, Goddard and Greer27,Reference Jang and Greer28 couple with light to create 3D photonic crystals,Reference Noda, Tomoda, Yamamoto and Chutinan29,Reference Arsenault, Clark, von Freymann, Cademartiri, Sapienza, Bertolotti, Evangellos, Wong, Kitaev, Manners, Wang, Sajeev, Diederik and Ozin30 produce negative refraction materials,Reference Soukoulis, Linden and Wegener31 and activate phonon scattering-driven thermal processes.Reference Dou, Jagt, Portela, Greer and Minnich32 Utilizing this emergence of new functionality at the nanoscale and proliferating these “size effects” onto 3D architectures have already proven successful. One notable example is the demonstration that hollow nanolattices with relative densities of ∼0.1%, made of 10-nm-thick brittle ceramic, recovered after compression in excess of 50% without sacrifice in strength or stiffnessReference Meza, Zelhofer, Clarke, Mateos, Kochmann and Greer3,Reference Meza, Das and Greer21 and had an exceptionally low dielectric constant (relative permittivity) of 1.06 at 1 MHz.Reference Lifson, Kim, Greer and Kim33,Reference Kim, Lifson, Rebecca, Greer and Kim34
Similar exceptional recoverability was also found in nano-architectures made of metallic glasses, materials that are notorious for catastrophic failure via rapid shear band initiation and propagation.Reference Liontas and Greer35 Another example is amorphous carbon nanolattices whose compressive strength approached the ideal material strength.Reference Bauer, Schroer, Schwaiger and Kraft5 These materials simultaneously attained ultra-lightweight, high strength and stiffness, and—in some cases—recoverability by combining the architecture and material size effects that emerge in nanomaterials. Manufacturing 3D nano-architected materials will enable the creation of new classes of materials, which do not currently exist, that will be able to address multiple technological challenges, especially those where a property and density need to be decoupled from one another.
In this issue
The focus of this issue of MRS Bulletin is all aspects of design, fabrication, mechanical behavior, and functionality of architected materials. Leading contributors to the field have provided discussions on (1) the manufacture and processing of architected materials; (2) their optimal design; (3) multiscale computational design tools; (4) extreme mechanical properties when endowed with micro- and nanoscale features; and (5) application of architected materials in electrochemical systems.
Architected materials are unique, in the sense that their performance is fundamentally controlled by geometry at multiple length scales, from the nano- to the macroscale, rather than chemical composition or processing alone. As a result, the realization of these materials is contingent upon the ability to faithfully reproduce the designed architecture. This presents fundamental challenges in fabrication due to the required 3D complexity, multiple length scales, range of material constituents, possibility of multiple materials in a single architecture, and overall manufacturing throughput. The SpadacciniReference Spadaccini36 article in this issue gives an overview of additive manufacturing processes that can provide solutions to some of these challenges in the manufacture of architected materials. The article demonstrates that while remarkable advancements in additive manufacturing for architected materials have been made, bringing these materials and processes to industrial realization remains a significant challenge.
Incessant improvements in additive manufacturing technologies along with the development of strategies to improve accuracy, such as machine parameter tuning, compensation strategies, and post-processing treatments (e.g., hot isostatic pressing, machining, electropolishing, and acid etching), have significantly improved the as-manufactured quality of architected materials. Yet, manufacturing flaws are unlikely to completely disappear in the foreseeable future. In their article, Pasini and GuestReference Pasini and Guest37 discuss methodologies to systematically assess morphology and dispersion of as-manufactured defects as a route to develop higher fidelity predictive models for defects in architected materials. They envision a workflow from fabrication of a statistically relevant set of architected materials of prescribed geometry and material, followed by metrology to assess variability between nominal and as-built architecture, uncertainty quantification to estimate the impact of defects, and robust topology optimization for the design of architected materials that are defect-insensitive.
Kochmann et al.Reference Kochmann, Hopkins and Valdevit38 present a survey of modeling techniques to describe and predict properties of architected cellular metamaterials and to optimize their topology and geometry toward tailoring their mechanical properties such as stiffness, strength, fracture toughness, and energy absorption. The approaches include classical finite element techniques, scale-bridging techniques such as homogenization and concurrent scale coupling, and effective continuum descriptions of the underlying discrete networks. Despite many existing approaches, a long list of open challenges remains, including models for the complex nonlinear, inelastic, and the rich nonlinear dynamic response of metamaterials, models for the nano- and microscales where material and structural feature sizes are of the same order, and neither classical micromechanical and atomistic techniques nor structural engineering tools are applicable. Most importantly, they show that the inclusion of fabrication-based tolerances and imperfections are essential and often neglected while assessing the performance of architected materials.
“Smaller is different” is a frequently used phrase in materials science; using nanoscale features in architected materials is powerful because it enables decoupling of historically coupled properties such as strength, toughness, and ductility. Schwaiger et al.Reference Schwaiger, Meza and Li39 discuss the emergence of fabrication methods that have enabled the creation of materials with controllable architectures down to the nanoscale. These micro- and nano-architected materials utilize both resilient architectures and size-affected constituent materials to achieve unprecedented mechanical properties such as ultrahigh strength at low density, recoverability after large applied strains in intrinsically brittle materials, and metamaterial properties such as chirality and negative static compressibility. Through an understanding of the governing principles behind these materials they also provide guidelines for the design of the next generation of nano-architected materials.
Energy storage is a key grand challenge facing our society today, and Pikul and LongReference Pikul and Long40 demonstrate that architected materials can play an essential role in next-generation electrochemical systems that attain unprecedented capabilities. For example, they discuss how the geometry and chemistry of architected materials can be engineered to tune electrochemical kinetics to enhance power density, efficiency, and lifetime of/in batteries and fuel cells. The article not only summarizes advances in energy storage offered by architected materials and highlights fabrication methods used to realize these advances, it also demonstrates that electrochemistry is an enabling tool for architected materials with functionality beyond energy storage and sensing.
Perspective
Throughout history, advances in materials and manufacturing technologies have led to the invention of new classes of materials that have had revolutionary societal impacts. The development of the blast furnace enabled the widespread use of cast iron for the great bridges, railway terminals, and civil buildings of the early 19th century. The advent of additive manufacturing technologies, along with true nanoengineering tools capable of resolving and manipulating matter at close-to-atomic levels over the last couple of decades, has opened the possibility to build particularly resilient materials and structures the way nature does.
Architected materials are a new class of materials culminating from the confluence of these technologies. These materials show promise for multifunctional applications, combining a mechanical function (such as stiffness and strength) with some other property (such as thermal or electrical conductivity), thereby making lightweight and efficient batteries, structural armor, and deployable materials a possibility. They also allow for real-time or even time-dependent tunability of properties with most recent advances reporting abilities to dynamically reconfigure metamaterial topologies as a function of electrochemical or acoustic stimuli.Reference Xia, Afshar, Yang, Portela, Kochmann, Di Leo and Greer41 While significant progress continues in bringing this new class of materials into a range of engineering applications, a number of challenges remain, including the development of scalable and cost-effective manufacturing methods.

Julia R. Greer is the Ruben F. and Donna Mettler Professor of Materials Science, Mechanics and Medical Engineering at the California Institute of Technology. Her research focuses on creating and characterizing classes of materials with multiscale microstructural hierarchy, which combine three-dimensional architectures with nanoscale-induced materials properties. Her awards include the American Association for Advances in Functional Materials-Heeger Award in 2019, the Vannevar Bush Faculty Fellowship in 2016, CNN’s 20/20 Visionary in 2016, Top-10 Breakthrough Technologies in 2015, and MIT Technology Review’s TR-35 Award, in 2008. She was named one of “100 Most Creative People” by Fast Company Magazine and a Young Global Leader by the World Economic Forum in 2014. She has authored or co-authored more than 150 publications. She serves as an associate editor for Nano Letters and Extreme Mechanics Letters. Greer can be reached by email at jrgreer@caltech.edu.

Vikram S. Deshpande has been a professor in the Department of Engineering at the University of Cambridge, UK, since 2010. His research interests include contributions in mechanics of materials, ranging from the design of micro-architected materials to modeling soft and active materials. His current research focuses on mechanical properties, including the development of models for their constitutive behavior that have been encapsulated into commercial finite element programs (e.g., ABAQUS, DYNA). He has written more than 240 journal articles and serves on the editorial boards of a number of journals in mechanics and biomechanics. Deshpande can be reached by email at vsd20@cam.ac.uk.







