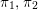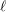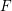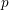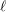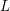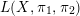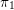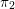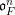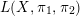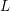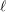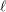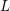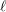1 Introduction
The integral representation of local
![]() $L$
-factors, of pairs of complex irreducible representations of general linear groups over a nonarchimedean local field
$L$
-factors, of pairs of complex irreducible representations of general linear groups over a nonarchimedean local field
![]() $F$
, was developed in the fundamental paper [Reference Jacquet, Piatetski-Shapiro and Shalika5] of Jacquet–Piatetski-Shapiro–Shalika. These
$F$
, was developed in the fundamental paper [Reference Jacquet, Piatetski-Shapiro and Shalika5] of Jacquet–Piatetski-Shapiro–Shalika. These
![]() $L$
-factors are Euler factors which are the greatest common divisors, in a certain sense, of families of integrals
$L$
-factors are Euler factors which are the greatest common divisors, in a certain sense, of families of integrals
![]() $I$
of Whittaker functions. For
$I$
of Whittaker functions. For
![]() $n\geqslant m$
, as a by-product of the definition, if
$n\geqslant m$
, as a by-product of the definition, if
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
are irreducible smooth complex (or
$\unicode[STIX]{x1D70B}_{2}$
are irreducible smooth complex (or
![]() $\ell$
-adic) representations of
$\ell$
-adic) representations of
![]() $\text{GL}_{n}(F)$
and
$\text{GL}_{n}(F)$
and
![]() $\text{GL}_{m}(F)$
respectively with Whittaker models
$\text{GL}_{m}(F)$
respectively with Whittaker models
![]() $W(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713})$
and
$W(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713})$
and
![]() $W(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}^{-1})$
, extended to all irreducible representations via the Langland’s classification, then it is known that there is a finite number
$W(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}^{-1})$
, extended to all irreducible representations via the Langland’s classification, then it is known that there is a finite number
![]() $r$
of Whittaker functions
$r$
of Whittaker functions
![]() $W_{i}\in W(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713})$
and
$W_{i}\in W(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713})$
and
![]() $W_{i}^{\prime }\in W(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}^{-1})$
, and a finite number of Schwartz functions
$W_{i}^{\prime }\in W(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}^{-1})$
, and a finite number of Schwartz functions
![]() $\unicode[STIX]{x1D6F7}_{i}$
on
$\unicode[STIX]{x1D6F7}_{i}$
on
![]() $F^{n}$
if
$F^{n}$
if
![]() $n=m$
, such that the
$n=m$
, such that the
![]() $L$
-factor
$L$
-factor
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
can be expressed as
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
can be expressed as
![]() $\sum _{i=1}^{r}I(X,W_{i},W_{i}^{\prime })$
, or
$\sum _{i=1}^{r}I(X,W_{i},W_{i}^{\prime })$
, or
![]() $\sum _{i=1}^{r}I(X,W_{i},W_{i}^{\prime },\unicode[STIX]{x1D6F7}_{i})$
when
$\sum _{i=1}^{r}I(X,W_{i},W_{i}^{\prime },\unicode[STIX]{x1D6F7}_{i})$
when
![]() $n=m$
. A natural question which thus arises is whether one can find an explicit family of such test vectors.
$n=m$
. A natural question which thus arises is whether one can find an explicit family of such test vectors.
A famous instance of test vectors is the essential vectors for generic representations (cf. [Reference Jacquet, Piatetski-Shapiro and Shalika4, Reference Jacquet6, Reference Matringe9]). It is shown in these references that these vectors are test vectors for
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
when
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
when
![]() $\unicode[STIX]{x1D70B}_{1}$
is a generic representation of
$\unicode[STIX]{x1D70B}_{1}$
is a generic representation of
![]() $\text{GL}_{n}(F)$
,
$\text{GL}_{n}(F)$
,
![]() $\unicode[STIX]{x1D70B}_{2}$
is an unramified standard module of
$\unicode[STIX]{x1D70B}_{2}$
is an unramified standard module of
![]() $\text{GL}_{m}(F)$
, and
$\text{GL}_{m}(F)$
, and
![]() $n>m$
.
$n>m$
.
Interesting partial results have been obtained in [Reference Kim7], and, as indicated in [Reference Kim7], the theory of derivatives and its interpretation in terms of restriction of Whittaker functions (cf. [Reference Cogdell and Piatetski-Shapiro3, Reference Matringe9]) should reduce the general problem to the cuspidal case. Here, we establish the cuspidal case: that for pairs of cuspidal representations
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
, we can choose
$\unicode[STIX]{x1D70B}_{2}$
, we can choose
![]() $r=1$
, and moreover, we exhibit explicit test vectors, in the interesting case, whenever
$r=1$
, and moreover, we exhibit explicit test vectors, in the interesting case, whenever
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is not equal to one. The fact that
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is not equal to one. The fact that
![]() $r$
can be chosen to be
$r$
can be chosen to be
![]() $1$
when
$1$
when
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})=1$
, for any pair of irreducible representations
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})=1$
, for any pair of irreducible representations
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
of
$\unicode[STIX]{x1D70B}_{2}$
of
![]() $\text{GL}_{n}(F)$
and
$\text{GL}_{n}(F)$
and
![]() $\text{GL}_{m}(F)$
, is explained in the proof of [Reference Jacquet, Piatetski-Shapiro and Shalika5, Theorem 2.7] and follows from standard facts on Kirillov models. We do not provide completely explicit test functions in this case, possibly a quite technical problem, and we in fact do not consider this case in the remainder of this article, as it is not needed for our application to reduction modulo
$\text{GL}_{m}(F)$
, is explained in the proof of [Reference Jacquet, Piatetski-Shapiro and Shalika5, Theorem 2.7] and follows from standard facts on Kirillov models. We do not provide completely explicit test functions in this case, possibly a quite technical problem, and we in fact do not consider this case in the remainder of this article, as it is not needed for our application to reduction modulo
![]() $\ell$
.
$\ell$
.
Before we state our main theorem, we explain our normalization of Haar measure (Section 4), as for our application to reduction modulo
![]() $\ell$
some care needs to be taken with the normalization. Let
$\ell$
some care needs to be taken with the normalization. Let
![]() $\mathfrak{o}_{F}$
denote the ring of integers of
$\mathfrak{o}_{F}$
denote the ring of integers of
![]() $F$
with unique maximal ideal
$F$
with unique maximal ideal
![]() $\mathfrak{p}_{F}$
, and let
$\mathfrak{p}_{F}$
, and let
![]() $q$
denote the cardinality of the residue field
$q$
denote the cardinality of the residue field
![]() $\mathfrak{o}_{F}/\mathfrak{p}_{F}$
and
$\mathfrak{o}_{F}/\mathfrak{p}_{F}$
and
![]() $p$
its characteristic. We fix our Haar measure on
$p$
its characteristic. We fix our Haar measure on
![]() $\text{GL}_{n}(F)$
to give the pro-
$\text{GL}_{n}(F)$
to give the pro-
![]() $p$
unipotent radical
$p$
unipotent radical
![]() $K_{n}^{1}$
of
$K_{n}^{1}$
of
![]() $\text{GL}_{n}(\mathfrak{o}_{F})$
volume one. It will turn out that this is a good choice of normalization for reduction modulo
$\text{GL}_{n}(\mathfrak{o}_{F})$
volume one. It will turn out that this is a good choice of normalization for reduction modulo
![]() $\ell$
for primes
$\ell$
for primes
![]() $\ell$
not equal to
$\ell$
not equal to
![]() $p$
because
$p$
because
![]() $K_{n}^{1}$
is a pro-
$K_{n}^{1}$
is a pro-
![]() $p$
subgroup. In particular, the volume of any pro-
$p$
subgroup. In particular, the volume of any pro-
![]() $p$
subgroup of
$p$
subgroup of
![]() $\text{GL}_{n}(F)$
which occurs in our computation will be a power of
$\text{GL}_{n}(F)$
which occurs in our computation will be a power of
![]() $q$
.
$q$
.
Now we state our main theorem. Let
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
be cuspidal complex, or
$\unicode[STIX]{x1D70B}_{2}$
be cuspidal complex, or
![]() $\ell$
-adic, representations of
$\ell$
-adic, representations of
![]() $\text{GL}_{n}(F)$
such that
$\text{GL}_{n}(F)$
such that
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is nontrivial, so that
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is nontrivial, so that
![]() $\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
for some unramified character
$\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
for some unramified character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $F^{\times }$
. Let
$F^{\times }$
. Let
![]() $e$
denote the common ramification index of
$e$
denote the common ramification index of
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
(see Section 6). We denote by
$\unicode[STIX]{x1D70B}_{2}$
(see Section 6). We denote by
![]() $W_{1}$
and
$W_{1}$
and
![]() $W_{2}$
the explicit Whittaker functions for
$W_{2}$
the explicit Whittaker functions for
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
, as constructed in [Reference Paskunas and Stevens12], with respect to a suitable nondegenerate character of the standard maximal unipotent subgroup of
$\unicode[STIX]{x1D70B}_{2}$
, as constructed in [Reference Paskunas and Stevens12], with respect to a suitable nondegenerate character of the standard maximal unipotent subgroup of
![]() $\text{GL}_{n}(F)$
and suitable maximal extended simple types in
$\text{GL}_{n}(F)$
and suitable maximal extended simple types in
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
.
$\unicode[STIX]{x1D70B}_{2}$
.
Theorem 9.1
. There is an integer
![]() $r$
such that
$r$
such that
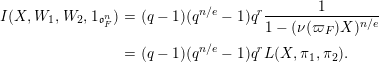 $$\begin{eqnarray}\displaystyle I(X,W_{1},W_{2},1_{\mathfrak{o}_{F}^{n}}) & = & \displaystyle (q-1)(q^{n/e}-1)q^{r}\frac{1}{1-(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{F})X)^{n/e}}\nonumber\\ \displaystyle & = & \displaystyle (q-1)(q^{n/e}-1)q^{r}L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I(X,W_{1},W_{2},1_{\mathfrak{o}_{F}^{n}}) & = & \displaystyle (q-1)(q^{n/e}-1)q^{r}\frac{1}{1-(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{F})X)^{n/e}}\nonumber\\ \displaystyle & = & \displaystyle (q-1)(q^{n/e}-1)q^{r}L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}).\nonumber\end{eqnarray}$$
The factor
![]() $q^{r}$
occurs in our computation as a product of volumes, with respect to certain quotient measures, of quotients of pro-
$q^{r}$
occurs in our computation as a product of volumes, with respect to certain quotient measures, of quotients of pro-
![]() $p$
subgroups related to the groups of Bushnell–Kutzko [Reference Bushnell and Kutzko2] in their explicit construction of
$p$
subgroups related to the groups of Bushnell–Kutzko [Reference Bushnell and Kutzko2] in their explicit construction of
![]() $\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}$
. Clearly, after our computation we could simply renormalize our measure by the factor
$\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}$
. Clearly, after our computation we could simply renormalize our measure by the factor
![]() $(q-1)(q^{n/e}-1)q^{r}$
and under the new normalization have an equality between the integral and the
$(q-1)(q^{n/e}-1)q^{r}$
and under the new normalization have an equality between the integral and the
![]() $L$
-factor, hence
$L$
-factor, hence
![]() $(W_{1},W_{2},1_{\mathfrak{o}_{F}^{n}})$
is a test vector in the sense described earlier. However, it is important to keep track of these factors for our application to reduction modulo
$(W_{1},W_{2},1_{\mathfrak{o}_{F}^{n}})$
is a test vector in the sense described earlier. However, it is important to keep track of these factors for our application to reduction modulo
![]() $\ell$
.
$\ell$
.
We now describe the proof of this theorem. In Section 7, we carefully choose an appropriate basis of
![]() $F^{n}$
and simple types in our cuspidal representations, so that the subgroup of
$F^{n}$
and simple types in our cuspidal representations, so that the subgroup of
![]() $\text{GL}_{n}(F)$
defined by these simple types decomposes well with respect to the Iwasawa decomposition and satisfies some other important properties (see Proposition 7.1). In Section 8, we analyze the support of the explicit Whittaker functions of Paskunas and Stevens in terms of this well chosen group (Proposition 8.4). This preparation, which constitutes a substantial amount of the path to our main result, then allows us to compute the integral in Section 9.
$\text{GL}_{n}(F)$
defined by these simple types decomposes well with respect to the Iwasawa decomposition and satisfies some other important properties (see Proposition 7.1). In Section 8, we analyze the support of the explicit Whittaker functions of Paskunas and Stevens in terms of this well chosen group (Proposition 8.4). This preparation, which constitutes a substantial amount of the path to our main result, then allows us to compute the integral in Section 9.
Our interest in test vectors originated in the study of
![]() $\ell$
-modular Rankin–Selberg
$\ell$
-modular Rankin–Selberg
![]() $L$
-factors, for
$L$
-factors, for
![]() $\ell \neq p$
, as introduced in [Reference Kurinczuk and Matringe8]. Let
$\ell \neq p$
, as introduced in [Reference Kurinczuk and Matringe8]. Let
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
be integral cuspidal
$\unicode[STIX]{x1D70B}_{2}$
be integral cuspidal
![]() $\ell$
-adic representations of
$\ell$
-adic representations of
![]() $\text{GL}_{n}(F)$
and
$\text{GL}_{n}(F)$
and
![]() $\text{GL}_{m}(F)$
, and
$\text{GL}_{m}(F)$
, and
![]() $\unicode[STIX]{x1D70F}_{1}=r_{\ell }(\unicode[STIX]{x1D70B}_{1})$
and
$\unicode[STIX]{x1D70F}_{1}=r_{\ell }(\unicode[STIX]{x1D70B}_{1})$
and
![]() $\unicode[STIX]{x1D70F}_{2}=r_{\ell }(\unicode[STIX]{x1D70B}_{2})$
their reductions modulo
$\unicode[STIX]{x1D70F}_{2}=r_{\ell }(\unicode[STIX]{x1D70B}_{2})$
their reductions modulo
![]() $\ell$
, which are cuspidal
$\ell$
, which are cuspidal
![]() $\ell$
-modular representations. By [Reference Kurinczuk and Matringe8, Theorem 3.13], the local factor
$\ell$
-modular representations. By [Reference Kurinczuk and Matringe8, Theorem 3.13], the local factor
![]() $L(X,\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2})$
always divides
$L(X,\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2})$
always divides
![]() $r_{\ell }(L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}))$
. In particular,
$r_{\ell }(L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}))$
. In particular,
![]() $L(X,\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2})=r_{\ell }(L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}))$
whenever
$L(X,\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2})=r_{\ell }(L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}))$
whenever
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})=1$
. Hence the interesting case, where a strict division can happen is when
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})=1$
. Hence the interesting case, where a strict division can happen is when
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is not equal to
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is not equal to
![]() $1$
, and, in particular,
$1$
, and, in particular,
![]() $n=m$
. In [Reference Mínguez10], it was shown that for banal representations the
$n=m$
. In [Reference Mínguez10], it was shown that for banal representations the
![]() $\ell$
-modular Godement–Jacquet
$\ell$
-modular Godement–Jacquet
![]() $L$
-factor is equal to the reduction modulo
$L$
-factor is equal to the reduction modulo
![]() $\ell$
of the
$\ell$
of the
![]() $\ell$
-adic Godement–Jacquet
$\ell$
-adic Godement–Jacquet
![]() $L$
-factor. It is thus natural to ask: if
$L$
-factor. It is thus natural to ask: if
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
are
$\unicode[STIX]{x1D70B}_{2}$
are
![]() $\ell$
-adic integral cuspidal representations of
$\ell$
-adic integral cuspidal representations of
![]() $\text{GL}_{n}(F)$
with banal reductions
$\text{GL}_{n}(F)$
with banal reductions
![]() $\unicode[STIX]{x1D70F}_{1}$
and
$\unicode[STIX]{x1D70F}_{1}$
and
![]() $\unicode[STIX]{x1D70F}_{2}$
, does one have
$\unicode[STIX]{x1D70F}_{2}$
, does one have
![]() $L(X,\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2})=r_{\ell }(L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}))$
? As a corollary of our main result on test vectors applied to
$L(X,\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2})=r_{\ell }(L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}))$
? As a corollary of our main result on test vectors applied to
![]() $\ell$
-adic Rankin–Selberg integrals, we answer this question in the affirmative.
$\ell$
-adic Rankin–Selberg integrals, we answer this question in the affirmative.
Corollary 10.1
. Let
![]() $\unicode[STIX]{x1D70F}_{1}$
and
$\unicode[STIX]{x1D70F}_{1}$
and
![]() $\unicode[STIX]{x1D70F}_{2}$
be two banal cuspidal
$\unicode[STIX]{x1D70F}_{2}$
be two banal cuspidal
![]() $\ell$
-modular representations of
$\ell$
-modular representations of
![]() $\text{GL}_{n}(F)$
, and
$\text{GL}_{n}(F)$
, and
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
be any cuspidal
$\unicode[STIX]{x1D70B}_{2}$
be any cuspidal
![]() $\ell$
-adic lifts, then
$\ell$
-adic lifts, then
In [Reference Kurinczuk and Matringe8], this corollary plays a key role in the classification of
![]() $L$
-factors of generic
$L$
-factors of generic
![]() $\ell$
-modular representations, and their relationship with
$\ell$
-modular representations, and their relationship with
![]() $\ell$
-adic
$\ell$
-adic
![]() $L$
-factors via reduction modulo
$L$
-factors via reduction modulo
![]() $\ell$
.
$\ell$
.
It would be interesting to pursue the methods of this paper for integral representations of other
![]() $L$
-factors, such as the Asai, exterior square, and symmetric square
$L$
-factors, such as the Asai, exterior square, and symmetric square
![]() $L$
-factors.
$L$
-factors.
2 Notations
Let
![]() $F$
be a nonarchimedean local field of residual characteristic
$F$
be a nonarchimedean local field of residual characteristic
![]() $p$
and residual cardinality
$p$
and residual cardinality
![]() $q$
. Throughout,
$q$
. Throughout,
![]() $R$
will denote one of the fields
$R$
will denote one of the fields
![]() $\mathbb{C}$
,
$\mathbb{C}$
,
![]() $\overline{\mathbb{Q}_{\ell }}$
, and
$\overline{\mathbb{Q}_{\ell }}$
, and
![]() $\overline{\mathbb{F}_{\ell }}$
and we assume that
$\overline{\mathbb{F}_{\ell }}$
and we assume that
![]() $\ell \neq p$
. For
$\ell \neq p$
. For
![]() $E$
any extension of
$E$
any extension of
![]() $F$
, we denote by
$F$
, we denote by
![]() $\mathfrak{o}_{E}$
the ring of integers of
$\mathfrak{o}_{E}$
the ring of integers of
![]() $E$
; by
$E$
; by
![]() $\unicode[STIX]{x1D71B}_{E}$
a uniformizer of
$\unicode[STIX]{x1D71B}_{E}$
a uniformizer of
![]() $E$
; by
$E$
; by
![]() $\mathfrak{p}_{E}=(\unicode[STIX]{x1D71B}_{E})$
the unique maximal ideal of
$\mathfrak{p}_{E}=(\unicode[STIX]{x1D71B}_{E})$
the unique maximal ideal of
![]() $\mathfrak{o}_{E}$
; by
$\mathfrak{o}_{E}$
; by
![]() $q_{E}$
the residual cardinality of
$q_{E}$
the residual cardinality of
![]() $E$
; and let
$E$
; and let
![]() $||_{E,R}:E^{\times }\rightarrow R^{\times }$
denote the unramified character defined by
$||_{E,R}:E^{\times }\rightarrow R^{\times }$
denote the unramified character defined by
![]() $|\unicode[STIX]{x1D71B}_{E}|_{E,R}=q_{E}^{-1}$
, thus
$|\unicode[STIX]{x1D71B}_{E}|_{E,R}=q_{E}^{-1}$
, thus
![]() $||_{E,\mathbb{C}}$
is the restriction of the absolute value to
$||_{E,\mathbb{C}}$
is the restriction of the absolute value to
![]() $E^{\times }$
normalized in the usual way. When the field
$E^{\times }$
normalized in the usual way. When the field
![]() $R$
considered is clear we remove the index
$R$
considered is clear we remove the index
![]() $R$
from
$R$
from
![]() $||_{E,R}$
, and when
$||_{E,R}$
, and when
![]() $E=F$
we remove the index
$E=F$
we remove the index
![]() $F$
as well.
$F$
as well.
Let
![]() $G_{n}=\text{GL}_{n}(F)$
,
$G_{n}=\text{GL}_{n}(F)$
,
![]() $K_{n}=\text{GL}_{n}(\mathfrak{o}_{F})$
,
$K_{n}=\text{GL}_{n}(\mathfrak{o}_{F})$
,
![]() $K_{n}^{1}=1+\text{Mat}_{n,n}(\mathfrak{p}_{F})$
, and let
$K_{n}^{1}=1+\text{Mat}_{n,n}(\mathfrak{p}_{F})$
, and let
![]() $Z_{n}$
be the center of
$Z_{n}$
be the center of
![]() $G_{n}$
. For
$G_{n}$
. For
![]() $g$
in
$g$
in
![]() $G_{n}$
, by abuse of notation, we denote by
$G_{n}$
, by abuse of notation, we denote by
![]() $|g|$
the quantity
$|g|$
the quantity
![]() $|\!\det (g)|$
. Put
$|\!\det (g)|$
. Put
![]() $\unicode[STIX]{x1D702}_{n}=(0~\cdots ~0~1)\in \text{Mat}_{1,n}(F)$
, and let
$\unicode[STIX]{x1D702}_{n}=(0~\cdots ~0~1)\in \text{Mat}_{1,n}(F)$
, and let
![]() $P_{n}$
be the standard mirabolic subgroup of
$P_{n}$
be the standard mirabolic subgroup of
![]() $G_{n}$
, that is, the set of all matrices
$G_{n}$
, that is, the set of all matrices
![]() $g$
in
$g$
in
![]() $G_{n}$
such that
$G_{n}$
such that
![]() $\unicode[STIX]{x1D702}_{n}g=\unicode[STIX]{x1D702}_{n}$
. Let
$\unicode[STIX]{x1D702}_{n}g=\unicode[STIX]{x1D702}_{n}$
. Let
![]() $N_{n}$
be the unipotent radical of the standard Borel subgroup of upper triangular matrices in
$N_{n}$
be the unipotent radical of the standard Borel subgroup of upper triangular matrices in
![]() $G_{n}$
. For
$G_{n}$
. For
![]() $k\in \mathbb{Z}$
, let
$k\in \mathbb{Z}$
, let
![]() $G_{n}^{(k)}=\{g\in G_{n}:~|g|_{F}=q^{-k}\}$
. For any subset
$G_{n}^{(k)}=\{g\in G_{n}:~|g|_{F}=q^{-k}\}$
. For any subset
![]() $X$
of
$X$
of
![]() $G_{n}$
, let
$G_{n}$
, let
![]() $X^{(k)}=X\cap G_{n}^{(k)}$
, and let
$X^{(k)}=X\cap G_{n}^{(k)}$
, and let
![]() $\mathbf{1}_{X}$
denote the characteristic function of
$\mathbf{1}_{X}$
denote the characteristic function of
![]() $X$
.
$X$
.
Let
![]() $\overline{\mathbb{Q}_{\ell }}$
denote an algebraic closure of the
$\overline{\mathbb{Q}_{\ell }}$
denote an algebraic closure of the
![]() $\ell$
-adic numbers,
$\ell$
-adic numbers,
![]() $\overline{\mathbb{Z}_{\ell }}$
denote its ring of integers, and
$\overline{\mathbb{Z}_{\ell }}$
denote its ring of integers, and
![]() $\overline{\mathbb{F}_{\ell }}$
denote its residue field which is an algebraic closure of the finite field of
$\overline{\mathbb{F}_{\ell }}$
denote its residue field which is an algebraic closure of the finite field of
![]() $\ell$
-elements.
$\ell$
-elements.
3 Representations with coefficients in
 $R$
$R$
We only consider smooth
![]() $R$
-representations, that is smooth representations with coefficients in
$R$
-representations, that is smooth representations with coefficients in
![]() $R$
, and we use
$R$
, and we use
![]() $\vee$
as an exponent to denote the contragredient. We call a representation on a
$\vee$
as an exponent to denote the contragredient. We call a representation on a
![]() $\overline{\mathbb{Q}_{\ell }}$
-vector space an
$\overline{\mathbb{Q}_{\ell }}$
-vector space an
![]() $\ell$
-adic representation, and a representation on an
$\ell$
-adic representation, and a representation on an
![]() $\overline{\mathbb{F}_{\ell }}$
-vector space an
$\overline{\mathbb{F}_{\ell }}$
-vector space an
![]() $\ell$
-modular representation. Let
$\ell$
-modular representation. Let
![]() $(\unicode[STIX]{x1D70B},{\mathcal{V}})$
be an irreducible
$(\unicode[STIX]{x1D70B},{\mathcal{V}})$
be an irreducible
![]() $\ell$
-adic representation of
$\ell$
-adic representation of
![]() $G_{n}$
. We call
$G_{n}$
. We call
![]() $\unicode[STIX]{x1D70B}$
integral if
$\unicode[STIX]{x1D70B}$
integral if
![]() ${\mathcal{V}}$
contains a
${\mathcal{V}}$
contains a
![]() $G_{n}$
-stable
$G_{n}$
-stable
![]() $\overline{\mathbb{Z}_{\ell }}$
-lattice. Notice that for an
$\overline{\mathbb{Z}_{\ell }}$
-lattice. Notice that for an
![]() $\ell$
-adic character
$\ell$
-adic character
![]() $\unicode[STIX]{x1D708}:G_{n}\rightarrow \overline{\mathbb{Q}_{\ell }}^{\times }$
this just means that
$\unicode[STIX]{x1D708}:G_{n}\rightarrow \overline{\mathbb{Q}_{\ell }}^{\times }$
this just means that
![]() $\unicode[STIX]{x1D708}$
takes values in
$\unicode[STIX]{x1D708}$
takes values in
![]() $\overline{\mathbb{Z}_{\ell }}^{\times }$
.
$\overline{\mathbb{Z}_{\ell }}^{\times }$
.
An
![]() $R$
-representation is called cuspidal if it is irreducible and never appears as a quotient of a properly parabolically induced representation. By [Reference Vignéras13, II 4.12], a cuspidal
$R$
-representation is called cuspidal if it is irreducible and never appears as a quotient of a properly parabolically induced representation. By [Reference Vignéras13, II 4.12], a cuspidal
![]() $\ell$
-adic representation is integral if and only if its central character is integral, hence the contragredient of a cuspidal
$\ell$
-adic representation is integral if and only if its central character is integral, hence the contragredient of a cuspidal
![]() $\ell$
-adic representation
$\ell$
-adic representation
![]() $\unicode[STIX]{x1D70B}$
is integral if and only if
$\unicode[STIX]{x1D70B}$
is integral if and only if
![]() $\unicode[STIX]{x1D70B}$
is integral. Let
$\unicode[STIX]{x1D70B}$
is integral. Let
![]() $\unicode[STIX]{x1D70B}$
be an integral cuspidal
$\unicode[STIX]{x1D70B}$
be an integral cuspidal
![]() $\ell$
-adic representation and
$\ell$
-adic representation and
![]() $\mathfrak{L}$
be a
$\mathfrak{L}$
be a
![]() $G_{n}$
-stable
$G_{n}$
-stable
![]() $\overline{\mathbb{Z}_{\ell }}$
-lattice in the space of
$\overline{\mathbb{Z}_{\ell }}$
-lattice in the space of
![]() $\unicode[STIX]{x1D70B}$
. Let
$\unicode[STIX]{x1D70B}$
. Let
![]() $r_{\mathfrak{L}}(\unicode[STIX]{x1D70B})$
be the
$r_{\mathfrak{L}}(\unicode[STIX]{x1D70B})$
be the
![]() $\ell$
-modular representation induced on the space
$\ell$
-modular representation induced on the space
![]() $\mathfrak{L}\otimes _{\overline{\mathbb{Z}_{\ell }}}\overline{\mathbb{F}_{\ell }}$
. This
$\mathfrak{L}\otimes _{\overline{\mathbb{Z}_{\ell }}}\overline{\mathbb{F}_{\ell }}$
. This
![]() $\ell$
-modular representation is also cuspidal (and irreducible) by [Reference Vignéras13, III 5.10], and hence independent of the choice of the lattice
$\ell$
-modular representation is also cuspidal (and irreducible) by [Reference Vignéras13, III 5.10], and hence independent of the choice of the lattice
![]() $\mathfrak{L}$
by the Brauer–Nesbitt principle [Reference Vignéras14, Theorem 1], we thus write
$\mathfrak{L}$
by the Brauer–Nesbitt principle [Reference Vignéras14, Theorem 1], we thus write
![]() $r_{\ell }(\unicode[STIX]{x1D70B})$
for
$r_{\ell }(\unicode[STIX]{x1D70B})$
for
![]() $r_{\mathfrak{L}}(\unicode[STIX]{x1D70B})$
and call
$r_{\mathfrak{L}}(\unicode[STIX]{x1D70B})$
and call
![]() $r_{\ell }(\unicode[STIX]{x1D70B})$
the reduction modulo
$r_{\ell }(\unicode[STIX]{x1D70B})$
the reduction modulo
![]() $\ell$
of
$\ell$
of
![]() $\unicode[STIX]{x1D70B}$
. We also say that
$\unicode[STIX]{x1D70B}$
. We also say that
![]() $\unicode[STIX]{x1D70B}$
lifts
$\unicode[STIX]{x1D70B}$
lifts
![]() $r_{\ell }(\unicode[STIX]{x1D70B})$
, and it follows from [Reference Vignéras13, III 5.10] that all cuspidal
$r_{\ell }(\unicode[STIX]{x1D70B})$
, and it follows from [Reference Vignéras13, III 5.10] that all cuspidal
![]() $\ell$
-modular representations lift to cuspidal
$\ell$
-modular representations lift to cuspidal
![]() $\ell$
-adic representations. Following [Reference Mínguez and Sécherre11, Remark 8.15], we call a cuspidal
$\ell$
-adic representations. Following [Reference Mínguez and Sécherre11, Remark 8.15], we call a cuspidal
![]() $\ell$
-modular representation
$\ell$
-modular representation
![]() $\unicode[STIX]{x1D70F}$
banal if
$\unicode[STIX]{x1D70F}$
banal if
![]() $\unicode[STIX]{x1D70F}\not \simeq \unicode[STIX]{x1D70F}\otimes ||_{F}$
(notice that the definition in [Reference Mínguez and Sécherre11, Remark 8.15] refers to a condition given in Proposition 8.9 of this reference, which in the cuspidal case reduces to the condition we give here). For
$\unicode[STIX]{x1D70F}\not \simeq \unicode[STIX]{x1D70F}\otimes ||_{F}$
(notice that the definition in [Reference Mínguez and Sécherre11, Remark 8.15] refers to a condition given in Proposition 8.9 of this reference, which in the cuspidal case reduces to the condition we give here). For
![]() $H$
a closed subgroup of
$H$
a closed subgroup of
![]() $G$
, we write
$G$
, we write
![]() $\text{Ind}_{H}^{G}$
for the functor of smooth induction taking representations of
$\text{Ind}_{H}^{G}$
for the functor of smooth induction taking representations of
![]() $H$
to representations of
$H$
to representations of
![]() $G$
, and write
$G$
, and write
![]() $\text{ind}_{H}^{G}$
for the functor of smooth induction with compact support.
$\text{ind}_{H}^{G}$
for the functor of smooth induction with compact support.
4 Normalization of Haar measures
We now discuss our normalization of Haar measures. The basic reference for
![]() $R$
-Haar measures is [Reference Vignéras14, I 2], but we also refer the reader to [Reference Kurinczuk and Matringe8, Section 2.2] for more details on the splitting of Haar measures with respect to standard decompositions. Let
$R$
-Haar measures is [Reference Vignéras14, I 2], but we also refer the reader to [Reference Kurinczuk and Matringe8, Section 2.2] for more details on the splitting of Haar measures with respect to standard decompositions. Let
![]() $dg$
be the Haar measure on
$dg$
be the Haar measure on
![]() $G_{n}$
normalized to give
$G_{n}$
normalized to give
![]() $K_{n}^{1}$
volume
$K_{n}^{1}$
volume
![]() $1$
.
$1$
.
We normalize the right Haar measure on
![]() $P_{n}$
so that
$P_{n}$
so that
![]() $dp(P_{n}\cap K_{n}^{1})=1$
, on
$dp(P_{n}\cap K_{n}^{1})=1$
, on
![]() $N_{n}$
so that
$N_{n}$
so that
![]() $dn(N_{n}\cap K_{n}^{1})=1$
, and on
$dn(N_{n}\cap K_{n}^{1})=1$
, and on
![]() $Z_{n}$
so that
$Z_{n}$
so that
![]() $dz(Z_{n}\cap K_{n}^{1})=1$
. For the remainder of this section, let
$dz(Z_{n}\cap K_{n}^{1})=1$
. For the remainder of this section, let
![]() $G$
denote a closed subgroup of
$G$
denote a closed subgroup of
![]() $G_{n}$
with Haar measure
$G_{n}$
with Haar measure
![]() $d_{G}g$
. For any open subgroup
$d_{G}g$
. For any open subgroup
![]() $U$
of
$U$
of
![]() $G$
, we define the Haar measure
$G$
, we define the Haar measure
![]() $d_{U}g$
on
$d_{U}g$
on
![]() $U$
as the restriction of
$U$
as the restriction of
![]() $d_{G}g$
, in particular
$d_{G}g$
, in particular
![]() $d_{U}g$
is normalized as soon as
$d_{U}g$
is normalized as soon as
![]() $d_{G}g$
is.
$d_{G}g$
is.
If
![]() $H$
is a closed subgroup of
$H$
is a closed subgroup of
![]() $G$
with right Haar measure
$G$
with right Haar measure
![]() $d_{H}h$
, and such that the modulus character of
$d_{H}h$
, and such that the modulus character of
![]() $G$
restricts to
$G$
restricts to
![]() $H$
as the modulus character of
$H$
as the modulus character of
![]() $H$
, we descend
$H$
, we descend
![]() $d_{G}g$
to a right-invariant measure
$d_{G}g$
to a right-invariant measure
![]() $d_{H\backslash G}g$
on
$d_{H\backslash G}g$
on
![]() $H\backslash G$
as explained in [Reference Vignéras14, I 2.8]. For
$H\backslash G$
as explained in [Reference Vignéras14, I 2.8]. For
![]() $f$
a smooth map from
$f$
a smooth map from
![]() $G$
to
$G$
to
![]() $R$
with compact support, denoting by
$R$
with compact support, denoting by
![]() $f^{H}$
the map on
$f^{H}$
the map on
![]() $H\backslash G$
defined by
$H\backslash G$
defined by
the usual relation is satisfied:
This implies that
![]() $d_{H\backslash G}g$
is normalized as soon as
$d_{H\backslash G}g$
is normalized as soon as
![]() $d_{G}g$
and
$d_{G}g$
and
![]() $d_{H}g$
are.
$d_{H}g$
are.
Indeed, if
![]() $K$
is a compact subgroup of
$K$
is a compact subgroup of
![]() $G$
, applying the equality above to
$G$
, applying the equality above to
![]() $f=\mathbf{1}_{K}$
, so that
$f=\mathbf{1}_{K}$
, so that
gives the relation
This gives for example the normalization
With these normalizations, we have the splitting
This splitting descends on
![]() $N_{n}\backslash G_{n}$
, in which case
$N_{n}\backslash G_{n}$
, in which case
![]() $dg$
denotes the normalized right-invariant measure on
$dg$
denotes the normalized right-invariant measure on
![]() $N_{n}\backslash G_{n}$
and
$N_{n}\backslash G_{n}$
and
![]() $dp$
the right-invariant measure on
$dp$
the right-invariant measure on
![]() $N_{n}\backslash P_{n}$
. Notice that with such normalizations, the volume of all pro-
$N_{n}\backslash P_{n}$
. Notice that with such normalizations, the volume of all pro-
![]() $p$
subgroups of
$p$
subgroups of
![]() $G_{n}$
, of
$G_{n}$
, of
![]() $P_{n}$
and of
$P_{n}$
and of
![]() $Z_{n}$
will be (positive or negative) powers of
$Z_{n}$
will be (positive or negative) powers of
![]() $q$
. Moreover, for such choices, reduction modulo
$q$
. Moreover, for such choices, reduction modulo
![]() $\ell$
commutes with integration (cf. [Reference Kurinczuk and Matringe8, Remark 2.1]), that is, if
$\ell$
commutes with integration (cf. [Reference Kurinczuk and Matringe8, Remark 2.1]), that is, if
![]() $f\in {\mathcal{C}}_{c}^{\infty }(X,\overline{\mathbb{Z}_{\ell }})$
for
$f\in {\mathcal{C}}_{c}^{\infty }(X,\overline{\mathbb{Z}_{\ell }})$
for
![]() $X$
equal to
$X$
equal to
![]() $G_{n}$
or any of the homogeneous spaces
$G_{n}$
or any of the homogeneous spaces
![]() $K\backslash L$
with
$K\backslash L$
with
![]() $L$
a subgroup of
$L$
a subgroup of
![]() $G_{n}$
considered above, then
$G_{n}$
considered above, then
![]() $\int _{X}f(x)\,dx\in \overline{\mathbb{Z}_{\ell }}$
, and
$\int _{X}f(x)\,dx\in \overline{\mathbb{Z}_{\ell }}$
, and
For the rest of this section, we suppose that
![]() $R$
has characteristic zero, and we recall some classical equalities, which all follow from Relation (1).
$R$
has characteristic zero, and we recall some classical equalities, which all follow from Relation (1).
For a finite set
![]() $A$
, we let
$A$
, we let
![]() $|A|$
denote its cardinality in
$|A|$
denote its cardinality in
![]() $R$
. Suppose that
$R$
. Suppose that
![]() $G=K$
compact, and
$G=K$
compact, and
![]() $U$
is an open subgroup of
$U$
is an open subgroup of
![]() $K$
, then
$K$
, then
Finally, if
![]() $V$
is a closed subgroup of
$V$
is a closed subgroup of
![]() $K$
(using the fact that
$K$
(using the fact that
![]() $K$
is unimodular, hence that
$K$
is unimodular, hence that
![]() $d_{K}(UV)=d_{K}(V^{-1}U^{-1})=d_{K}(VU)$
), one obtains
$d_{K}(UV)=d_{K}(V^{-1}U^{-1})=d_{K}(VU)$
), one obtains
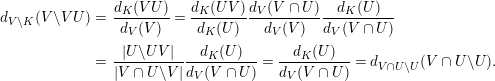 $$\begin{eqnarray}\displaystyle d_{V\backslash K}(V\backslash VU) & = & \displaystyle \frac{d_{K}(VU)}{d_{V}(V)}=\frac{d_{K}(UV)}{d_{K}(U)}\frac{d_{V}(V\cap U)}{d_{V}(V)}\frac{d_{K}(U)}{d_{V}(V\cap U)}\nonumber\\ \displaystyle & = & \displaystyle \frac{|U\backslash UV|}{|V\cap U\backslash V|}\frac{d_{K}(U)}{d_{V}(V\cap U)}=\frac{d_{K}(U)}{d_{V}(V\cap U)}=d_{V\cap U\backslash U}(V\cap U\backslash U).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{V\backslash K}(V\backslash VU) & = & \displaystyle \frac{d_{K}(VU)}{d_{V}(V)}=\frac{d_{K}(UV)}{d_{K}(U)}\frac{d_{V}(V\cap U)}{d_{V}(V)}\frac{d_{K}(U)}{d_{V}(V\cap U)}\nonumber\\ \displaystyle & = & \displaystyle \frac{|U\backslash UV|}{|V\cap U\backslash V|}\frac{d_{K}(U)}{d_{V}(V\cap U)}=\frac{d_{K}(U)}{d_{V}(V\cap U)}=d_{V\cap U\backslash U}(V\cap U\backslash U).\end{eqnarray}$$
By convention, from now on, we use the same letter for the measure on
![]() $G$
and its descent to
$G$
and its descent to
![]() $H\backslash G$
(and when the context is clear for its restriction to an open subgroup as well).
$H\backslash G$
(and when the context is clear for its restriction to an open subgroup as well).
5 Rankin–Selberg integrals and local factors
Let
![]() $\unicode[STIX]{x1D713}$
be an additive character of
$\unicode[STIX]{x1D713}$
be an additive character of
![]() $F$
which is trivial on
$F$
which is trivial on
![]() $\mathfrak{p}_{F}$
, but nontrivial on
$\mathfrak{p}_{F}$
, but nontrivial on
![]() $\mathfrak{o}_{F}$
. By abuse of notation, also denote by
$\mathfrak{o}_{F}$
. By abuse of notation, also denote by
![]() $\unicode[STIX]{x1D713}$
the nondegenerate character of
$\unicode[STIX]{x1D713}$
the nondegenerate character of
![]() $N_{n}$
defined for
$N_{n}$
defined for
![]() $x=(x_{i,j})\in N_{n}$
by
$x=(x_{i,j})\in N_{n}$
by
which is necessarily integral in the
![]() $\ell$
-adic case because
$\ell$
-adic case because
![]() $N_{n}$
is exhausted by its pro-
$N_{n}$
is exhausted by its pro-
![]() $p$
subgroups. If
$p$
subgroups. If
![]() $\unicode[STIX]{x1D70B}$
is a cuspidal representation of
$\unicode[STIX]{x1D70B}$
is a cuspidal representation of
![]() $G_{n}$
, then it is generic (cf. [Reference Bernstein and Zelevinsky1] in the complex or
$G_{n}$
, then it is generic (cf. [Reference Bernstein and Zelevinsky1] in the complex or
![]() $\ell$
-adic case, and [Reference Vignéras13, III 5.10] for
$\ell$
-adic case, and [Reference Vignéras13, III 5.10] for
![]() $R=\overline{\mathbb{F}_{\ell }}$
), meaning
$R=\overline{\mathbb{F}_{\ell }}$
), meaning
![]() $\text{dim}(\text{Hom}_{N_{n}}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713}))=1$
, and hence it has a unique Whittaker model
$\text{dim}(\text{Hom}_{N_{n}}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713}))=1$
, and hence it has a unique Whittaker model
![]() $W(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})$
, equal to the image of
$W(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})$
, equal to the image of
![]() $\unicode[STIX]{x1D70B}$
in
$\unicode[STIX]{x1D70B}$
in
![]() $\text{Ind}_{N_{n}}^{G_{n}}(\unicode[STIX]{x1D713})$
. Suppose that
$\text{Ind}_{N_{n}}^{G_{n}}(\unicode[STIX]{x1D713})$
. Suppose that
![]() $\unicode[STIX]{x1D70B}$
is an integral cuspidal
$\unicode[STIX]{x1D70B}$
is an integral cuspidal
![]() $\ell$
-adic representation of
$\ell$
-adic representation of
![]() $G_{n}$
, then the
$G_{n}$
, then the
![]() $\overline{\mathbb{Z}_{\ell }}$
-submodule
$\overline{\mathbb{Z}_{\ell }}$
-submodule
![]() $W_{e}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})$
of
$W_{e}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})$
of
![]() $W(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})$
consisting of all functions in
$W(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})$
consisting of all functions in
![]() $W(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})$
which take values in
$W(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})$
which take values in
![]() $\overline{\mathbb{Z}_{\ell }}$
is a
$\overline{\mathbb{Z}_{\ell }}$
is a
![]() $G_{n}$
-stable lattice in
$G_{n}$
-stable lattice in
![]() $\unicode[STIX]{x1D70B}$
(cf. [Reference Vignéras14, Theorem 2]). Then by definition
$\unicode[STIX]{x1D70B}$
(cf. [Reference Vignéras14, Theorem 2]). Then by definition
![]() $r_{\ell }(\unicode[STIX]{x1D70B})\simeq W_{e}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})\otimes _{\overline{\mathbb{Z}_{\ell }}}\overline{\mathbb{F}_{\ell }}$
, which is irreducible and cuspidal (cf. Section 2.1 and the references given there). Thus
$r_{\ell }(\unicode[STIX]{x1D70B})\simeq W_{e}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})\otimes _{\overline{\mathbb{Z}_{\ell }}}\overline{\mathbb{F}_{\ell }}$
, which is irreducible and cuspidal (cf. Section 2.1 and the references given there). Thus
![]() $W_{e}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})\otimes _{\overline{\mathbb{Z}_{\ell }}}\overline{\mathbb{F}_{\ell }}$
is a space of Whittaker functions for
$W_{e}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})\otimes _{\overline{\mathbb{Z}_{\ell }}}\overline{\mathbb{F}_{\ell }}$
is a space of Whittaker functions for
![]() $\unicode[STIX]{x1D70B}$
with values in
$\unicode[STIX]{x1D70B}$
with values in
![]() $\overline{\mathbb{F}_{\ell }}$
, hence equal to
$\overline{\mathbb{F}_{\ell }}$
, hence equal to
![]() $W(r_{\ell }(\unicode[STIX]{x1D70B}),r_{\ell }(\unicode[STIX]{x1D713}))$
. For
$W(r_{\ell }(\unicode[STIX]{x1D70B}),r_{\ell }(\unicode[STIX]{x1D713}))$
. For
![]() $W\in W_{e}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})$
, we write
$W\in W_{e}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713})$
, we write
![]() $r_{\ell }(W)$
for the image of
$r_{\ell }(W)$
for the image of
![]() $W$
in
$W$
in
![]() $W(r_{\ell }(\unicode[STIX]{x1D70B}),r_{\ell }(\unicode[STIX]{x1D713}))$
.
$W(r_{\ell }(\unicode[STIX]{x1D70B}),r_{\ell }(\unicode[STIX]{x1D713}))$
.
Finally, we recall the definition of the Rankin–Selberg local
![]() $L$
-factors for a pair of cuspidal
$L$
-factors for a pair of cuspidal
![]() $R$
-representations of
$R$
-representations of
![]() $G_{n}$
. The construction is originally due to Jacquet–Piatetski-Shapiro–Shalika [Reference Jacquet, Piatetski-Shapiro and Shalika5] for complex representations, and works equally well for
$G_{n}$
. The construction is originally due to Jacquet–Piatetski-Shapiro–Shalika [Reference Jacquet, Piatetski-Shapiro and Shalika5] for complex representations, and works equally well for
![]() $\overline{\mathbb{Q}_{\ell }}$
-representations. This construction was extended to a construction for representations over any algebraically closed field of characteristic prime to
$\overline{\mathbb{Q}_{\ell }}$
-representations. This construction was extended to a construction for representations over any algebraically closed field of characteristic prime to
![]() $p$
in [Reference Kurinczuk and Matringe8]. As we are ultimately interested in
$p$
in [Reference Kurinczuk and Matringe8]. As we are ultimately interested in
![]() $\mathbb{C},\overline{\mathbb{Q}_{\ell }}$
and
$\mathbb{C},\overline{\mathbb{Q}_{\ell }}$
and
![]() $\overline{\mathbb{F}_{\ell }}$
representations we give precise references to the construction in [Reference Kurinczuk and Matringe8].
$\overline{\mathbb{F}_{\ell }}$
representations we give precise references to the construction in [Reference Kurinczuk and Matringe8].
Let
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
be cuspidal representations of
$\unicode[STIX]{x1D70B}_{2}$
be cuspidal representations of
![]() $G_{n}$
,
$G_{n}$
,
![]() $W_{1}\in W(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713})$
,
$W_{1}\in W(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713})$
,
![]() $W_{2}\in W(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}^{-1})$
, and
$W_{2}\in W(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}^{-1})$
, and
![]() $\unicode[STIX]{x1D6F7}\in {\mathcal{C}}_{c}^{\infty }(F^{n})$
be a locally constant function from
$\unicode[STIX]{x1D6F7}\in {\mathcal{C}}_{c}^{\infty }(F^{n})$
be a locally constant function from
![]() $F^{n}$
to
$F^{n}$
to
![]() $R$
with compact support. By [Reference Kurinczuk and Matringe8, Proposition 3.3], for
$R$
with compact support. By [Reference Kurinczuk and Matringe8, Proposition 3.3], for
![]() $k\in \mathbb{Z}$
, the coefficients
$k\in \mathbb{Z}$
, the coefficients
are well defined and vanish for
![]() $k$
sufficiently negative. In fact, these coefficients vanish for
$k$
sufficiently negative. In fact, these coefficients vanish for
![]() $k$
sufficiently negative because both
$k$
sufficiently negative because both
![]() $W_{1}$
and
$W_{1}$
and
![]() $W_{2}$
vanish on
$W_{2}$
vanish on
![]() $P_{n}^{(k)}$
for such
$P_{n}^{(k)}$
for such
![]() $k$
, as a consequence of [Reference Jacquet, Piatetski-Shapiro and Shalika5, Proposition 2.2]. Hence the local Rankin–Selberg integral
$k$
, as a consequence of [Reference Jacquet, Piatetski-Shapiro and Shalika5, Proposition 2.2]. Hence the local Rankin–Selberg integral
is a formal Laurent series with coefficients in
![]() $R$
. In fact, by [Reference Kurinczuk and Matringe8, Theorem 3.5],
$R$
. In fact, by [Reference Kurinczuk and Matringe8, Theorem 3.5],
![]() $I(X,W_{1},W_{2},\unicode[STIX]{x1D6F7})\in R(X)$
is a rational function, and as
$I(X,W_{1},W_{2},\unicode[STIX]{x1D6F7})\in R(X)$
is a rational function, and as
![]() $W_{1}$
varies in
$W_{1}$
varies in
![]() $W(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713})$
,
$W(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713})$
,
![]() $W_{2}$
varies in
$W_{2}$
varies in
![]() $W(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}^{-1})$
, and
$W(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}^{-1})$
, and
![]() $\unicode[STIX]{x1D6F7}$
varies in
$\unicode[STIX]{x1D6F7}$
varies in
![]() ${\mathcal{C}}_{c}^{\infty }(F^{n})$
, the
${\mathcal{C}}_{c}^{\infty }(F^{n})$
, the
![]() $R$
-submodule of
$R$
-submodule of
![]() $R(X)$
spanned by
$R(X)$
spanned by
![]() $I(X,W_{1},W_{2},\unicode[STIX]{x1D6F7})$
is a fractional ideal of
$I(X,W_{1},W_{2},\unicode[STIX]{x1D6F7})$
is a fractional ideal of
![]() $R[X^{\pm 1}]$
, and has a unique generator
$R[X^{\pm 1}]$
, and has a unique generator
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
which is an Euler factor. We call
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
which is an Euler factor. We call
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
the local Rankin–Selberg
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
the local Rankin–Selberg
![]() $L$
-factor, and note that it does not depend on the choice of the character
$L$
-factor, and note that it does not depend on the choice of the character
![]() $\unicode[STIX]{x1D713}$
. If
$\unicode[STIX]{x1D713}$
. If
![]() $R=\overline{\mathbb{Q}_{\ell }}$
, it is shown in [Reference Kurinczuk and Matringe8, Corollary 3.6] that the
$R=\overline{\mathbb{Q}_{\ell }}$
, it is shown in [Reference Kurinczuk and Matringe8, Corollary 3.6] that the
![]() $L$
-factor is the inverse of a polynomial in
$L$
-factor is the inverse of a polynomial in
![]() $\overline{\mathbb{Z}_{\ell }}[X]$
, and thus it makes sense to talk of its reduction modulo
$\overline{\mathbb{Z}_{\ell }}[X]$
, and thus it makes sense to talk of its reduction modulo
![]() $\ell$
. Moreover, it follows from [Reference Kurinczuk and Matringe8, Theorem 3.13], that if
$\ell$
. Moreover, it follows from [Reference Kurinczuk and Matringe8, Theorem 3.13], that if
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
are two integral cuspidal
$\unicode[STIX]{x1D70B}_{2}$
are two integral cuspidal
![]() $\ell$
-adic representations of
$\ell$
-adic representations of
![]() $G_{n}$
, then one has
$G_{n}$
, then one has
Now by [Reference Jacquet, Piatetski-Shapiro and Shalika5, Proposition 8.1, (ii)], the
![]() $L$
-factor
$L$
-factor
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is equal to
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is equal to
![]() $1$
unless
$1$
unless
![]() $\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
for some unramified character
$\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
for some unramified character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $F^{\times }$
. Hence if
$F^{\times }$
. Hence if
![]() $\unicode[STIX]{x1D70B}_{2}\not \simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
then
$\unicode[STIX]{x1D70B}_{2}\not \simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
then
![]() $L(X,r_{\ell }(\unicode[STIX]{x1D70B}_{1}),r_{\ell }(\unicode[STIX]{x1D70B}_{2}))=r_{\ell }(L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}))=1$
.
$L(X,r_{\ell }(\unicode[STIX]{x1D70B}_{1}),r_{\ell }(\unicode[STIX]{x1D70B}_{2}))=r_{\ell }(L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}))=1$
.
For our computations to come, we use a decomposition of the Rankin–Selberg integral in the special case where
![]() $\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D70B}_{1}^{\vee }$
, in particular their central characters are inverse of each other. Thus we assume this is the case for the rest of this section. For
$\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D70B}_{1}^{\vee }$
, in particular their central characters are inverse of each other. Thus we assume this is the case for the rest of this section. For
![]() $k\in \mathbb{Z}$
, we set
$k\in \mathbb{Z}$
, we set
which, similarly to
![]() $c_{k}$
, vanishes for
$c_{k}$
, vanishes for
![]() $k$
sufficiently negative, and we put
$k$
sufficiently negative, and we put
Let
![]() $\unicode[STIX]{x1D6F7}\in {\mathcal{C}}_{c}^{\infty }(F^{n})$
be a
$\unicode[STIX]{x1D6F7}\in {\mathcal{C}}_{c}^{\infty }(F^{n})$
be a
![]() $K_{n}$
-invariant function, for
$K_{n}$
-invariant function, for
![]() $i\in \mathbb{Z}$
, we set
$i\in \mathbb{Z}$
, we set
which vanishes for
![]() $i$
sufficiently negative, and we put
$i$
sufficiently negative, and we put
As
![]() $G_{n}^{(k)}=\coprod _{i\in \mathbb{Z}}P_{n}^{(k-ni)}Z_{n}^{(ni)}K_{n}$
, from the splitting of Section 4 we find
$G_{n}^{(k)}=\coprod _{i\in \mathbb{Z}}P_{n}^{(k-ni)}Z_{n}^{(ni)}K_{n}$
, from the splitting of Section 4 we find
from which we deduce
Taking
![]() $\unicode[STIX]{x1D6F7}$
equal to the characteristic function
$\unicode[STIX]{x1D6F7}$
equal to the characteristic function
![]() $\mathbf{1}_{\mathfrak{o}_{F}^{n}}$
, we obtain the formula
$\mathbf{1}_{\mathfrak{o}_{F}^{n}}$
, we obtain the formula
The equality
![]() $Z(X,\mathbf{1}_{\mathfrak{o}_{F}^{n}})=(q-1/1-X^{n})$
is standard (cf. [Reference Mínguez10, Theorem 3.1]) except that in our setting, we get the extra constant
$Z(X,\mathbf{1}_{\mathfrak{o}_{F}^{n}})=(q-1/1-X^{n})$
is standard (cf. [Reference Mínguez10, Theorem 3.1]) except that in our setting, we get the extra constant
![]() $q-1$
from our choice of normalization on
$q-1$
from our choice of normalization on
![]() $Z_{n}$
, as we set
$Z_{n}$
, as we set
![]() $dz(Z_{n}\cap K_{n}^{1})=1$
instead of the usual
$dz(Z_{n}\cap K_{n}^{1})=1$
instead of the usual
![]() $dz(Z_{n}\cap K_{n})=1$
.
$dz(Z_{n}\cap K_{n})=1$
.
6 Simple types and reduction modulo
 $\ell$
$\ell$
For the beginning of this section we assume that
![]() $R=\mathbb{C}$
or
$R=\mathbb{C}$
or
![]() $\overline{\mathbb{Q}_{\ell }}$
. Let
$\overline{\mathbb{Q}_{\ell }}$
. Let
![]() $V$
be an
$V$
be an
![]() $n$
-dimensional
$n$
-dimensional
![]() $F$
-vector space, let
$F$
-vector space, let
![]() $\text{End}_{F}(V)$
denote the
$\text{End}_{F}(V)$
denote the
![]() $F$
-algebra
$F$
-algebra
![]() $\text{End}_{F}(V)$
of
$\text{End}_{F}(V)$
of
![]() $F$
-endomorphisms of
$F$
-endomorphisms of
![]() $V$
and let
$V$
and let
![]() $G$
denote the group
$G$
denote the group
![]() $\text{Aut}_{F}(V)$
of
$\text{Aut}_{F}(V)$
of
![]() $F$
-automorphisms of
$F$
-automorphisms of
![]() $V$
. Hence
$V$
. Hence
![]() $G$
identifies with
$G$
identifies with
![]() $G_{n}$
as soon as we choose a basis of
$G_{n}$
as soon as we choose a basis of
![]() $V$
. In [Reference Bushnell and Kutzko2], every cuspidal
$V$
. In [Reference Bushnell and Kutzko2], every cuspidal
![]() $R$
-representation of
$R$
-representation of
![]() $G$
is constructed explicitly as
$G$
is constructed explicitly as
![]() $\text{ind}_{\mathbf{J}}^{G}(\unicode[STIX]{x1D6EC})$
, where
$\text{ind}_{\mathbf{J}}^{G}(\unicode[STIX]{x1D6EC})$
, where
![]() $\mathbf{J}$
is an open and compact-mod-center subgroup of
$\mathbf{J}$
is an open and compact-mod-center subgroup of
![]() $G$
, and
$G$
, and
![]() $\unicode[STIX]{x1D6EC}$
is an irreducible representation of
$\unicode[STIX]{x1D6EC}$
is an irreducible representation of
![]() $\mathbf{J}$
of finite dimension. The pairs
$\mathbf{J}$
of finite dimension. The pairs
![]() $(\mathbf{J},\unicode[STIX]{x1D6EC})$
are called extended maximal simple types, and for any such pair
$(\mathbf{J},\unicode[STIX]{x1D6EC})$
are called extended maximal simple types, and for any such pair
![]() $\text{ind}_{\mathbf{J}}^{G}(\unicode[STIX]{x1D6EC})$
is (irreducible and) cuspidal by [Reference Bushnell and Kutzko2, Chapter 6]. We briefly explain the construction of the group
$\text{ind}_{\mathbf{J}}^{G}(\unicode[STIX]{x1D6EC})$
is (irreducible and) cuspidal by [Reference Bushnell and Kutzko2, Chapter 6]. We briefly explain the construction of the group
![]() $\mathbf{J}$
, focusing on the properties which we shall use.
$\mathbf{J}$
, focusing on the properties which we shall use.
An
![]() $\mathfrak{o}_{F}$
-lattice chain
$\mathfrak{o}_{F}$
-lattice chain
![]() ${\mathcal{L}}$
in
${\mathcal{L}}$
in
![]() $V$
is a nonempty set of
$V$
is a nonempty set of
![]() $\mathfrak{o}_{F}$
-lattices
$\mathfrak{o}_{F}$
-lattices
![]() $\{L_{i}:i\in \mathbb{Z}\}$
such that, for all
$\{L_{i}:i\in \mathbb{Z}\}$
such that, for all
![]() $i\in \mathbb{Z}$
,
$i\in \mathbb{Z}$
,
![]() $L_{i+1}\subsetneq L_{i}$
and there exists
$L_{i+1}\subsetneq L_{i}$
and there exists
![]() $e({\mathcal{L}})\in \mathbb{Z}$
such that
$e({\mathcal{L}})\in \mathbb{Z}$
such that
![]() $L_{i+e({\mathcal{L}})}=\unicode[STIX]{x1D71B}_{F}L_{i}$
. The construction of [Reference Bushnell and Kutzko2], starts with data
$L_{i+e({\mathcal{L}})}=\unicode[STIX]{x1D71B}_{F}L_{i}$
. The construction of [Reference Bushnell and Kutzko2], starts with data
![]() $(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
called maximal simple strata consisting of
$(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
called maximal simple strata consisting of
(1) an element
 $\unicode[STIX]{x1D6FD}\in \text{End}_{F}(V)$
which generates a simple field extension
$\unicode[STIX]{x1D6FD}\in \text{End}_{F}(V)$
which generates a simple field extension
 $E=F[\unicode[STIX]{x1D6FD}]$
;
$E=F[\unicode[STIX]{x1D6FD}]$
;(2) an
 $\mathfrak{o}_{F}$
-lattice chain
$\mathfrak{o}_{F}$
-lattice chain
 ${\mathcal{L}}$
in
${\mathcal{L}}$
in
 $V$
such that
$V$
such that
 $E^{\times }{\mathcal{L}}\subset {\mathcal{L}}$
(i.e., for any
$E^{\times }{\mathcal{L}}\subset {\mathcal{L}}$
(i.e., for any
 $x\in E^{\times }$
and
$x\in E^{\times }$
and
 $L\in {\mathcal{L}}$
we have
$L\in {\mathcal{L}}$
we have
 $xL\in {\mathcal{L}}$
); in particular
$xL\in {\mathcal{L}}$
); in particular
 ${\mathcal{L}}$
is an
${\mathcal{L}}$
is an
 $\mathfrak{o}_{E}$
-lattice chain, and it is required (as
$\mathfrak{o}_{E}$
-lattice chain, and it is required (as
 $(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
is maximal) that
$(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
is maximal) that
 $L_{i+1}=\unicode[STIX]{x1D71B}_{E}L_{i}$
;
$L_{i+1}=\unicode[STIX]{x1D71B}_{E}L_{i}$
;
which satisfy a technical condition (cf. [Reference Bushnell and Kutzko2, 1.5.5] where the simple strata we consider are among those denoted
![]() $[\mathfrak{A},-,0,\unicode[STIX]{x1D6FD}]$
).
$[\mathfrak{A},-,0,\unicode[STIX]{x1D6FD}]$
).
Let
![]() $(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
be a maximal simple strata. We denote by
$(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
be a maximal simple strata. We denote by
![]() $\mathfrak{A}=\mathfrak{A}({\mathcal{L}})$
the
$\mathfrak{A}=\mathfrak{A}({\mathcal{L}})$
the
![]() $\mathfrak{o}_{F}$
-order in
$\mathfrak{o}_{F}$
-order in
![]() $\text{End}_{F}(V)$
and
$\text{End}_{F}(V)$
and
![]() $\mathfrak{B}=\mathfrak{B}(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
the
$\mathfrak{B}=\mathfrak{B}(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
the
![]() $\mathfrak{o}_{E}$
-order in
$\mathfrak{o}_{E}$
-order in
![]() $\text{End}_{E}(V)$
defined by
$\text{End}_{E}(V)$
defined by
![]() ${\mathcal{L}}$
,
${\mathcal{L}}$
,
In [Reference Bushnell and Kutzko2, 3.1] Bushnell–Kutzko define compact open subgroups of
![]() $G$
denoted by
$G$
denoted by
![]() $H^{1}=H^{1}(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
,
$H^{1}=H^{1}(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
,
![]() $J^{1}=J^{1}(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
, and
$J^{1}=J^{1}(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
, and
![]() $J=J(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
. The properties we need are:
$J=J(\unicode[STIX]{x1D6FD},{\mathcal{L}})$
. The properties we need are:
(1) the groups
 $H^{1}\leqslant J^{1}$
are pro-
$H^{1}\leqslant J^{1}$
are pro-
 $p$
(by definition), are normalized by
$p$
(by definition), are normalized by
 $E^{\times }$
and are normal subgroups of
$E^{\times }$
and are normal subgroups of
 $J$
by [Reference Bushnell and Kutzko2, 3.1.15], moreover
$J$
by [Reference Bushnell and Kutzko2, 3.1.15], moreover
 $J\subset \text{Aut}_{\mathfrak{o}_{F}}(L_{0})$
(by definition).
$J\subset \text{Aut}_{\mathfrak{o}_{F}}(L_{0})$
(by definition).(2) Put
 $m=n/[E:F]$
, by [Reference Bushnell and Kutzko2, 3.1.15] we have
$m=n/[E:F]$
, by [Reference Bushnell and Kutzko2, 3.1.15] we have  $$\begin{eqnarray}\displaystyle J & = & \displaystyle \mathfrak{B}^{\times }J^{1},\qquad \mathfrak{B}^{\times }\cap J^{1}=1+\unicode[STIX]{x1D71B}_{E}\mathfrak{B}\qquad \text{and}\qquad \nonumber\\ \displaystyle & & \displaystyle J/J^{1}\simeq \mathfrak{B}^{\times }/(1+\unicode[STIX]{x1D71B}_{E}\mathfrak{B})\simeq G_{m}(k_{E}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J & = & \displaystyle \mathfrak{B}^{\times }J^{1},\qquad \mathfrak{B}^{\times }\cap J^{1}=1+\unicode[STIX]{x1D71B}_{E}\mathfrak{B}\qquad \text{and}\qquad \nonumber\\ \displaystyle & & \displaystyle J/J^{1}\simeq \mathfrak{B}^{\times }/(1+\unicode[STIX]{x1D71B}_{E}\mathfrak{B})\simeq G_{m}(k_{E}).\nonumber\end{eqnarray}$$
We then set
![]() $\mathbf{J}=\mathbf{J}(\unicode[STIX]{x1D6FD},{\mathcal{L}})=E^{\times }J$
, in particular
$\mathbf{J}=\mathbf{J}(\unicode[STIX]{x1D6FD},{\mathcal{L}})=E^{\times }J$
, in particular
![]() $\mathbf{J}$
is compact mod
$\mathbf{J}$
is compact mod
![]() $E^{\times }$
and hence compact mod
$E^{\times }$
and hence compact mod
![]() $F^{\times }$
. Notice that if
$F^{\times }$
. Notice that if
![]() $\unicode[STIX]{x1D70B}\simeq \text{ind}_{\mathbf{J}}^{G}\unicode[STIX]{x1D6EC}$
, the center
$\unicode[STIX]{x1D70B}\simeq \text{ind}_{\mathbf{J}}^{G}\unicode[STIX]{x1D6EC}$
, the center
![]() $F^{\times }$
of
$F^{\times }$
of
![]() $G$
acts by the central character
$G$
acts by the central character
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
of
![]() $\unicode[STIX]{x1D70B}$
through
$\unicode[STIX]{x1D70B}$
through
![]() $\unicode[STIX]{x1D6EC}$
. Finally, we note that the construction of
$\unicode[STIX]{x1D6EC}$
. Finally, we note that the construction of
![]() $\unicode[STIX]{x1D6EC}$
depends on our fixed additive character
$\unicode[STIX]{x1D6EC}$
depends on our fixed additive character
![]() $\unicode[STIX]{x1D713}$
(cf. [Reference Bushnell and Kutzko2, 3.2]).
$\unicode[STIX]{x1D713}$
(cf. [Reference Bushnell and Kutzko2, 3.2]).
The definitions above do not include the groups of the maximal simple types for level zero cuspidal representations (see [Reference Bushnell and Kutzko2, 5.5.10(b)]), although these can be considered formally as part of the construction described above for the maximal zero strata
![]() $(0,{\mathcal{L}})$
with
$(0,{\mathcal{L}})$
with
![]() $\unicode[STIX]{x1D6FD}=0$
and
$\unicode[STIX]{x1D6FD}=0$
and
![]() $e({\mathcal{L}})=1$
. In this case, we put
$e({\mathcal{L}})=1$
. In this case, we put
![]() $J=\mathfrak{A}^{\times }$
,
$J=\mathfrak{A}^{\times }$
,
![]() $\mathbf{J}=F^{\times }J$
,
$\mathbf{J}=F^{\times }J$
,
![]() $H^{1}=J^{1}=1+\unicode[STIX]{x1D71B}_{F}\mathfrak{A}$
, and
$H^{1}=J^{1}=1+\unicode[STIX]{x1D71B}_{F}\mathfrak{A}$
, and
![]() $J/J^{1}=\mathfrak{A}^{\times }/(1+\unicode[STIX]{x1D71B}_{F}\mathfrak{A})\simeq G_{n}(k_{F})$
.
$J/J^{1}=\mathfrak{A}^{\times }/(1+\unicode[STIX]{x1D71B}_{F}\mathfrak{A})\simeq G_{n}(k_{F})$
.
Now we consider
![]() $\overline{\mathbb{F}_{\ell }}$
-representations. It follows from [Reference Vignéras13, Chapitre IV] that the Bushnell–Kutzko classification of cuspidal
$\overline{\mathbb{F}_{\ell }}$
-representations. It follows from [Reference Vignéras13, Chapitre IV] that the Bushnell–Kutzko classification of cuspidal
![]() $\overline{\mathbb{Q}_{\ell }}$
-representations adapts well to
$\overline{\mathbb{Q}_{\ell }}$
-representations adapts well to
![]() $\overline{\mathbb{F}_{\ell }}$
-representations. We only need to know the following facts:
$\overline{\mathbb{F}_{\ell }}$
-representations. We only need to know the following facts:
Let
![]() $\unicode[STIX]{x1D70F}$
be a cuspidal
$\unicode[STIX]{x1D70F}$
be a cuspidal
![]() $\ell$
-modular representation of
$\ell$
-modular representation of
![]() $G$
. As we recalled in Section 3, there exists an integral cuspidal
$G$
. As we recalled in Section 3, there exists an integral cuspidal
![]() $\ell$
-adic representation
$\ell$
-adic representation
![]() $\unicode[STIX]{x1D70B}$
such that
$\unicode[STIX]{x1D70B}$
such that
![]() $\unicode[STIX]{x1D70F}=r_{\ell }(\unicode[STIX]{x1D70B})$
. Choose an extended maximal simple type
$\unicode[STIX]{x1D70F}=r_{\ell }(\unicode[STIX]{x1D70B})$
. Choose an extended maximal simple type
![]() $(\mathbf{J},\unicode[STIX]{x1D6EC})$
such that
$(\mathbf{J},\unicode[STIX]{x1D6EC})$
such that
![]() $\unicode[STIX]{x1D70B}\simeq \text{ind}_{\mathbf{J}}^{G}(\unicode[STIX]{x1D6EC})$
, as in the beginning of this section. A cuspidal
$\unicode[STIX]{x1D70B}\simeq \text{ind}_{\mathbf{J}}^{G}(\unicode[STIX]{x1D6EC})$
, as in the beginning of this section. A cuspidal
![]() $\ell$
-adic representation is integral if and only if its central character
$\ell$
-adic representation is integral if and only if its central character
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
is integral, by [Reference Vignéras13, II 4.13] (the direction integral implies integral central character being clear). We recall why this is true. First as
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
is integral, by [Reference Vignéras13, II 4.13] (the direction integral implies integral central character being clear). We recall why this is true. First as
![]() $\mathbf{J}$
is compact mod
$\mathbf{J}$
is compact mod
![]() $F^{\times }$
, we claim that the irreducible representation
$F^{\times }$
, we claim that the irreducible representation
![]() $\unicode[STIX]{x1D6EC}$
is integral if and only if
$\unicode[STIX]{x1D6EC}$
is integral if and only if
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
is integral. Again, one direction is clear. For the other, suppose that
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
is integral. Again, one direction is clear. For the other, suppose that
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
is integral and choose a random not necessarily
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
is integral and choose a random not necessarily
![]() $\mathbf{J}$
-stable lattice
$\mathbf{J}$
-stable lattice
![]() $\mathfrak{L}_{0}$
in the space
$\mathfrak{L}_{0}$
in the space
![]() $V_{\unicode[STIX]{x1D6EC}}$
of
$V_{\unicode[STIX]{x1D6EC}}$
of
![]() $\unicode[STIX]{x1D6EC}$
. It is stabilized by a compact open subgroup
$\unicode[STIX]{x1D6EC}$
. It is stabilized by a compact open subgroup
![]() $U$
of
$U$
of
![]() $\mathbf{J}$
, and choosing representatives
$\mathbf{J}$
, and choosing representatives
![]() $c_{1},\ldots ,c_{r}$
of
$c_{1},\ldots ,c_{r}$
of
![]() $\mathbf{J}/F^{\times }U$
, one has
$\mathbf{J}/F^{\times }U$
, one has
![]() $\unicode[STIX]{x1D6EC}(\mathbf{J})(\mathfrak{L}_{0})=\sum _{i=1}^{r}\unicode[STIX]{x1D6EC}(c_{i})(\mathfrak{L}_{0})$
, hence
$\unicode[STIX]{x1D6EC}(\mathbf{J})(\mathfrak{L}_{0})=\sum _{i=1}^{r}\unicode[STIX]{x1D6EC}(c_{i})(\mathfrak{L}_{0})$
, hence
![]() $\mathfrak{L}_{\unicode[STIX]{x1D6EC}}=\unicode[STIX]{x1D6EC}(\mathbf{J})(\mathfrak{L}_{0})$
is a
$\mathfrak{L}_{\unicode[STIX]{x1D6EC}}=\unicode[STIX]{x1D6EC}(\mathbf{J})(\mathfrak{L}_{0})$
is a
![]() $\mathbf{J}$
-stable lattice in
$\mathbf{J}$
-stable lattice in
![]() $V_{\unicode[STIX]{x1D6EC}}$
by [Reference Vignéras13, 9.3]. The induced
$V_{\unicode[STIX]{x1D6EC}}$
by [Reference Vignéras13, 9.3]. The induced
![]() $\overline{\mathbb{Z}_{\ell }}$
-representation
$\overline{\mathbb{Z}_{\ell }}$
-representation
![]() $\text{ind}_{\mathbf{J}}^{G}(\mathfrak{L}_{\unicode[STIX]{x1D6EC}})$
is then a lattice in
$\text{ind}_{\mathbf{J}}^{G}(\mathfrak{L}_{\unicode[STIX]{x1D6EC}})$
is then a lattice in
![]() $\unicode[STIX]{x1D70B}$
by [Reference Vignéras13, 9.3]. Moreover
$\unicode[STIX]{x1D70B}$
by [Reference Vignéras13, 9.3]. Moreover
![]() $\unicode[STIX]{x1D70F}=r_{\ell }(\unicode[STIX]{x1D70B})\simeq \text{ind}_{\mathbf{J}}^{G}(r_{\ell }(\unicode[STIX]{x1D6EC}))$
, and
$\unicode[STIX]{x1D70F}=r_{\ell }(\unicode[STIX]{x1D70B})\simeq \text{ind}_{\mathbf{J}}^{G}(r_{\ell }(\unicode[STIX]{x1D6EC}))$
, and
![]() $r_{\ell }(\unicode[STIX]{x1D6EC})$
is an irreducible representation of
$r_{\ell }(\unicode[STIX]{x1D6EC})$
is an irreducible representation of
![]() $\mathbf{J}$
by irreducibility of
$\mathbf{J}$
by irreducibility of
![]() $\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70F}$
.
Finally, we give another characterization of banal cuspidal representations: recall, from Section 3, by definition
![]() $\unicode[STIX]{x1D70F}$
is banal if and only if the cardinality of the cuspidal line
$\unicode[STIX]{x1D70F}$
is banal if and only if the cardinality of the cuspidal line
![]() $\mathbb{Z}_{\unicode[STIX]{x1D70F}}=\{||^{k}\unicode[STIX]{x1D70F},~k\in \mathbb{Z}\}$
is greater than
$\mathbb{Z}_{\unicode[STIX]{x1D70F}}=\{||^{k}\unicode[STIX]{x1D70F},~k\in \mathbb{Z}\}$
is greater than
![]() $1$
. By [Reference Mínguez and Sécherre11, Lemme 5.3], this cardinality is the same as the integer
$1$
. By [Reference Mínguez and Sécherre11, Lemme 5.3], this cardinality is the same as the integer
![]() $o(\unicode[STIX]{x1D70F})$
introduced in [Reference Mínguez and Sécherre11, Section 5.2, (5.4)]. From [Reference Mínguez and Sécherre11, Section 5.2, (5.4)],
$o(\unicode[STIX]{x1D70F})$
introduced in [Reference Mínguez and Sécherre11, Section 5.2, (5.4)]. From [Reference Mínguez and Sécherre11, Section 5.2, (5.4)],
![]() $o(\unicode[STIX]{x1D70F})$
is the order of
$o(\unicode[STIX]{x1D70F})$
is the order of
![]() $q^{n/e}$
in
$q^{n/e}$
in
![]() $\overline{\mathbb{F}_{\ell }}^{\times }$
, where
$\overline{\mathbb{F}_{\ell }}^{\times }$
, where
![]() $e=e(E/F)$
is the ramification index attached to
$e=e(E/F)$
is the ramification index attached to
![]() $(\mathbf{J},\unicode[STIX]{x1D6EC})$
which in particular does not depend on the choice of extended maximal simple type. Hence
$(\mathbf{J},\unicode[STIX]{x1D6EC})$
which in particular does not depend on the choice of extended maximal simple type. Hence
![]() $\unicode[STIX]{x1D70F}$
is banal if and only if
$\unicode[STIX]{x1D70F}$
is banal if and only if
![]() $q^{n/e}-1\neq 0$
in
$q^{n/e}-1\neq 0$
in
![]() $\overline{\mathbb{F}_{\ell }}$
.
$\overline{\mathbb{F}_{\ell }}$
.
7 The modified Paskunas–Stevens basis
For this section
![]() $R=\mathbb{C}$
or
$R=\mathbb{C}$
or
![]() $\overline{\mathbb{Q}_{\ell }}$
. Let
$\overline{\mathbb{Q}_{\ell }}$
. Let
![]() $\unicode[STIX]{x1D70B}$
be a cuspidal
$\unicode[STIX]{x1D70B}$
be a cuspidal
![]() $R$
-representation of
$R$
-representation of
![]() $G$
and
$G$
and
![]() $(\mathbf{J}=\mathbf{J}(\unicode[STIX]{x1D6FD},{\mathcal{L}}),\unicode[STIX]{x1D6EC})$
be an extended maximal simple type in
$(\mathbf{J}=\mathbf{J}(\unicode[STIX]{x1D6FD},{\mathcal{L}}),\unicode[STIX]{x1D6EC})$
be an extended maximal simple type in
![]() $\unicode[STIX]{x1D70B}$
. According to [Reference Paskunas and Stevens12, Corollaries 3.4 and 4.13], there exists an
$\unicode[STIX]{x1D70B}$
. According to [Reference Paskunas and Stevens12, Corollaries 3.4 and 4.13], there exists an
![]() $F$
-basis
$F$
-basis
![]() ${\mathcal{B}}=(v_{1},\ldots ,v_{n})$
of
${\mathcal{B}}=(v_{1},\ldots ,v_{n})$
of
![]() $V$
particularly suited to relating the Whittaker model of
$V$
particularly suited to relating the Whittaker model of
![]() $\unicode[STIX]{x1D70B}$
and the model
$\unicode[STIX]{x1D70B}$
and the model
![]() $\text{ind}_{\mathbf{J}}^{G}(\unicode[STIX]{x1D6EC})$
defined via type theory. In particular,
$\text{ind}_{\mathbf{J}}^{G}(\unicode[STIX]{x1D6EC})$
defined via type theory. In particular,
![]() ${\mathcal{B}}$
splits
${\mathcal{B}}$
splits
![]() ${\mathcal{L}}$
, that is,
${\mathcal{L}}$
, that is,
![]() $L_{k}=\bigoplus _{i=1}^{n}\mathfrak{p}_{F}^{a_{i}(k)}v_{i}$
with
$L_{k}=\bigoplus _{i=1}^{n}\mathfrak{p}_{F}^{a_{i}(k)}v_{i}$
with
![]() $a_{i}(k)\in \mathbb{Z}$
for all
$a_{i}(k)\in \mathbb{Z}$
for all
![]() $k\in \mathbb{Z}$
, and is such that if
$k\in \mathbb{Z}$
, and is such that if
![]() $N$
is the maximal unipotent subgroup of
$N$
is the maximal unipotent subgroup of
![]() $G$
attached to the maximal flag defined by
$G$
attached to the maximal flag defined by
![]() ${\mathcal{B}}$
, and if
${\mathcal{B}}$
, and if
![]() $\unicode[STIX]{x1D713}$
, by abuse of notation, denotes the nondegenerate character of
$\unicode[STIX]{x1D713}$
, by abuse of notation, denotes the nondegenerate character of
![]() $N$
defined for
$N$
defined for
![]() $x\in N$
by
$x\in N$
by
where
![]() $\text{Mat}_{{\mathcal{B}}}(x)$
denotes the matrix of
$\text{Mat}_{{\mathcal{B}}}(x)$
denotes the matrix of
![]() $x$
with respect to the basis
$x$
with respect to the basis
![]() ${\mathcal{B}}$
, then the triple
${\mathcal{B}}$
, then the triple
![]() $(J,\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D713})$
satisfies
$(J,\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D713})$
satisfies
Let
![]() $P$
be the mirabolic subgroup defined by
$P$
be the mirabolic subgroup defined by
We put
![]() ${\mathcal{M}}=(P\cap J)J^{1}$
, which is a group as
${\mathcal{M}}=(P\cap J)J^{1}$
, which is a group as
![]() $J^{1}$
is normal in
$J^{1}$
is normal in
![]() $J$
. It follows from [Reference Paskunas and Stevens12] that the image of
$J$
. It follows from [Reference Paskunas and Stevens12] that the image of
![]() ${\mathcal{M}}$
in
${\mathcal{M}}$
in
![]() $J/J^{1}\simeq G_{m}(k_{E})$
is isomorphic to
$J/J^{1}\simeq G_{m}(k_{E})$
is isomorphic to
![]() $P_{m}(k_{E})$
. We now explain how to extract this from [Reference Paskunas and Stevens12]: in the notation of [Reference Paskunas and Stevens12], our group
$P_{m}(k_{E})$
. We now explain how to extract this from [Reference Paskunas and Stevens12]: in the notation of [Reference Paskunas and Stevens12], our group
![]() $P$
is denoted
$P$
is denoted
![]() ${\mathcal{M}}_{F}$
and [Reference Paskunas and Stevens12, Corollary 4.8] shows that
${\mathcal{M}}_{F}$
and [Reference Paskunas and Stevens12, Corollary 4.8] shows that
In [Reference Paskunas and Stevens12, Section 4.1], Paskunas–Stevens introduce another mirabolic group they denote by
![]() ${\mathcal{M}}_{E}$
which satisfies
${\mathcal{M}}_{E}$
which satisfies
![]() $P\cap \mathfrak{B}^{\times }={\mathcal{M}}_{E}\cap \mathfrak{B}^{\times }$
by the equality just before [Reference Paskunas and Stevens12, Corollary 4.7], and they also denote by
$P\cap \mathfrak{B}^{\times }={\mathcal{M}}_{E}\cap \mathfrak{B}^{\times }$
by the equality just before [Reference Paskunas and Stevens12, Corollary 4.7], and they also denote by
![]() ${\mathcal{M}}_{\mathfrak{B}}$
the group
${\mathcal{M}}_{\mathfrak{B}}$
the group
![]() $({\mathcal{M}}_{E}\cap \mathfrak{B}^{\times })(1+\unicode[STIX]{x1D71B}_{E}\mathfrak{B})$
. Hence Equation (5) gives
$({\mathcal{M}}_{E}\cap \mathfrak{B}^{\times })(1+\unicode[STIX]{x1D71B}_{E}\mathfrak{B})$
. Hence Equation (5) gives
![]() ${\mathcal{M}}={\mathcal{M}}_{\mathfrak{B}}J^{1}$
as
${\mathcal{M}}={\mathcal{M}}_{\mathfrak{B}}J^{1}$
as
![]() $(1+\unicode[STIX]{x1D71B}_{E}\mathfrak{B})=\mathfrak{B}^{\times }\cap J^{1}$
. Finally, from the discussion after the proof of [Reference Paskunas and Stevens12, Lemma 4.10], the image of
$(1+\unicode[STIX]{x1D71B}_{E}\mathfrak{B})=\mathfrak{B}^{\times }\cap J^{1}$
. Finally, from the discussion after the proof of [Reference Paskunas and Stevens12, Lemma 4.10], the image of
![]() ${\mathcal{M}}_{\mathfrak{B}}$
in
${\mathcal{M}}_{\mathfrak{B}}$
in
![]() $\mathfrak{B}^{\times }/1+\unicode[STIX]{x1D71B}_{E}\mathfrak{B}\simeq G_{m}(k_{E})$
is isomorphic to
$\mathfrak{B}^{\times }/1+\unicode[STIX]{x1D71B}_{E}\mathfrak{B}\simeq G_{m}(k_{E})$
is isomorphic to
![]() $P_{m}(k_{E})$
, hence the same is true for the image of
$P_{m}(k_{E})$
, hence the same is true for the image of
![]() ${\mathcal{M}}$
in
${\mathcal{M}}$
in
![]() $J/J^{1}\simeq \mathfrak{B}^{\times }/1+\unicode[STIX]{x1D71B}_{E}\mathfrak{B}\simeq G_{m}(k_{E})$
. In particular, the following index will appear in our computation:
$J/J^{1}\simeq \mathfrak{B}^{\times }/1+\unicode[STIX]{x1D71B}_{E}\mathfrak{B}\simeq G_{m}(k_{E})$
. In particular, the following index will appear in our computation:
For
![]() $i\in \{1,\ldots ,n\}$
, the functions
$i\in \{1,\ldots ,n\}$
, the functions
![]() $a_{i}:\mathbb{Z}\rightarrow \mathbb{Z}$
satisfy the relation
$a_{i}:\mathbb{Z}\rightarrow \mathbb{Z}$
satisfy the relation
![]() $a_{i+e}(k)=a_{i}(k)+1$
. In particular, this holds for
$a_{i+e}(k)=a_{i}(k)+1$
. In particular, this holds for
![]() $i=n$
, and the map
$i=n$
, and the map
![]() $k\mapsto a_{n}(k)$
is increasing with values in
$k\mapsto a_{n}(k)$
is increasing with values in
![]() $\mathbb{Z}$
, so there is
$\mathbb{Z}$
, so there is
![]() $k_{0}$
between
$k_{0}$
between
![]() $1$
and
$1$
and
![]() $e$
such that
$e$
such that
![]() $a_{n}(k_{0})=a_{n}(k_{0}-1)+1$
, and then
$a_{n}(k_{0})=a_{n}(k_{0}-1)+1$
, and then
![]() $a_{n}(k_{0}+i)=a_{n}(k_{0})$
for
$a_{n}(k_{0}+i)=a_{n}(k_{0})$
for
![]() $i\in \{0,\ldots ,e-1\}$
. Hence by reindexing the lattice chain
$i\in \{0,\ldots ,e-1\}$
. Hence by reindexing the lattice chain
![]() ${\mathcal{L}}$
if necessary, by a translation,
${\mathcal{L}}$
if necessary, by a translation,
![]() $k\mapsto k-k_{0}$
, we can suppose that
$k\mapsto k-k_{0}$
, we can suppose that
We recall that
![]() $L_{0}=\bigoplus _{i=1}^{n}\mathfrak{p}_{F}^{a_{i}(0)}v_{i}$
, and we set
$L_{0}=\bigoplus _{i=1}^{n}\mathfrak{p}_{F}^{a_{i}(0)}v_{i}$
, and we set
![]() ${\mathcal{B}}^{\prime }=(\unicode[STIX]{x1D71B}_{F}^{a_{1}(0)}v_{1},\ldots ,\unicode[STIX]{x1D71B}_{F}^{a_{n}(0)}v_{n})$
, which we write as
${\mathcal{B}}^{\prime }=(\unicode[STIX]{x1D71B}_{F}^{a_{1}(0)}v_{1},\ldots ,\unicode[STIX]{x1D71B}_{F}^{a_{n}(0)}v_{n})$
, which we write as
![]() ${\mathcal{B}}^{\prime }=(w_{1},\ldots ,w_{n})$
.
${\mathcal{B}}^{\prime }=(w_{1},\ldots ,w_{n})$
.
We use this basis to identify
![]() $G$
with
$G$
with
![]() $G_{n}$
. With this choice, one has
$G_{n}$
. With this choice, one has
![]() $J\subset K_{n}$
because
$J\subset K_{n}$
because
![]() $J\subset \text{Aut}_{\mathfrak{o}_{F}}(L_{0})$
. The group
$J\subset \text{Aut}_{\mathfrak{o}_{F}}(L_{0})$
. The group
![]() $P$
identifies with
$P$
identifies with
![]() $P_{n}$
, the group
$P_{n}$
, the group
![]() $N$
identifies with
$N$
identifies with
![]() $N_{n}$
, and the character
$N_{n}$
, and the character
![]() $\unicode[STIX]{x1D713}$
of
$\unicode[STIX]{x1D713}$
of
![]() $N_{n}$
identifies with
$N_{n}$
identifies with
where
![]() $t_{i}=\unicode[STIX]{x1D71B}_{F}^{a_{i}(0)-a_{i+1}(0)}$
.
$t_{i}=\unicode[STIX]{x1D71B}_{F}^{a_{i}(0)-a_{i+1}(0)}$
.
For our computation to come, it will be useful to notice the following property of
![]() ${\mathcal{B}}^{\prime }$
: one has
${\mathcal{B}}^{\prime }$
: one has
for
![]() $k\in \{1,\ldots ,e-1\}.$
As
$k\in \{1,\ldots ,e-1\}.$
As
![]() $\unicode[STIX]{x1D71B}_{E}L_{k}=L_{k+1}$
for any
$\unicode[STIX]{x1D71B}_{E}L_{k}=L_{k+1}$
for any
![]() $k\in \mathbb{Z}$
, the properties above and the fact that
$k\in \mathbb{Z}$
, the properties above and the fact that
![]() $L_{k+e}=\unicode[STIX]{x1D71B}_{F}L_{k}$
, imply that the last row of
$L_{k+e}=\unicode[STIX]{x1D71B}_{F}L_{k}$
, imply that the last row of
![]() $\unicode[STIX]{x1D71B}_{E}^{i}\in G_{n}$
belongs to
$\unicode[STIX]{x1D71B}_{E}^{i}\in G_{n}$
belongs to
![]() $(\mathfrak{o}_{F})^{n}-(\mathfrak{p}_{F})^{n}$
for
$(\mathfrak{o}_{F})^{n}-(\mathfrak{p}_{F})^{n}$
for
![]() $i=0,\ldots ,e-1$
, and more generally that it belongs to
$i=0,\ldots ,e-1$
, and more generally that it belongs to
![]() $(\mathfrak{p}_{F}^{l})^{n}-(\mathfrak{p}_{F}^{l+1})^{n}$
if
$(\mathfrak{p}_{F}^{l})^{n}-(\mathfrak{p}_{F}^{l+1})^{n}$
if
![]() $i=le+r$
, with
$i=le+r$
, with
![]() $r\in \{0,\ldots ,e-1\}$
. As an immediate consequence, if we write an Iwasawa decomposition of
$r\in \{0,\ldots ,e-1\}$
. As an immediate consequence, if we write an Iwasawa decomposition of
![]() $\unicode[STIX]{x1D71B}_{E}^{i}$
,
$\unicode[STIX]{x1D71B}_{E}^{i}$
,
we can choose
![]() $z_{i}=I_{n}$
for
$z_{i}=I_{n}$
for
![]() $i=0,\ldots ,e-1$
, and more generally
$i=0,\ldots ,e-1$
, and more generally
![]() $z_{i}=\unicode[STIX]{x1D71B}_{F}^{l}I_{n}$
for
$z_{i}=\unicode[STIX]{x1D71B}_{F}^{l}I_{n}$
for
![]() $i=le+r$
, with
$i=le+r$
, with
![]() $r\in \{0,\ldots ,e-1\}$
. In particular
$r\in \{0,\ldots ,e-1\}$
. In particular
![]() $|p_{i}|=q^{-in/e}$
, for
$|p_{i}|=q^{-in/e}$
, for
![]() $i=0,\ldots ,e-1$
.
$i=0,\ldots ,e-1$
.
For clarity, we list the properties of the data
![]() $(J,\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D713}_{t})$
that we use.
$(J,\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D713}_{t})$
that we use.
Proposition 7.1. With the above choice of basis we have:
(1) The inclusion
 $J\subset K_{n}$
.
$J\subset K_{n}$
.(2) The space
 $\text{Hom}_{N_{n}\cap J}(\unicode[STIX]{x1D713}_{t},\unicode[STIX]{x1D6EC})\neq 0.$
$\text{Hom}_{N_{n}\cap J}(\unicode[STIX]{x1D713}_{t},\unicode[STIX]{x1D6EC})\neq 0.$
(3) Set
 ${\mathcal{M}}=(P_{n}\cap J)J^{1}$
, then
${\mathcal{M}}=(P_{n}\cap J)J^{1}$
, then
 $|J/{\mathcal{M}}|=q^{n/e}-1$
.
$|J/{\mathcal{M}}|=q^{n/e}-1$
.(4) The element
 $\unicode[STIX]{x1D71B}_{E}^{i}\in P_{n}K_{n}$
if and only if
$\unicode[STIX]{x1D71B}_{E}^{i}\in P_{n}K_{n}$
if and only if
 $i\in \{0,\ldots ,e-1\}$
and, in this case, if we choose
$i\in \{0,\ldots ,e-1\}$
and, in this case, if we choose
 $p_{i}\in P_{n}$
and
$p_{i}\in P_{n}$
and
 $k_{i}\in K_{n}$
, such that
$k_{i}\in K_{n}$
, such that
 $\unicode[STIX]{x1D71B}_{E}^{i}=p_{i}k_{i}$
, then we have
$\unicode[STIX]{x1D71B}_{E}^{i}=p_{i}k_{i}$
, then we have
 $|p_{i}|=|\unicode[STIX]{x1D71B}_{E}^{i}|=q^{-in/e}.$
$|p_{i}|=|\unicode[STIX]{x1D71B}_{E}^{i}|=q^{-in/e}.$
For the remainder, we consider the
![]() $k_{i}\in K_{n}$
and
$k_{i}\in K_{n}$
and
![]() $p_{i}\in P_{n}$
chosen in Proposition 7.1 Statement (4) as fixed.
$p_{i}\in P_{n}$
chosen in Proposition 7.1 Statement (4) as fixed.
As
![]() $P_{n}\cap J^{1}$
is a pro-
$P_{n}\cap J^{1}$
is a pro-
![]() $p$
subgroup of
$p$
subgroup of
![]() $P_{n}$
, and
$P_{n}$
, and
![]() $J^{1}$
is a pro-
$J^{1}$
is a pro-
![]() $p$
subgroup of
$p$
subgroup of
![]() $G_{n}$
, the volume
$G_{n}$
, the volume
is a power of
![]() $q$
thanks to our normalization of measures, and we write
$q$
thanks to our normalization of measures, and we write
A certain volume will appear in our later computation, we compute it in the next lemma.
Lemma 7.2. For any
![]() $i\in \{0,\ldots ,e-1\}$
, we have
$i\in \{0,\ldots ,e-1\}$
, we have
Proof. We have
the last equality thanks to Relation (3). Now,
![]() $dk(k_{i}Jk_{i}^{-1})=dk(J)$
. We also notice that
$dk(k_{i}Jk_{i}^{-1})=dk(J)$
. We also notice that
hence
As for any compact open subset
![]() $A$
of
$A$
of
![]() $P_{n}$
, one has
$P_{n}$
, one has
![]() $dp(pAp^{-1})=|p|dp(A)$
, as is easily seen by writing
$dp(pAp^{-1})=|p|dp(A)$
, as is easily seen by writing
![]() $dp=dgdu$
, with
$dp=dgdu$
, with
![]() $dg$
on
$dg$
on
![]() $G_{n-1}$
and
$G_{n-1}$
and
![]() $du$
on
$du$
on
![]() $U_{n}$
, we obtain the relation
$U_{n}$
, we obtain the relation
We then obtain from Relations (1) and (2):
 $$\begin{eqnarray}\displaystyle dk((P_{n}\cap k_{i}Jk_{i}^{-1})\backslash k_{i}Jk_{i}^{-1}) & = & \displaystyle \frac{dk(k_{i}Jk_{i}^{-1})}{dp(P_{n}\cap k_{i}Jk_{i}^{-1})}\nonumber\\ \displaystyle & = & \displaystyle q^{-in/e}\frac{dk(J)}{dp(P_{n}\cap J)}\nonumber\\ \displaystyle & = & \displaystyle q^{-in/e}dk((P_{n}\cap J)\backslash J).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle dk((P_{n}\cap k_{i}Jk_{i}^{-1})\backslash k_{i}Jk_{i}^{-1}) & = & \displaystyle \frac{dk(k_{i}Jk_{i}^{-1})}{dp(P_{n}\cap k_{i}Jk_{i}^{-1})}\nonumber\\ \displaystyle & = & \displaystyle q^{-in/e}\frac{dk(J)}{dp(P_{n}\cap J)}\nonumber\\ \displaystyle & = & \displaystyle q^{-in/e}dk((P_{n}\cap J)\backslash J).\nonumber\end{eqnarray}$$
Now by Relations (1) and (2) again, one has
 $$\begin{eqnarray}\displaystyle dk((P_{n}\cap J)\backslash J)) & = & \displaystyle \frac{dk(J)}{dp(P_{n}\cap J)}=\frac{dk(J)}{dk({\mathcal{M}})}\frac{dk({\mathcal{M}})}{dp(P_{n}\cap J)}\nonumber\\ \displaystyle & = & \displaystyle |J\backslash {\mathcal{M}}|dk(P_{n}\cap J\backslash {\mathcal{M}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle dk((P_{n}\cap J)\backslash J)) & = & \displaystyle \frac{dk(J)}{dp(P_{n}\cap J)}=\frac{dk(J)}{dk({\mathcal{M}})}\frac{dk({\mathcal{M}})}{dp(P_{n}\cap J)}\nonumber\\ \displaystyle & = & \displaystyle |J\backslash {\mathcal{M}}|dk(P_{n}\cap J\backslash {\mathcal{M}}).\nonumber\end{eqnarray}$$
Finally, because
![]() ${\mathcal{M}}=(P_{n}\cap J)J^{1}$
, applying Relation (3) gives:
${\mathcal{M}}=(P_{n}\cap J)J^{1}$
, applying Relation (3) gives:
by Proposition 7.1(3) and our definition of
![]() $r_{1}$
. This concludes the proof.◻
$r_{1}$
. This concludes the proof.◻
8 Explicit Whittaker functions of Paskunas–Stevens
In this section we continue to assume that
![]() $R=\mathbb{C}$
or
$R=\mathbb{C}$
or
![]() $\overline{\mathbb{Q}_{\ell }}$
. We now recall the definition and some properties of the explicit Whittaker functions of [Reference Paskunas and Stevens12]. We set
$\overline{\mathbb{Q}_{\ell }}$
. We now recall the definition and some properties of the explicit Whittaker functions of [Reference Paskunas and Stevens12]. We set
We extend
![]() $\unicode[STIX]{x1D713}_{t}$
to the group
$\unicode[STIX]{x1D713}_{t}$
to the group
![]() ${\mathcal{U}}$
as in [Reference Paskunas and Stevens12, Definition 4.2], and, by abuse of notation, denote this extension by
${\mathcal{U}}$
as in [Reference Paskunas and Stevens12, Definition 4.2], and, by abuse of notation, denote this extension by
![]() $\unicode[STIX]{x1D713}_{t}$
. We fix a normal compact open subgroup
$\unicode[STIX]{x1D713}_{t}$
. We fix a normal compact open subgroup
![]() ${\mathcal{N}}$
of
${\mathcal{N}}$
of
![]() ${\mathcal{U}}$
contained in
${\mathcal{U}}$
contained in
![]() $\ker (\unicode[STIX]{x1D713}_{t})$
. We also denote by
$\ker (\unicode[STIX]{x1D713}_{t})$
. We also denote by
![]() $\unicode[STIX]{x1D70C}$
the trace character of
$\unicode[STIX]{x1D70C}$
the trace character of
![]() $\unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D6EC}$
and
![]() $\unicode[STIX]{x1D70C}^{\vee }$
that of
$\unicode[STIX]{x1D70C}^{\vee }$
that of
![]() $\unicode[STIX]{x1D6EC}^{\vee }$
.
$\unicode[STIX]{x1D6EC}^{\vee }$
.
Definition 8.1. (Bessel functions)
For
![]() $j\in \mathbf{J}$
, we define
$j\in \mathbf{J}$
, we define
 $$\begin{eqnarray}\displaystyle {\mathcal{J}}(j) & = & \displaystyle |{\mathcal{N}}\backslash {\mathcal{U}}|^{-1}\mathop{\sum }_{{\mathcal{N}}\backslash {\mathcal{U}}}\unicode[STIX]{x1D713}_{t}(u)^{-1}\unicode[STIX]{x1D70C}(ju),\qquad \text{and}\nonumber\\ \displaystyle {\mathcal{J}}^{\vee }(j) & = & \displaystyle |{\mathcal{N}}\backslash {\mathcal{U}}|^{-1}\mathop{\sum }_{{\mathcal{N}}\backslash {\mathcal{U}}}\unicode[STIX]{x1D713}_{t}(u)\unicode[STIX]{x1D70C}^{\vee }(ju).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{J}}(j) & = & \displaystyle |{\mathcal{N}}\backslash {\mathcal{U}}|^{-1}\mathop{\sum }_{{\mathcal{N}}\backslash {\mathcal{U}}}\unicode[STIX]{x1D713}_{t}(u)^{-1}\unicode[STIX]{x1D70C}(ju),\qquad \text{and}\nonumber\\ \displaystyle {\mathcal{J}}^{\vee }(j) & = & \displaystyle |{\mathcal{N}}\backslash {\mathcal{U}}|^{-1}\mathop{\sum }_{{\mathcal{N}}\backslash {\mathcal{U}}}\unicode[STIX]{x1D713}_{t}(u)\unicode[STIX]{x1D70C}^{\vee }(ju).\nonumber\end{eqnarray}$$
The Bessel functions enjoy the following properties:
Proposition 8.2.
(1) We have the equality
 ${\mathcal{J}}(1)=1$
.
${\mathcal{J}}(1)=1$
.(2)
 ${\mathcal{J}}(uj)={\mathcal{J}}(ju)=\unicode[STIX]{x1D713}_{t}(u){\mathcal{J}}(j)$
for
${\mathcal{J}}(uj)={\mathcal{J}}(ju)=\unicode[STIX]{x1D713}_{t}(u){\mathcal{J}}(j)$
for
 $u\in {\mathcal{U}}$
and
$u\in {\mathcal{U}}$
and
 $j\in \mathbf{J}$
.
$j\in \mathbf{J}$
.(3) For all
 $j\in \mathbf{J}$
, we have the relation
$j\in \mathbf{J}$
, we have the relation  $$\begin{eqnarray}{\mathcal{J}}^{\vee }(j)={\mathcal{J}}(j^{-1}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{J}}^{\vee }(j)={\mathcal{J}}(j^{-1}).\end{eqnarray}$$
(4) For all
 $j_{1}$
and
$j_{1}$
and
 $j_{2}$
in
$j_{2}$
in
 $\mathbf{J}$
, we have
$\mathbf{J}$
, we have  $$\begin{eqnarray}\mathop{\sum }_{m\in {\mathcal{U}}\backslash {\mathcal{M}}}{\mathcal{J}}(j_{1}m^{-1}){\mathcal{J}}(mj_{2})={\mathcal{J}}(j_{1}j_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m\in {\mathcal{U}}\backslash {\mathcal{M}}}{\mathcal{J}}(j_{1}m^{-1}){\mathcal{J}}(mj_{2})={\mathcal{J}}(j_{1}j_{2}).\end{eqnarray}$$
Proof. See [Reference Paskunas and Stevens12, Proposition 5.3 and Theorem 5.6]. The third property follows from a simple change of variables, and the relation
![]() $\unicode[STIX]{x1D70C}^{\vee }(ab)=\unicode[STIX]{x1D70C}(b^{-1}a^{-1})$
for any
$\unicode[STIX]{x1D70C}^{\vee }(ab)=\unicode[STIX]{x1D70C}(b^{-1}a^{-1})$
for any
![]() $a$
and
$a$
and
![]() $b$
in
$b$
in
![]() $\mathbf{J}$
. The final property follows from [Reference Paskunas and Stevens12, Proposition 5.3, Property (v)], thanks to the bijection
$\mathbf{J}$
. The final property follows from [Reference Paskunas and Stevens12, Proposition 5.3, Property (v)], thanks to the bijection
![]() $m\leftrightarrow m^{-1}$
between
$m\leftrightarrow m^{-1}$
between
![]() ${\mathcal{M}}/{\mathcal{U}}$
and
${\mathcal{M}}/{\mathcal{U}}$
and
![]() ${\mathcal{U}}\backslash {\mathcal{M}}$
.◻
${\mathcal{U}}\backslash {\mathcal{M}}$
.◻
We can now define the explicit Whittaker functions
![]() $W$
and
$W$
and
![]() $W^{\vee }$
of Paskunas–Stevens following [Reference Paskunas and Stevens12, Section 5.2] and recall a first property.
$W^{\vee }$
of Paskunas–Stevens following [Reference Paskunas and Stevens12, Section 5.2] and recall a first property.
Definition 8.3. Both
![]() $W$
and
$W$
and
![]() $W^{\vee }$
are supported on
$W^{\vee }$
are supported on
![]() $N_{n}\mathbf{J}$
, and
$N_{n}\mathbf{J}$
, and
for
![]() $n\in N_{n}$
and
$n\in N_{n}$
and
![]() $j\in \mathbf{J}$
, whereas
$j\in \mathbf{J}$
, whereas
for
![]() $n\in N_{n}$
and
$n\in N_{n}$
and
![]() $j\in \mathbf{J}$
. Moreover,
$j\in \mathbf{J}$
. Moreover,
![]() $W$
belongs to
$W$
belongs to
![]() $W(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713}_{t})$
and
$W(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D713}_{t})$
and
![]() $W^{\vee }$
belongs to
$W^{\vee }$
belongs to
![]() $W(\unicode[STIX]{x1D70B}^{\vee },\unicode[STIX]{x1D713}_{t}^{-1})$
.
$W(\unicode[STIX]{x1D70B}^{\vee },\unicode[STIX]{x1D713}_{t}^{-1})$
.
We now prove further properties of
![]() $W$
and
$W$
and
![]() $W^{\vee }$
.
$W^{\vee }$
.
Proposition 8.4. For
![]() $l\geqslant 0$
, let
$l\geqslant 0$
, let
![]() $W_{l}=\mathbf{1}_{G_{n}^{(l)}}W,$
and
$W_{l}=\mathbf{1}_{G_{n}^{(l)}}W,$
and
![]() $W_{l}^{\vee }=\mathbf{1}_{G_{n}^{(l)}}W^{\vee }$
.
$W_{l}^{\vee }=\mathbf{1}_{G_{n}^{(l)}}W^{\vee }$
.
(1) The functions
 $(W_{l})\mid _{P_{n}K_{n}}$
and
$(W_{l})\mid _{P_{n}K_{n}}$
and
 $(W_{l})^{\vee }\mid _{P_{n}K_{n}}$
are zero unless
$(W_{l})^{\vee }\mid _{P_{n}K_{n}}$
are zero unless
 $l=in/e$
for some
$l=in/e$
for some
 $i\in \{0,\ldots ,e-1\}$
, and in this case
$i\in \{0,\ldots ,e-1\}$
, and in this case  $$\begin{eqnarray}(W_{l})\mid _{P_{n}K_{n}}=\mathbf{1}_{N_{n}\unicode[STIX]{x1D71B}_{E}^{i}J}W\mid _{P_{n}K_{n}},\qquad (W_{l}^{\vee })\mid _{P_{n}K_{n}}=\mathbf{1}_{N_{n}\unicode[STIX]{x1D71B}_{E}^{i}J}W^{\vee }\mid _{P_{n}K_{n}}.\end{eqnarray}$$
$$\begin{eqnarray}(W_{l})\mid _{P_{n}K_{n}}=\mathbf{1}_{N_{n}\unicode[STIX]{x1D71B}_{E}^{i}J}W\mid _{P_{n}K_{n}},\qquad (W_{l}^{\vee })\mid _{P_{n}K_{n}}=\mathbf{1}_{N_{n}\unicode[STIX]{x1D71B}_{E}^{i}J}W^{\vee }\mid _{P_{n}K_{n}}.\end{eqnarray}$$
(2) If
 $W_{in/e}(pk)\neq 0$
, then
$W_{in/e}(pk)\neq 0$
, then
 $i\in \{0,\ldots ,e-1\}$
,
$i\in \{0,\ldots ,e-1\}$
,
 $k\in P_{n}\unicode[STIX]{x1D71B}_{E}^{i}J$
, and, in fact,
$k\in P_{n}\unicode[STIX]{x1D71B}_{E}^{i}J$
, and, in fact,
 $k\in (P_{n}\cap K_{n})k_{i}J$
.
$k\in (P_{n}\cap K_{n})k_{i}J$
.(3) If
 $W_{in/e}(p\unicode[STIX]{x1D71B}_{E}^{i}j)\neq 0$
with
$W_{in/e}(p\unicode[STIX]{x1D71B}_{E}^{i}j)\neq 0$
with
 $p\in P_{n}$
and
$p\in P_{n}$
and
 $j\in J$
, then
$j\in J$
, then
 $p\in N_{n}(P_{n}\cap J)$
.
$p\in N_{n}(P_{n}\cap J)$
.
Proof. The first statement follows from the fact that
![]() $W$
is supported on
$W$
is supported on
![]() $N_{n}\mathbf{J}=\coprod _{i\in \mathbb{Z}}N_{n}\unicode[STIX]{x1D71B}_{E}^{i}J$
, this is a disjoint union because the absolute value of the determinant on
$N_{n}\mathbf{J}=\coprod _{i\in \mathbb{Z}}N_{n}\unicode[STIX]{x1D71B}_{E}^{i}J$
, this is a disjoint union because the absolute value of the determinant on
![]() $N_{n}\unicode[STIX]{x1D71B}_{E}^{i}J$
is
$N_{n}\unicode[STIX]{x1D71B}_{E}^{i}J$
is
![]() $q^{-ni/e}$
, and Statement (4) of Proposition 7.1. Hence, if
$q^{-ni/e}$
, and Statement (4) of Proposition 7.1. Hence, if
![]() $W_{in/e}(pk)\neq 0$
, then
$W_{in/e}(pk)\neq 0$
, then
![]() $W(pk)\neq 0$
, so
$W(pk)\neq 0$
, so
![]() $pk\in N_{n}\unicode[STIX]{x1D71B}_{E}^{l}J$
for a unique
$pk\in N_{n}\unicode[STIX]{x1D71B}_{E}^{l}J$
for a unique
![]() $l\in \{0,\ldots ,e-1\}$
, but this
$l\in \{0,\ldots ,e-1\}$
, but this
![]() $l$
must be equal to
$l$
must be equal to
![]() $i$
, and this gives the first assertion of the second statement. In particular
$i$
, and this gives the first assertion of the second statement. In particular
![]() $k\in p^{-1}N_{n}\unicode[STIX]{x1D71B}_{E}^{i}J\subset P_{n}\unicode[STIX]{x1D71B}_{E}^{i}J$
. But
$k\in p^{-1}N_{n}\unicode[STIX]{x1D71B}_{E}^{i}J\subset P_{n}\unicode[STIX]{x1D71B}_{E}^{i}J$
. But
![]() $P_{n}\unicode[STIX]{x1D71B}_{E}^{i}J=P_{n}p_{i}k_{i}J=P_{n}k_{i}J$
, hence
$P_{n}\unicode[STIX]{x1D71B}_{E}^{i}J=P_{n}p_{i}k_{i}J=P_{n}k_{i}J$
, hence
![]() $k\in P_{n}k_{i}J\cap K_{n}=(P_{n}\cap K_{n})k_{i}J$
. This proves the second statement. For the third, we observe that if
$k\in P_{n}k_{i}J\cap K_{n}=(P_{n}\cap K_{n})k_{i}J$
. This proves the second statement. For the third, we observe that if
![]() $W_{in/e}(p\unicode[STIX]{x1D71B}_{E}^{i}j)\neq 0$
, then
$W_{in/e}(p\unicode[STIX]{x1D71B}_{E}^{i}j)\neq 0$
, then
![]() $p\unicode[STIX]{x1D71B}_{E}^{i}j\in N_{n}\unicode[STIX]{x1D71B}_{E}^{i}J$
, hence
$p\unicode[STIX]{x1D71B}_{E}^{i}j\in N_{n}\unicode[STIX]{x1D71B}_{E}^{i}J$
, hence
![]() $p\in N_{n}\unicode[STIX]{x1D71B}_{E}^{i}Jj^{-1}\unicode[STIX]{x1D71B}_{E}^{-i}=N_{n}J$
, which implies that
$p\in N_{n}\unicode[STIX]{x1D71B}_{E}^{i}Jj^{-1}\unicode[STIX]{x1D71B}_{E}^{-i}=N_{n}J$
, which implies that
![]() $p\in N_{n}(P_{n}\cap J)$
.◻
$p\in N_{n}(P_{n}\cap J)$
.◻
9 Test vectors
Again, we assume that
![]() $R=\mathbb{C}$
, or
$R=\mathbb{C}$
, or
![]() $\overline{\mathbb{Q}_{\ell }}$
, and
$\overline{\mathbb{Q}_{\ell }}$
, and
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
are cuspidal
$\unicode[STIX]{x1D70B}_{2}$
are cuspidal
![]() $R$
-representations of
$R$
-representations of
![]() $G_{n}$
. We denote by
$G_{n}$
. We denote by
![]() $(\mathbf{J},\unicode[STIX]{x1D6EC})$
the extended maximal simple type of
$(\mathbf{J},\unicode[STIX]{x1D6EC})$
the extended maximal simple type of
![]() $\unicode[STIX]{x1D70B}_{1}$
, by
$\unicode[STIX]{x1D70B}_{1}$
, by
![]() $e=e(E/F)$
the ramification index of the field extension associated to
$e=e(E/F)$
the ramification index of the field extension associated to
![]() $(\mathbf{J},\unicode[STIX]{x1D6EC})$
, and by
$(\mathbf{J},\unicode[STIX]{x1D6EC})$
, and by
![]() $W,W^{\vee }$
the explicit Whittaker functions associated to
$W,W^{\vee }$
the explicit Whittaker functions associated to
![]() $\unicode[STIX]{x1D70B}_{1}$
(see Definition 8.3). This section is dedicated to proving our main result on test vectors.
$\unicode[STIX]{x1D70B}_{1}$
(see Definition 8.3). This section is dedicated to proving our main result on test vectors.
Theorem 9.1. Suppose that
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is nontrivial, so that
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is nontrivial, so that
![]() $\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
for some unramified character
$\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
for some unramified character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $F^{\times }$
. Then there is an integer
$F^{\times }$
. Then there is an integer
![]() $r$
such that
$r$
such that
We are now ready to prove the following crucial proposition. We recall that for all integers
![]() $l\geqslant 0$
, the restriction
$l\geqslant 0$
, the restriction
![]() $W_{l}$
has been defined in Proposition 8.4.
$W_{l}$
has been defined in Proposition 8.4.
Proposition 9.2. Let
![]() $F_{l}:(K_{n}\cap P_{n})\backslash K_{n}/J^{1}\rightarrow R$
be defined by
$F_{l}:(K_{n}\cap P_{n})\backslash K_{n}/J^{1}\rightarrow R$
be defined by
Then
![]() $F_{l}$
is nonzero if an only if
$F_{l}$
is nonzero if an only if
![]() $l=in/e$
and
$l=in/e$
and
![]() $i\in \{0,\ldots ,e-1\}$
, and in this case, it is supported on
$i\in \{0,\ldots ,e-1\}$
, and in this case, it is supported on
![]() $(K_{n}\cap P_{n})k_{i}J$
. Moreover, for
$(K_{n}\cap P_{n})k_{i}J$
. Moreover, for
![]() $i\in \{0,\ldots ,e-1\}$
, and for
$i\in \{0,\ldots ,e-1\}$
, and for
![]() $k\in (K_{n}\cap P_{n})k_{i}J$
, there is an integer
$k\in (K_{n}\cap P_{n})k_{i}J$
, there is an integer
![]() $r_{2}$
independent of
$r_{2}$
independent of
![]() $i$
such that
$i$
such that
Proof. If
![]() $F_{l}(k)$
is nonzero, then
$F_{l}(k)$
is nonzero, then
![]() $W_{l}(pkj)$
is nonzero at least for some
$W_{l}(pkj)$
is nonzero at least for some
![]() $p\in P_{n}$
and
$p\in P_{n}$
and
![]() $j\in J$
, but then according to Statements (1) and (2) of Proposition 8.4, this implies that
$j\in J$
, but then according to Statements (1) and (2) of Proposition 8.4, this implies that
![]() $l$
is of the form
$l$
is of the form
![]() $l=in/e$
with
$l=in/e$
with
![]() $i\in \{0,\ldots ,e-1\}$
, and
$i\in \{0,\ldots ,e-1\}$
, and
![]() $k\in (K_{n}\cap P_{n})k_{i}J$
. Moreover, from Statement (2) of the same proposition, we can write
$k\in (K_{n}\cap P_{n})k_{i}J$
. Moreover, from Statement (2) of the same proposition, we can write
![]() $k=p_{0}\unicode[STIX]{x1D71B}_{E}^{i}j_{0}$
for
$k=p_{0}\unicode[STIX]{x1D71B}_{E}^{i}j_{0}$
for
![]() $p_{0}\in P_{n}$
and
$p_{0}\in P_{n}$
and
![]() $j_{0}\in J$
. But now notice that for such a
$j_{0}\in J$
. But now notice that for such a
![]() $k$
, we have
$k$
, we have
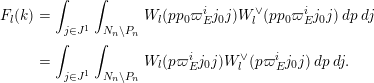 $$\begin{eqnarray}\displaystyle F_{l}(k) & = & \displaystyle \int _{j\in J^{1}}\int _{N_{n}\backslash P_{n}}W_{l}(pp_{0}\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)W_{l}^{\vee }(pp_{0}\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)\,dp\,dj\nonumber\\ \displaystyle & = & \displaystyle \int _{j\in J^{1}}\int _{N_{n}\backslash P_{n}}W_{l}(p\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)W_{l}^{\vee }(p\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)\,dp\,dj.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{l}(k) & = & \displaystyle \int _{j\in J^{1}}\int _{N_{n}\backslash P_{n}}W_{l}(pp_{0}\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)W_{l}^{\vee }(pp_{0}\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)\,dp\,dj\nonumber\\ \displaystyle & = & \displaystyle \int _{j\in J^{1}}\int _{N_{n}\backslash P_{n}}W_{l}(p\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)W_{l}^{\vee }(p\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)\,dp\,dj.\nonumber\end{eqnarray}$$
Hence by Statement (3) of Proposition 8.4
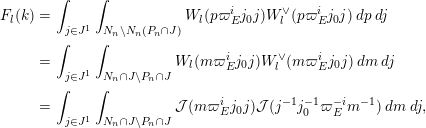 $$\begin{eqnarray}\displaystyle F_{l}(k) & = & \displaystyle \int _{j\in J^{1}}\int _{N_{n}\backslash N_{n}(P_{n}\cap J)}W_{l}(p\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)W_{l}^{\vee }(p\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)\,dp\,dj\nonumber\\ \displaystyle & = & \displaystyle \int _{j\in J^{1}}\int _{N_{n}\cap J\backslash P_{n}\cap J}W_{l}(m\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)W_{l}^{\vee }(m\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)\,dm\,dj\nonumber\\ \displaystyle & = & \displaystyle \int _{j\in J^{1}}\int _{N_{n}\cap J\backslash P_{n}\cap J}{\mathcal{J}}(m\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j){\mathcal{J}}(j^{-1}j_{0}^{-1}\unicode[STIX]{x1D71B}_{E}^{-i}m^{-1})\,dm\,dj,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{l}(k) & = & \displaystyle \int _{j\in J^{1}}\int _{N_{n}\backslash N_{n}(P_{n}\cap J)}W_{l}(p\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)W_{l}^{\vee }(p\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)\,dp\,dj\nonumber\\ \displaystyle & = & \displaystyle \int _{j\in J^{1}}\int _{N_{n}\cap J\backslash P_{n}\cap J}W_{l}(m\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)W_{l}^{\vee }(m\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j)\,dm\,dj\nonumber\\ \displaystyle & = & \displaystyle \int _{j\in J^{1}}\int _{N_{n}\cap J\backslash P_{n}\cap J}{\mathcal{J}}(m\unicode[STIX]{x1D71B}_{E}^{i}j_{0}j){\mathcal{J}}(j^{-1}j_{0}^{-1}\unicode[STIX]{x1D71B}_{E}^{-i}m^{-1})\,dm\,dj,\nonumber\end{eqnarray}$$
the last equality according to Proposition 8.2(3). Now, as
![]() $\mathbf{J}$
normalizes
$\mathbf{J}$
normalizes
![]() $J^{1}$
, and as for any
$J^{1}$
, and as for any
![]() $t\in G_{n}$
normalizing
$t\in G_{n}$
normalizing
![]() $J^{1}$
, the automorphism
$J^{1}$
, the automorphism
![]() $j\mapsto tjt^{-1}$
of
$j\mapsto tjt^{-1}$
of
![]() $J^{1}$
has modulus character equal to
$J^{1}$
has modulus character equal to
![]() $\mathbf{1}$
, because
$\mathbf{1}$
, because
![]() $J^{1}$
is an open subgroup of the unimodular group
$J^{1}$
is an open subgroup of the unimodular group
![]() $G_{n}$
, we have
$G_{n}$
, we have
 $$\begin{eqnarray}\displaystyle F_{l}(k) & = & \displaystyle \int _{j\in J^{1}}\int _{N_{n}\cap J\backslash P_{n}\cap J}{\mathcal{J}}(mj\unicode[STIX]{x1D71B}_{E}^{i}j_{0}){\mathcal{J}}(j_{0}^{-1}\unicode[STIX]{x1D71B}_{E}^{-i}(mj)^{-1})\,dm\,dj\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{n}\cap J\backslash {\mathcal{M}}}{\mathcal{J}}(m\unicode[STIX]{x1D71B}_{E}^{i}j_{0}){\mathcal{J}}(j_{0}^{-1}\unicode[STIX]{x1D71B}_{E}^{-i}m^{-1})\,dm.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{l}(k) & = & \displaystyle \int _{j\in J^{1}}\int _{N_{n}\cap J\backslash P_{n}\cap J}{\mathcal{J}}(mj\unicode[STIX]{x1D71B}_{E}^{i}j_{0}){\mathcal{J}}(j_{0}^{-1}\unicode[STIX]{x1D71B}_{E}^{-i}(mj)^{-1})\,dm\,dj\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{n}\cap J\backslash {\mathcal{M}}}{\mathcal{J}}(m\unicode[STIX]{x1D71B}_{E}^{i}j_{0}){\mathcal{J}}(j_{0}^{-1}\unicode[STIX]{x1D71B}_{E}^{-i}m^{-1})\,dm.\nonumber\end{eqnarray}$$
We write
which is indeed a power of
![]() $q$
as
$q$
as
![]() $H^{1}$
is pro-
$H^{1}$
is pro-
![]() $p$
. Moreover, as
$p$
. Moreover, as
![]() $H^{1}$
is normal in
$H^{1}$
is normal in
![]() $J$
, and as the integrand is invariant under
$J$
, and as the integrand is invariant under
![]() ${\mathcal{U}}$
thanks to Property (2) in Proposition 8.2
${\mathcal{U}}$
thanks to Property (2) in Proposition 8.2
the last equality thanks to Statement (4) of Proposition 8.2. ◻
Proposition 9.3. The coefficient
is zero unless
![]() $l=in/e$
for some
$l=in/e$
for some
![]() $i\in \{0,\ldots ,e-1\}$
, in which case there is an integer
$i\in \{0,\ldots ,e-1\}$
, in which case there is an integer
![]() $r$
such that
$r$
such that
Proof. By definition,
![]() $b_{l}$
is equal to
$b_{l}$
is equal to
with
![]() $dk(J^{1})=q^{r_{3}}$
(
$dk(J^{1})=q^{r_{3}}$
(
![]() $J^{1}$
is pro-
$J^{1}$
is pro-
![]() $p$
). So according to Proposition 9.2, this is zero if
$p$
). So according to Proposition 9.2, this is zero if
![]() $l\neq in/e$
for
$l\neq in/e$
for
![]() $i\in \{0,\ldots ,e-1\}$
, and if
$i\in \{0,\ldots ,e-1\}$
, and if
![]() $l=in/e$
for
$l=in/e$
for
![]() $i\in \{0,\ldots ,e-1\}$
, it is equal to
$i\in \{0,\ldots ,e-1\}$
, it is equal to
 $$\begin{eqnarray}\displaystyle q^{r_{3}}\int _{P_{n}\cap K_{n}\backslash (P_{n}\cap K_{n})k_{i}J}F_{l}(k)\,dk & = & \displaystyle q^{r_{2}+r_{3}}dk(P_{n}\cap K_{n}\backslash (P_{n}\cap K_{n})k_{i}J)\nonumber\\ \displaystyle & = & \displaystyle q^{r}(q^{n/e}-1)q^{-in/e},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle q^{r_{3}}\int _{P_{n}\cap K_{n}\backslash (P_{n}\cap K_{n})k_{i}J}F_{l}(k)\,dk & = & \displaystyle q^{r_{2}+r_{3}}dk(P_{n}\cap K_{n}\backslash (P_{n}\cap K_{n})k_{i}J)\nonumber\\ \displaystyle & = & \displaystyle q^{r}(q^{n/e}-1)q^{-in/e},\nonumber\end{eqnarray}$$
where we write
![]() $r=r_{1}+r_{2}+r_{3}$
, from Lemma 7.2.◻
$r=r_{1}+r_{2}+r_{3}$
, from Lemma 7.2.◻
If
![]() $\unicode[STIX]{x1D70B}$
is a cuspidal
$\unicode[STIX]{x1D70B}$
is a cuspidal
![]() $R$
-representation of
$R$
-representation of
![]() $G_{n}$
of ramification index
$G_{n}$
of ramification index
![]() $e$
, we denote by
$e$
, we denote by
![]() $R(\unicode[STIX]{x1D70B})$
its ramification group, that is the group of unramified characters
$R(\unicode[STIX]{x1D70B})$
its ramification group, that is the group of unramified characters
![]() $\unicode[STIX]{x1D708}$
of
$\unicode[STIX]{x1D708}$
of
![]() $F^{\times }$
which satisfy
$F^{\times }$
which satisfy
![]() $\unicode[STIX]{x1D708}\unicode[STIX]{x1D70B}\simeq \unicode[STIX]{x1D70B}$
. It follows from [Reference Bushnell and Kutzko2, 6.2.5], that
$\unicode[STIX]{x1D708}\unicode[STIX]{x1D70B}\simeq \unicode[STIX]{x1D70B}$
. It follows from [Reference Bushnell and Kutzko2, 6.2.5], that
![]() $R(\unicode[STIX]{x1D70B})$
is isomorphic to the group of
$R(\unicode[STIX]{x1D70B})$
is isomorphic to the group of
![]() $n/e$
th roots of unity in
$n/e$
th roots of unity in
![]() $R^{\times }$
, via
$R^{\times }$
, via
![]() $\unicode[STIX]{x1D708}\mapsto \unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{F})$
.
$\unicode[STIX]{x1D708}\mapsto \unicode[STIX]{x1D708}(\unicode[STIX]{x1D71B}_{F})$
.
Proof of Theorem 9.1.
We first suppose that
![]() $\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D70B}_{1}^{\vee }$
. By Equation (4), the integral
$\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D70B}_{1}^{\vee }$
. By Equation (4), the integral
![]() $I(X,W,W^{\vee },\mathbf{1}_{\mathfrak{o}_{F}^{n}})$
is equal to
$I(X,W,W^{\vee },\mathbf{1}_{\mathfrak{o}_{F}^{n}})$
is equal to
Now, as
![]() $WW^{\vee }=\sum _{l\in \mathbb{Z}}W_{l}W_{l}^{\vee }$
, by Statement (1) of Propositions 8.4 and 9.3, we have
$WW^{\vee }=\sum _{l\in \mathbb{Z}}W_{l}W_{l}^{\vee }$
, by Statement (1) of Propositions 8.4 and 9.3, we have
 $$\begin{eqnarray}\displaystyle \int _{(K_{n}\cap P_{n})\backslash K_{n}}I_{(0)}(X,\unicode[STIX]{x1D70C}(k)W,\unicode[STIX]{x1D70C}(k)W^{\vee })\,dk & = & \displaystyle \mathop{\sum }_{i=0}^{e-1}b_{in/e}q^{in/e}X^{in/e}\nonumber\\ \displaystyle =q^{r}(q^{n/e}-1)\mathop{\sum }_{i=0}^{e-1}X^{in/e} & = & \displaystyle q^{r}(q^{n/e}-1)\frac{1-X^{n}}{1-X^{n/e}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{(K_{n}\cap P_{n})\backslash K_{n}}I_{(0)}(X,\unicode[STIX]{x1D70C}(k)W,\unicode[STIX]{x1D70C}(k)W^{\vee })\,dk & = & \displaystyle \mathop{\sum }_{i=0}^{e-1}b_{in/e}q^{in/e}X^{in/e}\nonumber\\ \displaystyle =q^{r}(q^{n/e}-1)\mathop{\sum }_{i=0}^{e-1}X^{in/e} & = & \displaystyle q^{r}(q^{n/e}-1)\frac{1-X^{n}}{1-X^{n/e}}.\nonumber\end{eqnarray}$$
This gives the equality
On the other hand, and by [Reference Jacquet, Piatetski-Shapiro and Shalika5, Proposition 8.1], the factor
![]() $L(X,\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}^{\vee })$
is equal to
$L(X,\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}^{\vee })$
is equal to
Now in general, as we supposed that
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is not equal to
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is not equal to
![]() $1$
, we have
$1$
, we have
![]() $\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
for some unramified character
$\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
for some unramified character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $F^{\times }$
. However, we have
$F^{\times }$
. However, we have
On the other hand, we have
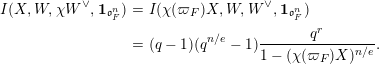 $$\begin{eqnarray}\displaystyle I(X,W,\unicode[STIX]{x1D712}W^{\vee },\mathbf{1}_{\mathfrak{o}_{F}^{n}}) & = & \displaystyle I(\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}_{F})X,W,W^{\vee },\mathbf{1}_{\mathfrak{o}_{F}^{n}})\nonumber\\ \displaystyle & = & \displaystyle (q-1)(q^{n/e}-1)\frac{q^{r}}{1-(\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}_{F})X)^{n/e}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I(X,W,\unicode[STIX]{x1D712}W^{\vee },\mathbf{1}_{\mathfrak{o}_{F}^{n}}) & = & \displaystyle I(\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}_{F})X,W,W^{\vee },\mathbf{1}_{\mathfrak{o}_{F}^{n}})\nonumber\\ \displaystyle & = & \displaystyle (q-1)(q^{n/e}-1)\frac{q^{r}}{1-(\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}_{F})X)^{n/e}}.\nonumber\end{eqnarray}$$
However,
and we are done.◻
10
 $L$
-factors of banal cuspidal
$L$
-factors of banal cuspidal
 $\ell$
-modular representations
$\ell$
-modular representations
In this section, we consider the cases
![]() $R=\overline{\mathbb{F}_{\ell }}$
, and
$R=\overline{\mathbb{F}_{\ell }}$
, and
![]() $R=\overline{\mathbb{Q}_{\ell }}$
. In the
$R=\overline{\mathbb{Q}_{\ell }}$
. In the
![]() $\overline{\mathbb{Q}_{\ell }}$
setting, we continue with the notations of the last section, and note that as
$\overline{\mathbb{Q}_{\ell }}$
setting, we continue with the notations of the last section, and note that as
![]() $\unicode[STIX]{x1D713}$
is integral, so are
$\unicode[STIX]{x1D713}$
is integral, so are
![]() $\unicode[STIX]{x1D713}_{t}$
and
$\unicode[STIX]{x1D713}_{t}$
and
![]() $\unicode[STIX]{x1D713}_{t}^{-1}$
. Our main theorem has the following interesting corollary.
$\unicode[STIX]{x1D713}_{t}^{-1}$
. Our main theorem has the following interesting corollary.
Corollary 10.1. Let
![]() $\unicode[STIX]{x1D70F}_{1}$
and
$\unicode[STIX]{x1D70F}_{1}$
and
![]() $\unicode[STIX]{x1D70F}_{2}$
be two banal cuspidal
$\unicode[STIX]{x1D70F}_{2}$
be two banal cuspidal
![]() $\ell$
-modular representations of
$\ell$
-modular representations of
![]() $G_{n}$
, and
$G_{n}$
, and
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
be any cuspidal
$\unicode[STIX]{x1D70B}_{2}$
be any cuspidal
![]() $\ell$
-adic lifts, then
$\ell$
-adic lifts, then
Proof. We already noticed in Section 5 that if
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is equal to
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is equal to
![]() $1$
, then
$1$
, then
whether
![]() $\unicode[STIX]{x1D70F}_{1}$
and
$\unicode[STIX]{x1D70F}_{1}$
and
![]() $\unicode[STIX]{x1D70F}_{2}$
are banal or not. Hence we only need to focus on the case when
$\unicode[STIX]{x1D70F}_{2}$
are banal or not. Hence we only need to focus on the case when
![]() $L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is not equal to
$L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2})$
is not equal to
![]() $1$
, that is
$1$
, that is
![]() $\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
for some unramified character
$\unicode[STIX]{x1D70B}_{2}\simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
for some unramified character
![]() $\unicode[STIX]{x1D712}$
. Let
$\unicode[STIX]{x1D712}$
. Let
![]() $W$
be the Stevens–Paskunas explicit Whittaker function associated to an extended maximal simple type of
$W$
be the Stevens–Paskunas explicit Whittaker function associated to an extended maximal simple type of
![]() $\unicode[STIX]{x1D70B}_{1}$
as in the statement of Theorem 9.1.
$\unicode[STIX]{x1D70B}_{1}$
as in the statement of Theorem 9.1.
Lemma 10.2. The explicit Whittaker functions
![]() $W$
and
$W$
and
![]() $\unicode[STIX]{x1D712}W^{\vee }$
lie in the
$\unicode[STIX]{x1D712}W^{\vee }$
lie in the
![]() $\overline{\mathbb{Z}_{\ell }}$
-submodules
$\overline{\mathbb{Z}_{\ell }}$
-submodules
![]() $W_{e}(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713}_{t})$
and
$W_{e}(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713}_{t})$
and
![]() $W_{e}(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}_{t}^{-1})$
respectively.
$W_{e}(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}_{t}^{-1})$
respectively.
Proof. As in the proof of Theorem 9.1, the representation
![]() $\unicode[STIX]{x1D70B}_{1}$
contains an extended maximal simple type
$\unicode[STIX]{x1D70B}_{1}$
contains an extended maximal simple type
![]() $(\mathbf{J}_{1},\unicode[STIX]{x1D6EC}_{1})$
and
$(\mathbf{J}_{1},\unicode[STIX]{x1D6EC}_{1})$
and
![]() $W$
is chosen to be the Paskunas–Stevens Whittaker function of Definition 8.3 relative to this data. As
$W$
is chosen to be the Paskunas–Stevens Whittaker function of Definition 8.3 relative to this data. As
![]() $\unicode[STIX]{x1D70B}_{1}$
is integral,
$\unicode[STIX]{x1D70B}_{1}$
is integral,
![]() $\unicode[STIX]{x1D6EC}_{1}$
is integral by the end of Section 6. This implies that the trace character
$\unicode[STIX]{x1D6EC}_{1}$
is integral by the end of Section 6. This implies that the trace character
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6EC}_{1}}$
of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6EC}_{1}}$
of
![]() $\unicode[STIX]{x1D6EC}_{1}$
has values in
$\unicode[STIX]{x1D6EC}_{1}$
has values in
![]() $\overline{\mathbb{Z}_{\ell }}$
. In particular the Bessel function
$\overline{\mathbb{Z}_{\ell }}$
. In particular the Bessel function
![]() ${\mathcal{J}}_{1}$
(see Definition 8.1) associated to the pair
${\mathcal{J}}_{1}$
(see Definition 8.1) associated to the pair
![]() $(\mathbf{J}_{1},\unicode[STIX]{x1D6EC}_{1})$
takes values in
$(\mathbf{J}_{1},\unicode[STIX]{x1D6EC}_{1})$
takes values in
![]() $\overline{\mathbb{Z}_{\ell }}$
. Hence, as
$\overline{\mathbb{Z}_{\ell }}$
. Hence, as
![]() $\unicode[STIX]{x1D713}_{t}$
is integral,
$\unicode[STIX]{x1D713}_{t}$
is integral,
![]() $W\in W_{e}(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713}_{t})$
(see Definition 8.3). Now,
$W\in W_{e}(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713}_{t})$
(see Definition 8.3). Now,
![]() $\unicode[STIX]{x1D70B}_{2}$
is of the form
$\unicode[STIX]{x1D70B}_{2}$
is of the form
![]() $\unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
with
$\unicode[STIX]{x1D712}\unicode[STIX]{x1D70B}_{1}^{\vee }$
with
![]() $\unicode[STIX]{x1D712}$
an unramified character of
$\unicode[STIX]{x1D712}$
an unramified character of
![]() $F^{\times }$
(which is integral as
$F^{\times }$
(which is integral as
![]() $\unicode[STIX]{x1D712}$
is unramified), so Proposition 8.2(3) implies that the Bessel function
$\unicode[STIX]{x1D712}$
is unramified), so Proposition 8.2(3) implies that the Bessel function
![]() $\unicode[STIX]{x1D712}{\mathcal{J}}_{1}^{\vee }$
is integral. We conclude that
$\unicode[STIX]{x1D712}{\mathcal{J}}_{1}^{\vee }$
is integral. We conclude that
![]() $\unicode[STIX]{x1D712}W^{\vee }$
belongs to
$\unicode[STIX]{x1D712}W^{\vee }$
belongs to
![]() $W_{e}(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}_{t}^{-1})$
(see Definition 8.3 again).◻
$W_{e}(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}_{t}^{-1})$
(see Definition 8.3 again).◻
Granted
![]() $W\in W_{e}(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713}_{t})$
and
$W\in W_{e}(\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D713}_{t})$
and
![]() $\unicode[STIX]{x1D712}W^{\vee }\in W_{e}(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}_{t})$
, we have
$\unicode[STIX]{x1D712}W^{\vee }\in W_{e}(\unicode[STIX]{x1D70B}_{2},\unicode[STIX]{x1D713}_{t})$
, we have
Notice that
![]() $r_{\ell }(q^{r}(q-1)(q^{n/e}-1))$
is nonzero if and only if
$r_{\ell }(q^{r}(q-1)(q^{n/e}-1))$
is nonzero if and only if
![]() $\unicode[STIX]{x1D70B}_{1}$
(hence
$\unicode[STIX]{x1D70B}_{1}$
(hence
![]() $\unicode[STIX]{x1D70B}_{2}$
) is banal by the end of Section 6. As the integral
$\unicode[STIX]{x1D70B}_{2}$
) is banal by the end of Section 6. As the integral
![]() $I(X,r_{\ell }(W),r_{\ell }(\unicode[STIX]{x1D712}W^{\vee }),r_{\ell }(\mathbf{1}_{\mathfrak{o}_{F}^{n}}))$
belongs to the fractional ideal
$I(X,r_{\ell }(W),r_{\ell }(\unicode[STIX]{x1D712}W^{\vee }),r_{\ell }(\mathbf{1}_{\mathfrak{o}_{F}^{n}}))$
belongs to the fractional ideal
![]() $(L(X,\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2}))$
of
$(L(X,\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2}))$
of
![]() $\overline{\mathbb{F}_{\ell }}[X^{\pm 1}]$
, we deduce that
$\overline{\mathbb{F}_{\ell }}[X^{\pm 1}]$
, we deduce that
![]() $r_{\ell }(L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}))$
divides
$r_{\ell }(L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}))$
divides
![]() $L(X,\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2})$
. As in any case, thanks to [Reference Kurinczuk and Matringe8, Theorem 3.13], the
$L(X,\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2})$
. As in any case, thanks to [Reference Kurinczuk and Matringe8, Theorem 3.13], the
![]() $L$
-factor
$L$
-factor
![]() $L(X,\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2})$
divides
$L(X,\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2})$
divides
![]() $r_{\ell }(L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}))$
, we deduce the desired equality.◻
$r_{\ell }(L(X,\unicode[STIX]{x1D70B}_{1},\unicode[STIX]{x1D70B}_{2}))$
, we deduce the desired equality.◻
Acknowledgments
We thank Paul Broussous and Shaun Stevens for stimulating discussions, and Jim Cogdell for bringing the test vector problem to our attention. We thank the referee for a very thorough review which improved greatly the presentation and clarified certain parts of the arguments. This work has benefited from the support of the Heilbronn Institute for Mathematical Research, GDRI 571 “French–British–German network in Representation Theory”, and from the grant ANR-13-BS01-0012 FERPLAY.