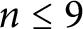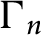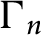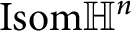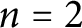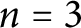Hyperbolic Coxeter groups of minimal growth rates in higher dimensions

Abstract

The cusped hyperbolic n-orbifolds of minimal volume are well known for $n\leq 9$ . Their fundamental groups are related to the Coxeter n-simplex groups $\Gamma _{n}$ . In this work, we prove that $\Gamma _{n}$ has minimal growth rate among all non-cocompact Coxeter groups of finite covolume in $\textrm{Isom}\mathbb H^{n}$ . In this way, we extend previous results of Floyd for $n=2$ and of Kellerhals for $n=3$ , respectively. Our proof is a generalization of the methods developed together with Kellerhals for the cocompact case.

1 Introduction

Let $\mathbb H^{n}$ denote the real hyperbolic n-space with its isometry group $\textrm{Isom}\mathbb H^{n}$ .

A hyperbolic Coxeter polyhedron $P\subset \mathbb H^{n}$ is a convex polyhedron of finite volume all of whose dihedral angles are integral submultiples of $\pi $ . Associated to P is the hyperbolic Coxeter group $\Gamma \subset \textrm{Isom}\mathbb H^{n}$ generated by the reflections in the bounding hyperplanes of P. By construction, $\Gamma $ is a discrete group with associated orbifold $O^{n}=\mathbb H^{n} / \Gamma $ of finite volume.

We focus on non-compact hyperbolic Coxeter polyhedra, having at least one ideal vertex $v_{\infty } \in \partial \mathbb H^{n}$ . Notice that the stabilizer of the vertex $v_{\infty }$ is isomorphic to an affine Coxeter group. The group $\Gamma $ is called non-cocompact, and its quotient space $O^{n}$ has at least one cusp.

The hyperbolic Coxeter group $\Gamma $ is the geometric realization of an abstract Coxeter system $(W,S)$ consisting of a group W with a finite generating set S together with the relations $s^{2}=1$ and $(ss^{\prime })^{m_{ss^{\prime }}}=1$ , where $m_{ss^{\prime }}=m_{s^{\prime }s}\in \{2,3,\ldots ,\infty \}$ for all $s,s^{\prime }\in S$ with $s\not =s^{\prime }$ . The growth series $f_{S}(t)$ of $W=(W,S)$ is given by

$$ \begin{align*}f_{S}(t)=1+\sum\limits_{k\ge1}a_{k}t^{k} \, , \end{align*} $$

where $a_{k}\in \mathbb Z$ is the number of elements in W with S-length k. The growth rate $\tau _{W}$ of $W=(W,S)$ is defined as the inverse of the radius of convergence of $f_{S}(t)$ .

We are interested in small growth rates of non-cocompact hyperbolic Coxeter groups in $\textrm{Isom}\mathbb H^{n}$ for $n\geq 2$ . For $n=2$ , Floyd [6] showed that the Coxeter group $\Gamma _{2} = [3,\infty ]$ generated by the reflections in the triangle with angles $\pi /2, \pi /3$ , and $0$ is the (unique) group of minimal growth rate. For $n=3$ , Kellerhals [13] proved that the tetrahedral group $\Gamma _{3}$ generated by the reflections in the Coxeter tetrahedron with symbol $[6,3,3]$ realizes minimal growth rate in a unique way.

Consider the hyperbolic Coxeter n-simplices and their reflection groups $\Gamma _{n} \subset \textrm{Isom}\mathbb H^{n}$ depicted in Table 1. For their volumes, we refer to [12]. Observe that $\Gamma _{n}$ is of minimal covolume among all non-cocompact hyperbolic Coxeter n-simplex groups.

Table 1 The hyperbolic Coxeter n-simplex group $\Gamma _{n}$ .

The aim of this work is to prove the following result in the context of growth rates.

Theorem Let $2\leq n \leq 9$ . Among all non-cocompact hyperbolic Coxeter groups of finite covolume in $\operatorname {Isom} \mathbb H^{n}$ , the group $\Gamma _{n}$ given in Table 1 has minimal growth rate, and as such the group is unique.

Our Theorem should be compared with the volume minimality results for cusped hyperbolic n-orbifolds $O^{n}$ for $2\le n \le 9$ . These results are due to Siegel [16] for $n=2$ , Meyerhoff [15] for $n= 3$ , Hild and Kellerhals [10] for $n=4$ , and Hild [9] for $n\le 9$ . Indeed, the fundamental group of $O^{n}$ is related to $\Gamma _{n}$ in all these cases.

The work is organized as follows. In Section 2.1, we set the background about hyperbolic Coxeter polyhedra and their associated reflection groups. Furthermore, we present a result of Felikson and Tumarkin about their combinatorics as given by [5, Theorem B], which will play a crucial role in our proof. In fact, we will exploit the (non-)simplicity of the Coxeter polyhedra in a most useful way. In Section 2.2, we discuss growth series and growth rates of Coxeter groups and introduce the notion of extension of a Coxeter graph. We also provide some illustrating examples. The monotonicity result of Terragni [18] for growth rates, presented in Theorem 2.2, will be another major ingredient in our proof. Finally, Section 3 is devoted to the proof of our result. We perform it in two steps by assuming that the Coxeter graph under consideration has an affine component of type $\widetilde A_{1}$ or not.

2 Hyperbolic Coxeter groups and growth rates

2.1 Coxeter polyhedra and their reflection groups

Let $\mathbb X^{n}$ denote one of the geometric n-spaces of constant curvature, the unit n-sphere $\mathbb S^{n}$ , the Euclidean n-space $\mathbb E^{n}$ , or the real hyperbolic n-space $\mathbb H^{n}$ . As usual, we embed $\mathbb X^{n}$ in a suitable quadratic space $\mathbb Y^{n+1}$ . In the Euclidean case, we take the affine model and write $\mathbb E^{n}=\{ x \in \mathbb E^{n+1} \mid x_{n+1}=0\}$ . In the hyperbolic case, we interpret $\mathbb H^{n}$ as the upper sheet of the hyperboloid in $\mathbb R^{n+1}$ , that is,

$$ \begin{align*} \mathbb H^{n}=\{x\in\mathbb R^{n+1}\mid \,\langle x,x\rangle_{n,1}\,=-1\,,\,x_{n+1}>0\}, \end{align*} $$

where $\,\langle x,x\rangle _{n,1}\,=x_{1}^{2}+\cdots +x_{n}^{2}-x_{n+1}^{2}$ is the standard Lorentzian form. Its boundary $\partial \mathbb H^{n}$ can be identified with the set

$$ \begin{align*} \partial \mathbb H^{n}=\{x\in\mathbb R^{n+1}\mid \,\langle x,x\rangle_{n,1}\,=0\,,\,\sum_{k=1}^{n+1}x_{k}^{2}=1\,,\,x_{n+1}>0\}. \end{align*} $$

In this picture, the isometry group of $\mathbb H^{n}$ is isomorphic to the group $O^{+}(n,1)$ of positive Lorentzian matrices leaving the bilinear form $\langle \,, \rangle _{n,1}$ and the upper sheet invariant.

It is well known that each isometry of $\mathbb X^{n}$ is a finite composition of reflections in hyperplanes, where a hyperplane $H=H_{v}$ in $\mathbb X^{n}$ is characterized by a normal unit vector $v \in \mathbb Y^{n+1}$ . Associated to $H_{v}$ are two closed half-spaces. We denote by $H^{-}_{v}$ the half-space in $\mathbb X^{n}$ with outer normal vector v.

A (convex) n-polyhedron $P= \cap _{i\in I} H_{i}^{-} \subset \mathbb X^{n}$ is the non-empty intersection of a finite number of half-spaces $H_{i}^{-}$ bounded by the hyperplanes $H_{i}=H_{v_{i}}$ for $i\in I$ . A facet of P is of the form $F_{i}=P\cap H_{i}$ for some $i\in I$ . In the sequel, for $\mathbb X^{n} \neq \mathbb S^{n}$ , we always assume that P is of finite volume. In the Euclidean case, this implies that P is compact, and in the hyperbolic case, P is the convex hull of finitely many points $v_{1},\ldots ,v_{k} \in \mathbb H^{n} \cup \partial \mathbb H^{n}$ . If $v_{i} \in \mathbb H^{n}$ , then $v_{i}$ is an ordinary vertex, and if $v_{i}\in \partial \mathbb H^{n}$ , then $v_{i}$ is an ideal vertex of P, respectively.

If all dihedral angles $\alpha _{ij}=\measuredangle (H_{i},H_{j})$ formed by intersecting hyperplanes $H_{i}, H_{j}$ in the boundary of P are either zero or of the form $\frac {\pi }{m_{ij}}$ for an integer $m_{ij} \geq 2$ , then P is called a Coxeter polyhedron in $\mathbb X^{n}$ . Observe that the Gram matrix $\text {Gr}(P)=(\langle v_{i}, v_{j}\rangle _{\mathbb Y^{n+1}})_{i,j\in I}$ is a real symmetric matrix with $1$ ’s on the diagonal and non-positive coefficients off the diagonal. In this way, the theory of Perron–Frobenius applies. For further details and references about Coxeter polyhedra in $\mathbb X^{n}$ , we refer to [4, 19, 20].

Let $P= \cap _{i=1}^{N} H_{i}^{-}\subset \mathbb X^{n}$ be a Coxeter n-polyhedron. Denote by $r_{i}=r_{H_{i}}$ the reflection in the bounding hyperplane $H_{i}$ of P, and let $G=G_{P}$ be the group generated by $r_{1}, \ldots , r_{N}$ . It follows that G is a discrete subgroup of finite covolume in $\textrm{Isom}\mathbb X^{n}$ , called a geometric Coxeter group.

A geometric Coxeter group $G\subset \textrm{Isom}\mathbb X^{n}$ with generating system $S=\{r_{1},\ldots ,r_{N}\}$ is the geometric realization of an abstract Coxeter system $(W,S)$ . In fact, we have $r_{i}^{2}=1$ and $(r_{i}r_{j})^{m_{ij}}=1$ with $m_{ij}=m_{ji}\in \{2,3,\ldots ,\infty \}$ as above. Here, $m_{ij}=\infty $ indicates that $r_{i}r_{j}$ is of infinite order.

For $\mathbb X^{n}= \mathbb S^{n}$ , G is a spherical Coxeter group and as such finite. For $\mathbb X^{n}= \mathbb E^{n}$ , G is a Euclidean or affine Coxeter group and of infinite order. By a result of Coxeter [3], the irreducible spherical and Euclidean Coxeter groups are entirely classified. In contrast to this fact, hyperbolic Coxeter groups are far from being classified. For a survey about partial classification results, we refer to [4].

For the description of abstract and geometric Coxeter groups, one commonly uses the language of weighted graphs and Coxeter symbols. Let $(W,S)$ be an abstract Coxeter system with generating system $S=\{s_{1},\ldots ,s_{N}\}$ and relations of the form $s_{i}^{2}=1$ and $s_{i}s_{j}^{m_{ij}}=1$ with $m_{ij}=m_{ji}\in \{2,3,\ldots ,\infty \}$ . The Coxeter graph of the Coxeter system $(W,S)$ is the non-oriented graph $\Sigma $ whose nodes correspond to the generators $s_{1},\ldots ,s_{N}$ . If $s_{i}$ and $s_{j}$ do not commute, their nodes $n_{i},n_{j}$ are connected by an edge with weight $m_{ij}\geq 3$ . We omit the weight $m_{ij}=3$ since it occurs frequently. The number N of nodes is the order of $\Sigma $ . A subgraph $\sigma \subset \Sigma $ corresponds to a special subgroup of $(W,S)$ , that is, a subgroup of the form $(W_{T},T)$ for a subset $T\subset S$ . Observe that the Coxeter graph $\Sigma $ is connected if $(W,S)$ is irreducible.

In the case of a geometric Coxeter group $G=(W,S)\subset \textrm{Isom}\mathbb X^{n}$ , we call its Coxeter graph $\Sigma $ spherical, affine, or hyperbolic, if $\mathbb X^{n}=\mathbb S^{n}, \mathbb E^{n}$ , or $\mathbb H^{n}$ , respectively. In Table 2, we reproduce all the connected affine Coxeter graphs, using the classical notation, with the exception of the three groups $\widetilde E_{6}, \widetilde E_{7}, \widetilde E_{8}$ (they will not appear in the following).

Table 2 Connected affine Coxeter graphs of order $n+1$ .

An abstract Coxeter group with a simple presentation can conveniently be described by its Coxeter symbol. For example, the linear Coxeter graph with edges of successive weights $k_{1},\ldots ,k_{N}\geq 3$ is abbreviated by the Coxeter symbol $[k_{1},\ldots ,k_{N}]$ . The Y-shaped graph made of one edge with weight p and of two strings of k and l edges emanating from a central vertex of valency $3$ is denoted by $[p,3^{k,l}]$ (see [12]).

Let us specify the context and consider a Coxeter polyhedron $P = \cap _{i=1}^{N} H_{i}^{-} \subset \mathbb H^{n}$ . Denote by $\Gamma = G_{P} \subset \textrm{Isom}\mathbb H^{n}$ its associated Coxeter group and by $\Sigma $ its Coxeter graph. Since P is of finite volume, the graph $\Sigma $ is connected. Furthermore, if P is not compact, then P has at least one ideal vertex.

Let $v \in \mathbb H^{n}$ be an ordinary vertex of P. Then, its link $L_{v}$ is the intersection of P with a small sphere of center v that does not intersect any facet of P not incident to v. It corresponds to a spherical Coxeter polyhedron of $ \mathbb S^{n-1}$ and therefore to a spherical Coxeter subgraph $\sigma $ of order n in $\Sigma $ .

Let $v_{\infty } \in \partial \mathbb H^{n}$ be an ideal vertex of P. Then, its link, denoted by $L_{\infty }$ , is given by the intersection of P with a sufficiently small horosphere centered at $v_{\infty }$ as above. The link $L_{\infty }$ corresponds to a Euclidean Coxeter polyhedron in $\mathbb E^{n-1}$ and is related to an affine Coxeter subgraph $\sigma _{\infty }$ of order $\geq n$ in $\Sigma $ .

More precisely, if $v_{\infty }$ is a simple ideal vertex, that is, $v_{\infty }$ is the intersection of exactly n among the N bounding hyperplanes of P, the Coxeter graph $\sigma _{\infty }$ is connected and of order n. Otherwise, $\sigma _{\infty }$ has $n_{c}(\sigma _{\infty }) \geq 2$ affine components, and we have the following formula:

(1) $$ \begin{align} n-1=\text{order}(\sigma_{\infty})-n_{c}(\sigma_{\infty}) . \end{align} $$

Recall that a polyhedron is simple if all of its vertices are simple.

As in the spherical and Euclidean cases, hyperbolic Coxeter simplices in $\mathbb H^{n}$ are all known, and they exist for $n\le 9$ (see [1] or [20]). A list of their Coxeter graphs, Coxeter symbols, and volumes can be found in [12]. Among the related Coxeter n-simplex groups, the group $\Gamma _{n}$ , as given in Table 1, is of minimal covolume.

The following structural result for simple hyperbolic Coxeter polyhedra due to Felikson and Tumarkin [5, Theorem B] will be a corner stone for the proof of our Theorem.

Theorem 2.1 Let $n \leq 9$ , and let $P\subset \mathbb H^{n}$ be a non-compact simple Coxeter polyhedron. If all facets of P are mutually intersecting, then P is either a simplex or isometric to the polyhedron $P_{0}$ whose Coxeter graph is depicted in Figure 1.

Figure 1 The Coxeter polyhedron $P_{0}\subset \mathbb H^{4}$ .

2.2 Growth rates and their monotonicity

Let $(W,S)$ be a Coxeter system and denote by $a_{k}\in \mathbb Z$ the number of elements $w\in W$ with S-length k. The growth series $f_{S}(t)$ of $(W,S)$ is defined by

$$ \begin{align*} f_{S}(t)=1+\sum\limits_{k\ge1}a_{k}t^{k}.\end{align*} $$

In the following, we list some properties of $f_{S}(t)$ . For references, we refer to [11].

There is a formula due to Steinberg expressing the growth series $f_{S}(t)$ of a Coxeter system $(W,S)$ in terms of its finite special subgroups $W_{T}$ for $T\subseteq S\,,$

(2) $$ \begin{align} \frac{1}{f_{S}(t^ {-1})}=\sum\limits_{{W_{T}<W\atop\scriptscriptstyle{{\vert W_{T}\vert<\infty}}}}\, \frac{(-1)^{\vert T\vert}}{f_{T}(t)}, \end{align} $$

where $W_{\varnothing }=\{1\}$ . By a result of Solomon, the growth polynomial of each term $f_{T}(t)$ in (2) can be expressed by means of its exponents $\{m_{1},m_{2},\ldots ,m_{p}\}$ according to the formula

(3) $$ \begin{align} f_{T}(t)=\prod\limits_{i=1}^ {p}\,[m_{i}+1], \end{align} $$

where $\,[k]=1+t+\cdots + t^{k-1}$ and, more generally, $\,[k_{1},\ldots ,k_{r}]:=[k_{1}]\cdots [k_{r}]\,$ . A complete list of the irreducible spherical Coxeter groups together with their exponents can be found in [14]. For example, the exponents of the Coxeter group $\text {A}_{n}$ with Coxeter graph are $\{1,2,\ldots ,n\}$ so that

(4) $$ \begin{align} f_{A_{n}}(t)=[2,\ldots,n+1]. \end{align} $$

Furthermore, the growth series of a reducible Coxeter system $(W,S)$ with factor groups $(W_{1},S_{1})$ and $(W_{2},S_{2})$ such that $S=(S_{1}\times \{1_{W_{2}}\})\cup (\{1_{W_{1}}\}\times S_{2})$ satisfies the product formula

$$ \begin{align*} f_{S}(t)=f_{S_{1}}(t)\cdot f_{S_{1}}(t). \end{align*} $$

In its disk of convergence, the growth series $f_{S}(t)$ is a rational function, which can be expressed as the quotient of coprime monic polynomials $p(t), q(t)\in \mathbb Z[t]$ of the same degree. The growth rate $\tau _{W}=\tau _{(W,S)}$ is defined by the inverse of the radius of convergence of $f_{S}(t)$ and can be expressed by

$$ \begin{align*} \tau_{W}=\limsup_{k\rightarrow\infty} {a_{k}}^{1/k}. \end{align*} $$

It is the inverse of the smallest positive real pole of $f_{S}(t)$ and hence an algebraic integer.

Important for the proof of our Theorem is the following result of Terragni [17] about the growth monotonicity.

Theorem 2.2 Let $(W,S)$ and $(W^{\prime },S^{\prime })$ be two Coxeter systems such that there is an injective map $ \iota :S\rightarrow S^{\prime } $ with $ m_{st} \le m^{\prime }_{\iota (s)\iota (t)}$ for all $ s,t\in S$ . Then, $\tau _{(W,S)}\le \tau _{(W^{\prime },S^{\prime })}.$

For $n\geq 2$ , consider a Coxeter group $\Gamma \subset \textrm{Isom}\mathbb H^{n}$ of finite covolume. By results of Milnor and de la Harpe, we know that $\tau _{\Gamma }>1$ . More precisely, and as shown by Terragni [17], $ \tau _{\Gamma } \geq \tau _{\Gamma _{9}} \approx 1.1380 $ , where $\Gamma _{9}$ is the Coxeter simplex group given in Table 1.

Next, we introduce another tool in the proof of our result, the (simple) extension of a Coxeter graph.

Definition 2.1 Let $\Sigma $ be an abstract Coxeter graph. A (simple) extension of $\Sigma $ is a Coxeter graph $\Sigma ^{\prime }$ obtained by adding one node linked with a (simple) edge to the Coxeter graph $\Sigma $ .

As a direct consequence of Theorem 2.2, if W is a Coxeter group with Coxeter graph $\Sigma $ , any extension $\Sigma ^{\prime }$ of $\Sigma $ encodes a Coxeter group $W^{\prime }$ such that $\tau _{W}\leq \tau _{W^{\prime }}$ .

Example 2.3 Consider an irreducible affine Coxeter graph of order $3$ as given in Table 2. Up to symmetry, the graph $\widetilde {A}_{2}$ has a unique extension given by the Coxeter graph at the top left in Figure 2. This graph describes the Coxeter tetrahedron $[3,3^{[3]}]$ of finite volume. The Coxeter graphs $\widetilde C_{2}$ and $\widetilde G_{2}$ give rise to the remaining five extensions depicted in Figure 2. By a result of Kellerhals [13], these six Coxeter graphs describe Coxeter tetrahedral groups $\Lambda $ of finite covolume in $\textrm{Isom}\mathbb H^{3}$ whose growth rates satisfy $\tau _{\Lambda }\geq \tau _{\Gamma _{3}}$ .

Figure 2 Extensions of $\widetilde A_{2}$ , $\widetilde C_{2}$ , and $\widetilde G_{2}$ .

Example 2.4 In a similar way, any extension of an irreducible affine Coxeter graph of order $4$ yields a Coxeter simplex group of finite covolume in $\textrm{Isom}\mathbb H^{4}$ . They are given in Figure 3. Notice that $\Gamma _{4}=[4,3^{2,1}]$ is part of them.

Figure 3 Extensions of $\widetilde A_{3}$ , $\widetilde B_{3}$ , and $\widetilde C_{3}$ .

Remark 2.5 When considering irreducible affine Coxeter graphs of order greater than or equal to $5$ , the resulting extensions do not always relate to hyperbolic Coxeter n-simplex groups of finite covolume. For example, among the extensions of $\widetilde {F_{4}}$ , the graph depicted in Figure 4 describes an infinite volume simplex in $\mathbb H^{5}$ .

Figure 4 An infinite volume $5$ -simplex.

3 Proof of the Theorem

Let $2 \leq n\leq 9$ , and consider the Coxeter simplex group $\Gamma _{n} \subset \textrm{Isom}\mathbb H^{n}$ whose Coxeter graph is depicted in Table 1. In this section, we provide the proof of our main result stated as follows.

Theorem For any $2 \leq n\leq 9$ , the group $\Gamma _{n} $ has minimal growth rate among all non-cocompact hyperbolic Coxeter groups of finite covolume in $\textrm{Isom}\mathbb H^{n}$ , and as such the group is unique.

For $n=2$ and for $n=3$ , the result has been established by Floyd [6] and Kellerhals [13]. Therefore, it suffices to prove the Theorem for $4\le n \le 9$ .

Observe that the growth rates of all Coxeter simplex groups in $\textrm{Isom}\mathbb H^{n}$ are known. Their list can be found in [17]. In particular, one deduces the following strict inequalities:

(5) $$ \begin{align} \tau_{\Gamma_{9}} \approx 1.1380 < \cdots < \tau_{\Gamma_{5}} \approx 1.2481 < \tau_{\Gamma_{4}} \approx 1.3717 , \end{align} $$

(6) $$ \begin{align} \tau_{\Gamma_{5}} < \tau_{\Gamma_{3}}\approx 1.2964 . \end{align} $$

For a fixed dimension n, one also checks that $\Gamma _{n}$ has minimal growth rate among (all the finitely many) non-cocompact Coxeter simplex groups $\Lambda \subset \textrm{Isom}\mathbb H^{n}$ .

As a consequence, we focus on hyperbolic Coxeter groups $\Gamma \subset \textrm{Isom}\mathbb H^{n}$ generated by at least $N \geq n+2$ reflections in the facets of a non-compact finite volume Coxeter polyhedron $P\subset \mathbb H^{n}$ . We have to show that $\tau _{\Gamma _{n}}<\tau _{\Gamma }$ , which yields unicity of the group $\Gamma _{n}$ with this property.

Suppose that the Coxeter polyhedron P is simple. By Theorem 2.1, P is either isometric to the polyhedron $P_{0}\subset \textrm{Isom}\mathbb H^{4}$ depicted in Figure 1, or P has a pair of disjoint facets. For the growth rate $\tau $ of the Coxeter group associated to $P_{0}$ , one easily checks with help of the software CoxIter [7, 8] that $\tau _{\Gamma _{4}} <\tau \approx 2.8383 $ . Hence, we can assume that P is not isometric to $P_{0}$ . If P has a pair of disjoint facets, then the Coxeter graph $\Sigma $ of P and its associated group $\Gamma $ contains a subgraph .

The property that the Coxeter graph $\Sigma $ contains such a subgraph of type $\widetilde A_{1} = [\infty ]$ allows us to conclude the proof, whether the polyhedron P is simple or not. In the following, we first look at this property and analyze it more closely.

3.1 In the presence of $\widetilde A_{1}$

We start by considering particular Coxeter graphs of order $4$ containing $\widetilde A_{1}$ . Their related growth rates will be useful when comparing with the one of $\Gamma $ . This approach is similar to the one developed in [2].

Let $W_{0} = [\infty ,3,3]$ be the abstract Coxeter group depicted in Figure 5. By means of the software CoxIter, one checks that

(7) $$ \begin{align} \tau_{\Gamma_{4}}< \tau_{W_{0}} \approx 1.4655 . \end{align} $$

Figure 5 The Coxeter group $W_{0}=[\infty ,3,3]$ .

Furthermore, consider the two abstract Coxeter groups $W_{1}=[3,\infty ,3]$ and $W_{2}=[\infty , 3^{1,1}]$ given in Figure 6.

Figure 6 The Coxeter groups $W_{1}=[3,\infty ,3]$ and $W_{2}=[\infty , 3^{1,1}]$ .

For their growth rates, we prove the following auxiliary result.

Lemma 3.1 $\tau _{W_{0}} < \tau _{W_{1}}$ and $ \tau _{W_{0}}< \tau _{W_{2}}$ .

Proof For $0\leq i\leq 2$ , denote by $f_{i}:=f_{W_{i}}$ the growth series of $W_{i}$ and by $R_{i}$ its radius of convergence. Recall that $R_{i}$ is the smallest positive pole of $f_{i}$ , and that $\tau _{W_{i}}=\frac 1{R_{i}}$ .

We establish the growth functions $f_{i}$ according to Steinberg’s formula (2). They are given as follows:

$$ \begin{align*} \begin{array}{lll} \frac{1}{f_{0}(t^{-1})}=& 1-\frac{4}{[2]}+\frac3{[2,2]}+\frac2{[2,3]}- \frac1{[2,2,3]}-\frac1{[2,3,4]} , \\ \\ \frac{1}{f_{1}(t^{-1})}= &1-\frac{4}{[2]}+\frac3{[2,2]} +\frac2{[2,3]}- \frac2{[2,2,3]} , \\ \\ \frac{1}{f_{2}(t^{-1})}=& 1-\frac{4}{[2]}+\frac3{[2,2]}+\frac2{[2,3]}- \frac1{[2,2,2]}-\frac1{[2,3,4]}. \end{array} \end{align*} $$

Hence, for any $t>0$ , one has the positive difference functions given by

$$ \begin{align*} \begin{array}{lll} \frac1{f_{0}(t^{-1})}-\frac{1}{f_{1}(t^{-1})}&=\frac1{[2,2,3]} - \frac1{[2,3,4]} =\frac{t^{2}+t^{3}}{[2,2,3,4]}> 0 , \\ \\ \frac1{f_{0}(t^{-1})}-\frac{1}{f_{2}(t^{-1})}&=\frac1{[2,2,2]} - \frac1{[2,2,3]} =\frac{t^{2}}{[2,2,2,3]} > 0. \end{array} \end{align*} $$

Therefore, for $i=1,2$ , and for $u=t^{-1}\in (0,1)$ , the smallest positive root $R_{0}$ of $\frac 1{f_{0}(u)}$ is strictly bigger than the one of $\frac 1{f_{i}(u)}$ . This finishes the proof.

As a first consequence, combining (5), (7), and Lemma 3.1, one obtains that

(8) $$ \begin{align} \tau_{\Gamma_{n}} <\tau_{W_{i}}, \quad \end{align} $$

for all $4\leq n \leq 9$ and $0\le i \le 2$ .

Next, suppose that the Coxeter graph $\Sigma $ of $\Gamma $ contains a subgraph $\widetilde A_{1}$ . Since $\Sigma $ is connected of order $N \geq n+2 \geq 6$ , the subgraph $\widetilde A_{1}$ is contained in a connected subgraph $\sigma $ of order $4$ in $\Sigma $ , which is related to a special subgroup W of $\Gamma $ . By Theorem 2.2, one has that $\tau _{W_{i}}\leq \tau _{W}$ for some $0\le i \le 2$ . By combining (8) with these findings, and by Theorem 2.2 and Lemma 3.1, one deduces that

(9) $$ \begin{align} \tau_{\Gamma_{n}} < \tau_{W_{0}} \le \tau_{W} \le \tau_{\Gamma} . \end{align} $$

This finishes the proof of the Theorem in the presence of a subgraph $\widetilde A_{1}$ in $\Sigma $ .

3.2 In the absence of $\widetilde A_{1}$

Suppose that the Coxeter graph $\Sigma $ with $N\geq n+2$ nodes does not contain a subgraph of type $\widetilde A_{1}$ . In particular, by Theorem 2.1, the corresponding Coxeter polyhedron $P \subset \textrm{Isom}\mathbb H^{n}$ is not simple, and it follows that $5\le n\le 9$ .

Consider a non-simple ideal vertex $v_{\infty }\in P$ . Its link $L_{\infty } \subset \mathbb E^{n-1}$ is described by a reducible affine subgraph $\sigma _{\infty }$ with $n_{c}=n_{c}(\infty )\geq 2$ components which satisfies ${ n-1=\text {order}(\sigma _{\infty })-n_{c}}$ by (1). In Table 3, we list all possible realizations for $\sigma _{\infty }$ by using the following notations.

Let $\widetilde \sigma _{k}$ be a connected affine Coxeter graph of order $k\geq 3$ as listed in Table 2, and denote by $\bigsqcup \limits _{k} \widetilde \sigma _{k}$ the Coxeter graph consisting of the components of type $\widetilde \sigma _{k}$ .

Observe that for any graph $\bigsqcup \limits _{k} \widetilde \sigma _{k}$ in Table 3, one has $3\leq \min \limits _{k} k \leq 5$ , and that the case $\min \limits _{k} k=5$ appears only when $n=9$ .

Among the different components of $\sigma _{\infty }$ , we consider the ones of smallest order $\geq 3$ together with their extensions.

Table 3 Reducible affine Coxeter graphs $\sigma _{\infty }$ with $n_{c}\geq 2$ components $\widetilde \sigma _{k}$ of order $k\geq 3$ such that $n=\text {order}(\sigma _{\infty })-n_{c}+1$ .

$\bullet \quad $ Assume that the graph $\sigma _{\infty }$ of the vertex link $L_{\infty }$ contains an affine component $\widetilde \sigma $ of order $3$ . By Example 2.3, we know that any extension of $\widetilde \sigma $ encodes a Coxeter tetrahedral group $\Lambda \subset \textrm{Isom}\mathbb H^{3}$ of finite covolume. The graph $\Sigma $ itself contains a subgraph $\sigma $ of order $4$ which in turn comprises $\widetilde \sigma $ . The Coxeter graph $\sigma $ corresponds to a special subgroup W of $\Gamma $ , and by Theorem 2.2, we deduce that $\tau _{\Lambda }\leq \tau _{W}$ .

Since $\tau _{\Gamma _{3}}\le \tau _{\Lambda }$ , and in view of (5) and (6), Theorem 2.2 yields the desired inequality

(10) $$ \begin{align} \tau_{\Gamma_{n}} < \tau_{\Gamma_{3}} \leq \tau_{\Lambda} \leq \tau_{W} \leq \tau_{\Gamma} , \end{align} $$

which finishes the proof in this case, and for $n=5$ and $n=6$ ; see Table 3.

$\bullet \quad $ Assume that the graph $\sigma _{\infty }$ contains an affine component $\widetilde \sigma $ of order $4$ . We apply the same reasoning as above. By Example 2.4, any extension of $\widetilde \sigma $ corresponds to a Coxeter 4-simplex group $\Lambda $ of finite covolume, and $\tau _{\Gamma _{4}} \leq \tau _{\Lambda }$ . Again, $\Sigma $ contains a subgraph $\sigma $ comprising $\widetilde \sigma $ . Hence, there exists a special subgroup W of $\Gamma $ described by $\sigma $ so that

(11) $$ \begin{align} \tau_{\Gamma_{n}} < \tau_{\Gamma_{4}} \leq \tau_{\Lambda} \leq \tau_{W} \leq \tau_{\Gamma} . \end{align} $$

By (10) and (11), the proof is finished in this case, and for $n=7$ and $n=8$ ; see Table 3.

$\bullet \quad $ Assume that $\sigma _{\infty }$ contains an affine component $\widetilde \sigma $ of order $5$ . By Table 3, one has $7\leq n\leq 9$ . It is not difficult to list all possible extensions of $\widetilde \sigma $ . There are exactly 15 such extensions. It turns out that there are 11 extensions that encode Coxeter $5$ -simplex groups of finite covolume, whereas the remaining 4 extensions describe $5$ -simplex groups $\Delta _{i}, i=1,\ldots ,4,$ of infinite covolume. These last four simplices arise by extending $\widetilde B_{4}$ , $\widetilde C_{4}$ , and $\widetilde F_{4}$ . They are given in Figure 7, together with their associated growth rates computed with CoxIter.

Figure 7 The Coxeter groups $\Delta _{i}, i=1,\ldots ,4$ .

In view of (5), it turns out that

(12) $$ \begin{align} \tau_{\Gamma_{5}}<\tau_{\Delta_{i}}, \quad \text{ for } i=1,\ldots,4 . \end{align} $$

As above, the component $\widetilde \sigma $ lies in a subgraph $\sigma $ of order $6$ in $\Sigma $ , and the latter corresponds to a special subgroup W of $\Gamma $ so that

$$ \begin{align*} \text{ either } \quad \tau_{\Lambda}\leq \tau_{W} \quad\text{ or } \quad \tau_{\Delta_{i}}\leq \tau_{W}, \quad \quad 1\leq i\leq 4\ , \end{align*} $$

where $\Lambda $ is a Coxeter $5$ -simplex group of finite covolume. Since $ \tau _{ \Gamma _{5}} \leq \tau _{\Lambda }$ , and by (5) and (12), one deduces that

(13) $$ \begin{align} \tau_{\Gamma_{n}} < \tau_{ \Gamma_{5}} \leq \tau_{W} \leq \tau_{\Gamma}. \end{align} $$

This finishes the proof of this case.

Finally, all the above considerations allow us to conclude the proof of the Theorem.