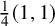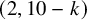Analytic torsion for log-Enriques surfaces and Borcherds product

Abstract

We introduce a holomorphic torsion invariant of log-Enriques surfaces of index two with cyclic quotient singularities of type $\frac {1}{4}(1,1)$ . The moduli space of such log-Enriques surfaces with k singular points is a modular variety of orthogonal type associated with a unimodular lattice of signature $(2,10-k)$ . We prove that the invariant, viewed as a function of the modular variety, is given by the Petersson norm of an explicit Borcherds product. We note that this torsion invariant is essentially the BCOV invariant in the complex dimension $2$ . As a consequence, the BCOV invariant in this case is not a birational invariant, unlike the Calabi-Yau case.

1 Introduction

The analytic torsion, which is a certain combination of the determinants of Hodge Laplacians on differential forms, is an invariant of Riemannian manifolds defined by Ray and Singer [40] as an analytic analogue of the Reidemeister torsion, the first topological invariant that is not a homotopy invariant. It was proved independently by Cheeger [11] and Müller [38] that the analytic torsion and the Reidemeister torsion agree on closed manifolds (Ray-Singer conjecture). Ray and Singer [41] also introduced a version of the analytic torsion for complex manifolds, usually referred to as the holomorphic torsion. The holomorphic torsion has found significant applications in Arakelov theory, canonical metrics and mirror symmetry. Unlike its real analogue, it depends on the geometry and complex structure of the underlying complex manifold [6] (the anomaly formula), which gives rise to interesting functions on moduli spaces. In this paper, we focus on this aspect of holomorphic torsion: that is, its connection with modular forms.

In fact, Ray and Singer already noticed the remarkable connection. Using Kronecker’s first limit formula, Ray and Singer [41] computed the analytic torsion for elliptic curves and found it to be given in terms of the Jacobi $\Delta $ -function, a modular form of weight $12$ on $\mathbf H/\textrm {SL}(2, \mathbf Z)$ . Their result has since then been extended to higher genus Riemann surfaces by Zograf [51], McIntyre-Takhtajan [35], Kokotov-Korotkin [28] and McIntyre-Park [36]; Zograf and McIntyre-Takhtajan studied the analytic torsion of Riemann surfaces with respect to the hyperbolic metric, while Kokotov-Korotkin and McIntyre-Park studied it with respect to the (degenerate) flat metric attached to an abelian differential of the Riemann surface.

In dimension two, motivated by string duality, the second author [43] studied the case of $2$ -elementary $K3$ surfaces – that is, pairs consisting of a $K3$ surface X and a holomorphic involution $\iota :\, X\longrightarrow X$ (acting nontrivially on holomorphic two forms) – and introduced an (equivariant) holomorphic torsion invariant for those surfaces. By the global Torelli theorem for $K3$ surfaces, the moduli space of 2-elementary K3 surfaces of fixed topological type is a modular variety of orthogonal type, so the holomorphic torsion invariant is viewed as a function on such modular varieties. On orthogonal modular varieties, Borcherds [8] constructed a class of automorphic forms with remarkable properties as singular theta lifts of elliptic modular forms. These automorphic forms are called Borcherds products. It is shown that the holomorphic torsion invariant of $2$ -elementary $K3$ surfaces is given by the Petersson norm of a certain series of Borcherds products [45], [30].

If $\iota $ is fixed point free, then the quotient $Y=X/\iota $ is an Enriques surface whose holomorphic torsion invariant is given by one of the most remarkable Borcherds products, the Borcherds $\Phi $ -function of rank $10$ . In this paper, we extend this result to a class of singular rational surfaces called log-Enriques surfaces introduced by D.-Q. Zhang [47]. As in the case of Enriques surfaces, a log-Enriques surface Y is expressed as a quotient $Y=X/\iota $ , where X is a $K3$ surface with rational double points called the canonical covering of Y, and $\iota $ is an anti-symplectic involution on X free from fixed points outside the singular points. To be precise, our log-Enriques surfaces are those of index two in the sense of Zhang [47]. To obtain a nice moduli space, we restrict ourselves to the case where X has only nodes as its singular points. A log-Enriques surface with this property is called good in this paper. Then a good log-Enriques surface can admit at most $10$ singular points, any of which is a cyclic quotient singularity of type $\frac {1}{4}(1,1)$ . It turns out that the moduli space of good log-Enriques surfaces of k singular points is again a Zariski open subset of a modular variety of orthogonal type of dimension $10-k$ attached to a unimodular lattice of signature $(2,10-k)$ . Let us write ${\mathcal M}_{k}$ for this modular variety. When $k=8$ , we have ${\mathcal M}_{8}^{\textrm {odd}}$ and ${\mathcal M}_{8}^{\textrm {even}}$ , according to the parity of the unimodular lattice of signature $(2,2)$ . For simplicity, we write ${\mathcal M}_{8}$ for ${\mathcal M}_{8}^{\textrm {odd}}$ and ${\mathcal M}_{8}^{\textrm {even}}$ when there is no possibility of confusion. For a good log-Enriques surface Y with k singular points, we write ${\varpi }(Y)\in {\mathcal M}_k$ for the isomorphism class of Y. Interestingly enough, ${\mathcal M}_{k}$ can be identified with a Zariski open subset of the Kähler moduli of a Del Pezzo surface V of degree $\deg V = k$ , the modular variety given by $\mathcal {KM}(V)=\Omega _{H(V, {\mathbf Z})}/O^{+}(H(V, {\mathbf Z}))$ , where $H(V, {\mathbf Z})$ is the total cohomology lattice of V, $O^{+}(H(V, {\mathbf Z}))$ is its automorphism group and $\Omega _{H(V, {\mathbf Z})}$ is the domain of type IV attached to $H(V, {\mathbf Z})$ . (See Theorem 2.10.)

Analogously to the Enriques lattice, the Del Pezzo lattice $H(V, {\mathbf Z})$ admits a reflective modular form $\Phi _{V}$ on $\Omega _{H(V, {\mathbf Z})}$ for $O^{+}(H(V, {\mathbf Z}))$ of weight $\deg V+4$ , which is nowhere vanishing on the Zariski open subset corresponding to ${\mathcal M}_{k}$ and characterises the Heegner divisor of norm $(-1)$ -vectors [44]. In addition, $\Phi _{V}$ is the denominator function of a generalised Kac-Moody algebra with explicit Fourier series expansion by Gritsenko and Nikulin [22], [23]. (See Section 8 for more about $\Phi _{V}$ .)

On the other hand, even though they are rational surfaces, every log-Enriques surface Y admits a Ricci flat Kähler orbifold metric [27]. Let $\tau (Y)$ denote the analytic torsion of Y in the sense of X. Ma [32] (suitably normalised by volume; see Section 8.1, especially Theorem 8.3 and Theorem 8.4 for the precise definition). Then our main result says that $\tau (Y)$ is given by some power of the Petersson norm of the Borcherds product $\Phi _{V}$ .

Theorem 1.1. There exists a constant $C_{k}>0$ depending only on k such that for every good log-Enriques surface Y with k singular points,

$$ \begin{align*}\tau(Y) = C_{k} \left\|\Phi_{V}({\varpi}(Y))\right\|^{-1/4},\\[-15pt] \end{align*} $$

where V is a Del Pezzo surface of degree k.

It is important to note that our torsion invariant is essentially the complex $2$ -dimensional analogue of the BCOV invariant (See [3], [19], [17], [20]). In higher dimensions, Bershadsky, Cecotti, Ooguri and Vafa [3] introduced a certain combination of holomorphic torsions, called the BCOV torsion, and predicted the mirror symmetry at genus one as an equivalence of the BCOV torsion and certain curve counting invariants at genus one. The corresponding holomorphic torsion invariant of Calabi-Yau threefolds, called the BCOV invariant, was introduced by Fang, Lu and the second author [19], who verified some predictions in [3]. Very recently, the BCOV invariant is extended to Calabi-Yau manifolds of arbitrary dimension by Eriksson, Freixas i Montplet and Mourougane [17], who have established the mirror symmetry at genus one for the Dwork family in arbitrary dimension [18]. The notion of the BCOV invariant is further extended to a certain class of pairs by Y. Zhang [49], who, together with L. Fu, has established the birational invariance of the BCOV invariants [50], [20]. According to mirror symmetry, the BCOV invariants correspond to the topological string amplitudes whose modular properties are important features. In the final section, we will interpret Theorem 1.1 in terms of the BCOV torsion so that the BCOV invariant of good log-Enriques surfaces is expressed as the Borcherds product $\Phi _{V}$ , an infinite product of expected type in mirror symmetry. As log-Enriques surfaces are rational, the BCOV invariant is not a birational invariant in this case.

We remark that the equivalence of the analytic torsion of Ricci flat Enriques surfaces and the Borcherds $\Phi $ -function [43] may be viewed as the limiting case $k=0$ . Since $\tau (Y)$ is the analytic torsion of a resolution of Y with respect to a degenerate Ricci flat metric, our theorem may be viewed as a two-dimensional analogue of the theorems of Kokotov-Korotkin [28] and McIntyre-Park [36], as mentioned above. Because of the isomorphism between the complex structure moduli of good log-Enriques surfaces and the Kähler moduli of Del Pezzo surfaces, in view of mirror symmetry at genus one as mentioned above, it may be worth asking if the Fourier coefficients of the elliptic modular form appearing in the infinite product expansion of $\Phi _{V}$ are interpreted as some counting invariants of Del Pezzo surfaces. We also remark that by Theorem 1.1 and the recent result of S. Ma [29], the analytic torsion of good log-Enriques surfaces is obtained from the Borcherds $\Phi $ -function of rank $10$ by manipulating quasi-pullbacks successively. See Section 8.3 for the details.

Our method of proof, which should have independent interest and which carries out the program proposed in [44, Question 5.18] for $2$ -elementary $K3$ surfaces, is to de-singularise the double covering of Y via the Eguchi-Hanson instanton to obtain a $2$ -elementary $K3$ surface $(\widetilde {X},\theta )$ and study the limiting behaviour of the (equivariant) analytic torsion of $(\widetilde {X},\theta )$ , as well as other constituents of the invariant $\tau (\widetilde {X}, \theta )$ of $(\widetilde {X}, \theta )$ , as $\widetilde {X}$ degenerates into the orbifold double covering X of Y. As a result, the ratio $\tau (Y)/\tau (\widetilde {X}, \theta )^{1/2}$ may be viewed as the (equivariant) analytic torsion of the Eguchi-Hanson instanton (compare Theorem 7.12). In [5], Bismut computed the behaviour of Quillen metrics when the exceptional divisor is blown down to a smooth point. In this paper, we study the same type of problem, where the blowing-up of ${\mathbf C}^{2}$ will be replaced by the Eguchi-Hanson instanton. We remark that Theorem 1.1 would be proved in the same way as in [43] by making use of the fundamental theorems for Quillen metrics such as the curvature formula, anomaly formula and embedding formula [4], [6], [7], [31], whose extensions to orbifolds were obtained by X. Ma [32], [33], if we could understand degenerations of log Enriques surfaces. On the other hand, it would be difficult to understand the geometric meaning of the ratio $\tau (Y)/\tau (\widetilde {X}, \theta )^{1/2}$ by this method. In the final section, we will observe that $\tau (Y)/\tau (\widetilde {X}, \theta )^{1/2}$ is the key factor in the exact comparison formula for the BCOV invariants for certain Calabi-Yau orbifolds.

This paper is organised as follows.

In Section 2, we recall log-Enriques surfaces and study their moduli space. In Section 3, we recall the notion of analytic torsion and also the holomorphic torsion invariant $\tau (\widetilde {X}, \theta )$ for $2$ -elementary $K3$ surfaces [43]. In Theorem 3.2, we will give an explicit formula for the analytic torsion of a $K3$ surface with respect to an arbitrary Kähler metric. In Section 4, we recall the Eguchi-Hanson instanton and construct a family of Kähler metrics $\{ \gamma _{\epsilon ,\delta } \}$ on $\widetilde {X}$ converging to an orbifold metric with uniformly bounded Ricci curvature. In Section 5, we study the behaviour of some constituents of the invariant $\tau (\widetilde {X}, \theta )$ with respect to the metric $\gamma _{\epsilon ,\delta }$ as $\epsilon \to 0$ . In Section 6, we derive some estimates for the heat kernels of $(\widetilde {X}, \gamma _{\epsilon ,\delta })$ . In Section 7, we determine the behaviour of (equivariant) analytic torsion of $(\widetilde {X}, \theta )$ with respect to the metric $\gamma _{\epsilon ,\delta }$ as $\epsilon \to 0$ and $\delta \to 0$ . In Section 8, we introduce a holomorphic torsion invariant for good log-Enriques surfaces and prove the main theorem. In Section 9, we study the relation between the invariant $\tau (Y)$ and the BCOV invariant.

2 log-Enriques surfaces

2.1 log-Enriques surfaces

Following D.-Q. Zhang [47], [48], we recall the notion of log-Enriques surfaces (of index $2$ ) and its basic properties.

Definition 2.1. An irreducible normal projective complex surface Y is called a log-Enriques surface if the following conditions are satisfied:

1. (1) Y is singular and has at most quotient singularities except rational double points. In particular, Y has the structure of a compact complex orbifold.

2. (2) The irregularity of Y vanishes: that is, $H^{1}(Y,{\mathcal O}_{Y})=0$ .

3. (3) Let $K_{Y}$ be the canonical line bundle of Y in the sense of orbifolds. Then

   $$ \begin{align*}K_{Y}\not\cong{\mathcal O}_{Y}, \qquad K_{Y}^{\otimes2}={\mathcal O}_{Y}. \end{align*} $$

Remark 2.2. For ${\mathfrak p} \in \textrm {Sing}\,Y$ , there exist a neighbourhood $U_{\mathfrak p}$ of ${\mathfrak p}$ in Y, a finite group $G_{\mathfrak p} \subset \textrm {GL}({\mathbf C}^{2})$ and a $G_{\mathfrak p}$ -invariant neighbourhood V of $0$ in ${\mathbf C}^{2}$ such that $(U_{\mathfrak p}, {\mathfrak p}) \cong (V/G_{\mathfrak p}, 0)$ . Then $K_{Y}|_{U_{\mathfrak p}}$ is defined as $(V \times {\mathbf C})/G_{\mathfrak p}$ , where the $G_{\mathfrak p}$ -action is given by $g\cdot (z,\zeta ) = (g\cdot z, \det (g)\zeta )$ .

Remark 2.3. Logarithmic Enriques surfaces in this paper are those of index two in Zhang’s papers [47], [48]. We only deal with log-Enriques surfaces of index two in this paper.

If a smooth complex surface satisfies conditions (2), (3), then it is an Enriques surface. For this reason, we impose that log-Enriques surfaces are singular. Then a log-Enriques surface is rational [47, Lemma 3.4]. By Zhang [47, Lemma 3.1], every singularity of a log-Enriques surface Y is the quotient of a rational double point by ${\mathbf Z}/2{\mathbf Z}$ and hence non-Gorenstein. Indeed, if ${\mathfrak p}\in \textrm {Sing}\,Y$ , then there exists by (1) an isomorphism of germs of analytic spaces $(Y,{\mathfrak p})\cong ({\mathbf C}^{2}/G,0)$ , where $G\subset \textrm {GL}({\mathbf C}^{2})$ is a finite group. By (3), the image of the homomorphism $\det \colon G\ni g\to \det g\in {\mathbf C}^{*}$ is $\pm 1$ . If $G_{0}:=\ker \det \subset G$ , then $G_{0}\subset \textrm {SL}({\mathbf C}^{2})$ is a normal subgroup of G of index $2$ , so that $(X,0)=({\mathbf C}^{2}/G_{0},0)$ is a rational double point. If $p\colon (X,0)\to (Y,0)$ denotes the projection induced by the inclusion of groups $G_{0}\subset G$ , then p induces an isomorphism of germs $(X/(G/G_{0}),0)\to (Y,0)$ , where $G/G_{0}\cong \{\pm 1\}\cong {\mathbf Z}/2{\mathbf Z}$ . By [47, Lemma 3.1], $(X, 0)$ is a rational double point of type $A_{2n-1}$ for some n. Since the homomorphism $\det ^{2} \colon G \to {\mathbf C}^{*}$ is trivial, $K_{Y}^{\otimes 2}$ is a holomorphic line bundle on Y in the ordinary sense.

2.2 The canonical double covering

Let Y be a log-Enriques surface, and let $\varXi \in H^{0}(Y,K_{Y}^{\otimes 2})\setminus \{0\}$ be a nowhere vanishing bicanonical form on Y in the sense of orbifolds. The canonical double covering of Y is defined as

$$ \begin{align*}X:=\{(y,\xi)\in K_{Y};\,\xi\otimes\xi=\varXi\}\subset K_{Y}, \end{align*} $$

which is equipped with the projection $p\colon X\to Y$ induced from the projection $K_{Y}\to Y$ . Then $p\colon X\to Y$ is a double covering, which ramifies only over $\textrm {Sing}\,Y$ . (Since $K_{Y, {\mathfrak p}} = {\mathbf C}/\pm 1$ for ${\mathfrak p} \in \textrm {Sing}(Y)$ , $p^{-1}({\mathfrak p})$ consists of a single point.) The canonical involution $\iota \colon X\to X$ is defined as the nontrivial covering transformation:

$$ \begin{align*}\iota(y,\xi)=(y,-\xi). \end{align*} $$

Since the ramification locus of $p \colon X \to Y$ is $\textrm {Sing}\,X$ , we have $X^{\iota } = \textrm {Sing}\,X$ and that $\iota $ has no fixed points on $X\setminus \textrm {Sing}\,X$ .

Let $\pi \colon \widetilde {X}\to X$ be the minimal resolution, and let ${\theta }\colon \widetilde {X}\to \widetilde {X}$ be the involution induced by the canonical involution $\iota $ . The involution $\theta $ is also called the canonical involution on $\widetilde {X}$ . We have the following commutative diagram:

(2.1)

Here the projection $p\colon X\to Y$ ramifies only at $\textrm {Sing}\,Y$ . In what follows, we denote by $X^{\iota }$ and $\widetilde {X}^{\theta }$ the sets of fixed points of $\iota $ and $\theta $ , respectively. Since $\iota $ has no fixed points on $X\setminus \mathrm {Sing}\,X$ , $\theta $ has no fixed points on $\widetilde {X}\setminus \pi ^{-1}(\mathrm {Sing}\,X)$ . Hence $\widetilde {X}\setminus \pi ^{-1}(\mathrm {Sing}\,X) \subset \widetilde {X} \setminus \widetilde {X}^{\theta }$ . In other words, $\widetilde {X}^{\theta } \subset \pi ^{-1}(\mathrm {Sing}\,X)$ .

Lemma 2.4. In the commutative diagram (2.1), the following hold:

1. (1) X is a $K3$ surface with rational double points, and

   $$ \begin{align*}X^{\iota}=\mathrm{Sing}\,X=p^{-1}(\mathrm{Sing}\,Y), \qquad \iota^{*}|_{H^{0}(X,K_{X})}=-1. \end{align*} $$

2. (2) $(\widetilde {X},\theta )$ is a $2$ -elementary $K3$ surface. Namely, $\theta $ acts nontrivially on holomorphic $2$ -forms on $\widetilde {X}$ . Moreover, there exists an integer $k\in \{1,\ldots ,10\}$ such that

   $$ \begin{align*}\widetilde{X}^{\theta}=E_{1}\amalg\ldots\amalg E_{k}, \qquad E_{i}\cong\mathbf{P}^{1}. \end{align*} $$
   The pair $(\widetilde {X},\theta )$ is called the $2$ -elementary $K3$ surface associated to Y.

Proof. See [47, Lemma 3.1, Th. 3.6] for (1) and [48, Lemma 2.1] for (2).

Lemma 2.5. Let Y, $Y'$ be log Enriques surfaces with canonical double coverings $p' \colon X' \to Y'$ and $p \colon X \to Y$ , respectively. Let $\varphi \colon Y' \to Y$ be a birational holomorphic map. Then the following hold:

1. (1) $\varphi ^{*}$ induces an isomorphism from $H^{0}(Y, K_{Y}^{\otimes 2})$ to $H^{0}(Y', K_{Y'}^{\otimes 2})$ .

2. (2) $\varphi ( \mathrm {Sing}\,Y') \subset \mathrm {Sing}\,Y$ .

3. (3) $\varphi $ lifts to a holomorphic map $f \colon X' \to X$ of canonical double coverings.

Proof. (1) Let $\Xi \in H^{0}(Y, K_{Y}^{\otimes 2})\setminus \{0\}$ and $\Xi ' \in H^{0}(Y', K_{Y'}^{\otimes 2})\setminus \{0\}$ . Then $\varphi ^{*}\Xi $ is a bicanonical from on $Y'\setminus (\mathrm {Sing}\,Y' \cup \varphi ^{-1}(\mathrm {Sing}\,Y))$ , and $\Xi '$ is nowhere vanishing. We get $\varphi ^{*}\Xi /\Xi ' \in {\mathcal O}(Y'\setminus (\mathrm {Sing}\,Y' \cup \varphi ^{-1}(\mathrm {Sing}\,Y))) = {\mathcal O}(Y'\setminus \varphi ^{-1}(\mathrm {Sing}\,Y)) = {\mathcal O}(Y\setminus \mathrm {Sing}\,Y) = {\mathcal O}(Y)={\mathbf C}$ , where the first and third equalities follow from the normality of $Y'$ and Y and the second equality follows from the Zariski Main Theorem. Hence $\varphi ^{*}\Xi = c\,\Xi '$ with some $c \in {\mathbf C}\setminus \{0\}$ , and $\varphi ^{*}$ is an isomorphism.

(2) Let $o \in \mathrm {Sing}\,Y'$ . Assume $\varphi (o) \in Y \setminus \mathrm {Sing}\,Y$ . There exist a neighbourhood U of $\varphi (o)$ and a nowhere vanishing canonical form $\eta \in H^{0}(U, K_{Y})$ . We can express $\Xi |_{U} = F\cdot \eta ^{\otimes 2}$ , $F \in {\mathcal O}^{*}(U)$ . Since $\varphi ^{*}\Xi $ and $\varphi ^{*}F$ are nowhere vanishing on $\varphi ^{-1}(U)$ , so is $\varphi ^{*}\eta ^{\otimes 2}$ . Hence $\varphi ^{*}\eta $ is nowhere vanishing. Since any singular point of $Y'$ is non-Gorenstein, we get a contradiction. Thus $\varphi (o) \in \mathrm {Sing}\,Y$ .

(3) Since $\varphi ^{*}\Xi $ is nowhere vanishing on $Y'\setminus \varphi ^{-1}(\mathrm {Sing}\,Y)$ , $\varphi $ has no critical points on $Y'\setminus \varphi ^{-1}(\mathrm {Sing}\,Y)$ . Since the restriction of $\varphi $ to $Y'\setminus \varphi ^{-1}(\mathrm {Sing}\,Y)$ is a closed map, $\varphi \colon Y'\setminus \varphi ^{-1}(\mathrm {Sing}\,Y) \to Y \setminus \mathrm {Sing}\,Y$ is an étale covering of degree one: that is, an isomorphism. $\varphi $ induces a holomorphic map $f \colon X' \setminus (p')^{-1}\varphi ^{-1}(\mathrm {Sing}\,Y) \to X\setminus p^{-1}(\mathrm {Sing}\,Y)$ such that $p\circ f = \varphi \circ p'$ . Since $p^{-1}(y)$ consists of a unique point for any $y\in \mathrm {Sing}\,Y$ , f extends to a map from $X'$ to X by setting $f(x') := p^{-1}(\varphi (p'(x')))$ for $x'\in (p')^{-1}\varphi ^{-1}(\mathrm {Sing}\,Y)$ . By construction, $p\circ f = \varphi \circ p'$ . By this equality and the bijectivity of the map $p\colon \mathrm {Sing}\,X \to \mathrm {Sing}\,Y$ , f is continuous. Since f is holomorphic on a Zariski open subset, $f \colon X'\to X$ is holomorphic by the normality of $X'$ .

2.3 The good model of a log-Enriques surface

The group $\mathbf {Z}/4\mathbf {Z}$ acts on $\mathbf {C}^{2}$ as the multiplication by $i=\sqrt {-1}$ : that is, $i(z_{1},z_{2}):=(iz_{1},iz_{2})$ . We define the cyclic quotient singularity of type $\frac {1}{4}(1,1)$ by

$$ \begin{align*}(\mathbf{C}^{2}/\langle i\rangle,0). \end{align*} $$

Its minimal resolution is the total space of the line bundle ${\mathcal O}_{\mathbf {P}^{1}}(-4)$

$$ \begin{align*}\varpi\colon({\mathcal O}_{\mathbf{P}^{1}}(-4),E) \to (\mathbf{C}^{2}/\langle i\rangle,0), \end{align*} $$

where the exceptional divisor $E=\varpi ^{-1}(0)$ is a $(-4)$ -curve: that is, $E^{2}=-4$ .

Definition 2.6. A log-Enriques surface Y is good if Y has only cyclic quotient singularities of type $\frac {1}{4}(1,1)$ .

Let Y be a log-Enriques surface, $p\colon X\to Y$ be its canonical double covering and $\pi \colon \widetilde {X}\to X$ be the minimal resolution. Then X and $\widetilde {X}$ are equipped with the canonical involutions $\iota $ and $\theta $ , respectively. Let $E=\pi ^{-1}(\mathrm {Sing}\,X)$ be the exceptional divisor of $\pi \colon \widetilde {X}\to X$ . Then $E \supset \widetilde {X}^{\theta } =\amalg _{i=1}^{k}E_{i}$ with $1\leq k\leq 10$ . Since $E_{i}$ is a $(-2)$ -curve of $\widetilde {X}$ , it is a $(-4)$ -curve of $\widetilde {X}/\theta $ , and its contraction produces a cyclic quotient singularity of type $\frac {1}{4}(1,1)$ .

Definition 2.7. The good model of a log-Enriques surface Y, denoted by $Y^{\natural }$ , is defined as the contraction of the disjoint union of $(-4)$ -curves $\widetilde {X}^{\theta }$ in $\widetilde {X}/\theta $ , where $(\widetilde {X},\theta )$ is the $2$ -elementary $K3$ surface associated to Y.

Another construction of $Y^{\natural }$ from Y is as follows [47, Th. 3.6], [48, Lemmas 1.4 and 2.1]. Let $\widetilde {Y}$ be the minimal resolution of Y with exceptional divisor $D \subset \widetilde {Y}$ . Let $Y^{\#}$ be the blowing-up of $\widetilde {Y}$ at $\mathrm {Sing}\,D$ . Then the proper transform of D consists of disjoint $(-4)$ -curves, say $\widetilde {D}_{1},\ldots , \widetilde {D}_{k}$ . Then $Y^{\#} \cong \widetilde {X}/\theta $ and $Y^{\natural }$ is obtained from $Y^{\#}$ by contracting the $\widetilde {D}_{i}$ s. (Notice that $\widetilde {Y}$ and $Y^{\#}$ are not log-Enriques surfaces.) As is verified easily, the composition of the rational map $Y^{\natural } \dashrightarrow Y^{\#}$ and the blowing-down $Y^{\#} \to Y$ extend to a holomorphic map from $Y^{\natural }$ to Y.

By construction, $Y^{\natural }$ has at most cyclic quotient singularities of type $\frac {1}{4}(1,1)$ . If Y is a good log-Enriques surface, then $Y=Y^{\natural }$ .

Proposition 2.8. Let Y be a log-Enriques surface. If there is a birational holomorphic map from a good log-Enriques surface $Y'$ to Y, then $Y'\cong Y^{\natural }$ .

Proof. Let $X^{\natural }$ (respectively, $X'$ ) be the canonical double covering of $Y^{\natural }$ (respectively, $Y'$ ), and let $\widetilde {X}^{\natural }$ (respectively, $\widetilde {X'}$ ) be the minimal resolution of $X^{\natural }$ (respectively, $X'$ ). The birational morphism $Y'\to Y$ induces a birational morphism $\psi \colon (X',\iota ') \to (X,\iota )$ by Lemma 2.5 (3), and this $\psi $ induces an isomorphism $f\colon (\widetilde {X}',\theta ')\to (\widetilde {X},\theta )=(\widetilde {X}^{\natural },\theta )$ , by the minimality of $K3$ surfaces. Hence $(\widetilde {X}'/\theta ',(\widetilde {X}')^{\theta '})\cong (\widetilde {X}^{\natural }/\theta ,(\widetilde {X}^{\natural })^{\theta })$ . Since the projection $\widetilde {X}'/\theta '\to Y'$ (respectively, $\widetilde {X}^{\natural }/\theta \to Y^{\natural }$ ) is obtained by contracting every component of $(\widetilde {X}')^{\theta '}$ (respectively, $(\widetilde {X}^{\natural })^{\theta }$ ) to a cyclic quotient singularity of type $\frac {1}{4}(1,1)$ , f induces an isomorphism from $Y'$ to Y.

By Proposition 2.8, every log-Enriques surface has a unique good model. By Zhang [47, Th. 3.6], [48, Th.4, Cor. 5, Lemma 2.3], one can associate to a log-Enriques surface another log-Enriques surface with a unique singular point in the canonical way. So log-Enriques surfaces of this type form another class to be studied. Because of the uniqueness (up to a scaling) of the Ricci-flat ALE hyperkähler metric on the minimal resolution of $A_{1}$ -singularity, in this paper, we focus on good log-Enriques surfaces.

In the rest of this section, we study the moduli space of good log-Enriques surfaces. Throughout this paper, we mean by lattice a free $\mathbf {Z}$ -module of finite rank equipped with a nondegenerate integral symmetric bilinear form. We often identify a lattice with its Gram matrix.

2.4 $2$ -elementary $K3$ surfaces and log-Enriques surfaces

A pair $(Z,\iota )$ is called a $2$ -elementary $K3$ surface if Z is a $K3$ surface and $\iota \colon Z\to Z$ is a holomorphic anti-symplectic involution. For a $2$ -elementary $K3$ surface $(Z,\iota )$ , we define

$$ \begin{align*}H^{2}(Z,\mathbf{Z})^{\pm}=\{l\in H^{2}(Z,\mathbf{Z});\,\iota^{*}(l)=\pm l\}, \end{align*} $$

which is equipped with the integral bilinear form induced from the intersection pairing on $H^{2}(Z,\mathbf {Z})$ . Then $H^{2}(Z,\mathbf {Z})$ is isometric to the $K3$ -lattice (compare [1])

$$ \begin{align*}{\Bbb L}_{K3}:={\mathbb U}\oplus{\mathbb U}\oplus{\mathbb U}\oplus{\mathbb E}_{8}(-1)\oplus{\mathbb E}_{8}(-1), \end{align*} $$

where ${\Bbb U}=\binom {0\,1}{1\,0}$ and ${\Bbb E}_{8}(-1)$ is the negative-definite even unimodular lattice of rank $8$ whose Gram matrix is given by the Cartan matrix of type $E_{8}$ . If r denotes the rank of $H^{2}(Z,\mathbf {Z})^{+}$ , then $H^{2}(Z,\mathbf {Z})^{+}$ (respectively, $H^{2}(Z,\mathbf {Z})^{-}$ ) has signature $(1,r-1)$ (respectively, $(2,20-r)$ ). For a $2$ -elementary $K3$ surface $(Z,\iota )$ , the topological type of $Z^{\iota }$ is determined by the isometry class of the lattice $H^{2}(Z,\mathbf {Z})^{-}$ .

Let Y be a good log-Enriques surface, and let $(\widetilde {X},\theta )$ be the corresponding $2$ -elementary $K3$ surface. Hence $(\widetilde {X}/\theta ,\widetilde {X}^{\theta })\to (Y,\mathrm {Sing}(Y))$ is the minimal resolution of the cyclic quotient singularities of type $\frac {1}{4}(1,1)$ of Y. We set

$$ \begin{align*}k:=\#\mathrm{Sing}(Y) \end{align*} $$

and define $\Lambda _{k}$ as the unimodular lattice of signature $(2,10-k)$ (except when $k=8$ , which requires modification). Under the identification with a lattice with its Gram matrix, we have

$$ \begin{align*}\Lambda_{k} = \begin{pmatrix} I_{2}&0 \\ 0&-I_{10-k} \end{pmatrix} \quad (k\not=8), \qquad \Lambda_{8} = \begin{pmatrix} I_{2}&0 \\ 0&-I_{2} \end{pmatrix} \mbox{ or } {\mathbb U}\oplus{\mathbb U} \quad (k=8). \end{align*} $$

According to the parity of $\Lambda _{8}$ , we set $\Lambda _{8}^{\mathrm {odd}} := I_{2}\oplus - I_{2}$ and $\Lambda _{8}^{\mathrm {even}} := {\mathbb U}\oplus {\mathbb U}$ . Since $\widetilde {X}^{\theta }$ consists of smooth rational curves, we deduce from Nikulin [39, Th. 4.2.2] that there is an isometry of lattices $\alpha \colon H^{2}(\widetilde {X},\mathbf {Z}) \cong {\Bbb L}_{K3}$ with

(2.2) $$ \begin{align} \alpha\colon H^{2}(\widetilde{X},\mathbf{Z})^{-} \cong \Lambda_{k}(2). \end{align} $$

Here $\Lambda _{k}(2)$ stands for the rescaling of $\Lambda _{k}$ , whose bilinear form is the double of that of $\Lambda _{k}$ . An isometry of lattices $\alpha \colon H^{2}(\widetilde {X},\mathbf {Z})\cong {\Bbb L}_{K3}$ satisfying equation (2.2) is called a marking of $(\widetilde {X},\theta )$ . We set

$$ \begin{align*}M_{k}:=\Lambda_{k}(2)^{\perp}, \end{align*} $$

where the orthogonal complement is considered in the $K3$ -lattice ${\Bbb L}_{K3}$ . A $2$ -elementary $K3$ surface $(Z,\iota )$ is of type $M_{k}$ if its invariant lattice $H^{2}(Z,\mathbf {Z})^+$ is isometric to $M_{k}$ .

We define

$$ \begin{align*}\Omega_{k}:=\{[\eta]\in\mathbf{P}(\Lambda_{k}\otimes\mathbf{C});\,\langle\eta,\eta\rangle=0,\,\langle\eta,\overline{\eta}\rangle>0\}. \end{align*} $$

Then $\Omega _{k}$ consists of two connected components $\Omega _{k}^{+}$ and $\Omega _{k}^{-}$ , each of which is isomorphic to the bounded symmetric domain of type IV of dimension $10-k$ . Let $O(\Lambda _{k})$ be the automorphism group of $\Lambda _{k}$ , and let $O^{+}(\Lambda _{k})\subset O(\Lambda _{k})$ be the subgroup of index $2$ consisting of elements preserving $\Omega _{k}^{\pm }$ . We define the orthogonal modular variety associated with $\Lambda _{k}$ by

$$ \begin{align*}{\mathcal M}_{k}:=\Omega_{k}/O(\Lambda_{k})=\Omega_{k}^{+}/O^{+}(\Lambda_{k}). \end{align*} $$

When $k=8$ , we define ${\mathcal M}_{8}^{\mathrm {odd}} := \Omega _{8}/O(\Lambda _{8}^{\mathrm {odd}})$ and ${\mathcal M}_{8}^{\mathrm {even}} := \Omega _{8}/O(\Lambda _{8}^{\mathrm {even}})$ . When there is no possibility of confusion, we write ${\mathcal M}_{8}$ for ${\mathcal M}_{8}^{\mathrm {odd}}$ and ${\mathcal M}_{8}^{\mathrm {even}}$ .

Since $\theta $ acts nontrivially on $H^{0}(\widetilde {X},\Omega ^{2}_{\widetilde {X}})$ , we deduce the inclusion from the Hodge decomposition $H^{0}(\widetilde {X},\Omega ^{2}_{\widetilde {X}})\subset H^{2}(\widetilde {X},\mathbf {C})^{-}$ . Since $H^{0}(\widetilde {X},\Omega ^{2}_{\widetilde {X}})$ is a complex line, it follows from the Riemann-Hodge bilinear relations that

$$ \begin{align*}\varpi(\widetilde{X},\theta,\alpha) := [\alpha(H^{0}(\widetilde{X},\Omega^{2}_{\widetilde{X}})]\in\Omega_{k}. \end{align*} $$

The point $\varpi (\widetilde {X},\theta ,\alpha )\in \Omega _{k}$ is called the period of $(\widetilde {X},\theta ,\alpha )$ . We define the period of $(\widetilde {X},\theta )$ as the $O(\Lambda _{k})$ -orbit of $\varpi (\widetilde {X},\theta ,\alpha )$ : that is,

$$ \begin{align*}\overline{\varpi}(\widetilde{X},\theta):=O(\Lambda_{k})\cdot[\alpha(H^{0}(\widetilde{X},\Omega^{2}_{\widetilde{X}})]\in{\mathcal M}_{k}. \end{align*} $$

By [43, Th. 1.8], the coarse moduli space of $2$ -elementary $K3$ surfaces of type $M_{k}$ is isomorphic via the period map to the analytic space ${\mathcal M}_{k}^{o}:={\mathcal M}_{k}\setminus {\mathcal D}_{k}$ , where ${\mathcal D}_{k}$ is the discriminant divisor

$$ \begin{align*}{\mathcal D}_{k}=(\bigcup_{d\in\Lambda_{k},\,d^{2}=-1}d^{\perp})/O(\Lambda_{k}), \qquad d^{\perp}:=\{[\eta]\in\Omega_{k};\,\langle\eta,d\rangle=0\}. \end{align*} $$

2.5 The period mapping for log-Enriques surfaces

Definition 2.9. The period of a good log-Enriques surface Y with k singular points is defined as the period of the corresponding $2$ -elementary $K3$ surface $(\widetilde {X},\theta )$ :

$$ \begin{align*}\overline{\varpi}(Y):=\overline{\varpi}(\widetilde{X},\theta)\in{\mathcal M}_{k}. \end{align*} $$

When $k=8$ , we define the parity of Y as that of the lattice $\Lambda _{8}$ defined by equation (2.2).

Theorem 2.10. The period mapping induces a bijection between the isomorphism classes of good log-Enriques surfaces with k singular points (and fixed parity when $k=8$ ) and ${\mathcal M}_{k}^{o}$ .

Proof. Let ${\mathcal N}_{k}$ be the isomorphism classes of good log-Enriques surfaces with k singular points (and fixed parity when $k=8$ ). By [43, Th. 1.8], we can identify ${\mathcal M}_{k}^{o}$ with the isomorphism classes of $2$ -elementary $K3$ surfaces of type $M_{k}$ via the period mapping. We define a map $f\colon {\mathcal N}_{k}\to {\mathcal M}_{k}^{o}$ by setting $f(Y)=(\widetilde {X},\theta )$ , where $(\widetilde {X},\theta )$ is the $2$ -elementary $K3$ surface associated to Y. Similarly, we define a map $g \colon {\mathcal M}_{k}^{o} \to {\mathcal N}_{k}$ by sending $(Z,\sigma ) \in {\mathcal M}_{k}^{o}$ to the surface obtained from $Z/\sigma $ by blowing down $Z^{\sigma }$ . Since $Z^{\sigma }$ consists of k disjoint $(-2)$ -curves, its image in $Z/\sigma $ consists of k disjoint $(-4)$ -curves so that $g(Z, \sigma )$ is a good log-Enriques surface with k singular points. Since $g=f^{-1}$ by [48, Lemmas 1.4 and 2.1], f is a bijection.

Since the (locally defined) family of $2$ -elementary $K3$ surfaces of type $M_{k}$ associated to a holomorphic family of good log-Enriques surfaces with k-singular points is again holomorphic, the period mapping for any holomorphic family of good log-Enriques surfaces with k-singular points is holomorphic. In what follows, we regard ${\mathcal M}_{k}^{o}$ as a coarse moduli space of good log-Enriques surfaces with k singular points (and fixed parity when $k=8$ ).

3 Analytic torsion for $K3$ surfaces and $2$ -elementary $K3$ surfaces

3.1 Analytic torsion

Let Z be a compact complex orbifold of dimension n, and let $\gamma $ be a Kähler form on Z in the sense of orbifolds. Let $\iota \colon Z\to Z$ be a holomorphic involution, and assume that $\iota $ preserves $\gamma $ . Let $A^{0,q}_{Z}$ be the space of smooth $(0,q)$ -forms on Z in the sense of orbifolds. Let $\square _{q}=(\bar {\partial }+\bar {\partial }^{*})^{2}$ be the Hodge-Kodaira Laplacian acting on $A^{0,q}_{Z}$ . Let

$$ \begin{align*}\zeta_{q}(s):=\sum_{\lambda\in\sigma(\square_{q})\setminus\{0\}}\lambda^{-s}\,\dim E(\lambda;\square_{q}) \end{align*} $$

be the spectral zeta function of $\square _{q}$ , where $E(\lambda ;\square _{q})$ is the eigenspace of $\square _{q}$ corresponding to the eigenvalue $\lambda $ . Similarly, let

$$ \begin{align*}\zeta_{q}(s)(\iota):=\sum_{\lambda\in\sigma(\square_{q})\setminus\{0\}}\lambda^{-s}\,\mathrm{Tr}\left[\iota^{*}|_{E(\lambda;\square_{q})}\right] \end{align*} $$

be the equivariant spectral zeta function of $\square _{q}$ . Since $(Z,\gamma )$ is a Kähler orbifold, $\zeta _{q}(s)$ and $\zeta _{q}(s)(\iota )$ converge absolutely when $\Re s>\dim Z$ , extend to meromorphic functions on $\mathbf {C}$ and are holomorphic at $s=0$ . After Ray-Singer [41] and Bismut [4], we make the following:

Definition 3.1. The analytic torsion of the Kähler orbilod $(Z,\gamma )$ is defined as

$$ \begin{align*}\tau(Z,\gamma):=\exp[-\sum_{q=0}^{n}(-1)^{q}q\,\zeta^{\prime}_{q}(0)]. \end{align*} $$

The equivariant analytic torsion of $(Z,\iota ,\gamma )$ is defined as

$$ \begin{align*}\tau_{\mathbf{Z}_{2}}(Z,\gamma)(\iota):=\exp[-\sum_{q=0}^{n}(-1)^{q}q\,\zeta^{\prime}_{q}(0)(\iota)]. \end{align*} $$

3.2 Analytic torsion for $K3$ surfaces

Theorem 3.2. Let Z be a $K3$ surface, let $\eta \in H^{0}(Z,K_{Z})\setminus \{0\}$ , and let $\gamma $ be a Kähler form on Z. Then the following formula holds:

$$ \begin{align*}\tau(Z,\gamma) = \exp \left[ -\frac{1}{24}\int_{Z} \log\left\{\frac{\eta\wedge\overline{\eta}}{\gamma^{2}/2!}\cdot\frac{\mathrm{Vol}(Z,\gamma)}{\|\eta\|_{L^{2}}^{2}}\right\}\,c_{2}(Z,\gamma) \right], \end{align*} $$

where $c_{i}(Z,\gamma )$ denotes the ith Chern form of $(TZ,\gamma )$ and $\|\eta \|_{L^{2}}^{2}:=\int _{Z}\eta \wedge \overline {\eta }$ .

Proof. Let $\omega $ be a Ricci-flat Kähler form on Z such that

(3.1) $$ \begin{align} \frac{\omega^{2}}{2!}=\eta\wedge\overline{\eta}. \end{align} $$

Since the $L^{2}$ -metric on $H^{2}(Z,{\mathcal O}_{Z})=H^{0}(Z,K_{Z})^{\lor }$ is independent of the choice of a Kähler metric on Z, we get by the anomaly formula for Quillen metrics [6]

(3.2) $$ \begin{align} \log\left(\frac{\tau(Z,\gamma)\,\mathrm{Vol}(Z,\gamma)}{\tau(Z,\omega)\,\mathrm{Vol}(Z,\omega)}\right) = \frac{1}{24}\int_{Z}\widetilde{c_{1}c_{2}}(TZ;\gamma,\omega), \end{align} $$

where $\widetilde {c_{1}c_{2}}(TZ;\gamma ,\omega )$ is the Bott-Chern secondary class [6] such that

$$ \begin{align*}-dd^{c}\widetilde{c_{1}c_{2}}(TZ;\gamma,\omega)=c_{1}(Z,\gamma)c_{2}(Z,\gamma)-c_{1}(Z,\omega)c_{2}(Z,\omega). \end{align*} $$

Since $c_{1}(Z,\omega )=0$ by the Ricci-flatness of $\omega $ and $\widetilde {c_{1}}(L;h,h')=\log (h/h')$ for a holomorphic line bundle L and Hermitian metrics h and $h'$ on L, and since

$$ \begin{align*}\widetilde{c_{1}c_{2}}(TZ;\gamma,\omega)=\widetilde{c_{1}}(TZ;\gamma,\omega)c_{2}(Z,\gamma)+c_{1}(Z,\omega)\widetilde{c_{2}}(TZ;\gamma,\omega) \end{align*} $$

by [21], we get by equation (3.1)

(3.3) $$ \begin{align} \widetilde{c_{1}c_{2}}(TZ;\gamma,\omega) = \widetilde{c_{1}}(TZ;\gamma,\omega)c_{2}(Z,\gamma) = \log\left(\frac{\gamma^{2}}{\omega^{2}}\right)c_{2}(Z,\gamma) = \log\left(\frac{\gamma^{2}/2!}{\eta\wedge\overline{\eta}}\right)c_{2}(Z,\gamma). \end{align} $$

Since $\mathrm {Vol}(Z,\gamma )/\mathrm {Vol}(Z,\omega )=\mathrm {Vol}(Z,\gamma )/\|\eta \|_{L^{2}}^{2}$ , we get by substituting equation (3.3) into equation (3.2)

(3.4) $$ \begin{align} \begin{aligned} \log\left(\frac{\tau(Z,\gamma)}{\tau(Z,\omega)}\right) &= -\log\left(\frac{\mathrm{Vol}(Z,\gamma)}{\|\eta\|_{L^{2}}^{2}}\right) - \frac{1}{24}\int_{Z} \log\left(\frac{\eta\wedge\overline{\eta}}{\gamma^{2}/2!}\right)\,c_{2}(Z,\gamma) \\ &= -\frac{1}{24}\int_{Z} \log\left\{\frac{\eta\wedge\overline{\eta}}{\gamma^{2}/2!}\cdot\frac{\mathrm{Vol}(Z,\gamma)}{\|\eta\|_{L^{2}}^{2}}\right\}\,c_{2}(Z,\gamma), \end{aligned} \end{align} $$

where we used the Gauss-Bonnet-Chern formula for Z to get the second equality.

Since $\omega $ is Ricci-flat, the Laplacians $\square _{0}$ and $\square _{2}$ are isospectral via the map $A^{0,0}_{Y}\ni f\mapsto f\overline {\eta }\in A^{0,2}_{Y}$ . Hence, for the Ricci-flat metric $\omega $ , we get the equality of meromorphic functions

(3.5) $$ \begin{align} \zeta_{0}(s)=\zeta_{2}(s) \end{align} $$

Since the Dolbeault complex is exact on the orthogonal complement of harmonic forms, we get the equality of meromorphic functions

(3.6) $$ \begin{align} \zeta_{0}(s)-\zeta_{1}(s)+\zeta_{2}(s)=0. \end{align} $$

By equations (3.5) and (3.6), we get

(3.7) $$ \begin{align} \tau(Z,\omega)=1. \end{align} $$

The result follows from equations (3.4) and (3.7).

3.3 Equivariant analytic torsion for $2$ -elementary $K3$ surfaces

Let Z be a $K3$ surface, and let $\iota \colon Z\to Z$ be an anti-symplectic holomorphic involution. Let $Z^{\iota }=\amalg _{\alpha }C_{\alpha }$ be the decomposition into the connected components. By Nikulin [39, Th. 4.2.2], every $C_{\alpha }$ is a compact Riemann surface unless $Z^{\iota }=\emptyset $ .

Let $\gamma $ be an $\iota $ -invariant Kähler form on Z, and let $\eta \in H^{2}(Z,K_{Z})\setminus \{0\}$ . Let

$$ \begin{align*}M:=H^{2}(Z,\mathbf{Z})^{+} \end{align*} $$

be the invariant sublattice of $H^{2}(Z,\mathbf {Z})$ with respect to the $\iota $ -action. We define

$$ \begin{align*}\tau_{M}(Z,\iota) := \mathrm{Vol}(Z,\gamma)^{\frac{14-r(M)}{4}}\tau_{\mathbf{Z}_{2}}(Z,\gamma)(\iota)\, A_{M}(Z,\iota,\gamma)\, \mathrm{Vol}(Z^{\iota},\gamma|_{Z^{\iota}})\tau(Z^{\iota},\gamma|_{Z^{\iota}}), \end{align*} $$

where we define

$$ \begin{align*}\tau(Z^{\iota},\gamma|_{Z^{\iota}}):=\prod_{\alpha}\tau(C_{\alpha},\gamma|_{C_{\alpha}}), \qquad \mathrm{Vol}(Z^{\iota},\gamma|_{Z^{\iota}}):=\prod_{\alpha}\mathrm{Vol}(C_{\alpha},\gamma|_{C_{\alpha}}) \end{align*} $$

and

$$ \begin{align*}A_{M}(Z,\iota,\gamma) := \exp \left[ \frac{1}{8}\int_{Z^{\iota}} \left.\log\left\{\frac{\eta\wedge\overline{\eta}}{\gamma^{2}/2!}\cdot\frac{\mathrm{Vol}(Z,\gamma)}{\|\eta\|_{L^{2}}^{2}}\right\}\right|_{Z^{\iota}}\, c_{1}(Z^{\iota},\gamma|_{Z^{\iota}}) \right]. \end{align*} $$

As before, $c_{1}(Z^{\iota },\gamma |_{Z^{\iota }})$ is the first Chern form of $(TZ^{\iota },\gamma |_{Z^{\iota }})$ .

Theorem 3.3. The number $\tau _{M}(Z,\iota )$ is independent of the choice of an $\iota $ -invariant Kähler form on Z.

Proof. See [43, Th. 5.7].

For an explicit formula for $\tau _{M}$ as a function on the moduli space of $2$ -elementary $K3$ surfaces, see [43], [45], [30]. By Theorem 3.2, we can rewrite $\tau _{M}(Z,\iota )$ as follows:

(3.8) $$ \begin{align} \begin{aligned} \tau_{M}(Z,\iota) &= \mathrm{Vol}(Z,\gamma)^{\frac{14-r(M)}{4}}\tau(Z,\gamma)\tau_{\mathbf{Z}_{2}}(Z,\gamma)(\iota)\, \mathrm{Vol}(Z^{\iota},\gamma|_{Z^{\iota}})\tau(Z^{\iota},\gamma|_{Z^{\iota}}) \\ &\quad\times A_{M}(Z,\iota,\gamma)\, \exp \left[ \frac{1}{24}\int_{Z} \log\left\{\frac{\eta\wedge\overline{\eta}}{\gamma^{2}/2!}\cdot\frac{\mathrm{Vol}(Z,\gamma)}{\|\eta\|_{L^{2}}^{2}}\right\}\,c_{2}(Z,\gamma) \right]. \end{aligned} \end{align} $$

4 A degenerating family of Kähler metrics

Let Y be a good log-Enriques surface. For an orbifold Kähler form $\gamma $ on Y, we write $\mathrm {Vol}(Y,\gamma )=\int _{Y}\gamma ^{2}/2!$ for the volume of $(Y,\gamma )$ . We set

$$ \begin{align*}k:=\#\mathrm{Sing}(Y)\in\{1,\ldots,10\}. \end{align*} $$

Let $(\widetilde {X},\theta )$ be the $2$ -elementary $K3$ surface associated to Y such that

$$ \begin{align*}\widetilde{X}^{\theta}=\amalg_{{\frak p}\in\mathrm{Sing}(Y)}E_{\frak p}, \qquad E_{\frak p}\cong\mathbf{P}^{1}. \end{align*} $$

Let

$$ \begin{align*}\pi\colon(\widetilde{X},\widetilde{X}^{\theta})\to(X,\mathrm{Sing}\,X) \end{align*} $$

be the blowing-down of the disjoint union of $(-2)$ -curves. Then

$$ \begin{align*}{\frak p}=\pi(E_{\frak p}). \end{align*} $$

In this section, we construct a two-parameter family of Kähler metrics $\{ \gamma _{\epsilon ,\delta } \}$ on $\widetilde {X}$ converging to an orbifold Kähler metric on X, which is obtained by glueing the Eguchi-Hanson instanton at each ${\mathfrak p}$ and a Kähler metric on X. In the subsequent sections, we study the limiting behaviour of various geometric quantities of $(\widetilde {X}, \gamma _{\epsilon ,\delta })$ to construct an invariant of the log-Enriques surface Y.

4.1 Eguchi-Hanson instanton

For $\epsilon \geq 0$ , let $F_{\epsilon }(z)$ be the function on $\mathbf {C}^{2}\setminus \{0\}$ defined by

$$ \begin{align*}F_{\epsilon}(z) := \sqrt{\|z\|^{4}+\epsilon^{2}}+\epsilon\,\log\left(\frac{\|z\|^{2}}{\sqrt{\|z\|^{4}+\epsilon^{2}}+\epsilon}\right). \end{align*} $$

On every compact subset of $\mathbf {C}^{2}\setminus \{0\}$ , we have $\lim _{\epsilon \to 0}F_{\epsilon }(z)=\|z\|^{2}$ . For all $\epsilon \geq 0$ and $\delta>0$ ,

$$ \begin{align*}F_{\epsilon}(\delta z)=\delta^{2}F_{\epsilon\delta^{-2}}(z). \end{align*} $$

Let $T^{*}\mathbf {P}^{1}$ be the holomorphic cotangent bundle of the projective line, and let $E\subset T^{*}\mathbf {P}^{1}$ be its zero section. Let

$$ \begin{align*}\varPi\colon(T^{*}\mathbf{P}^{1},E)\to(\mathbf{C}^{2}/\{\pm1\},0) \end{align*} $$

be the blowing-down of the zero section. Since

$$ \begin{align*}i\partial\bar{\partial}F_{\epsilon}(z) = i \left( \frac{\epsilon\,\partial\|z\|^{2}\wedge\bar{\partial}\|z\|^{2}}{\sqrt{\|z\|^{4}+\epsilon^{2}}+\epsilon)\sqrt{\|z\|^{4}+\epsilon^{2}}} + \frac{\|z\|^{2}\partial\bar{\partial}\|z\|^{2}}{\sqrt{\|z\|^{4}+\epsilon^{2}}+\epsilon} + \epsilon\,\partial\bar{\partial}\log\|z\|^{2} \right) \end{align*} $$

is a positive $(1,1)$ -form on $(\mathbf {C}^{2}\setminus \{0\})/\pm 1$ satisfying

$$ \begin{align*}\frac{(i\partial\bar{\partial}F_{\epsilon})^{2}}{2!}=(\sqrt{-1})^{2}dz_{1}\wedge d\bar{z}_{1}\wedge dz_{2}\wedge d\bar{z}_{2}, \end{align*} $$

its pull-back to $T^{*}\mathbf {P}^{1}$

$$ \begin{align*}\gamma^{\mathrm{EH}}_{\epsilon}:=\varPi^{*}(i\partial\bar{\partial}F_{\epsilon}) \end{align*} $$

extends to a Ricci-flat Kähler form on $T^{*}\mathbf {P}^{1}$ for $\epsilon>0$ , called the Eguchi-Hanson instanton. We write $\gamma ^{\mathrm {EH}}$ for $\gamma ^{\mathrm {EH}}_{1}$ . The coordinate change $z\mapsto \sqrt {\epsilon }z$ on $\mathbf {C}^{2}$ induces an isometry of Kähler manifolds

(4.1) $$ \begin{align} (T^{*}\mathbf{P}^{1},\gamma^{\mathrm{EH}}_{\epsilon})\cong(T^{*}\mathbf{P}^{1},\epsilon\gamma^{\mathrm{EH}}). \end{align} $$

When $\epsilon =0$ ,

$$ \begin{align*}i\partial\bar{\partial}F_{0}=i\partial\bar{\partial}\|z\|^{2} \end{align*} $$

is the Euclidean Kähler form on $\mathbf {C}^{2}/\{\pm 1\}$ and $\gamma ^{\mathrm {EH}}_{0}=\varPi ^{*}\{i\partial \bar {\partial }F_{0}(z)\}=\varPi ^{*}(i\partial \bar {\partial }\|z\|^{2})$ is a degenerate Kähler form on $T^{*}\mathbf {P}^{1}$ .

Let $\omega _{\mathrm {FS}}$ be the Fubini-Study form on $\mathbf {P}^{1}$ such that

$$ \begin{align*}[\omega_{\mathrm{FS}}]=c_{1}({\mathcal O}_{\mathbf{P}^{1}}(1)). \end{align*} $$

By the definition of $F_{\epsilon }$ , we get

$$ \begin{align*}\gamma^{\mathrm{EH}}_{\epsilon}|_{E} = \epsilon\varPi^{*}(i\partial\bar{\partial}\log\|z\|^{2})|_{E} = 2\pi\epsilon\,\omega_{\mathrm{FS}}. \end{align*} $$

4.2 Glueing of the Eguchi-Hanson instanton

4.2.1 A modification of the Eguchi-Hanson instanton

Let $B(r)\subset \mathbf {C}^{2}$ be the ball of radius $r>0$ centred at $0\in \mathbf {C}^{2}$ , and set

$$ \begin{align*}V(r):=B(r)/\{\pm1\}. \end{align*} $$

Let $\varPi \colon (\widetilde {V}(r),E)\to (V(r),0)$ be the blowing-up at the origin. Then $V(\infty )=\mathbf {C}^{2}/\pm 1$ and $\widetilde {V}(\infty )=T^{*}\mathbf {P}^{1}$ . For $z\in (\mathbf {C}^{2}\setminus \{0\})/\pm 1$ and $\epsilon \geq 0$ , we define

$$ \begin{align*}E(z,\epsilon):=F_{\epsilon}(z)-\|z\|^{2}. \end{align*} $$

Since the error term $E(z,\epsilon )$ is a $C^{\omega }$ function on $(V(4)\setminus V(1))\times [0,1]$ with $E(z,0)=0$ , there is a constant $C_{k}$ for all $k\geq 0$ with

(4.2) $$ \begin{align} \sup_{z\in V(4)\setminus V(1)}|\partial_{z}^{k}E(z,\epsilon)|\leq C_{k}\,\epsilon. \end{align} $$

Let $\rho (t)$ be a $C^{\infty }$ function on $\mathbf {R}$ such that $0\leq \rho (t)\leq 1$ on $\mathbf {R}$ , $\rho (t)=1$ for $t\leq 1$ and $\rho (t)=0$ for $t\geq 2$ . We set

$$ \begin{align*}\phi_{\epsilon}(z) := \rho(\|z\|)\,F_{\epsilon}(z)+\{1-\rho(\|z\|)\}\,\|z\|^{2} = \|z\|^{2}+\rho(\|z\|)\,E(z,\epsilon) \end{align*} $$

and we define a $(1,1)$ form on $V(\infty )\setminus \{0\}$ by

$$ \begin{align*}\kappa_{\epsilon}:=i\partial\bar{\partial}\phi_{\epsilon}. \end{align*} $$

Since $\phi _{\epsilon }(z)=F_{\epsilon }(z)$ on $V(1)$ , $\kappa _{\epsilon }$ extends to a real $(1,1)$ -form on $T^{*}\mathbf {P}^{1}$ , which is positive on $\widetilde {V}(1)$ . Since $\phi _{\epsilon }(z)=\|z\|^{2}+\rho (\|z\|)\,E(z,\epsilon )$ on $V(2)\setminus V(1)$ , there exists by equation (4.2) a constant $\epsilon (\rho )\in (0,1)$ depending only on the choice of the cut-off function $\rho $ such that $\kappa _{\epsilon }$ is a positive $(1,1)$ -form on $V(2)\setminus V(1)$ for $0<\epsilon \leq \epsilon (\rho )$ . As a result, $\{\kappa _{\epsilon }\}_{0<\epsilon \leq \epsilon (\rho )}$ is a family of Kähler forms on $T^{*}\mathbf {P}^{1}$ such that $\kappa _{\epsilon }=i\partial \bar {\partial }\|z\|^{2}$ on $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2)$ .

We have the following slightly refined estimate for the error term $E(z, \epsilon )$ . Set

$$ \begin{align*}E(z):=E(z,1)=E_{1}(z)+E_{2}(z), \end{align*} $$

where

$$ \begin{align*}E_{1}(z)=\sqrt{\|z\|^{4}+1}-\|z\|^{2}=\frac{1}{\sqrt{\|z\|^{4}+1}+\|z\|^{2}}, \quad E_{2}(z)=\log\frac{\|z\|^{2}}{\sqrt{\|z\|^{4}+1}+1}.\\[-15pt] \end{align*} $$

Then for any nonnegative integer k, there exists a constant $C_{k}>0$ such that

1. (i) $|\partial _{z}^{k}E_{1}(z)|\leq C_{k}(1+\|z\|)^{-(2+k)}$ for all $z\in V(\infty )\setminus \{0\}$ ;

2. (ii) $|\partial _{z}^{k}E_{2}(z)|\leq C_{k}(1+\|z\|)^{-(2+k)}$ for all $z\in V(\infty )\setminus V(2)$ ;

3. (iii) $|\partial _{z}^{k}E_{2}(z)|\leq C_{k}\|z\|^{-k}$ for all $z\in V(2)\setminus \{0\} k\geq 1$ ; $C_0 \log \|z\|^2$ for $k=0$ .

From these inequalities, we get

(4.3) $$ \begin{align} |\partial_{z}^{k}E(z)| \leq \begin{cases} \begin{array}{ll} C_{k}\|z\|^{-k} \ (k\geq 1; C_0 \log \|z\|^2, k=0) & (\forall\,z\in V(2)\setminus\{0\}), \\ C_{k}(1+\|z\|)^{-(2+k)} & (\forall\,z\in V(\infty)\setminus V(2)). \end{array} \end{cases} \\[-15pt]\nonumber\end{align} $$

Since $E(z,\epsilon )=\epsilon \,E(\frac {z}{\sqrt {\epsilon }},1)=\epsilon \,E(\frac {z}{\sqrt {\epsilon }})$ and hence $\partial _{z}^{k}E(z,\epsilon )=\epsilon ^{1-\frac {k}{2}}(\partial _{z}^{k}E)(\frac {z}{\sqrt {\epsilon }})$ , we get by equation (4.3)

(4.4) $$ \begin{align} |\partial_{z}^{k}E(z,\epsilon)| \leq \begin{cases} \begin{array}{ll} C_{k}\epsilon\|z\|^{-k} \ (k\geq 1; C_0 \epsilon (\log \|z\|^2 + \log \epsilon), k=0) & (\forall\,z\in V(2)\setminus\{0\}), \\ C_{k}\epsilon^{2}(\sqrt{\epsilon}+\|z\|)^{-(2+k)} & (\forall\,z\in V(\infty)\setminus V(2)). \end{array} \end{cases}\\[-15pt]\nonumber \end{align} $$

Here, to get the estimate on $V(2)\setminus \{0\}$ , we used the fact $\epsilon ^{2}(\sqrt {\epsilon } + \|z\|)^{-(2+k)} < \epsilon \|z\|^{-k}$ on $V(2) \setminus V(2\sqrt {\epsilon })$ . Replacing $\epsilon (\rho )$ by a smaller constant if necessary, we may assume by equation (4.4) the following inequality of Hermitian matrices for all $0<\epsilon \leq \epsilon (\rho )$ and $z\in V(\infty )\setminus V(2)$ :

(4.5) $$ \begin{align} \frac{1}{2}(\delta_{ij}) \leq (\delta_{ij}+\frac{\partial^{2}E(z,\epsilon)}{\partial z_{i}\partial\bar{z}_{j}}) \leq 2(\delta_{ij}).\\[-15pt]\nonumber \end{align} $$

Moreover, for $\|z\| \leq 2$ ,

(4.6) $$ \begin{align} |\partial_{\epsilon}E(z,\epsilon)|\leq C\,\epsilon \|z\|^{-2}.\\[-15pt]\nonumber \end{align} $$

Lemma 4.1. There exist constants $C_{1},C_{2}>0$ such that the following inequality of $(1,1)$ -forms on $T^{*}\mathbf {P}^{1}$ hold for all $0<\epsilon \leq \epsilon (\rho )$ :

$$ \begin{align*}C_{1}\gamma_{\epsilon}^{\mathrm{EH}}\leq\kappa_{\epsilon}\leq C_{2}\gamma_{\epsilon}^{\mathrm{EH}}. \end{align*} $$

Proof. (Step 1) On $\widetilde {V}(1)$ , we have $\kappa _{\epsilon }=\gamma _{\epsilon }^{\mathrm {EH}}$ . On $\widetilde {V}(2)\setminus \widetilde {V}(1)$ , it follows from equation (4.2) that there exist constants $C_{1},C_{2}>0$ independent of $\epsilon \in (0,\epsilon (\rho )]$ with $C_{1}\gamma _{\epsilon }^{\mathrm {EH}}\leq \kappa _{\epsilon }\leq C_{2}\gamma _{\epsilon }^{\mathrm {EH}}$ . Combining these two estimates, we get $C_{1}\gamma _{\epsilon }^{\mathrm {EH}}\leq \kappa _{\epsilon }\leq C_{2}\gamma _{\epsilon }^{\mathrm {EH}}$ on $\widetilde {V}(2)$ .

(Step 2) We compare $\kappa _{\epsilon }$ and $\gamma _{\epsilon }^{\mathrm {EH}}$ on $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2)$ . On $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2)$ , we have $\kappa _{\epsilon }=\gamma ^{\mathrm {EH}}_{0}$ . By equation (4.5), we have $\frac {1}{2}\gamma ^{\mathrm {EH}}_{\epsilon }\leq \gamma ^{\mathrm {EH}}_{0}\leq 2\gamma ^{\mathrm {EH}}_{\epsilon }$ on $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2)$ . Since $\kappa _{\epsilon }=\gamma ^{\mathrm {EH}}_{0}$ on $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2)$ , We get the desired estimate on $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2)$ . This completes the proof.

4.2.2 A family of Kähler metrics on $\widetilde {X}$

Since $E_{\frak p}$ is a $(-2)$ -curve on $\widetilde {X}$ , there exist a neighbourhood $U_{\frak p}$ of $E_{\frak p}$ in $\widetilde {X}$ and an isomorphism of pairs

$$ \begin{align*}\psi_{\frak p}\colon(U_{\frak p},E_{\frak p})\cong(\widetilde{V}(1),E). \end{align*} $$

We may and will assume that $\psi _{\frak p}$ extends to an isomorphism between an open subset of $\widetilde {X}$ containing $U_{\frak p}$ and $\widetilde {V}(4)$ . We write $V(r)_{{\frak p}}$ for $V(r)$ viewed as a neighbourhood of ${\frak p}\in \mathrm {Sing}(X)$ . In what follows, we identify $\widetilde {V}(r)_{{\frak p}}$ with $\psi _{\frak p}^{-1}(\widetilde {V}(r)_{{\frak p}})$ .

Let $\gamma $ be a $\theta $ -invariant Kähler form on X in the sense of orbifolds, which has a potential function on every $V(4)_{\frak p}$ . By modifying the potential of $\gamma $ on each $V(4)_{\frak p}$ (compare [43, Proof of Lemma 6.2]), there exists a Kähler form $\gamma _{0}$ on X in the sense of orbifolds such that

(4.7) $$ \begin{align} \gamma_{0}|_{X\setminus\bigcup_{{\frak p}\in\mathrm{Sing}(X)}V(2)_{\frak p}}=\gamma, \qquad \gamma_{0}|_{V(2)_{\frak p}}=i\partial\bar{\partial}\|z\|^{2} \quad (\forall\,{\frak p}\in\mathrm{Sing}(X)).\\[-17pt]\nonumber \end{align} $$

In particular, $\|z\|^{2}\in C^{\omega }(V(2)_{\frak p})$ is a potential function of $\gamma _{0}$ on every $V(2)_{\frak p}$ . Since $\phi _{\epsilon }(z)=\|z\|^{2}$ near $\partial V(2)_{\frak p}$ , we can glue the Kähler form $\kappa _{\epsilon }$ on $\bigcup _{{\frak p}\in \mathrm {Sing}(X)}\widetilde {V}(2)_{\frak p}$ and the Kähler form $\gamma _{0}$ on $X\setminus \bigcup _{{\frak p}\in \mathrm {Sing}(X)}\widetilde {V}(2)_{\frak p}$ by setting

(4.8) $$ \begin{align} \gamma_{\epsilon} := \begin{cases} \begin{array}{ll} \kappa_{\epsilon}&\mbox{on }\bigcup_{{\frak p}\in\mathrm{Sing}(X)}\widetilde{V}(2)_{\frak p}, \\ \gamma_{0}&\mbox{on }X\setminus\bigcup_{{\frak p}\in\mathrm{Sing}(X)}\widetilde{V}(2)_{\frak p}. \end{array} \end{cases}\\[-17pt]\nonumber \end{align} $$

By construction, $\{\gamma _{\epsilon }\}_{0<\epsilon \leq \epsilon (\rho )}$ is a family of $\theta $ -invariant Kähler forms on $\widetilde {X}$ .

Lemma 4.2. The family of Kähler forms $\{\gamma _{\epsilon }\}_{0<\epsilon \leq \epsilon (\rho )}$ on $\widetilde {X}$ satisfies the following:

1. (1) For all ${\frak p}\in \mathrm {Sing}(X)$ , $\gamma _{0}|_{V(2)_{\frak p}}=i\partial \bar {\partial }\|z\|^{2}$ .

2. (2) For all ${\frak p}\in \mathrm {Sing}(X)$ , $\gamma _{\epsilon }|_{\widetilde {V}(1)_{\frak p}}=\psi _{\frak p}^{*}\gamma ^{\mathrm {EH}}_{\epsilon }$ .

3. (3) On $\widetilde {X}$ , $\gamma _{\epsilon }$ converges to $\pi ^{*}\gamma _{0}$ in the $C^{\infty }$ -topology.

4. (4) There exist constants $C, C'>0$ independent of $\epsilon $ (but depending on $\rho $ ) such that $|\mathrm {Ric}(\gamma _{\epsilon })|_{\gamma _{\epsilon }}\leq C\cdot \epsilon $ on $\bigcup _{{\frak p}\in \mathrm {Sing}\,X}\widetilde {V}(2)_{\frak p}$ and $|\mathrm {Ric}(\gamma _{\epsilon })|_{\gamma _{\epsilon }}\leq C'$ on $\widetilde {X}$ .

Proof. By construction, (1), (2), (3) are obvious. Let us see (4). Since $\gamma _{\epsilon }^{\mathrm {EH}}$ is Ricci-flat and since $\kappa _{\epsilon }=\gamma _{\epsilon }^{\mathrm {EH}}$ on $\widetilde {V}(1)_{\frak p}$ , we get $\mathrm {Ric}(\kappa _{\epsilon })=\mathrm {Ric}(\gamma _{\epsilon }^{\mathrm {EH}})=0$ on $\widetilde {V}(1)_{\frak p}$ . On $\widetilde {V}(2)_{\frak p}\setminus \widetilde {V}(1)_{\frak p}$ , we get $|\mathrm {Ric}(\gamma _{\epsilon })|_{\gamma _{\epsilon }}=|\mathrm {Ric}(\kappa _{\epsilon })|_{\kappa _{\epsilon }}\leq C\cdot \epsilon $ by equation (4.2). This proves the first estimate. Since $\gamma _{\epsilon }=\gamma _{0}$ on $X\setminus \bigcup _{{\frak p}\in \mathrm {Sing}(X)}\widetilde {V}(2)_{\frak p}$ , we get the second estimate.

4.2.3 A two-parameter family of Kähler metrics on $T^{*}\mathbf {P}^{1}$

For later use, we introduce another small parameter $\delta>0$ . Instead of glueing in the Eguchi-Hanson instanton in the region $\widetilde {V}(2)-\widetilde {V}(1)$ , we now do it in the region $\widetilde {V}(2\delta )-\widetilde {V}(\delta )$ . This is effected by replacing the cut-off function $\rho (t)$ by $\rho _{\delta }(t)=\rho (\frac {t}{\delta })$ in defining the Kähler potential $\phi _{\epsilon }$ for the Kähler metric $\gamma _{\epsilon }$ such that $\rho _{\delta }(t)=1$ for $t\leq \delta $ and $\rho _{\delta }(t)=0$ for $t\geq 2\delta $ . This gives us the family of real $(1,1)$ -forms on $T^{*}\mathbf {P}^{1}$

$$ \begin{align*}\kappa_{\epsilon, \delta}:= i \partial \overline{\partial} \phi_{\epsilon, \delta},\\[-17pt] \end{align*} $$

where

$$ \begin{align*}\phi_{\epsilon, \delta}(z):=\|z\|^2 + \rho_{\delta}(\|z\|)E(z, \epsilon).\\[-17pt] \end{align*} $$

To verify the positivity of $\kappa _{\epsilon , \delta }$ , we see the relation between $\phi _{\epsilon }$ and $\phi _{\epsilon , \delta }$ . Since $F_{\epsilon }(\delta z)=\delta ^{2}F_{\epsilon /\delta ^{2}}(z)$ , we get $E(\delta z,\epsilon )=\delta ^{2}E(z,\epsilon /\delta ^{2})$ . Since $\phi _{\epsilon ,1}(z)=\phi _{\epsilon }(z)$ and $\phi _{\epsilon , \delta }(z)=\|\delta \cdot \frac {z}{\delta }\|^{2}+\rho (\frac {\|z\|}{\delta })E(\delta \cdot \frac {z}{\delta },\epsilon )$ , this implies that

$$ \begin{align*}\phi_{\epsilon, \delta}(z)=\delta^{2}\phi_{\epsilon/\delta^{2}}(z/\delta).\\[-17pt] \end{align*} $$

Hence if $0<\epsilon /\delta ^{2}\leq \epsilon (\rho )$ , then $\kappa _{\epsilon , \delta }=i\partial \bar {\partial }\phi _{\epsilon , \delta }$ is a positive $(1,1)$ -form on $T^{*}\mathbf {P}^{1}$ . In what follows, we define $\phi _{\epsilon , \delta }$ for $\epsilon ,\delta \in (0,1]$ with $0<\epsilon /\delta ^{2}\leq \epsilon (\rho )$ . Then $\{\kappa _{\epsilon ,\delta }\}_{0<\epsilon /\delta ^{2}\leq \epsilon (\rho ),\,\epsilon ,\delta \in (0,1]}$ is a family of Kähler forms on $T^{*}\mathbf {P}^{1}$ . Moreover, the relation $\phi _{\epsilon , \delta }(z)=\delta ^{2}\phi _{\epsilon /\delta ^{2}}(z/\delta )$ implies that the automorphism of $T^{*}\mathbf {P}^{1}$ induced from the one $z\mapsto z/\delta $ on $V(\infty )$ yields an isometry of Kähler manifolds $(T^{*}\mathbf {P}^{1},\kappa _{\epsilon , \delta })\cong (T^{*}\mathbf {P}^{1},\delta ^{2}\kappa _{\epsilon /\delta ^{2}})$ such that

(4.9) $$ \begin{align} (\widetilde{V}(2\delta),\kappa_{\epsilon, \delta})\cong(\widetilde{V}(2),\delta^{2}\kappa_{\epsilon/\delta^{2}}). \end{align} $$

Lemma 4.3. There exist constants $C_{1},C_{2}>0$ such that the following inequality of $(1,1)$ -forms on $T^{*}\mathbf {P}^{1}$ holds for all $\epsilon ,\delta \in (0,1]$ with $0<\epsilon /\delta ^{2}\leq \epsilon (\rho )$ :

$$ \begin{align*}C_{1}\kappa_{\epsilon}\leq\kappa_{\epsilon,\delta}\leq C_{2}\kappa_{\epsilon}.\\[-15pt] \end{align*} $$

Proof. (Step 1) By Lemma 4.3 (Step 1), we get $C_{1}\gamma _{\epsilon }^{\mathrm {EH}}\leq \kappa _{\epsilon }\leq C_{2}\gamma _{\epsilon }^{\mathrm {EH}}$ on $\widetilde {V}(2)$ . By equation (4.9) and the relation $\delta ^{2}\gamma _{\epsilon /\delta ^{2}}^{\mathrm {EH}}=\gamma _{\epsilon }^{\mathrm {EH}}$ , this implies the inequality $C_{1}\gamma _{\epsilon }^{\mathrm {EH}}\leq \kappa _{\epsilon ,\delta }\leq C_{2}\gamma _{\epsilon }^{\mathrm {EH}}$ on $\widetilde {V}(2\delta )$ . Hence we get $C_{1}C_{2}^{-1}\kappa _{\epsilon }\leq \kappa _{\epsilon ,\delta }\leq C_{2}C_{1}^{-1}\kappa _{\epsilon }$ on $\widetilde {V}(2\delta )$ .

(Step 2) Next we compare $\kappa _{\epsilon ,\delta }$ and $\kappa _{\epsilon }$ on $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2\delta )$ . By definition, we have $\kappa _{\epsilon ,\delta }=\gamma _{0}^{\mathrm {EH}}$ on $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2\delta )$ . Let $H_{\epsilon }$ be the automorphism of $T^{*}\mathbf {P}^{1}$ induced from the automorphism $z\mapsto \sqrt {\epsilon }z$ of $V(\infty )=\mathbf {C}^{2}/\pm 1$ . Then $H_{\epsilon }$ is an isomorphism from $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2\delta /\sqrt {\epsilon })$ to $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2\delta )$ inducing the isometries

(4.10) $$ \begin{align} (T^{*}\mathbf{P}^{1}\setminus\widetilde{V}(2\delta),\gamma_{\epsilon}^{\mathrm{EH}}) \cong (T^{*}\mathbf{P}^{1}\setminus\widetilde{V}(2\delta/\sqrt{\epsilon}),\epsilon\gamma^{\mathrm{EH}}), \end{align} $$

(4.11) $$ \begin{align} (T^{*}\mathbf{P}^{1}\setminus\widetilde{V}(2\delta),\gamma_{0}^{\mathrm{EH}}) \cong (T^{*}\mathbf{P}^{1}\setminus\widetilde{V}(2\delta/\sqrt{\epsilon}),\epsilon\gamma_{0}^{\mathrm{EH}}).\\[-15pt]\nonumber \end{align} $$

Since $\epsilon /\delta ^{2}\leq \epsilon (\rho )$ and hence $\delta /\sqrt {\epsilon }>1/\sqrt {\epsilon (\rho )}$ , we have the inclusion $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(\frac {2\delta }{\sqrt {\epsilon }}) \subset T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2/\sqrt {\epsilon (\rho )})$ . By equation (4.4), there exist constants $C^{\prime }_{1},C^{\prime }_{2}>0$ such that $C^{\prime }_{1}\gamma ^{\mathrm {EH}}\leq \gamma ^{\mathrm {EH}}_{0}\leq C^{\prime }_{2}\gamma ^{\mathrm {EH}}$ on $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2/\sqrt {\epsilon (\rho )})$ . This, together with equations (4.10) and (4.11), yields the inequality $C^{\prime }_{1}\gamma ^{\mathrm {EH}}_{\epsilon }\leq \gamma ^{\mathrm {EH}}_{0}\leq C^{\prime }_{2}\gamma ^{\mathrm {EH}}_{\epsilon }$ on $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2\delta )$ for all $\epsilon ,\delta \in (0,1]$ with $0<\epsilon /\delta ^{2}\leq \epsilon (\rho )$ . Since $\kappa _{\epsilon ,\delta }=\gamma _{0}^{\mathrm {EH}}$ on $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2\delta )$ , we get $C^{\prime }_{1}\gamma ^{\mathrm {EH}}_{\epsilon }\leq \kappa _{\epsilon ,\delta }\leq C^{\prime }_{2}\gamma ^{\mathrm {EH}}_{\epsilon }$ on $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2\delta )$ . By Lemma 4.1, this implies the inequality $C^{\prime \prime }_{1}\kappa _{\epsilon }\leq \kappa _{\epsilon ,\delta }\leq C^{\prime \prime }_{2}\kappa _{\epsilon }$ on $T^{*}\mathbf {P}^{1}\setminus \widetilde {V}(2\delta )$ , where $C^{\prime \prime }_{1},C^{\prime \prime }_{2}>0$ are constants independent of $\epsilon ,\delta \in (0,1]$ with $0<\epsilon /\delta ^{2}\leq \epsilon (\rho )$ . This completes the proof.

4.2.4 A two-parameter family of Kähler metrics on $\widetilde {X}$

Modifying the construction in equation (4.8), we introduce a two-parameter family of $\theta $ -invariant Kähler forms on $\widetilde {X}$ by

(4.12) $$ \begin{align} \gamma_{\epsilon,\delta} := \begin{cases} \begin{array}{ll} \kappa_{\epsilon,\delta}&\mbox{on }\bigcup_{{\frak p}\in\mathrm{Sing}(X)}\widetilde{V}(2)_{\frak p}, \\ \gamma_{0}&\mbox{on }X\setminus\bigcup_{{\frak p}\in\mathrm{Sing}(X)}\widetilde{V}(2)_{\frak p} \end{array} \end{cases}\\[-15pt]\nonumber \end{align} $$

for $\epsilon ,\delta \in (0,1]$ with $0<\epsilon /\delta ^{2}\leq \epsilon (\rho )$ .

Lemma 4.4. There exist constants $C_{1},C_{2}>0$ such that the following inequality of $(1,1)$ -forms on $\widetilde {X}$ hold for all $\epsilon ,\delta \in (0,1]$ with $0<\epsilon /\delta ^{2}\leq \epsilon (\rho )$ :

$$ \begin{align*}C_{1}\gamma_{\epsilon}\leq\gamma_{\epsilon,\delta}\leq C_{2}\gamma_{\epsilon}. \\[-15pt]\end{align*} $$

Proof. On $\bigcup _{{\frak p}\in \mathrm {Sing}(X)}\widetilde {V}(2)_{\frak p}$ , the result follows from Lemma 4.3. On $X\setminus \bigcup _{{\frak p}\in \mathrm {Sing}(X)}\widetilde {V}(2)_{\frak p}$ , the result is obvious since $\gamma _{\epsilon ,\delta }=\gamma _{\epsilon }=\gamma _{0}$ is independent of $\epsilon ,\delta $ there.

Lemma 4.5. There exists a constant $C_{3}>0$ such that the following estimate holds for all $\epsilon ,\delta \in (0,1]$ with $0<\epsilon /\delta ^{2}\leq \epsilon (\rho )$ :

$$ \begin{align*}|\mathrm{Ric}(\gamma_{\epsilon,\delta})|_{\gamma_{\epsilon,\delta}}\leq C_{3}(\epsilon\delta^{-4}+1).\\[-15pt] \end{align*} $$

Proof. Since $\gamma _{\epsilon ,\delta }=\gamma _{0}$ on $X\setminus \bigcup _{{\frak p}\in \mathrm {Sing}(X)}\widetilde {V}(2)_{\frak p}$ , it suffices to prove the estimate on $\bigcup _{{\frak p}\in \mathrm {Sing}(X)}\widetilde {V}(2)_{\frak p}$ . Since $\gamma _{\epsilon ,\delta }=i\partial \bar {\partial }\|z\|^{2}$ is a flat metric on $\bigcup _{{\frak p}\in \mathrm {Sing}(X)}\widetilde {V}(2)_{\frak p}\setminus \widetilde {V}(2\delta )_{\frak p}$ , it suffices to prove the estimate on $\bigcup _{{\frak p}\in \mathrm {Sing}(X)}\widetilde {V}(2\delta )_{\frak p}$ . By equation (4.9), we get on each $\widetilde {V}(2\delta )_{\frak p}$

$$ \begin{align*}|\mathrm{Ric}(\gamma_{\epsilon,\delta})|_{\gamma_{\epsilon,\delta}} = |\mathrm{Ric}(\delta^{2}\gamma_{\epsilon/\delta^{2}})|_{\gamma_{\epsilon,\delta}} = \delta^{-2}|\mathrm{Ric}(\gamma_{\epsilon/\delta^{2}})|_{\gamma_{\epsilon/\delta^{2}}} \leq \delta^{-2}C(\epsilon/\delta^{2}) = C\epsilon\delta^{-4}, \end{align*} $$

where we used Lemma 4.2 (4) to get the inequality $|\mathrm {Ric}(\gamma _{\epsilon /\delta ^{2}})|_{\gamma _{\epsilon /\delta ^{2}}}\leq C(\epsilon /\delta ^{2})$ on $\widetilde {V}(2\delta )_{\frak p}$ . This completes the proof.

Fix a nowhere vanishing holomorphic $2$ -form

$$ \begin{align*}\eta\in H^{0}(\widetilde{X},K_{\widetilde{X}})\setminus\{0\}. \end{align*} $$

Since $(\varPi ^{-1})^{*}(\eta |_{V(1)_{\frak p}})$ is a nowhere vanishing holomorphic $2$ -form on $V(1)_{\frak p}\setminus \{0\}$ , there exists by the Hartogs extension theorem a nowhere vanishing holomorphic function $f_{\frak p}(z)$ on $B(1)$ such that

$$ \begin{align*}(\varPi^{-1})^{*}(\eta|_{V(1)_{\frak p}})=f_{\frak p}(z)\,dz_{1}\wedge dz_{2} \end{align*} $$

and $f_{\frak p}(-z)=f_{\frak p}(z)$ . Since $\gamma _{\epsilon ,\delta }=\gamma _{\epsilon }$ on $\widetilde {V}(\delta )_{\frak p}$ and hence

$$ \begin{align*}\left.(\varPi^{-1})^{*}(\gamma_{\epsilon,\delta}^{2}/2!)\right|_{V(\delta)_{\frak p}\setminus\{0\}} = (i\partial\bar{\partial}F_{\epsilon})^{2}/2! = (i)^{2}dz_{1}\wedge d\bar{z}_{1}\wedge dz_{2}\wedge d\bar{z}_{2}, \end{align*} $$

we get the equality of functions on $\widetilde {V}(\delta )_{\frak p}$

(4.13) $$ \begin{align} \left.\frac{\eta\wedge\overline{\eta}}{\gamma_{\epsilon,\delta}^{2}/2!}\right|_{\widetilde{V}(\delta)_{\frak p}} = \pi^{*}|f_{\frak p}(z)|^{2}. \end{align} $$

In particular, we have the following:

1. (i) On each $\widetilde {V}(\epsilon )_{\frak p}$ , the volume form of $\gamma _{\epsilon ,\delta }$ is independent of $\epsilon \in (0,\epsilon (\rho )]$ .

2. (ii) $f_{\frak p}(0)$ is independent of $\delta \in (0,1]$ and the choice of the cut-off function $\rho $ .

Since $\gamma _{\epsilon ,\delta }$ converges to $\gamma _{0}$ outside $\bigcup _{{\frak p}\in \mathrm {Sing}(X)}\widetilde {V}(\delta )_{\frak p}$ , we get the continuity

(4.14) $$ \begin{align} \lim_{\epsilon\to0}\mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta})=\mathrm{Vol}(X,\gamma_{0}). \end{align} $$

4.3 Ricci-flat Kähler form on the blowing-down of $\widetilde {X}^{\theta }$

Recall that

$$ \begin{align*}\pi \colon ( \widetilde{X}, \widetilde{X}^{\theta} ) \to ( X, \mathrm{Sing}\,X ) \end{align*} $$

is the blowing-down of the disjoint union of $(-2)$ -curves $\widetilde {X}^{\theta } = \amalg _{{\mathfrak p} \in \mathrm {Sing}\,X} E_{\mathfrak p}$ . Then ${\frak p}=\pi (E_{\frak p})$ . Under the identification $\psi _{\frak p}\colon (U_{\frak p},E_{\frak p})\cong (\widetilde {V}(1)_{\frak p},E)$ , $\pi \colon \widetilde {X}\to X$ is identified with the blowing-down $\varPi \colon T^{*}\mathbf {P}^{1}\to \mathbf {C}^{2}/\{\pm 1\}$ on each $V(1)_{\frak p}$ .

By [26], there exists a Ricci-flat orbifold Kähler form $\omega _{\eta }$ on X such that

$$ \begin{align*}\pi^{*}\omega_{\eta}^{2}/2!=\eta\wedge\overline{\eta}. \end{align*} $$

By equation (4.13), we have

$$ \begin{align*}\left.\pi^{*}\omega_{\eta}^{2}/\gamma_{\epsilon,\delta}^{2}\right|_{\widetilde{V}(\delta)_{\frak p}}=\varPi^{*}|f_{\frak p}(z)|^{2}. \end{align*} $$

Since the right-hand side is independent of $\epsilon \in (0,1)$ , we get by putting $\epsilon \to 0$

$$ \begin{align*}\left.\omega_{\eta}^{2}/\gamma_{0}^{2}\right|_{\widetilde{V}(\delta)_{\frak p}}=|f_{\frak p}|^{2}. \end{align*} $$

Hence we get the following relation by regarding $\eta $ as a nowhere vanishing holomorphic $2$ -form on both $\widetilde {X}$ and X

$$ \begin{align*}\left.\frac{\eta\wedge\overline{\eta}}{\gamma_{\epsilon,\delta}^{2}/2!}\right|_{E_{\frak p}} = |f_{\frak p}(0)|^{2} = \frac{\eta\wedge\overline{\eta}}{\gamma_{0}^{2}}({\frak p}). \end{align*} $$

5 Behaviour of some geometric quantities under the degeneration

In this section, we study the behaviour of the second Chern form, the Bott-Chern term, and the analytic torsion of the fixed curves when $\gamma _{\epsilon ,\delta }$ converges to the orbifold metric $\gamma _{0}$ .

5.1 Behaviour of the second Chern form as $\epsilon \to 0$

Proposition 5.1. For any $\delta \in (0,1]$ , one has

$$ \begin{align*}\lim_{\epsilon\to0}\pi_{*}c_{2}(\widetilde{X},\gamma_{\epsilon,\delta}) = c_{2}(X,\gamma_{0})+\frac{3}{2}\sum_{{\frak p}\in\mathrm{Sing}(X)}\delta_{\frak p} \end{align*} $$

as currents on X, where $\delta _{\frak p}$ is the Dirac $\delta $ -current supported at ${\frak p}$ . In particular,

$$ \begin{align*}\frac{1}{24}\int_{Y}c_{2}(Y,\gamma_{0})=\frac{1}{32}(16-k). \end{align*} $$

Proof. Let $h\in C^{\infty }(X)$ . By the definition of the Kähler form $\gamma _{\epsilon ,\delta }$ , we have

(5.1) $$ \begin{align} \begin{aligned} \int_{\widetilde{X}}\pi^{*}h\cdot c_{2}(\widetilde{X},\gamma_{\epsilon,\delta}) &= \int_{X\setminus\bigcup_{{\frak p}\in\mathrm{Sing}(X)}\widetilde{V}(\delta)_{\frak p}}h\cdot c_{2}(X,\gamma_{\epsilon,\delta}) + \sum_{{\frak p}\in\mathrm{Sing}(X)}h({\frak p})\int_{\widetilde{V}(\delta)_{\frak p}}c_{2}(\widetilde{X},\gamma_{\epsilon,\delta}) \\ &\quad+ \sum_{{\frak p}\in\mathrm{Sing}(X)}\int_{\widetilde{V}(\delta)_{\frak p}}\pi^{*}\{h-h({\frak p})\}\cdot c_{2}(\widetilde{X},\gamma_{\epsilon,\delta}). \end{aligned} \end{align} $$

For $a>0$ , let $T_{a}(z):=az$ be the homothety of $\mathbf {C}^{2}$ and let $\widetilde {T}_{a}\colon T^{*}\mathbf {P}^{1}\to T^{*}\mathbf {P}^{1}$ be the biholomorphic map induced by $T_{a}$ . Then $\widetilde {T}_{\epsilon }$ induces an isometry of Kähler manifolds

$$ \begin{align*}\widetilde{T}_{\epsilon}\colon(\widetilde{V}(\epsilon^{-2}),\epsilon^{2}\,\gamma^{\mathrm{EH}}) \cong (\widetilde{V}(1),\gamma^{\mathrm{EH}}_{\epsilon^{2}}). \end{align*} $$

Under the identification $T^{*}\mathbf {P}^{1}\setminus E\cong V(\infty )\setminus \{0\}$ , we have the following estimates

$$ \begin{align*}\left\|\gamma^{\mathrm{EH}}(z) - i\partial\bar{\partial}\|z\|^{2}\right\|\leq C(1+\|z\|)^{-4}, \qquad \|c_{2}(T^{*}\mathbf{P}^{1},\gamma^{\mathrm{EH}})(z)\|\leq C(1+\|z\|)^{-6} \end{align*} $$

for $\|z\|\gg 1$ by equation (4.3), where $C>0$ is a constant and the norm is with respect to $\gamma ^{\mathrm {EH}}$ .

Since there is a constant $C'>0$ with $\left |h|_{V(\delta )_{\frak p}}(z)-h({\frak p})\right |\leq C'\|z\|/(1+\|z\|)$ on $V(\delta )_{\frak p}$ , we get

(5.2) $$ \begin{align} \begin{aligned} \,& \left| \int_{\widetilde{V}(\delta)_{\frak p}}\{\pi^{*}h-h({\frak p})\}\cdot c_{2}(\widetilde{X},\gamma_{\epsilon,\delta}) \right| = \left| \int_{\widetilde{V}(\delta)_{\frak p}} \pi^{*}\{h|_{V(\delta)_{\frak p}}-h({\frak p})\}\cdot c_{2}(T^{*}\mathbf{P}^{1},\gamma^{\mathrm{EH}}_{\epsilon}) \right| \\ &= \left| \int_{\widetilde{V}(\delta\sqrt{\epsilon}^{-1})}\widetilde{T}_{\epsilon}^{*} \pi^{*}\{h|_{V(\delta)_{\frak p}}-h({\frak p})\}\cdot c_{2}(T^{*}\mathbf{P}^{1},\gamma^{\mathrm{EH}}) \right| \\ &\leq \int_{V(\delta\sqrt{\epsilon}^{-1})}C'\frac{\sqrt{\epsilon}\|z\|}{1+\sqrt{\epsilon}\|z\|}\cdot\frac{C}{1+\|z\|^{6}}\,\frac{(\gamma^{\mathrm{EH}})^{2}}{2!} \leq C"\sqrt{\epsilon}\to0\quad(\epsilon\to0), \end{aligned} \end{align} $$

where $C^{\prime \prime }>0$ is a constant. By equations (5.1) and (5.2), we get

(5.3) $$ \begin{align} \begin{aligned} \lim_{\epsilon\to0}\int_{\widetilde{X}}\pi^{*}h\cdot c_{2}(\widetilde{X},\gamma_{\epsilon,\delta}) &= \int_{X\setminus\bigcup_{{\frak p}\in\mathrm{Sing}(X)}V(\delta)_{\frak p}}h\cdot c_{2}(X,\gamma_{0}) \\ &\quad + \sum_{{\frak p}\in\mathrm{Sing}(X)}h({\frak p})\int_{T^{*}\mathbf{P}^{1}}c_{2}(T^{*}\mathbf{P}^{1},\gamma^{\mathrm{EH}}) \\ &= \int_{X}h\cdot c_{2}(X,\gamma_{0}) + \sum_{{\frak p}\in\mathrm{Sing}(X)}h({\frak p})\int_{T^{*}\mathbf{P}^{1}}c_{2}(T^{*}\mathbf{P}^{1},\gamma^{\mathrm{EH}}), \end{aligned} \end{align} $$

where we used the vanishing of $c_{2}(X,\gamma _{0})$ on $V(\delta )_{\frak p}$ to get the second equality. Setting $h=1$ in equation (5.3) and comparing it with the formula [27, p.396 l.5], we get

(5.4) $$ \begin{align} \int_{T^{*}\mathbf{P}^{1}}c_{2}(T^{*}\mathbf{P}^{1},\gamma^{\mathrm{EH}})=\chi(\mathbf{P}^{1})-\frac{1}{|\mathbf{Z}_{2}|}=\frac{3}{2}. \end{align} $$

The first assertion follows from equations (5.3) and (5.4).

Since $\#\mathrm {Sing}(Y)=k$ , we get by the first assertion

$$ \begin{align*}2\int_{Y}c_{2}(Y,\gamma_{0}) = \int_{X}c_{2}(X,\gamma_{0}) = \int_{\widetilde{X}}c_{2}(\widetilde{X},\gamma_{\epsilon,\delta})-\frac{3}{2}\sum_{{\frak p}\in\mathrm{Sing}(X)}\int_{X}\delta_{\frak p} = 24-\frac{3}{2}k. \end{align*} $$

This proves the second assertion.

5.2 Behaviour of the Bott-Chern terms as $\epsilon \to 0$

Proposition 5.2. For any $\delta \in (0,1]$ , one has

$$ \begin{align*}\begin{aligned} \,& \lim_{\epsilon\to0} \int_{\widetilde{X}} \log \left\{ \frac{\eta\wedge\overline{\eta}}{\gamma_{\epsilon,\delta}^{2}/2!}\cdot\frac{\mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta})}{\|\eta\|_{L^{2}}^{2}} \right\}\, c_{2}(\widetilde{X},\gamma_{\epsilon,\delta}) \\ &= \int_{X} \log\left\{\frac{\eta\wedge\overline{\eta}}{\gamma_{0}^{2}/2!}\cdot\frac{\mathrm{Vol}(X,\gamma_{0})}{\|\eta\|_{L^{2}}^{2}}\right\}\,c_{2}(X,\gamma_{0}) + \frac{3}{2}\sum_{{\frak p}\in\mathrm{Sing}(X)}\log\left\{|f_{\frak p}(0)|^{2}\frac{\mathrm{Vol}(X,\gamma_{0})}{\|\eta\|_{L^{2}}^{2}}\right\}. \end{aligned} \end{align*} $$

Proof. Since $\gamma _{\epsilon ,\delta }$ converges to $\gamma _{0}$ outside $\bigcup _{{\frak p}\in \mathrm {Sing}(X)}\widetilde {V}(\delta )_{\frak p}$ , and since $\mathrm {Vol}(\widetilde {X},\gamma _{\epsilon ,\delta })$ converges to $\mathrm {Vol}(X,\gamma _{0})$ as $\epsilon \to 0$ , we get the convergence

$$ \begin{align*}\begin{aligned} \,& \left( \int_{\widetilde{X}\setminus\bigcup_{{\frak p}\in\mathrm{Sing}(X)}\widetilde{V}(\delta)_{\frak p}} + \sum_{{\frak p}\in\mathrm{Sing}(X)}\int_{\widetilde{V}(\delta)_{\frak p}} \right) \log \left\{ \frac{\eta\wedge\overline{\eta}}{\gamma_{\epsilon,\delta}^{2}/2!}\cdot\frac{\mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta})}{\|\eta\|_{L^{2}}^{2}} \right\} c_{2}(\widetilde{X},\gamma_{\epsilon,\delta}) \\ &\to \int_{\widetilde{X}\setminus\bigcup_{{\frak p}\in\mathrm{Sing}(X)}\widetilde{V}(\delta)_{\frak p}} \log \left\{ \frac{\eta\wedge\overline{\eta}}{\gamma_{0}^{2}/2!}\cdot\frac{\mathrm{Vol}(X,\gamma_{0})}{\|\eta\|_{L^{2}}^{2}} \right\} c_{2}(\widetilde{X},\gamma_{0}) \\ &\quad+ \lim_{\epsilon\to0} \sum_{{\frak p}\in\mathrm{Sing}(X)}\int_{\widetilde{V}(\delta)_{\frak p}} \left\{ \log\pi^{*}|f_{\frak p}(z)|^{2}c_{2}(\widetilde{X},\gamma_{\epsilon,\delta}) + \log\frac{\mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta})}{\|\eta\|_{L^{2}}^{2}}c_{2}(\widetilde{X},\gamma_{\epsilon,\delta}) \right\} \\ &= \int_{X\setminus\bigcup_{{\frak p}\in\mathrm{Sing}(X)}V(\delta)_{\frak p}} \log \left\{ \frac{\eta\wedge\overline{\eta}}{\gamma_{0}^{2}/2!}\cdot\frac{\mathrm{Vol}(X,\gamma_{0})}{\|\eta\|_{L^{2}}^{2}} \right\} c_{2}(X,\gamma_{0}) \\ &\quad+ \frac{3}{2}\sum_{{\frak p}\in\mathrm{Sing}(X)}\log \left(|f_{\frak p}(0)|^{2}\frac{\mathrm{Vol}(X,\gamma_{0})}{\|\eta\|_{L^{2}}^{2}}\right) \end{aligned} \end{align*} $$

as $\epsilon \to 0$ , where the last equality follows from Proposition 5.1. Since $c_{2}(X,\gamma _{0})=0$ on $\bigcup _{{\frak p}\in \mathrm {Sing}(X)}V(\delta )_{\frak p}$ , we get the result.

Corollary 5.3. For any $\delta \in (0,1]$ , one has

$$ \begin{align*}\begin{aligned} \lim_{\delta\to0}\lim_{\epsilon\to0}\tau(\widetilde{X},\gamma_{\epsilon,\delta}) &= \prod_{{\frak p}\in\mathrm{Sing}(X)}\left\{|f_{\frak p}(0)|^{2}\frac{\mathrm{Vol}(X,\gamma_{0})}{\|\eta\|_{L^{2}}^{2}}\right\}^{-\frac{1}{16}} \\ &\quad\times \exp \left( -\frac{1}{24}\int_{X} \log\left\{\frac{\eta\wedge\overline{\eta}}{\gamma_{0}^{2}/2!}\cdot\frac{\mathrm{Vol}(X,\gamma_{0})}{\|\eta\|_{L^{2}}^{2}}\right\}\, c_{2}(X,\gamma_{0}) \right). \end{aligned} \end{align*} $$

In particular, the limit $\lim _{\delta \to 0}\lim _{\epsilon \to 0}\tau (\widetilde {X},\gamma _{\epsilon ,\delta })$ is independent of the choice of $\rho $ .

Proof. By Theorem 3.2 and Proposition 5.2, we get the desired equality. The independence of the double limit $\lim _{\delta \to 0}\lim _{\epsilon \to 0}\tau (\widetilde {X},\gamma _{\epsilon ,\delta })$ from $\rho $ is obvious because the right-hand side is independent of the choice of $\rho $ .

Define the Fubini-Study form on $E_{\frak p}$ by

$$ \begin{align*}\omega_{\mathrm{FS}}(E_{\frak p}):=\left.\varPi^{*}\left(\frac{i}{2\pi}\partial\bar{\partial}\log\|z\|^{2}\right)\right|_{E_{\frak p}}. \end{align*} $$

Then for ${\frak p}\in \mathrm {Sing}(X)$ , we have

$$ \begin{align*}\gamma_{\epsilon,\delta}|_{E_{\frak p}}=\epsilon\,\omega_{\mathrm{FS}}(E_{\frak p}) \end{align*} $$

and an isomorphism of Kähler manifolds $(E_{\frak p},\omega _{\mathrm {FS}}(E_{\frak p}))\cong (\mathbf {P}^{1},\omega _{\mathrm {FS}})$ .

Proposition 5.4. For any $\delta \in (0,1]$ , one has

$$ \begin{align*}\lim_{\epsilon\to0}A_{M}(\widetilde{X},\theta,\gamma_{\epsilon,\delta}) = \prod_{{\frak p}\in\mathrm{Sing}(X)}\left\{|f_{\frak p}(0)|^{2}\frac{\mathrm{Vol}(X,\gamma_{0})}{\|\eta\|_{L^{2}}^{2}}\right\}^{\frac{1}{4}}. \end{align*} $$

Proof. Since $\gamma _{\epsilon ,\delta }|_{E_{\frak p}}=\epsilon \,\omega _{\mathrm {FS}}(E_{\frak p})$ , and since $\omega _{\mathrm {FS}}(E_{\frak p})$ is Kähler-Einstein, we get

$$ \begin{align*}c_{1}(\widetilde{X}^{\theta},\gamma_{\epsilon,\delta}|_{\widetilde{X}^{\theta}})|_{E_{\frak p}} = \chi(\mathbf{P}^{1})\,\omega_{\mathrm{FS}}(E_{\frak p}) = 2\,\omega_{\mathrm{FS}}(E_{\frak p}). \end{align*} $$

Since $(\eta \wedge \overline {\eta })/(\gamma _{\epsilon ,\delta }^{2}/2!)|_{E_{\frak p}}=|f_{\frak p}(0)|^{2}$ by equation (4.13), we get

$$ \begin{align*}\begin{aligned} \,& A_{M}(\widetilde{X},\theta,\gamma_{\epsilon,\delta}) = \exp \left[ \frac{1}{8}\int_{\widetilde{X}^{\theta}} \left.\log\left\{\frac{\eta\wedge\overline{\eta}}{\gamma_{\epsilon,\delta}^{2}/2!} \cdot \frac{\mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta})}{\|\eta\|_{L^{2}}^{2}}\right\}\right|_{\widetilde{X}^{\theta}}\, c_{1}(\widetilde{X}^{\theta},\gamma_{\epsilon,\delta}|_{\widetilde{X}^{\theta}}) \right] \\ &= \exp \left[ \frac{1}{4}\sum_{{\frak p}\in\mathrm{Sing}(X)}\int_{E_{\frak p}} \left.\log\left\{ |f_{\frak p}(0)|^{2}\frac{\mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta})}{\|\eta\|_{L^{2}}^{2}}\right\}\right|_{E_{\frak p}}\, \omega_{\mathrm{FS}}(E_{\frak p}) \right] \\ &= \exp \left[ \frac{1}{4}\sum_{{\frak p}\in\mathrm{Sing}(X)} \log\left\{ |f_{\frak p}(0)|^{2}\frac{\mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta})}{\|\eta\|_{L^{2}}^{2}}\right\} \right] \to \prod_{{\frak p}\in\mathrm{Sing}(X)}\left\{|f_{\frak p}(0)|^{2}\frac{\mathrm{Vol}(X,\gamma_{0})}{\|\eta\|_{L^{2}}^{2}}\right\}^{\frac{1}{4}} \end{aligned} \end{align*} $$

as $\epsilon \to 0$ , where we used equation (4.14) to get the last limit. This completes the proof.

5.3 Behaviour of the analytic torsion of the exceptional divisors

Proposition 5.5. For any $\delta \in (0,1]$ and ${\frak p}\in \mathrm {Sing}(X)$ , the following equality holds for all $\epsilon \in (0,\delta ^{2}\epsilon (\rho )]$ :

$$ \begin{align*}\frac{\mathrm{Vol}(E_{\frak p},\gamma_{\epsilon,\delta}|_{E_{\frak p}})\tau(E_{\frak p},\gamma_{\epsilon,\delta}|_{E_{\frak p}})} {\mathrm{Vol}(\mathbf{P}^{1},\omega_{\mathrm{FS}})\tau(\mathbf{P}^{1},\omega_{\mathrm{FS}})} = \epsilon^{1/3}. \end{align*} $$

Proof. We recall a formula of Bost [9, Prop. 4.4]. Let $(Z,g)$ be a compact Kähler manifold of dimension d, and let $\lambda>0$ be a constant. By [9, (4.2.4)], we get

(5.5) $$ \begin{align} \log\left(\frac{\tau(Z,\lambda g)}{\tau(Z,g)}\right) = \left( -\sum_{i=0}^{d}(-1)^{i}(d-i)\,h^{0,i}(Z)+\int_{Z}\mathrm{Td}'(TZ) \right) \log\lambda, \end{align} $$

where the characteristic class $\mathrm {Td}'(E)$ is defined as follows (compare [9, Prop. 4.4]). If $\xi _{i} (i=1,\ldots ,r=\mathrm {rk}(E))$ are the Chern roots of a vector bundle E, then

$$ \begin{align*}\mathrm{Td}'(E) := \mathrm{Td}(E)\cdot\sum_{i=1}^{r}\left(\frac{1}{\xi_{i}}-\frac{e^{-\xi_{i}}}{1-e^{-\xi_{i}}}\right). \end{align*} $$

Since

$$ \begin{align*}\mathrm{Td}'(x) = \frac{x}{1-e^{-x}}\left(\frac{1}{x}-\frac{e^{-x}}{1-e^{-x}}\right) = \frac{1}{2}+\frac{1}{6}x+O(x^{2}) \end{align*} $$

and hence $\int _{\mathbf {P}^{1}}\mathrm {Td}'(T\mathbf {P}^{1})=1/3$ , we get by equation (5.5) applied to $(Z,g)=(\mathbf {P}^{1},\omega _{\mathrm {FS}})$

(5.6) $$ \begin{align} \tau(E_{\frak p},\gamma_{\epsilon,\delta}|_{E_{\frak p}})/\tau(\mathbf{P}^{1},\omega_{\mathrm{FS}}) = \tau(\mathbf{P}^{1},\epsilon\,\omega_{\mathrm{FS}})/\tau(\mathbf{P}^{1},\omega_{\mathrm{FS}}) = \epsilon^{-2/3}. \end{align} $$

Since

(5.7) $$ \begin{align} \mathrm{Vol}(E_{\frak p},\gamma_{\epsilon,\delta}|_{E_{\frak p}})/\mathrm{Vol}(\mathbf{P}^{1},\omega_{\mathrm{FS}}) = \mathrm{Vol}(\mathbf{P}^{1},\epsilon\,\omega_{\mathrm{FS}})/\mathrm{Vol}(\mathbf{P}^{1},\omega_{\mathrm{FS}}) = \epsilon, \end{align} $$

the result follows from equations (5.6) and (5.7).

6 Spectrum and heat kernels under the degeneration

In this section, we prove a uniform lower bound of the kth eigenvalue of the Laplacian and also a certain uniform exponential decay of the heat kernel for the degenerating family of metrics $\gamma _{\epsilon ,\delta }$ .

6.1 Uniformity of Sobolev inequality

In order to study the limit of the analytic torsions $\tau (\widetilde {X}, \gamma _{\epsilon ,\delta })$ and $\tau _{{\mathbf Z}_{2}}(\widetilde {X}, \gamma _{\epsilon ,\delta })(\theta )$ in the next section, we need to establish a uniform Sobolev inequality. First, we consider our model space $(T^{*}\mathbf {P}^{1}, \gamma ^{\mathrm {EH}}_{\epsilon })$ , the Eguchi-Hanson instanton. Here $\gamma ^{\mathrm {EH}}_{\epsilon }$ is the Ricci-flat Kähler metric constructed in Section 5.1 on $\widetilde {V}(\infty )=T^{*}\mathbf {P}^{1}$ . Note that for $0<\epsilon \leq 1$ , under the identification $\Phi :\ ({\mathbf R}^4\!-\! B(\rho ))/\{\pm 1\} \simeq \widetilde {V}(\infty )\! -\! K$ outside a compact neighbourhood $K = \widetilde {V}(\rho ) \subset \widetilde {V}(\infty )$ of the zero section of $T^{*}\mathbf {P}^{1}$ induced by the identification $({\mathbf C}^2\!-\! B(\rho ))/\{\pm 1\} = V(\infty ) \!-\! V(\rho ) = \widetilde {V}(\infty ) \!-\! \widetilde {V}(\rho )$ , one has

$$ \begin{align*}\Phi^*(\gamma^{\mathrm{EH}}_{\epsilon})_{ij} = \delta_{ij} + O(r^{-4}) \end{align*} $$

uniformly in $\epsilon $ by equation (4.4).

Lemma 6.1. There is a constant C such that for all $0<\epsilon \leq 1$ , the following hold:

1. (1) For all $f\in C_0^{\infty }(\widetilde {V}(\infty ))$ ,

   $$ \begin{align*}\| f \|_{L^4(\widetilde{V}(\infty),\gamma^{\mathrm{EH}}_{\epsilon})} \leq C \| df \|_{L^2(\widetilde{V}(\infty),\gamma^{\mathrm{EH}}_{\epsilon})}.\end{align*} $$

2. (2) Similarly, for all $\alpha \in A^{0,2}_0(\widetilde {V}(\infty ))$ ,

   $$ \begin{align*}\| \alpha \|_{L^4(\widetilde{V}(\infty),\gamma^{\mathrm{EH}}_{\epsilon})} \leq C \| d\alpha \|_{L^2(\widetilde{V}(\infty),\gamma^{\mathrm{EH}}_{\epsilon})}.\end{align*} $$

3. (3) For all $\alpha \in A^{0,1}_0(\widetilde {V}(\infty ))$ ,

   $$ \begin{align*}\| \alpha \|^2_{L^4(\widetilde{V}(\infty),\gamma^{\mathrm{EH}}_{\epsilon})} \leq C^2 \left(\| \overline{\partial}\alpha \|^2_{L^2(\widetilde{V}(\infty),\gamma^{\mathrm{EH}}_{\epsilon})} + \| \overline{\partial}^*\alpha \|^2_{L^2(\widetilde{V}(\infty),\gamma^{\mathrm{EH}}_{\epsilon})}\right). \end{align*} $$

Here all norms are defined with respect to the metric $\gamma ^{\mathrm {EH}}_{\epsilon }$ .

Proof. Since $(\widetilde {V}(\infty ),\gamma ^{\mathrm {EH}}_{\epsilon })\cong (\widetilde {V}(\infty ),\epsilon \gamma ^{\mathrm {EH}})$ by equation (4.1), and since the inequalities (1), (2), (3) above are invariant under the scaling of metrics $\gamma ^{\mathrm {EH}}\mapsto \epsilon \gamma ^{\mathrm {EH}}$ , it suffices to prove (1), (2), (3) for $\gamma ^{\mathrm {EH}}$ . In the rest of the proof, all norms are defined with respect to $\gamma ^{\mathrm {EH}}$ . Identifying a function in $C_0^{\infty }(\widetilde {V}(\infty )\! -\! K)$ with the corresponding $\pm 1$ -invariant function on $\mathbf R^4$ with compact support via $\Phi $ , we deduce from the Sobolev inequality for $\mathbf R^4$ that

$$ \begin{align*}\|f\|_{L^4(\widetilde{V}(\infty))} \leq 2C\|df\|_{L^2(\widetilde{V}(\infty))}, \quad \forall f \in C_0^{\infty}(\widetilde{V}(\infty)\!-\! K),\end{align*} $$

where C is the Sobolev constant for $\mathbf R^4$ . By an argument using partition of unity, there is a constant $C_K> 0$ such that

$$ \begin{align*}\|f\|_{L^4(\widetilde{V}(\infty))} \leq C_K(\|df\|_{L^2(\widetilde{V}(\infty))} + \|f\|_{L^2(K)}), \quad \forall f \in C_0^{\infty}(\widetilde{V}(\infty)).\end{align*} $$

Assume that there is no constant $D> 0$ such that

$$ \begin{align*}\|f\|_{L^2(K)}\leq D\|df\|_{L^2(\widetilde{V}(\infty))}, \quad \forall f \in C_0^{\infty}(\widetilde{V}(\infty)).\end{align*} $$

Then for any $n \in \mathbf N$ , there is a function $f_n \in C_0^{\infty }(\widetilde {V}(\infty ))$ such that

$$ \begin{align*}\|f_n\|_{L^2(K)} = 1, \quad \|df_n\|_{L^2(\widetilde{V}(\infty))} \leq \frac{1}{n}.\end{align*} $$

Therefore, we have

$$ \begin{align*}\|f_n\|_{L^4(\widetilde{V}(\infty))}\leq C_K(1 + 1/n) \leq 2C_K.\end{align*} $$

Passing to a subsequence if necessary, it follows that the sequence $f_n$ has a weak limit $f_{\infty } \in L^4(\widetilde {V}(\infty ))$ with $df_{\infty }= 0$ as currents on $\widetilde {V}(\infty )$ . This implies that in $L^4(\widetilde {V}(\infty ))$ , $f_{\infty } = 0$ . On the other hand, let $K'$ be a sufficiently big compact subset of $\widetilde {V}(\infty )$ , whose open subset contains K. Now, for any compact subset $K' \subset \widetilde {V}(\infty )$ , there is a constant $C_{K'}> 0$ such that

$$ \begin{align*}\|f_n\|_{L^2(K')}\leq \mathrm{Vol}(K')^{1/2}\|f_n\|^{1/2}_{L^4(K')}\leq C_{K'} =\sqrt{2C_K\mathrm{Vol}(K')}.\end{align*} $$

Hence, by the Rellich lemma, we may assume (by again passing to a subsequence if necessary) that $f_n$ converges to $f_{\infty }$ strongly in $L^2(K')$ . Since $K \subset K'$ and hence the convergence $f_n \rightarrow f_{\infty }$ in $L^2(K)$ is strong, we see that $ \|f_{\infty }\|_{L^2(K)} = \lim _{n \rightarrow \infty } \|f_n\|_{L^2(K)} = 1$ . This is a contradiction. Hence there exists a constant D such that $ \|f\|_{L^2(K)}\leq D\|df\|_{L^2(\widetilde {V}(\infty ))}$ . By setting $C = CK(1 + D$ ), we have

$$ \begin{align*}\| f \|_{L^4(\widetilde{V}(\infty))} \leq C \| df \|_{L^2(\widetilde{V}(\infty))}.\end{align*} $$

This proves (1).

(2) is an immediate consequence of (1), and the isomorphism $C_0^{\infty }(\widetilde {V}(\infty ))\ni f\mapsto f\overline {\eta }\in A^{0,2}_{0}(\widetilde {V}(\infty ))$ , which commutes with the operations involved. To see (3), let $\alpha \in A^{0,1}_0(\widetilde {V}(\infty ))$ . Then by (1),

$$ \begin{align*}\| \alpha \|^2_{L^4(\widetilde{V}(\infty))} = \left( \int_{\widetilde{V}(\infty)} |\alpha|^4 dx\right)^{1/2} \leq C^2 \int_{\widetilde{V}(\infty)} |\, d|\alpha|\, |^2dx. \end{align*} $$

Using Kato’s inequality, we have

$$ \begin{align*}\int_{\widetilde{V}(\infty)} |\, d|\alpha|\, |^2dx \leq \int_{\widetilde{V}(\infty)} |\nabla\alpha|^2dx.\end{align*} $$

Now the Bochner formula [34, (1.4.63)] gives $(\overline {\partial }\overline {\partial }^* + \overline {\partial }^*\overline {\partial })\alpha = \nabla ^*\nabla \alpha $ since $(\widetilde {V}(\infty ),\gamma ^{\mathrm {EH}}_{\epsilon })$ is Ricci flat. Our result follows.

Lemma 6.2. There is a constant C such that for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ , and all $\alpha \in A^{0,q}_0(\widetilde {V}(\infty ))$ , $0\leq q\leq 2$ ,

$$ \begin{align*}\| \alpha \|^2_{L^4(\widetilde{V}(\infty),\kappa_{\epsilon,\delta})} \leq C^2 \left( \| \overline{\partial}\alpha \|^2_{L^{2}(\widetilde{V}(\infty),\kappa_{\epsilon,\delta})} + \| \overline{\partial}^*\alpha \|^2_{L^2(\widetilde{V}(\infty),\kappa_{\epsilon,\delta})} \right), \end{align*} $$

where the norms and $\bar {\partial }^{*}$ are defined with respect to the metric $\kappa _{\epsilon ,\delta }$ .

Proof. By Lemmas 4.1 and 4.3, there exist constants $C_{1},C_{2}>0$ such that

(6.1) $$ \begin{align} C_{1}\gamma^{\mathrm{EH}}_{\epsilon}\leq\kappa_{\epsilon,\delta}\leq C_{2}\gamma^{\mathrm{EH}}_{\epsilon} \end{align} $$

for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ . Here $\epsilon (\rho )$ is defined in Section 4.2.1, in the discussion following equation (4.2). Hence there is a constant $C_{3}>0$ such that

(6.2) $$ \begin{align} C_{3}^{-1}\| \alpha \|^2_{L^4(\widetilde{V}(\infty),\gamma^{\mathrm{EH}}_{\epsilon})} \leq \| \alpha \|^2_{L^4(\widetilde{V}(\infty),\kappa_{\epsilon,\delta})} \leq C_{3}\| \alpha \|^2_{L^4(\widetilde{V}(\infty),\gamma^{\mathrm{EH}}_{\epsilon})}, \end{align} $$

(6.3) $$ \begin{align} C_{3}^{-1}\| \overline{\partial}\alpha \|^2_{L^{2}(\widetilde{V}(\infty),\gamma^{\mathrm{EH}}_{\epsilon})} \leq \| \overline{\partial}\alpha \|^2_{L^{2}(\widetilde{V}(\infty),\kappa_{\epsilon,\delta})} \leq C_{3}\| \overline{\partial}\alpha \|^2_{L^{2}(\widetilde{V}(\infty),\gamma^{\mathrm{EH}}_{\epsilon})} \end{align} $$

for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ and $\alpha \in A^{0,q}_{0}(\widetilde {V}(\infty ))$ .

Let $\Lambda _{\epsilon .\delta }$ (respectively, $\Lambda _{\epsilon }$ ) be the Lefschetz operator defined as the adjoint of the multiplication by $\kappa _{\epsilon ,\delta }$ (respectively, $\gamma ^{\mathrm {EH}}_{\epsilon }$ ). Since $\overline {\partial }^{*}=\pm i\Lambda _{\epsilon ,\delta }\partial $ for $(0,q)$ -forms by the Kähler identity, there exists by equation (6.1) a constant $C_{4}>0$ such that

(6.4) $$ \begin{align} C_{4}^{-1}\| \overline{\partial}^*\alpha \|^2_{L^2(\widetilde{V}(\infty),\gamma^{\mathrm{EH}}_{\epsilon})} \leq \| \overline{\partial}^*\alpha \|^2_{L^2(\widetilde{V}(\infty),\kappa_{\epsilon,\delta})} \leq C_{4}\| \overline{\partial}^*\alpha \|^2_{L^2(\widetilde{V}(\infty),\gamma^{\mathrm{EH}}_{\epsilon})}. \end{align} $$

By Lemma 6.1 (3) and equations (6.2), (6.3) and (6.4), we get the result.

For the minimal resolution $\widetilde {X}$ and the family of Kähler metrics $\gamma _{\epsilon ,\delta }$ constructed in Section 5.2 using the Eguchi-Hanson instanton, we have

Proposition 6.3. There is a constant C such that for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ , and all $\alpha \in A^{0,q}(\widetilde {X})$ , $0\leq q\leq 2$ ,

$$ \begin{align*}\| \alpha \|^2_{L^4(\widetilde{X},\gamma_{\epsilon,\delta})} \leq C^2 \left( \| \overline{\partial}\alpha \|^2_{L^2(\widetilde{X},\gamma_{\epsilon,\delta})} + \| \overline{\partial}^*\alpha \|^2_{L^2(\widetilde{X},\gamma_{\epsilon,\delta})} + \|\alpha \|^2_{L^2(\widetilde{X},\gamma_{\epsilon,\delta})} \right), \end{align*} $$

where the norms are defined with respect to the metric $\gamma _{\epsilon ,\delta }$ .

Proof. Since $\gamma _{\epsilon ,\delta }=\kappa _{\epsilon ,\delta }$ on $\bigcup _{{\frak p}\in \mathrm {Sing}(X)}\widetilde {V}(\delta )_{\frak p}$ , the result follows from Lemma 6.2 and an easy partition of unity argument.

6.2 A uniform lower bound of spectrum

Let $\square _{\epsilon ,\delta }^{q}=(\bar {\partial }+\bar {\partial }^{*})^{2}$ (respectively, $\square _{0}^{q}$ ) be the Hodge-Kodaira Laplacian of $(\widetilde {X},\gamma _{\epsilon ,\delta })$ (respectively, $(X,\gamma _{0})$ ) acting on $(0,q)$ -forms. Let $\lambda _{\epsilon ,\delta }^{q}(k)$ (respectively, $\lambda _{0}^{q}(k)$ ) be the kth nonzero eigenvalue of the Laplacian $\square _{\epsilon ,\delta }^{q}$ (respectively, $\square _{0}^{q}$ ). Then the nonzero eigenvalues of $\square _{\epsilon ,\delta }^{q}$ are given by

$$ \begin{align*}0<\lambda_{\epsilon,\delta}^{q}(1)\leq\lambda_{\epsilon,\delta}^{q}(2) \leq\cdots\leq\lambda_{\epsilon,\delta}^{q}(k)\leq\lambda_{\epsilon,\delta}^{q}(k+1)\leq\cdots \end{align*} $$

and the set of corresponding eigenforms $\{\varphi _{k,\epsilon ,\delta }^{q}\}_{k\in \mathbf {N}}$ . We set $\lambda _{\epsilon ,\delta }^{q}(0)=0$ and list the corresponding eigenforms $\varphi _{0,\epsilon ,\delta }^{q}$ (here we abuse the notation as there would be $\dim H^0(\tilde X, \Omega ^q_{\tilde X})$ many of them) so that $\{\varphi _{k,\epsilon ,\delta }^{q}\}_{k=0}^{\infty }$ forms a complete orthonormal basis of $L^{0,q}_{\epsilon ,\delta }(\widetilde {X})$ , the $L^{2}$ -completion of $A^{0,q}(\widetilde {X})$ with respect to the norm associated to $\gamma _{\epsilon ,\delta }$ . Since

$$ \begin{align*}K_{\epsilon,\delta}^{q}(t,x,y)=\sum_{k=0}^{\infty}e^{-t\lambda_{\epsilon,\delta}^{q}(k)}\varphi_{k,\epsilon,\delta}^{q}(x)\otimes\varphi_{k,\epsilon,\delta}^{q}(y)^{*}, \end{align*} $$

we get

(6.5) $$ \begin{align} \begin{aligned} \left| K_{\epsilon,\delta}^{q}(t,x,y) \right| &\leq \sum_{k=0}^{\infty}e^{-t\lambda_{\epsilon,\delta}^{q}(k)}|\varphi_{k,\epsilon,\delta}^{q}(x)|\cdot|\varphi_{k,\epsilon,\delta}^{q}(y)| \\ &\leq \{\sum_{k=0}^{\infty}e^{-t\lambda_{\epsilon,\delta}^{q}(k)}|\varphi_{k,\epsilon,\delta}^{q}(x)|^{2}\}^{1/2} \{\sum_{k=0}^{\infty}e^{-t\lambda_{\epsilon,\delta}^{q}(k)}|\varphi_{k,\epsilon,\delta}^{q}(y)|^{2}\}^{1/2} \\ &= \sqrt{\mathrm{tr}\,K_{\epsilon,\delta}^{q}(t,x,x)}\sqrt{\mathrm{tr}\,K_{\epsilon,\delta}^{q}(t,y,y)}. \end{aligned} \end{align} $$

Proposition 6.4. If $q=0,2$ , then there are constants $A, C>0$ such that for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ , and $x,y\in \widetilde {X}$ , $t>0$ , the following inequality holds:

(6.6) $$ \begin{align} 0< \left| K_{\epsilon,\delta}^{q}(t,x,y) \right| \leq A e^{C(\epsilon\delta^{-4}+1)}(t^{-2}+1). \end{align} $$

Moreover, for all $(\epsilon ,\delta )\in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ , and for all $t>0$ , $q\geq 0$ , the following inequality holds:

(6.7) $$ \begin{align} \mathrm{Tr}\,e^{-t\,\square_{\epsilon,\delta}^{q}}\leq \mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta})Ae^{C(\epsilon\delta^{-4}+1)}(t^{-2}+1). \end{align} $$

Proof. (Case 1) Let $q=0$ . By Proposition 6.3, the Sobolev constant is uniform for $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ . By [10, Thms. 2.1 and 2.16], there are constants $A>0$ , $B\geq 0$ such that for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ , and $x,y\in \widetilde {X}$ , $t>0$ ,

(6.8) $$ \begin{align} 0< K_{\epsilon,\delta}^{q}(t,x,y) \leq A\,e^{Bt}t^{-2}. \end{align} $$

Let $q=2$ . By Lemma 4.5, the Lichnerowicz formula and [24, p.32 l.4-l.5], we have

(6.9) $$ \begin{align} | K_{\epsilon,\delta}^{q}(t,x,y) | \leq e^{t|\mathrm{Ric}\gamma_{\epsilon,\delta}|_{\infty}} | K_{\epsilon,\delta}^{0}(t,x,y) | \leq e^{C(\epsilon\delta^{-4}+1)t}Ae^{Bt}(t^{-2}+1). \end{align} $$

For $t\leq 1$ , we get equation (6.6) by equations (6.8) and (6.9). For $t\geq 1$ , since $\mathrm {tr}\,K_{\epsilon ,\delta }^{q}(t,x,x)$ is a decreasing function in t, we deduce equation (6.6) from equations (6.5), (6.8) and (6.9) and the inequality

$$ \begin{align*}\left| K_{\epsilon,\delta}^{q}(t,x,y) \right| \leq \sqrt{\mathrm{tr}\,K_{\epsilon,\delta}^{q}(1,x,x)}\sqrt{\mathrm{tr}\,K_{\epsilon,\delta}^{q}(1,y,y)} \leq 2e^{C(\epsilon\delta^{-4}+1)}Ae^{B}. \end{align*} $$

Since $\mathrm {Tr}\,e^{-t\,\square _{\epsilon ,\delta }^{q}}=\int _{\widetilde {X}}\mathrm {tr}\,K_{\epsilon ,\delta }^{q}(t,x,x)\,dx$ , we get equation (6.7) from equation (6.6).

(Case 2) Let $q=1$ . Since $\sum _{q}(-1)^{q}\mathrm {Tr}\,e^{-t\,\square _{\epsilon ,\delta }^{q}}=0$ for all $t>0$ , equation (6.7) for $q=1$ follows from equation (6.7) for $q=0,2$ . This completes the proof.

Write $\lambda _{\epsilon }^{q}(k)$ for $\lambda _{\epsilon ,1}^{q}(k)$ .

Lemma 6.5. There is a constant $\lambda>0$ such that for all $\epsilon \in (0,\epsilon (\rho )]$ and $q\geq 0$ ,

(6.10) $$ \begin{align} \lambda_{\epsilon}^{q}(1)\geq\lambda>0. \end{align} $$

Proof. Since $\dim \widetilde {X}=2$ and hence $\lambda _{\epsilon }^{1}(1)=\lambda _{\epsilon }^{0}(1)$ or $\lambda _{\epsilon }^{1}(1)=\lambda _{\epsilon }^{2}(1)$ , it suffices to prove equation (6.10) for $q=0,2$ . Assume that there is a sequence $\{\epsilon _{n}\}$ such that $\epsilon _{n}\to 0$ and $\lambda _{\epsilon _{n}}^{q}(1)\to 0$ as $n\to \infty $ for $q=0$ or $2$ . By the same argument as in [42, p.434–p.436] using the uniformity of the Sobolev constant (compare Proposition 6.3), there is a holomorphic q-form $\psi $ on $X \setminus \mathrm {Sing}\,X$ , which is possibly meromorphic on $\widetilde {X}$ , with the following properties:

1. (i) The complex conjugation $\overline {\varphi _{1,\epsilon _{n}}^{q}}$ converges to $\psi $ on every compact subset of $X\setminus \mathrm {Sing}(X)$ as $n\to \infty $ .

2. (ii) $\|\psi \|_{L^{2}}=1$ and $\pi ^{*}\psi \perp H^{0}(\widetilde {X},\Omega ^{q}_{\widetilde {X}})$ with respect to the degenerate Kähler metric $\pi ^{*}\gamma _{0}$ on $\widetilde {X}$ .

Since $\mathrm {Sing}\,X$ consists of isolated orbifold points, it follows from the Riemann extension theorem that $\psi $ extends to a holomorphic q-form on X in the sense of orbifolds. When $q=0$ , $\psi $ is a constant. When $q=2$ , since X has canonical singularities, $\pi ^{*}\psi $ is a holomorphic $2$ -form on $\widetilde {X}$ . In both cases, the condition $\pi ^{*}\psi \perp H^{0}(\widetilde {X},\Omega ^{q}_{\widetilde {X}})$ implies $\psi =0$ , which contradicts the other condition $\|\psi \|_{L^{2}}=1$ . This proves the result.

Lemma 6.6. There is a constant $\lambda '>0$ such that for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )]$ and $q\geq 0$ ,

$$ \begin{align*}\lambda_{\epsilon,\delta}^{q}(1)\geq\lambda'>0. \end{align*} $$

Proof. Firstly, we prove the inequality when $q=1$ . Since $\widetilde {X}$ is a $K3$ surface and hence $\ker \square _{\epsilon ,\delta }^{1}=0$ , we get by equation (6.10)

(6.11) $$ \begin{align} \lambda\,\|\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon})}^{2} \leq \|\bar{\partial}\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon})}^{2}+\|\bar{\partial}^{*}\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon})}^{2} = \|\partial\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon})}^{2} \end{align} $$

for all $\alpha \in A^{0,1}(\widetilde {X})$ , where we used the coincidence of the $\bar {\partial }$ -Laplacian and the $\partial $ -Laplacian for Kähler manifolds to get the equality in equation (6.11). By Lemma 4.4, there exist constants $C_{1}>0$ such that for all $\alpha \in A^{0,1}(\widetilde {X})$ ,

$$ \begin{align*}C_{1}^{-1}\|\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon})}^{2} \leq \|\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon,\delta})}^{2} \leq C_{1}\|\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon})}^{2}, \end{align*} $$

$$ \begin{align*}C_{1}^{-1}\|\partial\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon})}^{2} \leq \|\partial\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon,\delta})}^{2} \leq C_{1}\|\partial\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon})}^{2}. \end{align*} $$

Combining these inequalities and equation (6.11), we get for all $\alpha \in A^{0,1}(\widetilde {X})$

(6.12) $$ \begin{align} C_{1}^{-1}\lambda\,\|\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon,\delta})}^{2} \leq C_{1}\|\partial\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon,\delta})}^{2} = C_{1} \left( \|\bar{\partial}\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon,\delta})}^{2}+\|\bar{\partial}^{*}\alpha\|_{L^{2}(\widetilde{X},\gamma_{\epsilon,\delta})}^{2} \right). \end{align} $$

The result for $q=1$ follows from equation (6.12). Since $\bar {\partial }\varphi _{\epsilon ,\delta }^{0}(1)$ and $\bar {\partial }^{*}\varphi _{\epsilon ,\delta }^{2}(1)$ are nonzero eigenforms of $\square _{\epsilon ,\delta }^{1}$ , we get $\lambda '\leq \lambda _{\epsilon ,\delta }^{1}(1)\leq \lambda _{\epsilon ,\delta }^{0}(1)$ and $\lambda '\leq \lambda _{\epsilon ,\delta }^{1}(1)\leq \lambda _{\epsilon ,\delta }^{2}(1)$ .

Theorem 6.7. There are constants $\Lambda , C>0$ such that for all $k\in \mathbf {N}$ , $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ and $q\geq 0$ ,

$$ \begin{align*}\lambda_{\epsilon,\delta}^{q}(k)\geq\Lambda e^{-\frac{1}{2}C(\epsilon\delta^{-4}+1)}\,k^{1/2}. \end{align*} $$

Proof. By Proposition 6.4, we get for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ and $t\in (0,1]$

$$ \begin{align*}\sum_{i=1}^{k}e^{-t\lambda_{\epsilon,\delta}^{q}(i)} \leq h^{0,q}(\widetilde{X})+\sum_{i=1}^{\infty}e^{-t\lambda_{\epsilon,\delta}^{q}(i)} = \mathrm{Tr}\,e^{-t\square_{\epsilon,\delta}^{q}} \leq A'e^{C(\epsilon\delta^{-4}+1)} \,t^{-2}, \end{align*} $$

where $A'$ is a constant such that $A\mathrm {Vol}(\widetilde {X},\gamma _{\epsilon ,\delta }) \leq A'$ . Since $\lambda '/\lambda _{\epsilon ,\delta }^{q}(k)\leq 1$ by Lemma 6.6, substituting $t:=\lambda '/\lambda _{\epsilon ,\delta }^{q}(k)$ in this inequality and using $\lambda _{\epsilon ,\delta }^{q}(i)/\lambda _{\epsilon ,\delta }^{q}(k)\leq 1$ for $i\leq k$ , we get

$$ \begin{align*}k\,e^{-\lambda'} \leq \sum_{i=1}^{k}e^{-\frac{\lambda'\lambda_{\epsilon,\delta}^{q}(i)}{\lambda_{\epsilon,\delta}^{q}(k)}} \leq A'e^{C(\epsilon\delta^{-4}+1)}\,\left(\frac{\lambda'}{\lambda_{\epsilon,\delta}^{q}(k)}\right)^{-2}. \end{align*} $$

We get the result by setting $\Lambda :=(A')^{-1/2}\lambda ' e^{-\lambda '/2}$ .

Corollary 6.8. Let C and $\Lambda $ be the same constants as in Theorem 6.7, and set $\Lambda (R):=\Lambda e^{-\frac {1}{2}CR}$ and $\Psi (R):=\sum _{k=1}^{\infty }e^{-\frac {1}{2}\Lambda (R) k^{1/2}}$ . Then for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ and $t\geq 1$ , the following inequality holds:

$$ \begin{align*}0 < \mathrm{Tr}\,e^{-t\square_{\epsilon,\delta}^{q}}-h^{0,q}(\widetilde{X}) \leq \Psi(\epsilon\delta^{-4}+1)\,e^{-\frac{1}{2}\Lambda (1+\epsilon\delta^{-4})t}. \end{align*} $$

Proof. Since $\lambda _{\epsilon ,\delta }^{q}(k)\geq \frac {\Lambda (\epsilon \delta ^{-4}+1)}{2}(k^{1/2}+1)$ by Theorem 6.7, we get $\sum _{k=1}^{\infty }e^{-t\lambda _{\epsilon ,\delta }^{q}(k)} \leq e^{-t\Lambda (\epsilon \delta ^{-4}+1)/2}\sum _{k=1}^{\infty }e^{-\frac {1}{2}t\Lambda (\epsilon \delta ^{-4}+1) k^{1/2}} \leq \Psi (\epsilon \delta ^{-4}+1)\,e^{-t\Lambda (\epsilon \delta ^{-4}+1)/2}$ for $t\geq 1$ .

We also need an estimate for the heat kernel $K_{\epsilon ,\delta ,\infty }^{q}(t,x,y)$ of $(\widetilde {V}(\infty ),\kappa _{\epsilon ,\delta })$ .

Proposition 6.9. There are constants $A', C'>0$ such that for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ , $x\in \widetilde {V}(\infty )$ , $t>0$ and $q\geq 0$ , the following inequality holds:

$$ \begin{align*}\left|K_{\epsilon,\delta,\infty}^{q}(t,x,y)\right|\leq A'e^{C'(\epsilon\delta^{-4}+1)} (t^{-2}+1). \end{align*} $$

Proof. When $q=0$ , the result follows from Lemma 6.2 and [10, Thms. 2.1 and 2.16]. Let $q>0$ . Since $|\mathrm {Ric}(\gamma _{\epsilon ,\delta })|\leq C(\epsilon \delta ^{-4}+1)$ by Lemma 4.5, we deduce from [24, p.32 l.4-l.5] and the Lichnerowicz formula for $\square _{\epsilon ,\delta }^{q}$ that

$$ \begin{align*}0< \left| K_{\epsilon,\delta,\infty}^{q}(t,x,y) \right| \leq e^{C(\epsilon\delta^{-4}+1)t}K_{\epsilon,\delta,\infty}^{0}(t,x,y) \leq A\,e^{C(\epsilon\delta^{-4}+1)t}t^{-2}. \end{align*} $$

This proves the result for $t\leq 1$ . Since equation (6.5) remains valid for $K_{\epsilon ,\delta ,\infty }^{q}(t,x,y)$ by the fact that $K_{\epsilon ,\delta ,\infty }^{q}(t,x,y)$ is obtained as the limit $R\to \infty $ of the Dirichlet heat kernel of $\widetilde {V}(R)$ , the result for $t\geq 1$ also follows. This completes the proof.

7 Behaviour of (equivariant) analytic torsion

In the previous sections, the additional parameter $\delta $ is pretty harmless, and the results still hold in its presence. This parameter will play a more essential role in this section. Indeed, we shall prove the following:

Theorem 7.1. There exist constants $C_{0}(k),C_{1}(k)>0$ depending only on $k=\#\mathrm {Sing}(Y)$ such that

$$ \begin{align*}\lim_{\delta\to0}\lim_{\epsilon\to0}\tau(\widetilde{X},\gamma_{\epsilon, \delta})=C_{0}(k)\cdot\tau(X,\gamma_{0}), \end{align*} $$

$$ \begin{align*}\lim_{\delta\to0}\lim_{\epsilon\to0}\epsilon^{k/3}\tau_{\mathbf{Z}_{2}}(\widetilde{X},\gamma_{\epsilon, \delta})(\theta)=C_{1}(k)\cdot\tau_{\mathbf{ Z}_{2}}(X,\gamma_{0})(\iota). \end{align*} $$

7.1 Existence of limits

By Corollary 5.3, the first limit exists and is independent of the choice of a cut-off function $\rho $ . For the second limit, we have

Proposition 7.2. For any $\delta \in (0,1]$ , the number

$$ \begin{align*}\epsilon^{k/3}\tau_{\mathbf{Z}_{2}}(\widetilde{X},\gamma_{\epsilon,\delta})(\theta)\mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta}) \end{align*} $$

is independent of $\epsilon ,\delta \in (0,1]$ with $0<\epsilon \delta ^{-2}\leq \epsilon (\rho )$ . In particular, for any $\delta \in (0,1]$ , the following limit exists as $\epsilon \to 0$

$$ \begin{align*}\lim_{\epsilon\to0}\epsilon^{k/3}\tau_{\mathbf{Z}_{2}}(\widetilde{X},\gamma_{\epsilon,\delta})(\theta), \end{align*} $$

and the limit is independent of $\delta \in (0,1]$ and the choice of a cut-off function $\rho $ .

Proof. (Step 1) Let $g_{0},g_{1}$ be $\theta $ -invariant Kähler metrics on $\widetilde {X}$ . Let $\widetilde {\mathrm {Td}}_{\theta }(T\widetilde {X};g_{0},g_{1})^{(1,1)}$ be the Bott-Chern class such that

$$ \begin{align*}-dd^{c}\widetilde{\mathrm{Td}}_{\theta}(T\widetilde{X};g_{0},g_{1}) = \mathrm{Td}_{\theta}(T\widetilde{X},g_{0}) - \mathrm{Td}_{\theta}(T\widetilde{X},g_{1}). \end{align*} $$

By Bismut [4, Th. 2.5],

(7.1) $$ \begin{align} \log \left( \frac{\tau_{\mathbf{Z}_{2}}(\widetilde{X},g_{0})(\theta)\mathrm{Vol}(\widetilde{X},g_{0})}{\tau_{\mathbf{Z}_{2}}(\widetilde{X},g_{1})(\theta)\mathrm{ Vol}(\widetilde{X},g_{1})} \right) = \int_{\widetilde{X}^{\theta}} \widetilde{\mathrm{Td}}_{\theta}(T\widetilde{X};g_{0},g_{1}). \end{align} $$

Since

$$ \begin{align*}\mathrm{Td}_{\theta}(T\widetilde{X};g_{0},g_{1})^{(1,1)} = \frac{1}{8} {c_{1}(T\widetilde{X})|_{\widetilde{X}^{\theta}}c_{1}(T\widetilde{X}^{\theta})}(g_{0},g_{1}) - \frac{1}{12} {c_{1}(T\widetilde{X}^{\theta})^{2}}(g_{0},g_{1}) \end{align*} $$

by [43, Prop. 5.3], we have the following equality of Bott-Chern classes:

$$ \begin{align*}\begin{aligned} \widetilde{\mathrm{Td}}_{\theta}(T\widetilde{X};g_{0},g_{1})^{(1,1)} &= \frac{1}{8} \widetilde{c_{1}(T\widetilde{X})|_{\widetilde{X}^{\theta}}c_{1}(T\widetilde{X}^{\theta})}(g_{0},g_{1}) - \frac{1}{12} \widetilde{c_{1}(T\widetilde{X}^{\theta})^{2}}(g_{0},g_{1}) \\ &= \frac{1}{8} \widetilde{c_{1}}(T\widetilde{X};g_{0},g_{1})|_{\widetilde{X}^{\theta}}c_{1}(T\widetilde{X}^{\theta},g_{1}) + \frac{1}{8} c_{1}(T\widetilde{X},g_{0})|_{\widetilde{X}^{\theta}}\widetilde{c_{1}}(T\widetilde{X}^{\theta};g_{0},g_{1}) \\ &\quad - \frac{1}{12} \widetilde{c_{1}}(T\widetilde{X}^{\theta};g_{0},g_{1})\{c_{1}(T\widetilde{X}^{\theta},g_{0})+c_{1}(T\widetilde{X}^{\theta},g_{1})\}, \end{aligned} \end{align*} $$

where [21, Eq. (1.3.1.2)] is used to get the second equality. For a holomorphic line bundle L and Hermitian metrics $h_{0},h_{1}$ on L, we have

$$ \begin{align*}\widetilde{c_{1}}(L;h_{0},h_{1})=\log(h_{0}/h_{1}) \end{align*} $$

by [21, Eq. (1.2.5.1)]. (Our sign convention is different from the one in Gillet-Soulé [21]. Our $\widetilde {c_{1}}(L;h_{0},h_{1})$ is $-\widetilde {c_{1}}(L;h_{0},h_{1})$ in [21].) Hence

(7.2) $$ \begin{align} \begin{aligned} \widetilde{\mathrm{Td}}_{\theta}(T\widetilde{X};g_{0},g_{1})^{(1,1)} &\equiv \frac{1}{8} \left. \log\left(\frac{\det g_{0}}{\det g_{1}}\right) \right|_{\widetilde{X}^{\theta}} c_{1}(\widetilde{X}^{\theta},g_{1}) + \frac{1}{8} \left. c_{1}(\widetilde{X},g_{0}) \log\left(\frac{g_{0}}{g_{1}} \right|_{\widetilde{X}^{\theta}} \right) \\ &\quad - \frac{1}{12} \left. \log\left(\frac{g_{0}}{g_{1}} \right|_{\widetilde{X}^{\theta}} \right) \{c_{1}(\widetilde{X}^{\theta},g_{0})+c_{1}(\widetilde{X}^{\theta},g_{1})\} \\ &\qquad \mod \mathrm{Im}\,\partial+\mathrm{Im}\,\bar{\partial}. \end{aligned} \end{align} $$

(Step 2) We set $g_{0}=\gamma _{\epsilon ,\delta }$ and $g_{1}=\gamma _{\epsilon (\rho )}$ in Step 1. Since $g_{0}=\gamma _{\epsilon ,\delta }$ is Ricci-flat on a neighbourhood of $\widetilde {X}^{\theta }$ , we have

$$ \begin{align*}c_{1}(\widetilde{X},\gamma_{\epsilon,\delta})|_{\widetilde{X}^{\theta}}=0. \end{align*} $$

Since the volume form of EH instanton $i\partial \bar {\partial }F_{\epsilon }$ is the standard Euclidean volume form

$$ \begin{align*}\frac{(i\partial\bar{\partial}F_{\epsilon})^{2}}{2!}=i^{2}dz_{1}\wedge d\bar{z}_{1}\wedge dz_{2}\wedge d\bar{z}_{2} \end{align*} $$

and since $\gamma _{\epsilon ,\delta }=i\partial \bar {\partial }F_{\epsilon }$ on $\widetilde {V}(\delta )_{\frak p}$ , we get

$$ \begin{align*}\left. \left( \frac{\det\gamma_{\epsilon,\delta}}{\det\gamma_{\epsilon(\rho)}}\right) \right|_{\widetilde{X}^{\theta}} = \left. \left( \frac{\gamma_{\epsilon,\delta}^{2}/2!}{\gamma_{\epsilon(\rho)}^{2}/2!}\right) \right|_{\widetilde{X}^{\theta}} = 1. \end{align*} $$

If $E_{i}\cong \mathbf {P}^{1}$ is a component of $\widetilde {X}^{\theta }$ , then $(E_{i},\gamma _{\epsilon ,\delta }|_{E_{i}})\cong (\mathbf {P}^{1},\epsilon \,\omega _{\mathrm {FS}})$ and $(E_{i},\gamma _{\epsilon (\rho )}|_{E_{i}})\cong (\mathbf {P}^{1},\epsilon (\rho )\omega _{\mathrm {FS}})$ . Hence

$$ \begin{align*}\left.\frac{\gamma_{\epsilon,\delta}}{\gamma_{\epsilon(\rho)}}\right|_{\widetilde{X}^{\theta}}=\frac{\epsilon}{\epsilon(\rho)}. \end{align*} $$

Altogether, we get

(7.3) $$ \begin{align} \begin{aligned} \,& \int_{\widetilde{X}^{\theta}} \widetilde{\mathrm{Td}}_{\theta}(T\widetilde{X};\gamma_{\epsilon,\delta},\gamma_{\epsilon(\rho)})^{(1,1)} = -\int_{\widetilde{X}^{\theta}} \frac{1}{12} \left. \log\left(\frac{\gamma_{\epsilon,\delta}}{\gamma_{\epsilon(\rho)}} \right|{}_{\widetilde{X}^{\theta}} \right) \{c_{1}(\widetilde{X}^{\theta},\gamma_{\epsilon,\delta})+c_{1}(\widetilde{X}^{\theta},\gamma_{\epsilon(\rho)})\} \\ &= -\frac{\log(\epsilon/\epsilon(\rho))}{6} \int_{\widetilde{X}^{\theta}}c_{1}(\widetilde{X}^{\theta}) = -\frac{\log(\epsilon/\epsilon(\rho))}{6}\chi(\widetilde{X}^{\theta}) = -\frac{k}{3}\,\log\frac{\epsilon}{\epsilon(\rho)}, \end{aligned} \end{align} $$

where we used the fact $\widetilde {X}^{\theta }=E_{1}\amalg \cdots \amalg E_{k}$ , $k=\#\mathrm {Sing}\,X$ , $E_{i}\cong \mathbf {P}^{1}$ . This, together with equation (7.1), yields that

$$ \begin{align*}\epsilon^{k/3}\tau_{\mathbf{Z}_{2}}(\widetilde{X},\gamma_{\epsilon,\delta})(\theta)\mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta}) = \epsilon(\rho)^{k/3}\mathrm{Vol}(\widetilde{X},\gamma_{\epsilon(\rho)})\, \tau_{\mathbf{Z}_{2}}(\widetilde{X},\gamma_{\epsilon(\rho)})(\theta) \end{align*} $$

is independent of $\epsilon ,\delta \in (0,1]$ with $0<\epsilon \delta ^{-2}\leq \epsilon (\rho )$ .

(Step 3) Let $\chi $ be another cut-off function to glue Eguchi-Hanson instanton to the initial Kähler form $\gamma _{0}$ on X (compare Sections 5.2.1 and 5.2.3). Then there exists $\epsilon (\chi )\in (0,1)$ such that the function $\phi ^{\prime }_{\epsilon ,\delta }(z):=\|z\|^{2}+\chi _{\delta }(\|z\|)E(z,\epsilon )$ on $V(\infty )\setminus \{0\}$ is a potential of a Kähler form on $T^{*}\mathbf {P}^{1}=\widetilde {V}(\infty )$ for any $\epsilon ,\delta \in (0,1]$ with $0<\epsilon \delta ^{-2}\leq \epsilon (\chi )$ . Let $\gamma ^{\prime }_{\epsilon ,\delta }$ be the families of Kähler forms on $\widetilde {X}$ constructed in the same way as in equation (4.12), using $\kappa ^{\prime }_{\epsilon ,\delta }:=i\partial \bar {\partial }\phi ^{\prime }_{\epsilon ,\delta }$ instead of $\kappa _{\epsilon ,\delta }$ . By Step 2, we get

$$ \begin{align*}\epsilon^{k/3}\tau_{\mathbf{Z}_{2}}(\widetilde{X},\gamma^{\prime}_{\epsilon,\delta})(\theta)\mathrm{Vol}(\widetilde{X},\gamma^{\prime}_{\epsilon,\delta}) = \epsilon(\chi)^{k/3}\mathrm{Vol}(\widetilde{X},\gamma^{\prime}_{\epsilon(\chi)})\, \tau_{\mathbf{Z}_{2}}(\widetilde{X},\gamma^{\prime}_{\epsilon(\chi)})(\theta) \end{align*} $$

for any $\epsilon ,\delta \in (0,1]$ with $0<\epsilon \delta ^{-2}\leq \epsilon (\chi )$ . To prove the independence of the limit $\lim _{\epsilon \to 0}\epsilon ^{k/3}\tau _{\mathbf {Z}_{2}}(\widetilde {X},\gamma _{\epsilon ,\delta })(\theta )\mathrm {Vol}(\widetilde {X},\gamma _{\epsilon ,\delta })$ from the choice of $\rho $ , we must prove

(7.4) $$ \begin{align} \epsilon(\rho)^{k/3}\mathrm{Vol}(\widetilde{X},\gamma_{\epsilon(\chi)})\, \tau_{\mathbf{Z}_{2}}(\widetilde{X},\gamma_{\epsilon(\chi)})(\theta) = \epsilon(\chi)^{k/3}\mathrm{Vol}(\widetilde{X},\gamma^{\prime}_{\epsilon(\chi)})\, \tau_{\mathbf{Z}_{2}}(\widetilde{X},\gamma^{\prime}_{\epsilon(\chi)})(\theta). \end{align} $$

We set $g_{0}=\gamma _{\epsilon (\rho )}$ and $g_{1}=\gamma ^{\prime }_{\epsilon (\chi )}$ in equation (7.2). By the same computation as in equation (7.3), we get

$$ \begin{align*}\int_{\widetilde{X}^{\theta}} \widetilde{\mathrm{Td}}_{\theta}(T\widetilde{X};\gamma_{\epsilon(\rho)},\gamma^{\prime}_{\epsilon(\chi)})^{(1,1)} = -\frac{k}{3}\log\frac{\epsilon(\chi)}{\epsilon(\rho)}. \end{align*} $$

This, together with equation (7.1), yields equation (7.4). This completes the proof.

7.2 A comparison of heat kernels

Recall that $K_{\epsilon ,\delta }^{q}(t, x, y)$ denote the heat kernel of the Hodge-Kodaira Laplacian $\square _{q}^{\epsilon ,\delta }$ for the Kähler metric $\gamma _{\epsilon ,\delta }$ on $\widetilde {X}$ , and $K_{0}^q(t, x, y)$ the heat kernel of the Hodge-Kodaira Laplacian $\square _{q}^{0}$ for the Kähler metric $\gamma _{0}$ on X. For $0<r\leq 4$ , let

$$ \begin{align*}\widetilde{V}_r:=\bigcup_{{\frak p}\in\mathrm{Sing}(X)} \widetilde{V}(r)_{\frak p}, \qquad \widetilde{X}_r:=\widetilde{X}-\widetilde{V}_r. \end{align*} $$

Define $\widetilde {V}_{\infty }$ to be $\widetilde {V}_4$ extended by k copies of the infinite cone $(\mathbf C^2 - B(4))/\{\pm 1\}$ . The metric $\gamma _{\epsilon , \delta }|_{\widetilde {V}_4}$ similarly extends to a Kähler metric $\gamma _{\epsilon , \delta }^{\infty }$ on $\widetilde {V}_{\infty }$ . We denote by $K_{\epsilon , \delta , \infty }^q(t, x, y)$ the corresponding heat kernel on $\widetilde {V}_{\infty }$ . Similarly, we have the corresponding $X_r, V_r, V_{\infty }$ on X, with $X_r$ identified with $\widetilde {X}_r$ . Note that $V_{\infty }$ is just k copies of the infinite cone.

We first established some uniform estimates on the heat kernel $K_{\epsilon ,\delta }^{q}(t, x, y)$ , improving on Proposition 6.4 when the points are in specific regions.

Theorem 7.3. There are constants $A, C$ depending only on the Sobolev constant and dimension such that, for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ and $0\leq q\leq 2$ , we have

$$ \begin{align*}| K_{\epsilon}^q(t, x, z) | \leq Ae^{C(1+ \epsilon \delta^{-4})} \delta^{-4} e^{-\frac{\delta^2}{32t}}, \ \ \ \forall x \in \widetilde{X}_{3\delta}, \ \ z\in \widetilde{V}_{2\delta}, \ \ t>0.\end{align*} $$

Similarly, we have $\forall x \in \widetilde {X}_{3\delta }, \ z\in \widetilde {V}_{2\delta }, \ t>0$ ,

$$ \begin{align*}|d K_{\epsilon}^q(t, x, z)| \leq Ae^{C(1+ \epsilon \delta^{-4})} \delta^{-5} e^{-\frac{\delta^2}{32t}}, \ \ | d^*_{\epsilon, \delta} K_{\epsilon}^q(t, x, z) | \leq Ae^{C(1+ \epsilon \delta^{-4})} \delta^{-5} e^{-\frac{\delta^2}{32t}},\end{align*} $$

Here $d, \ d^*_{\epsilon , \delta }$ could act on either the x or z variable. Finally, for $0<r<2\delta $ , $x \in \widetilde {X}_{3\delta }, \ \ z\in \widetilde {V}_{2\delta , r} = \widetilde {V}_{2\delta }-\widetilde {V}_{r}$ , and $i\in \mathbf N$ ,

$$ \begin{align*}| \nabla^i K_{\epsilon, \delta}^q(t-s, x, z) | \leq C(i, \delta, r) e^{-\frac{\delta^2}{32t}} \end{align*} $$

for a constant $C(i, \delta , r)$ , depending on $i, \delta , r$ . Here $\nabla ^i$ denotes the ith covariant derivative with respect to the metric $\gamma _{\epsilon ,\delta }$ acting on either variable.

Proof. Throughout the proof, we fix $ x \in \widetilde {X}_{3\delta }, \ \ z\in \widetilde {V}_{2\delta }, \ \ t>0.$ Since the Ricci curvature of $\gamma _{\epsilon , \delta }$ is bounded by Lemma 4.5, the Sobolev estimate, together with the Moser iteration technique combined with the finite propagation speed argument as in Cheeger-Gromov-Taylor [13], gives the uniform estimate

$$ \begin{align*}| K_{\epsilon}^q(t, x, z) | \leq Ae^{C(1+ \epsilon \delta^{-4})} \delta^{-4} e^{-\frac{\delta^2}{32t}}.\end{align*} $$

Indeed, the finite propagation speed technique gives us the $L^2$ estimate

$$ \begin{align*}\| K_{\epsilon}^q(t, \cdot, \cdot) \|_{L^2(B_{\delta/4}(x)\times B_{\delta/4}(z) )} \leq c e^{-\frac{\delta^2}{16t}} \end{align*} $$

for some uniform constant c. Now Moser iteration as in [13][pages 16–26], together with semi-group domination [24], yields the desired estimate.

For the estimate on $ d K_{\epsilon }^q(t, x, z), \ d^*_{\epsilon , \delta } K_{\epsilon }^q(t, x, z)$ , let $\eta (r)$ be a smooth cut-off function that is identically $1$ for $|r|\leq \delta /8$ and identically $0$ for $|r|\geq \delta /4$ and $|\eta '| \leq \frac {16}{\delta }$ . We will continue to denote by $\eta $ its composition with a distance function (either $d(x, \cdot )$ or $d(z, \cdot )$ ). Note then

$$ \begin{align*} \|(d+d^*_{\epsilon, \delta} )_z[\eta K_{\epsilon}^q(t, \cdot, \cdot)] \|^2_{L^2(B_{\delta/4}(x)\times B_{\delta/4}(z) )}& = \|(d)_z[\eta K_{\epsilon}^q(t, \cdot, \cdot)] \|^2_{L^2(B_{\delta/4}(x)\times B_{\delta/4}(z) )} \\ &\quad + \|(d^*_{\epsilon, \delta} )_z[\eta K_{\epsilon}^q(t, \cdot, \cdot)] \|^2_{L^2(B_{\delta/4}(x)\times B_{\delta/4}(z) )}, \end{align*} $$

from which we deduce

$$ \begin{align*} \|(d)_z[ K_{\epsilon}^q(t, \cdot, \cdot)] \|_{L^2(B_{\delta/8}(x)\times B_{\delta/8}(z) )} & \leq \|(d+d^*_{\epsilon, \delta} )_z[\eta K_{\epsilon}^q(t, \cdot, \cdot)] \|_{L^2(B_{\delta/4}(x)\times B_{\delta/4}(z) )} \\ &\quad + \frac{16}{\delta} \| K_{\epsilon}^q(t, \cdot, \cdot) \|_{L^2(B_{\delta/4}(x)\times B_{\delta/4}(z) )} \\ & \leq \|(d+d^*_{\epsilon, \delta} )_z[ K_{\epsilon}^q(t, \cdot, \cdot)] \|_{L^2(B_{\delta/4}(x)\times B_{\delta/4}(z) )} \\ &\quad + \frac{32}{\delta} \| K_{\epsilon}^q(t, \cdot, \cdot) \|_{L^2(B_{\delta/4}(x)\times B_{\delta/4}(z) )}. \end{align*} $$

Now the same finite propagation speed technique gives

$$ \begin{align*}\|(d+d^*_{\epsilon, \delta} )_z[ K_{\epsilon}^q(t, \cdot, \cdot)] \|_{L^2(B_{\delta/4}(x)\times B_{\delta/4}(z) )} \leq c' e^{-\frac{\delta^2}{16t}}, \end{align*} $$

which in turn gives

$$ \begin{align*}\|(d)_z[ K_{\epsilon}^q(t, \cdot, \cdot)] \|_{L^2(B_{\delta/8}(x)\times B_{\delta/8}(z) )} \leq (c'+ c\frac{32}{\delta}) e^{-\frac{\delta^2}{32t}}. \end{align*} $$

The same method as above then yields

$$ \begin{align*}|(d)_z[ K_{\epsilon}^q(t, x, z)] | \leq Ae^{C(1+ \epsilon \delta^{-4})} \delta^{-5} e^{-\frac{\delta^2}{32t}}. \end{align*} $$

The others can be proven in exactly the same way.

Finally, for $0<r<2\delta $ , we note that the curvature tensor and its derivatives of $\gamma _{\epsilon ,\delta }$ are bounded in $\widetilde {V}_{2\delta , r} = \widetilde {V}_{2\delta }-\widetilde {V}_{r}$ by a constant depending on $\delta , r$ . Moreover, the injectivity radius of $\gamma _{\epsilon ,\delta }$ in $\widetilde {V}_{2\delta , r}$ is bounded away from zero by a constant depending on $\delta , r$ . Hence, by the elliptic estimate combined with the argument as before, we have, for $x \in \widetilde {X}_{3\delta }, \ \ z\in \widetilde {V}_{2\delta , r} = \widetilde {V}_{2\delta }-\widetilde {V}_{r}$ , and $i\in \mathbf N$ ,

$$ \begin{align*} | \nabla^i K_{\epsilon, \delta}^q(t-s, x, z) | \leq C(i, \delta, r) e^{-\frac{\delta^2}{32t}} \end{align*} $$

for a constant $C(i, \delta , r)$ depending on $i, \delta , r$ .

Theorem 7.4. There are constants $A, C$ depending only on the Sobolev constant and dimension such that, for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ and $0\leq q\leq 2$ , we have

$$ \begin{align*} | K_{\epsilon, \delta}^q(t, x, y)- K_{0}^q(t, x, y) | \leq Ae^{C(1+ \epsilon \delta^{-4})} \delta^{-9} e^{-\frac{\delta^2}{16t}} \mathrm{vol}(\partial \widetilde{X}_{2\delta}), \ \ \ \forall x, y \in \widetilde{X}_{3\delta}, \ \ t>0. \end{align*} $$

Furthermore, $\forall x, y \in \widetilde {X}_{3\delta }, \ \ t>0$ , we have the pointwise (although not necessarily uniform) convergence as $\epsilon \rightarrow 0$ ,

$$ \begin{align*}K_{\epsilon, \delta}^q(t, x, y)- K_{0}^q(t, x, y) \longrightarrow 0. \end{align*} $$

Proof. For $0<r\leq 4$ , we apply the Duhamel principle [11, (3.9)] to $K_{\epsilon , \delta }^q(t, x, y)- K_{0}^q(t, x, y)$ on $\widetilde {X}_r$ to obtain

$$ \begin{align*} K_{\epsilon, \delta}^q(t, x, y)- K_{0}^q(t, x, y) & = -\int_0^t\int_{\widetilde{X}_r} \left[ (\partial_t + \square_0^q) K_{\epsilon, \delta}^q(t-s, x, z) \right] \wedge * K_{0}^q(s, z, y) \\ &\quad + \int_0^t\int_{\partial \widetilde{X}_r} K_{\epsilon, \delta}^q(t-s, x, z) \wedge * d K_{0}^q(s, z, y)\\ &\quad + (-1)^{4q+1} \int_0^t\int_{\partial \widetilde{X}_r} * d K_{\epsilon, \delta}^q(t-s, x, z) \wedge K_{0}^q(s, z, y) \\ &\quad + (-1)^{4q+1} \int_0^t\int_{\partial \widetilde{X}_r} * K_{\epsilon, \delta}^q(t-s, x, z) \wedge d^* K_{0}^q(s, z, y) \\ &\quad + \int_0^t\int_{\partial \widetilde{X}_r} d^* K_{\epsilon, \delta}^q(t-s, x, z) \wedge * K_{0}^q(s, z, y). \end{align*} $$

Now fix $x, y \in \widetilde {X}_{3\delta }$ . First we let $r=2\delta $ . Then the first term on the right-hand side goes away, and we are left with only boundary terms. By Theorem 7.3, and noticing that similar estimates hold for the orbifold heat kernel

(7.5) $$ \begin{align} | K_{0}^q(t, x, z) | \leq C\delta^{-4} e^{-\frac{\delta^2}{32t}}, \ \ \ \forall x \in \widetilde{X}_{3\delta}, \ \ z\in \widetilde{V}_{2\delta}, \ \ t>0, \end{align} $$

as well as its derivatives, we deduce then that

$$ \begin{align*} | K_{\epsilon, \delta}^q(t, x, y)- K_{0}^q(t, x, y) | \leq Ae^{C(1+ \epsilon \delta^{-4})} \delta^{-9} e^{-\frac{\delta^2}{16t}} \mathrm{vol}(\partial \widetilde{X}_{2\delta}). \end{align*} $$

To prove the pointwise convergence, we let $r<2\delta $ and denote $\widetilde {V}_{2\delta , r}=\widetilde {V}_{2\delta }-\widetilde {V}_r$ . Then the Duhamel principle becomes

$$ \begin{align*} K_{\epsilon, \delta}^q(t, x, y)- K_{0}^q(t, x, y) & = -\int_0^t\int_{\widetilde{V}_{2\delta}, r} \left[ (\partial_t + \square_0^q) K_{\epsilon, \delta}^q(t-s, x, z) \right] \wedge * K_{0}^q(s, z, y) \\ &\quad + \int_0^t\int_{\partial \widetilde{X}_r} K_{\epsilon, \delta}^q(t-s, x, z) \wedge * d K_{0}^q(s, z, y)\\ &\quad + (-1)^{4q+1} \int_0^t\int_{\partial \widetilde{X}_r} * d K_{\epsilon, \delta}^q(t-s, x, z) \wedge K_{0}^q(s, z, y)\\ &\quad + (-1)^{4q+1} \int_0^t\int_{\partial \widetilde{X}_r} * K_{\epsilon, \delta}^q(t-s, x, z) \wedge d^* K_{0}^q(s, z, y) \\ &\quad + \int_0^t\int_{\partial \widetilde{X}_r} d^* K_{\epsilon, \delta}^q(t-s, x, z) \wedge * K_{0}^q(s, z, y). \end{align*} $$

We use the relation $ (\partial _t + \square _0^q) K_{\epsilon ,\delta }^q(t-s, x, z)= (\square _0^q-\square _{\epsilon ,\delta }^q) K_{\epsilon ,\delta }^q(t-s, x, z)$ to control the first integral. Since $\gamma _{\epsilon , \delta }= i \partial \overline {\partial } \phi _{\epsilon , \delta }$ , $\phi _{\epsilon , \delta }(z)=\|z\|^2 + \rho _{\delta }(\| z \|)E(z, \epsilon )$ , $\rho _{\delta }(t)=\rho (t/\delta )$ , $\rho (\cdot )\in C^{\infty }({\mathbf R})$ on $\widetilde {V}_{2\delta , r}$ and since $E(z,\epsilon )$ is a real analytic function on $\widetilde {V}_{3\delta ,r/2}\times [0,1)$ with $E(z,0)=0$ , $\frac {1}{\epsilon }(\square _{0}^{q} - \square _{\epsilon ,\delta }^{q})$ is a second order differential operator with coefficients in $C^{\infty }(\widetilde {V}_{3\delta ,r/2}\times [0,\epsilon (\rho )\delta ^{2}))$ . Hence there is a constant $C_{0}(\delta ,r)>0$ depending on $\delta $ , r but not on $\epsilon $ such that for all $(z,\epsilon ) \in \widetilde {V}_{3\delta ,r/2}\times [0,\epsilon (\rho )\delta ^{2})$ ,

$$ \begin{align*}|(\square_{0}^{q} - \square_{\epsilon,\delta}^{q}) K_{\epsilon,\delta}^{q}(t-s,x,z)| \leq \epsilon C_{0}(\delta,r) \sum_{k\leq 2} |\nabla_{z}^{k} K(t-s,x,z)|. \end{align*} $$

(This can also be deduced from equations (4.2), (4.4) and (4.6).)

By the second statement of Theorem 7.3 applied to the right-hand side, we have, for $x \in \widetilde {X}_{3\delta }, \ \ z\in \widetilde {V}_{2\delta , r}$ ,

$$ \begin{align*}| (\partial_t + \square_0^q) K_{\epsilon, \delta}^q(t-s, x, z) | =|(\square_0^q-\square_{\epsilon,\delta}^q) K_{\epsilon,\delta}^q(t-s, x, z)| \leq \epsilon C(\delta, r) e^{-\frac{\delta^2}{32t}} \end{align*} $$

for a constant $C(\delta , r)$ depending on $\delta , r$ but not on $\epsilon $ .

Combining with the uniform estimates in Theorem 7.4, we obtain, for $x, y \in \widetilde {X}_{3\delta }$ ,

$$ \begin{align*}| K_{\epsilon, \delta}^q(t, x, y)- K_{0}^q(t, x, y) | \leq \epsilon t C'(\delta, r) e^{-\frac{\delta^2}{16t}} + C^{\prime\prime}(\delta)t e^{-\frac{\delta^2}{16t}} \mathrm{vol}(\partial \widetilde{X}_r).\end{align*} $$

Now for any $\eta>0$ , we take r sufficiently small so that $ C^{\prime \prime }(\delta )t e^{-\frac {\delta ^2}{16t}} \mathrm {vol}(\partial \widetilde {X}_r)< \frac {\eta }{2}$ . Then we take $\epsilon $ sufficiently small such that $\epsilon t C'(\delta , r) e^{-\frac {\delta ^2}{16t}}< \frac {\eta }{2}$ . Hence

$$ \begin{align*}| K_{\epsilon, \delta}^q(t, x, y)- K_{0}^q(t, x, y) | < \eta.\end{align*} $$

This proves the pointwise convergence.

Remark 7.5. Since we have the Ricci curvature lower bound, the pointwise convergence of the heat kernels should also be a consequence of some general spectral convergence results due to Cheeger-Colding [12] for the case $q=0$ , Honda [25] for the case $q=1$ and Bei [2] for $q=n=2$ . See also [16].

Theorem 7.6. There is a constant C depending only on the Sobolev constant and dimension such that, for $\delta \leq 1$ ,

$$ \begin{align*} | K_{0}^q(t, x, y)- K_{0, \infty}^q(t, x, y) | \leq C e^{-\frac{1}{16t}} \mathrm{vol}(\partial V_4), \ \ \ \forall x, y \in V_{3\delta}, \ \ t>0. \end{align*} $$

Proof. The Duhamel principle [11, (3.9)] applied to $K_{0}^q(t, x, y)- K_{0, \infty }^q(t, x, y)$ on $V_4$ gives us

$$ \begin{align*} K_{0}^q(t, x, y)- K_{0, \infty}^q(t, x, y) & = \int_0^t\int_{\partial V_4} K_{0}^q(s, x, z) \wedge * d K_{0, \infty}^q(t-s, z, y) \\ &\quad + (-1)^{4q+1} \int_0^t\int_{\partial V_4} * d K_{0}^q(s, x, z) \wedge K_{0, \infty}^q(t-s, z, y) \\ &\quad + (-1)^{4q+1} \int_0^t\int_{\partial V_4} * K_{0}^q(s, x, z) \wedge d^* K_{0, \infty}^q(t-s, z, y) \\ &\quad + \int_0^t\int_{\partial V_4} d^* K_{0}^q(s, x, z) \wedge * K_{0, \infty}^q(t-s, z, y). \end{align*} $$

Thus we obtain, for $x, y\in V_{3\delta }, \delta \leq 1$ , using the estimate 7.5, except with the $\delta $ there replaced by a fixed constant, say $1/4$ , as well as a similar estimate for $K_{0, \infty }^q(t, x, y) $ ,

$$ \begin{align*}| K_{0}^q(t, x, y)- K_{0, \infty}^q(t, x, y) | \leq C e^{-\frac{1}{16t}} \mathrm{vol}(\partial V_4).\\[-40pt] \end{align*} $$

Our final task here is to compare the heat kernel $K_{\epsilon ,\delta }^{q}(t, x, y)$ with $K_{\epsilon , \delta , \infty }^q(t, x, y)$ , the heat kernel on $\widetilde {V}_{\infty }$ , when $x, y \in \widetilde {V}_{3\delta }$ .

Theorem 7.7. There are constants $A, C$ depending only on the Sobolev constant and dimension such that, for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ and $0\leq q\leq 2$ , we have

$$ \begin{align*} | K_{\epsilon,\delta}^{q}(t, x, y)- K_{\epsilon,\delta, \infty}^{q}(t, x, y) | \leq Ae^{C(1+ \epsilon \delta^{-4})} e^{-\frac{1}{16t}} \mathrm{vol}(\partial V_4), \ \ \ \forall x, y \in \widetilde{V}_{3\delta}, \ \ t>0. \end{align*} $$

Proof. The proof follows the same line as above. We apply the Duhamel principle to $K_{\epsilon ,\delta }^{q}(t, x, y)- K_{\epsilon ,\delta , \infty }^{q}(t, x, y)$ on $\widetilde {V}_{4}$ and use the heat kernel estimate in Theorem 7.3 as well as the analogous estimate for $K_{\epsilon ,\delta , \infty }^{q}(t, x, y)$ to obtain the desired estimate.

7.3 Partial analytic torsion

Recall that in Section 4.1, for a compact Kähler orbifold $(Z, \gamma )$ of dimension n,

$$ \begin{align*}\zeta_{q}(s)=\sum_{\lambda\in\sigma(\square_{q})\setminus\{0\}}\lambda^{-s}\,\dim E(\lambda;\square_{q}) = \frac{1}{\Gamma(s)} \int_0^{\infty} t^{s-1} \mathrm{Tr}(e^{-t\square_q }P^{\perp}_q) \, dt \end{align*} $$

with $P^{\perp }_q$ the orthogonal projection onto the orthogonal complement of $\mathrm {ker}\, \square _q$ and (the logarithm of) the analytic torsion

$$ \begin{align*}\ln \tau(Z,\gamma)=-\sum_{q=0}^{n}(-1)^{q}q\,\zeta^{\prime}_{q}(0)= -\zeta^{\prime}_{T}(0), \end{align*} $$

where

$$ \begin{align*}\zeta_{T}(s)=\frac{1}{\Gamma(s)} \int_0^{\infty} t^{s-1} \mathrm{Tr}_s(Ne^{-t\square}P^{\perp}) \, dt. \end{align*} $$

Here $\square $ denotes the Hodge-Kodaira Laplacian on $A^{0, *}(Z)$ , $P^{\perp }$ the orthogonal projection onto the orthogonal compliment of $\mathrm {ker}\, \square $ and $\mathrm {Tr}_s$ the supertrace on $A^{0, *}(Z)$ : that is, the alternating sum of the traces on each degree and N the so-called number operator, which simply multiplies a differential form by its degree.

By the Lidskii theorem,

$$ \begin{align*} \mathrm{Tr}_s(Ne^{-t\square}P^{\perp}) & = \int_Z \mathrm{tr}_s(N K(t, x, x)P^{\perp}(x, x)) \, dx \\ & = \sum_{q=0}^{n}(-1)^{q}q\,\int_Z \mathrm{tr}(K_q(t, x, x)P_q^{\perp}(x, x)) \, dx, \end{align*} $$

where $K(t, x, y)$ , $K_q(t, x, y)$ denotes the heat kernel of $\square $ , $\square _q$ , respectively, $P^{\perp }(x, x)$ the Schwartz kernel of $P^{\perp }$ and $\mathrm {tr}_s$ (abusing notation) also the pointwise supertrace.

At this point, it is convenient to introduce what is called ‘partial analytic torsion’ in [14]. For a domain $D\subset Z$ , we define

$$ \begin{align*}\zeta_{T}^{D, Z}(s)=\frac{1}{\Gamma(s)} \int_0^{\infty} t^{s-1} \int_D \mathrm{tr}_s(N K(t, x, x)P^{\perp}(x, x)) \, dx \, dt \end{align*} $$

and

(7.6) $$ \begin{align} \ln \tau(D, Z,\gamma)= -\left(\zeta_T^{D, Z}\right)'(0). \end{align} $$

Clearly

(7.7) $$ \begin{align} \ln \tau(Z,\gamma)=\ln \tau(D, Z,\gamma)+ \ln \tau(Z-D, Z,\gamma). \end{align} $$

Similarly, we can define the equivariant version $\tau _{\mathbf {Z}_{2}}(D, Z, \gamma )(\theta )$ for $\theta $ -invariant domain $D\subset Z$ . That is, we define

$$ \begin{align*}\zeta_{T, \theta}^{D, Z}(s)=\frac{1}{\Gamma(s)} \int_0^{\infty} t^{s-1} \int_D \mathrm{tr}_s(N K(t, x,\theta x)P^{\perp}(x, \theta x)) \, dx \, dt \end{align*} $$

and

(7.8) $$ \begin{align} \ln \tau_{\mathbf{Z}_{2}}(D, Z, \gamma)(\theta)= -\left(\zeta_{T, \theta}^{D, Z}\right)'(0). \end{align} $$

Then the discussion applies to the equivariant version as well.

7.4 Limit of partial analytic torsion I

Theorem 7.8. For $0<\delta \leq 1$ , we have

$$ \begin{align*}\lim_{\epsilon \rightarrow 0} \ln \tau(\widetilde{X}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta})= \ln \tau(X_{3\delta}, X, \gamma_{0}) \end{align*} $$

and

$$ \begin{align*}\lim_{\epsilon \rightarrow 0} \ln \tau_{\mathbf{Z}_{2}}(\widetilde{X}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta})(\theta) = \ln \tau_{\mathbf{Z}_{2}}(X_{3\delta}, X, \gamma_{0})(\iota). \end{align*} $$

Proof. (Step 1) Let

$$ \begin{align*}\mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x)) \sim \sum_{i=0}^{\infty} a_i^{\epsilon, \delta}(x)\, t^{i-2} \end{align*} $$

be the pointwise small time asymptotic expansion, and write

$$ \begin{align*} \zeta_{T}^{\widetilde{X}_{3\delta}, \widetilde{X}}(s) & = \frac{1}{\Gamma(s)} \left[ \int_1^{\infty} t^{s-1} \int_{\widetilde{X}_{3\delta}} \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x)P^{\perp}_{\epsilon, \delta}(x, x)) \, dx \, dt \right. \\ &\quad + \int_0^{1} t^{s-1} \int_{\widetilde{X}_{3\delta}} [ \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x))- \sum_{i=0}^{2} a_i^{\epsilon, \delta}(x)\, t^{i-2} ] \, dx \, dt \\ &\quad + \left. \sum_{i=0}^{1} \int_{\widetilde{X}_{3\delta}} \frac{a_i^{\epsilon, \delta}(x)}{s+ i-2} \, dx + \frac{1}{s} \int_{\widetilde{X}_{3\delta}}[ a_2^{\epsilon, \delta}(x) - \mathrm{tr}_s(N P_{\epsilon, \delta}(x, x))] \, dx \right] , \end{align*} $$

where $P_{\epsilon , \delta }(x, x)$ is the Schwartz kernel of $P_{\epsilon , \delta }$ , the orthogonal projection onto $\mathrm {ker}\, \square _{\epsilon , \delta }$ . We obtain

$$ \begin{align*} \ln \tau(\widetilde{X}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta}) & = - \int_1^{\infty} t^{-1} \int_{\widetilde{X}_{3\delta}} \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x)P^{\perp}_{\epsilon, \delta}(x, x)) \, dx \, dt \\ &\quad - \int_0^{1} t^{-1} \int_{\widetilde{X}_{3\delta}}\left[ \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x))- \sum_{i=0}^{2} a_i^{\epsilon, \delta}(x)\, t^{i-2}\right] \, dx \, dt \\ &\quad - \sum_{i=0}^{1} \int_{\widetilde{X}_{3\delta}} \frac{a_i^{\epsilon, \delta}(x)}{ i-2} \, dx + \Gamma'(1) \int_{\widetilde{X}_{3\delta}}\left[ a_2^{\epsilon, \delta}(x) - \mathrm{tr}_s(N P_{\epsilon, \delta}(x, x))\right] \, dx \end{align*} $$

and similarly for $\ln \tau (X_{3\delta }, X, \gamma _{0})$ . Since the asymptotic expansion depends only on the local data, we have $a_i^{\epsilon , \delta }(x)=a_i^{0}(x)$ on $\widetilde {X}_{3\delta }$ . Hence

(7.9) $$ \begin{align} \begin{aligned} \,& \ln \tau(\widetilde{X}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta}) - \ln \tau(X_{3\delta}, X, \gamma_{0}) \\ &= - \int_1^{\infty} t^{-1} \int_{\widetilde{X}_{3\delta}} \mathrm{tr}_s \left[ N K_{\epsilon, \delta}(t, x, x)P^{\perp}_{\epsilon, \delta}(x, x) - N K_{0}(t, x, x)P^{\perp}_{0}(x, x) \right] \, dx \, dt \\ &\quad - \int_0^{1} t^{-1} \int_{\widetilde{X}_{3\delta}}\left[ \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x) -N K_{0}(t, x, x)) \right] \, dx \, dt \\ &\quad - \Gamma'(1) \int_{\widetilde{X}_{3\delta}} \mathrm{tr}_s(N P_{\epsilon, \delta}(x, x) - N P_{0}(x, x))\, dx. \end{aligned} \end{align} $$

We estimate each term on the right-hand side.

(Step 2) Let $\Psi (\cdot )> 0$ and $\Lambda (\cdot )>0 $ be as defined in Corollary 6.8. By Corollary 6.8,

$$ \begin{align*}\begin{aligned} \int_{\widetilde{X}_{3\delta}}\left|\mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x)P^{\perp}_{\epsilon, \delta}(x, x))\right|\,dx &\leq \sum_{q\geq0}q\,(\mathrm{Tr}\,e^{-t\square_{\epsilon,\delta}}-h^{0,q}(\widetilde{X})) \\ &\leq \Psi(\epsilon\delta^{-4}+1)\,\exp[-\frac{1}{2}t\Lambda(\epsilon\delta^{-4}+1)] \end{aligned} \end{align*} $$

for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ and $t\geq 1$ . Hence for any $\nu>0$ , there is $T'=T'(\nu )>0$ depending only on $\nu $ such that for all $\epsilon ,\delta \in (0,1]$ with $\epsilon <\min \{\epsilon (\rho )\delta ^{2},\delta ^{4}\}$ , and $T>T'$ ,

(7.10) $$ \begin{align} \int_T^{\infty} t^{-1} \int_{\widetilde{X}_{3\delta}} \left|\mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x)P^{\perp}_{\epsilon, \delta}(x, x)) \right|\, dx \, dt \leq \Psi(2)\int_{T}^{\infty}e^{-\Lambda(2) t/2}\frac{dt}{t} < \nu \end{align} $$

and similarly for the same term involving $K_0$ . By Theorem 7.4 and Lebesgue dominated convergence theorem, there exists $\epsilon _0>0$ such that

(7.11) $$ \begin{align} \left| \int_1^{T} t^{-1} \int_{\widetilde{X}_{3\delta}} \mathrm{tr}_s[N( K_{\epsilon, \delta}(t, x, x)) - K_{0}(t, x, x))] \, dx \, dt \right| < \nu \end{align} $$

whenever $\epsilon < \epsilon _0$ . Similarly,

(7.12) $$ \begin{align} \left| \int_0^{1} t^{-1} \int_{\widetilde{X}_{3\delta}} \mathrm{tr}_s[N( K_{\epsilon, \delta}(t, x, x)) - K_{0}(t, x, x))] \, dx \, dt \right| < \nu \end{align} $$

whenever $\epsilon < \epsilon _0$ .

On the other hand,

(7.13) $$ \begin{align} \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x)P^{\perp}_{\epsilon, \delta}(x, x)) =\mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x)) - \mathrm{tr}_s(N P_{\epsilon, \delta}(x, x)) \end{align} $$

and similarly for $K_0$ . Recall $\ker \square _{0}=\ker \square _{\epsilon ,\delta }=\mathbf {C}\cdot 1\oplus \mathbf {C}\cdot \bar {\eta }$ . For $x\in \widetilde {X}_{3\delta }$ , we get

(7.14) $$ \begin{align} \mathrm{tr}_{s}[N(P_{\epsilon,\delta}(x,x)-P_{0}(x,x))] = \frac{2}{\|\eta\|_{L^{2}}^{2}} \left( \frac{\eta\wedge\bar{\eta}}{\gamma_{\epsilon,\delta}^{2}/2!}(x)-\frac{\eta\wedge\bar{\eta}}{\gamma_{0}^{2}/2!}(x) \right) =0, \end{align} $$

because $\gamma _{\epsilon ,\delta }=\gamma _{0}$ on $\widetilde {X}_{3\delta }$ . It follows from equations (7.11), (7.13) and (7.14) that

(7.15) $$ \begin{align} \left| \int_1^{T} t^{-1} \int_{\widetilde{X}_{3\delta}} \mathrm{tr}_s(N[ K_{\epsilon, \delta}(t, x, x)P^{\perp}_{\epsilon, \delta}(x, x)-K_0(t, x, x)P^{\perp}_0(x, x)]) \, dx \, dt \right| < \nu. \end{align} $$

Substituting equations (7.10), (7.11), (7.12), (7.14) and (7.15) into equation (7.9), we get

$$ \begin{align*}\left| \ln \tau(\widetilde{X}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta}) -\ln \tau(X_{3\delta}, X, \gamma_{0}) \right| < 3\nu \end{align*} $$

whenever $\epsilon < \epsilon _0$ . Since $\nu>0$ can be chosen arbitrarily small, this finishes the proof of the first formula.

To prove the result about the equivariant torsion, we follow the same line of argument, except with a simplification, since $\theta $ has no fixed points in $\widetilde {X}_{3\delta }$ . Indeed,

$$ \begin{align*} \ln \tau_{\mathbf{Z}_{2}}(\widetilde{X}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta})(\theta) & = - \int_1^{\infty} t^{-1} \int_{\widetilde{X}_{3\delta}} \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, \theta x)P^{\perp}_{\epsilon, \delta}(x, \theta x)) \, dx \, dt \\ &\quad - \int_0^{1} t^{-1} \int_{\widetilde{X}_{3\delta}} \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, \theta x))\, dx \, dt \\ &\quad - \Gamma'(1) \int_{\widetilde{X}_{3\delta}} \mathrm{tr}_s(N P_{\epsilon, \delta}(x, \theta x)\, dx \end{align*} $$

and

(7.16) $$ \begin{align} \begin{aligned} \,& \ln \tau_{\mathbf{Z}_{2}}(\widetilde{X}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta})(\theta) -\ln \tau_{\mathbf{Z}_{2}}(X_{3\delta}, X, \gamma_{0})(\iota) \\ &= - \int_1^{\infty} t^{-1} \int_{\widetilde{X}_{3\delta}} \mathrm{tr}_s \left[ N K_{\epsilon, \delta}(t, x, \theta x)P^{\perp}_{\epsilon, \delta}(x, \theta x) - N K_{0}(t, x, \theta x)P^{\perp}_{0}(x,\theta x) \right] \, dx \, dt \\ &\quad - \int_0^{1} t^{-1} \int_{\widetilde{X}_{3\delta}}\left[ \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x,\theta x) -N K_{0}(t, x,\theta x)) \right] \, dx \, dt \\ &\quad - \Gamma'(1) \int_{\widetilde{X}_{3\delta}} \mathrm{tr}_s(N P_{\epsilon, \delta}(x, \theta x) - N P_{0}(x,\theta x))\, dx. \end{aligned} \end{align} $$

Now we proceed as before.

7.5 Limit of partial analytic torsion II

To relate $\ln \tau (X_{3\delta }, X, \gamma _{0})$ to $\ln \tau (X, \gamma _{0})$ , by (7.7), it suffices to show

Theorem 7.9. We have

$$ \begin{align*}\lim_{\delta \rightarrow 0} \ln \tau(V_{3\delta}, X, \gamma_0)= 0, \ \ \ \lim_{\delta \rightarrow 0} \ln \tau_{\mathbf{Z}_{2}}(V_{3\delta}, X, \gamma_0)(\iota)=0. \end{align*} $$

Remark 7.10. This is closely related to [15], where analytic torsions on orbifolds defined from conical singularity pointview are shown to be the same as the ones defined from orbifold singularity pointview.

Proof. Again, the proofs for both formulas work the same, so we only present the first one. Moreover, the argument works for any orbifold singularity, but we will work with the cyclic quotient singularity of type $\frac {1}{4}(1,1)$ in our situation. First of all, by the same kind of argument as above, using Theorem 7.6 and $\mathrm {vol}(V_{3\delta }) \rightarrow 0$ as $\delta \rightarrow 0$ , one has

$$ \begin{align*}\lim_{\delta \rightarrow 0} \ln \tau(V_{3\delta}, X, \gamma_0)= \lim_{\delta \rightarrow 0} \ln \tau(V_{3\delta}, V_{\infty}, \kappa_0). \end{align*} $$

Now the right-hand side can be explicitly computed since the heat kernel is explicitly known. Indeed, as $V_{\infty }$ is just k copies of $\mathbf C^2/\mathbf Z_2$ , the (orbifold) heat kernel of $( V_{\infty }, \kappa _0)$ on the $(0,q)$ forms is $k\binom {n}{q}$ ( $n=2$ in our case) copies of

$$ \begin{align*}K_0(t, x,x')= \frac{1}{(4\pi t)^{n/2}}\left( e^{-\frac{|x-x'|^2}{4t}} + e^{-\frac{|x+x'|^2}{4t}} \right). \end{align*} $$

In terms of the polar coordinates $x=(r, y), y\in S^{2n-1}$ ,

$$ \begin{align*}K_0(t, x, x)= \frac{1}{(4\pi t)^{n/2}}(1+ e^{-r^2/t}). \end{align*} $$

Thus

$$ \begin{align*}\int_{V_{3\delta}} K_0(t, x, x) dx = c_n \delta^n t^{-n/2} + d_n \int_0^{\frac{3\delta}{t^{1/2}}} \xi^{n-1}e^{-\xi^2} d\xi, \end{align*} $$

where $c_n=\frac {3^n\omega _n}{n(4\pi )^{n/2}}$ , $d_n=\frac {\omega _n}{(4\pi )^{n/2}}$ , $\omega _n=\mathrm {vol}(S^{n-1})$ .

The second term has different asymptotic behaviours for $t\rightarrow 0$ and $t\rightarrow \infty $ . Since

$$ \begin{align*}\int_0^{\frac{3\delta}{t^{1/2}}} \xi^{n-1}e^{-\xi^2} d\xi= \int_0^{\infty} \xi^{n-1}e^{-\xi^2} d\xi -\int^\infty_{\frac{3\delta}{t^{1/2}}} \xi^{n-1}e^{-\xi^2} d\xi, \end{align*} $$

by some elementary inequality, it is a constant $d_n'=d_n \int _0^{\infty } \xi ^{n-1}e^{-\xi ^2} d\xi $ plus an exponentially decaying term as $t\rightarrow 0$ (or one could just invoke the known asymptotic for the complementary error function for a large argument). On the other hand, it is also straightforward to see that as $t \rightarrow \infty $ , the second term is $O(t^{-\frac {n-1}{2}})$ .

Set

$$ \begin{align*} \zeta_\delta(s) & = \frac{1}{\Gamma(s)}\int_0^\infty t^{s-1} \left(\int_{V_{3\delta}} K_0(t, x, x) dx\right) dt \\ & = \frac{1}{\Gamma(s)}\left[ \int_0^1 t^{s-1} \left(\int_{V_{3\delta}} K_0(t, x, x) dx\right) dt + \int_1^\infty t^{s-1} \left(\int_{V_{3\delta}} K_0(t, x, x) dx\right) dt \right], \end{align*} $$

where the first term is defined through analytic continuation from a region where the real part of s is sufficiently large, whereas the second term is defined through analytic continuation from a region where the real part of s is sufficiently negative. Therefore

$$ \begin{align*} \frac{1}{\Gamma(s)}\int_0^1 t^{s-1} \left(\int_{V_{3\delta}} K_0(t, x, x) dx\right) dt & = \frac{1}{\Gamma(s)} \frac{c_n\delta^n}{s-n/2} + \frac{d_n'}{\Gamma(s+1)} \\ &\quad - \frac{d_n}{\Gamma(s)}\int_0^1 t^{s-1}\int^\infty_{\frac{3\delta}{t^{1/2}}} \xi^{n-1}e^{-\xi^2} d\xi dt , \end{align*} $$

and

$$ \begin{align*} \frac{1}{\Gamma(s)}\int_1^\infty t^{s-1} \left(\int_{V_{3\delta}} K_0(t, x, x) dx\right) dt & = - \frac{1}{\Gamma(s)} \frac{c_n\delta^n}{s-n/2} \\ &\quad + \frac{d_n}{\Gamma(s)}\int_0^1 t^{s-1}\int_0^{\frac{3\delta}{t^{1/2}}} \xi^{n-1}e^{-\xi^2} d\xi dt. \end{align*} $$

Thus,

$$ \begin{align*}\zeta_\delta'(0) = -d_n'\Gamma'(1) -d_n \int_0^1 t^{-1}\int^\infty_{\frac{3\delta}{t^{1/2}}}\xi^{n-1}e^{-\xi^2} d\xi dt + d_n \int_0^1 t^{-1}\int^{\frac{3\delta}{t^{1/2}}}_0 \xi^{n-1}e^{-\xi^2} d\xi dt. \end{align*} $$

By a simple change of integration, we arrive at

$$ \begin{align*}\zeta_\delta'(0)= -d_n'\Gamma'(1) -d_n \int_{3\delta}^\infty 2\ln \frac{3\delta}{\xi} \xi^{n-1}e^{-\xi^2} d\xi + d_n \int_0^{3\delta} 2\ln \frac{3\delta}{\xi} \xi^{n-1}e^{-\xi^2} d\xi. \end{align*} $$

This has a logarithmic divergence ( $2d_n' \ln 3\delta $ ) as $\delta \rightarrow 0$ , but

$$ \begin{align*}\ln \tau(V_{3\delta}, V_{\infty}, \gamma_0)= - k\zeta_\delta'(0)\sum_{q=0}^n (-1)^q q \binom{n}{q} =0 \end{align*} $$

by combinatorial formula since $n\geq 2$ (in fact equal to $2$ in this case). The proof for the partial equivariant torsion is almost the same. We just need to insert the action of the involution $\theta $ into the heat kernel, which will result in only the $d_n$ terms similar to the above formulas.

Corollary 7.11. We have

$$ \begin{align*}\lim_{\delta \rightarrow 0}\lim_{\epsilon \rightarrow 0} \ln \tau(\widetilde{X}_{3\delta}, \widetilde{X}, \gamma_{\epsilon,\delta})= \ln \tau(X, \gamma_0), \ \ \ \end{align*} $$

$$ \begin{align*}\lim_{\delta \rightarrow 0}\lim_{\epsilon \rightarrow 0} \ln \tau_{\mathbf{Z}_{2}}(\widetilde{X}_{3\delta}, \widetilde{X}, \gamma_{\epsilon,\delta})(\iota) =\ln \tau_{\mathbf{Z}_{2}}(X, \gamma_0)(\iota). \end{align*} $$

Proof. Since $\ln \tau (X, \gamma _0)=\ln \tau (X_{3\delta },X, \gamma _0)+\ln \tau (V_{3\delta },X,\gamma _0)$ and $\ln \tau _{\mathbf {Z}_{2}}(X, \gamma _0)(\iota )=\ln \tau _{\mathbf {Z}_{2}}(X_{3\delta },X, \gamma _0)(\iota )+\ln \tau _{\mathbf {Z}_{2}}(V_{3\delta },X,\gamma _0)(\iota )$ by equation (7.7), we get by Theorem 7.9

$$ \begin{align*}\lim_{\delta\to0}\ln \tau(X_{3\delta},X, \gamma_0)=\ln \tau(X, \gamma_0), \qquad \lim_{\delta\to0}\ln \tau_{\mathbf{Z}_{2}}(X_{3\delta},X, \gamma_0)(\iota)=\ln \tau_{\mathbf{Z}_{2}}(X, \gamma_0)(\iota), \end{align*} $$

which, together with Theorem 7.8, yields the result.

7.6 Limit of partial analytic torsion III

On the other hand, we have

Theorem 7.12. The following equalities hold:

$$ \begin{align*}\lim_{\delta \rightarrow 0}\lim_{\epsilon \rightarrow 0} \ln \tau(\widetilde{V}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta}) = k\,\ln C_0^{\mathrm{EH}}(\rho), \end{align*} $$

$$ \begin{align*}\lim_{\delta \rightarrow 0}\lim_{\epsilon \rightarrow 0} \ln \left[\epsilon^{k/3}\tau_{\mathbf{Z}_{2}}(\widetilde{V}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta})(\theta)\right]=k\,\ln C_1^{\mathrm{EH}}(\rho), \end{align*} $$

where the constants $C_0^{\mathrm {EH}}(\rho )$ , $C_1^{\mathrm {EH}}(\rho )$ depend only on the cut-off function $\rho $ .

At this stage, the constants $C_0^{\mathrm {EH}}(\rho )$ , $C_1^{\mathrm {EH}}(\rho )$ may depend on $\rho $ . The fact that they are independent of $\rho $ will be postponed to the next subsection.

7.6.1 An integral expression of $\tau (\widetilde {V}_{3\delta }, \widetilde {X}, \gamma _{\epsilon , \delta })$ and $\tau _{\mathbf {Z}_{2}}(\widetilde {V}_{3\delta }, \widetilde {X}, \gamma _{\epsilon , \delta })(\theta )$

For the proof of Theorem 7.12, as before, we compute

$$ \begin{align*} \ln \tau(\widetilde{V}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta}) & = - \int_1^{\infty} t^{-1} \int_{\widetilde{V}_{3\delta}} \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x)P^{\perp}_{\epsilon, \delta}(x, x)) \, dx \, dt \\ &\quad - \int_0^{1} t^{-1} \int_{\widetilde{V}_{3\delta}}\left[ \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x))- \sum_{i=0}^{2} a_i^{\epsilon, \delta}(x)\, t^{i-2}\right] \, dx \, dt \\ &\quad - \sum_{i=0}^{1} \int_{\widetilde{V}_{3\delta}} \frac{a_i^{\epsilon, \delta}(x)}{ i-2} dx + \Gamma'(1) \int_{\widetilde{V}_{3\delta}}\left[ a_2^{\epsilon, \delta}(x) - \mathrm{tr}_s(N P_{\epsilon, \delta}(x, x))\right] dx, \end{align*} $$

where $a_i^{\epsilon , \delta }(x)$ are the coefficients of the pointwise small time asymptotic expansion for $\mathrm {tr}_s(N K_{\epsilon , \delta }(t, x, x))$ described in the proof of Theorem 7.8. Similarly,

$$ \begin{align*} \ln \tau_{\mathbf{Z}_{2}}(\widetilde{V}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta}) & = - \int_1^{\infty} t^{-1} \int_{\widetilde{V}_{3\delta}} \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, \theta(x))P^{\perp}_{\epsilon, \delta}(x, \theta(x))) \, dx \, dt \\ &\quad - \int_0^{1} \frac{dt}{t} \left[ \int_{\widetilde{V}_{3\delta}}\mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, \theta(x)))\,dx - \sum_{i=0}^{1}t^{i-1} \int_{E}b_i^{\epsilon, \delta}(z)\, dz\right] \\ &\quad + \int_{E} b_0^{\epsilon, \delta}(z) \, dz + \Gamma'(1) \left[ \int_{E}b_1^{\epsilon, \delta}(z)\,dz - \int_{\widetilde{V}_{3\delta}} \mathrm{tr}_s(N P_{\epsilon, \delta}(x, \theta(x)))\, dx\right] \end{align*} $$

with $b_i^{\epsilon , \delta }(x)$ the coefficients of the pointwise small time asymptotic expansion for $\mathrm {tr}_s(N K_{\epsilon , \delta }(t, x, \theta (x)))$ . We study the behaviour of each term on the right-hand side as $\epsilon \to 0$ and $\delta \to 0$ . For this, we set

$$ \begin{align*}\begin{aligned} I(\epsilon,\delta;\rho) &:= - \int_{0}^{1}\frac{dt}{t}\int_{\widetilde{V}(3\delta)}\left[ \mathrm{tr}_{s}(N K_{\epsilon, \delta,\infty}(t, x, x))- \sum_{i=0}^{2} a_{i}^{\epsilon, \delta}(x)\, t^{i-2}\right] \, dx \\ &\qquad - \sum_{i=0}^{1} \int_{\widetilde{V}(3\delta)} \frac{a_{i}^{\epsilon, \delta}(x)}{ i-2} \, dx + \Gamma'(1) \int_{\widetilde{V}(3\delta)}a_{2}^{\epsilon, \delta}(x) \, dx, \end{aligned} \end{align*} $$

$$ \begin{align*}\begin{aligned} J(\epsilon,\delta;\rho) &:= - \int_{0}^{1}\frac{dt}{t} \left[ \int_{\widetilde{V}(3\delta)}\mathrm{tr}_{s}(N K_{\epsilon, \delta,\infty}(t, x, \theta(x)))\, dx - \sum_{i=0}^{1}t^{i-1}\int_{E}b_{i}^{\epsilon, \delta}(z)\,dz \right] \\ &\qquad + \int_{E} b_{0}^{\epsilon, \delta}(z)\, dz + \Gamma'(1) \int_{E}b_{1}^{\epsilon, \delta}(z) \, dz. \end{aligned} \end{align*} $$

Since $K_{\epsilon , \delta ,\infty }(t, x, y)=\oplus _{q}K_{\epsilon , \delta ,\infty }^{q}(t, x, y)$ is $k$ -copies of the heat kernel of $(T^{*}\mathbf {P}^{1},\kappa _{\epsilon ,\delta })$ , $I(\epsilon ,\delta ;\rho )$ and $J(\epsilon ,\delta ;\rho )$ depend only on $\epsilon ,\delta \in (0,1]$ with $\epsilon \delta ^{-2}\leq \epsilon (\rho )$ and the cut-off function $\rho $ . Since $\widetilde {V}_{3\delta }$ is k-copies of $\widetilde {V}(3\delta )$ , we have

$$ \begin{align*}\begin{aligned} \ln \tau(\widetilde{V}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta}) &= -\int_1^{\infty} \frac{dt}{t} \int_{\widetilde{V}_{3\delta}} \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x)P^{\perp}_{\epsilon, \delta}(x, x)) \, dx \\ &\quad -\int_{0}^{1}\frac{dt}{t}\int_{\widetilde{V}_{3\delta}}\mathrm{tr}_{s}\{N K_{\epsilon,\delta}(t,x,x)-N K_{\epsilon,\delta,\infty}(t,x,x)\}dx \\ &\quad -\Gamma'(1)\int_{\widetilde{V}_{3\delta}}\mathrm{tr}_{s}(N P_{\epsilon,\delta}(x,x))\,dx+k\cdot I(\epsilon,\delta;\rho) \end{aligned} \end{align*} $$

and similarly

$$ \begin{align*}\begin{aligned} \ln \tau_{\mathbf{Z}_{2}}(\widetilde{V}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta}) &= -\int_1^{\infty} \frac{dt}{t} \int_{\widetilde{V}_{3\delta}} \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, \theta(x))P^{\perp}_{\epsilon, \delta}(x, \theta(x))) \, dx \\ &\quad -\int_{0}^{1}\frac{dt}{t}\int_{\widetilde{V}_{3\delta}}\mathrm{tr}_{s}\{N K_{\epsilon,\delta}(t,x,\theta(x))-N K_{\epsilon,\delta,\infty}(t,x,\theta(x))\}dx \\ &\quad -\Gamma'(1)\int_{\widetilde{V}_{3\delta}}\mathrm{tr}_{s}\{N P_{\epsilon,\delta}(x,\theta(x))\}\,dx+k\cdot J(\epsilon,\delta;\rho). \end{aligned} \end{align*} $$

7.6.2 Limit of the first integral

Proposition 7.13. The following equality holds:

$$ \begin{align*}\lim_{\delta\to0}\lim_{\epsilon\to0} \int_1^{\infty} \frac{dt}{t} \int_{\widetilde{V}_{3\delta}} \mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x)P^{\perp}_{\epsilon, \delta}(x, x)) \, dx=0. \end{align*} $$

The same is true for the first integral in the expression of $\ln \tau _{\mathbf {Z}_{2}}(\widetilde {V}_{3\delta }, \widetilde {X}, \gamma _{\epsilon , \delta })$ .

Proof. Let $\nu>0$ be arbitrary. As in the proof of Theorem 7.8 Step 2, there is $T=T(\nu )>0$ depending only on $\nu $ such that

(7.17) $$ \begin{align} \int_T^{\infty} t^{-1} \int_{\widetilde{V}_{3\delta}} \left|\mathrm{tr}_s(N K_{\epsilon, \delta}(t, x, x)P^{\perp}_{\epsilon, \delta}(x, x)) \right|\, dx \, dt < \nu \end{align} $$

for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \leq \min \{\epsilon (\rho )\delta ^{2}, \delta ^{4}\}$ , which will be assumed throughout the proof. By Theorem 7.7,

(7.18) $$ \begin{align} \left| \int_1^{T} t^{-1} \int_{\widetilde{V}_{3\delta}} \mathrm{tr}_s[N\{ K_{\epsilon, \delta}(t, x, x)) - K_{\epsilon, \delta,\infty}(t, x, x)\}] \, dx \, dt \right| \leq C(T)\, \mathrm{vol}(\widetilde{V}_{3\delta}), \end{align} $$

where $C(T)$ is a constant depending only on T. By equation (7.14), we get

(7.19) $$ \begin{align} \int_{\widetilde{V}_{3\delta}}\mathrm{tr}_{s}[N(P_{\epsilon,\delta}(x,x)]\,dx = \int_{\widetilde{V}_{3\delta}}\frac{2\eta\wedge\bar{\eta}}{\|\eta\|_{L^{2}}^{2}} \leq 2\frac{\|\eta\wedge\bar{\eta}/\gamma_{0}^{2}\|_{L^{\infty}}}{\|\eta\|_{L^{2}}}\mathrm{Vol}(\widetilde{V}_{3\delta}). \end{align} $$

By equations (7.13), (7.18) and (7.19), we get

(7.20) $$ \begin{align} \begin{aligned} \,& \left| \int_1^{T} t^{-1} \int_{\widetilde{V}_{3\delta}} \mathrm{tr}_s[N\{ K_{\epsilon, \delta}(t, x, x)P^{\perp}_{\epsilon, \delta}(x, x)-K_{\epsilon, \delta,\infty}(t, x,x)\}] \, dx \, dt \right| \\ & \leq \{C(T)+2\frac{\|\eta\wedge\bar{\eta}/\gamma_{0}^{2}\|_{L^{\infty}}}{\|\eta\|_{L^{2}}}\log T\}\, \mathrm{vol}(\widetilde{V}_{3\delta}). \end{aligned} \end{align} $$

By Proposition 6.9, there is a constant $A>0$ such that

(7.21) $$ \begin{align} \int_1^{T} t^{-1} \int_{\widetilde{V}_{3\delta}} \left| K_{\epsilon, \delta,\infty}(t, x,x) \right|\, dx \, dt \leq Ae^{C(\epsilon\delta^{-4}+1)T}\,\log T\cdot\mathrm{vol}(\widetilde{V}_{3\delta}) \end{align} $$

for all $\epsilon ,\delta \in (0,1]$ with $\epsilon\, \delta ^{-2}\leq \epsilon (\rho )$ . By equations (7.20) and (7.21), we get

(7.22) $$ \begin{align} \left| \int_1^{T} t^{-1} \int_{\widetilde{V}_{3\delta}} \mathrm{tr}_s[N K_{\epsilon, \delta}(t, x, x)P^{\perp}_{\epsilon, \delta}(x, x)] \, dx \, dt \right| \leq \widetilde{C}(T)\, \mathrm{vol}(\widetilde{V}_{3\delta}), \end{align} $$

where $\widetilde {C}(T)=C(T)+ (2\frac {\|\eta \wedge \bar {\eta }/\gamma _{0}^{2}\|_{L^{\infty }}}{\|\eta \|_{L^{2}}}+Ae^{2CT})\log T$ . Since $\nu>0$ can be chosen arbitrarily small, by taking into account that $\mathrm {vol}(\widetilde {V}_{3\delta }) $ goes to zero as $\delta \rightarrow 0$ , the result follows from equations (7.17) and (7.22).

7.6.3 Limit of the second integral

Proposition 7.14. The following equality holds:

$$ \begin{align*}\lim_{\delta\to0}\lim_{\epsilon\to0} \int_{0}^{1}\frac{dt}{t}\int_{\widetilde{V}_{3\delta}}\mathrm{tr}_{s}\{N K_{\epsilon,\delta}(t,x,x)-N K_{\epsilon,\delta,\infty}(t,x,x)\}dx=0. \end{align*} $$

The same is true for the second integral in the expression of $\ln \tau _{\mathbf {Z}_{2}}(\widetilde {V}_{3\delta }, \widetilde {X}, \gamma _{\epsilon , \delta })$ .

Proof. The proof is the same as above, using the estimate of Theorem 7.7. Indeed, we have, for all $\epsilon ,\delta \in (0,1]$ with $\epsilon \leq \min \{\epsilon (\rho )\delta ^{2}, \delta ^{4}\}$ , that there is a constant $C>0$ such that

$$ \begin{align*}|\mathrm{tr}_{s}\{N K_{\epsilon,\delta}(t,x,x)-N K_{\epsilon,\delta,\infty}(t,x,x)\}|\leq C\,t \end{align*} $$

for all $(x,t)\in \widetilde {V}_{3\delta }\times (0,1]$ . Hence

(7.23) $$ \begin{align} \left| \int_{0}^{1}\frac{dt}{t}\int_{\widetilde{V}_{3\delta}}\mathrm{tr}_{s}\{N K_{\epsilon,\delta}(t,x,x)-N K_{\epsilon,\delta,\infty}(t,x,x)\}dx \right| \leq C\,\mathrm{Vol}(\widetilde{V}_{3\delta},\gamma_{\epsilon, \delta}). \end{align} $$

By the fact that

$$ \begin{align*}\lim_{\delta\to0}\lim_{\epsilon\to0}\mathrm{Vol}(\widetilde{V}_{3\delta},\gamma_{\epsilon, \delta})= \lim_{\delta\to0}\mathrm{ Vol}(\widetilde{V}_{3\delta},\gamma_{0})=0, \end{align*} $$

we get the result.

7.6.4 Proof of Theorem 7.12

By equation (7.14), we get

$$ \begin{align*}\lim_{\delta\to0}\lim_{\epsilon\to0}\int_{\widetilde{V}_{3\delta}}\mathrm{tr}_{s}(N P_{\epsilon,\delta}(x,x))\,dx = \lim_{\delta\to0}\lim_{\epsilon\to0}\int_{\widetilde{V}_{3\delta}}\mathrm{tr}_{s}(N P_{\epsilon,\delta}(x,\theta(x)))\,dx =0. \end{align*} $$

From Propositions 7.13 and 7.14, it follows that

$$ \begin{align*}\lim_{\delta\to0}\lim_{\epsilon\to0} \ln \tau(\widetilde{V}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta}) = k\,\lim_{\delta\to0}\lim_{\epsilon\to0}I(\epsilon,\delta;\rho), \end{align*} $$

$$ \begin{align*}\lim_{\delta\to0}\lim_{\epsilon\to0} \ln\left[\epsilon^{k/3} \tau_{\mathbf{Z}_{2}}(\widetilde{V}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta})\right] = k\,\lim_{\delta\to0}\lim_{\epsilon\to0}\left[J(\epsilon,\delta;\rho)+\frac{1}{3}\ln\epsilon\right]. \end{align*} $$

Since the right-hand side depends only on the choice of $\rho $ , we get the result by setting

$$ \begin{align*}\ln C_{0}^{\mathrm{EH}}(\rho):=\lim_{\delta\to0}\lim_{\epsilon\to0}I(\epsilon,\delta;\rho), \qquad \ln C_{1}^{\mathrm{EH}}(\rho):=\lim_{\delta\to0}\lim_{\epsilon\to0}\left[J(\epsilon,\delta;\rho)+\frac{1}{3}\ln\epsilon\right]. \end{align*} $$

This completes the proof, provided that these double limits exist. This will be addressed in what follows.

Remark 7.15. $C_0^{\mathrm {EH}}(\rho )$ , respectively $C_1^{\mathrm {EH}}(\rho )$ , is renormalised (respectively, equivariant) analytic torsion for the asymptotically conical space $\widetilde {V}(\infty )=(T^{*}\mathbf {P}^{1},\gamma ^{\mathrm {EH}})$ .

7.7 Proof of Theorem 7.1

Since

$$ \begin{align*}\ln \tau(\widetilde{X}, \gamma_{\epsilon, \delta}) = \ln \tau(\widetilde{X}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta}) + \ln \tau(\widetilde{V}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta}) \end{align*} $$

and

$$ \begin{align*}\ln \tau_{\mathbf{Z}_{2}}(\widetilde{X}, \gamma_{\epsilon, \delta}) = \ln \tau_{\mathbf{Z}_{2}}(\widetilde{X}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta}) + \ln \tau_{\mathbf{Z}_{2}}(\widetilde{V}_{3\delta}, \widetilde{X}, \gamma_{\epsilon, \delta}) \end{align*} $$

by the definition of partial (equivariant) analytic torsion, we get by Corollary 7.11 and Theorem 7.12

(7.24) $$ \begin{align} \lim_{\delta\to0}\lim_{\epsilon\to0} \ln \tau(\widetilde{X}, \gamma_{\epsilon, \delta}) = \ln \tau(X, \gamma_{0}) + k\,\ln C_{0}^{\mathrm{EH}}(\rho), \end{align} $$

(7.25) $$ \begin{align} \lim_{\delta\to0}\lim_{\epsilon\to0} \ln\left[\epsilon^{k/3} \tau_{\mathbf{Z}_{2}}(\widetilde{X}, \gamma_{\epsilon, \delta})\right] = \ln \tau_{\mathbf{Z}_{2}}(X, \gamma_{0}) + k\,\ln C_{1}^{\mathrm{EH}}(\rho). \end{align} $$

As the double limits on the left-hand side of equations (7.24) and (7.25) exist by virtue of Corollary 5.3 and Proposition 7.2, so do the double limits in defining $\ln C_{0}^{\mathrm {EH}}(\rho )$ and $\ln C_{1}^{\mathrm {EH}}(\rho )$ .

On the other hand, again by Corollary 5.3 and Proposition 7.2, the double limits $\lim _{\delta \to 0}\lim _{\epsilon \to 0}\ln \tau (\widetilde {X}, \gamma _{\epsilon , \delta })$ and $\lim _{\delta \to 0}\lim _{\epsilon \to 0}\ln \left [\epsilon ^{k/3} \tau _{\mathbf {Z}_{2}}(\widetilde {X}, \gamma _{\epsilon , \delta })\right ]$ are independent of the choice of $\rho $ . Hence $C_{0}^{\mathrm {EH}}(\rho )$ and $C_{1}^{\mathrm {EH}}(\rho )$ in equations (7.24) and (7.25) are in fact independent of $\rho $ . This completes the proof of Theorem 7.1.

8 A holomorphic torsion invariant of log-Enriques surfaces

In this section, we introduce a holomorphic torsion invariant of log-Enriques surfaces and give its explicit formula as a function on the moduli space.

8.1 A construction of invariant

Theorem 8.1. There is a constant $C(k)$ depending only on $k=\#\mathrm {Sing}(Y)$ with

$$ \begin{align*}\begin{aligned} \tau_{M}(\widetilde{X},\theta) &= C(k)\mathrm{Vol}(Y,\gamma_{0})^{\frac{4-k}{4}}\,\tau(Y,\gamma_{0})^{2} \times \prod_{{\frak p}\in\mathrm{Sing}(X)}\left\{|f_{\frak p}(0)|^{2}\frac{\mathrm{Vol}(Y,\gamma_{0})}{\|\eta\|_{L^{2}(Y)}^{2}}\right\}^{\frac{5}{16}} \\ &\quad\times \exp \left( \frac{1}{12}\int_{Y} \log\left\{\frac{\eta\wedge\bar{\eta}}{\gamma_{0}^{2}/2!}\cdot\frac{\mathrm{Vol}(Y,\gamma_{0})}{\|\eta\|_{L^{2}(Y)}^{2}}\right\}\, c_{2}(Y,\gamma_{0}) \right). \end{aligned} \end{align*} $$

Here $f_{\frak p}$ is defined in the discussion immediately preceding equation (4.13).

Proof. Since $M_{k}^{\perp }\cong \Lambda _{k}(2)$ , we have $\frac {14-r(H^{2}(\widetilde {X},\mathbf {Z})^{+})}{4}=\frac {4-k}{4}$ . By its independence of the choice of $\theta $ -invariant Kähler metric on $\widetilde {X}$ , $\tau _{M}(\widetilde {X},\theta )$ is given by

$$ \begin{align*}& \lim_{\delta\to0}\lim_{\epsilon\to0} \tau(\widetilde{X},\gamma_{\epsilon,\delta})\tau_{\mathbf{Z}_{2}}(\widetilde{X},\gamma_{\epsilon,\delta})(\theta)\, \mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta})^{\frac{4-k}{4}} \mathrm{Vol}(\widetilde{X}^{\theta},\gamma_{\epsilon,\delta}|_{\widetilde{X}^{\theta}}) \tau(\widetilde{X}^{\theta},\gamma_{\epsilon,\delta}|_{\widetilde{X}^{\theta}}) \\ &\quad\times A_{M}(\widetilde{X},\theta,\gamma_{\epsilon,\delta})\, \exp \left( \frac{1}{24}\int_{\widetilde{X}} \log\left\{ \frac{\eta\wedge\bar{\eta}}{\gamma_{\epsilon,\delta}^{2}/2!} \cdot \frac{\mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta})}{\|\eta\|_{L^{2}(\widetilde{X})}^{2}} \right\}\, c_{2}(\widetilde{X},\gamma_{\epsilon,\delta}) \right) \\ &= \lim_{\delta\to0}\lim_{\epsilon\to0} \{\epsilon^{\frac{k}{3}}\tau(\widetilde{X},\gamma_{\epsilon,\delta})\tau_{\mathbf{Z}_{2}}(\widetilde{X},\gamma_{\epsilon,\delta})(\theta) \mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta})^{\frac{4-k}{4}} \} \\ &\quad\times \lim_{\delta\to0}\lim_{\epsilon\to0} \prod_{{\frak p}\in\mathrm{Sing}(X)}\epsilon^{-\frac{1}{3}}\mathrm{Vol}(E_{\frak p},\gamma_{\epsilon,\delta}|_{E_{\frak p}}) \tau(E_{\frak p},\gamma_{\epsilon,\delta}|_{E_{\frak p}}) \times \lim_{\delta\to0}\lim_{\epsilon\to0}A_{M}(\widetilde{X},\theta,\gamma_{\epsilon,\delta}) \\ &\quad\times \lim_{\delta\to0}\lim_{\epsilon\to0} \exp \left( \frac{1}{24}\int_{\widetilde{X}} \log \left\{ \frac{\eta\wedge\bar{\eta}}{\gamma_{\epsilon,\delta}^{2}/2!} \cdot \frac{\mathrm{Vol}(\widetilde{X},\gamma_{\epsilon,\delta})}{\|\eta\|_{L^{2}(\widetilde{X})}^{2}} \right\}\, c_{2}(\widetilde{X},\gamma_{\epsilon,\delta}) \right). \end{align*} $$

By equation (4.14), Propositions 5.2, 5.4, 5.5, Corollary 5.3 and Theorem 7.1, we get

$$ \begin{align*}\begin{aligned} \tau_{M}(\widetilde{X},\theta) &= (C_{0}^{\mathrm{EH}}C_{1}^{\mathrm{EH}})^{k}\,\tau(X,\gamma_{0})\tau_{\mathbf{Z}_{2}}(X,\gamma_{0})(\iota)\, \{2\mathrm{Vol}(Y,\gamma_{0})\}^{\frac{4-k}{4}} \\ &\quad\times \{\mathrm{Vol}(\mathbf{P}^{1},\omega_{\mathrm{FS}})\tau(\mathbf{P}^{1},\omega_{\mathrm{FS}})\}^{k} \times \prod_{{\frak p}\in\mathrm{Sing}(X)}\left\{|f_{\frak p}(0)|^{2}\frac{\mathrm{Vol}(X,\gamma_{0})}{\|\eta\|_{L^{2}(X)}^{2}}\right\}^{\frac{1}{4}+\frac{1}{16}} \\ &\quad\times \exp \left[ \frac{1}{24}\int_{X} \log\left\{\frac{\eta\wedge\bar{\eta}}{\gamma_{0}^{2}/2!}\cdot\frac{\mathrm{Vol}(X,\gamma_{0})}{\|\eta\|_{L^{2}(X)}^{2}}\right\}\, c_{2}(X,\gamma_{0}) \right]. \end{aligned} \end{align*} $$

Since

$$ \begin{align*}\tau(Y,\gamma_{0})^{2}=\tau(X,\gamma_{0})\tau_{\mathbf{Z}_{2}}(X,\gamma_{0})(\iota), \qquad \mathrm{Vol}(X,\gamma_{0})/\|\eta\|_{L^{2}(X)}^{2}=\mathrm{Vol}(Y,\gamma_{0})/\|\eta\|_{L^{2}(Y)}^{2}, \end{align*} $$

and since X is a double covering of Y, we get the result by setting

(8.1) $$ \begin{align} C(k)=2\{2^{-\frac{1}{4}}C_{0}^{\mathrm{EH}}C_{1}^{\mathrm{EH}}\mathrm{Vol}(\mathbf{P}^{1},\omega_{\mathrm{FS}})\tau(\mathbf{ P}^{1},\omega_{\mathrm{FS}})\}^{k}. \end{align} $$

This completes the proof.

Theorem 8.2. Let $\gamma $ be a Kähler form on Y in the sense of orbifolds. Then the following equality holds:

$$ \begin{align*}\frac{\tau(Y,\gamma)\mathrm{Vol}(Y,\gamma)}{\tau(Y,\omega_{\eta})\mathrm{Vol}(Y,\omega_{\eta})} = \left\{ \prod_{{\frak p}\in\mathrm{Sing}(Y)}\left(\frac{\omega_{\eta}^{2}}{\gamma^{2}}\right)({\frak p}) \right\}^{-\frac{5}{32}} \exp \left\{ -\frac{1}{24}\int_{Y} \log\left(\frac{\omega_{\eta}^{2}}{\gamma^{2}}\right)\,c_{2}(Y,\gamma) \right\}. \end{align*} $$

Proof. Let ${\frak p}\in \mathrm {Sing}(Y)$ , and let $({\mathcal U}_{\frak p},0)\subset (\mathbf {C}^{2},0)$ be an open subset that uniformises the germ $(Y,{\frak p})$ . We have an isomorphism $(Y,{\frak p})\cong (\mathbf {C}^{2}/\Gamma _{\frak p},0)$ of germs, where $\Gamma _{\frak p}=\mathbf {Z}/4\mathbf {Z}=\langle i\rangle $ , such that $\omega _{\eta }$ and $\gamma $ lift to Kähler metrics on ${\mathcal U}_{\frak p}$ . Following Ma [32], we define $Y^{\Sigma }$ as the union $Y^{\Sigma }:=Y^{i}\amalg Y^{i^{2}}\amalg Y^{i^{3}}$ , where $Y^{i^{\nu }}=\{{\frak p}^{i^{\nu }}\}_{{\frak p}\in \mathrm {Sing}(Y)}$ and the germ $(Y^{i^{\nu }},{\frak p}^{i^{\nu }})$ is equipped with orbifold structure $(Y^{i^{\nu }},{\frak p}^{i^{\nu }})\cong (\mathbf {C}^{2}/\langle i^{\nu }\rangle ,0)$ .

Recall that the characteristic class $\mathrm {Td}^{\Sigma }(TY)$ supported on the singular locus of Y appears in the Riemann-Roch theorem for orbifolds, for which we refer the reader to, for example, [32]. By the anomaly formula for Quillen metrics for orbifolds [32], we get

(8.2) $$ \begin{align} \begin{aligned} \,& \log \left( \frac{\tau(Y,\gamma)\mathrm{Vol}(Y,\gamma)}{\tau(Y,\omega_{\eta})\mathrm{Vol}(Y,\omega_{\eta})} \right) = \frac{1}{4}\int_{Y^{\Sigma}}\widetilde{\mathrm{Td}}^{\Sigma}(TY;\gamma,\omega_{\eta}) + \frac{1}{24}\int_{Y}\widetilde{c_{1}c_{2}}(TY;\gamma,\omega_{\eta}) \\ &= \frac{1}{4}\sum_{{\frak p}\in\mathrm{Sing}(Y)}\sum_{\nu=1}^{3} \left[ \left(\widetilde{\frac{\mathrm{Td}}{\mathrm{e}}}\right)_{\nu/2}(TU_{\frak p};\gamma,\omega_{\eta}) \right]^{(0,0)}({\frak p}) + \frac{1}{24}\int_{Y}\widetilde{c_{1}c_{2}}(TY;\gamma,\omega_{\eta})^{(2,2)}. \end{aligned} \end{align} $$

Here, for $\theta \in \mathbf {R}$ and a square matrix A, we define $\left ({\frac {\mathrm {Td}}{\mathrm {e}}}\right )_{\theta }(A):=\det \left (\frac {I}{I-e^{-(\pi i\theta +A)}}\right )$ , and $(\widetilde {\mathrm {Td}/\mathrm {e}})_{\theta }$ is the Bott-Chern secondary class associated to $\left (\mathrm {Td}/\mathrm {e}\right )_{\theta }(A)$ such that for any holomorphic vector bundle E and Hermitian metrics h, $h'$ on E

$$ \begin{align*}-dd^{c}\left(\widetilde{\frac{\mathrm{Td}}{\mathrm{e}}}\right)_{\theta}(E;h,h') = \left(\frac{\mathrm{Td}}{\mathrm{e}}\right)_{\theta}\left(-\frac{1}{2\pi i}R(E,h)\right) - \left(\frac{\mathrm{Td}}{\mathrm{e}}\right)_{\theta}\left(-\frac{1}{2\pi i}R(E,h')\right). \end{align*} $$

Similarly, $\widetilde {c_{1}c_{2}}$ is the Bott-Chern secondary class associated to the invariant polynomial $c_{1}(A)c_{2}(A)$ such that for any holomorphic vector bundle E and Hermitian metrics h, $h'$ on E

$$ \begin{align*}-dd^{c}\widetilde{c_{1}c_{2}}(E;h,h')=c_{1}(E,h)c_{2}(E,h)-c_{1}(E,h')c_{2}(E,h'). \end{align*} $$

For $A=\mathrm {diag}(\lambda _{1},\lambda _{2})$ , we have

$$ \begin{align*}\left(\frac{\mathrm{Td}}{\mathrm{e}}\right)_{\frac{\nu}{2}}(A)=\frac{1}{(1-i^{-\nu})^{2}}\{1-\frac{i^{-\nu}}{1-i^{-\nu}}c_{1}(A)+O(2)\}. \end{align*} $$

Thus we get

(8.3) $$ \begin{align} \begin{aligned} \sum_{\nu=1}^{3} \left[ \left(\widetilde{\frac{\mathrm{Td}}{\mathrm{e}}}\right)_{\frac{\nu}{2}}(TU_{\frak p};\gamma,\omega_{\eta}) \right]^{(0,0)} ({\frak p}) &= -\sum_{\nu=1}^{3}\frac{i^{-\nu}}{(1-i^{-\nu})^{3}}\,\widetilde{c_{1}}(TU_{\frak p};\gamma,\omega_{\eta})({\frak p}) \\ &= \frac{5}{8}\widetilde{c_{1}}(TU_{\frak p};\gamma,\omega_{\eta})({\frak p}) = -\frac{5}{8}\log\left(\omega_{\eta}^{2}/\gamma^{2}\right)({\frak p}). \end{aligned} \end{align} $$

On the other hand, by the same computations as in equation (3.3), we get

(8.4) $$ \begin{align} \widetilde{c_{1}c_{2}}(TY;\gamma,\omega_{\eta})^{(2,2)}=-\log\left(\omega_{\eta}^{2}/\gamma^{2}\right)\,c_{2}(TY,\gamma). \end{align} $$

Substituting equation (8.3) and equation (8.4) into equation (8.2), we get the result.

Theorem 8.3. For every Ricci-flat log-Enriques surface $(Y,\omega )$ , one has

$$ \begin{align*}\mathrm{Vol}(Y,\omega)^{\frac{4-k}{8}}\tau(Y,\omega)=C(k)^{-1}\,\tau_{M}(\widetilde{X},\theta)^{\frac{1}{2}}, \end{align*} $$

where $C(k)$ is the same constant as in Theorem 8.1.

Proof. We put $\gamma =\gamma _{0}$ in Theorem 8.2. Then we get by Theorem 8.1

$$ \begin{align*}\begin{aligned} \,& \tau(Y,\omega_{\eta})\mathrm{Vol}(Y,\omega_{\eta}) = \tau(Y,\gamma_{0})\mathrm{Vol}(Y,\gamma_{0})^{\frac{4-k}{8}}\mathrm{Vol}(Y,\gamma_{0})^{\frac{4+k}{8}} \\ &\qquad\qquad\qquad\qquad\quad\times \{ \prod_{{\frak p}\in\mathrm{Sing}(X)}\left(\frac{\omega_{\eta}^{2}}{\gamma_{0}^{2}}\right)({\frak p}) \}^{\frac{5}{32}} \exp \left[ \frac{1}{24}\int_{Y} \log\left(\frac{\omega_{\eta}^{2}}{\gamma_{0}^{2}}\right)\,c_{2}(Y,\gamma_{0}) \right] \\ &= C(k)^{-1}\tau_{M}(\widetilde{X},\theta)^{\frac{1}{2}}\mathrm{Vol}(Y,\gamma_{0})^{\frac{4+k}{8}} \times \prod_{{\frak p}\in\mathrm{Sing}(X)}\left\{|f_{\frak p}(0)|^{2}\frac{\mathrm{Vol}(Y,\gamma_{0})}{\|\eta\|_{L^{2}(Y)}^{2}}\right\}^{-\frac{5}{32}} \\ &\quad\times \exp \left[ -\frac{1}{24}\int_{Y} \log\left\{\frac{\eta\wedge\bar{\eta}}{\gamma_{0}^{2}/2!}\cdot\frac{\mathrm{Vol}(Y,\gamma_{0})}{\|\eta\|_{L^{2}(Y)}^{2}}\right\}\, c_{2}(Y,\gamma_{0}) \right] \\ &\quad\times \{ \prod_{{\frak p}\in\mathrm{Sing}(X)}\left(\frac{\omega_{\eta}^{2}}{\gamma_{0}^{2}}\right)({\frak p}) \}^{\frac{5}{32}} \exp \left[ \frac{1}{24}\int_{Y} \log\left(\frac{\eta\wedge\bar{\eta}}{\gamma_{0}^{2}/2!}\right)\,c_{2}(Y,\gamma_{0}) \right]. \end{aligned} \end{align*} $$

Since $|f_{\frak p}(0)|^{2}=[\eta \wedge \bar {\eta }/(\gamma _{0}^{2}/2!)]({\frak p})=[\omega _{\eta }^{2}/\gamma _{0}^{2}]({\frak p})$ , we get

$$ \begin{align*}\begin{aligned} \,& \tau(Y,\omega_{\eta})\mathrm{Vol}(Y,\omega_{\eta}) \\ &= C(k)^{-1}\tau_{M}(\widetilde{X},\theta)^{\frac{1}{2}}\mathrm{Vol}(Y,\gamma_{0})^{\frac{4+k}{8}} \times \prod_{{\frak p}\in\mathrm{Sing}(X)}\left(|f_{\frak p}(0)|^{2}\frac{\mathrm{Vol}(Y,\gamma_{0})}{\mathrm{Vol}(Y,\omega_{\eta})}\right)^{-\frac{5}{32}} \\ &\quad\times \{ \prod_{{\frak p}\in\mathrm{Sing}(X)}|f_{\frak p}(0)|^{2} \}^{\frac{5}{32}} \exp \left[ -\frac{1}{24}\int_{Y} \log\left\{\frac{\mathrm{Vol}(Y,\gamma_{0})}{\mathrm{Vol}(Y,\omega_{\eta})}\right\}\, c_{2}(Y,\gamma_{0}) \right] \\ &= C(k)^{-1}\tau_{M}(\widetilde{X},\theta)^{\frac{1}{2}}\mathrm{Vol}(Y,\gamma_{0})^{\frac{4+k}{8}} \left(\frac{\mathrm{Vol}(Y,\gamma_{0})}{\mathrm{Vol}(Y,\omega_{\eta})}\right)^{-\frac{5}{32}k} \exp\left[ -\frac{16-k}{32}\log\left(\frac{\mathrm{Vol}(Y,\gamma_{0})}{\mathrm{Vol}(Y,\omega_{\eta})}\right) \right] \\ &= C(k)^{-1}\tau_{M}(\widetilde{X},\theta)^{\frac{1}{2}}\mathrm{Vol}(Y,\omega_{\eta})^{\frac{4+k}{8}}, \end{aligned} \end{align*} $$

where we used the second assertion of Proposition 5.1 to get the second equality. This proves the result.

Theorem 8.4. Let $\gamma $ be a Kähler form on Y in the sense of orbifolds, and let $\varXi \in H^{0}(Y,K_{Y}^{\otimes 2})\setminus \{0\}$ be a nowhere vanishing bicanonical form on Y. Then

$$ \begin{align*}\begin{aligned} \tau_{k}(Y) &:= \tau(Y,\gamma)\mathrm{Vol}(Y,\gamma)\,\|\varXi\|_{L^{1}(Y)}^{-\frac{4+k}{8}} \left\{ \prod_{{\frak p}\in\mathrm{Sing}(Y)}\left(\frac{\gamma^{2}/2!}{|\varXi|}\right)({\frak p}) \right\}^{\frac{5}{32}} \\ &\quad\times \exp \left[ \frac{1}{24}\int_{Y} \log\left(\frac{|\varXi|}{\gamma^{2}/2!}\right)\,c_{2}(Y,\gamma) \right] \end{aligned} \end{align*} $$

is independent of the choices of $\gamma $ and $\varXi $ , where $|\varXi |:=\sqrt {\varXi \otimes \overline {\varXi }}$ is the Ricci-flat volume form on Y induced by $\varXi $ . In fact,

$$ \begin{align*}\tau_{k}(Y)=C(k)^{-1}\tau_{M}(\widetilde{X},\theta)^{\frac{1}{2}}. \end{align*} $$

Proof. Let $\omega $ be a Ricci-flat Kähler form on Y in the sense of orbifolds such that $\omega ^{2}/2!=|\varXi |$ . Since $\mathrm {Vol}(Y,\omega )=\|\varXi \|_{L^{1}(Y)}$ , we get by Theorem 8.3

(8.5) $$ \begin{align} \mathrm{Vol}(Y,\omega)\tau(Y,\omega) = \mathrm{Vol}(Y,\omega)^{\frac{4+k}{8}}\mathrm{Vol}(Y,\omega)^{\frac{4-k}{8}}\tau(Y,\omega) = C(k)^{-1}\,\|\varXi\|_{L^{1}(Y)}^{\frac{4+k}{8}}\,\tau_{M}(\widetilde{X},\theta)^{\frac{1}{2}}. \end{align} $$

Let $\xi \in H^{0}(\widetilde {X},K_{\widetilde {X}})$ be a nowhere vanishing holomorphic $2$ -form on $\widetilde {X}$ such that $(p\circ \pi )^{*}\varXi =\xi ^{\otimes 2}$ . Since $\omega =\omega _{\xi }$ : that is, $\omega ^{2}/2!=\xi \wedge \overline {\xi }=|\varXi |$ , we get by Theorem 8.2

(8.6) $$ \begin{align} \frac{\tau(Y,\gamma)\mathrm{Vol}(Y,\gamma)}{\tau(Y,\omega)\mathrm{Vol}(Y,\omega)} = \left\{ \prod_{{\frak p}\in\mathrm{Sing}(Y)}\left(\frac{|\varXi|}{\gamma^{2}/2!}\right)({\frak p}) \right\}^{-\frac{5}{32}} \exp \left[ -\frac{1}{24}\int_{Y} \log\left(\frac{|\varXi|}{\gamma^{2}/2!}\right)\,c_{2}(Y,\gamma) \right]. \end{align} $$

Comparing equation (8.5) and equation (8.6), we get

(8.7) $$ \begin{align} \begin{aligned} \tau(Y,\gamma)\mathrm{Vol}(Y,\gamma) &= C(k)^{-1}\tau_{M}(\widetilde{X},\theta)^{\frac{1}{2}}\,\|\varXi\|_{L^{1}(Y)}^{\frac{4+k}{8}} \left\{ \prod_{{\frak p}\in\mathrm{Sing}(Y)}\left(\frac{|\varXi|}{\gamma^{2}/2!}\right)({\frak p}) \right\}^{-\frac{5}{32}} \\ &\quad\times \exp \left[ -\frac{1}{24}\int_{Y} \log\left(\frac{|\varXi|}{\gamma^{2}/2!}\right)\,c_{2}(Y,\gamma) \right]. \end{aligned} \end{align} $$

From equation (8.7), we get $\tau _{k}(Y)=C(k)^{-1}\tau _{M}(\widetilde {X},\theta )^{1/2}$ . Since the right-hand side is independent of the choices of $\gamma $ and $\varXi $ , so is $\tau _{k}(Y)$ . This completes the proof.

8.2 Del Pezzo surfaces and an explicit formula for the invariant $\tau _{k}$

In this subsection, we give an explicit formula for $\tau _{k}$ as an automorphic function on the Kähler moduli of Del Pezzo surfaces. Let $1\leq k\leq 9$ . We define the unimodular Lorentzian lattices $L_{k}$ and ${\Bbb U}(-1)$ as

$$ \begin{align*}L_{k}:=\begin{pmatrix}1&0\\0&-I_{9-k}\end{pmatrix} \quad(k\not=8), \qquad L_{8} := \begin{pmatrix}1&0\\0&-1\end{pmatrix}\mbox{ or }\begin{pmatrix}0&1\\1&0\end{pmatrix}, \end{align*} $$

$$ \begin{align*}{\Bbb U}(-1):=\begin{pmatrix} 0&-1 \\ -1&0 \end{pmatrix}. \end{align*} $$

We fix an isometry of lattices $\Lambda _{k}\cong {\Bbb U}(-1)\oplus L_{k}$ and identify $\Lambda _{k}$ with ${\Bbb U}(-1)\oplus L_{k}$ .

Let V be a Del Pezzo surface of degree k: that is,

$$ \begin{align*}k = \deg V = \int_{V} c_{1}(V)^{2}. \end{align*} $$

Then $V = \mathrm {Bl}_{9-k}( {\mathbf P}^{2} )$ is the blowing-up of ${\mathbf P}^{2}$ at $9-k$ points in general position when $k\not =8$ . When $k=8$ , $V\cong \Sigma _{0}$ or $\Sigma _{1}$ , where $\Sigma _{n} = {\mathbf P}( {\mathcal O}_{{\mathbf P}^{1}} \oplus {\mathcal O}_{{\mathbf P}^{1}}(n) )$ is the Hirzebruch surface. Notice that $\Sigma _{0}={\mathbf P}^{1} \times {\mathbf P}^{1}$ and $\Sigma _{1}=\mathrm {Bl}_{1}( {\mathbf P}^{2} )$ . When $V\not \cong \Sigma _{0}$ , $H^{2}(V, {\mathbf Z})$ endowed with the cup product pairing is isometric to $L_{k}$ by identifying $H, E_{1},\ldots ,E_{9-k}$ with the standard basis of $L_{k}$ , where $H \in H^{2}(V, {\mathbf Z})$ is the class obtained from the hyperplane class of $H^{2}({\mathbf P}^{2}, {\mathbf Z})$ and $E_{i} (i=1,\ldots ,9-k)$ are the classes of exceptional divisors. Similarly, $H(V, {\mathbf Z})$ endowed with the Mukai pairing is isometric to $\Lambda _{k}$ . In what follows, we identify $L_{k}$ (respectively, $\Lambda _{k}$ ) with $H^{2}(V, {\mathbf Z})$ (respectively, $H(V, {\mathbf Z})$ ) in this way.

Recall that the type IV domain $\Omega _{k}$ associated with $\Lambda _{k}$ was defined in Section 2.4. We identify $\Omega _{H(V, {\mathbf Z})}$ with the tube domain $H^{2}(V, {\mathbf Z})\otimes {\mathbf R}+i\,{\mathcal C}_{H^{2}(V, {\mathbf Z})} \subset H^{2}(V, {\mathbf C})$ via the map

(8.8) $$ \begin{align} H^{2}(V, {\mathbf Z})\otimes{\mathbf R}+i\,{\mathcal C}_{H^{2}(V, {\mathbf Z})} \ni y\to[\exp(y)]:=\left[\left(1, y, y^{2}/2\right)\right]\in \Omega_{H(V, {\mathbf Z})}, \end{align} $$

where ${\mathcal C}_{H^{2}(V, {\mathbf Z})}:=\{v\in H^{2}(V, {\mathbf R}); \, v^{2}>0 \}$ is the positive cone of $H^{2}(V, {\mathbf R})$ . Through the isomorphism given by equation (8.8), $O(H(V,{\mathbf Z}))$ acts on $H^{2}(V, {\mathbf R})+i\,{\mathcal C}_{H^{2}(V, {\mathbf Z})}$ .

Let ${\mathcal K}_{V} \subset {\mathcal C}_{H^{2}(V, {\mathbf Z})}$ be the Kähler cone of V: that is, the cone of $H^{2}(V, {\mathbf R})$ consisting of Kähler classes on V. Let $\mathrm {Eff}(V) \subset H^{2}(V, {\mathbf R})$ be the effective cone of V: that is, the dual cone of the Kähler cone ${\mathcal K}_{V}$ .

Definition 8.5. Define the infinite product $\Phi _{V}(z)$ on $H^{2}(V, {\mathbf Z})\otimes \mathbf {R}+i\,{\mathcal K}_{V}$ by

$$ \begin{align*}\begin{aligned} \Phi_{V}(z) &:= e^{\pi i\langle c_{1}(V), z\rangle} \prod_{\alpha\in \mathrm{Eff}(V)} (1-e^{2\pi i\langle\alpha,z\rangle})^{c_{k}^{(0)}(\alpha^{2})} \\ &\qquad\times \prod_{\beta\in \mathrm{Eff}(V),\,\, \beta/2\equiv c_{1}(V)/2\mod H^{2}(V, {\mathbf Z})} (1-e^{\pi i\langle\beta,z\rangle})^{c_{k}^{(1)}(\beta^{2}/4)}, \end{aligned} \end{align*} $$

where $\{c_{k}^{(0)}(l)\}_{l\in \mathbf {Z}}$ , $\{c_{k}^{(1)}(l)\}_{l\in \mathbf {Z}+k/4}$ are defined by the generating functions

$$ \begin{align*}\sum_{l\in\mathbf{Z}}c_{k}^{(0)}(l)\,q^{l} = \frac{\eta(2\tau)^{8}\theta_{{\Bbb A}_{1}}(\tau)^{k}}{\eta(\tau)^{8}\eta(4\tau)^{8}}, \qquad \sum_{l\in\frac{k}{4}+\mathbf{Z}}c_{k}^{(1)}(l)\,q^{l} = -8\,\frac{\eta(4\tau)^{8}\theta_{{\Bbb A}_{1}+1/2}(\tau)^{k}}{\eta(2\tau)^{16}}. \end{align*} $$

Here $\theta _{{\Bbb A}_{1}+\epsilon /2}(\tau ):=\sum _{n\in \mathbf {Z}}q^{(n+\epsilon /2)^{2}}$ and $\eta (\tau ):=q^{1/24}\prod _{n>0}(1-q^{n})$ .

Let ${\mathcal C}_{H^{2}(V, {\mathbf Z})}^{+}$ be the connected component of ${\mathcal C}_{H^{2}(V, {\mathbf Z})}$ that contains ${\mathcal K}_{V}$ , and let $\Omega _{H(V, {\mathbf Z})}^{+}$ be the component of $\Omega _{H(V, {\mathbf Z})}$ corresponding to $H^{2}(V, {\mathbf R}) + i\,{\mathcal C}_{H^{2}(V, {\mathbf Z})}^{+}$ via the isomorphism given by equation (8.8). By Borcherds [8, Th. 13.3] (compare [44]), $\Phi _{V}(z)$ converges absolutely for those $z\in H^{2}(V, {\mathbf R}) + i\,{\mathcal K}_{V}$ with $\Im z\gg 0$ and extends to an automorphic form on $\Omega _{H(V, {\mathbf Z})}^{+}$ for $O^{+}(H(V, {\mathbf Z}))$ of weight $\deg V+4$ with zero divisor $\mathrm {div}(\Phi _{V})=\sum _{d\in H(V, {\mathbf Z}),\,d^{2}=-1}d^{\perp }$ under the identification $H^{2}(V, {\mathbf R}) + i\,{\mathcal C}_{H^{2}(V, {\mathbf Z})}^{+} \cong \Omega _{H(V, {\mathbf Z})}^{+}$ .

Recently, an explicit Fourier series expansion of $\Phi _{V}(z)$ is discovered by Gritsenko [22, Cor. 5.1]. It is also remarkable that $\Phi _{V}$ is the denominator function of a generalised Kac-Moody algebra, whose real and imaginary simple roots are explicitly given by the Fourier series expansion of $\Phi _{V}$ [23, §6.2, Th. 6.1 Eq. (6.1), (6.10)]. In this sense, the series of Borcherds products $\Phi _{V}$ associated to Del Pezzo surfaces is quite analogous to the Borcherds $\Phi $ -function of rank $10$ .

We define the Petersson norm of $\Phi _{V}(z)$ by

$$ \begin{align*}\|\Phi_{V}(z)\|^{2}:=\langle\Im z,\Im z\rangle^{4+\deg V}|\Phi_{V}(z)|^{2}, \end{align*} $$

where $z\in H^{2}(V, {\mathbf R}) + i\,{\mathcal C}_{H^{2}(V, {\mathbf Z})}^{+}$ . Then $\|\Phi _{V}\|^{2}$ is an $O^{+}(H(V, {\mathbf Z}))$ -invariant $C^{\infty }$ function on $\Omega _{H(V, {\mathbf Z})}^{+}$ . Hence $\|\Phi _{V}\|^{2}$ is identified with a $C^{\infty }$ function on ${\mathcal M}_{\deg V}$ in the sense of orbifolds.

Theorem 8.6. Let $1\leq k\leq 9$ . There exists a constant $\widetilde {C}(k)>0$ depending only on k such that for every $2$ -elementary $K3$ surface $(\widetilde {X},\theta )$ of type $M_{k}:=\Lambda _{k}(2)^{\perp }$ ,

$$ \begin{align*}\tau_{M_{k}}(\widetilde{X},\theta)=\widetilde{C}(k)\,\| \Phi_{V}(\overline{\varpi}(\widetilde{X},\theta)) \|^{-1/2}, \end{align*} $$

where $k = \deg V$ .

Proof. See [44, Th. 4.2 (1)] and [45, Th. 0.1].

Theorem 8.7. Let $1\leq k\leq 9$ . Then there exists a constant $C_{k}>0$ depending only on k such that for every good log-Enriques surface Y with $\#\mathrm {Sing}(Y) = \deg V$ ,

$$ \begin{align*}\tau_{\deg V}(Y) = C_{\deg V} \left\| \Phi_{V}(\overline{\varpi}(Y)) \right\|^{-1/4}. \end{align*} $$

Proof. We set $k = \deg V$ . When $k=2$ , we define $V=\Sigma _{0}$ when Y is of even type and $V=\Sigma _{1}$ when Y is of odd type. Let $(\widetilde {X},\theta )$ be the $2$ -elementary $K3$ surface of type $M_{k}$ associated to Y. By the definition of the period of Y, we have $\overline {\varpi }(Y)=\overline {\varpi }(\widetilde {X},\theta )$ . Hence

(8.9) $$ \begin{align} \left\|\Phi_{V}\left(\overline{\varpi}(Y)\right)\right\|=\|\Phi_{V}(\overline{\varpi}(\widetilde{X},\theta))\|. \end{align} $$

By Theorems 8.4, 8.6 and equation (8.9), we get

(8.10) $$ \begin{align} \begin{aligned} \tau_{k}(Y) &= C(k)^{-1}\tau_{M_{k}}(\widetilde{X},\theta)^{1/2} = C(k)^{-1}\widetilde{C}(k)\,\|\Phi_{V}(\overline{\varpi}(\widetilde{X},\theta))\|^{-1/4} \\ &= C(k)^{-1}\widetilde{C}(k)\,\left\|\Phi_{V}\left(\overline{\varpi}(Y)\right)\right\|^{-1/4}. \end{aligned} \end{align} $$

Setting $C_{k}:=C(k)^{-1}\widetilde {C}(k)$ in equation (8.10), we get the result.

8.3 The quasi-pullback of $\Phi _{V}$

We define the Kähler moduli of V by

$$ \begin{align*}\mathcal{KM}(V) := (H^{2}(V, {\mathbf R}) + i\,{\mathcal C}_{H^{2}(V, {\mathbf Z})}^{+})/O^{+}(H(V,{\mathbf Z})) \cong \Omega_{H(V,{\mathbf Z})}^{+}/O^{+}(H(V,{\mathbf Z})). \end{align*} $$

Since $H(V,{\mathbf Z}) \cong \Lambda _{\deg V}$ , we have $\mathcal {KM}(V)={\mathcal M}_{\deg V}$ , where the orthogonal modular variety ${\mathcal M}_{k}$ was defined in Section 2.4. Let $\pi \colon \widetilde {V}:=\mathrm {Bl}_{p}(V)\to V$ be the blow-up of V at p, and let $E:=\pi ^{-1}(p)$ be the exceptional curve of $\pi $ . Then we have a map of cohomologies $\pi ^{*}\colon H(V,{\mathbf Z})\to H(\widetilde {V},{\mathbf Z})$ , which induces the canonical identification

$$ \begin{align*}H(V,{\mathbf Z})\cong \pi^{*}H(V,{\mathbf Z}) = \{ [x]\in H(\widetilde{V},{\mathbf Z});\,\langle[E],x\rangle=0 \}. \end{align*} $$

Since $[E]$ is a norm $(-1)$ -vector of $H^{2}(\widetilde {V}, {\mathbf Z})$ , this implies that $\mathcal {KM}(V)$ is identified with a component of the Heegner divisor of norm $(-1)$ -vectors of $\mathcal {KM}(\widetilde {V})$ . Since $O(H(\widetilde {V}, {\mathbf Z}))$ acts transitively on the norm $(-1)$ -vectors of $H(\widetilde {V}, {\mathbf Z})$ except the case $\deg \widetilde {V} = 7$ – that is, $H(\widetilde {V}, {\mathbf Z}) \cong {\mathbb U}^{\oplus 2} \oplus \langle -1 \rangle $ – $\mathcal {KM}(V)$ coincides with the Heegner divisor of norm $(-1)$ -vectors of $\mathcal {KM}(\widetilde {V})$ when $\deg V \not =7$ . When $\deg V=7$ , the Heegner divisor of norm $(-1)$ -vectors of $\mathcal {KM}(\widetilde {V})$ consists of two components; one is given by $\mathcal {KM}(\varSigma _{0})$ , and the other is given by $\mathcal {KM}(\varSigma _{1})$ , where $\varSigma _{n} = {\mathbf P}( {\mathcal O}_{{\mathbf P}^{1}} \oplus {\mathcal O}_{{\mathbf P}^{1}}(n) )$ is the Hirzebruch surface. In the following theorem, we use the convention that a Del Pezzo surface of degree $0$ is an Enriques surface.

Theorem 8.8. $\Phi _{V}$ is the quasi-pullback of $\Phi _{\widetilde {V}}$ to $\mathcal {KM}(V) = [E]^{\perp }$ , up to a constant. Namely, in the infinite product expression in Definition 8.5, the following equality holds:

$$ \begin{align*}\Phi_{V} = \mathrm{Const}.\, \left. \frac{\Phi_{\widetilde{V}}(\cdot)}{\langle \cdot, [E]\rangle} \right|_{[E]^{\perp}}, \end{align*} $$

where $\langle z, [E] \rangle $ is the linear form on $H^{2}(\widetilde {V}, {\mathbf C})$ defined by the norm $(-1)$ -vector $[E]$ .

Proof. The result is a special case of [29, Th. 1.1]. See also [29, Example 3.17].

This theorem can be summarised in the following diagrams:

$$ \begin{align*}\begin{array}{lllllllllll} \mathcal{KM}(\mathrm{Enr}) &\supset &\mathcal{KM}(\mathrm{dP}_{1}) &\supset &\cdots &\supset &\mathcal{KM}(\mathrm{dP}_{7}) &\supset &\mathcal{KM}(\Sigma_{1}) &\supset &\mathcal{KM}({\mathbf P}^{2}) \\ \Phi_{\mathrm{Enr}} & \to & \Phi_{\mathrm{dP}_{1}} & \to & \cdots & \to & \Phi_{\mathrm{dP}_{7}} & \to & \Phi_{\Sigma_{1}} & \to & \Phi_{{\mathbf P}^{2}} \\ \eta_{1^{-8}2^{8}4^{-8}} & \to & \eta_{1^{-8}2^{8}4^{-8}} \theta & \to & \cdots & \to & \eta_{1^{-8}2^{8}4^{-8}} \theta^{7} & \to & \eta_{1^{-8}2^{8}4^{-8}} \theta^{8} & \to & \eta_{1^{-8}2^{8}4^{-8}} \theta^{9} \end{array} \end{align*} $$

and

$$ \begin{align*}\begin{array}{lllllllll} \mathcal{KM}(\mathrm{dP}_{7}) &\supset &\mathcal{KM}(\Sigma_{0}) \\ \Phi_{\mathrm{dP}_{7}} & \to & \Phi_{\Sigma_{0}} \\ \eta_{1^{-8}2^{8}4^{-8}} \theta^{7} & \to & \eta_{1^{-8}2^{8}4^{-8}} \theta^{8} \end{array} \end{align*} $$

where the inclusion implies the embedding as the discriminant divisor, the arrow in the second line implies the quasi-pullback (up to a constant), and the arrow in the third line describes the change of elliptic modular form for $\Gamma _{0}(4)$ corresponding to $\Phi _{V}$ . We remark that there are no inclusions of $\mathcal {KM}({\mathbf P}^{2})$ into $\mathcal {KM}(\Sigma _{0})$ .

9 The invariant $\tau _{k}$ and the BCOV invariant

9.1 The BCOV invariant of log-Enriques surfaces

In this subsection, we prove that the invariant $\tau _{k}$ is viewed as the BCOV invariant of good log-Enriques surfaces. Recall that for a compact connected Kähler orbifold $(V, \gamma )$ , the BCOV torsion $T_{\mathrm {BCOV}}(V,\gamma )$ is defined as

$$ \begin{align*}T_{\mathrm{BCOV}}(V,\gamma) := \exp( -\sum_{p,q\geq 0} (-1)^{p+q}pq\,\zeta_{p,q}'(0)), \end{align*} $$

where $\zeta _{p,q}(s)$ is the spectral zeta function of the Laplacian $\square _{p,q}$ acting on $(p,q)$ -forms on V in the sense of orbifolds. As before, the analytic torsion of the trivial line bundle on V is denoted by $\tau (V,\gamma )$ .

Lemma 9.1. If $\dim V = 2$ , then the following equality holds:

$$ \begin{align*}T_{\mathrm{BCOV}}(V,\gamma) = \tau(V,\gamma)^{-2}. \end{align*} $$

Proof. Since $\square _{p,q}$ and $\square _{2-q,2-p}$ are isospectral via the Hodge $*$ -operator, we have $\zeta _{p,q}(s) = \zeta _{2-q,2-p}(s)$ . Since $\square _{p,q}$ and $\square _{q,p}$ are isospectral via the complex conjugation, we have $\zeta _{p,q}(s)=\zeta _{q,p}(s)$ . Using these relations, we have

(9.1) $$ \begin{align} -\log T_{\mathrm{BCOV}}(V,\gamma) = 4\zeta^{\prime}_{0,0}(0) - 4\zeta^{\prime}_{0,1}(0) + \zeta^{\prime}_{1,1}(0). \end{align} $$

Since $\zeta _{0,0}(s) - \zeta _{0,1}(s) + \zeta _{0,2}(s) =0$ and $\zeta _{1,0}(s) - \zeta _{1,1}(s) + \zeta _{1,2}(s) =0$ , we have $4\zeta ^{\prime }_{0,0}(0) - 4\zeta ^{\prime }_{0,1}(0) = -4\zeta ^{\prime }_{0,2}(0)$ and $\zeta ^{\prime }_{1,1}(0) = \zeta ^{\prime }_{1,0}(0) + \zeta ^{\prime }_{1,2}(0) = \zeta ^{\prime }_{1,0}(0) + \zeta ^{\prime }_{0,1}(0) = 2\zeta ^{\prime }_{0,1}(0)$ . Substituting these into equation (9.1), we get the result.

Now we have the following:

Theorem 9.2. Let Y be a good log-Enriques surface with k singular points. Let $\gamma $ be a Kähler form on Y in the sense of orbifolds, and let $\varXi \in H^{0}(Y,K_{Y}^{\otimes 2})\setminus \{0\}$ be a nowhere vanishing bicanonical form on Y. Then

$$ \begin{align*}\begin{aligned} \tau_{\mathrm{BCOV}}(Y) &:= T_{\mathrm{BCOV}}(Y,\gamma)\mathrm{Vol}(Y,\gamma)^{-2}\,\|\varXi\|_{L^{1}(Y)}^{\frac{4+k}{4}} \left\{ \prod_{{\frak p}\in\mathrm{Sing}(Y)}\left(\frac{\gamma^{2}/2!}{|\varXi|}\right)({\frak p}) \right\}^{-\frac{5}{16}} \\ &\quad\times \exp \left[ -\frac{1}{12}\int_{Y} \log\left(\frac{|\varXi|}{\gamma^{2}/2!}\right)\,c_{2}(Y,\gamma) \right] \end{aligned} \end{align*} $$

is independent of the choices of $\gamma $ and $\varXi $ . In fact,

$$ \begin{align*}\tau_{\mathrm{BCOV}}(Y) = \tau_{k}(Y)^{-2} = C_{k}^{-2} \| \Phi_{V}( \overline{\varpi}(Y)) \|^{\frac{1}{2}}, \end{align*} $$

where $C_{k}$ is the same constant as in Theorem 8.7.

Proof. Since $\tau _{\mathrm {BCOV}}(Y)=\tau _{k}(Y)^{-2}$ by Theorem 8.4 and Lemma 9.1, we get the first claim. The second claim follows from Theorem 8.7.

We call $\tau _{\mathrm {BCOV}}(Y)$ the BCOV invariant of Y. When $\gamma $ is Ricci-flat and $|\varXi | = \gamma ^{2}/2!$ , we have the following simple expression:

(9.2) $$ \begin{align} \tau_{\mathrm{BCOV}}(Y) = T_{\mathrm{BCOV}}(Y,\gamma)\mathrm{Vol}(Y,\gamma)^{\frac{k-4}{4}}. \end{align} $$

As in the case of Enriques surfaces, the BCOV invariant of good log-Enriques surfaces is expressed by the Peterssion norm of a Borcherds product. In particular, the BCOV invariant of log-Enriques surfaces is not a birational invariant, for the birational equivalence classes of log-Enriques surfaces consist of a single class.

Problem 9.3. For a good log-Enriques surface Y, there exists a log-Enriques surface $Y'$ with a unique singular point admitting a birational morphism $Y\to Y'$ (compare [47]). In general, the singularity of $Y'$ is worse than those of Y. Can one construct a holomorphic torsion invariant of $Y'$ using some ALE instanton instead of the Eguchi-Hanson instanton? If this is the case, compare the holomorphic torsion invariants between Y and $Y'$ .

Problem 9.4. Let Y be a good log-Enriques surface. Let $p\colon \widetilde {Y}\to Y$ be a resolution such that $p^{-1}(\mathrm {Sing}\,Y)$ is a disjoint union of smooth $(-4)$ -curves. Compare the BCOV invariant of Y and that of the pair $(\widetilde {Y}, p^{-1}(\mathrm {Sing}\,Y))$ defined by Zhang [49].

Problem 9.5. Can one construct a holomorphic torsion invariant of log-Enriques surfaces with index $\geq 3$ and prove its automorphy?

9.2 The BCOV invariant of certain Borcea-Voisin type orbifolds

Let Y be a good log-Enriques surface with k singular points, and let X be the canonical double covering of Y. Then X is a nodal $K3$ surface with k nodes endowed with an anti-symplectic involution $\iota $ with a fixed point set $\mathrm {Sing}\,X =\{ p_{1}, \ldots , p_{k} \}$ . Let T be an elliptic curve. We define

$$ \begin{align*}V=V_{(X,\iota,T)} := (X\times T)/(\iota\times(-1)_{T}). \end{align*} $$

Then V is a Calabi-Yau orbifold of dimension $3$ . Let $\widetilde {V}$ be the Borcea-Voisin orbifold

$$ \begin{align*}\widetilde{V} = \widetilde{V}_{(\widetilde{X},\theta,T)} := (\widetilde{X}\times T)/(\theta\times(-1)_{T}), \end{align*} $$

where $\pi \colon \widetilde {X} \to X$ is the minimal resolution of X and $\theta $ is the involution on $\widetilde {X}$ induced from $\iota $ . As before, we set $E_{i}:=\pi ^{-1}(p_{i}) \cong {\mathbf P}^{1}$ . The birational morphism from $\widetilde {V}$ to V induced by $\pi $ is denoted again by $\pi $ . Then $\pi \colon \widetilde {V} \to V$ is a partial resolution such that the k cyclic quotient singularities of type $(\frac {1}{4},\frac {1}{4},\frac {1}{2})$ of V are replaced by the milder cyclic quotient singularities of type $(\frac {1}{2},\frac {1}{2},0)$ . As an application of some results in Section 8, we compare the BCOV invariants between $\widetilde {V}$ and V.

Let $\gamma _{X}$ (respectively, $\gamma _{\widetilde {X}}$ ) be a Ricci-flat Kähler from on X (respectively, $\widetilde {X}$ ), and let $\gamma _{T}$ be the flat Kähler form with $\mathrm {Vol}(V,\gamma _{T})=1$ . Let $\pi _{1} \colon V \to Y=X/\iota $ and $\pi _{2} \colon V \to T/(-1)_{T}$ be the projections. Similarly, let $\widetilde {\pi }_{1} \colon \widetilde {V} \to \widetilde {X}/\theta $ and $\widetilde {\pi }_{2} \colon \widetilde {V} \to T/(-1)_{T}$ be the projections. We define a Ricci-flat Kähler form $\gamma $ (respectively, $\widetilde {\gamma }$ ) on V (respectively, $\widetilde {V}$ ) by

$$ \begin{align*}\gamma := \pi_{1}^{*}\gamma_{X} + \pi_{2}^{*}\gamma_{T}, \qquad \widetilde{\gamma} := \widetilde{\pi}_{1}^{*}\gamma_{\widetilde{X}} + \widetilde{\pi}_{2}^{*}\gamma_{T}. \end{align*} $$

Since $\mathrm {Sing}(X\times T) = (\{ p_{1} \} \times T) \amalg \cdots \amalg (\{ p_{k} \} \times T)$ , we have

$$ \begin{align*}\begin{aligned} \mathrm{Sing}\,V &= (\{ p_{1} \} \times T/(-1)_{T}) \amalg\cdots\amalg (\{ p_{k} \} \times T/(-1)_{T}) \amalg (X^{\iota} \times T[2]) \\ &= (\{ p_{1} \} \times T/(-1)_{T}) \amalg\cdots\amalg (\{ p_{k} \} \times T/(-1)_{T}) \amalg (\mathrm{Sing}\,X \times T[2]), \end{aligned} \end{align*} $$

where $T[2]$ denotes the points of order $2$ of T. Similarly,

$$ \begin{align*}\mathrm{Sing}\,\widetilde{V} = \widetilde{X}^{\theta} \times T[2] = (E_{1}\times T[2]) \amalg\cdots\amalg (E_{k}\times T[2]). \end{align*} $$

Hence the $1$ -dimensional strata of $\mathrm {Sing}\,V$ (respectively, $\mathrm {Sing}\,\widetilde {V}$ ) consist of k-copies of the quotient $T/(-1)_{T}$ (respectively, $4$ -copies of $E_{1},\ldots ,E_{k}$ ), which are endowed with the flat orbifold Kähler form $\gamma _{T}$ (respectively, Kähler form $\gamma _{\widetilde {X}}|_{E_{i}}$ induced from $\gamma _{\widetilde {X}}$ ).

Recall from [46, (6.12)] that the orbifold BCOV invariant of V is defined by

(9.3) $$ \begin{align} \begin{aligned} \tau_{\mathrm{BCOV}}^{\mathrm{orb}}(V) &= T_{\mathrm{BCOV}}(V,\gamma)\mathrm{Vol}(V,\gamma)^{-3+\frac{\chi^{\mathrm{orb}}(V)}{12}}\mathrm{Vol}_{L^{2}}(H^{2}(V,{\mathbf Z}),\gamma)^{-1} \\ &\quad\times \prod_{i=1}^{k} \tau( \{ p_{i} \}\times (T/(-1)_{T}), \gamma_{T})^{-1}\mathrm{Vol}(T/(-1)_{T}, \gamma_{T})^{-1} \\ &= T_{\mathrm{BCOV}}(V,\gamma)\mathrm{Vol}(V,\gamma)^{-3+\frac{\chi^{\mathrm{orb}}(V)}{12}}\mathrm{Vol}_{L^{2}}(H^{2}(V,{\mathbf Z}),\gamma)^{-1} 2^{k}\tau( T, \gamma_{T})^{-\frac{k}{2}}, \end{aligned} \end{align} $$

where we used the facts $\tau (T/(-1)_{T},\gamma _{T}) = \tau (T,\gamma _{T})^{1/2}$ and $\mathrm {Vol}(T/(-1)_{T},\gamma _{T})=1/2$ to get the second equality and $\mathrm {Vol}_{L^{2}}(H^{2}(V,{\mathbf Z}),\gamma )$ is the covolume of the lattice $H^{2}(V,{\mathbf Z})_{\mathrm {fr}}:=H^{2}(V,{\mathbf Z})/\mathrm {Torsion}$ with respect to the $L^{2}$ metric induced by $\gamma $ . (In what follows, for a finitely generated ${\mathbf Z}$ -module M, we set $M_{\mathrm {fr}} := M/\mathrm {Tors}(M)$ .) For the definition of $\chi ^{\mathrm {orb}}(V)$ , see [46, (6.2)]. By [46, Prop. 6.2], $\chi ^{\mathrm { orb}}(V)$ coincides with the Euler characteristic of a crepant resolution of V. Similarly, we have

$$ \begin{align*}\begin{aligned} \tau_{\mathrm{BCOV}}^{\mathrm{orb}}(\widetilde{V}) &= T_{\mathrm{BCOV}}(\widetilde{V},\widetilde{\gamma}) \mathrm{Vol}(\widetilde{V},\widetilde{\gamma})^{-3+\frac{\chi^{\mathrm{orb}}(\widetilde{V})}{12}} \mathrm{Vol}_{L^{2}}(H^{2}(\widetilde{V},{\mathbf Z}),\widetilde{\gamma})^{-1} \\ &\quad\times \{\prod_{i=1}^{k}\tau(E_{i},\gamma_{\widetilde{X}}|_{E_{i}})\mathrm{Vol}(E_{i}, \gamma_{\widetilde{X}}|_{E_{i}})\}^{-4}. \end{aligned} \end{align*} $$

Let $q \colon X \times T \to V$ and $\widetilde {q} \colon \widetilde {X} \times T \to \widetilde {V}$ be the quotient maps. Let $H^{2}(X\times T, {\mathbf Z})^{+}$ (respectively, $H^{2}(\widetilde {X}\times T, {\mathbf Z})^{+}$ ) be the invariant subspace with respect to the $\iota \times (-1)_{T}$ (respectively, $\theta \times (-1)_{T}$ )-action on $X \times T$ (respectively, $\widetilde {X}\times T$ ). We define $H^{2}(X, {\mathbf Z})^{+}$ and $H^{2}(\widetilde {X}, {\mathbf Z})^{+}$ in the same way. Let $r:=\mathrm {rk}_{\mathbf Z} H^{2}(X, {\mathbf Z})^{+}$ and $\widetilde {r} := \mathrm {rk}_{\mathbf Z} H^{2}(\widetilde {X}, {\mathbf Z})^{+}$ . Then $\widetilde {r}=r+k=10+k$ . The maps of cohomologies

$$ \begin{align*}q^{*} \colon H^{2}(V,{\mathbf Z})_{\mathrm{fr}} \to H^{2}(X\times T, {\mathbf Z})^{+}_{\mathrm{fr}} = H^{2}(X,{\mathbf Z})^{+}_{\mathrm{fr}} \oplus H^{2}(T, {\mathbf Z}),\\[-42pt] \end{align*} $$

$$ \begin{align*}\widetilde{q}^{*} \colon H^{2}(\widetilde{V},{\mathbf Z})_{\mathrm{fr}} \to H^{2}(\widetilde{X}\times T, {\mathbf Z})^{+} = H^{2}(\widetilde{X},{\mathbf Z})^{+} \oplus H^{2}(T, {\mathbf Z}), \end{align*} $$

have finite cokernel. Let $\mathrm {disc}(H^{2}(X,{\mathbf Z})^{+}_{\mathrm {fr}})$ be the discriminant of the lattice $H^{2}(X,{\mathbf Z})^{+}_{\mathrm {fr}}$ with respect to the intersection pairing $\langle \cdot ,\cdot \rangle $ on $H^{2}(X,{\mathbf Z})_{\mathrm {fr}}\subset H^{2}(X,{\mathbf Q})$ . Namely, if $\{ {\mathbf e}_{1},\ldots ,{\mathbf e}_{r} \}$ is a basis of $H^{2}(X,{\mathbf Z})_{\mathrm {fr}}$ , then $\mathrm {disc}(H^{2}(X,{\mathbf Z})^{+}_{\mathrm {fr}}) := \det ( \langle {\mathbf e}_{i}, {\mathbf e}_{j} \rangle )$ . Obviously, $|\mathrm {Coker}\, q^{*}|$ , $|\mathrm {Coker}\, \widetilde {q}^{*}|$ , $\mathrm {disc}(H^{2}(X,{\mathbf Z})^{+}_{\mathrm {fr}})$ , $\mathrm {disc}(H^{2}(\widetilde {X},{\mathbf Z})^{+})$ depend only on k. Recall that the constant $C(k)$ was defined in equation (8.1), which is the kth power of the product of the normalised analytic torsion of the Eguchi-Hanson instanton and the analytic torsion of ${\mathbf P}^{1}$ endowed with the Fubini-Study metric, up to a universal constant.

Theorem 9.6. The following equality holds:

$$ \begin{align*}\frac{\tau_{\mathrm{BCOV}}^{\mathrm{orb}}(V)}{\tau_{\mathrm{BCOV}}^{\mathrm{orb}}(\widetilde{V})} = 2^{-k-4}C(k)^{8}\left(\frac{|\mathrm{Coker}\, q^{*}|}{|\mathrm{Coker}\, \widetilde{q}^{*}|}\right)^{-2} \left( \frac{|\mathrm{disc}(H^{2}(X,{\mathbf Z})^{+}_{\mathrm{fr}})|}{|\mathrm{disc}(H^{2}(\widetilde{X},{\mathbf Z})^{+})|} \right)^{-1}. \end{align*} $$

Proof. We express $T_{\mathrm {BCOV}}(V,\gamma )$ in terms of $\tau _{{\mathbf Z}_{2}}(X,\gamma _{X})(\iota )$ and $\tau (T,\gamma _{T})$ . As is easily verified, Lemmas 8.3–8.7 of [46] hold true for V without any change. Since $h^{1,1}(X)=20-k$ , the coefficient $21$ of $\zeta ^{T,+}(s)$ in [46, Lemma 8.8] should be replaced by $21-k$ . Hence, for V, the equality corresponding to [46, (8.28), p.357] becomes

$$ \begin{align*}\sum_{p,q}(-1)^{p+q}pq\,\zeta_{p,q}(s) = (24-k)\zeta^{T,+}(s) + 8\{ \zeta^{X,+}(s) - \zeta^{X,-}(s)\}. \end{align*} $$

As a result, we get the following equality as in the first equality of [46, (8.29), p.358]:

(9.4) $$ \begin{align} T_{\mathrm{BCOV}}(V,\gamma) = \tau_{{\mathbf Z}_{2}}(X,\gamma_{X})(\iota)^{-4}\tau(T,\gamma_{T})^{-(12-\frac{k}{2})}. \end{align} $$

By [46, (8.29), p.358 l.2-3], we have

(9.5) $$ \begin{align} T_{\mathrm{BCOV}}(\widetilde{V},\widetilde{\gamma}) = \tau_{{\mathbf Z}_{2}}(\widetilde{X},\gamma_{\widetilde{X}})(\theta)^{-4}\tau(T,\gamma_{T})^{-12}. \end{align} $$

Since $\widetilde {X}^{\theta }$ consists of k copies of mutually disjoint ${\mathbf P}^{1}$ , we get $\chi ^{\mathrm {orb}}(V) = \chi ^{\mathrm {orb}}( \widetilde {V} ) = \frac {1}{2}\chi (\widetilde {X}\times T) + \frac {3}{2}\chi ( \widetilde {X}^{\theta } \times T[2])=12k$ by [46, Prop. 6.1 and (6.3)]. Hence

(9.6) $$ \begin{align} \mathrm{Vol}(V,\gamma)^{-3+\frac{\chi^{\mathrm{orb}}(V)}{12}} = \mathrm{Vol}(V,\gamma)^{-3+k} = 2^{3-k}\,\mathrm{Vol}(X,\gamma_{X})^{-3+k}, \end{align} $$

where we used the fact $\mathrm {Vol}(T,\gamma _{T})=1$ and $\mathrm {Vol}(V,\gamma )=\mathrm {Vol}(X,\gamma _{X})\mathrm {Vol}(T,\gamma _{T})/2$ . Similarly,

(9.7) $$ \begin{align} \mathrm{Vol}(\widetilde{V},\widetilde{\gamma})^{-3+\frac{\chi^{\mathrm{orb}}(\widetilde{V})}{12}} = 2^{3-k}\,\mathrm{Vol}(\widetilde{X},\gamma_{\widetilde{X}})^{-3+k}. \end{align} $$

Let $\{{\mathbf f}_{1},\ldots ,{\mathbf f}_{r+1}\}$ be a basis of $H^{2}(V,{\mathbf Z})_{\mathrm {fr}}$ . By definition, we have

$$ \begin{align*}\mathrm{Vol}_{L^{2}}(H^{2}(V,{\mathbf Z}),\gamma)=|\det( \langle{\mathbf f}_{i},{\mathbf f}_{j}\rangle_{L^{2}} )|, \end{align*} $$

where $\langle \cdot ,\cdot \rangle _{L^{2}}$ denotes the $L^{2}$ inner product on $H^{2}(V,{\mathbf R})$ induced from $\gamma $ . Since $\mathrm {Vol}_{L^{2}}(H^{2}(T,{\mathbf Z}),\gamma _{T})=1$ , the same calculations as in [19, Lemma 13.4] yield that

(9.8) $$ \begin{align} \begin{aligned} \mathrm{Vol}_{L^{2}}(H^{2}(V,{\mathbf Z}),\gamma) &= |\mathrm{Coker}\,q^{*}|^{2}\,\mathrm{Vol}_{L^{2}}(H^{2}(X,{\mathbf Z})^{+}_{\mathrm{fr}}\oplus H^{2}(T,{\mathbf Z}),\gamma_{X}\oplus\gamma_{T}) \\ &= |\mathrm{Coker}\,q^{*}|^{2}\,\mathrm{Vol}_{L^{2}}(H^{2}(X,{\mathbf Z})^{+}_{\mathrm{fr}},\gamma_{X})\,\mathrm{Vol}(X,\gamma_{X})/2 \\ &= 2^{-(r+1)}|\mathrm{Coker}\,q^{*}|^{2}\,|\mathrm{disc}(H^{2}(X,{\mathbf Z})^{+}_{\mathrm{fr}})|\,\mathrm{Vol}(X,\gamma_{X}). \end{aligned} \end{align} $$

Similarly, we have

(9.9) $$ \begin{align} \mathrm{Vol}_{L^{2}}(H^{2}(\widetilde{V},{\mathbf Z}),\widetilde{\gamma}) = 2^{-(\widetilde{r}+1)}|\mathrm{Coker}\,\widetilde{q}^{*}|^{2}\,|\mathrm{disc}(H^{2}(\widetilde{X},{\mathbf Z})^{+})|\, \mathrm{Vol}(\widetilde{X},\gamma_{\widetilde{X}}). \end{align} $$

Substituting equations (9.4), (9.6) and (9.8) into equation (9.3) and using equation (3.7), we get

(9.10) $$ \begin{align} \begin{aligned} \tau_{\mathrm{BCOV}}^{\mathrm{orb}}(V) &= 2^{r+4}|\mathrm{Coker}\,q^{*}|^{-2}\,|\mathrm{disc}(H^{2}(X,{\mathbf Z})^{+}_{\mathrm{fr}})|^{-1} \\ &\quad\times \tau_{{\mathbf Z}_{2}}(X,\gamma_{X})(\iota)^{-4}\mathrm{Vol}(X,\gamma_{X})^{-4+k}\tau(T,\gamma_{T})^{-12} \\ &= 2^{r+4}|\mathrm{Coker}\,q^{*}|^{-2}\,|\mathrm{disc}(H^{2}(X,{\mathbf Z})^{+}_{\mathrm{fr}})|^{-1} \\ &\quad\times \tau(X,\gamma_{X})^{-4}\tau_{{\mathbf Z}_{2}}(X,\gamma_{X})(\iota)^{-4}\mathrm{Vol}(X,\gamma_{X})^{-4+k}\tau(T,\gamma_{T})^{-12} \\ &= 2^{r-k}|\mathrm{Coker}\,q^{*}|^{-2}\,|\mathrm{disc}(H^{2}(X,{\mathbf Z})^{+}_{\mathrm{fr}})|^{-1} \tau(Y,\gamma_{Y})^{-8}\mathrm{Vol}(Y,\gamma_{Y})^{-4+k}\tau(T,\gamma_{T})^{-12} \\ &= 2^{r-k}|\mathrm{Coker}\,q^{*}|^{-2}\,|\mathrm{disc}(H^{2}(X,{\mathbf Z})^{+}_{\mathrm{fr}})|^{-1}C(k)^{8} \tau_{M}(\widetilde{X},\theta)^{-4}\tau(T,\gamma_{T})^{-12}, \end{aligned} \end{align} $$

where we used the equality $\tau (Y,\gamma _{Y})^{2}=\tau (X,\gamma _{X})\tau _{{\mathbf Z}_{2}}(X,\gamma _{X})(\iota )$ to get the third equality and Theorem 8.3 to get the last equality. Similarly, substituting equations (9.5), (9.7) and (9.9) into [46, (6.12)], we get

(9.11) $$ \begin{align} \begin{aligned} \tau_{\mathrm{BCOV}}^{\mathrm{orb}}(\widetilde{V}) &= \tau_{{\mathbf Z}_{2}}(\widetilde{X},\gamma_{\widetilde{X}})(\theta)^{-4}\tau(T,\gamma_{T})^{-12} \{\prod_{i=1}^{k}\tau(E_{i},\gamma_{\widetilde{X}}|_{E_{i}})\mathrm{Vol}(E_{i}, \gamma_{\widetilde{X}}|_{E_{i}})\}^{-4} \\ &\quad\times 2^{3-k}\,\mathrm{Vol}(\widetilde{X},\gamma_{\widetilde{X}})^{-3+k} 2^{\widetilde{r}+1}|\mathrm{Coker}\,\widetilde{q}^{*}|^{-2}\,|\mathrm{disc}(H^{2}(\widetilde{X},{\mathbf Z})^{+})|^{-1} \mathrm{Vol}(\widetilde{X},\gamma_{\widetilde{X}})^{-1} \\ &= 2^{\widetilde{r}+4-k}|\mathrm{Coker}\,\widetilde{q}^{*}|^{-2}\,|\mathrm{disc}(H^{2}(\widetilde{X},{\mathbf Z})^{+})|^{-1}\tau(T,\gamma_{T})^{-12} \\ &\quad\times \tau_{{\mathbf Z}_{2}}(\widetilde{X},\gamma_{\widetilde{X}})(\theta)^{-4}\mathrm{Vol}(\widetilde{X},\gamma_{\widetilde{X}})^{-4+k} \{\prod_{i=1}^{k}\tau(E_{i},\gamma_{\widetilde{X}}|_{E_{i}})\mathrm{Vol}(E_{i}, \gamma_{\widetilde{X}}|_{E_{i}})\}^{-4} \\ &= 2^{r+4}|\mathrm{Coker}\,\widetilde{q}^{*}|^{-2}\,|\mathrm{disc}(H^{2}(\widetilde{X},{\mathbf Z})^{+})|^{-1} \tau_{M}(\widetilde{X},\theta)^{-4}\tau(T,\gamma_{T})^{-12}. \end{aligned} \end{align} $$

Comparing equation (9.10) and equation (9.11), we get the result.

We define the BCOV invariant of elliptic curve T as

$$ \begin{align*}\tau_{\mathrm{BCOV}}(T) := \mathrm{Vol}(T,\omega)^{-1}\,\tau_{\mathrm{BCOV}}(T,\omega)\, \exp\left[-\frac{1}{12}\int_{T} \log\left( \frac{i\,\xi\wedge\overline{\xi}}{\omega} \right)\,c_{1}(T,\omega)\right], \end{align*} $$

where $\omega $ is an arbitrary Kähler from on T. By [46, Th. 8.1], $\tau _{\mathrm {BCOV}}(T)$ is independent of the choice of $\omega $ and is expressed by the Petersson norm of the Dedekind $\eta $ -function. By definition, we have $\tau _{\mathrm {BCOV}}(T) = \tau (T,\gamma _{T})^{-1}$ . By equation (9.10), we have the following factorisation of the orbifold BCOV invariant of V.

Corollary 9.7. The following equality of BCOV invariants holds:

$$ \begin{align*}\tau_{\mathrm{BCOV}}^{\mathrm{orb}}(V) = 2^{r-k} |\mathrm{Coker}\,q^{*}|^{-2} |\mathrm{disc}( H^{2}(X,{\mathbf Z})^{+}_{\mathrm{fr}})|^{-1} \tau_{\mathrm{BCOV}}(Y)^{4}\tau_{\mathrm{BCOV}}(T)^{12}. \end{align*} $$

Proof. The result follows from equation (9.2) and the third equality of equation (9.10).

Remark 9.8. In [46, p.357 l.7], it seems that the equality $H^{2}(X,{\mathbf Z}) = H^{2}(S\times T,{\mathbf Z})^{+}$ does not hold in general. As the difference of these two quantities, $|\mathrm {Coker}\,\widetilde {q}^{*}|$ should appear in the formula for $\tau _{\mathrm {BCOV}}^{\mathrm {orb}}(\widetilde {V})$ as in equation (9.11).

Remark 9.9. In this subsection, for the sake of simplicity of notation, we adopt the definitions $\mathrm {Vol}(V,\gamma )=\int _{V}\gamma ^{3}/3!$ and $\langle \alpha , \beta \rangle _{L^{2}} = \int _{V} ({\mathcal H}\alpha ) \wedge \overline {*}({\mathcal H}\beta )$ , and so on, where ${\mathcal H}(\cdot )$ denotes the harmonic projection. If we follow the tradition in Arakelov geometry, it is more natural to define the $L^{2}$ -inner product by $\mathrm {Vol}(V,\gamma )=(2\pi )^{-\dim V}\int _{V}\gamma ^{3}/3!$ and $\langle \alpha , \beta \rangle _{L^{2}} = (2\pi )^{-\dim V}\int _{V} ({\mathcal H}\alpha ) \wedge \overline {*}({\mathcal H}\beta )$ , and so on. Notice that in [46], this latter definition is adopted.

Problem 9.10. Is the orbifold BCOV invariant [46] a birational invariant of Calabi-Yau orbifolds? (To our knowledge, it is still open that the BCOV invariant of KLT Calabi-Yau varieties [20] coincides with the orbifold BCOV invariant [46].) If the answer is affirmative, then it follows from Theorem 9.6 that the normalised analytic torsion of the Eguchi-Hanson instanton will essentially be given by the analytic torsion of ${\mathbf P}^{1}$ with respect to the Fubini-Study metric. Once a comparison formula for the BCOV invariants for birational Calabi-Yau orbifolds is obtained, then one will get a formula for the normalised analytic torsion of the Eguchi-Hanson instanton through Theorem 9.6.