The theory of frame ordering: observing motions in calmodulin complexes

Abstract

Large scale functional motions of molecules are studied experimentally using numerous molecular and biophysics techniques, the data from which are subsequently interpreted using diverse models of Brownian molecular dynamics. To unify all rotational physics techniques and motional models, the frame order tensor – a universal statistical mechanics theory based on the rotational ordering of rigid body frames – is herein formulated. The frame ordering is the fundamental physics that governs how motions modulate rotational molecular physics and it defines the properties and maximum information content encoded in the observable physics. Using the tensor to link residual dipolar couplings and pseudo-contact shifts, two distinct information-rich and atomic-level biophysical measurements from the field of nuclear magnetic resonance spectroscopy, to a number of basic mechanical joint models, a highly dynamic state of calmodulin (CaM) bound to a target peptide in a tightly closed conformation was observed. Intra- and inter-domain motions reveal the CaM complex to be entropically primed for peptide release.

Speculation

Extracting translational and rotational diffusive motion of molecules in the fields of biophysics and molecular physics from experimental data is an inverse problem. Today many of the most complex rotational models of this inverse problem derive from the Perrin (1934) and (1936) cornerstone publications on the Brownian diffusion of a free ellipsoid. We have extended Perrin's original work by describing the statistical mechanical ordering of a frame with time – or across an ensemble – attached to any part of a molecule. This fundamental theory results in a series of tensors that define the total physics content of all rotational biophysics and molecular physics techniques and facilitate the modelling of far more complex motions.

Introduction

Observing solution-state molecular dynamics (MD) is the key to understanding the fine details of how cellular machinery operates and how the energetics of macromolecules and flexible organic molecules influence their micro- to macroscopic properties. To this end there is not only a need to solve the three-dimensional (3D) structures of different dynamic states, but also to study the mechanics, distribution and fine control of the continuous Brownian transitions of the molecule between its infinite yet bounded states. Experimentally MD can be studied using diverse molecular physics techniques, many of which are modulated by stochastic rotational motions. Among others these include: dielectric dispersion (Perrin, 1934); fluorescence spectroscopy (Perrin, 1926, 1934, 1936; Weber, 1952; Belford et al., 1972); phosphorescence spectroscopy (Razi Naqvi et al., 1973; Austin et al., 1979); dynamic light scattering (Pecora, 1964, 1968); transient birefringence, linear dichroism, and optical rotation decay (Wegener et al., 1979); nuclear magnetic resonance (NMR) spectroscopy (Bloembergen et al., 1948; Woessner, 1962); and electron paramagnetic resonance spectroscopy (Freed, 1964). To extract the MD information from the ensemble or time averaged physics data, a statistical mechanical model of the underlying Brownian diffusion process is fit to the data.

For the global tumbling of a rigid molecule, the Einstein equations of Brownian molecular motion (Einstein, 1905) extended by Perrin for the free diffusion of an ellipsoid (Perrin, 1934, 1936) is an exact description for all rotational physics techniques. As this single ellipsoidal diffusion tensor is insufficient for multi-domain, tethered, or segmental rigid body motions, numerous mechanical joint models with varying internal degrees of freedom (DOF) have subsequently been developed. For two-domain molecules with a single-pivoted motion, time-dependent uniform distribution models of the Brownian diffusion tensor include: hinge models with one bending DOF (Harvey, 1979; Wegener, 1980); universal joints with two DOFs, equivalent to diffusion in a cone with no torsional motion (Wegener et al., 1980); the fully flexible universal joint with three DOFs as Euler angles {α, β, γ} and the torsion angle defined as α + γ (Wegener et al., 1980); and the hinged dumbbell model with three DOFs as one bending and two torsion angles {α, β ₁, β ₂} (Harvey et al., 1983; García de la Torre et al., 1985). The single pivot, 3DOF models are simply different parameterisations of the ball-and-socket or spherical mechanical joint. For three or more domains, one model includes the fully flexible universal joint extended to Y-shaped and double-jointed molecules (Wegener, 1982). For segmental motions in linear systems with multiple domains or rigid bodies, wormlike chain models are often used (Kratky and Porod, 1949).

Of all molecular physics techniques, NMR provides the greatest dynamic information content with multiple, independent sources of atomic-level information. Consequently many advanced statistical mechanical MD models specifically for NMR exist. For time-dependent, information-rich relaxation data, diverse two-domain models have been developed (Baber et al., 2001; Horne et al., 2007; Ryabov and Fushman, 2007; Wong et al., 2009). Using time-independent residual dipolar couplings (RDCs) and pseudo-contact shifts (PCSs), ensemble models for two-domain systems are often used (Bertini et al., 2004, 2007; Zweckstetter, 2008; Erdelyi et al., 2011; Yamamoto et al., 2011; Russo et al., 2013), sometimes incorporating non-rotational small-angle X-ray scattering (SAXS) data (Bertini et al., 2010). Ensemble sampling models for segmental motions in multi-domain systems and intrinsically disordered proteins using RDCs, SAXS and other data types have also been developed (Bernado et al., 2005; Nodet et al., 2009; Huang et al., 2014).

Despite the many advancements of the last century, MD modelling for analysing experimental data is in active development. To unify all rotational molecular physics data sources via individual mechanical models, herein a bridging and universal physics theory for single and multi-rigid-body motions will be developed based on the statistical mechanical ordering of reference frames – the frame order theory. The frame order link between model and experiment is established via equations for a single rotation matrix. A case study will be presented demonstrating multiple motional modes in a calmodulin (CaM)–peptide complex using experimental RDC and PCS NMR data.

Materials and methods

Sample preparation and NMR data collection

RDC and PCS values for CaM–IQ were previously measured (Russo et al., 2013) using the N60D CaM mutant from Bertini et al. (2003), and are presented in SI Section 7. In the N60D CaM system, a lanthanide ion can selectively bind to the second calcium binding site of the N-terminal domain. There are small structural changes at the lanthanide binding site which have been characterised previously by X-ray crystallography. They are so small that they are considered negligible. They also have no impact on the topic of this paper which is the long-range rigid body motions between domains and subdomains in a macromolecule. Mobile residues identified as those with published model-free order parameters (Frederick et al., 2007) less than 0.8 were excluded from the analysis (shown in SI Section 4 and listed in the frame order analysis script in SI Section 6.3).

Frame order theory for RDCs and PCSs

The RDCs and PCSs in molecules arise from the anisotropy of the magnetic susceptibility of the protein-attached paramagnetic lanthanide ions. In the case of RDCs the anisotropy of the magnetic susceptibility leads to alignment in the external magnetic field. PCSs are dominated by the anisotropy of the dipolar coupling between the anisotropic magnetic moment of the electron and the isotropic magnetic moment of the nuclear spin. The anisotropic magnetic moment of the electron is due to the anisotropy of the magnetic susceptibility of the lanthanide. Although linked by the anisotropy of the magnetic susceptibility of the lanthanide which causes both PCSs and RDCs to no longer average to zero, these anisotropic observables emanate from different physical processes and possess distinct MD information content. If rotational Brownian motions between the rigid bodies are present, then the lanthanide-tagged body exhibits the strongest alignment force in the magnetic field and the alignment of the non-lanthanide-tagged body is reduced by the MD. The RDC is a rank-2 dominated physical process due to the nuclear magnetic dipole–dipole coupling (see SI Section 1.2.1.1). It contains orientational information between two proximal atoms – the interatomic distance is generally known as covalently bonded atoms are primarily studied – and hence RDCs report on molecule-wide dynamic changes. In general, NMR parameters are considered to be local. However, RDCs and PCSs are global parameters that provide conformational restraints over infinite (RDCs) and long (PCSs) distances. This is due to the fact that, with paramagnetic metal ions, an alignment frame is created that is attached to a rigid molecular frame of a part of the molecule (in our case the N-terminal domain of CaM which carries the lanthanide). The orientation of all internuclear vectors is then related to this alignment tensor via the RDCs, irrespective of distance of these internuclear vectors from the metal ion. Thus the RDC is truly a long range (long = infinite) restraint. PCSs depend on the orientation and also the distance with an r ⁻³ dependence and therefore are shorter range but, depending on the metal, can reach up to 20–30 Å. The RDC can be expressed as

(1)$$D = d\hat{r}^{\rm T}\cdot A\cdot \hat{r},$$

where d is the magnetic dipole–dipole constant (Eq. (S33)), $\hat{r}$ is the interatomic unit vector between two adjacent spin-half nuclei, and A is the rank-2 symmetric and traceless molecular alignment tensor. As the fast vibrational and librational motions of the interatomic vector are statistically self-decoupled from the slower rigid body motions, the RDC due to a diminished frame ordering is

(2)$$D = d\hat{r}^{\rm T}\cdot {\overline A}\cdot \hat{r},$$

where $\overline{A}$ is the averaged and reduced alignment tensor. In contrast the PCS is due to the coupling of the nuclear magnetic dipole with the magnetic field induced by the lanthanide ion's unpaired electron (see SI Section 1.2.1.2). The PCS is a long distance constraint between the observed atom and lanthanide on the order of nanometres, containing both orientational and distance information – and hence it can report on global conformational changes. This global dynamic information content is however distinct from that of the RDC. The standard PCS value can be written as

(3)$$\delta = \displaystyle{c \over \left\vert {{r{\hskip-5pt}{\vskip1.7pt{_\sim}}}}_{\vskip-1pt{\rm LN}}\right\vert^5} \hat{r}_{{\rm LN}}^{\rm T} \cdot A\cdot \hat{r}_{\rm LN},$$

where c is the PCS constant, $\hat{r}_{{\rm LN}}$ is approximated by the lanthanide ion to nuclear unit vector, and $\vert {\mathop{r{\hskip-5pt}{\vskip1.8pt{_\sim}}_{\rm LN}}} \vert $ is the length of the vector (see Eq. (S35)). The PCS reduction is complicated by the inverse fifth power of the electron–nuclear distance which, unlike the RDC, is modulated by and coupled to the inter-body rotations. Hence the PCS is a convolution of rotational and translation information. As the decoupling of the ${\mathop{r{\hskip-5pt}{\vskip1.8pt{_\sim}}_{\rm LN}}}$ and A averaging is currently intractable and a reasonable approximation could not be found, instead a computationally expensive numerical integration was used to find an approximate solution by working around the frame ordering physics (SI Section 3). This low quality approximation circumvents the intrinsic frame order physics and in so slows the analysis by many orders of magnitude. It suffers from numerical precision artefacts especially for low amplitude modes of motions due to computational limitations resulting in non-uniform and inadequate sampling. The numerical sampling algorithm, model nesting simplification, and optimisation space simplification techniques employed – essential for speeding up the analysis – also decrease the quality of the results. Excluding optimisation and model failures (d'Auvergne and Gooley, 2006), observable in this analysis as a non-realistic average domain position far from expected or large steric clashes, for large amplitude motions the approximation would however be close to the exact result obtained from symbolic frame order equations. The rotation matrices of the numerical integration can be used to create a uniformly distributed ensemble of structures – and these structures will be bound by the same limits of the motional model used in the frame order matrix equation derivations (see ‘Frame order modelling of two domains’). As the same mathematical representation of motion is shared between the approximate numerical integration and the exact frame order matrix equations, the PCS and RDC analyses are hence compatible and the parameters of the mathematical model can be optimised simultaneously using both the PCS and RDC data.

Reduced alignment

The global molecular dynamic information in the RDCs and PCSs, excluding the PCS vector length modulation, is determined by the reduced alignment tensor $\overline{A}$. The alignment tensor averaging can be expressed as

(4)$$\overline{A} = \mathop \Bigg\langle \int \limits_0^{t_{{\rm max}}} R^{-1}\lpar {\Omega_t} \rpar \cdot A\cdot R\lpar {\Omega_t} \rpar {\rm d}t\Bigg\rangle$$

where the angular brackets denote the ensemble averaging, the time integration is for a single molecule over the evolution period of the physical interaction, and Ω _t are the three time-dependent angles describing the Brownian rotation of the rigid body. By writing this in index notation and rearranging, assuming that the molecular alignment and inter-body motions are not strongly coupled, the reduced alignment tensor can be seen to be linear combinations of the full alignment tensor multiplied by ᛞ⁽²⁾ frame order elements (Eqs (6) and (7) and SI Section 1.2.2). Using a rank-1, five-dimensional (5D) notation for the alignment tensors, this can be expressed as a product of a rank-2, 5D frame order superoperator, the elements of which are sums or differences of the ᛞ⁽²⁾ elements, and the original tensor (Eq. (S47)). Note that the alignment tensor is itself simply the anisotropic component of the first-degree frame order tensor ᛞ⁽¹⁾ (SI Section 1.2.3).

Integration of the RDC

Quadratic numerical integration is used for obtaining the frame order matrix elements of the pseudo-ellipse model, as symbolic integration for this model is intractable. However the surface area normalisation factor is simplified by series expansion to numerically implement a two-dimensional trigonometric function labelled the pseudo-elliptic cosine or pec(θ _x, θ _y) (SI Section 2.9.2).

Integration of the PCS

As the symbolic integration of the PCS is currently intractable due to the convoluted translational and rotational information, the frame order matrix equations derived in SI Section 2 are not applicable and numeric integration of the physical interaction must be used instead. Standard quadratic integration for the PCS over the three dimensions of the isotropic and pseudo-elliptic cones is however too computationally expensive. Instead, the orders of magnitude faster quasi-random integration technique using the Sobol’ point sequence (Sobol’, 1967) was used (SI Section 3.1.2). As Sobol’ point generation is slow, the points were oversampled and any points outside of the motional model half-angles where skipped and integration stopped once the desired number of points had been reached. Due to slow data transfer speeds between nodes, all attempts at parallelisation failed (SI Section 3.2). The most significant technique for speeding up the optimisation by many orders of magnitude is model nesting. As the most complex model consists of 15 parameters, an initial grid search for optimisation is not possible. Instead the optimised parameters from a simpler nested model are taken as the starting point for the more complex model and a grid search is only performed using the unique parameters of the complex model (SI Section 3.3). A number of other techniques were used to speed up optimisation including using a subset of measured PCS values for finding an initial solution (SI Section 3.4) and a few optimisation tricks including a lower quasi-random integration precision in the initial grid search, a zooming grid search, and a zooming precision optimisation where the number of Sobol’ points are increased (SI Section 3.5).

PCS structural noise

The analysis of the PCS is influenced by two significant sources of noise – the NMR experimental error and the structural noise associated with the 3D molecular structure. The closer the nuclear spin to the paramagnetic centre, the greater the influence of structural noise. This distance dependence is governed by the empirically derived equation:

(5)$$\sigma _{{\rm dist}} = \displaystyle{{\sqrt 3 \vert \delta \vert P_{{\rm RMSD}}} \over {r_{{\rm LN}}}},$$

where σ _dist is the distance standard deviation (SD) component of the structural noise, δ is the PCS value, P _RMSD is the atomic position root-mean-square deviation, and r _LN is the paramagnetic centre to spin distance. When close to the paramagnetic centre, this error source can exceed that of the NMR experiment. The equation for the angular component of the structural noise is however intractable, being influenced by distance, orientation in the alignment frame, and the magnetic susceptibility tensor geometry. Instead structural noise was simulated by randomising atomic positions 10 000 times over a multivariate normal distribution, back-calculating the PCS value using an alignment tensor calculated from the original data with the lanthanide position assumed fixed, and calculating the PCS SDs. This additional structural PCS error was combined with the experimental PCS error using variance addition.

The CaM–peptide reference frame

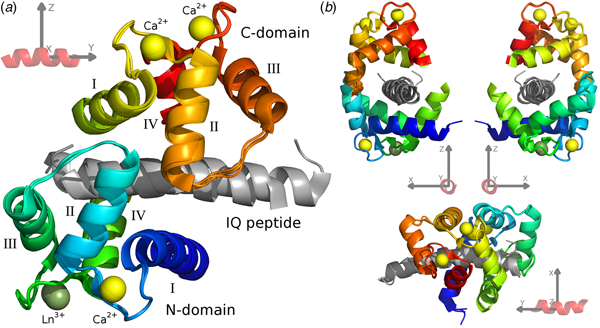
For the CaM–IQ complex, an imprecise reference frame can be defined by the common atoms of the three IQ peptides (Fig. 1). With an origin at the centre of the peptide, the positive and negative axes roughly point to the major structural features of the complex: the +x direction to the point of contact between the two closed domains, the CaM clamp opening; the −x direction to the melting point between the two domains; the ±y directions along the helical peptide axis; the +z direction to the centre of mass (CoM) of the C-domain; and the −z direction to the CoM of the N-domain.

Fig. 1. The CaM–IQ frame order average structure ensemble. (a) The 2BE6 X-ray crystallographic structure was broken into a non-moving body of the N-domain helices I and IV and calcium binding loops, and two moving rigid bodies for the frame order analyses – the N-domain helices II and III and interconnecting loop, and the C-domain – and the A, B, and C structures for each body superimposed. The moving bodies have been shifted to their motional average position. (b) Different orthogonal perspectives of a CaM–peptide reference frame used to visualise the MD. This synthetic frame is used to compare and describe the different CaM motions.

Frame order data analyses

The various two-domain motion models, linked via the frame order matrix to the RDC and PCS data, were optimised using software relax (d'Auvergne and Gooley, 2008). The optimisation space for the isotropic and pseudo-elliptic models contain multiple local minima which correspond to the permutations of the cone opening and torsion half-angles, hence axis permutations are used to sample all solutions (SI Section 2.13). Statistical model comparisons were performed with the gold standard for frequentist model selection – Akaike's information criterion (AIC) (Akaike, 1973; d'Auvergne and Gooley, 2003). Error analyses via Monte Carlo simulations were not feasible due to excessive computational times.

Pivoted motions in a structural ensemble

To compare with the single- and double-pivoted frame order models, a new protocol was designed to iteratively find all pivoted modes of motion in an ensemble of structures. This was applied to the A, B and C structures of the CaM–IQ X-ray ensemble (SI Section 5). The iterative Kabsch method for the fit-to-mean superimposition algorithm was modified so that the centroid position for translation and rotation of all structures is shared. The 3D position of the shared centroid or pivot point can be optimised by using the root-mean-square deviation (RMSD) as a maximum-likelihood estimate. One mode of pivoted motion can then be iteratively removed from the ensemble until no more rigid body motions are present. The full implementation is presented in SI Section 5.2.1.

Representations of the MD

Two new representations of MD have been developed to aid in the visualisation and comparison of different types of dynamics. The first is labelled as the ‘web-of-motion’ representation. This is used for ensembles of N structures where N is small. Here the equivalent heavy backbone atoms are connected using rods. The representation highlights the amplitudes, directions, and other features of the motions in 3D. The second representation is for an ensemble of N structures where N is large. The ensemble is simply shown with C_α backbone atoms shown as small spheres. The other backbone atoms are excluded to minimise clutter and not overwhelm the representation. This is used for the frame order results by approximating the MD using a uniformly distributed ensemble of 1000 structures.

Interatomic distance and parallax shift fluctuations

To decompose and visualise the motions in an ensemble of structures, two measures for comparing collections of atom pairs were devised – the interatomic distance fluctuations and the parallax shift fluctuations. These two measures of motions are close to orthogonal to each other and so represent different components of the motion. For the interatomic distance fluctuations, the corrected sample SD is calculated for the distances between each backbone C_α atom pair in the ensemble. The collection of all atom pairs produces a pairwise matrix of SD values which is frame and superimposition independent. The parallax shifts are calculated as the SD of distances between the interatomic vectors of an atom pair for all ensemble members and their projection onto their average vector. The parallax shift is calculated for the collection of all atom pairs, producing a pairwise matrix of SD values. This is a frame and superimposition dependent measure close to orthogonal to the interatomic distance fluctuations, assuming the interatomic vectors are not too divergent (it is orthogonal to the projection of the distance fluctuations onto the average vector). It is similar to an angle measure but, importantly, it is independent of the distance between the two atoms. For the frame order analyses, the uniform distribution models were approximated by discrete ensembles of 1000 structures generated by randomly selecting structures that satisfy the frame order model constraints.

Inter domain tensor comparisons

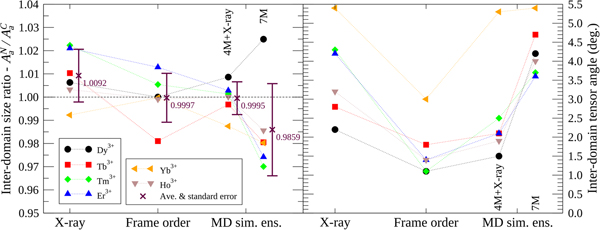
To compare the X-ray structures, frame order motional distributions and MD simulation ensembles, an inter-domain tensor comparison was performed (Fig. 5). In the reference frame of the N-domain, where alignment is strongest due to the bound lanthanide ion, full alignment tensors A ^C were predicted for the moving C-domain via an ensemble model. To this end, the structures were superimposed over the N-domain backbone heavy atoms and the full N-domain alignment tensors A ^N calculated using high precision lanthanide position optimisation with errors due to structural noise added to the PCS values. Within the same superimposition, the C-domain structures were then used to calculate a second alignment tensor A ^C with the addition of the PCS structural error but no lanthanide position optimisation. As this tensor calculation requires an ensemble of structures, the frame order uniform distribution models were roughly approximated using 1000 randomly selected structures. The frame order comparisons were tested on ensembles of 10 and 10 000 structures, but these suffered from counteracting sampling inaccuracy and numerical PCS truncation artefacts respectively (Fig. S86). Hence a perfect number of structures for the frame order ensemble approximation can never be reached and an extra error due to approximation is present in A ^C. If the ensemble model were a perfect description of the dynamics then, to within experimental error, the moving C-domain ensemble tensors should predict the non-moving N-domain tensors so that A ^C = A ^N. The N- and C-domain tensors are compared using two measures: the tensor size ratio defined as the ratio of anisotropic components A _a reflecting the absolute size of the traceless A tensors; and the inter-tensor angle. For the tensor size ratio A _a^N/A _a^C, the ideal value is one. This ratio however only includes one piece of geometric information from the five required to describe the symmetric and traceless tensor A. The inter-tensor angle measure is more comprehensive as it includes all of the geometrical and orientational tensor information. For the ideal model this angle should head to zero. Another error source of note is that these measures do not take the internal N-domain motions into account.

Data analysis

All theoretical derivations, experimental data, analysis scripts, and analysis methods are presented in the Supplementary Material.

Results

The theory of frame ordering

For a rigid body within a molecular system – ranging from single atoms all the way to molecular complexes – its orientational time dependence is described by the rotation matrix R(t) operating on the rigid body frame. To interpret the observed experimental data from rank-n rotational molecular physics processes, the frame order tensor is defined as

(6)$${\tf="TT58d178b9" \char "16DE}^{\left( n \right)}\left( t \right) = \overline {R^{\otimes n}\left( t \right)} .$$

The overbar is the statistical mechanics ensemble average, and ⊗n is the nth tensor power, or the outer product n times. It is a rank-2n, 3D orientational tensor describing the rotational ordering of the frame after time t. For a single molecule, an alternative frame order tensor is the time average of Eq. (6). The first-, second-, third-, and higher-degree frame order tensors {ᛞ⁽¹⁾, ᛞ⁽²⁾, ᛞ⁽³⁾, …} decompose the stochastic motions into elements that modulate rank-{1, 2, 3, …} physical processes. Depending on frame of reference and symmetries in the motions, only a subset of frame order matrix elements will be active and non-zero.

To drastically simplify the interpretation of frame order for non-freely diffusing rigid bodies, the time-dependent and independent components of the rotation matrix can be separated into transformation matrices as R(t) = E · F(t) · E ^T. The transformation E is from the motional average 3D position of the rigid body to the directional axes of the mechanical model (the motional eigenframe). As the starting 3D structure of the rigid body will not be at the average position, another time-independent component is required, namely the forwards rotation R _ave. The frame order tensor can then be expressed as

(7)$${\tf="TT58d178b9" \char "16DE}^{\lpar n \rpar }(t) = E^{\otimes n}\cdot \overline {F^{\otimes n}(t)} \cdot E^{{\rm T}\otimes n}\cdot R_{{\rm ave}}^{{\rm T}\otimes n}, $$

where T⊗n denotes the nth tensor power of the transposed matrix. When the directions of motion are orthogonal, as is often modelled, E and F are rotation matrices. In practice the 3D structure can be pre-rotated to the average position using R _ave.

The majority of rotational molecular physics techniques are dominated by rank n = 2 interactions and hence are modulated by the rank-4, second-degree frame order tensor ᛞ⁽²⁾. This tensor can be written as a 3D matrix of 3D matrices. The on-diagonal matrices are the second-degree ordering, or auto-correlations, of the frame axes to themselves whereas the off-diagonal matrices are the cross-correlations between the three axes. The frame order tensors are a logical extension of the non-zero subset of time-averaged rotation matrix elements and double-products $\overline {c_{ij}} $ and $\overline {c_{ij}c_{kl}} $ which appeared historically in Perrin's derivations (Perrin, 1936). These terms are the non-zero elements of ᛞ⁽¹⁾ and ᛞ⁽²⁾ from Eq. (6) under the condition of rigid-body free diffusion. Interestingly the free ellipsoid second-degree matrix starts as ᛞ⁽²⁾(0) = I ₁ and the matrix elements evolve mono-exponentially to ᛞ⁽²⁾(∞) = 1/3I ₂, where I _i are the rank-4 identity matrices (SI Section 1.5.1). When motions are more complicated than those of a free ellipsoid, Eqs. (6) and (7) drastically simplify the process of linking the dynamics model to the experimental physics. For the second-degree frame order tensor elements active for the rank-2 NMR processes of the experimental RDC and PCS data analysed herein, see the ‘Materials and methods’ section.

Frame order modelling of two domains

For the molecular two-body problem in which two rigid bodies are tethered by a flexible linker, the dynamics is represented by the spherical joint. This mechanical system consists of a single pivot point and three rotational DOF. Euler angles are a poor representation of this system so instead the more natural ‘tilt-and-torsion’ angles used for describing symmetrical spatial parallel mechanisms in the field of robotics was used (Korein, 1985; Crawford et al., 1999; Huang et al., 1999; Bonev and Gosselin, 2006) (SI Section 2.1.2). Starting with the z–y–z Euler angles {α, β, γ}, the torsion angle is defined as σ = α + γ, as in the fully flexible universal joint (Wegener et al., 1980), and the tilt angles are θ = β and ϕ = γ. The advantage of this angle system is that the mechanics of the tilt and torsion can be modelled independently. Three simple uniform distribution models of the torsion angle twisting include a restriction to within the opening half-angle ±σ _max, the torsionless model with the complete restriction of σ _max = 0, and the free rotor with unrestricted torsions. The tilt component was also modelled using simple uniform distributions including complete rigidity, an isotropic cone with an opening half-angle θ _max, and a pseudo-elliptic cone with maximum opening half-angles θ _x and θ _y. Nine different models were created as all combinations of the tilt and torsion submodels and were labelled as the rigid, rotor, free rotor, isotropic cone (normal, torsionless and free rotor), and pseudo-ellipse (normal, torsionless and free rotor). Additionally a more complicated double-pivoted motional system, the double rotor, was modelled using two torsion angles (Fig. S1). The full set of model parameters can be partitioned into the average domain position (translation and rotation), the pivot point(s), the motional eigenframe, and the half-angles restricting the MD (SI Sections 1 and 2). The use of a motional pivot allows for some translational freedom in the domains to be modelled, however not all of the uncoupled translational DOF can be modelled. In the case of CaM–IQ inter-domain motions, the PCS values for the non-tagged domain are less than 1 ppm, with most being below 0.3 ppm (Table S9). The result of this, together with the combined fixed 0.1 ppm NMR spectral errors and structural noise, is that the modelling of uncoupled translational freedom is not stable. More precise PCS and structural data would be required.

For each model, a rotation matrix within the motional eigenframe is defined using the active tilt-and-torsion parameters (Eq. (S74c)). The RDCs and PCSs are both time and ensemble averaged, hence devoid of time information, so the frame order tensor at t = ∞ is used (see the ‘Materials and methods’ section). As the models are uniform distributions, ᛞ⁽ⁿ⁾ is simply the normalised surface integral of the nth tensor power of the rotation matrix, within the limits of the motional model. The frame order ᛞ⁽¹⁾ and ᛞ⁽²⁾ equations for the models are presented in SI Section 2 and implemented in version 4 of the software relax (d'Auvergne and Gooley, 2008).

CaM–IQ X-ray structure and MD simulation

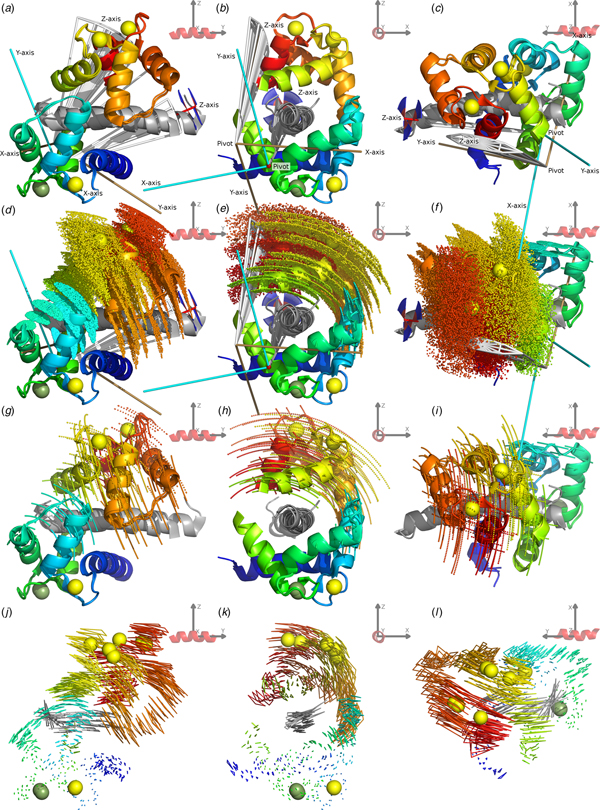
To demonstrate the frame order modelling, the 2BE6 X-ray crystallographic structure (Van Petegem et al., 2005) of CaM bound to the helical IQ domain of the Ca_V1.2 voltage-gated calcium channel was studied. The CaM–IQ X-ray structure consists of three distinct states A, B and C. These states are also seen in solution and the absence of separate peaks in the NMR spectrum for each state implies fast interconversion between these and additional states as found in Russo et al., (2013). For reference, a labelled representation of the CaM–IQ complex is shown in Fig. 1. To better understand this MD, a frame and superimposition dependent, iterative, pivoted motion finding algorithm was designed (see ‘Materials and methods’, ‘Pivoted motions in a structural ensemble’ and SI Section 5.2). Two dependent modes of motion were found in the reference frames of both the N- and C-domains (Figs 2, S35, S36). The primary mode has a mechanical pivot located within the non-moving domain and a rotation axis perpendicular to the axis between the two domains – it is a sliding of the moving N-domain over the peptide and non-moving C-domain, obliquely crossing the peptide axis. The secondary mode has its pivot located within the moving N-domain close to its CoM with an axis almost perpendicular to both the inter-domain axis and the peptide axis – it is the domain rolling along the IQ peptide. From the interatomic distance and parallax shift fluctuations (Figs 2f and i, S38, S39, S40), it is clear that the C-domain together with the IQ peptide form a rigid core, that intra-domain motion occurs in the loop between helices II and III and the termini of the N-domain, matching the direction of the secondary inter-domain motions (Fig. 3), and that the inter-domain contact point near the centre of both domains remains in a closed state. This agrees with the higher affinity of the C-domain for the target peptide (Van Petegem et al., 2005).

Fig. 2. The CaM–IQ 2BE6 X-ray crystallographic structure motions. (a–c) The C-domain backbone heavy atom superimposed structures A, B and C displayed from three different CaM-frame orientations. The N-domain Ca²⁺ atom positions show the primary motional mode of the domain sliding obliquely over the IQ peptide and non-moving C-domain. (d, e) The web-of-motion representation with equivalent backbone heavy atoms connected in the three crystal structures. This new representation enhances the visualisation of the primary motional modes. The C-domain superimposition best highlights the double-pivot motional system as found using a new iterative, pivoted motion finding algorithm. (g, h) The residual orthogonal motions after the first pivoted motion has been subtracted. This perpendicular secondary motional mode is a rolling of the N-domain over the IQ peptide. (f, i) Backbone C_α interatomic distance and C-domain superimposed parallax shift fluctuations respectively (see the ‘Materials and methods’ section). These inter-atom measures are a new type of representation that demonstrate the rigid C-domain and IQ peptide core, the inter and intra N-domain motions, and the maintenance of the closed CaM state.

Fig. 3. Combined CaM–IQ frame order dynamics (a–i) compared with the X-ray structure motions (j–l). The two rigid body frame order models consist of the C-domain moving as a pseudo-ellipse and the N-domain helices II, III and connecting loop moving as a torsionless pseudo-ellipse. (a–c) Geometric representations of the two pseudo-ellipse models, showing the pseudo-elliptic cones, z-axis torsional restriction (for the C-domain), motional eigenframes, and pivot points. (d–f) Distribution representation using 1000 uniformly distributed states, shown via the C_α atom positions displayed as small spheres. (g–i) Decomposition of the distributions in (d–f) showing equally spaced states solely along the motional eigenmodes, defined as the rotations about the motional eigenframe's axes. These motions are animated in the SI movies. (j–l) X-ray motions seen from the N-domain helices I and IV and calcium binding loop rigid body frame (with backbone heavy and Ca²⁺ atoms superimposed) represented as a web-of-motion, whereby equivalent backbone heavy atoms are connected between the three crystal structures. The correlation of the frame order motions is evident by the almost matching amplitude and direction of motional modes at the inter-domain contact point, as well as the similar position and orientation of the optimised pivot points and eigenframes. In the frame of the rigid C-domain, these motions would translate as the N-domain moving over the IQ peptide, opening as it slides towards the contact point.

In the CaM–IQ ensemble analysis using MD simulations and measured RDC and PCS data (Russo et al., 2013), two seven-state ensembles were created with simulation snapshot selection via quality (Q) factor optimisation: the X-ray structures with four simulation structures (4M + 2BE6); and seven simulation structures (7M). From the visual representation in the original publication and Figs S81 and S82, the primary inter-domain motional mode can be seen to be almost parallel to but with a slight rolling over the IQ peptide axis.

CaM–IQ motions were also predicted via Gaussian network models (SI Section 15) using the iGNM server (Li et al., 2016).

CaM–IQ frame order motions

Using the published RDC and PCS data (Russo et al., 2013), multiple frame order analyses were performed to identify and investigate two major motions – the CaM inter-domain motions and the N-domain sub-domain rigid body motions. To significantly improve the robustness to outlier PCS values, an extra error due to structural noise was simulated and added to the experimental PCS errors (see the ‘PCS structural noise’ section). For the analysis it is important to take this additional positional error in the 3D structures into account as it shifts the optimised lanthanide position away from the true position due to proximal atoms exhibiting the greatest errors with a hyperbolic distance dependence (Eq. (5)). A biased lanthanide position has a large effect on the optimised alignment tensor for the PCS but no effect on the RDC alignment tensor. The structural error contribution to the RDC results in an overall decrease in alignment tensor size (Zweckstetter and Bax, 2002). This structural noise effect is much smaller than the lanthanide position bias, and the generous 1 Hz RDC errors should cover the combined NMR spectral and structural noise components. The current analysis is also based on the differences in alignment between different domains and, as the effect of structural noise on RDC derived alignment tensors should be the same for all domains of the molecule, this noise is not expected to influence the results. Structural noise was also minimised by breaking the CaM–IQ structures into domains, superimposing the individual A, B and C components, and using the resultant ensemble of three structures. For the N-domain frame to which the lanthanide ion is bound, a per-lanthanide three-state ensemble analysis using the RDC and PCS data was performed on the superimposed X-ray structures to obtain the full A _i alignment tensors (d'Auvergne and Gooley, 2008). The input data for the frame order analyses consisted of the moving domain RDCs and PCSs together with the full A _i tensors. The ten tilt-and-torsion mechanical models were then optimised for the single A, B, and C structures and different superimposed ensembles of ABC (SI Section 10).

For the inter-domain motions, using AIC (Akaike, 1973; d'Auvergne and Gooley, 2003) the most parsimonious model was judged to be the rotor model (Table S11). However, the more complex pseudo-ellipse model was chosen as more physically meaningful, it has a similar optimised χ ² value yet consists of multiple modes of motion. The primary frame order MD mode in both models is identical, matching the X-ray mode – an oblique sliding of the moving domain over the peptide and non-moving domain, with a mechanical pivot in the core of the non-moving domain (Figs 2 and 3, S36, S67, S68). The minor secondary mode is the domain sliding along the peptide axis rather than rolling along it as in the X-ray ensemble. This is similar to the 4M + 2BE6 and 7M MD simulation ensemble primary mode. Although the double rotor can model the exact X-ray MD, including the secondary rolling, this motion is not supported by the NMR data. The amplitude of inter-domain motions is significantly greater than in the X-ray ensemble (Fig. 3, S36, Tables S5, S6, S19). The almost parallel rotations between the X-ray states for the first N-domain motional mode are {9.0°, 9.7°, 16.3°}, whereas the pseudo-ellipse torsion and cone half-angles are {σ _max, θ _y, θ _x} = {29.2°, 8.2°, 0.7°}. The pseudo-ellipse torsion angle hence produces a distribution of domain rotations greater than any of the X-ray structure rotations (Fig. 3).

Based on the internal motions in the X-ray ensemble (Fig. 2c), the N-domain was split and the whole CaM system analysed as a three segment rigid-body problem. Two frame order analyses were performed using different N-domain subdivisions – helices II and III and their connecting loop as the moving body, and helices I and IV moving together as a single unit. Using whole-protein combined AIC values, the first was judged to be the best fit to the data (Table S43). Model elimination based on RMSDs to the X-ray structures was essential for removing failed models (d'Auvergne and Gooley, 2006) prior to selecting the torsionless pseudo-ellipse (Table S33). The mechanical pivot and localisation of the MD are similar to the X-ray ensemble intra N-domain motions, yet the directions of the main modes of motion are different and the amplitudes are much greater (Figs 2 and 3, S76, S77). These motions are weaker or almost absent in the 4M + 2BE6 and 7M ensembles respectively (Fig. S83).

In both the inter- and intra-domain cases, the individual domain ABC superimposed structural ensembles statistically improved the fit in comparison with the individual structures due to the minimisation of structural noise. For the inter-domain motions the results for the structures and ensembles were comparable however for the smaller displacements of the intra N-domain motions the choice of structure or ensemble is significant (see all result tables in SI Section 10). Implicit in this analysis is the quality of the input structures, and that these input structures need have no relationship with the conformation landscape. Hence a single high quality structure is sufficient. In this case however the use of multiple structures improved the quality of the fit and allowed for finer motional details to be extracted. To validate the models chosen using AIC, the results were compared with the Bayesian information criterion (Schwarz, 1978) in Tables S11b, S24b, and S34b. The Bayesian-based statistic made no difference to the final models selected.

For the individual moving body CaM–IQ frame order results, no steric clashes were observed. The validation of the results by checking the metal position as in Russo et al. (2013) is not possible as the measure is not statistically independent in this analysis. The metal position is optimised using the N-domain data (see the ‘PCS structural noise’ section). It is then fixed and the frame order analysis predicts the reduced tensors using the full N-domain tensors for the C-terminal domain, i.e. the problem is implicitly constructed so that the full tensors for the N and C domains are one and the same. Hence the metal position and frame order results are statistically linked.

Discussion

Frame order

The theory of frame ordering developed in this paper is a new way of representing the fundamental aspects of rotational biophysics. It is the exact statistical mechanical description of the physics of how certain motions modulate the biophysical laboratory measurements. These motions are the real molecular dynamics, here abbreviated as MD – which should not be confused with their in silico prediction (MD simulation). Knowledge of the underlying physics is not necessary for modelling MD using biophysical measurements. However understanding the concept of frame order would significantly facilitate motional model development. Separately deriving the frame order equations for a dynamics model and the frame order based equations for each biophysical process simplifies the linking of complex models to the observables. Successful derivations of both components results in a direct set of equations linking the model to experiment, enabling standard and relatively fast non-linear optimisation of the model parameters. To avoid over-fitting the data, the frame order matrices can also be simulated to see if all aspects of the complex model affect the observables, as the frame order matrices contribute significantly to the inherent information bottleneck. Assuming complementary biophysical data can be measured, a simple extension of matrices of Eqs. (6) and (7) to include translation and skew information would allow for both orientational and translational processes to be studied.

For rank-1 biophysical processes, frame ordering can be visualised as a series of frames attached to different parts of a molecule. These frames match the order matrix at time zero, whereby the axes are of unit length. The presence of motions causes the ordering in certain directions to decrease with time. At infinite time – the often observed statistical mechanical average in a sample – the average axes of the frames may no longer be of unit length. The lengths will correspond to the eigenvalues of the order matrix (which in this case is the rank-2 first degree frame order matrix minus the identity matrix). For unrestricted motions all lengths would head to zero. If the motions are global, such as with free or constrained molecular diffusion, all of the frames attached to the molecule loose order equally. But if the motions are internal, different frames would have different reduced axis lengths. These reductions in the ordering of the frame directly modulate the rotational biophysics observables. For rank-2 biophysical processes, the time-dependent frame order matrices are the totality of the auto- and cross-correlation functions of the frame axes. The matrices at infinity are the plateaus of these correlation functions. There are 3⁴ = 81 correlation functions, though symmetry aspects of frame order, biophysical processes, and motions decrease the number of unique functions. In the context of modelling domain motions using non-local, multiple atom biophysical data, solely the theory of maximum occurrence (MO) has been developed (Bertini et al., 2004, 2007, 2010; Longinetti et al., 2006; Dasgupta et al., 2011). MO analyses RDC and PCS NMR data and optionally small angle X-ray scattering data, and the theory has been developed using data measured from the CaM N60D mutant for specific lanthanide binding (Bertini et al., 2003). This inverse problem modelling produces a map of the conformational space showing the maximum percentage of time for individual conformations. In the context of frame ordering, the physics of the rank-2 second degree matrix governs the topological uncertainty present in the MO conformational map due to components of the domain motions not being present in the measured data. Further approaches rely on MD simulation or Monte Carlo approaches (which is not guaranteed to be exhaustive) and then selecting subensembles which best fit the data to use for cross validation (Russo et al., 2013). Or the use of the MEDUSA multiconformational search algorithm for generating an ensemble of structures that fulfil the data (Blackledge et al., 1993).

CaM–peptide motions

The combined three segment whole-protein CaM–IQ frame order motions show strong consistencies between the two moving rigid bodies (Figs 3, S79, S80, SI movies), with close to collinear motional eigenframes, similarly positioned pivots and comparable amplitudes and directions of motion sliding over the IQ peptide. This implies that the inter-domain C-domain motions and N-terminal intra-domain helices II, III and connecting loop motions are one and the same. The minor differences are hypothesised to be due to experimental error as the propagation of uncertainty was computational infeasible to calculate. Although motional correlation information is absent from the NMR data, the motional average structure in the closed state implies strong correlations. This is because large scale decorrelated motions of the rigid bodies can be ruled out as only motions away from each other are sterically possible but this would result in a non-observed partial opening of the average structure (Fig. 1). In addition the contacting C-terminal ends of helix II in both domains have similar RMSDs (Fig. 4), the difference of 1.3 Å being easily bridged by side chain motions across the closed CaM clamp. This correlation is weakly present in the X-ray structures but absent from the MD simulation ensembles. The Gaussian network modelling also indicates some inter-domain correlation, though this is to be expected due to the elastic constraints applied across the inter-domain clamp opening implicit in analysing a closed CaM–IQ structure (SI Section 15). Comparing all ensembles, the three segment frame order analysis roughly approximated by a two-domain ensemble model, although similar to the 4M + 2BE6 ensemble for the tensor size ratio, best predicts the full moving domain alignment tensors (Figs 5, S86). Movies for the three rigid bodies moving linearly along the three motional eigenmodes of the frame order results are presented in Supplementary Movies S1, S2, and S3. These are in the reference frame of the N-domain helices I and IV and calcium binding loops and are simply animated versions of Figs 3g–i. Correlated rather than anti-correlated movements along the eigenmodes are shown as the anti-correlated versions result in significant overlap and steric clashes of the structures. Internal flexibility, which can account for the gaps between amino acid residues in the animation at the outer part of the distribution, has not been modelled and hence is not shown.

Fig. 4. Backbone C_α RMSDs in the N-domain helices I and IV frame of CaM–IQ using ensemble-based models, highlighting entropic differences. In the frame order analyses, approximated by 1000 structures, the inter-domain contact points near the centre of both domains have similar RMSDs. This allows the protein to remain in a closed state while the atoms furthest from the motional pivot in the N-domain move the greatest extent. The large pool of entropy in the closed CaM state decreases the entropic change ΔS between the peptide-bound and free forms of CaM, facilitating peptide release.

Fig. 5. Inter-domain alignment tensor comparison of CaM–IQ. Using ensemble-based models/approximations, the two A tensors in the non-moving frame ideally should match (see the ‘Materials and methods’ section). For the tensor size ratio measure A _a^N/A _a^C, which uses a single piece of geometric information, the average value is closest to the ideal of one for the frame order ensemble approximation but the deviations are smallest for the 4M MD simulation + X-ray 2BE6 ensemble. For the inter-tensor angle, which includes all five independent pieces of alignment tensor information, compared with the X-ray, 4M + X-ray, and 7M ensembles, the frame order angles are closest to the ideal of zero for all tensors.

From the perspective of the rigid core frame of the C-domain and IQ peptide, all motions are localised within the N-domain. As this domain moves in the +x direction of the clamp opening, the correlation of the motions results in the inter-helix angles of two N-domain EF-hands being sterically forced open. Propagating through the semi rigid α-helices via hydrogen bonds to the Ca²⁺ coordination centres, this forms a mechanical lever prying open and adding entropy to the N-domain coordination sites, decreasing their Ca²⁺ binding affinity.

Due to the pool of conformational entropy in the closed CaM–IQ complex (S _pool), compared with a rigid complex a much smaller entropy change (ΔS) is required for peptide binding and dissociation. Together with the weakened Ca²⁺ binding affinity, this primes the system for peptide release. The mechanical model also implies that the N-domain interacting residues of the CaM target peptides would control the size of S _pool. As the Gibbs free energy is similar for the different CaM–peptide complexes, ΔG = ΔH − TΔS ≈ − 50 kJ mol⁻¹ (Frederick et al., 2007), the regulation of S _pool is hypothesised to contribute significantly to the diversity of CaM binding entropies (ΔS) and compensating binding enthalpies (ΔH). The total value of S _pool was not estimated as, to be able to compare to measured ΔS values, the large contribution due to changes in the complex, multi-layered hydration shell needs to be separated from ΔS. This is however currently not feasible.

Frame order analyses were also performed on free CaM (Dasgupta et al., 2011) however the low data quality rendered the results too noisy to make any conclusions, and on the CaM–DAPk and CaM–DRP1p peptide complexes (Bertini et al., 2009) in which the observed motions were statistically insignificant (SI Sections 12, 13, 14). Hence frame order modelling solely using RDCs and PCSs requires high quality data and is insensitive to very low amplitude motions.

The current analysis is computationally expensive due to the numerical integration of the PCS circumventing the frame order physics. The derivation of an approximate PCS solution allowing for a symbolic representation of the frame order tensors would have a significant impact on the quality and modelling capabilities of the analysis and would decrease the non-parallelisable computation time by many orders of magnitude (see SI Section 3). The symbolic solution would also allow for deep insights into the inverse problem, including an understanding of which components of the MD can or cannot influence the experimental data. And the elimination of numerical precision, sampling, model nesting, and optimisation space simplification artefacts would allow for more motional information to be reliably extracted from the data.

The uniform distributions of the torsion angle and tilt component in the current set of models are an approximation for modelling the primary modes of motion of the macromolecule, specifically the direction, amplitude, and anisotropy of the motions. In the future, higher modes of motion could be modelled to reproduce more of the conformational landscape, for example using a Gaussian distribution and then adding higher moments including skew and kurtosis. Alternative decompositions of the complex distribution of ensemble of states might also yield useful information about the motion. However whether or not information about these higher modes of motion is present in the experimental data would need to be carefully validated. In the above modelling, steric clashes are not excluded in order to avoid artificial bias that certain parameter constraint algorithms can introduce. Steric clash based structure selection is only possible using the approximate PCS numerical integration algorithm and is not compatible with the continuous, non-ensemble model of the frame order matrix equations. Hence the final results were manually checked for any such issues. Note that a minor steric clash could either be a result of the simplistic modelling of a uniform distribution not taking higher modes of motion into account or simply due to the loss of motional information in the frame order averaging process resulting in the higher modes of motion not being present in the experimental data. As the modelling herein decomposes the MD into components of higher and higher order for the increasingly complex models, the final result should be considered not as the exact motion of the macromolecule but rather a representation of the simplest modes of that motion, and importantly those components that survive the averaging induced by the frame ordering process.

Implications for molecular physics

In summary, the statistical mechanics rank-2n frame order tensor is the universal physics theory linking the motional model to all rotational molecular physics techniques. The frame ordering defines the totality of the rotational MD information content of an experiment and the characteristics of that information. Only two steps are required to link the MD model to experimental data – the physics is first broken down in terms of frame order tensor elements, and then the MD model is expressed as a rotation matrix and converted to a frame order matrix. This was performed symbolically for rank-2 RDC data and numerically for multi-rank PCS data, both from the field of NMR, using rotor, double rotor, isotropic cone, and pseudo-elliptic cone models. Applying this to the CaM–IQ complex, a correlated inter-domain and intra N-domain motion was observed. The CaM clamp does not open despite the large scale internal motions, showing that the target peptide can regulate the entropic priming of its own release.