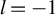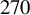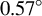1 Introduction
The construction of numerous high-power laser systems around the world[ Reference Danson, Haefner, Bromage, Butcher, Chanteloup, Chowdhury, Galvanauskas, Gizzi, Hein, Hillier, Hopps, Kato, Khazanov, Kodama, Korn, Li, Li, Limpert, Ma, Nam, Neely, Papadopoulos, Penman, Qian, Rocca, Shaykin, Siders, Spindloe, Szatmári, Trines, Zhu, Zhu and Zuegel 1 – Reference Li, Leng and Li 4 ] has enabled the development of novel particle (see reports of Bulanov et al.[ Reference Bulanov, Esarey, Schroeder, Bulanov, Esirkepov, Kando, Pegoraro and Leemans 5 ] and Esarey et al.[ Reference Esarey, Schroeder and Leemans 6 ] and references therein) and radiation sources[ Reference Nakamura, Koga, Esirkepov, Kando, Korn and Bulanov 7 – Reference Capdessus, King, Del Sorbo, Duff, Ridgers and McKenna 12 ] for multidisciplinary applications[ Reference Bulanov, Wilkens, Esirkepov, Korn, Kraft, Kraft, Molls and Khoroshkov 13 , Reference Weeks, Litvinenko and Madey 14 ]. Most of the improvements of the laser beams used for driving laser–matter interactions have been focused on increasing power, on-target intensity, total energy and the contrast of the compressed pulse. For example, the proposed facility[ Reference Bu, Xu, Xu, Ji, Li and Xu 3 , Reference Li, Leng and Li 4 ] that aims to cross the 100 PW limit is expected to be in development over the next decade. Concurrently, new optical techniques for producing helical wave-fronts[ Reference Leblanc, Denoeud, Chopineau, Mennerat, Martin and Quere 15 – Reference Porat, Lightman, Cohen and Pomerantz 20 ] are also being developed. There now exist multiple computational[ Reference Longman and Fedosejevs 17 , Reference Vieira, Trines, Alves, Fonseca, Mendonça, Bingham, Norreys and Silva 21 – Reference Blackman, Nuter, Korneev and Tikhonchuk 29 ] and experimental[ Reference Leblanc, Denoeud, Chopineau, Mennerat, Martin and Quere 15 , Reference Longman, Salgado, Zeraouli, Naniz, Pérez-Hernández, Eltahlawy, Volpe and Fedosejevs 18 , Reference Denoeud, Chopineau, Leblanc and Quéré 30 – Reference Aboushelbaya, Glize, Savin, Mayr, Spiers, Wang, Bourgeois, Spindloe, Bingham and Norreys 32 ] studies examining interactions of helical laser beams with plasmas. There are also some published works on the terawatt scale helical laser production using a chirped-pulse amplification system[ Reference Pan, Liang, Yu, Wang, Li and Li 19 , Reference Chen, Zheng, Lu, Wang, Cai, Wang, Zheng, Ai, Leng, Xu and Fan 33 ]. Even though the techniques for creating helical beams with higher power are yet to be applied at high-power high-intensity laser facilities, they offer an exciting opportunity to create laser pulses with a qualitatively different field typology that can have a profound impact on laser–plasma interactions and particle acceleration.
There are several laser-based electron acceleration approaches with different degrees of maturity. The most frequently used ones are laser wakefield acceleration[ Reference Esarey, Schroeder and Leemans 6 ], which utilizes plasma electric fields, and direct laser acceleration[ Reference Gibbon 34 ], which relies on the fields of the laser for the energy transfer inside a plasma (e.g., see the report of Arefiev et al.[ Reference Arefiev, Khudik, Robinson, Shvets, Willingale and Schollmeier 35 ]) or in vacuum[ Reference Stupakov and Zolotorev 36 ]. These mechanisms are typically realized using conventional laser pulses. In an attempt to improve electron acceleration, several studies also considered radially polarized laser beams[Reference Zïam, Thévenet, Lifschitz and Faure37] and higher-order Gaussian beams[Reference Sprangle, Esarey and Krall38]. Recently, there has been an increased interest in utilizing ultra-high-intensity laser beams with helical wave-fronts for electron acceleration in various setups, including vacuum acceleration[Reference Shi, Blackman, Stutman and Arefiev39–Reference Pae, Kim, Pathak, Ryu and Nam42], laser wakefield acceleration[Reference Vieira and Mendonça43, Reference Zhang, Chen, Schroeder, Luo, Zeng, Li, Yu, Weng, Ma, Yu, Sheng and Esarey44] and microstructural target electron acceleration[Reference Hu, Yu, Lu, Zhang, Zou, Zhang, Ge, Yin and Shao 45 ].
Conventional high-power laser systems[
Reference Danson, Haefner, Bromage, Butcher, Chanteloup, Chowdhury, Galvanauskas, Gizzi, Hein, Hillier, Hopps, Kato, Khazanov, Kodama, Korn, Li, Li, Limpert, Ma, Nam, Neely, Papadopoulos, Penman, Qian, Rocca, Shaykin, Siders, Spindloe, Szatmári, Trines, Zhu, Zhu and Zuegel
1
] generate linearly polarized (LP) laser beams without a twist to the laser wave-fronts, which prevents one from readily realizing the interactions utilizing ultra-high-intensity helical laser beams. The spatial structure of laser beams with helical wave-fronts can be viewed as a superposition of Laguerre–Gaussian (LG) modes, which is why these beams are often referred to as LG beams. An LG beam can potentially be produced from a standard LP Gaussian laser pulse in reflection from a fan-like structure[
Reference Shi, Shen, Zhang, Zhang, Wang and Xu
16
,
Reference Longman and Fedosejevs
17
,
Reference Porat, Lightman, Cohen and Pomerantz
20
]. This approach avoids transmissive optics and it is well-suited for generating high-power high-intensity LG beams at high efficiency. Achieving circularly polarized (CP) LG beams in conventional high-intensity laser systems is likely to be more challenging than achieving LP-LG beams, since a native Gaussian beam is LP and extra steps need to be taken to induce circular polarization. It is then imperative to study laser–plasma interactions involving LP-LG beams, as these beams are more likely to be achieved in the near-term at high-intensity laser systems such as ELI-NP[
Reference Radier, Chalus, Charbonneau, Thambirajah, Deschamps, David, Barbe, Etter, Matras, Ricaud, Leroux, Richard, Lureau, Baleanu, Banici, Gradinariu, Caldararu, Capiteanu, Naziru, Diaconescu, Iancu, Dabu, Ursescu, Dancus, Ur, Tanaka and Zamfir
2
] or the SG-II UP facility[
Reference Zhu, Zhu, Li, Zhu, Ma, Lu, Fan, Liu, Zhou, Xu, Zhang, Xie, Yang, Wang, Ouyang, Wang, Li, Yang, Fan, Sun, Liu, Li, Zhang, Tao, Sun, Zhu, Wang, Jiao, Ren, Li, Jiao, Huang and Lin
46
]. The focus of this paper is on electron acceleration in vacuum by an LP-LG laser beam following its reflection off a plasma with a sharp density gradient. This setup is sometimes referred to as the ‘reflection off a plasma mirror’[
Reference Thévenet, Leblanc, Kahaly, Vincenti, Vernier, Quéré and Faure
47
], but we minimize the use of the term ‘plasma mirror’ to avoid any confusion with the optical shutters employed for producing high-contrast pulses. Direct laser acceleration in vacuum by a conventional laser beam is generally considered to be ineffective. The key issue is the transverse electron expulsion caused by the transverse electric field of the laser. The expulsion terminates electron energy gain from the laser and leads to strong electron divergence. It must be stressed that the expulsion is closely tied to the topology of the laser field, which is dominated by the transverse electric and magnetic fields. In two recent publications[
Reference Shi, Blackman, Stutman and Arefiev
39
,
Reference Shi, Blackman and Arefiev
40
] we showed that a CP-LG beam with a properly chosen twist can be used to solve the expulsion problem. The wave-front twist creates a unique accelerating structure dominated by longitudinal laser electric and magnetic fields in the region close to the axis of the beam. The longitudinal electric field provides forward acceleration without causing electron divergence, while the longitudinal magnetic field provides transverse electron confinement. It was shown using 3D particle-in-cell (PIC) simulations that a CP-LG beam reflected off a plasma can generate dense bunches of ultra-relativistic electrons via the described mechanism[
Reference Shi, Blackman, Stutman and Arefiev
39
,
Reference Shi, Blackman and Arefiev
40
]. The distinctive features of this acceleration mechanism are the formation of multiple sub-
![]() $\unicode{x3bc} \mathrm{m}$
electron bunches, their relatively short acceleration distance (around
$\unicode{x3bc} \mathrm{m}$
electron bunches, their relatively short acceleration distance (around
![]() $100\ \unicode{x3bc} \mathrm{m}$
) and their high density (in the range of the critical density). The purpose of the current study is to identify the changes introduced by the change in polarization from circular to linear with the ultimate goal of determining whether the use of circular polarization is essential.
$100\ \unicode{x3bc} \mathrm{m}$
) and their high density (in the range of the critical density). The purpose of the current study is to identify the changes introduced by the change in polarization from circular to linear with the ultimate goal of determining whether the use of circular polarization is essential.
In this paper, we present results of a 3D PIC simulation for a 600 TW LP-LG laser beam reflected off a plasma with a sharp density gradient. We find that, despite the loss of axial symmetry introduced by switching from circular to linear polarization, the key features of electron acceleration are retained. Namely, the laser is still able to generate dense ultra-relativistic electron bunches, with the acceleration performed by the longitudinal laser electric field in the region close to the laser axis. In the most energetic bunch, the electron energy reaches 0.29 GeV (10% energy spread). The bunch has a charge of 6 pC, a duration of approximately 270 as and remarkably low divergence of
![]() ${0.57}^{\circ }$
(10 mrad). The normalized emittance in
${0.57}^{\circ }$
(10 mrad). The normalized emittance in
![]() $y$
and
$y$
and
![]() $z$
is
$z$
is
![]() ${\tilde{\varepsilon}}_{\textrm{rms},y}\approx 5\times {10}^{-7},{\tilde{\varepsilon}}_{\textrm{rms},z}\approx 4\times {10}^{-7}$
.
${\tilde{\varepsilon}}_{\textrm{rms},y}\approx 5\times {10}^{-7},{\tilde{\varepsilon}}_{\textrm{rms},z}\approx 4\times {10}^{-7}$
.
Such dense attosecond bunches can find applications in research and technology[ Reference Schönenberger, Mittelbach, Yousefi, McNeur, Niedermayer and Hommelhoff 48 , Reference Black, Niedermayer, Miao, Zhao, Solgaard, Byer and Leedle 49 ], with one specific application being free-electron lasers[ Reference Huang, Ding and Schroeder 50 ]. The rest of this paper is organized as follows. Section 2 presents the field structure of the LP-LG beam and the setup of our 3D PIC simulation. Section 3 discusses the formation of electron bunches that takes place during laser reflection off the plasma. Section 4 examines the energy gain by the electron bunches during their motion with the laser pulse. Section 5 summarizes our key results and discusses their implication.
2 Field structure of the linearly polarized Laguerre–Gaussian beam and simulation setup
In this section, we present the structure of the LP-LG beam that we use in our 3D PIC simulation to generate and accelerate electron bunches. The section also presents the simulation setup.
The wave-front structure of a helical beam can be parameterized using two indices: the twist index
![]() $l$
, which specifies the azimuthal dependence of the transverse electric and magnetic fields, and the radial index
$l$
, which specifies the azimuthal dependence of the transverse electric and magnetic fields, and the radial index
![]() $p$
, which specifies the radial dependence of the same fields in the focal plane. The polarization of the transverse laser fields is independent of their wave-front topology, so a helical beam can be LP or CP. Detailed expressions for all field components of an LP-LG beam are provided by Shi et al.[
Reference Shi, Blackman and Arefiev
40
]. We choose to omit these expressions here for compactness and instead we summarize the key features. The twist index
$p$
, which specifies the radial dependence of the same fields in the focal plane. The polarization of the transverse laser fields is independent of their wave-front topology, so a helical beam can be LP or CP. Detailed expressions for all field components of an LP-LG beam are provided by Shi et al.[
Reference Shi, Blackman and Arefiev
40
]. We choose to omit these expressions here for compactness and instead we summarize the key features. The twist index
![]() $l$
qualitatively changes the topology of the transverse and longitudinal fields. We are interested in the field structure close to the central axis. There are three distinct cases:
$l$
qualitatively changes the topology of the transverse and longitudinal fields. We are interested in the field structure close to the central axis. There are three distinct cases:
![]() $l = 0$
,
$l = 0$
,
![]() $\mid l\mid\ = 1$
and
$\mid l\mid\ = 1$
and
![]() $\mid l\mid\ >1$
. The case of
$\mid l\mid\ >1$
. The case of
![]() $l = 0$
corresponds to a conventional beam, with the near-axis field structure dominated by transverse electric and magnetic fields. In the case of
$l = 0$
corresponds to a conventional beam, with the near-axis field structure dominated by transverse electric and magnetic fields. In the case of
![]() $\mid l\mid\ >1$
, all laser fields vanish on the central axis. The case that is of interest to us is the case with
$\mid l\mid\ >1$
, all laser fields vanish on the central axis. The case that is of interest to us is the case with
![]() $\mid l\mid\ = 1$
, because in this case the longitudinal rather than transverse fields peak on the axis.
$\mid l\mid\ = 1$
, because in this case the longitudinal rather than transverse fields peak on the axis.
In our 3D PIC simulations, we use an LP 600 TW laser with
![]() $l = -1$
and
$l = -1$
and
![]() $p = 0$
. We consider a beam that propagates in the negative direction along the
$p = 0$
. We consider a beam that propagates in the negative direction along the
![]() $x$
-axis upon entering the simulation box. Detailed parameters of the laser beam are listed in Table 1. In order to facilitate a comparison with the results for a CP-LG beam published by Shi et al.[
Reference Shi, Blackman and Arefiev
40
] (right-CP with
$x$
-axis upon entering the simulation box. Detailed parameters of the laser beam are listed in Table 1. In order to facilitate a comparison with the results for a CP-LG beam published by Shi et al.[
Reference Shi, Blackman and Arefiev
40
] (right-CP with
![]() $l = -1$
and
$l = -1$
and
![]() $p = 0$
), we use the same peak power, pulse duration and spot size for our LP-LG beam. The electric and magnetic field structures of the LP-LG beam in the
$p = 0$
), we use the same peak power, pulse duration and spot size for our LP-LG beam. The electric and magnetic field structures of the LP-LG beam in the
![]() $\left(x,z\right)$
-plane and the
$\left(x,z\right)$
-plane and the
![]() $\left(y,z\right)$
-plane are shown in Figure 1. The plots illustrate the difference in topology between the transverse and longitudinal field components. The longitudinal electric and magnetic fields reach their highest amplitude along the axis of the laser beam (see Figures 1(b) and 1(c)). On the other hand, the transverse electric field shown in Figure 1(a) vanishes on the axis of the beam. The electric field structure in Figure 1 agrees with the analytical expression given in Appendix C and derived in paraxial approximation by assuming that the diffraction angle
$\left(y,z\right)$
-plane are shown in Figure 1. The plots illustrate the difference in topology between the transverse and longitudinal field components. The longitudinal electric and magnetic fields reach their highest amplitude along the axis of the laser beam (see Figures 1(b) and 1(c)). On the other hand, the transverse electric field shown in Figure 1(a) vanishes on the axis of the beam. The electric field structure in Figure 1 agrees with the analytical expression given in Appendix C and derived in paraxial approximation by assuming that the diffraction angle
![]() ${\theta}_{\textrm{d}}$
is small. The longitudinal fields are relatively strong even though
${\theta}_{\textrm{d}}$
is small. The longitudinal fields are relatively strong even though
![]() ${\theta}_{\textrm{d}}\ll 1$
. We have
${\theta}_{\textrm{d}}\ll 1$
. We have
![]() ${E}_{\parallel}^{\mathrm{max}}/{E}_{\perp}^{\mathrm{max}} = {B}_{\parallel}^{\mathrm{max}}/{B}_{\perp}^{\mathrm{max}}\approx 0.14$
for the considered LP-LG beam with
${E}_{\parallel}^{\mathrm{max}}/{E}_{\perp}^{\mathrm{max}} = {B}_{\parallel}^{\mathrm{max}}/{B}_{\perp}^{\mathrm{max}}\approx 0.14$
for the considered LP-LG beam with
![]() ${\theta}_{\textrm{d}}\approx 8.5\times {10}^{-2}$
, where
${\theta}_{\textrm{d}}\approx 8.5\times {10}^{-2}$
, where
![]() ${\theta}_{\textrm{d}} = {\lambda}_0/\pi {w}_0$
. Note that
${\theta}_{\textrm{d}} = {\lambda}_0/\pi {w}_0$
. Note that
![]() ${E}_{\parallel}^{\mathrm{max}}\approx 1.1\times {10}^{13}$
V/m and
${E}_{\parallel}^{\mathrm{max}}\approx 1.1\times {10}^{13}$
V/m and
![]() ${B}_{\parallel}^{\mathrm{max}}\approx 36$
kT. The peak normalized amplitude of the longitudinal field
${B}_{\parallel}^{\mathrm{max}}\approx 36$
kT. The peak normalized amplitude of the longitudinal field
![]() ${a}_{\ast} = \mid e\mid {E}_{\parallel}^{\mathrm{max}}/{m}_{\textrm{e}} c\omega$
for a given period-averaged power
${a}_{\ast} = \mid e\mid {E}_{\parallel}^{\mathrm{max}}/{m}_{\textrm{e}} c\omega$
for a given period-averaged power
![]() $P$
in PW is given by Equation (C21), where
$P$
in PW is given by Equation (C21), where
![]() $c$
is the speed of light,
$c$
is the speed of light,
![]() $\omega = 2\pi c/{\lambda}_0$
is the laser frequency and
$\omega = 2\pi c/{\lambda}_0$
is the laser frequency and
![]() $e$
and
$e$
and
![]() ${m}_{\textrm{e}}$
are the electron charge and mass, respectively. We find that
${m}_{\textrm{e}}$
are the electron charge and mass, respectively. We find that
![]() ${a}_{\ast}\approx 2.7$
for the considered power of 600 TW.
${a}_{\ast}\approx 2.7$
for the considered power of 600 TW.

Figure 1 Electric and magnetic field components of an LP-LG laser beam before it encounters the plasma. Panels (a) and (d) show
![]() ${E}_{y}$
; panels (b) and (e) show
${E}_{y}$
; panels (b) and (e) show
![]() ${E}_{x}$
; panels (c) and (f) show
${E}_{x}$
; panels (c) and (f) show
![]() ${B}_{x}$
. The left-hand column ((a)–(c)) shows the field structure in the
${B}_{x}$
. The left-hand column ((a)–(c)) shows the field structure in the
![]() $\left(x,z\right)$
-plane at
$\left(x,z\right)$
-plane at
![]() $y = 0$
. The right-hand column ((d)–(f)) shows the field structure in the
$y = 0$
. The right-hand column ((d)–(f)) shows the field structure in the
![]() $\left(y,z\right)$
-plane at the
$\left(y,z\right)$
-plane at the
![]() $x$
-position indicated with the dashed line in panels (a)–(c). All the snapshots are taken at
$x$
-position indicated with the dashed line in panels (a)–(c). All the snapshots are taken at
![]() $t\approx -9$
fs from the simulation with parameters listed in Table 1.
$t\approx -9$
fs from the simulation with parameters listed in Table 1.
Table 1 3D PIC simulation parameters. Here,
![]() ${n}_{\textrm{c}} = 1.8\times {10}^{27}$
m
${n}_{\textrm{c}} = 1.8\times {10}^{27}$
m
![]() ${}^{-3}$
is the critical density corresponding to the laser wavelength
${}^{-3}$
is the critical density corresponding to the laser wavelength
![]() ${\lambda}_0$
. The initial temperatures for electrons and ions are set to zero.
${\lambda}_0$
. The initial temperatures for electrons and ions are set to zero.

It is instructive to compare the field structure of the LP-LG beam to the field structure of the CP-LG beam from Shi et al.[
Reference Shi, Blackman and Arefiev
40
]. In both cases, the longitudinal electric and magnetic fields peak on the axis of the beam where the transverse field vanishes. However, in contrast to the CP-LG beam, the longitudinal electric and magnetic fields of the LP-LG beam lack axial symmetry (see Figures 1(e) and 1(f)). The difference in symmetry can be illustrated by constructing an LP-LG beam (
![]() $l = -1$
) from two co-propagating CP-LG beams. Following the notations of Shi et al.[
Reference Shi, Blackman and Arefiev
40
], we create a CP transverse electric field by adding
$l = -1$
) from two co-propagating CP-LG beams. Following the notations of Shi et al.[
Reference Shi, Blackman and Arefiev
40
], we create a CP transverse electric field by adding
![]() ${E}_{z} = i\sigma {E}_{y}$
, where
${E}_{z} = i\sigma {E}_{y}$
, where
![]() $\sigma = 1$
produces a right-CP wave and
$\sigma = 1$
produces a right-CP wave and
![]() $\sigma = -1$
produces a left-CP wave. We take a pair of CP-LG beams: one with
$\sigma = -1$
produces a left-CP wave. We take a pair of CP-LG beams: one with
![]() $l = -1$
,
$l = -1$
,
![]() $\sigma = -1$
and the other one with
$\sigma = -1$
and the other one with
![]() $l = -1$
,
$l = -1$
,
![]() $\sigma = 1$
. Their superposition produces an LP transverse electric field, because
$\sigma = 1$
. Their superposition produces an LP transverse electric field, because
![]() ${E}_{z}$
components of these beams cancel each other out. It was shown by Shi et al.[
Reference Shi, Blackman, Stutman and Arefiev
39
,
Reference Shi, Blackman and Arefiev
40
] that the longitudinal fields of the right- and left-CP-LG beams have different dependencies on
${E}_{z}$
components of these beams cancel each other out. It was shown by Shi et al.[
Reference Shi, Blackman, Stutman and Arefiev
39
,
Reference Shi, Blackman and Arefiev
40
] that the longitudinal fields of the right- and left-CP-LG beams have different dependencies on
![]() $r$
and
$r$
and
![]() $\phi$
. Specifically, the longitudinal field of the right-CP-LG beam (
$\phi$
. Specifically, the longitudinal field of the right-CP-LG beam (
![]() $l\sigma = -1$
) is axisymmetric, whereas the longitudinal field of the left-CP-LG beam (
$l\sigma = -1$
) is axisymmetric, whereas the longitudinal field of the left-CP-LG beam (
![]() $l\sigma = 1$
) has azimuthal dependence. Moreover, only the right-CP-LG beam contributes to the longitudinal fields on the axis, because the fields of the left-CP-LG beam vanish. The LP-LG beam inherits its azimuthal dependence from the left-CP-LG beam, which is the reason why the longitudinal fields still peak on the axis, but lose their symmetry as we move away from the axis.
$l\sigma = 1$
) has azimuthal dependence. Moreover, only the right-CP-LG beam contributes to the longitudinal fields on the axis, because the fields of the left-CP-LG beam vanish. The LP-LG beam inherits its azimuthal dependence from the left-CP-LG beam, which is the reason why the longitudinal fields still peak on the axis, but lose their symmetry as we move away from the axis.
As stated earlier, we want to contrast our results with those for a right-CP-LG beam that has the same power. The key player in electron acceleration is the longitudinal electric field of the laser, because it is this field that performs most of the acceleration for the electrons moving along the laser axis. We use the discussed decomposition for the LP-LG beam to compare the longitudinal field strength
![]() $\mid {E}_{x}\mid$
on the axis of the two beams. We have already shown that
$\mid {E}_{x}\mid$
on the axis of the two beams. We have already shown that
![]() $\mid {E}_{x}\mid$
of an LP-LG beam is equal to
$\mid {E}_{x}\mid$
of an LP-LG beam is equal to
![]() $\mid {E}_{x}\mid$
of a right-CP-LG beam whose transverse field amplitude is half of that in the LP-LG beam. The power of the right-CP-LG beam is two times lower than the power the LP-LG beam. Since the power scales as the square of the field strength, we immediately conclude that
$\mid {E}_{x}\mid$
of a right-CP-LG beam whose transverse field amplitude is half of that in the LP-LG beam. The power of the right-CP-LG beam is two times lower than the power the LP-LG beam. Since the power scales as the square of the field strength, we immediately conclude that
![]() $\mid {E}_{x}\mid$
in a right-CP-LG beam whose power is the same as the power of the LP-LG beam is going to be higher by a factor of
$\mid {E}_{x}\mid$
in a right-CP-LG beam whose power is the same as the power of the LP-LG beam is going to be higher by a factor of
![]() $\sqrt{2}$
. The loss of axial symmetry and the reduced field strength are likely to alter the injection and subsequent acceleration of electron bunches by the LP-LG beam compared to the case of the right-CP-LG beam from Shi et al.[
Reference Shi, Blackman and Arefiev
40
].
$\sqrt{2}$
. The loss of axial symmetry and the reduced field strength are likely to alter the injection and subsequent acceleration of electron bunches by the LP-LG beam compared to the case of the right-CP-LG beam from Shi et al.[
Reference Shi, Blackman and Arefiev
40
].
In our simulation performed using the PIC code EPOCH[
Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers
51
], the discussed LP-LG beam is reflected off a plasma with a sharp density gradient. In what follows, we provide details of the simulation setup that we use in the next sections to study electron injection and acceleration. The target is initially set as a fully ionized carbon plasma with electron density
![]() ${n}_{\textrm{e}} = 180{n}_{\textrm{c}}$
, where
${n}_{\textrm{e}} = 180{n}_{\textrm{c}}$
, where
![]() ${n}_{\textrm{c}}$
= 1.8
${n}_{\textrm{c}}$
= 1.8
![]() $\times {10}^{27}$
m
$\times {10}^{27}$
m
![]() ${}^{-3}$
is the critical density for the considered laser wavelength
${}^{-3}$
is the critical density for the considered laser wavelength
![]() ${\lambda}_0 = 0.8\ \unicode{x3bc} \mathrm{m}$
. Table 1 provides details regarding the density gradient. The focal plane of the beam in the absence of the plasma is located at
${\lambda}_0 = 0.8\ \unicode{x3bc} \mathrm{m}$
. Table 1 provides details regarding the density gradient. The focal plane of the beam in the absence of the plasma is located at
![]() $x = 0\ \unicode{x3bc} \mathrm{m}$
, which is also the location of the plasma surface. The resolution and the number of particles per cell in the PIC simulation are determined based on a convergence test, discussed in Appendix A. The test addresses the concern that the parameters of the accelerated electron bunches might be sensitive to simulation parameters[
Reference Shi, Blackman, Stutman and Arefiev
39
].
$x = 0\ \unicode{x3bc} \mathrm{m}$
, which is also the location of the plasma surface. The resolution and the number of particles per cell in the PIC simulation are determined based on a convergence test, discussed in Appendix A. The test addresses the concern that the parameters of the accelerated electron bunches might be sensitive to simulation parameters[
Reference Shi, Blackman, Stutman and Arefiev
39
].
3 Electron injection into the linearly polarized Laguerre–Gaussian laser beam
In this section we discuss the formation of electron bunches that takes place during laser reflection off the plasma. We refer to this process as the ‘electron injection’, because, once the bunches are formed, they continue surfing with the laser beam.
Figure 2 shows various aspects of electron injection. All snapshots are taken at
![]() $t = 9$
fs, with
$t = 9$
fs, with
![]() $t = 0$
fs being defined as the time when the peak of the laser envelope reaches
$t = 0$
fs being defined as the time when the peak of the laser envelope reaches
![]() $x = 0$
(in the absence of the plasma). The electron density,
$x = 0$
(in the absence of the plasma). The electron density,
![]() ${n}_{\textrm{e}}$
, in the
${n}_{\textrm{e}}$
, in the
![]() $\left(x,z\right)$
-plane is shown in Figure 2(a). At this point, most of the laser beam (incident from the right) has been reflected by the plasma. The reflection process generates bunches that are solid in the near-axis region, with the peak densities as high as
$\left(x,z\right)$
-plane is shown in Figure 2(a). At this point, most of the laser beam (incident from the right) has been reflected by the plasma. The reflection process generates bunches that are solid in the near-axis region, with the peak densities as high as
![]() ${n}_{\textrm{c}}$
. The plot of
${n}_{\textrm{c}}$
. The plot of
![]() ${n}_{\textrm{e}}$
integrated over the laser beam cross-section that is shown in Figure 7(a) of Appendix A provides additional information about the bunches. Figures 2(b) and 2(c) show the transverse areal density
${n}_{\textrm{e}}$
integrated over the laser beam cross-section that is shown in Figure 7(a) of Appendix A provides additional information about the bunches. Figures 2(b) and 2(c) show the transverse areal density
![]() ${\rho}_{\textrm{e}}$
and cell-averaged divergence angle
${\rho}_{\textrm{e}}$
and cell-averaged divergence angle
![]() $\left\langle \theta \right\rangle$
of the third bunch marked with a dashed rectangle in Figure 2(a). The divergence angle for an individual electron is defined as
$\left\langle \theta \right\rangle$
of the third bunch marked with a dashed rectangle in Figure 2(a). The divergence angle for an individual electron is defined as
![]() $\theta \equiv \arctan \left({p}_{\perp }/{p}_{x}\right)$
. The angle is averaged on every mesh cell of the
$\theta \equiv \arctan \left({p}_{\perp }/{p}_{x}\right)$
. The angle is averaged on every mesh cell of the
![]() $\left(y,z\right)$
-plane. It is instructive to compare the plots of
$\left(y,z\right)$
-plane. It is instructive to compare the plots of
![]() ${\rho}_{\textrm{e}}$
and
${\rho}_{\textrm{e}}$
and
![]() $\left\langle \theta \right\rangle$
to the results for the CP-LG laser beam presented by Shi et al.[
Reference Shi, Blackman and Arefiev
40
] for the same time instant (
$\left\langle \theta \right\rangle$
to the results for the CP-LG laser beam presented by Shi et al.[
Reference Shi, Blackman and Arefiev
40
] for the same time instant (
![]() $t = 9$
fs). In the case of the LP-LG beam, the areal density in the near-axis region is approximately two times lower, while the divergence angle in the same region is similar to that of the CP-LG beam. The biggest difference is the loss of axial symmetry. The LP-LG beam generates two dense side-lobes in addition to the on-axis part that has been discussed. To further illustrate the complex structure of the electron bunches generated by the LP-LG beam, Figures 2(d) and 2(e) provide 3D rendering of the electron density in the third bunch. It is clear from Figure 2(d) that the two side-lobes are slightly behind the on-axis region, which means that the phase of the laser field at their location is different. The divergence of the two lobes (shown in Figure 2(c)) is so high that they are likely to move away from the central axis while moving in the positive direction along the
$t = 9$
fs). In the case of the LP-LG beam, the areal density in the near-axis region is approximately two times lower, while the divergence angle in the same region is similar to that of the CP-LG beam. The biggest difference is the loss of axial symmetry. The LP-LG beam generates two dense side-lobes in addition to the on-axis part that has been discussed. To further illustrate the complex structure of the electron bunches generated by the LP-LG beam, Figures 2(d) and 2(e) provide 3D rendering of the electron density in the third bunch. It is clear from Figure 2(d) that the two side-lobes are slightly behind the on-axis region, which means that the phase of the laser field at their location is different. The divergence of the two lobes (shown in Figure 2(c)) is so high that they are likely to move away from the central axis while moving in the positive direction along the
![]() $x$
-axis with the laser beam.
$x$
-axis with the laser beam.

Figure 2 Structure of electron bunches shortly after laser reflection off the plasma (
![]() $t = 9$
fs). (a) Electron density on a log-scale, with the color representing
$t = 9$
fs). (a) Electron density on a log-scale, with the color representing
![]() $\log \left({n}_{\textrm{e}}/{n}_{\textrm{c}}\right)$
. The blue, red and green contours denote
$\log \left({n}_{\textrm{e}}/{n}_{\textrm{c}}\right)$
. The blue, red and green contours denote
![]() ${n}_{\textrm{e}} = 0.1{n}_{\textrm{c}}$
,
${n}_{\textrm{e}} = 0.1{n}_{\textrm{c}}$
,
![]() $0.5{n}_{\textrm{c}}$
and
$0.5{n}_{\textrm{c}}$
and
![]() ${n}_{\textrm{c}}$
, respectively. The dashed rectangle marks the third bunch, whose additional details are provided in the remaining panels. (b) Electron areal density
${n}_{\textrm{c}}$
, respectively. The dashed rectangle marks the third bunch, whose additional details are provided in the remaining panels. (b) Electron areal density
![]() ${\rho}_{\textrm{e}}$
in the third bunch. (c) Cell-averaged electron divergence angle
${\rho}_{\textrm{e}}$
in the third bunch. (c) Cell-averaged electron divergence angle
![]() $\left\langle \theta \right\rangle$
in the third bunch. (d), (e) 3D rendering of the electron density in the third bunch using different viewpoints.
$\left\langle \theta \right\rangle$
in the third bunch. (d), (e) 3D rendering of the electron density in the third bunch using different viewpoints.
To examine this expectation and to provide additional insights into electron bunch dynamics, we performed detailed particle tracking for the third bunch. We distinguish three groups of electrons based on their transverse position within the bunch at
![]() $t = 46$
fs. Figure 3(a) shows the areal density of the third bunch at
$t = 46$
fs. Figure 3(a) shows the areal density of the third bunch at
![]() $t = 46$
fs, while Figure 3(b) shows the three groups of electrons selected for tracking. The electrons are picked randomly from the entire electron population of the third bunch. Note that we choose
$t = 46$
fs, while Figure 3(b) shows the three groups of electrons selected for tracking. The electrons are picked randomly from the entire electron population of the third bunch. Note that we choose
![]() $t = 46$
fs rather than
$t = 46$
fs rather than
![]() $t = 9$
fs as our selection time in order to give enough time for the three groups to become visibly separated. The selected particles are tracked during the entire simulation (up to
$t = 9$
fs as our selection time in order to give enough time for the three groups to become visibly separated. The selected particles are tracked during the entire simulation (up to
![]() $t\approx 310$
fs) to determine their trajectories and energy gain.
$t\approx 310$
fs) to determine their trajectories and energy gain.

Figure 3 (a) Areal density of the electrons in the third bunch at time
![]() $t = 46$
fs. (b) Three groups of electrons (blue, green and red markers) selected from the third bunch at
$t = 46$
fs. (b) Three groups of electrons (blue, green and red markers) selected from the third bunch at
![]() $t = 46$
fs for tracking. The electrons in each group are selected randomly. (c) Transverse positions of the three groups of electrons from (b) at
$t = 46$
fs for tracking. The electrons in each group are selected randomly. (c) Transverse positions of the three groups of electrons from (b) at
![]() $t = -2.2$
fs. (d)–(f) Trajectories of the three groups of electrons in the transverse plane over the duration of the simulation. The line color shows electron energy. The markers show the electron locations at
$t = -2.2$
fs. (d)–(f) Trajectories of the three groups of electrons in the transverse plane over the duration of the simulation. The line color shows electron energy. The markers show the electron locations at
![]() $t = 46$
fs. (g)–(i) Time evolution of the longitudinal position for the same three groups of electrons, with (g) showing ‘blue’ electrons, (h) showing ‘green’ electrons and (i) showing ‘red’ electrons. The line color shows electron energy.
$t = 46$
fs. (g)–(i) Time evolution of the longitudinal position for the same three groups of electrons, with (g) showing ‘blue’ electrons, (h) showing ‘green’ electrons and (i) showing ‘red’ electrons. The line color shows electron energy.
Figures 3(d)–3(f) provide projections of electron trajectories onto the beam cross-section, where the color-coding is used to show electron energy along each trajectory. The markers correspond to the electron positions at
![]() $t = 46$
fs. To see the initial electron positions, we provide Figure 3(c) that shows electron positions in the
$t = 46$
fs. To see the initial electron positions, we provide Figure 3(c) that shows electron positions in the
![]() $\left(y,z\right)$
-plane at
$\left(y,z\right)$
-plane at
![]() $t = -2.2$
fs. As seen in Figure 3(d), the ‘blue’ electrons remain close to the axis of the laser beam and thus within the region with a strong longitudinal electric field throughout the simulation. The ‘green’ electrons (see Figure 3(e)) rotate around the axis and eventually leave the analysis window (
$t = -2.2$
fs. As seen in Figure 3(d), the ‘blue’ electrons remain close to the axis of the laser beam and thus within the region with a strong longitudinal electric field throughout the simulation. The ‘green’ electrons (see Figure 3(e)) rotate around the axis and eventually leave the analysis window (
![]() $y\in \left(-2,2\right){w}_0$
,
$y\in \left(-2,2\right){w}_0$
,
![]() $z\in \left(-2,2\right){w}_0$
). The ‘red’ electrons (see Figure 3(f)) are different because they are expelled directly outwards without any significant rotation. These electrons travel through the region with a significant transverse electric field. The long-term energy gain by these three groups of electrons is discussed in the next section.
$z\in \left(-2,2\right){w}_0$
). The ‘red’ electrons (see Figure 3(f)) are different because they are expelled directly outwards without any significant rotation. These electrons travel through the region with a significant transverse electric field. The long-term energy gain by these three groups of electrons is discussed in the next section.
4 Electron energy gain in the linearly polarized Laguerre–Gaussian laser beam
In Section 2 we showed that the reflection of an LP-PG beam produces dense electron bunches. These bunches can move with the laser beam, gaining energy. In this section we examine this energy gain.
Figures 3(g)–3(i) show how the energy of electrons in each group from Figure 3(b) changes over time. The magnitude of the longitudinal electron velocity
![]() ${v}_{x}$
is a major factor determining the electron energy gain. Electrons with smaller
${v}_{x}$
is a major factor determining the electron energy gain. Electrons with smaller
![]() $c-{v}_{x}$
can stay longer in the accelerating part of the laser wave-front while moving forward with the laser beam. Due to the fact that the considered electrons are ultra-relativistic, it is the divergence angle
$c-{v}_{x}$
can stay longer in the accelerating part of the laser wave-front while moving forward with the laser beam. Due to the fact that the considered electrons are ultra-relativistic, it is the divergence angle
![]() $\theta$
rather than the magnitude of the velocity that primarily influences
$\theta$
rather than the magnitude of the velocity that primarily influences
![]() ${v}_{x}$
, with
${v}_{x}$
, with
![]() ${v}_{x}\approx c\cos \theta$
. To assess the difference between
${v}_{x}\approx c\cos \theta$
. To assess the difference between
![]() ${v}_{x}$
and
${v}_{x}$
and
![]() $c$
, which can be extremely small, we use the vertical coordinate that shows
$c$
, which can be extremely small, we use the vertical coordinate that shows
![]() $\left(x- ct\right)/{\lambda}_0$
in Figures 3(g)–3(i). It is essentially the relative slip (in the units of
$\left(x- ct\right)/{\lambda}_0$
in Figures 3(g)–3(i). It is essentially the relative slip (in the units of
![]() ${\lambda}_0$
) between the electron and a point moving with the speed of light. The ‘blue’ electrons remain close to the beam axis and have the smallest
${\lambda}_0$
) between the electron and a point moving with the speed of light. The ‘blue’ electrons remain close to the beam axis and have the smallest
![]() $c-{v}_{x}$
. As seen in Figure 3(g), they slip by less than
$c-{v}_{x}$
. As seen in Figure 3(g), they slip by less than
![]() $0.2{\lambda}_0$
over 300 fs, which allows them to gain roughly 290 MeV. The ‘green’ electrons have a much bigger value of
$0.2{\lambda}_0$
over 300 fs, which allows them to gain roughly 290 MeV. The ‘green’ electrons have a much bigger value of
![]() $c-{v}_{x}$
because there is a transverse component of electron velocity associated with the rotation. As seen in Figure 3(h), they experience significant slipping over 100 fs, which prevents them from the prolonged acceleration required for a substantial energy gain. The ‘red’ electrons have the biggest transverse displacement early on, so that they are exposed to a strong transverse laser electric field. This field causes their transverse motion, and it also transfers energy to the electrons. This is the reason why the ‘red’ electrons shown in Figure 3(i) gain more energy than the ‘green’ electrons. However, their slipping causes them to experience a decelerating field before the laser beam has time to diverge. This is the underlying cause for the energy reduction at
$c-{v}_{x}$
because there is a transverse component of electron velocity associated with the rotation. As seen in Figure 3(h), they experience significant slipping over 100 fs, which prevents them from the prolonged acceleration required for a substantial energy gain. The ‘red’ electrons have the biggest transverse displacement early on, so that they are exposed to a strong transverse laser electric field. This field causes their transverse motion, and it also transfers energy to the electrons. This is the reason why the ‘red’ electrons shown in Figure 3(i) gain more energy than the ‘green’ electrons. However, their slipping causes them to experience a decelerating field before the laser beam has time to diverge. This is the underlying cause for the energy reduction at
![]() $t>100$
fs. The analysis of electron trajectories leads us to a conclusion that the most energetic electrons in our setup are the electrons that remain close to the axis of the beam. In what follows, we focus on their energy gain.
$t>100$
fs. The analysis of electron trajectories leads us to a conclusion that the most energetic electrons in our setup are the electrons that remain close to the axis of the beam. In what follows, we focus on their energy gain.
Before we proceed with the analysis of the electron acceleration, we take a closer look at the reflected fields. Figure 4(a) shows the transverse electric field away from the axis (
![]() $y = 0$
,
$y = 0$
,
![]() $z = 0.7{w}_0$
) and longitudinal magnetic field on the axis (
$z = 0.7{w}_0$
) and longitudinal magnetic field on the axis (
![]() $y = 0$
,
$y = 0$
,
![]() $z = 0$
) after the laser has been reflected by the plasma. As we have already seen, the electrons tend to bunch on the axis. The field of these electrons is difficult to separate from the longitudinal laser electric field. This is the reason why
$z = 0$
) after the laser has been reflected by the plasma. As we have already seen, the electrons tend to bunch on the axis. The field of these electrons is difficult to separate from the longitudinal laser electric field. This is the reason why
![]() ${B}_{\parallel }$
is plotted instead of
${B}_{\parallel }$
is plotted instead of
![]() ${E}_{\parallel }$
. The transverse field is plotted off-axis because it vanishes on the axis of the beam for the considered helical beam. The most striking feature compared to the CP-LG beam examined by Shi et al.[
Reference Shi, Blackman, Stutman and Arefiev
39
,
Reference Shi, Blackman and Arefiev
40
] is the appearance of higher-order harmonics in
${E}_{\parallel }$
. The transverse field is plotted off-axis because it vanishes on the axis of the beam for the considered helical beam. The most striking feature compared to the CP-LG beam examined by Shi et al.[
Reference Shi, Blackman, Stutman and Arefiev
39
,
Reference Shi, Blackman and Arefiev
40
] is the appearance of higher-order harmonics in
![]() ${E}_{y}$
. In contrast to
${E}_{y}$
. In contrast to
![]() ${E}_{y}$
,
${E}_{y}$
,
![]() ${B}_{\parallel }$
has a more regular shape. The spectra shown in Figure 4(b) confirm that
${B}_{\parallel }$
has a more regular shape. The spectra shown in Figure 4(b) confirm that
![]() ${E}_{y}$
contains odd harmonics due to high-harmonic generation effects[
Reference Teubner and Gibbon
52
], whereas
${E}_{y}$
contains odd harmonics due to high-harmonic generation effects[
Reference Teubner and Gibbon
52
], whereas
![]() ${B}_{\parallel }$
in the near-axis region seems to be unaffected by the harmonic generation. According to Zhang et al.[
Reference Zhang, Shen, Shi, Wang, Zhang, Wang, Xu, Yi and Xu
22
] and Denoeud et al.[
Reference Denoeud, Chopineau, Leblanc and Quéré
30
], the twist index
${B}_{\parallel }$
in the near-axis region seems to be unaffected by the harmonic generation. According to Zhang et al.[
Reference Zhang, Shen, Shi, Wang, Zhang, Wang, Xu, Yi and Xu
22
] and Denoeud et al.[
Reference Denoeud, Chopineau, Leblanc and Quéré
30
], the twist index
![]() ${l}_{n}$
of the harmonics generated during reflection of an LP-LG laser beam scales as
${l}_{n}$
of the harmonics generated during reflection of an LP-LG laser beam scales as
![]() ${l}_{n} = nl$
, where
${l}_{n} = nl$
, where
![]() $n$
is the harmonic order. The field profiles suggest that the analysis of electron acceleration in the near-axis region can be performed without taking into account the higher-order harmonics, which have a different Gouy phase shift.
$n$
is the harmonic order. The field profiles suggest that the analysis of electron acceleration in the near-axis region can be performed without taking into account the higher-order harmonics, which have a different Gouy phase shift.

Figure 4 Electric and magnetic fields after reflection of the LP-LG laser beam off the plasma. (a) Longitudinal profiles of the transverse electric field
![]() ${E}_{y}$
(red curve) and longitudinal magnetic field
${E}_{y}$
(red curve) and longitudinal magnetic field
![]() ${B}_{\parallel }$
(blue line) at
${B}_{\parallel }$
(blue line) at
![]() $t = 21$
fs. Here,
$t = 21$
fs. Here,
![]() ${B}_{\parallel }$
is plotted along the axis of the beam (
${B}_{\parallel }$
is plotted along the axis of the beam (
![]() $y = 0$
,
$y = 0$
,
![]() $z = 0$
), whereas
$z = 0$
), whereas
![]() ${E}_{y}$
is plotted at an off-axis location (
${E}_{y}$
is plotted at an off-axis location (
![]() $y = 0$
,
$y = 0$
,
![]() $z = 0.7{w}_0$
) where its amplitude has the highest value. (b) Frequency spectra of
$z = 0.7{w}_0$
) where its amplitude has the highest value. (b) Frequency spectra of
![]() ${E}_{y}$
(red line) and
${E}_{y}$
(red line) and
![]() ${B}_{\parallel }$
(blue line) from panel (a).
${B}_{\parallel }$
(blue line) from panel (a).
The momentum gain of the electrons moving along the axis of the laser beam can then be obtained by integrating the momentum balance equation:
where
![]() ${E}_{\parallel }$
is the on-axis component of the laser electric field. We neglect high-harmonic generation and beam scattering, so
${E}_{\parallel }$
is the on-axis component of the laser electric field. We neglect high-harmonic generation and beam scattering, so
![]() ${E}_{\parallel }$
is the real part of the on-axis field in the original beam given by Equation (C18). The longitudinal electric field has the same dependence on
${E}_{\parallel }$
is the real part of the on-axis field in the original beam given by Equation (C18). The longitudinal electric field has the same dependence on
![]() $x$
as the field of the CP-LG beam considered by Shi et al.[
Reference Shi, Blackman and Arefiev
40
]. For example, we have the following:
$x$
as the field of the CP-LG beam considered by Shi et al.[
Reference Shi, Blackman and Arefiev
40
]. For example, we have the following:
 $$\begin{align}{E}_{\parallel} = -\frac{E_{\ast}\sin \left(\Phi +{\Phi}_0\right)}{1+{x}^2/{x}_{\textrm{R}}^2},\end{align}$$
$$\begin{align}{E}_{\parallel} = -\frac{E_{\ast}\sin \left(\Phi +{\Phi}_0\right)}{1+{x}^2/{x}_{\textrm{R}}^2},\end{align}$$
for an electron that is staying close to the peak of the envelope, where
![]() ${E}_{\ast }$
is the peak amplitude of
${E}_{\ast }$
is the peak amplitude of
![]() ${E}_{\parallel }$
. Here
${E}_{\parallel }$
. Here
![]() ${\Phi}_0$
is a constant that can be interpreted as the injection phase for an electron that starts its acceleration at
${\Phi}_0$
is a constant that can be interpreted as the injection phase for an electron that starts its acceleration at
![]() $x\approx 0$
. The only difference between the fields of the CP-LG and LP-LG beams is their amplitude. Therefore, we can skip the derivation here and directly apply the result of Shi et al.[
Reference Shi, Blackman and Arefiev
40
]. We have the following longitudinal momentum gain for an electron injected into the laser beam close to the peak of the envelope:
$x\approx 0$
. The only difference between the fields of the CP-LG and LP-LG beams is their amplitude. Therefore, we can skip the derivation here and directly apply the result of Shi et al.[
Reference Shi, Blackman and Arefiev
40
]. We have the following longitudinal momentum gain for an electron injected into the laser beam close to the peak of the envelope:
 $$\begin{align}\frac{\Delta {p}_{\parallel }}{m_{\textrm{ec}}} = -{a}_{\ast}\frac{\pi^2{w}_0^2}{\lambda_0^2}\left\{\cos {\Phi}_0-\cos \left[{\Phi}_0-2\arctan \left(x/{x}_{\textrm{R}}\right)\right]\right\},\\[-22pt] \nonumber \end{align}$$
$$\begin{align}\frac{\Delta {p}_{\parallel }}{m_{\textrm{ec}}} = -{a}_{\ast}\frac{\pi^2{w}_0^2}{\lambda_0^2}\left\{\cos {\Phi}_0-\cos \left[{\Phi}_0-2\arctan \left(x/{x}_{\textrm{R}}\right)\right]\right\},\\[-22pt] \nonumber \end{align}$$
where
![]() ${a}_{\ast }$
is the normalized amplitude of the longitudinal field.
${a}_{\ast }$
is the normalized amplitude of the longitudinal field.
We obtain the terminal momentum gain by taking the limit of
![]() $x/{x}_{\textrm{R}}\to \infty$
in Equation (3), which yields the following:
$x/{x}_{\textrm{R}}\to \infty$
in Equation (3), which yields the following:
 $$\begin{align}\frac{\Delta {p}_{\parallel}^{\mathrm{term}}}{m_{\textrm{ec}}} = 2{a}_{\ast}\frac{\pi^2{w}_0^2}{\lambda_0^2}\cos \left({\Phi}_0-\pi \right).\end{align}$$
$$\begin{align}\frac{\Delta {p}_{\parallel}^{\mathrm{term}}}{m_{\textrm{ec}}} = 2{a}_{\ast}\frac{\pi^2{w}_0^2}{\lambda_0^2}\cos \left({\Phi}_0-\pi \right).\end{align}$$
One can understand the dependence on
![]() ${\Phi}_0$
by recalling that the electron is continuously slipping with respect to the forward-moving structure of
${\Phi}_0$
by recalling that the electron is continuously slipping with respect to the forward-moving structure of
![]() ${E}_{\parallel }$
as it moves with the laser pulse. Delayed injection into the accelerating phase means that the electron slips into the decelerating phase before the amplitude of
${E}_{\parallel }$
as it moves with the laser pulse. Delayed injection into the accelerating phase means that the electron slips into the decelerating phase before the amplitude of
![]() ${E}_{\parallel }$
becomes small due to the beam diffraction. As a result, the net momentum gain is reduced. The energy gain occurs only for
${E}_{\parallel }$
becomes small due to the beam diffraction. As a result, the net momentum gain is reduced. The energy gain occurs only for
![]() $\pi /2<{\Phi}_0<3\pi /2$
. The assumption that the electron is moving forward with ultra-relativistic velocity is no longer valid for
$\pi /2<{\Phi}_0<3\pi /2$
. The assumption that the electron is moving forward with ultra-relativistic velocity is no longer valid for
![]() $3\pi /2<{\Phi}_0<5\pi /2$
, which, in turn, invalidates the derived expression. It is useful to rewrite our result in terms of electron energy. We assume that the electron experiences a considerable energy gain due to the increase of its longitudinal momentum, so that the terminal energy is
$3\pi /2<{\Phi}_0<5\pi /2$
, which, in turn, invalidates the derived expression. It is useful to rewrite our result in terms of electron energy. We assume that the electron experiences a considerable energy gain due to the increase of its longitudinal momentum, so that the terminal energy is
![]() ${\varepsilon}^{\mathrm{term}}\approx {cp}_{\parallel}^{\mathrm{term}}\approx c\Delta {p}_{\parallel}^{\mathrm{term}}$
. We then have the following:
${\varepsilon}^{\mathrm{term}}\approx {cp}_{\parallel}^{\mathrm{term}}\approx c\Delta {p}_{\parallel}^{\mathrm{term}}$
. We then have the following:
 $$\begin{align}\frac{\varepsilon^{\mathrm{term}}}{m_{\textrm{e}}{c}^2} = 2{a}_{\ast}\frac{\pi^2{w}_0^2}{\lambda_0^2}\cos \left({\Phi}_0-\pi \right).\end{align}$$
$$\begin{align}\frac{\varepsilon^{\mathrm{term}}}{m_{\textrm{e}}{c}^2} = 2{a}_{\ast}\frac{\pi^2{w}_0^2}{\lambda_0^2}\cos \left({\Phi}_0-\pi \right).\end{align}$$
We now take into account the expression for
![]() ${a}_{\ast }$
in terms of the period-averaged power
${a}_{\ast }$
in terms of the period-averaged power
![]() $P$
given by Equation (C21) to obtain the following practical expression:
$P$
given by Equation (C21) to obtain the following practical expression:
In comparison to the acceleration by a CP-LG beam with the same power
![]() $P$
[
Reference Shi, Blackman and Arefiev
40
], the terminal energy in the LP-LG beam is lower by a factor of
$P$
[
Reference Shi, Blackman and Arefiev
40
], the terminal energy in the LP-LG beam is lower by a factor of
![]() $\sqrt{2}$
.
$\sqrt{2}$
.
Figure 5 provides information of the long-term electron acceleration in the 3D PIC simulation. Figure 5(a) shows the electron energy distribution as a function of
![]() $x$
at
$x$
at
![]() $t = 261$
fs. Note that the plot of
$t = 261$
fs. Note that the plot of
![]() ${n}_{\textrm{e}}$
integrated over the laser beam cross-section is shown in Figure 7(c) of Appendix A. By this point, the electrons have roughly traveled a distance of
${n}_{\textrm{e}}$
integrated over the laser beam cross-section is shown in Figure 7(c) of Appendix A. By this point, the electrons have roughly traveled a distance of
![]() $100{\lambda}_0$
with the laser beam. Note that
$100{\lambda}_0$
with the laser beam. Note that
![]() $t = 261$
fs is chosen as the time of the snapshot in order to facilitate a comparison with the results for the CP-LG beam presented by Shi et al.[
Reference Shi, Blackman and Arefiev
40
]. The pronounced bunching is maintained by the periodic accelerating structure of
$t = 261$
fs is chosen as the time of the snapshot in order to facilitate a comparison with the results for the CP-LG beam presented by Shi et al.[
Reference Shi, Blackman and Arefiev
40
]. The pronounced bunching is maintained by the periodic accelerating structure of
![]() ${E}_{\parallel }$
. The third bunch travels close to the peak of the laser envelope, which results in the highest electron energy gain. In what follows, we focus on this specific bunch.
${E}_{\parallel }$
. The third bunch travels close to the peak of the laser envelope, which results in the highest electron energy gain. In what follows, we focus on this specific bunch.

Figure 5 Result of the long-term electron acceleration in the reflected LP-LG laser beam close to the beam axis. (a) Electron energy distribution as a function of
![]() $x$
at
$x$
at
![]() $t = 261$
fs for electrons with
$t = 261$
fs for electrons with
![]() $r<1.5\ \unicode{x3bc} \mathrm{m}$
. The inset shows the third bunch that is marked with the dashed rectangle in the main plot. (b) Time evolution of the electron distribution over the divergence angle
$r<1.5\ \unicode{x3bc} \mathrm{m}$
. The inset shows the third bunch that is marked with the dashed rectangle in the main plot. (b) Time evolution of the electron distribution over the divergence angle
![]() $\theta$
in the third bunch (
$\theta$
in the third bunch (
![]() $r<2{w}_0$
). (c) Time evolution of the electron energy spectrum in the third bunch. The black dashed curve is the prediction obtained from Equation (3) with
$r<2{w}_0$
). (c) Time evolution of the electron energy spectrum in the third bunch. The black dashed curve is the prediction obtained from Equation (3) with
![]() ${\Phi}_0 = 0.8\pi$
. The start time of the acceleration is used as an adjustable parameter. (d) Electron energy versus the divergence angle in the third bunch shown in the inset of panel (a).
${\Phi}_0 = 0.8\pi$
. The start time of the acceleration is used as an adjustable parameter. (d) Electron energy versus the divergence angle in the third bunch shown in the inset of panel (a).
Figures 5(b) and 5(c) show the time evolution of the divergence angle and electron energy within the third bunch (see the dashed rectangle and the inset in Figure 5(a)). After an initial stage that lasts about 80 fs, the distribution over the divergence angle reaches its asymptotic shape. It can be seen from the snapshot in Figure 5(b) (taken at
![]() $t = 261$
fs) that the bunch is monoenergetic, with most electrons having a divergence angle that is less than 10 mrad. The time evolution of the energy spectrum, shown in Figure 5(c), confirms that the bunch accelerates roughly as a whole. The dashed curve is the solution given by Equation (3). We used the start time of the acceleration as an adjustable parameter because our model only captures the acceleration after the longitudinal motion becomes ultra-relativistic. The phase
$t = 261$
fs) that the bunch is monoenergetic, with most electrons having a divergence angle that is less than 10 mrad. The time evolution of the energy spectrum, shown in Figure 5(c), confirms that the bunch accelerates roughly as a whole. The dashed curve is the solution given by Equation (3). We used the start time of the acceleration as an adjustable parameter because our model only captures the acceleration after the longitudinal motion becomes ultra-relativistic. The phase
![]() ${\Phi}_0$
is another adjustable parameter that we use to match the time evolution of the electron energy in the bunch. We find that
${\Phi}_0$
is another adjustable parameter that we use to match the time evolution of the electron energy in the bunch. We find that
![]() ${\Phi}_0\approx 0.8\pi$
provides the best fit, the result of which is shown in Figure 5(c). The large energy spread at the early stage is likely due to the presence of the two lobes shown in Figure 2. The good agreement at later times indicates that our model captures relatively well the key aspects of the on-axis electron acceleration.
${\Phi}_0\approx 0.8\pi$
provides the best fit, the result of which is shown in Figure 5(c). The large energy spread at the early stage is likely due to the presence of the two lobes shown in Figure 2. The good agreement at later times indicates that our model captures relatively well the key aspects of the on-axis electron acceleration.
We find that the electron bunches retain noticeable asymmetry following their prolonged interaction with the laser beam. To illustrate the asymmetry, Figures 6(a) and 6(b) show the areal density
![]() ${\rho}_{\textrm{e}}$
and the cell-averaged divergence angle
${\rho}_{\textrm{e}}$
and the cell-averaged divergence angle
![]() $\theta$
in the cross-section of the third bunch at
$\theta$
in the cross-section of the third bunch at
![]() $t = 261$
fs. The bunch asymmetry is likely imprinted by the asymmetry in
$t = 261$
fs. The bunch asymmetry is likely imprinted by the asymmetry in
![]() ${E}_{x}$
shown in Figure 1(e). Since the electron bunches are moving slower than the laser wave-fronts, each bunch experiences a rotating
${E}_{x}$
shown in Figure 1(e). Since the electron bunches are moving slower than the laser wave-fronts, each bunch experiences a rotating
![]() ${E}_{x}$
. This can be shown by examining the field structure at the location of a forward-moving ultra-relativistic electron bunch. We calculate
${E}_{x}$
. This can be shown by examining the field structure at the location of a forward-moving ultra-relativistic electron bunch. We calculate
![]() ${E}_{x}$
in the beam cross-section using the analytical expression given in Appendix C. The longitudinal position is set by the expression
${E}_{x}$
in the beam cross-section using the analytical expression given in Appendix C. The longitudinal position is set by the expression
![]() $x = ct+{\Phi}_0{\lambda}_0/2\pi$
to mimic the longitudinal ultra-relativistic motion of an electron bunch. We set
$x = ct+{\Phi}_0{\lambda}_0/2\pi$
to mimic the longitudinal ultra-relativistic motion of an electron bunch. We set
![]() ${\Phi}_0 = 0.8\pi$
, as this was the injection phase determined by our analysis. Figures 6(c)–6(e) show
${\Phi}_0 = 0.8\pi$
, as this was the injection phase determined by our analysis. Figures 6(c)–6(e) show
![]() ${E}_{x}$
at
${E}_{x}$
at
![]() $\tilde{x} = 0.1$
, 0.45 and 2.3, respectively. These locations correspond to the snapshots in Figures 2, 3 and 5. The plots confirm that the field is indeed rotating, but they also show that the rotation is relatively slow, which is likely the reason why the asymmetry is retained by the electron bunch.
$\tilde{x} = 0.1$
, 0.45 and 2.3, respectively. These locations correspond to the snapshots in Figures 2, 3 and 5. The plots confirm that the field is indeed rotating, but they also show that the rotation is relatively slow, which is likely the reason why the asymmetry is retained by the electron bunch.

Figure 6 (a) Areal density
![]() ${\rho}_{\textrm{e}}$
and (b) cell-averaged divergence angle
${\rho}_{\textrm{e}}$
and (b) cell-averaged divergence angle
![]() $\theta$
in the cross-section of the third bunch at
$\theta$
in the cross-section of the third bunch at
![]() $t = 261$
fs and
$t = 261$
fs and
![]() $\tilde{x} = 2.3$
. (c)–(e) Snapshots of the longitudinal electric field
$\tilde{x} = 2.3$
. (c)–(e) Snapshots of the longitudinal electric field
![]() ${E}_{x}/{E}_{x0}$
in the cross-section of the laser beam at
${E}_{x}/{E}_{x0}$
in the cross-section of the laser beam at
![]() $\tilde{x} = 0.1$
,
$\tilde{x} = 0.1$
,
![]() $t = 9$
fs (c),
$t = 9$
fs (c),
![]() $\tilde{x} = 0.45$
,
$\tilde{x} = 0.45$
,
![]() $t = 46$
fs (d) and
$t = 46$
fs (d) and
![]() $\tilde{x} = 2.3$
,
$\tilde{x} = 2.3$
,
![]() $t = 261$
fs (e). Here,
$t = 261$
fs (e). Here,
![]() ${E}_{x}$
is calculated using the analytical expression Equation (C28) given in Appendix C and
${E}_{x}$
is calculated using the analytical expression Equation (C28) given in Appendix C and
![]() ${E}_{x0}$
is the amplitude of
${E}_{x0}$
is the amplitude of
![]() ${E}_{x}$
at
${E}_{x}$
at
![]() $\tilde{x} = 0$
,
$\tilde{x} = 0$
,
![]() $r = 0$
.
$r = 0$
.
We conclude this section by providing additional parameters of the most energetic electron bunch (the third bunch) generated by the considered 600 TW LP-LG laser beam. The electron energy in the bunch is 0.29 GeV with a full width at half maximum (FWHM) of approximately
![]() $10\%$
. The bunch has a charge of 9 pC and a duration of approximately 270 as. The divergence angle is as low as
$10\%$
. The bunch has a charge of 9 pC and a duration of approximately 270 as. The divergence angle is as low as
![]() ${0.57}^{\circ }$
(10 mrad). The normalized emittance in
${0.57}^{\circ }$
(10 mrad). The normalized emittance in
![]() $y$
is
$y$
is
![]() ${\tilde{\varepsilon}}_{\textrm{rms},y}\approx 1.6\times {10}^{-6}$
and the normalized emittance in
${\tilde{\varepsilon}}_{\textrm{rms},y}\approx 1.6\times {10}^{-6}$
and the normalized emittance in
![]() $z$
is
$z$
is
![]() ${\tilde{\varepsilon}}_{\textrm{rms},z}\approx 1.4\times {10}^{-6}$
.
${\tilde{\varepsilon}}_{\textrm{rms},z}\approx 1.4\times {10}^{-6}$
.
5 Summary and discussion
Using 3D PIC simulations, we have examined electron acceleration by a 600 TW LP-LG laser beam with
![]() $l = -1$
reflected off a plasma with a sharp density gradient. The simulations show that electrons can be effectively injected into the laser beam during its reflection. The electrons that are injected close to the laser axis experience a prolonged longitudinal acceleration by the longitudinal laser electric field. The simulations also show that the laser beam generates a train of mono-energetic ultra-relativistic electron bunches with a small divergence angle. The distinctive features of this acceleration mechanism are the formation of multiple sub-
$l = -1$
reflected off a plasma with a sharp density gradient. The simulations show that electrons can be effectively injected into the laser beam during its reflection. The electrons that are injected close to the laser axis experience a prolonged longitudinal acceleration by the longitudinal laser electric field. The simulations also show that the laser beam generates a train of mono-energetic ultra-relativistic electron bunches with a small divergence angle. The distinctive features of this acceleration mechanism are the formation of multiple sub-
![]() $\unicode{x3bc} \mathrm{m}$
electron bunches, their relatively short acceleration distance (around
$\unicode{x3bc} \mathrm{m}$
electron bunches, their relatively short acceleration distance (around
![]() $100\ \unicode{x3bc} \mathrm{m}$
) and their high density (in the range of the critical density).
$100\ \unicode{x3bc} \mathrm{m}$
) and their high density (in the range of the critical density).
An important conclusion from our study is that the key features that were previously reported for a CP-LG beam[ Reference Shi, Blackman, Stutman and Arefiev 39 , Reference Shi, Blackman and Arefiev 40 ] are retained in the case of an LP-LG laser beam. It is likely that experimentally it will be easier to generate a high-power LP-LG beam than a high-power CP-LG beam. This is because the laser beams at high-power laser facilities are LP. Changing the polarization introduces additional challenges and complications that our approach of using an LP-LG beam allows one to circumvent. We hope that this aspect will make it easier to perform a proof-of-principle experiment.
Even though there are key similarities, there are also differences in electron injection and acceleration between the cases of LP-LG and CP-LG beams. The injection into the LP-LG beam is more complex, leading to a formation of two side-lobes that accompany the on-axis bunch. The asymmetry of the longitudinal electric field causes the on-axis electron bunches to become asymmetric. In contrast to that, the bunches generated by a CP-LG beam are axisymmetrical. For two beams with the same power, the LP-LG beam has weaker on-axis electric and magnetic fields. The reduction in the field strength leads to a reduced energy gain, with the terminal electron energy being lower by roughly a factor of
![]() $\sqrt{2}$
.
$\sqrt{2}$
.
Our mechanism relies on electrons becoming relativistic during the injection process. It is this feature that allows the injected electrons to surf with the laser pulse without quickly slipping from an accelerating phase into an adjacent decelerating phase. Since the longitudinal laser electric field plays a critical role in the injection process, its amplitude needs to be relativistic to generate relativistic injected electrons. A reduction of the incident laser power can thus degrade the mono-energetic spectra of the electron bunches by reducing the amplitude of the longitudinal field. To examine this aspect, we ran an additional simulation with a reduced incident power of 60 TW. Even though the laser still generates electron bunches in this case, the bunches are no longer mono-energetic. The peak energy is also noticeably lower than the value predicted by Equation (6). The underlying cause is most likely the inability of electrons to stay for a prolonged period of time in an accelerating phase.
In this work, we primarily focused on the most energetic (third) electron bunch. The considered laser pulse generates five distinct electron bunches. Their parameters are given in Table 3 of Appendix A. We want to point out that the front and tail of the considered laser pulse are steeper than what one would expect for a Gaussian pulse with the same FWHM, which was a deliberate choice made to reduce the size of the moving window and thus computational costs. The electrons must be relativistic during their injection, so that they can start moving with the laser beam without significant slipping. If this is not the case, then the mono-energetic feature discussed earlier might be hard to achieve. A dedicated study is required to determine the role of the temporal shape of the laser pulse and its overall duration. We anticipate that a longer laser pulse would produce a large number of ultra-relativistic electron bunches. For example, an 800 fs 600 TW LP-LG laser beam[Reference Zhu, Zhu, Li, Zhu, Ma, Lu, Fan, Liu, Zhou, Xu, Zhang, Xie, Yang, Wang, Ouyang, Wang, Li, Yang, Fan, Sun, Liu, Li, Zhang, Tao, Sun, Zhu, Wang, Jiao, Ren, Li, Jiao, Huang and Lin46] contains roughly 300 cycles, so it has the potential to generate a similar number of bunches. Such a pre-modulated electron beam with high charge can potentially be used to generate coherent undulator radiation and to create a free-electron laser[Reference Huang, Ding and Schroeder50, Reference MacArthur, Lutman, Krzywinski and Huang53].
Table 2 Parameters used for the four simulations depicted in Figure 7.

Table 3 Parameters of all five electron bunches at
![]() $t$
= 261 fs.
$t$
= 261 fs.

Appendices
A Convergence test
It was shown by Shi et al.[
Reference Shi, Blackman, Stutman and Arefiev
39
] that the characteristics of the accelerated electron population in the setup considered in this paper can be sensitive to the resolution used by the 3D PIC simulation. We ran a series of 3D PIC simulations using a 600 TW LP-LG beam with
![]() $l = -1$
and
$l = -1$
and
![]() $p = 0$
to identify the simulation parameters that provide convergent results. In our convergence test, we varied the cell size and the number of macro-particles per cell. All relevant simulation parameters chosen for the convergence test are given in Table 2. The simulations were performed using EPOCH[
Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers
51
,
54
].
$p = 0$
to identify the simulation parameters that provide convergent results. In our convergence test, we varied the cell size and the number of macro-particles per cell. All relevant simulation parameters chosen for the convergence test are given in Table 2. The simulations were performed using EPOCH[
Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers
51
,
54
].
There are two features that we use to compare the simulations: the electron spectrum and the electron density. We use the linear density
![]() ${\Lambda}_{\textrm{e}}$
, which is the number density integrated in the cross-section of the laser beam. Figure 7(b) shows
${\Lambda}_{\textrm{e}}$
, which is the number density integrated in the cross-section of the laser beam. Figure 7(b) shows
![]() ${\Lambda}_{\textrm{e}}$
early in the simulation at
${\Lambda}_{\textrm{e}}$
early in the simulation at
![]() $t = 9$
fs. The formation of individual electron bunches is clearly visible in this plot. The curves for higher resolution simulations, that is, simulations #3 and #4, are similar, which suggests that reducing the cell size below
$t = 9$
fs. The formation of individual electron bunches is clearly visible in this plot. The curves for higher resolution simulations, that is, simulations #3 and #4, are similar, which suggests that reducing the cell size below
![]() $1/80\ \unicode{x3bc} \mathrm{m}$
may not be necessary. Figure 7(d) shows four bunches generated by the laser pulse after they travel a significant distance in vacuum. Again, the curves for simulations #3 and #4 are very similar.
$1/80\ \unicode{x3bc} \mathrm{m}$
may not be necessary. Figure 7(d) shows four bunches generated by the laser pulse after they travel a significant distance in vacuum. Again, the curves for simulations #3 and #4 are very similar.

Figure 7 (a), (c) Linear density profiles early in the formation process of electron bunches,
![]() $t = 9$
fs (panel (a)), and after the bunches have experienced prolonged acceleration,
$t = 9$
fs (panel (a)), and after the bunches have experienced prolonged acceleration,
![]() $t = 261$
fs (panel (c)). (b) Energy spectra of the third bunch (inside the dashed rectangle) from panel (a). (d) Energy spectra of the third bunch (inside the dashed rectangle) from panel (c). The legend in each plot provides the simulation number from Table 2.
$t = 261$
fs (panel (c)). (b) Energy spectra of the third bunch (inside the dashed rectangle) from panel (a). (d) Energy spectra of the third bunch (inside the dashed rectangle) from panel (c). The legend in each plot provides the simulation number from Table 2.
Electron bunches experience longitudinal acceleration while they travel in vacuum with the laser pulse. It is therefore important to check not only the density of the bunches, but also their energy spectrum
![]() $\mathrm{d}N/\mathrm{d}{\varepsilon}_{\textrm{e}}$
, where
$\mathrm{d}N/\mathrm{d}{\varepsilon}_{\textrm{e}}$
, where
![]() $N$
and
$N$
and
![]() ${\varepsilon}_{\textrm{e}}$
are the electron number and energy, respectively. Figure 7(b) shows the spectrum of the third bunch (inside the dashed rectangle) in Figure 7(a). Figure 7(d) shows the spectrum of the same bunch (inside the dashed rectangle in Figure 7(c)) after it has experienced extended acceleration. These spectra confirm that simulations #3 and #4 produce similar results. In the main text, we use the results of simulation #4. This simulation is deemed to be reliable based on the presented convergence test.
${\varepsilon}_{\textrm{e}}$
are the electron number and energy, respectively. Figure 7(b) shows the spectrum of the third bunch (inside the dashed rectangle) in Figure 7(a). Figure 7(d) shows the spectrum of the same bunch (inside the dashed rectangle in Figure 7(c)) after it has experienced extended acceleration. These spectra confirm that simulations #3 and #4 produce similar results. In the main text, we use the results of simulation #4. This simulation is deemed to be reliable based on the presented convergence test.
B Parameters of all the bunches generated by the linearly polarized Laguerre–Gaussian beam
In the main text, we focused on the most energetic bunch, which is the third bunch out of the five bunches generated by the considered 600 TW LP-LG laser beam. Table 3 provides various parameters for all five bunches. The parameters are calculated at
![]() $t = 261$
fs.
$t = 261$
fs.
C Longitudinal electric field of a linearly polarized Laguerre–Gaussian laser beam
Here we follow the notations introduced by Shi et al.[
Reference Shi, Blackman and Arefiev
40
] to provide analytical expressions for the fields of an LP helical beam in the paraxial approximation. Specifically, it is assumed that the diffraction angle, defined as
![]() ${\theta}_{\textrm{d}} = {w}_0/{x}_{\textrm{R}}$
, is small, where
${\theta}_{\textrm{d}} = {w}_0/{x}_{\textrm{R}}$
, is small, where
![]() ${w}_0$
is the beam waist and
${w}_0$
is the beam waist and
![]() ${x}_{\textrm{R}} = \pi {w}_0^2/{\lambda}_0$
is the Rayleigh range. We consider a beam propagating along the
${x}_{\textrm{R}} = \pi {w}_0^2/{\lambda}_0$
is the Rayleigh range. We consider a beam propagating along the
![]() $x$
-axis. Its transverse electric field is polarized along the
$x$
-axis. Its transverse electric field is polarized along the
![]() $y$
-axis. It is convenient to normalize
$y$
-axis. It is convenient to normalize
![]() $x$
to
$x$
to
![]() ${x}_{\textrm{R}}$
and
${x}_{\textrm{R}}$
and
![]() $y$
and
$y$
and
![]() $z$
to
$z$
to
![]() ${w}_0$
or
${w}_0$
or
![]() $w(x)$
:
$w(x)$
:
The solution of the wave equation corresponding to an LG beam is given by the following:
where
![]() $g$
is the envelope function with
$g$
is the envelope function with
![]() $\max (g) = 1$
,
$\max (g) = 1$
,
is the phase variable, and
 $$\begin{align}{\psi}_{\textrm{p},\textrm{l}}\left(\tilde{x},\tilde{r},\phi \right) &= {C}_{p,l}f{\left(\tilde{x}\right)}^{\mid l\mid +1+2p}{\left(1+{\tilde{x}}^2\right)}^{p}{L}_{p}^{\mid l\mid}\left(\frac{2{\tilde{r}}^2}{1+{\tilde{x}}^2}\right){\left(\sqrt{2}\tilde{r}\right)}^{\mid l\mid} \nonumber\\& \quad \times \exp \left[-{\tilde{r}}^2f\left(\tilde{x}\right)\right]\exp \left( il\phi \right)\end{align}$$
$$\begin{align}{\psi}_{\textrm{p},\textrm{l}}\left(\tilde{x},\tilde{r},\phi \right) &= {C}_{p,l}f{\left(\tilde{x}\right)}^{\mid l\mid +1+2p}{\left(1+{\tilde{x}}^2\right)}^{p}{L}_{p}^{\mid l\mid}\left(\frac{2{\tilde{r}}^2}{1+{\tilde{x}}^2}\right){\left(\sqrt{2}\tilde{r}\right)}^{\mid l\mid} \nonumber\\& \quad \times \exp \left[-{\tilde{r}}^2f\left(\tilde{x}\right)\right]\exp \left( il\phi \right)\end{align}$$
is a mode with a radial index
![]() $p$
and twist index
$p$
and twist index
![]() $l$
. Here we introduced the following:
$l$
. Here we introduced the following:
 $$\begin{align}f\left(\tilde{x}\right) = \frac{1-i\tilde{x}}{1+{\tilde{x}}^2} = \frac{1}{\sqrt{1+{\tilde{x}}^2}}\exp \left(-i\arctan\tilde{x}\right).\end{align}$$
$$\begin{align}f\left(\tilde{x}\right) = \frac{1-i\tilde{x}}{1+{\tilde{x}}^2} = \frac{1}{\sqrt{1+{\tilde{x}}^2}}\exp \left(-i\arctan\tilde{x}\right).\end{align}$$
The
![]() ${L}_{p}^{\mid l\mid }$
function is the generalized Laguerre polynomial and
${L}_{p}^{\mid l\mid }$
function is the generalized Laguerre polynomial and
![]() ${C}_{p,l}$
is a normalization constant. The modes
${C}_{p,l}$
is a normalization constant. The modes
![]() ${\psi}_{p,l}\left(\tilde{x},\tilde{r},\phi \right)$
are orthonormal at a given
${\psi}_{p,l}\left(\tilde{x},\tilde{r},\phi \right)$
are orthonormal at a given
![]() $\tilde{x}$
[
Reference Allen, Beijersbergen, Spreeuw and Woerdman
55
], with the following:
$\tilde{x}$
[
Reference Allen, Beijersbergen, Spreeuw and Woerdman
55
], with the following:
 $$\begin{align}{C}_{p,l} = \sqrt{\frac{2p!}{\pi \left(p+|l|\right)!}},\end{align}$$
$$\begin{align}{C}_{p,l} = \sqrt{\frac{2p!}{\pi \left(p+|l|\right)!}},\end{align}$$
such that
 $$\begin{align}{\int}_0^{2\pi } \mathrm{d}\phi {\int}_0^{\infty }{\psi}_{l,p}\left(\tilde{x},\tilde{r},\phi \right){\psi}_{p,l}^{\ast}\left(\tilde{x},\tilde{r},\phi \right)\tilde{r}\mathrm{d}\tilde{r} = 1.\end{align}$$
$$\begin{align}{\int}_0^{2\pi } \mathrm{d}\phi {\int}_0^{\infty }{\psi}_{l,p}\left(\tilde{x},\tilde{r},\phi \right){\psi}_{p,l}^{\ast}\left(\tilde{x},\tilde{r},\phi \right)\tilde{r}\mathrm{d}\tilde{r} = 1.\end{align}$$
The period-averaged power in this beam is as follows:
where
![]() $c$
is the speed of light. Note that
$c$
is the speed of light. Note that
![]() ${E}_0$
is not the peak amplitude of
${E}_0$
is not the peak amplitude of
![]() ${E}_{y}$
in the case of an LG beam.
${E}_{y}$
in the case of an LG beam.
The mode considered in the main text has
![]() $p = 0$
and
$p = 0$
and
![]() $l = -1$
. The next equation then follows from Equation (C5):
$l = -1$
. The next equation then follows from Equation (C5):
 $$\begin{align}{E}_{y} &= {E}_0g\left(\xi \right){C}_{0,-1}{\left[f\left(\tilde{x}\right)\right]}^2\sqrt{2}\tilde{r}\exp \left[-{\tilde{r}}^2f\left(\tilde{x}\right)\right] \nonumber\\& \quad \times\exp \left(- i\phi \right)\exp \left(2i\tilde{x}/{\theta}_{\textrm{d}}^2- i\omega t\right).\end{align}$$
$$\begin{align}{E}_{y} &= {E}_0g\left(\xi \right){C}_{0,-1}{\left[f\left(\tilde{x}\right)\right]}^2\sqrt{2}\tilde{r}\exp \left[-{\tilde{r}}^2f\left(\tilde{x}\right)\right] \nonumber\\& \quad \times\exp \left(- i\phi \right)\exp \left(2i\tilde{x}/{\theta}_{\textrm{d}}^2- i\omega t\right).\end{align}$$
As shown by Shi et al.[ Reference Shi, Blackman and Arefiev 40 ], the corresponding longitudinal electric field is as follows:
 $$\begin{align}{E}_{x} = \frac{i{\theta}_{\textrm{d}}}{2}\left(\frac{1}{\tilde{r}}{e}^{{i}\phi}-2f\tilde{r}\cos \phi \right){E}_{y},\end{align}$$
$$\begin{align}{E}_{x} = \frac{i{\theta}_{\textrm{d}}}{2}\left(\frac{1}{\tilde{r}}{e}^{{i}\phi}-2f\tilde{r}\cos \phi \right){E}_{y},\end{align}$$
where it is taken into account that
![]() $p = 0$
and
$p = 0$
and
![]() $l = -1$
. The longitudinal electric field on the axis is given by the following:
$l = -1$
. The longitudinal electric field on the axis is given by the following:
It is convenient to rewrite this expression by introducing the phase as follows:
and amplitude:
so that
The expression for
![]() $P$
, recast in terms of the normalized amplitude, is as follows:
$P$
, recast in terms of the normalized amplitude, is as follows:
and reads as follows:
 $$\begin{align}P = {a}_{\ast}^2\frac{\pi^4}{2}{\left(\frac{w_0}{\lambda_0}\right)}^4\frac{m_{\textrm{e}}^2{c}^5}{e^2}.\end{align}$$
$$\begin{align}P = {a}_{\ast}^2\frac{\pi^4}{2}{\left(\frac{w_0}{\lambda_0}\right)}^4\frac{m_{\textrm{e}}^2{c}^5}{e^2}.\end{align}$$
It follows from this relation that:
 $$\begin{align}{a}_{\ast}\approx 50{\left(\frac{\lambda_0}{w_0}\right)}^2{\left(P\kern0.22em \left[ \mathrm{PW}\right]\kern0.1em \right)}^{1/2}.\end{align}$$
$$\begin{align}{a}_{\ast}\approx 50{\left(\frac{\lambda_0}{w_0}\right)}^2{\left(P\kern0.22em \left[ \mathrm{PW}\right]\kern0.1em \right)}^{1/2}.\end{align}$$
In the main text, we examine the field structure of
![]() ${E}_{x}$
away from the axis. The corresponding expression follows from Equation (C14):
${E}_{x}$
away from the axis. The corresponding expression follows from Equation (C14):
 $$\begin{align}{E}_{x} = {iE}_{x0}{e}^{i{\Phi}_{\ast }}\frac{e^{-{r}_{\ast}^2}}{1+{\tilde{x}}^2}\left[1-2\left(1-i\tilde{x}\right){r}_{\ast}^2\cos \phi {e}^{-i\phi}\right],\end{align}$$
$$\begin{align}{E}_{x} = {iE}_{x0}{e}^{i{\Phi}_{\ast }}\frac{e^{-{r}_{\ast}^2}}{1+{\tilde{x}}^2}\left[1-2\left(1-i\tilde{x}\right){r}_{\ast}^2\cos \phi {e}^{-i\phi}\right],\end{align}$$
where, for compactness, we used the following notations:
The real part, under the assumption that
![]() $g\left(\xi \right)$
has no imaginary part, is given by the following:
$g\left(\xi \right)$
has no imaginary part, is given by the following:
 $$\begin{align}\kern0.1em \mathrm{Re}({E}_{x}) = -{E}_{x0}\frac{e^{-{r}_{\ast}^2}}{1+{\tilde{x}}^2} & \left[\left(1-2{y}_{\ast}^2+2\tilde{x}{y}_{\ast }{z}_{\ast}\right)\right. \nonumber\\& \left.\quad \times \sin {\Phi}_{\ast }+2{y}_{\ast}\left(\tilde{x}{y}_{\ast }+{z}_{\ast}\right)\cos {\Phi}_{\ast}\right],\end{align}$$
$$\begin{align}\kern0.1em \mathrm{Re}({E}_{x}) = -{E}_{x0}\frac{e^{-{r}_{\ast}^2}}{1+{\tilde{x}}^2} & \left[\left(1-2{y}_{\ast}^2+2\tilde{x}{y}_{\ast }{z}_{\ast}\right)\right. \nonumber\\& \left.\quad \times \sin {\Phi}_{\ast }+2{y}_{\ast}\left(\tilde{x}{y}_{\ast }+{z}_{\ast}\right)\cos {\Phi}_{\ast}\right],\end{align}$$
where
![]() ${y}_{\ast} = {r}_{\ast}\cos \phi$
and
${y}_{\ast} = {r}_{\ast}\cos \phi$
and
![]() ${z}_{\ast} = {r}_{\ast}\sin \phi$
.
${z}_{\ast} = {r}_{\ast}\sin \phi$
.
Data availability
The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
Code availability
PIC simulations were performed with the fully relativistic open-access 3D PIC code EPOCH[ 54 ].
Acknowledgments
Y.S. acknowledges the support by USTC Research Funds of the Double First-Class Initiative, Strategic Priority Research Program of CAS (Grant No. XDA25010200), CAS Project for Young Scientists in Basic Research (Grant No. YSBR060) and Newton International Fellows Alumni follow-on funding. D.R.B. and A.A. acknowledge the support by the National Science Foundation (Grant No. PHY 1903098). Simulations were performed with EPOCH (developed under UK EPSRC Grants EP/G054950/1, EP/G056803/1, EP/G055165/1 and EP/M022463/1). The simulations and numerical calculations in this paper have been done on the supercomputing system in the Supercomputing Center of University of Science and Technology of China. This research used the resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231.