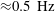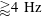Drag forces on a bed particle in open-channel flow: effects of pressure spatial fluctuations and very-large-scale motions

Abstract

The fluctuating drag forces acting on spherical roughness elements comprising the bed of an open-channel flow have been recorded along with synchronous measurements of the surrounding velocity field using stereoscopic particle image velocimetry. The protrusion of the target particle, equipped with a force sensor, was systematically varied between zero and one-half diameter relative to the hexagonally packed adjacent spheres. Premultiplied spectra of drag force fluctuations were found to have bimodal shapes with a low-frequency (${\approx}0.5~\text{Hz}$) peak corresponding to the presence of very-large-scale motions (VLSMs) in the turbulent flow. The high-frequency ($\gtrapprox 4~\text{Hz}$) region of the drag force spectra cannot be explained by velocity time series extracted from points around the particle, but instead appears to be dominated by the action of pressure gradients in the overlying flow field. For small particle protrusions, this high-frequency region contributes a majority of the drag force variance, while the relative importance of the low-frequency drag force fluctuations increases with increasing protrusion. The amplitude of high-frequency drag force fluctuations is modulated by the VLSMs irrespective of particle protrusion. These results provide some insight into the mechanics of bed particle stability and indicate that the optimum conditions for particle entrainment may occur when a low-pressure region embedded in the high-velocity portion of a VLSM overlays a particle.

1 Introduction

Estimation of drag forces acting on aquatic surfaces are of interest in many areas of hydraulic and eco-hydraulic engineering, including the assessment of: friction factor; the initiation and rate of sediment transport; appropriate flow regimes for aquatic plants, invertebrates and other biota; and general flow–structure interaction problems (e.g. Ancey et al. 2008; Nikora et al. 2012; Dey 2014; Kidanemariam & Uhlmann 2017). This paper will focus on the assessment of drag force fluctuations acting on stationary bed roughness elements. Such considerations are important in order to refine bulk approaches to estimating sediment transport conditions such as threshold Shields parameter (Shields 1936) and include more information about the natural variability of roughness elements and the turbulent velocity field.

The total drag force acting on a bed particle is the sum of pressure and viscous stresses integrated over the particle surface. The surface stresses are related to the velocity field according to the mass and momentum conservation equations supplemented with appropriate boundary conditions. Sufficiently high-resolution velocity measurements to utilise conservation equations are, however, seldom available, and therefore simplified models describing the interrelations of the velocity field and drag are required. The standard approach is to present the instantaneous drag force ( $F$ ) proportional to squared velocity as

(1.1) $$\begin{eqnarray}F(t)={\textstyle \frac{1}{2}}C_{D}\unicode[STIX]{x1D70C}u^{2}A,\end{eqnarray}$$

where $\unicode[STIX]{x1D70C}$ is the fluid density, $u(t)$ is the streamwise velocity component at some representative point near the particle, $t$ is time, $A$ is the particle exposed frontal area, $C_{D}(D^{+})$ is the drag coefficient which absorbs particle shape effects, $D^{+}=Du_{\ast }/\unicode[STIX]{x1D708}$ is the roughness Reynolds number which represents the balance between pressure and viscous drag, $D$ is particle diameter, $u_{\ast }$ is the shear velocity, and $\unicode[STIX]{x1D708}$ is the fluid kinematic viscosity. Dwivedi et al. (2010) presented (1.1) in the frequency ( $f$ ) domain as

(1.2) $$\begin{eqnarray}S_{F}(f)=\left\{\frac{1}{2}C_{D}\unicode[STIX]{x1D70C}A\bar{u}\right\}^{2}\left(\frac{4}{\bar{u}^{2}}S_{u}(f)+\frac{2}{\bar{u}^{4}}\int _{-\infty }^{\infty }S_{u}(f^{\prime })S_{u}(f-f^{\prime })\,\text{d}f^{\prime }\right),\end{eqnarray}$$

where $S_{u}$ and $S_{F}$ are spectra of velocity and force fluctuations, respectively. Equation (1.2) is derived for conditions of a Gaussian velocity probability distribution. When $\bar{u}\gg u^{\prime }$ , the second term on the right-hand side of (1.2) can be neglected. In this case (1.2) indicates a linear relationship between drag fluctuations and velocity fluctuations ( $F^{\prime }\propto u^{\prime }$ ). For $\bar{u}\approx u^{\prime }$ the higher-order term ( $F^{\prime }\propto u^{\prime 2}$ ) becomes important. The prime symbol here indicates a deviation from the time-average value, i.e. $F^{\prime }=F-\bar{F}$ and $u^{\prime }=u-\bar{u}$ . Models relating drag force spectra to velocity spectra are important because the latter have received significantly more experimental attention and are comparatively better understood. Such relationships, however, may not be universally applicable; Dwivedi et al. (2010), for example, reported a break from the expected behaviour at high frequencies attributed to vortex shedding from roughness elements.

A number of studies report data on drag and lift forces acting on sediment particles via pressure measurements (e.g. Hofland 2005; Detert, Nikora & Jirka 2010; Amir, Nikora & Stewart 2014; Celik, Diplas & Dancey 2014), direct force measurements (e.g. Schmeeckle, Nelson & Shreve 2007; Dwivedi et al. 2010) and via numerical simulations (e.g. Chan-Braun, García-Villalba & Uhlmann 2011, 2013; Mazzuoli & Uhlmann 2017). There remains, however, a shortage of data to evaluate mechanisms responsible for drag force generation and to test and refine models coupling velocity and drag force fluctuations. The aim of this paper is to address this shortage with comprehensive measurements and analysis of the instantaneous drag forces acting on roughness elements combined with synchronous measurements of the surrounding velocity field. The main focus is on the identification of the key features of drag spectra and establishing their interrelations with the turbulence structure of the overlying flow. We use spherical roughness elements as an idealised gravel bed particle and adopt the same flow conditions as Cameron, Nikora & Stewart (2017) so that potential links between drag force and the very-large-scale motions (VLSMs or superstructures; e.g. Kim & Adrian 1999; Hutchins & Marusic 2007) identified in that study can be examined. The role of particle exposure, which was originally demonstrated by Fenton & Abbott (1977) to contribute significantly to particle stability, is explored through systematic manipulation of the particle protrusion.

The structure of the paper is as follows: in § 2 we describe our instrumentation including particle image velocimetry (PIV) set-up and the development of an instrumented particle for measuring drag force; in § 3 we present statistical distributions of fluid velocities, drag forces and coupled statistics of velocity–drag interrelations; finally in § 4 we summarise our main findings.

2 Experimental set-up

A set of experiments were conducted using a drag measurement device and stereoscopic PIV in the Aberdeen Open Channel Facility (AOCF). The AOCF consists of an 18 m long by 1.18 m wide recirculating open-channel flume and an instrumental carriage which traverses the length of the flume and houses the PIV system and the support instrumentation. An entrance tank fitted with flow-straightening vanes and honeycomb panels secures a uniform transverse velocity distribution free from large-scale turbulence at the channel entrance. The water level at the free-fall exit of the channel is regulated by a vertical slat weir. Uniform flow was established for a given flow rate by iteratively adjusting the weir and measuring the water surface profile using ultrasonic displacement sensors attached to the flume carriage. Using this procedure, the deviation of flow depth along the 18 m long channel can be held to 0.5 mm, which is approximately the limit of bed flatness and deflections of the channel under load and thermal expansion. The drag measurement device and the PIV system are described in the following sections.

2.1 Drag measurement device

The drag measurement device consists of a 16 mm diameter nylon sphere bonded with epoxy resin to a pair of AE-801 (Kronex Technologies Corp.) sensor elements in a parallel configuration (figure 1 a,b). The sensor elements consist of a $5~\text{mm}\times 0.95~\text{mm}$ by 0.15 mm thick silicon beam with a strain-sensitive resistor implanted on each side. The parallel configuration of the beam elements was selected so that the device would be sensitive predominantly to the applied drag force rather than the torque, which would be measured by a single beam configuration. That is, we expect the output of the device to be somewhat independent of the elevation ( $\unicode[STIX]{x0394}z$ , figure 1 b) at which a force is applied. Figure 1(c) presents data obtained from a finite element model of the structural configuration and indicates that a force applied at the top of the spherical particle will give a measured force approximately 2 % higher than a force applied at the bottom of the sphere. The measured drag force is also weakly sensitive to transverse and vertical loads due to imperfections in the assembly and installation of the device. The off-axis sensitivity was estimated from mechanical loading tests to be approximately 1 %. The addition of two passive resistors to the two embedded resistors on the AE-801 elements completed a half Wheatstone bridge circuit which was supplied with an excitation voltage of 3 V. The bridge output was sampled with a 24-bit analogue-to-digital converter at 2000 Hz. Each AE-801 element was sampled independently and the outputs subsequently averaged.

Figure 1. (a) Drag measurement device; (b) exaggerated deflected shape of the AE-801 strain gauge elements; (c) relative sensitivity to a unit drag force load at $\unicode[STIX]{x0394}z$ ; (d) transfer function of the drag measurement device.

A calibrated device sensitivity of $20~\text{mV}~\text{V}^{-1}$ per newton of applied load was estimated by applying a sequence of precision static loads. The calibrated resolution of the system associated with the 24-bit sampling was $1.5\times 10^{-7}~\text{N}$ . The dynamic response of the sensor was estimated from the rapid unloading response curve (edge response) which can be differentiated to obtain the impulse response and subsequently Fourier-transformed to obtain the amplitude response function (figure 1 d). The response function indicates that measured forces are damped at frequencies beyond 100 Hz, probably due to a thin layer of room-temperature-vulcanising silicon that was applied to waterproof the sensor elements. Frequencies of interest in this study were found to be less than 20 Hz, and over this range the drag measurement device has near-unity gain. Recorded drag forces were found to drift slowly with changes in water temperature. The time scale of the offset drift, however, was significantly larger than that of the turbulence-induced drag force fluctuations, allowing the drift to be removed from the recorded data by a high-pass filter.

The drag measurement device was installed through a hole in the base of the flume and attached to a micrometer adjuster which permitted precision manipulation of the sphere protrusion ( $P$ , figure 1 a). The action of the adjuster translates the instrumented sphere purely in the vertical direction. The surrounding particles remained in a fixed position throughout the experiments.

Figure 2. ‘Mini’ mode PIV configuration (a), and transfer function (b) of ‘mini’ mode (circles) and ‘macro’ mode (squares). The transfer function is separable such that $T(\unicode[STIX]{x1D706}_{x}^{-1},\unicode[STIX]{x1D706}_{y}^{-1},\unicode[STIX]{x1D706}_{z}^{-1})=T(\unicode[STIX]{x1D706}_{x}^{-1})T(\unicode[STIX]{x1D706}_{y}^{-1})T(\unicode[STIX]{x1D706}_{z}^{-1})$ and $\unicode[STIX]{x1D706}_{x}$ , $\unicode[STIX]{x1D706}_{y}$ and $\unicode[STIX]{x1D706}_{z}$ are wavelengths in the corresponding $x$ , $y$ and $z$ directions.

2.2 Stereoscopic particle image velocimetry

Two configurations of stereoscopic PIV were employed: a near-bed high-resolution ‘mini’ mode (in the streamwise-vertical plane), and a flow depth scale ‘macro’ mode (in the transverse-vertical plane). Both ‘mini’ and ‘macro’ mode measurement planes intersected the centre of the test particle (figure 1 a) in such a way that much of the flow field around the upper hemisphere was measured, including the regions where maximum correlation between velocity and drag are typically found (e.g. Dwivedi et al. 2010; Chan-Braun et al. 2013). The ‘mini’ mode (figure 2 a) is a two-camera system with a measurement plane extending $50~\text{mm}\times 20~\text{mm}$ (streamwise $\times$ vertical). Glass-bottomed ‘boats’ sit at the water surface allowing optical access to the flow domain for the cameras and the laser light sheet. The presence of the ‘boats’ disturbs a thin region ( ${\approx}2~\text{mm}$ ) of the flow field near the free surface but has no influence on the near-bed velocity field. As the cameras are oriented at a downwards angle of $45^{\circ }$ , measurement of the flow region below the roughness tops is possible, although some regions very close to the roughness elements needed to be excluded from the analysis due to bright reflections of the laser. The ‘macro’ mode is a four-camera configuration with a measurement plane extending 330 mm in the transverse direction and covering the flow region from the roughness tops to the free surface. This set-up is equivalent to that used in Cameron et al. (2017) and is described in further detail there. Both ‘mini’ and ‘macro’ systems employ Dalsa 4M60 cameras equipped with Nikon 60 mm lenses with aperture set to $\text{f}/16$ . The ‘mini’ mode was sampled at 160 frames per second (f.p.s.), resulting in 80 vector fields per second, while the ‘macro’ mode was sampled at 64 f.p.s. and 100 f.p.s. depending on the flow depth. The camera positions and view angles are calibrated by taking images of a precision dot grid array positioned at different points within the camera field of view. The result of the calibration procedure is a function which relates three-dimensional coordinates within the flow field to two-dimensional image coordinates while fully accounting for refraction at the air–glass–water interfaces. Seeding particles were neutrally buoyant 10–20  $\unicode[STIX]{x03BC}$ m diameter titania-coated hollow glass spheres for the ‘mini’ mode and silver-coated hollow glass spheres with diameters between 20 and 32  $\unicode[STIX]{x03BC}$ m for the ‘macro’ mode. Both seeding types were custom manufactured by Microsphere Technology Ltd. An Oxford Lasers 100 mJ, 532 nm Nd:YAG laser provided the light source for both modes. The light sheet thickness was 1.2 mm and 2.4 mm for the ‘mini’ and ‘macro’ modes, respectively. The measurements from both modes were analysed using an iterative deformation PIV algorithm with $64~\text{pixel}\times 64~\text{pixel}$ Blackman-weighted interrogation regions. The transfer functions (figure 2 b), which indicate the low-pass filtering of the velocity by the combined effects of interrogation region size and the light sheet thickness, indicate a nominal resolution of around 3 mm for the ‘macro’ mode and 1 mm for the ‘mini’ mode.

2.3 Flow configurations

The entire bed of the flume was covered with a single layer of $D=16~\text{mm}$ diameter glass spheres in a hexagonally close-packed arrangement. Positioning of the spheres was regulated by perforated stainless-steel plates attached to the bed of the flume. Flow conditions (table 1) were selected to be the same as those used in Cameron et al. (2017). The flows are hydraulically rough and subcritical, with roughness Reynolds numbers $D^{+}=605$ and Froude numbers less than one. A large ratio of channel width to flow depth secures near-two-dimensional flow (Cameron et al. 2017) upstream of the test particle, which was located along the centreline of the flume.

Table 1. Flow conditions for the experiments: $H$ is flow depth above the roughness tops; $B=1180~\text{mm}$ is channel width; $D=16~\text{mm}$ is particle diameter; $Q$ is flow rate; $S_{0}$ is bed surface slope; $U=Q/BH$ is the bulk velocity; $u_{\ast }=\sqrt{gHS_{0}}$ is shear velocity; $R=UH/\unicode[STIX]{x1D708}$ is the bulk Reynolds number; $Fr=U/\sqrt{gH}$ is the Froude number; the $+$ superscript denotes normalisation with the viscous length scale $\unicode[STIX]{x1D708}/u_{\ast }$ ; $\unicode[STIX]{x1D708}$ is fluid kinematic viscosity; and $g$ is acceleration due to gravity.

The studied parameter space (table 2) consists of five flow configurations and nine protrusions ( $P$ ) of the instrumented particle. We ran four types of experiments: (1) short-term (20 min) drag-only measurements, (2) long-term (90 min) drag measurements, (3) synchronous ‘macro’ mode PIV with drag measurements, and (4) synchronous ‘mini’ mode PIV with drag measurements (table 2). It was not practicable to utilise all measurement type/parameter space combinations due to the large storage and processing time requirements for PIV. Instead, a subset of combinations (table 2) were selected encompassing the full extent of the parameter space and optimised to favour long recording times to minimise sampling uncertainty. The short-term drag-only measurements were used only to capture the mean drag force where the measurement duration needed to be kept short to limit the instrument drift. Higher-order statistics were computed using the long-term drag measurements after removing instrument drift with a high-pass filter with a kernel size of 10 min.

Table 2. Experiment matrix: $\dagger$ , drag force measurements, 20 min duration, 2000 Hz; $\ddagger$ , drag force measurements, 90 min, 2000 Hz; $\#$ , synchronous PIV ‘macro’ mode and drag force measurements, 20 min, 50 Hz ( $\text{H030},\ldots ,\text{H070}$ ), 32 Hz (H095, H120); $\Vert$ , synchronous PIV ‘mini’ mode and drag force measurements, 30 min, 80 Hz.

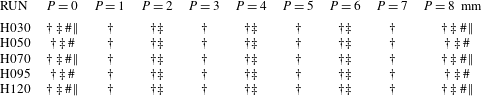
3 Results

3.1 Velocity field

Distributions of double-averaged mean velocity and second-order moments are presented in figure 3 where the overbar and angle brackets are used to denote the time and space averaging operations, respectively. The mean velocity ( $\langle \bar{u}\rangle /u_{\ast }$ ) scales reasonably well with $z/D$ with only a small influence of flow depth. The relative offsets between the velocity profiles when plotted versus $z/H$ reflects the expected trend of increasing friction factor ( ${\sim}u_{\ast }^{2}/U^{2}$ ) with decreasing relative submergence ( $H/D$ ; e.g. Stewart et al. 2018). Analysis in Cameron et al. (2017) indicated that for these flows the measured velocity distributions support a logarithmic range up to $z/H\approx 0.5$ with a von Kármán coefficient of $\unicode[STIX]{x1D705}=0.38$ .

The near-bed normalised velocity variances (figure 3 b,d) generally collapse when plotted versus $z/D$ , whereas in the outer flow the distributions scale with $z/H$ . Immediately above the roughness tops neither scaling holds and the velocity variance is a function of the relative submergence ( $H/D$ ). This submergence effect is often observed in open-channel flows (e.g. Bayazit 1976) but not yet well understood. The linearity of the covariance term $\langle \overline{u^{\prime }w^{\prime }}\rangle$ confirms the two-dimensionality of the studied flows. Higher-order statistics, correlation functions and spectra for these flows are reported in Cameron et al. (2017).

Figure 3. Mean streamwise velocity and velocity variance. The roughness tops are at $z=0$ .

Noting the potential link between turbulence generated in the wake of particles and drag force indicated by Dwivedi et al. (2010), the near-bed turbulent kinetic energy ( $\text{TKE}=0.5\overline{u_{i}^{\prime }u_{i}^{\prime }}$ , where $u_{i}$ is the $i$ th velocity component) is shown in figure 4. The high-protrusion case shows a strong enhancement of TKE behind the particle, reflecting instability of the shear layer that forms between the retarded flow behind the particle and the unobstructed overhead flow. The low-protrusion case in comparison exhibits very weak wake turbulence. Power spectra for the vertical velocity component (figure 4 h) at the point $0.25D$ above the top and $0.75D$ downstream of the centre of the particle (where the highest TKE occurs) indicate a quasi-periodicity of the wake turbulence at around 20 Hz with only a minor influence of the flow depth. Spectra for the streamwise velocity component (figure 4 g) also indicate enhanced energy around 20 Hz but no sharp local maxima are observed, i.e. the energy is spread over a larger range of scales. The relationship between the wake turbulence and the particle drag force will be considered in § 3.3.

Figure 4. (a–f) Turbulent kinetic energy in the near-bed region. (g,h) Spectra of the streamwise and vertical velocity extracted at the position marked by the filled circle in (a–f). Symbols as in figure 3; grey lines, $P=8~\text{mm}$ ; black lines, $P=0~\text{mm}$ . Note that the spheres represented by dashed lines are displaced from the light sheet due to the hexagonal packing.

3.2 Drag force

Short records of measured drag force are shown in figure 5 for the zero ( $P=0$ ) and maximum ( $P=8$ ) protrusion cases. It is readily apparent that the higher-protrusion case corresponds to larger-amplitude and longer-wavelength force fluctuations. It is also interesting to note that the zero-protrusion case features frequent negative drag force events. We will, in this section, further explore the recorded drag force time series using moments of the drag force probability distribution and spectra.

Mean drag force and the higher-order moments of the drag force probability distribution are presented as a function of particle protrusion in figure 6. We find the expected trend of increasing mean drag and drag variance with increasing protrusion, reflecting increased exposure of the instrumented particle to the flow. The mean drag generally increases with decreasing flow depth consistent with the trend for mean velocity (figure 3 c). The zero-protrusion cases show slightly larger drag than the estimated value $\unicode[STIX]{x1D70F}_{0}A_{p}$ , where $\unicode[STIX]{x1D70F}_{0}=\unicode[STIX]{x1D70C}g\bar{H}S_{0}$ is the bed shear stress, $A_{p}=\sqrt{3}D^{2}/2$ is the plan area of the hexagonal region assigned to a particle, $\bar{H}$ is the mean flow depth, $S_{0}$ is the bed slope, $\unicode[STIX]{x1D70C}$ is the fluid density and $g$ is acceleration due to gravity. The difference between the measured and estimated values indicates that the target particle experiences slightly higher drag force than the average particle, probably due to some randomness in the heights of the surrounding particle tops and the non-uniform distribution of bed shear stress due to sidewall effects. The drag force variance increases with increasing flow depth, similar to the trend previously noted for the near-bed velocity variance. The drag force skewness is small ( ${\sim}0.5$ ) while the drag force kurtosis approaches the value for Gaussian distributions (i.e. zero) with increasing protrusion. Chan-Braun et al. (2011) in comparison reported significantly higher kurtosis values of 7.1 and 2.0 for zero-protrusion spheres in a square packing arrangement and transitionally rough flows with a $D^{+}$ of 11 and 49, respectively. At higher roughness Reynolds number ( $D^{+}=119$ ), Mazzuoli & Uhlmann (2017) found a drag force kurtosis of 0.6, within the range reported in figure 6(d).

Figure 5. Time series of measured drag force; black line, ‘H120, $P=0$ ’; grey line, ‘H120, $P=8$ ’.

Figure 6. Statistics of drag force for different protrusions ( $P$ ) and flow depths. Symbols as in figure 3.

Spectra of drag force fluctuations (figure 7) have a similar shape to those of Dwivedi et al. (2010) with a characteristic high-frequency hump. We observe a general collapse of the high-frequency part of the spectra for the different protrusions while the low-frequency region is stratified according to protrusion. The premultiplied spectra exhibit bimodal shapes with characteristic frequencies marked as $f_{1}$ (low frequency) and $f_{2}$ (high frequency) in figure 7. The local maxima in the spectra are useful statistics to evaluate the scaling relationship with protrusion and flow depth and for comparison with near-bed velocity spectra. The characteristic frequencies and their corresponding premultiplied spectral magnitude are extracted for all experiments and collated in figure 8. It is surprising to see that $f_{1}$ and $f_{2}$ and the spectral magnitude at the $f_{2}$ frequency are generally independent of protrusion. Figure 8(b) indicates that the drag force variance is dominated by the high-frequency contributions at low protrusion, transitioning to a low-frequency-dominated process at high protrusion. The spectral magnitude at the $f_{1}$ frequency scales with protrusion in a similar way to the squared exposed frontal area ( $A^{2}$ , equation (1.1), figure 8 b). The near-bed velocity variance in comparison (figure 3 d) is nearly constant in the range $z=0$ to $z=0.5D$ . This suggests that much of the increase in drag force variance with increasing protrusion is associated with increased exposure of the particle to the flow. Spectral magnitudes are higher for the larger flow depths, consistent with the trend for drag force variance previously identified. We will explore the behaviour of the drag force data further in the following section by considering potential interrelations between the velocity field and the drag force.

Figure 7. (a–e) Spectra and (f–j) premultiplied spectra of drag force fluctuations.

Figure 8. (a) Frequency and (b) magnitude of the low-frequency ( $f_{1}$ , dashed lines) and high-frequency ( $f_{2}$ , solid lines) characteristic scales of drag force fluctuations. Symbols as per figure 3. The shaded regions in (a) indicate characteristic frequencies of velocity field fluctuations. The particle squared frontal area ( $A^{2}$ ) is overlaid in (b) for comparison.

3.3 Velocity–drag interrelations

In order to make an initial comparison between the drag force and the velocity field, we have overlaid shaded regions in figure 8(a) corresponding to the characteristic frequencies of wake-scale motions (WSMs), large-scale motions (LSMs) and very-large-scale motions (VLSMs) obtained from near-bed premultiplied velocity spectra. The wake frequency range is extracted from a premultiplied version of the spectra in figure 4(h), while the LSM and VLSM ranges are from Cameron et al. (2017) although presented here in the frequency domain rather than in the wavenumber domain. The VLSM frequencies appear in a narrow range and align closely with the $f_{1}$ drag frequency. It is not yet clear how VLSMs scale in rough-bed open-channel flow. The narrow frequency range over which they appear in this case probably results from the number of other experimental parameters that were held constant (e.g. $D$ , $u_{\ast }$ , $B$ and the streamwise length from the channel entrance to the measurement location). Neither the LSM nor wake frequencies align with $f_{2}$ , suggesting that these may not be responsible for the high-frequency hump in the drag force spectra.

Figure 9. Correlation between drag force and streamwise velocity.

Figure 10. (a) Correlation between drag force and streamwise velocity. (b) Drag force–streamwise velocity coherence function. (c) Phase angle diagram. Symbols as per figure 3; black lines, $P=0$ ; grey lines, $P=8$ . The dashed line in (c) has slope $-(0.05)2\unicode[STIX]{x03C0}f$ .

3.3.1 Correlation function

The correlation function between drag force and the streamwise velocity component $R_{Fu}(\unicode[STIX]{x1D6E5}_{t},y,z)=\overline{F^{\prime }(t)u^{\prime }(y,z,t+\unicode[STIX]{x1D6E5}_{t})}/(\unicode[STIX]{x1D70E}_{F}\unicode[STIX]{x1D70E}_{u})$ with $\unicode[STIX]{x1D70E}_{F}=\overline{F^{\prime }F^{\prime }}^{0.5}$ and $\unicode[STIX]{x1D70E}_{u}=\overline{u^{\prime }u^{\prime }}^{0.5}$ is presented in figure 9 for $\unicode[STIX]{x1D6E5}_{t}=0$ and in figure 10(a) for $y=0$ . The correlation function is a measure of the linear dependence of $F^{\prime }$ on $u^{\prime }$ that is suggested by (1.2) when $\bar{u}\gg u^{\prime }$ . The high-protrusion cases in figure 9 show depth scale regions of positive correlation near the protruding particle with adjacent regions of negative correlation. A similar pattern for two-point velocity correlations was attributed to the presence of space-filling depth-scale counter-rotating vortices (VLSMs) in Cameron et al. (2017). The maximum correlation coefficient of around 0.7 for the high-protrusion cases indicates that a majority of the drag force variance is associated with streamwise velocity fluctuations. A similar maximum correlation of 0.72 was reported by Celik et al. (2014) for near-fully protruding spheres. The no-protrusion cases in comparison have relatively lower correlation and mechanisms other than linear coupling with the streamwise velocity may be required to explain drag force fluctuations. Figure 10(a) shows the correlation function for the high-protrusion cases after scaling the time lag with the bulk velocity to form a pseudo- $x$ coordinate ( $x_{\ast }=-\unicode[STIX]{x1D6E5}_{t}U$ ). The correlation contours are slanted relative to the bed such that the time lag to maximise the correlation is dependent on the vertical coordinate $z$ . This pattern probably reflects the typical inclination of turbulent structures in the flow (e.g. Adrian 2007). Appreciable correlation is found several flow depths upstream and downstream of the particle, indicating that large-scale turbulent structures significantly contribute to the drag force fluctuations.

3.3.2 Coherence function and phase angle diagram

Potential correlations between velocity and drag can also be explored in the frequency domain via the coherence function and the phase angle diagram (figures 10 b and 10 c, respectively). The coherence function is estimated as $|S_{Fu}|^{2}/(S_{F}S_{u})$ and the phase angle as $\text{arg}(S_{Fu})$ , where $S_{Fu}$ is the complex-valued cross-spectral density function of drag and velocity with velocity extracted from a point 4 mm above the top of the particle. For the high-protrusion case, we observe that the coherence is near 1.0 for low frequencies, indicating that in this range most of the drag force fluctuation can be explained by a linear dependence on the velocity fluctuation. The coherence drops rapidly with increasing frequency, and at scales corresponding to the high-frequency hump in the drag spectra there is no appreciable coherence. Coherence for the low-protrusion cases is generally lower than for $P=8~\text{mm}$ . Coherence values less than one indicate either nonlinear coupling between drag and the point velocity fluctuations, or that additional factors are responsible for the drag force fluctuations. We have checked the velocity–drag coherence and the squared velocity–drag coherence with all velocity components at all measured points around the particle but were unable to find substantial coherence at the high frequencies.

The phase angle diagram indicates the phase shift between velocity and drag fluctuations and should only be interpreted for frequencies at which the coherence is significantly greater than zero. In this range we find zero phase for the low-protrusion case and linear phase change for the high-protrusion case, indicating that velocity fluctuations lead drag force fluctuations by around 0.05 s ( ${\sim}1.5D/U$ ). The dependence of phase angle on protrusion probably results from the elevation difference between the point above the particle where velocity was measured and the resultant drag force. Chan-Braun et al. (2011) indicated that for zero-protrusion spheres the resultant drag force was near the top of the particle, i.e. close to the point where we extracted the measured velocity fluctuations. With increasing protrusion, it is reasonable to assume that the resultant drag force shifts downwards towards the centre of the particle. This elevation difference combined with the typical inclination of the correlation contours (figure 10 a) probably leads to the observed phase difference being proportional to protrusion.

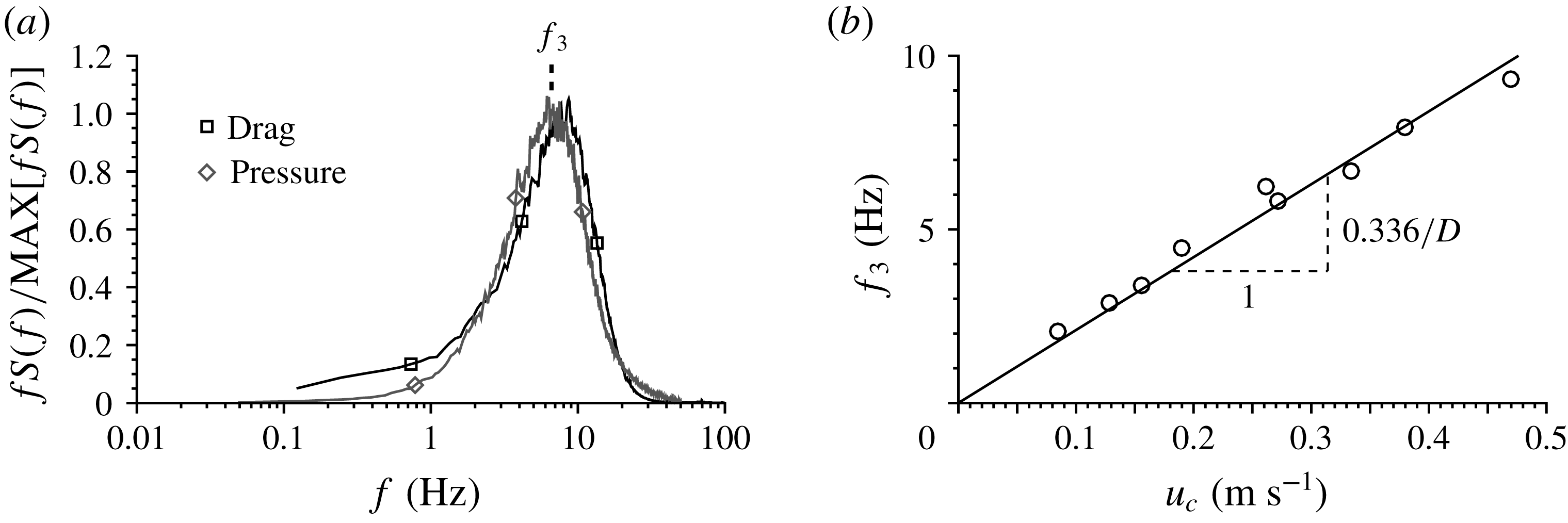
Figure 11. (a) Comparison between premultiplied spectra of drag force and differential pressure (H120, $P=0$ ). (b) Characteristic frequency of differential pressure versus convection velocity. The pressure data were recorded by Amir et al. (2014) and reanalysed here.

3.3.3 Role of pressure fluctuations

Data presented so far suggest that the low-frequency peak in the drag force spectra is associated with VLSMs, given the correspondence between their respective frequencies (figure 8 a) and high coherence at these scales. The high-frequency peak in the drag force spectra, however, cannot be explained by wake turbulence, as the frequencies do not match (figure 8 a) and there is no coherence between drag and velocity at these scales. Furthermore, the amplitude of wake turbulence depends on protrusion (figure 4 h) whereas the drag force fluctuations at the $f_{2}$ scale are independent of protrusion (figure 8 b). Therefore, we require an alternative mechanism to explain the high-frequency part of the drag force spectrum.

We propose that the high-frequency drag force fluctuations represent a passive response to the passage of turbulent pressure fluctuations. By ‘passive’ we refer to pressure fluctuations that occur naturally as part of the turbulent flow and are not induced or modified by the presence of the particle. Such advected pressure fluctuations have previously been proposed by Smart & Habersack (2007) to be an important lift-force-generating mechanism in gravel-bed rivers. Pressure fluctuations at scales larger than the particle diameter will impose a pressure gradient across the particle, resulting in net drag and lift force fluctuations. In this case, the drag force is proportional to the pressure difference between points separated by the particle size $D$ , or in the spectral domain,

(3.1) $$\begin{eqnarray}kS_{F}(k)\propto [\text{sin}(0.5kD)]^{2}kS_{p}(k),\end{eqnarray}$$

where $kS_{p}(k)$ is the premultiplied pressure spectra, $k=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}$ is wavenumber and $\text{sin}(0.5kD)$ is the transfer function of a differencing filter of scale $D$ . If the pressure spectrum has power-law type (i.e. $S_{p}(k)\propto k^{-n}$ ), equation (3.1) will form local maxima for $n<3$ . With $n=7/3$ for the inertial subrange (e.g. Monin & Yaglom 2007), the maximum occurs at $kD/2\unicode[STIX]{x03C0}=0.308$ , or applying Taylor’s hypothesis $f_{max}=0.308u_{c}/D$ , where $u_{c}$ is the convection velocity of the pressure fluctuations. This relationship cannot be tested using the drag force data presented here, as $u_{c}$ is near-constant for all experiments. The ‘drag’ measurements of Amir et al. (2014), however, were obtained over a range of flow conditions and are re-evaluated here. Amir et al. (2014) used differential pressure sensors embedded in spherical particles with zero protrusion to estimate drag forces. Their ‘run 8’ has identical flow and bed conditions to our case ‘H120, $P=0$ ’, enabling the direct comparison of spectra for the two cases in figure 11(a). The spectra show excellent agreement, confirming that the data of Amir et al. (2014) are a suitable analogue to the present drag force data. The frequency ( $f_{3}$ , figure 11 a) corresponding to the maximum in the premultiplied differential pressure spectra is presented as a function of convection velocity for all nine flow conditions of Amir et al. (2014) in figure 11(b). The convection velocity was estimated directly from correlation functions between adjacent sensors in a streamwise array of instrumented particles. The best-fitting trend through the data in figure 11(b) has a slope of $0.336/D$ , close to the $0.308/D$ predicted for $k^{-7/3}$ pressure spectra. Pressure fluctuations away from solid boundaries, however, are difficult to measure directly and their spectral distribution remains uncertain.

Advecting pressure fluctuations may also explain the time-shifted correlation between drag and lift forces observed by Hofland (2005), Dwivedi (2010), Chan-Braun et al. (2013), Amir et al. (2014), Celik et al. (2014), and Mazzuoli & Uhlmann (2017) and illustrated in figure 12(b). This pattern can be understood by considering the passage of a high- or low-pressure region (figure 12 a) with a corresponding drag–lift–drag cycle. Such a cycle can be particularly important for the entrainment of low-protrusion particles which may require an initial lift force to dislodge them followed by a high drag force to displace them downstream. The contribution of advecting pressure fluctuations to drag force fluctuations would be confirmed from the cross-spectral density function of pressure above a particle and drag force. We would expect coherence near 1.0 in the high frequencies, with a corresponding phase angle of $90^{\circ }$ indicating that the pressure gradient is synchronous with the drag force. Such data, however, are not yet available. Mazzuoli & Uhlmann (2017) also interpreted the shape of the drag–lift correlation function as the result of the passage of turbulent structures in the flow. However, in their conceptual model, coherent vortical motions were hypothesised to be responsible for the generation of drag and lift forces on the particles rather than spatial pressure fluctuations. Although pressure fluctuations are in principle non-local, i.e. they may depend on velocity fluctuations far from the point under consideration (e.g. Tsinober 2001), a majority of the pressure fluctuation has been found to be associated with local vortical motions (e.g. Robinson 1991). The model of Mazzuoli & Uhlmann (2017) and that presented here may be compatible in that local vortical motions may induce the pressure fluctuations proposed to be responsible for the generation of the high-frequency drag and lift forces.

Figure 12. (a) Schematic illustrating passage of a low-pressure region and corresponding drag and lift response. (b) Typical correlation function between drag and lift forces acting on a particle.

Figure 13. Amplitude modulation: correlation between low-frequency velocity fluctuations and the envelope of high-frequency drag force fluctuations.

3.3.4 Amplitude modulation

Recent evidence has emerged (e.g. Mathis, Hutchins & Marusic 2009; Marusic, Mathis & Hutchins 2010) that VLSMs interact with near-bed turbulence by modulating the amplitude of small-scale velocity fluctuations. It would be interesting to see if the high-frequency part of the drag force spectra was similarly modulated. Such modulation would have implications for sediment entrainment – a process governed by extreme drag and lift force fluctuations which may require superposition of events at different scales. We test for modulation effects following the approach of Mathis et al. (2009) using the correlation coefficient $R_{\hat{F}\ddot{u} }(y,z,\unicode[STIX]{x1D6E5}_{t}=0)=\overline{\hat{F}^{\prime }(t)\ddot{u} ^{\prime }(y,z,t+\unicode[STIX]{x1D6E5}_{t})}/(\unicode[STIX]{x1D70E}_{\hat{F}}\unicode[STIX]{x1D70E}_{\ddot{u} })$ , where $\unicode[STIX]{x1D70E}_{\hat{F}}=\overline{\hat{F}^{\prime }\hat{F}^{\prime }}^{\,0.5}$ and $\unicode[STIX]{x1D70E}_{\ddot{u} }=\overline{\ddot{u} ^{\prime }\ddot{u} ^{\prime }}^{\,0.5}$ . Here $\unicode[STIX]{x1D6E5}_{t}$ is a time lag, $\ddot{u}$ is the streamwise velocity component filtered by a low-pass filter and $\hat{F}$ is the low-frequency part of the envelope of the high-frequency drag force fluctuations. We use a cut-off frequency of 4 Hz to separate the high and low frequencies and the Hilbert transform is used to extract the envelope. Figure 13 indicates a maximum correlation coefficient of around 0.35 which is generally independent of protrusion and flow depth. It is interesting to see relatively high modulation for the zero-protrusion case even though the correlation measured between drag and velocity was low (figures 9 and 10). This suggests that the low-frequency velocity fluctuations may still be important for these cases even though their direct contribution to the drag force variance is small. We note also that the maximum correlation is found some distance above the top of the particle. Examination of the time-shifted correlation (not shown) $R_{\hat{F}\ddot{u} }(y,z,\unicode[STIX]{x0394}t)$ indicates that the maximum correlation is shifted due to a combination of inclined turbulence structures and a phase shift by which the high-frequency drag fluctuations lead the low-frequency velocity field by a short time. Such phase shifts between large and small scales have previously been reported (e.g. Bandyopadhyay & Hussain 1984; Jacobi & McKeon 2013; Tsuji, Marusic & Johansson 2016) and may relate to a preferential alignment of the small scales at the interfaces between large-scale structures. A precise description of the interaction, however, awaits further study.

4 Conclusions

Measurements of drag force fluctuations acting on spherical particles in open-channel flow reveal that the premultiplied spectra have a bimodal shape characterised by a low-frequency peak and a high-frequency peak. With increasing particle protrusion, the drag force variance becomes increasingly dominated by the contributions from the low-frequency process. The low-frequency spectral peak is associated with high coherence between the streamwise velocity component and the drag force and probably results from the action of very-large-scale motions. High-frequency drag force fluctuations, previously thought to be related to wake turbulence, however, do not show appreciable coherence with point velocity measurements around the particle. Instead, we propose that the high-frequency region of the drag force spectra is dominated by the action of pressure gradients in the overlying turbulent flow. The invariance of the high-frequency spectral magnitude to particle protrusion and the scaling of the peak frequency with convection velocity are consistent with this hypothesis. Models which relate drag or lift forces to the squared local flow velocity can therefore only account for a fraction of the drag force fluctuation and should be supplemented with additional terms to incorporate the contribution of turbulent pressure fluctuations. These findings are relevant to sediment transport processes, indicating that the key mechanism of particle entrainment may change from transient pressure events at low protrusion to high-velocity events associated with VLSMs at high protrusion. Neither of these mechanisms are accounted for in current sediment transport models. Additionally, we find that high-frequency drag force fluctuations interact with low-frequency velocity fluctuations via an amplitude modulation process. This suggests that the presence of VLSMs may be important to drag forces and particle entrainment even at low particle protrusion where their direct contribution is relatively small. Further data are required to test the sensitivity of particle drag force to turbulent pressure fluctuations. Direct tests, however, would require synchronous measurements of drag force and the overlying pressure field which is still difficult to obtain experimentally. The indicated role of VLSMs in the entrainment of sediment particles could be examined by combining mobile bed particles and PIV measurements of velocity fields corresponding to the instant of entrainment.