1 Introduction
Survey-based contingent valuation (CV) techniques are commonly used to value the potential effects of a policy change when market-based valuation of those effects is not possible. The results of these analyses are often intended to inform policy decisions, which are made within the context of formal policymaking institutions – such as Congress or state legislatures – that structure these decisions in a specific manner. In particular, policymaking institutions are commonly designed to reduce the large number of potential options for addressing any given policy problem to a binary choice between the continuation of current policy and a single, specified alternative (Jones, Reference Jones2001; Simon, Reference Simon1996; Workman, Reference Workman2015).Footnote 1 Policymakers are often faced with these decisions in controversial, highly politicized contexts, where a significant level of conflict exists between different populations and perspectives. Thus, it is important that analyses intended to inform these decisions are designed in a manner consistent with their structure, at least if the analyses are to have maximum informational value for policymakers.
In this research we develop an approach for conducting CV exercises in a manner consistent with the decision structure typically faced by policymakers. In brief, the approach starts by presenting survey respondents with information on the future conditions that are likely to occur under the current policy and a single, defined alternative policy option or operational change. Then, we provide respondents with an opportunity to indicate whether they would prefer to continue with current policy or adopt the defined alternative, absent any financial considerations for their household. Doing so allows us to define a reference utility level for each respondent specific to his or her preferences – their unpreferred policy option. Finally, we close the exercise by asking respondents whether they would be willing to pay a randomly selected dollar amount in order to implement their preferred policy option. Because we established a conceptually consistent reference utility level across respondents, the responses to the valuation question can serve as the basis for estimating respondent willingness to pay (WTP) for their preferred policy option using a single welfare measure – a Hicksian compensating surplus measure.
The data generated from this exercise allow for an estimate of WTP for the defined policy alternative, relative to leaving policy unchanged (and vice versa). More importantly, we illustrate how the estimates can be combined to provide an estimate of “net WTP” for the defined policy alternative (continuation of current policy) compared to the continuation of current policy (defined policy alternative). In doing so, these analyses provide information relevant to the type of decision that policymakers often face while remaining consistent with the standard assumptions underlying CV exercises. We apply our approach within the context of policy governing the storage of used nuclear fuel (UNF) in the United States, valuing the policy option of constructing an interim storage facility (ISF) relative to a continuation of current policy, wherein UNF is stored on-site at or near commercial nuclear generating plants.
We proceed by first discussing the role of baselines in the context of CV exercises generally, and in the context of these analyses conducted with an eye toward policymaking institutions specifically. We then transition to describing the development of a CV approach consistent with the structure of decisions generated by U.S. policymaking institutions. Next we provide background information on UNF management policy in the United States. We then detail the data and analytic techniques used to estimate net WTP for an ISF. Finally, we close by discussing the implications of our approach and results for CV research and the future of UNF management policy in the United States.
2 Contingent valuation analysis and the policymaking process: the role of baselines in a dynamic world
The traditional approach to CV exercises conducted in a policy context typically involves describing the potential effects that may occur as a result of a given policy change and then asking individuals whether they would be willing to pay some positive dollar amount for those effects. In this approach, the potential policy-induced changes are described relative to a given baseline, typically (but not always) implied to be the current levels of the goods in question (e.g., Carson & Louviere, Reference Carson and Louviere2011; Carson & Czajkowski, Reference Carson, Czajkowski, Hess and Daly2014). If the policy change induces effects that will continue to occur over time, as is almost always the case with policy change, then the implied baseline is the current levels of the relevant goods, amenities, and outcomes extended over time; the analyses use a “current-level” baseline. Analysts then generate an estimate of the value of the effects of the potential policy change, relative to that baseline. While the theory underlying nonmarket valuation is flexible in referencing either an initial (Hicksian compensating) or subsequent (Hicksian equivalent) reference point (Freeman, Herriges & Kling, Reference Freeman, Herriges and Kling2014), in practice exercises conducted relative to a current-level baseline are the predominant approach for valuing nonmarket welfare changes.
Although this approach generates a plausible estimate of WTP for the effects of a policy change relative to the current-level baseline, such estimates are of limited – or even no – value to policymakers, at least absent additional information. The complex and dynamic nature of the world means that current levels of a particular good, amenity, or outcome are rarely maintained over time, even without any change in policy. This is true in the environmental context, where a constantly evolving landscape generates continuous changes in goods or amenities (e.g., beaches, vegetation, air quality, animal species, irrigation, or river flows) even if the policy governing that landscape remains unchanged (Jones et al., Reference Jones, Berrens, Jenkins-Smith, Silva, Carlson, Ripberger, Gupta and Carlson2016; Carson & Czajkowski, Reference Carson, Czajkowski, Hess and Daly2014; Hanley et al., Reference Hanley, Czajkowski, Hanley-Nickolls and Redpath2010).Footnote 2 This perspective also applies in a social context, where changing economic and social conditions produce continual changes in homelessness, unemployment, family structure, educational attainment and just about any other outcome we care about societally, absent any policy change.Footnote 3
In such a dynamic world, policymakers almost never face a decision where they are choosing between a policy that would maintain current levels of the relevant goods, amenities, or outcomes for the foreseeable future and an alternative policy option that would set a different trajectory for those goods, amenities, or outcomes. Rather, they face a choice between no policy change, which sets a given trajectory for the various goods, amenities, and outcomes that individuals may value (one that almost always departs from the current level) and a defined policy alternative, which will set a future trajectory that differs from both the current level and the trajectory that would be realized under continuation of current policy.Footnote 4
The value of estimates generated by an approach designed to mirror the structure of the choices facing policymakers is clearly recognized by the organizations responsible for providing policy analysis to these institutions and is incorporated into their products. For example, when projecting the budgetary effects of a potential policy change, the Congressional Budget Office (CBO) projects the effects of proposed legislation relative to the spending that would occur if the legislation were not enacted, rather than to a stagnant baseline of current spending levels extended over time. Similarly, federal environmental impact statements (EIS) required under the National Environmental Policy Act (NEPA) must include a “No Action Alternative” that describes, as a baseline, the evolving state of environmental resources if no policy change occurs. We argue that the same logic should be extended to CV exercises and in the following section we develop a general approach for doing so.
2.1 Implications for CV design to inform policy decisions
Structuring a CV exercise in a manner designed to generate information directly relevant to policy decisions is broadly similar to the typical CV exercise, but there are also a number of important differences. First, it is important to explicitly present information on the trajectories of the bundle of potentially valued goods, amenities, and outcomes projected to be realized over a defined time frame under two conditions, one where policy remains unchanged and a second where a specified policy alternative is adopted. The trajectories for these two policy options could be described relative to some common baseline – most likely a current-level baseline – or they could be described directly relative to one another. In our application below we apply the latter approach, but in a later section of this paper we discuss what an application of the former would entail. Regardless of the specific basis of comparison, this approach of explicitly describing the trajectories of two policy options differs from the typical approach of describing the effects of a policy change relative to some implicit baseline.
After describing the trajectories predicted to occur under the two policy options it is important to make clear to the respondent that if this choice occurred in an actual policymaking context one of the options would be adopted and implemented. That is, it is important to clarify that the two presented options represent the set of possible policy responses and are to be evaluated relative to one another, as opposed to some absolute baseline or another possible policy alternative. In this setup, a vote for one of the options necessarily constitutes a vote against the other option. After respondents are given this information, the respondents are asked to indicate which policy they prefer in the absence of any financial considerations for their household. This step in the exercise establishes the reference utility level as respondents’ “unpreferred” policy option. We discuss the implications of this reference utility level in greater detail below.
Upon ascertaining respondents’ preferred (and unpreferred) policy option, the exercise proceeds by informing the respondent that the option they selected would require additional resources if it were to be adopted and implemented. Although it is commonly perceived that maintaining current policy requires only current resource levels, such perceptions are usually inaccurate. In perhaps the clearest demonstration of this reality, Medicare projections indicate that a substantial amount of additional public investment will be required to continue the current policy (Congressional Budget Office, 2016). Thus, the final step of the exercise asks individuals whether they would be willing to pay a randomly selected dollar amount, in the form of additional taxes, to facilitate adoption and implementation of the option they prefer.
This approach to valuation is appealing for two reasons. First, as noted above, it mirrors the structure of choices that policymakers are likely to face – leave policy unchanged or adopt a specified policy alternative. Such choices typically entail both benefits and costs associated with each policy option and the relevant question from policymakers’ perspective is whether the levels of a multidimensional bundle of goods, amenities, and outcomes that would accrue if they voted to change policy exceed the levels that would be obtained if they voted for policy to remain unchanged. Therefore, the choice is a relative one, rather than an absolute one. Second, our approach allows us to use a single welfare measure to generate a relative valuation of the two policy options – a compensating surplus measure of WTP. Indeed, our approach places a clear policy choice in an unbiased voting context, and then frames a second voting question as an income-constrained WTP measure, regardless of which policy option is preferred by the respondent. This can be contrasted with the classic referendum format that posits a vote for or against a single policy option (e.g., see Arrow et al., Reference Arrow, Solow, Portney, Leamer, Radner and Schuman1993; Welsh et al., Reference Welsh, Bishop, Phillips and Baumgartner1995 and discussion in Jones et al., Reference Jones, Berrens, Jenkins-Smith, Silva, Carlson, Ripberger, Gupta and Carlson2016). We explain this argument, and its connected approach, further.
Consider a policy choice where there is considerable public debate in the policy domain and all policy options require continuing or ongoing payments by taxpayers in some form, which is the case in nearly every policy area (see Mitchell & Carson, Reference Mitchell and Carson1989, p. 38 for a similar articulation). Above we described how collective choice institutions, such as legislatures or executive branch agencies, collapse the multitude of potential policy options into something approximating a binary format in such cases. This results in policymakers facing the choice of whether to vote to keep policy unchanged – resulting in bundle
![]() $\unicode[STIX]{x1D703}^{0}$
– or to vote for the defined policy alternative, which will result in bundle
$\unicode[STIX]{x1D703}^{0}$
– or to vote for the defined policy alternative, which will result in bundle
![]() $\unicode[STIX]{x1D703}^{1}$
. In such scenarios, CV exercises typically define the implied property right as residing in the continuation of current policy (i.e., the compensating surplus) and then estimate WTP to acquire the policy change using a Hicksian welfare measure, thus assuming that the policy change produces utility increments. When considered in the policymaking context, it is clear that such an approach is problematic for at least three reasons. First, at the point where policymakers are faced with the choice of voting to either leave policy unchanged or adopt a defined alternative, property rights are undefined or ambiguous. Indeed, at that point bundle
$\unicode[STIX]{x1D703}^{1}$
. In such scenarios, CV exercises typically define the implied property right as residing in the continuation of current policy (i.e., the compensating surplus) and then estimate WTP to acquire the policy change using a Hicksian welfare measure, thus assuming that the policy change produces utility increments. When considered in the policymaking context, it is clear that such an approach is problematic for at least three reasons. First, at the point where policymakers are faced with the choice of voting to either leave policy unchanged or adopt a defined alternative, property rights are undefined or ambiguous. Indeed, at that point bundle
![]() $\unicode[STIX]{x1D703}^{0}$
is no more of a “right” than bundle
$\unicode[STIX]{x1D703}^{0}$
is no more of a “right” than bundle
![]() $\unicode[STIX]{x1D703}^{1}$
. This calls into question the practice of using the continuation of current policy as the reference level of utility. Second, in complex operational settings, such as storing nuclear waste or managing a river system, both continuation of current policy and adoption of a defined alternative will typically require additional taxpayer support going forward. Third, the very fact that debate over policy options is occurring within the formal political process suggests that a nontrivial portion of the population considers each of the policy alternatives (the continuation of current policy or the defined alternative) to be utility decrements. This calls into question the typical assumption that a given policy option uniformly enhances individual utility (Viscusi, Reference Viscusi2015). In such cases, members of the population are divided according to individualized, heterogeneous perceptions of utility increments and decrements for a given policy proposal. The relevant valuation measures are therefore: (i) WTP for the defined policy alternative (among those viewing policy change as an increment); and (ii) WTP for maintaining current policy and thus avoiding the defined policy alternative (among those viewing the defined policy change as a decrement).Footnote
5
Together, these inconsistencies with the reality of the policy process suggest that traditional CV exercises – even those ostensibly conducted in a policy context – provide information of only limited relevance to policymakers.
$\unicode[STIX]{x1D703}^{1}$
. This calls into question the practice of using the continuation of current policy as the reference level of utility. Second, in complex operational settings, such as storing nuclear waste or managing a river system, both continuation of current policy and adoption of a defined alternative will typically require additional taxpayer support going forward. Third, the very fact that debate over policy options is occurring within the formal political process suggests that a nontrivial portion of the population considers each of the policy alternatives (the continuation of current policy or the defined alternative) to be utility decrements. This calls into question the typical assumption that a given policy option uniformly enhances individual utility (Viscusi, Reference Viscusi2015). In such cases, members of the population are divided according to individualized, heterogeneous perceptions of utility increments and decrements for a given policy proposal. The relevant valuation measures are therefore: (i) WTP for the defined policy alternative (among those viewing policy change as an increment); and (ii) WTP for maintaining current policy and thus avoiding the defined policy alternative (among those viewing the defined policy change as a decrement).Footnote
5
Together, these inconsistencies with the reality of the policy process suggest that traditional CV exercises – even those ostensibly conducted in a policy context – provide information of only limited relevance to policymakers.
Our approach addresses these issues by designing our elicitation exercise to first identify the policy option that (relative to a defined alternative) is preferred by an individual respondent in terms of providing an incremental welfare change.Footnote 6 In doing so, we are effectively defining respondents’ reference utility level as that which they would have received from their unpreferred policy alternative. Having defined the reference utility level for each respondent, we then ask the respondent whether they would vote for their preferred alternative at some randomly assigned annual tax payment amount. This approach is conceptually consistent across respondents in that we inquire about their WTP for their preferred alternative (i.e., WTP for the increment) using a Hicksian compensating surplus measure. However, the policy option representing a respondent’s preferred alternative – the policy providing the perceived welfare increment – is allowed to vary according to their values, tastes, and preferences.
This valuation approach rests on the assumption that the two policy options presented to respondents can be validly compared relative to one another. Given our previous discussion of the structure of decisions within policymaking institutions we believe this assumption to be uncontroversial. Specifically, given the binary nature of the policy choice, WTP for the preferred option can be readily interpreted as WTP to avoid the unpreferred option. Furthermore, it is both valid and informative to combine the WTP estimates for each policy option to arrive at a single estimate of “net WTP” for one of the policy options, most likely the defined policy alternative although net WTP for continuation of current policy could also be easily calculated. This calculation is done in a manner that includes the valuations of individuals on both sides of the analytical ledger – both those for and those against the policy.Footnote 7 We acknowledge that our approach would be problematic if the goal of the exercise was estimating an absolute value for the goods, amenities, and outcomes generated by a given policy option. However, that is not the goal of this exercise – it would be inconsistent with the structure of policy decisions, where choices are not absolute, but relative. Indeed, when faced with a formal decision in policymaking institutions, policymakers do not choose to vote for a given policy option according to whether they believe it will return a level of goods, amenities, and outcomes that exceed some absolute threshold. Rather, they consider whether a specified option for changing policy is superior to leaving policy unchanged. Our approach mirrors that decision structure, and thus facilitates an estimate of the relative value of the two policy options at hand. Put differently, we estimate the net value difference (in dollars) between the two options under consideration. In the following section we provide an overview of policy governing UNF storage in the United States, which serves as the empirical context for application of the approach described above. By design, we apply our approach in a context with highly charged conflict over policy options.
3 Used nuclear fuel storage policy
Used nuclear fuel storage policy in the United States represents an issue where policymakers are currently embroiled in a highly technical and value-laden debate about how to manage growing stocks of UNF as we work toward a socially acceptable and technically feasible permanent disposal solution, such as the construction of a deep geologic repository. As part of this debate, the Blue Ribbon Commission on America’s Nuclear Future (BRC) recently recommended that the United States “establish a program that leads to the timely development of one or more consolidated storage facilities” as a possible alternative to the current practice of storing UNF “on-site” at or near the facilities that produced the material (BRC, 2012).
Consolidating UNF into one or more interim storage sites is attractive to some because it reduces some of the risks associated with current practices. For example, a number of on-site storage facilities are currently located near rivers and oceans, making them vulnerable to the sort of flooding that affected the UNF storage pools at Fukushima. In addition, most of the UNF that is currently stored on-site in the United States is stored in cooling pools or dry casks that were not specifically designed to protect the material from human-caused disasters like terrorism or the potential long-term effects of natural wear and tear or corrosion. Compounding these vulnerabilities, a number of these on-site facilities are located near large population centers, which means that a single incident may affect a large number of people in a short period of time. Consolidated interim storage could reduce these risks by storing UNF farther from population centers, in regions of the country that are less vulnerable to natural disasters, and in containers that are specifically designed to withstand corrosion and terrorist attacks.Footnote 8
Though attractive, some argue that the benefits of interim storage would require a rather substantial cost and the generation of a new set of risks that cannot be justified. For instance, consolidated interim storage would require that we transport UNF from the temporary storage facilities where it was produced to an off-site facility. This process, some argue, would increase the likelihood of an accident and, in the long run, expose more people to the risks associated with the material because each person along the transportation corridor is now vulnerable (Freudenburg, Reference Freudenburg1991; also see National Research Council, 2006).
Because of the real and perceived risk reduction tradeoffs associated with this set of contrasting alternatives, it is possible – and indeed likely – that some members of the public will prefer to discontinue current on-site storage practices and commence construction of an ISF, whereas others will prefer to maintain current practice and continue to store UNF on-site.
4 Valuation exercise for the policy options
To obtain data that would allow us to estimate the value of constructing an ISF relative to continued on-site storage, we fielded a web-based survey that contained a multistage elicitation exercise that followed the approach outlined in Section 2. We administered the survey on June 28–29, 2014 to a sample of 812 adults (age 18 and older) that reside in the United States. We designed and programed the survey in-house and purchased the sample frame from Survey Sampling International (SSI). Survey Sampling International provided access to a large pool of potential respondents, and recruited respondents to match national characteristics such as region of residence, gender, and race/ethnicity.Footnote 9 Before commencing the elicitation exercise, the survey provided background information on UNF and posed the following two questions intended to measure baseline support for each of the two UNF storage policies:Footnote 10
Using a scale from one to seven, where one means strongly oppose and seven means strongly support, how do you feel about the current practice of storing used nuclear fuel at or near nuclear power plants?
Using a scale from one to seven, where one means strongly oppose and seven means strongly support, how do you feel about constructing one or more interim storage facilities for consolidating used nuclear fuel in the U.S.?
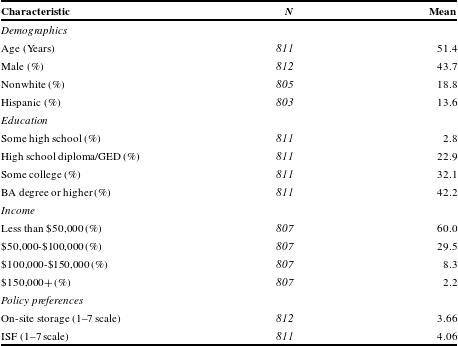
In addition to sample summary statistics, Table 1 summarizes the baseline levels of support for each UNF storage policy option.
The elicitation exercise began by presenting respondents with the following lead-in text, table, and question:Footnote 11
Government officials will consider many factors when deciding how to store used nuclear fuel. One factor is whether various options are personally worthwhile to people like you. In the next question, we will describe the effects of two specific options being considered for storage of used nuclear fuel. We would like you to tell us which of these two options you would prefer.
People might consider several factors when deciding which option they prefer, including the cost of each option and the expected effects of each option.

Think about a situation in which you had an opportunity to vote for Option 1 or Option 2. Keeping in mind all of the potential effects described for each option above, and if adoption of either option would not cost you anything, would you vote for Option 1 or Option 2?
1 - Option 1
2 - Option 2
3 - Would choose not to vote for either option
We highlight two features of this approach to value elicitation. First, the approach presents respondents with a binary choice between two options – the continuation of current policy or the defined alternative – and asks respondents which of the two options they prefer. In doing so, the approach mirrors the decision structure that policymakers face, thus rendering the results of the value elicitation more informative to policy decisions than the typical CV exercise. Second, despite clear differences from the standard approach to value elicitation in CV exercises, the elicitation approach we present above maintains consistency with the assumptions underlying the CV technique, as well as methodological best practices. For example, we previously described how the elicitation approach generates a relative valuation of, as well as an estimate of the net difference between, the two policy options using a single welfare measure – a compensating surplus measure of WTP. In addition, the value elicitation is conducted in an incentive-compatible referendum format and emphasizes the consequentiality of the exercise (Carson & Groves, Reference Carson and Groves2007).
Table 1 Sample summary statistics.
With these features of the elicitation exercise in mind, we turn to describing the policy preferences that respondents expressed in this stage of the exercise. In response to the question inquiring which of the policy options they preferred, 256 (32%) respondents said that they would vote to continue on-site storage, 359 (44%) said that they would vote for the interim storage option, and 197 (24%) said that they would not vote. We consider respondents who state they would not vote to be indifferent between the two policy options and thus have no relative preference.
To gain additional insight into these results we model the choice to vote for any policy option – relative to choosing not to vote – as a function of demographic characteristics and baseline support for the two storage policies. More formally, we estimate
where the probability that respondent
![]() $i$
chooses to vote,
$i$
chooses to vote,
![]() $V$
, for any policy option is a function of a vector of demographic characteristics
$V$
, for any policy option is a function of a vector of demographic characteristics
![]() $X$
and baseline support for each of the two UNF storage policies
$X$
and baseline support for each of the two UNF storage policies
![]() $S$
;
$S$
;
![]() $\text{logit}^{-1}(x)=e^{x}/(1+e^{x})$
. The results from this model are presented in the first column of Table 2. All else equal, older respondents and respondents who identified as racial minorities were less likely to vote in the exercise than younger and nonminority respondents, respectively. Respondents who reported higher levels of education and income, by comparison, were more likely to vote in the exercise than their less educated and lower earning peers. Finally, as observed in actual referenda and elections, participation was higher among respondents who demonstrated a clear preference for the policies on the ballot (Brady, Verba & Schlozman, Reference Brady, Verba and Schlozman1995).
$\text{logit}^{-1}(x)=e^{x}/(1+e^{x})$
. The results from this model are presented in the first column of Table 2. All else equal, older respondents and respondents who identified as racial minorities were less likely to vote in the exercise than younger and nonminority respondents, respectively. Respondents who reported higher levels of education and income, by comparison, were more likely to vote in the exercise than their less educated and lower earning peers. Finally, as observed in actual referenda and elections, participation was higher among respondents who demonstrated a clear preference for the policies on the ballot (Brady, Verba & Schlozman, Reference Brady, Verba and Schlozman1995).
Table 2 Logistic regression models of the choice between voting and not voting in the exercise and voting for on-site storage versus interim storage facility.

Note: *
![]() $p<0.10$
; **
$p<0.10$
; **
![]() $p<0.05$
; ***
$p<0.05$
; ***
![]() $p<0.01$
. Standard errors in parentheses next to coefficient estimate.
$p<0.01$
. Standard errors in parentheses next to coefficient estimate.
Among respondents who stated that they would vote in the referendum (expressed a preference for one of the two policy options) we analyzed support for on-site storage, relative to an ISF, using the following model:
where the probability that respondent
![]() $i$
chooses to vote for the on-site storage policy option
$i$
chooses to vote for the on-site storage policy option
![]() $O$
is a function of the same demographic characteristics and baseline policy support measures specified in equation (1) above. Results from this model are presented in column 2 of Table 2. As expected, policy choices depend on baseline policy support. Respondents who support on-site storage were more likely to select the on-site storage option than respondents who oppose on-site storage. The opposite is true of respondents who support interim storage – they were significantly less likely to select the on-site storage option than respondents who oppose interim storage. This finding provides an important validity check for the exercise – it provides evidence that respondents thought about the question and voted in a manner consistent with their preferences.
$O$
is a function of the same demographic characteristics and baseline policy support measures specified in equation (1) above. Results from this model are presented in column 2 of Table 2. As expected, policy choices depend on baseline policy support. Respondents who support on-site storage were more likely to select the on-site storage option than respondents who oppose on-site storage. The opposite is true of respondents who support interim storage – they were significantly less likely to select the on-site storage option than respondents who oppose interim storage. This finding provides an important validity check for the exercise – it provides evidence that respondents thought about the question and voted in a manner consistent with their preferences.
With this understanding of the determinants of choosing to vote and – among voters – expressed policy preferences, we move to describing the next stage of the elicitation exercise, the single-bounded polychotomous choice valuation question. In this stage we presented the 615 respondents who said that they would vote for one of the two options with the following text and question:
The option you chose will be more expensive to operate in the long term [near-term]Footnote 12 , and will increase the cost to taxpayers. The tax would be added to your electricity bill. As a taxpayer, would you vote for this option? As you think about your answer, please remember that if this proposal passes, you would have less money for household expenses, charities, groceries, or car payments.
Would you vote for this option if adoption of this option would cost your household $[12, 24, 72, 120, 360, 780, or 1200] in increased taxes every year for the foreseeable future?
1 - Definitely no
2 - Probably no
3 - Not sure
4 - Probably yes
5 - Definitely yes
Table 3 presents the responses to this question. The table presents responses separately for individuals who expressed a preference for on-site storage in the first stage of the elicitation exercise and those who expressed a preference for an ISF. The results indicate that, of the 256 respondents who stated they would vote for the on-site storage policy option at no cost, approximately 35% would probably or definitely vote yes to paying the randomly assigned tax payment amount. Of the 359 individuals who expressed a preference for the ISF policy option at no cost, about 40% said that they would probably or definitely vote yes to paying the randomly assigned tax payment amount.
Table 3 Vote choice with required tax payment by initial policy preference.

Note:
![]() $N$
in parentheses next to percentage.
$N$
in parentheses next to percentage.
We leverage the responses to the question above – together with the randomly assigned tax payment amounts – to estimate relative WTP for the policy options in both parametric and nonparametric frameworks. We begin with the parametric estimates by fitting a series of logistic regression models to the data.Footnote 13 For the first model we restrict the sample to respondents who stated a preference for an ISF (relative to on-site storage) in the initial stage of the elicitation exercise and estimate the following logit model:
where the probability of observing vote choice
![]() $C$
– indicating that the individual would pay additional taxes for the policy option – for respondent
$C$
– indicating that the individual would pay additional taxes for the policy option – for respondent
![]() $i$
is a function of the randomly assigned tax payment amount
$i$
is a function of the randomly assigned tax payment amount
![]() $P$
and a logistically distributed error term
$P$
and a logistically distributed error term
![]() $u$
. To reduce hypothetical bias, we only assign a “Yes” (
$u$
. To reduce hypothetical bias, we only assign a “Yes” (
![]() $C=1$
) response to respondents who said “Definitely yes” in response to the valuation question. All other respondents, including those who said “Probably yes,” are coded as “No” (
$C=1$
) response to respondents who said “Definitely yes” in response to the valuation question. All other respondents, including those who said “Probably yes,” are coded as “No” (
![]() $C=0$
). This decision is motivated by Blumenschein et al.’s (Reference Blumenschein, Johannesson, Blomquist, Liljas and O’Conor1998) work finding that the difference between hypothetical and real WTP is substantially reduced when “Probably yes” responses are treated as “No” votes as opposed to “Yes” votes. Results from estimation of this model are shown in the first column of Table 4.
$C=0$
). This decision is motivated by Blumenschein et al.’s (Reference Blumenschein, Johannesson, Blomquist, Liljas and O’Conor1998) work finding that the difference between hypothetical and real WTP is substantially reduced when “Probably yes” responses are treated as “No” votes as opposed to “Yes” votes. Results from estimation of this model are shown in the first column of Table 4.
Table 4 Logistic regression models predicting bid acceptance, by preferred policy option and inclusion of covariates.

Note: *
![]() $p<0.10$
; **
$p<0.10$
; **
![]() $p<0.05$
; ***
$p<0.05$
; ***
![]() $p<0.01$
; standard errors in parentheses next to coefficient estimate; 90% confidence intervals in brackets next to mean WTP estimates.
$p<0.01$
; standard errors in parentheses next to coefficient estimate; 90% confidence intervals in brackets next to mean WTP estimates.
Our second model uses the same sample and variable classification as the first. However, we build upon the model in equation (3) by including demographic characteristics,
![]() $X$
, and baseline policy support,
$X$
, and baseline policy support,
![]() $S$
, as covariates in the model. The specific covariates we include are the same as those in equation (1).Footnote
14
The model we estimate, the results of which are shown in the second column of Table 4, can be written as:
$S$
, as covariates in the model. The specific covariates we include are the same as those in equation (1).Footnote
14
The model we estimate, the results of which are shown in the second column of Table 4, can be written as:
Our third and fourth models are identical in structure to the first and second models, respectively, but the sample for these models is restricted to the respondents who stated a preference for on-site storage in the initial stage of the elicitation exercise. The results from these models are shown in the third and fourth columns of Table 4.
The parameter estimates in Table 4 provide a basis for estimating mean WTP for an ISF (on-site storage), relative to on-site storage (an ISF). Following Blomquist, Dickie and O’Conor (Reference Blomquist, Dickie and O’Conor2011), we estimate mean WTP using the following equation:
where
![]() $\unicode[STIX]{x1D711}$
is the estimated coefficient on the tax payment amount from the models described above (see Table 4) and
$\unicode[STIX]{x1D711}$
is the estimated coefficient on the tax payment amount from the models described above (see Table 4) and
![]() $z$
is the effect of the covariates when they are evaluated at their respective means. This calculation produces a mean WTP for an ISF of approximately $30 when the covariates are not included in the calculation (i.e., the bid-only model), and $16 when they are included.Footnote
15
These estimates can be interpreted as the mean WTP for an ISF among individuals who indicated that they preferred the ISF option to on-site storage.
$z$
is the effect of the covariates when they are evaluated at their respective means. This calculation produces a mean WTP for an ISF of approximately $30 when the covariates are not included in the calculation (i.e., the bid-only model), and $16 when they are included.Footnote
15
These estimates can be interpreted as the mean WTP for an ISF among individuals who indicated that they preferred the ISF option to on-site storage.
We use the same approach to estimate mean WTP for individuals who indicated that they prefer on-site storage, relative to an ISF. The calculations indicate that individuals who prefer on-site storage have a mean WTP of approximately $20 when the calculations are based on the model that excludes covariates; mean WTP drops to about $10 when basing the calculations on the model with the covariates.
4.1 Estimating net WTP
Above we describe how policymaking institutions structure decisions in a manner such that policymakers consider whether a specified option for changing policy is superior to the continuation of current policy – they pose a relative choice. Our elicitation exercise mirrors this structure in that it asks respondents which policy option they prefer, relative to a defined alternative policy. Thus, although the mean WTP results in Table 4 have a stand-alone interpretation, the structure of the elicitation exercise also allows them to be compared directly to one another; they can be combined into a single estimate of “net WTP”. We do this by subtracting estimated mean WTP for individuals who prefer on-site storage – scaled by the proportion of individuals who indicated they preferred the on-site option in the first stage of the valuation exercise – from estimated mean WTP for individuals who prefer an ISF, scaled by the proportion of individuals who indicated they preferred the ISF option. Based on the results of the models without covariates, this procedure generates a net WTP of about $7 for an ISF.Footnote 16 Applying this approach to the results of models with covariates produces a mean net WTP of about $4 in favor of an ISF. Net WTP estimates are presented in Table 5 below.
Along with subtracting the separate mean WTP estimates for the two policy options from the stand-alone models to obtain an estimate of net WTP, we can also recover an estimate of net WTP for an ISF (or on-site storage) through estimation of a single model. To accomplish this, we include in our analytic sample all respondents who stated a policy preference – either an ISF or on-site storage – and estimate the following logit model:
which expands the model in equation (3) by including
![]() $\unicode[STIX]{x1D713}F_{i}$
, which indicates that the respondent preferred the ISF policy option in the first stage of the exercise and an interaction term
$\unicode[STIX]{x1D713}F_{i}$
, which indicates that the respondent preferred the ISF policy option in the first stage of the exercise and an interaction term
![]() $\unicode[STIX]{x1D706}_{1}(P_{i}\ast F_{i})$
, that allows the relationship between the tax payment amount and bid acceptance to vary according to the policy option that an individual selected.
$\unicode[STIX]{x1D706}_{1}(P_{i}\ast F_{i})$
, that allows the relationship between the tax payment amount and bid acceptance to vary according to the policy option that an individual selected.
Table 5 Logistic regression models predicting bid acceptance for preferred policy option, by inclusion of covariates.

Note: *
![]() $p<0.10$
; **
$p<0.10$
; **
![]() $p<0.05$
; ***
$p<0.05$
; ***
![]() $p<0.01$
; standard errors in parentheses next to coefficient estimate.
$p<0.01$
; standard errors in parentheses next to coefficient estimate.
The results from this model are shown in the first column of Table 5. Note that the parameter estimates in columns one and three of Table 4 can be recovered from this single model. For instance, the intercept in column one is
![]() $-$
1.710, which is equivalent to the intercept of this model (
$-$
1.710, which is equivalent to the intercept of this model (
![]() $-$
2.551) plus the estimated coefficient on Vote (0.841). As such, we can use the estimates from this model to reproduce the separate mean WTP estimates presented in Table 4. More importantly, though, we can use the estimates from this model to directly estimate net WTP for an ISF. To do so, we apply equation (5) twice, once when the indicator for preferring an ISF is one (i.e.,
$-$
2.551) plus the estimated coefficient on Vote (0.841). As such, we can use the estimates from this model to reproduce the separate mean WTP estimates presented in Table 4. More importantly, though, we can use the estimates from this model to directly estimate net WTP for an ISF. To do so, we apply equation (5) twice, once when the indicator for preferring an ISF is one (i.e.,
![]() $F=1$
) and a second time when the indicator for preferring an ISF is zero (i.e.,
$F=1$
) and a second time when the indicator for preferring an ISF is zero (i.e.,
![]() $F=0$
). Because the parameter estimates in columns 1 and 3 of Table 4 can be recovered from this single model, the estimates of mean WTP for an ISF and on-site storage are identical to those presented earlier. We then combine these estimates of mean WTP for an ISF and on-site storage into a single estimate of net WTP for an ISF using the procedure described above (i.e., subtracting the estimates that are weighted by the proportion of individuals who prefer the respective options). Doing so reproduces the estimates of net WTP we calculated from the stand-alone models – this estimate is presented in Table 5.
$F=0$
). Because the parameter estimates in columns 1 and 3 of Table 4 can be recovered from this single model, the estimates of mean WTP for an ISF and on-site storage are identical to those presented earlier. We then combine these estimates of mean WTP for an ISF and on-site storage into a single estimate of net WTP for an ISF using the procedure described above (i.e., subtracting the estimates that are weighted by the proportion of individuals who prefer the respective options). Doing so reproduces the estimates of net WTP we calculated from the stand-alone models – this estimate is presented in Table 5.
Following this logic, we can also estimate net WTP in a single model that includes the covariates:
This model expands upon the previous model by including demographic characteristics
![]() $X$
, and baseline policy support
$X$
, and baseline policy support
![]() $S$
, as well as interaction terms
$S$
, as well as interaction terms
![]() $\unicode[STIX]{x1D706}_{2}(X_{i}\ast F_{i})$
and
$\unicode[STIX]{x1D706}_{2}(X_{i}\ast F_{i})$
and
![]() $\unicode[STIX]{x1D706}_{3}(S_{i}\ast F_{i})$
that allow the estimated coefficients on
$\unicode[STIX]{x1D706}_{3}(S_{i}\ast F_{i})$
that allow the estimated coefficients on
![]() $X$
and
$X$
and
![]() $S$
to vary by the policy option (
$S$
to vary by the policy option (
![]() $F$
) that was selected in the first stage of the value elicitation exercise. The results from this model are shown in the second column of Table 5. Again, the parameter estimates from columns two and four in Table 4 are comparable to estimates that can be recovered from this single model, so we can use this model to reproduce the mean WTP estimates that were derived from those models. We can also use the procedure described above to directly estimate net WTP for an ISF from this single model. Unsurprisingly, the estimate of net WTP for an ISF (about $4) mirrors the one generated from the two separate models.
$F$
) that was selected in the first stage of the value elicitation exercise. The results from this model are shown in the second column of Table 5. Again, the parameter estimates from columns two and four in Table 4 are comparable to estimates that can be recovered from this single model, so we can use this model to reproduce the mean WTP estimates that were derived from those models. We can also use the procedure described above to directly estimate net WTP for an ISF from this single model. Unsurprisingly, the estimate of net WTP for an ISF (about $4) mirrors the one generated from the two separate models.
4.2 Nonparametric WTP estimates
To this point we have provided parametric estimates of WTP. To calculate nonparametric estimates of mean WTP for an ISF and on-site storage, we again restrict the samples according to the preference that respondents indicated in the first stage of the elicitation exercise (an ISF sample and an on-site sample), and then we apply the lower bound Turnbull estimation technique presented in Haab and McConnell (Reference Haab and McConnell2002) on both samples.
Table 6 Frequency distribution of bid acceptance, by preferred policy option.

Note: Lower bound WTP estimated using Turnbull procedure outlined in Haab and McConnell (Reference Haab and McConnell2002). The lower bound on the confidence intervals for on-site storage were
![]() $-$
4.24 and
$-$
4.24 and
![]() $-$
1.36; these are truncated at zero to facilitate interpretation.
$-$
1.36; these are truncated at zero to facilitate interpretation.
Table 6 presents these calculations. The lower bound Turnbull estimate of WTP for an ISF is about $22, and the estimate for on-site storage is approximately $13. When scaled by the proportion of respondents who supported the respective policy options in stage one of the exercise, the estimates fall to roughly $10 and $4, respectively. These estimates provide conservative (lower bound) estimates of average household WTP for an ISF when on-site storage is the policy alternative, and, alternatively WTP for on-site storage when an ISF is the alternative. As before, they can also be used to calculate a net WTP for an ISF by subtracting the scaled estimate for individuals who prefer on-site storage ($4.04) from the scaled estimate for individuals who prefer an ISF ($9.55). This produces a net WTP of approximately $5.50 for an ISF, which is in line with the parametric estimates.
Our estimates of net WTP are of particular interest to policymakers as they provide information that is directly relevant to the decision they face; should we continue to invest in on-site storage, or should we construct an interim storage facility? These results, like the parametric results outlined above, favor the construction of an ISF, but the net value of an ISF over the continuation of on-site storage is fairly modest.
5 An approach for estimating absolute WTP for the continuation of current policy and a policy alternative
To this point, the paper develops and executes a “relative” approach to valuation that generates an estimate of WTP for a preferred policy option relative to an unpreferred alternative. This approach is designed to more directly inform policy decisions, as the elicitation exercise is structured in a manner that mirrors the decisions that policymakers commonly face.
It is also possible, however, to imagine a scenario where estimates of the “absolute” (i.e., relative to a current-level baseline) nonmarket values of two policy options – most likely the continuation of current policy and a single, defined alternative – are needed. With slight modifications, the approach we developed above can generate such estimates. In particular, it would require the analyst to construct two separate elicitation exercises, one that compared the continuation of current policy to a current-level baseline and a second that compared the defined alternative to the same, current-level baseline. Survey respondents could then be randomly assigned to each CV exercise, which would proceed in the manner of a typical CV exercise and WTP could then be estimated for both for the continuation of current policy and for the defined alternative policy option, relative to a current-level baseline. Implementation of such an approach would allow the analyst to estimate WTP for two separate policy options – maintaining current policy or adopting and implementing the alternative – each compared to a fictitious unchanging state as specified in the current-level baseline. We note that because these two estimates share a common baseline they can, in theory, be directly compared to one another to provide an estimate of net WTP for either alternative. Of course, whether this theoretical comparability plays out empirically remains to be seen. We plan to directly address this question in future research.
6 Discussion and conclusions
This research has considered how WTP for policy options can be estimated in a manner that is of direct relevance to choices commonly confronted by policymakers in legislatures and government agencies. We began by considering the choice of baselines used to generate such estimates, arguing that legislative and agency decision-makers are typically confronted with binary choices between pairs of options, in which one option is evaluated relative to the other rather than against some fixed, absolute threshold.Footnote 17 We have also argued that, for all options including the continuation of current policy, the relevant characterization is a specific choice that comes at a stipulated cost. In that way, the question we pose is: what are people willing to pay for their preferred option relative to their alternative (less-preferred) option? We contend that this is the kind of information that is necessary to provide a comparative estimate of net WTP that will be of most relevance to policymakers. Of course, it is still theoretically and sometimes practically important to know something about a population’s WTP for an option in comparison to some kind of absolute or fixed baseline, and we have described an approach to CV that will provide “absolute” estimates while theoretically preserving our ability to estimate net WTP for a policy option.
To demonstrate our approach, we estimated WTP for two distinct options for managing UNF in the United States: continue on-site storage at or near the nuclear generators where the waste was produced (the continuation of current policy) or transport the material to one or more regional interim storage facilities where it can be sequestered away from large populations, environmentally sensitive areas, and secured from natural and human threats (the defined policy alternative). Our approach allowed us to estimate WTP for an ISF (relative to on-site storage), WTP for on-site storage (relative to an ISF), and subsequently, the net WTP for an ISF. Results indicate that the mean WTP for an ISF (relative to on-site storage) ranges from $7 to $13, depending on the specification. Mean WTP for on-site storage (relative to an ISF) is also positive, but a bit lower, at $3 to $7. When combined, our results indicate a net mean WTP for an ISF of approximately $8–11, depending upon the estimation approach. In other words, the head-to-head comparison that is most relevant to policymakers favors the construction of an ISF, but the net value of an ISF over the continuation of on-site storage is fairly modest.
With these results in mind, imagine that we had instead undertaken a more conventional CV exercise in which we only estimated WTP for an ISF in relation to a current-level baseline. Such an approach would have several features and associated implications for the decisions that policymakers face. Most notably, we would not be able to answer the question that is most relevant to them – should we continue to invest in on-site storage or should we construct an ISF? Instead, we would have generated a “one-sided” estimate of WTP for an ISF and no information about WTP to continue on-site storage. This predicament would leave us with two options. On the one hand, we could stop here and provide this incomplete information to policymakers. On the other hand, we could answer the question they care about, by assuming that WTP to continue on-site storage is zero (equivalent to current levels). Our results do not support this assumption. WTP to continue on-site storage is almost as high as WTP for an ISF. As such, this assumption would cause us to significantly overestimate the gap between WTP for an ISF and WTP to continue on-site storage.
This problem is not specific to the nuclear waste policy domain. Rather, failure to estimate a “net” or “relative” WTP for a prospective policy change is likely to result in a superfluous or flawed analysis from the standpoint of policymakers when: (1) some portion of the population values the continuation of current policy more than the defined policy alternative; and (2) it is difficult for the portion of the population that prefers the current policy to avoid, opt out of, or ignore the effects of the policy change. When both of these conditions are met, the portion of the population that values the continuation of current policy but is forced to consume the policy change may suffer an unavoidable loss in utility if the defined alternative is implemented. The bias generated by one-sided WTP estimates will be largest in instances where value conflict is high (a relatively large portion of the population holds positive values for the continuation of current policy) and free disposability is highly constrained (it is nearly impossible for those who prefer to continue current policy to avoid the policy change and its effects). We expect cases where high conflict over values will almost always coincide with an inability of participants to opt out. Unless the participants are purely self-regarding, the affected values will have implications for other people and society that will matter for – and affect the utility of – those who are engaged in the disagreement over values.
Though some researchers contend that these conditions are rarely met (e.g., Haab & McConnell, Reference Haab and McConnell1997), the environmental economics literature is replete with examples in which policy changes inflict utility losses on portions of the population (e.g., Castle & Berrens, Reference Castle and Berrens1993; Cameron & Quiggin, Reference Cameron and Quiggin1994; Wilson, Reference Wilson1999; Jones et al., Reference Jones, Berrens, Jenkins-Smith, Silva, Carlson, Ripberger, Gupta and Carlson2016). In these instances, utility from both the continuation of current policy and defined alternative options must be elicited and in order to recover unbiased estimates of WTP within the relevant population.
In light of these considerations, we urge analysts to think about the reality of the policy process and the needs of policymakers when they are designing CV exercises. In the United States, the policymaking process is designed to reduce the large number of potential options for addressing policy problems to a binary choice between the continuation of current policy and a single alternative (Jones, Reference Jones2001; Simon, Reference Simon1996). Often times, policymakers have to choose one of these two options in high-conflict and high-stakes settings, where their decisions will benefit some and burden others. In these settings, CV exercises should be conducted in a manner consistent with the decision that policymakers face – should we continue to invest in the current policy, or should we adopt the specified alternative? In this paper, we have developed and tested the efficacy of an approach to CV that will provide information directly relevant to this question.
Appendix A. Background information about used nuclear fuel storage that was provided to respondents on the survey
Now we need to provide essential information for you to consider before answering additional questions. We ask that you read the following three paragraphs carefully so that everyone taking the survey has the same minimum level of factual information.
Used nuclear fuel is highly radioactive and must be safeguarded for thousands of years or chemically reprocessed, which is not economically feasible in the United States today. In 2010 the government halted construction of a deep underground facility inside Yucca Mountain in Nevada that had been intended for permanent storage and disposal of UNF.
Currently, used nuclear fuel in the United States is stored at more than 100 temporary storage sites in 39 states. This used fuel is stored in cooling pools “on-site” at nuclear power plants and decommissioned facilities. As part of the nation’s UNF storage policy, the government is trying to decide whether this used fuel should continue to be stored on-site, or whether it should be transported to interim storage facilities until a permanent repository can be constructed.
Key arguments that are made FOR current “on-site” storage practices include the following:
-
∙ Keeping the UNF at current facilities until a permanent repository is constructed would ensure that the radioactive materials have to be moved only once instead of twice.
-
∙ Packaging and transportation of UNF from nuclear facilities to interim storage facilities is risky.
-
∙ Storing fuel “on-site” at nuclear facilities is less expensive than building interim storage facilities and buys time for finding permanent future solutions.
-
∙ Current storage at nuclear power plants has not caused any accidents that have exposed the U.S. public to radiation, and with significant investment, current storage sites can be made safer from terrorists and other threats such as flooding.
Key arguments that are made AGAINST current “on-site” storage practices include the following:
-
∙ Storing UNF at nuclear facilities does not provide adequate protection from terrorists, and increasing security would require substantial effort, time, and money.
-
∙ Some nuclear power plants where UNF is stored are near rivers and oceans where flooding is possible, and many are near large population centers, making huge numbers of U.S. residents vulnerable to risks from flooding and other accidents. On rare occasions, UNF has leaked radiation into the cooling pools.
-
∙ Large volumes of these materials are accumulating that require expensive security; yet current practices do not provide a permanent solution.
-
∙ Some of these sites have been dismantled or shutdown, resulting in “stranded” UNF. Expensive security measures must be maintained to protect these stored nuclear materials. Interim storage facilities could help consolidate this used fuel.
Though nuclear power plants will continue to store some UNF in their cooling pools, much of the radioactive materials currently at more than 100 temporary storage sites in 39 states could be consolidated at a smaller number of facilities. The President’s Blue Ribbon Commission on America’s Nuclear Future recognized that constructing underground repositories for permanent storage and disposal of UNF will take decades, and the Commission recommended building interim storage sites in the next 10–15 years where UNF could be consolidated, stored, and better secured while one or more permanent nuclear repositories are being developed. These interim storage sites would meet all technical and safety requirements set by the U.S. Nuclear Regulatory Commission, the U.S. Environmental Protection Agency, and state regulatory agencies.
Key arguments that are made FOR interim storage sites include the following:
-
∙ Interim sites can be constructed sooner (within 10–15 years) to safely store UNF for up to a hundred years, which is longer than feasible for temporary storage at nuclear power plants, and allow more time to develop permanent repositories.
-
∙ Interim sites would consolidate UNF while providing better protection from terrorists and allowing the radioactive materials to cool and be packaged for eventual shipment to a permanent repository.
-
∙ Interim sites would reduce the growing amount of radioactive materials currently being stored at nuclear power plants, many of which are near large population centers, rivers, and oceans where flooding is possible.
-
∙ Interim sites would allow removal of “stranded” UNF from ten sites and eventually other sites where nuclear reactors have been dismantled or shutdown, but expensive security measures must be continued to protect the stored nuclear materials. Those savings could partially pay for constructing interim storage sites.
Key arguments that are made AGAINST interim storage sites include the following:
-
∙ Building interim sites might lead to delaying the more politically difficult solution of building permanent repositories, which may take 30 or 40 years to construct.
-
∙ Transporting UNF by barge, train, or truck to interim sites is more risky than continuing temporary storage at the sites of operating or dismantled nuclear power plants.
-
∙ Expanding current “on-site” storage practices at or near existing operational nuclear power plants is cheaper and politically more acceptable than building consolidated interim storage facilities.
-
∙ No members of the public have yet been harmed by current practices for temporarily storing UNF, and even though many of today’s sites are near large population centers, security can be improved to reduce the risks of terrorist attacks and flooding.








