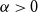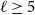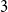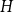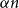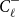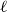1. Introduction
A
![]() $k$
-uniform hypergraph
$k$
-uniform hypergraph
![]() $H$
consists of a vertex set
$H$
consists of a vertex set
![]() $V(H)$
together with a set of edges
$V(H)$
together with a set of edges
![]() $E(H)\subseteq V(H)^{(k)}=\{S\subseteq V(H)\,:\,\vert S\vert =k\}$
. Throughout this note, if not stated otherwise, by hypergraph we always mean a
$E(H)\subseteq V(H)^{(k)}=\{S\subseteq V(H)\,:\,\vert S\vert =k\}$
. Throughout this note, if not stated otherwise, by hypergraph we always mean a
![]() $3$
-uniform hypergraph. Given a hypergraph
$3$
-uniform hypergraph. Given a hypergraph
![]() $F$
, the extremal number of
$F$
, the extremal number of
![]() $F$
for
$F$
for
![]() $n$
vertices,
$n$
vertices,
![]() $\textrm{ex}(n,F)$
, is the maximum number of edges an
$\textrm{ex}(n,F)$
, is the maximum number of edges an
![]() $n$
-vertex hypergraph can have without containing a copy of
$n$
-vertex hypergraph can have without containing a copy of
![]() $F$
. Determining the value of
$F$
. Determining the value of
![]() $\textrm{ex}(n,F)$
, or the Turán density
$\textrm{ex}(n,F)$
, or the Turán density
![]() $\pi (F) = \lim _{n \to \infty } \frac{\textrm{ex}(n,F)}{\binom{n}{3}}$
, is one of the core problems in combinatorics. In particular, the problem of determining the Turán density of the complete
$\pi (F) = \lim _{n \to \infty } \frac{\textrm{ex}(n,F)}{\binom{n}{3}}$
, is one of the core problems in combinatorics. In particular, the problem of determining the Turán density of the complete
![]() $3$
-uniform hypergraph on four vertices, i.e.,
$3$
-uniform hypergraph on four vertices, i.e.,
![]() $\pi \left(K_4^{(3)}\right)$
, was asked by Turán in 1941 [Reference Turán13] and Erdős [Reference Erdős4] offered 1000
$\pi \left(K_4^{(3)}\right)$
, was asked by Turán in 1941 [Reference Turán13] and Erdős [Reference Erdős4] offered 1000
![]() $\$$
for its resolution. Despite receiving a lot of attention (see for instance the survey by Keevash [Reference Keevash8]) this problem, and even the seemingly simpler problem of determining
$\$$
for its resolution. Despite receiving a lot of attention (see for instance the survey by Keevash [Reference Keevash8]) this problem, and even the seemingly simpler problem of determining
![]() $\pi \left(K_4^{(3)-}\right)$
, where
$\pi \left(K_4^{(3)-}\right)$
, where
![]() $K_4^{(3)-}$
is the
$K_4^{(3)-}$
is the
![]() $K_4^{(3)}$
minus one edge, remain open.
$K_4^{(3)}$
minus one edge, remain open.
Several variations of this type of problem have been considered, see for instance [Reference Balogh, Clemen and Lidický1, Reference Glebov, Král’ and Volec7, Reference Reiher, Rödl and Schacht12] and the references therein. The one that we are concerned with in this note asks how large the minimum codegree of an
![]() $F$
-free hypergraph can be. Given a hypergraph
$F$
-free hypergraph can be. Given a hypergraph
![]() $H$
and
$H$
and
![]() $S\subseteq V$
, we define the degree
$S\subseteq V$
, we define the degree
![]() $d(S)$
of
$d(S)$
of
![]() $S$
(in
$S$
(in
![]() $H$
) as the number of edges containing
$H$
) as the number of edges containing
![]() $S$
, i.e.,
$S$
, i.e.,
![]() $d(S)=\vert \{e\in E(H)\,:\,S\subseteq e\}\vert$
. If
$d(S)=\vert \{e\in E(H)\,:\,S\subseteq e\}\vert$
. If
![]() $S=\{v\}$
or
$S=\{v\}$
or
![]() $S=\{u,v\}$
(and
$S=\{u,v\}$
(and
![]() $H$
is
$H$
is
![]() $3$
-uniform), we omit the parentheses and speak of
$3$
-uniform), we omit the parentheses and speak of
![]() $d(v)$
or
$d(v)$
or
![]() $d(uv)$
as the degree of
$d(uv)$
as the degree of
![]() $v$
or codegree of
$v$
or codegree of
![]() $u$
and
$u$
and
![]() $v$
, respectively. We further write
$v$
, respectively. We further write
![]() $\delta (H)=\delta _1(H)=\min _{v\in V(H)} d(v)$
and
$\delta (H)=\delta _1(H)=\min _{v\in V(H)} d(v)$
and
![]() $\delta _2(H)=\min _{uv\in V(H)^{(2)}}d(uv)$
for the minimum degree and the minimum codegree of
$\delta _2(H)=\min _{uv\in V(H)^{(2)}}d(uv)$
for the minimum degree and the minimum codegree of
![]() $H$
, respectively.
$H$
, respectively.
Given a hypergraph
![]() $F$
and
$F$
and
![]() $n\in \mathbb{N}$
, Mubayi and Zhao [Reference Mubayi and Zhao11] introduced the codegree Turán number
$n\in \mathbb{N}$
, Mubayi and Zhao [Reference Mubayi and Zhao11] introduced the codegree Turán number
![]() $\textrm{ex}_2(n,F)$
of
$\textrm{ex}_2(n,F)$
of
![]() $n$
and
$n$
and
![]() $F$
as the maximum
$F$
as the maximum
![]() $d$
such that there is an
$d$
such that there is an
![]() $F$
-free hypergraph
$F$
-free hypergraph
![]() $H$
on
$H$
on
![]() $n$
vertices with
$n$
vertices with
![]() $\delta _2(H)\geq d$
. Moreover, they defined the codegree Turán density of
$\delta _2(H)\geq d$
. Moreover, they defined the codegree Turán density of
![]() $F$
as
$F$
as
and proved that this limit always exists. It is not hard to see that
The codegree Turán density is known only for a few (non-trivial) hypergraphs (and blow-ups of these), see the table in [Reference Balogh, Clemen and Lidický1]. The first result that determined
![]() $\gamma (F)$
exactly is due to Mubayi [Reference Mubayi9] who showed that
$\gamma (F)$
exactly is due to Mubayi [Reference Mubayi9] who showed that
![]() $\gamma (\mathbb F) = 1/2$
, where
$\gamma (\mathbb F) = 1/2$
, where
![]() $\mathbb F$
denotes the ‘Fano plane’. Later, using a computer assisted proof, Falgas–Ravry, Pikhurko, Vaughan, and Volec [Reference Falgas-Ravry, Pikhurko, Vaughan and Volec6] proved that
$\mathbb F$
denotes the ‘Fano plane’. Later, using a computer assisted proof, Falgas–Ravry, Pikhurko, Vaughan, and Volec [Reference Falgas-Ravry, Pikhurko, Vaughan and Volec6] proved that
![]() $\gamma \left(K_4^{(3)-}\right)=1/4$
. As far as we know, the only other hypergraph for which the codegree Turán density is known is
$\gamma \left(K_4^{(3)-}\right)=1/4$
. As far as we know, the only other hypergraph for which the codegree Turán density is known is
![]() $F_{3,2}$
, a hypergraph with vertex set [5] and edges
$F_{3,2}$
, a hypergraph with vertex set [5] and edges
![]() $123$
,
$123$
,
![]() $124$
,
$124$
,
![]() $125$
, and
$125$
, and
![]() $345$
[Reference Falgas–Ravry, Marchant, Pikhurko and Vaughan5]. The problem of determining the codegree Turán density of
$345$
[Reference Falgas–Ravry, Marchant, Pikhurko and Vaughan5]. The problem of determining the codegree Turán density of
![]() $K_4^{(3)}$
remains open, and Czygrinow and Nagle [Reference Czygrinow and Nagle2] conjectured that
$K_4^{(3)}$
remains open, and Czygrinow and Nagle [Reference Czygrinow and Nagle2] conjectured that
![]() $\gamma \left(K_4^{(3)}\right)=1/2$
. For more results concerning
$\gamma \left(K_4^{(3)}\right)=1/2$
. For more results concerning
![]() $\pi (F)$
,
$\pi (F)$
,
![]() $\gamma (F)$
, and other variations of the Turán density see [Reference Balogh, Clemen and Lidický1].
$\gamma (F)$
, and other variations of the Turán density see [Reference Balogh, Clemen and Lidický1].
Given an integer
![]() $\ell \geq 3$
, a tight cycle
$\ell \geq 3$
, a tight cycle
![]() $C_\ell$
is a hypergraph with vertex set
$C_\ell$
is a hypergraph with vertex set
![]() $\{v_1, \dots, v_\ell \}$
and edge set
$\{v_1, \dots, v_\ell \}$
and edge set
![]() $\{v_iv_{i+1}v_{i+2}\,:\,i\in \mathbb{Z}/\ell \mathbb{Z}\}$
. Moreover, we define
$\{v_iv_{i+1}v_{i+2}\,:\,i\in \mathbb{Z}/\ell \mathbb{Z}\}$
. Moreover, we define
![]() $C_\ell ^{-}$
as
$C_\ell ^{-}$
as
![]() $C_\ell ^{}$
minus one edge. In this note, we prove that the Turán codegree density of
$C_\ell ^{}$
minus one edge. In this note, we prove that the Turán codegree density of
![]() $C_\ell ^{-}$
is zero for every
$C_\ell ^{-}$
is zero for every
![]() $\ell \geq 5$
.
$\ell \geq 5$
.
Theorem 1.1. Let
![]() $\ell \geq 5$
be an integer. Then
$\ell \geq 5$
be an integer. Then
![]() $\gamma \left(C_{\ell }^{-}\right)=0$
.
$\gamma \left(C_{\ell }^{-}\right)=0$
.
The previously known best upper bound was given by Balogh, Clemen, and Lidický [Reference Balogh, Clemen and Lidický1] who used flag algebras to prove that
![]() $\gamma \left(C_{\ell }^-\right)\leq 0.136$
.
$\gamma \left(C_{\ell }^-\right)\leq 0.136$
.
2. Proof of Theorem 1.1
For singletons, pairs, and triples, we may omit the set parentheses and commas. For a hypergraph
![]() $H=(V,E)$
and
$H=(V,E)$
and
![]() $v\in V$
, the link of
$v\in V$
, the link of
![]() $v$
(in
$v$
(in
![]() $H$
) is the graph
$H$
) is the graph
![]() $L_v=(V\setminus v,\{e\setminus v\,:\,v\in e\in E\})$
. For
$L_v=(V\setminus v,\{e\setminus v\,:\,v\in e\in E\})$
. For
![]() $x,y\in V$
, the neighbourhood of
$x,y\in V$
, the neighbourhood of
![]() $x$
and
$x$
and
![]() $y$
(in
$y$
(in
![]() $H$
) is the set
$H$
) is the set
![]() $N(xy)=\{z\in V\,:\,xyz\in E\}$
. For positive integers
$N(xy)=\{z\in V\,:\,xyz\in E\}$
. For positive integers
![]() $\ell, k$
and a hypergraph
$\ell, k$
and a hypergraph
![]() $F$
on
$F$
on
![]() $k$
vertices, denote the
$k$
vertices, denote the
![]() $\ell$
-blow-up of
$\ell$
-blow-up of
![]() $F$
by
$F$
by
![]() $F(\ell )$
. This is the
$F(\ell )$
. This is the
![]() $k$
-partite hypergraph
$k$
-partite hypergraph
![]() $F(\ell )=(V, E)$
with
$F(\ell )=(V, E)$
with
![]() $V = V_1 \dot \cup \dots \dot \cup V_k$
,
$V = V_1 \dot \cup \dots \dot \cup V_k$
,
![]() $|V_i| = \ell$
for
$|V_i| = \ell$
for
![]() $1\leq i \leq k$
, and
$1\leq i \leq k$
, and
![]() $E = \{v_{i_1}v_{i_2} v_{i_3}\,:\, v_{i_j} \in V_{i_j} \text{ and } i_1 i_2 i_3 \in E(F)\}$
.
$E = \{v_{i_1}v_{i_2} v_{i_3}\,:\, v_{i_j} \in V_{i_j} \text{ and } i_1 i_2 i_3 \in E(F)\}$
.
In their seminal paper, Mubayi and Zhao [Reference Mubayi and Zhao11] proved the following supersaturation result for the codegree Turán density.
Proposition 2.1 (Mubayi and Zhao [Reference Mubayi and Zhao11]). For every hypergraph
![]() $F$
and
$F$
and
![]() $\varepsilon \gt 0$
, there are
$\varepsilon \gt 0$
, there are
![]() $n_0$
and
$n_0$
and
![]() $\delta \gt 0$
such that every hypergraph
$\delta \gt 0$
such that every hypergraph
![]() $H$
on
$H$
on
![]() $n\geq n_0$
vertices with
$n\geq n_0$
vertices with
![]() $\delta _2(H)\geq (\gamma (F)+\varepsilon )n$
contains at least
$\delta _2(H)\geq (\gamma (F)+\varepsilon )n$
contains at least
![]() $\delta n^{v(F)}$
copies of
$\delta n^{v(F)}$
copies of
![]() $F$
. Consequently, for every positive integer
$F$
. Consequently, for every positive integer
![]() $\ell$
,
$\ell$
,
![]() $\gamma (F) = \gamma (F(\ell ))$
.
$\gamma (F) = \gamma (F(\ell ))$
.
Proof of Theorem
1.1. We begin by noting that it is enough to show that
![]() $\gamma \left(C_5^-\right) = 0$
. Indeed, we shall prove by induction that
$\gamma \left(C_5^-\right) = 0$
. Indeed, we shall prove by induction that
![]() $\gamma \left(C_{\ell }^-\right)=0$
for every
$\gamma \left(C_{\ell }^-\right)=0$
for every
![]() $\ell \geq 5$
. For
$\ell \geq 5$
. For
![]() $\ell =6$
, the result follows since
$\ell =6$
, the result follows since
![]() $C_6^-$
is a subgraph of
$C_6^-$
is a subgraph of
![]() $C_3(2)$
. Hence, by Proposition 2.1, we have
$C_3(2)$
. Hence, by Proposition 2.1, we have
![]() $\gamma \left(C_6^-\right)\leq \gamma (C_3(2))=\gamma (C_3)=0$
. For
$\gamma \left(C_6^-\right)\leq \gamma (C_3(2))=\gamma (C_3)=0$
. For
![]() $\ell =7$
, note that
$\ell =7$
, note that
![]() $C_7^-$
is a subgraph of
$C_7^-$
is a subgraph of
![]() $C_5^-(2)$
. To see that, let
$C_5^-(2)$
. To see that, let
![]() $v_1,\dots,v_5$
be the vertices of a
$v_1,\dots,v_5$
be the vertices of a
![]() $C_5^-$
with edge set
$C_5^-$
with edge set
![]() $\{v_iv_{i+1}v_{i+2}\,:\,i\neq 4\}$
, where the indices are taken modulo
$\{v_iv_{i+1}v_{i+2}\,:\,i\neq 4\}$
, where the indices are taken modulo
![]() $5$
. Now add one copy
$5$
. Now add one copy
![]() $v^{\prime}_2$
of
$v^{\prime}_2$
of
![]() $v_2$
and one copy
$v_2$
and one copy
![]() $v^{\prime}_3$
of
$v^{\prime}_3$
of
![]() $v_3$
. Then
$v_3$
. Then
![]() $v_1v_3v_2v_4v^{\prime}_3v_5v^{\prime}_2$
is the cyclic ordering of a
$v_1v_3v_2v_4v^{\prime}_3v_5v^{\prime}_2$
is the cyclic ordering of a
![]() $C_7^-$
with the missing edge being
$C_7^-$
with the missing edge being
![]() $v^{\prime}_3v_5v^{\prime}_2$
. Therefore, if
$v^{\prime}_3v_5v^{\prime}_2$
. Therefore, if
![]() $\gamma \left(C_5^-\right)=0$
, then, by Proposition 2.1, we have
$\gamma \left(C_5^-\right)=0$
, then, by Proposition 2.1, we have
![]() $\gamma \left(C_7^-\right)=0$
. Finally, for
$\gamma \left(C_7^-\right)=0$
. Finally, for
![]() $\ell \geq 8$
,
$\ell \geq 8$
,
![]() $\gamma \left(C_\ell ^-\right)=0$
follows by induction using the same argument and observing that
$\gamma \left(C_\ell ^-\right)=0$
follows by induction using the same argument and observing that
![]() $C_\ell ^-$
is a subgraph of
$C_\ell ^-$
is a subgraph of
![]() $C_{\ell -3}^-(2)$
.
$C_{\ell -3}^-(2)$
.
Given
![]() $\varepsilon \in (0,1)$
, consider a hypergraph
$\varepsilon \in (0,1)$
, consider a hypergraph
![]() $H=(V,E)$
on
$H=(V,E)$
on
![]() $n\geq \big (\frac{2}{\varepsilon }\big )^{5/\varepsilon ^2+2}$
vertices with
$n\geq \big (\frac{2}{\varepsilon }\big )^{5/\varepsilon ^2+2}$
vertices with
![]() $\delta _2(H)\geq \varepsilon n$
. We claim that
$\delta _2(H)\geq \varepsilon n$
. We claim that
![]() $H$
contains a copy of a
$H$
contains a copy of a
![]() $C_5^-$
.
$C_5^-$
.
Given
![]() $v,b\in V$
,
$v,b\in V$
,
![]() $S\subseteq V$
, and
$S\subseteq V$
, and
![]() $P\subseteq (V\setminus S)^{2}$
, we say that
$P\subseteq (V\setminus S)^{2}$
, we say that
![]() $(v,S,b,P)$
is a nice picture if it satisfies the following (see Figure 1):
$(v,S,b,P)$
is a nice picture if it satisfies the following (see Figure 1):
-
(i)
 $S\subseteq N_{L_v}(b)$
, where
$S\subseteq N_{L_v}(b)$
, where
 $N_{L_v}(b)$
is the neighbourhood of
$N_{L_v}(b)$
is the neighbourhood of
 $b$
in the link
$b$
in the link
 $L_v$
.
$L_v$
. -
(ii) For every vertex
 $u\in S$
and ordered pair
$u\in S$
and ordered pair
 $(x,y)\in P$
, the sequence
$(x,y)\in P$
, the sequence
 $ubxy$
is a path of length
$ubxy$
is a path of length
 $3$
in
$3$
in
 $L_v$
.
$L_v$
.
Note that if
![]() $(v,S,b,P)$
is a nice picture and there exists
$(v,S,b,P)$
is a nice picture and there exists
![]() $u\in S$
and
$u\in S$
and
![]() $(x,y)\in P$
such that
$(x,y)\in P$
such that
![]() $uxy\in E$
, then
$uxy\in E$
, then
![]() $ubvxy$
is a copy of
$ubvxy$
is a copy of
![]() $C_5^-$
(with the missing edge being
$C_5^-$
(with the missing edge being
![]() $yub$
)
$yub$
)

Figure 1. A nice picture
![]() $(v,S,b,P)$
.
$(v,S,b,P)$
.
To find such a copy of
![]() $C_5^-$
in
$C_5^-$
in
![]() $H$
, we are going to construct a sequence of nested sets
$H$
, we are going to construct a sequence of nested sets
![]() $S_t\subseteq S_{t-1}\subseteq \ldots \subseteq S_0$
, where
$S_t\subseteq S_{t-1}\subseteq \ldots \subseteq S_0$
, where
![]() $t=\lceil 5/\varepsilon ^2+1\rceil$
, such that for
$t=\lceil 5/\varepsilon ^2+1\rceil$
, such that for
![]() $1\leq i\leq t$
there are nice pictures
$1\leq i\leq t$
there are nice pictures
![]() $(v_i,S_i,b_i,P_i)$
satisfying
$(v_i,S_i,b_i,P_i)$
satisfying
![]() $v_i\in S_{i-1}$
,
$v_i\in S_{i-1}$
,
![]() $|S_i|\geq \big (\frac{\varepsilon }{2}\big )^{i+1}n\geq 1$
and
$|S_i|\geq \big (\frac{\varepsilon }{2}\big )^{i+1}n\geq 1$
and
![]() $|P_i|\geq \varepsilon ^2 n^2/5$
. Suppose that such a sequence exists. Then by the pigeonhole principle, there exist two indices
$|P_i|\geq \varepsilon ^2 n^2/5$
. Suppose that such a sequence exists. Then by the pigeonhole principle, there exist two indices
![]() $i,j \in [t]$
such that
$i,j \in [t]$
such that
![]() $P_i\cap P_j\neq \emptyset$
and
$P_i\cap P_j\neq \emptyset$
and
![]() $i\lt j$
. Let
$i\lt j$
. Let
![]() $(x,y)$
be an element of
$(x,y)$
be an element of
![]() $P_i\cap P_j$
. Hence, we obtain a nice picture
$P_i\cap P_j$
. Hence, we obtain a nice picture
![]() $(v_i,S_i,b_i,P_i)$
,
$(v_i,S_i,b_i,P_i)$
,
![]() $v_j\in S_i$
and
$v_j\in S_i$
and
![]() $(x,y)\in P_i$
such that
$(x,y)\in P_i$
such that
![]() $v_jxy \in E$
(since
$v_jxy \in E$
(since
![]() $xy$
is an edge in
$xy$
is an edge in
![]() $L_{v_j}$
). Consequently,
$L_{v_j}$
). Consequently,
![]() $v_jb_iv_ixy$
is a copy of
$v_jb_iv_ixy$
is a copy of
![]() $C_5^-$
in
$C_5^-$
in
![]() $H$
.
$H$
.
It remains to prove that the sequence described above always exists. We construct it recursively. Let
![]() $S_0\subseteq V$
be an arbitrary subset of size
$S_0\subseteq V$
be an arbitrary subset of size
![]() $\varepsilon n/2$
. Suppose we already found the sets
$\varepsilon n/2$
. Suppose we already found the sets
![]() $S_i$
for
$S_i$
for
![]() $0\leq i\lt k\leq t$
, with the respective nice pictures
$0\leq i\lt k\leq t$
, with the respective nice pictures
![]() $(v_i,S_i,b_i,P_i)$
for
$(v_i,S_i,b_i,P_i)$
for
![]() $1\leq i\lt k$
. Now we want to construct
$1\leq i\lt k$
. Now we want to construct
![]() $(v_k,S_k,b_k,P_k)$
. Pick
$(v_k,S_k,b_k,P_k)$
. Pick
![]() $v_k\in S_{k-1}$
arbitrarily. The minimum codegree of
$v_k\in S_{k-1}$
arbitrarily. The minimum codegree of
![]() $H$
implies that
$H$
implies that
![]() $\delta (L_{v_k})\geq \varepsilon n$
and thus for every
$\delta (L_{v_k})\geq \varepsilon n$
and thus for every
![]() $u\in S_{k-1}$
, we have that
$u\in S_{k-1}$
, we have that
![]() $d_{L_{v_k}}(u)\geq \varepsilon n$
. Observe that
$d_{L_{v_k}}(u)\geq \varepsilon n$
. Observe that
and therefore, by an averaging argument there is a vertex
![]() $b_k\in V\setminus v_k$
such that the subset
$b_k\in V\setminus v_k$
such that the subset
![]() $S_k\,:\!=\,N_{L_{v_k}}(b_k)\cap S_{k-1}\subseteq S_{k-1}$
is of size at least
$S_k\,:\!=\,N_{L_{v_k}}(b_k)\cap S_{k-1}\subseteq S_{k-1}$
is of size at least
![]() $|S_k|\geq \big (\frac{\varepsilon }{2}\big )^{k+1} n$
. Let
$|S_k|\geq \big (\frac{\varepsilon }{2}\big )^{k+1} n$
. Let
![]() $P_k$
be all the pairs
$P_k$
be all the pairs
![]() $(x,y) \in (V\setminus S_k)^2$
such that for every vertex
$(x,y) \in (V\setminus S_k)^2$
such that for every vertex
![]() $v\in S_k$
, the sequence
$v\in S_k$
, the sequence
![]() $v,b_k,x,y$
forms a path of length
$v,b_k,x,y$
forms a path of length
![]() $3$
in
$3$
in
![]() $L_{v_k}$
. Since
$L_{v_k}$
. Since
![]() $|S_k|\leq \varepsilon n/2$
and
$|S_k|\leq \varepsilon n/2$
and
![]() $\delta (L_{v_k})\geq \varepsilon n$
, it is easy to see that
$\delta (L_{v_k})\geq \varepsilon n$
, it is easy to see that
![]() $|P_k|\geq (\varepsilon n/2)(\varepsilon n/2-1) \geq \varepsilon ^2n^2/5$
. That is to say
$|P_k|\geq (\varepsilon n/2)(\varepsilon n/2-1) \geq \varepsilon ^2n^2/5$
. That is to say
![]() $(v_k, S_k, b_k, P_k)$
is a nice picture satisfying the desired conditions.
$(v_k, S_k, b_k, P_k)$
is a nice picture satisfying the desired conditions.
3. Concluding remarks
A famous result by Erdős [Reference Erdős3] asserts that a hypergraph
![]() $F$
satisfies
$F$
satisfies
![]() $\pi (F)=0$
if
$\pi (F)=0$
if
![]() $F$
is tripartite (i.e.,
$F$
is tripartite (i.e.,
![]() $V(F)=X_1\dot \cup X_2 \dot \cup X_3$
and for every
$V(F)=X_1\dot \cup X_2 \dot \cup X_3$
and for every
![]() $e\in E(F)$
we have
$e\in E(F)$
we have
![]() $\vert e\cap X_i\vert = 1$
for every
$\vert e\cap X_i\vert = 1$
for every
![]() $i\in [3]$
). Note that if
$i\in [3]$
). Note that if
![]() $H$
is tripartite, then every subgraph of
$H$
is tripartite, then every subgraph of
![]() $H$
is tripartite as well and there are tripartite hypergraphs
$H$
is tripartite as well and there are tripartite hypergraphs
![]() $H$
with
$H$
with
![]() $\vert E(H) \vert =\tfrac{2}{9} \binom{\vert V(H)\vert }{3}$
. Therefore, if
$\vert E(H) \vert =\tfrac{2}{9} \binom{\vert V(H)\vert }{3}$
. Therefore, if
![]() $F$
is not tripartite, then
$F$
is not tripartite, then
![]() $\pi (F)\geq 2/9$
. In other words, Erdős’ result implies that there are no Turán densities in the interval
$\pi (F)\geq 2/9$
. In other words, Erdős’ result implies that there are no Turán densities in the interval
![]() $(0,2/9)$
. It would be interesting to understand the behaviour of the codegree Turán density in the range close to zero.
$(0,2/9)$
. It would be interesting to understand the behaviour of the codegree Turán density in the range close to zero.
Question 3.1. Is it true that for every
![]() $\xi \in (0,1]$
, there exists a hypergraph
$\xi \in (0,1]$
, there exists a hypergraph
![]() $F$
such that
$F$
such that
Mubayi and Zhao [Reference Mubayi and Zhao11] answered this question affirmatively if we consider the codegree Turán density of a family of hypergraphs instead of a single hypergraph.
Since
![]() $C_5^{-}$
is not tripartite, we have that
$C_5^{-}$
is not tripartite, we have that
![]() $\pi (C_5^{-})\geq 2/9$
. The following construction attributed to Mubayi and Rödl (see e.g. [Reference Balogh, Clemen and Lidický1]) provides a better lower bound. Let
$\pi (C_5^{-})\geq 2/9$
. The following construction attributed to Mubayi and Rödl (see e.g. [Reference Balogh, Clemen and Lidický1]) provides a better lower bound. Let
![]() $H=(V,E)$
be a
$H=(V,E)$
be a
![]() $C_5^{-}$
-free hypergraph on
$C_5^{-}$
-free hypergraph on
![]() $n$
vertices. Define a hypergraph
$n$
vertices. Define a hypergraph
![]() $\widetilde H$
on
$\widetilde H$
on
![]() $3n$
vertices with
$3n$
vertices with
![]() $V(\widetilde H)= V_1\dot \cup V_2\dot \cup V_3$
such that
$V(\widetilde H)= V_1\dot \cup V_2\dot \cup V_3$
such that
![]() $\widetilde H[V_i]=H$
for every
$\widetilde H[V_i]=H$
for every
![]() $i\in [3]$
plus all edges of the form
$i\in [3]$
plus all edges of the form
![]() $e=\{v_1,v_2,v_3\}$
with
$e=\{v_1,v_2,v_3\}$
with
![]() $v_i\in V_i$
. Then, it is easy to check that
$v_i\in V_i$
. Then, it is easy to check that
![]() $\widetilde H$
is also
$\widetilde H$
is also
![]() $C_5^{-}$
-free. We may recursively repeat this construction starting with
$C_5^{-}$
-free. We may recursively repeat this construction starting with
![]() $H$
being a single edge and obtain an arbitrarily large
$H$
being a single edge and obtain an arbitrarily large
![]() $C_5^{-}$
-free hypergraph with density
$C_5^{-}$
-free hypergraph with density
![]() $1/4-o(1)$
. In fact, those hypergraphs are
$1/4-o(1)$
. In fact, those hypergraphs are
![]() $C_\ell ^-$
-free for every
$C_\ell ^-$
-free for every
![]() $\ell$
not divisible by three. The following is a generalisation of a conjecture in [Reference Mubayi, Pikhurko and Sudakov10].
$\ell$
not divisible by three. The following is a generalisation of a conjecture in [Reference Mubayi, Pikhurko and Sudakov10].
Conjecture 3.2. If
![]() $\ell \geq 5$
is not divisible by three, then
$\ell \geq 5$
is not divisible by three, then
![]() $\pi \left(C_\ell ^{-}\right) = \frac{1}{4}\,$
.
$\pi \left(C_\ell ^{-}\right) = \frac{1}{4}\,$
.