Does telling white lies signal pro-social preferences?

Abstract

The opportunity to tell a white lie (i.e., a lie that benefits another person) generates a moral conflict between two opposite moral dictates, one pushing towards telling the truth always and the other pushing towards helping others. Here we study how people resolve this moral conflict. What does telling a white lie signal about a person’s pro-social tendencies? To answer this question, we conducted a two-stage 2x2 experiment. In the first stage, we used a Deception Game to measure aversion to telling a Pareto white lie (i.e., a lie that helps both the liar and the listener), and aversion to telling an altruistic white lie (i.e., a lie that helps the listener at the expense of the liar). In the second stage we measured altruistic tendencies using a Dictator Game and cooperative tendencies using a Prisoner’s dilemma. We found three major results: (i) both altruism and cooperation are positively correlated with aversion to telling a Pareto white lie; (ii) both altruism and cooperation are negatively correlated with aversion to telling an altruistic white lie; (iii) men are more likely than women to tell an altruistic white lie, but not to tell a Pareto white lie. Our results shed light on the moral conflict between prosociality and truth-telling. In particular, the first finding suggests that a significant proportion of people have non-distributional notions of what the right thing to do is, irrespective of the economic consequences, they tell the truth, they cooperate, they share their money.

1 Introduction

Moral decision-making in communication often concerns the choice whether to tell the truth or to deceive. While it is generally agreed that it is bad to tell lies that increase your benefit at the expense of that of another person (black lies), moral philosophers have long argued about if and when telling a lie that increases the benefit of another person (white lie) is morally acceptable. We find Socrates pointing out to one of his interlocutors in Plato’s Republic that, “when any of our so-called friends are attempting, through madness or ignorance, to do something bad, isn’t it a useful drug for preventing them?”—suggesting that, given the circumstances, deception might be the “good” thing to do (Plato [1997]). At the other end of the spectrum we find Immanuel Kant, for whom good intentions or consequences cannot justify an act of lying. For Kant, telling even a white lie is “by its mere form a crime of a human being against his own person and a worthlessness that must make him contemptible in his own eyes.” (Kant [1996]).

This raises the question whether prosocial agents would tell such “useful” lies, or condemn them, as Kant did. Prosocial behaviour, that is, behaviour intended to benefit other people or society as a whole, is widely considered the right course of action in situations in which there is a conflict between one’s own benefit and that of others. The Golden Rule, which encapsulates the essence of prosociality, is indeed “found in some form in almost every ethical tradition” (Blackburn [2003]). Thus, a prosocial person, when facing the decision of whether to tell a white lie or not may experience a conflict between two diverging moral dictates, one pushing towards lying for the benefit of others and the other pushing towards telling the truth regardless of circumstance.

Since most human interaction revolves around communication and involves some degree of prosociality, understanding how this conflict is resolved is not only interesting from the theoretical point of view of moral philosophy, but also from a more practical point of view. For instance, taking verbatim an example from Erat and Gneezy [2012] “should a supervisor give truthful feedback to a poorly performing employee, even when such truthful feedback has the potential to reduce the employee’s confidence and future performance?” What does telling a white lie signal about the supervisor’s prosocial tendencies?

The focus of the present paper is on this type of question and, more generally, the moral conflict between lying aversion and prosocial behaviour.

To measure prosocial tendencies and aversion to telling white lies we build on previous studies in behavioural economics, which place economic games into experimental settings. Specifically, the Dictator Game (DG), due to its setup, has proven useful in measuring altruistic proclivities in recruited subjects. In a standard DG, one player (the dictator) is given an initial endowment and is asked to decide how much of it, if any, to transfer to a passive player (the recipient), who is given nothing. The anonymity and confidentiality of decisions are ensured to rule out incentives (such as reputation) to share their endowment with the recipient. Although the theory of homo œconomicus predicts that dictators keep the whole endowment for themselves, research has shown that a significant proportion of dictators allocate a non-trivial share to recipients (Camerer [2003], Engel [2011], Forsythe et al. [1994], Kahneman et al. [1986]).

Akin to the manner in which the DG is used in research as the paradigmatic game with which to investigate altruism, extensive use has been made of the Prisoner’s Dilemma (PD) in experimental settings in order to investigate cooperative behaviour in agents. In the standard one-shot two-player PD, both players can either cooperate or defect. If a player cooperates, he pays c and bestows b>c on the other player while, if he defects, he pays and gives 0. Clearly homo œconomicus would defect in any case since, irrespective of the strategy of the other, the optimal strategy is to give 0. Yet in day-to-day life people often do cooperate and, perhaps unsurprisingly, research has shown that even in anonymous one-shot PD experiments a significant percentage of people choose to cooperate (see, e.g., Rapoport [1965]).

More recently, behavioural scientists have delved into choices people make regarding deception in different circumstances and under different conditions. Unlike cooperation and altruism, lying aversion is not measured by a unique and standard economic game and (at least) three different models have been put forward (Gneezy et al. [2013]). However, irrespective of the model used, findings all point to the same direction: while the classic approach in economics assumes that people are selfish and that lying in itself does not involve any cost, accumulating evidence suggests that a significant amount of people are lie-averse in economic and social interactions (Abeler et al. [2014], Cappelen et al. [2013], Erat and Gneezy [2012], Gneezy [2005], Gneezy et al. [2013], Hurkens and Kartik [2009], Lundquist et al. [2009], Weisel and Shalvi [2015]).

Recent research has also shed light on when people are more likely to use deception. Shalvi et al. [2011] find that “observing desired counterfactuals attenuates the degree to which people perceive lies as unethical”. Wiltermuth [2011] finds that people are more likely to cheat when the benefit of doing so is split between themselves and another person, even when the other beneficiary is a stranger with whom they had no interaction. Gino et al. [2013] distinguish among the mechanisms that may drive this increased willingness to cheat when the spoils are split with others. They suggest that the ability to justify self-serving actions as appropriate when others benefit is a stronger driver for unethical behaviour than pure concern for others. They also find that people cheat more when the number of beneficiaries increases and that individuals feel less guilty about their dishonest behaviour when others benefit from it. Conrads et al. [2013] examine the impact of two prevalent compensation schemes, individual piece-rates (under which each individual gets one compensation unit for each unit they produce) and team incentives (under which the production of the team is pooled and each individual receives one half of a compensation unit per unit of the joint production output). They find that lying is more prevalent under team incentives than under the individual piece-rates scheme. Thus, their results add to the evidence in Wiltermuth [2011] and Gino et al. [2013] suggesting that individuals are more willing to lie when the benefits of doing so are shared with others. Cohen et al. [2009] test whether groups lie more than individuals. They find that groups are more inclined to lie than individuals when deception is guaranteed to best serve their economic interest, but lie relatively less than individuals when honesty can be used strategically. Their results suggest that groups are more strategic than individuals in that they will use or avoid deception in order to maximise their economic outcome.

A few previous studies have investigated the relation between prosocial behaviour and aversion to telling white lies. Shalvi and de Dreu [2014] show that oxytocin, a neuropeptide known to promote affiliation and cooperation with others, promotes group-serving dishonesty. Levine and Schweitzer [2014] report that people who tell white lies are perceived as more moral than those who tell the truth. In a subsequent work, Levine and Schweitzer [2015] show that trusters in a trust game allocate more money to people who have told a white lie in a previous game than to people who have told the truth. This result provides evidence that telling a white lie signals prosocial behavior to observers. However, Levine and Schweitzer [2015] do not measure trustees’ behavior and thus it remains unclear whether those who tell white lies are really more prosocial than those who tell the truth. One corollary of the results of the current paper is that the answer to this question is positive in the case of altruistic white lies (those that benefit the other person at the expense of the liar), but negative in the case of Pareto white lies (those that benefit both the other person and the liar).

More closely related to our work is that of Cappelen et al. [2013], which explores the correlation between altruism in the DG and aversion to telling a Pareto white lie (PWL), providing evidence that people telling a Pareto white lie give significantly less in the Dictator Game. Our work builds on and extends the results of this paper.

Indeed, although these results represent a good starting point, more research is needed to develop a better understanding of the relation between aversion to telling a white lie and prosocial behaviour. First of all, most everyday situations are better modelled by a PD, rather than a DG. Since altruism in the DG and cooperation in the PD are different behaviours (virtually all altruistic people cooperate, but the converse does not hold - see Capraro et al. [2014a], it is also important to investigate the correlation between cooperation in the PD and aversion to telling a white lie. Second, many white lies are not Pareto optimal, but involve a cost for the liar (altruistic white lies, AWL). Thus, it is important to go beyond Pareto white lies and explore also the correlation between prosocial behaviour and altruistic white lies.

To fill this gap, we implemented a 2x2 experiment, in which subjects play a two-stage game. In the first stage they play one out of two possible treatments in a variation of the Deception Game introduced by Gneezy et al. [2013]. In these treatments they have the opportunity to tell either a Pareto or an altruistic white lie. In the second stage subjects are assigned to either the PD or the DG. We have evidence for three major results: (i) both altruism and cooperation are positively correlated with aversion to telling a Pareto white lie; (ii) both altruism and cooperation are negatively correlated with aversion to telling an altruistic white lie; (iii) men are more likely than women to tell an altruistic white lie, but not to tell a Pareto white lie.

2 Experimental design and procedure

We set up a two-stage experiment in which we first collect data on subjects’ lying aversion; followed by data regarding their prosocial preferences. In the first stage, subjects were directed to one of two variations on the Deception Game, in the spirit of Gneezy et al. [2013]. One variation serves to measure aversion to tell an altruistic white lie; the other variation serves to measure aversion to tell a Pareto white lie. In the second stage of the experiment, the players were randomly assigned to either the DG or the PD. Comprehension questions were asked for each of the four games, before any decision could be made. Subjects failing any of the comprehension questions were automatically excluded from the survey. In the next subsections we describe the experimental design. Full experimental instructions are reported in Appendix A.

2.1 Stage 1: Measure of lying-aversion

In the first stage of the experiment, subjects played a Deception Game akin to that of Gneezy et al. [2013] with Pareto White Lies (PWL) and Altruistic White Lies (AWL) treatments. As in Gneezy et al. [2013] two players are paired and the first player has the opportunity to tell a white lie. However, unlike Gneezy et al. [2013], in our Deception game the payoffs of both players depend only on Player 1’s choice and not on whether Player 2 believes that Player 1 is telling the truth or telling a lie. In our Deception Game, Player 2 is passive and does not make any decision. We use this variant because we are interested in looking at the relation between Player 1’s lying aversion and their prosocial tendencies. Our design allows us to avoid confounding effects due to the beliefs that Player 1 may have about the beliefs of Player 2. Since in our design Player 2 does not make any decision, the beliefs that Player 1 may have about Player 2 do not play any role and a prosocial Player 1 will always tell a white lie, regardless of their beliefs regarding Player 2.

Specifically, in our Deception Game, Player 1 is assigned to group i, where i∈{1, 2}. The group allocation is communicated only to Player 1. Player 1 can choose between two possible strategies. Option A: telling the number of the group they were assigned to; or Option B: telling the number of the other group. Players in the AWL condition were told that the payoff for each player would be determined as follows:

• • Option A: Player 1 and Player 2 earn $0.10 each.

• • Option B: Player 1 earns $0.09 and Player 2 earns $ 0.30.

Players in the PWL condition, on the other hand, were told that the payoff for each player would be determined as follows:

• • Option A: Player 1 and Player 2 earn $ 0.10 each.

• • Option B: Player 1 and Player 2 earn $ 0.15 each.

2.2 Stage 2: Measure of prosociality

In the second stage of the game, all subjects were randomly assigned to either a one-shot anonymous Dictator Game (DG) or a one-shot anonymous Prisoner’s Dilemma (PD) to assess the extent of their altruism toward, or cooperation with, unrelated individuals.

In the DG, dictators were given an initial endowment of $ 0.20 and were asked to decide how much money, if any, to transfer to a recipient, who was given nothing. Each dictator was informed that the recipient they were matched with would have no active role and would receive only the amount of money the dictator decides to give. In the PD, subjects were given an initial endowment of $ 0.10 and were asked to decide whether to transfer the $ 0.10 to the other subject (cooperate) or not (defect). Each time a subject transfers their $0.10, the other subject earns $0.20. Each subject was informed that the subject they were matched with would be facing the same decision problem.

We deliberately chose to use the word ”transfer”, rather than “give”, “cooperate”, or similar words, in order to minimise possible framing effects caused by the moral weight associated with names of the strategies.

3 Results

Subjects living in the United States were recruited via the crowd-sourcing internet marketplace Amazon Mechanical Turk (Paolacci et al. [2010], Horton et al. [2011], Bartneck et al. [2015]). A total of 1212 subjects (59% males, mean age = 33.83) passed the comprehension questions and participated in our experiment.

In the first stage of the experiment, 614 subjects played in the AWL treatment while 598 subjects were assigned to the PWL treatment. Pareto white lies were told extremely more frequently than altruistic white lies: whilst only 23% of the subjects chose to tell an altruistic white lie, 83% of the subjects lied in the PWL treatment (Wilcoxon Rank sum, p < .0001). These results are qualitatively in line with those reported by Erat and Gneezy [2012], who found that 43% of people lie in their AWL treatment and 76% of subjects lie in their PWL treatment. The effect of demographic questions on lying aversion will be discussed separately.

In the second stage of the experiment, 697 subjects were assigned to the DG, while 515 played the PD. Dictators on average transferred 22% of their endowment, whilst in the PD cooperation was chosen 35% of the time. Linear regression predicting DG donation as a function of the three main demographic variables (sex, age, and education level) shows that women donated more than men (coeff = 1.74, p < .0001), that older people donated slightly more than younger people (coeff =0.03, p=0.048) and that education level has no significant effect on DG donations (coeff = 0.04, p=0.78).¹ On the other hand, logit regression predicting cooperation as a function of the three main demographic variables shows that none of them has a significant effect on cooperative behaviour (all p’s >0.15).

3.1 Altruism and lying-aversion

Figure 1 reports the average (normalized) DG donation of liars and honests in both the AWL and the PWL treatments and suggests that honest people were more altruistic than liars in the PWL treatment, but less altruistic than liars in the AWL treatment. To confirm this we use linear regression predicting DG donation using a dummy variable, which takes value 1 (resp. 0) if the subject has told the truth (resp. a lie). Results show that, in the AWL treatment, honest people were almost significantly less altruistic than liars (coeff =−1.14, p = 0.063), and that, in the PWL treatment, honest people were significantly more altruistic than liars (coeff = 1.43, p = 0.035).

Next we examine whether these differences are predicted by individual differences in demographics. To do this, we repeat the linear regressions including controls on the three main demographic variables (sex, age, and level of education). Results show that, in the AWL treatment, honest people were significantly less altruistic than liars (coeff =−1.33, p = 0.03), and that, in the PWL treatment, honest people were almost significantly more altruistic than liars (coeff = 1.26, p = 0.06). In both cases, the only significant demographic variable is the gender of the subject (AWL: coeff = 1.74, p = 0.0008, PWL: coeff = 1.79, p = 0.0008). The full regression table is reported in Appendix B, Table 1. Thus, although the difference in altruism between liars and honest people is partly driven by the gender of the subject, it remains significant or close to significant also after controlling for this variable, suggesting existence of a true effect of aversion to telling a white lie on altruistic behaviour in the Dictator Game.

Figure 1: Average (normalized) DG donation of liars and honests in both the AWL and the PWL treatments. Error bars represent the standard errors of the means. In the Pareto white lies treatment, honest people tend to me more altruistic than liars (linear regression with no control on socio-demographic variables: coeff = 1.43, p = 0.035; with control: coeff = 1.26, p = 0.06). In the altruistic white lies treatment, honest people tend to be less altruistic than liars (linear regression with no control on socio-demographic variables: coeff = −1.14, p = 0.063; with control: coeff = −1.33, p = 0.03).

3.2 Cooperation and lying-aversion

Figure 2 reports the average PD cooperation of liars and honests in both the AWL and the PWL treatments and suggests that, as in the DG case, honest people were more cooperative than liars in the PWL treatment, but less cooperative than liars in the AWL treatment. To confirm this we use logit regression predicting PD cooperation using a dummy variable, which takes value 1 (resp. 0) if the subject has told the truth (as opposed to a lie). Results show that, in the AWL treatment, honest people were much less altruistic than liars (coeff =−1.25, p < .0001), and that, in the PWL treatment, honest people were significantly more altruistic than liars (coeff = 0.71, p = 0.04).

Next we examine whether these differences are driven by demographic differences. To do this, we repeat the logit regressions including controls on the three main demographic variables. Results show that, in the AWL treatment, honest people were less altruistic than liars (coeff =−1.31, p < .0001), and that, in the PWL treatment, honest people were more altruistic than liars (coeff = 0.79, p = 0.02). In both cases, none of the demographic variables is significant (only gender has an almost-significant effect (p = 0.08), but only in the PWL treatment). Full regression table is reported in Appendix B, Table 2.

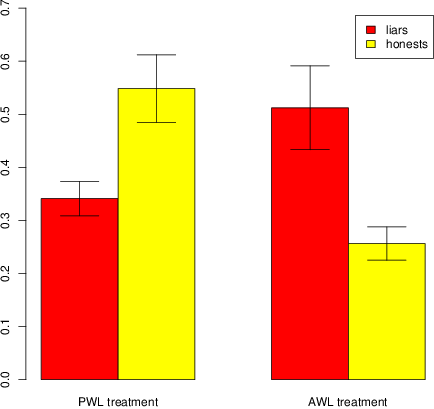
Figure 2: Average PD cooperation of liars and honests in both the AWL and the PWL treatments. Error bars represent the standard errors of the means. In the Pareto white lies treatment, honest people tend to be more cooperative than liars (logit regression with no control on socio-demographic variables: = 0.71, p = 0.04; with control: coeff = 0.79, p = 0.02). In the altruistic white lies treatment, honest people tend to be less cooperative than liars (logit regression with no control on socio-demographic variables: coeff =−1.25, p < .0001; with control: coeff =−1.31, p < .0001).

3.3 Gender differences in deception

Gender differences in deceptive behaviour have attracted considerable attention since the work of Dreber and Johannesson [2008], who found that men are more likely than women to tell a black lie, that is, a lie that benefits the liar at the expense of the listener. In the context of white lies, Erat and Gneezy [2012] found that women are more likely than men to tell an altruistic lie, but men are more likely than women to tell a Pareto white lie. Interestingly, the latter result was not replicated by Cappelen et al. [2013], who found no gender differences in lying aversion in the context of Pareto white lies. In line with this latter result, we also find no gender differences in the PWL treatment. Indeed, logit regression predicting the probability of telling a Pareto white lie as a function of sex, age, and level of education shows no significant effect of gender (coeff = 0.25, p = 0.25) and age (coeff =−0.01, p = 0.47) and, if anything, shows a significant negative effect of the level of education (coeff =−0.18, p = 0.04). Interestingly, in the context of altruistic white lies, we even find the reverse correlation of that reported by Erat and Gneezy [2012]. In our sample, men are slightly more likely than women to tell an altruistic white lie (26% vs 18%). The difference is statistically significant as shown by logit regression predicting the probability of telling an altruistic white lie as a function of sex, age, and level of education (gender: coeff = 0.50, p=0.02; age: coeff =−0.00, p = 0.85; education: coeff =−0.02, p = 0.73). We refer the reader to Figure 3 for a visual representation of gender differences in deceptive behaviour.

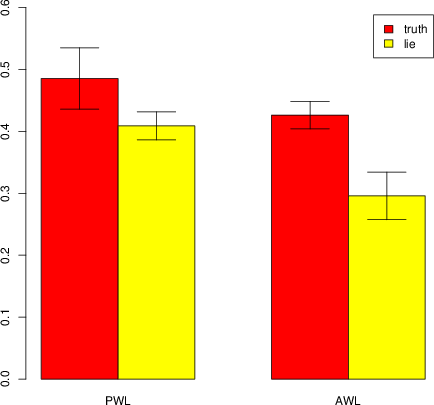
Figure 3: Proportion of females across treatments divided between liars and honests. In the Pareto white lie treatment, there is no statistically significant gender difference in deceptive behaviour. On the other hand, in the altruistic white lie treatment, we found that women are significantly more likely than men to tell the truth.

4 Discussion

We conducted this experiment to explore the relation between cooperation, altruism, and aversion to telling white lies among subjects. Cooperative tendencies were measured through the Prisoner’s Dilemma (PD); altruistic tendencies were measured through the Dictator Game (DG); and lying-aversion was measured using a Deception Game. The setup of our Deception Game was such that if Player 1 chose to lie then there would be an increase in monetary outcome for both players (the Pareto white lie variant, PWL) or an increase in monetary outcome for Player 2 at a small cost to Player 1 (the altruistic white lie variant, AWL). Our design differed from previous versions of the Deception Game in that the payoffs of both players depend only on the decision of the first player. This design allows us to study the correlation between Player 1’s lying-aversion and prosocial tendencies without adding the potentially confounding factor that Player 1 may have beliefs about the behaviour of Player 2.

Our results provide evidence of three major findings: (i) both altruism and cooperation are positively correlated with aversion to telling a Pareto white lie; (ii) both altruism and cooperation are negatively correlated with aversion to telling an altruistic white lie; (iii) men are more likely than women to tell an altruistic white lie, but not to tell a Pareto white lie.

These results make several contributions to the literature. The positive correlation between altruism and aversion to telling a Pareto white lie was also found by Cappelen et al. [2013]. Our results replicate and extend this finding as they also show that the same correlation holds true when considering cooperative behaviour (as opposed to altruistic behaviour), and that these correlations disappear and are actually even reversed when considering altruistic white lies (as opposed to Pareto white lies). These are not trivial extensions. Indeed, a positive correlation between altruism in the DG and aversion to telling a Pareto white lie can, in principle, be explained by assuming that there are two types of agents: (i) non-purely utilitarian agents, who aim at maximising the social welfare and choose the strategy that maximises their payoff in case multiple strategies give rise to the same social welfare (e.g., Charness and Rabin [2002],Capraro [2013]); and (ii) purely egalitarian agents, who minimise payoff differences, irrespective of their own payoff (e.g., with suitable values for the parameters of the models, Fehr and Schmidt [1999]), Bolton and Ockenfels [2000]. Assuming this type distribution, non-purely utilitarian agents always tell Pareto white lies (because they increase the social welfare) and give nothing in the DG (because giving does not increase the social welfare); and purely egalitarian agents give half in the DG, yet are indifferent between telling a Pareto white lie or not in the Deception Game (since they both minimise payoff differences). Thus, if the proportion of utilitarian agents is large enough, this would generate a positive correlation between altruism in the DG and aversion to tell a Pareto white lie, that would be consistent with the findings in Cappelen et al. [2013].

On the other hand, explaining our results using distributional preferences is much harder. Indeed, to explain the negative correlation between cooperation in the PD and telling a PWL, one must assume that the majority of utilitarian people actually defect in the PD. But this assumption clashes with the very nature of utilitarian people—that of maximising the total welfare and thus cooperation in the PD.

One potential explanation for our findings is that subjects have two possible degrees of moral motivation (low or high) towards either of two moral principles (utilitarianism and deontology). Utilitarian people follow distributional preferences for maximising the social welfare; deontological people follow non-distributional preferences for doing what they think it is the right thing to do. We assume that these types of individuals act as follows:

• • High utilitarian people give half in the DG, cooperate in the PD, and lie in the AWL and in the PWL.

• • High deontological people give half in the DG, cooperate in the PD, and tell the truth in the AWL and in the PWL.

• • Low utilitarian people keep in the DG, keep in the PD, tell the truth in the AWL and are indifferent in the PWL.

• • Low deontological people keep in the DG, keep in the PD, tell the truth in the AWL and are indifferent in the PWL.

According to this partition, the positive correlation between truth-telling and DG-donation/PD-cooperation in the PWL treatment would be driven by high deontological subjects; and the negative correlation between truth-telling and DG-donation/PD-cooperation in the AWL treatment would be driven by low utilitarian and low deontological subjects.

There might be high utilitarian subjects as well, but they do not show up because we have only one case per subject. An interesting direction for future research is therefore to do a within-subject design with many trials, using different payoffs, aimed at establishing the position of each subject in a two-dimensional space.

Of course, more research is needed also to support the existence of a possibly non-distributional “deontological domain”, containing all those actions that a particular individual considers to be morally right independently of their economic consequences, and to classify the actions belonging to this domain. For instance, here we have focussed on altruism and cooperation, as they are the most studied prosocial behaviours. However, they are not the only ones. Future research may be devoted to understanding whether the same correlations with truth-telling hold for other prosocial behaviours, such as benevolence (i.e., acting in such a way as to increase the other’s payoff beyond one’s own, (Capraro et al. [2014b] and hyper-altruism (i.e., weighting the other’s payoff more than one’s own, (Crockett et al. [2014], Capraro [2015]). More generally, it is likely that this “deontological domain” extends what Peysakhovich et al. [2014] call ‘cooperative phenotype’. In other words, one possible interpretation of our results is that the ‘cooperative phenotype’ extends beyond social dilemmas and regards also truth-telling when lying is Pareto optimal and lying when it is costly for the liar, but benefits the other person.

Additionally, our results connect to the work of Levine and Schweitzer [2015], which reported that telling white lies (both altruistic and Pareto optimal) signals prosocial tendencies in observers: third parties, when playing in the role of trusters in the Trust Game, allocate more money to people who have told a white lie in a previous Deception Game than to those who have told the truth. However, Levine and Schweitzer [2015] did not measure trustee’s behavior and so it remained unclear whether people telling a white lie were really more prosocial than those telling the truth. Our results provide evidence that this is true in the case of altruistic white lies, but false in the case of Pareto white lies. Further research may shed light on the origin of this false belief.

Finally, our results add to the literature regarding gender differences in deceptive behaviour. Dreber and Johannesson [2008] found that men were more likely than women to tell black lies (e.g., lies that increase the liar’s benefit at the expense of the listener). A similar result was shown by Friesen and Gangadharan [2012], who found that men are more likely than women to behave dishonestly for their own benefit. Yet, Childs [2012] failed to replicate this gender effect using a very similar design to that in Dreber and Johannesson [2008]. In the context of white lies, Erat and Gneezy [2012] reported that women are more likely than men to tell an altruistic white lie, but men are more likely than women to tell a Pareto white lie. This latter result was not replicated by Cappelen et al. [2013], who found no gender differences in telling a Pareto white lie. In line with the latter result, our results also show no gender difference in telling a Pareto white lie. But, interestingly, we found gender differences in telling an altruistic white lie, but in the opposite direction than that reported in Erat and Gneezy [2012]: we found that men are more likely than women to tell an altruistic white lie. Taken together, these results suggest that it may be premature to draw general conclusions about whether there are general gender differences in lying, and call for further studies.