Hostname: page-component-7b9c58cd5d-dlb68 Total loading time: 0 Render date: 2025-03-14T00:55:32.612Z Has data issue: false hasContentIssue false
  • English
  • Français

Proper 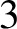$3$-colorings of 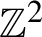$\mathbb {Z}^{2}$ are Bernoulli

Part of: Special processes Ergodic theory

Published online by Cambridge University Press:  27 April 2022

GOURAB RAY  and
YINON SPINKA Open the ORCID record for YINON SPINKA [Opens in a new window]
GOURAB RAY*
Affiliation:
Department of Mathematics, University of Victoria, Victoria, BC, Canada V8W 2Y2
YINON SPINKA
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC, Canada V6T 1Z2 School of Mathematical Sciences, Tel Aviv University, Tel Aviv 6997801, Israel (e-mail: yinon@math.ubc.ca)
*
e-mail: gourabray@uvic.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

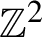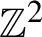We consider the unique measure of maximal entropy for proper 3-colorings of $\mathbb {Z}^{2}$ , or equivalently, the so-called zero-slope Gibbs measure. Our main result is that this measure is Bernoulli, or equivalently, that it can be expressed as the image of a translation-equivariant function of independent and identically distributed random variables placed on $\mathbb {Z}^{2}$ . Along the way, we obtain various estimates on the mixing properties of this measure.

Keywords

coloringBernoullifactor of iid

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory 37A60: Dynamical systems in statistical mechanics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 6 , June 2023 , pp. 2002 - 2027
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achlioptas, D., Molloy, M., Moore, C. and Van Bussel, F.. Rapid mixing for lattice colourings with fewer colours. J. Stat. Mech. Theory Exp. 2005(10) (2005), P10012.CrossRefGoogle Scholar
Adams, S.. Følner independence and the amenable Ising model. Ergod. Th. & Dynam. Sys. 12(4) (1992), 633–657.CrossRefGoogle Scholar
Boyle, M.. Open problems in symbolic dynamics. Contemp. Math. 469 (2008), 69–118.CrossRefGoogle Scholar
Chandgotia, N., Peled, R., Sheffield, S. and Tassy, M.. Delocalization of uniform graph homomorphisms from ${\mathbb{Z}}^2$ to $\mathbb{Z}$ . Comm. Math. Phys. 387(2) (2021), 621–647.CrossRefGoogle Scholar
Conze, J. P.. Entropie d’un groupe abélien de transformations. Z. Wahrsch. Verwandte Gebiete 25(1) (1972), 11–30.CrossRefGoogle Scholar
den Hollander, F. and Steif, J. E.. Mixing properties of the generalized $T,{T}^{-1}$ -process. J. Anal. Math. 72(1) (1997), 165–202.CrossRefGoogle Scholar
den Hollander, F. and Steif, J. E.. On K-automorphisms, Bernoulli shifts and Markov random fields. Ergod. Th. & Dynam. Sys. 17(2) (1997), 405–415.CrossRefGoogle Scholar
Duminil-Copin, H.. Lectures on the Ising and Potts models on the hypercubic lattice. PIMS-CRM Summer School in Probability. Springer, Cham, 2017, pp. 35–161.CrossRefGoogle Scholar
Duminil-Copin, H., Harel, M., Laslier, B., Raoufi, A. and Ray, G.. Logarithmic variance for the height function of square-ice. Preprint, 2022, arXiv:1911.00092.CrossRefGoogle Scholar
Feldheim, O. N. and Spinka, Y.. Long-range order in the 3-state antiferromagnetic Potts model in high dimensions. J. Eur. Math. Soc. (JEMS) 21(5) (2019), 1509–1570.CrossRefGoogle Scholar
Galvin, D., Kahn, J., Randall, D. and Sorkin, G.. Phase coexistence and torpid mixing in the 3-coloring model on . SIAM J. Discrete Math. 29(3) (2015), 1223–1244.CrossRefGoogle Scholar
Goldberg, L. A., Jalsenius, M., Martin, R. and Paterson, M.. Improved mixing bounds for the anti-ferromagnetic Potts model on ${{\textsf{Z}}}^2$ . LMS J. Comput. Math. 9 (2006), 1–20.CrossRefGoogle Scholar
Grimmett, G. R.. The Random-Cluster Model (Grundlehren der mathematischen Wissenschaften, 333). Springer, Berlin, 2006.CrossRefGoogle Scholar
Häggström, O., Jonasson, J. and Lyons, R.. Coupling and Bernoullicity in random-cluster and Potts models. Bernoulli 8(3) (2002), 275–294.Google Scholar
Hoffman, C.. A Markov random field which is K but not Bernoulli. Israel J. Math. 112(1) (1999), 249–269.CrossRefGoogle Scholar
Hoffman, C.. A family of nonisomorphic Markov random fields. Israel J. Math. 142(1) (2004), 345–366.CrossRefGoogle Scholar
Kammeyer, J. W.. A complete classification of the two-point extensions of a multidimensional Bernoulli shift. J. Anal. Math. 54 (1990), 113–163.CrossRefGoogle Scholar
Katznelson, Y. and Weiss, B.. Commuting measure-preserving transformations. Israel J. Math. 12(2) (1972), 161–173.CrossRefGoogle Scholar
Ledrappier, F.. Un champ Markovien peut être d’entropie nulle et mélangeant. C. R. Acad. Sci. Paris 287(7) (1978), A561–A563.Google Scholar
Lieb, E. H.. Residual entropy of square ice. Condensed Matter Physics and Exactly Soluble Models. Eds. B. Nachtergaele, J. P. Solovej and J. Yngvason. Springer, Berlin, 2004, pp. 461–471.CrossRefGoogle Scholar
Nam, D., Sly, A. and Zhang, L.. Ising model on trees and factors of IID. Comm. Math. Phys. 389 (2022), 1009–1046.CrossRefGoogle Scholar
Ornstein, D.. Ergodic Theory, Randomness and Dynamical Systems (Yale Mathematical Monographs, 5). Yale University Press, New Haven, CT, 1974.Google Scholar
Ornstein, D. and Weiss, B.. Finitely determined implies very weak Bernoulli. Israel J. Math. 17(1) (1974), 94–104.CrossRefGoogle Scholar
Ornstein, D. and Weiss, B.. -actions and the Ising model, unpublished, 1977.Google Scholar
Peled, R.. High-dimensional Lipschitz functions are typically flat. Ann. Probab. 45(3) (2017), 1351–1447.CrossRefGoogle Scholar
Peled, R. and Spinka, Y.. Rigidity of proper colorings of ${\mathbb{Z}}^d$ . Preprint, 2020, arXiv:1808.03597.Google Scholar
Peled, R. and Spinka, Y.. Three lectures on random proper colorings of ${\mathbb{Z}}^d$ . Preprint, 2020, arXiv:2001.11566.Google Scholar
Rudolph, D. J. and Schmidt, K.. Almost block independence and Bernoullicity of ${\mathbb{Z}}^d$ -actions by automorphisms of compact abelian groups. Invent. Math. 120(1) (1995), 455–488.CrossRefGoogle Scholar
Sheffield, S.. Random Surfaces. Société Mathématique de France, Paris, 2005.Google Scholar
Shields, P. C.. Almost block independence. Z. Wahrsch. Verwandte Gebiete 49(1) (1979), 119–123.CrossRefGoogle Scholar
Slawny, J.. Ergodic properties of equilibrium states. Comm. Math. Phys. 80(4) (1981), 477–483.CrossRefGoogle Scholar
Sly, A. and Zhang, L.. Stationary distributions for the voter model in $d\ge 3$ are factors of IID. Preprint, 2022, arXiv:1908.09450.CrossRefGoogle Scholar
Spinka, Y.. Finitary codings for spatial mixing Markov random fields. Ann. Probab. 48(3) (2020), 1557–1591.CrossRefGoogle Scholar
Thouvenot, J.-P.. Convergence en moyenne de l’information pour l’action de ${\mathbb{Z}}^2$ . Z. Wahrsch. Verwandte Gebiete 24(2) (1972), 135–137.CrossRefGoogle Scholar
van den Berg, J. and Maes, C.. Disagreement percolation in the study of Markov fields. Ann. Probab. 22(2) (1994), 749–763.Google Scholar
van den Berg, J. and Steif, J. E.. On the existence and nonexistence of finitary codings for a class of random fields. Ann. Probab. 27 (1999), 1501–1522.Google Scholar