Towards an estimation of sub-sea-ice platelet-layer volume with multi-frequency electromagnetic induction sounding

Abstract

Ice-platelet clusters modify the heat and mass balance of sea ice near Antarctic ice shelves and provide a unique habitat for ice-associated organisms. The amount and distribution of these ice crystals below the solid sea ice provide insight into melt rates and circulation regimes in the ice-shelf cavities, which are difficult to observe directly. However, little is known about the circum-Antarctic volume of the sub-sea-ice platelet layer, because observations have mostly been limited to point measurements. In this study, we present a new application of multi-frequency electromagnetic (EM) induction sounding to quantify platelet-layer properties. Combining in situ data with the theoretical response yields a bulk platelet-layer conductivity of 1154 ± 271 mS m^–1 and ice-volume fractions of 0.29-0.43. Calibration routines and uncertainties are discussed in detail to facilitate future studies. Our results suggest that multi-frequency EM induction sounding is a promising method to efficiently map platelet-layer volume on a larger scale than has previously been feasible.

Introduction

The Antarctic coastline is fringed by ice shelves, floating extensions of continental ice sheets (Le Brocq and others, 2010). Basal melt of ice shelves leads to the formation of water masses that are fresher and less dense than the surrounding ocean body (Mahoney and others, 2011). As the sea-water freezing point depends on pressure (Foldvik and Kvinge, 1974), the water becomes supercooled when the less dense plume rises. Ice platelets nucleate in the supercooled water, but the process of ice formation varies (Smith and others, 2001). Near the Ekström Ice Shelf in the eastern Weddell Sea, large amounts of ice platelets rise from the cavity below the ice shelf and accumulate underneath the sea ice (Eicken and Lange, 1989; Hoppmann and others, 2015). In McMurdo Sound, near the Ross Ice Shelf, platelet growth is often associated with in situ formation of ice platelets directly underneath the sea ice (Smith and others, 2001) or is interpreted as a combination of the two processes (Jeffries and others, 1993; Dempsey and others, 2010).

The resulting sub-sea-ice platelet layer, hereafter referred to as the platelet layer, may contribute significantly to the heat and mass balance of adjacent sea ice (Eicken and Lange, 1989) and represents a unique ice habitat (Arrigo and others, 1993). The additional buoyancy modifies the sea-ice freeboard, influencing satellite remote sensing near coastal areas in Antarctica (Rack and others, 2013; Price and others, 2014). Furthermore, the platelet layer is a direct indicator of ocean/ice-shelf interaction, and the amount of basal ice-shelf melt might be reflected in the volume of ice platelets found below landfast sea ice (Hoppmann and others, 2015), a region much more accessible than the cavities below ice shelves.

The total volume of ice platelets below the sea ice is a product of the layer thickness, the area and the ice-volume fraction. The platelet layer is up to several meters thick, usually determined with a thickness gauge, and the horizontal extent is given by point measurements. Previous investigations of ice-volume fractions in McMurdo Sound used estimates from core holes, ice-temperature profiles and horizontal thin sections. Results ranged from 0.2 to ˃0.5, while a recent study found an ice-volume fraction of 0.25 ± 0.06 using heat-flux calculations (Gough and others, 2012). At Atka Bay, Günther and Dieckmann (1999) calculated a value of 0.46, based on consideration of sea-ice isostasy. Kipfstuhl (1991) and Hoppmann and others (2015) compared their sea-ice thickness observations to a localized growth model and estimated ice-volume fractions of 0.2 and 0.25 ± 0.1, respectively.

One physical parameter which depends on the ice-volume fraction of the platelet layer is the electrical conductivity. Differences in conductivity are fundamental for sea-ice thickness retrieval with electromagnetic (EM) induction sounding, a common method typically applied with airborne (Haas and others, 2009) or ground-based devices (Kovacs and Morey, 1991; Haas and others, 1997; Haas, 1998; Reid and others, 2003). In general, a single frequency in the range 3000-10 000 Hz is used to estimate the distance of the sensor to the ice/water interface. The method is based on the assumption that sea ice can be described as a single level layer with negligible electrical conductivity (˂100mS m^–1; e.g. Reid and others, 2006) compared to sea water (e.g. 2690 mS m^–1 in the winter Weddell Sea). This is a reasonable assumption for most offshore sea ice, but in the presence of a porous platelet layer it becomes invalid. In this case, a single-layer assumption will lead to either an overestimation of the solid sea-ice thickness (Rack and others, 2013) or an underestimation of total (solid ice + platelet layer) thickness with no possibility to resolve both layers. Single-frequency systems are sensitive to the thickness and the electrical bulk conductivity of the platelet layer, but do not provide enough observational constraints for an unambiguous resolution of layer thicknesses and conductivities. Therefore, those systems are not able to resolve multiple sea-ice layers with different electrical parameters. In exploration geophysics, it is therefore common to resolve a multilayered subsurface structure using either multiple frequencies, several transmitter/receiver configurations, or a combination of the two.

The aim of this study is to lay the foundations for rapid estimation of large-scale platelet-layer volumes, without the need for time-consuming sea-ice drilling experiments. We focus here on the analysis of multi-frequency EM induction sounding data at platelet-free calibration sites with known sea-ice thickness to assess calibration coefficients and data uncertainties for the individual instrumental frequencies. We apply calibration coefficients and uncertainties to a more complex situation with a platelet layer, to derive limitations for the parameterization of the platelet-layer conductivity and to investigate its relationship to ice-volume fraction.

Method

We used a commercial EM induction sensor (GEM-2, Geophex Ltd) for multi-frequency soundings on sea ice with an underlying platelet layer at several survey sites in Atka Bay. An estimation of instrumental uncertainties requires knowledge of the subsurface structure. At Atka Bay, these requirements were not fulfilled since the electrical bulk conductivity of the platelet layer is unknown and its estimation is a major goal of this study. Therefore, two additional datasets over simpler geophysical calibration targets were acquired to calculate the calibration coefficients and the uncertainties of the measurements. These calibrations were conducted over level sea ice in the central Weddell Sea (no platelet layer) and over the North Sea in Germany, where no sea ice was present (sea water only). Figure 1 shows the sea-ice survey and calibration sites.

Fig. 1. Map of sea-ice study sites. (a) Enlarged map of Atka Bay, showing the survey sites with an underlying platelet layer (white triangles). Background: TerraSAR-X image from 15 November 2012, provided by the German Aerospace Center (DLR). (b) Calibration sites in the Weddell Sea without a platelet layer (black triangles). Blue areas indicate the locations of ice shelves (Fretwell and others, 2013; Bedmap2).

Multi-frequency EM sounding

The GEM-2 instrument (Fig. 2) is a ground-based induction sensor with promising specifications for multilayer sea-ice thickness retrieval. It can be used either in horizontal or vertical coplanar mode with a transmitter/receiver coil spacing of 1.66 m. The coil spacing is a critical parameter, since, together with the chosen frequency, it limits the sounding depth. Although the coil spacing of the GEM-2 is small compared with the much used single-frequency Geonics EM-31 (3.67 m), it was considered to be sufficient for our purposes. The GEM-2 instrument can be operated simultaneously with up to five frequencies in a range 330-96 000 Hz. For calibration measurements in the Weddell and North Seas we used frequencies of 1530, 5310, 18 330, 63 030 and 93 090 Hz. At Atka Bay we used slightly different frequencies (450-93 030 Hz) at a sampling rate of 10 Hz.

Fig. 2. Multi-frequency EM induction sounding data are recorded with the GEM-2 at different heights above sea ice. The signal directly depends on the distances to the conductive layers. Photograph by Sandra Schwegmann, 24 June 2013.

During operation, a primary EM field is generated by the transmitter coil of the EM instrument. The primary field induces a secondary magnetic field in all nearby conductive layers. The receiver coil measures the superimposed signal of all resulting magnetic fields. The EM response is defined as the relative secondary field, which is the secondary field divided by the primary field. It can be expressed as a complex number with the in-phase, I (real part), and the quadrature, Q (imaginary part). In-phase and quadrature are dimensionless and are recorded in parts per million (ppm). An alternative representation is given by the amplitude, Amp, and phase, φ , where φ = arctan (Q/I) and Amp

In practice, the primary field is often suppressed at the receiver coil to measure the minor secondary field at sufficient resolution. This is realized in the GEM-2 with a bucking coil, which is connected in series with the receiver coil, but has the opposite polarity (Won and others, 2003). The bucking coil has a defined area, number of turns and distance to the transmitter (1.035 m) to cancel the primary field at the receiver location with an equal current.

According to Frischknecht and others (1991), three types of systematic errors exist in in-phase and quadrature recordings, due to improper adjustment and calibration of the sensor: (1) zero-level offsets, I_c and Q _c, (2) scaling coefficients, A, and (3) phase-mixing coefficients, P_c, have to be applied to the measured in-phase and quadrature components, I _m and Q _m. The corrected in-phase, I, and quadrature, Q, are calculated as

(1)

and

(2)

A similar approach has been presented by Deszcz-Pan and others (1998), Reid and Bishop (2004), Brodie and Sambridge (2006) and Minsley and others (2012). Because of systematic errors in our instrument, we corrected our data according to Eqns (1) and (2) to get reliable results.

Bucking coil bias

We compared field data to numerical one-dimensional forward models (Anderson, 1979) to obtain the calibration coefficients at specific calibration sites. Model parameters were the EM frequency and the coil spacing and orientation, as well as the thickness and conductivity of multiple layers.

We found a significant bias between the actual GEM-2 response and the forward models at all sites and all frequencies. This deviation could not be explained with either realistic calibration coefficients, or with the layer conductivities at the calibration sites. We finally found that the bucking coil picked up, in addition to the primary field, a signal from the subsurface (secondary field), which could not be described with a constant factor, as described in the literature and performed during the internal instrumental processing. To account for the secondary field measured by the bucking coil, we implemented the bucking coil in our forward models as a second receiver and subtracted the result from the receiver response. By doing so, we achieved good agreement between data and forward models with realistic calibration coefficients.

Relation between electrical conductivity and porosity

Archie’s law relates the bulk electrical conductivity, σ of a porous layer to the porosity, Φ, the brine conductivity, σb, and the cementation factor, m (Archie, 1942):

(3)

We used this law to convert (1) brine conductivity and brine volume of sea ice to bulk conductivity of the solid sea-ice layer and (2) bulk conductivity of the platelet layer to the actual ice-volume fraction. The empirical factor, m, depends, to a large extent, on the material grain shape and pore geometry (Salem and Chilingarian, 1999). Previous studies have often used a value of 1.75 for solid sea ice, and a range 1.55-2.2 is reported in the literature (Reid and others, 2006). Because of the different structure of the unconsolidated platelet layer, with higher connectivity and brine volume than solid sea ice, the cementation factor of solid sea ice might not be applicable to the platelet layer. We therefore tested a broad range of cementation factors from 1.5 to 2.5, values which are usually used for saturated sandstones (Glover and others, 1997). These structures are more likely to describe the connected pores of the platelet layer.

Field data

Atka Bay

We investigated properties of the platelet layer at Atka Bay at three sites between November 2012 and January 2013, operating from the German research station Neumayer III. The sites ATKA03, ATKA11 and ATKA24 (Fig. 1; Table 1 ) represent different fast-ice regimes. At ATKA11, where we repeated EM data acquisition five times, sea ice was ∼4 months old, formed after a breakout in August 2012. Consequently, ATKA11 showed thinner sea ice than all the other sites. We found older first-year sea ice at ATKA24 and thicker rafted sea ice at ATKA03. A detailed description of the sea-ice conditions is given by Hoppmann and others (2015). At each site, we removed the snow and acquired multi-frequency EM data in 0.1 m steps in sensor altitude from the sea-ice surface to a maximum height of 2 m above the sea ice (Fig. 2).

Table 1. Summary of GEM-2 datasets at Atka Bay. Date format is day/month. IT: measured sea-ice thickness (snow was removed); PLT: measured platelet-layer thickness; F: measured freeboard; T: air temperature measured at Neumayer III station; σi estimated sea-ice conductivity; σpl estimated platelet-layer conductivity

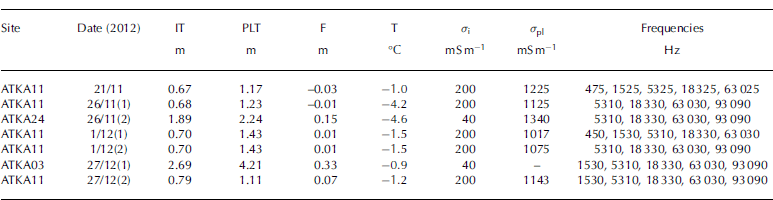
After the EM sounding, we measured the freeboard, F, the sea-ice thickness, IT, and the platelet-layer thickness, PLT, with a modified thickness gauge through 0.05 m drillholes (Table 1 ). Individual ice platelets up to 0.1 m in diameter were observed. Manual sea-ice thickness measurements yielded an uncertainty of ˂0.1 m for solid sea ice. But we could only determine the platelet-layer thickness with an accuracy of ∼0.3 m, as verified by an underwater camera (Hoppmann and others, 2015). The platelet layer often consisted of internal dense layers, and in the vicinity of sea water the platelet layer was generally looser than in the middle of the layer. Surprisingly, we often found a less dense layer next to the solid sea ice. For our further calculations, however, we assumed a homogeneous platelet layer.

To determine conductivities of the water column and the interstitial platelet-layer water, we used a conductivity-temperature-depth (CTD) probe (CTD75M, Sea & Sun Technology GmbH) to perform in total 22 down- and upward casts between 21 November 2012 and 7 January 2013. The instrument was operated through core holes 0.1 m in diameter, with a maximum depth range of 250 m. Small ice crystals regularly blocked the conductivity cell while the instrument was operating in the platelet layer, resulting in spuriously low conductivity values. We tried to minimize this risk by repeated up- and downward movements of the instrument. As the downward casts still contained spurious data, we determined from the undisturbed upward casts an average sea-water conductivity of 2690 mS m ^–1 below the platelet layer.

To compare the electrical conductivity of the solid sea-ice layer with results from the GEM-2, we retrieved several sea-ice cores and measured temperature and salinity profiles at 0.1 m intervals. Brine volume (porosity) was calculated according to Cox and Weeks (1983) and Leppäranta and Manninen (1988). Brine conductivity, σ _b , was determined after Stogryn and Desargant (1985) and Reid and others (2006). The bulk conductivity of the solid sea-ice layer, σ , was then calculated using Eqn (3) and a cementation factor, m = 1.75 (Reid and others, 2006).

Weddell Sea and North Sea

Electromagnetic calibration data from sites with no platelet layer were acquired in the central Weddell Sea at 12 sites during two winter expeditions with the German icebreaker RV Polarstern between June and September 2013 (Table 2). Sea-ice thickness was measured with a thickness gauge, and the conductivity of the sea water was obtained by the keel salinometer of RV Polarstern (IT and σ_w in Table 2 ).

Table 2. Summary of Weddell Sea and North Sea calibrations operated with frequencies 1530, 5310, 18 330, 63 030 and 93 090 Hz. Date format is day/month. IT: measured sea-ice thickness (snow was removed); F: measured freeboard; T: air temperature measured by Polarstern; σ _i : estimated sea-ice conductivity; σw: sea-water conductivity measured by Polarstern (daily average, Weddell Sea data) and by a handheld instrument (North Sea data). Note the low sea-water conductivity in the North Sea due to the inflow of fresh water (site 13)

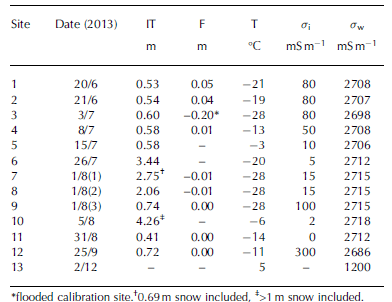
On first-year sea ice the snow was removed, which made surface flooding visible at site 3 ( Table 2 ). On multi-year sea ice, where it was not possible to remove the snow in the footprint area, we placed the GEM-2 on top of the snow and consequently included a second layer of 0 m Sm ^–1 in the forward models (site 7). At site 10, we were not able to estimate the snow depth because of internal icy layers, and consequently used the same conductivity for the sea ice and the snow layer. The bulk conductivity, a , of the solid sea ice was obtained in the same way as at Atka Bay.

An additional calibration dataset was acquired from the North Sea over mixed ocean and river inflow water at the mouth of the river Weser near Bremerhaven, Germany (last calibration in Table 2 ). The conductivity of the sea water was measured with a handheld conductivity meter (1200 mS m^–1 ) . Without the presence of a sea-ice layer the EM response could be modelled as an ideal homogeneous half-space.

Results

Calibration coefficients and uncertainties were calculated using the calibration data from the Weddell Sea and the North Sea. Coefficients were then applied to the Atka Bay data to estimate sea-ice and platelet-layer conductivities and the ice-volume fraction of the platelet layer.

GEM-2 uncertainties

Calibration coefficients and uncertainties were obtained by manually minimizing the difference between the GEM-2 data and theoretical forward models. Figure 3a and b show typical 63 030 Hz EM responses for different heights above sea water for the Weddell Sea calibrations. For the forward model (blue dashed line) the sea-ice layer was initially assumed to be non-conductive (0 mS m ^–1) and a conductivity of 2700 m Sm ^–1 was assigned to the sea water. The uncorrected datasets for in-phase and quadrature (Fig. 3a and b) differ significantly from each other and from the forward models. Reasons for this variability may originate from an incorrect calibration of the GEM-2 in general, the dependence of the EM response on environmental temperatures, the influence of sea-ice conductivity and variabilities of the drillhole sea-ice thickness estimations within the footprint of the instrument.

Fig. 3. Raw EM data (63030 Hz) for all Weddell Sea datasets. (a) In-phase, (b) quadrature and (c) enlargement of box in (b). The forward models (blue dashed curves) were calculated by assuming a homogeneous half-space of 2700 mS m ^–1 and resistive sea ice (0mS m ^–1) . Two additional forward models with increasing sea-ice conductivities (50 and 100 mS m ¹) are shown in (c).

We therefore categorize the deviation from the forward models into two main parts: first, imprecise calibration of the individual frequencies as a mean offset to the forward models (systematic error); and second, the influence of environmental temperature, sea-ice conductivity and uncertainties of thickness estimations as the inter-variability between different calibrations. The first factor can be corrected by averaging the calibration coefficients for each frequency over all calibrations. The second factor describes the uncertainty of these mean calibration coefficients.

Zero-level offset coefficients, I _c0 and Q _c0 (Table 3), were measured by lifting the GEM-2 with RV Polarstern’s crane and acquiring data from several meters above ground. This free-air response was obtained for ∼30 min once the instrument was in temperature equilibrium. To investigate the long-term drift and the temperature dependency, these measurements were carried out multiple times. Although the crane measurements were conducted at temperatures from 24 to -10°C, we did not observe a strong temperature dependence of the zero-level offsets for any frequency. Once the instrument was in temperature equilibrium, the instrumental noise (I _n and Q _n) was determined as the standard deviation of the time series. Mean scaling, A, and phase-mixing coefficients, P_c, were obtained at each site (Table 2) by manually minimizing the root-mean-square error (rmse) between in-phase and quadrature data and the forward models. It was necessary to use different zero-level offset coefficients, I_c and Q _c, than those obtained from the free-air experiment to reach a satisfactory agreement with the forward models. These changes significantly increased the standard deviation and, thus, the uncertainty of zero-level offset coefficients of the individual frequencies. The average of all calibration coefficients, the standard deviations from individual calibration sites and the instrumental noise are summarized in Table 2 ) to calculate these coefficients, because the signal values were low and calibration coefficients depended mainly on the estimated sea-ice conductivity.

The sea-ice conductivities, a _i , for the forward models were determined with the local maximum of quadrature components of frequencies 63 030 and 93 090 Hz, which are assumed to be the most sensitive to sea-ice conductivity, due to their low penetration depth. This method was applied because it is almost independent of any zero-level offset, scaling and phase-mixing corrections. In Figure 3c this is shown for theoretical forward-model curves. One particular example, the calibration at flooded site 3 (Table 2), exhibits a conductivity of 1700 mS m ¹ for the top 20 cm and the local maximum is shifted significantly to higher values (Fig. 3b, red). Small conductivity changes were also necessary to fit the local maximum for non-flooded calibration sites. Estimated sea-ice conductivities, a _i , are summarized in Table 2.Using Eqns (1) and (2), all calibration data were corrected with the mean coefficients, I _c, Q _c, A and P_c (Table 3). The total uncertainty for the in-phase component, ∆I, was calculated with the Gaussian law of error propagation according to

(4)

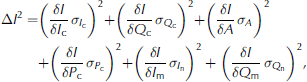
under the assumption that the uncertainty of the measured in-phase and quadrature signal, I _m and Q _m, is described by the noise, I_n and Q _n, and the uncertainty of the remaining contributions is given by the standard deviations of the calibration coefficients. The calculation for ∆Q was performed accordingly. The corrected data (dots), the respective forward models (solid curves) and the estimated uncertainties (ellipses) for in-phase and quadrature are shown for one example dataset (site 1, Table 2 ) in Figure 4.

Fig. 4. Data from calibration site 1 ( Table 2) with applied calibration coefficients. The instrument was lifted from zero (large dots) to 2m (smaller dots) over 0.53m thick sea ice with a conductivity of 80 mS m¹ . The semi-axes of the ellipses indicate the in-phase and quadrature uncertainties. The forward models (solid curves) for 0–3 m are shown for the different frequencies.

Using forward models as in Figure 4 and increasing the sea-ice thickness in 0.1 m steps (sea ice with 100 mS m¹ ), over a depth of 10 m, the calculated uncertainties exceed in 3 m depth the difference of two consecutive responses. This means that it is possible to resolve solid sea ice up to 3 m thick at an accuracy of 0.1 m with GEM-2 specifications and given uncertainties.

Sea-ice conductivity

The conductivity of the solid sea ice was estimated for all calibration and survey sites by aligning the measured quadrature components of the two highest frequencies (63 030 and 93 090 Hz) to the modelled data. This procedure yielded sea-ice conductivities of 200 mS m ¹ for thin sea ice (˂1 m) at ATKA11 and conductivities of 4 0 m Sm ^–1 for thicker sea ice at ATKA03 and ATKA24 (Table 1).

Brine porosity and conductivity were used to calculate the reference bulk conductivity values (Eqn (3)). The conductivities of the three ATKA11 sea-ice cores were 139 ± 113, 141 ± 1 0 2 and 149 ± 77 m Sm ^–1 . These high standard deviations were mostly due to high conductivities at the ice/ water interface. If these were omitted, overall conductivities reduced to 100 ± 18, 114 ± 73 and 127 ± 47 mS m ^–1. Sea-ice cores at ATKA03 and ATKA24 yielded a sea-ice conductivity of 56 ± 23 and 101 ± 35 mS m ^–1, respectively.

In the Weddell Sea, nine sea-ice cores (1 m) gave sea-ice conductivities between 35 and 72 mS m ^–1, with an average of 56 14 mS m ^–1. The highest standard deviation in a single core was 55 mS m ^–1. A thicker sea-ice core of 1.77m yielded a bulk sea-ice conductivity of 17 8 mS m ^–1.

In contrast, sea-ice conductivities based on forward-model fitting at 63 030 and 93 090 Hz ranged from 0 to 100 m Sm ^–1 (with one outlier of 300 mS m ¹ ) for thin sea ice (˂1 m) and from 2 to 1 5 m Sm ^–1 for thicker sea ice (˃1 m; Table 2 ). A value of 300 mS m ¹ is a rather high conductivity for first-year sea ice, and may be explained by the presence of surface flooding or internal layers. Excluding the outlier (300 mS m ^–1), the conductivities from the sea-ice cores are in the same range as the conductivities from our results obtained by the GEM-2.

Bulk platelet-layer conductivity

The sea-ice conductivity at each site at Atka Bay was used as an input parameter for a series of forward models, together with the known thicknesses of solid sea ice and the platelet layer. We varied the electrical conductivity of the platelet layer using the full range of physically plausible conductivities, from a fully resistive layer (0 m Sm ^–1) to conductive sea water (2700mS m ^–1) in steps of 50 m Sm ^–1 . From the series of forward models (e.g. ATKA11 at 18 330 Hz; Fig. 5) we calculated the best fit between the corrected GEM-2 data (applied calibration coefficients) and the forward models, based on the local minimum of the rmse (Fig. 6). This procedure was repeated at all sites at Atka Bay for both in-phase and quadrature components and for each frequency. We found that the best fit of in-phase and quadrature components did not always result in the same bulk platelet-layer conductivity. Assuming that both components should yield the same conductivity, we applied an additional phase correction at each site for every frequency. The new phase-mixing coefficients were averaged and included in the uncertainty estimation (Pc2, σPc2; Table 3 ). The averaged coefficients were again applied to both components for all frequencies at all sites, except at ATKA03, where the signal was too insensitive to the bulk platelet-layer conductivity, due to generally low signal values on the thick sea ice. We repeated the estimation of bulk platelet-layer conductivity by finding the local minimum of the rmse and also considered the upper and lower limit of the in-phase (Fig. 6) and quadrature uncertainties.

Table 3. Calibration coefficients for all frequencies. Noise of in-phase, I_n, and quadrature, Q _n, components estimated by long time series; zero-level offset coefficients, I_c0 and Qc₀, measured with a crane away from any conductive material. Zero-level offset coefficients, I_c and Q _c, scaling coefficients, A, and phase-mixing coefficients, P _c, obtained by minimizing the difference between field data and forward models. P _c2 are the phase-mixing coefficients adjusted for the Atka Bay datasets. x is the arithmetic average and σ the 1σ standard deviation of the individual calibration coefficients

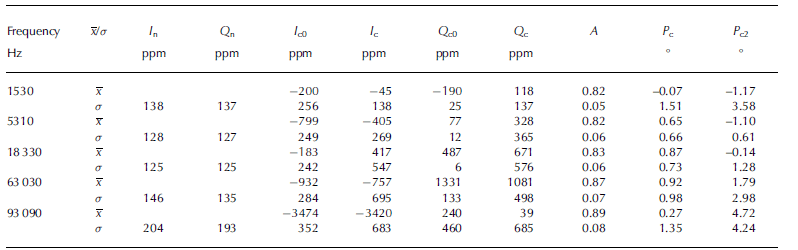
Fig. 5. Corrected dataset and corresponding uncertainties for the (a) in-phase and (b) quadrature 18330 Hz component at ATKA11 (1 December 2012). The forward models were calculated assuming various platelet-layer conductivities (color bar).

Fig. 6. Root-mean-square errors (rmse) were calculated for the in-phase component (Fig. 5a) to find the smallest difference between this dataset and individual forward models. This is shown for the best fit, for the lower limit of uncertainties and for the upper limit. The bulk platelet-layer conductivity is, in this example, 1000 mS m ¹ with a difference of 250mS m^–1 to the lower and 200 mS m ¹ to the upper limit.

We excluded the 450 Hz frequency and the in-phase component of the 1530 Hz channel from the analysis, due to a poor signal-to-noise ratio. We found that the quadrature component of the two highest frequencies only weakly depended on the bulk-conductivity variations of the platelet layer at most sites, and we thus excluded these from further analysis. Based on the small penetration depth of these frequencies and the typical thickness of the fast ice, this was not unexpected.

The local minima of the rmse of all processed frequencies and components were averaged by survey site (Fig. 7) and by individual frequencies (Fig. 8). For individual sites we found mean bulk platelet-layer conductivities in the range 1017-1340 mS m ^–1 (Fig. 7, best fit). The mean of these values resulted in a bulk platelet-layer conductivity of 1154 mS m¹ (Fig. 7, solid black line). The mean value of the lower uncertainty limit was 883 mS m ¹ and of the upper uncertainty limit 1425 m Sm ^–1, which resulted in an overall uncertainty of ±271 m Sm ^–1 . We observed highest bulk platelet-layer conductivity at ATKA24, the site with a thicker sea ice and platelet layer (1.89+ 2.24m) than at ATKA11. Here we assume that an internal conductive layer was located in the platelet layer.

Fig. 7. Bulk platelet-layer conductivities. The results obtained using different frequencies are averaged and shown for the individual sites. The conductivities and the corresponding standard deviations are shown for the best fit, and the lower and upper limit of uncertainties. Dataset date format is day-month of 2012.

Fig. 8. Bulk platelet-layer conductivities. The results obtained at the different sites are averaged and shown for the individual frequencies. The conductivities and the corresponding standard deviations are shown for the best fit, and the lower and upper limit of uncertainties.

We observed a frequency dependence of the bulk platelet-layer conductivity (Fig. 8), where higher frequencies tended to result in higher conductivities, even though upper layers may be, in general, more consolidated. Whether the reason for this relationship is a calibration error or insufficient description of the layering by the forward models is not known.

Ice-volume fraction of platelet layer

The next step was to convert the layer conductivity to porosity. We used Archie’s law (Eqn (3)), where the brine conductivity, σ _b , is the conductivity of the liquid phase in the platelet layer. To a first-order approximation, σ _b can be described by the conductivity of the sea-water column below.

In eight down- and two upward CTD casts, the water in the platelet layer appeared to be much fresher than the sea water (1800 vs 2690 mS m^–1), but we interpret these low values as an interaction between ice platelets and the conductivity sensor. We assumed cementation factors, m, between 1.5 and 2.5. Applying these parameters to different brine conductivities, σ _b , and bulk platelet-layer conductivities, σ , with lower and upper limits of uncertainties, we found a range of ice-volume fractions (1-Φ, where Φ is porosity; Table 4 ).

Table 4. Ice-volume fractions of the platelet layer assuming different values for cementation factor, m, conductivities of interstitial water in the platelet layer, σ _b , and bulk platelet-layer conductivities, σ , of the lower uncertainty limit (883 mS m^–1 ), the best fit (1154 mS m^–1 ) and the upper uncertainty limit (1425 mS m^–1)

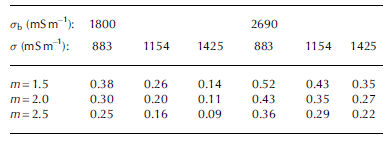
The resulting ice-volume fractions were in the range 0.16-0.26 for sea-water conductivities σ _b = 1800 mS m^–1which we considered to be spuriously low. For regular sea water of σ _b = 2690 mS m^–1 the ice-volume fractions were in the range 0.29-0.43. Accounting for the lower and upper uncertainty limits, ice-volume fractions for spuriously low brine conductivity, σ _b , were 0.09-0.38, and for sea-water brine conductivity they were 0.22-0.52. The ice-volume fraction was equally influenced by the choice of cementation factor, m, and brine conductivity, σ_b.

Discussion

We have shown that, for given thicknesses of solid sea ice and the platelet layer, it is possible to use multi-frequency EM induction soundings to resolve the bulk platelet-layer conductivity within an uncertainty range of 271 m Sm^–1. The uncertainty is mainly governed by the inter-variability between calibrations, rather than by the instrumental noise of the GEM-2. Consequently, the uncertainties of the calibration coefficients can be reduced significantly with proper calibrations. As stated above, we are able to resolve with GEM-2 data a solid sea-ice layer of 3 m with an accuracy of 0.1 m, based on calculated uncertainties. Reducing the uncertainty by 50% will allow us to resolve solid sea ice of up to 4.20 m at an accuracy of 0.1 m. ATKA03 with its 2.69 m solid sea ice and 4.21 m platelet layer could not be resolved by the set-up used. Theoretical calculations, however, showed that it would be possible to resolve these layers with frequencies up to 18 330 Hz by further reducing the uncertainties.

During our first operations of the GEM-2 at Atka Bay fast ice, we tested different frequency configurations in order to evaluate its potential (Table 1 ). Frequencies of 1530, 5310, 18 330, 63 030 and 93 090 Hz showed promising results, as the various frequencies are sensitive to different depths, while a frequency as low as 450 Hz was too noisy. In general, lower frequencies are more sensitive to deeper structures, and higher frequencies to the shallower sea ice. With the two highest frequencies, we obtained sea-ice conductivities similar to those from independent results of sea-ice cores. This can be very useful for other studies, especially for a non-destructive determination of sea-ice properties (e.g. Haas and others, 2008). Although first-year sea ice is generally more electrically conductive than thick sea ice, the sea-ice conductivities from forward-model fitting at ATKA11 were with 200 mS m^–1 unexpectedly high. At this site the freeboards were close to zero, and a slushy snow/ice interface was observed after the snow was removed, which probably influenced the GEM-2 recordings.

For further GEM-2 studies, where an absolute calibration is desired, we strongly suggest calculating calibration coefficients and uncertainties for all the individual frequencies. Nevertheless, the instrument can still be used in a traditional way for single-frequency sea-ice thickness retrievals, similar to an EM-31, where an exponential fit to calibration data at a single frequency is used to directly determine the sea-ice thickness (e.g. Haas and others, 1997). The advantages of the GEM-2 over the EM-31 are the different sounding depths, due to several frequencies, and recording of in-phase and quadrature. The two components provide independent measurements at a single frequency and thereby reduce the ambiguity of the recorded signal, which is important for the determination of the calibration coefficients. The in-phase component of the EM-31 is often at saturation, and the apparent conductivity is calculated with the quadrature component. In general, the in-phase component is more sensitive to deeper structures than the quadrature component.

Correcting the Atka Bay data with the calibration coefficients revealed that an additional phase shift had to be applied. This is possibly linked to the fundamentally different temperature regimes at the calibration sites, where the mean calibration coefficients were obtained. Slightly different frequency configurations had only a minor influence. This highlights the importance of careful calibration measurements for future field campaigns. We measured environmental temperatures during all our surveys, but could not see a strong temperature dependence of individual measurements, although the instrument was in temperature equilibrium with its surroundings.

While the uncertainty associated with the GEM-2 data mainly affects the estimation of platelet-layer conductivity, the subsequent conversion to ice-volume fraction strongly depends on physical assumptions of pore and ice-platelet shapes. For example, we assume that the pore-water is connected, which would generally indicate a low value for the cementation factor, m, in Archie’s law (Glover, 2009). A lower value indicates spherical pores and grains (Salem and Chilingarian, 1999), but this is not the case for individual disk-shaped ice platelets within the platelet layer. Using thin sections for sea-ice cores from Atka Bay, Hoppmann and others (2015) found randomly oriented ice platelets (which agrees with recent findings of Gough and others, 2012). This factor might again result in a lower value of m, due to less angularity. However, to date, no studies exist that describe the cementation factor, m, for the platelet layer using independent measurements. Instead, we calculated a brine platelet-layer conductivity with a range of values, 1.5-2.5, normally observed in sandstones (Glover and others, 1997). In general, we get better agreement with results from recent studies (Gough and others, 2012; Hoppmann and others, 2015) with higher cementation factors or lower brine conductivities.

The brine conductivity, a _b , measured by CTD casts creates an additional uncertainty. Hoppmann and others (2015) showed that the platelet layer was already thinning when the GEM-2 surveys were conducted (November 2012-January 2013), due to the inflow of warm water masses. Hence, the brine conductivity may have decreased due to ice melt in late December. Nevertheless, these melt rates and the associated freshening do not explain the low conductivities (∼-1800mS m^{– 1}) recorded. Also, the bulk platelet-layer conductivity at ATKA11 on 27 December (Fig. 7) did not decrease compared with earlier calibrations.

Apart from the physical assumptions of the platelet layer and the conversion of conductivities to ice-volume fraction, we assumed the ideal case of two layers, which are level within the footprint of the sensor. We tried to compensate for this effect by measuring sea-ice thickness in the footprint range of the instrument through several drillholes. This assumption most likely does not hold for thicker sea ice and platelet layers, where sub-ice topographies or internal layers may be present more often.With frequencies more sensitive to the solid sea-ice layer and the significant extension of the frequency range to lower values, we are confident that we can resolve both platelet layer thickness and conductivity using a geophysical inversion scheme. The result of the inversion might be that a two-layer case is not sufficient; instead it may be necessary to have several platelet layers to explain the apparent relationship (Fig. 8) between bulk platelet-layer conductivity and frequency. However, data inversion is only possible when the bias of the bucking coil is included in inversion algorithms.

Conclusion

This study is a step towards sub-sea-ice platelet-layer volume estimation of Antarctic fast ice with EM induction sounding. We used the multi-frequency ground-based instrument GEM-2, operated at frequencies of 450-93 090 Hz. We compared measurements at sites of known sea-ice and platelet-layer thicknesses at Atka Bay with two-layered forward models, deriving a mean bulk platelet-layer conductivity of 1154 ± 2 7 1 mS m^{– 1}. Assuming a range of cementation factors for the platelet layer, we obtained ice-volume fractions of 0.29-0.43, while values of 0.25 ± 0.06 and 0.25 ± 0.1 have recently been found by other methods (Gough and others, 2012; Hoppmann and others, 2015). Using the quadrature component of higher frequencies, 63 030 and 93 090 Hz, we were able to estimate conductivities of the solid sea-ice layer. Accurate calibrations are required to reduce the uncertainties of multi-frequency EM measurements to make them useful for the determination of the platelet-layer volume. Comparisons of calibration data and forward models revealed that it is crucial to include the signal response of the bucking coil in the theoretical calculations. In general, multi-frequency soundings are superior to single-frequency soundings and may also improve sea-ice thickness retrieval over deformed and porous sea ice that has similar macroscale properties to the platelet layer in Antarctica. Our results provide elemental physical constraints for the layer conductivities and ice-volume fractions. As we continue this work, we intend to conduct a joint analysis of all frequencies using a geophysical inversion to retrieve platelet-layer thickness and conductivities simultaneously. Multi-frequency EM induction sounding will enable us to survey ice-platelet volume below the Antarctic near-coastal sea ice on a much larger scale than by direct measurements through drillholes. Our method can also be applied to data from multi-frequency airborne sensors, which have recently been developed (Pfaffhuber and others, 2012).