INTRODUCTION
In ruminants, the extent of digestion of feeds and their nutrients depends on: (i) the magnitudes of the fractional rate of fermentation (k d) in the rumen and the fractional rate of passage (kp) from the rumen, (ii) the length of time that feed components are exposed to the enzymatic reactions and their absorption in the small intestine and (iii) possible fermentation in the hindgut. As fibre digestion is greater in the rumen than in any other compartment of the gastro-intestinal tract, the longer the fibre particulate remains in the rumen the greater the extent of fibre digestion is likely to be. The kp influences the retention of the particulate matter in the rumen. In addition to the extent of digestion of feeds, kp has also been related to maximal voluntary dry matter intake (DMI), amount of ruminally undegraded protein, efficiency of microbial growth, extent of methane loss and susceptibility of animals to bloating (Okine et al. Reference Okine, Mathison, Kaske, Kennelly and Christopherson1998).
Clauss et al. (Reference Clauss, Hummel and Streich2006) indicated that the ratio between the rates of passage of liquids and solids is different between browsers and grazers, probably because grazers (or ruminants under a grazing condition) retain solids (fibre) for a longer period of time than browsers. Therefore, it is possible that the passage rate in goats (intermediate to concentrate selector) may be similar to that of cattle and sheep (grazers) when fed high-forage diets. However, Clauss & Lechner-Doll (Reference Clauss and Lechner-Doll2001) had previously concluded that browsers are not able to retain particles for as long as grazers because their retention selectivity factor in the rumen is narrower (1·14–1·80 mm) than grazers (1·56–2·80 mm), indicating that browsers may have a faster kp.
Mathematical models can be useful for describing and predicting the biological mechanisms involved in digestion of feeds by ruminants. In fact, nutrition mathematical models rely heavily on accurate predictions of kp to determine ruminal digestibility of feeds and their nutrients (Cannas et al. Reference Cannas, Tedeschi, Fox, Pell and Van Soest2004; Fox et al. Reference Fox, Tedeschi, Tylutki, Russell, van Amburgh, Chase, Pell and Overton2004; Tedeschi et al. Reference Tedeschi, Chalupa, Janczewski, Fox, Sniffen, Munson, Kononoff and Boston2008) and to allow different strategies for feeding and management of ruminant animals throughout the world. Different approaches have been used in predicting kp from empirical equations (Cannas & Van Soest Reference Cannas, Van Soest, McNamara, France and Beever2000; Seo et al. Reference Seo, Tedeschi, Lanzas, Schwab and Fox2006) to more complex dynamic models (Seo et al. Reference Seo, Lanzas, Tedeschi and Fox2007, Reference Seo, Lanzas, Tedeschi, Pell and Fox2009). Empirical equations can provide enough descriptive information of the variables involved and their relationship with dependent variables.
The objectives of the present paper were: (i) to develop and evaluate empirical equations to predict kp of forage in goats using chemical composition of the diet, (ii) to compare the predictions of the newly developed equation with those equations proposed by Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000) for ruminants and (iii) to perform a sensitivity analysis of influential variables that could impact the kp for goats.
MATERIALS AND METHODS
Database description
Table 1 shows the range of chemical composition of the diets, body weight (BW), DMI and number of data points for the development and evaluation databases.
Table 1. Summary of animal and diet composition of the development and evaluation studies*
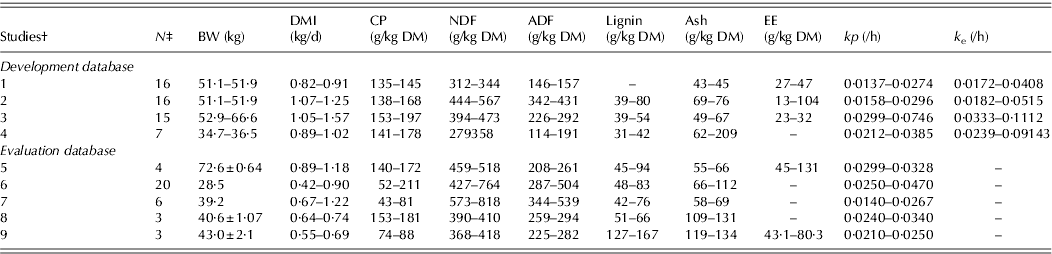
* BW, body weight; DMI, dry matter intake; CP, crude protein; NDF, neutral detergent fibre; ADF, acid detergent fibre; EE, ether extract; kp , calculated fractional passage rate and k e is calculated fractional rate of escape of particles from the rumen. Values are minimum and maximum or mean±s.e.
† Studies 1,Gurung et al. Reference Gurung, Solaiman, Rankins, Mcelhenny, Aguilar-Caballero, Torres-Acosta, Ducoing-Watty, Cerrillo-Soto, Juárez-Reyes and Martinez-Kawas2008; 2, Kendricks et al. Reference Kendricks, Gurung, Rankins, Solaiman, Abdrahim and Mcelhenny2009; 3, Wolc et al. Reference Wolc, Solaiman and Gurung2009; 4, J. Bartlett, personal communication; 5, Solaiman et al. Reference Solaiman, Smoot and Owens2002; 6, Coleman et al. Reference Coleman, Hart and Sahlu2003; 7, Hadjigeorgiou et al. Reference Hadjigeorgiou, Gordon and Milne2001; 8, Alcaide et al. Reference Alcaide, García and Aguilera2000; and 9, Yanez Ruiz et al. Reference Yanez Ruiz, Martin Garcia, Moumen and Molina Alcaide2004.
‡ Number of data points, considering all combinations of animals, diets and periods of Latin square designs.
Development database
The data from four studies that sequentially measured the concentration of a forage marker, ytterbium (Yb), in the faeces were gathered into a development database. Briefly, study 1 was comprised of a Latin square design with four mature Boer crossbred wether goats (51·4 kg BW) fed 0·37 of marked bermudagrass hay and 0·63 of concentrate containing 0, 0·13, 0·25 or 0·38 of distillers’ dried grains with solubles (Gurung et al. Reference Gurung, Solaiman, Rankins, Mcelhenny, Aguilar-Caballero, Torres-Acosta, Ducoing-Watty, Cerrillo-Soto, Juárez-Reyes and Martinez-Kawas2008); all 16 (4×4) data points were used. Study 2 investigated the impact of levels of peanut skins (0, 0·10, 0·20 and 0·30), substituting soybean meal in the concentrate portion of the diet of four mature Boer crossbred wether goats (70·6 kg BW) fed 0·45 of marked bermudagrass hay (Kendricks et al. Reference Kendricks, Gurung, Rankins, Solaiman, Abdrahim and Mcelhenny2009); all 16 (4×4) data points were used. Study 3 had four mature wether goats (58·5 kg BW) fed 0·40 concentrate, 0·30 bermudagrass hay and 0·30 of Lespedeza cuneata and/or alfalfa at four different ratios (0:30, 10:20, 20:10 and 30:0, respectively) in a Latin square design (Wolc et al. Reference Wolc, Solaiman and Gurung2009); only 15 out of 16 (4×4) data points were used. The marking technique used by Wolc et al. (Reference Wolc, Solaiman and Gurung2009) differed from the other studies in that they used rumen gelatine capsule containing Yb acetate to mark all feed particles (forages and concentrates) in the rumen. A limitation of this technique is that some Yb acetate probably remained free (i.e. unattached to any particle), escaped the rumen and reached the faeces in a free form, thus providing a faster kp than expected. Finally, study 4 also used an incomplete Latin square design to determine the impact of four levels of broiler litter (0, 0·13, 0·25 and 0·50) in the diet of wether goats (35·7 kg BW) (J. Bartlett, personal communication); only seven out of ten data points were used. The animals in study 4 were smaller (lighter) than in the other studies used for the development database. Study 3 had faecal collections at 0, 6, 12, 24, 36, 48, 60, 72, 96 and 120 h (ten time points), studies 1 and 2 had the same time points as study 3 plus faecal collection at 84 h (11 time points) and study 4 had 19 times of faecal collections (0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, 108 and 120 h) after feeding the marker.
Evaluation database
Independent studies published in the literature were gathered into an evaluation database. Study 5 was comprised of four mature Nubian wether goats (72·6 kg BW) fed 0·45 bermudagrass hay and 0·55 concentrate, which had four levels of EasiFlo cottonseed replacing corn and soybean meal, so that diet dry matter (DM) contained 0, 0·16, 0·33 or 0·50 of EasiFlo cottonseed; Yb was used as a marker (Solaiman et al. Reference Solaiman, Smoot and Owens2002). For study 6, 20 different hays cut at two or three stages of maturity from cool-season and warm-season plant species were fed to yearling Alpine wether goats (28·5 kg BW) and the passage rate was determined using Yb (Coleman et al. Reference Coleman, Hart and Sahlu2003). The aim of study 7 was to investigate the digestibility of temperate forages with or without ammonia treatment using 12 Scottish cashmere male goats (39·2 kg BW); n-alkane was the marker used for temperate forages (Hadjigeorgiou et al. Reference Hadjigeorgiou, Gordon and Milne2001). For study 8, four dry non-pregnant Granadina goats (40·6 kg BW) were fed with three diets based on alfalfa and combinations of beet pulp and oat grain; chromium mordant technique was used to mark alfalfa (Alcaide et al. Reference Alcaide, García and Aguilera2000). Finally, study 9 also used dry non-pregnant Granadina goats (43 kg BW) to determine the ruminal degradation profiles and passage rates of olive leaves with or without supplementation with barley and faba beans; the chromium mordant technique was also used (Yanez Ruiz et al. Reference Yanez Ruiz, Martin Garcia, Moumen and Molina Alcaide2004). These studies were selected because of their diversity of feed, animal and environment information.
Determination of the ruminal fractional passage rate
The direct comparison and use of the published kp from different studies may not be adequate because different studies may use different methodologies in fitting the data to passage rate models. Therefore, the raw data of the development database studies were used to estimate the kp using the GnG1 models (Vieira et al. Reference Vieira, Tedeschi and Cannas2008a, Reference Vieira, Tedeschi and Cannasb). The GnG1 models are based on the Gamma distribution and were selected because of their robustness, flexibility to describe different marker profiles and ability to standardize the method of determination of the age-dependent fractional passage rate among studies. The data were fitted to GnG1 models of at least two and to up to 12 orders of time dependency (e.g. compartments) in the rumen (n=2–12) and one-time dependency post-rumen (i.e. G2G1–G12G1). The GnG1 Models software (http://nutritionmodels.tamu.edu/gng1.htm, verified June 19 2011) was used to fit the data. Briefly, the parameter estimates are the order of time dependency related to transference mechanisms of the particles from the raft (unmixed) pool to the escapable (mixed) pool in the rumen (n), transit time, representing the time of an escaped particle to transit from the reticulo-omasal orifice to the faeces (τ, measured in h), asymptotic age-dependent fractional rate for transference of particles from the raft to the escapable pool (L r or λ r, measured /h), fractional rate of escape of particles from the escapable pool (k e, /h), and the mass ratio between the marker dose and NDF mass in the raft pool (C0, g/g) (Vieira et al. Reference Vieira, Tedeschi and Cannas2008b). The kp was computed based on the parameters λ r, k e and n using Eqn (1) as proposed by Ellis et al. (Reference Ellis, Matis, Hill, Murphy, Fahey, Collins, Mertens and Moser1994).
where kp is the overall fractional passage rate (/h); λ r is the asymptotic age-dependent fractional rate for transference of particles from the raft to the escapable pool (/h); k e is the calculated fractional rate of escape of particles from the escapable pool (/h); and n is the order of time dependency.
Statistical analyses
All statistical analyses were performed with SAS v. 9.2 (SAS 2008) using PROC REG and PROC MIXED. The following variables, expressed either as g/kg DM or as daily intake (g/kg BW), were used in a stepwise selection process using PROC REG to predict kp either as observed kp values or as the logarithm of observed kp values: BW, dietary DM, crude protein (CP), neutral detergent fibre (NDF), acid detergent fibre (ADF), hemicellulose, lignin, ash, ether extract (EE) and the ratio of lignin to NDF. In addition, the logarithm of NDF, lignin and lignin to NDF ratio were used as independent dietary variables. Preliminary analyses indicated these variables were nonlinearly related to kp. This nonlinear relationship of the kp with other variables is in accordance with the work by Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000). As some of the studies did not have all variables, some variables (i.e. hemicellulose and ADF) were omitted in order to increase the number of data points in a parallel regression analysis. In the first random coefficient model, the PROC MIXED was used to evaluate the contribution of study, diet and animal variations to the total variance in predicting the average observed kp. The effects of study, and diet and animal within study, were assumed to be random effects and the variance component was used for the variance–(co)variance matrix structure (Littell et al. Reference Littell, Milliken, Stroup, Wolfinger and Schabenberger2006). Additionally, a second random coefficient model (statistical model shown in Eqn (2)) was evaluated to estimate the empirical equation based on the fixed effect of the selected independent variables after adjustment for study effect (St-Pierre Reference St-Pierre2001). The kp adjusted for study effects (kp adj) was computed with the fixed effects and the residue estimates (μ+X ij+ε ij; Eqn (2)). The approximate coefficient of determination was calculated as the regression of kp adj on the fixed effect variables (X i). The plot of studentized residuals on predicted values was used to assess outliers, which were removed if outside of the range −2·5 to +2·5.
where Y ij is the dependent variable, μ is the overall mean, X ij is the ith-independent variable of the jth study, Studyj is the random effect of the jth study on the intercept, X ij×Studyj is the random interaction between the ith-independent variable and the jth study, study is identically, independently and normally distributed ![]() and ε ij is the identically, independently and normally distributed uncontrolled, random error
and ε ij is the identically, independently and normally distributed uncontrolled, random error ![]() .
.
Equation evaluation
A random coefficient model similar to that shown in Eqn (2) was used to remove the effect of study from the intercept and the slope and the adjusted, observed kp was used to determine the equation adequacy. The adequacy of the predictions of the kp of the evaluation database was assessed as described by Tedeschi (Reference Tedeschi2006). Equation precision was measured with the coefficient of determination (R 2) of the linear regression between observed and predicted values and the simultaneous F-test of the intercept and slope (H 0: intercept=0 and slope=1), whereas the accuracy (Cb) was determined based on the concordance correlation coefficient (CCC) and the mean square error of prediction (MSEP) and its decomposition into mean bias, systematic bias and random errors (Tedeschi Reference Tedeschi2006). The Cb statistic measures how far (or close) the regression line deviates from the Y=X line. Evaluations were performed by means of the Model Evaluation System v. 3.1.11 (http://nutritionmodels.tamu.edu/mes.htm, verified June 19 2011) as discussed by Tedeschi (Reference Tedeschi2006). In addition to the prediction equation derived in the present study, the equation proposed by Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000) (CVS) to predict kp (Eqn (3)) was also tested with the evaluation database.

where kp CVS is the fractional passage rate predicted by the Cannas & Van Soest's (Reference Cannas, Van Soest, McNamara, France and Beever2000) equation (/h), NDF is expressed as a g/kg BW, and CP is expressed as a g/kg dry matter.
Sensitivity analysis
Sensitivity analysis was performed using the Monte Carlo technique, which randomly samples input variables based on a probability density distribution to assess their concurrent impact on the value and distribution of output variables. The Monte Carlo simulation was performed with @Risk v. 5.7 (Palisade Corporation 2010) using 10 000 iterations and Latin hypercube sampling as discussed by McKay et al. (Reference Mckay, Beckman and Conover1979). The determination of most influential variables on the simulation output was accomplished by using standardized regression coefficients (SRC) (Kutner et al. Reference Kutner, Nachtsheim, Neter and Li2005). The SRC reflects the change in the s.d. of the dependent (output) variable associated with 1 unit change in the s.d. of the independent (input) variable at a ceteris paribus condition, that is, when all other input variables are fixed, unchanged (Helton & Davis Reference Helton and Davis2002). Spearman correlations were assigned to input variables to maintain the expected correlations between independent variables during the simulations.
RESULTS AND DISCUSSION
The G2G1 model consistently had a lower sum of squares of errors and greater relative likelihood probabilities (data not shown) than other GnG1 versions (Vieira et al. Reference Vieira, Tedeschi and Cannas2008a). Therefore, the G2G1 model was chosen to converge the passage profiles of all studies of the development database. Figure 1 depicts the marker concentration profiles and the fitted line for selected treatments of the development database studies.
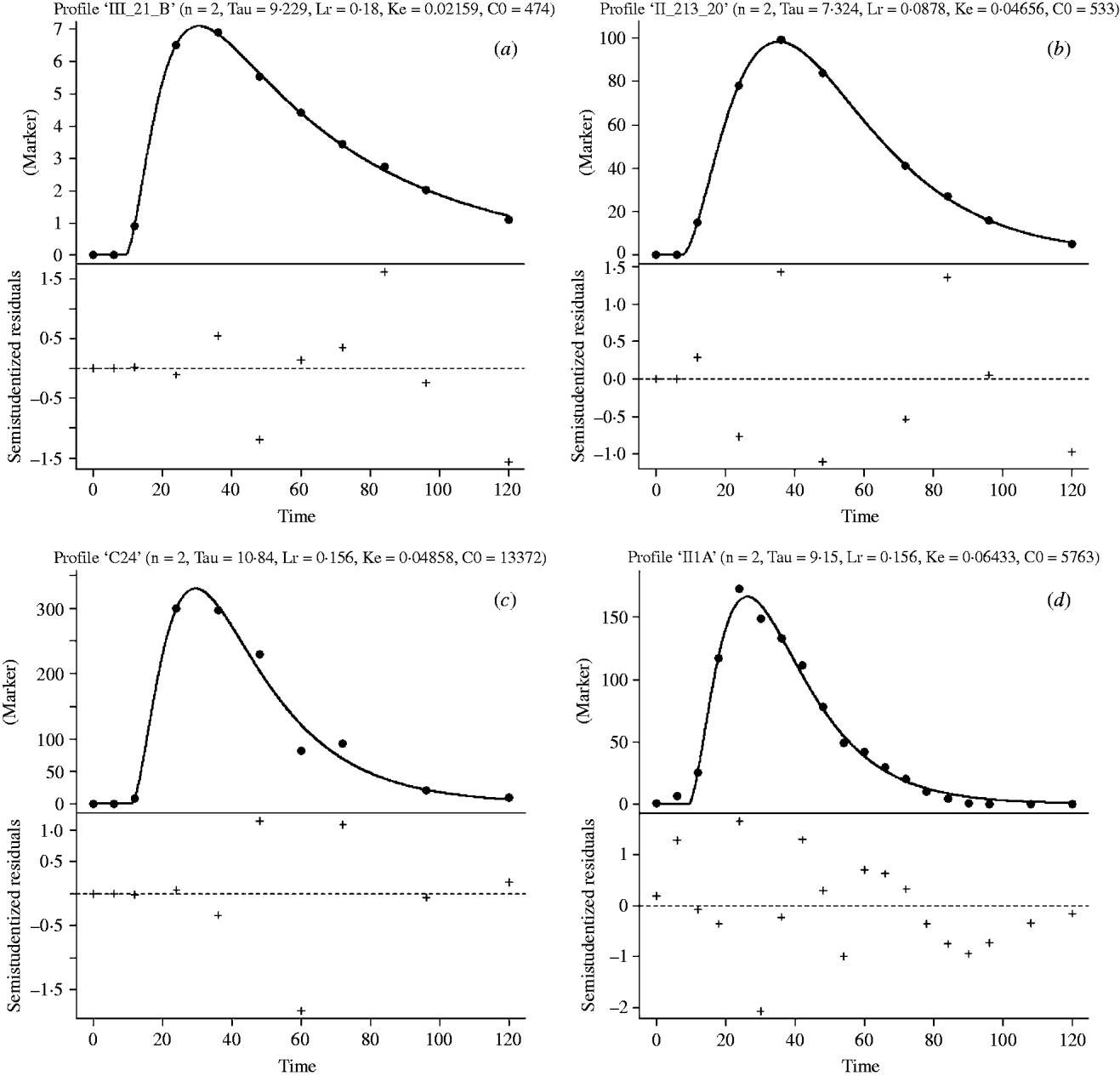
Fig. 1. Marker concentration (marker) profiles (blue dots) and G2G1 fitting line (solid, dark line) in the top part of the graphics and studentized residuals in the bottom part of the graphics versus incubation time (h, X-axis) of selected treatments from studies 1 (a), 2 (b), 3 (c) and 4 (d) of the development database. The parameter estimates shown in the top part of the graphics are: n is the order of time dependency; L r is the asymptotic age-dependent fractional rate for transference of particles from the raft to the escapable pool (/h); σ is the transit time that represents the time of an escaped particle to transit from the reticulo-omasal orifice to the faeces (h); k e is the calculated fractional rate of escape of particles from the escapable pool (/h); and C0 is the mass ratio between the marker dose and NDF mass in the raft pool (g/g).
Development of empirical equations
For the untransformed kp, hemicellulose (g/kg BW), BW (kg), natural logarithm of lignin to NDF ratio and ash (g/kg BW) were selected by the stepwise selection process. These variables explained 0·714 of the variation and had a root of mean square error (RMSE) of 0·0069/h with 38 data points (Eqn (4)).
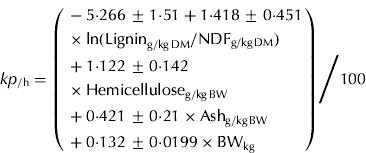
When the ln(kp) was used as the dependent variable, hemicellulose (g/kg DM), BW (kg), NDF (g/kg DM) and ADF (g/kg BW) were selected; they explained 0·747 of the variation and had RMSE of 0·189 ln(kp) (0·0121/h) with 38 data points (Eqn (5)).
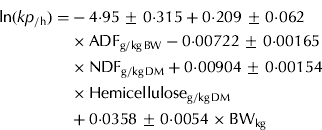
The ln(kp) yielded slightly better predictions than the original, untransformed kp, and the residual plot of the ln(kp) had a more homoskedastic variance (not shown). Therefore, the ln(kp) was selected for further evaluation.
In the present study, nonetheless, few data points were used because of missing values for some dietary variables across studies. Thus, a reduced model that did not contain certain variables with missing values (i.e. lignin, cellulose and hemicellulose) was re-fitted; therefore including more data points. With the reduced model, the ln(kp) equation contained CP (g/kg BW), ADF (g/kg BW), ln(NDF) (g/kg BW) and BW (kg) as independent variables. These variables explained 0·722 of the variation and had an RMSE of 0·202 ln(kp) (0·0122/h) with 54 data points (Eqn (6)).

Equation (6) suggests that kp increases with dietary CP, ln(NDF) and BW but decreases with dietary ADF, as shown by their coefficient estimates. These variables are in agreement with Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000), in which kp was positively correlated with NDF and CP. The dairy NRC (2001) also uses dietary NDF in predicting kp of dry forage, and the work of Seo et al. (Reference Seo, Tedeschi, Lanzas, Schwab and Fox2006) confirmed that kp of forage is related to forage proportion in the diet of dairy cows. In contrast to these publications, Eqn (6) included CP (g/kg BW), suggesting that CP is important in the kp of goats in addition to fibre and body size for the present data. However, note that the coefficient of variation (s.d. divided by the mean) of the CP coefficient estimate was c. 0·38, which is quite large.
As ADF is not always reported as it should be, an additional regression excluding ADF was also performed and Eqn (6) was re-fitted using NDF, DM, CP, ash and BW. Equation (7) explained only 0·595 of the variation of the ln(kp) and had RMSE of 0·241 ln(kp) (0·0127/h) with 54 data points. Interestingly, CP was no longer significant when ADF was not included as an independent variable.

Development of empirical equations adjusted for study effects
The first random coefficient model analysis indicated the (co)variance of study, animal and diet accounted for 0·564, 0·158 and 0·00002 of the total variance, respectively. Even though study accounted for more than 0·50 of the random variation, its (co)variance estimate was not significantly different from zero (P=0·134). Similarly, the diet (co)variance was not significantly different from zero (P=0·479). However, there was a very strong trend for the animal (co)variance to be different from zero (P=0·059). The average kp was 0·0283/h.
The second random coefficient model was performed using the variables identified in Eqn (7), but the random effect of study was included in the statistical model as shown in Eqn (2). The parameter estimates of the fixed effects are shown in Eqn (8). The approximate R 2 was 0·623 with a RMSE of 0·196 ln(kp) (0·0122/h). As Eqn (8) is adjusted for the impact of studies, it should be used to predict kp for goats.

Evaluation of empirical equations
Equation (8) was used to predict the kp using the animal and dietary information of the evaluation database. Studies in the evaluation database were also analysed as random factors. The study (co)variance affected mostly the intercept (σ Study2=0·399, P=0·130) rather than the slope (σ Study2=0·013, P=0·403) of the regression of observed on predicted mean kp. The intercept was greatly affected by studies 6 and 7, probably because of the lighter BW of the animals; their points are more sparsely distributed than the other studies. Figure 2 depicts the plot of observed and predicted values. After adjusting for study effects, Eqn (8) was able to account for c. 0·46 of the variation in the observed kp. Even though the intercept and slope differed simultaneously (P<0·001) from zero and unity, respectively, the slope was not different (P=0·172) from unity. This suggests that Eqn (8) was able to predict kp, but there was a significant mean bias. In fact, Eqn (8) underpredicted the mean kp by 0·0129/h. The CCC was extremely low (0·22; theoretical range from 0 to 1) with an accuracy of 0·33 (theoretical range from 0 to 1). The root of MSEP (RMSEP) was 0·0139/h and the decomposition of the MSEP indicated that 0·86 of this error was associated with mean bias, 0·132 was due to random errors, and only 0·0076 was caused by systematic bias.
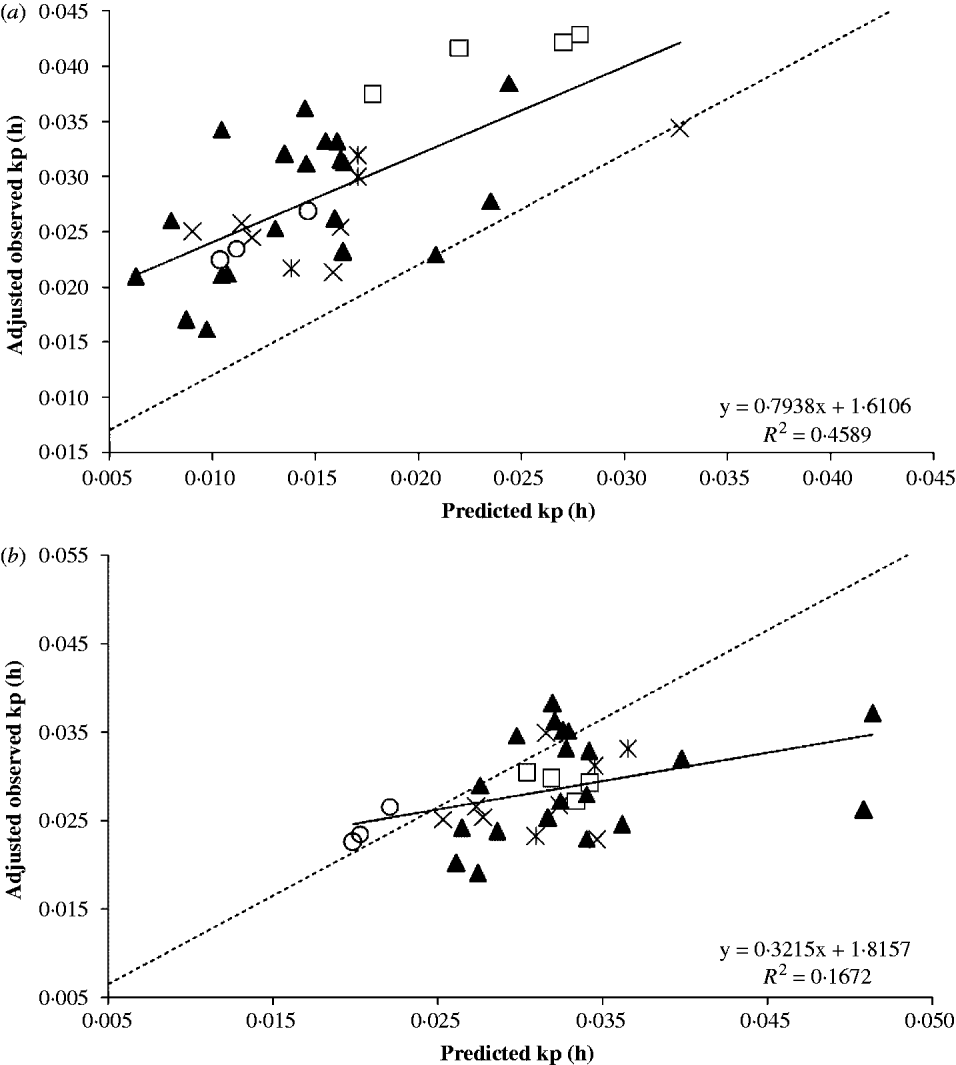
Fig. 2. Regression between observed fractional passage rates (kp) adjusted to study effect and predicted kp using (a) the developed empirical equation or (b) the equation published by Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000). Symbols are data from study 5 (□), study 6 (▴), study 7 (×), study 8 (*) and study 9 (○). The dashed line is the Y=X line.
These findings suggested the G2G1 model may underpredict the kp or that reported values for kp in the evaluation database are overpredicted. In fact, simple models or one compartment model (Grovum & Williams Reference Grovum and Williams1973; Mertens & Loften Reference Mertens and Loften1980) may overpredict the kp because it does not account for the age-dependent fractional rate between compartments within the rumen (λ r in Eqn (1)) before the marked particulate effectively escapes the rumen. The reported kp in the literature is more likely to be associated with k e in Eqn (1), shown in Table 1, than with the kp calculated with GnG1 models. The averages±standard deviations (s.d.) of calculated kp and k e in the development database were 0·028±0·0115 and 0·041±0·0212/h, respectively. The difference between kp and k e is 0·0135/h, which is similar to the mean bias of 0·0129/h. This remarkably similar difference and the negligible systematic bias suggest that Eqn (8) can predict the true fractional passage rate, assuming two compartments in the rumen. Furthermore, predicted values by Eqn (8) could be adjusted for the mean bias that was found when evaluating literature data by simply adding 0·0129/h to Eqn (8) as shown in Eqn (9). The reason for this discrepancy is likely because the literature data were based on one compartment in the rumen using a time-independent fractional rate.

A similar meta-regression was performed with Eqn (3) (Cannas & Van Soest Reference Cannas, Van Soest, McNamara, France and Beever2000). The precision was less than Eqn (8) (R 2 of 0·17) but as expected, the accuracy was greater (mean bias of 0·00344/h, RMSEP of 0·00716/h, CCC of 0·34 and accuracy of 0·83), probably because the authors used literature data that are comparable to the values in the evaluation database of the present study. This means that their kp were computed using time-independent models. The decomposition of MSEP indicated a more equally distribution of the MSEP among mean bias (0·23), systematic bias (0·363) and random errors (0·406) than Eqn (8).
A revision of the equation published by Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000) (Eqn (3)) has been developed (L. O. Tedeschi, personal communication; Eqn (10)) by adjusting for the study effects of the database used by Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000).
When using the evaluation database to evaluate the revised equation of Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000) (Eqn (10)), a slightly improved R 2 was obtained of 0·24, RMSEP of 0·00625/h and CCC of 0·39. However, mean bias (−0·00366/h) was similar with the sign changed, and accuracy decreased slightly (Cb=0·79). The major enhancement in using the kp CVS2 for study effects (Eqn (10)) was the partitioning of the MSEP that decreased the systematic bias from 0·363 to 0·139, suggesting that the adjustment for studies allows for a more consistent prediction.
Even though there was a slight improvement in the Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000) equation when their study effects were accounted for, the adequacy of Eqn (10) was less than Eqn (9) in predicting kp for goats. Therefore, either equation could be used for predictive purposes.
Sensitivity analysis
The data from the development and evaluation databases (N=90 data points) were combined to identify the most likely distribution of CP (g/kg DM), NDF (g/kg DM), BW (kg) and DMI (kg/d) of goats consuming high-forage-based diets under confinement conditions. The best distribution fit for CP (g/kg DM) was the normal distribution with mean=132 and s.d.=41·7; for NDF (g/kg DM) it was the Weibull distribution with alpha and beta parameters equal to 1·40 and 244·3, respectively; for BW (kg) it was the normal distribution with mean=46 and s.d.=12·4; and for DMI (kg/d) it was the beta general distribution with alpha1 and alpha2 parameters of 2·58 and 3·56, respectively. The correlation between CP (g/kg DM) and NDF (g/kg DM) was −0·695 and for BW (kg) and DMI (kg/d) it was 0·725. These correlations are in agreement with those obtained from the database of Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000) of −0·77 and 0·87, respectively.
Figure 3 shows the SRC for the simulated predictions of kp using Eqns (3) and (8). Both equations were positively related to DMI (kg/d) and negatively related to BW (kg/d) with varying intensities (different SRC values). Interestingly, however, whereas NDF (g/kg DM) had a negative impact on the kp predicted with Eqn (8) (for each s.d. increase in the NDF value, kp would decrease by 37% of its s.d.), it had a positive impact on Eqn (3) (for each s.d. increase in the NDF value, kp would increase by 69% of its s.d.). The mean and s.d. for the kp predicted with Eqn (3) were 0·034 and 0·0056/h and for Eqn (8) they were 0·022 and 0·0079/h, respectively. Therefore, assuming the s.d. of NDF was 155 g/kg DM, an increase in dietary NDF by the s.d. value would increase the kp from Eqn (3) by 0·0039/h whereas the kp from Eqn (8) would be decreased by 0·0029/h. The inclusion of dietary CP in the prediction equation greatly impacted on the kp predicted by the equation of Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000), which was based on papers in which time-independent models were probably used, in contrast to the present study. This is likely to be the same for the present evaluation database, as discussed above. Even though DMI affected both empirical equations, it had a greater impact in Eqn (8) than in Eqn (3), in which the SRC was 1·66 times greater (1·13/0·68). A possible explanation for these discrepancies in directions and intensities (SRC values) between these empirical equations is that the fitting technique used in obtaining the kp in each case was different. For Eqn (8), the G2G1 model (Vieira et al. Reference Vieira, Tedeschi and Cannas2008a, Reference Vieira, Tedeschi and Cannasb) was used, whereas the studies in the database used by Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000) might have used the G1G1 model, which is probably the same model used by the studies in the present evaluation database.

Fig. 3. SRC obtained from Monte Carlo simulation of predictions of fractional passage rate using (a) the developed empirical equation or (b) the equation published by Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000). Generated with @Risk 5·7.
Figure 4a has the distribution of simulated predicted kp using Eqns (3) and (8). Equation (8) had a wider distribution (P<0·01 was 0·0105–0·0362/h) compared with Eqn (3) (P<0·01 was 0·0253–0·0434/h, not shown). The least value that Eqn (3) is likely to predict in practice is about 0·0217/h (lower P<0·001) and the greatest kp that Eqn (8) is likely to predict is 0·044/h (upper P<0·001). This suggests that, assuming the kp predictions of Eqn (9), it is likely to have an upper limit of kp around 0·0569/h (0·044+0·0129/h). In fact, the greatest kp of the evaluation database was 0·047/h. The partial correlation between the simulated kp of Eqns (3) and (9) was low (r=0·32), indicating that these equations are not compatible even though the mean predicted values are similar (0·0335 and 0·0349/h, respectively, Fig. 5). The distribution of kp shown in Fig. 4 does not support the claim that browsing ruminants have faster kp than grazing ruminants (Hoffmann Reference Hoffmann1989), even though most of the ruminants used in scientific experimentations are not free-ranging animals and therefore a direct comparison with grazing ruminants may not be adequate because animals cannot exert their normal behaviour of feed selection.

Fig. 4. Histogram of the distributions of predicted fractional passage rate (/h) using Monte Carlo simulation technique of the empirical equation published by Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000) and the developed empirical equation without (a, Eqn (8)) or with (b, Eqn (9)) adjustment for the mean bias. Generated with @Risk 5·7.

Fig. 5. Scatter plot of predicted fractional passage rate (/h) using Monte Carlo simulation technique of the developed empirical equation (Eqn (9), Y-axis) and the equation published by Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000) (X-axis). The shaded area is the confidence ellipse assuming bivariate normal distribution. Generated with @Risk 5·7.
Figure 4b suggests that 0·748 of the simulated kp from Eqn (9) are within P<0·01 of the simulated kp from Cannas & Van Soest (Reference Cannas, Van Soest, McNamara, France and Beever2000) or the P<0·01 of Eqn (9) (0·0244–0·0501/h) contains 0·973 of the simulated kp values with Cannas & Van Soest's (Reference Cannas, Van Soest, McNamara, France and Beever2000) equation (not shown). These findings support the hypothesis that the kp in goats may behave like cattle and sheep when fed high-forage diets (Clauss et al. Reference Clauss, Hummel and Streich2006). The average NDF of the development and evaluation databases was 0·50 g/kg DM, ranging from 0·28 to 0·82 g/kg DM.
Implications
The current results suggest that kp of goats is impacted differently by dietary nutrients when compared with grazers such as cattle and sheep. The sensitivity analysis indicated a theoretical upper limit of 0·0569/h for kp for goats based on the developed empirical equation. Furthermore, standardization of the prediction of the true kp is needed among different laboratories so that improvements in the predictions of kp for goats can be achieved. Data with different dietary compositions are needed to further evaluate the equation devised in the present paper.


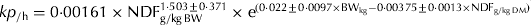 ) had an
) had an 





