Exploring novel target structures for manipulating relativistic laser–plasma interaction

Abstract

The improved laser-to-pedestal contrast ratio enabled by current high-power laser pulse cleaning techniques allows the fine features of the target survive before the main laser pulse arrives. We propose to introduce the nano-fabrication technologies into laser–plasma interaction to explore the novel effects of micro-structures. We found out that not only laser-driven particle sources but also the laser pulse itself can be manipulated by specifically designed micro-cylinder and -tube targets, respectively. The proposal was supported by full-3D particle-in-cell simulations and successful proof-of-principle experiments for the first time. We believe this would open a way to manipulate relativistic laser–plasma interaction at the micro-size level.

1 Introduction

The prospect of realizing compact particle accelerators and x-ray sources based on high-power lasers has gained numerous attention. Utilization of all the proposed schemes in the field requires the laser–matter interaction process to be repeatable or moreover, controllable. This has been very challenging at ultra-high light intensities (typically ${>}10^{18}~\text{W}/\text{cm}^{2}$ ) for the following reasons: first, the laser pulse is always associated with a long pedestal (pico-seconds to nano-seconds), which would create a pre-plasma on the target before the femtosecond (fs) main pulse arrives. The target condition would be dramatically changed compared to the initial setup, laying a barrier for precise prediction and control on the interaction; second, in the domain of laser–plasma interaction (LPI), flat foils have been the most commonly used ones in the overdense regime. The parameter space for the target is thus 2D: thickness versus density. A combination of these two parameters gives only a limited room to manipulate the interaction and strongly restricts the possibilities one could explore.

Recently, laser-to-pedestal contrast ratios as high as $10^{10}$ has been achieved due to the newly developed laser pulse cleaning techniques^[1]. Further, using of a plasma mirror can increase the contrast by 2–4 orders of magnitude^[2–4]. With these advancements, we now propose to manipulate the interaction process by introducing the 3D nano-fabrication technique into LPI. The current 3D direct laser-writing (DLW) technique can produce repeatable structures with at a resolution as high as 100 nm^[5]. The high laser contrast guarantees that the fine structures will survive until the main pulse arrives. The use of the micro-optical elements provides another degree of freedom (other than density and thickness) that makes it possible to micro-engineer LPIs. Hence various LPI applications can be tuned for optimal performance.

Based on experiments in the Scarlet facility in the Ohio State University and 3D PIC simulations with the code VLPL^[6], our approach focuses on exploring novel effects of micro-engineered structured targets. These structures will be specifically designed to manipulate either the high-energy particle sources (electrons, ions, etc.) or the relativistic fs laser pulses.

In this paper, we summarize our investigations on two typical structures: micro-cylinder and micro-tube targets. Although the main results of our research have been previously published in letter style journals (Refs. [7, 8]), here we extend the discussions to offer a more complete presentation of the salient physics. As will be shown in the following sections, the micro-cylinder targets serve to manipulate laser–electron acceleration and the micro-tube targets are dedicated to manipulating the laser intensity.

Figure 1. Scanning electron microscope (SEM) images of micro-cylinder targets: (a) wire spatial distribution, (b) the orientation of the wires with respect to the Silicon substrate. Laser is incident parallel to the wires (white arrow); (c–e) 3D PIC simulations of laser propagating between the micro-wires. (f) The electron phase-space distribution for the micro-cylinder (MC) target and flat target. The laser amplitude, pulse duration and spot size are $a_{0}=21$ ( $\times \,10^{21}~\text{W}/\text{cm}^{2}$ ),  $\unicode[STIX]{x1D70F}_{0}=40$  fs and $w_{0}=4\unicode[STIX]{x1D706}_{0}$ , respectively.

2 Micro-cylinder targets-manipulating laser–electron acceleration

A simplest structure we started with is micro-cylinder target. It is an array of cylinders at the size of tens of micron in length and several micron in diameter. These cylinders are periodically distributed on a substrate with a spatial period of several micron. Nowadays, manufacturing such structure is readily accessible^[9]. For the target we used in our experiments, inclined silicon (Si) cylinders were periodically grown with $1.5~\unicode[STIX]{x03BC}\text{m}$ diameter, 15– $25~\unicode[STIX]{x03BC}\text{m}$ length and $7~\unicode[STIX]{x03BC}\text{m}$ spacing on a $450~\unicode[STIX]{x03BC}\text{m}$ Si substrates, as seen in Figures 1(a) and 1(b). Detailed target making process can be found in Ref. [7].

To get a basic idea of how the laser interacts with the cylinders, we did a full-3D PIC simulation first. The simulation was carried out in a box with $48\unicode[STIX]{x1D706}_{0}\times 20\unicode[STIX]{x1D706}_{0}\times 20\unicode[STIX]{x1D706}_{0}$ in $x\times y\times z$ directions, respectively ( $\unicode[STIX]{x1D706}_{0}=0.8~\unicode[STIX]{x03BC}\text{m}$ is the laser wavelength). The incident laser pulse is polarized in the $y$ direction and propagates along the $x$ direction. The laser field has a profile of $a_{y}=a_{0}e^{-(r/w_{0})^{2}}\sin ^{2}(\unicode[STIX]{x1D70B}t/2\unicode[STIX]{x1D70F})\sin (\unicode[STIX]{x1D714}_{0}t)$ . Here $r=\sqrt{y^{2}+z^{2}}$ , $w_{0}$ is the laser spot size, $\unicode[STIX]{x1D714}_{0}$ is the laser frequency, $a_{0}=eE_{L}/(m_{e}\unicode[STIX]{x1D714}_{0}c)$ is the normalized laser electric field amplitude, $e$ and $m_{e}$ are fundamental charge and electron mass, $E_{L}$ is the laser electric field and $c$ is the speed of light in vacuum, respectively. We chose $a_{0}=21$ , $\unicode[STIX]{x1D70F}=40$  fs and $w_{0}=4\unicode[STIX]{x1D706}_{0}$ based on the Scarlet facility. Periodic carbon micro-wires with a length of $20\unicode[STIX]{x1D706}_{0}$ , diameter of $1.5\unicode[STIX]{x1D706}_{0}$ and spatial spacing of $7.25\unicode[STIX]{x1D706}_{0}$ are placed $10\unicode[STIX]{x1D706}_{0}$ from the left boundary. The electron density of the wires is $n_{e}=300n_{c}$ and they are attached to an aluminum (Al) foil of $n_{Al}=25n_{c}$ density [ $n_{c}=m\unicode[STIX]{x1D714}_{0}^{2}/(4\unicode[STIX]{x1D70B}e^{2})$ is the critical density]. The cylinders are attached to the Al foil with an inclined angle of $22.5^{\circ }$ off the target normal direction to mimic the experimental setup. The entire target is cold and pre-ionized. In our simulations, we employed periodic boundary condition for the laser field in the transverse ( $y$  and  $z$ ) directions and absorbing boundary conditions for the particles.

The simulation results are shown in Figure 1(c)–1(f). We assume the laser pulse enters the array and hits right between the cylinders. The transverse laser field pulled a significant amount of electrons out of the nearest four wires. These electrons are micro-bunched in the transverse direction due to the oscillation nature of the laser field. Hence the spatial period is about one laser wavelength. The electron bunches are injected into the laser pulse and accelerated forward via direct laser acceleration (DLA) mechanism^{[7, 10–12]}. These highly energetic electrons propagate along with the laser pulse. When the latter reaches the substrate, electrons have acquired significant kinetic energy to pass through the substrate and escape the target, while the laser is reflected.

A great advantage of the micro-cylinder target is the huge enhancement for electron energy. Figure 1(f) shows the electron momentum for the micro-cylinder targets. As a baseline comparison, the result of a flat interface without the wires (using the same laser) is also presented. It is apparent that the direct acceleration enabled by the cylinders enormously boosts the peak momentum of electrons. One can also identify the micro-bunches. Coming to the spectrum in Figure 2(a), electrons with energies up to 90 MeV are produced in the former compared to 20 MeV maximum electron energies in flat targets. The total number of relativistic electrons with energies above 1 MeV is enhanced by a factor of 25 with the structured interface compared to flat targets. An exponential fit to the electron energy distribution from the micro-wire array target yields $kT_{e}=16$  MeV, much higher than the ponderomotive scaling at the same intensity ( $kT_{e}=7$  MeV)^[13].

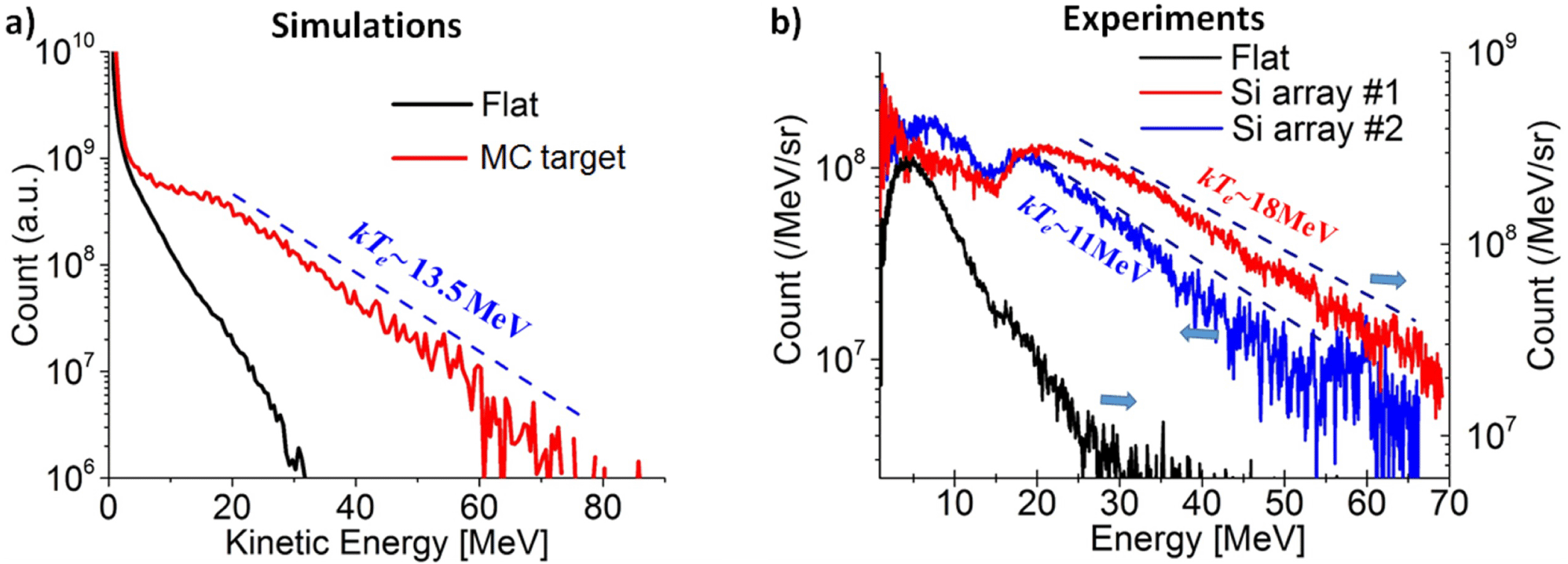
Figure 2. (a) The electron energy distribution for the MC target (red solid) and the flat foil (black solid); (b) experimental results from two experimental shots, with Si array target (shot #1 and #2) and a flat target (flat solid).

A first principle-of-proof experiment was carried out using the Si-array targets introduced in Figures 1(a) and 1(b). The laser in the SCARLET facility delivered 4–5 J of energy on target with pulse contrast better than $10^{9}$ . The 40 fs duration laser pulse was focused with an $F/2.2$ on-axis parabola to a $3~\unicode[STIX]{x03BC}\text{m}$ full-width at half-maximum (FWHM) focal spot, reaching a peak intensity ${\sim}1\times 10^{21}~\text{W}/\text{cm}^{2}$ ^[7]. To prevent laser back-reflections from damaging the front-end optics, the wires were grown at $22.5^{\circ }$ with respect to the flat substrate normal [Figure 1(a)]. The laser propagation direction was parallel to the wires and electrons escaping the rear side of the target were collected with a magnetic spectrometer coupled to imaging plate detectors. The instrument collected electrons at $30^{\circ }$ from the laser axis and $52.5^{\circ }$ from rear target normal.

The experimental results are presented in Figure 2(b). For the flat target, the cut-off energies of the electron beam is around 30 MeV. Significant enhancement was observed with the Si-array target. The cut-off energies from the two shots reach 70 and 60 MeV. They both exhibit a low energy population in the range of 0.5–20 MeV and a high-energy population that extends to 60–70 MeV range. An exponential fit to spectra in the high-energy region gives $kT_{e}\sim 18$ and ${\sim}11$  MeV, respectively. The variation of the spectrum could be a result of the laser beam alignment, which will be discussed later.

The well-matched results between our simulations and experiments indicate the great advantage of the micro-cylinder targets on electron acceleration. Further studies have shown that electrons can also be guided by the cylinders due to the self-generated electrostatic and magnetic fields in the vicinity of the structures^[14].

These well-organized micro-structured targets open a way to generate various energetic electron sources at demand. By changing the length and spatial period, the electron cut-off energy and the population can be manipulated. For instance, in some applications the total beam charge or the laser-to-electron conversion efficiency is superior. A short and dense cylinder array, as shown in Figure 3(a), is more efficient. When the pursue is on the peak electron energy for secondary applications, a long and well-separated cylinder target in Figure 3(b) is more appropriate. We ran 2D simulations with the two typical structures proposed above. Due to the increasing of the interface from the short and dense array, a large amount of electrons are heated up. Their peak energy does not rise compared to the flat foil, as seen in Figure 3(c); however, the population of electrons with moderate energies is enormously enhanced, leading to a much higher absorption efficiency. These electrons are mostly restricted within the substrate due to the sheath field at its rear surface. On the contrary, the long and sparse cylinders, as proven by the above simulations and experiments, provide high cut-off energy electron sources while the population is much lower. In Figure 3(c), we noticed that the maximum energy from the long and sparse structure is almost three times as the one from the short ones. The total electron energy over 1 MeV, however, is about $1/3$ of the latter.

The fact that one can work in different regimes to produce desired particle sources based on the micro-cylinder targets enriches the concept of manipulation. We would expect optimized performance on various applications, such as laser ion acceleration, x-ray emission and so on, by choosing the best geometry of interest.

Figure 3. 2D simulations on laser interacting with (a) a short and dense cylinder array target and (b) a long and sparse one. The electron energy distribution for both targets are shown in (c). The electron spectrum for a flat target is added for comparison. The cylinders and substrates [the gray area in (a) and (b)] are made of carbon. The laser amplitude, pulse duration and spot size are $a_{0}=21\times 10^{21}~\text{W}/\text{cm}^{2}$ ,  $\unicode[STIX]{x1D70F}_{0}=40$  fs and $w_{\text{y}}=3\unicode[STIX]{x1D706}_{0}$ , respectively.

3 Micro-tube targets manipulating laser intensity

The second structure we explored is the micro-tube targets. The target consists of periodic hollow micro-tubes attached to a flat substrate [Figure 4(a)]. They can be printed using two-photon lithography process available on most commercial 3D printers with a featured resolution around 200 nm. When a laser is incident on such a target, there is a great and certain chance that it will enter one of the tubes. We first introduce the results of 3D PIC simulations on a laser propagating within a single tube.

The simulation box is $40\unicode[STIX]{x1D706}_{0}\times 12\unicode[STIX]{x1D706}_{0}\times 12\unicode[STIX]{x1D706}_{0}$ in $x\times y\times z$ directions. The laser pulse is polarized along the $y$ -axis. A single carbon tube is placed $10\unicode[STIX]{x1D706}_{0}$ from the left boundary, with a diameter of $6\unicode[STIX]{x1D706}_{0}$ . The electron density of the tube when fully ionized is $n_{e}=300n_{c}$ and the thickness of the wall is $\unicode[STIX]{x1D706}_{0}$ . The whole target is cold and pre-ionized. The cell size is $0.02\unicode[STIX]{x1D706}_{0}\times 0.1\unicode[STIX]{x1D706}_{0}\times 0.1\unicode[STIX]{x1D706}_{0}$ to resolve the fine structure and the time step is $\unicode[STIX]{x1D6E5}t=0.008T_{0}$ to suppress the numerical instability for high plasma density. A laser beam with a duration of 40 fs and intensity of $5.3\times 10^{21}~\text{W}/\text{cm}^{2}$ propagates from the left boundary and enters the target.

Figure 4. Scheme of laser–micro-tube interaction. (a) Design of a relativistic fs laser impinging on a periodic micro-tube target. (b) Iso-surface plots for the laser intensity distribution before and after it enters the tube. The section of the tube shown above is $32~\unicode[STIX]{x03BC}\text{m}$ long; the length of the simulated tube is $120~\unicode[STIX]{x03BC}\text{m}$ . (c) Light intensity distribution on the $x$ – $y$ plane for the input pulse and in-tube pulse.

Not surprisingly, electrons are extracted from the inner boundary and accelerated. A more exciting fact is that the laser intensity inside the tube is boosted by a factor of ${\sim}3$ compared to the initial incident intensity. A peak intensity of $1.5\times 10^{22}~\text{W}/\text{cm}^{2}$ is reached after the pulse has propagated a distance of $8~\unicode[STIX]{x03BC}\text{m}$ from the entrance aperture, as seen in Figures 4(b) and 4(c).

Figure 5. Laser field distribution at $t=$ (a)  $14T_{0}$ , (b)  $22T_{0}$ and (c)  $30T_{0}$ . The averaged laser intensity distribution in the $y$ – $z$ plane is shown for (d) the input laser and (e) in-tube laser.

Since the total laser energy is fixed and the pulse duration does not change before and after entering the tube [see in Figure 4(b) the pulse length], it must be that the laser beam is somehow focused within the tube. Figures 5(a)–5(c) show the process of the laser interacting with the structure. Apparently, the presence of an aperture boundary to the incident laser beam induces redistribution of the light intensity in the tube. A hot spot area appears at round $x=20\unicode[STIX]{x1D706}_{0}$ . The intensity distribution in the $y$ – $z$ plane is shown in Figures 5(e) and 5(d). A tight focal spot with an FWHM of $1.8~\unicode[STIX]{x03BC}\text{m}$ is achieved inside the tube compared to $2.9~\unicode[STIX]{x03BC}\text{m}$ (FWHM) for the input beam.

We attribute the ‘squeezing’ of laser pulse into the tube to the diffraction effect. Two types of diffractions exist depending on the aperture size. When the aperture diameter is relatively small (comparable to the laser wavelength) the diffraction is in the far-field Fraunhofer regime, where the light beam diverges dramatically after passing through the aperture. Hence there is no intensity enhancement. However, if the aperture size is large compared to the wavelength, in the near-field region the diffraction is Fresnel-like, where a hot spot area is formed with enhanced intensity. In our simulations, the aperture inner diameter is $6\unicode[STIX]{x1D706}_{0}$ . Thus it is the Fresnel-like diffraction that leads to a smaller spot size and a higher intensity within the tube.

When the laser enters the tube after diffracted by the aperture, it is also optically restricted by the boundary. Figure 6(a) illustrates how the intensity is redistributed by varying the tube inner diameter. An optimized enhancement is observed at an inner radius of $3\unicode[STIX]{x1D706}_{0}$ . This is a result from the competition between the diffraction effect and the total laser energy contained in the tube. For instance, tube radius beyond $3\unicode[STIX]{x1D706}_{0}$ would let more laser energy in but the diffraction is weaker. On the contrary, a smaller tube size is only able to contain a very limited portion of the laser energy. In fact if the tube size is below the diffraction limit, the laser beam might be blocked and cannot get into the tube at all.

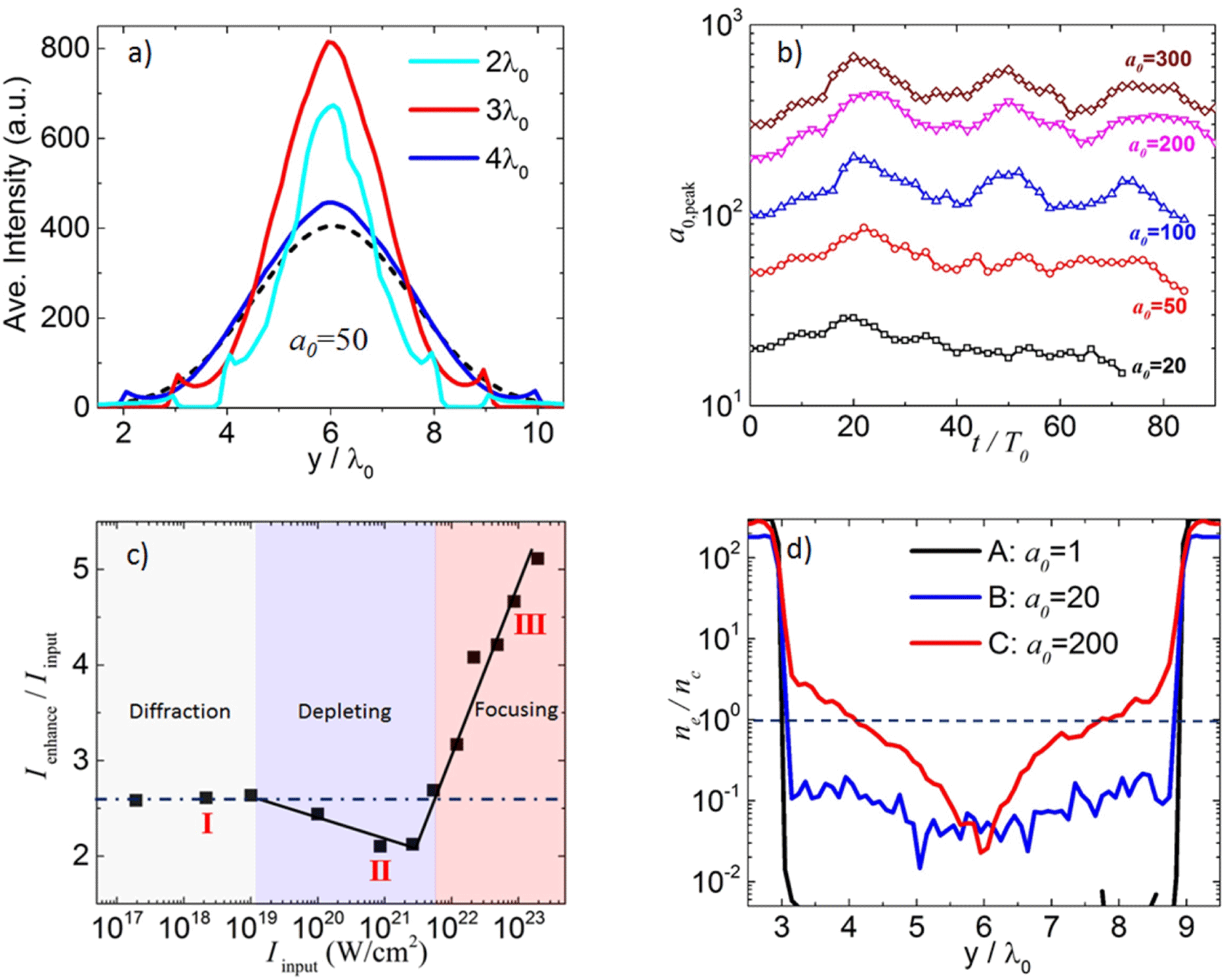
Figure 6. (a) The intensity profile on the $y$ -axis for inner radius of $2\unicode[STIX]{x1D706}_{0}$ (cyan solid), $3\unicode[STIX]{x1D706}_{0}$ (red solid) and $4\unicode[STIX]{x1D706}_{0}$ (blue solid). The initial pulse profile is denoted in black dashed. (b) The peak in-tube intensity as a function of simulation time for input laser amplitude of $a_{0}=20$ , 50, 100, 200, 300, respectively. (c) The intensification factor versus the input laser intensity. (d) The averaged electrons density distribution on the $y$ -axis for $a_{0}=1$ , 20 and 200.

Diffraction could happen multiple times provided the tube is sufficiently long. We did a series of 3D simulations by fixing the tube geometry while changing the incident laser amplitude. For all amplitudes especially the ones over $a_{0}=100$ , the enhanced peak intensity exhibits clear oscillations over time, as seen in Figure 6(b). It indicates multiple diffractions within the tube: the laser is diffracted, focused, diverged and diffracted again. As diffraction is only geometry related, the oscillating period should be independent of the laser intensity. This is clearly illustrated in Figure 6(b), where the period is roughly $25T_{0}$ for all the laser amplitudes.

We define the intensified factor as the ratio between the peak intensity of the in-tube laser and input laser. This ratio is derived from simulations and plotted as a function of the incident laser intensities in Figure 6(c). As discussed above, the intensification factor should be intensity irrelevant should diffraction be the only mechanism. Yet we identified three distinctive scaling laws in the full range. In the first regime (I), the intensification is constant for all lasers, suggesting a pure diffraction effect. When the laser intensity rises into the second regime (II), the enhancement declines marginally. A more exciting scaling appears in the third regime (III). Here the intensification increases dramatically as the input intensities go up. A factor of 5 is achieved at $10^{23}~\text{W}/\text{cm}^{2}$ .

The trend shown in Figure 6(c) suggests that intensity does play a role on the enhancement, which cannot be fully explained by diffraction. We infer that the abnormal scaling in regimes II and III comes from the plasma effect induced by the laser field itself. To explain it, we chose three typical laser amplitudes in different regimes, averaged the electron density along the propagation direction and extracted the value on the $y$ -axis. The corresponding density profiles are presented in Figure 6(d). In the first regime, i.e., $a_{0}=1$ , the laser field is too weak to keep electrons within the tube. There is no plasma effect and the intensification is due to pure diffraction. Thus this regime is named the diffraction regime. When the laser intensity goes to the second regime, say $a_{0}=20$ , a relatively low density plasma ( ${<}0.1n_{c}$ ) is created inside the tube. They tend to deplete the laser energy. One sees a slightly lower intensification factor here. This is denoted as the depletion regime. In the third regime, the laser field is so strong that it pulls a substantial amount of electrons out of the tube. These electrons form overdense plasma embedded by the boundary. The tube aperture is modified in a way that the effective inner diameter is reduced. The laser energy bounded within the tube thus becomes more concentrated, which leads to a rising intensification factor. One then works in the focusing regime.

Figure 7. The averaged (a) electrostatic field (E-field) and (b) magnetic field (B-field) of the tube. The color bar shows the field strength normalized by the incident laser field amplitude $E_{0}$ and $B_{0}$ , while the arrows denote the orientation. We are looking to the opposite of the laser propagation direction. The orientation of the B-field in (b) is clock-wise.

Based on the above analysis, we can roughly estimate the thresholds that define the three regimes. Electrons extracted from the tube boundary are accelerated forward by the DLA mechanism. Since a laser beam propagates at approximately the speed of light in vacuum $c$ , only an electron that is accelerated to be close to $c$ in half of the laser period can stay in the acceleration phase and move along with the laser pulse. Otherwise, it will slip into the deceleration phase, where the orientation of laser field is flipped. In that case, the electron would be scattered off instead of being attracted toward the axis. This requirement defines the first threshold – the laser intensity must be relativistic at the tube inner boundary:

(1) $$\begin{eqnarray}a_{r=r_{0}}\geqslant 1.\end{eqnarray}$$

It gives $I_{0}\approx 1.6\times 10^{19}~\text{W}/\text{cm}^{2}$ for the pulse profile and tube size we employed, consistent with the one shown in Figure 6(c).

The second threshold appears when the embedded electron density reaches critical density by the inner boundary. We estimated it by considering the balance between the charge-separation field and the laser field. Assuming the averaged plasma density drops linearly to zero from the boundary to the axis [from Figure 6(d)] $\bar{n}_{e}(r)=(r/r_{0})\bar{n}_{r_{0}}$ , the peak charge-separation field at the boundary is $\bar{E}_{r_{0}}\sim 4\unicode[STIX]{x1D70B}e\bar{n}_{r_{0}}r_{0}/3$ . On the other hand, the effective laser field averaged over one laser period is $\langle |E_{L,r_{0}}\sin (\unicode[STIX]{x1D714}_{0}t)|\rangle /2$ [the $1/2$ factor stems from the fact that only the part $E_{y}>0$ contributes to the electrons from the upper boundary ( $y>6\unicode[STIX]{x1D706}_{0}$ ) and vice versa]. Thus one has $\bar{a}_{r_{0}}=a_{0}/e\unicode[STIX]{x1D70B}$ ( $e\approx 2.72$ ). By balancing the two fields $\bar{E}_{y}\sim \bar{E}_{r}$ at $r=r_{0}$ , we obtain the second threshold

(2) $$\begin{eqnarray}a_{\text{thr}}\approx \frac{2\unicode[STIX]{x1D70B}^{2}e}{3}\biggl(\frac{r_{0}}{\unicode[STIX]{x1D706}_{0}}\biggr)\biggl(\frac{\bar{n}_{r_{0}}}{n_{c}}\biggr),\quad (e\approx 2.72)\end{eqnarray}$$

which is $a_{\text{thr}}\approx 53\;(I_{0}\approx 6\times 10^{21}~\text{W}/\text{cm}^{2})$ for $r_{0}=3\unicode[STIX]{x1D706}_{0}$ , in agreement with the one observed in Figure 6(c).

From the scaling law one sees that the micro-tube targets are able to boost light intensity up to $10^{23}~\text{W}/\text{cm}^{2}$ based on today’s high-power laser systems, well in the exotic near-quantum electro-dynamics (QED) regime. By manipulating the laser intensity, optimizing the outcome of LPI becomes possible.

The tubes can also guide the energetic particles for secondary applications. In Figure 7 we show the averaged electric and magnetic fields generated by the tube. The pulled-out electrons induce a positively charged tube, in which the charge-separation field is pointing toward the axis, as illustrated in Figure 7(a). Meanwhile, a return current is created within the tube wall to compensate the current carried by the forward going energetic electron bunches. A remarkable poloidal magnetic field surrounding the tube is built up as clearly seen in Figure 7(b). The strengths of both fields are comparable to each other; hence, an electron moving at the speed close to $c$ along the laser propagation direction is balanced by the E- and B-forces. The highly electrons are then guided by the tube, forming a collimated beam when exiting the structure. This is a very favorable feature for many secondary applications. For instance, one can attach an array of micro-tube to a flat foil, as shown in Figure 4(a). Due to the intensification effect and the induced highly collimated electron bunches, the generation of high-energy protons and gamma rays can be greatly enhanced^{[8, 15]}.

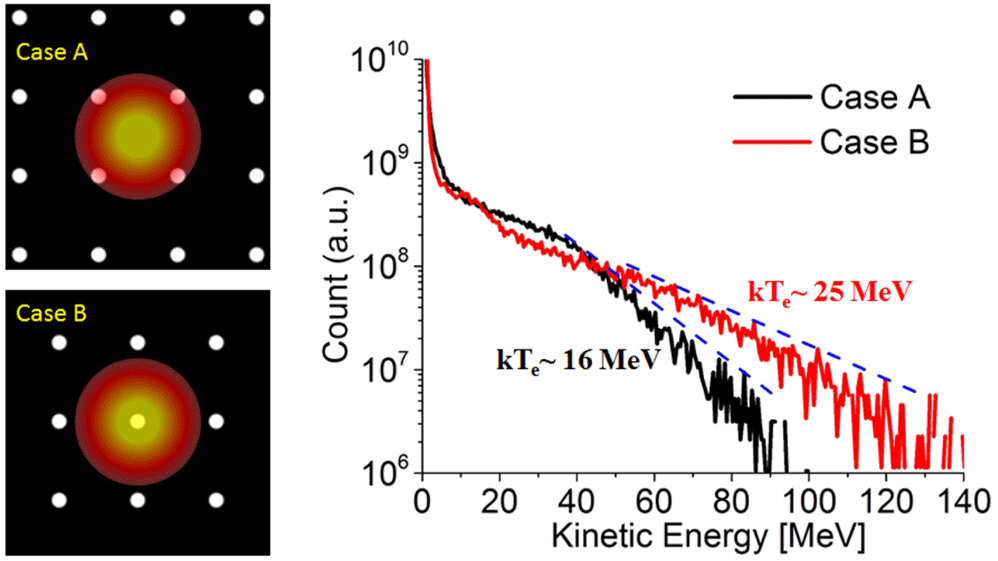
Figure 8. The laser hitting between the wires in Case A and right on a wire in Case B. The right column shows the energy spectra for both cases. All other simulation parameters are the same as in Figure 1.

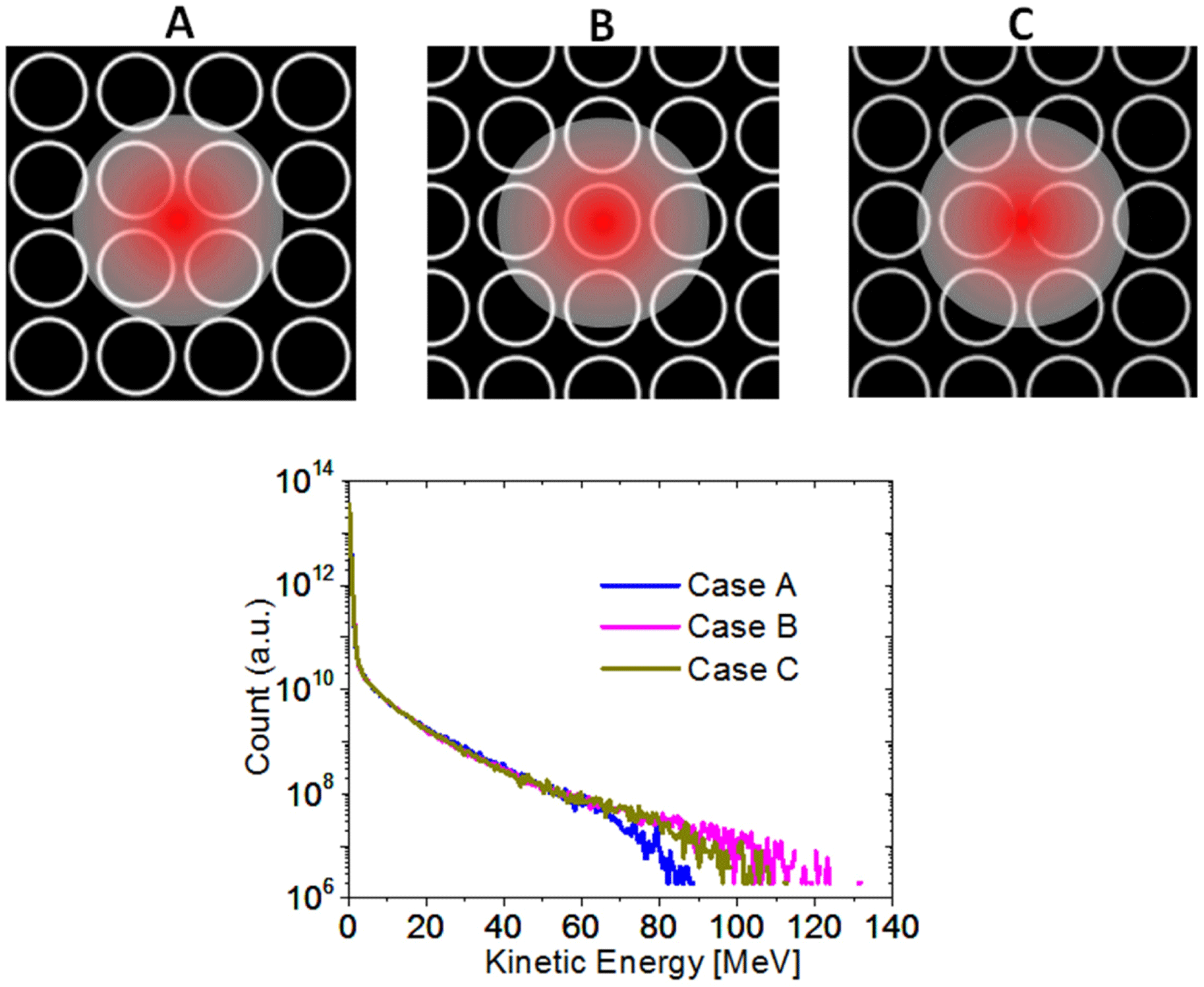
Figure 9. Laser interacting with smaller tubes with inner diameter of $3\unicode[STIX]{x1D706}_{0}$ . Case A, B and C show the three different landing spots of the laser beam. The corresponding electron spectra are listed in the lower row. The laser pulse is of peak intensity $10^{21}~\text{W}/\text{cm}^{2}$ , duration 40 fs and spot size $8\unicode[STIX]{x1D706}_{0}$ .

4 Alignment

In reality, using the micro-structures requires that the laser hits at least one unit with a certain chance. This can be done by improving the alignment technique so that the laser beam enters the unit precisely, though it is challenging. We propose to use a compact array of many identical units and make sure that the laser spot covers at least one unit.

For the micro-cylinder target, we consider two extreme cases: the laser hits right between the wires (case A) and the laser hits right on a wire (case B). The corresponding spectra from 3D simulations are listed in Figure 8.

Both of them exhibit similar distribution. The cut-off energy and temperature is higher for the latter because the laser intensity on the wire is higher than in Case A. These two cases draw the energy boundary for the structure we used, i.e., 90–130 MeV in energy and 16–25 MeV in temperature. It is still a well-defined region where there is plenty of room for further manipulation.

The alignment issue for micro-tube targets is more critical. On the one hand, with an array of closely placed tubes, the laser missing one tube would hit another (at least part of it). The worst scenario would be the laser lands right between the tubes. This could be improved if the open area is much higher compared to the walls. In terms of enhanced electron acceleration for secondary applications, we propose to use a relatively small tube aperture size so that the laser would cover several of them wherever it goes.

In the following 3D simulations, we use a $10^{21}~\text{W}/\text{cm}^{2}$ , 40 fs laser and reduce the tube diameter by half to $3\unicode[STIX]{x1D706}_{0}$ . In this case the laser spot size (full-width at $1/e$ ) $8\unicode[STIX]{x1D706}_{0}$ would interact with at least four tubes as shown in Figure 9. Three different laser-landing locations are tested in Cases A, B and C. Again, the cut-off energy varies in some degree but still in a very delicate range from 90–120 MeV.

5 Discussions and conclusions

We have shown through experiments and full-3D PIC simulations that, the new added degree of freedom – the target shape, allows for manipulating LPI at the micro-meter level. They can be applied to various aspects such as target normal sheath acceleration of ions^[16–21], $x/\unicode[STIX]{x1D6FE}$ -ray emission ^[22] and generation of MeV-positron beams^[23]. Both the cut-off energy and the population can be manipulated by adjusting the length and spatial period of the well-organized structures. Experiments are under way to demonstrate the prospect of micro-cylinder and micro-tube targets.

It should also be noted that other structured interfaces have also been studied through simulations on enhancing the laser-to-target energy conversion efficiency and altering the incident laser pulse^[24–36]. In our work, we propose the concept of manipulation relativistic LPI by not only enhancing the absorption efficiency but also intensifying the laser pulse itself and furthermore, creating the particle sources at demand.