Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-15T15:56:39.394Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramanujan Congruences for p-k(n)

Published online by Cambridge University Press:  20 November 2018

A. O. L. Atkin
A. O. L. Atkin*
Affiliation:
The Atlas Computer Laboratory, Chilton, Didcot, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let

1

2

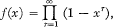
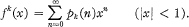
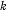Thus p-1(n) = p(n) is just the partition function, for which Ramanujan (4) found congruence properties modulo powers of 5, 7, and 11. Ramanathan (3) considers the generalization of these congruences modulo powers of 5 and 7 for all ; unfortunately his results are incorrect, because of an error in his Lemma 4 on which his main theorems depend. This error is essentially a misquotation of the results of Watson (5), which one may readily understand in view of Watson's formidable notation.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 67 - 78
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Atkin, A. O. L., Proof of a conjecture of Ramanujan, Glasgow Math. J., 8 (1967), 14–32.Google Scholar
2. Atkin, A. O. L. and O'Brien, J. N., Some properties of pin) and c(n) modulo powers of 13, Trans. Amer. Math. Soc, 126 (1967), 442–459.Google Scholar
3. Ramanathan, K. G., Identities and congruences of the Ramanujan type, Can. J. Math., 2 1950), 168–178.Google Scholar
4. Ramanujan, S., Some properties of pin), the number of partitions of n, Proc. Cambridge Phil. Soc, 19 (1919), 207–210.Google Scholar
5. Watson, G. N., Ramanujans Vermutung ûber Zerfâllungsanzahlen, J. fiir Math., 179 (1938), 97–128.Google Scholar
6. Weber, H., Lehrbuch der Algebra, Vol. 3 (Brunswick, 1908; reprinted Chelsea, N.Y.).Google Scholar