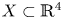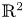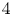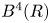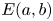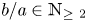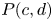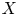1. Notation
Here we gather some common notation. We work in ![]() $\mathbb {R}^4 \equiv \mathbb {C}^2$ with the standard symplectic form
$\mathbb {R}^4 \equiv \mathbb {C}^2$ with the standard symplectic form ![]() $\omega = ({i}/{2}) \sum _{k=1}^2\,dz_k \wedge d\overline {z}_k$. The moment map is
$\omega = ({i}/{2}) \sum _{k=1}^2\,dz_k \wedge d\overline {z}_k$. The moment map is
We use coordinates ![]() $(r, s)$ on
$(r, s)$ on ![]() $\mathbb {R}_{\ge 0}^2$. Given a subset
$\mathbb {R}_{\ge 0}^2$. Given a subset ![]() $\Omega \subset \mathbb {R}_{\ge 0}^2$ we define the corresponding toric domain
$\Omega \subset \mathbb {R}_{\ge 0}^2$ we define the corresponding toric domain ![]() $X_{\Omega } := \mu ^{-1}(\Omega ) \subset \mathbb {C}^2$. A toric star-shaped domain
$X_{\Omega } := \mu ^{-1}(\Omega ) \subset \mathbb {C}^2$. A toric star-shaped domain ![]() $X_{\Omega }$ has
$X_{\Omega }$ has ![]() $\partial \Omega$ transversal to the radial vector field
$\partial \Omega$ transversal to the radial vector field ![]() $X_{\rm rad} = r ({\partial }/{\partial r}) + s ({\partial }/{\partial s})$ of
$X_{\rm rad} = r ({\partial }/{\partial r}) + s ({\partial }/{\partial s})$ of ![]() $\mathbb {R}_{>0}^2$. In the case when this subset
$\mathbb {R}_{>0}^2$. In the case when this subset ![]() $\Omega$ is of the form
$\Omega$ is of the form
we say that ![]() $X_{\Omega }$ is (toric) convex if
$X_{\Omega }$ is (toric) convex if ![]() $f$ is concave, and
$f$ is concave, and ![]() $X_{\Omega }$ is (toric) concave if
$X_{\Omega }$ is (toric) concave if ![]() $f$ is convex. Examples of toric domains which are both convex and concave are symplectic (closed) ellipsoids. We define the (open) ellipsoid
$f$ is convex. Examples of toric domains which are both convex and concave are symplectic (closed) ellipsoids. We define the (open) ellipsoid ![]() $E(a,b) := X_{\Delta (a,b)}$ with
$E(a,b) := X_{\Delta (a,b)}$ with ![]() $0< a\leq b$, where
$0< a\leq b$, where ![]() $\Delta (a,b) := \{0 \le r < a, 0 \le s < b - {br}/{a} \}$. The ball of capacity
$\Delta (a,b) := \{0 \le r < a, 0 \le s < b - {br}/{a} \}$. The ball of capacity ![]() $R$ is denoted by
$R$ is denoted by ![]() $B^4(R) = E(R,R)$. We say that an ellipsoid
$B^4(R) = E(R,R)$. We say that an ellipsoid ![]() $E(a,b)$ is integral if
$E(a,b)$ is integral if ![]() $ {b}/{a} \in \mathbb {N}_{\geq 2}$. The polydisk
$ {b}/{a} \in \mathbb {N}_{\geq 2}$. The polydisk ![]() $P(c,d): = X_{\Box (c,d)}$ with
$P(c,d): = X_{\Box (c,d)}$ with ![]() $0< c \leq d$, where
$0< c \leq d$, where ![]() $\Box (a,b) := \{0 \le r < a, 0 \le s < b\}$. A product Lagrangian torus is a torus
$\Box (a,b) := \{0 \le r < a, 0 \le s < b\}$. A product Lagrangian torus is a torus
Given subsets ![]() $U, V \subset \mathbb {R}^4$ we write
$U, V \subset \mathbb {R}^4$ we write ![]() $\Phi : U \hookrightarrow V$ to mean that there exists a Hamiltonian diffeomorphism
$\Phi : U \hookrightarrow V$ to mean that there exists a Hamiltonian diffeomorphism ![]() $\Phi$ of
$\Phi$ of ![]() $\mathbb {R}^4$ embedding
$\mathbb {R}^4$ embedding ![]() $U$ into
$U$ into ![]() ${\rm int}(V)$. If
${\rm int}(V)$. If ![]() $\Phi$ is not emphasized, we simply denote such an embedding by
$\Phi$ is not emphasized, we simply denote such an embedding by ![]() $U \hookrightarrow V$.
$U \hookrightarrow V$.
We will denote by ![]() ${\mathcal {L}}(X)$ the set of Lagrangian tori in a domain
${\mathcal {L}}(X)$ the set of Lagrangian tori in a domain ![]() $X \subset \mathbb {C}^2$ which are Hamiltonian isotopic in
$X \subset \mathbb {C}^2$ which are Hamiltonian isotopic in ![]() $\mathbb {C}^2$ to a product torus. The space
$\mathbb {C}^2$ to a product torus. The space ![]() ${\mathcal {L}}(X)$ is equipped with the smooth topology.
${\mathcal {L}}(X)$ is equipped with the smooth topology.
2. Introduction
A fundamental problem in symplectic topology is to understand the space of Lagrangian submanifolds, denoted by ![]() ${\mathcal {L}}(X)$, of a given manifold
${\mathcal {L}}(X)$, of a given manifold ![]() $X$, and in particular the action of the Hamiltonian group
$X$, and in particular the action of the Hamiltonian group ![]() ${\rm Ham}(X)$ on
${\rm Ham}(X)$ on ![]() $\mathcal {L}(X)$. We will describe some steps in this direction when the symplectic manifold is a domain in
$\mathcal {L}(X)$. We will describe some steps in this direction when the symplectic manifold is a domain in ![]() $\mathbb {R}^4$, including balls, integral ellipsoids, and polydisks. Our Lagrangian submanifolds are tori, and for simplicity we will restrict attention to those which are Hamiltonian isotopic to a product torus
$\mathbb {R}^4$, including balls, integral ellipsoids, and polydisks. Our Lagrangian submanifolds are tori, and for simplicity we will restrict attention to those which are Hamiltonian isotopic to a product torus ![]() $L(r,s)$ defined in (1). Recall that when
$L(r,s)$ defined in (1). Recall that when ![]() $X = \mathbb {R}^4$ the only known Lagrangian tori which do not fall into this category are Hamiltonian isotopic to scalings of the Chekanov torus, see [Reference Chekanov and SchlenkCS10].
$X = \mathbb {R}^4$ the only known Lagrangian tori which do not fall into this category are Hamiltonian isotopic to scalings of the Chekanov torus, see [Reference Chekanov and SchlenkCS10].
The Lagrangian tori in a given domain ![]() $X$ are described up to Hamiltonian diffeomorphism in
$X$ are described up to Hamiltonian diffeomorphism in ![]() $\mathbb {R}^4$ by the (Hamiltonian) shape invariant
$\mathbb {R}^4$ by the (Hamiltonian) shape invariant
The study of the shape invariant was initiated by Eliashberg in [Reference EliashbergEli91]. Note that ![]() ${\rm Sh}_{H}(X)$ contains strictly more information than the possible area classes of embedded Lagrangian tori (which we simply called the shape invariant in [Reference Hind and ZhangHZ21]). Indeed the product tori
${\rm Sh}_{H}(X)$ contains strictly more information than the possible area classes of embedded Lagrangian tori (which we simply called the shape invariant in [Reference Hind and ZhangHZ21]). Indeed the product tori ![]() $L(1,2)$ and
$L(1,2)$ and ![]() $L(2,3)$ have integral Maslov
$L(2,3)$ have integral Maslov ![]() $2$ bases with the same area classes, but as stated in Theorem 2.1,
$2$ bases with the same area classes, but as stated in Theorem 2.1, ![]() $L(1,2) \hookrightarrow B(3+\epsilon )$ for any arbitrarily small
$L(1,2) \hookrightarrow B(3+\epsilon )$ for any arbitrarily small ![]() $\epsilon >0$ while there is no such embedding from
$\epsilon >0$ while there is no such embedding from ![]() $L(2,3)$.
$L(2,3)$.
It is often convenient to work with the reduced Hamiltonian shape invariant denoted by ![]() ${\rm Sh}_{H}^+(X) := {\rm Sh}_{H}(X) \cap {\{r \leq s\}}$. As examples, the Hamiltonian shape invariants of balls
${\rm Sh}_{H}^+(X) := {\rm Sh}_{H}(X) \cap {\{r \leq s\}}$. As examples, the Hamiltonian shape invariants of balls ![]() $B^4(R)$ and polydisks
$B^4(R)$ and polydisks ![]() $P(c,d)$ were worked out by the first author and Opshtein in [Reference Hind and OpshteinHO20], and the current authors computed the Hamiltonian shape invariant of integral ellipsoids in Theorem 1.8 in [Reference Hind and ZhangHZ21].
$P(c,d)$ were worked out by the first author and Opshtein in [Reference Hind and OpshteinHO20], and the current authors computed the Hamiltonian shape invariant of integral ellipsoids in Theorem 1.8 in [Reference Hind and ZhangHZ21].
Theorem 2.1 [Reference Hind and OpshteinHO20, Reference Hind and ZhangHZ21]
We have the following computations of the reduced Hamiltonian shape invariants.
(i) When
 $X = B^4(R)$,
$X = B^4(R)$,
 \[ {\rm Sh}_{H}^+(B^4(R)) = \bigg\{ (r,s) \in \mathbb{R}_{>0}^2 \, \bigg| \, r+s < R \mbox{ or } r < \frac{R}{3} \bigg\} \cap \{r \leq s\}. \]
\[ {\rm Sh}_{H}^+(B^4(R)) = \bigg\{ (r,s) \in \mathbb{R}_{>0}^2 \, \bigg| \, r+s < R \mbox{ or } r < \frac{R}{3} \bigg\} \cap \{r \leq s\}. \]
(ii) When
 $X = E(a,b)$ with
$X = E(a,b)$ with  $ {b}/{a} \in \mathbb {N}_{\geq 2}$,
$ {b}/{a} \in \mathbb {N}_{\geq 2}$,
 \[ {\rm Sh}_{H}^+(E(a,b)) =\bigg\{ (r,s) \in \mathbb{R}_{>0}^2 \, \bigg| \, \frac{r}{a} + \frac{s}{b} <1 \mbox{ or } r < \frac{a}{2} \bigg\} \cap \{r \leq s\}. \]
\[ {\rm Sh}_{H}^+(E(a,b)) =\bigg\{ (r,s) \in \mathbb{R}_{>0}^2 \, \bigg| \, \frac{r}{a} + \frac{s}{b} <1 \mbox{ or } r < \frac{a}{2} \bigg\} \cap \{r \leq s\}. \]
(iii) When
 $X = P(c,d)$ with
$X = P(c,d)$ with  $0< c \leq d$,
$0< c \leq d$,
 \[ {\rm Sh}_{H}^+(P(c,d)) = \bigg\{ (r,s) \in \mathbb{R}_{>0}^2 \, \bigg| \, \begin{array}{l} r< c\\ s< d \end{array} \mbox{ or } r < \frac{c}{2}\bigg\}\cap \{r \leq s\}. \]
\[ {\rm Sh}_{H}^+(P(c,d)) = \bigg\{ (r,s) \in \mathbb{R}_{>0}^2 \, \bigg| \, \begin{array}{l} r< c\\ s< d \end{array} \mbox{ or } r < \frac{c}{2}\bigg\}\cap \{r \leq s\}. \]
Remark 2.2 (i) Note that the subsets ![]() ${\rm Sh}_H^+$ of the basic toric domains in Theorem 2.1 are all formed, modulo the intersection with
${\rm Sh}_H^+$ of the basic toric domains in Theorem 2.1 are all formed, modulo the intersection with ![]() $\{r \leq s\}$, by the moment image
$\{r \leq s\}$, by the moment image ![]() $\mu (X)$ plus a vertical long strip.
$\mu (X)$ plus a vertical long strip.
(ii) The proof of statement (ii) in Theorem 2.1 utilized some results from Siegel [Reference SiegelSie22]; the results in the current paper are independent of Theorem 2.1.
2.1 Hamiltonian knottedness
There exists a Hamiltonian diffeomorphism of ![]() $\mathbb {R}^4$ mapping
$\mathbb {R}^4$ mapping ![]() $L(r,s)$ onto
$L(r,s)$ onto ![]() $L(r', s')$ if and only if
$L(r', s')$ if and only if ![]() $\{r,s\} = \{r', s'\}$, see [Reference ChekanovChe96]. Hence, there is a well-defined projection map
$\{r,s\} = \{r', s'\}$, see [Reference ChekanovChe96]. Hence, there is a well-defined projection map
mapping a Lagrangian torus in ![]() $L \in {\mathcal {L}}(X)$ to the unique
$L \in {\mathcal {L}}(X)$ to the unique ![]() $(r,s)$ such that
$(r,s)$ such that ![]() $r \le s$ and
$r \le s$ and ![]() $L$ is Hamiltonian isotopic to
$L$ is Hamiltonian isotopic to ![]() $L(r,s)$.
$L(r,s)$.
This map is continuous. Indeed, by Weinstein's neighborhood theorem, a sequence of Lagrangians ![]() $L_n \to L$ in
$L_n \to L$ in ![]() $\mathcal {L}(X)$ can be thought of as sections of
$\mathcal {L}(X)$ can be thought of as sections of ![]() $T^* L$ or, up to a Hamiltonian diffeomorphism, as sections of the normal bundle
$T^* L$ or, up to a Hamiltonian diffeomorphism, as sections of the normal bundle ![]() $T^* L(r,s)$ of a product torus, where
$T^* L(r,s)$ of a product torus, where ![]() $\mathcal {P}(L)=(r,s)$. Such sections are Hamiltonian isotopic to constant sections, which correspond to
$\mathcal {P}(L)=(r,s)$. Such sections are Hamiltonian isotopic to constant sections, which correspond to ![]() $L(r_n,s_n)$, for
$L(r_n,s_n)$, for ![]() $(r_n, s_n)$ converging to
$(r_n, s_n)$ converging to ![]() $(r,s)$.
$(r,s)$.
The Hamiltonian diffeomorphism group ![]() ${\rm Ham}(X)$ acts on
${\rm Ham}(X)$ acts on ![]() ${\mathcal {L}}(X)$ and preserves the fibers of
${\mathcal {L}}(X)$ and preserves the fibers of ![]() $\mathcal {P}$. Paths in a fiber correspond to Lagrangian isotopies with a fixed area class
$\mathcal {P}$. Paths in a fiber correspond to Lagrangian isotopies with a fixed area class ![]() $(r,s) \in {\rm Sh}_{H}^+(X)$, and these are realized by a Hamiltonian isotopy in
$(r,s) \in {\rm Sh}_{H}^+(X)$, and these are realized by a Hamiltonian isotopy in ![]() $X$, see Theorem 0.4.2 in [Reference ChaperonCha83]. Hence, path connected components of the fibers are precisely the orbits of
$X$, see Theorem 0.4.2 in [Reference ChaperonCha83]. Hence, path connected components of the fibers are precisely the orbits of ![]() ${\rm Ham}(X)$, and if a fiber over a point
${\rm Ham}(X)$, and if a fiber over a point ![]() $(r,s)$ happens to be disconnected, then we have embeddings
$(r,s)$ happens to be disconnected, then we have embeddings ![]() $L(r,s) \hookrightarrow X$ which are not Hamiltonian isotopic in
$L(r,s) \hookrightarrow X$ which are not Hamiltonian isotopic in ![]() $X$. This motivates the following definition.
$X$. This motivates the following definition.
Definition 2.3 Suppose the product Lagrangian torus ![]() $L(r,s)$ embeds into
$L(r,s)$ embeds into ![]() $X$ by inclusion, i.e.
$X$ by inclusion, i.e. ![]() $(r,s) \in \mu (X)$. Then we call an embedded Lagrangian torus in
$(r,s) \in \mu (X)$. Then we call an embedded Lagrangian torus in ![]() $X$ unknotted if it is in the same component as
$X$ unknotted if it is in the same component as ![]() $L(r,s)$, and knotted if it lies in another component.
$L(r,s)$, and knotted if it lies in another component.
More explicitly, if ![]() $L(r,s) \subset X$, then an embedded Lagrangian torus
$L(r,s) \subset X$, then an embedded Lagrangian torus ![]() $L \in \mathcal {P}^{-1}((r,s))$ is unknotted if there exists a Hamiltonian isotopy in
$L \in \mathcal {P}^{-1}((r,s))$ is unknotted if there exists a Hamiltonian isotopy in ![]() ${\boldsymbol X}$, denoted by
${\boldsymbol X}$, denoted by ![]() $\{\Phi _t\}_{t \in [0,1]}$, such that
$\{\Phi _t\}_{t \in [0,1]}$, such that ![]() $\Phi _0 = {\mathbb 1}_X$ and
$\Phi _0 = {\mathbb 1}_X$ and ![]() $\Phi _1(L) = L(r,s)$. Note that, for
$\Phi _1(L) = L(r,s)$. Note that, for ![]() $(r,s)$ with
$(r,s)$ with ![]() $r \neq s$, even though all Lagrangian tori in the fiber
$r \neq s$, even though all Lagrangian tori in the fiber ![]() $\mathcal {P}^{-1}((r,s))$ are conjectured to be Hamiltonian isotopic in
$\mathcal {P}^{-1}((r,s))$ are conjectured to be Hamiltonian isotopic in ![]() $\mathbb {R}^4$, they are not necessarily Hamiltonian isotopic in
$\mathbb {R}^4$, they are not necessarily Hamiltonian isotopic in ![]() $X$. In other words, the action of
$X$. In other words, the action of ![]() ${\rm Ham}(X)$ on a fiber of
${\rm Ham}(X)$ on a fiber of ![]() $\mathcal {P}$ may not be transitive.
$\mathcal {P}$ may not be transitive.
Remark 2.4 The (un)knottedness defined in Definition 2.3 is identical to that for symplectic embeddings discussed in [Reference McDuffMcD91, Reference McDuffMcD09, Reference Cristofaro-GardinerCG19, Reference Gutt and UsherGU19].
Our first result says that for some basic domains many fibers of the projection ![]() $\mathcal {P}$ are indeed disconnected, so knotted Lagrangian tori are quite common.
$\mathcal {P}$ are indeed disconnected, so knotted Lagrangian tori are quite common.
Theorem 2.5 Let ![]() $X=B^4(R)$. Then for any area classes
$X=B^4(R)$. Then for any area classes
there exist knotted Lagrangian tori in the fiber ![]() $\mathcal {P}^{-1}((r,s))$.
$\mathcal {P}^{-1}((r,s))$.
Theorem 2.6 Let ![]() $X=E(a,b)$ with
$X=E(a,b)$ with ![]() $k: = {b}/{a} \in \mathbb {N}_{\ge 2}$. Then for any area classes
$k: = {b}/{a} \in \mathbb {N}_{\ge 2}$. Then for any area classes
there exist knotted Lagrangian tori in the fiber ![]() $\mathcal {P}^{-1}((r,s))$.
$\mathcal {P}^{-1}((r,s))$.
Theorem 2.7 Let ![]() $X= P(c,d)$. Then for any area classes
$X= P(c,d)$. Then for any area classes
there exist knotted Lagrangian tori in the fiber ![]() $\mathcal {P}^{-1}((r,s))$.
$\mathcal {P}^{-1}((r,s))$.
The shaded parts in Figure 1 illustrate those regions claimed in Theorems 2.5, 2.6, and 2.7, respectively, where there exist knotted Lagrangian tori. Their proofs will be given in § 5.3. In fact, these results quickly follow from the path lifting properties that are systematically studied in § 2.2.

Figure 1. Regions that admit knotted Lagrangian tori.
We remark that knotted Lagrangian tori in the ball were originally constructed by Vianna [Reference ViannaVia14]. The exotic Lagrangian torus constructed by Chekanov [Reference ChekanovChe96] is not considered here as is it not Hamiltonian isotopic to a product torus in ![]() $\mathbb {C}^2$.
$\mathbb {C}^2$.
Detecting Hamiltonian knotted Lagrangian tori has connections to symplectic embeddings, and sometimes we can detect more knotted Lagrangian tori in both ![]() $E(a,b)$ and
$E(a,b)$ and ![]() $B^4(R)$ by using our path lifting results together with the existence of symplectic embeddings. We will discuss this in detail in § 2.3.
$B^4(R)$ by using our path lifting results together with the existence of symplectic embeddings. We will discuss this in detail in § 2.3.
It is also interesting to study Lagrangian knottedness in closed symplectic manifolds. In our case, we show that the knotted Lagrangians in the ball described by Theorem 2.5 are still not Hamiltonian isotopic to the corresponding product in the compactification ![]() $\mathbb {C} P^2$. Here we view
$\mathbb {C} P^2$. Here we view ![]() $\mathbb {C} P^2$ as the union of the ball
$\mathbb {C} P^2$ as the union of the ball ![]() $B(R)$ and the line at infinity, which is a symplectic sphere of area
$B(R)$ and the line at infinity, which is a symplectic sphere of area ![]() $R$. Thus, we can strengthen Theorem 2.5 as follows.
$R$. Thus, we can strengthen Theorem 2.5 as follows.
Theorem 2.8 For any point ![]() $(r,s)$ in (4), there exists a Lagrangian torus
$(r,s)$ in (4), there exists a Lagrangian torus ![]() $L \subset B^4(R) \subset \mathbb {C} P^2$ such that:
$L \subset B^4(R) \subset \mathbb {C} P^2$ such that:
(i)
 $\mathcal {P}(L) = (r,s)$;
$\mathcal {P}(L) = (r,s)$;(ii)
 $L$ is not Hamiltonian isotopic to
$L$ is not Hamiltonian isotopic to  $L(r,s)$ in
$L(r,s)$ in  $\mathbb {C} P^2$.
$\mathbb {C} P^2$.
We remark that Theorem 2.8 does not exclude the possibility that ![]() $L$ is isotopic to another product torus in
$L$ is isotopic to another product torus in ![]() $\mathbb {C} P^2$. Indeed, according to [Reference Shelukhin, Tonkonog and ViannaSTV18], § 7, it is plausible to conjecture that almost all Lagrangian tori in
$\mathbb {C} P^2$. Indeed, according to [Reference Shelukhin, Tonkonog and ViannaSTV18], § 7, it is plausible to conjecture that almost all Lagrangian tori in ![]() $\mathbb {C} P^2$ are Hamiltonian isotopic to product tori.
$\mathbb {C} P^2$ are Hamiltonian isotopic to product tori.
2.2 Path lifting
The main results in § 2.1 are consequences of a novel analysis of the path lifting problem of the projection ![]() $\mathcal {P}$. To start, let us give the following key definition.
$\mathcal {P}$. To start, let us give the following key definition.
Definition 2.9 A smooth path ![]() $\gamma : [0,T] \to {\rm Sh}_{H}^+(X)$ where
$\gamma : [0,T] \to {\rm Sh}_{H}^+(X)$ where ![]() $\gamma (0)=(r_0, s_0)$ lifts to
$\gamma (0)=(r_0, s_0)$ lifts to ![]() ${\mathcal {L}}(X)$ if there exists a smooth family of embedded Lagrangian tori in
${\mathcal {L}}(X)$ if there exists a smooth family of embedded Lagrangian tori in ![]() $X$, denoted by
$X$, denoted by ![]() $\{L_t\}_{t \in [0,T]}$, with
$\{L_t\}_{t \in [0,T]}$, with ![]() $\mathcal {P}(L_t) = \gamma (t)$ and
$\mathcal {P}(L_t) = \gamma (t)$ and ![]() $L_0 = L(r_0, s_0)$.
$L_0 = L(r_0, s_0)$.
In other words, unless stated otherwise, we will always assume our lifts start from an inclusion, and so a necessary condition for a lift is that ![]() $\gamma (0) \in \mu (X)$. In addition, denote by
$\gamma (0) \in \mu (X)$. In addition, denote by ![]() $\mu (X)^+ : = \mu (X) \cap \{r\leq s\}$.
$\mu (X)^+ : = \mu (X) \cap \{r\leq s\}$.
Example 2.10 For any smooth path ![]() $\gamma : [0,T] \to \mu (X)^+ \subset {\rm Sh}_{H}^+(X)$, it lifts to
$\gamma : [0,T] \to \mu (X)^+ \subset {\rm Sh}_{H}^+(X)$, it lifts to ![]() ${\mathcal {L}}(X)$ since one can consider the family of product Lagrangian tori
${\mathcal {L}}(X)$ since one can consider the family of product Lagrangian tori ![]() $\{L(r_t, s_t)\}_{t \in [0,T]}$ with area classes smoothly changing along
$\{L(r_t, s_t)\}_{t \in [0,T]}$ with area classes smoothly changing along ![]() $\gamma$.
$\gamma$.
We call any path in Example 2.10 a Type-I path, and any other path in ![]() ${\rm Sh}_{H}^+(X)$ starting in
${\rm Sh}_{H}^+(X)$ starting in ![]() $\mu (X)^+$ a Type-II path. We will elaborate on the subtlety of this path lifting from the following three perspectives, with more details given in § 7.
$\mu (X)^+$ a Type-II path. We will elaborate on the subtlety of this path lifting from the following three perspectives, with more details given in § 7.
(1) (Concatenation) One can build up a path that lifts to
 $\mathcal {L}(X)$ via a series of concatenations of multiple sub-paths in either Type-I or Type-II, see Corollary 5.6 and also the left picture in Figure 18.
$\mathcal {L}(X)$ via a series of concatenations of multiple sub-paths in either Type-I or Type-II, see Corollary 5.6 and also the left picture in Figure 18.(2) (Non-uniqueness) The path liftings are not unique. There exist paths
 $\gamma$ having two lifts
$\gamma$ having two lifts  $\{L_t\}_{t \in [0,T]}$ and
$\{L_t\}_{t \in [0,T]}$ and  $\{L'_t\}_{t \in [0, T]}$ such that
$\{L'_t\}_{t \in [0, T]}$ such that  $L_T$ and
$L_T$ and  $L'_T$ lie in different components of the fiber over
$L'_T$ lie in different components of the fiber over  $\gamma (T)$, see Remark 5.7.
$\gamma (T)$, see Remark 5.7.(3) (Orientation) Again, the right picture in Figure 18 shows that there exist paths with
 $\gamma (0), \gamma (T) \in \mu (X)$ such that
$\gamma (0), \gamma (T) \in \mu (X)$ such that  $\gamma$ lifts but its reserve
$\gamma$ lifts but its reserve  $\overline {\gamma }: = \{\gamma (T-t)\}_{t \in [0,T]}$ does not lift.
$\overline {\gamma }: = \{\gamma (T-t)\}_{t \in [0,T]}$ does not lift.
Next, we give both necessary and sufficient conditions (unfortunately not quite the same) for paths in the reduced (Hamiltonian) shape invariant of balls, integral ellipsoids, and polydisks to lift. For simplicity, we will state the results only for certain Type-II paths. More general paths can be considered via concatenations mentioned previously (see Corollary 5.6).
Theorem 2.11 (Path lifting for  $B^4(R)$)
$B^4(R)$)
Let ![]() $\gamma = \{\gamma (t)\}_{t \in [0,T]}$ be a path in
$\gamma = \{\gamma (t)\}_{t \in [0,T]}$ be a path in ![]() ${\rm Sh}_H^+(B^4(R))$ with
${\rm Sh}_H^+(B^4(R))$ with ![]() $\gamma (0) \in \mu (B^4(R))^+$ but
$\gamma (0) \in \mu (B^4(R))^+$ but ![]() $\gamma (T) \notin \mu (B^4(R))^+$. Denote
$\gamma (T) \notin \mu (B^4(R))^+$. Denote ![]() $\gamma (t) = (r_t, s_t)$, then we have the following conclusions.
$\gamma (t) = (r_t, s_t)$, then we have the following conclusions.
(I) If
 $ {r_t}/{s_t}$ is non-increasing and
$ {r_t}/{s_t}$ is non-increasing and  $2r_t + s_t \geq R$ for all
$2r_t + s_t \geq R$ for all  $t \in [0, T]$, then
$t \in [0, T]$, then  $\gamma$ does not lift to
$\gamma$ does not lift to  ${\mathcal {L}}(B^4(R))$.
${\mathcal {L}}(B^4(R))$.(II) The path
 $\gamma$ does lift to
$\gamma$ does lift to  ${\mathcal {L}}(B^4(R))$ if there exists a
${\mathcal {L}}(B^4(R))$ if there exists a  $t_*$ with
$t_*$ with  $0 \le t_* \le T$ satisfying:
$0 \le t_* \le T$ satisfying:
(i)
 $\gamma |_{[0, t_*]} \in \mu (B^4(R))^+$;
$\gamma |_{[0, t_*]} \in \mu (B^4(R))^+$;(ii)
 $2r_{t_*} + s_{t_*} < R$;
$2r_{t_*} + s_{t_*} < R$;(iii)
 $0< r_t < {R}/{3}$ for any
$0< r_t < {R}/{3}$ for any  $t \in [t_*,T]$.
$t \in [t_*,T]$.
Theorem 2.12 (Path lifting for integral  $E(a,b)$)
$E(a,b)$)
Let ![]() $\gamma = \{\gamma (t)\}_{t \in [0,T]}$ be a path in
$\gamma = \{\gamma (t)\}_{t \in [0,T]}$ be a path in ![]() ${\rm Sh}_H^+(E(a,b))$ with
${\rm Sh}_H^+(E(a,b))$ with ![]() $k: = {b}/{a} \in \mathbb {N}_{\geq 2}$,
$k: = {b}/{a} \in \mathbb {N}_{\geq 2}$, ![]() $\gamma (0) \in \mu (E(a,b))^+$ but
$\gamma (0) \in \mu (E(a,b))^+$ but ![]() $\gamma (T) \notin \mu (E(a,b))^+$. Denote
$\gamma (T) \notin \mu (E(a,b))^+$. Denote ![]() $\gamma (t) = (r_t, s_t)$, then we have the following conclusions.
$\gamma (t) = (r_t, s_t)$, then we have the following conclusions.
(I) If
 $ {r_t}/{s_t}$ is non-increasing and
$ {r_t}/{s_t}$ is non-increasing and  $(k+1)r_t + s_t \geq b$ for all
$(k+1)r_t + s_t \geq b$ for all  $t \in [0,T]$, then
$t \in [0,T]$, then  $\gamma$ does not lift to
$\gamma$ does not lift to  ${\mathcal {L}}(E(a,b))$.
${\mathcal {L}}(E(a,b))$.(II) The path
 $\gamma$ does lift to
$\gamma$ does lift to  ${\mathcal {L}}(E(a,b))$ if there exists a
${\mathcal {L}}(E(a,b))$ if there exists a  $t_*$ with
$t_*$ with  $0 \le t_* \le T$ satisfying:
$0 \le t_* \le T$ satisfying:
(i)
 $\gamma |_{[0, t_*]} \in \mu (E(a,b))^+$;
$\gamma |_{[0, t_*]} \in \mu (E(a,b))^+$;(ii) either one of the following conditions holds,
(1)
 $(k-1) r_{t_*} \leq s_{t_*}$ and
$(k-1) r_{t_*} \leq s_{t_*}$ and  $(k+1)r_{t_*} + s_{t_*} < b$, or
$(k+1)r_{t_*} + s_{t_*} < b$, or(2)
 $(k-1) r_{t_*} > s_{t_*}$ and
$(k-1) r_{t_*} > s_{t_*}$ and  $0< r_{t_*}< {a}/{2}$;
$0< r_{t_*}< {a}/{2}$;
(iii)
 $0< r_{t}< {a}/{2}$ for all
$0< r_{t}< {a}/{2}$ for all  $t \in [t_*,T]$.
$t \in [t_*,T]$.
Theorem 2.13 (Path lifting for  $P(c,d)$)
$P(c,d)$)
Let ![]() $\gamma = \{\gamma (t)\}_{t \in [0,T]}$ be a path in
$\gamma = \{\gamma (t)\}_{t \in [0,T]}$ be a path in ![]() ${\rm Sh}_H^+(P(c,d))$ with
${\rm Sh}_H^+(P(c,d))$ with ![]() $\gamma (0) \in \mu (P(c,d))^+$ but
$\gamma (0) \in \mu (P(c,d))^+$ but ![]() $\gamma (T) \notin \mu (P(c,d))^+$. Denote
$\gamma (T) \notin \mu (P(c,d))^+$. Denote ![]() $\gamma (t) = (r_t, s_t)$, then we have the following conclusions.
$\gamma (t) = (r_t, s_t)$, then we have the following conclusions.
(I) If
 $ {r_t}/{s_t}$ is non-increasing and
$ {r_t}/{s_t}$ is non-increasing and  $r_t + s_t \geq d$ for all
$r_t + s_t \geq d$ for all  $t \in [0, T]$, then
$t \in [0, T]$, then  $\gamma$ does not lift to
$\gamma$ does not lift to  ${\mathcal {L}}(P(c,d))$.
${\mathcal {L}}(P(c,d))$.(II) The path
 $\gamma$ does lift to
$\gamma$ does lift to  ${\mathcal {L}}(P(c,d))$ if there exists a
${\mathcal {L}}(P(c,d))$ if there exists a  $t_*$ with
$t_*$ with  $0 \le t_* \le T$ satisfying:
$0 \le t_* \le T$ satisfying:
(i)
 $\gamma |_{[0, t_*]} \in \mu (P(c,d))^+$;
$\gamma |_{[0, t_*]} \in \mu (P(c,d))^+$;(ii)
 $r_{t_*} + s_{t_*} < d$;
$r_{t_*} + s_{t_*} < d$;(iii)
 $0< r_t < {c}/{2}$ for any
$0< r_t < {c}/{2}$ for any  $t \in [t_*,T]$.
$t \in [t_*,T]$.
Example 2.14 (1) The left picture in Figure 2 shows a path ![]() $\gamma _1$ that does not lift to
$\gamma _1$ that does not lift to ![]() $\mathcal {L}(B^4(R))$, while the right-hand side shows a path
$\mathcal {L}(B^4(R))$, while the right-hand side shows a path ![]() $\gamma _2$ that does lift. This is implied by Theorem 2.11.
$\gamma _2$ that does lift. This is implied by Theorem 2.11.

Figure 2. Path ![]() $\gamma _1$ does not lift to
$\gamma _1$ does not lift to ![]() $\mathcal {L}(B^4(R))$ but
$\mathcal {L}(B^4(R))$ but ![]() $\gamma _2$ does lift.
$\gamma _2$ does lift.
(2) The left picture in Figure 3 shows a path ![]() $\gamma _1$ that does not lift to
$\gamma _1$ that does not lift to ![]() $\mathcal {L}(E(a,b))$, while the right-hand side shows a path
$\mathcal {L}(E(a,b))$, while the right-hand side shows a path ![]() $\gamma _2$ that does lift. This is implied by Theorem 2.12. In particular, for path
$\gamma _2$ that does lift. This is implied by Theorem 2.12. In particular, for path ![]() $\gamma _2$, condition (II-ii-2) of Theorem 2.12 applies.
$\gamma _2$, condition (II-ii-2) of Theorem 2.12 applies.

Figure 3. Path ![]() $\gamma _1$ does not lift to
$\gamma _1$ does not lift to ![]() $\mathcal {L}(E(a,b))$ but
$\mathcal {L}(E(a,b))$ but ![]() $\gamma _2$ does lift.
$\gamma _2$ does lift.
(3) The left picture in Figure 4 shows a path ![]() $\gamma _1$ that does not lift to
$\gamma _1$ that does not lift to ![]() $\mathcal {L}(P(c,d))$, while the right-hand side shows a path
$\mathcal {L}(P(c,d))$, while the right-hand side shows a path ![]() $\gamma _2$ that does lift. This is implied by Theorem 2.13.
$\gamma _2$ that does lift. This is implied by Theorem 2.13.

Figure 4. Path ![]() $\gamma _1$ does not lift to
$\gamma _1$ does not lift to ![]() $\mathcal {L}(P(c,d))$ but
$\mathcal {L}(P(c,d))$ but ![]() $\gamma _2$ does lift.
$\gamma _2$ does lift.
Remark 2.15 In Figure 3, suppose we deform ![]() $\gamma _1$ such that the starting point lies in the shaded region, the endpoint is unchanged, and the new
$\gamma _1$ such that the starting point lies in the shaded region, the endpoint is unchanged, and the new ![]() $\gamma _1$ intersects
$\gamma _1$ intersects ![]() $\{(k+1)r + s < b\}$ only in the shaded region. Then Theorem 2.12 is not strong enough to determine whether this path lifts or not. Indeed, such a
$\{(k+1)r + s < b\}$ only in the shaded region. Then Theorem 2.12 is not strong enough to determine whether this path lifts or not. Indeed, such a ![]() $\gamma _1$ does not satisfy condition (I) in Theorem 2.12 since the new starting point lies below the line
$\gamma _1$ does not satisfy condition (I) in Theorem 2.12 since the new starting point lies below the line ![]() $(k+1)r + s = b$. But the new
$(k+1)r + s = b$. But the new ![]() $\gamma _1$ does not satisfy condition (II) in Theorem 2.12 either, since there exist no
$\gamma _1$ does not satisfy condition (II) in Theorem 2.12 either, since there exist no ![]() $(r_{t_*}, s_{t_*})$ on the new
$(r_{t_*}, s_{t_*})$ on the new ![]() $\gamma _1$ which lie in the region described by condition (II-ii) in Theorem 2.12.
$\gamma _1$ which lie in the region described by condition (II-ii) in Theorem 2.12.
The obstructions (I) in Theorems 2.11 and 2.12 can be viewed as a single result (where for the case ![]() $B^4(R)$, we set
$B^4(R)$, we set ![]() $k = 1$) and it will be proved in § 4.2; obstruction (I) in Theorem 2.13 has a similar proof, given in § 4.3. Results (II) in Theorems 2.11, 2.12, and 2.13, which will be proved in § 5.2, are consequences of a general path lifting criterion that works for any toric domains in
$k = 1$) and it will be proved in § 4.2; obstruction (I) in Theorem 2.13 has a similar proof, given in § 4.3. Results (II) in Theorems 2.11, 2.12, and 2.13, which will be proved in § 5.2, are consequences of a general path lifting criterion that works for any toric domains in ![]() $\mathbb {R}^4$, see Corollary 5.6 in § 5.1.
$\mathbb {R}^4$, see Corollary 5.6 in § 5.1.
2.3 Symplectic embeddings
If there exists a Hamiltonian diffeomorphism ![]() $f:X \hookrightarrow Y$, then we have
$f:X \hookrightarrow Y$, then we have ![]() ${\rm Sh}_{H}^+(X) \subset {\rm Sh}_{H}^+(Y)$ (see Proposition 7.1 in [Reference Hind and ZhangHZ21]). Given its natural scaling properties, we can therefore think of
${\rm Sh}_{H}^+(X) \subset {\rm Sh}_{H}^+(Y)$ (see Proposition 7.1 in [Reference Hind and ZhangHZ21]). Given its natural scaling properties, we can therefore think of ![]() ${\rm Sh}_{H}^+(X)$ as a kind of set-valued symplectic capacity. For a possible relation between this set-valued symplectic capacity and classical
${\rm Sh}_{H}^+(X)$ as a kind of set-valued symplectic capacity. For a possible relation between this set-valued symplectic capacity and classical ![]() $\mathbb {R}_{\geq 0}$-valued symplectic capacities, see § 1.2.1 in [Reference Hind and ZhangHZ21]. Some resulting obstructions to symplectic embeddings were explored in Theorem 1.6 in [Reference Hind and ZhangHZ21], however at least in the case when
$\mathbb {R}_{\geq 0}$-valued symplectic capacities, see § 1.2.1 in [Reference Hind and ZhangHZ21]. Some resulting obstructions to symplectic embeddings were explored in Theorem 1.6 in [Reference Hind and ZhangHZ21], however at least in the case when ![]() $X$ and
$X$ and ![]() $Y$ are ellipsoids the obstructions turn out to be fairly weak, and are all consequences of Gromov's non-squeezing together with the volume constraint.
$Y$ are ellipsoids the obstructions turn out to be fairly weak, and are all consequences of Gromov's non-squeezing together with the volume constraint.
Now we analyze embedding obstructions coming from shapes from the path lifting perspective. Observe that if ![]() $\gamma :[0,T] \to {\rm Sh}_H^+(X)$ is a path with
$\gamma :[0,T] \to {\rm Sh}_H^+(X)$ is a path with ![]() $\gamma (0) \in \mu (X)^+ \cap \mu (Y)^+$, then, given our symplectic embedding
$\gamma (0) \in \mu (X)^+ \cap \mu (Y)^+$, then, given our symplectic embedding ![]() $\phi : X \hookrightarrow Y$, if
$\phi : X \hookrightarrow Y$, if ![]() $\gamma$ lifts as
$\gamma$ lifts as ![]() $\{L_t\}_{t \in [0,T]}$ to
$\{L_t\}_{t \in [0,T]}$ to ![]() ${\mathcal {L}}(X)$, then
${\mathcal {L}}(X)$, then ![]() $\{\phi (L_t)\}_{t \in [0, T]}$ gives a lift to
$\{\phi (L_t)\}_{t \in [0, T]}$ gives a lift to ![]() ${\mathcal {L}}(Y)$, although this lift to
${\mathcal {L}}(Y)$, although this lift to ![]() ${\mathcal {L}}(Y)$ may not satisfy our usual initial condition, that is,
${\mathcal {L}}(Y)$ may not satisfy our usual initial condition, that is, ![]() $\phi (L_0) = L(\mathcal {P}(\gamma (0)))$, a product torus in
$\phi (L_0) = L(\mathcal {P}(\gamma (0)))$, a product torus in ![]() $Y$. However, applying a Hamiltonian diffeomorphism of
$Y$. However, applying a Hamiltonian diffeomorphism of ![]() $Y$, the initial condition can be satisfied if
$Y$, the initial condition can be satisfied if ![]() $\phi (L_0)$ is unknotted in
$\phi (L_0)$ is unknotted in ![]() $Y$. Hence, we produce either examples of knotted Lagrangian tori in
$Y$. Hence, we produce either examples of knotted Lagrangian tori in ![]() $Y$ or potentially stronger embedding obstructions from
$Y$ or potentially stronger embedding obstructions from ![]() $X$ to
$X$ to ![]() $Y$. We have several consequences in these two directions.
$Y$. We have several consequences in these two directions.
2.3.1 Detecting knotted Lagrangian tori
The following result provides another approach (cf. Theorems 2.5, 2.6, and 2.7) to detect knotted Lagrangian tori. It will be proved in § 8.1.
Theorem 2.16 We can detect knotted Lagrangian tori in the following three cases.
(1) Suppose there exists a symplectic embedding
 $\phi :E(1,x) \hookrightarrow B^4(R)$ for
$\phi :E(1,x) \hookrightarrow B^4(R)$ for  $1< R< x$. If
$1< R< x$. If  $(r,s) \in \mu (E(1,x))^+ \cap \mu (B^4(R))^+$ with
$(r,s) \in \mu (E(1,x))^+ \cap \mu (B^4(R))^+$ with  $2r+s >R$, then the embedded Lagrangian torus
$2r+s >R$, then the embedded Lagrangian torus  $\phi (L(r,s))$ is knotted in the fiber
$\phi (L(r,s))$ is knotted in the fiber  $\mathcal {P}^{-1}((r,s))$ of
$\mathcal {P}^{-1}((r,s))$ of  $B^4(R)$.
$B^4(R)$.(2) Suppose there exists a symplectic embedding
 $\phi :E(1,x) \hookrightarrow E(a,b)$ for
$\phi :E(1,x) \hookrightarrow E(a,b)$ for  $1< a < b=ka < x$ with
$1< a < b=ka < x$ with  $k \in \mathbb {N}_{\ge 2}$. If
$k \in \mathbb {N}_{\ge 2}$. If  $(r,s) \in \mu (E(1,x))^+ \cap \mu (E(a,b))^+$ with
$(r,s) \in \mu (E(1,x))^+ \cap \mu (E(a,b))^+$ with  $(k+1)r+s > b$, then the embedded Lagrangian torus
$(k+1)r+s > b$, then the embedded Lagrangian torus  $\phi (L(r,s))$ is knotted in the fiber
$\phi (L(r,s))$ is knotted in the fiber  $\mathcal {P}^{-1}((r,s))$ of
$\mathcal {P}^{-1}((r,s))$ of  $E(a,b)$.
$E(a,b)$.(3) Suppose there exists a symplectic embedding
 $\phi :E(1,x) \hookrightarrow P(c,d)$ for
$\phi :E(1,x) \hookrightarrow P(c,d)$ for  $1< c < d < x$. If
$1< c < d < x$. If  $(r,s) \in \mu (E(1,x))^+ \cap \mu (P(c,d))^+$ with
$(r,s) \in \mu (E(1,x))^+ \cap \mu (P(c,d))^+$ with  $r+s > d$, then the embedded Lagrangian torus
$r+s > d$, then the embedded Lagrangian torus  $\phi (L(r,s))$ is knotted in the fiber
$\phi (L(r,s))$ is knotted in the fiber  $\mathcal {P}^{-1}((r,s))$ of
$\mathcal {P}^{-1}((r,s))$ of  $P(c,d)$.
$P(c,d)$.
We emphasize that the knotted Lagrangian tori produced by Theorems 2.5, 2.6, and 2.7 are actually subsets of those which follow from Theorem 2.16 together with symplectic embedding results. In what follows, we provide examples to support this. One can quickly see the difference by comparing Figure 1 with Figures 5 and 6. In particular, we produce knotted Lagrangian tori with area class ![]() $(r,s)$ such that
$(r,s)$ such that ![]() $r> {R}/{3}$,
$r> {R}/{3}$, ![]() $r > {a}/{2}$, and
$r > {a}/{2}$, and ![]() $r > {c}/{2}$, respectively, in the examples below. To obtain this enhancement we require information about symplectic embeddings, while the knotted Lagrangian tori in Theorems 2.5, 2.6, and 2.7 are detected directly via the path lifting properties.
$r > {c}/{2}$, respectively, in the examples below. To obtain this enhancement we require information about symplectic embeddings, while the knotted Lagrangian tori in Theorems 2.5, 2.6, and 2.7 are detected directly via the path lifting properties.
Remark 2.17 We remark that since the ![]() $\phi$ in Theorem 2.16 are defined on ellipsoids, the knotted embedded tori
$\phi$ in Theorem 2.16 are defined on ellipsoids, the knotted embedded tori ![]() $\phi (L(r,s))$ extend to embedded polydisks
$\phi (L(r,s))$ extend to embedded polydisks ![]() $\phi (P(r,s))$, which of course must also be knotted.
$\phi (P(r,s))$, which of course must also be knotted.

Figure 5. Knotted Lagrangian tori in ![]() $B(2)$ and
$B(2)$ and ![]() $E(a,b)$ lie in the shaded regions.
$E(a,b)$ lie in the shaded regions.

Figure 6. Knotted Lagrangian tori in ![]() $P(1,2)$ lie in the shaded region.
$P(1,2)$ lie in the shaded region.
Example 2.18 (1) Let ![]() $\phi : E(1,4) \hookrightarrow B^4(2)$ be a symplectic embedding. We know such an embedding exists, see [Reference OpshteinOps07, Reference McDuff and SchlenkMcDS12]. Any
$\phi : E(1,4) \hookrightarrow B^4(2)$ be a symplectic embedding. We know such an embedding exists, see [Reference OpshteinOps07, Reference McDuff and SchlenkMcDS12]. Any ![]() $(r,s)$ in the shaded region in the left picture of Figure 5 satisfies criterion (1) of Theorem 2.16. Therefore,
$(r,s)$ in the shaded region in the left picture of Figure 5 satisfies criterion (1) of Theorem 2.16. Therefore, ![]() $\phi (L(r,s))$ is knotted in the fiber
$\phi (L(r,s))$ is knotted in the fiber ![]() $\mathcal {P}^{-1}((r,s))$ of
$\mathcal {P}^{-1}((r,s))$ of ![]() $B^4(2)$.
$B^4(2)$.
(2) Now let ![]() $k \in \mathbb {N}_{\ge 2}$ and consider a symplectic embedding
$k \in \mathbb {N}_{\ge 2}$ and consider a symplectic embedding ![]() $\phi : E({ka}/({k+1}), (k+1)a) \hookrightarrow E(a,b)$. We verify in Appendix A that such embeddings do exist. Then, by Theorem 2.16(2) we see that
$\phi : E({ka}/({k+1}), (k+1)a) \hookrightarrow E(a,b)$. We verify in Appendix A that such embeddings do exist. Then, by Theorem 2.16(2) we see that ![]() $\phi (L(r,s))$ is knotted in the fiber
$\phi (L(r,s))$ is knotted in the fiber ![]() $\mathcal {P}^{-1}((r,s))$ of
$\mathcal {P}^{-1}((r,s))$ of ![]() $E(a,b)$ provided
$E(a,b)$ provided ![]() $(r,s) \in \mu (E( {ka}/({k+1}), (k+1)a))^+ \cap \mu (E(a,b))^+$ with
$(r,s) \in \mu (E( {ka}/({k+1}), (k+1)a))^+ \cap \mu (E(a,b))^+$ with ![]() $(k+1)r+s > b$ or, in other words,
$(k+1)r+s > b$ or, in other words,
Comparing with Theorem 2.6, this gives additional points in the region ![]() $ {a}/{2} < r < {b}/({k+1})$.
$ {a}/{2} < r < {b}/({k+1})$.
Note that in the case of the ball ![]() $B(R)$ we find knotted monotone Lagrangian tori projecting under
$B(R)$ we find knotted monotone Lagrangian tori projecting under ![]() $\mathcal {P}$ to the interval
$\mathcal {P}$ to the interval ![]() $\{(t,t) | {R}/{3} < t < {2R}/{5} \}$. Vianna's work [Reference ViannaVia14] produces monotone tori projecting to the larger interval
$\{(t,t) | {R}/{3} < t < {2R}/{5} \}$. Vianna's work [Reference ViannaVia14] produces monotone tori projecting to the larger interval ![]() $\{(t,t) | {R}/{3} < t < {R}/{2} \}$.
$\{(t,t) | {R}/{3} < t < {R}/{2} \}$.
(3) Let ![]() $\phi : E(1,4) \hookrightarrow P(1, 2)$ be a symplectic embedding. We know such an embedding exists, see [Reference Cristofaro-Gardiner, Frenkel and SchlenkCGFS17]. Any
$\phi : E(1,4) \hookrightarrow P(1, 2)$ be a symplectic embedding. We know such an embedding exists, see [Reference Cristofaro-Gardiner, Frenkel and SchlenkCGFS17]. Any ![]() $(r,s)$ in the shaded region in the left picture of Figure 6 satisfies criterion (3) of Theorem 2.16. Therefore,
$(r,s)$ in the shaded region in the left picture of Figure 6 satisfies criterion (3) of Theorem 2.16. Therefore, ![]() $\phi (L(r,s))$ is knotted in the fiber
$\phi (L(r,s))$ is knotted in the fiber ![]() $\mathcal {P}^{-1}((r,s))$ of
$\mathcal {P}^{-1}((r,s))$ of ![]() $P(1, 2)$.
$P(1, 2)$.
Both the shaded regions in Figure 5 and the shaded region in Figure 6 contain strictly more points than those given by Theorems 2.5, 2.6, and 2.7. However, we need to confirm the existence of a symplectic embedding when applying Theorem 2.16, which is sometimes non-trivial, see Proposition A.1 in Appendix A.
Here are a few immediate corollaries of Theorem 2.16 which can be compared with results on stabilized symplectic embeddings, see Theorem 1.1 in [Reference McDuffMcD18] or Theorems 1.1 and 1.3 in [Reference Cristofaro-Gardiner, Hind and SiegelCGHS22].
Corollary 2.19 Denote by ![]() $\overline {E(1,x)}$ the closure of the open ellipsoid
$\overline {E(1,x)}$ the closure of the open ellipsoid ![]() $E(1,x)$ in
$E(1,x)$ in ![]() $\mathbb {C}^2$. We have the following conclusions.
$\mathbb {C}^2$. We have the following conclusions.
(1) If
 $\overline {E(1,x)} \hookrightarrow B^4(R)$ and the image of
$\overline {E(1,x)} \hookrightarrow B^4(R)$ and the image of  $L( {x}/({x+1}), {x}/({x+1})) \subset \partial \overline {E(1,x)}$ is unknotted in
$L( {x}/({x+1}), {x}/({x+1})) \subset \partial \overline {E(1,x)}$ is unknotted in  $B^4(R)$, then
$B^4(R)$, then  $R\geq {3x}/({x+1})$.
$R\geq {3x}/({x+1})$.(2) If
 $\overline {E(1,x)} \hookrightarrow E(a,b)$ with
$\overline {E(1,x)} \hookrightarrow E(a,b)$ with  $k : = {b}/{a} \in \mathbb {N}_{\geq 2}$ and the image of
$k : = {b}/{a} \in \mathbb {N}_{\geq 2}$ and the image of  $L( {x}/({x+k-1}), {(k-1)x}/({x+k-1})) \subset \partial \overline {E(1,x)}$ is unknotted in
$L( {x}/({x+k-1}), {(k-1)x}/({x+k-1})) \subset \partial \overline {E(1,x)}$ is unknotted in  $E(a,b)$, then
$E(a,b)$, then  $a\geq {2x}/({x+k-1})$.
$a\geq {2x}/({x+k-1})$.(3) If
 $\overline {E(1,x)} \hookrightarrow P(c,d)$ with
$\overline {E(1,x)} \hookrightarrow P(c,d)$ with  $k: = {d}/{c} \in \mathbb {R}_{>0}$ and the image of
$k: = {d}/{c} \in \mathbb {R}_{>0}$ and the image of  $L( {x}/({x+2k-1}), {(2k-1)x}/({x+2k-1})) \subset \partial \overline {E(1,x)}$ is unknotted in
$L( {x}/({x+2k-1}), {(2k-1)x}/({x+2k-1})) \subset \partial \overline {E(1,x)}$ is unknotted in  $P(c,d)$, then
$P(c,d)$, then  $c \geq {2x}/({x+2k-1})$.
$c \geq {2x}/({x+2k-1})$.
Proof. (1) The description of ![]() ${\rm Sh}_H^+(B^4(R))$ in Theorem 2.1 together with our embedding
${\rm Sh}_H^+(B^4(R))$ in Theorem 2.1 together with our embedding ![]() $L( {x}/({x+1}), {x}/({x+1})) \subset \overline {E(1, x)} \hookrightarrow B^4(R)$ implies that
$L( {x}/({x+1}), {x}/({x+1})) \subset \overline {E(1, x)} \hookrightarrow B^4(R)$ implies that ![]() $R > {2x}/({x+1})$. Then
$R > {2x}/({x+1})$. Then
Hence, Theorem 2.16(1) implies that ![]() $R \geq 2 \cdot {x}/({x+1}) + {x}/({x+1}) = {3x}/({x+1})$.
$R \geq 2 \cdot {x}/({x+1}) + {x}/({x+1}) = {3x}/({x+1})$.
(2) Without loss of generality, assume ![]() $1 \leq a$ and
$1 \leq a$ and ![]() $x \geq b$. As
$x \geq b$. As ![]() $L( {x}/({x+k-1}), {(k-1)x}/({x+k-1})) \subset \overline {E(1,x)} \hookrightarrow E(a,b)$ we have
$L( {x}/({x+k-1}), {(k-1)x}/({x+k-1})) \subset \overline {E(1,x)} \hookrightarrow E(a,b)$ we have ![]() $( {x}/({x+k-1}), {(k-1)x}/({x+k-1})) \in {\rm Sh}_H^+(E(a,b))$. Therefore,
$( {x}/({x+k-1}), {(k-1)x}/({x+k-1})) \in {\rm Sh}_H^+(E(a,b))$. Therefore,
since this point lies on the line ![]() $s = (k-1)r$ and any points in
$s = (k-1)r$ and any points in ![]() ${\rm Sh}_H^+(E(a,b) \setminus \mu ^+(E(a,b))$ have
${\rm Sh}_H^+(E(a,b) \setminus \mu ^+(E(a,b))$ have ![]() $s > kr$ (cf. Figure 3). Hence, Theorem 2.16(2) implies that
$s > kr$ (cf. Figure 3). Hence, Theorem 2.16(2) implies that ![]() $b \geq (k+1) \cdot {x}/({x+k-1}) + {(k-1)x}/({x+k-1}) = {2kx}/({x+k-1})$. Dividing by
$b \geq (k+1) \cdot {x}/({x+k-1}) + {(k-1)x}/({x+k-1}) = {2kx}/({x+k-1})$. Dividing by ![]() $k$ on both sides, we obtain the desired conclusion.
$k$ on both sides, we obtain the desired conclusion.
(3) Without loss of generality, assume ![]() $1\leq c \leq d \leq x$. Now
$1\leq c \leq d \leq x$. Now ![]() $L( {x}/({x+2k-1}), {(2k-1)x}/({x+2k-1})) \subset \overline {E(1,x)} \hookrightarrow P(c,d)$ implies that
$L( {x}/({x+2k-1}), {(2k-1)x}/({x+2k-1})) \subset \overline {E(1,x)} \hookrightarrow P(c,d)$ implies that ![]() $( {x}/({x+2k-1}), {(2k-1)x}/({x+2k-1})) \in {\rm Sh}_H^+(P(c,d))$. Therefore,
$( {x}/({x+2k-1}), {(2k-1)x}/({x+2k-1})) \in {\rm Sh}_H^+(P(c,d))$. Therefore,
since this point lies on the line ![]() $s = (2k-1)r$ and any points in
$s = (2k-1)r$ and any points in ![]() ${\rm Sh}_H^+(P(a,b) \setminus \mu ^+(P(a,b))$ have
${\rm Sh}_H^+(P(a,b) \setminus \mu ^+(P(a,b))$ have ![]() $s > 2kr$ (cf. Figure 4). Hence, Theorem 2.16(3) implies that
$s > 2kr$ (cf. Figure 4). Hence, Theorem 2.16(3) implies that ![]() $d \geq {x}/({x+2k-1}) + {(2k-1)x}/({x+2k-1}) = {2kx}/({x+2k-1})$. Dividing by
$d \geq {x}/({x+2k-1}) + {(2k-1)x}/({x+2k-1}) = {2kx}/({x+2k-1})$. Dividing by ![]() $k$ on both sides, we obtain the desired conclusion.
$k$ on both sides, we obtain the desired conclusion.
Remark 2.20 A symplectic embedding ![]() $\overline {E(1,x)} \hookrightarrow X$ is clearly a stronger condition than the existence of a family of Hamiltonian embeddings
$\overline {E(1,x)} \hookrightarrow X$ is clearly a stronger condition than the existence of a family of Hamiltonian embeddings ![]() $L(r,s) \hookrightarrow X$ for
$L(r,s) \hookrightarrow X$ for ![]() $(r,s) \in \partial E(1,x)$. However, since the bounds in Corollary 2.19 precisely match those in [Reference Cristofaro-Gardiner, Hind and SiegelCGHS22] we are naturally led to expect a close relation between Lagrangian isotopies and stabilized embeddings
$(r,s) \in \partial E(1,x)$. However, since the bounds in Corollary 2.19 precisely match those in [Reference Cristofaro-Gardiner, Hind and SiegelCGHS22] we are naturally led to expect a close relation between Lagrangian isotopies and stabilized embeddings ![]() $E(1,x) \times \mathbb {C} \hookrightarrow X \times \mathbb {C}$. This will be explored elsewhere.
$E(1,x) \times \mathbb {C} \hookrightarrow X \times \mathbb {C}$. This will be explored elsewhere.
2.3.2 Embedding obstructions
The obstructions to the symplectic embedding between toric domains are usually given by certain symplectic capacities, for instance, Ekeland–Hofer capacity [Reference Ekeland and HoferEH90], embedded contact homology (ECH) capacities [Reference HutchingsHut11], Gutt–Hutchings capacities [Reference Gutt and HutchingsGH18], etc. Almost all of them are constructed via dynamical information, e.g. closed Reeb orbits, on ![]() $\partial X$ when it is viewed as a contact manifold with the contact structure induced by the standard primitive of the symplectic structure on
$\partial X$ when it is viewed as a contact manifold with the contact structure induced by the standard primitive of the symplectic structure on ![]() $\mathbb {R}^4$. Until now, the cases that have been studied the most are toric concave domains and toric convex domains. By using the reduced (Hamiltonian) shape invariants, we are able to obtain embedding obstructions for a large family of toric star-shaped domains that are beyond the cases of toric concave or convex (see, e.g., the toric domain from the subset in
$\mathbb {R}^4$. Until now, the cases that have been studied the most are toric concave domains and toric convex domains. By using the reduced (Hamiltonian) shape invariants, we are able to obtain embedding obstructions for a large family of toric star-shaped domains that are beyond the cases of toric concave or convex (see, e.g., the toric domain from the subset in ![]() $\mathbb {R}_{\geq 0}^2$ bounded by the orange curve in Figure 19). Here is the result, which will be proved in § 8.2.
$\mathbb {R}_{\geq 0}^2$ bounded by the orange curve in Figure 19). Here is the result, which will be proved in § 8.2.
Theorem 2.21 Let ![]() $X \subset \mathbb {R}^4$ be a toric domain and
$X \subset \mathbb {R}^4$ be a toric domain and ![]() $E(a,b)$ an ellipsoid with
$E(a,b)$ an ellipsoid with ![]() $k = {b}/{a} \in \mathbb {N}_{\geq 1}$. Suppose
$k = {b}/{a} \in \mathbb {N}_{\geq 1}$. Suppose ![]() $X \not \subset E(a,b)$. If there exists an ellipsoid
$X \not \subset E(a,b)$. If there exists an ellipsoid ![]() $E$ satisfying the following conditions:
$E$ satisfying the following conditions:
(i)
 $E \subset X \cap E(a,b)$, and
$E \subset X \cap E(a,b)$, and  $E \not \subset E( {ak}/({k+1}), b)$;
$E \not \subset E( {ak}/({k+1}), b)$;(ii) there exists an oriented path
(8)with \begin{equation} \gamma = \{(r_t, s_t) \in \mathbb{R}^2 \,| \, r_t \leq s_t\}_{t \in [0,T]} \subset \mu(X) \cap \mu \bigg(E\bigg(\frac{ak}{k+1}, b\bigg)\bigg)^{c} \end{equation}
\begin{equation} \gamma = \{(r_t, s_t) \in \mathbb{R}^2 \,| \, r_t \leq s_t\}_{t \in [0,T]} \subset \mu(X) \cap \mu \bigg(E\bigg(\frac{ak}{k+1}, b\bigg)\bigg)^{c} \end{equation} $(r_0, s_0) \in \mu (E)$,
$(r_0, s_0) \in \mu (E)$,  $(r_T, s_T) \notin \mu (E(a,b))$, and the ratio
$(r_T, s_T) \notin \mu (E(a,b))$, and the ratio  $ {r_t}/{s_t}$ non-increasing;
$ {r_t}/{s_t}$ non-increasing;
then there is no embedding ![]() $X \hookrightarrow E(a,b)$.
$X \hookrightarrow E(a,b)$.
We illustrate the strength of Theorem 2.21 via the following corollaries. They provide obstructions to symplectic embeddings without computing any symplectic capacities.
Corollary 2.22 Let ![]() $E(a,b)$ be a symplectic ellipsoid with
$E(a,b)$ be a symplectic ellipsoid with ![]() $k: = {b}/{a}\in \mathbb {N}_{\geq 2}$. If there exists a symplectic embedding
$k: = {b}/{a}\in \mathbb {N}_{\geq 2}$. If there exists a symplectic embedding ![]() $E(1,x) \hookrightarrow E(a,b)$ with
$E(1,x) \hookrightarrow E(a,b)$ with ![]() $1< a < 1 + {1}/{k}$, then
$1< a < 1 + {1}/{k}$, then ![]() $b \geq x$.
$b \geq x$.
Proof. Suppose ![]() $x>b$, then see the left picture in Figure 7. Referring to Theorem 2.21 where
$x>b$, then see the left picture in Figure 7. Referring to Theorem 2.21 where ![]() $X = E(1,x)$, the desired ellipsoid
$X = E(1,x)$, the desired ellipsoid ![]() $E= X_{\Delta (1,b)}$ where
$E= X_{\Delta (1,b)}$ where ![]() $\Delta (1,b)$ is the triangle with vertices
$\Delta (1,b)$ is the triangle with vertices ![]() $(0,0)$,
$(0,0)$, ![]() $(1,0)$, and
$(1,0)$, and ![]() $(0, b)$, and the desired path is the bold path (with arrow)
$(0, b)$, and the desired path is the bold path (with arrow) ![]() $\gamma$ in the picture. Therefore, Theorem 2.21 implies the contradiction.
$\gamma$ in the picture. Therefore, Theorem 2.21 implies the contradiction.

Figure 7. Embedding obstructions from path lifting.
Remark 2.23 The result in Corollary 2.22 can also be derived from ECH capacities assuming a computational fact on the ECH capacities of 4-dimensional ellipsoids, namely Proposition 1.2 in [Reference HutchingsHut11]. Explicitly, suppose ![]() $b< x$, let
$b< x$, let ![]() $c_k^{\rm ECH}$ denote the
$c_k^{\rm ECH}$ denote the ![]() $k$th ECH capacity. One can verify that
$k$th ECH capacity. One can verify that ![]() $c^{\rm ECH}_{k+1}(E(1,x)) > ak = b = c^{\rm ECH}_{k+1}(E(a,b)).$
$c^{\rm ECH}_{k+1}(E(1,x)) > ak = b = c^{\rm ECH}_{k+1}(E(a,b)).$
Corollary 2.24 Consider toric domains ![]() $B^4(20)$ and
$B^4(20)$ and ![]() $X_{\Omega }$ where the boundary
$X_{\Omega }$ where the boundary ![]() $\partial \Omega \cap \mathbb {R}_{>0}^2$ is piecewise linear with vertices
$\partial \Omega \cap \mathbb {R}_{>0}^2$ is piecewise linear with vertices ![]() $(0, 24), (2, 17), (19, 0)$, see the right picture in Figure 7. Then
$(0, 24), (2, 17), (19, 0)$, see the right picture in Figure 7. Then ![]() $X_{\Omega }$ does not symplectically embed into
$X_{\Omega }$ does not symplectically embed into ![]() $B^4(20)$.
$B^4(20)$.
Proof. By taking ![]() $E = B^4(16)$ as the triangle
$E = B^4(16)$ as the triangle ![]() $\Delta (16, 16)$ with vertices
$\Delta (16, 16)$ with vertices ![]() $(0,0)$,
$(0,0)$, ![]() $(16,0)$, and
$(16,0)$, and ![]() $(0, 16)$ in the picture and
$(0, 16)$ in the picture and ![]() $\gamma$ as the bold path (with arrow) in the picture, Theorem 2.21 implies the desired conclusion.
$\gamma$ as the bold path (with arrow) in the picture, Theorem 2.21 implies the desired conclusion.
Remark 2.25 This embedding obstruction can also be derived from Gutt–Hutchings capacities denoted by ![]() $c_k^{\rm GH}$ and constructed in [Reference Gutt and HutchingsGH18]. Explicitly, consider the second Gutt–Hutchings capacity. Since
$c_k^{\rm GH}$ and constructed in [Reference Gutt and HutchingsGH18]. Explicitly, consider the second Gutt–Hutchings capacity. Since ![]() $X_{\Omega }$ is a toric concave domain, by Theorem 1.14 in [Reference Gutt and HutchingsGH18], one can verify that
$X_{\Omega }$ is a toric concave domain, by Theorem 1.14 in [Reference Gutt and HutchingsGH18], one can verify that ![]() $c_2^{\rm GH}(X_{\Omega }) = 21 > 20 = c_2^{\rm GH}(B^4(20))$.
$c_2^{\rm GH}(X_{\Omega }) = 21 > 20 = c_2^{\rm GH}(B^4(20))$.
Finally, we include an example which seems beyond the reach of existing capacities: it is toric but not star-shaped, convex, nor concave.
Corollary 2.26 Fix ![]() $S> {2R}/{3}$ and
$S> {2R}/{3}$ and ![]() $R-S< u< {S}/{2}$, and define
$R-S< u< {S}/{2}$, and define
Then there is no symplectic embedding ![]() $X_{S,u} \hookrightarrow B^4(R)$.
$X_{S,u} \hookrightarrow B^4(R)$.
Proof. Denote by
Suppose there exists a symplectic embedding ![]() $X_{S,u} \hookrightarrow B^4(R)$. As the ball
$X_{S,u} \hookrightarrow B^4(R)$. As the ball ![]() $\overline {B^4(S)}$ in
$\overline {B^4(S)}$ in ![]() $X_{S,u}$ is closed, any such embedding extends to a slightly larger ball. Therefore, we have a symplectic embedding
$X_{S,u}$ is closed, any such embedding extends to a slightly larger ball. Therefore, we have a symplectic embedding ![]() $X_{S,u}(\delta ) \hookrightarrow B^4(R)$ for some sufficiently small
$X_{S,u}(\delta ) \hookrightarrow B^4(R)$ for some sufficiently small ![]() $\delta >0$. One can choose
$\delta >0$. One can choose ![]() $\delta$ such that
$\delta$ such that ![]() $S + \delta < R$.
$S + \delta < R$.
In order to apply Theorem 2.21, let us take ![]() $E(a,b) = B^4(R)$ where
$E(a,b) = B^4(R)$ where ![]() $a = b = R$ and
$a = b = R$ and ![]() $k = 1$ as well as
$k = 1$ as well as ![]() $E = B^4(S + \delta )$. Explicitly, (the closure of)
$E = B^4(S + \delta )$. Explicitly, (the closure of) ![]() $E$ is the triangle
$E$ is the triangle ![]() $\Delta (S+\delta, S+\delta )$ in Figure 8 with vertices
$\Delta (S+\delta, S+\delta )$ in Figure 8 with vertices ![]() $(0,0)$,
$(0,0)$, ![]() $(S+\delta, 0)$, and
$(S+\delta, 0)$, and ![]() $(0, S+\delta )$. Note that
$(0, S+\delta )$. Note that ![]() $X_{S,u}(\delta ) \not \subset B^4(R)$ because the product Lagrangian torus
$X_{S,u}(\delta ) \not \subset B^4(R)$ because the product Lagrangian torus ![]() $L(u, R-u) \in X_{S,u}(\delta ) \backslash B^4(R)$. Moreover,
$L(u, R-u) \in X_{S,u}(\delta ) \backslash B^4(R)$. Moreover, ![]() $E$ satisfies
$E$ satisfies
where the second relation comes from our hypothesis that ![]() $S+\delta > S> {2R}/{3} > {R}/{2}$. This verifies condition (i) in Theorem 2.21.
$S+\delta > S> {2R}/{3} > {R}/{2}$. This verifies condition (i) in Theorem 2.21.

Figure 8. Embedding obstructions from path lifting.
For condition (ii) in Theorem 2.21, let us take a path ![]() $\gamma$ simply as
$\gamma$ simply as
that is, the bold line segment (with arrow) in Figure 8. Obviously, ![]() $\gamma \subset \mu (X_{S, u}(\delta ))$. Meanwhile, observe that
$\gamma \subset \mu (X_{S, u}(\delta ))$. Meanwhile, observe that ![]() $\gamma (0) = (u, S-u)$ lies above the line
$\gamma (0) = (u, S-u)$ lies above the line ![]() $s = R -2r$ that describes the hypotenuse of the ellipsoid
$s = R -2r$ that describes the hypotenuse of the ellipsoid ![]() $E( {R}/{2}, R)$ when
$E( {R}/{2}, R)$ when ![]() $S-u > R - 2u$ or
$S-u > R - 2u$ or ![]() $u>R-S$, and
$u>R-S$, and ![]() $\gamma (0)$ lies in
$\gamma (0)$ lies in ![]() $\{r \le s\}$ provided
$\{r \le s\}$ provided ![]() $u< S/2$. (Parameters
$u< S/2$. (Parameters ![]() $u$ satisfying both of these conditions exist when
$u$ satisfying both of these conditions exist when ![]() $S>2R/3$.)
$S>2R/3$.)
Hence, Theorem 2.21 is verified, and there are no symplectic embeddings ![]() $X_{S,u}(\delta ) \hookrightarrow B^4(R)$.
$X_{S,u}(\delta ) \hookrightarrow B^4(R)$.
Remark 2.27 Corollary 2.26 follows from the computation of the shape invariant in Theorem 2.1(i) (applied to ![]() $L(u, R-u)$) only when
$L(u, R-u)$) only when ![]() $u> {R}/{3}$.
$u> {R}/{3}$.
Discussion. For both Corollaries 2.22 and 2.24, one can deform the domain ![]() $E(1,x)$ or
$E(1,x)$ or ![]() $X_{\Omega }$ to any star-shaped domains as long as we can find the desired ellipsoid
$X_{\Omega }$ to any star-shaped domains as long as we can find the desired ellipsoid ![]() $E$ and a bold path (with arrow)
$E$ and a bold path (with arrow) ![]() $\gamma$ as above, then still the embedding obstructions hold by Theorem 2.21. However, the classical symplectic capacities may not apply at all to the deformed domains. Moreover, the following two remarks are particularly interesting.
$\gamma$ as above, then still the embedding obstructions hold by Theorem 2.21. However, the classical symplectic capacities may not apply at all to the deformed domains. Moreover, the following two remarks are particularly interesting.
(1) In order to obtain the conclusion of Corollary 2.22, it is necessary to apply the obstruction from path lifting (instead of merely comparing the Hamiltonian shape invariants). Indeed, from ![]() ${\rm Sh}_H^+(E(1,x)) \subset {\rm Sh}_H^+(E(a,b))$, we only know that
${\rm Sh}_H^+(E(1,x)) \subset {\rm Sh}_H^+(E(a,b))$, we only know that
In other words, ![]() $a \geq 1$ and
$a \geq 1$ and ![]() $ {b}/{2} \geq x - {a}/{2} \cdot x$ (which is
$ {b}/{2} \geq x - {a}/{2} \cdot x$ (which is ![]() $b \geq (2 - a)x$). Under the hypothesis that
$b \geq (2 - a)x$). Under the hypothesis that ![]() $1< a < 1 + {1}/{k}$, we have
$1< a < 1 + {1}/{k}$, we have ![]() $2-a> 1- {1}/{k}$, which implies that
$2-a> 1- {1}/{k}$, which implies that ![]() $b \geq (1- {1}/{k})x$, and it is weaker than the conclusion of Corollary 2.22.
$b \geq (1- {1}/{k})x$, and it is weaker than the conclusion of Corollary 2.22.
(2) The point ![]() $(2,17)$ on
$(2,17)$ on ![]() $\partial \Omega$ in the hypothesis of Corollary 2.24 is crucial in the sense that it lies above the line
$\partial \Omega$ in the hypothesis of Corollary 2.24 is crucial in the sense that it lies above the line ![]() $2r+s = 20$, so there is a sufficiently large space to produce the desired path
$2r+s = 20$, so there is a sufficiently large space to produce the desired path ![]() $\gamma \subset \mu (E(10, 20))^{c}$. Curiously, the obstruction
$\gamma \subset \mu (E(10, 20))^{c}$. Curiously, the obstruction ![]() $c^{\rm GH}_2(X_{\Omega }) > c^{\rm GH}_2(B^4(20))$ shows exactly this geometric property. It would be interesting to obtain an accurate relation between the path lifting obstruction and the capacities
$c^{\rm GH}_2(X_{\Omega }) > c^{\rm GH}_2(B^4(20))$ shows exactly this geometric property. It would be interesting to obtain an accurate relation between the path lifting obstruction and the capacities ![]() $c^{\rm GH}_k$.
$c^{\rm GH}_k$.
2.4 Related work
The papers [Reference Entov, Ganor and MembrezEGM18, Reference Shelukhin, Tonkonog and ViannaSTV18] study the star-shape of both open and closed symplectic manifolds. The star-shape is defined relative to a fixed Lagrangian torus ![]() $L_0$ and in our language describes which linear paths have lifts starting at
$L_0$ and in our language describes which linear paths have lifts starting at ![]() $L_0$. Here, rather than Hamiltonian isotopy class, lifts are defined in terms of flux, which makes sense on a general symplectic manifold. One of the main results in [Reference Entov, Ganor and MembrezEGM18] that relates to our work is a series of computations and estimations (via Poisson bracket invariant in [Reference Buhovsky, Entov and PolterovichBEP12]) of the star-shape with different starting Lagrangians
$L_0$. Here, rather than Hamiltonian isotopy class, lifts are defined in terms of flux, which makes sense on a general symplectic manifold. One of the main results in [Reference Entov, Ganor and MembrezEGM18] that relates to our work is a series of computations and estimations (via Poisson bracket invariant in [Reference Buhovsky, Entov and PolterovichBEP12]) of the star-shape with different starting Lagrangians ![]() $L_0$ in
$L_0$ in ![]() $\mathbb {C}^n$.
$\mathbb {C}^n$.
With more sophisticated algebraic machinery, e.g. Fukaya algebra, [Reference Shelukhin, Tonkonog and ViannaSTV18] enhances [Reference Entov, Ganor and MembrezEGM18] in various ways. A consequence of the main result in [Reference Shelukhin, Tonkonog and ViannaSTV18] is that for toric Fano varieties, the star-shape relative to the monotone Lagrangian fiber coincides with the moment polytope. In the case of ![]() $B(R)$ this implies that linear paths starting from
$B(R)$ this implies that linear paths starting from ![]() $( {R}/{3}, {R}/{3}) \in \Delta (R,R)$ have lifts only if the path lies completely in the moment image
$( {R}/{3}, {R}/{3}) \in \Delta (R,R)$ have lifts only if the path lies completely in the moment image ![]() $\Delta (R,R)$. We note that
$\Delta (R,R)$. We note that ![]() $( {R}/{3}, {R}/{3})$ lies precisely on the boundary of our ‘flexible region’
$( {R}/{3}, {R}/{3})$ lies precisely on the boundary of our ‘flexible region’ ![]() $\{2r + s < R\}$, so the result matches Theorem 2.11. In this case our results cover more general paths, and we give constructions showing the constraints are often sharp. However, we emphasize that our obstructions rely on the non-triviality of certain moduli spaces of holomorphic curves, which are only established for simple domains.
$\{2r + s < R\}$, so the result matches Theorem 2.11. In this case our results cover more general paths, and we give constructions showing the constraints are often sharp. However, we emphasize that our obstructions rely on the non-triviality of certain moduli spaces of holomorphic curves, which are only established for simple domains.
The paper [Reference Shelukhin, Tonkonog and ViannaSTV18] also gives constructions of path lifts in ![]() $\mathbb {C} P^2$ and other toric manifolds. While saying that two Lagrangians are not symplectomorphic in
$\mathbb {C} P^2$ and other toric manifolds. While saying that two Lagrangians are not symplectomorphic in ![]() $\mathbb {C} P^2$ is a stronger condition than Hamiltonian knottedness in the ball, if a path lifts in
$\mathbb {C} P^2$ is a stronger condition than Hamiltonian knottedness in the ball, if a path lifts in ![]() $\mathbb {C} P^2$ the corresponding Lagrangian isotopy may intersect the line at infinity, and so these lifts do not imply lifting in the ball.
$\mathbb {C} P^2$ the corresponding Lagrangian isotopy may intersect the line at infinity, and so these lifts do not imply lifting in the ball.
For detecting Hamiltonian knotted Lagrangian tori, Theorem 3.2 in Ono's work [Reference OnoOno15] detects the existence of knotted Lagrangian tori in ![]() $P(c,c)$ with the area classes lying the following region
$P(c,c)$ with the area classes lying the following region
Note that this covers a larger region than that defined by (6) from Theorem 2.7 when ![]() $c = d$, but our result Theorem 2.7 applies to more general
$c = d$, but our result Theorem 2.7 applies to more general ![]() $c$ and
$c$ and ![]() $d$.
$d$.
3. Background and preliminary
3.1 Shape invariant
Given an exact symplectic manifold ![]() $(M^{2n}, \omega = d\lambda )$ with a fixed primitive
$(M^{2n}, \omega = d\lambda )$ with a fixed primitive ![]() $\lambda$, the shape invariant of this
$\lambda$, the shape invariant of this ![]() $(M, \omega = d\lambda )$, denoted by
$(M, \omega = d\lambda )$, denoted by ![]() ${\rm Sh}(M, \lambda )$, is defined as the collection of all possible area classes of embedded Lagrangian tori. More explicitly, for any Lagrangian embedding
${\rm Sh}(M, \lambda )$, is defined as the collection of all possible area classes of embedded Lagrangian tori. More explicitly, for any Lagrangian embedding ![]() $\phi : \mathbb {T}^n \hookrightarrow M^{2n}$, the pullback
$\phi : \mathbb {T}^n \hookrightarrow M^{2n}$, the pullback ![]() $\phi ^*\lambda$ represents a cohomology class in
$\phi ^*\lambda$ represents a cohomology class in ![]() $H^1(\mathbb {T}^n; \mathbb {R})$. By choosing an integral basis
$H^1(\mathbb {T}^n; \mathbb {R})$. By choosing an integral basis ![]() $e: = (e_1,\ldots,e_n)$ of
$e: = (e_1,\ldots,e_n)$ of ![]() $H_1(\mathbb {T}^n; \mathbb {Z})$, the following evaluation
$H_1(\mathbb {T}^n; \mathbb {Z})$, the following evaluation
induces a map from Lagrangian embeddings to elements in ![]() $\mathbb {R}^n$. Of course, the set of values from (9) depends on
$\mathbb {R}^n$. Of course, the set of values from (9) depends on ![]() $\lambda$ and
$\lambda$ and ![]() $e$, where a different choice of
$e$, where a different choice of ![]() $\lambda$ results in a uniform shift in
$\lambda$ results in a uniform shift in ![]() $\mathbb {R}^n$ and a different choice of
$\mathbb {R}^n$ and a different choice of ![]() $e$ results in a transformation by an element in
$e$ results in a transformation by an element in ![]() ${\rm GL}(n, \mathbb {Z})$. In particular, the action by
${\rm GL}(n, \mathbb {Z})$. In particular, the action by ![]() ${\rm GL}(n, \mathbb {Z})$ provides a certain symmetry of
${\rm GL}(n, \mathbb {Z})$ provides a certain symmetry of ![]() ${\rm Sh}(M, \lambda )$. It is Sikorav's work [Reference SikoravSik89] and Eliashberg's work [Reference EliashbergEli91] that first observed the application of the shape invariant to the study of the rigidity of symplectic or contact embeddings. For further development in this direction, see [Reference MüllerMül19, Reference Rosen and ZhangRZ21, Reference Hind and ZhangHZ21].
${\rm Sh}(M, \lambda )$. It is Sikorav's work [Reference SikoravSik89] and Eliashberg's work [Reference EliashbergEli91] that first observed the application of the shape invariant to the study of the rigidity of symplectic or contact embeddings. For further development in this direction, see [Reference MüllerMül19, Reference Rosen and ZhangRZ21, Reference Hind and ZhangHZ21].
In this paper, we consider a restrictive version of the shape invariant, called the Hamiltonian shape invariant, and our ![]() $(M^{2n}, \omega = d\lambda ) = (X, \omega _{\rm std} = d\lambda _{\rm std})$ for a toric domain
$(M^{2n}, \omega = d\lambda ) = (X, \omega _{\rm std} = d\lambda _{\rm std})$ for a toric domain ![]() $X$ in
$X$ in ![]() $(\mathbb {R}^4, \omega _{\rm std})$. It is defined in (2) as the collection of all possible area classes
$(\mathbb {R}^4, \omega _{\rm std})$. It is defined in (2) as the collection of all possible area classes ![]() $(r,s) \in \mathbb {R}_{>0}^2$ that admit
$(r,s) \in \mathbb {R}_{>0}^2$ that admit ![]() $L(r,s) \hookrightarrow X$, and it is denoted by
$L(r,s) \hookrightarrow X$, and it is denoted by ![]() ${\rm Sh}_H(X)$. Observe that in this set-up, there is no dependence of the primitive and we have a canonical choice of the basis
${\rm Sh}_H(X)$. Observe that in this set-up, there is no dependence of the primitive and we have a canonical choice of the basis ![]() $e = (e_1, e_2)$, where
$e = (e_1, e_2)$, where ![]() $e_1$ is the standard circle in
$e_1$ is the standard circle in ![]() $L(r,s)$, lying in the first
$L(r,s)$, lying in the first ![]() $\mathbb {R}^2$-factor of
$\mathbb {R}^2$-factor of ![]() $\mathbb {R}^4$, bounding the disk with area
$\mathbb {R}^4$, bounding the disk with area ![]() $r$ and
$r$ and ![]() $e_2$ is the standard circle in
$e_2$ is the standard circle in ![]() $L(r,s)$, lying in the second
$L(r,s)$, lying in the second ![]() $\mathbb {R}^2$-factor of
$\mathbb {R}^2$-factor of ![]() $\mathbb {R}^4$, bounding the disk with area
$\mathbb {R}^4$, bounding the disk with area ![]() $s$. Then the only symmetry we have is via the reflection
$s$. Then the only symmetry we have is via the reflection ![]() $(r,s) \mapsto (s,r)$, which induces a simplified version, the reduced Hamiltonian shape invariant denoted by
$(r,s) \mapsto (s,r)$, which induces a simplified version, the reduced Hamiltonian shape invariant denoted by ![]() ${\rm Sh}_H^+(X) := {\rm Sh}_H(X) \cap \{r \leq s\}$.
${\rm Sh}_H^+(X) := {\rm Sh}_H(X) \cap \{r \leq s\}$.
The explicit computations of ![]() ${\rm Sh}_H(X)$ as a subset in
${\rm Sh}_H(X)$ as a subset in ![]() $\mathbb {R}_{>0}^2$, even for basic toric domains such as balls, ellipsoids, and polydisks, were carried out quite recently, see [Reference Hind and OpshteinHO20, Reference Hind and ZhangHZ21]. Theorem 2.1 in the introduction summarizes the corresponding results. These results are consequences of a sophisticated analysis of holomorphic curves forming part of symplectic field theory (SFT).
$\mathbb {R}_{>0}^2$, even for basic toric domains such as balls, ellipsoids, and polydisks, were carried out quite recently, see [Reference Hind and OpshteinHO20, Reference Hind and ZhangHZ21]. Theorem 2.1 in the introduction summarizes the corresponding results. These results are consequences of a sophisticated analysis of holomorphic curves forming part of symplectic field theory (SFT).
A slightly different version of the shape invariant, which is formulated via the flux of a Lagrangian isotopy (in particular, applied on closed manifolds such as ![]() $\mathbb {C} P^n$ and
$\mathbb {C} P^n$ and ![]() $S^2 \times S^2$), has been studied in [Reference Entov, Ganor and MembrezEGM18, Reference Shelukhin, Tonkonog and ViannaSTV18]. These works point out the intriguing relations between the shape invariant and Poisson-bracket invariants in [Reference Buhovsky, Entov and PolterovichBEP12] and the SYZ fibration in [Reference Strominger, Yau and ZaslowSYZ96], respectively.
$S^2 \times S^2$), has been studied in [Reference Entov, Ganor and MembrezEGM18, Reference Shelukhin, Tonkonog and ViannaSTV18]. These works point out the intriguing relations between the shape invariant and Poisson-bracket invariants in [Reference Buhovsky, Entov and PolterovichBEP12] and the SYZ fibration in [Reference Strominger, Yau and ZaslowSYZ96], respectively.
3.2 Symplectic field theory
Lagrangian embeddings ![]() $\phi : L(s,t) \hookrightarrow X$ can be effectively studied via SFT. It is a modern machinery, originally formulated in the work [Reference Eliashberg, Givental and HoferEGH00] and further developed in [Reference Bourgeois, Eliashberg, Hofer, Wysocki and ZehnderBEH+03, Reference HoferHof06, Reference Cieliebak and MohnkeCM18], that can associate a variety of algebraic invariants to a symplectic cobordism. Our work, however, does not rely on this full algebraic machinery, which is indeed still under development. The proofs in the current paper require only compactness and deformation theorems for (somewhere injective) holomorphic curves, modulo some references to ECH and to earlier works of the authors. The input from these earlier works is used to establish existence of a holomorphic curve in Lemma 4.1 (which can be avoided using Remark 4.2) and then in the bubbling analysis of both § 4.1.2 and the main proof in § 4.2, where Lemma 3.7 of [Reference Hind and OpshteinHO20] is a key ingredient.
$\phi : L(s,t) \hookrightarrow X$ can be effectively studied via SFT. It is a modern machinery, originally formulated in the work [Reference Eliashberg, Givental and HoferEGH00] and further developed in [Reference Bourgeois, Eliashberg, Hofer, Wysocki and ZehnderBEH+03, Reference HoferHof06, Reference Cieliebak and MohnkeCM18], that can associate a variety of algebraic invariants to a symplectic cobordism. Our work, however, does not rely on this full algebraic machinery, which is indeed still under development. The proofs in the current paper require only compactness and deformation theorems for (somewhere injective) holomorphic curves, modulo some references to ECH and to earlier works of the authors. The input from these earlier works is used to establish existence of a holomorphic curve in Lemma 4.1 (which can be avoided using Remark 4.2) and then in the bubbling analysis of both § 4.1.2 and the main proof in § 4.2, where Lemma 3.7 of [Reference Hind and OpshteinHO20] is a key ingredient.
Topologically, our symplectic cobordism is the complement ![]() $W: = X \backslash U_g^*L$ where
$W: = X \backslash U_g^*L$ where ![]() $L = \phi (L(r,s))$ and
$L = \phi (L(r,s))$ and ![]() $U^*_gL$ is the unit codisk bundle of
$U^*_gL$ is the unit codisk bundle of ![]() $L$ with respect to some metric
$L$ with respect to some metric ![]() $g$ on
$g$ on ![]() $L$; our metrics will always be flat. With a preferred almost complex structure
$L$; our metrics will always be flat. With a preferred almost complex structure ![]() $J$ on
$J$ on ![]() $W$, the central objects in SFT are
$W$, the central objects in SFT are ![]() $J$-holomorphic curves
$J$-holomorphic curves ![]() $C: (S^2 \backslash \{p_1,\ldots, p_m\}, j) \to (W, J)$, where the asymptotic ends from punctures
$C: (S^2 \backslash \{p_1,\ldots, p_m\}, j) \to (W, J)$, where the asymptotic ends from punctures ![]() $p_i$ correspond to Reeb orbits on
$p_i$ correspond to Reeb orbits on ![]() $\partial X$ (positive ends) and on
$\partial X$ (positive ends) and on ![]() $S_g^*L : = \partial U_g^*L$ (negative ends). In fact, the Reeb orbits on
$S_g^*L : = \partial U_g^*L$ (negative ends). In fact, the Reeb orbits on ![]() $S_g^*L$ can readily be classified (see Proposition 3.1 in [Reference Hind and OpshteinHO20]). More concretely, we say a Reeb orbit on
$S_g^*L$ can readily be classified (see Proposition 3.1 in [Reference Hind and OpshteinHO20]). More concretely, we say a Reeb orbit on ![]() $S_g^*L$ is of the type
$S_g^*L$ is of the type ![]() $(-m,-n)$, denoted by
$(-m,-n)$, denoted by ![]() $\gamma _{(m, n)}$, if its projection to
$\gamma _{(m, n)}$, if its projection to ![]() $L$ lies in the homology class
$L$ lies in the homology class ![]() $(-m, -n) \in H^1(\mathbb {T}^2, \mathbb {Z})$. Note that for a
$(-m, -n) \in H^1(\mathbb {T}^2, \mathbb {Z})$. Note that for a ![]() $J$-holomorphic plane
$J$-holomorphic plane ![]() $C: (S^2 \backslash \{p\}, j) \to (W, J)$ with only one asymptotic end on
$C: (S^2 \backslash \{p\}, j) \to (W, J)$ with only one asymptotic end on ![]() $\gamma _{(-m, -n)}$, by Stokes’ theorem, its area is
$\gamma _{(-m, -n)}$, by Stokes’ theorem, its area is
A useful algebraic invariant of ![]() $C$ is its Fredholm index. Denote by
$C$ is its Fredholm index. Denote by ![]() $\{\gamma _i^+\}_{i=1}^{s_+}$ the collection of positive asymptotic orbits and
$\{\gamma _i^+\}_{i=1}^{s_+}$ the collection of positive asymptotic orbits and ![]() $\{\gamma _i^-\}_{i=1}^{s_-}$ the collection of negative asymptotic orbits. Without loss of generality, let us assume these Reeb orbits are either non-degenerate or Morse–Bott, that is, they may come in smooth families, and
$\{\gamma _i^-\}_{i=1}^{s_-}$ the collection of negative asymptotic orbits. Without loss of generality, let us assume these Reeb orbits are either non-degenerate or Morse–Bott, that is, they may come in smooth families, and ![]() $S_i^+$ and
$S_i^+$ and ![]() $S_i^-$ are the leaf spaces of the associated Morse–Bott submanifolds. Fix a symplectic trivialization
$S_i^-$ are the leaf spaces of the associated Morse–Bott submanifolds. Fix a symplectic trivialization ![]() $\tau$ of
$\tau$ of ![]() $C^*TW$ along these Reeb orbits, and
$C^*TW$ along these Reeb orbits, and ![]() $c_1^{\tau }(C^*TW)$ denotes the first Chern number with respect to this trivialization
$c_1^{\tau }(C^*TW)$ denotes the first Chern number with respect to this trivialization ![]() $\tau$. Then
$\tau$. Then
 \begin{align} {\rm ind}(C) & = (s_+ + s_- - 2) + 2c_1^{\tau}(C^*TW) \nonumber\\ & \quad + \bigg(\sum_{i=1}^{s^+} {\rm CZ}^{\tau}(\gamma_i^+) + \frac{\dim S_i^+}{2}\bigg) - \bigg(\sum_{i=1}^{s_-} {\rm CZ}^{\tau}(\gamma_i^-) - \frac{\dim S_i^+}{2}\bigg), \end{align}
\begin{align} {\rm ind}(C) & = (s_+ + s_- - 2) + 2c_1^{\tau}(C^*TW) \nonumber\\ & \quad + \bigg(\sum_{i=1}^{s^+} {\rm CZ}^{\tau}(\gamma_i^+) + \frac{\dim S_i^+}{2}\bigg) - \bigg(\sum_{i=1}^{s_-} {\rm CZ}^{\tau}(\gamma_i^-) - \frac{\dim S_i^+}{2}\bigg), \end{align}
where ![]() ${\rm CZ}^{\tau}$ is the Conley–Zehnder index with respect to
${\rm CZ}^{\tau}$ is the Conley–Zehnder index with respect to ![]() $\tau$, which can be computed as the Robbin–Salamon index (see [Reference Robbin and SalamonRS93]). Note that
$\tau$, which can be computed as the Robbin–Salamon index (see [Reference Robbin and SalamonRS93]). Note that ![]() ${\rm ind}(C)$ is independent of the choice of symplectic trivialization
${\rm ind}(C)$ is independent of the choice of symplectic trivialization ![]() $\tau$. When specifying
$\tau$. When specifying ![]() $\gamma _i^{-} = \gamma _{(-m_i, n_i)}$ for
$\gamma _i^{-} = \gamma _{(-m_i, n_i)}$ for ![]() $i \in \{1,\ldots, s_-\}$ and taking
$i \in \{1,\ldots, s_-\}$ and taking ![]() $\tau$ as the complex trivialization of the contact planes induced by complexifying the trivialization of the 2-torus, the index formula (10) can be computed by
$\tau$ as the complex trivialization of the contact planes induced by complexifying the trivialization of the 2-torus, the index formula (10) can be computed by
 \begin{equation} {\rm ind}(C) = (s_+ + s_- -2) + \bigg(\sum_{i=1}^{s^+} {\rm CZ}^{\tau}(\gamma_i^+) + \frac{\dim S_i^+}{2}\bigg) + 2 \sum_{i=1}^{s_-} (m_i + n_i). \end{equation}
\begin{equation} {\rm ind}(C) = (s_+ + s_- -2) + \bigg(\sum_{i=1}^{s^+} {\rm CZ}^{\tau}(\gamma_i^+) + \frac{\dim S_i^+}{2}\bigg) + 2 \sum_{i=1}^{s_-} (m_i + n_i). \end{equation}
For more detailed elaboration, see Example 4.1 in [Reference Hind and ZhangHZ21]. Sometimes, the toric domain ![]() $X$ can be compactified to be a closed symplectic manifold by adding certain curves at infinity. In this paper, we are particularly interested in the following two cases.
$X$ can be compactified to be a closed symplectic manifold by adding certain curves at infinity. In this paper, we are particularly interested in the following two cases.
(i) Ball ![]() $B^4(R)$, where
$B^4(R)$, where ![]() $B^4(R)$ can be compactified to
$B^4(R)$ can be compactified to ![]() $\mathbb {C} P^2(R)$ with the area of the line at infinity
$\mathbb {C} P^2(R)$ with the area of the line at infinity ![]() $S_{\infty }$ being
$S_{\infty }$ being ![]() $R$. Then we study
$R$. Then we study ![]() $C$ without positive ends, but with a topological invariant given by its intersection number with
$C$ without positive ends, but with a topological invariant given by its intersection number with ![]() $S_{\infty }$. We denote the intersection by
$S_{\infty }$. We denote the intersection by ![]() $d$. Then the corresponding formula in (11) is
$d$. Then the corresponding formula in (11) is
 \begin{equation} {\rm ind}(C) = (s_- -2) + 6d + 2 \sum_{i=1}^{s_-} (m_i + n_i). \end{equation}
\begin{equation} {\rm ind}(C) = (s_- -2) + 6d + 2 \sum_{i=1}^{s_-} (m_i + n_i). \end{equation} (ii) Polydisks ![]() $P(c,d)$, where
$P(c,d)$, where ![]() $P(c,d)$ can be compactified to
$P(c,d)$ can be compactified to ![]() $S^2(c) \times S^2(d)$ with two factors having areas
$S^2(c) \times S^2(d)$ with two factors having areas ![]() $c$ and
$c$ and ![]() $d$, by adding two curves
$d$, by adding two curves ![]() $\{\infty \} \times S^2(b)$ and
$\{\infty \} \times S^2(b)$ and ![]() $S^2(a) \times \{\infty \}$. Then we study
$S^2(a) \times \{\infty \}$. Then we study ![]() $C$ without positive ends, but with a topological invariant given by its intersection with these two curves at infinity. We denote by
$C$ without positive ends, but with a topological invariant given by its intersection with these two curves at infinity. We denote by ![]() $(d_1, d_2)$ the bidegree labeling the two intersection numbers. Then the corresponding formula in (11) is
$(d_1, d_2)$ the bidegree labeling the two intersection numbers. Then the corresponding formula in (11) is
 \begin{equation} {\rm ind}(C) = (s_- -2) + 4 (d_1 + d_2) + 2 \sum_{i=1}^{s_-} (m_i + n_i). \end{equation}
\begin{equation} {\rm ind}(C) = (s_- -2) + 4 (d_1 + d_2) + 2 \sum_{i=1}^{s_-} (m_i + n_i). \end{equation}
A useful technique in SFT is neck-stretching, via a sequence of deformations of almost complex structures on the symplectic cobordism ![]() $W$. The standard SFT compactness theorem in [Reference Bourgeois, Eliashberg, Hofer, Wysocki and ZehnderBEH+03] promises the existence of a limit curve
$W$. The standard SFT compactness theorem in [Reference Bourgeois, Eliashberg, Hofer, Wysocki and ZehnderBEH+03] promises the existence of a limit curve ![]() $C_{\rm lim}$, more precisely, a pseudo-holomorphic building consisting of curves in different levels matched in a possibly complicated way. However, the two invariants introduced above,
$C_{\rm lim}$, more precisely, a pseudo-holomorphic building consisting of curves in different levels matched in a possibly complicated way. However, the two invariants introduced above, ![]() ${\rm area}(C)$ and
${\rm area}(C)$ and ![]() ${\rm ind}(C)$, converge in the limit and behave in a rather controllable manner. To be precise, if
${\rm ind}(C)$, converge in the limit and behave in a rather controllable manner. To be precise, if ![]() $C_{\rm lim}$ is obtained by gluing different sub-buildings
$C_{\rm lim}$ is obtained by gluing different sub-buildings ![]() $\{C_i\}_{i =1}^n$ along matching orbits
$\{C_i\}_{i =1}^n$ along matching orbits ![]() $\{\gamma _i\}_{i=1}^m$, then
$\{\gamma _i\}_{i=1}^m$, then
and
 \begin{equation} {\rm ind}(C_{\rm lim}) = \sum_{i=1}^n {\rm ind}(C_i) - \sum_{i=1}^m {\rm dim}\,S_i, \end{equation}
\begin{equation} {\rm ind}(C_{\rm lim}) = \sum_{i=1}^n {\rm ind}(C_i) - \sum_{i=1}^m {\rm dim}\,S_i, \end{equation}
where ![]() $S_i$ is the leaf space of
$S_i$ is the leaf space of ![]() $\gamma _i$ for
$\gamma _i$ for ![]() $i \in \{1,\ldots, m\}$. For more details, see Proposition 3.3 in [Reference Hind and OpshteinHO20]. In what follows, we will see that the combination of
$i \in \{1,\ldots, m\}$. For more details, see Proposition 3.3 in [Reference Hind and OpshteinHO20]. In what follows, we will see that the combination of ![]() ${\rm area}(C)$ and
${\rm area}(C)$ and ![]() ${\rm ind}(C)$ actually yield quite strong constraints on the possible configurations of
${\rm ind}(C)$ actually yield quite strong constraints on the possible configurations of ![]() $C_{\rm lim}$. This will be essential to the study of embeddings
$C_{\rm lim}$. This will be essential to the study of embeddings ![]() $L(r,s) \hookrightarrow X$. These ideas were also used in both [Reference Hind and OpshteinHO20, Reference Hind and ZhangHZ21] in the computations of the (Hamiltonian) shape invariant.
$L(r,s) \hookrightarrow X$. These ideas were also used in both [Reference Hind and OpshteinHO20, Reference Hind and ZhangHZ21] in the computations of the (Hamiltonian) shape invariant.
4. Obstructions to path liftings
In this section, we will prove the obstruction to a path lifting, that is, obstruction (I) in Theorems 2.11, 2.12, and 2.13. We will deal with Theorems 2.11 and 2.12 together, although 2.11 could also be proved using a compactification as in our proof of Theorem 2.13. Before the main proof we first establish the existence of a certain holomorphic cylinder, and then analyze possible degenerations of moduli spaces of genus ![]() $0$ curves with Fredholm index at least equal to the number of negative ends.
$0$ curves with Fredholm index at least equal to the number of negative ends.
4.1 Preparations
4.1.1 Existence of a holomorphic cylinder
The following lemma, Lemma 4.1, guarantees the existence of a holomorphic cylinder which will initiate our main proof.
Recall that ![]() $L(r_0, s_0)$ is the product torus in
$L(r_0, s_0)$ is the product torus in ![]() $\mathbb {C}^2$ with area classes
$\mathbb {C}^2$ with area classes ![]() $r_0$ and
$r_0$ and ![]() $s_0$. We assume
$s_0$. We assume ![]() $L(r_0, s_0) \subset E(a,b)$, that is,
$L(r_0, s_0) \subset E(a,b)$, that is, ![]() $kr_0 + s_0 < b$. Recall that
$kr_0 + s_0 < b$. Recall that ![]() $\gamma _{(m,n)}$ denotes the closed Reeb orbits of type
$\gamma _{(m,n)}$ denotes the closed Reeb orbits of type ![]() $(-m, -n)$ on the unit co-sphere bundle
$(-m, -n)$ on the unit co-sphere bundle ![]() $S^*_gL(r_0, s_0)$ with respect to a preferred flat metric
$S^*_gL(r_0, s_0)$ with respect to a preferred flat metric ![]() $g$ on
$g$ on ![]() $L(r_0, s_0)$. Since
$L(r_0, s_0)$. Since ![]() $L(r_0, s_0) \subset E(a,b)$, rescaling the metric
$L(r_0, s_0) \subset E(a,b)$, rescaling the metric ![]() $g$, we may assume this unit codisk bundle
$g$, we may assume this unit codisk bundle ![]() $U_g^*L(r_0, s_0)$ sits inside
$U_g^*L(r_0, s_0)$ sits inside ![]() $E(a,b)$. As discussed in § 3.2, the complement
$E(a,b)$. As discussed in § 3.2, the complement ![]() $E(a,b)\backslash U_g^*L(r_0, s_0)$ is a symplectic cobordism and the deformed complex structure, denoted by
$E(a,b)\backslash U_g^*L(r_0, s_0)$ is a symplectic cobordism and the deformed complex structure, denoted by ![]() $J_0$, gives a compatible almost complex structure with cylindrical ends. Denote by
$J_0$, gives a compatible almost complex structure with cylindrical ends. Denote by ![]() $\gamma _b$ the long closed Reeb orbit on
$\gamma _b$ the long closed Reeb orbit on ![]() $\partial E(a,b)$ with period
$\partial E(a,b)$ with period ![]() $b$.
$b$.
In order to guarantee non-degeneracy, when working with holomorphic curves asymptotic to ellipsoids we will always increase ![]() $b$ slightly so that
$b$ slightly so that ![]() $ {b}/{a} \notin \mathbb {Q}$. As the perturbation can be arbitrarily small this does not affect the statements of any of our results. Here, with our fixed trivialization
$ {b}/{a} \notin \mathbb {Q}$. As the perturbation can be arbitrarily small this does not affect the statements of any of our results. Here, with our fixed trivialization ![]() $\tau$ as in § 3.2, the longer orbit
$\tau$ as in § 3.2, the longer orbit ![]() $\gamma _b$ of
$\gamma _b$ of ![]() $E(a,b)$ has its Conley–Zehnder index given by
$E(a,b)$ has its Conley–Zehnder index given by ![]() ${\rm CZ}^{\tau }(\gamma _b) = 2\,\lfloor {b}/{a} \rfloor + 3$.
${\rm CZ}^{\tau }(\gamma _b) = 2\,\lfloor {b}/{a} \rfloor + 3$.
Lemma 4.1 There exists a ![]() $J_0$-holomorphic cylinder in the symplectic cobordism
$J_0$-holomorphic cylinder in the symplectic cobordism
with a positive end on ![]() $\gamma _b$, the longer Reeb orbit of
$\gamma _b$, the longer Reeb orbit of ![]() $\partial E(a,b)$, and with a negative end on a Reeb orbit
$\partial E(a,b)$, and with a negative end on a Reeb orbit ![]() $\gamma _{k,1}$ on
$\gamma _{k,1}$ on ![]() $S^*_gL(r_0, s_0)$ (where recall
$S^*_gL(r_0, s_0)$ (where recall ![]() $k = {b}/{a}$).
$k = {b}/{a}$).
Outline of the proof of Lemma 4.1. One proof of this is to analyze a neck-stretching argument in [Reference Hind and ZhangHZ21] which produces a union of curves in the cobordism ![]() $E(a,b)\backslash U_g^*L(r_0, s_0)$, checking that one of the curves must be a cylinder as required. We also give a direct geometric construction in Remark 4.2 of a cylinder which is holomorphic for some almost complex structure (a result which is actually enough for our purposes).
$E(a,b)\backslash U_g^*L(r_0, s_0)$, checking that one of the curves must be a cylinder as required. We also give a direct geometric construction in Remark 4.2 of a cylinder which is holomorphic for some almost complex structure (a result which is actually enough for our purposes).
Proof of Lemma 4.1 There exists a thin and long ellipsoid denoted by ![]() $E(\epsilon, \epsilon S)$ which can be embedded inside the unit codisk bundle
$E(\epsilon, \epsilon S)$ which can be embedded inside the unit codisk bundle ![]() $U_g^*L(r_0, s_0)$. Here,
$U_g^*L(r_0, s_0)$. Here, ![]() $\epsilon$ is sufficiently small and we require
$\epsilon$ is sufficiently small and we require ![]() $S>k+1$. Up to symplectomorphism, we have the following inclusions,
$S>k+1$. Up to symplectomorphism, we have the following inclusions,
Denote by ![]() $\beta$ the short closed Reeb orbit of
$\beta$ the short closed Reeb orbit of ![]() $\partial E(\epsilon, \epsilon S)$ with period
$\partial E(\epsilon, \epsilon S)$ with period ![]() $\epsilon$. By an appropriate deformation of the almost complex structure, we can view
$\epsilon$. By an appropriate deformation of the almost complex structure, we can view ![]() $E(a,b) \backslash E(\epsilon, \epsilon S)$ as a symplectic cobordism with respect to an almost complex structure (still) denoted by
$E(a,b) \backslash E(\epsilon, \epsilon S)$ as a symplectic cobordism with respect to an almost complex structure (still) denoted by ![]() $J_0$. By Theorem 5.8 in [Reference Hind and ZhangHZ21], there exists a
$J_0$. By Theorem 5.8 in [Reference Hind and ZhangHZ21], there exists a ![]() $J_0$-holomorphic cylinder with positive end
$J_0$-holomorphic cylinder with positive end ![]() $\gamma _b$ and negative end
$\gamma _b$ and negative end ![]() $\beta ^{k+1}$.Footnote 1 Then by a neck-stretching along the boundary
$\beta ^{k+1}$.Footnote 1 Then by a neck-stretching along the boundary ![]() $S_g^*L(r_0, s_0)$ as in [Reference Hind and ZhangHZ21], Lemma 6.1, the limiting building
$S_g^*L(r_0, s_0)$ as in [Reference Hind and ZhangHZ21], Lemma 6.1, the limiting building ![]() $C_{\rm lim}$ contains
$C_{\rm lim}$ contains ![]() $(k+2)$-many curves in
$(k+2)$-many curves in ![]() $E(a,b) \backslash U_g^*L(r_0, s_0)$, denoted by
$E(a,b) \backslash U_g^*L(r_0, s_0)$, denoted by ![]() $\{F_1,\ldots, F_{k+2}\}$. Lemma 6.1 in [Reference Hind and ZhangHZ21] also implies that for each
$\{F_1,\ldots, F_{k+2}\}$. Lemma 6.1 in [Reference Hind and ZhangHZ21] also implies that for each ![]() $i \in \{1,\ldots, k+2\}$, we have
$i \in \{1,\ldots, k+2\}$, we have ![]() ${\rm ind}(F_i) = 1$. Moreover, since we have only one positive end, the argument in the proof of the ‘only if’ part of Theorem 1.4 in [Reference Hind and ZhangHZ21] implies that all but one of the
${\rm ind}(F_i) = 1$. Moreover, since we have only one positive end, the argument in the proof of the ‘only if’ part of Theorem 1.4 in [Reference Hind and ZhangHZ21] implies that all but one of the ![]() $F_i$ are planes and the remaining curve is a cylinder with positive end on
$F_i$ are planes and the remaining curve is a cylinder with positive end on ![]() $\gamma _b$. Without loss of generality, assume
$\gamma _b$. Without loss of generality, assume ![]() $F_1$ is the cylinder. Moreover, suppose the negative end of
$F_1$ is the cylinder. Moreover, suppose the negative end of ![]() $F_i$ has type
$F_i$ has type ![]() $(-k_i, -l_i)$. Since the negative ends bound a cycle in
$(-k_i, -l_i)$. Since the negative ends bound a cycle in ![]() $T^* L(r_0, s_0)$ we see
$T^* L(r_0, s_0)$ we see
 \begin{equation} \sum_{i=1}^{k+2} k_i = \sum_{i=1}^{k+2} l_i = 0. \end{equation}
\begin{equation} \sum_{i=1}^{k+2} k_i = \sum_{i=1}^{k+2} l_i = 0. \end{equation} So far, we have implicitly assumed our ![]() $J_0$ is generic in order to guarantee curves of non-negative index. However, we would like to work with a
$J_0$ is generic in order to guarantee curves of non-negative index. However, we would like to work with a ![]() $J_0$ such that the
$J_0$ such that the ![]() $z_1$ and
$z_1$ and ![]() $z_2$ axes are complex (and, hence, are finite energy planes, say
$z_2$ axes are complex (and, hence, are finite energy planes, say ![]() $P_1$ and
$P_1$ and ![]() $P_2$, asymptotic to
$P_2$, asymptotic to ![]() $\gamma _a$ and
$\gamma _a$ and ![]() $\gamma _b$, respectively). As these axes are disjoint from
$\gamma _b$, respectively). As these axes are disjoint from ![]() $L(r_0, s_0)$, it is easy to check that they are not covered by any of our limiting curves, and so we may still assume regularity.
$L(r_0, s_0)$, it is easy to check that they are not covered by any of our limiting curves, and so we may still assume regularity.
Since the axes are complex, positivity of intersection implies that for ![]() $i \ge 2$ the
$i \ge 2$ the ![]() $F_i$ are asymptotic to a Reeb orbits representing classes with
$F_i$ are asymptotic to a Reeb orbits representing classes with ![]() $k_i \le 0$ and
$k_i \le 0$ and ![]() $l_i \le 0$. As the curves have index
$l_i \le 0$. As the curves have index ![]() $1$, the index formula implies that
$1$, the index formula implies that ![]() $k_i + l_i =-1$, so the only possibilities are
$k_i + l_i =-1$, so the only possibilities are ![]() $(k_i, l_i) = (-1,0)$ or
$(k_i, l_i) = (-1,0)$ or ![]() $(k_i, l_i) = (0,-1)$. Identifying any matching asymptotic orbits and adding a disk inside
$(k_i, l_i) = (0,-1)$. Identifying any matching asymptotic orbits and adding a disk inside ![]() $E(\epsilon, \epsilon S)$, our holomorphic building can be compactified to form a homology class in the ellipsoid with boundary
$E(\epsilon, \epsilon S)$, our holomorphic building can be compactified to form a homology class in the ellipsoid with boundary ![]() $\gamma _b$. Since
$\gamma _b$. Since ![]() $P_1$ represents a class with boundary
$P_1$ represents a class with boundary ![]() $\gamma _a$, it has intersection number
$\gamma _a$, it has intersection number ![]() $+1$ with the compactified building. Then by positivity of intersection, we see that at most one
$+1$ with the compactified building. Then by positivity of intersection, we see that at most one ![]() $F_i$ is asymptotic to an orbit in the class
$F_i$ is asymptotic to an orbit in the class ![]() $(0,-1)$.
$(0,-1)$.
Suppose first that exactly one ![]() $F_i$ for
$F_i$ for ![]() $i \ge 2$ is asymptotic to an orbit of type
$i \ge 2$ is asymptotic to an orbit of type ![]() $(0,-1)$. Then
$(0,-1)$. Then ![]() $F_1$ is asymptotic to an orbit of type
$F_1$ is asymptotic to an orbit of type ![]() $(k,1)$ as required.
$(k,1)$ as required.
Alternatively, all ![]() $F_i$ for
$F_i$ for ![]() $i \ge 2$ are asymptotic to orbits of type
$i \ge 2$ are asymptotic to orbits of type ![]() $(-1,0)$ and
$(-1,0)$ and ![]() $F_1$ is asymptotic to an orbit of type
$F_1$ is asymptotic to an orbit of type ![]() $(k+1,0)$. In this case the limiting building has intersection number at least
$(k+1,0)$. In this case the limiting building has intersection number at least ![]() $k+1$ with
$k+1$ with ![]() $P_2$. However we can compute Siefring's generalized intersection number (see (4-3) in [Reference SiefringSie11]) to be
$P_2$. However we can compute Siefring's generalized intersection number (see (4-3) in [Reference SiefringSie11]) to be
Indeed, trivializing the contact planes in ![]() $E(a,b)$ along
$E(a,b)$ along ![]() $\partial P_2$ by using an identification
$\partial P_2$ by using an identification ![]() $\Phi$ with the
$\Phi$ with the ![]() $z_1$ plane, in the notation from [Reference SiefringSie11] we have
$z_1$ plane, in the notation from [Reference SiefringSie11] we have ![]() $i^{\Phi }(P_2, P_2)=0$ and
$i^{\Phi }(P_2, P_2)=0$ and ![]() $\Omega ^{\Phi }(P_2, P_2) = k$.
$\Omega ^{\Phi }(P_2, P_2) = k$.
As our limiting holomorphic building has a single unmatched positive end on ![]() $\gamma _b$ and (after we compactify with the disk inside
$\gamma _b$ and (after we compactify with the disk inside ![]() $E(\epsilon, \epsilon S)$) is homotopic relative to its compactified positive boundary to
$E(\epsilon, \epsilon S)$) is homotopic relative to its compactified positive boundary to ![]() $P_2$, Theorem 2.2 from [Reference SiefringSie11] implies that
$P_2$, Theorem 2.2 from [Reference SiefringSie11] implies that ![]() $k$ is an upper bound for the intersections between the curves in our limiting building and
$k$ is an upper bound for the intersections between the curves in our limiting building and ![]() $P_2$. This is a contradiction if the building contains
$P_2$. This is a contradiction if the building contains ![]() $k+1$ planes asymptotic to
$k+1$ planes asymptotic to ![]() $(-1,0)$.
$(-1,0)$.
Remark 4.2 For an alternative proof of Lemma 4.1, at least for a carefully chosen ![]() $J_0$, we observe it is, in fact, possible to write down such a holomorphic cylinder directly. To do this we fix a circle
$J_0$, we observe it is, in fact, possible to write down such a holomorphic cylinder directly. To do this we fix a circle ![]() $\Gamma = \{\theta _1 - k \theta _2 =0 \}$ in the torus
$\Gamma = \{\theta _1 - k \theta _2 =0 \}$ in the torus ![]() $\mathbb {T}^2$, and identify all fibers of the moment map
$\mathbb {T}^2$, and identify all fibers of the moment map ![]() $\mu$ with the same
$\mu$ with the same ![]() $\mathbb {T}^2$, suitably collapsed over the axes. In the moment image
$\mathbb {T}^2$, suitably collapsed over the axes. In the moment image ![]() $\mu (E(a,b))$ let
$\mu (E(a,b))$ let ![]() $\sigma$ be a curve which coincides with the line through
$\sigma$ be a curve which coincides with the line through ![]() $(r_0, s_0)$ of slope
$(r_0, s_0)$ of slope ![]() $ {1}/{k}$ at one end, and the vertical line through
$ {1}/{k}$ at one end, and the vertical line through ![]() $(0,b)$ at the other. Then
$(0,b)$ at the other. Then ![]() $\sigma \times \Gamma$ is a cylinder in
$\sigma \times \Gamma$ is a cylinder in ![]() $E(a,b)$, which is symplectic provided
$E(a,b)$, which is symplectic provided ![]() $\sigma$ never has slope
$\sigma$ never has slope ![]() $-k$. We can find such paths exactly because
$-k$. We can find such paths exactly because ![]() $b > ka$. Moreover, our cylinder coincides with the trivial cylinder over the Reeb orbits at each end, so we can find an almost complex structure
$b > ka$. Moreover, our cylinder coincides with the trivial cylinder over the Reeb orbits at each end, so we can find an almost complex structure ![]() $J_0$ making the cylinder holomorphic.
$J_0$ making the cylinder holomorphic.
4.1.2 Degenerations of moduli spaces
Here we analyze possible degenerations of a moduli space of genus ![]() $0$ curves with Fredholm index bounded below by the number of negative ends. In any degeneration we can isolate a particular limiting curve, and the main Lemma 4.4 shows that areas of curves in the new moduli space are bounded above by the areas of the original moduli space.
$0$ curves with Fredholm index bounded below by the number of negative ends. In any degeneration we can isolate a particular limiting curve, and the main Lemma 4.4 shows that areas of curves in the new moduli space are bounded above by the areas of the original moduli space.
Given an isotopy of Lagrangian submanifolds ![]() $\{L_t\}_{t \in [0,1]}$, corresponding compatible almost complex structures
$\{L_t\}_{t \in [0,1]}$, corresponding compatible almost complex structures ![]() $J_t$ on the complement of
$J_t$ on the complement of ![]() $L_t$, and a sequence of
$L_t$, and a sequence of ![]() $J_{t_n}$-holomorphic curves
$J_{t_n}$-holomorphic curves ![]() $\{C_n\}_{n \in \mathbb {N}}$ with (negative) ends on the Lagrangian submanifolds
$\{C_n\}_{n \in \mathbb {N}}$ with (negative) ends on the Lagrangian submanifolds ![]() $\{L_{t_n}\}_{n \in \mathbb {N}}$, the standard SFT-compactness implies that if
$\{L_{t_n}\}_{n \in \mathbb {N}}$, the standard SFT-compactness implies that if ![]() $t_n \to t_*$ and the
$t_n \to t_*$ and the ![]() $C_n$ have bounded area, for example if they appear in the same moduli space, then the
$C_n$ have bounded area, for example if they appear in the same moduli space, then the ![]() $C_n$ converge to a
$C_n$ converge to a ![]() $J_{t_*}$-holomorphic building
$J_{t_*}$-holomorphic building ![]() $C_{\rm lim}$. To be precise, the standard SFT-compactness applies to a sequence of
$C_{\rm lim}$. To be precise, the standard SFT-compactness applies to a sequence of ![]() ${J_n}$-holomorphic curves
${J_n}$-holomorphic curves ![]() $C_n$ in a fixed cobordism, however we can use Fukaya's trick (see § 2.1 in [Reference Shelukhin, Tonkonog and ViannaSTV18]) to transfer the moving boundary conditions on
$C_n$ in a fixed cobordism, however we can use Fukaya's trick (see § 2.1 in [Reference Shelukhin, Tonkonog and ViannaSTV18]) to transfer the moving boundary conditions on ![]() $L_{t_n}$ to a sequence of almost complex structures on a fixed cobordism as required. Hence, we still obtain compactness as in [Reference Bourgeois, Eliashberg, Hofer, Wysocki and ZehnderBEH+03]. A careful study of
$L_{t_n}$ to a sequence of almost complex structures on a fixed cobordism as required. Hence, we still obtain compactness as in [Reference Bourgeois, Eliashberg, Hofer, Wysocki and ZehnderBEH+03]. A careful study of ![]() $C_{\rm lim}$ plays an important role in the proof of obstruction (I) in Theorems 2.11 and 2.12. In particular, the following technical lemma, Lemma 4.3, is useful to us.
$C_{\rm lim}$ plays an important role in the proof of obstruction (I) in Theorems 2.11 and 2.12. In particular, the following technical lemma, Lemma 4.3, is useful to us.
Let ![]() $C$ denote a curve with
$C$ denote a curve with ![]() ${\rm ind}(C) = e$, one positive end on
${\rm ind}(C) = e$, one positive end on ![]() $\gamma _b$, and
$\gamma _b$, and ![]() $e$-many negative ends on the Lagrangian torus
$e$-many negative ends on the Lagrangian torus ![]() $L_0$. For instance, the cylinder provided by Lemma 4.1 satisfies this condition with
$L_0$. For instance, the cylinder provided by Lemma 4.1 satisfies this condition with ![]() $L_o = L(r_0, s_0)$, since by (11)
$L_o = L(r_0, s_0)$, since by (11)
Denote by ![]() $\mathcal {M}_{C}(t)$ for
$\mathcal {M}_{C}(t)$ for ![]() $t \in [0,1]$ the moduli space corresponding to the curve
$t \in [0,1]$ the moduli space corresponding to the curve ![]() $C$ with boundary conditions on
$C$ with boundary conditions on ![]() $L_t$. Suppose the universal moduli space of the
$L_t$. Suppose the universal moduli space of the ![]() $\mathcal {M}_C(t)$ is not compact, that is, there exist a degeneration at
$\mathcal {M}_C(t)$ is not compact, that is, there exist a degeneration at ![]() $t_* \in [0,1]$ with a limiting building
$t_* \in [0,1]$ with a limiting building ![]() $C_{\rm lim} \notin \mathcal {M}_C(t_*)$. The proof of Lemma 3.7 in [Reference Hind and OpshteinHO20, p. 552] shows there exists a curve of
$C_{\rm lim} \notin \mathcal {M}_C(t_*)$. The proof of Lemma 3.7 in [Reference Hind and OpshteinHO20, p. 552] shows there exists a curve of ![]() $C_{\rm lim}$ in
$C_{\rm lim}$ in ![]() $E(a,b) \backslash U_g^*L_{t_*}$, which we denote by
$E(a,b) \backslash U_g^*L_{t_*}$, which we denote by ![]() $C_0$, having
$C_0$, having ![]() ${\rm ind}(C_0) \geq \# \,\mbox {negative ends of } C_0$. We denote by
${\rm ind}(C_0) \geq \# \,\mbox {negative ends of } C_0$. We denote by ![]() $C_1,\ldots, C_k$ the components (as connected sub-buildings of
$C_1,\ldots, C_k$ the components (as connected sub-buildings of ![]() $C_{\rm lim}$ consisting of curves in
$C_{\rm lim}$ consisting of curves in ![]() $E(a,b) \backslash U_g^*L_{t_*}$ and in the symplectization
$E(a,b) \backslash U_g^*L_{t_*}$ and in the symplectization ![]() $T^*L_{t_*}\backslash 0_{L_{t_*}}$) of the complement of
$T^*L_{t_*}\backslash 0_{L_{t_*}}$) of the complement of ![]() $C_0$ in
$C_0$ in ![]() $C_{\rm lim}$ such that each
$C_{\rm lim}$ such that each ![]() $C_i$ matches with
$C_i$ matches with ![]() $C_0$ at only one negative end of
$C_0$ at only one negative end of ![]() $C_0$. See Figure 9 for an example of
$C_0$. See Figure 9 for an example of ![]() $C_{\rm lim}$. Suppose
$C_{\rm lim}$. Suppose ![]() $C_i$ for
$C_i$ for ![]() $i \in \{1,\ldots, k\}$ admits
$i \in \{1,\ldots, k\}$ admits ![]() $e_i$-many negative ends, while the cardinality of the unmatched ends of
$e_i$-many negative ends, while the cardinality of the unmatched ends of ![]() $C_0$ is denoted by
$C_0$ is denoted by ![]() $e_0$ (hence, the total number of the negative ends of
$e_0$ (hence, the total number of the negative ends of ![]() $C_{\rm lim}$ is
$C_{\rm lim}$ is ![]() $\sum _{i=0}^k e_i$). Finally, as shown in Figure 9, suppose the negative ends of the curves in
$\sum _{i=0}^k e_i$). Finally, as shown in Figure 9, suppose the negative ends of the curves in ![]() $E(a,b) \backslash U_g^*L_{t_*}$ from the component
$E(a,b) \backslash U_g^*L_{t_*}$ from the component ![]() $C_i$ have type
$C_i$ have type ![]() $\{(-m_i^{j}, -n_i^{j})\}_{j = 1,\ldots, l_i}$. Then we have the following result.
$\{(-m_i^{j}, -n_i^{j})\}_{j = 1,\ldots, l_i}$. Then we have the following result.
Lemma 4.3 Suppose ![]() $C_0$ contains the positive end
$C_0$ contains the positive end ![]() $\gamma _b$. Then, with
$\gamma _b$. Then, with ![]() $(-m_i^j, -n_i^j)$ defined as above, we have
$(-m_i^j, -n_i^j)$ defined as above, we have ![]() $\sum _{i=1}^k \sum _{j=1}^{l_i} (m_i^j + n_i^j) \leq 0$.
$\sum _{i=1}^k \sum _{j=1}^{l_i} (m_i^j + n_i^j) \leq 0$.

Figure 9. A limit curve in ![]() $\mathcal {M}_C(t_*)$.
$\mathcal {M}_C(t_*)$.
Outline of the proof of Lemma 4.3. We will compare the indices of the various components ![]() $C_i$ with the index of the limiting building using (15). Together with an analysis of matching ends we will derive the result.
$C_i$ with the index of the limiting building using (15). Together with an analysis of matching ends we will derive the result.
Proof of Lemma 4.3 First, by the index matching formula (15), we have
 \begin{equation} e = {\rm ind}(C_{\rm lim}) = \bigg(\sum_{i=0}^k {\rm ind}(C_i) \bigg) - k, \quad \mbox{which is} \quad \sum_{i=0}^k {\rm ind}(C_i) = e+k. \end{equation}
\begin{equation} e = {\rm ind}(C_{\rm lim}) = \bigg(\sum_{i=0}^k {\rm ind}(C_i) \bigg) - k, \quad \mbox{which is} \quad \sum_{i=0}^k {\rm ind}(C_i) = e+k. \end{equation}
Since ![]() $e = \#\,\mbox {negative ends of } C_{\rm lim} = e_0 + \cdots + e_k$, by regrouping these terms, (17) is equivalent to the relation
$e = \#\,\mbox {negative ends of } C_{\rm lim} = e_0 + \cdots + e_k$, by regrouping these terms, (17) is equivalent to the relation ![]() $\big ({\rm ind}(C_0) - (e_0+k)\big ) + \sum _{i=1}^k ({\rm ind}(C_i) - e_i) =0.$ Moreover, since
$\big ({\rm ind}(C_0) - (e_0+k)\big ) + \sum _{i=1}^k ({\rm ind}(C_i) - e_i) =0.$ Moreover, since ![]() $e_0 +k$ equals the
$e_0 +k$ equals the ![]() $\# \, \mbox {negative ends of } C_0$, by assumption,
$\# \, \mbox {negative ends of } C_0$, by assumption, ![]() ${\rm ind}(C_0) \geq e_0+k$, so
${\rm ind}(C_0) \geq e_0+k$, so
 \begin{equation} \sum_{i=1}^k ({\rm ind}(C_i) - e_i) \leq 0. \end{equation}
\begin{equation} \sum_{i=1}^k ({\rm ind}(C_i) - e_i) \leq 0. \end{equation}
Second, let us focus on a component ![]() $C_i$ for
$C_i$ for ![]() $i \in \{1,\ldots, k\}$. Since
$i \in \{1,\ldots, k\}$. Since ![]() $C_0$ already occupies the only positive end
$C_0$ already occupies the only positive end ![]() $\gamma _b$, each such
$\gamma _b$, each such ![]() $C_i$ only has ends on
$C_i$ only has ends on ![]() $L_{t_*}$. By a further decomposition, suppose
$L_{t_*}$. By a further decomposition, suppose ![]() $C_i$ consists of
$C_i$ consists of ![]() $Q_i$-many sub-components lying entirely in the symplectization
$Q_i$-many sub-components lying entirely in the symplectization ![]() $T^*L_{t_*} \backslash 0_{L_{t_*}}$, denoted by
$T^*L_{t_*} \backslash 0_{L_{t_*}}$, denoted by ![]() $\{u_i^j\}_{j=1,\ldots, Q_i}$. Each
$\{u_i^j\}_{j=1,\ldots, Q_i}$. Each ![]() $u_i^j$ has
$u_i^j$ has ![]() $e_i^j$-many negative ends and
$e_i^j$-many negative ends and ![]() $s_i^j$-many positive ends. In particular,
$s_i^j$-many positive ends. In particular, ![]() $\sum _{j=1}^{Q_i} e_i^j = e_i$. Similarly,
$\sum _{j=1}^{Q_i} e_i^j = e_i$. Similarly, ![]() $C_i$ consists of
$C_i$ consists of ![]() $R_i$-many curves in
$R_i$-many curves in ![]() $E(a,b) \backslash U_g^*L_{t_*}$, denoted by
$E(a,b) \backslash U_g^*L_{t_*}$, denoted by ![]() $\{v_i^j\}_{j=1,\ldots, R_i}$. Each
$\{v_i^j\}_{j=1,\ldots, R_i}$. Each ![]() $v_i^j$ has
$v_i^j$ has ![]() $r^j_i$-many negative ends on
$r^j_i$-many negative ends on ![]() $L_{t_*}$, of type
$L_{t_*}$, of type ![]() $\{(-m_i^{j,l}, -n_i^{j, l})\}_{l = 1,\ldots, r_i^j}$. See Figure 10 for an example of this decomposition of
$\{(-m_i^{j,l}, -n_i^{j, l})\}_{l = 1,\ldots, r_i^j}$. See Figure 10 for an example of this decomposition of ![]() $C_i$. Note that
$C_i$. Note that ![]() $\sum _{j=1}^{Q_i} s_i^j = (\sum _{j=1}^{R_i} r_i^j) + 1$ since there is one extra end matching with
$\sum _{j=1}^{Q_i} s_i^j = (\sum _{j=1}^{R_i} r_i^j) + 1$ since there is one extra end matching with ![]() $C_0$. By Proposition 3.4(b) in [Reference Hind and OpshteinHO20], curves
$C_0$. By Proposition 3.4(b) in [Reference Hind and OpshteinHO20], curves ![]() $u_i^j$ in the symplectization have index
$u_i^j$ in the symplectization have index ![]() ${\rm ind}(u_i^j) = 2s_i^j + e_i^j -2$. In addition, curves
${\rm ind}(u_i^j) = 2s_i^j + e_i^j -2$. In addition, curves ![]() $v_i^j$ in
$v_i^j$ in ![]() $E(a,b) \backslash U_g^*L_{t_*}$ have index
$E(a,b) \backslash U_g^*L_{t_*}$ have index ![]() ${\rm ind}(v_i^j) = r_i^j -2 + 2 \sum _{l=1}^{r_i^j} (m_i^{j,l} + n_i^{j, l})$ by the formula (11). Then by the index matching formula (15) again,
${\rm ind}(v_i^j) = r_i^j -2 + 2 \sum _{l=1}^{r_i^j} (m_i^{j,l} + n_i^{j, l})$ by the formula (11). Then by the index matching formula (15) again,
 \begin{align*} {\rm ind}(C_i) - e_i & = \bigg(\sum_{j=1}^{R_i} {\rm ind}(v_i^j) + \sum_{j=1}^{Q_i} {\rm ind}(u_i^j) - \sum_{j=1}^{R_i} r_i^j \bigg) - e_i\\ & = \sum_{j=1}^{R_i} \bigg(r_i^j -2 + 2 \sum_{l=1}^{r_i^j} (m_i^{j,l} + n_i^{j, l})\bigg) \\ &\quad + \sum_{j=1}^{Q_i} \big(2s_i^j + e_i^j -2 \big) - \sum_{j=1}^{R_i} r_i^j - \sum_{j=1}^{Q_i} e_i^j\\ & = 2 \bigg(- R_i + \sum_{j=1}^{R_i} \sum_{l=1}^{r_i^j}(m_i^{j,l} + n_i^{j, l}) - Q_i + \sum_{j=1}^{Q_i} s_i^j \bigg). \end{align*}
\begin{align*} {\rm ind}(C_i) - e_i & = \bigg(\sum_{j=1}^{R_i} {\rm ind}(v_i^j) + \sum_{j=1}^{Q_i} {\rm ind}(u_i^j) - \sum_{j=1}^{R_i} r_i^j \bigg) - e_i\\ & = \sum_{j=1}^{R_i} \bigg(r_i^j -2 + 2 \sum_{l=1}^{r_i^j} (m_i^{j,l} + n_i^{j, l})\bigg) \\ &\quad + \sum_{j=1}^{Q_i} \big(2s_i^j + e_i^j -2 \big) - \sum_{j=1}^{R_i} r_i^j - \sum_{j=1}^{Q_i} e_i^j\\ & = 2 \bigg(- R_i + \sum_{j=1}^{R_i} \sum_{l=1}^{r_i^j}(m_i^{j,l} + n_i^{j, l}) - Q_i + \sum_{j=1}^{Q_i} s_i^j \bigg). \end{align*}
Now, for such a decomposition of ![]() $C_i$ having genus
$C_i$ having genus ![]() $0$, we can associate a tree to it by adding a vertex for each curve and each asymptotic end, and an edge between the vertex for a curve and each of its asymptotic end. We identify the two vertices corresponding to matching asymptotic ends. Since the Euler characteristic of a tree is always
$0$, we can associate a tree to it by adding a vertex for each curve and each asymptotic end, and an edge between the vertex for a curve and each of its asymptotic end. We identify the two vertices corresponding to matching asymptotic ends. Since the Euler characteristic of a tree is always ![]() $1$, we have
$1$, we have
 \[ R_i + Q_i - \bigg(\sum_{j=1}^{Q_i} s_i^j -1\bigg) = 1, \quad \mbox{which implies} \ Q_i + R_i - \sum_{j=1}^{Q_i} s_i^j = 0. \]
\[ R_i + Q_i - \bigg(\sum_{j=1}^{Q_i} s_i^j -1\bigg) = 1, \quad \mbox{which implies} \ Q_i + R_i - \sum_{j=1}^{Q_i} s_i^j = 0. \]
Therefore, we obtain the following relation,
 \[ {\rm ind}(C_i) - e_i = 2 \bigg(\sum_{j=1}^{R_i} \sum_{l=1}^{r_i^j}(m_i^{j,l} + n_i^{j, l}) \bigg). \]
\[ {\rm ind}(C_i) - e_i = 2 \bigg(\sum_{j=1}^{R_i} \sum_{l=1}^{r_i^j}(m_i^{j,l} + n_i^{j, l}) \bigg). \]
Finally, summing over all ![]() $i = \{1,\ldots, k\}$, we have
$i = \{1,\ldots, k\}$, we have
 \begin{align*} 2 \sum_{i=1}^k \sum_{j=1}^{l_i} (m_i^j + n_i^j) & = 2 \sum_{i=1}^k \sum_{j=1}^{R_i} \sum_{l=1}^{r_i^j}(m_i^{j,l} + n_i^{j, l}) \\ & = 2 \sum_{i=1}^k ({\rm ind}(C_i) - e_i) \leq 0, \end{align*}
\begin{align*} 2 \sum_{i=1}^k \sum_{j=1}^{l_i} (m_i^j + n_i^j) & = 2 \sum_{i=1}^k \sum_{j=1}^{R_i} \sum_{l=1}^{r_i^j}(m_i^{j,l} + n_i^{j, l}) \\ & = 2 \sum_{i=1}^k ({\rm ind}(C_i) - e_i) \leq 0, \end{align*}
where ![]() $l_i = \sum _{j=1}^{R_i} r_i^j$ and the last step comes from (18). Thus, we complete the proof.
$l_i = \sum _{j=1}^{R_i} r_i^j$ and the last step comes from (18). Thus, we complete the proof.

Figure 10. A decomposition of ![]() $C_i$.
$C_i$.
A corollary of Lemma 4.3 is the following useful result. Denote by ![]() $\mathcal {M}_{C_0}(t)$ the moduli space of the curve
$\mathcal {M}_{C_0}(t)$ the moduli space of the curve ![]() $C_0$ in Lemma 4.3 (so, in particular, we are assuming the curves have a single positive end
$C_0$ in Lemma 4.3 (so, in particular, we are assuming the curves have a single positive end ![]() $\gamma _b$) with moving boundary conditions on
$\gamma _b$) with moving boundary conditions on ![]() $L_t$. Recall that
$L_t$. Recall that ![]() $L_t$ is a Lagrangian isotopy which will cover a path
$L_t$ is a Lagrangian isotopy which will cover a path ![]() $\gamma (t) = (r(t), s(t))$ in the shape of
$\gamma (t) = (r(t), s(t))$ in the shape of ![]() $E(a,b)$. Denote by
$E(a,b)$. Denote by ![]() ${\rm area}_{C_0}(t)$ the (time-dependent) area of a curve in
${\rm area}_{C_0}(t)$ the (time-dependent) area of a curve in ![]() $\mathcal {M}_{C_0}(t)$ with boundary on
$\mathcal {M}_{C_0}(t)$ with boundary on ![]() $L_t$, and similarly define
$L_t$, and similarly define ![]() ${\rm area}_C(t)$ where
${\rm area}_C(t)$ where ![]() $C$ is the curve we started from whose moduli space degenerated into
$C$ is the curve we started from whose moduli space degenerated into ![]() $C_{\rm lim}$. We note that these area formulas only depend on the moduli space of
$C_{\rm lim}$. We note that these area formulas only depend on the moduli space of ![]() $C$ or
$C$ or ![]() $C_0$, and actually only on the homology class of
$C_0$, and actually only on the homology class of ![]() $C_0$ and
$C_0$ and ![]() $C$. Thus, they are well defined even if the corresponding moduli space is empty and, in particular,
$C$. Thus, they are well defined even if the corresponding moduli space is empty and, in particular, ![]() ${\rm area}_C(t)$ is defined when
${\rm area}_C(t)$ is defined when ![]() $t > t_*$. Recall that
$t > t_*$. Recall that ![]() $t_* \in [0,1]$ is the moment where
$t_* \in [0,1]$ is the moment where ![]() $C$ degenerates.
$C$ degenerates.
Proposition 4.4 Suppose ![]() $r(t) / s(t)$ is non-increasing with respect the parameter
$r(t) / s(t)$ is non-increasing with respect the parameter ![]() $t \in [0,1]$ and the moduli space of
$t \in [0,1]$ and the moduli space of ![]() $C$ degenerates at time
$C$ degenerates at time ![]() $t_*$. Then
$t_*$. Then ![]() ${\rm area}_{C_0}(t) \leq {\rm area}_{C}(t)$ for all
${\rm area}_{C_0}(t) \leq {\rm area}_{C}(t)$ for all ![]() $t \in [t_*,1]$.
$t \in [t_*,1]$.
Proof. We know that ![]() ${\rm area}_{C_0}(t_*) \leq {\rm area}_{C_{\rm lim}}(t_*) = {\rm area}_{C}(t_*)$ since
${\rm area}_{C_0}(t_*) \leq {\rm area}_{C_{\rm lim}}(t_*) = {\rm area}_{C}(t_*)$ since ![]() $C_0$ is a component of
$C_0$ is a component of ![]() $C_{\rm lim}$, it suffices to prove the conclusion for
$C_{\rm lim}$, it suffices to prove the conclusion for ![]() $t \in (t_*,1]$. Arguing by contradiction, suppose there exists some
$t \in (t_*,1]$. Arguing by contradiction, suppose there exists some ![]() $t' \in (t_*, 1]$ such that
$t' \in (t_*, 1]$ such that ![]() ${\rm area}_{C_0}(t') > {\rm area}_{C}(t')$. Note that for any
${\rm area}_{C_0}(t') > {\rm area}_{C}(t')$. Note that for any ![]() $t \in [t_*,1]$, we have
$t \in [t_*,1]$, we have
 \begin{align*} {\rm area}_C(t) & = \sum_{i=0}^k {\rm area}_{C_i}(t) \\ & = {\rm area}_{C_0}(t) + \bigg(\sum_{i=1}^k\sum_{j=1}^{l_i} m_i^j\bigg) r_t + \bigg(\sum_{i=1}^k\sum_{j=1}^{l_i} n_i^j\bigg) s_t, \end{align*}
\begin{align*} {\rm area}_C(t) & = \sum_{i=0}^k {\rm area}_{C_i}(t) \\ & = {\rm area}_{C_0}(t) + \bigg(\sum_{i=1}^k\sum_{j=1}^{l_i} m_i^j\bigg) r_t + \bigg(\sum_{i=1}^k\sum_{j=1}^{l_i} n_i^j\bigg) s_t, \end{align*}
since, for homological reasons, curves in the symplectization contribute ![]() $0$ to the area. For brevity, let
$0$ to the area. For brevity, let ![]() $M := \sum _{i=1}^k\sum _{j=1}^{l_i} m_i^j$ and
$M := \sum _{i=1}^k\sum _{j=1}^{l_i} m_i^j$ and ![]() $N: = \sum _{i=1}^k\sum _{j=1}^{l_i} n_i^j$.
$N: = \sum _{i=1}^k\sum _{j=1}^{l_i} n_i^j$.
Arguing by contradiction, the relation ![]() ${\rm area}_{C_0}(t') > {\rm area}_{C}(t')$ above implies that
${\rm area}_{C_0}(t') > {\rm area}_{C}(t')$ above implies that ![]() $Mr_{t'} + Ns_{t'} <0$. Meanwhile, since at
$Mr_{t'} + Ns_{t'} <0$. Meanwhile, since at ![]() $t= t_*$ each
$t= t_*$ each ![]() $C_i$ for
$C_i$ for ![]() $i \in \{1,\ldots, k\}$ is a holomorphic curve, we have
$i \in \{1,\ldots, k\}$ is a holomorphic curve, we have ![]() $\sum _{i=1}^k {\rm area}_{C_i}(t_*) >0$, which is equivalent to
$\sum _{i=1}^k {\rm area}_{C_i}(t_*) >0$, which is equivalent to ![]() $Mr_{t_*} + Ns_{t_*} >0$. Hence, since the function
$Mr_{t_*} + Ns_{t_*} >0$. Hence, since the function ![]() $Mr_t + Ns_t$ is continuous with respect to time
$Mr_t + Ns_t$ is continuous with respect to time ![]() $t$, the intermediate value theorem implies that there exists
$t$, the intermediate value theorem implies that there exists ![]() $t_{{\dagger} } \in (t_*, t')$ such that
$t_{{\dagger} } \in (t_*, t')$ such that
There are two cases as follows, see Figure 11, depending on the relative position between ![]() $(r_{t_*}, s_{t_*})$ and the line
$(r_{t_*}, s_{t_*})$ and the line ![]() $Mr + Ns =0$. In the left picture, the condition
$Mr + Ns =0$. In the left picture, the condition ![]() $Mr_{t_*} + N s_{t_*} >0$ implies that the lower half plane given by the division of the line
$Mr_{t_*} + N s_{t_*} >0$ implies that the lower half plane given by the division of the line ![]() $Mr + Ns = 0$ is the positive region. In particular, for any
$Mr + Ns = 0$ is the positive region. In particular, for any ![]() $r = s(>0)$, we have
$r = s(>0)$, we have
This contradicts Lemma 4.3. In the right picture, the condition ![]() $Mr_{t_*} + N s_{t_*} >0$ implies that the upper half plane given by the division of the line
$Mr_{t_*} + N s_{t_*} >0$ implies that the upper half plane given by the division of the line ![]() $Mr + Ns = 0$ is the positive region. By our hypothesis that
$Mr + Ns = 0$ is the positive region. By our hypothesis that ![]() $ {r(t)}/{s(t)}$ is non-increasing,
$ {r(t)}/{s(t)}$ is non-increasing, ![]() $\gamma |_{t >t_*}$ remains above the line
$\gamma |_{t >t_*}$ remains above the line ![]() $Mr + Ns = 0$, contradicting the existence of a
$Mr + Ns = 0$, contradicting the existence of a ![]() $t_{{\dagger} }$.
$t_{{\dagger} }$.

Figure 11. Relative position between ![]() $(r_{t_*}, s_{t_*})$ and
$(r_{t_*}, s_{t_*})$ and ![]() $Mr + Ns = 0$.
$Mr + Ns = 0$.
4.2 Proof of obstruction (I) in Theorems 2.11 and 2.12
Outline. We will trace the moduli space of the cylinder constructed in Lemma 4.1 under our Lagrangian isotopy. The idea is that if an isotopy as in obstruction (I) existed, then the area of any curves would decrease to ![]() $0$, and hence as holomorphic curves have positive area we deduce there must be a degeneration to a non-trivial building. But by Proposition 4.4, we can then work instead with a moduli space of curves from the limiting building whose areas would also decrease to
$0$, and hence as holomorphic curves have positive area we deduce there must be a degeneration to a non-trivial building. But by Proposition 4.4, we can then work instead with a moduli space of curves from the limiting building whose areas would also decrease to ![]() $0$, giving a contradiction.
$0$, giving a contradiction.
Proof. Suppose by contradiction that a path ![]() $\gamma = \{(r_t, s_t)\}_{t \in [0,1]}$ as in obstruction (I) admits a lift
$\gamma = \{(r_t, s_t)\}_{t \in [0,1]}$ as in obstruction (I) admits a lift ![]() $\{L_t\}_{t \in [0,1]}$.
$\{L_t\}_{t \in [0,1]}$.
Denote by ![]() ${\mathcal {M}}_1(t)$ the moduli space consisting of cylinders with positive end
${\mathcal {M}}_1(t)$ the moduli space consisting of cylinders with positive end ![]() $\gamma _b$ and negative end
$\gamma _b$ and negative end ![]() $\gamma _{k,1}$ on the moving boundary
$\gamma _{k,1}$ on the moving boundary ![]() $L_t$. By Lemma 4.1, we know that
$L_t$. By Lemma 4.1, we know that ![]() ${\mathcal {M}}_1(0) \neq \emptyset$, that is, there exists a
${\mathcal {M}}_1(0) \neq \emptyset$, that is, there exists a ![]() $C^{(1)} \in {\mathcal {M}}_1(0)$. As before, the area of curves in
$C^{(1)} \in {\mathcal {M}}_1(0)$. As before, the area of curves in ![]() ${\mathcal {M}}_1(t)$ will be denoted by
${\mathcal {M}}_1(t)$ will be denoted by ![]() ${\rm area}_{C^{(1)}}(t)$.
${\rm area}_{C^{(1)}}(t)$.
By (11) each ![]() $C^{(1)}_t \in \mathcal {M}_1(t)$ has its index equal to
$C^{(1)}_t \in \mathcal {M}_1(t)$ has its index equal to
 \begin{align*} {\rm ind}(C^{(1)}_t) & = (1+1-2) + 0 + (2 + 2k + 1) - \big (2(k+1) + \tfrac{1}{2} - \tfrac{1}{2}\big) \\ & = (2k+3) - (2k+2) = 1. \end{align*}
\begin{align*} {\rm ind}(C^{(1)}_t) & = (1+1-2) + 0 + (2 + 2k + 1) - \big (2(k+1) + \tfrac{1}{2} - \tfrac{1}{2}\big) \\ & = (2k+3) - (2k+2) = 1. \end{align*}
Hence, since ![]() ${\rm ind}(C^{(1)}_t) = 1> -1 = 2 \cdot {\rm genus} (C^{(1)}_t) - 2 + \# \Gamma _{\rm even}$, where
${\rm ind}(C^{(1)}_t) = 1> -1 = 2 \cdot {\rm genus} (C^{(1)}_t) - 2 + \# \Gamma _{\rm even}$, where ![]() $\# \Gamma _{\rm even}$ is the number of asymptotic ends with even CZ indices, curves in
$\# \Gamma _{\rm even}$ is the number of asymptotic ends with even CZ indices, curves in ![]() ${\mathcal {M}}_1(t)$ are automatically regular (see Theorem 1 in [Reference WendlWen10]). Thus,
${\mathcal {M}}_1(t)$ are automatically regular (see Theorem 1 in [Reference WendlWen10]). Thus, ![]() ${\mathcal {M}}_1(t)$ is non-empty for an open subset of
${\mathcal {M}}_1(t)$ is non-empty for an open subset of ![]() $t \in [0,1]$.
$t \in [0,1]$.
Now suppose that the moduli space is compact. Then ![]() $\mathcal {M}_1(0) \neq \emptyset$ together with automatic regularity implies that
$\mathcal {M}_1(0) \neq \emptyset$ together with automatic regularity implies that ![]() ${\mathcal {M}}_1(1) \neq \emptyset$. However, any curve
${\mathcal {M}}_1(1) \neq \emptyset$. However, any curve ![]() $C^{(1)}_1 \in \mathcal {M}_1(1)$ has
$C^{(1)}_1 \in \mathcal {M}_1(1)$ has
This is in contradiction to our assumption that ![]() $(r_1, s_1) \notin \mu (E(a,b))^+$. Hence, the moduli space is not compact and we have a degeneration at some time
$(r_1, s_1) \notin \mu (E(a,b))^+$. Hence, the moduli space is not compact and we have a degeneration at some time ![]() $t_* \in [0,1]$, that is, we have a holomorphic building
$t_* \in [0,1]$, that is, we have a holomorphic building ![]() $C^{(1)}_{\rm lim}$ which is a limit of curves
$C^{(1)}_{\rm lim}$ which is a limit of curves ![]() $C_n \in \mathcal {M}_1(t_n)$ with
$C_n \in \mathcal {M}_1(t_n)$ with ![]() $t_n \to t_*$. The argument (20) implies that the degeneration point
$t_n \to t_*$. The argument (20) implies that the degeneration point ![]() $(r_{t_*}, s_{t_*})$ in fact occurs inside
$(r_{t_*}, s_{t_*})$ in fact occurs inside ![]() ${\rm int}(\mu (E(a,b)^+)$.
${\rm int}(\mu (E(a,b)^+)$.
By § 3.3 in [Reference Hind and OpshteinHO20], ![]() $C^{(1)}_{\rm lim}$ contains a top-level curve, denoted by
$C^{(1)}_{\rm lim}$ contains a top-level curve, denoted by ![]() $C^{(2)}$, of index at least
$C^{(2)}$, of index at least ![]() $e$ and with
$e$ and with ![]() $e$ negative ends. We claim that
$e$ negative ends. We claim that ![]() $C^{(2)}$ must have a positive end; we can then check that for index reasons it must be asymptotic to
$C^{(2)}$ must have a positive end; we can then check that for index reasons it must be asymptotic to ![]() $\gamma _b$. Indeed, suppose not, then
$\gamma _b$. Indeed, suppose not, then ![]() $C^{(2)}$ can be thought of as a curve in
$C^{(2)}$ can be thought of as a curve in ![]() $\mathbb {C}^2 \setminus L_{t^*}$ and by Lemma 3.7 in [Reference Hind and OpshteinHO20] the curve
$\mathbb {C}^2 \setminus L_{t^*}$ and by Lemma 3.7 in [Reference Hind and OpshteinHO20] the curve ![]() $C^{(2)}$ has area at least
$C^{(2)}$ has area at least ![]() $r_{t_*}$. As any curve in
$r_{t_*}$. As any curve in ![]() ${\mathcal {M}}_1(t_*)$ has area
${\mathcal {M}}_1(t_*)$ has area ![]() $b - kr_{t_*} - s_{t_*}$, we must then have
$b - kr_{t_*} - s_{t_*}$, we must then have ![]() $r_{t_*} \leq {\rm area}_{C^{(1)}}(t_*) < b - kr_{t_*} - s_{t_*}$, which is equivalent to
$r_{t_*} \leq {\rm area}_{C^{(1)}}(t_*) < b - kr_{t_*} - s_{t_*}$, which is equivalent to ![]() $(k+1)r_{t_*} + s_{t_*} < b$, contradicting our assumption (I) on the path.
$(k+1)r_{t_*} + s_{t_*} < b$, contradicting our assumption (I) on the path.
Denote by ![]() $\mathcal {M}_2(t)$ the moduli space corresponding to the curve
$\mathcal {M}_2(t)$ the moduli space corresponding to the curve ![]() $C^{(2)}$ above with the moving boundary condition on
$C^{(2)}$ above with the moving boundary condition on ![]() $L_t$ for
$L_t$ for ![]() $t \in [t_*,1]$ and again we define
$t \in [t_*,1]$ and again we define ![]() ${\rm area}_{C^{(2)}}(t)$ to be the area of curves. If needed, consider
${\rm area}_{C^{(2)}}(t)$ to be the area of curves. If needed, consider ![]() $\mathcal {M}_2(t)$ with extra marked points, so the resulting index is exactly equal to
$\mathcal {M}_2(t)$ with extra marked points, so the resulting index is exactly equal to ![]() $e$ (instead of at least
$e$ (instead of at least ![]() $e$). Then Proposition 4.4 implies that curves in the moduli space of
$e$). Then Proposition 4.4 implies that curves in the moduli space of ![]() $C^{(2)}$ will not survive until
$C^{(2)}$ will not survive until ![]() $t =1$. In fact, there must be a degeneration before time
$t =1$. In fact, there must be a degeneration before time ![]() $t_1$, where
$t_1$, where ![]() $\gamma |_{t=t_1}$ lies outside
$\gamma |_{t=t_1}$ lies outside ![]() $\mu (E(a,b))$. Indeed, otherwise there will exists some curve denoted by
$\mu (E(a,b))$. Indeed, otherwise there will exists some curve denoted by ![]() $C^{(2)}_{t_1} \in \mathcal {M}_2(t_1)$ that results in the following contradiction,
$C^{(2)}_{t_1} \in \mathcal {M}_2(t_1)$ that results in the following contradiction,
Therefore, the moduli space ![]() $\mathcal {M}_2(t)$ is not compact over
$\mathcal {M}_2(t)$ is not compact over ![]() $[t_*,1]$ and it will degenerate again at some
$[t_*,1]$ and it will degenerate again at some ![]() $t_{**} \in (t_*, t_1)$. We repeat the argument above by considering the limit building
$t_{**} \in (t_*, t_1)$. We repeat the argument above by considering the limit building ![]() $C^{(2)}_{\rm lim}$ from a degeneration of
$C^{(2)}_{\rm lim}$ from a degeneration of ![]() $C^{(2)}$ and pick the preferred top curve
$C^{(2)}$ and pick the preferred top curve ![]() $C^{(3)}$ as above. Next by Proposition 4.4 again, we will get a further degeneration, now within the time interval
$C^{(3)}$ as above. Next by Proposition 4.4 again, we will get a further degeneration, now within the time interval ![]() $(t_{**}, t_1)$, and so on.
$(t_{**}, t_1)$, and so on.
We note that this process must terminate, and hence the desired contradiction is given by an inductive argument. To see this, suppose we have a sequence of ![]() $C^{(k)}$ asymptotic to
$C^{(k)}$ asymptotic to ![]() $L_k \to L_{\infty }$. Using Fukaya's trick again there exists a family of global diffeomorphisms mapping our
$L_k \to L_{\infty }$. Using Fukaya's trick again there exists a family of global diffeomorphisms mapping our ![]() $L_k$ to an
$L_k$ to an ![]() $\tilde {L}_{\infty }$, where
$\tilde {L}_{\infty }$, where ![]() $\tilde {L}_{\infty }$ lies very close to
$\tilde {L}_{\infty }$ lies very close to ![]() $L_{\infty }$ but has rational area class, that is,
$L_{\infty }$ but has rational area class, that is, ![]() $\tilde {L}_{\infty }$ is Hamiltonian isotopic to an
$\tilde {L}_{\infty }$ is Hamiltonian isotopic to an ![]() $L(\delta m, \delta n)$ with
$L(\delta m, \delta n)$ with ![]() $m,n \in \mathbb {N}$. We may assume that the almost complex structures on the complement of the
$m,n \in \mathbb {N}$. We may assume that the almost complex structures on the complement of the ![]() $L_k$ push forward to tame almost complex structures on the complement of
$L_k$ push forward to tame almost complex structures on the complement of ![]() $\tilde {L}_{\infty }$. By construction, our
$\tilde {L}_{\infty }$. By construction, our ![]() $C^{(k)}$ have a positive end, and in a degeneration of
$C^{(k)}$ have a positive end, and in a degeneration of ![]() $C^{(k)}$ the curve
$C^{(k)}$ the curve ![]() $C^{(k+1)}$ is the only curve in the limiting building with an end on
$C^{(k+1)}$ is the only curve in the limiting building with an end on ![]() $\partial E(a,b)$. Therefore, the other top-level curves in the limit, when pushed forward to the complement of
$\partial E(a,b)$. Therefore, the other top-level curves in the limit, when pushed forward to the complement of ![]() $\tilde {L}_{\infty }$, have area at least
$\tilde {L}_{\infty }$, have area at least ![]() $\delta$. Hence, in the complement of
$\delta$. Hence, in the complement of ![]() $\tilde {L}_{\infty }$, the areas of the
$\tilde {L}_{\infty }$, the areas of the ![]() $C^{(k)}$ decrease by at least
$C^{(k)}$ decrease by at least ![]() $\delta$ at each step, and so indeed our recursion is finite.
$\delta$ at each step, and so indeed our recursion is finite.
4.3 Proof of obstruction (I) in Theorem 2.13
Outline. The proof of the obstruction to the path lifting in the polydisks ![]() $P(c,d)$ is similar to the proof in balls and integral ellipsoids. The only variation is that we start from a curve that is different from that from Lemma 4.1 or Remark 4.2.
$P(c,d)$ is similar to the proof in balls and integral ellipsoids. The only variation is that we start from a curve that is different from that from Lemma 4.1 or Remark 4.2.
Proof. Suppose by contradiction that path ![]() $\gamma = \{(r_t, s_t)\}_{t \in [0,1]}$ admits a lift
$\gamma = \{(r_t, s_t)\}_{t \in [0,1]}$ admits a lift ![]() $\{L_t\}_{t \in [0,1]}$. Compactify
$\{L_t\}_{t \in [0,1]}$. Compactify ![]() $P(c,d)$ to
$P(c,d)$ to ![]() $S^2(c) \times S^2(d)$ with two factors having areas
$S^2(c) \times S^2(d)$ with two factors having areas ![]() $c$ and
$c$ and ![]() $d$. Denote by
$d$. Denote by ![]() $\mathcal {M}_1(t)$ the moduli space consisting of finite energy planes that intersect
$\mathcal {M}_1(t)$ the moduli space consisting of finite energy planes that intersect ![]() $S^2(c) \times \{\infty \}$ only once (i.e. it is of bidegree
$S^2(c) \times \{\infty \}$ only once (i.e. it is of bidegree ![]() $(0,1))$ and has its negative asymptotic end
$(0,1))$ and has its negative asymptotic end ![]() $\gamma _{(0,1)}$ on the moving boundary
$\gamma _{(0,1)}$ on the moving boundary ![]() $L_t$ for
$L_t$ for ![]() $t \in [0,1]$. The moduli space
$t \in [0,1]$. The moduli space ![]() $\mathcal {M}_1(0)$ is non-empty since we can simply write out (the image of) a curve
$\mathcal {M}_1(0)$ is non-empty since we can simply write out (the image of) a curve ![]() $C^{(1)}$ explicitly as follows:
$C^{(1)}$ explicitly as follows:
and by (13) ![]() ${\rm ind}(C^{(1)}) = -1 + 2\cdot 2 +2\cdot (-1) = 1$, plus the automatic regularity can be verified.
${\rm ind}(C^{(1)}) = -1 + 2\cdot 2 +2\cdot (-1) = 1$, plus the automatic regularity can be verified.
Now, suppose that the moduli space is compact, then ![]() $\mathcal {M}_1(1) \neq \emptyset$. Any curve
$\mathcal {M}_1(1) \neq \emptyset$. Any curve ![]() $C^{(1)}_1 \in \mathcal {M}_1(1)$ satisfies
$C^{(1)}_1 \in \mathcal {M}_1(1)$ satisfies ![]() ${\rm area}(C_1^{(1)}) = d - s_1 >0$, which contradicts our assumption that
${\rm area}(C_1^{(1)}) = d - s_1 >0$, which contradicts our assumption that ![]() $(r_1, s_1) \notin \mu (P(c,d))^+$. Hence, we have a degeneration at some time
$(r_1, s_1) \notin \mu (P(c,d))^+$. Hence, we have a degeneration at some time ![]() $t_* \in [0,1]$ with a limit curve a holomorphic building
$t_* \in [0,1]$ with a limit curve a holomorphic building ![]() $C_{\rm lim}^{(1)}$. By § 3.3 in [Reference Hind and OpshteinHO20],
$C_{\rm lim}^{(1)}$. By § 3.3 in [Reference Hind and OpshteinHO20], ![]() $C_{\rm lim}^{(1)}$ contains a top-level curve
$C_{\rm lim}^{(1)}$ contains a top-level curve ![]() $C^{(2)}$ of index at least
$C^{(2)}$ of index at least ![]() $e$ with
$e$ with ![]() $e$ negative ends. This curve
$e$ negative ends. This curve ![]() $C^{(2)}$ intersects
$C^{(2)}$ intersects ![]() $S^2(c) \times \{\infty \}$ since otherwise, by [Reference Hind and OpshteinHO20, Lemma 3.7], it has area at least
$S^2(c) \times \{\infty \}$ since otherwise, by [Reference Hind and OpshteinHO20, Lemma 3.7], it has area at least ![]() $r_{t_*}$ and then
$r_{t_*}$ and then
which contradicts our assumption (I) on the path.
Denote by ![]() $\mathcal {M}_2(t)$ the moduli space corresponding to the curve
$\mathcal {M}_2(t)$ the moduli space corresponding to the curve ![]() $C^{(2)}$ above with moving boundary on
$C^{(2)}$ above with moving boundary on ![]() $L_t$ for
$L_t$ for ![]() $t \in [t_*,1]$. It is readily checked that the same conclusion in Lemma 4.3 holds if we replace the assumption ‘contains the positive end
$t \in [t_*,1]$. It is readily checked that the same conclusion in Lemma 4.3 holds if we replace the assumption ‘contains the positive end ![]() $\gamma _b$’ with ‘intersects
$\gamma _b$’ with ‘intersects ![]() $S^2(c) \times \{\infty \}$’. Then Proposition 4.4, whose argument only involves areas, implies that
$S^2(c) \times \{\infty \}$’. Then Proposition 4.4, whose argument only involves areas, implies that ![]() $\mathcal {M}_2(t)$ is not compact, so it will degenerate again at
$\mathcal {M}_2(t)$ is not compact, so it will degenerate again at ![]() $t_{**} \in (t_*, t_1)$ where
$t_{**} \in (t_*, t_1)$ where ![]() $t_1$ is the first time that
$t_1$ is the first time that ![]() $\gamma$ intersects the line segment
$\gamma$ intersects the line segment ![]() $\{(r, d) \in \mathbb {R}_{>0}^2 \,| \, 0< r< {c}/{2}\}$. The rest of the proof goes exactly the same as that in § 4.2, and thus we get the desired conclusion.
$\{(r, d) \in \mathbb {R}_{>0}^2 \,| \, 0< r< {c}/{2}\}$. The rest of the proof goes exactly the same as that in § 4.2, and thus we get the desired conclusion.
5. Construction of path lifting
5.1 Path lifting criterion
In this section we construct our path lifts. The main result is the following theorem giving a Hamiltonian isotopy with controlled support between an inclusion and a rolled up Lagrangian. The domains of interest are the ![]() $Q(a,b)$ defined here.
$Q(a,b)$ defined here.
Definition 5.1 The domain ![]() $Q(a,b) \subset \mathbb {C}^2$ is defined by
$Q(a,b) \subset \mathbb {C}^2$ is defined by
where
a quadrilateral region in ![]() $\mathbb {R}^2$.
$\mathbb {R}^2$.
Theorem 5.2 Let ![]() $0 < a < b$ and
$0 < a < b$ and ![]() $\epsilon >0$. Then there exists a Hamiltonian isotopy of the Lagrangian tori denoted by
$\epsilon >0$. Then there exists a Hamiltonian isotopy of the Lagrangian tori denoted by ![]() $\{L_t\}_{t \in [0,1]}$ with
$\{L_t\}_{t \in [0,1]}$ with ![]() $L_0 = L(a,b)$ such that the following conclusions hold:
$L_0 = L(a,b)$ such that the following conclusions hold:
(1) for every
 $t \in [0,1]$, the Lagrangian
$t \in [0,1]$, the Lagrangian  $L_t \subset Q(a + \epsilon,b + \epsilon )$;
$L_t \subset Q(a + \epsilon,b + \epsilon )$;(2)
 $L_1 \subset Q(a + \epsilon, a + \epsilon )$.
$L_1 \subset Q(a + \epsilon, a + \epsilon )$.
Remark 5.3 The existence of a Hamiltonian diffeomorphism with the property (2) has been established in [Reference Hind and ZhangHZ21, Theorem 6.3], which, in turn, relied on § 6 in [Reference Hind and OpshteinHO20]. These proofs however essentially wrote down the torus ![]() $L_1$ and then applied general methods to show the
$L_1$ and then applied general methods to show the ![]() $L_1$ to be Hamiltonian isotopic to
$L_1$ to be Hamiltonian isotopic to ![]() $L(a,b)$, hence losing control of the support of the isotopy. The improvement here is that the whole isotopy is fairly explicit, allowing us to add conclusion (1) in Theorem 5.2. This condition is, of course, vital for the quantitative study of isotopies in the current paper.
$L(a,b)$, hence losing control of the support of the isotopy. The improvement here is that the whole isotopy is fairly explicit, allowing us to add conclusion (1) in Theorem 5.2. This condition is, of course, vital for the quantitative study of isotopies in the current paper.
Proof of Theorem 5.2 The following lemma will be used. It is well known and can be proved by applying a symplectic conjugation mapping the disks ![]() $D(a)$ to rectangles
$D(a)$ to rectangles ![]() $(0,1) \times (0,a)$. Let
$(0,1) \times (0,a)$. Let ![]() $D(c)$ denote an open round disk in the plane, centered at the origin and with area
$D(c)$ denote an open round disk in the plane, centered at the origin and with area ![]() $c$.
$c$.
Lemma 5.4 Let ![]() $\epsilon >0$. There exists a function
$\epsilon >0$. There exists a function ![]() $G$ with compact support in
$G$ with compact support in ![]() $D(2a + \epsilon )$ and
$D(2a + \epsilon )$ and ![]() $0 \le G \le a + \epsilon$ such that the corresponding Hamiltonian flow
$0 \le G \le a + \epsilon$ such that the corresponding Hamiltonian flow ![]() $\phi ^t_G$ satisfies
$\phi ^t_G$ satisfies ![]() $\phi ^t_G(D(a)) \subset D((1+t)a + \epsilon )$ and
$\phi ^t_G(D(a)) \subset D((1+t)a + \epsilon )$ and ![]() $\phi ^1_G(D(a)) \cap D(a) = \emptyset$.
$\phi ^1_G(D(a)) \cap D(a) = \emptyset$.
We use coordinates ![]() $(z,w)$ on
$(z,w)$ on ![]() $\mathbb {C}^2$. We define a product Lagrangian torus
$\mathbb {C}^2$. We define a product Lagrangian torus ![]() $\tilde {L}(a,b)$ in
$\tilde {L}(a,b)$ in ![]() $\mathbb {C}^2$ by
$\mathbb {C}^2$ by
where ![]() $[0,1] \times [0,b]$ is a rectangle in
$[0,1] \times [0,b]$ is a rectangle in ![]() $w$-plane. Let
$w$-plane. Let ![]() $w = x + \sqrt {-1} y$. Note that a smoothing of
$w = x + \sqrt {-1} y$. Note that a smoothing of ![]() $\tilde {L}(a,b)$ is symplectomorphic to our standard product by a symplectomorphism on
$\tilde {L}(a,b)$ is symplectomorphic to our standard product by a symplectomorphism on ![]() $\mathbb {C}$ that interchanges the disk
$\mathbb {C}$ that interchanges the disk ![]() $D(b)$ with the rectangle
$D(b)$ with the rectangle ![]() $[0,1] \times [0,b]$ in the
$[0,1] \times [0,b]$ in the ![]() $w$-plane.
$w$-plane.
Consider a product Hamiltonian function
where ![]() $\chi : [0,a+\epsilon ] \to [0,1]$ is a smooth function, extended by zero outside
$\chi : [0,a+\epsilon ] \to [0,1]$ is a smooth function, extended by zero outside ![]() $[0, a+\epsilon ]$, such that for a sufficiently small
$[0, a+\epsilon ]$, such that for a sufficiently small ![]() $\delta >0$ we have:
$\delta >0$ we have:
(i)
 $\chi |_{[0,\delta ]} = 1$,
$\chi |_{[0,\delta ]} = 1$,  $\chi |_{[a+\epsilon -\delta, a+\epsilon ]} = 0$, and
$\chi |_{[a+\epsilon -\delta, a+\epsilon ]} = 0$, and  $\chi |_{[2\delta, a+\epsilon -2\delta ]}$ is linear of slope
$\chi |_{[2\delta, a+\epsilon -2\delta ]}$ is linear of slope  $-1/(a + \epsilon + \delta$);
$-1/(a + \epsilon + \delta$);(ii)
 $\chi |_{[\delta,2\delta ]}$ is concavely decreasing and
$\chi |_{[\delta,2\delta ]}$ is concavely decreasing and  $\chi |_{[a+\epsilon -2\delta, a+\epsilon -\delta ]}$ is convexly decreasing.
$\chi |_{[a+\epsilon -2\delta, a+\epsilon -\delta ]}$ is convexly decreasing.
See Figure 12 for the pictures of ![]() $\chi (y)$ and
$\chi (y)$ and ![]() $-\chi '(y)$. The function
$-\chi '(y)$. The function ![]() $G(z)$ is defined by Lemma 5.4.
$G(z)$ is defined by Lemma 5.4.

Figure 12. Graphs of ![]() $\chi (y)$ and
$\chi (y)$ and ![]() $-\chi '(y)$.
$-\chi '(y)$.
By the product rule we have ![]() $dH(z,w) = \chi '(y) G(z) \,{{d}y} + \chi (y) \,dG(z)$. Using the standard symplectic structure on
$dH(z,w) = \chi '(y) G(z) \,{{d}y} + \chi (y) \,dG(z)$. Using the standard symplectic structure on ![]() $\mathbb {C}^2$, that is,
$\mathbb {C}^2$, that is, ![]() $\omega _{\rm std} = \omega _{\rm std,\mathbb {C}}+{{d}x} \wedge {{d}y}$, we can write down the Hamiltonian vector field
$\omega _{\rm std} = \omega _{\rm std,\mathbb {C}}+{{d}x} \wedge {{d}y}$, we can write down the Hamiltonian vector field ![]() $X_H$ (via the Hamiltonian equation
$X_H$ (via the Hamiltonian equation ![]() $-dH = \iota _{X_H} \omega _{\rm std}$), namely
$-dH = \iota _{X_H} \omega _{\rm std}$), namely
where ![]() $X_{G(z)}$ is the Hamiltonian vector field generated by the function
$X_{G(z)}$ is the Hamiltonian vector field generated by the function ![]() $G(z)$ above with respect to
$G(z)$ above with respect to ![]() $\omega _{\rm std,\mathbb {C}}$. Therefore, the resulting Hamiltonian diffeomorphism of
$\omega _{\rm std,\mathbb {C}}$. Therefore, the resulting Hamiltonian diffeomorphism of ![]() $H$ is
$H$ is
Now, apply the Hamiltonian diffeomorphism ![]() $\phi ^1_H$ to
$\phi ^1_H$ to ![]() $\tilde {L}(a,b)$, and Figure 13 shows a schematic picture of how the projection to the
$\tilde {L}(a,b)$, and Figure 13 shows a schematic picture of how the projection to the ![]() $w$-plane changes (indicated by the shaded part). For later use, we label the rectangle
$w$-plane changes (indicated by the shaded part). For later use, we label the rectangle ![]() $S: = [0,1] \times [a+\epsilon, b]$. By our choice of
$S: = [0,1] \times [a+\epsilon, b]$. By our choice of ![]() $\epsilon$ and
$\epsilon$ and ![]() $\delta$ as above,
$\delta$ as above,
Therefore, the bottom part of the rectangle which is moved by ![]() $\phi _H^1$ is contained in the rectangle
$\phi _H^1$ is contained in the rectangle ![]() $[0,2] \times [0, a+\epsilon ]$ and touches neither the line
$[0,2] \times [0, a+\epsilon ]$ and touches neither the line ![]() $x = 1$ nor
$x = 1$ nor ![]() $x=2$.
$x=2$.

Figure 13. Behavior of ![]() $\phi _H^1(L(a,b))$ on the
$\phi _H^1(L(a,b))$ on the ![]() $w$-plane.
$w$-plane.
On the other hand, for the behavior on the ![]() $z$-plane, there are two extreme cases.
$z$-plane, there are two extreme cases.
(a) For
 $w \in I$, i.e.
$w \in I$, i.e.  $w = (x,0)$ for
$w = (x,0)$ for  $x \in [0,1]$, since
$x \in [0,1]$, since  $\chi (0) = 1$, the first factor in (22) is simply
$\chi (0) = 1$, the first factor in (22) is simply  $\phi _G^1(z)$ which by definition displaces
$\phi _G^1(z)$ which by definition displaces  $\partial D(a)$ (since it displaces
$\partial D(a)$ (since it displaces  $D(a)$).
$D(a)$).(b) For
 $w$ near
$w$ near  $S$, where
$S$, where  $S$ is the upper part of the rectangle as in Figure 13, since
$S$ is the upper part of the rectangle as in Figure 13, since  $\chi (y) = 0$, the second factor in (22) is identity, so
$\chi (y) = 0$, the second factor in (22) is identity, so  $\partial D(a)$ stays the same.
$\partial D(a)$ stays the same.
Next, we also consider a Hamiltonian isotopy ![]() $\{\psi _t\}_{t \in [0,1]}$ on the
$\{\psi _t\}_{t \in [0,1]}$ on the ![]() $w$-plane that wraps the region
$w$-plane that wraps the region ![]() $S$ around the deformed
$S$ around the deformed ![]() $w$-projection to overlap the rectangle
$w$-projection to overlap the rectangle ![]() $[0,1] \times [0,a+\epsilon ]$, see Figure 14. Although on the
$[0,1] \times [0,a+\epsilon ]$, see Figure 14. Although on the ![]() $w$-plane, there are intersection points of
$w$-plane, there are intersection points of ![]() $\psi _t|_{S}(S)$ with the line segment
$\psi _t|_{S}(S)$ with the line segment ![]() $I$, by our construction, viewed in four dimensions there will be no extra intersections. Indeed, for any point
$I$, by our construction, viewed in four dimensions there will be no extra intersections. Indeed, for any point ![]() $(z,w)$ with
$(z,w)$ with ![]() $w$ near
$w$ near ![]() $S$, the corresponding
$S$, the corresponding ![]() $z \in D(a)$, but by case (a) above for any point
$z \in D(a)$, but by case (a) above for any point ![]() $(z,w)$ with
$(z,w)$ with ![]() $w \in I$, the corresponding
$w \in I$, the corresponding ![]() $z$ lies in
$z$ lies in ![]() $\phi _G^1(D(a))$ which is disjoint from
$\phi _G^1(D(a))$ which is disjoint from ![]() $D(a)$. Continuing this wrapping construction as shown in Figure 15, we can wrap all of
$D(a)$. Continuing this wrapping construction as shown in Figure 15, we can wrap all of ![]() $S$ into the shaded region Figure 15, which is a subset of
$S$ into the shaded region Figure 15, which is a subset of ![]() $[0,1] \times [0,a+\epsilon ]$, union with an arbitrarily small neighborhood, say of width
$[0,1] \times [0,a+\epsilon ]$, union with an arbitrarily small neighborhood, say of width ![]() $\delta \ll \epsilon$, of the sides
$\delta \ll \epsilon$, of the sides ![]() $[0,1] \times \{0\}$,
$[0,1] \times \{0\}$, ![]() $\{0\} \times [0, a+ \epsilon ]$ and
$\{0\} \times [0, a+ \epsilon ]$ and ![]() $[0,1] \times \{a+\epsilon \}$.
$[0,1] \times \{a+\epsilon \}$.

Figure 14. Wrap the region ![]() $S$.
$S$.

Figure 15. More wrappings.
The Hamiltonian isotopy of interest is the image, under a symplectomorphism ![]() ${\mathbb 1} \times \Phi$, of the concatenation of the two constructions above,
${\mathbb 1} \times \Phi$, of the concatenation of the two constructions above,
Here ![]() $\Phi$ is a symplectomorphism of the
$\Phi$ is a symplectomorphism of the ![]() $w$-plane that maps
$w$-plane that maps
(i)
 $[-\delta,2] \times [-\delta,a+\epsilon + \delta ] \cup [0,1] \times [a,y]$ into
$[-\delta,2] \times [-\delta,a+\epsilon + \delta ] \cup [0,1] \times [a,y]$ into  $D(a+y+ 3\epsilon )$ for
$D(a+y+ 3\epsilon )$ for  $y \geq a+\epsilon$; and
$y \geq a+\epsilon$; and(ii) each horizontal rectangle
 $[-\delta,2] \times [-\delta,y]$ into
$[-\delta,2] \times [-\delta,y]$ into  $D(2y+\epsilon )$ for
$D(2y+\epsilon )$ for  $y \in [0,a+\epsilon ]$.
$y \in [0,a+\epsilon ]$.
See Figure 16 for a layer-by-layer picture of such a map ![]() $\Phi$ for part (ii). The existence of such symplectomorphisms follows Lemma 3.1.5 in the book [Reference SchlenkSch05].
$\Phi$ for part (ii). The existence of such symplectomorphisms follows Lemma 3.1.5 in the book [Reference SchlenkSch05].

Figure 16. The map ![]() $\Phi$ on
$\Phi$ on ![]() $[0,2] \times [0, a+\epsilon ]$.
$[0,2] \times [0, a+\epsilon ]$.
Note that both ![]() $\Phi ( [0,1] \times [0,b] )$ and
$\Phi ( [0,1] \times [0,b] )$ and ![]() $D(b)$ lie inside
$D(b)$ lie inside ![]() $D(a+b+ 3\epsilon )$. Therefore, without loss of generality, we may assume
$D(a+b+ 3\epsilon )$. Therefore, without loss of generality, we may assume ![]() $\Phi ( [0,1] \times [0,b] ) = D(b)$, that is, our isotopy starts at the standard product
$\Phi ( [0,1] \times [0,b] ) = D(b)$, that is, our isotopy starts at the standard product ![]() $L(a,b)$.
$L(a,b)$.
We need to keep track of the moment image ![]() $(\pi |z|^2, \pi |w|^2)$ along the Hamiltonian isotopy and have the following observations.
$(\pi |z|^2, \pi |w|^2)$ along the Hamiltonian isotopy and have the following observations.
Case ![]() $\alpha$. Let
$\alpha$. Let ![]() $(z,w) = (z, (x,y)) \in \tilde {L}(a,b)$ with
$(z,w) = (z, (x,y)) \in \tilde {L}(a,b)$ with ![]() $y \in [0, a+ \epsilon ]$. We denote the image of
$y \in [0, a+ \epsilon ]$. We denote the image of ![]() $(z,w)$ under
$(z,w)$ under ![]() $\phi ^t_H$ by
$\phi ^t_H$ by ![]() $(z', w')$, and this point is described by (22). In particular, the
$(z', w')$, and this point is described by (22). In particular, the ![]() $y$ coordinate is invariant under the flow. Hence, under the symplectomorphism
$y$ coordinate is invariant under the flow. Hence, under the symplectomorphism ![]() ${\mathbb 1} \times \Phi$, we get the relation
${\mathbb 1} \times \Phi$, we get the relation
For the bound on ![]() $\pi |\Phi (w')|^2$ we are applying condition (ii) on
$\pi |\Phi (w')|^2$ we are applying condition (ii) on ![]() $\Phi$. For the condition on
$\Phi$. For the condition on ![]() $z'$, by (22) we note that
$z'$, by (22) we note that ![]() $z' = \phi ^t_{\chi G}(z) = \phi ^{t\chi }_G(z)$ where
$z' = \phi ^t_{\chi G}(z) = \phi ^{t\chi }_G(z)$ where ![]() $z \in D(a)$, since
$z \in D(a)$, since ![]() $G$ is independent of time. But
$G$ is independent of time. But
and so by Lemma 5.4
as required.
The relation (24) yields
and then, importantly,
Such points ![]() $(z', w')$ are then fixed by the flow
$(z', w')$ are then fixed by the flow ![]() $\psi _t$.
$\psi _t$.
Case ![]() $\beta$. Let
$\beta$. Let ![]() $(z,w) = (z, (x,y)) \in \tilde {L}(a,b)$ with
$(z,w) = (z, (x,y)) \in \tilde {L}(a,b)$ with ![]() $y \in [a +\epsilon, b]$. Such points are fixed by
$y \in [a +\epsilon, b]$. Such points are fixed by ![]() $\phi ^t_H$, and the flow of
$\phi ^t_H$, and the flow of ![]() $\psi _t$ fixes the
$\psi _t$ fixes the ![]() $z$ coordinate and leaves the
$z$ coordinate and leaves the ![]() $w$ coordinate inside an
$w$ coordinate inside an ![]() $\epsilon$ neighborhood of
$\epsilon$ neighborhood of ![]() $[0,1] \times [0,b]$. This region is mapped close to
$[0,1] \times [0,b]$. This region is mapped close to ![]() $D(a+b)$ by
$D(a+b)$ by ![]() $\Phi$, using property (i).
$\Phi$, using property (i).
Therefore, we obtain a Lagrangian isotopy with its moment image lying in regions corresponding to either case ![]() $\alpha$ or case
$\alpha$ or case ![]() $\beta$ as above. The following graph illustrates these regions, for brevity, when
$\beta$ as above. The following graph illustrates these regions, for brevity, when ![]() $\epsilon \to 0$.
$\epsilon \to 0$.

The union of these regions is contained in an arbitrarily small neighborhood of the quadrilateral region defined by ![]() $q(a,b) \subset \mathbb {R}^2$ in our hypothesis. We note in
$q(a,b) \subset \mathbb {R}^2$ in our hypothesis. We note in ![]() ${\rm Case}\,\beta$ the points
${\rm Case}\,\beta$ the points ![]() $\psi _1(z,w)$ lie in an
$\psi _1(z,w)$ lie in an ![]() $\epsilon$ neighborhood of
$\epsilon$ neighborhood of ![]() $D(a) \times [0,1] \times [0,a]$. Therefore, by property (i) of
$D(a) \times [0,1] \times [0,a]$. Therefore, by property (i) of ![]() $\Phi$, the image under
$\Phi$, the image under ![]() ${\mathbb 1} \times \Phi$ lies close to
${\mathbb 1} \times \Phi$ lies close to ![]() $D(a) \times D(2a)$ and the moment image is described only by the lower trapezium in the graph above. In other words, at
$D(a) \times D(2a)$ and the moment image is described only by the lower trapezium in the graph above. In other words, at ![]() $t=1$ the moment image of the Lagrangian isotopy (23) lies in an arbitrarily small neighborhood of
$t=1$ the moment image of the Lagrangian isotopy (23) lies in an arbitrarily small neighborhood of ![]() $q(a,a)$. Hence, we complete the proof.
$q(a,a)$. Hence, we complete the proof.
In constructing lifts, our strategy will be to divide ![]() $\gamma$ into segments, and on each segment lift either by inclusions or by the rolled up Lagrangian embeddings described in Theorem 5.2. The following lemma says that a Hamiltonian isotopy is enough to piece these lifts together. In other words, we are free to concatenate paths with endpoints lying in the same path component of a fiber.
$\gamma$ into segments, and on each segment lift either by inclusions or by the rolled up Lagrangian embeddings described in Theorem 5.2. The following lemma says that a Hamiltonian isotopy is enough to piece these lifts together. In other words, we are free to concatenate paths with endpoints lying in the same path component of a fiber.
Lemma 5.5 Let ![]() $\gamma : [0,2] \to \mathbb {R}^2$ and
$\gamma : [0,2] \to \mathbb {R}^2$ and ![]() $L_t$,
$L_t$, ![]() $0 \le t \le 1$ and
$0 \le t \le 1$ and ![]() $M_t$,
$M_t$, ![]() $1 \le t \le 2$ be smooth families of Lagrangian tori in
$1 \le t \le 2$ be smooth families of Lagrangian tori in ![]() $\mathcal {L}(X)$ such that
$\mathcal {L}(X)$ such that ![]() $\mathcal {P}(L_t) = \gamma (t)$ and
$\mathcal {P}(L_t) = \gamma (t)$ and ![]() $\mathcal {P}(M_t) = \gamma (t)$ and
$\mathcal {P}(M_t) = \gamma (t)$ and ![]() $L_1$ is Hamiltonian isotopic to
$L_1$ is Hamiltonian isotopic to ![]() $M_1$ in
$M_1$ in ![]() $X$, that is,
$X$, that is, ![]() $L_1$ and
$L_1$ and ![]() $M_1$ lie in the same component of the fiber over
$M_1$ lie in the same component of the fiber over ![]() $\gamma (1)$. Then
$\gamma (1)$. Then ![]() $\gamma (t)$ has a smooth lift
$\gamma (t)$ has a smooth lift ![]() $N_t$ with
$N_t$ with ![]() $N_t = L_t$ for
$N_t = L_t$ for ![]() $t<1-\epsilon$ and
$t<1-\epsilon$ and ![]() $N_t = M_t$ for
$N_t = M_t$ for ![]() $t>1+\epsilon$.
$t>1+\epsilon$.
Proof. Let ![]() $\Phi _t \in {\rm Ham}(X)$ be a Hamiltonian flow with
$\Phi _t \in {\rm Ham}(X)$ be a Hamiltonian flow with ![]() $\Phi _0 = \rm {I}$ and
$\Phi _0 = \rm {I}$ and ![]() $\Phi _1(L_1) = M_1$. First we replace
$\Phi _1(L_1) = M_1$. First we replace ![]() $L_t$ by
$L_t$ by ![]() $\tilde {L}_t = \Phi _{f(t)}(L_t)$ where
$\tilde {L}_t = \Phi _{f(t)}(L_t)$ where ![]() $f(t)=0$ for
$f(t)=0$ for ![]() $t<1-\epsilon$ and
$t<1-\epsilon$ and ![]() $f(1)=1$. Then
$f(1)=1$. Then ![]() $\tilde {L}_t$ and
$\tilde {L}_t$ and ![]() $M_t$ together give a continuous lift of
$M_t$ together give a continuous lift of ![]() $\gamma (t)$.
$\gamma (t)$.
To smooth a possible corner at ![]() $\tilde {L}_1 = M_1$ we first identify a neighborhood of
$\tilde {L}_1 = M_1$ we first identify a neighborhood of ![]() $M_1$ in
$M_1$ in ![]() $X$ with a neighborhood of the zero section in
$X$ with a neighborhood of the zero section in ![]() $T^* \mathbb {T}^2$. Then Lagrangian tori near
$T^* \mathbb {T}^2$. Then Lagrangian tori near ![]() $M_1$ can be identified with the graphs of closed
$M_1$ can be identified with the graphs of closed ![]() $1$ forms
$1$ forms ![]() $\alpha = r \,d\theta _1 + s\,d\theta _2 + dg$ where
$\alpha = r \,d\theta _1 + s\,d\theta _2 + dg$ where ![]() $\theta _1$,
$\theta _1$, ![]() $\theta _2$ are coordinates on
$\theta _2$ are coordinates on ![]() $\mathbb {T}^2$ and
$\mathbb {T}^2$ and ![]() $g(\theta _1, \theta _2)$ is a smooth function. Here
$g(\theta _1, \theta _2)$ is a smooth function. Here ![]() $r$ and
$r$ and ![]() $s$ are uniquely defined, and
$s$ are uniquely defined, and ![]() $g$ is also uniquely defined if we insist that
$g$ is also uniquely defined if we insist that ![]() $\int g =0$. Moreover, we may assume that up to a translation the map
$\int g =0$. Moreover, we may assume that up to a translation the map ![]() $\mathcal {P}$ is given by
$\mathcal {P}$ is given by ![]() $\mathcal {P}({\rm {gr}}(\alpha )) = (r,s)$. Now finding a smooth lift just requires replacing the family of
$\mathcal {P}({\rm {gr}}(\alpha )) = (r,s)$. Now finding a smooth lift just requires replacing the family of ![]() $g$ corresponding to
$g$ corresponding to ![]() $\tilde {L}_t$ and
$\tilde {L}_t$ and ![]() $M_t$ by a smooth family of functions.
$M_t$ by a smooth family of functions.
Let ![]() $X_{\Omega }$ be a toric domain in
$X_{\Omega }$ be a toric domain in ![]() $\mathbb {R}^4$ with moment image
$\mathbb {R}^4$ with moment image ![]() $\Omega$. Recall that a Type-I path is a path that entirely lies in
$\Omega$. Recall that a Type-I path is a path that entirely lies in ![]() $\Omega ^+: = \Omega \cap \{r \leq s\}$ and any other path with starting point in
$\Omega ^+: = \Omega \cap \{r \leq s\}$ and any other path with starting point in ![]() $\Omega ^+$ is a Type-II path. The following corollary of Theorem 5.2 provides our key sufficient condition to lift a general path.
$\Omega ^+$ is a Type-II path. The following corollary of Theorem 5.2 provides our key sufficient condition to lift a general path.
Corollary 5.6 (Path lifting criterion)
Let ![]() $X_{\Omega } \subset \mathbb {R}^4$ be a toric domain and let
$X_{\Omega } \subset \mathbb {R}^4$ be a toric domain and let ![]() $\gamma = \{(r_t, s_t)\,|\, r_t < s_t\}_{t \in [0,T]}$ be an oriented path in
$\gamma = \{(r_t, s_t)\,|\, r_t < s_t\}_{t \in [0,T]}$ be an oriented path in ![]() ${\rm Sh}^+_H(X_{\Omega })$. Then
${\rm Sh}^+_H(X_{\Omega })$. Then ![]() $\gamma$ lifts to
$\gamma$ lifts to ![]() $\mathcal {L}(X_{\Omega })$ if it can be decomposed as a concatenation of sub-paths of Type-I and Type-II such that each Type-II path has the following property. Suppose the Type-II sub-path has domain
$\mathcal {L}(X_{\Omega })$ if it can be decomposed as a concatenation of sub-paths of Type-I and Type-II such that each Type-II path has the following property. Suppose the Type-II sub-path has domain ![]() $[t_0, t_1] \subset [0,1]$. Then there exists a
$[t_0, t_1] \subset [0,1]$. Then there exists a ![]() $t_* \in (t_0, t_1]$ and
$t_* \in (t_0, t_1]$ and ![]() $\epsilon >0$ such that:
$\epsilon >0$ such that:
(II-i)
 $\gamma |_{[t_0, t_*]} \subset \Omega ^{+}$ but
$\gamma |_{[t_0, t_*]} \subset \Omega ^{+}$ but  $\gamma |_{[t_*,t_1]} \not \subset \Omega ^+$;
$\gamma |_{[t_*,t_1]} \not \subset \Omega ^+$;(II-ii)
 $q(r_{t_*} + \epsilon, s_{t_*} + \epsilon ) \subset {\rm int}(\Omega )$, and, if
$q(r_{t_*} + \epsilon, s_{t_*} + \epsilon ) \subset {\rm int}(\Omega )$, and, if  $t_1 \neq T$, then also
$t_1 \neq T$, then also  $q(r_{t_1}, s_{t_1}) \subset {\rm int}(\Omega )$;
$q(r_{t_1}, s_{t_1}) \subset {\rm int}(\Omega )$;(II-iii)
 $q(r_t + \epsilon, r_t + \epsilon ) \subset {\rm int}(\Omega )$ for all
$q(r_t + \epsilon, r_t + \epsilon ) \subset {\rm int}(\Omega )$ for all  $t \in [t_*, t_1]$.
$t \in [t_*, t_1]$.
Proof of Corollary 5.6 By Example 2.10, any Type-I sub-path and the part ![]() $\gamma |_{[0, t_*]}$ of a Type-II sub-path always lifts via product tori, so we need to consider the part
$\gamma |_{[0, t_*]}$ of a Type-II sub-path always lifts via product tori, so we need to consider the part ![]() $\gamma |_{[t_*, t_1]}$ of a Type-II sub-path, which is not entirely contained in
$\gamma |_{[t_*, t_1]}$ of a Type-II sub-path, which is not entirely contained in ![]() $\Omega ^+$. By condition (II-iii) these segments lift using the family of rolled up embeddings described by Theorem 5.2. To do this, starting from the Lagrangian
$\Omega ^+$. By condition (II-iii) these segments lift using the family of rolled up embeddings described by Theorem 5.2. To do this, starting from the Lagrangian ![]() $\psi _1(\phi _H^1(L(a,b)))$ as in Figure 15, we can continuously change the areas of the disk
$\psi _1(\phi _H^1(L(a,b)))$ as in Figure 15, we can continuously change the areas of the disk ![]() $D(a)$ in the
$D(a)$ in the ![]() $z$-plane to be the given
$z$-plane to be the given ![]() $r_t$ and the height
$r_t$ and the height ![]() $b$ of the rectangle in Figure 13 to be the given
$b$ of the rectangle in Figure 13 to be the given ![]() $s_t$, for
$s_t$, for ![]() $t \in [t_*, t_1]$. The construction still applies since
$t \in [t_*, t_1]$. The construction still applies since ![]() $r_t < s_t$ for all
$r_t < s_t$ for all ![]() $t \in [0,1]$, and the resulting Lagrangian
$t \in [0,1]$, and the resulting Lagrangian ![]() $L_t$ is Hamiltonian isotopic to the product Lagrangian torus
$L_t$ is Hamiltonian isotopic to the product Lagrangian torus ![]() $L(r_t, s_t)$ since we can run the constructions
$L(r_t, s_t)$ since we can run the constructions ![]() $\psi _t$ and
$\psi _t$ and ![]() $\phi _H^t$ above in reverse (cf. the requirement of the condition
$\phi _H^t$ above in reverse (cf. the requirement of the condition ![]() $a< b$ for the constructions above). Moreover, the image of
$a< b$ for the constructions above). Moreover, the image of ![]() $L_t$ lies in an arbitrarily small neighborhood of
$L_t$ lies in an arbitrarily small neighborhood of ![]() $Q(r_t, r_t)$
$Q(r_t, r_t)$
It remains to adjust things so that our Lagrangian embeddings match at the endpoints of the segments, and by Lemma 5.5 it is enough to show these embeddings are Hamiltonian isotopic in ![]() $X_{\Omega }$. But at an endpoint
$X_{\Omega }$. But at an endpoint ![]() $t_1$ say, Theorem 5.2 gives such an isotopy from the product to the rolled up torus with support in a neighborhood of
$t_1$ say, Theorem 5.2 gives such an isotopy from the product to the rolled up torus with support in a neighborhood of ![]() $Q(r_{t_1}, s_{t_1})$, and by condition (II-ii) we have that
$Q(r_{t_1}, s_{t_1})$, and by condition (II-ii) we have that ![]() $Q(r_{t_1} + \epsilon, s_{t_1} + \epsilon ) \subset X_{\Omega }$. In this way, we get the desired conclusion.
$Q(r_{t_1} + \epsilon, s_{t_1} + \epsilon ) \subset X_{\Omega }$. In this way, we get the desired conclusion.
5.2 Proof of criterion (II) in Theorems 2.11, 2.12, and 2.13
5.2.1 Proof of Theorem 2.11(II)
We will show that a path ![]() $\gamma$ as described in Theorem 2.11(II) satisfies the lifting criterion in Corollary 5.6. Assuming the path is not of Type-I, it is already of Type-II and no decomposition into sub-paths is necessary. Our
$\gamma$ as described in Theorem 2.11(II) satisfies the lifting criterion in Corollary 5.6. Assuming the path is not of Type-I, it is already of Type-II and no decomposition into sub-paths is necessary. Our ![]() $t_*$ is given, and condition (II-i) follows since the path is Type-II.
$t_*$ is given, and condition (II-i) follows since the path is Type-II.
Recall that the moment image ![]() $\mu (B^4(R))$ is the right triangle
$\mu (B^4(R))$ is the right triangle ![]() $\Delta (R,R)$ in the
$\Delta (R,R)$ in the ![]() $(r,s)$ plane with vertices
$(r,s)$ plane with vertices ![]() $(0,0)$,
$(0,0)$, ![]() $(R,0)$ and
$(R,0)$ and ![]() $(0,R)$. Condition (II-ii) in Corollary 5.6,
$(0,R)$. Condition (II-ii) in Corollary 5.6, ![]() $q(r_{t_*}, s_{t_*}) \subset {\rm int}(\Delta (R,R))$, is equivalent to the condition that the vertex
$q(r_{t_*}, s_{t_*}) \subset {\rm int}(\Delta (R,R))$, is equivalent to the condition that the vertex ![]() $(r_{t_*}, r_{t_*}+s_{t_*})$ lies strictly below the hypotenuse of
$(r_{t_*}, r_{t_*}+s_{t_*})$ lies strictly below the hypotenuse of ![]() $\Delta (R,R)$. Since the equation of the hypotenuse is
$\Delta (R,R)$. Since the equation of the hypotenuse is ![]() $r+s = R$, the condition is
$r+s = R$, the condition is
as given in Theorem 2.11.
Similarly, condition (II-iii) in Corollary 5.6 is equivalent ![]() $r_t < {R}/{3}$ for
$r_t < {R}/{3}$ for ![]() $t \in [0, T]$. Thus, we complete the proof.
$t \in [0, T]$. Thus, we complete the proof.
5.2.2 Proof of Theorem 2.12(II)
As for Theorem 2.11(II) we need to check that the conditions in Theorem 2.11(II) imply the path ![]() $\gamma$ satisfies the conditions in Corollary 5.6. These are automatic if
$\gamma$ satisfies the conditions in Corollary 5.6. These are automatic if ![]() $\gamma$ is of Type-I, otherwise we think of
$\gamma$ is of Type-I, otherwise we think of ![]() $\gamma$ as a single path of Type-II.
$\gamma$ as a single path of Type-II.
Recall that ![]() $\mu (E(a,b))$ is the right triangle
$\mu (E(a,b))$ is the right triangle ![]() $\Delta (a,b)$ with vertices
$\Delta (a,b)$ with vertices ![]() $(0,0)$,
$(0,0)$, ![]() $(a,0)$, and
$(a,0)$, and ![]() $(0, b)$. We have two cases for condition (II-ii) of Corollary 5.6, due to the comparison between the slope of the hypotenuse of this triangle and the slope of the hypotenuse of the quadrilateral region
$(0, b)$. We have two cases for condition (II-ii) of Corollary 5.6, due to the comparison between the slope of the hypotenuse of this triangle and the slope of the hypotenuse of the quadrilateral region ![]() $q(r_{t_*}, s_{t_*})$ (see Figure 17). The slope
$q(r_{t_*}, s_{t_*})$ (see Figure 17). The slope ![]() $H_1$ is
$H_1$ is ![]() $- ({r_{t_*} + s_{t_*}})/{r_*}$ while the slope of
$- ({r_{t_*} + s_{t_*}})/{r_*}$ while the slope of ![]() $H_2$ is
$H_2$ is ![]() $-k = {-b}/{a}$. Then for the first case where
$-k = {-b}/{a}$. Then for the first case where ![]() $- ({r_{t_*} + s_{t_*}})/{r_*} \leq -k$ (which is equivalent to
$- ({r_{t_*} + s_{t_*}})/{r_*} \leq -k$ (which is equivalent to ![]() $(k-1) r_{t_*} \leq s_{t_*}$), we have
$(k-1) r_{t_*} \leq s_{t_*}$), we have ![]() $q(r_{t_*}, s_{t_*}) \subset {\rm int}(\Delta (a,b))$ if and only if the vertex
$q(r_{t_*}, s_{t_*}) \subset {\rm int}(\Delta (a,b))$ if and only if the vertex ![]() $(r_{t_*}, r_{t_*}+s_{t_*})$ lies strictly below the hypothenuse
$(r_{t_*}, r_{t_*}+s_{t_*})$ lies strictly below the hypothenuse ![]() $H_2$. Since the line represented by
$H_2$. Since the line represented by ![]() $H_2$ is
$H_2$ is ![]() $ {r}/{a} + {s}/{b} = 1$, we require
$ {r}/{a} + {s}/{b} = 1$, we require
which, writing ![]() $a = b/k$, is equivalent to
$a = b/k$, is equivalent to ![]() $(k+1)r_{t_*} + s_{t_*} < b$ as in Theorem 2.12(II-ii-1). Similarly, for the second case where
$(k+1)r_{t_*} + s_{t_*} < b$ as in Theorem 2.12(II-ii-1). Similarly, for the second case where ![]() $- ({r_{t_*} + s_{t_*}})/{r_*} > -k$ (which is equivalent to
$- ({r_{t_*} + s_{t_*}})/{r_*} > -k$ (which is equivalent to ![]() $(k-1) r_{t_*} > s_{t_*}$), we have
$(k-1) r_{t_*} > s_{t_*}$), we have ![]() $q(r_{t_*}, s_{t_*}) \subset {\rm int}(\Delta (a,b))$ if and only if the vertex
$q(r_{t_*}, s_{t_*}) \subset {\rm int}(\Delta (a,b))$ if and only if the vertex ![]() $(2r_*, 0)$ lies strictly on the left of
$(2r_*, 0)$ lies strictly on the left of ![]() $(a,0)$, that is,
$(a,0)$, that is, ![]() $2r_{t_*} < a$ as in Theorem 2.12(II-ii-2).
$2r_{t_*} < a$ as in Theorem 2.12(II-ii-2).

Figure 17. Comparisons of slopes.
For condition (II-iii) in Corollary 5.6, note that the slope of the hypotenuse ![]() $H_1$ of the quadrilateral region
$H_1$ of the quadrilateral region ![]() $q(r_{t}, r_{t})$ is always
$q(r_{t}, r_{t})$ is always ![]() $-2$ which is no greater than the slope of the hypotenuse
$-2$ which is no greater than the slope of the hypotenuse ![]() $H_2$ (since we assume
$H_2$ (since we assume ![]() $k \geq 2$). Therefore, the condition is equivalent to
$k \geq 2$). Therefore, the condition is equivalent to ![]() $2r_t < a$ as in Theorem 2.12. Thus, we complete the proof.
$2r_t < a$ as in Theorem 2.12. Thus, we complete the proof.
5.2.3 Proof of Theorem 2.13(II)
Recall that the moment image ![]() $\mu (P(c,d))$ is the rectangle
$\mu (P(c,d))$ is the rectangle ![]() $\Box (c,d)$ with vertices
$\Box (c,d)$ with vertices ![]() $(0,0)$,
$(0,0)$, ![]() $(c,0)$,
$(c,0)$, ![]() $(0,d)$, and
$(0,d)$, and ![]() $(c,d)$. Condition (II-ii) in Corollary 5.6,
$(c,d)$. Condition (II-ii) in Corollary 5.6, ![]() $q(r_{t_*}, s_{t_*}) \subset {\rm int}(\Box (a,b))$, is equivalent to the vertex
$q(r_{t_*}, s_{t_*}) \subset {\rm int}(\Box (a,b))$, is equivalent to the vertex ![]() $(2r_*, 0)$ lying on the left of
$(2r_*, 0)$ lying on the left of ![]() $(c,0)$ and the height
$(c,0)$ and the height ![]() $r_* + s_*$ being lower than
$r_* + s_*$ being lower than ![]() $d$. In other words, we require
$d$. In other words, we require
Similarly, condition (II-iii), ![]() $q(r_{t}, r_{t}) \subset {\rm int}(\Box (c,d))$, is determined by the vertex
$q(r_{t}, r_{t}) \subset {\rm int}(\Box (c,d))$, is determined by the vertex ![]() $(2r_t, 0)$, and requires
$(2r_t, 0)$, and requires ![]() $r_t < {c}/{2}$ for
$r_t < {c}/{2}$ for ![]() $t \in [t_*,T]$. As these conditions are fulfilled by the path in Theorem 2.13 we complete the proof as before.
$t \in [t_*,T]$. As these conditions are fulfilled by the path in Theorem 2.13 we complete the proof as before.
5.3 Proof of Theorems 2.5, 2.6, and 2.7
Now, we are ready to see how these path lifting criteria easily imply the existence of knotted Lagrangian tori in ![]() $B^4(R)$,
$B^4(R)$, ![]() $E(a,b)$, and
$E(a,b)$, and ![]() $P(c,d)$. We will give the proof of these three theorems simultaneously.
$P(c,d)$. We will give the proof of these three theorems simultaneously.
For any area classes ![]() $(r,s)$ in the given region (4) or (5) or (6), consider the path
$(r,s)$ in the given region (4) or (5) or (6), consider the path ![]() $\gamma = \{\gamma (t)\}_{t \in [0,1]}$ with
$\gamma = \{\gamma (t)\}_{t \in [0,1]}$ with
where ![]() $(r, s_*) \notin \Delta (R,R)$ or
$(r, s_*) \notin \Delta (R,R)$ or ![]() $(r, s_*) \notin \Delta (a,b)$ or
$(r, s_*) \notin \Delta (a,b)$ or ![]() $(r, s_*) \notin \Box (c,d)$, respectively. By Theorem 2.1, we know
$(r, s_*) \notin \Box (c,d)$, respectively. By Theorem 2.1, we know ![]() $\gamma \subset {\rm Sh}_H^+(B^4(R))$,
$\gamma \subset {\rm Sh}_H^+(B^4(R))$, ![]() $\gamma \subset {\rm Sh}_H^+(E(a,b))$, and
$\gamma \subset {\rm Sh}_H^+(E(a,b))$, and ![]() $\gamma \subset {\rm Sh}_H^+(P(c,d))$, respectively. Choose a path
$\gamma \subset {\rm Sh}_H^+(P(c,d))$, respectively. Choose a path ![]() $\tilde {\gamma }$ that sits entirely inside
$\tilde {\gamma }$ that sits entirely inside ![]() $\Delta (R,R)^+$ or
$\Delta (R,R)^+$ or ![]() $\Delta (a,b)^+$ or
$\Delta (a,b)^+$ or ![]() $\Box (c,d)^+$ such that the whole of
$\Box (c,d)^+$ such that the whole of ![]() $\tilde {\gamma }$ satisfies condition (II-iii) of Theorem 2.11, 2.12, or 2.13, respectively, and such that
$\tilde {\gamma }$ satisfies condition (II-iii) of Theorem 2.11, 2.12, or 2.13, respectively, and such that ![]() $\tilde {\gamma }$ starts at a point satisfying condition (II-ii) and ends at
$\tilde {\gamma }$ starts at a point satisfying condition (II-ii) and ends at ![]() $(r,s)$. Now, consider the concatenation
$(r,s)$. Now, consider the concatenation
Then by condition (II) in Theorem 2.11, 2.12, or 2.13, respectively, we know ![]() $\tilde {\gamma } \# \gamma$ lifts to a Lagrangian isotopy of tori. In particular, there exists a Lagrangian sub-isotopy which projects via
$\tilde {\gamma } \# \gamma$ lifts to a Lagrangian isotopy of tori. In particular, there exists a Lagrangian sub-isotopy which projects via ![]() $\mathcal {P}$ to
$\mathcal {P}$ to ![]() $\gamma$, starting from
$\gamma$, starting from ![]() $(r,s)$. If there do not exist any knotted Lagrangian tori in the fiber
$(r,s)$. If there do not exist any knotted Lagrangian tori in the fiber ![]() $\mathcal {P}^{-1}((r,s))$, then up to Hamiltonian isotopy in
$\mathcal {P}^{-1}((r,s))$, then up to Hamiltonian isotopy in ![]() $B^4(R)$ or
$B^4(R)$ or ![]() $E(a,b)$ or
$E(a,b)$ or ![]() $P(c,d)$, we can assume this sub-isotopy starts from the product Lagrangian torus
$P(c,d)$, we can assume this sub-isotopy starts from the product Lagrangian torus ![]() $L(r,s)$. Then, by Definition 2.9,
$L(r,s)$. Then, by Definition 2.9, ![]() $\gamma$ lifts and it contradicts condition (I) in Theorem 2.11, 2.12, or 2.13, respectively. Thus, we complete the proof.
$\gamma$ lifts and it contradicts condition (I) in Theorem 2.11, 2.12, or 2.13, respectively. Thus, we complete the proof.
Remark 5.7 We note that the paths ![]() $\tilde {\gamma }$ used in the proof above are examples of paths in the shape with non-unique lifts. Indeed, the proof shows that the lift of
$\tilde {\gamma }$ used in the proof above are examples of paths in the shape with non-unique lifts. Indeed, the proof shows that the lift of ![]() $\tilde {\gamma } \# \gamma$ at the endpoint of
$\tilde {\gamma } \# \gamma$ at the endpoint of ![]() $\tilde {\gamma }$ is a knotted Lagrangian torus, but as it lies in the moment image
$\tilde {\gamma }$ is a knotted Lagrangian torus, but as it lies in the moment image ![]() $\tilde {\gamma }$ also admits a lift to a family of product tori.
$\tilde {\gamma }$ also admits a lift to a family of product tori.
6. Hamiltonian knottedness in  $\mathbb {C} P^2$
$\mathbb {C} P^2$
In this section, we give the proof of Theorem 2.8.
Proof of Theorem 2.8 By the wrapping construction from Theorem 5.2, we find a Lagrangian torus, denoted by ![]() $L_{r,s}$, with area classes
$L_{r,s}$, with area classes ![]() $(r,s)$ and lying inside
$(r,s)$ and lying inside ![]() $B^4(R)$, so also lying inside
$B^4(R)$, so also lying inside ![]() $\mathbb {C} P^2$. To distinguish
$\mathbb {C} P^2$. To distinguish ![]() $L_{r,s}$ from the fiber
$L_{r,s}$ from the fiber ![]() $L(r,s)$ inside
$L(r,s)$ inside ![]() $\mathbb {C} P^2$, we will use the
$\mathbb {C} P^2$, we will use the ![]() $\Psi$-invariant considered in [Reference Shelukhin, Tonkonog and ViannaSTV18]. This computes the minimal area of Maslov 2 holomorphic disks with boundary on the corresponding Lagrangian torus. By Theorem 4.4 in [Reference Shelukhin, Tonkonog and ViannaSTV18],
$\Psi$-invariant considered in [Reference Shelukhin, Tonkonog and ViannaSTV18]. This computes the minimal area of Maslov 2 holomorphic disks with boundary on the corresponding Lagrangian torus. By Theorem 4.4 in [Reference Shelukhin, Tonkonog and ViannaSTV18], ![]() $\Psi (L)$ is well-defined for any embedded Lagrangian tori in
$\Psi (L)$ is well-defined for any embedded Lagrangian tori in ![]() $\mathbb {C} P^2$, in particular, it is independent of the almost complex structure and invariant under the Hamiltonian isotopy. We will obtain the desired conclusion by showing that
$\mathbb {C} P^2$, in particular, it is independent of the almost complex structure and invariant under the Hamiltonian isotopy. We will obtain the desired conclusion by showing that ![]() $\Psi (L(r,s)) \neq \Psi (L_{r,s})$.
$\Psi (L(r,s)) \neq \Psi (L_{r,s})$.
For the fiber ![]() $L(r,s)$, with respect to the standard almost complex structure
$L(r,s)$, with respect to the standard almost complex structure ![]() $J_{0}$ on
$J_{0}$ on ![]() $\mathbb {C} P^2$, there are three (standard) Maslov 2
$\mathbb {C} P^2$, there are three (standard) Maslov 2 ![]() $J_{0}$-holomorphic disks with boundaries on
$J_{0}$-holomorphic disks with boundaries on ![]() $L(r,s)$, denoted by
$L(r,s)$, denoted by ![]() $D_1, D_2, D_3$, intersecting the three edges of moment image
$D_1, D_2, D_3$, intersecting the three edges of moment image ![]() $\mu (\mathbb {C} P^2(R))$ once for each and with areas
$\mu (\mathbb {C} P^2(R))$ once for each and with areas
Since ![]() $(r,s)$ satisfies
$(r,s)$ satisfies ![]() $2r+s >R$, we have
$2r+s >R$, we have ![]() $R-r-s< r$, that is,
$R-r-s< r$, that is, ![]() ${\rm area}(D_3) <{\rm area}(D_1) < {\rm area}(D_2)$. In particular, by definition,
${\rm area}(D_3) <{\rm area}(D_1) < {\rm area}(D_2)$. In particular, by definition, ![]() $\Psi (L(r,s)) \leq R - r- s$.
$\Psi (L(r,s)) \leq R - r- s$.
On the other hand, for the wrapped Lagrangian torus ![]() $L_{r,s}$, we claim that
$L_{r,s}$, we claim that ![]() $\Psi (L_{r,s}) \geq r$. This leads to the desired conclusion that
$\Psi (L_{r,s}) \geq r$. This leads to the desired conclusion that ![]() $\Psi (L_{r,s}) > \Psi (L(r,s))$, in particular, not equal. To obtain this claim, we will divide the Maslov 2 disks
$\Psi (L_{r,s}) > \Psi (L(r,s))$, in particular, not equal. To obtain this claim, we will divide the Maslov 2 disks ![]() $D$ with boundary on
$D$ with boundary on ![]() $L_{r,s}$ into the following two classes:
$L_{r,s}$ into the following two classes:
For the family ![]() ${\rm I\ }$, since
${\rm I\ }$, since ![]() $L_{r,s}$ is Hamiltonian isotopic to
$L_{r,s}$ is Hamiltonian isotopic to ![]() $L(r,s)$ in
$L(r,s)$ in ![]() $\mathbb {C}^2$, a computation of the
$\mathbb {C}^2$, a computation of the ![]() $\Psi$ invariant in
$\Psi$ invariant in ![]() $\mathbb {C}^2$ implies that any holomorphic disk
$\mathbb {C}^2$ implies that any holomorphic disk ![]() $D$ will have
$D$ will have ![]() ${\rm area}(D) \geq r$. For the family
${\rm area}(D) \geq r$. For the family ![]() ${\rm II}$, we will prove it by contrapositive as follows.
${\rm II}$, we will prove it by contrapositive as follows.
Suppose there exists ![]() $D \in {\rm II}$ with intersection number
$D \in {\rm II}$ with intersection number ![]() $d \geq 1$ but with
$d \geq 1$ but with ![]() ${\rm area}(D)< r$. Let
${\rm area}(D)< r$. Let ![]() $(-m, -n)$ be the homology class of the boundary. Then the Maslov
$(-m, -n)$ be the homology class of the boundary. Then the Maslov ![]() $2$ condition gives
$2$ condition gives
and the area is
By our hypothesis ![]() $r< {R}/{3}$ and
$r< {R}/{3}$ and ![]() $d \geq 1$, we see that if
$d \geq 1$, we see that if ![]() ${\rm area}(D) < r$, then
${\rm area}(D) < r$, then ![]() $n \leq -1$.
$n \leq -1$.
Now, similarly to the proof of Theorem 2.5, consider the following straight line path ![]() $\gamma (t) = (r, (1-t) s + ts_*)$ in
$\gamma (t) = (r, (1-t) s + ts_*)$ in ![]() ${\rm Sh}^+_H(B^4(R))$, for
${\rm Sh}^+_H(B^4(R))$, for ![]() $t \in [0,1]$ but with sufficiently large
$t \in [0,1]$ but with sufficiently large ![]() $S$. Note that this path lifts to a Lagrangian isotopy
$S$. Note that this path lifts to a Lagrangian isotopy ![]() $\{L_t\}_{t \in [0,1]}$, starting from
$\{L_t\}_{t \in [0,1]}$, starting from ![]() $L_{r,s}$. Viewing
$L_{r,s}$. Viewing ![]() $\{L_t\}_{t \in [0,1]}$ inside
$\{L_t\}_{t \in [0,1]}$ inside ![]() $\mathbb {C} P^2$, if the corresponding family of holomorphic disks
$\mathbb {C} P^2$, if the corresponding family of holomorphic disks ![]() $D_t$ persists, then, as the degree is fixed (since the
$D_t$ persists, then, as the degree is fixed (since the ![]() $L_t$ lie in the ball disjoint from the line at infinity) and
$L_t$ lie in the ball disjoint from the line at infinity) and ![]() $n \leq -1$, we will have
$n \leq -1$, we will have ![]() ${\rm area}(D_1) = d(R-3r) + r + n(s_*-r)$ which is negative for
${\rm area}(D_1) = d(R-3r) + r + n(s_*-r)$ which is negative for ![]() $s_*$ sufficiently large and a contradiction.
$s_*$ sufficiently large and a contradiction.
Alternatively the family of disks is not compact, and we have bubbling into the union of a Maslov ![]() $0$ and a Maslov
$0$ and a Maslov ![]() $2$ disk. As
$2$ disk. As ![]() ${\rm area}(D_t)$ is a decreasing function of
${\rm area}(D_t)$ is a decreasing function of ![]() $t$ the Maslov
$t$ the Maslov ![]() $2$ component will also have area less than
$2$ component will also have area less than ![]() $r$, and the calculation above shows that it will be asymptotic to a class
$r$, and the calculation above shows that it will be asymptotic to a class ![]() $(-m_1, -n_1)$ with
$(-m_1, -n_1)$ with ![]() $n_1 <0$. Thus, the new family of Maslov
$n_1 <0$. Thus, the new family of Maslov ![]() $2$ disks again will have decreasing area and cannot persist until time
$2$ disks again will have decreasing area and cannot persist until time ![]() $t=1$ (the degree can only decrease after a degeneration by positivity of intersection). Arguing by induction, we have a contradiction as in § 4.2.
$t=1$ (the degree can only decrease after a degeneration by positivity of intersection). Arguing by induction, we have a contradiction as in § 4.2.
In this way, we have shown that any Maslov 2 disk ![]() $D \in {\rm II}$ must have area at least
$D \in {\rm II}$ must have area at least ![]() $r$. Together with the argument for the disks in the family
$r$. Together with the argument for the disks in the family ![]() ${\rm I}$, we obtain the desired claim, and thus complete the proof.
${\rm I}$, we obtain the desired claim, and thus complete the proof.
Remark 6.1 Proposition 2.8 also follows directly from Corollary 6.7 in [Reference Shelukhin, Tonkonog and ViannaSTV18] on the straight line path of the shape invariant. More precisely, if ![]() $L_{r,s}$ is Hamiltonian isotopic to the fiber
$L_{r,s}$ is Hamiltonian isotopic to the fiber ![]() $L(r,s)$ inside
$L(r,s)$ inside ![]() $\mathbb {C} P^2$, then Corollary 6.7 in [Reference Shelukhin, Tonkonog and ViannaSTV18] proves that the longest straight line starting from
$\mathbb {C} P^2$, then Corollary 6.7 in [Reference Shelukhin, Tonkonog and ViannaSTV18] proves that the longest straight line starting from ![]() $L_{r,s}$ stops at the boundary of
$L_{r,s}$ stops at the boundary of ![]() $\mu (\mathbb {C} P^2)$, while our straight line path chosen in the proof of Theorem 2.8 above can go (vertically) far beyond
$\mu (\mathbb {C} P^2)$, while our straight line path chosen in the proof of Theorem 2.8 above can go (vertically) far beyond ![]() $\mu (\mathbb {C} P^2)$. This provides the requested contradiction. We include the argument above for completeness as the Corollary 6.7 ultimately relies on similar considerations.
$\mu (\mathbb {C} P^2)$. This provides the requested contradiction. We include the argument above for completeness as the Corollary 6.7 ultimately relies on similar considerations.
The holomorphic disks in the above proof could be substituted for finite energy curves as in § 4.1. However, degenerations of holomorphic disks are slightly simpler to analyze.
7. An exotic example
As explained in the introduction, path lifting can be subtle for various reasons. In this section, we illustrate this complexity via an exotic example. Consider ![]() $\gamma _1$ and
$\gamma _1$ and ![]() $\gamma _2$ in
$\gamma _2$ in ![]() ${\rm Sh}_H^+(E(a,b))$ with
${\rm Sh}_H^+(E(a,b))$ with ![]() $k: = {b}/{a} = 3$ shown in Figure 18. In the left picture,
$k: = {b}/{a} = 3$ shown in Figure 18. In the left picture, ![]() $\gamma _1$ when viewed with either orientation lifts from
$\gamma _1$ when viewed with either orientation lifts from ![]() ${\rm Sh}_H^+(E(a,b))$ to a closed loop of Lagrangians. The picture indicates the concatenation points (two places labeled by crosses), and the sub-paths change types from Type-I to Type-II, then back to Type-I (see § 2.2).
${\rm Sh}_H^+(E(a,b))$ to a closed loop of Lagrangians. The picture indicates the concatenation points (two places labeled by crosses), and the sub-paths change types from Type-I to Type-II, then back to Type-I (see § 2.2).

Figure 18. Path ![]() $\gamma _1$ lifts, but path
$\gamma _1$ lifts, but path ![]() $\gamma _2$ lifts only viewed clockwise.
$\gamma _2$ lifts only viewed clockwise.
On the other hand, in the right picture, the path ![]() $\gamma _2$ is a small perturbation of
$\gamma _2$ is a small perturbation of ![]() $\gamma _1$ as a geometric path. If we view it clockwise, then this is an example showing a certain monodromy phenomenon. Note that
$\gamma _1$ as a geometric path. If we view it clockwise, then this is an example showing a certain monodromy phenomenon. Note that ![]() $\gamma _2$ lifts by condition (II) in Theorem 2.12 and the picture indicates the concatenation point as the lower cross. Explicitly, it starts from a Type-I sub-path, followed by a Type-II sub-path. This Type-II sub-path ends at the same point as the starting point. Meanwhile, since this Type-II sub-path never comes back to the ‘flexible’ region below the line
$\gamma _2$ lifts by condition (II) in Theorem 2.12 and the picture indicates the concatenation point as the lower cross. Explicitly, it starts from a Type-I sub-path, followed by a Type-II sub-path. This Type-II sub-path ends at the same point as the starting point. Meanwhile, since this Type-II sub-path never comes back to the ‘flexible’ region below the line ![]() $4r +s = b$, as in the left picture, the Lagrangian torus at the endpoint is not a product torus. Therefore, this closed loop
$4r +s = b$, as in the left picture, the Lagrangian torus at the endpoint is not a product torus. Therefore, this closed loop ![]() $\gamma _2$ lifts but not as a loop of Lagrangian tori.
$\gamma _2$ lifts but not as a loop of Lagrangian tori.
Finally, if we view ![]() $\gamma _2$ counterclockwise, i.e. considering its reverse path
$\gamma _2$ counterclockwise, i.e. considering its reverse path ![]() $\overline {\gamma }_2$, then it does not lift. Otherwise, the sub-path from the starting point to the upper cross will lift, and it violates the obstruction, i.e. condition (I) in Theorem 2.12. This shows that the orientation in the path lifting also matters.
$\overline {\gamma }_2$, then it does not lift. Otherwise, the sub-path from the starting point to the upper cross will lift, and it violates the obstruction, i.e. condition (I) in Theorem 2.12. This shows that the orientation in the path lifting also matters.
8. Obstructions to symplectic embeddings
In this section, we will demonstrate how to use path lifting to obstruct symplectic embeddings between domains in ![]() $\mathbb {R}^4$. Let us start from the following result.
$\mathbb {R}^4$. Let us start from the following result.
Proposition 8.1 Let ![]() $X, Y$ be two toric domains in
$X, Y$ be two toric domains in ![]() $\mathbb {R}^4$, and let
$\mathbb {R}^4$, and let ![]() $\gamma$ be a path in
$\gamma$ be a path in ![]() ${\rm Sh}_H^{+}(X)$ that lifts to a Lagrangian isotopy of tori in
${\rm Sh}_H^{+}(X)$ that lifts to a Lagrangian isotopy of tori in ![]() $\mathcal {L}(X)$, denoted by
$\mathcal {L}(X)$, denoted by ![]() $\{L_t\}_{t \in [0, T]}$. If there exists a symplectic embedding
$\{L_t\}_{t \in [0, T]}$. If there exists a symplectic embedding ![]() $X \hookrightarrow Y$ such that the image of
$X \hookrightarrow Y$ such that the image of ![]() $L_0$ is unknotted in
$L_0$ is unknotted in ![]() $Y$, then
$Y$, then ![]() $\gamma$ lies in
$\gamma$ lies in ![]() ${\rm Sh}_H^{+}(Y)$ and lifts to
${\rm Sh}_H^{+}(Y)$ and lifts to ![]() $\mathcal {L}(Y)$.
$\mathcal {L}(Y)$.
Proof. The first conclusion comes directly from Proposition 7.1 in [Reference Hind and ZhangHZ21]. It suffices to prove the second conclusion. Suppose ![]() $\gamma = \{(r_t, s_t) \in {\rm Sh}_H^+(X) \,|\, t \in [0,T]\}$. Since
$\gamma = \{(r_t, s_t) \in {\rm Sh}_H^+(X) \,|\, t \in [0,T]\}$. Since ![]() $\gamma$ lifts to
$\gamma$ lifts to ![]() $\mathcal {L}(X)$, the corresponding Lagrangian isotopy of tori
$\mathcal {L}(X)$, the corresponding Lagrangian isotopy of tori ![]() $L = \{L_t\}_{t \in [0, T]}$ satisfies
$L = \{L_t\}_{t \in [0, T]}$ satisfies ![]() $\mathcal {P}(L_t) = (r_t, s_t)$. Suppose the symplectic embedding
$\mathcal {P}(L_t) = (r_t, s_t)$. Suppose the symplectic embedding ![]() $X \hookrightarrow Y$ is
$X \hookrightarrow Y$ is ![]() $\phi$, and consider the Lagrangian isotopy
$\phi$, and consider the Lagrangian isotopy
Similarly to Proposition 7.1 in [Reference Hind and ZhangHZ21], we know ![]() $\mathcal {P}(\phi (L_t)) = (r_t, s_t)$ for any
$\mathcal {P}(\phi (L_t)) = (r_t, s_t)$ for any ![]() $t \in [0, T]$. Meanwhile, by assumption,
$t \in [0, T]$. Meanwhile, by assumption, ![]() $\phi (L_0)$ is unknotted in
$\phi (L_0)$ is unknotted in ![]() $Y$, so by definition there exists a Hamiltonian isotopy
$Y$, so by definition there exists a Hamiltonian isotopy ![]() $\Psi = \{\Psi _t\}_{t \in [0,T]}$ of
$\Psi = \{\Psi _t\}_{t \in [0,T]}$ of ![]() $Y$ such that
$Y$ such that ![]() $\Psi _1(\phi (L_0)) = L(r_0, s_0)$. Then the following Lagrangian isotopy of tori in
$\Psi _1(\phi (L_0)) = L(r_0, s_0)$. Then the following Lagrangian isotopy of tori in ![]() $Y$,
$Y$,
is the desired lift of ![]() $\gamma$ in
$\gamma$ in ![]() ${\rm Sh}_H^+(Y)$ since
${\rm Sh}_H^+(Y)$ since ![]() ${\rm Ham}(Y)$ preserves the fibers of
${\rm Ham}(Y)$ preserves the fibers of ![]() $\mathcal {P}$. In other words,
$\mathcal {P}$. In other words, ![]() $\gamma \subset {\rm Sh}_H^+(Y)$ lifts to
$\gamma \subset {\rm Sh}_H^+(Y)$ lifts to ![]() $\mathcal {L}(Y)$ by
$\mathcal {L}(Y)$ by ![]() $\tilde {L}$, and we complete the proof.
$\tilde {L}$, and we complete the proof.
8.1 Proof of Theorem 2.16
We will only give the proof of criterion (1); criteria (2) and (3) can be proved in a similar manner.
For the given ![]() $(r,s)$, consider the straight line path
$(r,s)$, consider the straight line path ![]() $\gamma$ starting at
$\gamma$ starting at ![]() $(r,s)$ and ending at
$(r,s)$ and ending at ![]() $(0,x)$. Since it is a straight line with
$(0,x)$. Since it is a straight line with ![]() $2r+s >R$ and
$2r+s >R$ and ![]() $x>R$, this path
$x>R$, this path ![]() $\gamma$ lies entirely outside the ‘flexible’ region below the line
$\gamma$ lies entirely outside the ‘flexible’ region below the line ![]() $2r+s =R$. Meanwhile, again
$2r+s =R$. Meanwhile, again ![]() $x>R$ implies that
$x>R$ implies that ![]() $\gamma$ will escape the moment image
$\gamma$ will escape the moment image ![]() $\Delta (R,R)$ eventually. Then, on the one hand, since
$\Delta (R,R)$ eventually. Then, on the one hand, since ![]() $\gamma$ lies entirely in the moment image
$\gamma$ lies entirely in the moment image ![]() $\Delta (1,x)$, Example 2.10 implies that it lifts to
$\Delta (1,x)$, Example 2.10 implies that it lifts to ![]() $\mathcal {L}(E(1,x))$. On the other hand, if
$\mathcal {L}(E(1,x))$. On the other hand, if ![]() $\phi (L(r, s))$ is unknotted under the embedding
$\phi (L(r, s))$ is unknotted under the embedding ![]() $\phi : E(1,x) \hookrightarrow B^4(R)$, then Proposition 8.1 implies that
$\phi : E(1,x) \hookrightarrow B^4(R)$, then Proposition 8.1 implies that ![]() $\gamma \subset {\rm Sh}_H^+(B^4(R))$ and it lifts as well. However, this contradicts Theorem 2.11(I). Therefore, we obtain the desired conclusion.
$\gamma \subset {\rm Sh}_H^+(B^4(R))$ and it lifts as well. However, this contradicts Theorem 2.11(I). Therefore, we obtain the desired conclusion.
8.2 Proof of Theorem 2.21
Assumption (ii) implies that ![]() $\gamma$ lifts to
$\gamma$ lifts to ![]() $\mathcal {L}(X)$ since
$\mathcal {L}(X)$ since ![]() $\gamma$ lies entirely in
$\gamma$ lies entirely in ![]() $\mu (X)^+$. In particular, the starting point
$\mu (X)^+$. In particular, the starting point ![]() $(r_0, s_0)$ can be realized as the inclusion of the product Lagrangian torus
$(r_0, s_0)$ can be realized as the inclusion of the product Lagrangian torus ![]() $L(r_0, s_0) \hookrightarrow X$. Now, suppose that there exists a symplectic embedding
$L(r_0, s_0) \hookrightarrow X$. Now, suppose that there exists a symplectic embedding ![]() $\phi : X \hookrightarrow E(a,b)$. By the first condition in assumption (i), we have
$\phi : X \hookrightarrow E(a,b)$. By the first condition in assumption (i), we have
where ![]() $i$ is the inclusion. Replacing
$i$ is the inclusion. Replacing ![]() $E$ by a slightly smaller closed ellipsoid, Corollary 1.6 in [Reference McDuffMcD09] proves that the space of symplectic embeddings from
$E$ by a slightly smaller closed ellipsoid, Corollary 1.6 in [Reference McDuffMcD09] proves that the space of symplectic embeddings from ![]() $E$ to
$E$ to ![]() $E(a,b)$ denoted by
$E(a,b)$ denoted by ![]() ${\rm Emb}(E, E(a,b))$ is connected, and then the condition
${\rm Emb}(E, E(a,b))$ is connected, and then the condition ![]() $E \subset E(a,b)$ implies that every symplectic embedding from
$E \subset E(a,b)$ implies that every symplectic embedding from ![]() $E$ to
$E$ to ![]() $E(a,b)$ is isotopic to the inclusion. In particular, the product Lagrangian torus
$E(a,b)$ is isotopic to the inclusion. In particular, the product Lagrangian torus ![]() $L(r_0,s_0) \subset E$ is unknotted under the symplectic embedding
$L(r_0,s_0) \subset E$ is unknotted under the symplectic embedding ![]() $\phi \circ i$. Then Proposition 8.1 implies that
$\phi \circ i$. Then Proposition 8.1 implies that ![]() $\gamma \subset {\rm Sh}_H^+(E(a,b))$ and it lifts to
$\gamma \subset {\rm Sh}_H^+(E(a,b))$ and it lifts to ![]() $\mathcal {L}(E(a,b))$. This contradicts Theorem 2.12(I), and therefore we obtain the desired contradiction. Figure 19 shows a schematic picture of this proof, where
$\mathcal {L}(E(a,b))$. This contradicts Theorem 2.12(I), and therefore we obtain the desired contradiction. Figure 19 shows a schematic picture of this proof, where ![]() $E = E_{\Delta (E_r, E_s)}$ and the moment image
$E = E_{\Delta (E_r, E_s)}$ and the moment image ![]() $\Delta (E_r, E_s)$ is shown as the triangle with vertices
$\Delta (E_r, E_s)$ is shown as the triangle with vertices ![]() $(0,0)$,
$(0,0)$, ![]() $(E_r, 0)$, and
$(E_r, 0)$, and ![]() $(0, E_s)$, the image
$(0, E_s)$, the image ![]() $\mu (X)$ is described via the profile curve (without arrow), and the obstruction is given by
$\mu (X)$ is described via the profile curve (without arrow), and the obstruction is given by ![]() $\gamma$, shown as the bold path (with arrow).
$\gamma$, shown as the bold path (with arrow).

Figure 19. The obstruction is given by the bold path.
Acknowledgements
This work was completed when the second author held the position of CRM-ISM Postdoctoral Research Fellow at CRM, University of Montreal, and the second author thanks this institute for its warm hospitality. We also thank an anonymous referee for a thorough report.
Conflicts of Interest
None.
Appendix A
This section verifies the following result, up to a rescaling by ![]() $ {a}/({k+1})$, that was used in Example 2.18(2).
$ {a}/({k+1})$, that was used in Example 2.18(2).
Proposition A.1 For any ![]() $k \in \mathbb {N}$,
$k \in \mathbb {N}$, ![]() $E(k, (k+1)^2) \hookrightarrow E(k+1, k(k+1))$.
$E(k, (k+1)^2) \hookrightarrow E(k+1, k(k+1))$.
From Hutchings’ work [Reference HutchingsHut11] and McDuff's work [Reference McDuffMcD11], there exists a complete characterization of four-dimensional ellipsoid embeddings, that is,
Here, ![]() $\mathcal {N}(a,b)$ denotes an infinite sequence of numbers consisting of all the non-negative linear combinations
$\mathcal {N}(a,b)$ denotes an infinite sequence of numbers consisting of all the non-negative linear combinations ![]() $ma + nb$ (for
$ma + nb$ (for ![]() $m, n \in \mathbb {Z}_{\geq 0}$) in a non-decreasing order (with repetitions), and
$m, n \in \mathbb {Z}_{\geq 0}$) in a non-decreasing order (with repetitions), and ![]() $\mathcal {N}(a,b)_k$ is the
$\mathcal {N}(a,b)_k$ is the ![]() $k$th entry in
$k$th entry in ![]() $\mathcal {N}(a,b)$, similarly to
$\mathcal {N}(a,b)$, similarly to ![]() $\mathcal {N}(c,d)_k$ and
$\mathcal {N}(c,d)_k$ and ![]() $\mathcal {N}(c,d)$. In fact, there exists a nice geometric description of
$\mathcal {N}(c,d)$. In fact, there exists a nice geometric description of ![]() $\mathcal {N}(a,b)$ (see § 3.3 in [Reference HutchingsHut11]). Denote by
$\mathcal {N}(a,b)$ (see § 3.3 in [Reference HutchingsHut11]). Denote by ![]() $\Delta _{a,b}(t)$ the closed right triangle in
$\Delta _{a,b}(t)$ the closed right triangle in ![]() $\mathbb {R}^2$ with vertices
$\mathbb {R}^2$ with vertices ![]() $(0,0)$,
$(0,0)$, ![]() $( {t}/{a}, 0)$, and
$( {t}/{a}, 0)$, and ![]() $(0, {t}/{b})$ for
$(0, {t}/{b})$ for ![]() $t \geq 0$, and denote
$t \geq 0$, and denote
Then the characterization (A.1) is equivalent to the statement that ![]() $E(c,d) \hookrightarrow E(a,b)$ if and only if
$E(c,d) \hookrightarrow E(a,b)$ if and only if ![]() $t_2 \leq t_1$ whenever
$t_2 \leq t_1$ whenever ![]() $\mathcal {R}_{c,d}(t_2) = \mathcal {R}_{a,b}(t_1)$. Since
$\mathcal {R}_{c,d}(t_2) = \mathcal {R}_{a,b}(t_1)$. Since ![]() $\mathcal {R}_{a,b}(t)$ and
$\mathcal {R}_{a,b}(t)$ and ![]() $\mathcal {R}_{c,d}(t)$ are non-decreasing functions of
$\mathcal {R}_{c,d}(t)$ are non-decreasing functions of ![]() $t$, (A.1) is further equivalent to the following statement:
$t$, (A.1) is further equivalent to the following statement:
We emphasize that the statement (A.1) (as well as (A.3)), are not always easy to verify. However, the equivalent statement (A.3) has the advantage that some elementary geometry propositions can be applied. For instance, in terms of counting lattice points, the well-known Pick's theorem is very useful. Explicitly, for any polygon with integer vertices and without holes,
The proof of Proposition A.1 turns out to be a nice combination of the criterion (A.3) and Pick's theorem (A.4).
Proof of Proposition A.1 By (A.3), it suffices to show ![]() ${\mathcal {R}}_{k,(k+1)^2}(t) \geq {\mathcal {R}}_{k+1,k(k+1)}(t)$ for any
${\mathcal {R}}_{k,(k+1)^2}(t) \geq {\mathcal {R}}_{k+1,k(k+1)}(t)$ for any ![]() $t \geq 0$. We will prove this in two steps. First, we have the following result.
$t \geq 0$. We will prove this in two steps. First, we have the following result.
Lemma A.2 For any ![]() $k \in \mathbb {N}$ and
$k \in \mathbb {N}$ and ![]() $A \in \mathbb {Z}_{\geq 0}$, we have
$A \in \mathbb {Z}_{\geq 0}$, we have
Proof of Lemma A.2 For the right triangle ![]() ${\Delta }_{k+1,k(k+1)}(Ak(k+1))$, its
${\Delta }_{k+1,k(k+1)}(Ak(k+1))$, its ![]() $x$-intercept is
$x$-intercept is ![]() $ {t}/{a} = {Ak(k+1)}/({k+1}) = Ak$ and its
$ {t}/{a} = {Ak(k+1)}/({k+1}) = Ak$ and its ![]() $y$-intercept is
$y$-intercept is ![]() $ {t}/{b} = {Ak(k+1)}/{k(k+1)} = A$, where both
$ {t}/{b} = {Ak(k+1)}/{k(k+1)} = A$, where both ![]() $Ak, k \in \mathbb {Z}_{\geq 0}$. Then Pick's theorem applies, and (A.4) implies that
$Ak, k \in \mathbb {Z}_{\geq 0}$. Then Pick's theorem applies, and (A.4) implies that
Meanwhile, by elementary counting, ![]() $\#\left \{\mbox {boundary lattice points}\right \} = 2A + Ak$. Therefore, we get the desired conclusion for
$\#\left \{\mbox {boundary lattice points}\right \} = 2A + Ak$. Therefore, we get the desired conclusion for ![]() ${\mathcal {R}}_{k+1,k(k+1)}(Ak(k+1))$.
${\mathcal {R}}_{k+1,k(k+1)}(Ak(k+1))$.
For the right triangle ![]() ${\Delta }_{k,(k+1)^2}(Ak(k+1))$, let us introduce the following notation,
${\Delta }_{k,(k+1)^2}(Ak(k+1))$, let us introduce the following notation,
where ![]() $C \in \mathbb {N}$ and
$C \in \mathbb {N}$ and ![]() $0 \leq C \leq k$, and
$0 \leq C \leq k$, and
where ![]() $B \in \mathbb {N}$ and
$B \in \mathbb {N}$ and ![]() $0 \leq B \leq k$. Here is a useful observation.
$0 \leq B \leq k$. Here is a useful observation.
Claim A.3 Either ![]() $B=C=0$ or
$B=C=0$ or ![]() $B + C = k+1$. In the second case we have
$B + C = k+1$. In the second case we have ![]() $\lfloor {Bk}/({k+1}) \rfloor = B-1$.
$\lfloor {Bk}/({k+1}) \rfloor = B-1$.
Proof of Claim A.3 First we note that if ![]() $B=0$, then
$B=0$, then ![]() $A$ is a multiple of
$A$ is a multiple of ![]() $k+1$ and so also
$k+1$ and so also ![]() $C=0$. Henceforth, then we suppose
$C=0$. Henceforth, then we suppose ![]() $B>0$.
$B>0$.
We have
Therefore, we can write ![]() $kB = m(k+1) + C$ where
$kB = m(k+1) + C$ where ![]() $m \ge 0$ is an integer. More explicitly,
$m \ge 0$ is an integer. More explicitly, ![]() $m = \lfloor {kB}/({k+1}) \rfloor$. As
$m = \lfloor {kB}/({k+1}) \rfloor$. As ![]() $B> 0$ we have
$B> 0$ we have ![]() $m < B$, but if
$m < B$, but if ![]() $m \le B-2$, then
$m \le B-2$, then
a contradiction. Hence, ![]() $m = B-1$ and we get
$m = B-1$ and we get ![]() $C = kB - (k+1)(B-1) = k+1 - B$. It is easy to check that
$C = kB - (k+1)(B-1) = k+1 - B$. It is easy to check that ![]() $B+C=k+1$ implies
$B+C=k+1$ implies ![]() $\lfloor {Bk}/({k+1}) \rfloor = B-1$, and, therefore, we get the desired claim.
$\lfloor {Bk}/({k+1}) \rfloor = B-1$, and, therefore, we get the desired claim.
Next, we will count lattice points in ![]() $\Delta _{k, (k+1)^2}(Ak(k+1))$. Divide
$\Delta _{k, (k+1)^2}(Ak(k+1))$. Divide ![]() ${\Delta }_{k,(k+1)^2}(Ak(k+1))$ into two parts as in Figure A.1, one small triangle
${\Delta }_{k,(k+1)^2}(Ak(k+1))$ into two parts as in Figure A.1, one small triangle ![]() $\Delta _{\rm small}$ and one trapezoid
$\Delta _{\rm small}$ and one trapezoid ![]() $P_{\rm trapezoid}$. Here the horizontal line
$P_{\rm trapezoid}$. Here the horizontal line ![]() $y=bk$ is excluded from
$y=bk$ is excluded from ![]() $\Delta _{\rm small}$ and considered as part of
$\Delta _{\rm small}$ and considered as part of ![]() $P_{\rm trapezoid}$. In the case when
$P_{\rm trapezoid}$. In the case when ![]() $B=C=0$ we make no division and
$B=C=0$ we make no division and ![]() $P_{\rm trapezoid}$ can be used to denote our original closed triangle
$P_{\rm trapezoid}$ can be used to denote our original closed triangle ![]() $\Delta _{k, (k+1)^2}(Ak(k+1))$. The way we cut in Figure A.1 guarantees that there are no lattice points on the hypotenuse of
$\Delta _{k, (k+1)^2}(Ak(k+1))$. The way we cut in Figure A.1 guarantees that there are no lattice points on the hypotenuse of ![]() $\Delta _{\rm small}$ except possibly at the endpoints. Indeed, since the slope of
$\Delta _{\rm small}$ except possibly at the endpoints. Indeed, since the slope of ![]() ${\Delta }_{k,(k+1)^2}(Ak(k+1))$ is
${\Delta }_{k,(k+1)^2}(Ak(k+1))$ is ![]() $- {k}/{(k+1)^2}$, moving from the vertex
$- {k}/{(k+1)^2}$, moving from the vertex ![]() $(A(k+1), 0)$ to the vertex
$(A(k+1), 0)$ to the vertex ![]() $(0, {Ak}/({k+1}))$, only when the
$(0, {Ak}/({k+1}))$, only when the ![]() $x$ coordinate decreases by a multiple of
$x$ coordinate decreases by a multiple of ![]() $(k+1)^2$ can we see a lattice point on the hypotenuse of
$(k+1)^2$ can we see a lattice point on the hypotenuse of ![]() ${\Delta }_{k,(k+1)^2}(Ak(k+1))$. There are at most
${\Delta }_{k,(k+1)^2}(Ak(k+1))$. There are at most ![]() $\lfloor {A}/({k+1}) \rfloor$-many non-zero multiples of
$\lfloor {A}/({k+1}) \rfloor$-many non-zero multiples of ![]() $(k+1)^2$ in the interval
$(k+1)^2$ in the interval ![]() $[0, A(k+1)]$ and the smallest is
$[0, A(k+1)]$ and the smallest is
Meanwhile, it is easy to verify that the corresponding ![]() $y$-coordinate is
$y$-coordinate is ![]() $bk$.
$bk$.

Figure A.1. A division of ![]() ${\Delta }_{k,(k+1)^2}(Ak(k+1))$.
${\Delta }_{k,(k+1)^2}(Ak(k+1))$.
Now ![]() $P_{\rm trapezoid}$ is a polygon with integer vertices and without holes. Hence, Pick's theorem applies, and (A.4) implies that
$P_{\rm trapezoid}$ is a polygon with integer vertices and without holes. Hence, Pick's theorem applies, and (A.4) implies that
Moreover, by an elementary counting, ![]() $\#\{\mbox {boundary lattice points}\} = (A+B+b)(k+1)$. Therefore,
$\#\{\mbox {boundary lattice points}\} = (A+B+b)(k+1)$. Therefore,
We note this formula applies in all cases, including when ![]() $B=0$ and
$B=0$ and ![]() $P_{\rm trapezoid}$ is a triangle.
$P_{\rm trapezoid}$ is a triangle.
For the small triangle ![]() $\Delta _{\rm small}$, up to an integer shift (explicitly shifted down by
$\Delta _{\rm small}$, up to an integer shift (explicitly shifted down by ![]() $bk$), it suffices to consider the following triangle in Figure A.2. In particular, the top horizontal line intersecting the triangle and with integer intercept is
$bk$), it suffices to consider the following triangle in Figure A.2. In particular, the top horizontal line intersecting the triangle and with integer intercept is ![]() $y = \lfloor {Bk}/({k+1}) \rfloor$. In the case when the triangle is non-trivial, that is
$y = \lfloor {Bk}/({k+1}) \rfloor$. In the case when the triangle is non-trivial, that is ![]() $B \neq 0$, Claim A.3 above says that
$B \neq 0$, Claim A.3 above says that ![]() $\lfloor {Bk}/({k+1}) \rfloor = B-1$. There are no lattice points in the interior of the hypotenuse of the triangle in Figure A.2, and for each
$\lfloor {Bk}/({k+1}) \rfloor = B-1$. There are no lattice points in the interior of the hypotenuse of the triangle in Figure A.2, and for each ![]() $\ell \in \{1,\ldots, B-1\}$, the intersection of the line
$\ell \in \{1,\ldots, B-1\}$, the intersection of the line ![]() $y = \ell$ with this triangle admits
$y = \ell$ with this triangle admits ![]() $(B(k+1) - \ell (k+2))$-many lattice points on its the interior. Then
$(B(k+1) - \ell (k+2))$-many lattice points on its the interior. Then
 \begin{align} \# \left\{\!\!\begin{array}{c} \mbox{lattice points} \\ \mbox{in } \Delta_{\rm small} \end{array}\!\!\right\} & = \sum_{\ell=1}^{B-1} (B(k+1) - \ell(k+2)) \nonumber\\ & = B(B-1)(k+1) - \frac{B(B-1)(k+2)}{2} \nonumber\\ & = \frac{B(B-1)k}{2} . \end{align}
\begin{align} \# \left\{\!\!\begin{array}{c} \mbox{lattice points} \\ \mbox{in } \Delta_{\rm small} \end{array}\!\!\right\} & = \sum_{\ell=1}^{B-1} (B(k+1) - \ell(k+2)) \nonumber\\ & = B(B-1)(k+1) - \frac{B(B-1)(k+2)}{2} \nonumber\\ & = \frac{B(B-1)k}{2} . \end{align}
(Again we note this formula remains valid in the case when ![]() $B=0$, that is, the triangle is empty and there are no lattice points.)
$B=0$, that is, the triangle is empty and there are no lattice points.)

Figure A.2. Line-by-line counting in ![]() $\Delta _{\rm small}$.
$\Delta _{\rm small}$.
Hence, by summing up the lattices points in ![]() $P_{\rm trapezoid}$ (as in (A.5)) and in
$P_{\rm trapezoid}$ (as in (A.5)) and in ![]() $\Delta _{\rm small}$ (as in (A.6)), we have
$\Delta _{\rm small}$ (as in (A.6)), we have
 \begin{align*} {\mathcal{R}}_{k,(k+1)^2}(Ak(k+1))& = \# \left\{\!\!\begin{array}{c} \mbox{lattice points} \\ \mbox{in } P_{\rm trapezoid} \end{array}\!\!\right\} + \#\left\{\!\!\begin{array}{c} \mbox{lattice points} \\ \mbox{in } \Delta_{\rm small} \end{array}\!\!\right\}\\ & = \frac{bk(k+1)(A+B)}{2} +1 + \frac{(A+B+b)(k+1)}{2} + \frac{B(B-1)k}{2}\\ & = \frac{1}{2} kA(A+1) + (A+1), \end{align*}
\begin{align*} {\mathcal{R}}_{k,(k+1)^2}(Ak(k+1))& = \# \left\{\!\!\begin{array}{c} \mbox{lattice points} \\ \mbox{in } P_{\rm trapezoid} \end{array}\!\!\right\} + \#\left\{\!\!\begin{array}{c} \mbox{lattice points} \\ \mbox{in } \Delta_{\rm small} \end{array}\!\!\right\}\\ & = \frac{bk(k+1)(A+B)}{2} +1 + \frac{(A+B+b)(k+1)}{2} + \frac{B(B-1)k}{2}\\ & = \frac{1}{2} kA(A+1) + (A+1), \end{align*}
where the final step comes from a series of simplifications using the relation ![]() $B = A - b(k+1)$. Thus, we complete the proof of Lemma A.2.
$B = A - b(k+1)$. Thus, we complete the proof of Lemma A.2.
Suppose now that ![]() $t = Ak(k+1) + s$ where
$t = Ak(k+1) + s$ where ![]() $0< s< k(k+1)$. Observe that the graph of
$0< s< k(k+1)$. Observe that the graph of ![]() ${\mathcal {R}}_{k+1,k(k+1)}(t)$ is horizontal with jumps when
${\mathcal {R}}_{k+1,k(k+1)}(t)$ is horizontal with jumps when ![]() $s = a(k+1)$ for integers
$s = a(k+1)$ for integers ![]() $a$. Thus, to establish our proposition, we may assume
$a$. Thus, to establish our proposition, we may assume ![]() $s=a(k+1)$ with
$s=a(k+1)$ with ![]() $1 \le a \le k-1$. Then we have
$1 \le a \le k-1$. Then we have
It remains to estimate ![]() ${\mathcal {R}}_{k,(k+1)^2}((Ak+a)(k+1)) - {\mathcal {R}}_{k,(k+1)^2}(Ak(k+1))$, and we aim to obtain at least
${\mathcal {R}}_{k,(k+1)^2}((Ak+a)(k+1)) - {\mathcal {R}}_{k,(k+1)^2}(Ak(k+1))$, and we aim to obtain at least ![]() $(A+1)a$ as in (A.7) (see Figure A.3). To this end, we use the same notation as above, but also introduce
$(A+1)a$ as in (A.7) (see Figure A.3). To this end, we use the same notation as above, but also introduce
where ![]() $D \in \mathbb {N}$ and
$D \in \mathbb {N}$ and ![]() $0 \leq D \leq k$. Note that
$0 \leq D \leq k$. Note that ![]() $d-c \le 1$. Moreover:
$d-c \le 1$. Moreover:
(i) if
 $d=c$, then
$d=c$, then  $a \le k+1 - C$ and
$a \le k+1 - C$ and  $D=C+a$;
$D=C+a$;(ii) if
 $d=c+1$, then
$d=c+1$, then  $D = C+a - (k+1)$.
$D = C+a - (k+1)$.
When condition (i) is satisfied the triangle intersects no new rows with integer intercepts; this is automatically the case when ![]() $B=0$. When condition (ii) is satisfied, the new triangle intersects
$B=0$. When condition (ii) is satisfied, the new triangle intersects ![]() $y=d$ and the row contains
$y=d$ and the row contains
lattice points. Meanwhile, the lengths of the other rows increase by ![]() $a(1 + {1}/{k})$, so we count the number of additional lattice points as
$a(1 + {1}/{k})$, so we count the number of additional lattice points as
where the ![]() $(a+1)$ terms come in blocks of length
$(a+1)$ terms come in blocks of length ![]() $a$ and the
$a$ and the ![]() $a$ terms in blocks of length
$a$ terms in blocks of length ![]() $k-a$. Therefore, depending whether the sum ends with
$k-a$. Therefore, depending whether the sum ends with ![]() $(a+1)$ (if
$(a+1)$ (if ![]() $c-kb \le a$) or
$c-kb \le a$) or ![]() $a$ terms (if
$a$ terms (if ![]() $c-kb \ge a+1$), we have
$c-kb \ge a+1$), we have
 \[ \#\left\{\!\!\begin{array}{c} \mbox{additional} \\ \mbox{points}\end{array}\!\!\right\} = \begin{cases} a + (k+1)ab + (c-kb)(a+1) & \mbox{if} \ c-kb \leq a, \\ a+ (k+1)ab + a(c-kb +1) & \mbox{if} \ c-kb \geq a+1. \end{cases} \]
\[ \#\left\{\!\!\begin{array}{c} \mbox{additional} \\ \mbox{points}\end{array}\!\!\right\} = \begin{cases} a + (k+1)ab + (c-kb)(a+1) & \mbox{if} \ c-kb \leq a, \\ a+ (k+1)ab + a(c-kb +1) & \mbox{if} \ c-kb \geq a+1. \end{cases} \]
It is easy to obtain the desired ![]() $(A+1)a$-many additional lattice points when
$(A+1)a$-many additional lattice points when ![]() $B = C =0$. If not, then Claim A.3 implies that
$B = C =0$. If not, then Claim A.3 implies that ![]() $b+c = A-1$ and
$b+c = A-1$ and ![]() $c-kb = B-1$, and a further simplification gives
$c-kb = B-1$, and a further simplification gives
 \[ \#\left\{\!\!\begin{array}{c} \mbox{additional} \\ \mbox{points}\end{array}\!\!\right\} = \begin{cases} aA + B-1 & \mbox{if} \ c-kb \leq a, \\ (A+1)a & \mbox{if} \ c-kb \geq a+1 .\end{cases} \]
\[ \#\left\{\!\!\begin{array}{c} \mbox{additional} \\ \mbox{points}\end{array}\!\!\right\} = \begin{cases} aA + B-1 & \mbox{if} \ c-kb \leq a, \\ (A+1)a & \mbox{if} \ c-kb \geq a+1 .\end{cases} \]
Therefore, it suffices to focus on the case where ![]() $c-kb \leq a$.
$c-kb \leq a$.

Figure A.3. Count additional lattice points in the shaded region.
If ![]() $d=c$, then by item (i) above,
$d=c$, then by item (i) above, ![]() $D = C+ a = k+1 - B + a$, which implies that
$D = C+ a = k+1 - B + a$, which implies that ![]() $B-1= a + k - D \ge a$. Thus, we get at least
$B-1= a + k - D \ge a$. Thus, we get at least ![]() $(A+1)a$-many additional lattice points as required. If
$(A+1)a$-many additional lattice points as required. If ![]() $d = c+1$, then we have an extra row so the cardinality of the additional points in total is
$d = c+1$, then we have an extra row so the cardinality of the additional points in total is ![]() $aA + B + \lfloor {(k+1)D}/{k} \rfloor$ by (A.8). Item (ii) above implies that
$aA + B + \lfloor {(k+1)D}/{k} \rfloor$ by (A.8). Item (ii) above implies that ![]() $D = a - B$ and then we have
$D = a - B$ and then we have
Therefore, we complete the proof of Proposition A.1.
Remark A.4 Since ![]() ${\rm Vol}(E(k, k+1)^2) = {\rm Vol}(E(k+1, k(k+1))) = {k(k+1)^2}/{2}$, the symplectic embedding guaranteed by Proposition A.1 is volume-filling.
${\rm Vol}(E(k, k+1)^2) = {\rm Vol}(E(k+1, k(k+1))) = {k(k+1)^2}/{2}$, the symplectic embedding guaranteed by Proposition A.1 is volume-filling.