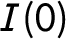Balance as a Pre-Estimation Test for Time Series Analysis

Abstract

It is understood that ensuring equation balance is a necessary condition for a valid model of times series data. Yet, the definition of balance provided so far has been incomplete and there has not been a consistent understanding of exactly why balance is important or how it can be applied. The discussion to date has focused on the estimates produced by the general error correction model (GECM). In this paper, we go beyond the GECM and beyond model estimates. We treat equation balance as a theoretical matter, not merely an empirical one, and describe how to use the concept of balance to test theoretical propositions before longitudinal data have been gathered. We explain how equation balance can be used to check if your theoretical or empirical model is either wrong or incomplete in a way that will prevent a meaningful interpretation of the model. We also raise the issue of “ $I(0)$ balance” and its importance.

1 Introduction

Since De Boef and Keele’s (2008) influential article “Taking Time Seriously,” debates over how to appropriately model dynamics in time series data have proliferated. This is typified by the “Symposium on Time Series Error Correction Methods in Political Science” in Political Analysis (volume 24, number 1), where seven articles debated the situations under which the use of the GECM is appropriate. There was one subject upon which all of the participating authors agreed: The necessity of estimating models with balanced equations.¹ And yet, Freeman (2016, 50) laments at the end of the symposium that “It now is clear that equation balance is not understood by political scientists.”²

Despite the agreement about its importance, the definition of “equation balance” in the symposium is incomplete.³ The lack of understanding of balance in political science is understandable given that Banerjee et al. (1993) dedicate less than five pages to it, and the econometric literature as a whole provides only a cursory discussion of the principle (Maddala and Kim 1998; Mankiw and Shapiro 1986, 251–252), and virtually no practical advice. Complicating matters further is the recent literature on bounds approaches to testing equilibrium relationships between variables (Pesaran, Shin, and Smith 2001; Philips 2018; Webb, Linn, and Lebo 2019, 2020). While these works do not directly reference balance, they raise questions about how balance applies when using the bounds approaches.

In this paper, we focus on the issue of equation balance, with the hope of providing concrete guidance to applied researchers who model time series data. We extend the discussion of balance beyond the focal point of the symposium: the estimates produced by the GECM.

We begin by completing the definition of equation balance by introducing what we call “ $I(0)$ balance.” We then explain why balance matters for applied researchers, discussing equation balance both theoretically and empirically. Finally, we show how the concept of balance can be applied before any model is estimated.

2 What is Balance? What is I(0) Balance?

We denote a variable that needs to be differenced d times in order to transform it into a covariance stationary process as $I(d)$ , where d is the order of integration.⁴ Following convention, we define cointegration as the linear combination of two or more variables with the same order of integration which produces a variable with a lower order of integration (Engle and Granger 1987). For example, if $X_1\sim ~I(1)$ and $X_2\sim ~I(1)$ and $Y\sim ~I(1)$ and $\beta _1 X_1 + \beta _2 X_2 + \beta _3 Y = Z\sim ~I(0)$ , then $X_1$ , $X_2$ , and Y are cointegrated.

Cointegration represents a type of long-run equilibrium between nonstationary variables. When $Z_t$ deviates from its expected value (the cointegrating equilibrium), some of the nonstationary variables respond such that they bring $Z_t$ back to equilibrium. The nonstationary series do not have their own equilibria, but they have an equilibrium relative to each other. This is a different type of equilibrium than that between two or more $I(0)$ series, in which each variable has its own stationary equilibrium (Webb et al. 2020), and the temporary deviation of one variable from its equilibrium causes the other to deviate temporarily from its equilibrium.

A model is defined as balanced “if and only if the regressand and the regressors (either individually or collectively, as a co-integrated set) are of the same order of integration” (Banerjee et al. 1993, 166). In other words, a model is balanced when the collection of variables on the right-hand side (RHS) of the equation are collectively of the same order of integration as the variable on the left-hand side (LHS).⁵ Without cointegration, the order of integration of the RHS is equal to the highest order of integration of all variables on the RHS. With cointegration, the order of integration may be lower. From a theoretical perspective, this is the only requirement for a model to be balanced. There is an additional empirical consideration, however. For the purposes of estimation, it is also necessary that there is a re-parameterization of the empirical model in which the regressand is $I(0)$ and the equation is balanced (Banerjee et al. 1993, 167–168). We call this “ $I(0)$ balance.” If this is not the case, the distributions for some or all of the usual tests of statistical inference—most commonly t and F statistics—will not have standard distributions.⁶ If a researcher wishes to use a model that is balanced but not $I(0)$ balanced, a new test statistic and its distribution has to be derived, which is not a simple matter.

Consider, for example, a simple model:

(1) $$ \begin{align} Y_{1,t} = \beta_1 X_{1,t} + \epsilon_{t}, \end{align} $$

where $Y_{1,t}$ and $X_{1,t} \sim I(1)$ . The order of integration of the LHS is I(1) and, so long as the order of integration of $\epsilon _{t}$ is less than 2, the order of integration of the RHS is $I(1)$ . The equation is balanced. If $Y_{1,t}$ and $X_{1,t}$ cointegrate such that $Y_{1,t} - \beta _1X_{1,t} = Z_{1,t} \sim I(0)$ and $\epsilon _{t} \sim I(0)$ , then the equation is $I(0)$ balanced. The equation can be rewritten such that the regressand is I(0):

(2) $$ \begin{align} Y_{1,t} - \beta_1 X_{1,t}= Z_{1,t} = \epsilon_{t}. \end{align} $$

However, if $Y_{1,t}$ and $X_{1,t}$ do not cointegrate, there is no way of writing (1) such that the LHS is $I(0)$ . Further, balance for (2) in the absence of cointegration implies that $\epsilon _{t}\sim I(1)$ . The result is that the t-statistic for $\beta _1$ will not have a standard distribution. This produces the spurious correlation described by Granger and Newbold (1974).⁷ Generally, empirical models that are not $I(0)$ balanced will have nonstationary errors, which violates the assumptions of most time series estimators, making inference dubious. As Maddala and Kim (1998, 252) note, one should avoid estimating such equations. This is because while an $I(0)$ unbalanced equation can be used for diagnostic purposes, such as the Dickey–Fuller test, it requires the use of test statistics with nonstandard distributions.⁸

3 Two Ways to Apply Balance Before Model Estimation

Balance matters because a theoretical or empirical model that is not balanced is wrong—or at least incomplete in some important way. An analogy may be helpful. Balance also applies to chemical equations, which describe how a combination of entities react to produce new entities. The entities on the LHS of the equation represent the chemicals being combined, and the entities on the RHS represent the chemicals that are produced. The law of conservation of mass requires the same amount of mass before and after the reaction, so the number of particles of each type on the LHS must add up to the number on the RHS. This “equation balance” is a necessary condition for a theorized chemical equation to be correct. If the chemist has a theory that implies an unbalanced chemical equation, she does not even need to enter the lab to know her theory is faulty.

For time series models, the analogous principle is that the order of integration on the LHS must be preserved on the RHS. For example, an $I(0)$ LHS variable with a stationary equilibrium cannot be the product of $I(1)$ RHS variables without equilibria, unless those RHS variables co-integrate to produce an $I(0)$ process with a cointegrating equilibrium. The principle of equation balance can be applied at multiple stages of the research process. What we describe below are tests for two necessary conditions before model estimation.

3.1 Using Balance to Test the Theoretical Model

When a researcher is developing a theory, they should ask: 1. What type of data-generating process (DGP) do I believe produced my variables? and 2. Given 1, is my theoretical model balanced? By doing this, the political scientist (like the chemist) can place a check on her theory. Once the researcher has determined the theoretical expectations regarding the orders of (co)integration of the variables in her model, she should ask if the model implies balance. If it does not, there is no point in developing an empirical model until she has reconsidered her theory and developed a balanced theoretical model. The way in which balance is achieved also has important implications for the expected equilibrium relationships between the variables. Balance achieved through all variables being $I(0)$ implies a distinct type of dynamic relationship than does balance achieved through the cointegration of $I(1)$ variables. In some cases, balance is only achieved by theorizing no long-run relationship. For example, if a researcher has theoretical reason to believe media tone about the economy is $I(1)$ , a theory stipulating it is caused by levels of an $I(0)$ consumer sentiment variable is not balanced unless the theory also includes other $I(1)$ causal factors. If media tone is $I(1)$ , a model that only includes an $I(0)$ consumer sentiment regressor and an $I(0)$ error term:

(3) $$ \begin{align} tone_{t} = \beta_0 + \beta_1 CS_{t} + \epsilon_{t} \end{align} $$

is incorrect or incomplete. All changes in consumer sentiment will dissipate over time and so cannot explain the nondissipating changes in media tone.

Could balance be achieved by allowing the error term to be $I(1)$ ? The model would not be balanced by the strict definition—which requires the regressand and regressors collectively to have the same order of integration—and achieving balance through the error term has two consequences. First, while (3) with $I(1)$ errors is not strictly wrong, it is very much incomplete, and will lead to a misinterpretation of the dynamic relationship between the LHS and RHS variables. It implies that the nondissipating changes in media tone are being driven by some $I(1)$ variable that has been excluded from the model (resulting in an $I(1)$ error term). The $I(0)$ consumer sentiment regressor may have an effect on media tone, but only in that it explains short-term deviations from the underlying long-term changes:

(4) $$ \begin{align} \Delta tone_{t} = \beta_0 + \beta_1 CS_{t} + \epsilon_{t}. \end{align} $$

This is distinct from (3), and implies no long-run relationship between $CS_{t} $ and $tone_{t}$ .

Second, because (3) is not $I(0)$ balanced, the resulting $I(1)$ error will produce problems for estimation and inference. The t- and F-statistics used in hypothesis tests may not be distributed as expected, leading to mistaken inference. In short, allowing the errors to be $I(1)$ is a way to claim the model is incomplete (rather than wrong), but the incompleteness directly leads to the wrong interpretation of the dynamic relationships between variables, and incorrect inference.

We suggest political scientists go beyond drawing arrows from one variable to the other and focusing only on a couple of variables of interest in their model, and instead consider the dynamic properties of all included variables and how they relate. When articulating a theoretical model for these purposes, the principles of the Empirical Implications of Theoretical Models movement might provide guidance, as might past empirical work. In Economics, there is a tradition of compiling evidence regarding the order of integration (and cointegration) of commonly used variables. This is a practice that political scientists might emulate.

We are not suggesting that researchers need to add extensive expositions on the dynamics of all their time series, but we are suggesting that most researchers can and should do more to indicate their theoretical expectations regarding the relationships of interest—specifically, the nature of the equilibrium between the dependent variable and the independent variables. We discuss a laudable (and rare) example of this in the Supplementary Appendix.

3.2 Using Balance to Test the Empirical Model Before Estimation

Once a researcher has developed a theory that passes the balance test and chosen a corresponding empirical model, she should test the order of integration of each of her variables and, if it is part of her theory, whether or not any variables that are $I(1)$ (or higher) cointegrate. There are issues of power with many of the tests of integration and cointegration, and so a grain (or many grains) of salt should be applied when interpreting those results.⁹ Further, different tests can produce contradictory results. See Webb et al. (2020) for a helpful discussion of these problems. It is not our intention to provide an order of (co)integrarion pretest procedure, but the interested reader is encouraged to refer to Enders (2004, Chapter 4) and Costantini and Sen (2016). We also discuss in Section 4 how the concept of balance can assist the researcher when interpreting these empirical tests, and how it can be used in combination with newer bounds testing procedures (Webb et al. 2019, 2020; Pesaran et al. 2001; Philips 2018). We do note that the empirical orders of (co)integration might differ from the theoretical even if the theory is correct. For example, the DGP for a variable might be $I(0)$ but with an autoregressive parameter near 1, making it near integrated. Unless the collected data covers a very long period of time, the variable will likely behave as if it were $I(1)$ over the period that it is observed. This means that it is for all empirical purposes, such as estimation of the empirical model, an $I(1)$ variable.

What if the empirical evidence regarding integration and cointegration does not meet theoretical expectations? Having derived such expectations, the researcher can decide if the theoretical model is still balanced under the updated beliefs. If not, she knows something is wrong with the theory, without needing to estimate an empirical model. Extending the chemical-equation analogy, if the chemist’s theory implies a balanced chemical equation $(X + Y = Z)$ based on beliefs about chemicals X, Y, and Z but, after examining the chemicals, discovers X has more particles of a particular type than originally believed, the chemist knows that her theory is wrong without mixing the chemicals. Further theorizing is required.

If the researcher decides the empirical evidence regarding the orders of integration and cointegration of the variables match her theoretical expectations, she can now check if her empirical model meets the requirement of $I(0)$ balance. That is, there must be some reparameterization of the empirical model such that it is balanced and the LHS is $I(0)$ . Note that if such a re-parameterization exists, it is not necessary to use the re-parameterized form for estimation. It is sufficient that it exists (Banerjee et al. 1993, 167–168).

Typical examples of re-parameterized models are standard and general error correction models (ECMs). Consider the autoregressive distributed lag (ADL) model:

(5) $$ \begin{align} y_{t} = \alpha_1 y_{t-1} + \beta_0 + \beta_1 x_{t} + \beta_2 x_{t-1} + \epsilon_{t}, \end{align} $$

where $y_{t}$ and $x_{t}$ are both $I(1)$ . The equation is balanced. The order of integration on the LHS is $I(1)$ and the order of integration of the RHS is equal to the highest order of integration of all variables on the RHS—also $I(1)$ . The common reparameterization of the ADL is the standard ECM:

(6) $$ \begin{align} \Delta y_{t} = \alpha_0 + \gamma (y_{t-1} + \kappa_1 x_{t-1}) + \kappa_0 \Delta x_{t} + \epsilon_{t}. \end{align} $$

If $y_{t}$ and $x_{t}$ are cointegrated, this equation is balanced, and importantly it is $I(0)$ balanced—both sides are $I(0)$ . If $y_{t}\sim ~I(1)$ , then $\Delta y_{t}\sim ~I(0)$ , as is the case for $x_{t}$ , and co-integration means $(y_{t-1} + \kappa _1 x_{1t-1})\sim ~I(0)$ . Without co-integration, the equation is not $I(0)$ balanced—the LHS is $I(0)$ but the RHS is $I(1)$ because $(y_{t-1} + \kappa _1 x_{1t-1})\sim ~I(1)$ .

If there is no re-parameterization in which the model is balanced and the regressand is $I(0)$ , the researcher may decide there are theoretically or empirically justified restrictions that can be placed on one or more parameters in the model such that there is. For example, setting $\gamma $ to 0 in (6), which implies no long-run relationship, achieves $I(0)$ balance without co-integration. As a further example, if $y_{t}\sim ~I(1)$ and $x_{t}\sim ~I(0)$ , $I(0)$ balance can be achieved in the lagged dependent variable model by placing the restriction $\alpha _1 = 1$ .

(7) $$ \begin{align} y_{t} = \alpha_1 y_{t-1} + \beta_0 + \beta_1 x_{t} + \epsilon_{t}. \end{align} $$

(8) $$ \begin{align} \kern-9pt y_{t} = y_{t-1} + \beta_0 + \beta_1 x_{t} + \epsilon_{t}. \end{align} $$

(9) $$ \begin{align} \kern-43pt \Delta y_{t}= \beta_0 + \beta_1 x_{t} + \epsilon_{t}. \end{align} $$

The regressand $\Delta y_{t}$ is $I(0)$ and the regressor $x_{t}$ is $I(0)$ .

In general, if restrictions are required, the researcher must decide if they are valid, keeping in mind that such restrictions may change the theoretical implications of the model. It is only at this point that the researcher should proceed with estimating a model. Restrictions required for $I(0)$ balance must be placed on the model prior to estimation.¹⁰

We acknowledge that what we are recommending can result in the researcher using the data to update their theoretical or empirical model. While this is common in time-series analysis, it is still a concern. Our intent is that by recommending that researchers consider balance before empirically examining the data, our procedure should: (a) prevent the researcher from proposing a theoretical model that was doomed to not match the data (because it was unbalanced) and (b) provide a more principled way of updating our beliefs by narrowing down the range of possible theoretical and empirical models.

4 Determining if a Model is Balanced and I(0) Balanced

The following procedure, outlined in Figure 1, determines if a model is balanced.¹¹ It applies equally if it is a theoretical model or an empirical model for which you are checking balance.¹²

Figure 1 Determining balance.

A prerequisite for checking balance is determining orders of integration and cointegration: for theoretical models, based on theoretical expectations; and for empirical models, based on tests that can be inconclusive. For now, we assume orders of (co)integration are knowable, and revisit the issue of uncertainty later. The researcher should proceed as follows: (1) Determine the order of integration of the variable on the LHS, theoretically or empirically. (2) Determine the order of integration of variables on the RHS. To reiterate, without cointegration, the order of integration of the RHS is equal to the highest order of integration of all variables on the RHS. With cointegration, the order of integration may be lower, keeping in mind that cointegration can occur between the Xs, between the Xs and Y, or both. For example, if all $I(1)$ variables on the RHS combine to produce an $I(0)$ process and the only remaining variables are $I(0)$ , the order of integration for the RHS is $I(0)$ . However, if $X_1\sim ~I(1)$ and $X_2\sim ~I(1)$ cointegrate to produce an $I(0)$ process, but $X_3\sim ~I(1)$ is also on the RHS, the order of integration for the RHS variables is $I(1)$ .¹³ (3) Restrict model parameters as is justified. (4) Use the following procedure for checking model balance.¹⁴ Begin by asking if the regressand is $I(0)$ .

(i) If yes and all regressors are individually $I(0)$ , you have balance and $I(0)$ balance. For example, if $y_{t}\sim ~I(0)$ and $x_{t}\sim ~I(0)$ , the ADL(1,1) model with one lag of the independent variable and one lag of the dependent variable:

(10) $$ \begin{align} y_{t} = \alpha_1 y_{t-1} + \beta_0 + \beta_1 x_{t} + \beta_2 x_{t-1} + \epsilon_{t} \end{align} $$

is $I(0)$ balanced, and the standard ECM:

(11) $$ \begin{align} \Delta y_{t} = \alpha_0 + \gamma (y_{t-1} + \kappa_1 x_{t-1}) + \kappa_0 \Delta x_{t} + \epsilon_{t} \end{align} $$

is $I(0)$ balanced. The first difference (FD) model:

(12) $$ \begin{align} \Delta y_{t} = \alpha_0 + \kappa_0 \Delta x_{1t} + \epsilon_{t} \end{align} $$

is also $I(0)$ balanced (if $y_{t}\sim ~I(0)$ , then $\Delta y_{t}\sim ~I(0)$ ). However, it is important to note that (12) represents a different relationship between X and Y than (10) or (11).

(ii) If the regressand is $I(0)$ but some regressors are not, ask if there is a linear combination of these non- $I(0)$ regressors that is $I(0)$ . If so, you have balance, and $I(0)$ balance. If not, you do not have balance. For example, if $y_{t}\sim ~I(0)$ , $x_{1t}\sim ~I(1)$ , and $x_{2t}\sim ~I(1)$ :

(13) $$ \begin{align} y_{t} = \alpha_1 y_{t-1} + \beta_0 + \beta_1 x_{1t} + \beta_2 x_{1t-1} + \beta_3 x_{2t} + \beta_4 x_{2t-1} + \epsilon_{t} \end{align} $$

is $I(0)$ balanced only if: $\beta _1 x_{1t} + \beta _2 x_{1t-1} + \beta _3 x_{2t} + \beta _4 x_{2t-1}\sim ~I(0)$ .

(iii) If the order of integration of the regressand is $I(d>0)$ , and all regressors are $I(0)$ , you do not have balance. For example, if $y_{t}\sim ~I(1)$ and $x_{t}\sim ~I(0)$ , the finite distributed lag model with one lag of the independent variable:

(14) $$ \begin{align} y_{t} = \beta_0 + \beta_1 x_{t} + \beta_2 x_{t-1} + \epsilon_{t} \end{align} $$

is not balanced and therefore not $I(0)$ balanced.

(iv) If the regressand is $I(d>0)$ and the regressors are collectively $I(d)$ , the equation is balanced. For example, if $y_{t}\sim ~I(1)$ and $x_{t}\sim ~I(1)$ , the ADL(1,1) is balanced:

(15) $$ \begin{align} y_{t} = \alpha_1 y_{t-1} + \beta_0 + \beta_1 x_{t} + \beta_2 x_{t-1} + \epsilon_{t}. \end{align} $$

However, when we seek an $I(0)$ balanced re-parameterization, we discover additional requirements. In the ECM re-parameterization:

(16) $$ \begin{align} \Delta y_{t} = \alpha_0 + \gamma (y_{t-1} + \kappa_1 x_{t-1}) + \kappa_0 \Delta x_{t} + \epsilon_{t}, \end{align} $$

the regressand is $I(0)$ but in order for the regressors to be collectively $I(0)$ , it must either be the case that $(y_{t-1} + \kappa _1 x_{1t-1})\sim ~I(0)$ or $\gamma =0$ . The first case implies Y and X cointegrate. The second case implies the appropriate equation is the FD model:

(17) $$ \begin{align} \Delta y_{t} = \alpha_0 + \kappa_0 \Delta x_{t} + \epsilon_{t}. \end{align} $$

Similarly, if $y_{t}\sim ~I(1)$ , $x_{1t}\sim ~I(1)$ and $x_{2t}\sim ~I(0)$ , the ADL(1,1) is balanced:

(18) $$ \begin{align} y_{t} = \rho y_{t-1} + \beta_0 + \beta_1 x_{1t} + \beta_2 x_{1t-1} + \beta_3 x_{2t} + \beta_4 x_{2t-1} + \epsilon_{t}. \end{align} $$

The LHS is $I(1)$ , and the RHS is $I(1)$ because $x_{1t}$ and $y_{t-1}$ are independently and collectively $I(1)$ . However, the following ECM re-parameterization with a $I(0)$ regressand:

(19) $$ \begin{align} \Delta y_{t} = \alpha_0 + \gamma (y_{t-1} + \kappa_1 x_{1t-1}) + \kappa_0 \Delta x_{1t} + \beta_3 x_{2t} + \beta_4 x_{2t-1} + \epsilon_{t}, \end{align} $$

requires either $y_{t-1} + \kappa _1 x_{1t-1}\sim ~I(0)$ (cointegration) or $\gamma =0$ to obtain $I(0)$ balance.

If the regressand is $I(d>0)$ but the regressors are collectively of some other order of integration, you do not have balance. For example, if $y_{t}\sim ~I(1)$ , $x_{1t}\sim ~I(1),$ and $x_{2t}\sim ~I(1)$ , the model:

(20) $$ \begin{align} y_{t} = \beta_0 + \beta_1 x_{1t} + \beta_2 x_{2t} + \epsilon_{t} \end{align} $$

is not balanced if $x_{1t}$ and $x_{2t}$ cointegrate to be $I(0)$ .

As discussed, empirically determining the order of integration and cointegration can be difficult. There are a number of tests for both, and their appropriateness depends on assumptions about the deterministic elements in the DGP (e.g., structural breaks and trending) (Webb et al. 2020). Enders (2004) provides a procedure to follow when testing the order of integration. These procedures are useful, but testing is complicated by the low power of these tests when T is small and by the possibility of contradictory results. Fortunately, there have been recent advances in this area. If the empirical evidence is relatively unambiguous that the regressand is $I(1)$ , but the order of integration of the regressors is unknown, the researcher can use the bounds procedure described by Pesaran et al. (2001) and Philips (2018) to determine if the regressors cointegrate with the lag of the regressand to produce a balanced model. Further, Webb et al. (2019) outline a bounds approach to test for cointegration between the regressand and regressors when the order of integration of one or both are unknown. A key feature of the bounds approach described in Webb et al. (2020) is that it is not necessary to know what type of equilibrium (cointegrating or stationary) is being tested. There are two trade-offs for this advantage. The first is that the bounds tests can produce indeterminate results. The second is that determining if there is a long-run equilibrium relationship leaves the practitioner without knowledge of the nature of that relationship. The concept of balance may be of assistance here both when interpreting traditional tests and bounds procedures.

Sometimes, the practitioner has strong priors about the dynamic nature of their data and the type of equilibrium relationship that might exist. If so, the balance approach can help by limiting the interpretation to models that meet the conditions of balance. When a researcher has established theoretical expectations regarding the order of integration of each variable in the theoretical model, these can be used as priors when interpreting traditional tests of integration and cointegration. Consider the case in which tests of integration confirm the theoretical expectation that the regressand is $I(0)$ and that the same holds for all regressors but one. For that final regressor, X, tests of integration are unclear. In this situation, balance requires that either X is $I(0)$ or there is an $I(1)$ covariate that cointegrates with X that is missing from the model. If the researcher believes that the second possibility is theoretically or empirical unlikely, this then suggests that X is $I(0)$ .

If the practitioner does not want to rely on traditional tests and instead use the bounds approach, the balance approach can still be useful. First, starting with a theoretical model that meets the conditions of balance increases the probability that the practitioner will find an equilibrium. Second, if an equilibrium is found using the bounds approach, having begun with a strong theoretical model gives the practitioner some justification for suggesting what type of equilibrium has been found. Third, the balance approach may be able to narrow down the type of dynamic relationship that exists between the variables. This could be used to narrow the bounds used in the bounds approach, making a definitive result more likely.

Using priors in a Bayesian approach (Brandt and Freeman 2006) can also allow the researcher to avoid making a definitive decision regarding the order of integration and cointegration of the variables. Instead, she can use the theoretical expectations and empirical evidence to place priors on one’s model that reflect her uncertain beliefs. Unfortunately, the consequences of mis-specifying the priors is largely unknown (Maddala and Kim 1998, 263–295), but the principle of balance might provide guidance regarding the priors. At minimum, the priors should suggest a balanced model.

The Johansen test (1991) also provides a means of testing for cointegration when the order of integration of the variables is unknown. It has the advantage of being applicable to multiple time series models. A downside is that the probability of incorrectly finding cointegration increases when stationary variables are included in the potential cointegration relationship (Philips 2018). Because violations of balance result in nonstationary residuals, we advocate testing residuals for white noise as an overall test of equation balance. The limitation is that the failure to pass a white noise test may instead be due to misspecification.

5 Examples

In the Supplementary Appendix, we discuss two influential articles and show how they could have benefited from applying the concept of balance theoretically and empirically.

6 Conclusion

The Political Analysis symposium identified equation balance as among the largest unaddressed problems in the applied time series literature. Practitioners have lacked a complete definition of equation balance, and how to assess it theoretically and empirically. We hope this paper begins to fill this void. While our focus has been single equation models, these issues apply equally to multiple equation time series and panel data models, where the balance requirements apply to each equation and to each case. Further, the discussion of balance in political science has almost exclusively focused on the GECM. But these principles are useful prior to the estimation of any model. Of course, we have outlined necessary, not sufficient, conditions for a good model. Balance is the beginning, but not the end, of the process to determine if a model is a good representation of reality.