Introduction
In Canada, avalanche hazards to structures, transportation corridors and residential areas are often mitigated by hazard or risk mapping, whereby the element at risk is situated in an area where avalanche return periods are acceptably long, and/or potential impact pressures are acceptably small (Reference Jamieson, Stethem, Schaerer and McClungJamieson and others, 2002, p. 14–17). When the risk from avalanches cannot be reduced to acceptable levels by location planning, mitigation measures such as avalanche control programs or defense structures may be applied.
The hazard- or risk-mapping process includes several steps in defining the avalanche problem and hazard areas. Some of the commonly applied methods include: terrain analysis of maps and aerial photographs; field studies of terrain; study of vegetation for signs of past avalanches; use of oral and written records of avalanches; weather and snow records; study of surficial materials; application of statistical models; and application of dynamic models (Reference Jamieson, Stethem, Schaerer and McClungJamieson and others, 2002, p. 9–10). While not all of these methods may be suitable for a particular problem, experts will typically combine several of these methods in their analysis, weighting the estimates in which they have greater confidence. Thus, application of statistical avalanche models is only one method used for some avalanche problems. This method is discussed in this paper for its applicability to a dataset consisting of avalanche paths with small vertical fall heights, hereafter called short slopes.
It has been found in practice that short slopes tend to run proportionately farther than larger slopes, and therefore the models developed for particular mountain ranges using statistical methods may not be applicable to short slopes (Reference McClung and LiedMcClung and Lied, 1987; Reference Nixon and McClungNixon and McClung, 1993).This finding motivated our study of short slopes, in which data obtained from short avalanche paths in four Canadian mountain ranges (Fig. 1) are analyzed using the multiple regressionmethod (e.g. Reference Lied and BakkehøiLied and Bakkehøi, 1980) and the run-out ratio method (e.g. Reference McClung and MearsMcClung and Mears, 1991). The results of analyses using these two different methods are compared and length-scale effects in the models are discussed. Finally, additional data from the Swiss Alps and the Chic Choc Range in Québec, Canada, are used to test the ability of the models to predict runout distances for paths not used to build the models.

Fig. 1. Location of study areas within Canada.
The preferred method for estimating avalanche runout distances in a path uses direct evidence from long-term observations of avalanches (Reference McClung and SchaererMcClung and Schaerer, 1993, p. 115). In paths where little or no direct evidence of avalanche activity is available (e.g. paths with no historical records or no forest), runout models may be the preferred or only method available to estimate extreme runout distances for avalanches. One commonly used modelling technique is called the regression method, which is a statistical evaluation of known avalanche runouts in a mountain range, applied to a given avalanche path within the range. Reference Bovis and MearsBovis and Mears (1976) and Reference Lied and BakkehøiLied and Bakkehøi (1980) first used topographic terrain parameters to estimate runout distances for paths in the United States and Norway, respectively. Reference Lied and BakkehøiLied and Bakkehøi (1980) introduced the reference β point in the runout zone from which to measure runout distances, which they defined as the position at which the slope angle first reaches 10° when proceeding downslope from the starting position (Fig. 2). The corresponding β angle is defined as the angle (measured from the horizontal) at the β point to the starting position of the avalanche path. It is common to quantify extreme runout distances by using the α angle, defined as the angle (measured from the horizontal) at the extreme runout position observed in the field to the starting position of the avalanche path. The parameter α is similar to that used by Reference ScheideggerScheidegger (1973) to estimate the average friction coefficient for large landslides. For a group of avalanche paths in Norway, Reference Lied and ToppeLied and Toppe (1989) showed that β was the only statistically significant predictor for α, and developed regression equations relating the α angle to the β angle. Similar expressions have been developed in Canada and the United States (Reference McClung, Mears and SchaererMcClung and others, 1989), Iceland (Reference JóhannessonJóhannesson, 1998), Austria (Reference Lied, Weiler, Bakkehøi and HopfLied and others, 1995) and Japan (Reference Fujisawa, Tsunaki and KamiishiFujisawa and others, 1993).

Fig. 2. Geometry of example avalanche path showing most terrain variables used in analyses. x-y coordinate system is shown with origin at lower left of figure.
A second statistical method used for estimating extreme runout distances is known as the runout ratio method. Reference McClung and MearsMcClung and Mears (1991) found that the extreme runout positions for avalanche paths in a particular mountain range fit an extreme-value probability density function similar to that used for water discharge from floods. They defined the runout ratio, Δx/Xβ, as the ratio of the horizontal distance from the β point to the extreme runout position, Δx, to the horizontal reach from the starting position to the β point, Xβ (Fig. 2). The runout ratio can take on positive or negative values, with a negative value indicating that the extreme runout position is located upslope of the defined β point location (typically 10° slope angle). The non-exceedance probability, P, is defined as the fraction of runout ratios in a particular mountain range that do not exceed a given ratio. Studies conducted for several ranges around the world (e.g. Reference McClung and MearsMcClung and Mears, 1991; Reference Nixon and McClungNixon and McClung, 1993) have found significant statistical relationships between the runout ratio and the extreme-value non-exceedance probability (e.g. R2 > 0.95) when applied to paths in a single mountain range (Reference MearsMears, 1992, p. 26). These results also show that each mountain range comprises a different population and thus each range should be analyzed separately.
In contrast to previous studies of slopes with a mean vertical fall height typically around 700 m, Reference McKittrick and BrownMcKittrick and Brown (1993) analyzed a dataset of mostly shorter slopes in southwest Montana, U.S.A., with a mean vertical fall height of 248 m. They defined the β point for their dataset as the location where the slope angle first decreases to 18°, rather than the conventional 10°. Although they offered no physical explanation of the improved fit of their data for a β point at 18°, other studies have found that locking of particles in the avalanche flow may begin at slope angles of about 25°, and that large, dry avalanches may begin a decelerating phase at this slope angle (Reference Gubler, Hiller, Klausegger and SuterGubler and others, 1986; Reference McClung and MearsMcClung and Mears, 1995). Considering this another way, most avalanche dynamics models predict that the frontal velocity will increase then decrease, approximating a semi-ellipse along a parabolic path (e.g. Reference Bartelt and SalmBartelt and Salm, 1998). Consequently, deceleration and locking should begin near the halfway point, measured horizontally. For an extreme avalanche running on a parabolic profile from a 38° slope in the starting zone to a 5° slope in the runout zone, deceleration should begin where the slope angle is approximately 21°. Based on these two observations, there may be a physical basis for using higher slope angles for defining the location of the β point, particularly for shorter slopes in which the mass may not reach a high velocity (e.g. >30ms-1) before beginning to decelerate.
As early as 1987, Reference McClung and LiedMcClung and Lied (1987) noted that their models likely did not apply well to paths with a vertical fall height of <350m, and scale effects were noted for both their regression and runout ratio models. Reference MearsMears (1989) and Reference McClung and MearsMcClung and Mears (1991) noted the importance of length-scale effects for data from the Colorado Rocky Mountains and the Sierra Nevada Range of California. Their findings and the work of Reference Nixon and McClungNixon and McClung (1993) suggest that the runout ratio decreases with increasing horizontal reach (Xβ), and illustrate the importance of scale effects in statistical runout modelling.These results support the hypothesis that extreme avalanches on smaller slopes run out proportionately farther than on taller slopes.
Methods
Field studies included a detailed topographic survey and estimation of the extreme runout position for each path using either vegetative indicators or historical records of extreme avalanches. As with previous studies (e.g. Reference McClung and MearsMcClung and Mears, 1991; Reference McKittrick and BrownMcKittrick and Brown, 1993), the goal of the runout survey was to identify the location of the “100 year” return period event, commonly referred to as the “extreme” runout position. However, the true return period for the interpreted extreme runout position likely represents return periods of 30–300 years, introducing unavoidable random variation in the data (Reference McClung and MearsMcClung and Mears, 1991).
Paths were selected in the four mountain ranges based on several criteria, including: vertical fall height; reasonable access by vehicle and foot; well-defined path characteristics (e.g. starting and runout zones); well-defined extreme run-out position; and no run-up on the opposite side of the valley or runout into a water body. Data were collected at 48 avalanche paths: 16 in the Coast Mountains, 10 in the Columbia Mountains, 15 in the Rockies and 7 paths in the Chic Choc Range or other parts of Québec. The Coast, Columbia and Rocky Mountain ranges are located in British Columbia and Alberta in western Canada, and the remaining paths are located in Québec, in the eastern part of Canada (Fig. 1). The paths vary from 48°47′ to 51°38′ N latitude and from 65°55′ to 123°10′W longitude. Elevations of the starting zones of the paths range approximately from 85 to 2500 mabovemean sea level. Thus, a geographically diverse sample set was obtained both in terms of latitude and longitude and in terms of elevation. See Jones (Reference Jones2002, p. 31–48) for a detailed discussion of field methods.
Descriptive Statistics
The data used in this study consist of 19 terrain variables, for which the mean, standard deviation, median and range of the variables are shown on Table 1. Two of the 48 avalanche paths were rejected from the analyses for reasons discussed further below, and thus statistics for the remaining 46 paths are presented.
Table 1. Descriptive statistics for the short-slope database
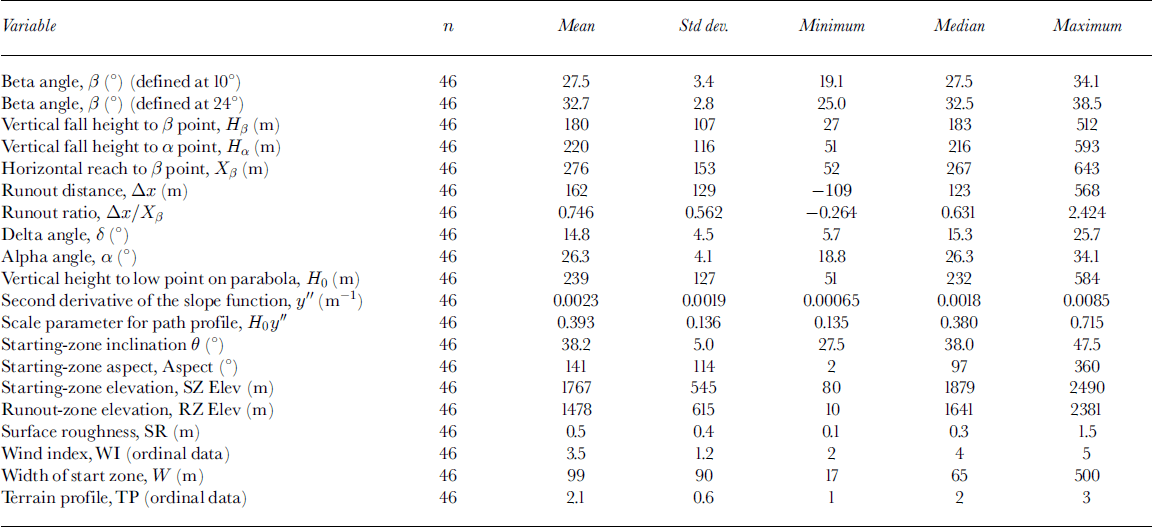
The total number of sites (N) in this dataset, 48, is considered to be sufficiently large to analyze using both parametric and extreme-value statistical techniques. From the central limit theorem (Reference Kennedy and NevilleKennedy and Neville, 1986, p. 117– 121), if N ≥ 30, the normal approximation for the mean and variance of a response variable can be used with good precision even for an extreme-value distribution. However, the number of sites from the individual mountain ranges varies from 7 to 16 paths, which is well below this recommended sample size of 30. Thus, only statistics for the combined ranges are presented.
Using the α and β angles as defined previously (Fig. 2), we redefine the β point as the position at which the slope angle first reaches 24° when proceeding downslope from the starting zone. Jones (Reference Jones2002, p. 58–61) provides a statistical argument to support a β point at 24° for short slopes. We also present statistics for β defined at 10° for comparison to previous studies and testing in the multiple regression model.
The delta angle, δ, is defined by sighting from the extreme runout position to the β point, with the angle measured from the horizontal. This is a measure of the average slope angle in the runout zone.
The runout ratio relates the horizontal distances Δx and Xβ to the reference slope angles α, β and δ (Reference McClung and MearsMcClung and Mears, 1991)
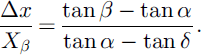
The vertical distance, Hβ, is measured from the starting position to the β point, and Hα is the vertical distance from the starting position to the extreme runout position.
H0 is defined as the vertical distance measured from the starting position to the lowest point on a polynomial parabolic curve y = ax2 + bx + c fitted to the terrain profile of a path (Fig. 2), the location where the first derivative (slope of the polynomial curve), y′, is zero. The second derivative of the polynomial curve, y′′ (Fig. 2), has a value of 2a and is the radius of curvature of the path profile (Reference Lied and BakkehøiLied and Bakkehøi, 1980). H0y′′ is the product of H0 and y′′, and serves as a dimensionless scale parameter (Reference Lied and BakkehøiLied and Bakkehøi, 1980).
The starting-zone inclination, θ, starting-zone aspect and starting-zone elevation, SZ Elev, are average values measured in the starting zone. The runout-zone elevation, RZ Elev, is an average value measured in the runout zone. The surface roughness is an approximate measure of the height of irregularity in the ground surface, measured in metres. The wind index for each avalanche starting zone, WI, was assigned one of five ordinal values according to Reference SchaererSchaerer (1977). The average width of the starting zone, W, was measured at the top of the starting zone.
The terrain profile variable, TP, is related to the radius of curvature, y′′, but accounts for the very abrupt change in curvature in hockey-stick profiles (Fig. 3). A value of 1 represents a slope with a nearly linear transition from the track to the runout zone; 2 represents a path with a concave parabolic shape and a relatively smooth transition from the track to the runout zone; and 3 represents a path with a hockey-stick profile in which there is an abrupt transition from a relatively steep slope to a slope at or near 0° in the runout zone (Reference MartinelliMartinelli, 1986). This type of profile may be commonly found where a steep slope meets a gently sloping or flat alluvial or glaciofluvial plain in a valley bottom.

Fig. 3. Examples of terrain profile types used for defining the TP variable.
The primary purpose of introducing the TP variable was to distinguish between hockey-stick and non-hockey-stick profiles in the dataset. However, better discrimination between paths in the dataset was found, and better results were obtained, when a three-class TP variable was used. The three-class variable is a partially subjective categorical variable, but we believe that different experts would classify paths similarly, and thusTP is a reproducible variable. Paths with hockey-stick profiles were common in the dataset, with 10 of the 48 paths (21%) classified as hockey sticks, 8 (17%) classified as linear planar and 30 (62%) classified as concave parabolas.
Alpha-Regression Model
Multiple regression was used to relate various independent predictor variables to the response variable, in this case the α angle used to define the extreme runout position. Fifteen predictor variables for α were chosen for the regression (Table 2).
Table 2. Spearman rank correlations between the response variable, α, and the predictor variables used to develop the alpha-regression model
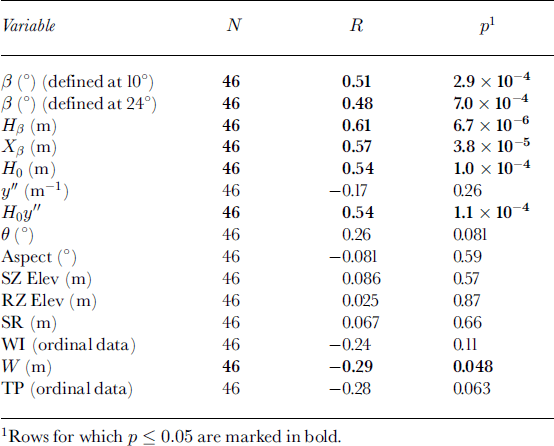
Spearman rank correlations between the predictor variables and α are shown in Table 2, and significant variables (p < 0.05) are highlighted. Seven of the 14 variables are significant at the 5% level and these were used to build the regression model. Two other predictor variables (θ andTP) showed correlations of borderline significance with α (0.05 < p < 0.1) and were also used in the regression. Backward-elimination multiple regression was used with these nine predictor variables to obtain the best fit of the predicted values of α to the observed values.
Two significant outliers, excluded from Table 1, were identified and removed from the analyses because they did not reach a slope angle of <28° upslope of the interpreted location of the extreme runout position (continuously steep paths (Reference McClungMcClung, 2001)), and a third was removed that had a much greater vertical fall height (Hα = 593 m) than the other paths, leaving a subset (n) of 45 paths for the regression. Variables were then systematically removed from the regression (backward elimination) when they were found to have a minimal effect on the model (i.e. variable F values less than a specified threshold at each regression step). Using a threshold F value at the 1% significance level, all variables but H0y′′, H0, TP, β (defined at 24°) and Xβ were eliminated from the regression. Additional analyses showed that β and Xβ could also be removed from the regression with minimal effect on the results. The remaining three predictor variables in the regression equation were H0y′′, H0 andTP. Removal of any of these three variables had a strong adverse effect on the fit, and thus the preferred regression is
This model has an adjusted R2 of 0.65, a standard error of regression (SE) of 2.5°, a significance level of 10-4 and utilizes 45 of the avalanche paths in the dataset. The subscript P is used to denote a runout estimate in probabilistic terms, in which it is assumed that runout distances expressed in terms of αP are approximately normally distributed. A chosen exceedance value of P (0 < P < 1) defines the number of α values for which P × 100% of the values in a normal distribution will not be less than the given value of αP. In order to avoid confusion with the similar (but opposite) term used for the runout ratio model, we use the term threshold probability to refer to the exceedance probability in the case of the alpha-regression model and non-exceedance probability in the case of the runout ratio model (Reference McClung and MearsMcClung and Mears, 1991).The term CP provides an estimation interval for αP and is used to estimate an individual value of αP for a given threshold probability P (0.5 < P < 1) (Reference Walpole and MyersWalpole and Myers, 1985, p. 371). Reference McClungMcClung (2001) notes that for P > 0.9 and normally distributed data, CP reduces to the z value of the normal distribution.
The three predictor variables chosen for this model are relatively simple topographic parameters that can be derived from a slope profile surveyed in the field or taken from a topographic map if a suitably scaled and detailed map is available. A summary of the regression is shown inTable 3.
Table 3. Results of multiple regression for α. Model-adjusted R2 = 0.65, n = 45, SE = 2.5°, p < 10-4

Unlike previous studies (e.g. Reference Bakkehøi, Domaas and LiedBakkehøi and others, 1983; Reference Nixon and McClungNixon and McClung, 1993), we found that although β is significantly correlated with α for this dataset when defined at either 10° or 24° (R = 0.51 and 0.48, respectively, from Table 2), it does not provide a good single-variable regression for α (e.g. R2 = 0.26, SE = 3.6° regressing α on β defined at 10° point). Four of the other predictor variables have higher significance levels with α, and higher F values in the regression. The final regression shown in Equation (2) is independent of where one defines the β point, so this definition becomes unimportant once it is established that β is not one of the top three predictors for multivariate regression for α for this dataset.
Runout Ratio Method
Reference McClung and LiedMcClung and Lied (1987) and Reference McClung and MearsMcClung and Mears (1991) showed that a Gumbel distribution in the form
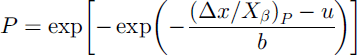
provides a good model for extreme avalanche runout distances. In this model, the runout ratio, Δx/Xβ, is the continuous random variable, u and b are the location and scale parameters, respectively, and P is the non-exceedance probability (threshold probability). A chosen value of P represents the runout ratio for which P 100% of the values in the dataset will not exceed that given value. Equation (3) can be rewritten as
where −ln(−ln(P)) is termed the reduced variate. By assigning appropriate non-exceedance values P for each observed runout ratio in the dataset based on their rank order, it is possible to solve for u and b using least-squares linear regression techniques (Reference McClung and MearsMcClung and Mears, 1991).
Based on the poor fit of the regression line to the data with the β point defined at 10°, additional linear regressions were conducted by varying the β point definition from 10° through 27°. For our short-slope dataset, the best fit of the data to a Gumbel distribution occurs when the β point is defined at 24° (Reference JonesJones, 2002, p. 58–61). Using this definition, R2 is maximized at 0.98 and the standard error of regression, SE, is minimized at 0.080 (Fig. 4). The resulting regression equation relating the runout ratio to the non-exceedance probability is

Fig. 4. Runout ratio fitted to an extreme-value (Gumbel) probability distribution for 46 avalanche paths in combined mountain ranges. β point defined at 24°.
This regression uses data from 46 of the 48 avalanche paths in the dataset (minus the two outliers discussed in the previous section), combines paths from all four mountain ranges and is hereafter termed the four-range model. Similar analyses were done with individual mountain ranges, but the fit for individual ranges was either equal to or poorer than the fit obtained with the combined ranges (Reference JonesJones, 2002, p. 62). Because the β point was redefined in this study as the location where the slope first reaches 24°, there is little point in comparing the scale and location parameters from this model to parameters from previously developed models.
Two long-running avalanche paths (high runout ratios) were noted during the analyses, both of which had runout zones that were within partly confined stream channels. Channelization of avalanche flow in the runout zone may have contributed to the longer runout distances (Reference McClungMcClung, 2001). These paths were included in the analyses since it is important the models are applicable for estimating extreme runout associated with long-running avalanche paths.
All previous work in the field of statistical avalanche-run-out estimation has emphasized, as one of its underlying assumptions, that each region or mountain range constitutes a separate population of extreme runout distances, and that each region must be analyzed separately (Reference MearsMears, 1992, p. 26). This analysis shows that a suitable model can be developed to represent short slopes in several mountain ranges in Canada, with all measured paths combined into one dataset. The four mountain ranges used in this study have very different climate characteristics, and represent all three of the generalized snow climates: maritime, continental and intermountain (Reference McClung and SchaererMcClung and Schaerer, 1993, p. 17–18).
Length-Scale Effects
As with previous studies (e.g. Reference McClung and MearsMcClung and Mears, 1991), the model developed for the short-slope dataset exhibits a scale effect when the runout ratio is used to define runout distance.The coefficients of the Spearman rank correlations of the runout ratio, Δx/Xβ, with either Hβ or Xβ are both -0.55 (n = 46), which are highly significant (p < 10-4). The negative correlations with the runout ratio show that proportionately longer runout distances are associated with shorter paths in the dataset, which is consistent with the findings of Reference McClung and MearsMcClung and Mears (1991) and Reference Nixon and McClungNixon and McClung (1993). The relationship between the runout ratio and the horizontal reach is clearly illustrated in Figure 5, in which the runout ratio is seen as a decreasing function of increasing horizontal reach. The vertical line drawn at Xβ = 300 m shows that there is a smaller range of runout ratios (-0.5 < Δx/Xβ < 1.0) associated with paths with horizontal reaches greater than approximately 300 m than with paths with horizontal reaches less than 300 m. Thus, although some of the scale effect between larger slopes and short slopes is reduced with this model, there is still a scale effect for the runout ratio in the short-slope dataset.

Fig. 5. Plot of the runout ratio υs the horizontal reach for the short-slope dataset, illustrating the length-scale effect in the runout ratio model.
Both Reference McClung and LiedMcClung and Lied (1987) and Reference McClung and MearsMcClung and Mears (1991) found that slopes with a vertical drop of <350m did not fit well into their dataset, and consequently trimmed these paths from their dataset. Additional analyses with our dataset indicate that the best-fit linear regression is found when the dataset is limited to slopes with a vertical fall height (Hα) of <275m, measured from the starting position to the extreme runout position (Reference JonesJones, 2002, p. 64). This may function as an approximate upper limit for which this “short-slope” model may be most applicable.
The scale effect for the alpha-regression model, although visually less pronounced than that observed with the runout ratio method, is still significant (Fig. 6). The Spearman rank correlation coefficients of Hβ, Hβ and Xβ with α are 0.44 (p < 10-2), 0.61 (p < 10-5) and 0.57 (p < 10-4), respectively, indicating that decreasing α (increasing runout distance) is associated with decreasing vertical fall height and horizontal reach (smaller path size) for this regression model. Thus, scale effects within the dataset need to be considered when using models developed using both the runout ratio and alpha-regression methods.

Fig. 6. Plot of observed α υs the horizontal reach for the short-slope dataset, illustrating the length-scale effect in the alpha-regression model.
For the Canadian short-slope dataset, the mean α is 26.3° (standard deviation (SD) of 4.1°, N = 46). Reference McClung and LiedMcClung and Lied (1987) report a mean α of 31.1° (SD of 6.4°, N = 212) for a dataset from western Norway, and Reference McClung, Mears and SchaererMcClung and others (1989) report a mean α of 27.8° (SD of 3.5°, N = 127) for a dataset of taller Canadian paths. Conducting t tests for the differences of the means, we find that the mean α for the short-slope dataset is significantly lower than mean values for both the Canadian taller slope (t = 2.2, 70 degrees of freedom (df), p = 0.02) and Norwegian (t = 6.4, df = 180, p < 10-6) datasets.
One important model limitation is that Equation (2) begins to fail for relatively larger paths with H0 approximately greater than 500 m. Large paths may tend to have higher values of α (e.g. 40° maximum observed for the Canadian Purcell and Rocky Mountain ranges (Reference McClung, Mears and SchaererMcClung and others, 1989)), but values of H0 approximately greater than 500 m result in α > 45°, which are unreasonably high values of α for extreme avalanches, and much higher than those typically noted in the literature.
Comparison of Runout Ratio and Alpha-Regression Methods
In the previous sections, avalanche runout models were developed using two different methods: the runout ratio (Equation (5)) and the alpha-regression method (Equation (2)). Both methods yield models that provide reasonably good fits to the sample of avalanche paths from this study. We follow the approach of Nixon and Reference McClung and SchaererMcClung (1993) for quantitatively comparing runout estimates by randomly selecting two avalanche paths from each mountain range, for a total of eight avalanche paths (Table 4). To compare the models in an unbiased manner, values for both the runout distance, ΔxP, and the equivalent αP angle are presented. The results in Table 4 show that at higher values of P (0.9 and 0.99) the runout ratiomethod estimates longer runout distances than the alpha-regression method for most paths, with the exception of the Brohm Ridge and Mont Jacques Cartier Saddle paths at P = 0.90. This is consistent with the findings of Reference Nixon and McClungNixon and McClung (1993), and is explained by the fact that runout estimates based on the assumption that runout follows an extreme value distribution should be higher than estimates based on runout following a normal distribution. This result is most profound for the highest threshold probabilities analyzed (P = 0.99), where the runout ratio method estimates runout distances 1.5–4 times the distance estimated with the regression method. High threshold probabilities (e.g. P = 0.90, P = 0.99) may be relevant for some engineering applications such as land-use planning.
Table 4. Comparison of runout distances and α angles for eight paths for the alpha-regression model αP = 21.11 + 22.41H0y′′ - 3.02TP + 0.01H0 - CPSE (Equation (2)) and the four-range model (Δx/XP )β = 0.494 - 0.441 ln(- ln(P)) (Equation (5))
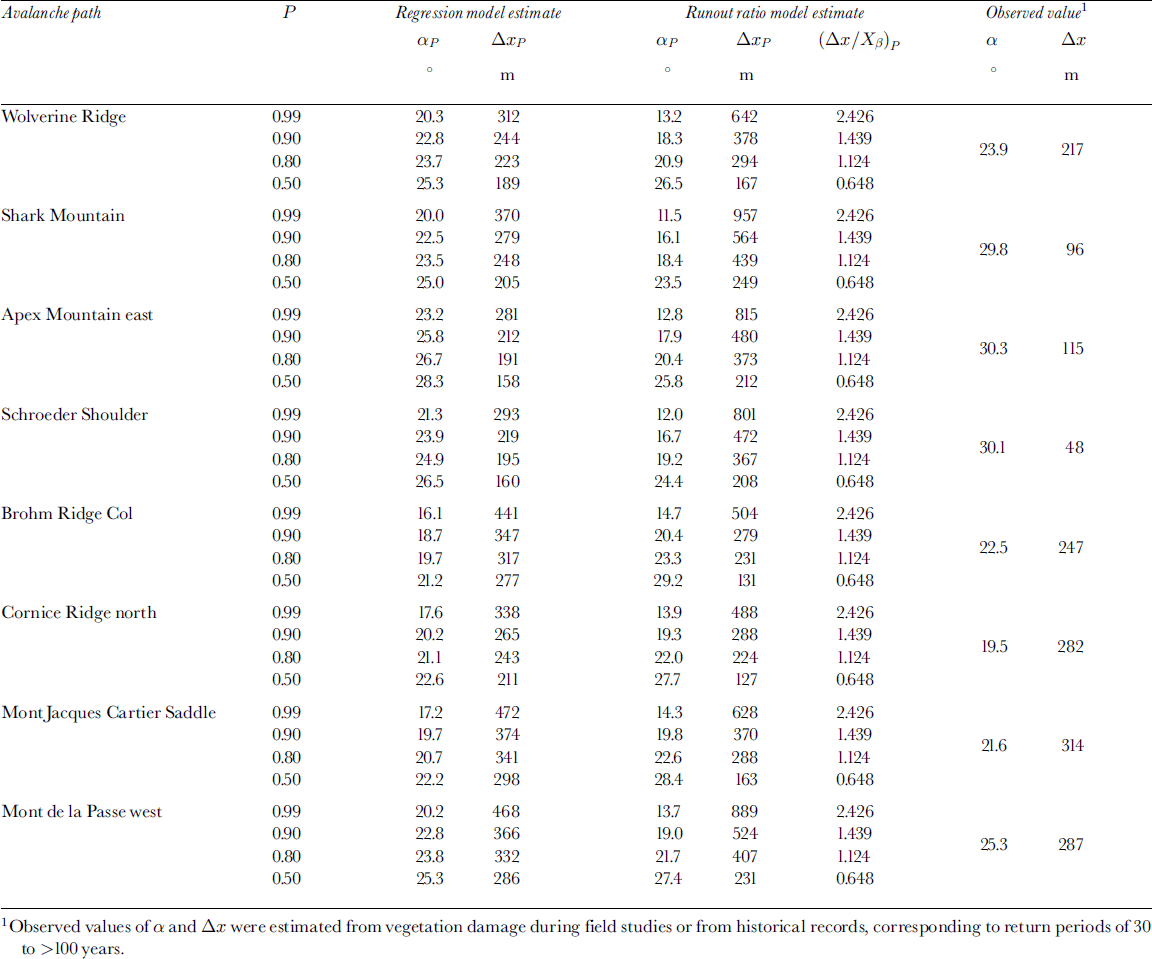
At very high values of P (e.g. P ≥ 0.90), the runout ratio method estimates equivalent α values that appear to be unreasonably low (Table 4). A review of the literature (e.g. Reference Lied and BakkehøiLied and Bakkehøi, 1980; Reference MartinelliMartinelli, 1986; Reference McClung and MearsMcClung and Mears, 1991; Reference Nixon and McClungNixon and McClung, 1993; Reference JóhannessonJóhannesson, 1998) shows that minimum observed α values are in the range 14–20° for most studies of avalanche runout. Exceptionally low values are in the range 14–16°, with only one recorded α angle of 14° in the Colorado Rocky Mountains (Reference MartinelliMartinelli, 1986). The lowest observed α angle from the short-slope dataset is 19° (Table 1). Table 4 shows that for P = 0.99 the runout ratio method estimates equivalent αP angles of 12–15°, implying that this model may be overly conservative at high threshold probabilities. The alpha-regression model estimates more realistic αP angles of 16– 23° for P = 0.99.
Proposed Physical Effects of Variables in Multiple Regression Model
The three independent variables used in the regression model, H0y′′, H0 andTP, are topographic parameters taken from the terrain profile for each path. While all three variables are statistically important parts of the regression model, the physical effectof each variable should be discussed to evaluate their individual contribution to the model.
The variable H0y′′ was found to be statistically significant in earlier studies (e.g. Reference Lied and BakkehøiLied and Bakkehøi, 1980; Reference McClung and LiedMcClung and Lied, 1987; Reference Lied, Weiler, Bakkehøi and HopfLied and others, 1995; Reference JóhannessonJóhannesson, 1998), but in all studies except for Reference Lied, Weiler, Bakkehøi and HopfLied and others (1995) was left out of the regression since it did not substantially improve the fit. In this study, H0y′′ is strongly and positively correlated with α (Table 2), which means that higher values of H0y′′ are associated with shorter runout distances. By assuming that the extreme runout position and the vertex of the fitted parabola for a path coincide, it is possible to show that H0y′′ is directly proportional to tan α. Thus, by geometry, H0y′′ is a promising predictor variable for α, even without the tangent transformation and allowing for statistical scatter of the extreme runouts with respect to the vertex. This was shown to be true in this study.
H0 is also strongly and positively correlated with α, while y′′ is not significantly correlated with α (Table 2). Interpretation of these correlations shows that paths with higher values of y′′ (highly curved) and higher values of H0 (taller slopes) are associated with higher values of α, or relatively shorter runout distances.This agrees with the hypothesis of this study that shorter slopes have relatively longer runout distances than taller slopes in this dataset. In terms of avalanche dynamics, highly curved paths have higher energy losses associated with slope angles that decrease markedly down the path, and consequently reduced runout potential. The lowest amount of energy loss would be associated with a perfectly linear slope, for which y′′ approaches 0. While shorter slopes have relatively longer runout distances, as the strong positive correlation with α suggests, there is also a curvature effect in the model with respect to y′′. Thus, H0y′′ may be a more important predictor variable for α than either H0 or y′′ alone.
The variable TP is negatively correlated with α, but only at the 6% significance level. This variable is highly related to the radius of curvature, y′′, but accounts for the very abrupt change in slope associated with hockey-stick profiles. Based on the negative correlation of TP with α, paths with higher values ofTP (i.e. hockey-stick profiles) are associated with lower values of α, and consequently longer runout distances (Fig. 7). This finding agrees with Reference MartinelliMartinelli, 1986 and Reference McClung and LiedMcClung and Lied (1987) who observed unusually long runout distances associated with short-track, hockey-stick profile paths. One possible physical interpretation for this phenomenon is that fast-moving snow may become partly fluidized upon reaching an abrupt slope transition associated with paths with hockey-stick profiles (Reference MartinelliMartinelli, 1986; Reference McClung and LiedMcClung and Lied, 1987; personal communication from K. Lied, 2002). Consequentially, extreme avalanches in these paths might flow greater distances because of entrained air and reduced frictional drag (Reference MartinelliMartinelli, 1986). Another explanation for this phenomenon is that there is a tendency for snow to be deposited at a sharp slope transition and for the remaining snow to override the material trapped in the transition area (Reference McClung and MearsMcClung and Mears, 1995). The material trapped at the transition may serve to reduce frictional forces at the transition, resulting in relatively longer runout distances.

Fig. 7. Box-and-whisker plot showing the relationship between observed α and the terrain profile variable, TP. Maximum, minimum, 25th and 75th percentiles and median are shown for each range of TP.
A third possible explanation is that the TP variable is simply compensating for the quadratic fit of the curves to the hockey-stick profiles. Both Reference Lied and BakkehøiLied and Bakkehøi (1980) and Reference MartinelliMartinelli, 1986 fit their paths using parabolas, similar to this study. It may be the case in these paths that the β points for the fitted curves should be located farther up-slope than the β point at the transition of the hockey stick. Thus, when terrain parameters are taken from parabolas fitted to path profiles, avalanche paths with hockey-stick profiles run farther in relation to paths with other profiles. From a practical perspective, higher values of TP (i.e. TP = 3 for hockey sticks) are associated with lower values of α, as shown by the negative contribution of TP to the alpha-regression model (Equation (2)) and shown graphically in Figure 7. Therefore, for conservative estimates of runout, one would prefer to choose higher values of TP in the model if unsure of which category of TP to apply to the path profile.
Testing the Short-Slope Runout Models
In order to assess the usefulness of the runout models developed in this project, we analyzed 13 additional short-slope avalanche paths that were not included in the development of the models. Five of these paths are from the Chic Choc Mountain range in Québec, and thus are geographically within the area represented by this study. The other eight paths are from the Swiss Alps, thus representing a different sample in terms of geography and possibly climate. These additional paths have vertical fall heights of 59–320m with a mean of 220 m, which is the same mean vertical fall height (Hα) shown inTable 1.
A plot of residuals (observed - predicted) for α vs predicted α for the alpha-regression model shows that observed α angles are within one standard error of regression for all of the Québec paths and five of the eight Swiss paths (Fig. 8). Measured α angles are within two standard errors of regression for all of the paths. One notable trend in Figure 8 is that the model consistently underestimated runout for the Swiss paths, although only three of these estimates were more than one standard error of regression from the observed values. The most likely explanation for this trend is that these three Swiss data represent avalanches with longer return periods than the majority of paths in the short-slope dataset (personal communication from S. Margreth, 2002). On average, the Swiss paths may have longer return periods than the paths used to develop the Canadian regression model, which have return periods more likely in the range 30 to >100 years. This would explain why the model consistently underestimates runout for the Swiss data. Another possible reason is that the Swiss data represent a different statistical population than the Canadian dataset, and thus the regression model does not work well for predicting run-out for paths outside of the four tested Canadian mountain ranges. Additional data from other mountain ranges would be useful for testing whether the applicability of these models is limited to the four Canadian mountain ranges.

Fig. 8. Plot of residuals (observed minus predicted α) vs predicted α using the alpha-regression model Equation (2)), with P = 0.50. Dashed lines show the mean ±1 SE (2.5°).
Whenthe four-range runout ratiomodel is used to predict runout for the 13 additional paths, a trend similar to that for the regression model can be observed (Fig. 9). The results shown in Figure 9 represent a non-exceedance probability of 0.5, since this is a mean value for the paths in the dataset. The model provides good runout estimates for all of the Québec paths, within15m of the observed runout in three cases.

Fig. 9. Plot of residuals (observed minus predicted Δx) υs predicted Δx using the four-range runout ratio model (Equation (5)) with P = 0.50.
Similar to the alpha-regression model, the runout ratio model underestimates runout for three or four of the Swiss paths. However, the runout estimates for four of the eight paths were within 80 m of the observed runout distances, which are reasonably good estimates given the amount of uncertainty associated with avalanche runout modelling.
Summary
In this paper, we presented and compared two methods for estimating runout distances for short-slope avalanche paths: one using the alpha-regression and the other using the run-out ratio method. For both models, the reference β point from which to measure runout distances was redefined for short slopes to be the position where the slope in the path first reaches 24° proceeding downslope from the starting zone. This definition provided better fits of the short-slope data using both normal and extreme-value probability distribution functions. Two avalanche paths with very steep runout zones were removed from the analyses, leaving 46 paths available to develop the runout models.
A run out model was developed by regressing eight potential predictor variables on the α angle. This model uses three of these variables, H0y′′, TP and H0, for the regression and provides a significant fit of the data to a normal distribution (adjusted R2 = 0.65, SE = 2.5°). Scale effects and the proposed physical explanations of the independent predictor variables on the alpha-regression model were discussed.
The runout ratio method was used to develop a model for estimating runout distances that fit a Gumbel extreme-value distribution function. The four-range model includes data from the four Canadian mountain ranges and is well fit by a Gumbel distribution (R2 = 0.98, SE = 0.080). Use of all four ranges in this analysis shows that there is little difference between mountain ranges in terms of runout distances for short slopes using the runout ratio method. Two long-running avalanche paths with runout zones within partly confined stream channels were noted in the analyses for the models. Channelization of the avalanche flow in the runout zone probably contributed to longer runout distances in these paths, and should be considered when estimating runouts.
A comparison of the two statistical methods shows that the runout ratiomethod estimates more conservative (longer) runout distances than the alpha-regression method for most threshold probabilities. This effect is very pronounced for the higher-threshold probabilities (e.g. P = 0.99), where the runout ratio method estimates runout distances up to four times that estimated by the alpha-regression method.
When terrain parameters are taken from parabolas fitted to path profiles, avalanches in paths with hockey-stick profiles tend to run farther in relation to paths with parabolic or almost linear profiles. This has important implications for estimating runout distances for short slopes, particularly when applied to land-use planning.
The models were tested using data from 13 additional short-slope avalanche paths, eight from the Swiss Alps and five from the Chic Choc range in Québec. Both models provide good runout estimates for the five Québec paths. Both models tend to underestimate runout distances for the Swiss paths when compared to the observed runout. However, both models provide reasonable estimates of runout for four of the eight Swiss paths, showing that these models may be used with caution for other ranges, taking into account the uncertainty associated with the models (i.e. using appropriate threshold probabilities). Additional studies would be required to assess the suitability of the models for individual mountain ranges not represented in this study.
This study included 48 avalanche paths, which was sufficient to build models for combined mountain ranges but was not sufficient data for properly assessing each range individually. Thus, a larger dataset could be developed that includes more paths in the individual ranges. There also may be important climatic variations within these ranges that influence runout distances. Further studies could look into specific climate variables (e.g. 30 year maximum water equivalent of snowfall) and assess their effect on runout distances.
Acknowledgements
For financial support while the first author was a graduate student at the University of Calgary we are grateful to the British Columbia Ministry of Transportation, the Association of Professional Engineers, Geologists and Geophysicists of Alberta, the Department of Civil Engineering at the University of Calgary, and to Canada’s Natural Sciences and Engineering Research Council. For their contributions to this project including advice, guidance, resources and identifying field sites we thank: J. Bennetto, H. Bluer, G. Bonwick, F. Bouchart, D. Clapp, M. Deschenes, C. Diezfelbinger, D. Germain, J. Goodrich, P. Hein, B. Hétu, P. Jordan, P. Kimmel, K. Lied, D. McClung, L. McKittrick, B. McLeod, B. McMahon, M. Maes, L. Nkemdirim, P. Schaerer, R. Schroeder, R. Siggers, D. Skjonsberg, C. Stethem and D. Wilson. For field assistance we are grateful to K. Paulig and G. Johnson. For providing additional data for testing the models we thank D. Germain, B. Hétu and S. Margreth. Finally, we would like to thank the two anonymous reviewers and the editor, F. Sandersen, for their helpful comments and suggestions that greatly improved this paper.







