Article contents
On the Pontrjagin classes of spray manifolds
Published online by Cambridge University Press: 11 December 2023
Abstract
The characterization of projectively flat Finsler metrics on an open subset in 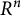 $R^n$ is the Hilbert’s fourth problem in the regular case. Locally projectively flat Finsler manifolds form an important class of Finsler manifolds. Every Finsler metric induces a spray on the manifold via geodesics. Therefore, it is a natural problem to investigate the geometric and topological properties of manifolds equipped with a spray. In this paper, we study the Pontrjagin classes of a manifold equipped with a locally projectively flat spray and show that such manifold must have zero Pontrjagin classes.
$R^n$ is the Hilbert’s fourth problem in the regular case. Locally projectively flat Finsler manifolds form an important class of Finsler manifolds. Every Finsler metric induces a spray on the manifold via geodesics. Therefore, it is a natural problem to investigate the geometric and topological properties of manifolds equipped with a spray. In this paper, we study the Pontrjagin classes of a manifold equipped with a locally projectively flat spray and show that such manifold must have zero Pontrjagin classes.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Canadian Mathematical Society
References
- 1
- Cited by



