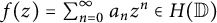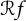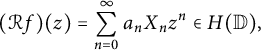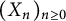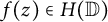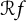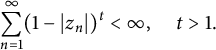1 Introduction and main results
It has been folklore since the early history of random analytic functions
![]() $(\mathcal {R} f)(z)= \sum _{k=0}^{\infty } \pm a_k z^k$
that the behaviors of
$(\mathcal {R} f)(z)= \sum _{k=0}^{\infty } \pm a_k z^k$
that the behaviors of
![]() $\mathcal {R} f$
exhibit often a dichotomy according to whether the coefficients
$\mathcal {R} f$
exhibit often a dichotomy according to whether the coefficients
![]() $\{a_k\}_{k=0}^{\infty }$
are square-summable or not. In principle, if
$\{a_k\}_{k=0}^{\infty }$
are square-summable or not. In principle, if
![]() $\sum |a_k|^2<\infty $
, then
$\sum |a_k|^2<\infty $
, then
![]() $\mathcal {R} f$
behaves reasonably well, and otherwise, wildly.
$\mathcal {R} f$
behaves reasonably well, and otherwise, wildly.
Relevant to the theme in this note are geometric conditions on the zero sequence
![]() $\{z_n\}_{n=1}^{\infty }$
of an analytic function over the unit disk, among which the best known one is perhaps the Blaschke condition, i.e.,
$\{z_n\}_{n=1}^{\infty }$
of an analytic function over the unit disk, among which the best known one is perhaps the Blaschke condition, i.e.,
 $$ \begin{align*}\sum_{n=1}^{\infty} (1-|z_n|)<\infty.\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty} (1-|z_n|)<\infty.\end{align*} $$
For functions in the Hardy space
![]() $H^p(\mathbb {D}) \ (p>0)$
over the unit disk, the zero sets are characterized as those sequences satisfying the Blaschke condition [Reference Duren4].
$H^p(\mathbb {D}) \ (p>0)$
over the unit disk, the zero sets are characterized as those sequences satisfying the Blaschke condition [Reference Duren4].
In the random setting, Littlewood’s theorem from 1930 [Reference Littlewood10] implies that
 $$ \begin{align*}(\mathcal{R}f)(z)=\sum_{n=0}^\infty \pm a_n z^n \in H^p(\mathbb{D})\end{align*} $$
$$ \begin{align*}(\mathcal{R}f)(z)=\sum_{n=0}^\infty \pm a_n z^n \in H^p(\mathbb{D})\end{align*} $$
almost surely for all
![]() $p>0$
if
$p>0$
if
![]() $f(z)=\sum _{n=0}^{\infty }a_n z^n \in H^2(\mathbb {D})$
. It follows that the zero sequence of
$f(z)=\sum _{n=0}^{\infty }a_n z^n \in H^2(\mathbb {D})$
. It follows that the zero sequence of
![]() $\mathcal {R} f$
satisfies the Blaschke condition almost surely. A converse statement holds as well, due to Nazarov, Nishry, and Sodin, who showed in 2013 [Reference Nazarov, Nishry and Sodin12] that if
$\mathcal {R} f$
satisfies the Blaschke condition almost surely. A converse statement holds as well, due to Nazarov, Nishry, and Sodin, who showed in 2013 [Reference Nazarov, Nishry and Sodin12] that if
![]() $f\notin H^2(\mathbb {D})$
, then
$f\notin H^2(\mathbb {D})$
, then
 $$ \begin{align*}\sum_{n=1}^{\infty}(1-|z_n(\omega)|)=\infty\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty}(1-|z_n(\omega)|)=\infty\end{align*} $$
almost surely, where
![]() $\{z_n(\omega )\}_{n=1}^{\infty }$
is the zero sequence of
$\{z_n(\omega )\}_{n=1}^{\infty }$
is the zero sequence of
![]() $\mathcal {R} f$
.
$\mathcal {R} f$
.
The purpose of this note is two-fold: firstly, we hope to gain more insight into the square-summable case, for which the quantity
![]() $\sum (1-|z_n(\omega )|)$
, as well as another notion
$\sum (1-|z_n(\omega )|)$
, as well as another notion
![]() $L(\mathcal {R} f)$
(see (1) below), defines an a.s. finite random variable whose quantitative property is of interests to us; secondly, and perhaps more importantly, we hope to gain more insight for the failure of the Blaschke condition in the non-square-summable territory for which much less is known in the literature.
$L(\mathcal {R} f)$
(see (1) below), defines an a.s. finite random variable whose quantitative property is of interests to us; secondly, and perhaps more importantly, we hope to gain more insight for the failure of the Blaschke condition in the non-square-summable territory for which much less is known in the literature.
Definition 1.1. A function
![]() $f(z)\in H(\mathbb {D})$
is said to be in the class
$f(z)\in H(\mathbb {D})$
is said to be in the class
![]() $\mathfrak {B} _t~(t\ge 1)$
if its zero set
$\mathfrak {B} _t~(t\ge 1)$
if its zero set
![]() $\{z_n\}_{n=1}^{\infty }$
satisfies the
$\{z_n\}_{n=1}^{\infty }$
satisfies the
![]() $B_t$
-condition:
$B_t$
-condition:
 $$ \begin{align*} \sum_{n=1}^{\infty}(1-|z_n|)^t<\infty. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^{\infty}(1-|z_n|)^t<\infty. \end{align*} $$
Remark. We shall use the class
![]() $\mathfrak {B}_1$
and the Blaschke class interchangeably.
$\mathfrak {B}_1$
and the Blaschke class interchangeably.
We shall indeed treat three kinds of randomization methods in this note.
Definition 1.2. A random variable X is called Bernoulli if
![]() $\mathbb {P}(X=1)=\mathbb {P}(X=-1)=\frac {1}{2}$
, Steinhaus if it is uniformly distributed on the unit circle, and by
$\mathbb {P}(X=1)=\mathbb {P}(X=-1)=\frac {1}{2}$
, Steinhaus if it is uniformly distributed on the unit circle, and by
![]() $N(0,1)$
, we mean the law of a Gaussian variable with zero mean and unit variance. Moreover, for
$N(0,1)$
, we mean the law of a Gaussian variable with zero mean and unit variance. Moreover, for
![]() $X\in \{\text {Bernoulli, Steinhaus, } N(0,1)\}$
, a standard X sequence is a sequence of independent, identically distributed X variables, denoted by
$X\in \{\text {Bernoulli, Steinhaus, } N(0,1)\}$
, a standard X sequence is a sequence of independent, identically distributed X variables, denoted by
![]() $\{\epsilon _n\}_{n\geq 0}$
,
$\{\epsilon _n\}_{n\geq 0}$
,
![]() $\{e^{2\pi i\alpha _n}\}_{n\geq 0}$
and
$\{e^{2\pi i\alpha _n}\}_{n\geq 0}$
and
![]() $\{\xi _n\}_{n\geq 0}$
, respectively. Lastly, a standard random sequence
$\{\xi _n\}_{n\geq 0}$
, respectively. Lastly, a standard random sequence
![]() $\{X_n\}_{n\geq 0}$
refers to either a standard Bernoulli, Steinhaus, or Gaussian
$\{X_n\}_{n\geq 0}$
refers to either a standard Bernoulli, Steinhaus, or Gaussian
![]() $N(0,1)$
sequence.
$N(0,1)$
sequence.
Theorem 1.3. Let
![]() $f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
,
$f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
,
![]() $\mathcal {R} f(z)=\sum _{k=0}^{\infty }a_k X_k z^k$
, where
$\mathcal {R} f(z)=\sum _{k=0}^{\infty }a_k X_k z^k$
, where
![]() $\{X_k\}_{k=0}^{\infty }$
is a standard random sequence, and let
$\{X_k\}_{k=0}^{\infty }$
is a standard random sequence, and let
![]() $\{z_n(\omega )\}_{n=1}^{\infty }$
be the zero sequence of
$\{z_n(\omega )\}_{n=1}^{\infty }$
be the zero sequence of
![]() $\mathcal {R} f$
, repeated according to multiplicity and ordered by nondecreasing modules. Then the following statements are equivalent for any
$\mathcal {R} f$
, repeated according to multiplicity and ordered by nondecreasing modules. Then the following statements are equivalent for any
![]() $t>1$
:
$t>1$
:
-
(i)
 $\mathcal {R} f\in \mathfrak {B}_t$
a.s.
$\mathcal {R} f\in \mathfrak {B}_t$
a.s.
 $;$
$;$
-
(ii)
 $\mathbb {E}(\sum _{n=1}^{\infty }(1-|z_n(\omega )|)^t)<\infty ;$
$\mathbb {E}(\sum _{n=1}^{\infty }(1-|z_n(\omega )|)^t)<\infty ;$
-
(iii)
 $\int _0^1 (\log (\sum _{k=0}^{\infty } |a_k|^2 r^{2k}))(1-r)^{t-2}dr<\infty .$
$\int _0^1 (\log (\sum _{k=0}^{\infty } |a_k|^2 r^{2k}))(1-r)^{t-2}dr<\infty .$
Corollary 1.4. Let
![]() $f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
and
$f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
and
![]() $\mathcal {R} f(z)=\sum _{k=0}^{\infty }a_k X_k z^k$
, where
$\mathcal {R} f(z)=\sum _{k=0}^{\infty }a_k X_k z^k$
, where
![]() $\{X_k\}_{k\geq 0}$
is a standard random sequence. Then
$\{X_k\}_{k\geq 0}$
is a standard random sequence. Then
![]() $\mathcal {R} f\in \mathfrak {B}_2$
almost surely if and only if
$\mathcal {R} f\in \mathfrak {B}_2$
almost surely if and only if
 $$ \begin{align*}\int_0^1 \log\big(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}\big)dr<\infty.\end{align*} $$
$$ \begin{align*}\int_0^1 \log\big(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}\big)dr<\infty.\end{align*} $$
As a complement, for
![]() $t=1$
, we obtain more information when
$t=1$
, we obtain more information when
![]() $f \in H^2$
as follows. Let
$f \in H^2$
as follows. Let
We observe that
![]() $L(f)$
is not really a measure of the size of f, since, for any g nonvanishing on
$L(f)$
is not really a measure of the size of f, since, for any g nonvanishing on
![]() $\mathbb {D}$
with
$\mathbb {D}$
with
![]() $g(0)=1$
, one has
$g(0)=1$
, one has
![]() $L(fg)=L(f)$
. By Theorem 2.3 in [Reference Duren4], both
$L(fg)=L(f)$
. By Theorem 2.3 in [Reference Duren4], both
are a.s. finite random variables if and only if
![]() $f\in H^2$
. Next, we obtain quantitative estimates for these two random variables, which complement the known results on the classical Blaschke condition.
$f\in H^2$
. Next, we obtain quantitative estimates for these two random variables, which complement the known results on the classical Blaschke condition.
Theorem 1.5. Let
![]() $f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
,
$f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
,
![]() $\mathcal {R} f(z)=\sum _{k=0}^{\infty }a_k X_k z^k$
, where
$\mathcal {R} f(z)=\sum _{k=0}^{\infty }a_k X_k z^k$
, where
![]() $\{X_k\}_{k=0}^{\infty }$
is a standard random sequence, and let
$\{X_k\}_{k=0}^{\infty }$
is a standard random sequence, and let
![]() $\{z_n(\omega )\}_{n=1}^{\infty }$
be the zero sequence of
$\{z_n(\omega )\}_{n=1}^{\infty }$
be the zero sequence of
![]() $\mathcal {R} f$
, repeated according to multiplicity and ordered by nondecreasing modules. Then the following statements are equivalent:
$\mathcal {R} f$
, repeated according to multiplicity and ordered by nondecreasing modules. Then the following statements are equivalent:
-
(i)
 $f\in H^2;$
$f\in H^2;$
-
(ii)
 $\mathcal {R} f\in \mathfrak {B}_1$
a.s.
$\mathcal {R} f\in \mathfrak {B}_1$
a.s.
 $;$
$;$
-
(iii)
 $\mathbb {E}\left (\sum _{n=1}^{\infty }\left (1-|z_{n}(w)|\right )\right )<\infty ;$
$\mathbb {E}\left (\sum _{n=1}^{\infty }\left (1-|z_{n}(w)|\right )\right )<\infty ;$
-
(iv)
 $\mathbb {E}\left (e^{L(\mathcal {R} f)}\right )<\infty .$
$\mathbb {E}\left (e^{L(\mathcal {R} f)}\right )<\infty .$
The rest of this note is devoted to the proofs of Theorems 1.3 and 1.5, ending with remarks on the zero sets of random analytic functions in the Bergman spaces.
2 Preliminaries
In this section, we introduce a key tool needed for our proofs. We motivate the estimate in [Reference Nazarov, Nishry and Sodin12] for Rademacher random variables by considering first the easier case of a standard Gaussian sequence
![]() $\{X_k\}_{k\geq 0}$
. For
$\{X_k\}_{k\geq 0}$
. For
![]() $f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
, we assume
$f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
, we assume
![]() $|a_0|=1$
and set
$|a_0|=1$
and set
 $$ \begin{align*}\widehat{F}_r(\theta)=\mathcal{R} f(re^{i\theta})/(\sum_{k=0}^{\infty} |a_k|^2 r^{2k})^{\frac{1}{2}}.\end{align*} $$
$$ \begin{align*}\widehat{F}_r(\theta)=\mathcal{R} f(re^{i\theta})/(\sum_{k=0}^{\infty} |a_k|^2 r^{2k})^{\frac{1}{2}}.\end{align*} $$
Then, for any
![]() $r\in (0,1)$
, we rewrite
$r\in (0,1)$
, we rewrite
 $$ \begin{align*} \widehat{F}_r(\theta)=\sum _{k=0}^{\infty} \widehat{a}_k(r) X_k e^{ik\theta}, \end{align*} $$
$$ \begin{align*} \widehat{F}_r(\theta)=\sum _{k=0}^{\infty} \widehat{a}_k(r) X_k e^{ik\theta}, \end{align*} $$
which is a random Fourier series satisfying the condition
![]() $\sum _{k=0}^{\infty } |\widehat {a}_k(r)|^2=1$
. Consequently, for each
$\sum _{k=0}^{\infty } |\widehat {a}_k(r)|^2=1$
. Consequently, for each
![]() $\theta $
, the random variable
$\theta $
, the random variable
![]() $ \widehat {F}_r(\theta )$
is a standard complex-valued Gaussian variable. In particular,
$ \widehat {F}_r(\theta )$
is a standard complex-valued Gaussian variable. In particular,
![]() $\mathbb {E}(|\log |\widehat {F}_{r}(\theta )||)$
is a positive constant (which can be estimated by
$\mathbb {E}(|\log |\widehat {F}_{r}(\theta )||)$
is a positive constant (which can be estimated by
![]() $\sqrt {\frac {2}{\pi }}\int _0^{\infty }|\log x|e^{-x^2/2}dx \thickapprox 0.87928$
). Now, the following equation, together with Theorem 2.3 in [Reference Duren4], implies that the zeros of
$\sqrt {\frac {2}{\pi }}\int _0^{\infty }|\log x|e^{-x^2/2}dx \thickapprox 0.87928$
). Now, the following equation, together with Theorem 2.3 in [Reference Duren4], implies that the zeros of
![]() $\mathcal {R} f$
satisfy the standard Blaschke condition almost surely if and only if
$\mathcal {R} f$
satisfy the standard Blaschke condition almost surely if and only if
![]() $f\in H^2$
:
$f\in H^2$
:
 $$ \begin{align*} \int_0^{2\pi}\log|\mathcal{R} f(r e^{i\theta})|\frac{d\theta}{2\pi} =\frac{1}{2}\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}) +\int_0^{2\pi}\log |\widehat{F}_{r}(\theta) |\frac{d\theta}{2\pi}. \end{align*} $$
$$ \begin{align*} \int_0^{2\pi}\log|\mathcal{R} f(r e^{i\theta})|\frac{d\theta}{2\pi} =\frac{1}{2}\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}) +\int_0^{2\pi}\log |\widehat{F}_{r}(\theta) |\frac{d\theta}{2\pi}. \end{align*} $$
Then, for the Rademacher case, the remarkable estimate of Nazarov, Nishry, and Sodin [Reference Nazarov, Nishry and Sodin12, Corollary 1.2] provides a uniform bound for
![]() $r \in (0,1)$
:
$r \in (0,1)$
:
For the Steinhaus case, by [Reference Offord13, Reference Ullrich16, Reference Ullrich17], one has indeed
In particular, the estimate (2) holds for all three standard randomization methods.
3 Proof of Theorem 1.3
Motivated by Theorem 2 in [Reference Heilper5], we have the following.
Lemma 3.1. Let
![]() $\{z_n\}_{n=1}^{\infty }$
be the zero sequence of a function
$\{z_n\}_{n=1}^{\infty }$
be the zero sequence of a function
![]() $f\in H(\mathbb {D})$
and let
$f\in H(\mathbb {D})$
and let
![]() $t>1$
be a real number. Then
$t>1$
be a real number. Then
![]() $\sum _{n=1}^{\infty }(1-|z_n|)^t<\infty $
if and only if
$\sum _{n=1}^{\infty }(1-|z_n|)^t<\infty $
if and only if
where
![]() $dA$
denotes the area measure on
$dA$
denotes the area measure on
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
Proof Since
![]() $(\log |z|)(1-|z|)^{t-2}$
is area-integrable, without loss of generality, we assume
$(\log |z|)(1-|z|)^{t-2}$
is area-integrable, without loss of generality, we assume
![]() $|f(0)|=1$
. Assume first that
$|f(0)|=1$
. Assume first that
![]() $\sum _{n=1}^{\infty }(1-|z_n|)^t<\infty $
, where
$\sum _{n=1}^{\infty }(1-|z_n|)^t<\infty $
, where
![]() $\{z_n\}_{n=1}^{\infty }$
are repeated according to multiplicity and ordered by nondecreasing modules. The counting function
$\{z_n\}_{n=1}^{\infty }$
are repeated according to multiplicity and ordered by nondecreasing modules. The counting function
![]() $n(r)$
denotes the number of zeros of
$n(r)$
denotes the number of zeros of
![]() $f(z)$
in the disk
$f(z)$
in the disk
![]() $|z|<r$
. Denote by
$|z|<r$
. Denote by
![]() $N(r):=\int _{0}^{r}\frac {n(s)}{s}ds$
the integrated counting function. By using integration-by-parts, twice, one has
$N(r):=\int _{0}^{r}\frac {n(s)}{s}ds$
the integrated counting function. By using integration-by-parts, twice, one has
 $$ \begin{align} \nonumber &\frac{1}{2\pi}\int_{|z|<r}(\log |f(z)|)(1-|z|)^{t-2}dA(z) \\ &\quad=C_1(r)\int_0^r N(s)(1-s)^{t-2}ds \\ \nonumber &\quad=\frac{C_1(r)}{t-1}\bigg[-N(r)(1-r)^{t-1}+C_2(r)\int_0^r (1-s)^{t-1}n(s)ds\bigg]\\ \nonumber &\quad=\frac{C_1(r)}{t-1}\bigg[-N(r)(1-r)^{t-1}-\frac{C_2(r)}{t}n(r)(1-r)^{t}+\frac{C_2(r)}{t}\sum_{|z_n|<r}(1-|z_n|)^t\bigg], \end{align} $$
$$ \begin{align} \nonumber &\frac{1}{2\pi}\int_{|z|<r}(\log |f(z)|)(1-|z|)^{t-2}dA(z) \\ &\quad=C_1(r)\int_0^r N(s)(1-s)^{t-2}ds \\ \nonumber &\quad=\frac{C_1(r)}{t-1}\bigg[-N(r)(1-r)^{t-1}+C_2(r)\int_0^r (1-s)^{t-1}n(s)ds\bigg]\\ \nonumber &\quad=\frac{C_1(r)}{t-1}\bigg[-N(r)(1-r)^{t-1}-\frac{C_2(r)}{t}n(r)(1-r)^{t}+\frac{C_2(r)}{t}\sum_{|z_n|<r}(1-|z_n|)^t\bigg], \end{align} $$
where
![]() $C_1(r)$
is bounded because of the monotonicity of
$C_1(r)$
is bounded because of the monotonicity of
![]() $\int _0^{2\pi } \log |f(re^{i\theta })|d\theta $
in r and
$\int _0^{2\pi } \log |f(re^{i\theta })|d\theta $
in r and
![]() $C_2(r)$
is bounded since
$C_2(r)$
is bounded since
![]() $n(s)$
vanishes when s is small. Then, the necessity follows by letting
$n(s)$
vanishes when s is small. Then, the necessity follows by letting
![]() $r\rightarrow 1^-$
.
$r\rightarrow 1^-$
.
Now, we assume (3). Then by Jensen’s formula, we have
![]() $\int _0^1 N(r)(1-r)^{t-2}dr<\infty $
. The monotonicity of
$\int _0^1 N(r)(1-r)^{t-2}dr<\infty $
. The monotonicity of
![]() $N(r)$
yields
$N(r)$
yields
![]() $N(r)=o\left (\frac {1}{(1-r)^{t-1}}\right )$
. Since
$N(r)=o\left (\frac {1}{(1-r)^{t-1}}\right )$
. Since
![]() $n(s)$
is nondecreasing, we obtain
$n(s)$
is nondecreasing, we obtain
 $$ \begin{align*} (r-r^2)n(r^2)\leq\int_{r^2}^r n(s)ds=o\left(\frac{1}{(1-r)^{t-1}}\right), \end{align*} $$
$$ \begin{align*} (r-r^2)n(r^2)\leq\int_{r^2}^r n(s)ds=o\left(\frac{1}{(1-r)^{t-1}}\right), \end{align*} $$
which implies
![]() $n(r)=o\left (\frac {1}{(1-r)^t}\right )$
. This, together with (4), yields the sufficiency. The proof is complete now.
$n(r)=o\left (\frac {1}{(1-r)^t}\right )$
. This, together with (4), yields the sufficiency. The proof is complete now.
Proof of Theorem 1.3
We shall show that (i)
![]() $\Leftrightarrow $
(iii) and (iii)
$\Leftrightarrow $
(iii) and (iii)
![]() $\Rightarrow $
(ii) since (ii)
$\Rightarrow $
(ii) since (ii)
![]() $\Rightarrow $
(i) is trivial. Firstly, we consider (i)
$\Rightarrow $
(i) is trivial. Firstly, we consider (i)
![]() $\Leftrightarrow $
(iii). As above, we may assume
$\Leftrightarrow $
(iii). As above, we may assume
![]() $|f(0)|=1$
. Set
$|f(0)|=1$
. Set
![]() $\widehat {F}_r(\theta )=\mathcal {R} f(re^{i\theta })/(\sum _{k=0}^{\infty } |a_k|^2 r^{2k})^{\frac {1}{2}}$
. We observe that
$\widehat {F}_r(\theta )=\mathcal {R} f(re^{i\theta })/(\sum _{k=0}^{\infty } |a_k|^2 r^{2k})^{\frac {1}{2}}$
. We observe that
 $$ \begin{align*} &\frac{1}{2\pi}\int_{|z|<s} (\log|\mathcal{R} f(z)|)(1-|z|)^{t-2} dA(z)\\ &\quad=C_1(s)\bigg\{\frac{1}{2}\int_0^s(\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}))(1-r)^{t-2}dr\\ &\qquad\qquad\quad+\frac{1}{2\pi}\int_0^s\int_0^{2\pi}(\log|\widehat{F}_r(\theta)|)(1-r)^{t-2}d\theta dr\bigg\}, \end{align*} $$
$$ \begin{align*} &\frac{1}{2\pi}\int_{|z|<s} (\log|\mathcal{R} f(z)|)(1-|z|)^{t-2} dA(z)\\ &\quad=C_1(s)\bigg\{\frac{1}{2}\int_0^s(\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}))(1-r)^{t-2}dr\\ &\qquad\qquad\quad+\frac{1}{2\pi}\int_0^s\int_0^{2\pi}(\log|\widehat{F}_r(\theta)|)(1-r)^{t-2}d\theta dr\bigg\}, \end{align*} $$
where
![]() $C_1(s)$
is bounded by the monotonicity of
$C_1(s)$
is bounded by the monotonicity of
![]() $ \int _0^{2\pi }\log |\mathcal {R} f(re^{i\theta })|d\theta $
in r. By the estimate (2), for any
$ \int _0^{2\pi }\log |\mathcal {R} f(re^{i\theta })|d\theta $
in r. By the estimate (2), for any
![]() $t>1$
and
$t>1$
and
![]() $s\in [0,1]$
, we obtain
$s\in [0,1]$
, we obtain
where C is an absolute constant. Therefore, we obtain
if and only if
 $$ \begin{align*} \int_0^1 (\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}))(1-r)^{t-2}dr<\infty. \end{align*} $$
$$ \begin{align*} \int_0^1 (\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}))(1-r)^{t-2}dr<\infty. \end{align*} $$
This, together with Lemma 3.1, proves (i)
![]() $\Leftrightarrow $
(iii). Next, (iii)
$\Leftrightarrow $
(iii). Next, (iii)
![]() $\Rightarrow $
(ii). By Jensen’s formula,
$\Rightarrow $
(ii). By Jensen’s formula,
 $$ \begin{align*} N_{\mathcal{R}f}(r) =\frac{1}{2}\log\left(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}\right)+\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta-\log|X_{0}|. \end{align*} $$
$$ \begin{align*} N_{\mathcal{R}f}(r) =\frac{1}{2}\log\left(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}\right)+\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta-\log|X_{0}|. \end{align*} $$
Integrating with respect to r over
![]() $(0,1)$
and taking the expectation give us
$(0,1)$
and taking the expectation give us
 $$ \begin{align*} \mathbb{E}&\left(\int_0^1 N_{\mathcal{R}f}(r)(1-r)^{t-2}dr\right)\\ &\quad=\frac{1}{2}\int_0^1 (\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}))(1-r)^{t-2}dr\\ &\qquad+\mathbb{E}\left(\frac{1}{2\pi}\int_0^1\int_{0}^{2\pi}(\log|\widehat{F}_{r}(\theta)|) (1-r)^{t-2}d\theta dr\right) -\frac{\mathbb{E}(\log|X_{0}|)}{t-1}. \end{align*} $$
$$ \begin{align*} \mathbb{E}&\left(\int_0^1 N_{\mathcal{R}f}(r)(1-r)^{t-2}dr\right)\\ &\quad=\frac{1}{2}\int_0^1 (\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k}))(1-r)^{t-2}dr\\ &\qquad+\mathbb{E}\left(\frac{1}{2\pi}\int_0^1\int_{0}^{2\pi}(\log|\widehat{F}_{r}(\theta)|) (1-r)^{t-2}d\theta dr\right) -\frac{\mathbb{E}(\log|X_{0}|)}{t-1}. \end{align*} $$
Then (5), together with the assumption (iii), yields that
![]() $\mathbb {E}(\int _0^1 N_{\mathcal {R}f}(r)(1-r)^{t-2}dr)$
is finite. Therefore,
$\mathbb {E}(\int _0^1 N_{\mathcal {R}f}(r)(1-r)^{t-2}dr)$
is finite. Therefore,
![]() $\int _0^1 N_{\mathcal {R}f}(r)(1-r)^{t-2} dr<\infty $
a.s. By the monotonicity of
$\int _0^1 N_{\mathcal {R}f}(r)(1-r)^{t-2} dr<\infty $
a.s. By the monotonicity of
![]() $N_{\mathcal {R}f}(r)$
, we have
$N_{\mathcal {R}f}(r)$
, we have
![]() $N_{\mathcal {R}f}(r)=o\left (\frac {1}{(1-r)^{t-1}}\right )$
a.s. Further, since
$N_{\mathcal {R}f}(r)=o\left (\frac {1}{(1-r)^{t-1}}\right )$
a.s. Further, since
![]() $n_{\mathcal {R}f}(s)$
is nondecreasing, we get
$n_{\mathcal {R}f}(s)$
is nondecreasing, we get
 $$ \begin{align} (r-r^2)n_{\mathcal{R}f}(r^2)\leq\int_{r^2}^r n_{\mathcal{R}f}(s)ds=o\bigg(\frac{1}{(1-r)^{t-1}}\bigg)\quad \text{a.s.} \end{align} $$
$$ \begin{align} (r-r^2)n_{\mathcal{R}f}(r^2)\leq\int_{r^2}^r n_{\mathcal{R}f}(s)ds=o\bigg(\frac{1}{(1-r)^{t-1}}\bigg)\quad \text{a.s.} \end{align} $$
Thus,
![]() $n_{\mathcal {R}f}(r)=o\left (\frac {1}{(1-r)^t}\right )$
a.s. Then we use integration-by-parts twice to obtain
$n_{\mathcal {R}f}(r)=o\left (\frac {1}{(1-r)^t}\right )$
a.s. Then we use integration-by-parts twice to obtain
 $$ \begin{align*} \sum_{n=1}^{\infty}(1-|z_n(\omega)|)^t =&\int_0^1 (1-r)^t dn_{\mathcal{R}f}(r) \leq t\int_0^1 \frac{(1-r)^{t-1}}{r}n_{\mathcal{R}f}(r) dr\\ =&t(t-1)\int_0^1 N_{\mathcal{R}f}(r)(1-r)^{t-2}dr, \end{align*} $$
$$ \begin{align*} \sum_{n=1}^{\infty}(1-|z_n(\omega)|)^t =&\int_0^1 (1-r)^t dn_{\mathcal{R}f}(r) \leq t\int_0^1 \frac{(1-r)^{t-1}}{r}n_{\mathcal{R}f}(r) dr\\ =&t(t-1)\int_0^1 N_{\mathcal{R}f}(r)(1-r)^{t-2}dr, \end{align*} $$
which implies that
![]() $\mathbb {E}(\sum _{n=1}^{\infty }(1-|z_n(\omega )|)^t)<\infty $
and completes the proof.
$\mathbb {E}(\sum _{n=1}^{\infty }(1-|z_n(\omega )|)^t)<\infty $
and completes the proof.
4 Proof of Theorem 1.5
Let
![]() $\{X_k\}_{k=0}^{\infty }$
be a standard random sequence. By the Kolmogorov 0-1 law [Reference Cinlar3, Theorem 5.12, p. 86] and Theorem 2.3 in [Reference Duren4], one has
$\{X_k\}_{k=0}^{\infty }$
be a standard random sequence. By the Kolmogorov 0-1 law [Reference Cinlar3, Theorem 5.12, p. 86] and Theorem 2.3 in [Reference Duren4], one has
![]() $ \mathbb {P} (\mathcal {R} f\in \mathfrak {B}_1)\in \{0,1\}, $
for any
$ \mathbb {P} (\mathcal {R} f\in \mathfrak {B}_1)\in \{0,1\}, $
for any
![]() $ f\in H(\mathbb {D}).$
By [Reference Nazarov, Nishry and Sodin12], this probability is one if and only if
$ f\in H(\mathbb {D}).$
By [Reference Nazarov, Nishry and Sodin12], this probability is one if and only if
![]() $ f \in H^2$
. So Theorem 1.5 complements their result.
$ f \in H^2$
. So Theorem 1.5 complements their result.
Let X be a measurable space, with
![]() $\nu $
a probability measure on it. Assume that g is a measurable function on X such that
$\nu $
a probability measure on it. Assume that g is a measurable function on X such that
![]() $||g||_{L^{p_0}(X, d\nu )}<\infty $
for some
$||g||_{L^{p_0}(X, d\nu )}<\infty $
for some
![]() $p_0>0$
. Then by [Reference Rudin14, p. 71], we know that
$p_0>0$
. Then by [Reference Rudin14, p. 71], we know that
Hence, for any
![]() $f\in H(\mathbb {D})$
,
$f\in H(\mathbb {D})$
,
where
![]() $f_r(z)=f(rz), \ (0<r<1)$
. The double limit above is not commutative, and there exists
$f_r(z)=f(rz), \ (0<r<1)$
. The double limit above is not commutative, and there exists
![]() $f \in H(\mathbb {D})$
such that
$f \in H(\mathbb {D})$
such that
Actually, for both terms to be finite, respectively, one has
Here, the first equivalence follows from Theorem 2.3 in [Reference Duren4]. We observe that, however, if
![]() $f\in \cup _{p>0}H^p$
, then
$f\in \cup _{p>0}H^p$
, then
Indeed, by the canonical factorization theorem [Reference Duren4, p. 24], one can easily prove the following equality which leads to (7):
It is curious to us that, despite its apparently simple looking, this equality is not recorded in the literature, up to the best of our knowledge. For several related statements, one can consult pages 17, 22, 23, 26 in [Reference Duren4]. We summarize the above discussion as the following lemma.
Lemma 4.1. If
![]() $f\in \cup _{p>0}H^p$
, then
$f\in \cup _{p>0}H^p$
, then
![]() $\lim _{p\rightarrow 0^+}||f||_{H^p}=e^{L(f)}$
.
$\lim _{p\rightarrow 0^+}||f||_{H^p}=e^{L(f)}$
.
Remark. The polynomial version of Lemma 4.1 is well-known [Reference Borwein and Erdélyi1], and useful in number theory, in connection with the so-called Mahler measure
![]() $M(g)$
[Reference McKee and Smyth11, Reference Smyth15], which is defined for a polynomial g with complex coefficients by
$M(g)$
[Reference McKee and Smyth11, Reference Smyth15], which is defined for a polynomial g with complex coefficients by
![]() $\log M(g)=\frac {1}{2\pi }\int _0^{2\pi }\log |g(e^{i\theta })|d\theta $
. An application of the Jensen formula shows that
$\log M(g)=\frac {1}{2\pi }\int _0^{2\pi }\log |g(e^{i\theta })|d\theta $
. An application of the Jensen formula shows that
![]() $M(g)=|a_n| \prod _{j=1}^n \text {max}(1, |z_j|),$
where
$M(g)=|a_n| \prod _{j=1}^n \text {max}(1, |z_j|),$
where
![]() $a_n$
is the leading coefficient of g, and
$a_n$
is the leading coefficient of g, and
![]() $\{z_j\}_{j=1}^n$
the complex roots. It is an elementary fact that
$\{z_j\}_{j=1}^n$
the complex roots. It is an elementary fact that
![]() $M(g)=\lim _{p\rightarrow 0^+}||g||_p.$
$M(g)=\lim _{p\rightarrow 0^+}||g||_p.$
We are now ready to prove Theorem 1.5.
Proof of Theorem 1.5
(iii)
![]() $\Rightarrow $
(ii) and (iv)
$\Rightarrow $
(ii) and (iv)
![]() $\Rightarrow $
(ii) are trivial. For (i)
$\Rightarrow $
(ii) are trivial. For (i)
![]() $\Rightarrow $
(ii), if
$\Rightarrow $
(ii), if
![]() $f \in H^2$
, then it follows from Littlewood’s theorem (see [Reference Kahane8, p. 54], [Reference Littlewood9, Reference Littlewood10]) that
$f \in H^2$
, then it follows from Littlewood’s theorem (see [Reference Kahane8, p. 54], [Reference Littlewood9, Reference Littlewood10]) that
![]() $\mathcal {R} f \in \mathfrak {B}_1$
almost surely since
$\mathcal {R} f \in \mathfrak {B}_1$
almost surely since
![]() $\mathfrak {B}_1$
contains
$\mathfrak {B}_1$
contains
![]() $H^p$
for every
$H^p$
for every
![]() $p>0$
. Now, for (i)
$p>0$
. Now, for (i)
![]() $\Rightarrow $
(iii), without loss of generality, we assume
$\Rightarrow $
(iii), without loss of generality, we assume
![]() $|a_0|=1$
. Recall that
$|a_0|=1$
. Recall that
![]() $\widehat {F}_r(\theta )=\mathcal {R} f(re^{i\theta })/(\sum _{k=0}^{\infty } |a_k|^2 r^{2k})^{\frac {1}{2}}$
. By Jensen’s formula,
$\widehat {F}_r(\theta )=\mathcal {R} f(re^{i\theta })/(\sum _{k=0}^{\infty } |a_k|^2 r^{2k})^{\frac {1}{2}}$
. By Jensen’s formula,
 $$ \begin{align*} N_{\mathcal{R}f}(r) &=\frac{1}{2\pi}\int_{0}^{2\pi}\log|\mathcal{R}f(re^{i\theta})|d\theta-\log|\mathcal{R}f(0)|\\ &=\frac{1}{2}\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k})+\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta-\log|X_{0}|. \end{align*} $$
$$ \begin{align*} N_{\mathcal{R}f}(r) &=\frac{1}{2\pi}\int_{0}^{2\pi}\log|\mathcal{R}f(re^{i\theta})|d\theta-\log|\mathcal{R}f(0)|\\ &=\frac{1}{2}\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k})+\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta-\log|X_{0}|. \end{align*} $$
Taking the expectation yields
 $$ \begin{align*} \mathbb{\mathbb{E}}(N_{\mathcal{R}f}(r)) =\frac{1}{2}\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k})+\mathbb{E}\left(\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta\right) -\mathbb{E}(\log|X_{0}|). \end{align*} $$
$$ \begin{align*} \mathbb{\mathbb{E}}(N_{\mathcal{R}f}(r)) =\frac{1}{2}\log(\sum_{k=0}^{\infty} |a_k|^2 r^{2k})+\mathbb{E}\left(\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta\right) -\mathbb{E}(\log|X_{0}|). \end{align*} $$
Since
![]() $f\in H^{2}$
, by the estimate (2), we know that
$f\in H^{2}$
, by the estimate (2), we know that
![]() $\lim _{r\rightarrow 1^-}\mathbb {E}(N_{\mathcal {R}f}(r))$
is finite. This, together with Fubini’s theorem, yields that
$\lim _{r\rightarrow 1^-}\mathbb {E}(N_{\mathcal {R}f}(r))$
is finite. This, together with Fubini’s theorem, yields that
![]() $\int _{0}^{1}\mathbb {E}(n_{\mathcal {R}f}(t))dt$
is finite, which is, in turn, equivalent to that
$\int _{0}^{1}\mathbb {E}(n_{\mathcal {R}f}(t))dt$
is finite, which is, in turn, equivalent to that
![]() $\mathbb {E}(\sum _{n=1}^{\infty }(1-|z_{n}(\omega )|))$
is finite by applying integration-by-parts and Fubini’s theorem to
$\mathbb {E}(\sum _{n=1}^{\infty }(1-|z_{n}(\omega )|))$
is finite by applying integration-by-parts and Fubini’s theorem to
![]() $\sum _{n=1}^{\infty }(1-|z_{n}(\omega )|)=\int _0^1 (1-t)dn_{\mathcal {R}f}(t).$
$\sum _{n=1}^{\infty }(1-|z_{n}(\omega )|)=\int _0^1 (1-t)dn_{\mathcal {R}f}(t).$
Next, we show (i)
![]() $\Rightarrow $
(iv). According to Littlewood’s theorem and Lemma 4.1, if
$\Rightarrow $
(iv). According to Littlewood’s theorem and Lemma 4.1, if
![]() $f\in H^2$
, then
$f\in H^2$
, then
![]() $e^{L(\mathcal {R} f)}=\lim _{p\rightarrow 0^+}||\mathcal {R} f||_{H^p}$
a.s. Taking the expectation yields
$e^{L(\mathcal {R} f)}=\lim _{p\rightarrow 0^+}||\mathcal {R} f||_{H^p}$
a.s. Taking the expectation yields
 $$ \begin{align*} \mathbb{E} e^{L(\mathcal{R} f)}=\mathbb{E}(\lim _{p\rightarrow0^+}||\mathcal{R} f||_{H^p})\leq \mathbb{E}(||\mathcal{R} f||_{H^2})\leq(\sum_{k=0}^{\infty} |a_k|^2)^{\frac{1}{2}}<\infty, \end{align*} $$
$$ \begin{align*} \mathbb{E} e^{L(\mathcal{R} f)}=\mathbb{E}(\lim _{p\rightarrow0^+}||\mathcal{R} f||_{H^p})\leq \mathbb{E}(||\mathcal{R} f||_{H^2})\leq(\sum_{k=0}^{\infty} |a_k|^2)^{\frac{1}{2}}<\infty, \end{align*} $$
as desired, where the second inequality is due to an application of Jensen’s inequality.
It remains to show (ii)
![]() $\Rightarrow $
(i). Recall that
$\Rightarrow $
(i). Recall that
![]() $\mathcal {R} f\in \mathfrak {B}_1$
a.s. if and only if
$\mathcal {R} f\in \mathfrak {B}_1$
a.s. if and only if
![]() $L(\mathcal {R} f)<\infty $
a.s. We observe that
$L(\mathcal {R} f)<\infty $
a.s. We observe that
 $$ \begin{align*} L(\mathcal{R} f)=\lim_{r\rightarrow1^-}\frac{1}{2}\log(\sum_{k=0}^{\infty}|a_k|^2 r^{2k}) +\lim_{r\rightarrow1^-}\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta. \end{align*} $$
$$ \begin{align*} L(\mathcal{R} f)=\lim_{r\rightarrow1^-}\frac{1}{2}\log(\sum_{k=0}^{\infty}|a_k|^2 r^{2k}) +\lim_{r\rightarrow1^-}\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta. \end{align*} $$
The limit
![]() $\lim _{r\to 1^-}\frac {1}{2\pi }\int _{0}^{2\pi }\log |\widehat {F}_{r}(\theta )|d\theta $
exists since
$\lim _{r\to 1^-}\frac {1}{2\pi }\int _{0}^{2\pi }\log |\widehat {F}_{r}(\theta )|d\theta $
exists since
![]() $L(\mathcal {R} f)$
is finite almost surely and
$L(\mathcal {R} f)$
is finite almost surely and
![]() $\sum _{k=0}^{\infty } |a_k|^2 r^{2k}$
increases monotonically with r. By Fatou’s lemma and (2), we get
$\sum _{k=0}^{\infty } |a_k|^2 r^{2k}$
increases monotonically with r. By Fatou’s lemma and (2), we get
 $$ \begin{align*} \lim_{r\rightarrow1^-}\bigg|\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta\bigg|<\infty \quad\text{a.s.}, \end{align*} $$
$$ \begin{align*} \lim_{r\rightarrow1^-}\bigg|\frac{1}{2\pi}\int_{0}^{2\pi}\log|\widehat{F}_{r}(\theta)|d\theta\bigg|<\infty \quad\text{a.s.}, \end{align*} $$
which yields
![]() $f\in H^2$
.
$f\in H^2$
.
As an application, from Theorem 1.5, one can easily deduce the following, since both statements are equivalent to
![]() $f \in H^2$
. It is of interests to us to find a direct proof for this result, which, however, eludes our repeated efforts. The corresponding deterministic statement is clearly false.
$f \in H^2$
. It is of interests to us to find a direct proof for this result, which, however, eludes our repeated efforts. The corresponding deterministic statement is clearly false.
Corollary 4.2. Let
![]() $f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
and
$f(z)=\sum _{k=0}^{\infty }a_k z^k\in H(\mathbb {D})$
and
![]() $\{X_k\}_{k=0}^{\infty }$
be a standard random sequence. Then
$\{X_k\}_{k=0}^{\infty }$
be a standard random sequence. Then
where
![]() $L^+(f):=\lim _{r\rightarrow 1^-}\frac {1}{2\pi }\int _{0}^{2\pi }\log ^+|f(re^{i\theta })|d\theta .$
$L^+(f):=\lim _{r\rightarrow 1^-}\frac {1}{2\pi }\int _{0}^{2\pi }\log ^+|f(re^{i\theta })|d\theta .$
5 The Bergman spaces
In 1974, Horowitz showed that the zero sets of the Bergman space
![]() $A^p$
, for any
$A^p$
, for any
![]() $p>0$
, satisfy the following for any
$p>0$
, satisfy the following for any
![]() $\varepsilon>0$
[Reference Horowitz6]:
$\varepsilon>0$
[Reference Horowitz6]:
 $$ \begin{align} \sum_{n=1}^{\infty} (1-|z_n|)\bigg(\log\frac{1}{1-|z_n|}\bigg)^{-1-\varepsilon}<\infty. \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty} (1-|z_n|)\bigg(\log\frac{1}{1-|z_n|}\bigg)^{-1-\varepsilon}<\infty. \end{align} $$
Let
![]() $f(z)=\sum _{k=0}^{\infty }a_k z^k\in A^p$
for some
$f(z)=\sum _{k=0}^{\infty }a_k z^k\in A^p$
for some
![]() $p>0$
. By [Reference Cheng, Fang and Liu2],
$p>0$
. By [Reference Cheng, Fang and Liu2],
![]() $\mathcal {R} f\in A^q $
almost surely for some
$\mathcal {R} f\in A^q $
almost surely for some
![]() $q>0$
, hence, the zero set
$q>0$
, hence, the zero set
![]() $\{z_n(\omega )\}_{n=1}^{\infty }$
of
$\{z_n(\omega )\}_{n=1}^{\infty }$
of
![]() $\mathcal {R} f$
satisfies (8) almost surely. We have conjectured the following for
$\mathcal {R} f$
satisfies (8) almost surely. We have conjectured the following for
![]() $\mathcal {R} f$
when
$\mathcal {R} f$
when
![]() $f \in A^p$
:
$f \in A^p$
:
 $$ \begin{align} \sum_{n=1}^{\infty} (1-|z_n(\omega)|)\bigg(\log\frac{1}{1-|z_n(\omega)|}\bigg)^{-1}<\infty\quad \text{a.s.} \quad ? \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty} (1-|z_n(\omega)|)\bigg(\log\frac{1}{1-|z_n(\omega)|}\bigg)^{-1}<\infty\quad \text{a.s.} \quad ? \end{align} $$
This is negated below.
By arguing similarly as in the proof of Lemma 3.1, we obtain that the zero set
![]() $\{z_{n}\}_{n=1}^{\infty }$
of
$\{z_{n}\}_{n=1}^{\infty }$
of
![]() $f\in H(\mathbb {D})$
satisfies
$f\in H(\mathbb {D})$
satisfies
 $$ \begin{align} \sum_{n=1}^{\infty}\left(1-|z_{n}|\right)\left(\log\frac{1}{1-|z_{n}|}\right)^{-1}<\infty \end{align} $$
$$ \begin{align} \sum_{n=1}^{\infty}\left(1-|z_{n}|\right)\left(\log\frac{1}{1-|z_{n}|}\right)^{-1}<\infty \end{align} $$
if and only if
 $$ \begin{align} \int_{\mathbb{D}}(\log|f(z)|) (1-|z|)^{-1}\left(\log\frac{e}{1-|z|}\right)^{-2}dA(z)<\infty. \end{align} $$
$$ \begin{align} \int_{\mathbb{D}}(\log|f(z)|) (1-|z|)^{-1}\left(\log\frac{e}{1-|z|}\right)^{-2}dA(z)<\infty. \end{align} $$
Moreover, arguments similar to those in the proof of Theorem 1.3, yield a random version that the zero set
![]() $\{z_{n}(\omega )\}_{n=1}^{\infty }$
of
$\{z_{n}(\omega )\}_{n=1}^{\infty }$
of
![]() $\mathcal {R} f$
satisfies (10) almost surely if and only if
$\mathcal {R} f$
satisfies (10) almost surely if and only if
 $$ \begin{align} \int_0^1 \big(\log ( \sum_{k=0}^{\infty} |a_k|^2 r^{2k}) \big) (1-r)^{-1} \left(\log\frac{e}{1-r}\right)^{-2} dr<\infty. \end{align} $$
$$ \begin{align} \int_0^1 \big(\log ( \sum_{k=0}^{\infty} |a_k|^2 r^{2k}) \big) (1-r)^{-1} \left(\log\frac{e}{1-r}\right)^{-2} dr<\infty. \end{align} $$
In order to negate (9), it suffices to find
![]() $f\in A^p$
such that (12) fails. Let
$f\in A^p$
such that (12) fails. Let
 $$ \begin{align*}f_t(z)=\sum_{n=1}^{\infty} 2^{nt} z^{2^n}, \quad 0<t<1/p\end{align*} $$
$$ \begin{align*}f_t(z)=\sum_{n=1}^{\infty} 2^{nt} z^{2^n}, \quad 0<t<1/p\end{align*} $$
be a lacunary series. By [Reference Jevtić, Vukotić and Arsenović7, Theorem 8.1.1],
![]() $f_t \in A^p$
if and only if
$f_t \in A^p$
if and only if
![]() $t<1/p$
. Set
$t<1/p$
. Set
![]() $g_t(r) = \sum _{n=1}^{\infty } 2^{2nt} r^{2^{n+1}}$
. We claim that if
$g_t(r) = \sum _{n=1}^{\infty } 2^{2nt} r^{2^{n+1}}$
. We claim that if
![]() $t>0$
, then
$t>0$
, then
 $$ \begin{align} g_t(r) \asymp \left(\frac{1}{1-r}\right)^{2t}. \end{align} $$
$$ \begin{align} g_t(r) \asymp \left(\frac{1}{1-r}\right)^{2t}. \end{align} $$
Let
![]() $r_N=1-\frac {1}{2^N}$
. By monotonicity in r, it suffices to show that
$r_N=1-\frac {1}{2^N}$
. By monotonicity in r, it suffices to show that
 $$ \begin{align*} g_t(r_N)= \sum_{n=1}^{\infty} 2^{2nt} r_N^{2^{n+1}} \asymp 2^{2Nt}. \end{align*} $$
$$ \begin{align*} g_t(r_N)= \sum_{n=1}^{\infty} 2^{2nt} r_N^{2^{n+1}} \asymp 2^{2Nt}. \end{align*} $$
Note that
![]() $r_N^{2^{n+1}} $
is bounded above and below when
$r_N^{2^{n+1}} $
is bounded above and below when
![]() $1\leq n \leq N$
. Hence,
$1\leq n \leq N$
. Hence,
 $$ \begin{align*}\sum_{n=1}^{N} 2^{2nt} r_N^{2^{n+1}} \asymp \sum_{n=1}^{N} 2^{2nt} \asymp 2^{2Nt}.\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{N} 2^{2nt} r_N^{2^{n+1}} \asymp \sum_{n=1}^{N} 2^{2nt} \asymp 2^{2Nt}.\end{align*} $$
Additionally,
 $$ \begin{align*} \sum_{n=N+1}^{\infty}2^{2nt} r_N^{2^{n+1}} \lesssim \sum_{n=N+1}^{\infty} 2^{2nt} e^{-2^{n+1-N}} \lesssim 2^{2Nt}. \end{align*} $$
$$ \begin{align*} \sum_{n=N+1}^{\infty}2^{2nt} r_N^{2^{n+1}} \lesssim \sum_{n=N+1}^{\infty} 2^{2nt} e^{-2^{n+1-N}} \lesssim 2^{2Nt}. \end{align*} $$
Therefore, the assertion (13) follows, and we deduce that (12) fails for
![]() $f_t$
.
$f_t$
.
Acknowledgments
The authors would like to thank the anonymous referee for careful reading of the manuscript and for his/her insightful comments and suggestions which helped to make the paper more readable. The authors also thank Prof. Pham Trong Tien for his valuable discussion.