I. INTRODUCTION
Technological advances in camera sensor technologies made possible the introduction of commercial plenoptic cameras on the global market at reasonable prices, opening the possibility of integrating such cameras in numerous applications from different domains. Light field (LF) images provide both spatial and angular information by making use of microlens arrays and high-resolution image sensors to capture 4D LF data. The specific nature of the plenoptic image calls for specific lossless coding method designs for LF image applications, e.g., depth estimation of 4D LFs, view synthesis for LF cameras, and medical imaging to name a few.
The traditional codecs for lossless image coding, such as JPEG-LS [Reference Weinberger, Seroussi and Sapiro1] and CALIC [Reference Wu and Memon2], follow a predictive coding paradigma applied to a small causal neighborhood, and do not take advantage of the specific nature of the plenoptic image. The current state-of-the-art codec for lossless image coding, Free Lossless Image Format (FLIF) [Reference Sneyers and Wuille3], was developed based on modern coding techniques and shows significant performance improvement compared to traditional codecs especially when employed for LF-image coding.
One way of representing the LF image is to use the so-called macro-pixels (MPs), where each MP corresponds to the image data of size $N \times N$![]() collected by a microlens. The LF image is stored as an array of MPs, denoted here by lenslet image. Another way is to use an $N \times N$
collected by a microlens. The LF image is stored as an array of MPs, denoted here by lenslet image. Another way is to use an $N \times N$![]() array of LF views, also known as sub-aperture images, where each view selects one pixel from each MP. LF-image coding was the topic of different grand challenges in international conferences and symposiums where different approaches were proposed based on one of these representations for lossy and lossless coding applications.
array of LF views, also known as sub-aperture images, where each view selects one pixel from each MP. LF-image coding was the topic of different grand challenges in international conferences and symposiums where different approaches were proposed based on one of these representations for lossy and lossless coding applications.
In the view synthesis domain, several approaches were proposed for LF image synthesis based on machine learning (ML) tools. The LF images are first preprocessed by heavily cropping the $N \times N$![]() array of views and the proposed methods are applied only to the array of middle views, representing around one-quarter of the captured LF image. The corner views are used as reference views and the remaining in-between views are usually synthesized one at a time.
array of views and the proposed methods are applied only to the array of middle views, representing around one-quarter of the captured LF image. The corner views are used as reference views and the remaining in-between views are usually synthesized one at a time.
In our prior work, we have investigated the potential offered by ML tools in lossless coding applications. In [Reference Schiopu, Liu and Munteanu4], we proposed the first deep-learning-based pixel-wise prediction method for coding ultra-high resolution images. In [Reference Schiopu and Munteanu5], an improved method is proposed by employing a deep-learning-based dual prediction method. In [Reference Schiopu and Munteanu6], we proposed the first deep-learning-based MP-wise prediction method for LF-image coding. In this paper, we propose a deep-learning-based method which synthesizes the entire $N \times N$![]() array of LF image views, in one step, based on a small subset of efficiently selected reference views. Furthermore, we propose a deep-learning-based method for lossless coding of LF images using the synthesized LF image, which further advances over our findings in [Reference Schiopu and Munteanu6]. The CALIC-based reference codec employed in [Reference Schiopu, Liu and Munteanu4] for pixel-wise coding of the prediction errors was extended in [Reference Schiopu and Munteanu6] to MP-wise coding, and it is employed here for the proposed method which makes use of a novel and more complex neural network architecture.
array of LF image views, in one step, based on a small subset of efficiently selected reference views. Furthermore, we propose a deep-learning-based method for lossless coding of LF images using the synthesized LF image, which further advances over our findings in [Reference Schiopu and Munteanu6]. The CALIC-based reference codec employed in [Reference Schiopu, Liu and Munteanu4] for pixel-wise coding of the prediction errors was extended in [Reference Schiopu and Munteanu6] to MP-wise coding, and it is employed here for the proposed method which makes use of a novel and more complex neural network architecture.
In summary, the novel contributions of this paper are as follows:
(1) an efficient deep-learning-based lossless codec for LF images;
(2) a novel deep-learning-based MP synthesis method for synthesizing in one step the entire LF image captured by the image sensor;
(3) an efficient deep-learning-based MP prediction based on the prior information provided by the synthesized image;
(4) efficient view configurations for reference view selection for MP synthesis and lossless coding of LF images;
(5) a novel causal neighborhood based on the MP structure for the CALIC binary mode employed in the basic reference codec [Reference Schiopu and Munteanu6].
The remainder of this paper is organized as follows. Section II outlines the state-of-the-art methods in the view synthesis and LF-image coding domains. Section III describes the proposed method for lossless coding of LF images based on a MP synthesis technique. Section IV presents the experimental validation and performance analysis of this work. Finally, section V draws the conclusions.
II. STATE-OF-THE-ART
The traditional state-of-the-art codecs for lossless image coding were designed to follow a predictive coding paradigm whereby the value of the current pixel is predicted using a linear combination of the values in the small causal neighborhood of the current pixel. JPEG-LS [Reference Weinberger, Seroussi and Sapiro1] is one of the most popular lossless codecs which operates on a three-pixel causal neighborhood to predict the current pixel. CALIC [Reference Wu and Memon2] is one of the most efficient lossless codecs which operates on a six-pixel causal neighborhood and applies a complex context modeling scheme to predict the current pixel. In a recent work, the FLIF codec [Reference Sneyers and Wuille3] was proposed by Sneyers and Wuille for lossless image coding applications which achieves an average improvement of $14\%$![]() [7] compared to WebP [8]. FLIF is based on the Meta-Adaptive Near-zero Integer Arithmetic Coding technique which offers an improved performance when dealing with LF images.
[7] compared to WebP [8]. FLIF is based on the Meta-Adaptive Near-zero Integer Arithmetic Coding technique which offers an improved performance when dealing with LF images.
In the lossless coding domain, different approaches were proposed for encoding the data extracted from different parts of the LF processing pipeline. In [Reference Perra9], a method based on a predictive coding approach is proposed for raw plenoptic image compression. In [Reference Helin, Astola, Rao and Tabus10], the method encodes the LF image as a set of views using a sparse modeling predictor guided by a disparity-based image segmentation. In [Reference Schiopu, Gabbouj, Gotchev and Hannuksela11], the authors proposed a context modeling method for compressing each view based on one reference view. In [Reference Santos, Assuncao, da Silva Cruz, Tavora, Fonseca-Pinto and Faria12], the authors study the impact of the reversible color transformations and of alternative data arrangements applied to different codecs.
The data rate of LFs is a challenging aspect for camera devices, especially for capturing LF videos. In the lossy compression domain, LF coding is an important topic which triggered a lot of interest in the compression community and in standardization bodies such as JPEG [30] and MPEG [31]. Several solutions were proposed by modifying the HEVC standard [Reference Sullivan, Ohm, Han and Wiegand13] to take into account the specific nature of the plenoptic image [Reference Liu, Wang, Li, Xiong, Wu and Zeng14–Reference Verhack, Sikora, Lange, Jongebloed, Van Wallendael and Lambert18]. In [Reference Tabus, Helin and Astola19], the authors propose a method for scalable lossy-to-lossless coding based on depth information. The method encodes a set of reference views by employing the standard codec, e.g., JPEG 2000 [Reference Skodras, Christopoulos and Ebrahimi29], and a set of dependent views based on sparse prediction computed based on the reference set and the geometrical information from depth map images. Moreover, the LF compression topic was well studied in several competitions or special sessions at international conferences where many approaches were proposed. The current state-of-the-art method was proposed in [Reference Zhong, Schiopu, Cornelis, Lu, Yuan and Munteanu20], where dedicated intra-coding methods based on dictionary learning, directional prediction, and optimized linear prediction were proposed to ensure a high coding efficiency.
In the view synthesis domain, several solutions are proposed based on ML tools. In [Reference Kalantari, Wang and Ramamoorthi21], a learning-based approach is proposed to synthesize each LF image view from a sparse set of reference views. The method employs a disparity estimation network, a warping algorithm, and a color prediction network to synthesize a single view in the LF image. In [Reference Wang, Liu, Wang, Hou, Sun and Tan22], an end-to-end deep-learning-based view synthesis method is proposed based on a system of 2D convolutions applied to stacked epipolar plane images and of 3D convolutions for detail-restoration. In [Reference Jiang, Le Pendu and Guillemot23], the authors propose a lossy compression scheme based on depth image-based view synthesis technique, where four reference views are compressed by HEVC and used to reconstruct a cropped version of the LF image. For all these methods, the raw LF images captured by a Lytro Illum camera were preprocessed by Lytro Power Tools Beta software (not available anymore) to obtain LF images represented as an array of $14 \times 14$![]() views, with a $541 \times 376$
views, with a $541 \times 376$![]() view resolution. The LF images are then heavily cropped and only the middle $7\times 7$
view resolution. The LF images are then heavily cropped and only the middle $7\times 7$![]() or $8\times 8$
or $8\times 8$![]() array of LF views are representing the captured LF image. One may note that the cropped LF image stores only around one-quarter of the captured LF image, i.e., $({7}/{14})^2$
array of LF views are representing the captured LF image. One may note that the cropped LF image stores only around one-quarter of the captured LF image, i.e., $({7}/{14})^2$![]() or $({8}/{14})^2.$
or $({8}/{14})^2.$![]()
In this paper, the raw LF images captured by a Lytro Illum camera are preprocessed by Dansereau's MATLAB Toolbox [Reference Dansereau, Pizarro and Williams24] to obtain LF images represented as an array of $15 \times 15$![]() views, with a $625 \times 434$
views, with a $625 \times 434$![]() view resolution. This paper tackles the more complex problems of MP synthesis and lossless coding of LF images applied to the entire LF image without cropping it. The goal of the proposed MP synthesis method is to provide valuable prior information for the proposed MP prediction method used by the MP-wise lossless image codec.
view resolution. This paper tackles the more complex problems of MP synthesis and lossless coding of LF images applied to the entire LF image without cropping it. The goal of the proposed MP synthesis method is to provide valuable prior information for the proposed MP prediction method used by the MP-wise lossless image codec.
III. PROPOSED METHOD
The raw LF images are preprocessed by the MATLAB Toolbox [Reference Dansereau, Pizarro and Williams24] to obtain a 5-dimensional data structure denoted by $LF(x,\,y,\,k,\,\ell, \,c),$![]() where $(x,\,y)$
where $(x,\,y)$![]() selects a specific light ray propagation angle stored by a MP in an $N \times N$
selects a specific light ray propagation angle stored by a MP in an $N \times N$![]() array, $(k,\,\ell )$
array, $(k,\,\ell )$![]() corresponds to the location of a specific MP in the camera macrolens array of size $N_{mr} \times N_{mc},$
corresponds to the location of a specific MP in the camera macrolens array of size $N_{mr} \times N_{mc},$![]() and c is the primary color, $c=1,\,2,\,\ldots, \,N_{ch}$
and c is the primary color, $c=1,\,2,\,\ldots, \,N_{ch}$![]() . For the LF images acquired by Lytro Illum cameras, the captured LF matrix is of size $N \times N \times N_{mr} \times N_{mc} \times N_{ch}=15 \times 15 \times 434 \times 625 \times 3$
. For the LF images acquired by Lytro Illum cameras, the captured LF matrix is of size $N \times N \times N_{mr} \times N_{mc} \times N_{ch}=15 \times 15 \times 434 \times 625 \times 3$![]() . Let us denote $M_{k,\ell, c}$
. Let us denote $M_{k,\ell, c}$![]() as the current MP found at the position $(k,\,\ell )$
as the current MP found at the position $(k,\,\ell )$![]() in the microlens matrix, $M_{k,\ell, c}= LF(x,\,y,\,k,\,\ell, \,c),$
in the microlens matrix, $M_{k,\ell, c}= LF(x,\,y,\,k,\,\ell, \,c),$![]() where $x = 1,\,2,\,\ldots, \, N$
where $x = 1,\,2,\,\ldots, \, N$![]() , $y = 1,\,2,\,\ldots, \,N,$
, $y = 1,\,2,\,\ldots, \,N,$![]() and $c = 1,\,2,\,\ldots, \,N_{ch}.$
and $c = 1,\,2,\,\ldots, \,N_{ch}.$![]() Since the proposed method is applied in turn for each color channel c, we simplify the notations by dropping the color index and refer to $M_{k,\ell, c}$
Since the proposed method is applied in turn for each color channel c, we simplify the notations by dropping the color index and refer to $M_{k,\ell, c}$![]() as $M_{k,\ell }$
as $M_{k,\ell }$![]() . The LF image is stored using the lenslet image structure [Reference Schiopu and Munteanu6], denoted by LL, which represents the LF image as an array of MPs. The LL matrix is set as follows:
. The LF image is stored using the lenslet image structure [Reference Schiopu and Munteanu6], denoted by LL, which represents the LF image as an array of MPs. The LL matrix is set as follows:

where LL is of size $(N \cdot N_{mr}) \times (N \cdot N_{mc}) \times N_{ch}.$![]()
The proposed method is depicted in Fig. 1 and contains three main stages:
(B1) lossless coding of reference views;
(B2) MP synthesis based on reference views;
(B3) lossless coding of remaining views based on synthesized image.
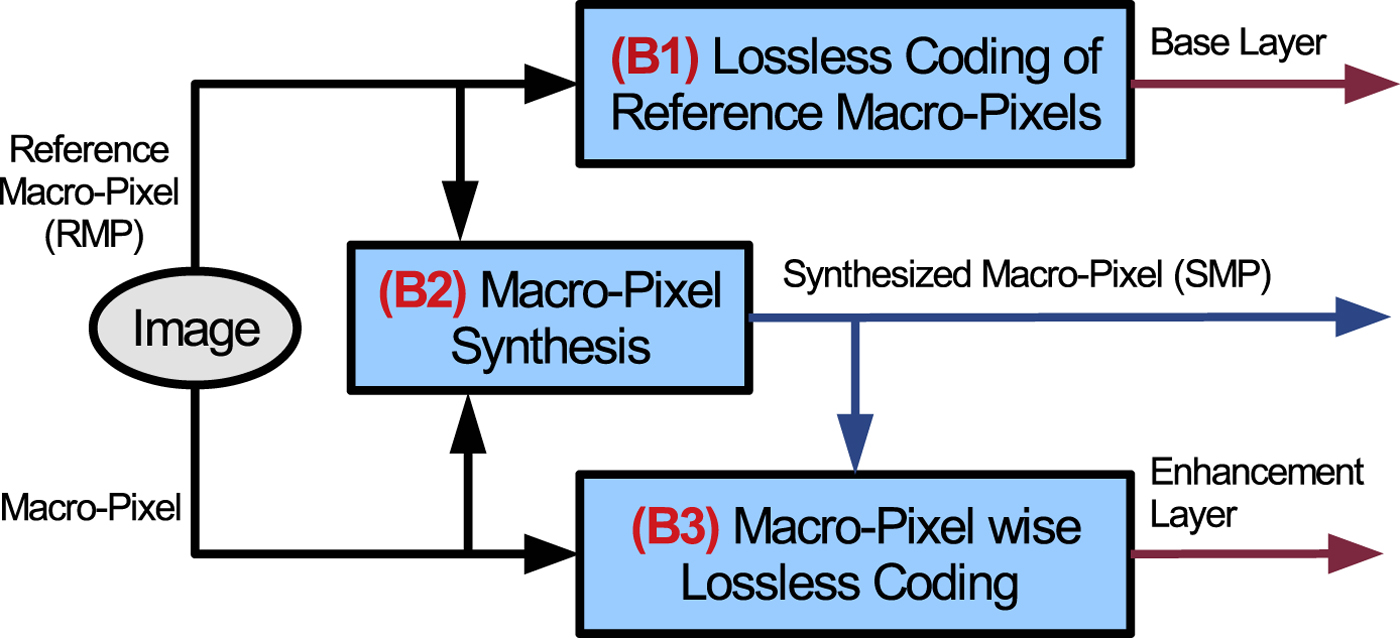
Fig. 1. The proposed method.
Section A presents the selection of reference views. Section B describes the method employed for lossless coding of reference views. Section C describes the proposed MP synthesis method. Section D describes the proposed method for lossless coding of remaining views. Section E describes the proposed neural network design. Section F presents an overview of the proposed method.
A) Reference view selection
In this paper, the problems of MP synthesis and lossless coding of LF images are studied by varying from small to large the number of reference views selected for view synthesis. Four view configurations are employed for selecting an increasing squared number of reference views. Since the MP structure has a squared size, the configurations are carefully designed to have a symmetric shape.
Figure 2(B1) depicts the proposed view configurations of size $f \times f,\,\; f=2,\,3,\,4,\,5,$![]() each used to select a specific set of $f^2$
each used to select a specific set of $f^2$![]() reference views from the array of $15\times 15$
reference views from the array of $15\times 15$![]() views, i.e., by selecting $f^2$
views, i.e., by selecting $f^2$![]() pixels from each MP. The selected views are stored using equation (1) as a reference LF image based on the corresponding RMPs of size $f \times f.$
pixels from each MP. The selected views are stored using equation (1) as a reference LF image based on the corresponding RMPs of size $f \times f.$![]() Let us denote $R^f_{k,\ell }$
Let us denote $R^f_{k,\ell }$![]() as the RMP extracted from $M_{k,\ell }$
as the RMP extracted from $M_{k,\ell }$![]() based on the configuration $f\times f.$
based on the configuration $f\times f.$![]() The top-left part of Fig. 2(B1) depicts the case of the $2 \times 2$
The top-left part of Fig. 2(B1) depicts the case of the $2 \times 2$![]() configuration where each RMP stores the array of $2 \times 2$
configuration where each RMP stores the array of $2 \times 2$![]() pixels corresponding to the set of views $S_2=\{(4,\,\;4),\, (4,\,\;12),\, (12,\,\;4),\, (12,\,\;12)\}.$
pixels corresponding to the set of views $S_2=\{(4,\,\;4),\, (4,\,\;12),\, (12,\,\;4),\, (12,\,\;12)\}.$![]() Hence, $R^2_{k,\ell }$
Hence, $R^2_{k,\ell }$![]() is set using $S_2$
is set using $S_2$![]() as follows:
as follows:
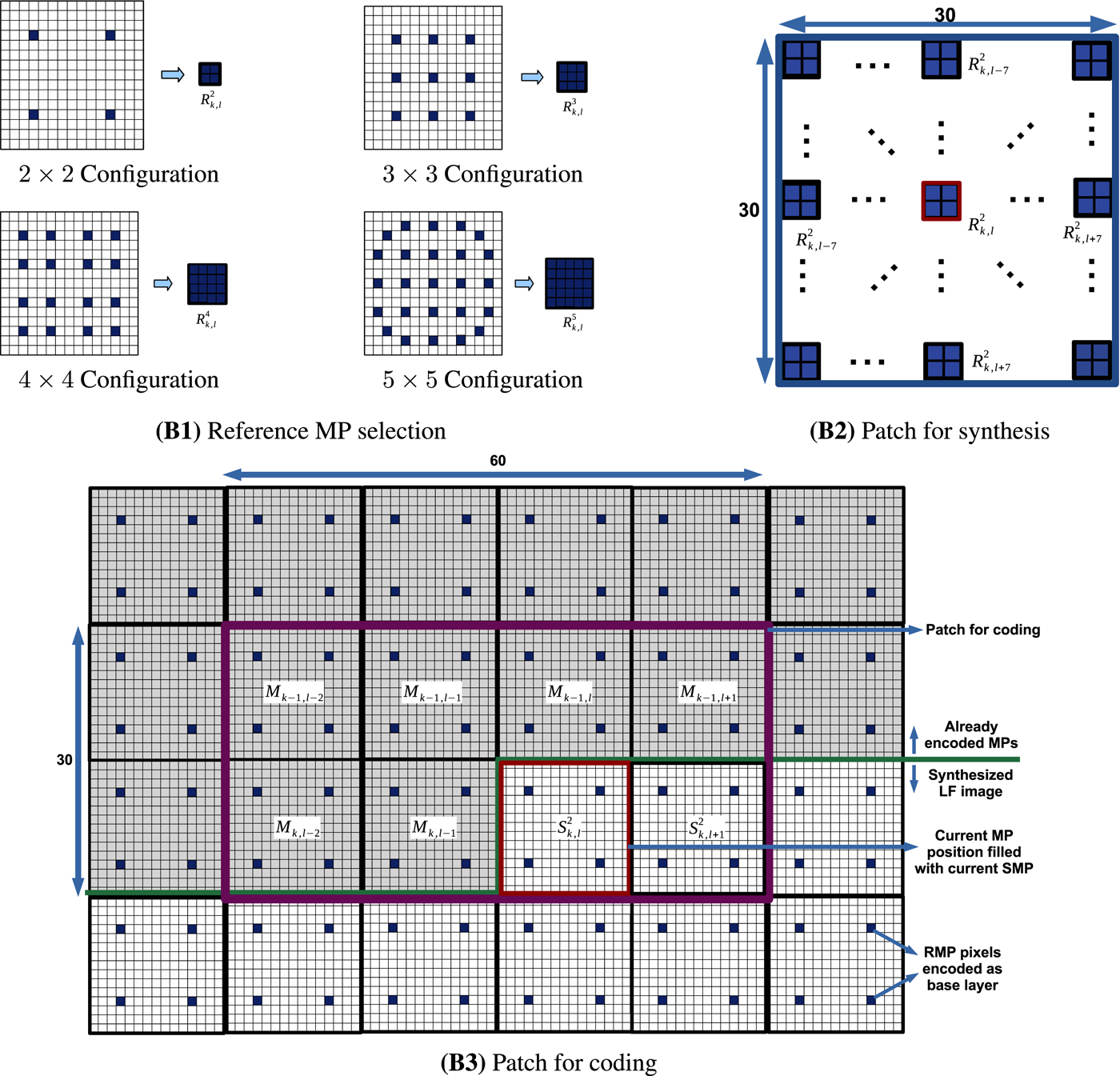
Fig. 2. (B1) The four view configurations used to form the reference macro-pixel (RMP): the $2\times 2$![]() configuration selects RMPs of size $2\times 2$
configuration selects RMPs of size $2\times 2$![]() , the $3\times 3$
, the $3\times 3$![]() configuration selects RMPs of size $3\times 3$
configuration selects RMPs of size $3\times 3$![]() , the $4\times 4$
, the $4\times 4$![]() configuration selects RMPs of size $4\times 4$
configuration selects RMPs of size $4\times 4$![]() , the $5\times 5$
, the $5\times 5$![]() configuration selects RMPs of size $5\times 5$
configuration selects RMPs of size $5\times 5$![]() . (B2) The structure of the patch for synthesis of size $30\times 30$
. (B2) The structure of the patch for synthesis of size $30\times 30$![]() . In the case of $2\times 2$
. In the case of $2\times 2$![]() configuration, the patch selects an array of $15\times 15$
configuration, the patch selects an array of $15\times 15$![]() RMPs around the current MP position. (B3) The structure of the patch for coding of size $30\times 60$
RMPs around the current MP position. (B3) The structure of the patch for coding of size $30\times 60$![]() for the case of $2\times 2$
for the case of $2\times 2$![]() configuration. The patch collects six MPs in the causal neighborhood and two synthesized macro-pixels (SMPs) in the non-causal neighborhood of the current MP position marked with a red square. Blue denotes the position of the reference view pixels in the MP. White denotes the position of the synthesized view pixels in the MP. Gray denotes the already encoded pixel positions.
configuration. The patch collects six MPs in the causal neighborhood and two synthesized macro-pixels (SMPs) in the non-causal neighborhood of the current MP position marked with a red square. Blue denotes the position of the reference view pixels in the MP. White denotes the position of the synthesized view pixels in the MP. Gray denotes the already encoded pixel positions.
The $2\times 2$![]() configuration was proposed to study the MP synthesis performance when the synthesized LF image is generated based on a minimum number of reference views, and the coding performance when the synthesized LF image is affected by high distortion. While the $5\times 5$
configuration was proposed to study the MP synthesis performance when the synthesized LF image is generated based on a minimum number of reference views, and the coding performance when the synthesized LF image is affected by high distortion. While the $5\times 5$![]() configuration was proposed to study the MP synthesis performance when the synthesized LF image is generated based on a large number of reference views, and the coding performance when the synthesized LF image is affected by low distortion. The four proposed view configurations were found optimal after complex experiments.
configuration was proposed to study the MP synthesis performance when the synthesized LF image is generated based on a large number of reference views, and the coding performance when the synthesized LF image is affected by low distortion. The four proposed view configurations were found optimal after complex experiments.
B) Lossless coding of reference views
In this paper, the selected reference views are encoded lossless in the first stage as a base layer. The corresponding reference LF image is encoded by employing the pixel-wise REP-CNN method [Reference Schiopu and Munteanu5] using network models trained for each color matrix.
The tests showed that the set of reference views is too small for an MP-wise entropy codec, such as the reference codec proposed in [Reference Schiopu and Munteanu6], to take advantage of the MP structure specific to LF images and to offer a consistent improvement over the REP-CNN method [Reference Schiopu and Munteanu5]. Similar results are obtained by employing either REP-CNN [Reference Schiopu and Munteanu5] or MP-CNN [Reference Schiopu and Munteanu6]. Moreover, the base layer has a small weight in the total bitrate.
C) Macro-pixel synthesis
In the second stage, the proposed deep-learning-based MP synthesis method is employed to synthesize the entire LF image based on the selected reference views. The novelty of this paper is that the entire set of views captured by the LF image is synthesized in one step.
In this paper, the patch for synthesis is formed by collecting an array of $30 \times 30$![]() pixels from the reference LF image. The patch collects the RMPs found in the close neighborhood of the current MP position as an array of $n_R\times n_R = {30}/{f}\times {30}/{f}$
pixels from the reference LF image. The patch collects the RMPs found in the close neighborhood of the current MP position as an array of $n_R\times n_R = {30}/{f}\times {30}/{f}$![]() RMPs, which collects a set of RMPs found at a maximum of $p^f=\lfloor {n_R}/{f} \rfloor$
RMPs, which collects a set of RMPs found at a maximum of $p^f=\lfloor {n_R}/{f} \rfloor$![]() RMP positions from the current RMP, $R^f_{k,\ell },$
RMP positions from the current RMP, $R^f_{k,\ell },$![]() as follows:
as follows:
Figure 2(B2) depicts the case of the $2 \times 2$![]() configuration where the patch for synthesis collects the neighboring RMPs found at a maximum of $p^2=7$
configuration where the patch for synthesis collects the neighboring RMPs found at a maximum of $p^2=7$![]() positions, and generates an array of $n_R\times n_R =15 \times 15$
positions, and generates an array of $n_R\times n_R =15 \times 15$![]() RMPs.
RMPs.
If $n_R=2n,$![]() then the patch for synthesis collects the RMPs found between the n top-left RMP positions and the n − 1 bottom-right RMP positions. For the $4\times 4$
then the patch for synthesis collects the RMPs found between the n top-left RMP positions and the n − 1 bottom-right RMP positions. For the $4\times 4$![]() configuration, the patch for synthesis collects only the central part of the RMPs found at the edge of the $8 \times 8$
configuration, the patch for synthesis collects only the central part of the RMPs found at the edge of the $8 \times 8$![]() array of RMPs.
array of RMPs.
The proposed neural network described in Section E is employed to compute the synthesized LF image. Note that the synthesized LF image is stored similarly in a lenslet structure using equation (1) and based on the corresponding SMPs of size $15 \times 15,$![]() denoted by $S^f_{k,\ell },$
denoted by $S^f_{k,\ell },$![]() where $(k,\, \ell )$
where $(k,\, \ell )$![]() is the MP's position in the matrix of microlenses, and $f\times f$
is the MP's position in the matrix of microlenses, and $f\times f$![]() is the selected reference view configuration. Therefore, for each $M_{k,\ell }$
is the selected reference view configuration. Therefore, for each $M_{k,\ell }$![]() and a reference view configuration $f\times f$
and a reference view configuration $f\times f$![]() , the method generates a corresponding $(R^f_{k,\ell },\, \; S^f_{k,\ell })$
, the method generates a corresponding $(R^f_{k,\ell },\, \; S^f_{k,\ell })$![]() pair.
pair.
D) Lossless coding of remaining views
In the third stage, the proposed deep-learning-based method for lossless coding based on the synthesized LF image is employed to encode the fine-details of the LF image corresponding to the synthesized view positions.
The proposed deep-learning-based MP prediction method takes advantage of the prior information found in the non-causal neighborhood of the current MP position in the synthesize LF image and provides an improved MP prediction compared to our previous work from [Reference Schiopu and Munteanu6]. The MP-CNN model [Reference Schiopu and Munteanu6] cannot be employed for MP synthesis due to the specific design of forming the patch based on six MP from the causal neighborhood stored as a MP volume.
In this paper, the patch for coding depicted in Fig. 2(B3) is formed by collecting an array of $30\times 60$![]() pixels from eight MPs selected as follows:
pixels from eight MPs selected as follows:
(i) the six MPs found in the causal neighborhood of the current MP: on the n (Northern), w (Western), $nw,\, ne,\, ww,$
 and nww MP positions in the LF image, i.e., $M_{k-1,\ell },\, M_{k,\ell -1},\, M_{k-1,\ell -1},\, M_{k-1,\ell +1},\, M_{k,\ell -2},$
and nww MP positions in the LF image, i.e., $M_{k-1,\ell },\, M_{k,\ell -1},\, M_{k-1,\ell -1},\, M_{k-1,\ell +1},\, M_{k,\ell -2},$ and $M_{k-1,\ell -2};$
and $M_{k-1,\ell -2};$
(ii) the two SMPs found in the non-causal neighborhood of the current MP: on the current MP position and e (Eastern) MP position in the synthesized LF image, i.e., $S^f_{k,\ell }$
 and $S^f_{k,\ell +1}.$
and $S^f_{k,\ell +1}.$
The MPs found outside the image edge are filled with zeros. The proposed neural network architecture described in Section E is employed to compute the MP prediction used for lossless coding.
In our prior work [Reference Schiopu and Munteanu6], we proposed a basic reference codec built based on the CALIC [Reference Wu and Memon2] architecture and designed for lossless coding of LF images. The reference codec uses a MP-wise coding strategy and it is employed also here for encoding based on the propose MP prediction the remaining views as the enhancement layer.
In this paper, the reference codec from [Reference Schiopu and Munteanu6] was further adapted to take advantage of the specific LF structure by employing a novel causal neighborhood for generating the modeling context in the CALIC binary mode.
In the CALIC architecture [Reference Wu and Memon2], before employing the predictive coding scheme via context modeling of prediction errors, the authors proposed to check if the current pixel values can be encoded based on the neighboring pixel values using a simple binary mode routine rather than based on prediction errors. The CALIC binary mode [Reference Wu and Memon2] consists in first collecting six pixels in the following causal neighborhood $M_{k,\ell }(x-1,\, y )$![]() , $M_{k,\ell }(x, \, y-1)$
, $M_{k,\ell }(x, \, y-1)$![]() , $M_{k,\ell }(x-1,\, y-1)$
, $M_{k,\ell }(x-1,\, y-1)$![]() , $M_{k,\ell }(x-1,\, y+1)$
, $M_{k,\ell }(x-1,\, y+1)$![]() , $M_{k,\ell }(x-2,\, y ),$
, $M_{k,\ell }(x-2,\, y ),$![]() and $M_{k,\ell }(x, \, y-2)$
and $M_{k,\ell }(x, \, y-2)$![]() of the current position $M_{k,\ell }(x,\,y)$
of the current position $M_{k,\ell }(x,\,y)$![]() , depicted by purple squares in Fig. 3, and then checking if it has no more than two different values, denoted by $I_1$
, depicted by purple squares in Fig. 3, and then checking if it has no more than two different values, denoted by $I_1$![]() and $I_2$
and $I_2$![]() . If true, then the binary mode is triggered, otherwise the predictive coding scheme is employed. In the binary mode, the current value, denoted I, is encoded by a symbol s set as follows: $s=0,$
. If true, then the binary mode is triggered, otherwise the predictive coding scheme is employed. In the binary mode, the current value, denoted I, is encoded by a symbol s set as follows: $s=0,$![]() if $I=I_1$
if $I=I_1$![]() ; $s=1,$
; $s=1,$![]() if $I=I_2;$
if $I=I_2;$![]() and $s=2,$
and $s=2,$![]() otherwise. Symbol s is encoded using a binary pattern generated based on the positions of $I_1$
otherwise. Symbol s is encoded using a binary pattern generated based on the positions of $I_1$![]() and $I_2$
and $I_2$![]() in the causal neighborhood, resulting in 32 modeling contexts [Reference Wu and Memon2].
in the causal neighborhood, resulting in 32 modeling contexts [Reference Wu and Memon2].
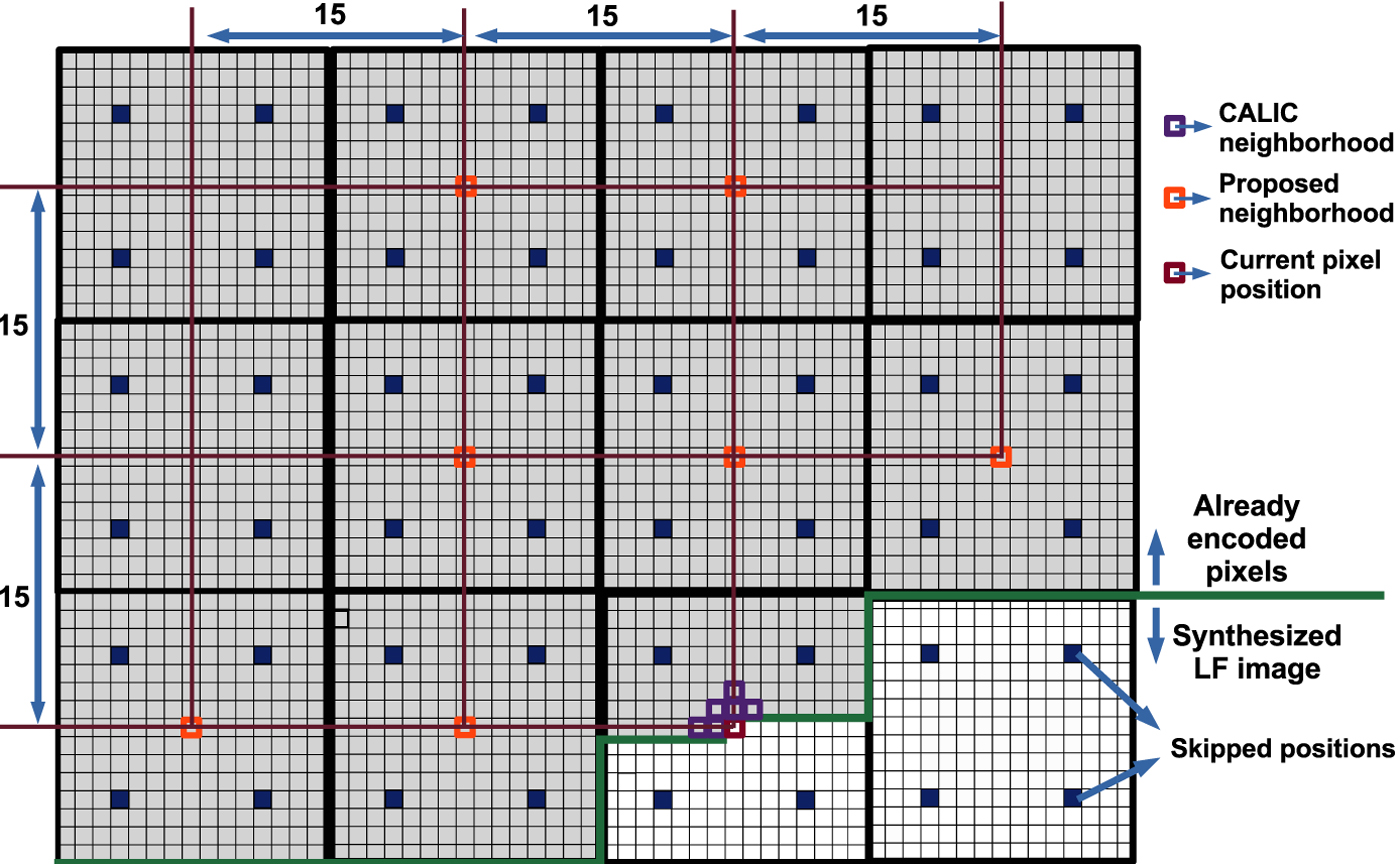
Fig. 3. The proposed neighborhood for generating the binary mode context in the basic reference codec [Reference Schiopu and Munteanu6]. Blue denotes the position of the reference view pixels in the MP. White denotes the position of the synthesized view pixels in the MP. Gray denotes the already encoded pixel positions. The red square denotes the current pixel position. The purple squares denote the CALIC binary mode context. The orange squares denote the proposed binary mode context.
In this paper, we propose the use of the following causal neighborhood in the binary mode routine: $M_{k-1, \ell }(x,y)$![]() , $M_{k, \ell -1}(x, y)$
, $M_{k, \ell -1}(x, y)$![]() , $M_{k-1, \ell -1}(x,y)$
, $M_{k-1, \ell -1}(x,y)$![]() , $M_{k-1, \ell +1}(x, y)$
, $M_{k-1, \ell +1}(x, y)$![]() , $M_{k-2, \ell }(x, y)$
, $M_{k-2, \ell }(x, y)$![]() , $M_{k, \ell -2}(x, y),$
, $M_{k, \ell -2}(x, y),$![]() and $M_{k-2, \ell -1}(x,y),$
and $M_{k-2, \ell -1}(x,y),$![]() depicted by orange squares in Fig. 3. One may note that the proposed neighborhood selects the pixels found on the same current position, $(x,\, y),$
depicted by orange squares in Fig. 3. One may note that the proposed neighborhood selects the pixels found on the same current position, $(x,\, y),$![]() in the neighboring MPs, rather than in the local neighborhood of the current MP, $M_{k,\ell }.$
in the neighboring MPs, rather than in the local neighborhood of the current MP, $M_{k,\ell }.$![]() Since we propose a seven pixel neighborhood, 64 modeling contexts are obtained. One can note that by increasing the number of pixels in the causal neighborhood from 6 to 7, the number of cases when the binary mode can be triggered is decreased since the constraint of finding no more than two different values becomes harder to satisfy and the proposed method will relay more on the proposed prediction.
Since we propose a seven pixel neighborhood, 64 modeling contexts are obtained. One can note that by increasing the number of pixels in the causal neighborhood from 6 to 7, the number of cases when the binary mode can be triggered is decreased since the constraint of finding no more than two different values becomes harder to satisfy and the proposed method will relay more on the proposed prediction.
The proposed change is applied only when all the pixels in the neighborhood are available. Our tests have showed that the proposed neighborhood has an opposite effect when employing it in the predictive coding scheme. In this case the coding contexts are not divers enough and the codding error is decoupled from the local neighborhood.
The reference codec was adapted to skip the coding of the pixels corresponding to the RMPs already encoded in base layer. For each configuration depicted in Fig. 2(B1) a binary mask is used to signal the skipped positions in the current MP, marked with blue squares in Fig. 3.
One may note that a deep-learning-based algorithm is employed at each stage of the proposed lossless coding method. Figure 1 shows that the total bitrate of the compressed LF image is obtained by concatenating the base layer, corresponding to the encoded reference views, and the enhancement layer, corresponding to the fine-details encoded for the synthesized view positions for lossless reconstruction.
E) Proposed network design
In this paper, we propose a novel neural network design which follows a multi-resolution feature extraction paradigm. The proposed architecture is depicted in Fig. 4(a) and it is inspired from the U-net architecture [Reference Ronneberger, Fischer and Brox25] (designed for biomedical image segmentation) and from the Residual Learning paradigma [Reference He, Zhang, Ren and Sun26] (designed for training time reduction).
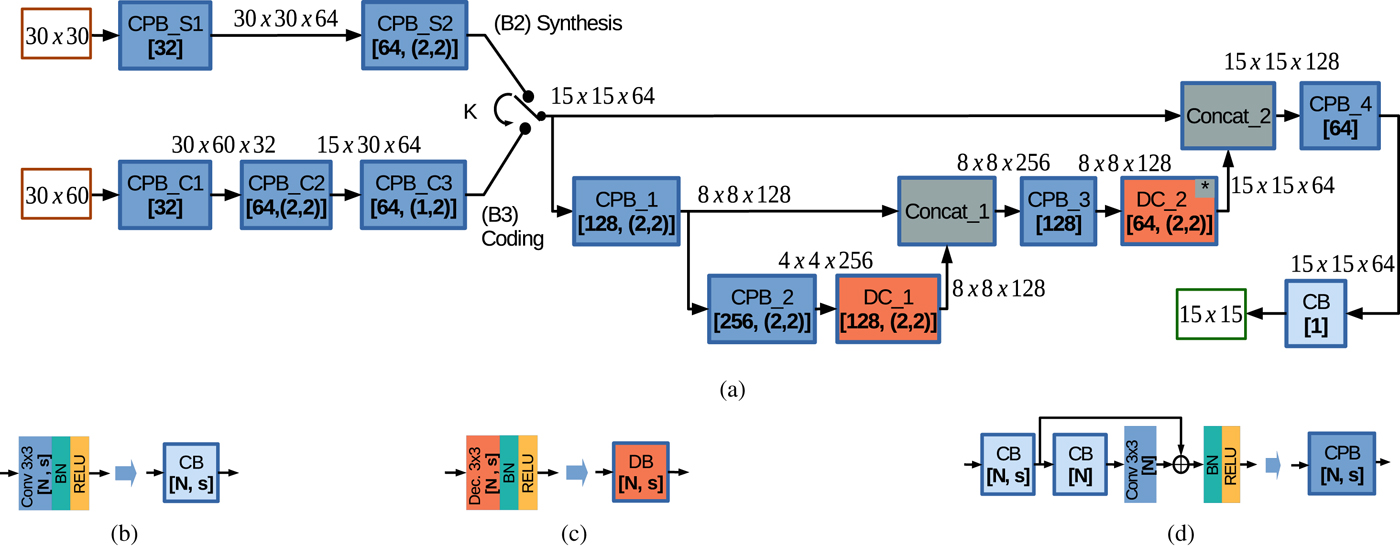
Fig. 4. (a) The proposed network design. When switch K is set to the (B2) Synthesis branch, the MP Syntheses based on Convolutional Neural Network (MPS-CNN) model is obtained. When switch K is set to the (B3) Coding branch, the Prediction using SMPs based on Convolutional Neural Network (PSMP-CNN) model is obtained. (b) The layer structure of the Convolution Block (CB). (c) The layer structure of the Deconvolution Block (DB). (d) The layer structure of the Convolution-based Processing Block (CPB) built based on the Residual Learning paradigma.
The network is built based on the following types of blocks of layers:
(a) The Convolution Block (CB) is depicted in Fig. 4(b) and contains the following sequence of layers: one convolution layer with a $3\times 3$
 window, N filters, and stride $s=(s_1,\,s_2);$
window, N filters, and stride $s=(s_1,\,s_2);$ followed by a Batch Normalization (BN) layer and a RELU activation layer.
followed by a Batch Normalization (BN) layer and a RELU activation layer.(b) The Deconvolution Block (DB) is depicted in Fig. 4(c) and contains the following sequence of layers: one deconvolution layer with a $3\times 3$
 window, N filters, and stride $s=(s_1,\,s_2);$
window, N filters, and stride $s=(s_1,\,s_2);$ followed by a BN layer and a RELU activation layer. Note that in proposed architecture, in the second DC block denoted by DC_2, an extra cropping layer is inserted after the deconvolution layer to remove the first line and column of the input patch and to generate an output patch having the MP size of $15 \times 15.$
followed by a BN layer and a RELU activation layer. Note that in proposed architecture, in the second DC block denoted by DC_2, an extra cropping layer is inserted after the deconvolution layer to remove the first line and column of the input patch and to generate an output patch having the MP size of $15 \times 15.$
(c) The Convolution-based Processing Block (CPB) is depicted in Fig. 4(d) and contains the equivalent of three CB blocks, where the first CB is used to decrease the resolution by setting the stride s and the other two CB blocks are used to design a modified version of the Residual Learning building block [Reference He, Zhang, Ren and Sun26].
One may note that, in this paper, we adopt the strategy of inserting a BN layer between a convolution layer and an activation layer. In the CPB block, the residual is added before applying the BN and RELU activation layers. For all convolution layers the input patch is padded in such a way that the output patch has the same size as the input.
The proposed network is employed for both MP synthesis and MP prediction. Since the patches for synthesis and coding have a different size, they are first processed by two separate branches:
(i) when switch K is set to the (B2) Synthesis branch, the MP Syntheses based on Convolutional Neural Network (MPS-CNN) is obtained;
(ii) when switch K is set to the (B3) Coding branch, the Prediction using Synthesized MPs based on Convolutional Neural Network (PSMP-CNN) is obtained.
The synthesis branch is depicted in the top-left corner of Fig. 4(a) and is processing the $30\times 30$![]() synthesis patch based on two CPB blocks: CPB_S1 with 32 filters, and CPB_S2 with 64 filters and stride $s = (2,\,2).$
synthesis patch based on two CPB blocks: CPB_S1 with 32 filters, and CPB_S2 with 64 filters and stride $s = (2,\,2).$![]() The coding branch is depicted in the middle-left part of Fig. 4(a) and is processing the $30\times 60$
The coding branch is depicted in the middle-left part of Fig. 4(a) and is processing the $30\times 60$![]() coding patch based on three CPB blocks: CPB_C1 with 32 filters, CPB_C2 with 64 filters and stride $s = (2,\,2),$
coding patch based on three CPB blocks: CPB_C1 with 32 filters, CPB_C2 with 64 filters and stride $s = (2,\,2),$![]() CPB_C3 with 64 filters and stride $s = (1,\,2)$
CPB_C3 with 64 filters and stride $s = (1,\,2)$![]() . Both branches are processing the patch from initial resolution down to $15\times 15$
. Both branches are processing the patch from initial resolution down to $15\times 15$![]() resolution. The remaining structure is using the U-net multi-resolution paradigma for further processing the patches at three resolutions: $15\times 15$
resolution. The remaining structure is using the U-net multi-resolution paradigma for further processing the patches at three resolutions: $15\times 15$![]() , $8\times 8$
, $8\times 8$![]() , and $4\times 4$
, and $4\times 4$![]() . In the proposed design, the last CB block contains only one filter so that it can output the MP prediction of the current MP.
. In the proposed design, the last CB block contains only one filter so that it can output the MP prediction of the current MP.
One may note that the number of filters of CPB blocks is increasing up to 256 for the $4\times 4$![]() resolution. The number of filters in the DB blocks is set as half the number of input channels. The concatenation layers are concatenating an equal number of activation maps after a CPB block is processing the current and lower resolutions. The total number of parameters of MPS-CNN and PSMP-CNN models is around 3 million. The stochastic gradient descend optimizer is used with the Nesterov momentum activated, and the momentum parameter set to $0.9.$
resolution. The number of filters in the DB blocks is set as half the number of input channels. The concatenation layers are concatenating an equal number of activation maps after a CPB block is processing the current and lower resolutions. The total number of parameters of MPS-CNN and PSMP-CNN models is around 3 million. The stochastic gradient descend optimizer is used with the Nesterov momentum activated, and the momentum parameter set to $0.9.$![]()
In this paper, the training procedure employs the mean square error (MSE) loss function. Let $\Theta _{MPS-CNN}$![]() be the set of all learned parameters of the MPS-CNN model, $X_i$
be the set of all learned parameters of the MPS-CNN model, $X_i$![]() the $i^{th}$
the $i^{th}$![]() patch for synthesis in the training set, and $Y_i$
patch for synthesis in the training set, and $Y_i$![]() the currently predicted MP. Let $F(\cdot )$
the currently predicted MP. Let $F(\cdot )$![]() be the function which processes $X_i$
be the function which processes $X_i$![]() using $\Theta _{MPS-CNN}$
using $\Theta _{MPS-CNN}$![]() to compute the MP prediction as $\hat {Y_i} = F(\Theta _{MPS-CNN},\, X_i)$
to compute the MP prediction as $\hat {Y_i} = F(\Theta _{MPS-CNN},\, X_i)$![]() . The loss function can be formulated as follows:
. The loss function can be formulated as follows:
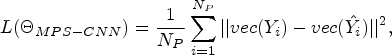
where $N_P$![]() is the size of the training set. Similarly, equation (4) can be formulated for the PSMP-CNN model.
is the size of the training set. Similarly, equation (4) can be formulated for the PSMP-CNN model.
F) Overview
The workflow of the proposed method is presented in Fig. 5. The proposed method extends our previous work on MP-wise coding [Reference Schiopu and Munteanu6]. The novel contributions of this paper compared to [Reference Schiopu and Munteanu6] can be summarized as follows:
(1) The proposed method takes advantage of the MP synthesis technique and generates a synthesized LF image using steps B1 and B2 of the algorithm.
(2) The patch for coding in [Reference Schiopu and Munteanu6] is a volume of size $N\times N\times 6$
 which collects six neighboring MPs, while the proposed patch for coding is a matrix of size $2N \times 4N$
which collects six neighboring MPs, while the proposed patch for coding is a matrix of size $2N \times 4N$ which collects six neighboring MPs and two neighboring SMPs.
which collects six neighboring MPs and two neighboring SMPs.(3) The two models are completely different. MP-CNN [Reference Schiopu and Munteanu6] uses a sequence of 3D convolutions to process the patch, while PSMP-CNN was inspired from the Unet architecture to process the patches at different resolutions, and it is based on 2D convolutions.
(4) The reference codec from [Reference Schiopu and Munteanu6] was further adapted to take advantage of the MP structure by introducing a MP-based causal neighborhood for the CALIC binary mode.
(5) The compression results presented in Section IV below show that the proposed method offers an average improvement of $12.5\%$
 over our MP-CNN of [Reference Schiopu and Munteanu6].
over our MP-CNN of [Reference Schiopu and Munteanu6].

Fig. 5. The workflow of the proposed method.
The proposed method can be adapted to other LF structures. A conventional LF dataset obtained with a multi-camera setup can be re-mapped to an MP data structure by appropriate re-ordering of light rays. In general, for an MP structure of $N\times M$![]() pixels, one can generate the patch for synthesis of size $2N\times 2M,$
pixels, one can generate the patch for synthesis of size $2N\times 2M,$![]() and a similar patch for coding of size $2N \times 4M.$
and a similar patch for coding of size $2N \times 4M.$![]() No other changes are necessary for the proposed network design or the MP-wise entropy codec. A similar strategy for selecting the reference views can be derived.
No other changes are necessary for the proposed network design or the MP-wise entropy codec. A similar strategy for selecting the reference views can be derived.
IV. EXPERIMENTAL EVALUATION
The experimental evaluation is carried out on the EPFL dataset [Reference Rerabek and Ebrahimi27], which contains 118 lenslet images. The images are captured in the RGB colormap with the Lytro Illum B01 camera with a 10-bit representation. After preprocessing it using the MATLAB Toolbox [Reference Dansereau, Pizarro and Williams24] a 16-bit representation is obtained, available as MATLAB files in [28]. In our tests only the first 8 bits representation of the images is used. After rearranging using equation (1) the 5-dimensional LF structure of each LF image, having $15\times 15 \times 625 \times 434 \times 3$![]() size, the 3-dimensional lenslet structure, LL, of size $9375 \times 6510 \times 3$
size, the 3-dimensional lenslet structure, LL, of size $9375 \times 6510 \times 3$![]() is obtained.
is obtained.
The dataset was divided into the Training Set of 10 images and Test Set of 108 images. In this paper, we set the Training Set as in [Reference Schiopu and Munteanu6] and train our models on the same 10 LF images. For each image in the Training Set, $200\,000$![]() patches are randomly selected for synthesis and $200\,000$
patches are randomly selected for synthesis and $200\,000$![]() patches for coding. Therefore, $N_P=2\,000\,000$
patches for coding. Therefore, $N_P=2\,000\,000$![]() patches for synthesis are used to train each MPS-CNN model, and $N_P=2\,000\,000$
patches for synthesis are used to train each MPS-CNN model, and $N_P=2\,000\,000$![]() patches for coding are used to train each PSMP-CNN model. For each view configuration, one MPS-CNN model and one PSMP-CNN model are trained for each color channel, during 32 epochs, and using a batch size of 500 patches; all the trained models are available online [32]. Since the reference LF image is encoded using the REP-CNN method [Reference Schiopu and Munteanu5], one REP-CNN model was trained for each color channel. Hence, in this paper, a total number of 36 models were trained for the proposed experimental setup.
patches for coding are used to train each PSMP-CNN model. For each view configuration, one MPS-CNN model and one PSMP-CNN model are trained for each color channel, during 32 epochs, and using a batch size of 500 patches; all the trained models are available online [32]. Since the reference LF image is encoded using the REP-CNN method [Reference Schiopu and Munteanu5], one REP-CNN model was trained for each color channel. Hence, in this paper, a total number of 36 models were trained for the proposed experimental setup.
In our work, we use the following training procedure: a $90\DIFdel {\%}$![]() –$10\%$
–$10\%$![]() ratio for splitting the training samples into training−validation data; if we denote the learning rate at epoch i as $\eta _i,$
ratio for splitting the training samples into training−validation data; if we denote the learning rate at epoch i as $\eta _i,$![]() then $\eta _{i+1}= (f_d)^{\lfloor {i}/{n_{s}}\rfloor }\cdot \eta _i,\, \forall i=1,\,2,\,\ldots, \,32,$
then $\eta _{i+1}= (f_d)^{\lfloor {i}/{n_{s}}\rfloor }\cdot \eta _i,\, \forall i=1,\,2,\,\ldots, \,32,$![]() where $f_d=0.2$
where $f_d=0.2$![]() is the decay rate, $n_{s}=5$
is the decay rate, $n_{s}=5$![]() is the decay step, and $\eta _1=5\times 10^{-4}$
is the decay step, and $\eta _1=5\times 10^{-4}$![]() is the learning rate at the first epoch. The training procedure is similar to [Reference Schiopu and Munteanu5,Reference Schiopu and Munteanu6].
is the learning rate at the first epoch. The training procedure is similar to [Reference Schiopu and Munteanu5,Reference Schiopu and Munteanu6].
A) Macro-pixel synthesis results
Figure 6 shows the synthesis results for three LF images in the dataset. The pseudo-colored images show the mean absolute error over the three color channels corresponding to the randomly selected view $(7,\,7)$![]() in the LF image. The distribution of the residual error was truncated for absolute errors represented on more than 4 bits (i.e., larger than 15) by replacing them with the escape symbol 16. One can note that the shades of blue corresponding to absolute mean errors represented on 1–2 bits are the dominant colors of the pseudo-colored images shown in Fig. 6.
in the LF image. The distribution of the residual error was truncated for absolute errors represented on more than 4 bits (i.e., larger than 15) by replacing them with the escape symbol 16. One can note that the shades of blue corresponding to absolute mean errors represented on 1–2 bits are the dominant colors of the pseudo-colored images shown in Fig. 6.

Fig. 6. Pseudo-colored images of the mean absolute error computed over the color channels for one view in the LF images. The mean absolute errors with more than 4-bit representation (i.e., larger than 15) are replaced by the escape symbol 16. The top-to-bottom rows show the synthesized view $(7,\,7)$![]() for each of the four view configurations: $2\times 2$
for each of the four view configurations: $2\times 2$![]() , $3\times 3$
, $3\times 3$![]() , $4\times 4$
, $4\times 4$![]() , and respectively $5\times 5$
, and respectively $5\times 5$![]() .
.
Figure 7(a) shows the results for each LF image in the dataset, where the distortion is measured using the PSNR metric computed between the original image, LL, and the synthesized image, $\hat {LL},$![]() as follows:
as follows:

$N_{LL} = (N\cdot N_{mr}) \times (N\cdot N_{mc}) \times N_{ch} = 9375 \times 6510 \times 3$![]() .
.

Fig. 7. Evaluation of the one-step synthesis results of the macro-pixel synthesis. (a) Synthesis results for each image in the Test Set. (b) Rate-distortion results for the Test Set. (c) Rate-distortion results for the Red and white building image. (d) Rate-distortion results for the Sophie and Vincent 2 image.
Figure 7(b) and Table 1 show the average rate-distortion results over the Test Set of 108 images for one-step MP synthesis, where the bitrate is computed as bits per channel (bpc). Moreover, the table shows the average weight of the base layer in the total image bitrate, denoted $p_{BR},$![]() computed as the ration between the base layer bitrate and the total bitrate. One may note that MPS-CNN achieves an average performance of 29.82 dB when only ${4}/{225} = 1.77\%$
computed as the ration between the base layer bitrate and the total bitrate. One may note that MPS-CNN achieves an average performance of 29.82 dB when only ${4}/{225} = 1.77\%$![]() of the views are selected as reference views and are encoded in $2.3\%$
of the views are selected as reference views and are encoded in $2.3\%$![]() of the total bitrate, while an average performance of 36.19 dB is achieved when ${25}/{225}=11.11\%$
of the total bitrate, while an average performance of 36.19 dB is achieved when ${25}/{225}=11.11\%$![]() of views are encoded in $15.40\%$
of views are encoded in $15.40\%$![]() of total bitrate. An improvement of around 2 dB increase is achieved with each increment of side f of the $f \times f$
of total bitrate. An improvement of around 2 dB increase is achieved with each increment of side f of the $f \times f$![]() view configurations.
view configurations.
Table 1. Lossless compression results of RMP and one-step synthesis results of SMP

Figures 7(c) and 7(d) show the rate-distortion results for two LF images from the Test Set. One may note that the image's content plays an important role in view synthesis applications and that MPS-CNN can achieve results of around 36.5 dB distortion base on only four reference views, and up to 43 dB distortion based on 25 reference views.
B) Lossless compression results
The proposed codec is denoted by MP Synthesis and Coding based on Convolutional Neural Network (MPSC-CNN) and encodes the LF images as follows:
(B1) REP-CNN [Reference Schiopu and Munteanu5] is employed to encode lossless the reference views;
(B2) MPS-CNN is employed to synthesize the LF image;
(B3) PSMP-CNN is employed to compute the MP prediction based on the synthesized image, and the MP-wise CALIC-based Reference codec [Reference Schiopu and Munteanu6] is employed to encode lossless the residual errors of the remaining views.
The performance of the following methods is compared:
(M1) the JPEG 2000 codec [Reference Skodras, Christopoulos and Ebrahimi29] based on the OpenJPEG implementation [33], the active reference software for JPEG 2000 [34], where the code runs with the “−r 1” parameter for a lossless compression setting;
(M2) the HEVC video codec [Reference Sullivan, Ohm, Han and Wiegand13] with all intra configuration; HEVC encodes the pseudo-video-sequence created using the spiral stacking scan pattern [Reference Helin, Astola, Rao and Tabus10,Reference Santos, Assuncao, da Silva Cruz, Tavora, Fonseca-Pinto and Faria12]; the fast x265 library [35] is used with the veryslow preset and the lossless parameter;
(M3) the JPEG-LS codec [Reference Weinberger, Seroussi and Sapiro1];
(M4) the CALIC codec [Reference Wu and Memon2] based on the authors implementation available online [36];
(M5) the CMS method [Reference Schiopu, Gabbouj, Gotchev and Hannuksela11] designed to encode 193 views out of the 225 views, where the remaining views are encoded using CALIC [Reference Wu and Memon2];
(M6) the FLIF codec [Reference Sneyers and Wuille3] based on the implementation available online [7];
(M7) the MP-CNN method [Reference Schiopu and Munteanu6], our preliminary work on MP-wise prediction, where the models are trained based on patches selected from the same training set;
(M8) the PredNN method [Reference Schiopu, Liu and Munteanu4], the first paper on pixel-wise CNN-based prediction, where the model is trained based on patches collected from the same training set; for each LF image more than 183 million patches are processed, one for each pixel and for each color matrix;
(M9) the REP-CNN method [Reference Schiopu and Munteanu5], the first deep-learning-based dual prediction method for pixel-wise prediction based on a similar training process as M8;
(M10) the proposed MPSC-CNN codec employed for the $2\times 2$
 configuration of reference views;
configuration of reference views;(M11) the proposed MPSC-CNN codec employed for the $3\times 3$
 configuration of reference views;
configuration of reference views;(M12) the proposed MPSC-CNN codec employed for the $4\times 4$
 configuration of reference views;
configuration of reference views;(M13) the proposed MPSC-CNN codec employed for the $5\times 5$
 configuration of reference views.
configuration of reference views.
Figure 8 shows the lossless compression results for each image in the dataset using the Relative Compression (RC) metric which is used to compare the compression results of a method MX relative to our proposed method M13. The RC result for a method MX is computed as follows:
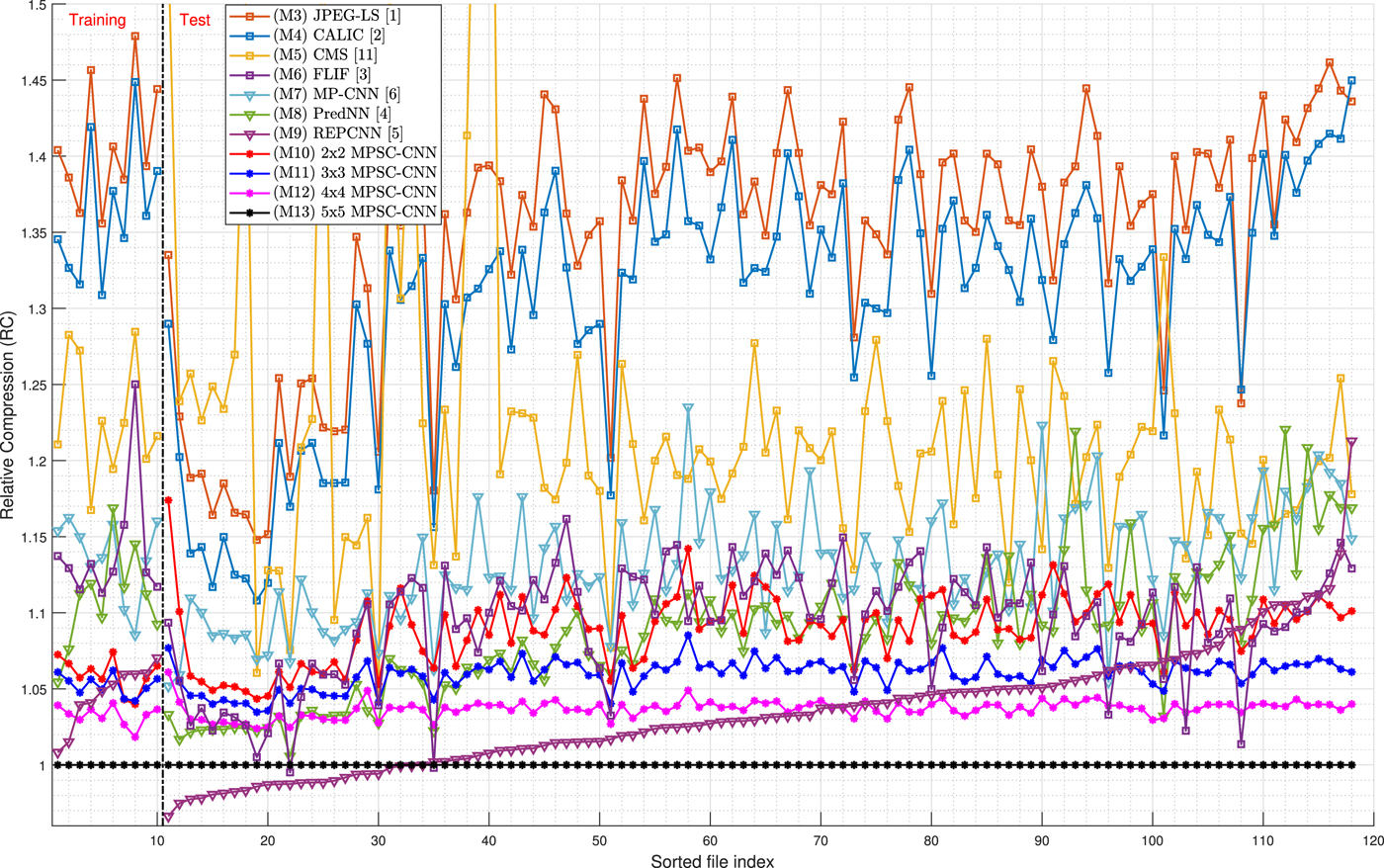
Fig. 8. Lossless compression results.
Table 2 shows the average results for the Test Set. Method M13, the proposed method based on the $5\times 5$![]() configuration, achieves the following average performance over the set of test images:
configuration, achieves the following average performance over the set of test images:
(i) $29.9\%$
 improvement compared to CALIC [Reference Wu and Memon2], a traditional lossless image codec;
improvement compared to CALIC [Reference Wu and Memon2], a traditional lossless image codec;(ii) $12.5\%$
 improvement compared to our previous method [Reference Schiopu and Munteanu6];
improvement compared to our previous method [Reference Schiopu and Munteanu6];(iii) $9.1\%$
 improvement compared to FLIF [Reference Sneyers and Wuille3], the current state-of-the-art lossless image codec; and
improvement compared to FLIF [Reference Sneyers and Wuille3], the current state-of-the-art lossless image codec; and(iv) $3\%$
 improvement compared to REP-CNN [Reference Schiopu and Munteanu5].
improvement compared to REP-CNN [Reference Schiopu and Munteanu5].
Table 2. Lossless compression results of for the Test Set (108 images)

From the complexity perspective, the proposed method requires the inference of two patches when encoding one MP. The MP-CNN model [Reference Schiopu and Munteanu6] requires the inference of a single patch when encoding one MP, however, the inference time of a 3D convolution is higher than of a 2D convolution. The two deep-learning-based pixel-wise prediction models, PredNN [Reference Schiopu, Liu and Munteanu4] and REP-CNN [Reference Schiopu and Munteanu5], require the inference of 225 patches when encoding one MP.
V. CONCLUSIONS
The paper proposed a novel approach for MP synthesis and lossless coding of LF image. Four view configurations are selecting an increasing number of reference views. The MPS-CNN model is employed for MP synthesis. The PSMP-CNN model is employed for MP prediction for coding. The MPSC-CNN codec employs the two models for lossless coding.
MPS-CNN is able to synthesize in one step the entire LF image captured by the image sensor (all $15^2$![]() views) based on a small subset of reference views ($2^2,\, 3^2,\, 4^2,\, 5^2$
views) based on a small subset of reference views ($2^2,\, 3^2,\, 4^2,\, 5^2$![]() ). While the current state-of-the-art methods are employed only to the middle LF image views ($7^2$
). While the current state-of-the-art methods are employed only to the middle LF image views ($7^2$![]() or $8^2$
or $8^2$![]() ), representing around one-quarter of the image, and the views are usually synthesized each one at a time. The synthesized LF image provides valuable prior information used to improve the MP prediction for lossless coding applications.
), representing around one-quarter of the image, and the views are usually synthesized each one at a time. The synthesized LF image provides valuable prior information used to improve the MP prediction for lossless coding applications.
The proposed MPSC-CNN codec based on the LF image synthesized using $5^2$![]() reference views outperforms the traditional codecs with an average improvement of $29.9\%$
reference views outperforms the traditional codecs with an average improvement of $29.9\%$![]() and the most recent state-of-the-art codec with an average improvement of $9.1\%.$
and the most recent state-of-the-art codec with an average improvement of $9.1\%.$![]()
FINANCIAL SUPPORT
This research work is funded by Agentschap Innoveren & Ondernemen (VLAIO) within the research project imec icon ILLUMINATE HBC.2018.0201, and by the research project VUB-SRP M3D2.
CONFLICT OF INTEREST
None.
Ionut Schiopu received his B.Sc. degree in Automatic Control and Computer Science, in 2009, and his M.Sc. degree in Advanced Techniques in Systems and Signals, in 2011, from Politehnica University of Bucharest, Romania, and his Ph.D. degree, in February 2016, from Tampere University of Technology, Finland. In the period between March 2016 and June 2017, he was a postdoctoral researcher at Tampere University of Technology, Finland. Since July 2017, he is a postdoctoral researcher at Vrije Universiteit Brussel, Belgium. His research interests are design and optimization of machine learning tools for image and video coding applications, view synthesis, depth estimation, entropy coding based on context modeling, and image segmentation for coding.
Adrian Munteanu received his M.Sc. degree in Electronics and Telecommunications from Politehnica University of Bucharest, Romania, in 1994, his M.Sc. degree in Biomedical Engineering from University of Patras, Greece, in 1996, and his Ph.D. degree in Applied Sciences (Magna Cum Laudae) from Vrije Universiteit Brussel, Belgium, in 2003. In the period 2004–2010, he was a post-doctoral fellow with the Fund for Scientific Research Flanders, Belgium. Since 2007, he is a professor at the Department of Electronics and Informatics of Vrije Universiteit Brussel, Belgium. His research interests include image, video and 3D graphics coding, distributed visual processing, 3D graphics, error-resilient coding, multimedia transmission over networks, and statistical modeling. He is author of more than 300 journal and conference publications, book chapters, and contributions to standards, and holds seven patents in image and video coding. He served as Associate Editor for IEEE Transactions on Multimedia. He serves as Associate Editor for IEEE Transactions on Image Processing.












