HEVC intra prediction acceleration based on texture direction and prediction unit modes reuse

Abstract

The new High Efficiency Video Coding (HEVC) standard achieves higher encoding efficiency when compared to its predecessors such as H.264/AVC. One of the factors responsible for this improvement is the new intra prediction method, which introduces a larger number of prediction directions resulting in an enhanced rate-distortion (RD) performance obtained at the cost of higher computational complexity. This paper proposes an algorithm to accelerate the intra mode decision, reducing the complexity of intra coding. The acceleration procedure takes into account the texture local directionality information and explores the correlation of intra modes across levels of the hierarchical tree structure used in HEVC. Experimental results show that the proposed algorithm provides a decrease of 39.22 and 43.88% in the HEVC intra prediction processing time on average, for all-intra high efficiency (AI-HE) and low complexity (AI-LC) configurations, respectively, with a small degradation in encoding efficiency (BD-PSNR loss of 0.1 dB for AI-HE and 0.8 dB for AI-LC on average).

I. INTRODUCTION

Although current H.264/AVC [1] encoders are already able to decrease bit-rates by 50% when compared to previous standards [2], recent high resolution video applications and multimedia services require even higher efficiency in video compression at much lower bit-rates. To comply with these demands for higher compression efficiency, a new video compression standard called High Efficiency Video Coding (HEVC) [3,4] was developed by the Joint Collaborative Team on Video Coding (JCT-VC) of ITU-T and ISO/IEC, with the main goal of reaching a better tradeoff between efficiency and complexity than that of the H.264/AVC standard.

Recent performance results obtained from comparisons between the H.264/AVC and HEVC showed that the latter can achieve an average bit-rate improvement of about 34.3% for random-access configuration and 36.8% for low-delay configuration when compared to H.264/AVC [5], considering the same image quality. However, for the all-intra (AI) configuration only a small bit-rate reduction of about 21.9% was obtained, with a complexity increase similar to that of the random-access configuration [5].

In AI configuration all frames are encoded using only intra prediction so that no temporal reference frames are used [6]. Since the AI case avoids the high cost of the motion estimation process and requires less frame memory than inter-frame encoding, its use is justified when one needs a simpler, cheaper, and less energy-demanding codec.

The AI configuration is also interesting for use in low complexity devices such as wireless video cameras, mobile phones, and PDAs, which usually have less available processing power or limited energy supplies [7,8].

The AI coding is also useful in video surveillance setups, portable studio quality cameras and digital cinema distribution networks [9,10], since it enables quick and simple editing without the loss of quality that occurs when editing inter-frame encoded video. Therefore, research on the acceleration of HEVC AI video coding is relevant for many distinct applications areas.

To reduce the computational complexity of HEVC AI configuration, this article proposes a fast intra prediction mode decision algorithm, which utilizes the edge information of the luminance frame texture to speed-up the best intra prediction mode selection. Furthermore, the proposed intra mode decision algorithm also explores the correlation between the orientation of the dominant edge of the current prediction unit (PU) and the orientations of the dominant edges of the PUs at previous tree depth levels.

Preliminary results of this research effort were published at [11]. This article extends that work by providing a complexity and encoding efficiency evaluation for the two test conditions of the all intra configuration, presenting experimental results for all-intra high efficiency (AI-HE) and all-intra low complexity (AI-LC) conditions obtained using the HM12 reference software [12]. Moreover, a preliminary proposal of an algorithm for intra mode fast choice targeting multiview video coding applications was published at [13], which is based on the method described in this paper. In that work, an inter-view prediction method which exploits the relationship between the intra mode directions of adjacent views was developed to accelerate the intra prediction process in multiview video encoding applications. The remainder of this paper is organized as follows. Section II outlines the intra prediction method used in HEVC. Section III briefly reviews related works about intra prediction complexity reduction. Section IV presents in detail the fast intra mode decision algorithm being proposed. Experimental results and comparisons with related works are presented in Section V. Finally, the conclusions are drawn in Section VI.

II. INTRA PREDICTION IN HEVC

In HEVC, each video frame is divided into a number of square blocks of equal size called coding tree blocks (CTBs). Each CTB can be partitioned into one or more CUs using a multilevel quadtree structure, where the CTBs are the roots of each coding tree. The CTB size can vary from 16×16 up to 64×64 luma samples [4]. Each CTB can be composed of only one coding unit (CU) or can be split into multiple CUs, using a quadtree structure [14], where the CTBs are the roots of each coding tree. The CU dimensions can vary from 8×8 up to the CTB dimensions and each leaf CU is also partitioned into prediction units (PUs). In the case of intra coded CU the partition can consist of one 2N × 2N PU or four N × N PUs, where N is half of the CU size.

The CU can be further divided into transform units (TUs) [4] so that each TU represents a block of prediction residues that is transformed and quantized. When the transformation process of the prediction residue starts, each CU becomes the root of a tree of TUs, in which the residual block is divided according to a quadtree structure and a transform is applied for each leaf node of the quadtree [15]. This transform tree is called residual quadtree (RQT).

An example of the hierarchical CU quadtree structure adopted in HEVC is presented in Fig. 1, in which a frame from the Objects sequence is presented. In this figure, each 64×64 CTB corresponds to a 64×64 CU, which can be partitioned into smaller square CUs.

Fig. 1. HEVC hierarchical CU quadtree structure.

The HEVC intra prediction process has some similarities with that adopted in H.264/AVC, since the PU to be encoded is predicted using the reference samples from the neighboring PUs (left and upper) [16].

The intra coding procedure used in the HEVC provides a total of 33 intra prediction directions [3], as well as two additional prediction modes: DC and planar [3] as presented in Fig. 2. The best performing mode of these 35 is identified through a complex search procedure that evaluates each and every of the modes and selects the one that results in the highest encoding performance, considering the rate-distortion (RD) values.

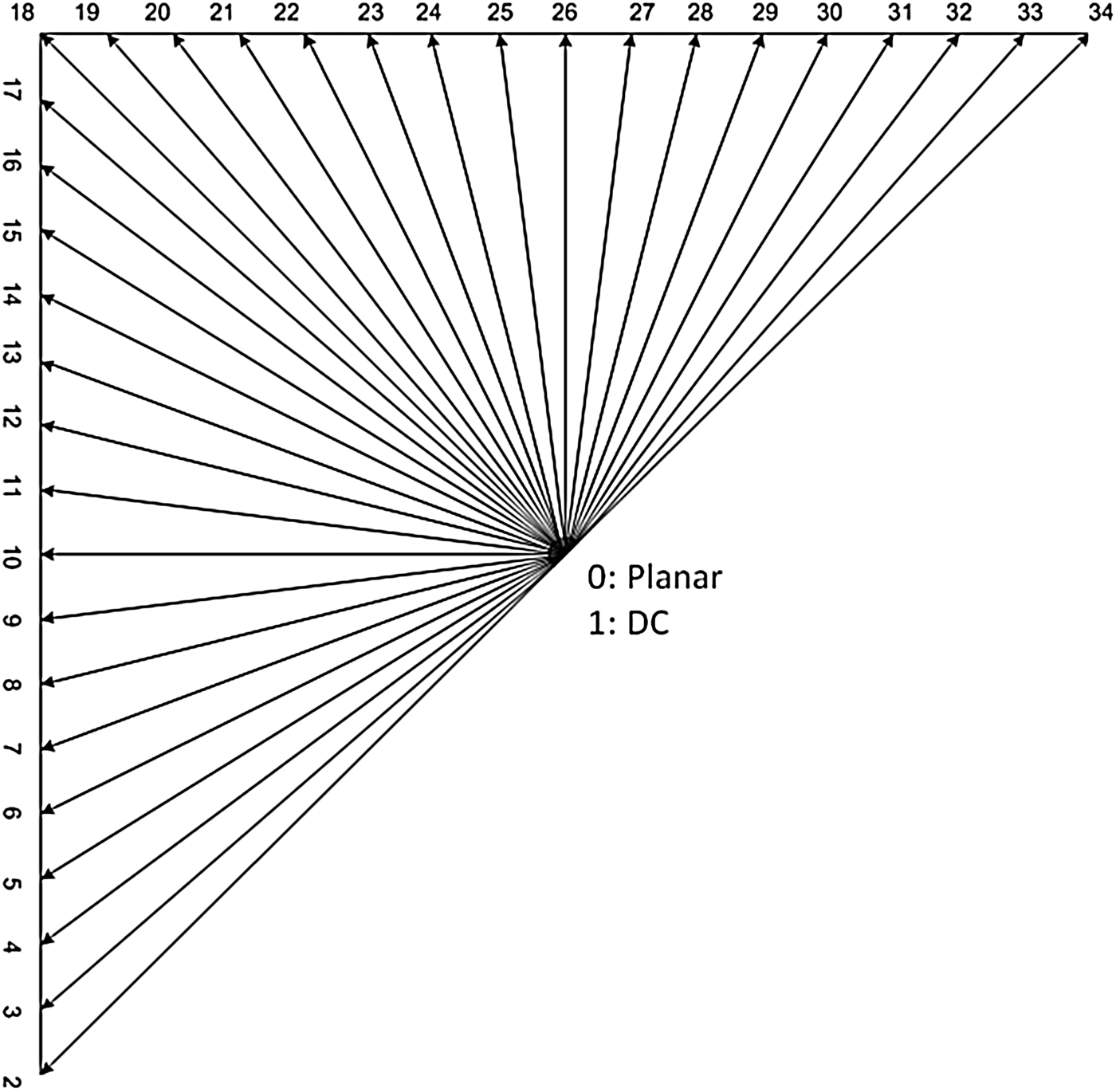
Fig. 2. HEVC intra prediction modes.

To identify the most time consuming components of HEVC reference software (HM), the complexity of the HM encoder was recently profiled in [17,18]. The results show that in the AI configuration case, about a quarter of the total encoding time is spent on rate-distortion optimized quantization (RDOQ) and 16% of time is spent in the intra prediction [17]. To decrease the computational complexity of intra prediction, a rough mode decision (RMD) process was included in the HEVC reference software since HM 2.0 [19] to diminish the number of intra modes to be evaluated during the RDOQ stage. In this process, all the 35 modes available are tested to select the modes which will compose a subset of candidate prediction modes. This subset is formed by choosing the modes that resulted in the smallest RD cost computed using the sum of absolute Hadamard transformed differences (HSAD) and the corresponding number of bits for each prediction mode [4,20], as shown in Fig. 3.

Fig. 3. RMD process.

Unlike H.264/AVC where only one most probable mode (MPM) is used, HEVC includes three MPMs owing to the increased number of intra prediction directions [4]. The three MPMs are chosen based on the intra modes employed in the left and top neighboring PUs of the current PU. By default, the first two MPMs are the modes of both neighboring PUs (left and top) and the third MPM is assigned with modes planar, DC, or angular (mode 26), in this order, considering the assignment of the first two modes, not being possible to duplicate them. Meanwhile, in the cases where the top and left PUs have the same intra mode, this mode and the two closest directional modes are chosen to compose the set of three MPMs [20].

In the next stage, RD cost of each prediction mode belonging to the subset is computed and the best mode (in terms of RD cost) is selected. The definition of the RQT to be used for encoding the residue obtained using the selected intra prediction mode concludes the process.

Recently, a specific profiling of the HM intra prediction procedure was performed to evaluate the computational complexity of the three major modules that compose this process [21]. In this profiling, the first module evaluated is the “N candidate selection”, which is based on HSAD cost and it defines the N modes with the smallest cost. The second module is the “Simplified RD calculation”, in which the N candidate modes selected in first module are evaluated to find the mode with the lowest RD cost. Finally, the third module “Full RD calculation” is computed using the intra mode chosen in the second step and it is applied only once for each PU [21].

The results of this complexity analysis show that the percentages of processing time spent on each of these modules are 19.4, 55.56, and 22.7%, respectively.

Since the second module (Simplified RD calculation) represents 55.56% of the time in the intra prediction process, it is a natural candidate for optimization to reduce the overall HEVC intra prediction complexity. A key parameter of this module is the number of candidate modes selected in the first module, where the more candidates the more complex is the intra coding process. Therefore, this work proposes a fast intra mode decision which optimizes the second module, as well as the first one, considering the PU texture edge orientation and the correlation between the intra modes of PUs at adjacent tree depth levels. In this way, a smaller and more effective candidate modes subset is selected, reducing the computational complexity of the HM intra mode decision. The details of the proposed acceleration method will be presented in Section IV.

III. RELATED WORKS

Some works have been published describing methods that aim to reduce the computation load of the HEVC intra prediction step. In the work published by Zhao et al. [22] a RMD process is performed to reduce the number of intra mode candidates to be evaluated in the rate-distortion optimization (RDO) process. This work also exploits the strong correlation among the neighboring PUs, to identify a MPM, which is added to the candidate mode set. In the work published by Kim et al. [23], a fast CU size decision algorithm for intra coding is proposed to early terminate the CU splitting process before further checking the RD cost of splitting into sub-CUs. The work proposed by Jiang et al. [24] takes a different approach: a gradient direction histogram is computed for each CU and based on this histogram a small subset of the candidate modes are selected as input for the RDO process. The method proposed by Tian and Goto [25] presents a two-stage PU size decision algorithm to accelerate the HEVC intra coding. In first stage, before the intra prediction process begins, the texture complexity of each LCU and its sub-blocks are evaluated to filter out useless PUs, thereby, if the complexity of LCU is considered high, large PUs are excluded from processing; if it is considered low, small PUs (8×8 and 4×4) are filtered out. In the second stage, during the intra coding process, the PU sizes of already encoded neighboring PUs are utilized to decide if the use of small PU candidates in the current PU encoding should be tried or skipped. In the method proposed by Kim et al. [26] an early termination of intra prediction is performed based on the intra prediction mode used in the previous depth PU and on the block size of current depth TU. In addition, the number of candidates of the RMD is further reduced before the RDO procedure, and the intra mode of the previous depth PU is always included in the candidates list for intra mode decision. In the work published by Zhang et al. [27], an adaptive fast mode decision for HEVC intra prediction is proposed which analyses the PUs texture characteristics to reduce the number of candidate modes to be evaluated in RDO process. The method proposed by Silva et al. [28] exploits the correlation of the PUs encoding modes across the HEVC tree structure levels, considering 8×8 and 32×32 PUs sizes. In the method proposed by Zhang and Ma [29], a 2:1 downsampling is applied to the prediction residual and then, a Hadamard transform of the downsampled prediction residual is computed to derive the sum of absolute HSAD used in a RMD process. Furthermore, a gradual search to reduce the number of modes for Hadamard cost calculation and an early termination scheme is applied to speed up the RDO process.

IV. INTRA MODE DECISION ACCELERATION ALGORITHM

As mentioned in the Section II, the algorithm used in HM to choose the best intra prediction mode includes a RMD step, which selects a subset of candidate modes to be used in the prediction of each PU. However, the need to evaluate in advance all the available 33 angular modes to compose this subset remains. Thus, the computational cost is still quite large, and the encoding time is still significant.

The main focus of this article is to propose a new and efficient algorithm to accelerate the HEVC intra prediction decision process. This algorithm is based on three main propositions:

1. 1. Define a reduced subset of angular modes selected considering the dominant edge orientation of the PU texture to determine which modes will be evaluated in the intra mode decision;

2. 2. Explore the correlation among the selected intra prediction modes in the neighbor PUs at the adjacent tree depth levels; and

3. 3. Refine the defined subset of modes adding a new one when a boundary-mode is included in the subset of candidate modes.

The next subsections will present the experiments conducted to gather data that support the presented propositions as well as a detailed description of the proposed algorithm.

A) Preliminary experiments

Some preliminary experiments were performed to evaluate the effectiveness of the propositions. Two experiments were carried out. The first experiment had as goal finding through experimentation the best size of the subset referenced in Proposition 1, considering both complexity reduction ratios and quality losses. The second experiment quantified the magnitude of the correlation between the intra modes selected in PUs at adjacent tree depth levels. This information was then used to decide if this correlation should be exploited to simplify the current PU intra mode choice.

In the first experiment, the 33 directional prediction modes defined in the HEVC standard were divided into smaller sets of modes. To compose these sets, the 33 modes were categorized in four major prediction directions: horizontal, vertical, 45^° diagonal and 135^° diagonal [30]. Each subset was composed of fifteen directional modes, as illustrated in Fig. 4. These subsets composition are presented in equations (1)–(4):

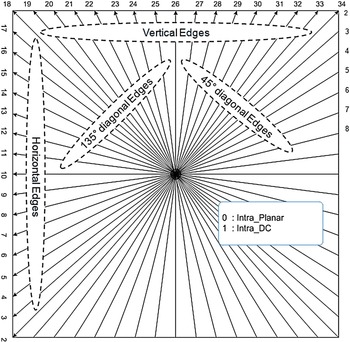
Fig. 4. Edge orientation subsets.

(1) $$\eqalign{{eVerSubset}&=\lcub 19,20,21,22,23,24,25,26,27,28,29,30,\cr & \quad \quad 31,32,33\rcub,}$$

(2) $$eHorSubset=\lcub 3,4,5,6,7,8,9,10,11,12,13,14,15,16,17\rcub ,$$

(3) $$e 45^{\circ} {Subset} =\{27,28,29,30,31,32,33,34,2,3,4,5,6,7,8\},$$

(4) $$\eqalign{e 135^{\circ}{Subset}&=\lcub 11,12,13,14,15,16,17,18,19,20,21,22,\cr & \quad \quad 23,24,25 \rcub.}$$

To determine the usefulness of each directional prediction mode in relation to the local orientation of the texture and compose the directional subset of modes, a group of experiments was performed using the test video sequences recommended in [31] with the all intra configuration and the four quantization parameter values commonly used to test HEVC encoding performance: 22, 27, 32 and 37. In these experiments, statistical information about the frequency of use of the modes included in each of the four subsets of fifteen modes was gathered and then analyzed to identify the eight directional modes (as adopted in the H.264 standard) most often chosen for each of the four edge directions listed before (vertical, horizontal, 45^°, 135^°). Afterwards, similar experiments were performed with seven, nine and ten angular modes per subset.

The analysis of the results showed that subsets composed of nine modes yielded the best tradeoff between performance and complexity reduction, as inferred from the information presented in the graphs of Figs 5 and 6.

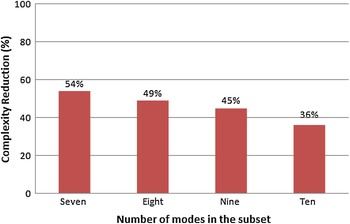
Fig. 5. Complexity reduction for each subset size evaluated.

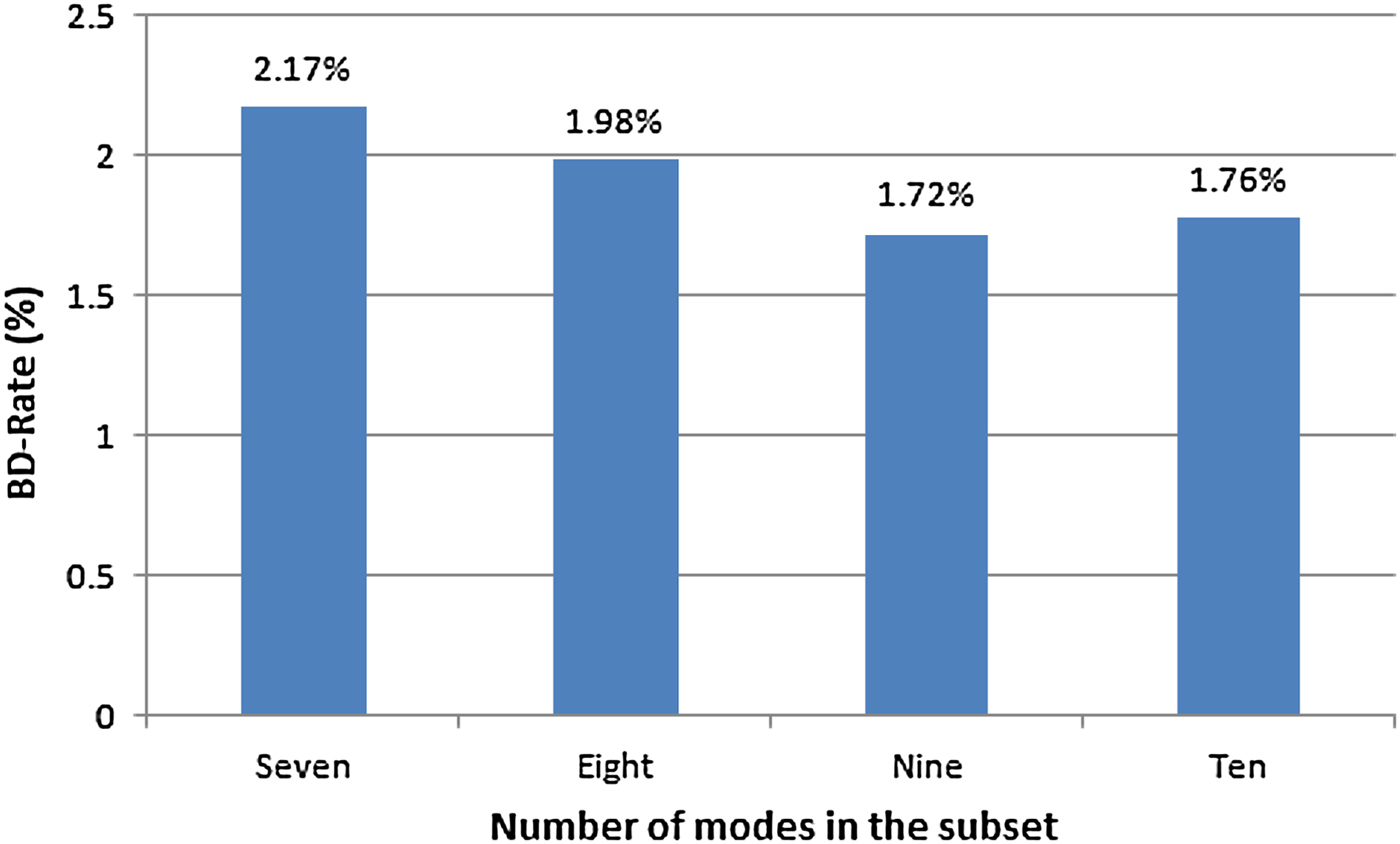
Fig. 6. BD-rate for each subset size evaluated.

From these figures, it is possible to notice that a significant complexity reduction (45%) in the intra mode decision was achieved when the subset of nine modes was used. Taking into account this considerable reduction of complexity and the small degradation of BD-rate encoding efficiency (1.72%), this subset size was selected to be used in the proposed algorithm. Thus, each subset of nine angular modes was associated with one edge orientation (horizontal, vertical, 45^°, 135^°), and a non-directional subset [30] was defined to be used when the PU texture does not have a dominant orientation. The composition of these five subsets of nine angular modes is presented in equations (5)–(9), and also graphically represented in Fig. 7.

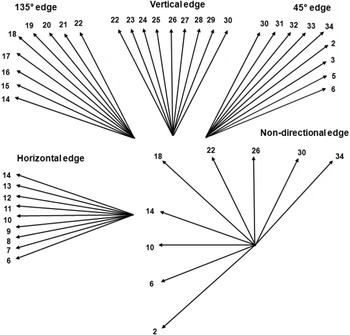
Fig. 7. Subsets of modes for each of the five edge directions.

(5) $$eVerSubset=\left\{22,23,24,25,26,27,28,29,30\right\},$$

(6) $$eHorSubset =\left\{6,7,8,9,10,11,12,13,14\right\},$$

(7) $$e45^{\circ}{Subset}=\left\{30,31,32,33,34,2,3,5,6\right\},$$

(8) $$e135^{\circ}{Subset}=\left\{14,15,16,17,18,19,20,21,22\right\},$$

(9) $$eNonDirSubset=\left\{2,6,10,14,18,22,26,30,34\right\}.$$

The non-directional subset was composed from the three most frequently chosen modes of each directional subset (modes 22, 26 and 30 from vertical subset; 6, 10 and 14 from horizontal subset; 30, 34 and 2 from 45^° subset; and 14, 18 and 22 from 135^° subset).

The second experiment aimed to evaluate the correlation between the edge orientation of the intra mode chosen for the current PU and the mode edge orientation of the PUs already encoded at the previous tree depth levels. This analysis was achieved to determine if there was empirical evidence to support the advantage of reuse of modes subset used in PUs encoding at adjacent tree levels. The test video sequences specified in [31] were intra encoded with quantization parameters 22, 27, 32, and 37. It is important to highlight that the correlation between the tree depth levels for all PU sizes (64×64, 32×32, 16×16, 8×8, and 4×4 PUs) were evaluated. This analysis intended to verify if the best mode chosen for the current PU had the same orientation (e.g. horizontal edge) as that of the intra mode selected in the PU coded at previous tree depth level. The results of this analysis, considering the average results for all tested video sequences, are presented in Table 1.

Table 1. Inter-level relationship between the PUs mode orientation.

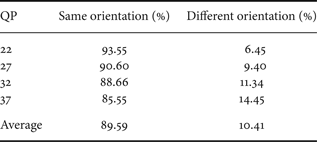
From these results it can be concluded that in most cases, the intra mode selected as the best mode in the PU that is being encoded (current PU) is included in the same directional subset (i.e. has the same orientation) as the mode selected in the PU encoded at the previous depth level was included. This observation motivated the addition of a new test in the proposed algorithm to verify if the dominant edge orientation of the PU to be encoded is the same orientation as the edge of the PU coded at previous tree depth level. If the result of this test is true, the subset of candidate modes of the PU coded at previous depth level is used to encode the current PU, as it will be presented in more detail in the algorithm description, in the next section.

B) Proposed algorithm

This subsection presents a detailed description of the proposed fast intra prediction mode choice algorithm.

The flowchart presented in Fig. 8 provides a diagrammatical representation of the major operations that constitute the algorithm as well as their sequencing.

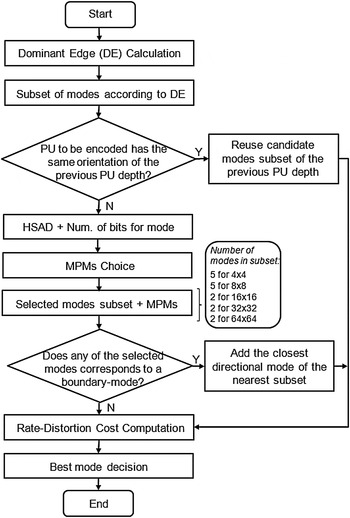
Fig. 8. Flowchart of the proposed intra mode decision acceleration algorithm.

As shown in the flowchart, the first step of the algorithm is an analysis of the PU texture which computes the dominant edge orientation.

The dominant edge orientation of each 4×4 PU is calculated based on the luminance values of its pixels as follows. The 4×4 PU is divided in four 2×2 blocks: Block 0, Block 1, Block 2, and Block 3, as illustrated in Fig. 9, and then the average luminance of each block is calculated. These averages were denoted as c0, c1, c2, and c3, respectively.

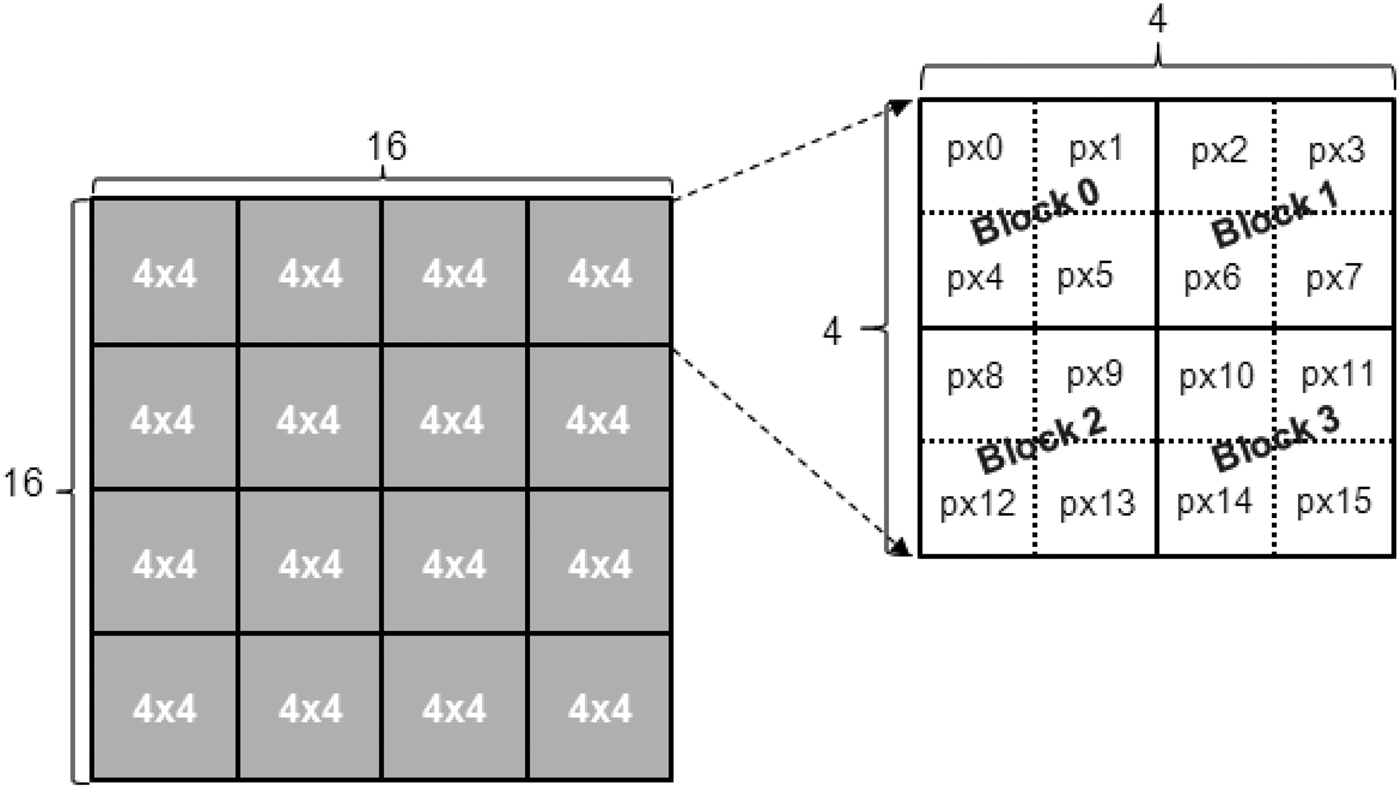
Fig. 9. 16×16 PU edge computation.

These values are then used in equations (10)–(14) [30] to compute five orientation indicator strengths:

(10) $$eV = \vert c_0 -c_1 +c_2 -c_3 \vert, $$

(11) $$eH=\vert c_0 +c_1 -c_2 -c_3 \vert, $$

(12) $$e45^{\circ} =\vert \sqrt 2 \ast \left( c_0 -c_3 \right) \vert, $$

(13) $$e135^{\circ}=\vert \sqrt 2 \ast \left( c_1 -c_2 \right) \vert, $$

(14) $$eND = \vert 2 \ast \left( c_0 -c_1 -c_2 +c_3 \right) \vert, $$

where eV means vertical edge, eH means horizontal edge, e45^° corresponds to diagonal 45^° edge, e135^° corresponds to diagonal 135^° edge, and eND corresponds to non-directional edge.

The dominant edge orientation is determined from these edge strengths, as that one with the largest value, following equation (15), where the symbol DomOr means dominant orientation.

(15) $$DomOr = \mathop{\arg \max \left\{eOr\right\}}\limits_{Or\in \{V,H,45^{\circ},135^{\circ},ND\}}.$$

For PUs sizes larger than 4×4, such as the 16×16 PU in Fig. 9, a slightly different procedure is performed. Initially, the averages of the strengths for each edge direction (horizontal, vertical, 45^°, 135^°, and non-directional) are computed over all the 4×4 PUs that compose the larger PU. Then, the direction with the highest average value is defined as the direction of the dominant edge of the larger PU (e.g. 16×16 PU).

The second step of the proposed algorithm is the definition of the subset of modes to be evaluated, considering the edge strength. Five subsets of angular modes are defined, each one composed of nine angular modes taken from the full set of 33 angular modes defined in HEVC, as explained in the Section IV.A.

The subsets composition presented previously in equations (5)–(9), is illustrated in Fig. 10.

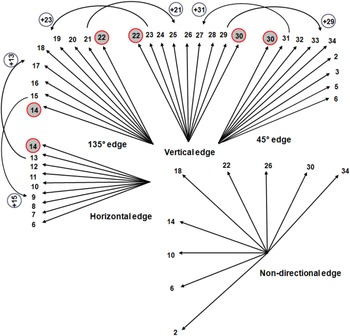
Fig. 10. Subsets of modes for the five edge directions with the additional boundary-mode test representation.

The proposed intra prediction process will use only one of the five subsets according to the edge orientation, DomOr, defined by equation (15).

The third step considers the edge information of the luminance frame texture to find the correlation between the current PU and the PUs encoded at the previous tree levels. This edge information is useful because according to the edge orientation (horizontal, vertical, 45^°, 135^° or non-directional) of the current PU texture and the edge orientation of the PUs already encoded at previous tree depth levels, it is possible to verify if these PUs have the same texture edge orientation and, if this is true, the candidate intra modes used previously can be reused to encode the current PU. Thus, in this algorithm step, a new test is performed to verify if the dominant edge orientation of the current PU has the same orientation as that used in the PU at the immediately lower tree depth level, the subset of candidate modes of the previous PU depth is assumed to be a good choice for the current PU prediction, and so it is used in the intra prediction of the latter, as illustrated in Fig. 11. Under these circumstances the next steps of the algorithm are skipped and the RD cost computation is immediately performed, as shown in Fig. 8. However, if the reuse is not advisable, the fourth step of the algorithm is started and the HSAD calculation is carried out, after which the fifth step, the MPMs choice is performed. Both fourth and fifth steps are described in the Section II. In the sixth step, the subset of modes is defined according to the PU size and the MPMs chosen are added to this subset.

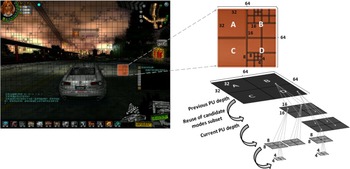
Fig. 11. Candidate modes subset reuse of PUs at adjacent tree depth levels.

The seventh algorithm step considers a possible addition of one more mode to the selected candidate modes subset. If one of the selected candidate modes corresponds to a boundary-mode (a mode that is at a boundary of two neighboring subsets), the direction-wise closest mode of the nearest subset is added to the set of candidate modes. This process is illustrated in Fig. 10, where the modes 14, 22, and 30 are the boundary-modes. Finally, the next algorithm steps are the RD cost calculation and the best intra prediction mode decision.

V. RESULTS AND COMPARISONS

The proposed algorithm was implemented in the HM12 [12]. In order to compare the encoding performance of the proposed algorithm with the performance of the unmodified HM12, a group of simulations were carried out using a computer equipped with an Intel^® Xeon^®, E5520 (2.27 GHz) processor, 24 GBytes of RAM and running the Windows Server 2008 HPC R2 operating system. Each simulation was scheduled to run on a single CPU core to allow comparisons of execution times. The simulations used four quantization parameters (QP): 22, 27, 32, and 37. The following test sequences were used: “People on Street” and “Steam Locomotive” sequences with 2560× 1600 resolution, “BQTerrace” and “Kimono” sequences with 1920× 1088 resolution, “SlideShow” sequence with 1280× 720 resolution, “ChinaSpeed” sequence with 1024× 768 resolution and “Objects” sequence with 640× 480 resolution. These sequences were encoded using two test cases: AI-HE and AI-LC configurations [3].

The results were obtained as follows. Initially, a group of simulations were performed, using the test sequences indicated above. These sequences were encoded using the unmodified HM12 reference software for the two test cases mentioned (AI-HE and AI-LC); afterwards, the same sequences were encoded using the proposed algorithm implemented in the HM12.

The coding efficiency was evaluated using the Bjontegaard delta measure [32,33]. Moreover, to compare the performance and complexity of the proposed algorithm in relation to the HM12 reference software, some complementary performance indicators were computed, namely the average percentage bit-rate difference (Δ Bitrate), average encoding time percentage difference (Δ Time) and the average luminance PSNR difference (Δ PSNRY) as defined by equations (16), (17) and (18).

(16) $$\Delta {PSNRY}={PSNRY}_{proposed} -{PSNRY}_{HM 12.0},$$

(17) $$ \Delta {Bitrate} = \displaystyle{{({Bitrate}_{proposed} -{Bitrate}_{{HM}12.0} )} \over {{Bitrate}_{{HM}12.0}}} \ast 100,$$

(18) $$ \Delta {Time} = \displaystyle{{{{Time}_{proposed}} - {Time}_{{HM}12.0}} \over {{Time}_{{HM}12.0}}} \ast 100.$$

Table 2 lists detailed results, comparing the performance and complexity of the proposed algorithm with results obtained using the unmodified HM 12, when AI-HE configuration is applied. The proposed algorithm achieves an encoding time reduction of up to 42.76% in relation to HM12 (about 39% on average) with slight degradation in encoding efficiency (BD-PSNR loss of 0.1 dB and BD-rate increase of 1.46% on average).

Table 2. Comparison of proposed algorithm with HM12 (high efficiency configuration).

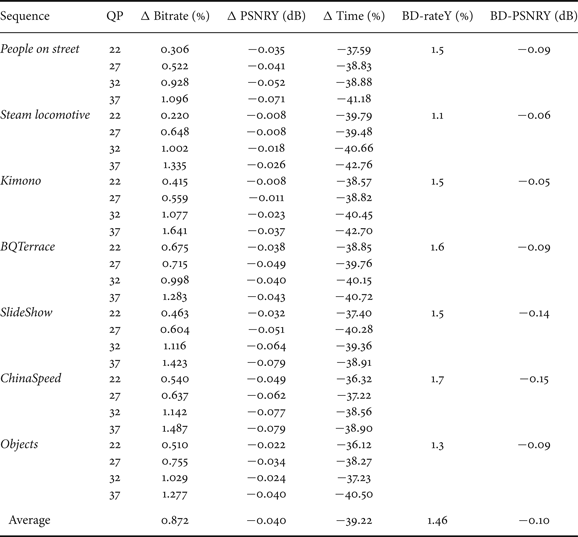
Table 3 presents the results for the proposed algorithm in relation to HM12, when AI-LC configuration is used. From these results, it is possible to verify that the encoding processing time was reduced by 43.88% on average, with a small degradation of 0.08 dB in BD-PSNR and an increase of 1.41% in BD-rate.

Table 3. Comparison of proposed algorithm with HM12 (low complexity configuration).

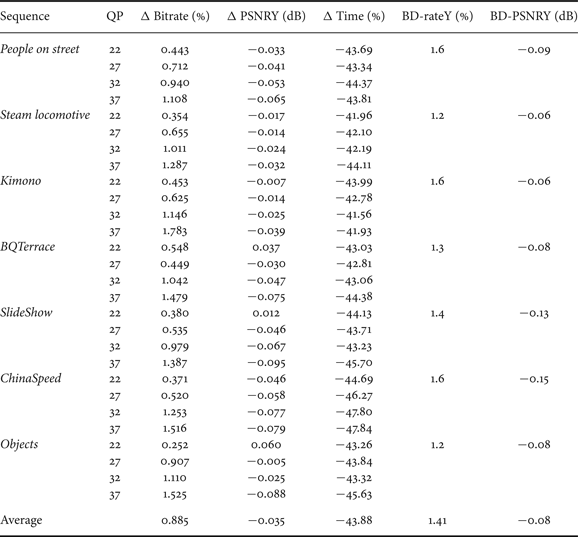
Figure 12 presents the plots of the RD curves for the BQTerrace test sequence (HD 1080p) to illustrate the obtained results. Each point in the curves represents one QP value. From this figure it is possible to conclude that the encoding efficiency of HM12 modified with the inclusion of the algorithm proposed in this paper is very similar to that reached with the unmodified HM12 reference software, thus introducing a minimal loss in performance, which is almost imperceptible in Fig. 12. The graph of Fig. 12 was plotted from the experiment performed using the AI-LC configuration. The full set of results for the BQTerrace and other test sequences encoded with AI-LC configuration are presented in Table 3.

Fig. 12. RD-curves of the proposed algorithm (BQTerrace 1920×1080 pixels).

Figure 13 shows the encoding times versus bit-rate for different QP values comparing the algorithm presented in this article and the HM12 results. From this figure, it is possible to verify that the proposed algorithm provides significant time savings in relation to HM12.

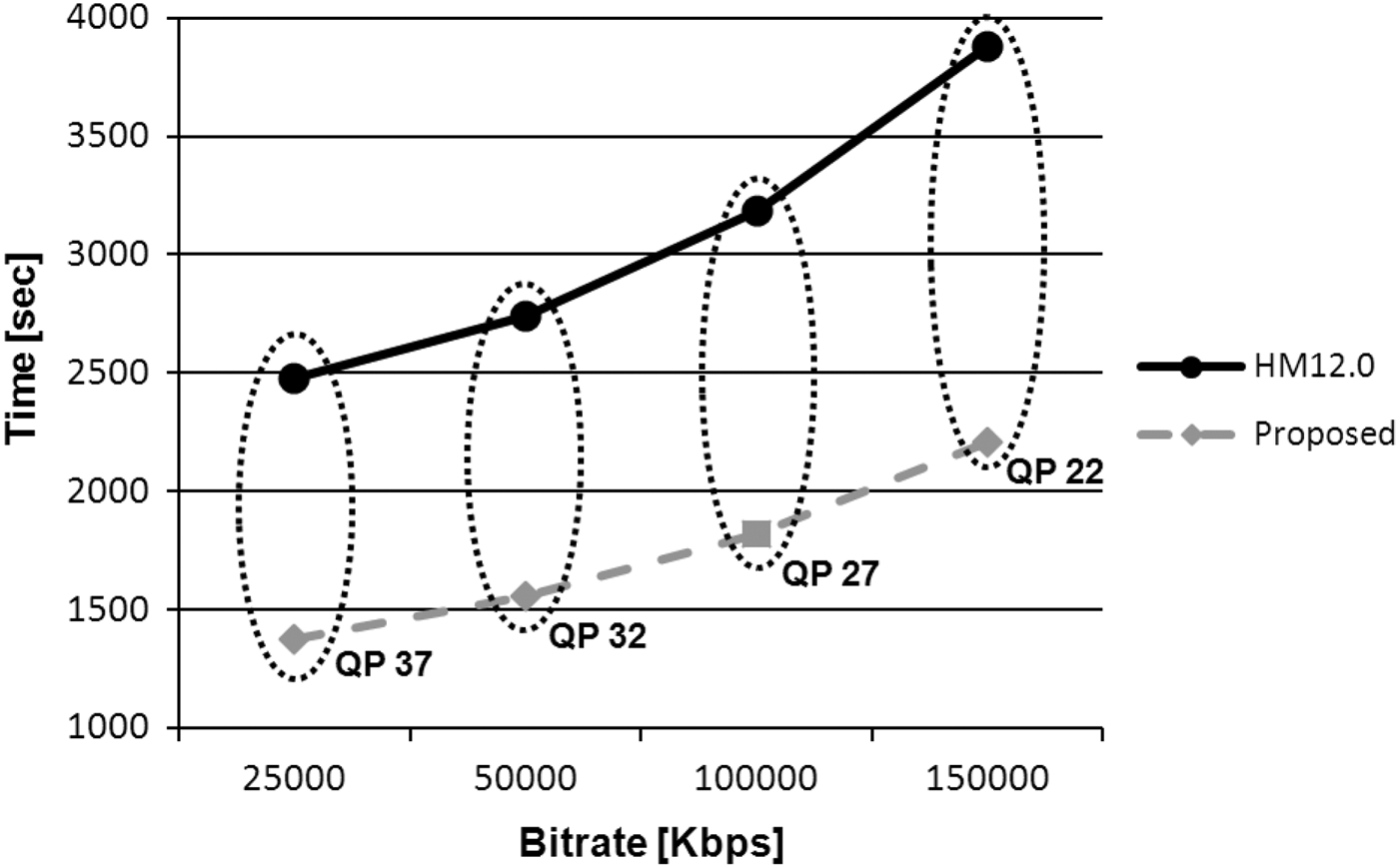
Fig. 13. Encoder time comparison of the proposed algorithm in relation to HM12 (BQTerrace 1920×1080 pixels).

Comparing the proposed algorithm with those described in the related works, it is possible to conclude that our work presents higher computation time savings than that presented by [22]. Since the method developed in [22] has been partially adopted in HM version 2.0 (and followers) and the algorithm proposed in the present work was tested on HM version 12.0 (already includes the procedure from HM 2.0), the computational savings introduced by our algorithm add to the savings introduced by [22]. The proposed algorithm presents better results than [23], which saves 24% encoding time on average, in the AI-HE configuration. Comparing to [24], our algorithm exceeds the complexity reduction reported in that work, which reports a 19.99% average complexity reduction for the AI-LC case. Concerning encoding efficiency, the algorithm presented in [24] incurred an average increase of 0.74% in bit-rate and an average decrease of 0.04 dB in PSNR when compared to the HM 4.0. When compared with [25], our work outperforms the complexity reduction of 30.71% in AI-HE case and presents similar results (44.91% on average) in AI-LC case. The algorithm proposed in this paper surpasses the encoding time reduction achieved by [26], up to 22.99% in AI-HE case and 26.16% in AI-LC case. Our work complexity reduction performance also exceeds that presented in [27] which saves only 15% of encoding time in the AI-HE configuration and 20% in AI-LC configuration. Our algorithm also exceeds the encoding time reduction presented by [28], which evaluates the correlations between adjacent tree level PU orientation for 8×8 and 32×32 PUs sizes only, while in this work the similarities for all PU sizes (64×64, 32×32, 16×16, 8×8, and 4×4 PUs) were evaluated. In comparison with [28], which saves around 24% of encoding time on average in AI-HE case, our algorithm achieves a reduction of 39.22% on average when this same case is considered, reaching a higher complexity reduction. When compared with [29], the results obtained in our work surpass the complexity reduction of 38% reported in that work. Concerning encoding efficiency, our work also reaches better performance than [29], which reports an increase in BD-Rate of 2.9%, while our algorithm presented an increase of 1.46% on average in AI-HE case and 1.41% in AI-LC case.

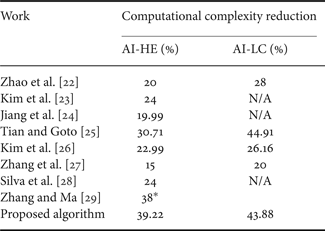
The comparison of the complexity reduction results obtained in this article with that presented in the related works is summarized in Table 4. Since some works published result data just for one of the two cases considered (AI-HE and AI-LC), the missing results are indicated as “Not Available” (N/A). Concerning Zhang and Ma [29], just one result column is presented because that work did not specify which test case was used (HE or LC), indicating only that the AI configuration was used.

Table 4. Complexity reduction comparison of proposed algorithm with related works.

* Only informed the AI configuration and did not mention the test condition used.

N/A, not available.

From this table it is possible to conclude that the proposed algorithm presents the highest complexity reduction when the AI-HE configuration is applied. Regarding AI-LC configuration, the proposed algorithm achieves similar results to those presented by [25], which has reached the best results in complexity reduction when this test case is considered.

VI. CONCLUSIONS

This article presented an algorithm which exploits the luminance texture directionality and intra mode relationship across the tree depth levels to accelerate the procedure used to find the best prediction mode used in the HEVC intra prediction coding. The proposed algorithm was focused on the AI configuration. Experimental evaluations using high efficiency and low complexity test conditions were conducted achieving important complexity reductions with negligible encoding efficiency degradations.

The algorithm computes the dominant edge orientation of the PU to be encoded considering the PU texture directionality, determining a reduced subset of modes to be evaluated in the mode decision process. The proposed algorithm also exploits the similarities between the edge orientation of the PUs intra modes encoded at previous tree level and the dominant edge orientation of the current PU to define the reuse of the previous PU modes subset. In addition, a boundary-mode test is included to selectively add a new intra mode direction to the subset of candidate modes to be evaluated in the intra mode decision process.

Experimental results show that when compared with the HM12, the encoding processing time was reduced by 39.22% on average when the AI-HE configuration was applied and about 44% on average when the AI-LC configuration is used. The proposed algorithm achieved this complexity reduction with a negligible drop in encoding efficiency: an average BD-PSNR loss of 0.01 dB for AI-HE configuration and 0.08 dB for AI-LC configuration. Furthermore, the proposed fast intra mode decision achieved higher complexity reduction ratios than the best competing HEVC intra prediction speedup methods published in the literature, namely [22–29], when the AI-HE configuration was applied, and similar results to those obtained by [25] which presented the best encoding time reduction when the AI-LC configuration was considered.