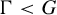1. Introduction
How can a given group act by isometries on a hyperbolic space? The aim of this paper is to study this question for irreducible lattices in a semisimple Lie group G of rank
![]() $\geq 2$
. Haettel [Reference Haettel13] addressed the case where all simple factors of the ambient product G have rank
$\geq 2$
. Haettel [Reference Haettel13] addressed the case where all simple factors of the ambient product G have rank
![]() $\geq 2$
and showed, in that case, that the isometric actions of the lattice on hyperbolic spaces are all degenerate (see below for a more precise formulation). In this paper, we allow G to have simple factors of rank one. Since rank-one simple groups have a natural geometric action on a proper hyperbolic space (namely, a rank-one symmetric space), the lattices in G do admit non-degenerate actions on hyperbolic spaces via their projections on the rank-one simple factors of G. We show that, up to a natural equivalence, those are the only actions of lattices in G on hyperbolic spaces.
$\geq 2$
and showed, in that case, that the isometric actions of the lattice on hyperbolic spaces are all degenerate (see below for a more precise formulation). In this paper, we allow G to have simple factors of rank one. Since rank-one simple groups have a natural geometric action on a proper hyperbolic space (namely, a rank-one symmetric space), the lattices in G do admit non-degenerate actions on hyperbolic spaces via their projections on the rank-one simple factors of G. We show that, up to a natural equivalence, those are the only actions of lattices in G on hyperbolic spaces.
1.1. Generalities on actions on hyperbolic spaces
Before stating our main theorem, we now explain some general facts about actions on hyperbolic spaces. First of all, any group has isometric actions on hyperbolic spaces that fix a bounded set, as well as actions that fix a point at infinity. Such actions can therefore not be used to deduce anything about the group: from our viewpoint, they are degenerate and we will disregard them. Moreover, given an action on a hyperbolic space, one could make a larger hyperbolic space containing the first one as a quasi-convex subspace, maintaining the group action. This can be done, for example, by attaching equivariantly geodesic rays. To take this possibility into account, it is natural to also rule out actions that admit a quasi-convex invariant set that is not coarsely dense. In view of all this, we define coarsely minimal actions (Definition 4.1) by, essentially, ruling out the pathological behaviours discussed above. Arguably, those are the most general actions that one might want to classify. Moreover, actions on hyperbolic spaces that admit an equivariant quasi-isometry should be considered equivalent, and we capture this in Definition 4.2, where there is a subtlety to deal with actions where given subgroups fix a bounded set rather than single points.
1.2. Rigidity of hyperbolic actions
We say that a lattice
![]() $\Gamma $
in a product group
$\Gamma $
in a product group
![]() ${G = G_1 \times \cdots \times G_N}$
is irreducible if the closure of the projection of
${G = G_1 \times \cdots \times G_N}$
is irreducible if the closure of the projection of
![]() $\Gamma $
to any proper sub-product has finite index. It follows from results of Margulis [Reference Margulis17, Theorem II.6.7] that if each
$\Gamma $
to any proper sub-product has finite index. It follows from results of Margulis [Reference Margulis17, Theorem II.6.7] that if each
![]() $G_i$
is a simple algebraic group over a local field, then
$G_i$
is a simple algebraic group over a local field, then
![]() $\Gamma $
is irreducible if and only if
$\Gamma $
is irreducible if and only if
![]() $\Gamma $
has no finite index subgroup that splits as a direct product in a non-trivial way. Here is the main result of this paper.
$\Gamma $
has no finite index subgroup that splits as a direct product in a non-trivial way. Here is the main result of this paper.
Theorem 1.1. Let
![]() $N \geq n \geq 0$
be integers. Let
$N \geq n \geq 0$
be integers. Let
![]() $G=\prod _{i=1}^N G_i$
be a product of N centreless simple Lie groups, where for all
$G=\prod _{i=1}^N G_i$
be a product of N centreless simple Lie groups, where for all
![]() $i \in \{1, \ldots , n\}$
, the factor
$i \in \{1, \ldots , n\}$
, the factor
![]() $G_i$
has real rank-one, and for all
$G_i$
has real rank-one, and for all
![]() $j \in \{n+1, \ldots , N\}$
, the factor
$j \in \{n+1, \ldots , N\}$
, the factor
![]() $G_j$
has real rank at least two. Let
$G_j$
has real rank at least two. Let
![]() $\Gamma < G$
be a lattice. Assume that
$\Gamma < G$
be a lattice. Assume that
![]() $n\ge 2$
or that
$n\ge 2$
or that
![]() $N>n$
. If
$N>n$
. If
![]() $N>1$
, assume in addition that
$N>1$
, assume in addition that
![]() $\Gamma $
is irreducible.
$\Gamma $
is irreducible.
Then any coarsely minimal isometric action of
![]() $\Gamma $
on a geodesic hyperbolic space is equivalent to one of the actions
$\Gamma $
on a geodesic hyperbolic space is equivalent to one of the actions
where each
![]() $X_i$
is the rank-one symmetric space of the factor
$X_i$
is the rank-one symmetric space of the factor
![]() $G_i$
.
$G_i$
.
As mentioned above, we refer to Definition 4.2 for the precise notion of equivalence appearing in the theorem.
In the special case where G consists only of a single higher rank factor, that is the case where
![]() $n=0$
and
$n=0$
and
![]() $N=1$
, our considerations recover for Lie groups the main theorem of [Reference Haettel13].
$N=1$
, our considerations recover for Lie groups the main theorem of [Reference Haettel13].
Corollary 1.2. Let G be a simple Lie group of real rank
![]() $\geq 2$
, and
$\geq 2$
, and
![]() $\Gamma <G$
a lattice. Then
$\Gamma <G$
a lattice. Then
![]() $\Gamma $
does not admit any coarsely minimal isometric action on a geodesic hyperbolic space.
$\Gamma $
does not admit any coarsely minimal isometric action on a geodesic hyperbolic space.
One can also view Theorem 1.1 as a generalization of the main result from Margulis’ paper [Reference Margulis16], where he studied possible amalgam decompositions of lattices in higher rank.
1.3. Hyperbolic structures
The setup adopted here is inspired by the notion of hyperbolic structures, defined in [Reference Abbott, Balasubramanya and Osin1] to capture cobounded actions on hyperbolic spaces. Coarsely minimal actions provide a similar but broader setup (see [Reference Abbott, Balasubramanya and Osin1, Proposition 3.12] for a comparison). In what follows, we regard a hyperbolic structure as an equivalence class (in the sense of Definition 4.2) of cobounded actions on hyperbolic spaces. It is a general fact that any such action is either coarsely minimal or the hyperbolic space being acted on is bounded (giving rise to what is called the trivial structure). While a coarsely minimal action may fail to be cobounded in general, it is worth noting that Theorem 1.1 yields another rigidity feature of higher rank lattices, namely the following corollary.
Corollary 1.3. Let
![]() $\Gamma < G$
be as in Theorem 1.1. Then any coarsely minimal isometric
$\Gamma < G$
be as in Theorem 1.1. Then any coarsely minimal isometric
![]() $\Gamma $
-action on a geodesic hyperbolic space is cobounded.
$\Gamma $
-action on a geodesic hyperbolic space is cobounded.
Indeed, since the projection
![]() $\Gamma \to G_i$
has dense image, the result follows from Theorem 1.1 because the
$\Gamma \to G_i$
has dense image, the result follows from Theorem 1.1 because the
![]() $G_i$
-action on the model space
$G_i$
-action on the model space
![]() $X_i$
is cocompact.
$X_i$
is cocompact.
By Corollary 1.3, the number of hyperbolic structures up to equivalence on
![]() $\Gamma $
is the number of coarsely minimal
$\Gamma $
is the number of coarsely minimal
![]() $\Gamma $
-actions up to equivalence plus one. Therefore, in the language of [Reference Abbott, Balasubramanya and Osin1], Theorem 1.1 implies that the lattices under consideration have exactly
$\Gamma $
-actions up to equivalence plus one. Therefore, in the language of [Reference Abbott, Balasubramanya and Osin1], Theorem 1.1 implies that the lattices under consideration have exactly
![]() $n+1$
inequivalent hyperbolic structures. Note that in [Reference Abbott, Balasubramanya and Osin1], for every integer
$n+1$
inequivalent hyperbolic structures. Note that in [Reference Abbott, Balasubramanya and Osin1], for every integer
![]() $n \geq 1$
, the authors construct a finitely generated group
$n \geq 1$
, the authors construct a finitely generated group
![]() $\Gamma $
admitting precisely n distinct hyperbolic structures; irreducible lattices in higher rank semisimple Lie groups provide naturally occurring examples of that same phenomenon. Note that any lattice in a higher rank simple Lie group has only the trivial hyperbolic structure by [Reference Haettel13] or Corollary 1.2.
$\Gamma $
admitting precisely n distinct hyperbolic structures; irreducible lattices in higher rank semisimple Lie groups provide naturally occurring examples of that same phenomenon. Note that any lattice in a higher rank simple Lie group has only the trivial hyperbolic structure by [Reference Haettel13] or Corollary 1.2.
Example 1.4. (Groups with
 $n \geq 2$
non-trivial hyperbolic structures)
$n \geq 2$
non-trivial hyperbolic structures)
Let
![]() $n \geq 2$
be an integer. Let also K be a totally real number field of degree n. Such a field can be constructed as a subextension of degree n in
$n \geq 2$
be an integer. Let also K be a totally real number field of degree n. Such a field can be constructed as a subextension of degree n in
![]() ${\mathbb Q}(\cos (2\pi /p))$
, where p is any prime congruent to
${\mathbb Q}(\cos (2\pi /p))$
, where p is any prime congruent to
![]() $1$
modulo
$1$
modulo
![]() $2n$
(in the special case of
$2n$
(in the special case of
![]() $n =2$
, one can of course simply take
$n =2$
, one can of course simply take
![]() ${K = {\mathbb Q}(\sqrt 2)}$
). Let
${K = {\mathbb Q}(\sqrt 2)}$
). Let
![]() $\mathcal O$
be the ring of integers of K. Then K has exactly n inequivalent embeddings as subfields of
$\mathcal O$
be the ring of integers of K. Then K has exactly n inequivalent embeddings as subfields of
![]() ${\mathbb R}$
, whose restrictions to
${\mathbb R}$
, whose restrictions to
![]() $\mathcal O$
have dense image. The corresponding diagonal embedding of
$\mathcal O$
have dense image. The corresponding diagonal embedding of
![]() $\mathcal O$
in
$\mathcal O$
in
![]() ${\mathbb R}^n$
has discrete image. Consequently, the group
${\mathbb R}^n$
has discrete image. Consequently, the group
embeds as an irreducible lattice in the product of n copies of
![]() $\operatorname {SL}_2({\mathbb R})$
. Theorem 4.4 implies that it has precisely n non-trivial hyperbolic structures that arise from its actions on the hyperbolic plane via the projections
$\operatorname {SL}_2({\mathbb R})$
. Theorem 4.4 implies that it has precisely n non-trivial hyperbolic structures that arise from its actions on the hyperbolic plane via the projections
![]() $\operatorname {pr}_1,\ldots ,\operatorname {pr}_n$
.
$\operatorname {pr}_1,\ldots ,\operatorname {pr}_n$
.
Example 1.5. (A group with a single non-trivial hyperbolic structure)
Consider the quadratic form
![]() $q(x_1,\ldots ,x_5)=x_1^2+x_2^2+x_3^2+\sqrt {2}x_4^2-x_5^2$
, its orthogonal group
$q(x_1,\ldots ,x_5)=x_1^2+x_2^2+x_3^2+\sqrt {2}x_4^2-x_5^2$
, its orthogonal group
![]() $\operatorname {SO}(q)= \{ {g\in \operatorname {SL}_5}\mid {q\circ g=q} \} $
and let
$\operatorname {SO}(q)= \{ {g\in \operatorname {SL}_5}\mid {q\circ g=q} \} $
and let
![]() $\Gamma =\operatorname {SO}(q)_{{\mathbb Z}[\sqrt {2}]}$
be the group of its integer points. This group has only one non-trivial hyperbolic structure, because
$\Gamma =\operatorname {SO}(q)_{{\mathbb Z}[\sqrt {2}]}$
be the group of its integer points. This group has only one non-trivial hyperbolic structure, because
![]() $\Gamma $
is an irreducible lattice in the semisimple real Lie group
$\Gamma $
is an irreducible lattice in the semisimple real Lie group
![]() ${\operatorname {SO}}(4,1)\times \operatorname {SO}(3,2)$
that has a single rank-one factor
${\operatorname {SO}}(4,1)\times \operatorname {SO}(3,2)$
that has a single rank-one factor
![]() ${\operatorname {SO}}(4,1)\simeq \operatorname {Isom}(\mathbb H^4)$
and another simple
${\operatorname {SO}}(4,1)\simeq \operatorname {Isom}(\mathbb H^4)$
and another simple
![]() $\operatorname {SO}(3,2)$
factor of rank two.
$\operatorname {SO}(3,2)$
factor of rank two.
1.4. Outline of proofs
In the proofs, we will use boundary theory as outlined in [Reference Bader and Furman3]. Roughly, given a group
![]() $\Gamma $
, one can associate to it a Lebesgue space B, called
$\Gamma $
, one can associate to it a Lebesgue space B, called
![]() $\Gamma $
-boundary, which on one hand has very strong ergodic properties, and on the other hand has the property that whenever
$\Gamma $
-boundary, which on one hand has very strong ergodic properties, and on the other hand has the property that whenever
![]() $\Gamma $
acts on a compact space Z, there is a
$\Gamma $
acts on a compact space Z, there is a
![]() $\Gamma $
-equivariant map
$\Gamma $
-equivariant map
![]() $B\longrightarrow \operatorname {Prob}(Z)$
, called a boundary map. In the case of a group
$B\longrightarrow \operatorname {Prob}(Z)$
, called a boundary map. In the case of a group
![]() $\Gamma $
acting nicely on a hyperbolic space X, as in Theorem 1.1, a key step consists in constructing an equivariant measurable map
$\Gamma $
acting nicely on a hyperbolic space X, as in Theorem 1.1, a key step consists in constructing an equivariant measurable map
![]() $\Phi :B \longrightarrow \partial X$
into the Gromov boundary of X. To do so, one starts from a boundary map into
$\Phi :B \longrightarrow \partial X$
into the Gromov boundary of X. To do so, one starts from a boundary map into
![]() $\operatorname {Prob}(\bar X)$
—the space of probability measures on a certain compactification of X—and uses the ergodic properties of the
$\operatorname {Prob}(\bar X)$
—the space of probability measures on a certain compactification of X—and uses the ergodic properties of the
![]() $\Gamma $
-action on B in conjunction with the geometric properties for the
$\Gamma $
-action on B in conjunction with the geometric properties for the
![]() $\Gamma $
-action on X, to show that the map
$\Gamma $
-action on X, to show that the map
![]() $\Phi $
takes values in Dirac measures
$\Phi $
takes values in Dirac measures
![]() $\Phi (x)=\delta _{\phi (x)}$
, where
$\Phi (x)=\delta _{\phi (x)}$
, where
![]() $\phi (x)\in \partial X\subset \bar {X}$
. The case where X is a proper Gromov-hyperbolic space had been considered already in [Reference Bader and Furman3], and indeed the main result of §3 is a direct generalization of [Reference Bader and Furman3, Theorem 3.2].
$\phi (x)\in \partial X\subset \bar {X}$
. The case where X is a proper Gromov-hyperbolic space had been considered already in [Reference Bader and Furman3], and indeed the main result of §3 is a direct generalization of [Reference Bader and Furman3, Theorem 3.2].
The fact that X is potentially a non-proper space causes several issues. One of them requires to study the relation between the horofunction compactification
![]() $\bar X$
and the Gromov boundary
$\bar X$
and the Gromov boundary
![]() $\partial X$
. Similar considerations appear in the work by Duchesne [Reference Duchesne9] and by Maher and Tiozzo [Reference Maher and Tiozzo15]. Related ideas appeared already in the much earlier work [Reference Margulis16] of Margulis, where he studied actions of higher rank lattices on trees of possibly infinite valency. Another issue is that the space
$\partial X$
. Similar considerations appear in the work by Duchesne [Reference Duchesne9] and by Maher and Tiozzo [Reference Maher and Tiozzo15]. Related ideas appeared already in the much earlier work [Reference Margulis16] of Margulis, where he studied actions of higher rank lattices on trees of possibly infinite valency. Another issue is that the space
![]() $\operatorname {Bdd}_C(X)$
of C-bounded subsets of X, which is naturally quasi-isometric to X, need no longer be separable. This causes critical separability issues when dealing with boundary maps. To circumvent those difficulties, we introduce in §2 a new type of ergodicity of boundary
$\operatorname {Bdd}_C(X)$
of C-bounded subsets of X, which is naturally quasi-isometric to X, need no longer be separable. This causes critical separability issues when dealing with boundary maps. To circumvent those difficulties, we introduce in §2 a new type of ergodicity of boundary
![]() $\Gamma $
-spaces, called coarse metric ergodicity. We show in Theorem 2.7 that it is always satisfied by Furstenberg–Poisson boundaries. In the context of Theorem 1.1, we also show that the standard Furstenberg–Poisson boundary of G also enjoys the coarse metric ergodicity as a
$\Gamma $
-spaces, called coarse metric ergodicity. We show in Theorem 2.7 that it is always satisfied by Furstenberg–Poisson boundaries. In the context of Theorem 1.1, we also show that the standard Furstenberg–Poisson boundary of G also enjoys the coarse metric ergodicity as a
![]() $\Gamma $
-space (Proposition 2.9). In §3, we construct boundary maps for any non-degenerate isometric
$\Gamma $
-space (Proposition 2.9). In §3, we construct boundary maps for any non-degenerate isometric
![]() $\Gamma $
-action on a hyperbolic space X, under the sole hypothesis of existence of an amenable coarsely metrically ergodic
$\Gamma $
-action on a hyperbolic space X, under the sole hypothesis of existence of an amenable coarsely metrically ergodic
![]() $\Gamma $
-space (Theorem 3.1).
$\Gamma $
-space (Theorem 3.1).
In §4, we focus again on the case where
![]() $\Gamma $
is a higher rank lattice, as in our main theorem. In this case, the
$\Gamma $
is a higher rank lattice, as in our main theorem. In this case, the
![]() $\Gamma $
-boundary of
$\Gamma $
-boundary of
![]() $\Gamma $
splits as a product, with factors corresponding to the factors of the ambient locally compact group G. Due to the ergodicity properties of
$\Gamma $
splits as a product, with factors corresponding to the factors of the ambient locally compact group G. Due to the ergodicity properties of
![]() $\Gamma $
-boundaries, we see that when
$\Gamma $
-boundaries, we see that when
![]() $\Gamma $
acts nicely on a hyperbolic space X, the boundary map from the
$\Gamma $
acts nicely on a hyperbolic space X, the boundary map from the
![]() $\Gamma $
-boundary to
$\Gamma $
-boundary to
![]() $\partial X$
factors through one of the algebraic factors of the ambient group G. At this point, there are two cases to analyse. The first case is when the said factor is of rank
$\partial X$
factors through one of the algebraic factors of the ambient group G. At this point, there are two cases to analyse. The first case is when the said factor is of rank
![]() $\geq 2$
: we have to show that this cannot occur. This is done in §4.4 by adapting the Weyl group method of Bader and Furman [Reference Bader and Furman2]. The second case is that the factor as above corresponds to a rank-one factor
$\geq 2$
: we have to show that this cannot occur. This is done in §4.4 by adapting the Weyl group method of Bader and Furman [Reference Bader and Furman2]. The second case is that the factor as above corresponds to a rank-one factor
![]() $G_i$
of G. In that case, we have to show that X is equivalent to the model symmetric space
$G_i$
of G. In that case, we have to show that X is equivalent to the model symmetric space
![]() $X_i$
for
$X_i$
for
![]() $G_i$
. This is done in §§4.5 and 4.6. By hypothesis, the group G has at least two factors in this case, and the projection of
$G_i$
. This is done in §§4.5 and 4.6. By hypothesis, the group G has at least two factors in this case, and the projection of
![]() $\Gamma $
to
$\Gamma $
to
![]() $G_i$
has dense image. To show the equivalence between
$G_i$
has dense image. To show the equivalence between
![]() $X_i$
and X, metric properties are transferred from
$X_i$
and X, metric properties are transferred from
![]() $X_i$
to X via the boundary map. A key ingredient is that bounded subsets of
$X_i$
to X via the boundary map. A key ingredient is that bounded subsets of
![]() $X_i$
correspond to precompact subsets of
$X_i$
correspond to precompact subsets of
![]() $G_i$
, and the latter property can be rephrased in terms of the boundedness of Radon–Nikodym derivatives for the action on the
$G_i$
, and the latter property can be rephrased in terms of the boundedness of Radon–Nikodym derivatives for the action on the
![]() $G_i$
-boundary.
$G_i$
-boundary.
Remark 1.6. In a draft version of this paper that was circulated as a preprint, we had adopted a more general setup, encompassing irreducible lattices in products whose factors were allowed to be simple algebraic groups over local fields or standard rank-one groups in the sense of [Reference Caprace, Cornulier, Monod and Tessera8]. However, the strategy used in that version was hampered by the measurability issues alluded to above, related to the inseparability of the space
![]() $\operatorname {Bdd}_C(X)$
. This is resolved here using coarse metric ergodicity. It is likely that Theorem 1.1 nevertheless extends to the general setup we had originally envisaged. A possible approach to establish this would be to generalize Proposition 2.9 beyond the Lie group case.
$\operatorname {Bdd}_C(X)$
. This is resolved here using coarse metric ergodicity. It is likely that Theorem 1.1 nevertheless extends to the general setup we had originally envisaged. A possible approach to establish this would be to generalize Proposition 2.9 beyond the Lie group case.
2. Coarse metric ergodicity
2.1. Definitions
The goal of this section is to introduce a coarse version of metric ergodicity. Let us recall some definitions before recalling metric ergodicity and discussing why we need a different version.
Let G be a second countable locally compact group (abbreviated lcsc group). This includes the case of a countable discrete group
![]() $\Gamma $
. A Lebesgue G-space is a Lebesgue space
$\Gamma $
. A Lebesgue G-space is a Lebesgue space
![]() $(\Omega ,\mu )$
with a measurable, measure class preserving action map
$(\Omega ,\mu )$
with a measurable, measure class preserving action map
![]() $G\times \Omega \longrightarrow \Omega $
. A Borel G-space V is a standard Borel space V with a Borel action map
$G\times \Omega \longrightarrow \Omega $
. A Borel G-space V is a standard Borel space V with a Borel action map
![]() $G\times V\longrightarrow V$
. By a Lebesgue map
$G\times V\longrightarrow V$
. By a Lebesgue map
![]() $\Omega \to V$
, we mean an equivalence class of functions from
$\Omega \to V$
, we mean an equivalence class of functions from
![]() $\Omega $
to V, defined almost everywhere and up to an almost everywhere identification, which has a Borel measurable representative.
$\Omega $
to V, defined almost everywhere and up to an almost everywhere identification, which has a Borel measurable representative.
The Lebesgue G-space
![]() $\Omega $
is metrically ergodic if, given any separable metric space S and continuous homomorphism
$\Omega $
is metrically ergodic if, given any separable metric space S and continuous homomorphism
![]() $\pi \colon G\to \operatorname {Isom}(S)$
, the only G-equivariant measurable maps
$\pi \colon G\to \operatorname {Isom}(S)$
, the only G-equivariant measurable maps
![]() $\Omega \to S$
are constant. (Ergodicity in the usual sense corresponds to taking
$\Omega \to S$
are constant. (Ergodicity in the usual sense corresponds to taking
![]() $S=\{0,1\}$
and
$S=\{0,1\}$
and
![]() $\pi $
trivial.)
$\pi $
trivial.)
Roughly, the relevance of metric ergodicity in our setting is that, given a higher rank lattice
![]() $\Gamma $
acting on a hyperbolic space X, we will need to rule out the existence of certain
$\Gamma $
acting on a hyperbolic space X, we will need to rule out the existence of certain
![]() $\Gamma $
-equivariant maps
$\Gamma $
-equivariant maps
![]() $B\to \partial X^{(3)}$
, where B is a
$B\to \partial X^{(3)}$
, where B is a
![]() $\Gamma $
-boundary and
$\Gamma $
-boundary and
![]() $\partial X^{(3)}$
is the space of distinct triples of boundary points of X. We are not aware of a natural way of endowing
$\partial X^{(3)}$
is the space of distinct triples of boundary points of X. We are not aware of a natural way of endowing
![]() $\partial X^{(3)}$
with a separable metric. Instead, we can endow it with a ‘coarsely separable’ metric and we will apply coarse metric ergodicity to this metric. Since it does not cost any additional work, we will actually deal with coarse metrics in the following sense.
$\partial X^{(3)}$
with a separable metric. Instead, we can endow it with a ‘coarsely separable’ metric and we will apply coarse metric ergodicity to this metric. Since it does not cost any additional work, we will actually deal with coarse metrics in the following sense.
Definition 2.1. A coarse metric on a set U is a function
![]() $d:U\times U\to [0,\infty )$
such that there exists
$d:U\times U\to [0,\infty )$
such that there exists
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $x,y,z \in U$
,
$x,y,z \in U$
,
The function d is a C-coarse metric on U.
Two coarse metrics are coarsely equivalent if their difference is uniformly bounded.
Remark 2.2. Every C-coarse metric d lies within bounded distance of a genuine metric
![]() $d'$
. Indeed, one can start with d, change it so that
$d'$
. Indeed, one can start with d, change it so that
![]() $d(x,x)=0$
and then set
$d(x,x)=0$
and then set
![]() $d_1(x,y)=\max \{d(x,y),d(y,x)\}$
. At this point, it is readily checked that
$d_1(x,y)=\max \{d(x,y),d(y,x)\}$
. At this point, it is readily checked that
![]() $d_1$
is again a C-coarse metric and to get
$d_1$
is again a C-coarse metric and to get
![]() $d'$
, one can add to it C times the discrete
$d'$
, one can add to it C times the discrete
![]() $\{0,1\}$
-metric.
$\{0,1\}$
-metric.
Definition 2.3. Let G be an lcsc group. A Lebesgue G-space
![]() $\Omega $
is said to be coarsely metrically ergodic if every Borel coarse metric d, defined on some conull subset
$\Omega $
is said to be coarsely metrically ergodic if every Borel coarse metric d, defined on some conull subset
![]() $\Omega _0\subseteq \Omega $
and G-invariant as a Lebesgue map
$\Omega _0\subseteq \Omega $
and G-invariant as a Lebesgue map
![]() $\Omega \times \Omega \to [0,\infty )$
, is essentially bounded, that is, there exists
$\Omega \times \Omega \to [0,\infty )$
, is essentially bounded, that is, there exists
![]() $R>0$
such for almost every (a.e.) pair
$R>0$
such for almost every (a.e.) pair
![]() $(x,x')\in \Omega _0\times \Omega _0$
, we have
$(x,x')\in \Omega _0\times \Omega _0$
, we have
![]() $d(x,x')\leq R$
. Equivalently, by Remark 2.2, if every G-invariant Borel metric on any
$d(x,x')\leq R$
. Equivalently, by Remark 2.2, if every G-invariant Borel metric on any
![]() $\Omega _0$
as above is essentially bounded.
$\Omega _0$
as above is essentially bounded.
Example 2.4. If B is a doubly ergodic G-space, that is, the diagonal G-action on
![]() $B\times B$
is ergodic, then B is coarsely metrically ergodic. This follows easily from the fact that given a G-invariant Borel coarse metric d on B, the subsets
$B\times B$
is ergodic, then B is coarsely metrically ergodic. This follows easily from the fact that given a G-invariant Borel coarse metric d on B, the subsets
![]() $\Delta _R=\{(b,b'): d(b,b')\leq R\}\subseteq B\times B$
are G-invariant and their union is the whole
$\Delta _R=\{(b,b'): d(b,b')\leq R\}\subseteq B\times B$
are G-invariant and their union is the whole
![]() $B\times B$
. Hence, one of them needs to have positive measure, and hence full measure by ergodicity.
$B\times B$
. Hence, one of them needs to have positive measure, and hence full measure by ergodicity.
Remark 2.5. Coarse metric ergodicity does not imply ergodicity, as any finite space with a trivial action is clearly coarsely metrically ergodic. However, it is easy to see that any coarsely metrically ergodic space has a finite number of ergodic components.
Note that in the definition of coarse metric ergodicity, we do not assume separability of d, merely that it is Borel. An example to keep in mind is the discrete
![]() $\{0,1\}$
-metric, which is Borel, but not separable unless
$\{0,1\}$
-metric, which is Borel, but not separable unless
![]() $\Omega $
is countable. A coarse metric space is coarsely separable if it is covered by a countable collection of balls of a fixed radius. By the following remark, essentially all coarse metrics of concern to us are coarsely separable.
$\Omega $
is countable. A coarse metric space is coarsely separable if it is covered by a countable collection of balls of a fixed radius. By the following remark, essentially all coarse metrics of concern to us are coarsely separable.
Remark 2.6. Given an lcsc group G, every G-invariant coarse metric on an ergodic space
![]() $\Omega $
is coarsely separable by the following argument. The space is an exhaustion of countably many concentric balls of growing radii, so there exists a radius r and a non-null r-ball. Translating this ball by a dense countable subgroup of G (which acts ergodically due to the weak* continuity of the G-representation on
$\Omega $
is coarsely separable by the following argument. The space is an exhaustion of countably many concentric balls of growing radii, so there exists a radius r and a non-null r-ball. Translating this ball by a dense countable subgroup of G (which acts ergodically due to the weak* continuity of the G-representation on
![]() $L^\infty (\Omega )$
), we find a countable collection of non-null r-balls whose union is of full measure.
$L^\infty (\Omega )$
), we find a countable collection of non-null r-balls whose union is of full measure.
2.2. Examples
A first source of coarsely metrically ergodic actions of a group
![]() $\Gamma $
is given by doubly ergodic
$\Gamma $
is given by doubly ergodic
![]() $\Gamma $
-spaces, as pointed out in Example 2.4. For our purposes, we need amenable
$\Gamma $
-spaces, as pointed out in Example 2.4. For our purposes, we need amenable
![]() $\Gamma $
-spaces
$\Gamma $
-spaces
![]() $B_-$
and
$B_-$
and
![]() $B_+$
such that the
$B_+$
such that the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $B_-\times B_+$
is coarsely metrically ergodic, see Theorem 3.1 below. Our main source for such
$B_-\times B_+$
is coarsely metrically ergodic, see Theorem 3.1 below. Our main source for such
![]() $\Gamma $
-spaces is provided by the following theorem.
$\Gamma $
-spaces is provided by the following theorem.
Theorem 2.7. Let G be an lcsc group. Let
![]() $\mu $
be a spread-out generating probability measure on G, and let
$\mu $
be a spread-out generating probability measure on G, and let
![]() $B_-$
and
$B_-$
and
![]() $B_+$
be the corresponding past and future Furstenberg–Poisson boundaries, that is, the Furstenberg–Poisson boundaries associated with the measures
$B_+$
be the corresponding past and future Furstenberg–Poisson boundaries, that is, the Furstenberg–Poisson boundaries associated with the measures
![]() $\check {\mu }$
and
$\check {\mu }$
and
![]() $\mu $
correspondingly. Then,
$\mu $
correspondingly. Then,
![]() $B_-$
and
$B_-$
and
![]() $B_+$
are amenable Lebesgue G-spaces such that the diagonal G-action on
$B_+$
are amenable Lebesgue G-spaces such that the diagonal G-action on
![]() $B_-\times B_+$
is metrically ergodic and coarsely metrically ergodic.
$B_-\times B_+$
is metrically ergodic and coarsely metrically ergodic.
In the case where
![]() $\mu $
is a symmetric measure, we obtain a single amenable G-space B, equal to
$\mu $
is a symmetric measure, we obtain a single amenable G-space B, equal to
![]() $B_-$
and
$B_-$
and
![]() $B_+$
. We emphasize that the coarse metric ergodicity of the G-action on
$B_+$
. We emphasize that the coarse metric ergodicity of the G-action on
![]() $B \times B$
should not be expected to hold for the same reason as in Example 2.4, since the G-action on
$B \times B$
should not be expected to hold for the same reason as in Example 2.4, since the G-action on
![]() $B \times B \times B \times B$
need not be ergodic: indeed, in the case where G is a rank-one simple Lie group, the space B can be identified with the visual boundary of the symmetric space of G, and
$B \times B \times B \times B$
need not be ergodic: indeed, in the case where G is a rank-one simple Lie group, the space B can be identified with the visual boundary of the symmetric space of G, and
![]() $B \times B \times B \times B$
is the space of
$B \times B \times B \times B$
is the space of
![]() $4$
-tuple of distinct points. The cross-ratio is a G-invariant function on that space.
$4$
-tuple of distinct points. The cross-ratio is a G-invariant function on that space.
Instead, the proof of Theorem 2.7 relies on the following lemma.
Lemma 2.8. (Cf. [Reference Bader and Furman3, Lemma 2.8])
Let G be an lcsc group and let
![]() $\mu $
be a spread-out generating probability measure on G. Let
$\mu $
be a spread-out generating probability measure on G. Let
![]() $(B_-,\nu _-)$
and
$(B_-,\nu _-)$
and
![]() $(B_+,\nu _+)$
be the corresponding past and future Furstenberg–Poisson boundaries. Given a positive measure subset
$(B_+,\nu _+)$
be the corresponding past and future Furstenberg–Poisson boundaries. Given a positive measure subset
![]() $E\subset B_-\times B_+$
and
$E\subset B_-\times B_+$
and
![]() $\epsilon>0$
, there is
$\epsilon>0$
, there is
![]() $g\in G$
and a positive measure subset
$g\in G$
and a positive measure subset
![]() $E_1^-\subset E^-\cap g^{-1}E^-$
, where
$E_1^-\subset E^-\cap g^{-1}E^-$
, where
![]() $E^{-}$
is the projection of E to
$E^{-}$
is the projection of E to
![]() $B_-$
, so that for every
$B_-$
, so that for every
![]() $b_-\in E_1^-$
,
$b_-\in E_1^-$
,
![]() $\nu _+(gE_{b_-})>1-\epsilon $
, where
$\nu _+(gE_{b_-})>1-\epsilon $
, where
![]() $E_{b_-}=\{b_+ \in B_+ \mid (b_-,b_+)\in E)\}$
.
$E_{b_-}=\{b_+ \in B_+ \mid (b_-,b_+)\in E)\}$
.
Proof of Theorem 2.7
The fact that
![]() $B_-$
and
$B_-$
and
![]() $B_+$
are amenable Lebesgue G-spaces such that the diagonal G-action on
$B_+$
are amenable Lebesgue G-spaces such that the diagonal G-action on
![]() $B_-\times B_+$
is metrically ergodic is proven in [Reference Bader and Furman3, Theorem 2.7]. We will show that diagonal G-action on
$B_-\times B_+$
is metrically ergodic is proven in [Reference Bader and Furman3, Theorem 2.7]. We will show that diagonal G-action on
![]() $B_-\times B_+$
is coarsely metrically ergodic.
$B_-\times B_+$
is coarsely metrically ergodic.
Fix a G-invariant Borel metric
![]() $d:(B_-\times B_+)^2\to [0,\infty )$
. By Remark 2.6 and upon normalization, we assume, as we may, that d is
$d:(B_-\times B_+)^2\to [0,\infty )$
. By Remark 2.6 and upon normalization, we assume, as we may, that d is
![]() $1$
-separable. We will show that for a.e.
$1$
-separable. We will show that for a.e.
![]() $b_-\in B_-$
, the essential diameter of
$b_-\in B_-$
, the essential diameter of
![]() $\{b_-\}\times B_+$
is bounded by
$\{b_-\}\times B_+$
is bounded by
![]() $3$
. By symmetry, for a.e.
$3$
. By symmetry, for a.e.
![]() $b_+\in B_+$
, the essential diameter of
$b_+\in B_+$
, the essential diameter of
![]() $B_-\times \{b_+\}$
is bounded by
$B_-\times \{b_+\}$
is bounded by
![]() $3$
, and thus the essential diameter of
$3$
, and thus the essential diameter of
![]() $B_-\times B_+$
is bounded by
$B_-\times B_+$
is bounded by
![]() $6$
.
$6$
.
We find a countable collection
![]() $A_i$
of non-null
$A_i$
of non-null
![]() $1$
-balls whose union is of full measure. We consider the projection
$1$
-balls whose union is of full measure. We consider the projection
![]() $B_-\times B_+\to B_-$
and for every i, we let
$B_-\times B_+\to B_-$
and for every i, we let
![]() $A_i^-$
be the image of
$A_i^-$
be the image of
![]() $A_i$
. For every natural n, we let
$A_i$
. For every natural n, we let
![]() $A_{i,n}^-$
be the set of those
$A_{i,n}^-$
be the set of those
![]() $b_-\in A_i^-$
such that
$b_-\in A_i^-$
such that
Note that there exists
![]() $N_i$
such that the sets
$N_i$
such that the sets
![]() $A_{i,n}^-$
are non-null for every
$A_{i,n}^-$
are non-null for every
![]() $n\geq N_i$
. Using the symbol
$n\geq N_i$
. Using the symbol
![]() $\circeq $
for equation up to null-sets, we get
$\circeq $
for equation up to null-sets, we get
![]() $A_{i}^-\circeq \bigcup _{n\geq N_i}~ A_{i,n}^-$
. We let
$A_{i}^-\circeq \bigcup _{n\geq N_i}~ A_{i,n}^-$
. We let
![]() $A_{i,n}$
be the preimage of
$A_{i,n}$
be the preimage of
![]() $A_{i,n}^-$
in
$A_{i,n}^-$
in
![]() $A_i$
and get
$A_i$
and get
 $$ \begin{align*} A_{i}\circeq\bigcup_{n\geq N_i}~ A_{i,n} \quad \mbox{and} \quad B_+\times B_-\circeq \bigcup_i~ A_{i}\circeq\bigcup_{i,{n\geq N_i}}~ A_{i,n}. \end{align*} $$
$$ \begin{align*} A_{i}\circeq\bigcup_{n\geq N_i}~ A_{i,n} \quad \mbox{and} \quad B_+\times B_-\circeq \bigcup_i~ A_{i}\circeq\bigcup_{i,{n\geq N_i}}~ A_{i,n}. \end{align*} $$
By modifying the sets
![]() $A_{i,n}$
, we assume as we may that for every
$A_{i,n}$
, we assume as we may that for every
![]() $i',n',i",n"$
,
$i',n',i",n"$
,
![]() $A_{i',n'}^-\cap A_{i",n"}^-$
is either non-null or empty, upon throwing away the preimages of the intersection in case it is null. By Fubini, for a.e.
$A_{i',n'}^-\cap A_{i",n"}^-$
is either non-null or empty, upon throwing away the preimages of the intersection in case it is null. By Fubini, for a.e.
![]() $b_-\in B_-$
, for a.e.
$b_-\in B_-$
, for a.e.
![]() $b_+\in B_+$
,
$b_+\in B_+$
,
![]() $(b_-,b_+)\in \bigcup _{i,{n\geq N_i}}~ A_{i,n}$
. We fix a generic
$(b_-,b_+)\in \bigcup _{i,{n\geq N_i}}~ A_{i,n}$
. We fix a generic
![]() $b_-\in B_-$
and consider the full measure subset of the fibre over
$b_-\in B_-$
and consider the full measure subset of the fibre over
![]() $b_-$
,
$b_-$
,
 $$ \begin{align*} D=(\{b_-\}\times B_+)\cap \bigg(\bigcup_{i,{n\geq N_i}}~ A_{i,n}\bigg). \end{align*} $$
$$ \begin{align*} D=(\{b_-\}\times B_+)\cap \bigg(\bigcup_{i,{n\geq N_i}}~ A_{i,n}\bigg). \end{align*} $$
We claim that the set D is bounded by
![]() $3$
. To see this, let us fix
$3$
. To see this, let us fix
![]() $b_{+}^{\prime },b_+^{\prime \prime }\in B_+$
such that
$b_{+}^{\prime },b_+^{\prime \prime }\in B_+$
such that
![]() $(b_-,b_{+}^{\prime }),(b_-,b_+^{\prime \prime })\in D$
. Fix
$(b_-,b_{+}^{\prime }),(b_-,b_+^{\prime \prime })\in D$
. Fix
![]() $i',n',i",n"$
such that
$i',n',i",n"$
such that
![]() $(b_-,b_{+}^{\prime })\in A_{i',n'}$
,
$(b_-,b_{+}^{\prime })\in A_{i',n'}$
,
![]() $(b_-,b_+^{\prime \prime })\in A_{i",n"}$
and
$(b_-,b_+^{\prime \prime })\in A_{i",n"}$
and
![]() $n'>N_{i'}$
,
$n'>N_{i'}$
,
![]() $n">N_{i"}$
. Set
$n">N_{i"}$
. Set
Let E be the preimage of
![]() $E^-$
in
$E^-$
in
![]() $A_{i',n'}$
and note that it is non-null. By Lemma 2.8, there exist
$A_{i',n'}$
and note that it is non-null. By Lemma 2.8, there exist
![]() $g\in G$
and a non-null subset
$g\in G$
and a non-null subset
![]() $E_1^-$
in
$E_1^-$
in
![]() $E^-\cap g^{-1}E^-$
such that for every
$E^-\cap g^{-1}E^-$
such that for every
![]() $b_{-}^{\prime }\in E_1^-$
,
$b_{-}^{\prime }\in E_1^-$
,
where
![]() $E_{b_{-}^{\prime }}=\{b_+\mid (b_{-}^{\prime },b_+)\in E\}$
. Fixing such
$E_{b_{-}^{\prime }}=\{b_+\mid (b_{-}^{\prime },b_+)\in E\}$
. Fixing such
![]() $b_{-}^{\prime }$
, we conclude that the set
$b_{-}^{\prime }$
, we conclude that the set
![]() $gE_{b_{-}^{\prime }}$
is bounded by
$gE_{b_{-}^{\prime }}$
is bounded by
![]() $1$
and it intersects both sets
$1$
and it intersects both sets
![]() $A_{i',n'}$
and
$A_{i',n'}$
and
![]() $A_{i",n"}$
. We conclude that
$A_{i",n"}$
. We conclude that
![]() $d((b_-,b_{+}^{\prime }),(b_-,b_+^{\prime \prime }))<3$
. This finishes the proof.
$d((b_-,b_{+}^{\prime }),(b_-,b_+^{\prime \prime }))<3$
. This finishes the proof.
For lattices in a semisimple Lie group G, one can realize the unique G-invariant measure class on
![]() $G/P$
as a Furstenberg–Poisson boundary, leading to the following proposition.
$G/P$
as a Furstenberg–Poisson boundary, leading to the following proposition.
Proposition 2.9. Let G be a semisimple Lie group and
![]() $\Gamma <G$
a lattice. Let
$\Gamma <G$
a lattice. Let
![]() $P<G$
be a minimal parabolic and endow the coset space
$P<G$
be a minimal parabolic and endow the coset space
![]() $G/P$
with the unique G-invariant measure class and consider it as a Lebesgue
$G/P$
with the unique G-invariant measure class and consider it as a Lebesgue
![]() $\Gamma $
-space. Then
$\Gamma $
-space. Then
![]() $G/P$
is an amenable Lebesgue
$G/P$
is an amenable Lebesgue
![]() $\Gamma $
-space such that the diagonal
$\Gamma $
-space such that the diagonal
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $G/P\times G/P$
is metrically ergodic and coarsely metrically ergodic.
$G/P\times G/P$
is metrically ergodic and coarsely metrically ergodic.
Proof. We fix a maximal compact subgroup
![]() $K<G$
. In [Reference Furstenberg10], Furstenberg proved that all bounded harmonic functions on the symmetric space
$K<G$
. In [Reference Furstenberg10], Furstenberg proved that all bounded harmonic functions on the symmetric space
![]() $G/K$
are represented via a Poisson formula as bounded measurable functions on
$G/K$
are represented via a Poisson formula as bounded measurable functions on
![]() $G/P$
with respect to a certain G-quasi-invariant measure
$G/P$
with respect to a certain G-quasi-invariant measure
![]() $\nu \in \operatorname {Prob}(G/P)$
, namely the unique K-invariant measure. Following the discretization process applied by Furstenberg in the special case of the hyperbolic plane, Lyons and Sullivan obtained in [Reference Lyons and Sullivan14, Theorem 5] a discretization scheme which applies to any *-recurrent discrete subset of a Riemannian manifold of bounded geometry (see [Reference Lyons and Sullivan14, §7] for the definition of *-recurrent), an example of such a setting being the orbit of
$\nu \in \operatorname {Prob}(G/P)$
, namely the unique K-invariant measure. Following the discretization process applied by Furstenberg in the special case of the hyperbolic plane, Lyons and Sullivan obtained in [Reference Lyons and Sullivan14, Theorem 5] a discretization scheme which applies to any *-recurrent discrete subset of a Riemannian manifold of bounded geometry (see [Reference Lyons and Sullivan14, §7] for the definition of *-recurrent), an example of such a setting being the orbit of
![]() $\Gamma $
on
$\Gamma $
on
![]() $G/K$
. Their discretization procedure for the pair
$G/K$
. Their discretization procedure for the pair
![]() $(G/K,\Gamma .K)$
commutes with the symmetries of the pair, and thus provides a probability measure
$(G/K,\Gamma .K)$
commutes with the symmetries of the pair, and thus provides a probability measure
![]() $\mu $
on
$\mu $
on
![]() $\Gamma $
for which the bounded
$\Gamma $
for which the bounded
![]() $\mu $
-harmonic functions are exactly the restriction to
$\mu $
-harmonic functions are exactly the restriction to
![]() $\Gamma $
of the bounded harmonic functions on
$\Gamma $
of the bounded harmonic functions on
![]() $G/K$
. That is, the future Furstenberg–Poisson boundary
$G/K$
. That is, the future Furstenberg–Poisson boundary
![]() $B_+$
of
$B_+$
of
![]() $(\Gamma ,\mu )$
is
$(\Gamma ,\mu )$
is
![]() $(G/P,\nu )$
. The main theorem of [Reference Ballmann and Ledrappier4] shows further that the measure
$(G/P,\nu )$
. The main theorem of [Reference Ballmann and Ledrappier4] shows further that the measure
![]() $\mu $
could be chosen to be symmetric, that is,
$\mu $
could be chosen to be symmetric, that is,
![]() $\check {\mu }=\mu $
. This shows that the past Furstenberg–Poisson boundary
$\check {\mu }=\mu $
. This shows that the past Furstenberg–Poisson boundary
![]() $B_-$
of
$B_-$
of
![]() $(\Gamma ,\mu )$
is
$(\Gamma ,\mu )$
is
![]() $(G/P,\nu )$
as well. We are thus done by Theorem 2.7.
$(G/P,\nu )$
as well. We are thus done by Theorem 2.7.
2.3. Coarse invariance
One can also make a further coarsification.
Definition 2.10. A coarse metric on a G-space U is said to be coarsely invariant if there exists
![]() $C>0$
such that for every
$C>0$
such that for every
![]() $x,y\in U$
and
$x,y\in U$
and
![]() $g\in G$
,
$g\in G$
,
![]() $|d(gx,gy)-d(x,y)|<C$
.
$|d(gx,gy)-d(x,y)|<C$
.
This coarsification turns out to not correspond to a more restrictive type of ergodicity.
Lemma 2.11. Assume
![]() $\Gamma $
is a countable group and
$\Gamma $
is a countable group and
![]() $\Omega $
is a coarsely metrically ergodic Lebesgue
$\Omega $
is a coarsely metrically ergodic Lebesgue
![]() $\Gamma $
-space. Then every coarsely invariant Borel coarse metric on
$\Gamma $
-space. Then every coarsely invariant Borel coarse metric on
![]() $\Omega $
is bounded. In fact, every coarsely invariant Borel function
$\Omega $
is bounded. In fact, every coarsely invariant Borel function
![]() $\Omega \times \Omega \to [0,\infty )$
which is coarsely symmetric and satisfies the coarse triangle inequality is a bounded coarse metric.
$\Omega \times \Omega \to [0,\infty )$
which is coarsely symmetric and satisfies the coarse triangle inequality is a bounded coarse metric.
Proof. Given a coarsely invariant coarse metric d on
![]() $\Omega $
, observe that
$\Omega $
, observe that
![]() $d'(x,y)=\sup \{d(gx,gy)\mid g\in \Gamma \}$
is a
$d'(x,y)=\sup \{d(gx,gy)\mid g\in \Gamma \}$
is a
![]() $\Gamma $
-invariant measurable coarse metric. Its boundedness implies the boundedness of d. The last part of the lemma follows from the fact that the function
$\Gamma $
-invariant measurable coarse metric. Its boundedness implies the boundedness of d. The last part of the lemma follows from the fact that the function
![]() $x\mapsto d'(x,x)$
is automatically bounded, by Remark 2.5.
$x\mapsto d'(x,x)$
is automatically bounded, by Remark 2.5.
Remark 2.12. We could say that
![]() $\Omega $
is coarsely coarse metrically ergodic, but we honestly think this is too much.
$\Omega $
is coarsely coarse metrically ergodic, but we honestly think this is too much.
2.4. Countable quotients
The following lemma shows that up to coarse equivalence, every coarsely separable coarse metric is pulled back from a countable quotient.
Lemma 2.13. Let d be a coarsely separable coarse metric on U. Then there exists a countable measurable quotient
![]() $\pi :U\to V$
and a coarse metric
$\pi :U\to V$
and a coarse metric
![]() $d'$
on V such that d is coarsely equivalent to the metric
$d'$
on V such that d is coarsely equivalent to the metric
![]() $\pi ^{*}d'$
, defined by
$\pi ^{*}d'$
, defined by
![]() $d(x,y)=d'(\pi (x),\pi (y))$
.
$d(x,y)=d'(\pi (x),\pi (y))$
.
Proof. We choose a countable C-dense subset V in U, identify it with
![]() $\mathbb {N}$
and define
$\mathbb {N}$
and define
![]() $\pi $
inductively, sending points at the C-ball around
$\pi $
inductively, sending points at the C-ball around
![]() $v\in V$
to v, unless their
$v\in V$
to v, unless their
![]() $\pi $
value was already determined. We set
$\pi $
value was already determined. We set
![]() $d'=d|_V$
.
$d'=d|_V$
.
2.5. Spaces of probabilities
Given a Borel space U, we endow the space
![]() $\operatorname {Prob}(U)$
with the Borel structure generated by the evaluation maps associated with all bounded Borel functions on U. We will need Proposition 2.15 below to rule out the existence of maps from the (double) boundary of the lattices we will be considering to various probability spaces
$\operatorname {Prob}(U)$
with the Borel structure generated by the evaluation maps associated with all bounded Borel functions on U. We will need Proposition 2.15 below to rule out the existence of maps from the (double) boundary of the lattices we will be considering to various probability spaces
![]() $\operatorname {Prob}(U)$
, including for U the space of distinct boundary triples of a hyperbolic space being acted on.
$\operatorname {Prob}(U)$
, including for U the space of distinct boundary triples of a hyperbolic space being acted on.
If U is a standard Borel space, then
![]() $\operatorname {Prob}(U)$
is also a standard Borel space. If
$\operatorname {Prob}(U)$
is also a standard Borel space. If
![]() $\pi :U\to V$
is a Borel map, then the induced map
$\pi :U\to V$
is a Borel map, then the induced map
![]() $\pi _*:\operatorname {Prob}(U)\to \operatorname {Prob}(V)$
is a Borel map.
$\pi _*:\operatorname {Prob}(U)\to \operatorname {Prob}(V)$
is a Borel map.
We assume henceforth that the Borel space U is endowed with a coarse metric d. In that case, we define the function
by setting
 $$ \begin{align*} \bar{d}(\mu_1,\mu_2)&=\inf \{r>0\mid \text{there exists } \mbox{ a Borel set } A \mbox{ in U},\\ &\quad\operatorname{diam}(A)< r,~\mu_1(A),\mu_2(A)>1/2\}. \end{align*} $$
$$ \begin{align*} \bar{d}(\mu_1,\mu_2)&=\inf \{r>0\mid \text{there exists } \mbox{ a Borel set } A \mbox{ in U},\\ &\quad\operatorname{diam}(A)< r,~\mu_1(A),\mu_2(A)>1/2\}. \end{align*} $$
Note that
![]() $\bar {d}(\mu ,\mu )$
might be arbitrarily large, so this is not necessarily a coarse metric. However, we have the following.
$\bar {d}(\mu ,\mu )$
might be arbitrarily large, so this is not necessarily a coarse metric. However, we have the following.
Lemma 2.14. The function
![]() $\bar {d}$
is symmetric and it satisfies the coarse triangle inequality: the difference
$\bar {d}$
is symmetric and it satisfies the coarse triangle inequality: the difference
![]() $\bar d(\mu _1,\mu _2)-\bar d(\mu _1,\mu _0)-\bar d(\mu _0,\mu _2)$
is uniformly bounded from above. The restriction of
$\bar d(\mu _1,\mu _2)-\bar d(\mu _1,\mu _0)-\bar d(\mu _0,\mu _2)$
is uniformly bounded from above. The restriction of
![]() $\bar {d}$
to U via the identification
$\bar {d}$
to U via the identification
![]() $x\mapsto \delta _x$
gives the coarse metric
$x\mapsto \delta _x$
gives the coarse metric
![]() $(x,y) \mapsto \max \{d(x,y),d(y,x)\}$
which is at a bounded distance away from d.
$(x,y) \mapsto \max \{d(x,y),d(y,x)\}$
which is at a bounded distance away from d.
Moreover, if U is a countable set and d is a Borel coarse metric on U, then
![]() $\bar {d}$
is a Borel function.
$\bar {d}$
is a Borel function.
Proof. The first assertions of the lemma are straightforward. For the last assertion under the extra hypothesis that U is countable, we observe that the infimum in the definition of
![]() $\bar d$
could be taken over the countable collection of the finite subsets of U. This ensures that
$\bar d$
could be taken over the countable collection of the finite subsets of U. This ensures that
![]() $\bar d$
is indeed Borel.
$\bar d$
is indeed Borel.
Proposition 2.15. Let
![]() $\Gamma $
be a countable group and
$\Gamma $
be a countable group and
![]() $\Omega $
be a coarsely metrically ergodic Lebesgue
$\Omega $
be a coarsely metrically ergodic Lebesgue
![]() $\Gamma $
-space. Let U be a Borel space and consider the Borel structure on
$\Gamma $
-space. Let U be a Borel space and consider the Borel structure on
![]() $\operatorname {Prob}(U)$
generated by evaluation at bounded Borel functions on U. If there exists a Borel
$\operatorname {Prob}(U)$
generated by evaluation at bounded Borel functions on U. If there exists a Borel
![]() $\Gamma $
-map from
$\Gamma $
-map from
![]() $\Omega $
to
$\Omega $
to
![]() $\operatorname {Prob}(U)$
, then every
$\operatorname {Prob}(U)$
, then every
![]() $\Gamma $
-invariant Borel, coarsely separable coarse metric on U has bounded
$\Gamma $
-invariant Borel, coarsely separable coarse metric on U has bounded
![]() $\Gamma $
-orbits.
$\Gamma $
-orbits.
Proof. We assume
![]() $f:\Omega \to \operatorname {Prob}(U)$
is a Borel
$f:\Omega \to \operatorname {Prob}(U)$
is a Borel
![]() $\Gamma $
-map and d is a coarsely separable
$\Gamma $
-map and d is a coarsely separable
![]() $\Gamma $
-invariant Borel coarse metric on U, and we argue to show that the
$\Gamma $
-invariant Borel coarse metric on U, and we argue to show that the
![]() $\Gamma $
-orbits in U are d-bounded. Since the restriction of
$\Gamma $
-orbits in U are d-bounded. Since the restriction of
![]() $\bar {d}$
to U is at a bounded distance away from d (see Lemma 2.14), it is enough to show that
$\bar {d}$
to U is at a bounded distance away from d (see Lemma 2.14), it is enough to show that
![]() $\operatorname {Prob}(U)$
contains a
$\operatorname {Prob}(U)$
contains a
![]() $\bar {d}$
-bounded subset.
$\bar {d}$
-bounded subset.
We let
![]() $\pi :U\to V$
and
$\pi :U\to V$
and
![]() $d'$
be as in Lemma 2.13, so that the pull back
$d'$
be as in Lemma 2.13, so that the pull back
![]() $\pi ^{*}d'$
is coarsely equivalent to d. It follows
$\pi ^{*}d'$
is coarsely equivalent to d. It follows
![]() $\overline {\pi ^{*}d'}$
is coarsely equivalent to
$\overline {\pi ^{*}d'}$
is coarsely equivalent to
![]() $\bar {d}$
. By Lemma 2.14,
$\bar {d}$
. By Lemma 2.14,
![]() $\bar {d'}$
is Borel, symmetric and it satisfies the coarse triangle inequality. Hence, the same applies also to
$\bar {d'}$
is Borel, symmetric and it satisfies the coarse triangle inequality. Hence, the same applies also to
![]() $\overline {\pi ^{*}d'}=(\pi _*)^{*}\bar {d'}$
.
$\overline {\pi ^{*}d'}=(\pi _*)^{*}\bar {d'}$
.
By Lemma 2.11,
![]() $f^{*}\overline {\pi ^{*}d'}$
is a bounded coarse metric on
$f^{*}\overline {\pi ^{*}d'}$
is a bounded coarse metric on
![]() $\Omega $
. We deduce that
$\Omega $
. We deduce that
![]() $\operatorname {Prob}(U)$
contains a
$\operatorname {Prob}(U)$
contains a
![]() $\overline {\pi ^{*}d'}$
-bounded subset. The proof is now complete, as this subset is
$\overline {\pi ^{*}d'}$
-bounded subset. The proof is now complete, as this subset is
![]() $\bar {d}$
-bounded.
$\bar {d}$
-bounded.
2.6. Barycentre maps
The last result in this section is not about coarse metric ergodicity, but it fits here since we are discussing the spaces
![]() $\operatorname {Prob}(U)$
. Let U be a Borel space and d a measurable metric on U. Roughly, we will construct ‘barycentres’ for probability measures, and the property that we will need is roughly that measures with bounded Radon–Nykodim derivatives with respect to each other have approximately the same barycentre.
$\operatorname {Prob}(U)$
. Let U be a Borel space and d a measurable metric on U. Roughly, we will construct ‘barycentres’ for probability measures, and the property that we will need is roughly that measures with bounded Radon–Nykodim derivatives with respect to each other have approximately the same barycentre.
We denote by
![]() $\operatorname {Bdd}(U)$
the space of non-empty d-bounded subsets of U. Given a measure
$\operatorname {Bdd}(U)$
the space of non-empty d-bounded subsets of U. Given a measure
![]() $m\in \operatorname {Prob}(U)$
and
$m\in \operatorname {Prob}(U)$
and
![]() $\epsilon \in (0,1/2)$
, we define
$\epsilon \in (0,1/2)$
, we define
and we let
![]() $\beta _\epsilon (m)$
be the union of all Borel sets A in U of diameter less than
$\beta _\epsilon (m)$
be the union of all Borel sets A in U of diameter less than
![]() $r_\epsilon (m)+1$
and
$r_\epsilon (m)+1$
and
![]() $m(A)\geq 1-\epsilon $
. Note that since
$m(A)\geq 1-\epsilon $
. Note that since
![]() $1-\epsilon <1$
, the infimum in the definition of
$1-\epsilon <1$
, the infimum in the definition of
![]() $r_\epsilon $
is taken over a non-empty set and
$r_\epsilon $
is taken over a non-empty set and
![]() $\beta _\epsilon (m)$
is a non-empty subset of U.
$\beta _\epsilon (m)$
is a non-empty subset of U.
Lemma 2.16. Let U be a Borel space and d a measurable metric on U. For every
![]() $\epsilon \in (0,1/2)$
and for every
$\epsilon \in (0,1/2)$
and for every
![]() $m\in \operatorname {Prob}(U)$
,
$m\in \operatorname {Prob}(U)$
,
![]() $\beta _\epsilon (m)$
is a non-empty d-bounded subset of U, and the map
$\beta _\epsilon (m)$
is a non-empty d-bounded subset of U, and the map
![]() $\beta _\epsilon :\operatorname {Prob}(U)\to \operatorname {Bdd}(U)$
is equivariant under all isometries of U. Moreover, given
$\beta _\epsilon :\operatorname {Prob}(U)\to \operatorname {Bdd}(U)$
is equivariant under all isometries of U. Moreover, given
![]() $C\geq 1$
, if
$C\geq 1$
, if
![]() $m_1,m_2\in \operatorname {Prob}(U)$
are such that for every measurable
$m_1,m_2\in \operatorname {Prob}(U)$
are such that for every measurable
![]() $E\subseteq U$
, we have
$E\subseteq U$
, we have
then
where
![]() $R=r_{\epsilon /C}(m_1)+1$
.
$R=r_{\epsilon /C}(m_1)+1$
.
Proof. By the fact that
![]() $1-\epsilon>1/2$
, all the Borel subsets A with
$1-\epsilon>1/2$
, all the Borel subsets A with
![]() $m(A)\geq 1-\epsilon $
intersect in pairs, so the diameter of
$m(A)\geq 1-\epsilon $
intersect in pairs, so the diameter of
![]() $\beta _\epsilon (m)$
is bounded by
$\beta _\epsilon (m)$
is bounded by
![]() $2r_\epsilon (m)+2$
. Equivariance is clear.
$2r_\epsilon (m)+2$
. Equivariance is clear.
Let now
![]() $C,m_1,m_2$
as in the last statement. Note that every Borel subset A of U with
$C,m_1,m_2$
as in the last statement. Note that every Borel subset A of U with
![]() $m_1(A)\geq 1-\epsilon /C$
satisfies
$m_1(A)\geq 1-\epsilon /C$
satisfies
![]() $m_2(U\setminus A)\leq Cm_1(U\setminus A) \leq \epsilon $
, and hence
$m_2(U\setminus A)\leq Cm_1(U\setminus A) \leq \epsilon $
, and hence
![]() $m_2(A)\geq 1-\epsilon $
. It follows that
$m_2(A)\geq 1-\epsilon $
. It follows that
![]() $r_{\epsilon }(m_2)\leq r_{\epsilon /C}(m_1)$
.
$r_{\epsilon }(m_2)\leq r_{\epsilon /C}(m_1)$
.
If
![]() $u\in \beta _{\epsilon }(m_2)$
, then by definition, u belongs to a Borel set A with
$u\in \beta _{\epsilon }(m_2)$
, then by definition, u belongs to a Borel set A with
![]() $m_2(A)\geq 1-\epsilon $
and diameter less than
$m_2(A)\geq 1-\epsilon $
and diameter less than
![]() $r_{\epsilon }(m_2)+1\leq r_{\epsilon /C}(m_1)+1$
. Fix any Borel set B of diameter less than
$r_{\epsilon }(m_2)+1\leq r_{\epsilon /C}(m_1)+1$
. Fix any Borel set B of diameter less than
![]() $r_{\epsilon /C}(m_1)+1$
and
$r_{\epsilon /C}(m_1)+1$
and
![]() $m_1(B)\geq 1-\epsilon /C$
. Then,
$m_1(B)\geq 1-\epsilon /C$
. Then,
![]() $m_2(B)\geq 1-\epsilon $
and we get
$m_2(B)\geq 1-\epsilon $
and we get
![]() $A\cap B\neq \emptyset $
. In particular, u lies within
$A\cap B\neq \emptyset $
. In particular, u lies within
![]() $r_{\epsilon /C}(m_1)+1$
of B, whence of
$r_{\epsilon /C}(m_1)+1$
of B, whence of
![]() $\beta _{\epsilon /C}(m_1)$
.
$\beta _{\epsilon /C}(m_1)$
.
3. Boundary maps
In this section, we fix a countable group
![]() $\Gamma $
and discuss boundary maps associated to various hyperbolic structures on
$\Gamma $
and discuss boundary maps associated to various hyperbolic structures on
![]() $\Gamma $
. In particular, we prove Theorem 3.1 below. The novel aspect of this theorem is that the Gromov hyperbolic spaces it deals with are not assumed to be proper. Recall that the Gromov boundary of a proper Gromov hyperbolic space is compact and the associated action is a convergence group action. Boundary maps associated with such actions were considered in [Reference Bader and Furman3, Theorem 3.2].
$\Gamma $
. In particular, we prove Theorem 3.1 below. The novel aspect of this theorem is that the Gromov hyperbolic spaces it deals with are not assumed to be proper. Recall that the Gromov boundary of a proper Gromov hyperbolic space is compact and the associated action is a convergence group action. Boundary maps associated with such actions were considered in [Reference Bader and Furman3, Theorem 3.2].
Given a Lebesgue
![]() $\Gamma $
-space
$\Gamma $
-space
![]() $\Omega $
and a standard Borel
$\Omega $
and a standard Borel
![]() $\Gamma $
-space V, we denote by
$\Gamma $
-space V, we denote by
![]() $\operatorname {Map}_\Gamma (\Omega ,V)$
the space of equivalence classes of measurable
$\operatorname {Map}_\Gamma (\Omega ,V)$
the space of equivalence classes of measurable
![]() $\Gamma $
-equivariant maps
$\Gamma $
-equivariant maps
![]() $f:\Omega \to V$
, that is, those measurable maps that satisfy
$f:\Omega \to V$
, that is, those measurable maps that satisfy
![]() $f(g.\omega )=g.f(\omega )$
for a.e.
$f(g.\omega )=g.f(\omega )$
for a.e.
![]() $g\in \Gamma $
and a.e.
$g\in \Gamma $
and a.e.
![]() $\omega \in \Omega $
. Two such maps
$\omega \in \Omega $
. Two such maps
![]() $f, f':\Omega \to V$
are identified if
$f, f':\Omega \to V$
are identified if
![]() $f(\omega )=f'(\omega )$
for a.e.
$f(\omega )=f'(\omega )$
for a.e.
![]() $\omega \in \Omega $
. Any such map f is equivalent to
$\omega \in \Omega $
. Any such map f is equivalent to
![]() $f_0:\Omega \to V$
such that for every
$f_0:\Omega \to V$
such that for every
![]() $g\in \Gamma $
, we have
$g\in \Gamma $
, we have
![]() $f_0(g.\omega )=g.f_0(\omega )$
a.e.
$f_0(g.\omega )=g.f_0(\omega )$
a.e.
![]() $\omega \in \Omega $
[Reference Zimmer18, Proposition B.5].
$\omega \in \Omega $
[Reference Zimmer18, Proposition B.5].
In the following theorem,
![]() $(X,d)$
is a separable Gromov hyperbolic space,
$(X,d)$
is a separable Gromov hyperbolic space,
![]() $\Gamma $
a countable group and
$\Gamma $
a countable group and
![]() $\Gamma \longrightarrow \operatorname {Isom}(X,d)$
a homomorphism. We denote by
$\Gamma \longrightarrow \operatorname {Isom}(X,d)$
a homomorphism. We denote by
![]() $\partial X$
the associated Gromov boundary, which is a Polish space on which
$\partial X$
the associated Gromov boundary, which is a Polish space on which
![]() $\Gamma $
acts by homeomorphisms, let
$\Gamma $
acts by homeomorphisms, let
![]() $\partial X^2$
be its square and
$\partial X^2$
be its square and
the subset of pairs of distinct boundary points. Since X is not assumed to be proper,
![]() $\partial X$
is not necessarily compact. Yet,
$\partial X$
is not necessarily compact. Yet,
![]() $\partial X$
is a standard Borel space and so are
$\partial X$
is a standard Borel space and so are
![]() $\partial X^{(2)}\subset \partial X^2$
. The action of
$\partial X^{(2)}\subset \partial X^2$
. The action of
![]() $\Gamma $
on all these spaces is Borel.
$\Gamma $
on all these spaces is Borel.
Theorem 3.1. (Compare [Reference Bader and Furman3, Theorem 3.2])
Let
![]() $\Gamma $
be a countable group. Assume
$\Gamma $
be a countable group. Assume
![]() $B_-$
and
$B_-$
and
![]() $B_+$
are amenable Lebesgue
$B_+$
are amenable Lebesgue
![]() $\Gamma $
-spaces such that the diagonal
$\Gamma $
-spaces such that the diagonal
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $B_-\times B_+$
is ergodic and coarsely metrically ergodic. Let
$B_-\times B_+$
is ergodic and coarsely metrically ergodic. Let
![]() $(X,d)$
be a separable, Gromov hyperbolic (possibly non-proper), geodesic metric space and let
$(X,d)$
be a separable, Gromov hyperbolic (possibly non-proper), geodesic metric space and let
![]() $\Gamma $
act on X by isometries. Assume that
$\Gamma $
act on X by isometries. Assume that
![]() $\Gamma $
does not fix a bounded set in X and does not fix a point or a pair of points in
$\Gamma $
does not fix a bounded set in X and does not fix a point or a pair of points in
![]() $\partial X$
.
$\partial X$
.
Then there exist
![]() $\phi _-\in \operatorname {Map}_\Gamma (B_-,\partial X)$
,
$\phi _-\in \operatorname {Map}_\Gamma (B_-,\partial X)$
,
![]() $\phi _+\in \operatorname {Map}_\Gamma (B_+,\partial X)$
such that the image of the map
$\phi _+\in \operatorname {Map}_\Gamma (B_+,\partial X)$
such that the image of the map
![]() $\phi _{\bowtie }\in \operatorname {Map}_\Gamma (B_-\times B_+,\partial X^2)$
given by
$\phi _{\bowtie }\in \operatorname {Map}_\Gamma (B_-\times B_+,\partial X^2)$
given by
is contained, modulo a null set, in the set of distinct pairs
![]() $\partial X^{(2)}\subset \partial X^2$
. Moreover, each of the following assertions holds:
$\partial X^{(2)}\subset \partial X^2$
. Moreover, each of the following assertions holds:
-
(i)
 $\operatorname {Map}_\Gamma (B_-,\operatorname {Prob}(\partial X))=\{ \delta \circ \phi _-\}$
and
$\operatorname {Map}_\Gamma (B_-,\operatorname {Prob}(\partial X))=\{ \delta \circ \phi _-\}$
and
 $\operatorname {Map}_\Gamma (B_+,\operatorname {Prob}(\partial X))=\{ \delta \circ \phi _+\}$
;
$\operatorname {Map}_\Gamma (B_+,\operatorname {Prob}(\partial X))=\{ \delta \circ \phi _+\}$
; -
(ii)
 $\operatorname {Map}_\Gamma (B_-\times B_+,\partial X) = \{ \phi _-\circ \operatorname {pr}_-,\phi _+\circ \operatorname {pr}_+\}$
;
$\operatorname {Map}_\Gamma (B_-\times B_+,\partial X) = \{ \phi _-\circ \operatorname {pr}_-,\phi _+\circ \operatorname {pr}_+\}$
; -
(iii)
 $\operatorname {Map}_\Gamma (B_-\times B_+,\partial X^{(2)}) = \{ \phi _{\bowtie },\ \tau \circ \phi _{\bowtie }\}$
, where
$\operatorname {Map}_\Gamma (B_-\times B_+,\partial X^{(2)}) = \{ \phi _{\bowtie },\ \tau \circ \phi _{\bowtie }\}$
, where
 $\tau (\xi ,\xi ')=(\xi ',\xi )$
.
$\tau (\xi ,\xi ')=(\xi ',\xi )$
.
The rest of this section is devoted to the proof of this theorem.
3.1. The horoclosure of a separable metric space
Let
![]() $(X, d)$
be a separable metric space. We consider the vector space of functions from X to
$(X, d)$
be a separable metric space. We consider the vector space of functions from X to
![]() $\mathbb {R}$
endowed with the topology of pointwise convergence, that is, the product space
$\mathbb {R}$
endowed with the topology of pointwise convergence, that is, the product space
![]() $\mathbb {R}^X$
, and the constant function
$\mathbb {R}^X$
, and the constant function
![]() $\mathbf {1}\in \mathbb {R}^X$
. We endow
$\mathbf {1}\in \mathbb {R}^X$
. We endow
![]() $\mathbb {R}^X/\mathbb {R}\cdot \mathbf {1}$
with the quotient topological vector space structure. We map X to
$\mathbb {R}^X/\mathbb {R}\cdot \mathbf {1}$
with the quotient topological vector space structure. We map X to
![]() $\mathbb {R}^X$
by
$\mathbb {R}^X$
by
![]() $x\mapsto d(\cdot ,x)$
and consider its image in
$x\mapsto d(\cdot ,x)$
and consider its image in
![]() $\mathbb {R}^X/\mathbb {R}\cdot \mathbf {1}$
. We denote the closure of the image of X in
$\mathbb {R}^X/\mathbb {R}\cdot \mathbf {1}$
. We denote the closure of the image of X in
![]() $\mathbb {R}^X/\mathbb {R}\cdot \mathbf {1}$
by
$\mathbb {R}^X/\mathbb {R}\cdot \mathbf {1}$
by
![]() $\bar {X}$
and call it the horoclosure of X. We denote the obvious map
$\bar {X}$
and call it the horoclosure of X. We denote the obvious map
![]() $X\to \bar {X}$
by i and the preimage of
$X\to \bar {X}$
by i and the preimage of
![]() $\bar {X}$
in
$\bar {X}$
in
![]() $\mathbb {R}^X$
by
$\mathbb {R}^X$
by
![]() $\tilde {X}$
. Elements of
$\tilde {X}$
. Elements of
![]() $\bar {X}$
(and, by abuse of notation, also elements of
$\bar {X}$
(and, by abuse of notation, also elements of
![]() $\tilde {X}$
) are called horofunctions. It is a common practice to fix a base point
$\tilde {X}$
) are called horofunctions. It is a common practice to fix a base point
![]() $x\in X$
and to consider the subspace
$x\in X$
and to consider the subspace
It is well known that the horoclosure of X is a compactification of it.
Lemma 3.2.
![]() $\bar {X}$
is a compact metrizable space and the map
$\bar {X}$
is a compact metrizable space and the map
![]() $i:X\to \bar {X}$
is an injective continuous map. For a fixed
$i:X\to \bar {X}$
is an injective continuous map. For a fixed
![]() $x\in X$
, the map
$x\in X$
, the map
![]() $\tilde {X}_x\to \bar {X}$
is a homeomorphism.
$\tilde {X}_x\to \bar {X}$
is a homeomorphism.
Proof. The fact that i is continuous is obvious. For
![]() $x\neq y$
in X, note that the difference function
$x\neq y$
in X, note that the difference function
![]() $d(x,\cdot )-d(y,\cdot )$
is not constant, as it attains different values at x and y. Thus, i is injective. We now fix
$d(x,\cdot )-d(y,\cdot )$
is not constant, as it attains different values at x and y. Thus, i is injective. We now fix
![]() $x\in X$
. First, we note that
$x\in X$
. First, we note that
![]() $\tilde {X}_x$
is closed subset of
$\tilde {X}_x$
is closed subset of
 $$ \begin{align*} \prod_{y\in X} [-d(x,y),d(x,y)] \subset \prod_{y\in X} \mathbb{R}=\mathbb{R}^X, \end{align*} $$
$$ \begin{align*} \prod_{y\in X} [-d(x,y),d(x,y)] \subset \prod_{y\in X} \mathbb{R}=\mathbb{R}^X, \end{align*} $$
and thus it is compact. Fixing a countable dense subset
![]() $X_0$
in X, the obvious map
$X_0$
in X, the obvious map
![]() $\tilde {X}_x\to \mathbb {R}^X \to \mathbb {R}^{X_0}$
is a continuous injection (as
$\tilde {X}_x\to \mathbb {R}^X \to \mathbb {R}^{X_0}$
is a continuous injection (as
![]() $\tilde {X}_x$
consists of continuous functions), and hence a homeomorphism onto its image. The image is a Frechet space, and thus metrizable. It follows that
$\tilde {X}_x$
consists of continuous functions), and hence a homeomorphism onto its image. The image is a Frechet space, and thus metrizable. It follows that
![]() $\tilde {X}_x$
is metrizable. Since the natural map
$\tilde {X}_x$
is metrizable. Since the natural map
![]() $\tilde {X}_x\to \bar {X}$
is also a continuous bijection, we conclude that it is a homeomorphism, and deduce that
$\tilde {X}_x\to \bar {X}$
is also a continuous bijection, we conclude that it is a homeomorphism, and deduce that
![]() $\bar {X}$
is compact and metrizable.
$\bar {X}$
is compact and metrizable.
Loosely speaking, we often identify X with
![]() $i(X) \subset \bar {X}$
. Note, however, that the image of X is in general not open in
$i(X) \subset \bar {X}$
. Note, however, that the image of X is in general not open in
![]() $\bar {X}$
, and the map i is not a homeomorphism onto its image.
$\bar {X}$
, and the map i is not a homeomorphism onto its image.
We decompose
![]() $\tilde {X}$
as follows:
$\tilde {X}$
as follows:
 $$ \begin{align*} \begin{aligned} \tilde{X}^b &= \{ {h\in \tilde{X}}\mid{ f \mbox{ is bounded from below}} \} , \\ \tilde{X}^u &= \{ {h\in \tilde{X}}\mid{ f \mbox{ is unbounded from below}} \}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \tilde{X}^b &= \{ {h\in \tilde{X}}\mid{ f \mbox{ is bounded from below}} \} , \\ \tilde{X}^u &= \{ {h\in \tilde{X}}\mid{ f \mbox{ is unbounded from below}} \}. \end{aligned} \end{align*} $$
This decomposition is constant on the fibres of
![]() $\tilde {X}\to \bar {X}$
, and thus gives a corresponding decomposition
$\tilde {X}\to \bar {X}$
, and thus gives a corresponding decomposition
![]() $\bar {X}=\bar {X}^b\cup \bar {X}^u$
. Clearly, we have
$\bar {X}=\bar {X}^b\cup \bar {X}^u$
. Clearly, we have
![]() $i(X) \subseteq \bar X^b$
so that
$i(X) \subseteq \bar X^b$
so that
![]() $\bar X^b$
is dense in
$\bar X^b$
is dense in
![]() $\bar X$
.
$\bar X$
.
Lemma 3.3. The decompositions
![]() $\tilde {X}=\tilde {X}^b\cup \tilde {X}^u$
and
$\tilde {X}=\tilde {X}^b\cup \tilde {X}^u$
and
![]() $\bar {X}=\bar {X}^b\cup \bar {X}^u$
are measurable and
$\bar {X}=\bar {X}^b\cup \bar {X}^u$
are measurable and
![]() $\operatorname {Isom}(X)$
-equivariant.
$\operatorname {Isom}(X)$
-equivariant.
Proof. The equivariance of the decompositions is obvious. Fix a dense countable subset
![]() $X_0$
in X and use the fact that
$X_0$
in X and use the fact that
![]() $\tilde {X}$
consists of continuous functions to note that
$\tilde {X}$
consists of continuous functions to note that
 $$ \begin{align*} \tilde{X}^u=\bigcap_{n\in \mathbb{N}}\bigcup_{x\in X_0} \{ {h\in \tilde{X}}\mid{ h(x)\leq -n } \} , \end{align*} $$
$$ \begin{align*} \tilde{X}^u=\bigcap_{n\in \mathbb{N}}\bigcup_{x\in X_0} \{ {h\in \tilde{X}}\mid{ h(x)\leq -n } \} , \end{align*} $$
and thus
![]() $\tilde {X}^u \subset \tilde {X}$
is measurable. Fixing
$\tilde {X}^u \subset \tilde {X}$
is measurable. Fixing
![]() $x\in X$
, using the measurability of
$x\in X$
, using the measurability of
![]() $\tilde {X}^u_x$
, we observe that
$\tilde {X}^u_x$
, we observe that
![]() $\bar {X}^u\subset \bar {X}$
is measurable.
$\bar {X}^u\subset \bar {X}$
is measurable.
3.2. The horoclosure of a hyperbolic metric space
We now assume, in addition, that the separable metric space
![]() $(X,d)$
is geodesic and Gromov hyperbolic (as before, it is possibly non-proper), and that there is a
$(X,d)$
is geodesic and Gromov hyperbolic (as before, it is possibly non-proper), and that there is a
![]() $\Gamma $
-action on it for some group
$\Gamma $
-action on it for some group
![]() $\Gamma $
.
$\Gamma $
.
The following lemma will allow us to use coarse metric ergodicity in the setting of Theorem 4.4 to exclude the existence of
![]() $\Gamma $
-maps to
$\Gamma $
-maps to
![]() $\bar {X}^b$
.
$\bar {X}^b$
.
Lemma 3.4. There is a Borel coarsely separable pseudo-metric on
![]() $\bar {X}^b$
on which
$\bar {X}^b$
on which
![]() $\Gamma $
acts by isometries. Moreover, if the
$\Gamma $
acts by isometries. Moreover, if the
![]() $\Gamma $
-action on X is unbounded, then the
$\Gamma $
-action on X is unbounded, then the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $\bar {X}^b$
is unbounded.
$\bar {X}^b$
is unbounded.
Proof. We will show the analogous statement for
![]() $\tilde {X}^b$
rather than
$\tilde {X}^b$
rather than
![]() $\bar {X}^b$
, and we note that the pseudo-metric we construct below passes to
$\bar {X}^b$
, and we note that the pseudo-metric we construct below passes to
![]() $\bar {X}^b$
(since the sets
$\bar {X}^b$
(since the sets
![]() $\tilde {I}(h)$
below do not change when adding a constant to h).
$\tilde {I}(h)$
below do not change when adding a constant to h).
We first show that the function
is measurable and
![]() $\operatorname {Isom}(X)$
-invariant, and that for every
$\operatorname {Isom}(X)$
-invariant, and that for every
![]() $h\in \tilde {X}^b$
, the set
$h\in \tilde {X}^b$
, the set
is bounded in X.
To see that
![]() $\inf $
is measurable, we fix a dense countable subset
$\inf $
is measurable, we fix a dense countable subset
![]() $X_0$
in X and we use the continuity of the functions in
$X_0$
in X and we use the continuity of the functions in
![]() $\tilde {X}^b$
to observe that
$\tilde {X}^b$
to observe that
The invariance of this function under
![]() $\operatorname {Isom}(X)$
is clear.
$\operatorname {Isom}(X)$
is clear.
Fix
![]() $h \in \tilde {X}^b$
. We now argue that
$h \in \tilde {X}^b$
. We now argue that
![]() $\tilde {I}(h)$
is of diameter bounded by
$\tilde {I}(h)$
is of diameter bounded by
![]() $C=8+4\delta $
, where
$C=8+4\delta $
, where
![]() $\delta $
is the hyperbolicity constant associated with the thin triangle property of X. Without loss of generality, we assume that
$\delta $
is the hyperbolicity constant associated with the thin triangle property of X. Without loss of generality, we assume that
![]() $\inf (h)=0$
. Assuming the negation, we fix two points
$\inf (h)=0$
. Assuming the negation, we fix two points
![]() $x,x'$
satisfying
$x,x'$
satisfying
![]() $d(x,x')>C$
and
$d(x,x')>C$
and
![]() $h(x),h(x')<1$
. We consider a finite sequence of points
$h(x),h(x')<1$
. We consider a finite sequence of points
![]() $x_0,x_1,\ldots ,x_n$
on a geodesic segment from x to
$x_0,x_1,\ldots ,x_n$
on a geodesic segment from x to
![]() $x'$
such that
$x'$
such that
![]() $x_0=x$
,
$x_0=x$
,
![]() $x_n=x'$
and
$x_n=x'$
and
![]() $d(x_i,x_{i+1})<1$
. We consider the image of h in
$d(x_i,x_{i+1})<1$
. We consider the image of h in
![]() $\bar {X}$
along with its neighbourhood given by
$\bar {X}$
along with its neighbourhood given by
We fix a point
![]() $y\in X$
whose image in
$y\in X$
whose image in
![]() $\bar {X}$
is in U. We thus have
$\bar {X}$
is in U. We thus have
We consider geodesic segments from y to x and from y to
![]() $x'$
and, using that
$x'$
and, using that
![]() $x,x'$
and y are the vertices of a thin triangle, we fix i such that
$x,x'$
and y are the vertices of a thin triangle, we fix i such that
![]() $x_i$
lies at distance at most
$x_i$
lies at distance at most
![]() $1+\delta $
from these segments. Thus,
$1+\delta $
from these segments. Thus,
 $$ \begin{align*} \begin{aligned} &d(y,x_i)+d(x_i,x)\leq d(y,x)+2+2\delta,\\ &d(y,x_i)+d(x_i,x')\leq d(y,x')+2+2\delta. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &d(y,x_i)+d(x_i,x)\leq d(y,x)+2+2\delta,\\ &d(y,x_i)+d(x_i,x')\leq d(y,x')+2+2\delta. \end{aligned} \end{align*} $$
Note that
![]() $d(x,x_i)+d(x_i,x')=d(x,x')$
. Upon possibly interchanging the roles of x and
$d(x,x_i)+d(x_i,x')=d(x,x')$
. Upon possibly interchanging the roles of x and
![]() $x'$
, we will assume that
$x'$
, we will assume that
![]() $d(x,x_i)\geq d(x,x')/2$
. In particular,
$d(x,x_i)\geq d(x,x')/2$
. In particular,
![]() $d(x,x_i)\geq C/2$
. Taking
$d(x,x_i)\geq C/2$
. Taking
![]() $j=0$
in equation (3.1), we now have
$j=0$
in equation (3.1), we now have
 $$ \begin{align*} 0 &= \inf(h) \\ & \leq h(x_i) \\ & < 1+d(y,x_i)+h(x)-d(y,x) \\ &\leq 1+(d(y,x)+2+2\delta- d(x_i,x))+h(x)-d(y,x)\\ &< (3+h(x))+2\delta-d(x_i,x) \\ & \leq 4+2\delta-C/2 =0. \end{align*} $$
$$ \begin{align*} 0 &= \inf(h) \\ & \leq h(x_i) \\ & < 1+d(y,x_i)+h(x)-d(y,x) \\ &\leq 1+(d(y,x)+2+2\delta- d(x_i,x))+h(x)-d(y,x)\\ &< (3+h(x))+2\delta-d(x_i,x) \\ & \leq 4+2\delta-C/2 =0. \end{align*} $$
This is a contradiction, and thus indeed the diameter of
![]() $\tilde {I}(h)$
is bounded by C.
$\tilde {I}(h)$
is bounded by C.
We can now define the required pseudo-metric
![]() $\rho $
by setting
$\rho $
by setting
This is the pull-back of a metric, so it is a pseudo-metric, and
![]() $\Gamma $
clearly acts on it by isometries. The fact that the
$\Gamma $
clearly acts on it by isometries. The fact that the
![]() $\tilde {I}(\cdot )$
are bounded implies the claim on unboundedness of the action. Moreover, coarse separability follows from separability of X and (uniform) boundedness of the
$\tilde {I}(\cdot )$
are bounded implies the claim on unboundedness of the action. Moreover, coarse separability follows from separability of X and (uniform) boundedness of the
![]() $\tilde {I}(\cdot )$
. What is left to show is that
$\tilde {I}(\cdot )$
. What is left to show is that
![]() $\rho $
is Borel, and to do so, we have to show that for all
$\rho $
is Borel, and to do so, we have to show that for all
![]() $r\in \mathbb R$
, we have that
$r\in \mathbb R$
, we have that
![]() $\Delta _r=\{(h,h'): \rho (h,h')> r\}\subseteq \tilde {X}^b \times \tilde {X}^b$
is Borel. Expanding the definitions,
$\Delta _r=\{(h,h'): \rho (h,h')> r\}\subseteq \tilde {X}^b \times \tilde {X}^b$
is Borel. Expanding the definitions,
![]() $\Delta _r$
is the set of pairs
$\Delta _r$
is the set of pairs
![]() $(h,h')$
such that
$(h,h')$
such that
![]() $\tilde {I}(h)$
and
$\tilde {I}(h)$
and
![]() $\tilde {I}(h')$
lie at Hausdorff distance more than r. In turn, this means that there exists
$\tilde {I}(h')$
lie at Hausdorff distance more than r. In turn, this means that there exists
![]() $x\in \tilde {I}(h)\cap X_0$
such that all
$x\in \tilde {I}(h)\cap X_0$
such that all
![]() $y\in \tilde {I}(h')\cap X_0$
lie at distance more than r from x, or that the same holds switching the roles of h and
$y\in \tilde {I}(h')\cap X_0$
lie at distance more than r from x, or that the same holds switching the roles of h and
![]() $h'$
(to justify the ‘
$h'$
(to justify the ‘
![]() $\cap X_0$
’, note that
$\cap X_0$
’, note that
![]() $\tilde {I}(h)\cap X_0$
is dense in
$\tilde {I}(h)\cap X_0$
is dense in
![]() $\tilde {I}(h)$
in view of the continuity of h, and similarly for
$\tilde {I}(h)$
in view of the continuity of h, and similarly for
![]() $h'$
). Denoting
$h'$
). Denoting
![]() $\tilde {J}(z)=\{k\in \tilde {X}^b: z\in \tilde {I}(k)\}$
for
$\tilde {J}(z)=\{k\in \tilde {X}^b: z\in \tilde {I}(k)\}$
for
![]() $z\in Z$
, the first case is further equivalent to
$z\in Z$
, the first case is further equivalent to
![]() $h'$
not lying in
$h'$
not lying in
![]() $\bigcup _{y\in X_0 : d(x,y)\leq r} \tilde {J}(y)$
, which is the subset of
$\bigcup _{y\in X_0 : d(x,y)\leq r} \tilde {J}(y)$
, which is the subset of
![]() $\tilde {X}^b$
of all k such that
$\tilde {X}^b$
of all k such that
![]() $\tilde {I}(k)$
contains some
$\tilde {I}(k)$
contains some
![]() $y\in X_0$
within distance r of x (the other case is similar). Hence, we have
$y\in X_0$
within distance r of x (the other case is similar). Hence, we have
 $$ \begin{align*} \Delta_r&=\bigcup_{x\in X_0}\bigg( \tilde{J}(x) \times \bigg(\tilde{X}^b-\bigcup_{y\in X_0 : d(x,y)\leq r}\tilde{J}(y)\bigg) \bigg)\\ &\quad\cup \bigcup_{y\in X_0} \bigg( \bigg(\tilde{X}^b-\bigcup_{x\in X_0 : d(x,y)\leq r} \tilde{J}(y)\bigg)\times \tilde{J}(x)\bigg). \end{align*} $$
$$ \begin{align*} \Delta_r&=\bigcup_{x\in X_0}\bigg( \tilde{J}(x) \times \bigg(\tilde{X}^b-\bigcup_{y\in X_0 : d(x,y)\leq r}\tilde{J}(y)\bigg) \bigg)\\ &\quad\cup \bigcup_{y\in X_0} \bigg( \bigg(\tilde{X}^b-\bigcup_{x\in X_0 : d(x,y)\leq r} \tilde{J}(y)\bigg)\times \tilde{J}(x)\bigg). \end{align*} $$
Hence,
![]() $\Delta _r$
is Borel provided that all
$\Delta _r$
is Borel provided that all
![]() $\tilde J(z)$
are Borel. However,
$\tilde J(z)$
are Borel. However,
![]() $\tilde J(z)=\{k\in \tilde {X}^b: k(z)<\inf (k)+1\}$
, so it is measurable in view of the measurability of
$\tilde J(z)=\{k\in \tilde {X}^b: k(z)<\inf (k)+1\}$
, so it is measurable in view of the measurability of
![]() $\inf $
, as required.
$\inf $
, as required.
3.3. The Gromov boundary
While the construction of the Gromov boundary
![]() $\partial X$
is fairly standard, it is commonly taken under a properness assumption on X. In preparation for our more general discussion, we review this construction (for X possibly non-proper) below, and we also relate it to horoclosures. As is common, we fix from now on a base point
$\partial X$
is fairly standard, it is commonly taken under a properness assumption on X. In preparation for our more general discussion, we review this construction (for X possibly non-proper) below, and we also relate it to horoclosures. As is common, we fix from now on a base point
![]() $o\in X$
. For
$o\in X$
. For
![]() $x\in X$
, we use the shorthand notation
$x\in X$
, we use the shorthand notation
![]() $|x|=d(o,x)$
. Gromov products will be taken, unless otherwise stated, with respect to o. That is, for
$|x|=d(o,x)$
. Gromov products will be taken, unless otherwise stated, with respect to o. That is, for
![]() $x,y\in X$
, we set
$x,y\in X$
, we set
In our discussion below, we fix
![]() $\delta>0$
such that for every
$\delta>0$
such that for every
![]() $x,y,z\in X$
, we have
$x,y,z\in X$
, we have
We recall that a sequence of points
![]() $(x_n)$
in X is said to converge to infinity if the real numbers
$(x_n)$
in X is said to converge to infinity if the real numbers
![]() $(x_n,x_m)$
approach infinity when both indices m and n tend to infinity.
$(x_n,x_m)$
approach infinity when both indices m and n tend to infinity.
Lemma 3.5. Assume
![]() $(x_n)$
is a sequence of points in X which converges in
$(x_n)$
is a sequence of points in X which converges in
![]() $\bar {X}$
and denote
$\bar {X}$
and denote
![]() $\bar {h}=\lim x_n$
. Then,
$\bar {h}=\lim x_n$
. Then,
![]() $(x_n)$
converges to infinity if and only if
$(x_n)$
converges to infinity if and only if
![]() $\bar {h}\in \bar {X}^u$
. In that case, if
$\bar {h}\in \bar {X}^u$
. In that case, if
![]() $(x^{\prime }_n)$
is another sequence in X satisfying
$(x^{\prime }_n)$
is another sequence in X satisfying
![]() $\lim x^{\prime }_n =\bar {h}$
, then
$\lim x^{\prime }_n =\bar {h}$
, then
![]() $(x_n,x^{\prime }_n) \to \infty $
.
$(x_n,x^{\prime }_n) \to \infty $
.
Proof. We will denote the lift of
![]() $\bar {h}$
in
$\bar {h}$
in
![]() $\tilde {X}_o$
by h and show that
$\tilde {X}_o$
by h and show that
![]() $(x_n)$
converges to infinity if and only if
$(x_n)$
converges to infinity if and only if
![]() $h\in \tilde {X}^u_o$
. Note that for every
$h\in \tilde {X}^u_o$
. Note that for every
![]() $x\in X$
, we have
$x\in X$
, we have
![]() $d(x_n,x)-|x|\to h(x)$
.
$d(x_n,x)-|x|\to h(x)$
.
Assuming first
![]() $(x_n)$
converges to infinity, we will show that
$(x_n)$
converges to infinity, we will show that
![]() $h\in \tilde {X}^u_o$
. Fix
$h\in \tilde {X}^u_o$
. Fix
![]() $r>0$
. Fix N such that for
$r>0$
. Fix N such that for
![]() $n,m>N$
,
$n,m>N$
,
![]() $(x_n,x_m)>r$
. Fix
$(x_n,x_m)>r$
. Fix
![]() $m>N$
, note that
$m>N$
, note that
![]() $|x_m|\geq r$
and let x be a point on a geodesic segment from o to
$|x_m|\geq r$
and let x be a point on a geodesic segment from o to
![]() $x_m$
with
$x_m$
with
![]() $|x|=r$
. Then, by hyperbolicity,
$|x|=r$
. Then, by hyperbolicity,
Thus,
As r was arbitrary, we get indeed that
![]() $h\in \tilde {X}^u_o$
.
$h\in \tilde {X}^u_o$
.
Assuming now
![]() $h\in \tilde {X}^u$
, we will show that
$h\in \tilde {X}^u$
, we will show that
![]() $(x_n)$
converges to infinity. Fix
$(x_n)$
converges to infinity. Fix
![]() $r>0$
. Fix x such that
$r>0$
. Fix x such that
![]() $h(x)<-r$
. Fix N such that for every
$h(x)<-r$
. Fix N such that for every
![]() $n>N$
,
$n>N$
,
![]() $d(x_n,x)-|x_n|<-r$
and observe that for such n,
$d(x_n,x)-|x_n|<-r$
and observe that for such n,
Then, by hyperbolicity, for
![]() $n,m>N$
,
$n,m>N$
,
As r was arbitrary, we deduce indeed that the sequence
![]() $(x_n)$
converges to infinity.
$(x_n)$
converges to infinity.
In the setting of the former paragraph, if
![]() $(x^{\prime }_n)$
is another sequences in X satisfying
$(x^{\prime }_n)$
is another sequences in X satisfying
![]() $x^{\prime }_n \to \bar {h}$
, fixing
$x^{\prime }_n \to \bar {h}$
, fixing
![]() $N'\geq N$
such that for every
$N'\geq N$
such that for every
![]() $n>N'$
,
$n>N'$
,
![]() $d(x^{\prime }_n,x)-|x^{\prime }_n|<-r$
, the same computation shows that
$d(x^{\prime }_n,x)-|x^{\prime }_n|<-r$
, the same computation shows that
![]() $(x_n,x^{\prime }_n)> r/2-\delta $
. Thus indeed, we obtain
$(x_n,x^{\prime }_n)> r/2-\delta $
. Thus indeed, we obtain
![]() $(x_n,x^{\prime }_n) \to \infty $
.
$(x_n,x^{\prime }_n) \to \infty $
.
Two sequences which converge to infinity,
![]() $(x_n)$
and
$(x_n)$
and
![]() $(y_n)$
, are said to be equivalent if
$(y_n)$
, are said to be equivalent if
![]() $(x_n,y_n) \to \infty $
. We conclude that if
$(x_n,y_n) \to \infty $
. We conclude that if
![]() $(x_n)$
and
$(x_n)$
and
![]() $(x^{\prime }_n)$
are two sequences in X satisfying
$(x^{\prime }_n)$
are two sequences in X satisfying
then
![]() $(x_n)$
is equivalent to
$(x_n)$
is equivalent to
![]() $(x^{\prime }_n)$
.
$(x^{\prime }_n)$
.
A point in
![]() $\partial X$
is, by definition, an equivalence class of sequences which converge to infinity. We denote by
$\partial X$
is, by definition, an equivalence class of sequences which converge to infinity. We denote by
![]() $\pi $
the unique map
$\pi $
the unique map
satisfying
For a point
![]() $\xi \in \partial X$
and
$\xi \in \partial X$
and
![]() $r>0$
, we set
$r>0$
, we set
We note that the collection of sets
![]() $U(\xi ,r)$
forms a basis for a topology and endow
$U(\xi ,r)$
forms a basis for a topology and endow
![]() $\partial X$
with this topology. In fact, one can extend the sets
$\partial X$
with this topology. In fact, one can extend the sets
![]() $U(\xi ,r)$
to
$U(\xi ,r)$
to
![]() $X\cup \partial X$
, and define a topology there using the extended sets as bases.
$X\cup \partial X$
, and define a topology there using the extended sets as bases.
Lemma 3.6. The map
![]() $\pi $
is continuous and
$\pi $
is continuous and
![]() $\operatorname {Isom}(X)$
-equivariant.
$\operatorname {Isom}(X)$
-equivariant.
Proof. The equivariance of
![]() $\pi $
is obvious. To show continuity, we fix a point
$\pi $
is obvious. To show continuity, we fix a point
![]() $\bar {h}\in \bar {X}^u$
and show the continuity of
$\bar {h}\in \bar {X}^u$
and show the continuity of
![]() $\pi $
at
$\pi $
at
![]() $\bar {h}$
. Thus, we fix
$\bar {h}$
. Thus, we fix
![]() $r>0$
and argue to show that there exists a neighbourhood V of
$r>0$
and argue to show that there exists a neighbourhood V of
![]() $\bar {h}$
in
$\bar {h}$
in
![]() $\bar {X}^u$
such that
$\bar {X}^u$
such that
![]() $\pi (V)\subset U(\pi (\bar {h}),r)$
. We will denote the lift of
$\pi (V)\subset U(\pi (\bar {h}),r)$
. We will denote the lift of
![]() $\bar {h}$
in
$\bar {h}$
in
![]() $\tilde {X}^u_o$
by h, set
$\tilde {X}^u_o$
by h, set
![]() $t=2(r+\delta )$
and fix a point
$t=2(r+\delta )$
and fix a point
![]() $x\in X$
such that
$x\in X$
such that
![]() $h(x)<-t$
. We let
$h(x)<-t$
. We let
![]() $V\subset \bar {X}^u_o$
be the open neighbourhood of
$V\subset \bar {X}^u_o$
be the open neighbourhood of
![]() $\bar {h}$
corresponding to the set
$\bar {h}$
corresponding to the set
![]() $\{h'\in \tilde {X}^u_o \mid h'(x)<-t\}$
. Fix
$\{h'\in \tilde {X}^u_o \mid h'(x)<-t\}$
. Fix
![]() $\bar {h}'\in V$
and denote its lift in
$\bar {h}'\in V$
and denote its lift in
![]() $\tilde {X}_o^u$
by
$\tilde {X}_o^u$
by
![]() $h'$
. Let
$h'$
. Let
![]() $(x_n)$
and
$(x_n)$
and
![]() $(x^{\prime }_n)$
be sequences in X converging to
$(x^{\prime }_n)$
be sequences in X converging to
![]() $\bar {h}$
and
$\bar {h}$
and
![]() $\bar {h}'$
, respectively. In particular, we have
$\bar {h}'$
, respectively. In particular, we have
Fix N such that for every
![]() $n>N$
, both
$n>N$
, both
![]() $(d(x_n,x)-|x_n|)<-t$
and
$(d(x_n,x)-|x_n|)<-t$
and
![]() $(d(x^{\prime }_n,x)-|x^{\prime }_n|)<-t$
. Note that for
$(d(x^{\prime }_n,x)-|x^{\prime }_n|)<-t$
. Note that for
![]() $n>N$
,
$n>N$
,
and similarly
![]() $(x^{\prime }_n,x)>t/2$
. Thus, we have
$(x^{\prime }_n,x)>t/2$
. Thus, we have
It follows that
![]() $\liminf (x_n,x^{\prime }_n)\geq r$
and, in particular,
$\liminf (x_n,x^{\prime }_n)\geq r$
and, in particular,
Therefore,
![]() $\pi (\bar {h}')\in U(\pi (\bar {h}),r)$
and we conclude that indeed
$\pi (\bar {h}')\in U(\pi (\bar {h}),r)$
and we conclude that indeed
![]() $\pi (V)\subset U(\pi (\bar {h}),r)$
.
$\pi (V)\subset U(\pi (\bar {h}),r)$
.
Here and in the following, we use the term ‘
![]() $\Gamma $
-map’ to mean a measurable
$\Gamma $
-map’ to mean a measurable
![]() $\Gamma $
-equivariant map between spaces equipped with a
$\Gamma $
-equivariant map between spaces equipped with a
![]() $\Gamma $
-action.
$\Gamma $
-action.
The following lemma will be used, similarly to Lemma 3.4, in conjunction with coarse metric ergodicity to exclude the existence of
![]() $\Gamma $
-maps to
$\Gamma $
-maps to
![]() $\partial X^{(3)}$
.
$\partial X^{(3)}$
.
Lemma 3.7. Let
![]() $\Gamma $
be a countable group acting by isometries on the separable hyperbolic space X. Then there is a Borel coarsely separable pseudo-metric
$\Gamma $
be a countable group acting by isometries on the separable hyperbolic space X. Then there is a Borel coarsely separable pseudo-metric
![]() $\rho $
on
$\rho $
on
![]() $\partial X^{(3)}$
such that the natural
$\partial X^{(3)}$
such that the natural
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $\partial X^{(3)}$
is an action by isometries of
$\partial X^{(3)}$
is an action by isometries of
![]() $\rho $
. Moreover, if
$\rho $
. Moreover, if
![]() $\mathcal U\subseteq \Gamma $
acts on X with unbounded orbits, then the
$\mathcal U\subseteq \Gamma $
acts on X with unbounded orbits, then the
![]() $\mathcal U$
-orbits in
$\mathcal U$
-orbits in
![]() $(\partial X^{(3)},\rho )$
are also unbounded.
$(\partial X^{(3)},\rho )$
are also unbounded.
Proof. Denote
![]() $\mathcal T=\partial X^{(3)}$
for convenience. Fix a
$\mathcal T=\partial X^{(3)}$
for convenience. Fix a
![]() $\Gamma $
-invariant dense subset A of X.
$\Gamma $
-invariant dense subset A of X.
We claim that there exists a
![]() $\Gamma $
-equivariant map
$\Gamma $
-equivariant map
![]() $\tau :\mathcal T\to \operatorname {Bdd}(A)$
with the property that for any
$\tau :\mathcal T\to \operatorname {Bdd}(A)$
with the property that for any
![]() $x\in X$
, we have that
$x\in X$
, we have that
![]() $\mathcal T_x=\tau ^{-1}(\{B\in \operatorname {Bdd}(X): x\in B\})\subseteq \mathcal T$
is closed.
$\mathcal T_x=\tau ^{-1}(\{B\in \operatorname {Bdd}(X): x\in B\})\subseteq \mathcal T$
is closed.
To show the claim, we will in fact first define a closed subset
![]() $\mathcal T_x$
for each
$\mathcal T_x$
for each
![]() $x\in A$
and then set
$x\in A$
and then set
![]() $\tau (t)=\{x\in A: t\in \mathcal T_x\}$
. Let
$\tau (t)=\{x\in A: t\in \mathcal T_x\}$
. Let
![]() $\delta>0$
be a hyperbolicity constant for X. For
$\delta>0$
be a hyperbolicity constant for X. For
![]() $x\in A$
, let
$x\in A$
, let
![]() $T_x\subseteq X^3$
be the set of all triples
$T_x\subseteq X^3$
be the set of all triples
![]() $(x_1,x_2,x_3)$
such that
$(x_1,x_2,x_3)$
such that
![]() ${d(x_i,x_j)> d(x_i,x)+d(x,x_j)-10\delta }$
for all distinct
${d(x_i,x_j)> d(x_i,x)+d(x,x_j)-10\delta }$
for all distinct
![]() $i,j\in \{1,2,3\}$
. We then define
$i,j\in \{1,2,3\}$
. We then define
![]() $\mathcal T_x$
to be the intersection of
$\mathcal T_x$
to be the intersection of
![]() $\mathcal T$
with closure of
$\mathcal T$
with closure of
![]() $T_x$
(taken in
$T_x$
(taken in
![]() $(X\cup \partial X)^3$
). Notice that
$(X\cup \partial X)^3$
). Notice that
![]() $\tau (t)$
defined as above is then a bounded, non-empty subset of A, and that
$\tau (t)$
defined as above is then a bounded, non-empty subset of A, and that
![]() $\tau $
is
$\tau $
is
![]() $\Gamma $
-equivariant.
$\Gamma $
-equivariant.
We can now pull-back the Hausdorff distance
![]() $d_{\textrm {Haus}}$
on
$d_{\textrm {Haus}}$
on
![]() $\operatorname {Bdd}(A)$
to
$\operatorname {Bdd}(A)$
to
![]() $\mathcal T$
, that is, we set
$\mathcal T$
, that is, we set
![]() $\rho (t,t')=d_{\textrm {Haus}}(\tau (t),\tau (t'))$
. Clearly,
$\rho (t,t')=d_{\textrm {Haus}}(\tau (t),\tau (t'))$
. Clearly,
![]() $\rho $
is a pseudo-metric and
$\rho $
is a pseudo-metric and
![]() $\Gamma $
acts on
$\Gamma $
acts on
![]() $\mathcal T$
by isometries of
$\mathcal T$
by isometries of
![]() $\rho $
. Moreover, orbits are unbounded since
$\rho $
. Moreover, orbits are unbounded since
![]() $(\mathcal T,\rho )$
is
$(\mathcal T,\rho )$
is
![]() $\Gamma $
-equivariantly isometrically embedded in
$\Gamma $
-equivariantly isometrically embedded in
![]() $\operatorname {Bdd}(A)$
, and on the latter, the
$\operatorname {Bdd}(A)$
, and on the latter, the
![]() $\Gamma $
-orbits are unbounded since orbits are unbounded in X (a similar argument applies to subsets of
$\Gamma $
-orbits are unbounded since orbits are unbounded in X (a similar argument applies to subsets of
![]() $\Gamma $
). Coarse separability also arises from this isometric embedding together with separability of X, which gives coarse separability of
$\Gamma $
). Coarse separability also arises from this isometric embedding together with separability of X, which gives coarse separability of
![]() $\operatorname {Bdd}(A)$
. It remains to show that
$\operatorname {Bdd}(A)$
. It remains to show that
![]() $\rho $
is Borel. To do so, it suffices to show that for all
$\rho $
is Borel. To do so, it suffices to show that for all
![]() $r\in \mathbb R$
, we have that
$r\in \mathbb R$
, we have that
![]() $\Delta _r=\{(t,t'): \rho (t,t')> r\}\subseteq \mathcal T \times \mathcal T$
is Borel. Expanding the definitions,
$\Delta _r=\{(t,t'): \rho (t,t')> r\}\subseteq \mathcal T \times \mathcal T$
is Borel. Expanding the definitions,
![]() $\Delta _r$
is the set of pairs
$\Delta _r$
is the set of pairs
![]() $(t,t')$
such that
$(t,t')$
such that
![]() $\tau (t)$
and
$\tau (t)$
and
![]() $\tau (t')$
lie at Hausdorff distance more than r. In turn, this means that there exists
$\tau (t')$
lie at Hausdorff distance more than r. In turn, this means that there exists
![]() $x\in \tau (t)$
such that all
$x\in \tau (t)$
such that all
![]() $y\in \tau (t')$
lie at distance more than r from x, or that the same holds switching the roles of t and
$y\in \tau (t')$
lie at distance more than r from x, or that the same holds switching the roles of t and
![]() $t'$
. The first case is further equivalent to
$t'$
. The first case is further equivalent to
![]() $t'$
not lying in
$t'$
not lying in
![]() $\bigcup _{y\in A : d(x,y)\leq r} \mathcal T_y$
, so that
$\bigcup _{y\in A : d(x,y)\leq r} \mathcal T_y$
, so that
![]() $\tau (t)$
does not contain any y with
$\tau (t)$
does not contain any y with
![]() $d(x,y)\leq r$
(and the other case is similar). Hence, we have
$d(x,y)\leq r$
(and the other case is similar). Hence, we have
 $$ \begin{align*}\Delta_r=\bigcup_{x\in A}\bigg( \mathcal T_x \times \bigg(\mathcal T-\bigcup_{y\in A : d(x,y)\leq r} \mathcal T_y\bigg) \bigg)\cup\bigcup_{y\in A} \bigg( \bigg(\mathcal T-\bigcup_{x\in A : d(x,y)\leq r} \mathcal T_y\bigg)\times \mathcal T_x\bigg).\end{align*} $$
$$ \begin{align*}\Delta_r=\bigcup_{x\in A}\bigg( \mathcal T_x \times \bigg(\mathcal T-\bigcup_{y\in A : d(x,y)\leq r} \mathcal T_y\bigg) \bigg)\cup\bigcup_{y\in A} \bigg( \bigg(\mathcal T-\bigcup_{x\in A : d(x,y)\leq r} \mathcal T_y\bigg)\times \mathcal T_x\bigg).\end{align*} $$
Since all
![]() $\mathcal T_x$
are closed,
$\mathcal T_x$
are closed,
![]() $\Delta _r$
is Borel, as required.
$\Delta _r$
is Borel, as required.
3.4. Atom-less measures
We now show a result needed in the next section, but not needed for the proof of Theorem 3.1; we include it here since we established the setup for its proof.
The result provides a
![]() $\Gamma $
-map from atom-less probability measures on
$\Gamma $
-map from atom-less probability measures on
![]() $\partial X$
to probability measures on
$\partial X$
to probability measures on
![]() $\partial X^{(3)}$
.
$\partial X^{(3)}$
.
Given a hyperbolic space X, denote by
![]() $\operatorname {Prob}_c(\partial X)$
the set of all atom-less probability measures on the standard Borel space
$\operatorname {Prob}_c(\partial X)$
the set of all atom-less probability measures on the standard Borel space
![]() $\partial X$
.
$\partial X$
.
Lemma 3.8. Let
![]() $\Gamma $
be a countable group acting by isometries on the hyperbolic space X. Then there is a
$\Gamma $
be a countable group acting by isometries on the hyperbolic space X. Then there is a
![]() $\Gamma $
-map
$\Gamma $
-map
Moreover, for all
![]() $\mu ,\nu \in \operatorname {Prob}_c(\partial X)$
with
$\mu ,\nu \in \operatorname {Prob}_c(\partial X)$
with
![]() $\mu $
absolutely continuous with respect to
$\mu $
absolutely continuous with respect to
![]() $\nu $
, we have
$\nu $
, we have
 $$ \begin{align*} \bigg\| \frac{d\Psi(\mu)}{d\Psi(\nu)}\bigg\|_\infty\leq \bigg(\bigg\|\frac{d\mu}{d\nu}\bigg\|_\infty\bigg)^3. \end{align*} $$
$$ \begin{align*} \bigg\| \frac{d\Psi(\mu)}{d\Psi(\nu)}\bigg\|_\infty\leq \bigg(\bigg\|\frac{d\mu}{d\nu}\bigg\|_\infty\bigg)^3. \end{align*} $$
Proof. We have a
![]() $\Gamma $
-map
$\Gamma $
-map
In fact, the assumption that
![]() $\mu $
has no atoms on a space
$\mu $
has no atoms on a space
![]() $\partial X$
implies that
$\partial X$
implies that
![]() $\mu \times \mu \times \mu $
gives zero mass to the diagonals in
$\mu \times \mu \times \mu $
gives zero mass to the diagonals in
![]() $\partial X \times \partial X\times \partial X$
, and so is fully supported on
$\partial X \times \partial X\times \partial X$
, and so is fully supported on
![]() $\partial X^{(3)}$
. We thus get a well-defined map
$\partial X^{(3)}$
. We thus get a well-defined map
as required.
To prove the moreover part, let
![]() $\mu ,\nu \in \operatorname {Prob}_c(\partial X)$
and let
$\mu ,\nu \in \operatorname {Prob}_c(\partial X)$
and let
![]() $f\in L^\infty (\partial X)$
be the Radon–Nikodym derivative of
$f\in L^\infty (\partial X)$
be the Radon–Nikodym derivative of
![]() $\mu $
with respect to
$\mu $
with respect to
![]() $\nu $
. Then
$\nu $
. Then
![]() $(x,y,z)\mapsto f(x)f(y)f(z)$
is the Radon–Nikodym derivative of
$(x,y,z)\mapsto f(x)f(y)f(z)$
is the Radon–Nikodym derivative of
![]() $\Phi (\mu )$
with respect to
$\Phi (\mu )$
with respect to
![]() $\Phi (\nu )$
, so that
$\Phi (\nu )$
, so that
![]() $\|{d\Phi (\mu )}/{d\Phi (\nu )}\|_\infty = (\|{d\mu }/{d\nu }\|_\infty )^3$
. The measures
$\|{d\Phi (\mu )}/{d\Phi (\nu )}\|_\infty = (\|{d\mu }/{d\nu }\|_\infty )^3$
. The measures
![]() $\Psi (\mu )$
and
$\Psi (\mu )$
and
![]() $\Psi (\nu )$
are push-forward measures of
$\Psi (\nu )$
are push-forward measures of
![]() $\Phi (\mu )$
and
$\Phi (\mu )$
and
![]() $\Phi (\nu )$
, and push-forwards do not increase the
$\Phi (\nu )$
, and push-forwards do not increase the
![]() $L^\infty $
norm of Radon–Nikodym derivatives, so we obtain the required bound.
$L^\infty $
norm of Radon–Nikodym derivatives, so we obtain the required bound.
3.5. Proof of Theorem 3.1
We are now ready to prove Theorem 3.1. By hypothesis, the group
![]() $\Gamma $
is a countable group acting by isometries on the hyperbolic space X, without fixing any bounded subset of X, any point of
$\Gamma $
is a countable group acting by isometries on the hyperbolic space X, without fixing any bounded subset of X, any point of
![]() $\partial X$
and any pair of points of
$\partial X$
and any pair of points of
![]() $\partial X$
.
$\partial X$
.
We start with some preliminary claims that we will use a few times.
First of all, we exclude the existence of
![]() $\Gamma $
-maps with various targets.
$\Gamma $
-maps with various targets.
Claim 3.9. We have
 $$ \begin{align*} \operatorname{Map}_\Gamma(B_-,\operatorname{Prob}(\bar X^b)) & =\operatorname{Map}_\Gamma(B_+,\operatorname{Prob}(\bar X^b))\\ &=\operatorname{Map}_\Gamma(B_-\times B_+,\operatorname{Prob}(\partial X^{(3)}))\\ &=\varnothing. \end{align*} $$
$$ \begin{align*} \operatorname{Map}_\Gamma(B_-,\operatorname{Prob}(\bar X^b)) & =\operatorname{Map}_\Gamma(B_+,\operatorname{Prob}(\bar X^b))\\ &=\operatorname{Map}_\Gamma(B_-\times B_+,\operatorname{Prob}(\partial X^{(3)}))\\ &=\varnothing. \end{align*} $$
Proof. Recall Lemmas 3.4 and 3.7 about the existence of Borel coarsely separable pseudo-metrics on
![]() $\bar X^b$
and on
$\bar X^b$
and on
![]() $\partial X^{(3)}$
, respectively, on which
$\partial X^{(3)}$
, respectively, on which
![]() $\Gamma $
acts by isometries with unbounded orbits. Then, in view of Proposition 2.15, all sets of
$\Gamma $
acts by isometries with unbounded orbits. Then, in view of Proposition 2.15, all sets of
![]() $\Gamma $
-maps in the statement need to be empty (note that any pseudo-metric is a coarse metric).
$\Gamma $
-maps in the statement need to be empty (note that any pseudo-metric is a coarse metric).
We shall make use of the following general observation with
![]() $\Omega $
being
$\Omega $
being
![]() $B_-$
,
$B_-$
,
![]() $B_+$
or
$B_+$
or
![]() ${B_-\times B_+}$
. Note that these Lebesgue
${B_-\times B_+}$
. Note that these Lebesgue
![]() $\Gamma $
-spaces are ergodic.
$\Gamma $
-spaces are ergodic.
Claim 3.10. Let
![]() $\Gamma \curvearrowright \Omega $
be an ergodic action and
$\Gamma \curvearrowright \Omega $
be an ergodic action and
![]() $\Gamma \curvearrowright V$
be a Borel action on a Polish space. Suppose
$\Gamma \curvearrowright V$
be a Borel action on a Polish space. Suppose
![]() $V=V_0\cup V_1$
with
$V=V_0\cup V_1$
with
![]() $V_0\cap V_1=\varnothing $
is a decomposition into
$V_0\cap V_1=\varnothing $
is a decomposition into
![]() $\Gamma $
-invariant Borel sets and suppose
$\Gamma $
-invariant Borel sets and suppose
![]() $\operatorname {Map}_\Gamma (\Omega ,\operatorname {Prob}(V_0))=\varnothing $
. Then the inclusion
$\operatorname {Map}_\Gamma (\Omega ,\operatorname {Prob}(V_0))=\varnothing $
. Then the inclusion
![]() $\operatorname {Prob}(V_1)\subset \operatorname {Prob}(V)$
gives an identification
$\operatorname {Prob}(V_1)\subset \operatorname {Prob}(V)$
gives an identification
Proof. Consider a measurable
![]() $\Gamma $
-equivariant map
$\Gamma $
-equivariant map
![]() $\phi \colon \Omega \longrightarrow \operatorname {Prob}(V)$
. We also define
$\phi \colon \Omega \longrightarrow \operatorname {Prob}(V)$
. We also define
![]() $f_0,f_1\colon \Omega \to [0,1]$
by setting
$f_0,f_1\colon \Omega \to [0,1]$
by setting
![]() $f_i(\omega )=\phi (\omega )(V_i)$
. These are
$f_i(\omega )=\phi (\omega )(V_i)$
. These are
![]() $\Gamma $
-invariant measurable functions. By ergodicity,
$\Gamma $
-invariant measurable functions. By ergodicity,
![]() $f_i(\omega )=c_i$
constants and
$f_i(\omega )=c_i$
constants and
![]() $c_i\ge 0$
with
$c_i\ge 0$
with
![]() $c_0+c_1=1$
. Assuming
$c_0+c_1=1$
. Assuming
![]() $c_0>0$
, one obtains a contradiction, because the normalized restriction
$c_0>0$
, one obtains a contradiction, because the normalized restriction
![]() $\phi _0(\omega )=c_0^{-1}\cdot \phi (\omega )|_{V_0}$
is a
$\phi _0(\omega )=c_0^{-1}\cdot \phi (\omega )|_{V_0}$
is a
![]() $\Gamma $
-map to
$\Gamma $
-map to
![]() $\operatorname {Prob}(V_0)$
, which are ruled out by assumption. Hence,
$\operatorname {Prob}(V_0)$
, which are ruled out by assumption. Hence,
![]() $c_0=0$
and
$c_0=0$
and
![]() $\phi (\omega )$
gives full mass to
$\phi (\omega )$
gives full mass to
![]() $V_1$
, and hence
$V_1$
, and hence
![]() $\phi $
can be considered as a
$\phi $
can be considered as a
![]() $\Gamma $
-map
$\Gamma $
-map
![]() $\Omega \longrightarrow \operatorname {Prob}(V_1)$
.
$\Omega \longrightarrow \operatorname {Prob}(V_1)$
.
Claim 3.11. For all
![]() $\psi _-\in \operatorname {Map}(B_-,\operatorname {Prob}(\partial X))$
and
$\psi _-\in \operatorname {Map}(B_-,\operatorname {Prob}(\partial X))$
and
![]() $\psi _+\in \operatorname {Map}(B_+,\operatorname {Prob}(\partial X))$
, the diagonal
$\psi _+\in \operatorname {Map}(B_+,\operatorname {Prob}(\partial X))$
, the diagonal
![]() $\Delta = \{ {(t,t)}\mid {t\in \partial X} \} \subset \partial X^2$
satisfies
$\Delta = \{ {(t,t)}\mid {t\in \partial X} \} \subset \partial X^2$
satisfies
for a.e.
![]() $(x,y)\in B_-\times B_+$
.
$(x,y)\in B_-\times B_+$
.
Proof. Given a probability measure
![]() $\eta \in \operatorname {Prob}(\partial X)$
, denote by
$\eta \in \operatorname {Prob}(\partial X)$
, denote by
![]() $\operatorname {Atom}(\eta )$
the set of atoms of
$\operatorname {Atom}(\eta )$
the set of atoms of
![]() $\eta $
; and for
$\eta $
; and for
![]() $\epsilon>0$
, by
$\epsilon>0$
, by
![]() $\operatorname {Atom}_\epsilon (\eta )= \{ {a}\mid {\eta (\{a\})\ge \epsilon } \} $
the subset of atoms with weight
$\operatorname {Atom}_\epsilon (\eta )= \{ {a}\mid {\eta (\{a\})\ge \epsilon } \} $
the subset of atoms with weight
![]() $\ge \epsilon $
. The cardinality of
$\ge \epsilon $
. The cardinality of
![]() $\operatorname {Atom}_\epsilon (\eta )$
is bounded by
$\operatorname {Atom}_\epsilon (\eta )$
is bounded by
![]() $\lceil 1/\epsilon \rceil $
and
$\lceil 1/\epsilon \rceil $
and
![]() $\operatorname {Atom}(\eta )$
is at most countable. Let
$\operatorname {Atom}(\eta )$
is at most countable. Let
![]() $\alpha ,\beta \in \operatorname {Prob}(\partial X)$
be two probability measures. A standard application of Fubini’s theorem shows that
$\alpha ,\beta \in \operatorname {Prob}(\partial X)$
be two probability measures. A standard application of Fubini’s theorem shows that
where the non-zero terms correspond to
![]() $t\in \operatorname {Atom}(\alpha )\cap \operatorname {Atom}(\beta )$
.
$t\in \operatorname {Atom}(\alpha )\cap \operatorname {Atom}(\beta )$
.
For
![]() $(x,y)\in B_-\times B_+$
, observe that the sets
$(x,y)\in B_-\times B_+$
, observe that the sets
![]() $\operatorname {Atom}(\psi _-(x))$
,
$\operatorname {Atom}(\psi _-(x))$
,
![]() $\operatorname {Atom}(\psi _+(y))$
and their intersection vary measurably and
$\operatorname {Atom}(\psi _+(y))$
and their intersection vary measurably and
![]() $\Gamma $
-equivariantly.
$\Gamma $
-equivariantly.
Assume, towards contradiction, that
![]() $\psi _-(x)\times \psi _+(y)(\Delta )>0$
. This is equivalent to asserting that for some
$\psi _-(x)\times \psi _+(y)(\Delta )>0$
. This is equivalent to asserting that for some
![]() $\epsilon>0$
, the set
$\epsilon>0$
, the set
has positive measure. Since the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $B_-\times B_+$
is ergodic, we deduce that this set is conull, and the cardinality of the set
$B_-\times B_+$
is ergodic, we deduce that this set is conull, and the cardinality of the set
![]() $A(x,y)=\operatorname {Atom}_\epsilon (\psi _-(x))\cap \operatorname {Atom}_\epsilon (\psi _+(y))$
is essentially constant.
$A(x,y)=\operatorname {Atom}_\epsilon (\psi _-(x))\cap \operatorname {Atom}_\epsilon (\psi _+(y))$
is essentially constant.
By Fubini’s theorem for a.e.
![]() $x\in B_-$
, we have
$x\in B_-$
, we have
![]() $A(x,y)=A(x,y')$
for a.e.
$A(x,y)=A(x,y')$
for a.e.
![]() $y,y'\in B_+$
. Thus,
$y,y'\in B_+$
. Thus,
![]() $A(x,-)$
is essentially independent of the second variable. For the same reason, it is essentially independent of the first variable; hence,
$A(x,-)$
is essentially independent of the second variable. For the same reason, it is essentially independent of the first variable; hence,
![]() $A(x,y)=A$
for a fixed finite subset
$A(x,y)=A$
for a fixed finite subset
![]() $A\subset \partial X$
. Since the map
$A\subset \partial X$
. Since the map
![]() $(x,y)\mapsto A(x,y)=A$
is equivariant, it follows that
$(x,y)\mapsto A(x,y)=A$
is equivariant, it follows that
![]() $\Gamma $
has a finite orbit O on
$\Gamma $
has a finite orbit O on
![]() $\partial X$
. By hypothesis,
$\partial X$
. By hypothesis,
![]() $\Gamma $
does not fix a point or a pair of points in
$\Gamma $
does not fix a point or a pair of points in
![]() $\partial X$
, so that
$\partial X$
, so that
![]() $|O|\geq 3$
. By considering the restriction of the pseudo-metric on
$|O|\geq 3$
. By considering the restriction of the pseudo-metric on
![]() $\partial X^{(3)}$
from Lemma 3.7 to the finite set of triples of distinct points in O, we obtain a
$\partial X^{(3)}$
from Lemma 3.7 to the finite set of triples of distinct points in O, we obtain a
![]() $\Gamma $
-invariant orbit in
$\Gamma $
-invariant orbit in
![]() $\partial X^{(3)}$
, contradicting that the action on
$\partial X^{(3)}$
, contradicting that the action on
![]() $\partial X^{(3)}$
has unbounded orbits.
$\partial X^{(3)}$
has unbounded orbits.
Hence,
![]() $\psi _-(x)\times \psi _+(y)(\Delta )=0$
almost everywhere on
$\psi _-(x)\times \psi _+(y)(\Delta )=0$
almost everywhere on
![]() $B_-\times B_+$
, as claimed.
$B_-\times B_+$
, as claimed.
End of proof of Theorem 3.1.
Since the actions
![]() $\Gamma \curvearrowright B_-$
,
$\Gamma \curvearrowright B_-$
,
![]() $\Gamma \curvearrowright B_+$
are amenable, the spaces
$\Gamma \curvearrowright B_+$
are amenable, the spaces
![]() $\operatorname {Map}_\Gamma (B_\pm ,\operatorname {Prob}(\bar X))$
are not empty. Consider the
$\operatorname {Map}_\Gamma (B_\pm ,\operatorname {Prob}(\bar X))$
are not empty. Consider the
![]() $\Gamma $
-invariant Borel decomposition
$\Gamma $
-invariant Borel decomposition
![]() $\bar {X}=\bar {X}^b\cup \bar {X}^u$
. In view of Claims 3.9 and 3.10, we have
$\bar {X}=\bar {X}^b\cup \bar {X}^u$
. In view of Claims 3.9 and 3.10, we have
and post-composing with the
![]() $\Gamma $
-map
$\Gamma $
-map
![]() $\pi _*:\operatorname {Prob}(\bar X^u)\to \operatorname {Prob}(\partial X)$
(see §3.3), we obtain
$\pi _*:\operatorname {Prob}(\bar X^u)\to \operatorname {Prob}(\partial X)$
(see §3.3), we obtain
Let us choose some measurable
![]() $\Gamma $
-equivariant maps
$\Gamma $
-equivariant maps
Consider the partition of
![]() $(\partial X)^3$
into
$(\partial X)^3$
into
![]() $\Gamma $
-invariant Borel sets
$\Gamma $
-invariant Borel sets
where
![]() $\Delta _{ij}= \{ {(\xi _1,\xi _2,\xi _3)}\mid {\xi _i=\xi _j} \} $
,
$\Delta _{ij}= \{ {(\xi _1,\xi _2,\xi _3)}\mid {\xi _i=\xi _j} \} $
,
![]() $\Delta _{123}= \{ {(\xi ,\xi ,\xi )}\mid {\xi \in \partial X} \} $
,
$\Delta _{123}= \{ {(\xi ,\xi ,\xi )}\mid {\xi \in \partial X} \} $
,
![]() $\Delta ^{\prime }_{ij}=\Delta _{ij}\setminus \Delta _{123}$
.
$\Delta ^{\prime }_{ij}=\Delta _{ij}\setminus \Delta _{123}$
.
Note that
![]() $\operatorname {Map}_\Gamma (B_-\times B_+,\operatorname {Prob}(\partial X^{(3)}))=\varnothing $
by Claim 3.9. Therefore, using Claim 3.10, every measurable
$\operatorname {Map}_\Gamma (B_-\times B_+,\operatorname {Prob}(\partial X^{(3)}))=\varnothing $
by Claim 3.9. Therefore, using Claim 3.10, every measurable
![]() $\Gamma $
-map
$\Gamma $
-map
![]() $\Psi :B_{-}\times B_{+}\longrightarrow \operatorname {Prob}((\partial X)^3)$
gives full measure to
$\Psi :B_{-}\times B_{+}\longrightarrow \operatorname {Prob}((\partial X)^3)$
gives full measure to
![]() $\Delta _{12}\cup \Delta ^{\prime }_{13}\cup \Delta ^{\prime }_{23}$
. We shall apply this to the map
$\Delta _{12}\cup \Delta ^{\prime }_{13}\cup \Delta ^{\prime }_{23}$
. We shall apply this to the map
Note that Claim 3.11 implies that almost everywhere,
![]() $\Psi (x,y)(\Delta _{12})=0$
.
$\Psi (x,y)(\Delta _{12})=0$
.
Let
![]() $\Delta $
denote the diagonal in
$\Delta $
denote the diagonal in
![]() $\partial X \times \partial X$
. The projection
$\partial X \times \partial X$
. The projection
![]() $\Delta ^{\prime }_{13}\to \Delta $
,
$\Delta ^{\prime }_{13}\to \Delta $
,
![]() $(\xi ,\eta ,\xi )\mapsto (\xi ,\xi )$
shows that
$(\xi ,\eta ,\xi )\mapsto (\xi ,\xi )$
shows that
Moreover, the first term of the right-hand side vanishes by Claim 3.11, so that
![]() $\Psi (x,y)(\Delta ^{\prime }_{13})\le \tfrac 12\psi _-(x)\times \psi _-(x)(\Delta )$
. Similarly, using the projection
$\Psi (x,y)(\Delta ^{\prime }_{13})\le \tfrac 12\psi _-(x)\times \psi _-(x)(\Delta )$
. Similarly, using the projection
![]() $\Delta ^{\prime }_{23}\to \Delta $
,
$\Delta ^{\prime }_{23}\to \Delta $
,
![]() $(\eta ,\xi ,\xi )\mapsto (\xi ,\xi )$
gives
$(\eta ,\xi ,\xi )\mapsto (\xi ,\xi )$
gives
We conclude that
 $$ \begin{align*} 1 &= \Psi(x,y)(\Delta^{\prime}_{13})+ \Psi(x,y)(\Delta^{\prime}_{23}) \\ &\leq \tfrac{1}{2}\psi_-(x)\times\psi_-(x)(\Delta) + \tfrac{1}{2}\psi_+(y)\times\psi_+(y)(\Delta) \\ &\leq 1, \end{align*} $$
$$ \begin{align*} 1 &= \Psi(x,y)(\Delta^{\prime}_{13})+ \Psi(x,y)(\Delta^{\prime}_{23}) \\ &\leq \tfrac{1}{2}\psi_-(x)\times\psi_-(x)(\Delta) + \tfrac{1}{2}\psi_+(y)\times\psi_+(y)(\Delta) \\ &\leq 1, \end{align*} $$
so that
![]() $\psi _-(x)\times \psi _-(y)(\Delta )=\psi _+(y)\times \psi _+(y)(\Delta )=1$
. Recall that, by Fubini’s theorem, for any probability measure
$\psi _-(x)\times \psi _-(y)(\Delta )=\psi _+(y)\times \psi _+(y)(\Delta )=1$
. Recall that, by Fubini’s theorem, for any probability measure
![]() $\nu $
, one has
$\nu $
, one has
![]() $\nu \times \nu (\Delta )=1$
if and only if
$\nu \times \nu (\Delta )=1$
if and only if
![]() $\nu $
is a Dirac measure
$\nu $
is a Dirac measure
![]() $\nu =\delta _z$
for some z. Hence, there exist maps
$\nu =\delta _z$
for some z. Hence, there exist maps
![]() $\phi _\pm :B_\pm \longrightarrow \partial X$
so that
$\phi _\pm :B_\pm \longrightarrow \partial X$
so that
The maps
![]() $\phi _\pm :B_{\pm} \longrightarrow \partial X$
are measurable and
$\phi _\pm :B_{\pm} \longrightarrow \partial X$
are measurable and
![]() $\Gamma $
-equivariant because the maps
$\Gamma $
-equivariant because the maps
![]() $\psi _\pm :B_\pm \longrightarrow \operatorname {Prob}(\partial X)$
are.
$\psi _\pm :B_\pm \longrightarrow \operatorname {Prob}(\partial X)$
are.
We also note that, since
![]() $\Psi (\Delta _{12})=0$
almost everywhere, we have
$\Psi (\Delta _{12})=0$
almost everywhere, we have
![]() $\phi _-(x)\ne \phi _+(y)$
for a.e.
$\phi _-(x)\ne \phi _+(y)$
for a.e.
![]() $(x,y)\in B_-\times B_+$
. Therefore, the map
$(x,y)\in B_-\times B_+$
. Therefore, the map
![]() $\phi _{\bowtie }=\phi _{-}\times \phi _+$
can be viewed as a measurable
$\phi _{\bowtie }=\phi _{-}\times \phi _+$
can be viewed as a measurable
![]() $\Gamma $
-equivariant map
$\Gamma $
-equivariant map
![]() $B_-\times B_+ \longrightarrow \partial X^{(2)}$
into distinct pairs.
$B_-\times B_+ \longrightarrow \partial X^{(2)}$
into distinct pairs.
Next, we show that
![]() $\phi _\pm $
are essentially unique. Indeed, we showed that every
$\phi _\pm $
are essentially unique. Indeed, we showed that every
![]() $\psi _\pm \in \operatorname {Map}_\Gamma (B_\pm ,\operatorname {Prob}(\partial X))$
takes values in Dirac measures. Assume we have two pairs of
$\psi _\pm \in \operatorname {Map}_\Gamma (B_\pm ,\operatorname {Prob}(\partial X))$
takes values in Dirac measures. Assume we have two pairs of
![]() $\Gamma $
-maps
$\Gamma $
-maps
![]() $\psi ^i_\pm :B_\pm \to \operatorname {Prob}(\partial X)$
with
$\psi ^i_\pm :B_\pm \to \operatorname {Prob}(\partial X)$
with
![]() $i=1,2$
. Consider the
$i=1,2$
. Consider the
![]() $\Gamma $
-maps
$\Gamma $
-maps
![]() $B_{\pm }\longrightarrow \operatorname {Prob}(\partial X)$
given by
$B_{\pm }\longrightarrow \operatorname {Prob}(\partial X)$
given by
![]() $z\mapsto \tfrac 12(\psi ^1_\pm (z)+\psi ^2_\pm (z))$
. Such a map has the form
$z\mapsto \tfrac 12(\psi ^1_\pm (z)+\psi ^2_\pm (z))$
. Such a map has the form
![]() $z\mapsto \delta _{\phi _\pm (z)}$
only if
$z\mapsto \delta _{\phi _\pm (z)}$
only if
![]() $\psi ^1_\pm (z)=\psi ^2_\pm (z)=\delta _{\phi _\pm (z)}$
.
$\psi ^1_\pm (z)=\psi ^2_\pm (z)=\delta _{\phi _\pm (z)}$
.
Next, consider an arbitrary map
![]() $\theta \in \operatorname {Map}_\Gamma (B_-\times B_+,\partial X)$
, consider the measurable
$\theta \in \operatorname {Map}_\Gamma (B_-\times B_+,\partial X)$
, consider the measurable
![]() $\Gamma $
-equivariant map to be defined by
$\Gamma $
-equivariant map to be defined by
Using the
![]() $\Gamma $
-equivariant Borel decomposition
$\Gamma $
-equivariant Borel decomposition
![]() $(\partial X)^3=\partial X^{(3)}\cup \Delta ^{\prime }_{12}\cup \Delta ^{\prime }_{13}\cup \Delta _{23}$
and ergodicity of the
$(\partial X)^3=\partial X^{(3)}\cup \Delta ^{\prime }_{12}\cup \Delta ^{\prime }_{13}\cup \Delta _{23}$
and ergodicity of the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $B_-\times B_+$
, we deduce that
$B_-\times B_+$
, we deduce that
![]() $\Theta (x,y)$
lies in one of these sets for a.e.
$\Theta (x,y)$
lies in one of these sets for a.e.
![]() $(x,y)$
. Lemma 3.7 combined with coarse metric ergodicity of
$(x,y)$
. Lemma 3.7 combined with coarse metric ergodicity of
![]() $B_-\times B_+$
rules out the set of distinct triples
$B_-\times B_+$
rules out the set of distinct triples
![]() $\partial X^{(3)}$
. Since the
$\partial X^{(3)}$
. Since the
![]() $23$
-components of
$23$
-components of
![]() $\Theta $
is just
$\Theta $
is just
![]() $\phi _{\bowtie }$
, and the latter take values in the space of distinct pairs
$\phi _{\bowtie }$
, and the latter take values in the space of distinct pairs
![]() $\partial X^{(2)}$
, rule out
$\partial X^{(2)}$
, rule out
![]() $\Delta _{23}$
. It follows that, up to a null set, either
$\Delta _{23}$
. It follows that, up to a null set, either
![]() $\Theta (x,y)\in \Delta ^{\prime }_{12}$
or
$\Theta (x,y)\in \Delta ^{\prime }_{12}$
or
![]() $\Theta (x,y)\in \Delta ^{\prime }_{13}$
. This corresponds to
$\Theta (x,y)\in \Delta ^{\prime }_{13}$
. This corresponds to
![]() $\theta =\psi _-\circ \operatorname {pr}_-$
or
$\theta =\psi _-\circ \operatorname {pr}_-$
or
![]() $\theta =\psi _+\circ \operatorname {pr}_+$
as claimed in assertion (ii).
$\theta =\psi _+\circ \operatorname {pr}_+$
as claimed in assertion (ii).
Finally, notice that assertion (iii) can be deduced from assertion (ii) by looking at the coordinates in
![]() $(\partial X)^{(2)}$
.
$(\partial X)^{(2)}$
.
4. Classification of actions on hyperbolic spaces
In this section, we prove Theorem 1.1.
4.1. Lattices acting on hyperbolic spaces
Recall that a subset A of a metric space is coarsely dense if there exists a constant R such that X is the R-neighbourhood of A. Recall moreover that given a group
![]() $\Gamma $
acting on a hyperbolic space X, its limit set is the set of boundary points that are equivalence classes of sequence of points
$\Gamma $
acting on a hyperbolic space X, its limit set is the set of boundary points that are equivalence classes of sequence of points
![]() $\gamma x$
for some fixed
$\gamma x$
for some fixed
![]() $x\in X$
.
$x\in X$
.
Definition 4.1. We say that an action
![]() $\Gamma \curvearrowright X$
on a hyperbolic space is coarsely minimal if X is unbounded, the limit set of
$\Gamma \curvearrowright X$
on a hyperbolic space is coarsely minimal if X is unbounded, the limit set of
![]() $\Gamma $
in
$\Gamma $
in
![]() $\partial X$
is not a single point and every quasi-convex
$\partial X$
is not a single point and every quasi-convex
![]() $\Gamma $
-invariant subset of X is coarsely dense.
$\Gamma $
-invariant subset of X is coarsely dense.
Note that coarse minimality is a stronger requirement than asking that the orbits of
![]() $\Gamma $
have full limit set. Indeed, consider for example, the free group
$\Gamma $
have full limit set. Indeed, consider for example, the free group
![]() $F_2$
acting on its Cayley tree T, which is the universal cover of a graph with
$F_2$
acting on its Cayley tree T, which is the universal cover of a graph with
![]() $1$
vertex and two loops. Glueing, for each n, an interval of length n to that vertex, one obtains a locally infinite graph whose universal cover is a tree
$1$
vertex and two loops. Glueing, for each n, an interval of length n to that vertex, one obtains a locally infinite graph whose universal cover is a tree
![]() $\tilde T$
on which
$\tilde T$
on which
![]() $F_2$
acts with full limit set. The tree T embeds as a convex
$F_2$
acts with full limit set. The tree T embeds as a convex
![]() $F_2$
-invariant subtree of
$F_2$
-invariant subtree of
![]() $\tilde T$
, but T is not coarsely dense in
$\tilde T$
, but T is not coarsely dense in
![]() $\tilde T$
, so that the
$\tilde T$
, so that the
![]() $F_2$
-action on
$F_2$
-action on
![]() $\tilde T$
is not coarsely minimal.
$\tilde T$
is not coarsely minimal.
Notice that if H is an infinite normal subgroup of infinite index of the hyperbolic G, then the action of H on a Cayley graph of G is coarsely minimal, but not cobounded.
Given a metric space X and
![]() $C\geq 0$
, denote by
$C\geq 0$
, denote by
![]() $\operatorname {Bdd}_C(X)$
the set of all closed subsets of diameter at most C, endowed with the Hausdorff metric. Notice that
$\operatorname {Bdd}_C(X)$
the set of all closed subsets of diameter at most C, endowed with the Hausdorff metric. Notice that
![]() $\operatorname {Bdd}_C(X)$
is quasi-isometric to X.
$\operatorname {Bdd}_C(X)$
is quasi-isometric to X.
Definition 4.2. Two actions
![]() $\Gamma \curvearrowright X_1,X_2$
on metric spaces
$\Gamma \curvearrowright X_1,X_2$
on metric spaces
![]() $X_1,X_2$
are equivalent if there exists an equivariant quasi-isometry
$X_1,X_2$
are equivalent if there exists an equivariant quasi-isometry
![]() $X_1\to \operatorname {Bdd}_{C}(X_2)$
for some
$X_1\to \operatorname {Bdd}_{C}(X_2)$
for some
![]() $C\geq 0$
.
$C\geq 0$
.
The reason for having
![]() $\operatorname {Bdd}_{C}(X_2)$
instead of
$\operatorname {Bdd}_{C}(X_2)$
instead of
![]() $X_2$
is that we want to allow the situation where some group element has a fixed point in
$X_2$
is that we want to allow the situation where some group element has a fixed point in
![]() $X_1$
but merely a bounded orbit in
$X_1$
but merely a bounded orbit in
![]() $X_2$
; for example, we want to declare all actions on bounded metric spaces to be equivalent.
$X_2$
; for example, we want to declare all actions on bounded metric spaces to be equivalent.
We note that the definition above is very similar to [Reference Abbott, Balasubramanya and Osin1, Definition 3.5] and, in fact, the two definitions are easily seen to be equivalent for cobounded actions.
Remark 4.3. Consider an action
![]() $\Gamma \curvearrowright X$
on a geodesic hyperbolic space.
$\Gamma \curvearrowright X$
on a geodesic hyperbolic space.
-
(1) If the action is cobounded, then it is coarsely minimal.
The following two items follow from a construction well known to experts, namely taking the coarse convex hull of an orbit and approximating it with a graph; this is explained, for example, in [Reference Gruber, Sisto and Tessera12, Remark 4].
-
(2) If the limit set of
 $\Gamma $
is not a single point, then there is a coarsely minimal action
$\Gamma $
is not a single point, then there is a coarsely minimal action
 $\Gamma \curvearrowright Y$
on a geodesic hyperbolic space Y and an equivariant quasi-isometric embedding
$\Gamma \curvearrowright Y$
on a geodesic hyperbolic space Y and an equivariant quasi-isometric embedding
 $Y\to X$
.
$Y\to X$
. -
(3) If
 $\Gamma $
is countable and
$\Gamma $
is countable and
 $\Gamma \curvearrowright X$
is coarsely minimal, then
$\Gamma \curvearrowright X$
is coarsely minimal, then
 $\Gamma \curvearrowright X$
is equivalent to an action on a separable geodesic hyperbolic space (in fact, a graph).
$\Gamma \curvearrowright X$
is equivalent to an action on a separable geodesic hyperbolic space (in fact, a graph).
Consider a semisimple Lie group
![]() $G=G_1\times \cdots \times G_N$
without compact factors. Assume that either
$G=G_1\times \cdots \times G_N$
without compact factors. Assume that either
![]() $N\geq 2$
or
$N\geq 2$
or
![]() $N=1$
and
$N=1$
and
![]() $G=G_1$
has rank at least 2.
$G=G_1$
has rank at least 2.
Re-order the factors in such a way that
![]() $G_i$
is rank-one if and only if
$G_i$
is rank-one if and only if
![]() $1\le i\le n$
for some
$1\le i\le n$
for some
![]() $n\leq N$
.
$n\leq N$
.
We now re-state our main theorem.
Theorem 4.4. Let
![]() $\Gamma $
be an irreducible lattice in
$\Gamma $
be an irreducible lattice in
![]() $G=G_1\times \cdots \times G_N$
as above. Then every coarsely minimal action of
$G=G_1\times \cdots \times G_N$
as above. Then every coarsely minimal action of
![]() $\Gamma $
on a geodesic hyperbolic space is equivalent to the action
$\Gamma $
on a geodesic hyperbolic space is equivalent to the action
for some
![]() $i \in \{1, \ldots , n\}$
, where
$i \in \{1, \ldots , n\}$
, where
![]() $X_i$
is the symmetric space for
$X_i$
is the symmetric space for
![]() $G_i$
.
$G_i$
.
Let us extend the notation of the theorem by denoting
![]() $X_j$
, for
$X_j$
, for
![]() $j>n$
, the symmetric space for
$j>n$
, the symmetric space for
![]() $G_j$
.
$G_j$
.
Let
![]() $\Gamma \curvearrowright (X,d)$
be a coarsely minimal action of
$\Gamma \curvearrowright (X,d)$
be a coarsely minimal action of
![]() $\Gamma $
on the geodesic hyperbolic space X. Denote by
$\Gamma $
on the geodesic hyperbolic space X. Denote by
![]() $d_i$
the pseudo-metric on
$d_i$
the pseudo-metric on
![]() $\Gamma $
corresponding to
$\Gamma $
corresponding to
![]() $\Gamma \curvearrowright X_i$
(with respect to some basepoint
$\Gamma \curvearrowright X_i$
(with respect to some basepoint
![]() $x_i$
, for
$x_i$
, for
![]() $i\leq n$
), and d the pseudo-metric corresponding to
$i\leq n$
), and d the pseudo-metric corresponding to
![]() $\Gamma \curvearrowright (X,d)$
.
$\Gamma \curvearrowright (X,d)$
.
4.2. Ruling out elementary actions
To be able to apply Theorem 3.1, we have to rule out that
![]() $\Gamma $
fixes a pair of points in
$\Gamma $
fixes a pair of points in
![]() $\partial X$
(the case that it fixes one point being ruled out by hypothesis). If that were the case, the subgroup
$\partial X$
(the case that it fixes one point being ruled out by hypothesis). If that were the case, the subgroup
![]() $\Gamma '$
of index at most 2 of
$\Gamma '$
of index at most 2 of
![]() $\Gamma $
that fixes a boundary point would admit the quasimorphism described in [Reference Caprace, Cornulier, Monod and Tessera8, Proposition 3.7]. According to [Reference Burger and Monod6, Reference Burger and Monod7],
$\Gamma $
that fixes a boundary point would admit the quasimorphism described in [Reference Caprace, Cornulier, Monod and Tessera8, Proposition 3.7]. According to [Reference Burger and Monod6, Reference Burger and Monod7],
![]() $\Gamma '$
does not admit unbounded quasimorphisms, so that according to [Reference Caprace, Cornulier, Monod and Tessera8, Lemma 3.8], the action
$\Gamma '$
does not admit unbounded quasimorphisms, so that according to [Reference Caprace, Cornulier, Monod and Tessera8, Lemma 3.8], the action
![]() $\Gamma \curvearrowright X$
has a single limit point, contradicting the coarse minimality of the action. From now on, we will assume that
$\Gamma \curvearrowright X$
has a single limit point, contradicting the coarse minimality of the action. From now on, we will assume that
![]() $\Gamma $
does not fix a point or a pair of points in X.
$\Gamma $
does not fix a point or a pair of points in X.
Finally, we can assume that X is separable by Remark 4.3.
4.3. Boundary map from one factor
For every
![]() $1\leq i \leq N$
, we let
$1\leq i \leq N$
, we let
![]() $B_i=G_i/P_i$
and we let
$B_i=G_i/P_i$
and we let
![]() $\nu _i$
be a measure in the Haar class on
$\nu _i$
be a measure in the Haar class on
![]() $B_i$
, and similarly we denote
$B_i$
, and similarly we denote
![]() $B=G/P=B_1\times \cdots \times B_N$
. Note that we are in the setting of Proposition 2.9 about coarse metric ergodicity.
$B=G/P=B_1\times \cdots \times B_N$
. Note that we are in the setting of Proposition 2.9 about coarse metric ergodicity.
Theorem 3.1 affords now two
![]() $\Gamma $
-maps
$\Gamma $
-maps
![]() $B\to \partial X$
satisfying various properties. The first of these properties implies that these two maps must coincide almost everywhere. We assume henceforth that both maps are identical, and we denote it by
$B\to \partial X$
satisfying various properties. The first of these properties implies that these two maps must coincide almost everywhere. We assume henceforth that both maps are identical, and we denote it by
![]() $\phi \colon B\to \partial X$
.
$\phi \colon B\to \partial X$
.
Claim 4.5. The map
![]() $\phi $
factors through one of
$\phi $
factors through one of
![]() $B_i$
. In other words, there is an index
$B_i$
. In other words, there is an index
![]() $i\in \{1,\ldots ,N\}$
and a
$i\in \{1,\ldots ,N\}$
and a
![]() $\Gamma $
-map
$\Gamma $
-map
![]() $B_i\ {\buildrel {\phi _i}\over \longrightarrow}\ \partial X$
such that
$B_i\ {\buildrel {\phi _i}\over \longrightarrow}\ \partial X$
such that
Proof. The equivariant map
![]() $\phi :B \longrightarrow \partial X$
cannot be essentially constant, because
$\phi :B \longrightarrow \partial X$
cannot be essentially constant, because
![]() $\Gamma $
does not have a fixed point in
$\Gamma $
does not have a fixed point in
![]() $\partial X$
. Fix an
$\partial X$
. Fix an
![]() $i\in \{1,\ldots ,N\}$
so that
$i\in \{1,\ldots ,N\}$
so that
![]() $\phi $
is not essentially constant over the
$\phi $
is not essentially constant over the
![]() $B_i$
-factor of
$B_i$
-factor of
![]() $B=B_1\times \cdots \times B_N$
. We let
$B=B_1\times \cdots \times B_N$
. We let
![]() $B'$
be the product of the other factors, and identify
$B'$
be the product of the other factors, and identify
![]() $B\simeq B_i\times B'$
. Using this identification, we consider the map
$B\simeq B_i\times B'$
. Using this identification, we consider the map
By Theorem 3.1(iii), we have three cases:
![]() $\Phi (B\times B)$
is contained in the diagonal
$\Phi (B\times B)$
is contained in the diagonal
![]() $\Delta \subset \partial X^2$
,
$\Delta \subset \partial X^2$
,
![]() $\Phi =\phi _{\bowtie }$
or
$\Phi =\phi _{\bowtie }$
or
![]() $\Phi =\tau \circ \phi _{\bowtie }$
, where
$\Phi =\tau \circ \phi _{\bowtie }$
, where
![]() $\phi _{\bowtie }=\phi \times \phi $
and
$\phi _{\bowtie }=\phi \times \phi $
and
![]() $\tau (\xi ,\eta )=(\eta ,\xi )$
. In the first case, we see that
$\tau (\xi ,\eta )=(\eta ,\xi )$
. In the first case, we see that
![]() $\phi (x,y)$
is independent of
$\phi (x,y)$
is independent of
![]() $y\in B'$
and therefore descends to a
$y\in B'$
and therefore descends to a
![]() $\Gamma $
-map
$\Gamma $
-map
![]() $B_i\to \partial X$
as required. In the second and third cases,
$B_i\to \partial X$
as required. In the second and third cases,
![]() $\phi $
is independent of
$\phi $
is independent of
![]() $x\in B_i$
, contradicting our choice of i.
$x\in B_i$
, contradicting our choice of i.
From now on, we fix the index
![]() $i \in \{1, \ldots , N\}$
afforded by Claim 4.5.
$i \in \{1, \ldots , N\}$
afforded by Claim 4.5.
4.4. The factor
 $B_i$
is associated with a rank-one factor
$B_i$
is associated with a rank-one factor
We now explain that the factor
![]() $B_i$
afforded by Claim 4.5 is associated with a rank-one factor, that is,
$B_i$
afforded by Claim 4.5 is associated with a rank-one factor, that is,
![]() $i\leq n$
. We argue by contradiction, assuming
$i\leq n$
. We argue by contradiction, assuming
![]() $i>n$
, that is,
$i>n$
, that is,
![]() $G_i$
is of higher rank.
$G_i$
is of higher rank.
As before, we let
![]() $P_i<G_i$
be a minimal parabolic. In the following, we will omit the index i and denote
$P_i<G_i$
be a minimal parabolic. In the following, we will omit the index i and denote
![]() $P=P_i$
. Let
$P=P_i$
. Let
![]() $A<P$
be a maximal split torus. We let
$A<P$
be a maximal split torus. We let
![]() $W=N_{G_i}(A)/Z_{G_i}(A)$
be the corresponding Weyl group and let
$W=N_{G_i}(A)/Z_{G_i}(A)$
be the corresponding Weyl group and let
![]() $S\subset W$
be the standard Coxeter generators associated with the positivity defined by P. Letting
$S\subset W$
be the standard Coxeter generators associated with the positivity defined by P. Letting
![]() $Z=Z_{G_i}(A)$
be the centralizer of A, we note that W acts naturally on
$Z=Z_{G_i}(A)$
be the centralizer of A, we note that W acts naturally on
![]() $G_i/Z$
by
$G_i/Z$
by
![]() $G_i$
-automorphisms.
$G_i$
-automorphisms.
As usual, we identify the set S with the set of simple roots of
![]() $G_i$
associated with the pair
$G_i$
associated with the pair
![]() $(A,P)$
. Any subset T of S generates a subgroup
$(A,P)$
. Any subset T of S generates a subgroup
![]() $W_T<W$
and it corresponds to a standard parabolic
$W_T<W$
and it corresponds to a standard parabolic
![]() $P_T<G_i$
containing
$P_T<G_i$
containing
![]() $P=P_\varnothing $
. All the subgroups of
$P=P_\varnothing $
. All the subgroups of
![]() $G_i$
containing P are of this form. Denoting by
$G_i$
containing P are of this form. Denoting by
![]() $\pi _T:G_i/Z\to G_i/P_T$
the standard map coming from the inclusion
$\pi _T:G_i/Z\to G_i/P_T$
the standard map coming from the inclusion
![]() $Z<P<P_T$
, we note that
$Z<P<P_T$
, we note that
We let
![]() $\pi =\pi _\varnothing :G_i/Z\to G_i/P$
be the standard map and let
$\pi =\pi _\varnothing :G_i/Z\to G_i/P$
be the standard map and let
![]() $w_0\in W$
be the longest element (with respect to the word distance induced by S). It is a standard fact that the map
$w_0\in W$
be the longest element (with respect to the word distance induced by S). It is a standard fact that the map
![]() $\pi \times \pi \circ w_0:G_i/Z\to G_i/P\times G_i/P$
is injective and its image is Zariski open (this image is the big cell in the Bruhat decomposition of
$\pi \times \pi \circ w_0:G_i/Z\to G_i/P\times G_i/P$
is injective and its image is Zariski open (this image is the big cell in the Bruhat decomposition of
![]() $G_i/P\times G_i/P$
).
$G_i/P\times G_i/P$
).
We also endow
![]() $G_i/Z$
with the Haar measure class. By the preceding paragraph, we may identify it, as measured
$G_i/Z$
with the Haar measure class. By the preceding paragraph, we may identify it, as measured
![]() $G_i$
-spaces, with
$G_i$
-spaces, with
![]() $B_i\times B_i=G_i/P\times G_i/P$
via the map
$B_i\times B_i=G_i/P\times G_i/P$
via the map
![]() $\pi \times \pi \circ w_0$
.
$\pi \times \pi \circ w_0$
.
We set
![]() $\phi _i:B_i\to \partial X$
to be the map given in Claim 4.5. Note that
$\phi _i:B_i\to \partial X$
to be the map given in Claim 4.5. Note that
![]() $\phi _i$
is not essentially constant, as
$\phi _i$
is not essentially constant, as
![]() $\partial X$
has no
$\partial X$
has no
![]() $\Gamma $
-fixed points. We thus may find a bounded measurable function
$\Gamma $
-fixed points. We thus may find a bounded measurable function
![]() $f_0:\partial X \to \mathbb {C}$
such that
$f_0:\partial X \to \mathbb {C}$
such that
![]() $f_0\circ \phi _i$
is not essentially constant. We fix such a function
$f_0\circ \phi _i$
is not essentially constant. We fix such a function
![]() $f_0$
.
$f_0$
.
We consider the map
![]() $\psi =\phi _i\circ p_1:B_i\times B_i\longrightarrow \partial X$
, where
$\psi =\phi _i\circ p_1:B_i\times B_i\longrightarrow \partial X$
, where
![]() $p_1:B_i\times B_i\longrightarrow B_i$
is the projection on the first factor. Under our identifications
$p_1:B_i\times B_i\longrightarrow B_i$
is the projection on the first factor. Under our identifications
![]() $B_i = G_i/P$
and
$B_i = G_i/P$
and
![]() $B_i\times B_i = G_i/Z$
, the projection
$B_i\times B_i = G_i/Z$
, the projection
![]() $p_1$
is identified with the map
$p_1$
is identified with the map
![]() $ \pi = \pi _\varnothing \colon G_i/Z \to G_i/P$
. We set
$ \pi = \pi _\varnothing \colon G_i/Z \to G_i/P$
. We set
By Theorem 3.1(ii), we conclude that
![]() $U<W$
is of index at most 2.
$U<W$
is of index at most 2.
We shall now show that U is contained in a proper parabolic subgroup
![]() $W_T$
of W. Consider now the algebra
$W_T$
of W. Consider now the algebra
![]() $L^\infty (G_i/Z)$
and its subalgebra
$L^\infty (G_i/Z)$
and its subalgebra
![]() $\pi ^{*}(L^\infty (G_i/P))$
consisting of functions pulled back from
$\pi ^{*}(L^\infty (G_i/P))$
consisting of functions pulled back from
![]() $L^\infty (G_i/P)$
under
$L^\infty (G_i/P)$
under
![]() $\pi :G_i/Z\to G_i/P$
(which we identify with
$\pi :G_i/Z\to G_i/P$
(which we identify with
![]() $p_1:B_i\times B_i\to B_i$
). Consider the subalgebra
$p_1:B_i\times B_i\to B_i$
). Consider the subalgebra
This is a weak*-closed
![]() $G_i$
-invariant subalgebra of
$G_i$
-invariant subalgebra of
![]() $L^\infty (G_i/Z)$
. By Mackey’s point realization theorem, this algebra coincides with the subalgebra of functions pulled back from a
$L^\infty (G_i/Z)$
. By Mackey’s point realization theorem, this algebra coincides with the subalgebra of functions pulled back from a
![]() $G_i$
-factor of
$G_i$
-factor of
![]() $G_i/Z$
. As all functions in it are pulled back from
$G_i/Z$
. As all functions in it are pulled back from
![]() $G_i/P$
, this factor is of the form
$G_i/P$
, this factor is of the form
![]() $G_i/P_T$
for some
$G_i/P_T$
for some
![]() $T\subset S$
. As the algebra includes the non-constant function
$T\subset S$
. As the algebra includes the non-constant function
![]() $f_0\circ \psi $
, we conclude that
$f_0\circ \psi $
, we conclude that
![]() $P_T\neq G_i$
, and thus
$P_T\neq G_i$
, and thus
![]() $T\neq S$
and
$T\neq S$
and
![]() $W_T\neq W$
. We have that
$W_T\neq W$
. We have that
![]() $\pi _T\circ u=\pi _T$
for every
$\pi _T\circ u=\pi _T$
for every
![]() $u\in U$
, and thus
$u\in U$
, and thus
![]() $U<W_T$
. It follows that
$U<W_T$
. It follows that
![]() $W_T$
is of index
$W_T$
is of index
![]() $2$
in W and, in particular, it is a normal subgroup.
$2$
in W and, in particular, it is a normal subgroup.
To obtain a contradiction and conclude this step of the proof, we use that W is an irreducible finite Coxeter group with
![]() $|W|>2$
, since
$|W|>2$
, since
![]() $G_i$
is simple of rank
$G_i$
is simple of rank
![]() $\geq 2$
. Therefore, there is
$\geq 2$
. Therefore, there is
![]() $t \in T$
and
$t \in T$
and
![]() $s \in S \setminus T$
such that s and t do not commute. In particular,
$s \in S \setminus T$
such that s and t do not commute. In particular,
![]() $sts$
is a reduced word in W. Since
$sts$
is a reduced word in W. Since
![]() $W_T$
has index
$W_T$
has index
![]() $2$
, we have
$2$
, we have
![]() $sts \in W_T$
. By [Reference Bourbaki5, Corollary 1 in Ch. IV, §1, no. 1.8], we deduce that
$sts \in W_T$
. By [Reference Bourbaki5, Corollary 1 in Ch. IV, §1, no. 1.8], we deduce that
![]() $s \in T$
, which is a contradiction.
$s \in T$
, which is a contradiction.
4.5. Bounded in
 $G_i$
is d-bounded
$G_i$
is d-bounded
Next, we show that d is ‘smaller’ than
![]() $d_i$
for i as in Claim 4.5.
$d_i$
for i as in Claim 4.5.
Claim 4.6. There exist
![]() $L,C$
so that for all
$L,C$
so that for all
![]() $\gamma ,\gamma '$
, we have
$\gamma ,\gamma '$
, we have
Proof. As G is of higher rank, we deduce from §4.4 that
![]() $N>1$
and, in particular, we get that
$N>1$
and, in particular, we get that
![]() $\operatorname {pr}_i(\Gamma )$
is dense in
$\operatorname {pr}_i(\Gamma )$
is dense in
![]() $G_i$
. Hence, in the metric
$G_i$
. Hence, in the metric
![]() $d_i$
any pair of points is connected by a
$d_i$
any pair of points is connected by a
![]() $(1,1)$
-quasi-geodesic, and to prove the claim, it suffices to show that sequences that are bounded in
$(1,1)$
-quasi-geodesic, and to prove the claim, it suffices to show that sequences that are bounded in
![]() $G_i$
are bounded in
$G_i$
are bounded in
![]() $(\Gamma ,d)$
. In other words, it suffices to show that any sequence
$(\Gamma ,d)$
. In other words, it suffices to show that any sequence
![]() $\{\gamma _j\}$
in
$\{\gamma _j\}$
in
![]() $\Gamma $
for which
$\Gamma $
for which
![]() $\{\operatorname {pr}_i(\gamma _j)\}$
is precompact in
$\{\operatorname {pr}_i(\gamma _j)\}$
is precompact in
![]() $G_i$
, one has
$G_i$
, one has
Let
![]() $\mu =\phi _*\nu _i\in \operatorname {Prob}(\partial X)$
be the push-forward of the measure
$\mu =\phi _*\nu _i\in \operatorname {Prob}(\partial X)$
be the push-forward of the measure
![]() $\nu _i$
on
$\nu _i$
on
![]() $B_i$
. By the metric ergodicity of
$B_i$
. By the metric ergodicity of
![]() $B_i$
,
$B_i$
,
![]() $\mu $
has no atomic part. Indeed, if it had, we would get a countable invariant subset of
$\mu $
has no atomic part. Indeed, if it had, we would get a countable invariant subset of
![]() $\partial X$
and upon endowing it with the discrete metric, in view of the metric ergodicity of
$\partial X$
and upon endowing it with the discrete metric, in view of the metric ergodicity of
![]() $B_i$
, we will conclude that this set contains a single point which is
$B_i$
, we will conclude that this set contains a single point which is
![]() $\Gamma $
-invariant, which contradicts the hypothesis.
$\Gamma $
-invariant, which contradicts the hypothesis.
By Lemma 3.8, we have a
![]() $\Gamma $
-map
$\Gamma $
-map
where, as before,
![]() $\operatorname {Prob}_c(\partial X)$
is the set of all atom-less probability measures on
$\operatorname {Prob}_c(\partial X)$
is the set of all atom-less probability measures on
![]() $\partial X$
.
$\partial X$
.
We assume that
![]() $\{\gamma _j\}$
is such that
$\{\gamma _j\}$
is such that
![]() $\{\operatorname {pr}_i(\gamma _j)\}$
is precompact in
$\{\operatorname {pr}_i(\gamma _j)\}$
is precompact in
![]() $G_i$
. We now need the following lemma.
$G_i$
. We now need the following lemma.
Lemma 4.7. Given any precompact subset
![]() $\{\gamma _j\}\subseteq G_i$
, the corresponding Radon–Nikodym derivatives are uniformly bounded, that is, we have
$\{\gamma _j\}\subseteq G_i$
, the corresponding Radon–Nikodym derivatives are uniformly bounded, that is, we have
 $$ \begin{align*} \sup_{j\ge 1} \bigg\|\frac{d\gamma_j\nu_i}{d\nu_i}\bigg\|_\infty<+\infty. \end{align*} $$
$$ \begin{align*} \sup_{j\ge 1} \bigg\|\frac{d\gamma_j\nu_i}{d\nu_i}\bigg\|_\infty<+\infty. \end{align*} $$
Proof. Since
![]() $\nu _i$
is the Patterson–Sullivan measure for
$\nu _i$
is the Patterson–Sullivan measure for
![]() $G_i$
, we have for any
$G_i$
, we have for any
![]() $g\in G_i$
and a.e.
$g\in G_i$
and a.e.
![]() $\xi \in \partial X_i$
,
$\xi \in \partial X_i$
,
where
![]() $\delta _i$
is a constant associated with the symmetric space
$\delta _i$
is a constant associated with the symmetric space
![]() $X_i$
for
$X_i$
for
![]() $G_i$
and
$G_i$
and
![]() $\beta (g,\xi )$
is the Busemann function. Since the Busemann function is bounded by the distance in
$\beta (g,\xi )$
is the Busemann function. Since the Busemann function is bounded by the distance in
![]() $X_i$
,
$X_i$
,
![]() $|\beta (g,\xi )|\le d_i(go,o)$
, the lemma is proved.
$|\beta (g,\xi )|\le d_i(go,o)$
, the lemma is proved.
Hence, by Lemma 4.7, we have
 $$ \begin{align*} \sup_{j\ge 1} \bigg\|\frac{d\gamma_j\nu_i}{d\nu_i}\bigg\|_\infty=C<+\infty. \end{align*} $$
$$ \begin{align*} \sup_{j\ge 1} \bigg\|\frac{d\gamma_j\nu_i}{d\nu_i}\bigg\|_\infty=C<+\infty. \end{align*} $$
We thus have the same bound on the Radon–Nikodym derivatives of
![]() $\mu $
$\mu $
 $$ \begin{align*} \sup_{j\ge 1} \bigg\|\frac{d\gamma_j\mu}{d\mu}\bigg\|_\infty\le C \end{align*} $$
$$ \begin{align*} \sup_{j\ge 1} \bigg\|\frac{d\gamma_j\mu}{d\mu}\bigg\|_\infty\le C \end{align*} $$
and also, by the ‘moreover’ part of Lemma 3.8,
 $$ \begin{align*} \sup_{j\ge 1} \bigg\|\frac{d\Psi(\gamma_j\mu)}{d\Psi(\mu)}\bigg\|_\infty\le C^3. \end{align*} $$
$$ \begin{align*} \sup_{j\ge 1} \bigg\|\frac{d\Psi(\gamma_j\mu)}{d\Psi(\mu)}\bigg\|_\infty\le C^3. \end{align*} $$
Setting
![]() $U=\operatorname {Prob}(\partial X^{(3)})$
, recall the maps
$U=\operatorname {Prob}(\partial X^{(3)})$
, recall the maps
![]() $\beta _\epsilon :\operatorname {Prob}(\partial X^{(3)})\to \operatorname {Bdd}(\partial X^{(3)})$
from §2.6, which are
$\beta _\epsilon :\operatorname {Prob}(\partial X^{(3)})\to \operatorname {Bdd}(\partial X^{(3)})$
from §2.6, which are
![]() $\Gamma $
-equivariant (as they are equivariant with respect to all isometries). Fix
$\Gamma $
-equivariant (as they are equivariant with respect to all isometries). Fix
![]() ${\epsilon \in (0,1/2)}$
and set
${\epsilon \in (0,1/2)}$
and set
![]() $R=r_{\epsilon /C}(\Psi (\mu ))+1$
. Fixing j and applying Lemma 2.16 with
$R=r_{\epsilon /C}(\Psi (\mu ))+1$
. Fixing j and applying Lemma 2.16 with
![]() $m_1=\Psi (\mu )$
and
$m_1=\Psi (\mu )$
and
![]() $m_2=\Psi (\gamma _j\mu )$
, we get
$m_2=\Psi (\gamma _j\mu )$
, we get
Since
![]() $N_R(\beta _{\epsilon /C}(\Psi (\mu )))$
is a bounded subset of
$N_R(\beta _{\epsilon /C}(\Psi (\mu )))$
is a bounded subset of
![]() $\partial X^{(3)}$
, we get that the sequence
$\partial X^{(3)}$
, we get that the sequence
![]() $\{\gamma _j\}$
has bounded orbits in
$\{\gamma _j\}$
has bounded orbits in
![]() $\partial X^{(3)}$
, whence it is bounded in
$\partial X^{(3)}$
, whence it is bounded in
![]() $(\Gamma ,d)$
by the ‘moreover’ part of Lemma 3.7.
$(\Gamma ,d)$
by the ‘moreover’ part of Lemma 3.7.
4.6. Unbounded in
 $G_i$
is d-unbounded
$G_i$
is d-unbounded
Claim 4.8. There exist
![]() $L,C$
so that for all
$L,C$
so that for all
![]() $\gamma ,\gamma '$
, we have
$\gamma ,\gamma '$
, we have
Proof. Let
![]() $\gamma _0\in \Gamma $
be a loxodromic element for
$\gamma _0\in \Gamma $
be a loxodromic element for
![]() $\Gamma \curvearrowright X$
, which exists by Gromov’s classification of actions on hyperbolic spaces [Reference Gromov11, §8]. Since the identity map
$\Gamma \curvearrowright X$
, which exists by Gromov’s classification of actions on hyperbolic spaces [Reference Gromov11, §8]. Since the identity map
![]() $(\Gamma ,d_i)\to (\Gamma ,d)$
is coarsely Lipschitz,
$(\Gamma ,d_i)\to (\Gamma ,d)$
is coarsely Lipschitz,
![]() $\gamma _0$
is loxodromic for
$\gamma _0$
is loxodromic for
![]() $\Gamma \curvearrowright X_i$
as well. Let us choose a constants A so that for each
$\Gamma \curvearrowright X_i$
as well. Let us choose a constants A so that for each
![]() $j\geq 0$
, we have
$j\geq 0$
, we have
![]() $j/A\leq d_i(1,\gamma _0^j)\leq Aj$
and
$j/A\leq d_i(1,\gamma _0^j)\leq Aj$
and
![]() $j/A\leq d(1,\gamma _0^j)\leq Aj$
. Note that, up to increasing A, since
$j/A\leq d(1,\gamma _0^j)\leq Aj$
. Note that, up to increasing A, since
![]() $G_i$
is rank-one and
$G_i$
is rank-one and
![]() $\gamma _0$
is loxodromic, the set
$\gamma _0$
is loxodromic, the set
is A-dense in
![]() $X_i$
, where we denote by
$X_i$
, where we denote by
![]() $K_i$
a maximal compact subgroup of
$K_i$
a maximal compact subgroup of
![]() $G_i$
. This is because, since
$G_i$
. This is because, since
![]() $K_i$
acts transitively on
$K_i$
acts transitively on
![]() $\partial X$
, there exists a constant C such that given any two points on a sphere around
$\partial X$
, there exists a constant C such that given any two points on a sphere around
![]() $x_i$
, there is an element of
$x_i$
, there is an element of
![]() $K_i$
that moves the first point C-close to the second one.
$K_i$
that moves the first point C-close to the second one.
Since the rank of
![]() $G_i$
equals one, we know by hypothesis that
$G_i$
equals one, we know by hypothesis that
![]() $N>1$
and, in particular, we get that
$N>1$
and, in particular, we get that
![]() $\operatorname {pr}_i(\Gamma )$
is dense in
$\operatorname {pr}_i(\Gamma )$
is dense in
![]() $G_i$
. Approximating elements of
$G_i$
. Approximating elements of
![]() $K_i$
by elements of
$K_i$
by elements of
![]() $\Gamma $
, we get that the set
$\Gamma $
, we get that the set
is
![]() $A+1$
-dense in
$A+1$
-dense in
![]() $\Gamma $
for the metric
$\Gamma $
for the metric
![]() $d_i$
. Enlarging A if necessary, let us further assume that
$d_i$
. Enlarging A if necessary, let us further assume that
![]() $d(1,\gamma )\leq Ad_i(1,\gamma )+A$
for all
$d(1,\gamma )\leq Ad_i(1,\gamma )+A$
for all
![]() $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
Consider an arbitrary
![]() $\gamma \in \Gamma $
. Using the above, we find
$\gamma \in \Gamma $
. Using the above, we find
![]() $\kappa \in \Gamma $
such that
$\kappa \in \Gamma $
such that
![]() $d_i(1,\kappa )\leq 1$
and
$d_i(1,\kappa )\leq 1$
and
![]() $d_i(\kappa \gamma ,\gamma _0^j)\leq A+1$
for some
$d_i(\kappa \gamma ,\gamma _0^j)\leq A+1$
for some
![]() $j\geq 0$
. Therefore, we obtain
$j\geq 0$
. Therefore, we obtain
 $$ \begin{align*} d_i(1,\gamma) &= d_i(\kappa,\kappa\gamma)\\ &\leq d_i(1,\gamma_0^j)+A+2\\ & \leq Aj+A+2\\ & \leq A^2d(1,\gamma_0^j)+A+2\\ &\leq A^2 (d(1,\kappa)+d(\kappa,\kappa\gamma)+d(\kappa\gamma,\gamma_0^j))+A+2\\ & \leq A^2d(1,\gamma)+A^3+2A^2+3A+2, \end{align*} $$
$$ \begin{align*} d_i(1,\gamma) &= d_i(\kappa,\kappa\gamma)\\ &\leq d_i(1,\gamma_0^j)+A+2\\ & \leq Aj+A+2\\ & \leq A^2d(1,\gamma_0^j)+A+2\\ &\leq A^2 (d(1,\kappa)+d(\kappa,\kappa\gamma)+d(\kappa\gamma,\gamma_0^j))+A+2\\ & \leq A^2d(1,\gamma)+A^3+2A^2+3A+2, \end{align*} $$
as required.
4.7. Conclusion
We have seen in §4.4 that the rank of
![]() $G_i$
is
$G_i$
is
![]() $1$
. Claims 4.6 and 4.8 imply that there is a
$1$
. Claims 4.6 and 4.8 imply that there is a
![]() $\Gamma $
-equivariant quasi-isometric embedding
$\Gamma $
-equivariant quasi-isometric embedding
![]() $f:X_i\to \operatorname {Bdd}_C(X)$
for some
$f:X_i\to \operatorname {Bdd}_C(X)$
for some
![]() $C\geq 0$
(since
$C\geq 0$
(since
![]() $(\Gamma ,d_i)$
is
$(\Gamma ,d_i)$
is
![]() $\Gamma $
-equivariantly quasi-isometric to
$\Gamma $
-equivariantly quasi-isometric to
![]() $X_i$
, and there is a
$X_i$
, and there is a
![]() $\Gamma $
-equivariant quasi-isometric embedding
$\Gamma $
-equivariant quasi-isometric embedding
![]() $(\Gamma ,d_i)\to X$
). Since
$(\Gamma ,d_i)\to X$
). Since
![]() $X_i$
is hyperbolic, the image of that quasi-isometric embedding is quasi-convex. Since the
$X_i$
is hyperbolic, the image of that quasi-isometric embedding is quasi-convex. Since the
![]() $\Gamma $
-action on X is coarsely minimal, it follows that the
$\Gamma $
-action on X is coarsely minimal, it follows that the
![]() $\Gamma $
-action on X is cobounded, so that the quasi-isometric embedding
$\Gamma $
-action on X is cobounded, so that the quasi-isometric embedding
![]() $(\Gamma ,d_i)\to X$
is in fact a quasi-isometry. This proves that
$(\Gamma ,d_i)\to X$
is in fact a quasi-isometry. This proves that
![]() $\Gamma \curvearrowright X_i$
is indeed equivalent to
$\Gamma \curvearrowright X_i$
is indeed equivalent to
![]() $\Gamma \curvearrowright X$
, as required.
$\Gamma \curvearrowright X$
, as required.
Acknowledgements
The authors would like to acknowledge the following support: U.B. was supported by ISF Moked 713510 grant number 2919/19; P.-E.C. was supported by the FWO and the F.R.S.-FNRS under the EOS programme (project ID 40007542); A.F. was supported in part by NSF Grant DMS 2005493; U.B. and A.F. were supported by BSF Grant 2018258. This project was started at the Oberwolfach workshop ‘Geometric structures in group theory’ number 1726. The authors are thankful to the Oberwolfach Institute for hosting the workshop and to the organizers. The authors are grateful to the referee for valuable comments and suggestions.