1. INTRODUCTION
As human society progresses and becomes more sophisticated, our demand for new ideals, new capabilities, and new environments intensifies, resulting in ever increasing complexity of human-made systems, which span from physical systems and technologies to organizations, social, political, and economic systems. Complexity has been recognized as an important feature and mechanism of biosystems, societal systems, and technology development processes. However, for engineered systems, the notion of complexity often points to unintended, undesirable, and must-avoid system properties.
One may note that the increasing complexity of engineered systems comes from increasingly complex and highly sophisticated functional requirements. For example, increasing demands for performance, safety, ease of operation, comfort of ride, and least environmental impact have led to today's complex automobiles. Over the process of product evolution, the capabilities or functionalities of the automobile were added incrementally, with special cares being made to make sure that unintended actions of, and interactions between, the components be eliminated or at least minimized. A major issue with developing complex engineered systems is that the sheer number of, and intricate interdependencies among, the system components imply uncertainty and unknowns to the engineers, making it difficult for them to ensure the valid operation range for the system to survive its expected mission. The strategy of current engineering approaches to complex systems can be characterized as “multilevel divide and concur,” that is, decomposing tasks into smaller ones and finding their solutions until the achievable solutions are attained, while limiting interactions among the subsolutions at every step of the process. As systems become ever more complex and a large number of engineering teams are involved, “limiting interactions” becomes practically impossible, which, in the extreme cases, can leave the success of the final systems to chance.
In contrast, it is intriguing to consider that nature “faces” all the uncertainties and unknowns, and yet natural systems are “designed” to live with these uncertainties and unknowns as an inherent part of their capabilities. We observe that human design and natural “design” are very distinct from each other: human design is more purpose or function driven and takes a top-down approach to avoid possible complexity problems, while natural “design” is arguably less purposeful and follows a bottom-up approach by making complexity as a “solution” to deal with the arising uncertainties and unknowns (Ashby, Reference Ashby1958). The research on system biology (Kitano, Reference Kitano2002), self-configurable systems (Subramanian & Katz, Reference Subramanian and Katz2000), and component-based design (Kopetz, Reference Kopetz1998) has explored the formation of adaptive systems from both natural and human-made perspectives. Most adaptive systems developed to date, including adaptive structures and adaptive control systems, are based on the prespecified system configurations. When the changes of task and operation environment exceed the configuration bound, the system will not be able to respond. Further, as systems become more complex, devising “adaptability” into the system may face the same problem described above. In our research, we introduce a cellular and self-organizing (CSO) approach to building adaptive systems. In this approach, a mechanical system is composed of multiple mechanical cells (or simply mCells), which can be either identical (for homogeneous systems) or distinct (for heterogeneous systems). Further, the formation of such systems is based on a set of bottom-up, dynamical, and self-organized mechanisms. It is fully understood that the CSO approach will not be able to compete with the traditional methods in a short term for many applications. However, the paradigm shift from component based to cell based and from top down to bottom up promises an alternative future for developing complex engineered systems.
Both multiagent systems and self-organizing systems have been highlighted in many engineering fields, such as computer science, industrial engineering, and material science. Much research has been done to investigate the properties and benefits of such systems and the ways to build them. One critical design research question is as follows: How can a designer connect the design of mechanical cells/agents and their interactions with functional requirements (or tasks)? In our research, we propose a field-based behavior regulation (FBR) approach as a basis for cells to interact with each other and with their task environment. In this approach, a cell is a sensor–operator unit that can perform a range of actions. At a given time, a cell's behavior can be self-regulated based on the cell's “field position” at that moment. The field position of a cell is determined by the task requirements and the environmental situation that can be sensed by the cell. When a CSO system is composed of multiple mCells, at any given time, different cells may exhibit different or similar behaviors. This cellular differentiation is achieved locally through field-based regulation, unlike conventional modular (Gu et al., Reference Gu, Hashemian, Sosale and Rivin1997; Gershenson et al., Reference Gershenson, Prasad and Allamneni1999) or component-based (Kopetz, Reference Kopetz1998) approaches in which differentiation of components is predetermined at design time and does not change during system operation.
In the rest of this paper, we review the related work in Section 2 and then introduce our CSO framework in Section 3. In Section 4, we present the FBR approach, and in Section 5 we demonstrate the effectiveness of our approach through simulation-based case studies. Section 6 draws conclusions and points out future research directions.
2. RELATED WORK
Much research has been done to investigate multiagent and self-organizing systems, and to develop methods for designing such systems. Self-organization and emergent behavior as two major features of such systems have been popular research topics in the area of complex systems (e.g., von Neumann, Reference von Neumann and Burks1966; Fukuda & Kawauchi, Reference Fukuda and Kawauchi1990; Weisbuch, Reference Weisbuch and Ryckebusch1991; Bojinov et al., Reference Bojinov, Casal and Hogg2000; Butler et al., Reference Butler, Kotay, Rus and Tomita2001; Wolfram, Reference Wolfram2002; Gershenson, Reference Gershenson, Bogg and Geyer2007; Zouein, Reference Zouein2009). Self-organization is the system-level organization through the limited local interactions of the constituent components, while emergence represents the concept of the patterns, often unpredictable ones, which are exhibited in the system level organization. Holland (Reference Holland1992) and Gell-Mann (Reference Gell-Mann1994) extended the research to nonhomogeneous systems and pointed out the nonlinearity between local and global, which becomes the biggest challenge of such systems. To further address the problem, the game of life (Gardner, Reference Gardner1970) and more cellular automata based fractals have been explored (Wolfram, Reference Wolfram2002).
In the field of engineering design, design for adaptability and design of reconfigurable systems have been investigated in the past decade. In their work focusing on vehicle design, Ferguson and Lewis (Reference Ferguson and Lewis2006) introduced a method of designing effective reconfigurable systems that focuses on determining how the design variables of a system change, as well as investigating the stability of a reconfigurable system through the application of a state-feedback controller. This method is based on multiobjective optimization and allows systems to adjust their design variables by dynamically optimizing in response to changing conditions. The adaptability of such systems is limited by the range of change of the variables and by the preconceivable changing situations. Martin and Ishii (Reference Martin and Ishii2002) proposed a design for variety approach that allows quick reconfiguration of products but mainly aims to reduce time to market by addressing generational product variation. Indices have been developed for generational variance to help designers reduce the development time of future evolutionary products (Martin & Ishii, Reference Martin and Ishii2002). In addition to developing design methods for reconfigurable systems, various reconfigurable robotics have been developed mostly by computer scientists. Fukuda and Nakagawa (Reference Fukuda and Nakagawa1988) developed a dynamically reconfigurable robotic system known as DRRS. Unsal et al. (Reference Unsal, Kilic and Khosla2001) focused on creating very simplistic i-Cube systems (with cubes being able to attached to each other) in order to investigate whether they can fully realize the full potential of this class of systems. PolyBot has gone through several updates over the years (Yim et al., Reference Yim, Duff and Roufas2000, Reference Yim, Zhang and Duff2002) but acquired notoriety by being the first robot that “demonstrated sequentially two topologically distinct locomotion modes by self-configuration. SuperBot (Shen et al., Reference Shen, Krivokon, Chiu, Everist, Rubenstein and Venkatesh2006) is composed of a series of homogeneous modules each of which has three joints and three points of connection. Control of SuperBot is naturally inspired and achieved through what the authors describe as the “hormone” control algorithm (Salemi et al., Reference Salemi, Shen and Will2001; Shen et al., Reference Shen, Salemi and Will2002, Reference Shen, Will, Galstyan and Chuong2004).
Biomimetic design methods allow designers to identify appropriate natural systems or mechanisms from which to draw design inspirations. The idea of using DNA and genes to capture genotypes of systems is not new. Inspired by nature's evolution process, genetic algorithm (Goldberg, Reference Goldberg1989) and genetic programming (Koza, Reference Koza1992) have been established to model problems using bit string (genetic algorithm) or functional tree (genetic programming) genes and to solve problems by evolving the best solution(s) from a population through reproduction, mutation, recombination, natural selection, and survival of fitness. This approach has been taken to solve various engineering problems, including design optimization, configuration design, and design automation (Koza, Reference Koza1992; Fogel et al., Reference Fogel, Owens and Walsh1996; Parmee, Reference Parmee1997; Bentley, Reference Bentley1999; Koza et al., Reference Koza, Bennett, Andre and Keane1999; Bonnie & Malaga, Reference Bonnie and Malaga2000; Lee et al., Reference Lee, Ma and Antonsson2001; Maher, Reference Maher2001; Vajna & Clement, Reference Vajna and Clement2002; Fan et al., Reference Fan, Seo, Hu, Rosenberg and Goodman2003). In addition to direct encoding where genotype codes map to the phenotypes directly, recently researchers have explored indirect coding method, called computational embryogeny (Kumar & Bentley, Reference Kumar and Bentley2000), to evolve rules that build or develop corresponding phenotypes (Yogev & Antonsson, Reference Yogev and Antonsson2007). Although these computational methods have been successfully applied to solve optimization problems with specific fitness functions, effectively integrating the methods into our proposed CSO systems design and development framework remains a key challenge. Aiming to develop machines that can replicate and repair themselves, Lipson (Reference Lipson2007) and his colleagues (Zykov et al., Reference Zykov, Mytilinaios, Adams and Lipson2005) investigated and demonstrated autonomous self-replication in the context of homogeneously composed systems composed of cube modules, and the type of system that has the capability if damaged to construct a detached functional copy of its nonfunctioning self through a technique called continuous self-modeling (Bongard et al., Reference Bongard, Zykov and Lipson2006). In order to make modular robots to solve self-adaptive tasks, a distributed constraint maintenance approach has been developed that allows networked agents to perform self-adaptation through satisfying their local constraints (Yu & Nagpal, Reference Yu and Nagpal2011).
Our previous work on CSO generated a design DNA concept and associated system formation mechanisms (Zouein, Reference Zouein2009; Jin et al., Reference Jin, Zouein and Lu2010). This research extends the previous research by expanding the concept of design DNA from a static specification to a dynamic and probabilistic representation, and then introducing a new field-based control mechanism to utilize the potentials of such systems for increased robustness and resilience. In addition, while most current approaches for multiagent systems design require agents to have global unique identifiers for cooperation and while some methods such as the digital hormone model (Shen et al., Reference Shen, Will, Galstyan and Chuong2004) require explicit local interactions, our FBR approach allows agents to respond to the field of the task environment spontaneously and interact with other cells or agents only implicitly, rather than deliberately, as a result of their actions in the task field.
3. CSO SYSTEMS
The goals of our research on CSO systems are twofold. First, we aim to develop systems that are flexible in responding to various known or unknown tasks, robust in achieving given tasks under changing environment situations, and resilient in dealing with partial system failures. Second, we are interested in developing a similar-to-nature bottom-up and self-organizing based design method for future complex engineered systems development.
To illustrate our intuitions, we compare engineered systems with natural systems from a design perspective. As shown in Table 1, in this comparison, the natural systems are divided into two categories: dynamical systems (e.g., planetary system) and biological systems (e.g., animals and plants), and the “design perspective” is captured by dividing analysis into four levels:
• Physical substrate: the physical units that constitute the system;
• Mechanism: the ways by which the system attains its behavior;
• Capability: the manifestation of external effects of the system, desired or not; and
• Adaptation: the ways by which the system changes itself.
Table 1. Comparison of engineered systems and natural systems

As shown in Table 1, conventional engineered systems are designed and built based on physical components that can be structured in various ways. The mechanism is realized by the designer-specified organization of the behaviors of the components. The desired functions are achieved through the working mechanisms of the constrained, or organized, component behaviors. These systems cannot change themselves in any explicit or implicit way in response to the changes of task and operation environment; hence, there is no adaptation.
Natural dynamical systems are formed based on objects such as planets or particles. Their mechanisms are completely self-organized based on the relationships, such as gravity, between the objects. While dynamical systems do not perform “functions” per se, they do exhibit their “capabilities” by reaching their attractors and maintaining stability around these attractors through spontaneous processes of the individual objects. Furthermore, the chaotic attractors of dynamical systems can be considered as the mechanism that can increase the variety of the stable states of the system, and hence the richness of strange attractors can be considered as a feature of adaptability.
Common to all biological systems, cellular structure is indispensable for these systems to grow into complex configurations (Vincent et al., Reference Vincent, Bogatyreva and Bogatyrev2006; Audesirk et al., Reference Audesirk, Audesirk and Byers2007). Unlike dynamical systems where no shared information is present from an object's point of view, each cell in a biological system possesses a “description,” called DNA, of the whole system and is able to interpret this locally shared information to generate local actions (i.e., producing adequate proteins). The self-organizing behavior is still spontaneous but guided by DNA. The separation of description of the system from the system itself makes it possible to “copy” and “vary” the description independently from changing the system. Therefore, mutation and natural selection together create an evolution framework for open-ended adaptation (Watson & Crick, Reference Watson and Crick1953; von Neumann, Reference von Neumann and Burks1966).
Learning from what nature “does” has led us to treat self-organizing as the key concept that needs to be implemented in future adaptive engineered systems. Self-organizing has profound implications in dealing with complexity. First, it is spontaneous, and hence does not require prespecifying “who should do what in what ways,” allowing high-level uncertainty under unpredictable situations. Second, if arranged properly, increasing system complexity can be a solution to dealing with high-level environment complexity. The challenge, however, is how one can devise and guide self-organizing so that desired system-level emergent behaviors and functions can be achieved.
In our proposed CSO systems framework, shown in Table 2, three concepts are fundamental, namely, mCells, fields, and design-DNA (dDNA). The mCellls constitute the physical substrate for system formation, and they are the entities that self-organize themselves for emergent system behaviors and functions. The concept of field is needed to bring tasks and environmental constraints into the mCells' self-organizing framework. Like dynamical systems, where gravity fields are basic means for planets to self-organize, we need some fields in which our mCells can self-organize. Unlike dynamical systems, however, our fields must be able to capture tasks and make “completing tasks” part of the “attractor landscape.” Because our fields are artifacts to be designed and so is the self-organizing behavior of mCells in response to these fields, we need a mechanism to guide the mCells. For this, we introduce dDNA, which contains both system information and the information needed for finding and evolving into “attractors.” Again, the explicit description of the system using dDNA allows open-ended adaptation through genetic evolution, which is a future research topic. The details of these concepts together with the elaborations are described in the next section.
Table 2. The CSO Systems Framework

Note: CSO, cellular self-organizing; dDNA, design-DNA.
4. THE MODEL AND CONCEPTS
In this section, we elaborate the discussion of the last section by introducing definitions of the concepts discussed above. Through the process of describing definitions, we also introduce the field-based mechanisms that are needed to realize self-organization. Because in this paper we focus on self-organization aspect of the CSO systems, we will skip the detailed discussion of the definition of design-DNA, of which more information can be found in Zouein (Reference Zouein2009) and Jin et al. (Reference Jin, Zouein and Lu2010).
An mCell is the basic element or unit of a mechanical CSO system:
Definition 1. mCell: mCell = {Cu, S, A, B}, where Cu is the control unit, S = {s 1, s 2, . . .} is the sensory information, A = {a 1, a 2, . . .} are capable actions, and B is the behavior set (see Definitions 3 and 4 below).■
Almost all existing cellular systems, such as Superbot (Shen et al., Reference Shen, Krivokon, Chiu, Everist, Rubenstein and Venkatesh2006) and Miche (Gilpin et al., Reference Gilpin, Kotay, Rus and Vasilescu2008), can be modeled using this definition. The mCell is the smallest structural and functional unit of a CSO system. Although for a CSO system design, either homogeneous with identical mCells or heterogeneous with different mCells, the appearance or the structure of its mCells may be different, an mCell should be able to sense the environment around it, process material, energy, and/or information as it action, and make a decision on its next action. Of course, mCells have a limited number of sensors, a limited range for each sensor, a limited communication range with others, and a limited number of possible actions.
Definition 2. State: State = {SC, A C}, where S C ⊂ S and A C ⊂ A are current information being sensed and current actions being performed, respectively.■
State is used to represent the situation of an mCell. It is the combination of the current sensor information Sc and the current actions Ac. This definition of state parallels the sensor–motor description of cognitive systems (von Foerster, Reference von Foerster, Inhelder, Gracia and Voneche1977).
Definition 3. Behavior: b = {S C, A C} → A N, where S C ⊂ S and A C ⊂ A are current sensor information and actions, respectively, and A N ⊂ A are the next step actions.■
A behavior b designates the next possible actions for a given situation or state. Because mCells need to behave in different situations or states, the complete behavior of an mCell i can be defined by its behavior set B i = {b i1, . . . , b im}. The Cu of the mCell should be able to judge the situation and determine the next possible actions based on B i.
Definition 4. Behaviors of system: BoS = {B 1, B 2, . . . , B n}, where B 1, B 2, . . . , B n are behavior sets of each of n mCells in the system.■
The BoS can also be viewed as the complete design information of a CSO system. This BoS is supposed to be designed by designers. If all mCells share the same behavior set B (i.e., B 1 = B 2 = · · · = B n = B), then we have a homogeneous CSO system. Otherwise, the CSO system is said to be heterogeneous.
From the above four definitions, one may see that the concept of mCell resembles partly that of biological cell. A biological cell serves its purpose by producing proteins, while an mCell produces local actions; a biological cell can only process the signals that its receptors on the membrane can catch, whereas mCells rely on the sensors they have. Furthermore, biological cells hold “design information” stored in DNA. Similarly, mCells hold the design information through dDNA, which contains the corresponding set of behaviors.
As mentioned above, incorporating task requirements into the self-organizing system as “attractors” is a challenge. We address this challenge with the following definitions of function requirements and fields.
Definition 5. Functional requirement: FR i = {S i, A i}, where S i and A i form a specific state or situation.■
There are two reasons why a functional requirement holds the similar construct of the state described above. First, this representation allows us to specify “desired states” of the system. These desired states can be goal states or transient states that a designer deems to be necessary. Second, using the state construct to represent functional requirements allows mCells to recognize whether the function is achieved by examining their sensor information and actions for given functional requirements.
It is worth mentioning that our definition of functional requirement based on both sensory information S i and action A i is more general than the conventional function definition that uses only action A i. When S i = Ø our definition is a conventional function. The general functional requirement representation allows designers to specify circumstances (i.e., sensory information) in addition to actions.
At present, we explore CSO systems with homogeneous mCells. As in biological systems where stem cells can differentiate themselves into different organ cells by expressing only specific portions of their DNA, we consider that the initial homogeneous mCells with multiple behavioral capabilities (e.g., B = {b 1, b 2, b 3, b 4, b 5, b 6, b 7}) will, during the process of emergence, differentiate and find their “specialty” behaviors (e.g., B s = {b 3, b 4}) during the period of task execution. We expect that this self-organized emergence may create functional blocks consisting of multiple mCells, as organs forming in biological systems or attractors in dynamical systems. Once a task is accomplished and another task arises, or the environment changes, the functional blocks may dissolve by themselves and the mCells will continue to renew their differentiation and form new functional blocks.
It is expected that the enormous size of the potential behaviors resulted from the cellular formation of the system, that is, the large sets of BoS = {B 1, B 2, . . . , B n} provides a functional base for “unforeseeable” functional requirements and environment changes, increasing the system flexibility and robustness, respectively; and that the redundancy of mCells together with the large number of mCells makes the role of a single mCell insignificant during the emergence of the system behaviors. Failures with one or more single mCells can be dealt with by other similar mCells, leading to high-level system resilience.
From a design perspective, however, developing CSO systems is a challenging task. As much as we attempt to understand how biological systems develop their emergence, we face enormous challenges in developing such fruitful emergence in our engineered systems. In this research, we attempt to generate “guided emergence” by providing rules for mCells to self-organize and for desired system behaviors to emerge. Two fundamental issues must be addressed. The first relates to design information representation. We have introduced a dDNA-based representation scheme to capture CSO system information at the cellular level (Jin et al., Reference Jin, Zouein and Lu2010; Zouein et al., Reference Zouein, Chen and Jin2010). The second issue has to do with devising mechanisms to guide self-organization. In the following, we introduce a field-based approach to allow mCells to self-regulate their behaviors in order to induce system-level emergence of reaching “attractors.”
5. FBR
In physical systems, the concept of field is everywhere (e.g., gravity field, electrical field, magnetic field, and electromagnetic field). Objects operating in the fields can “sense” the field and react to it by following physical principles. In the biological world, the function of an organism is realized by a collection of different types of cells working together. The distribution of the chemical signals, called morphogen, controls the biological regulation and hence the shape and organ formation. Through the developmental process, stem cells differentiate into different cell types by responding to specific morphogen distributions.
In our CSO systems, mCells need a similar differentiation capability in order to self-organize and collectively become a functional system. Instead of producing different proteins, differentiated mCells produce different i. Instead of being triggered by chemical signals, the mCells differentiation must be triggered by the functional requirements and environmental constraints. To realize such behaviors, we extend the concept of physical field and chemical field into more general “fields” and introduce an FBR, for guiding cellular self-organization in CSO systems.
For a CSO system, the sensory capabilities of its mCells are predefined and given. In this case, whenever a task (defined by its FRs) and an operation environment (which may or may not be fully known) are given, we can define a task field that captures the external world to an mCell encompassing both task requirements and environmental conditions. We have:
Definition 6. Sensory information and sensing: sInfo = SNS (FR, Env), where FR is the functional requirements, Env is the environment situation, and SNS is the sensing operator.■
Definition 7. Task field and field formation: tField = FLD (sInfo), where sInfo = (s 1, . . . , s n) is the sensory information and FLD is the field formation operator.■
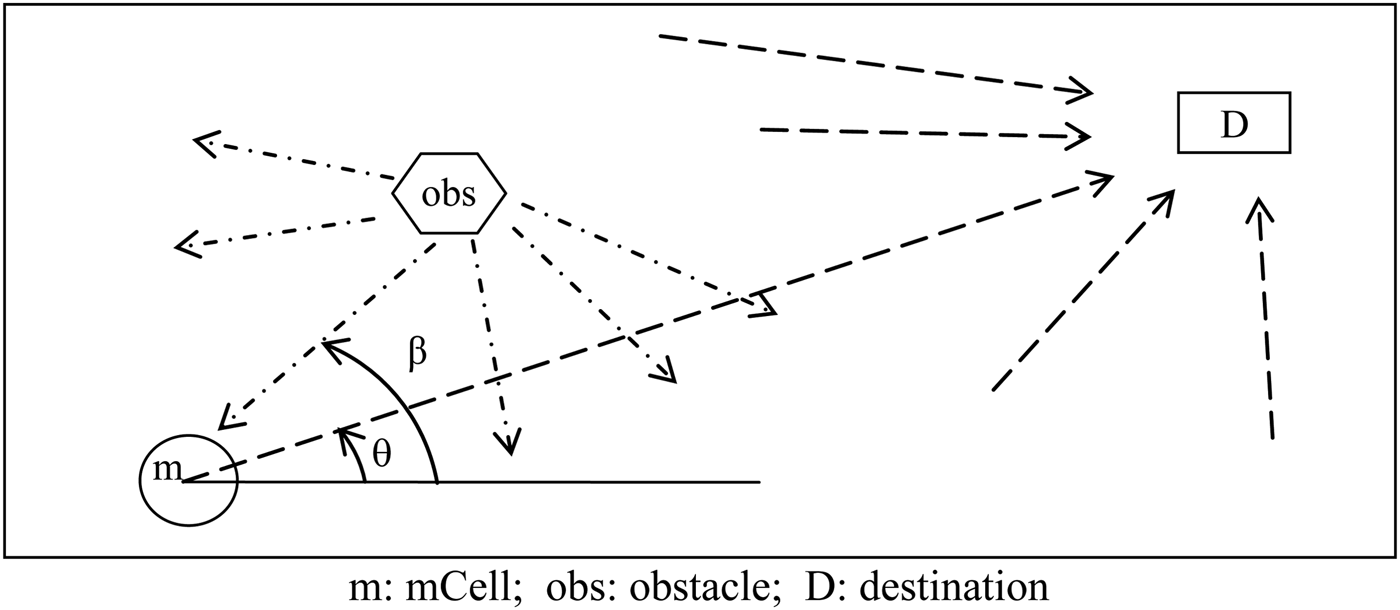
From Definition 7 it can be seen that we define the task field relative to a specific mCell and its sensing capability. Figure 1a shows a simple example of a tField. An mCell m is moving to its destination d with the potential of encountering an obstacle obs in a two-dimensional space. In this case, the destination D can be considered as an attractor that creates an attraction field (indicated as broken directed lines), capturing the task requirements; and in a similar way, the obstacle, obs, creates a repelling field (indicated as dotted directed lines), characterizing the operation environment. It can be seen from Figure 1a that the tField serves as a “complete” context for an mCell to operate in this specific example.

Fig. 1. An example of a task field and a behavior field.
Because mCell differentiation is about behavior distribution, an mCell must be able to determine its behavior based on the given task field. Therefore, we introduce a concept called behavior field, or bField, to capture the potential distribution of preferable behaviors an mCell can choose in a given task field. We further use FBR FT to denote the transformation from a task field into a behavior field and introduce the following definition:
Definition 8. Behavior field and field transformation: bField = FBR FT(tField, B), where FBR FT is the field based regulation (FBR) operator for field transformation, bField is the behavior field, and tField is the task field.■
According to Definition 8, how behaviors should be distributed is largely dependent on the field transformation operator FBR FT. There can be different ways to represent a bField. One may associate “rewards,” “risks,” or “probability” with different “locations” for an mCell to perform different behaviors. The “locations” can be defined as real two- or three-dimension spaces or n-dimension virtual spaces, depending on the task domain and mCell properties. Figure 1b shows a simple example of a bField. An mCell m is moving in the task field composed of the destination D's attraction field and the obstacle obs's repelling field. Based on some given field transformation operator, FBR FT, the mCell m creates a bField around itself denoted by the curved dark line around m in Figure 1b.
In this research, we associate an mCell's “behavior distribution” with its surrounding “locations,” and we further call this distribution behavior profile, or bProfile. Therefore, we introduce the following definition, which is a specific case of Definition 8:
Definition 8b. Behavior profile and field transformation: bProfile = FBR FT (tField, B), where bProfile = {(b 1, p 1), . . . , (b n, p n)}; [b i ∈ B, 0 ≤ p i ≤ 1, 1≤ i ≤ n] indicates (behavior, probability) pairs for an mCell to choose its actions; n is the total number of possible behaviors that the mCell can perform; tField is the task field; and B is mCell's behavior set.■
The dark line in Figure 1b mentioned above indicates the “behavior profile” for mCell m. Given a behavior profile at a given time, an mCell still needs to “make a decision” to select a behavior. We introduce the second FBR operator as follows:
Definition 9. Behavior selection and behavior selector: b = FBR BS (bProfile), where FBR BS is the FBR operator for behavior selection; bProfile = {(b 1, p 1), . . . , (b n, p n)}; [b i ∈ B, 0 ≤ p i ≤ 1, 1≤ i ≤ n]; and b is selected behavior b ∈ B.■
Summarizing the above definitions, for an mCell m at time t for given functional requirements FR and environmental situation Env, the behavior or action of the mCell is chosen by following the self-organizing operations:
From Equation (1), we can see that an mCell's sensing capability (i.e., SNS), its capability of forming an internally useful task field (i.e., FLD), and its FBR based field transformation (i.e., FBR FT) and behavior selection (i.e., FBR BS) completely determine the mCells self-organizing behavior. Interactions between mCells can be introduced by devising constraints between mCells that influence an mCell's SNS, FLD, FBR capabilities and consequently its behavior. The system stabilities and functions are achieved around the “attractors” of the mCells. For different task domains, these capabilities should be designed and devised differently so that the overall performance of the emergent behavior is desirable. In the following, we describe examples of how these self-organizing capabilities can be designed and implemented in computer simulations.
6. CASE STUDIES AND DISCUSSION
To investigate how our approach can be applied to CSO systems design, a set of computer simulation-based case studies were carried out with the intention of addressing the following questions:
• What constitutes the task and behavior fields?
• What is the benefit of using the concept of behavior field?
• How will locally regulated behaviors emerge into desired global effects?
• How will the field transformation (FBR FT) and behavior selection (FBR BS) impact the global system behavior?
In the following subsections, we present two case studies. The first case study is designed to investigate the concept of field and the second one for demonstrating FBR effectiveness.
6.1. Case study 1: Single exploration mCell
The overall task for this case study is for one mCell to travel to a given destination in an unknown environment. The two functional requirements are
• FR1 = “Move to destination” and
• FR2 = “Avoid obstacle.”
The mCell can decide the direction of movement, so the two behaviors are
• b 1 = “Move to the direction toward destination” and
• b 2 = “Move away from the direction to obstacle.”
We further assume that the obstacles between the mCell and the destination can be everywhere with any density and that the mCell can always sense the direction of the destination and can sense the locations of the obstacles only when they are within a certain range. Given the two functional requirements, the sensor information and current actions, an mCell needs to decide which “action,” that is, direction, to take.
6.1.1. Task field
The task field for this example is composed of the attraction field of the destination and the repelling fields of various obstacles, and more than one obstacle can exist at any time. We use parameter θ to represent the attraction field and β the repelling field, as show in Figure 2. Combining the two, we have task field for mCell m:
where n is the number of obstacles.

Fig. 2. Tasks field for mCell m.
6.1.2. Behavior regulation
In this case study, mCells can sense the task field and always know where the destination (i.e., θ) is and where obstacles (i.e., β1, β2, . . . , βn) are. As mentioned above, field-driven behavior regulation has two steps, that is,
Step 1. Transform tField into bField through FBR FT.
Step 2. Select a specific behavior/action through FBR BS.
Behavior field and FBRFT
In this example, the bField, or bProfile, determines the likelihood in which an mCell is taking its next move into direction α and the likelihood the mCell is avoiding this direction owing to the existence of obstacles. The distribution of these two likelihoods around the 360-degree circle around an mCell constitutes the bField or bProfile of the mCell. Specifically, for one destination and one obstacle, we introduce the following FBR FT:
 $$\eqalign{bField_m \lpar \rm \alpha \rpar & = FRB_{FT} \lpar tField_m \comma \; B\rpar = \lcub \alpha \comma \; \,p_{\rm \alpha} \comma \; q_{\rm \alpha} \rcub \cr & = \!\left\{ {\rm \alpha} \comma \displaystyle{1 \over {\sqrt 2\pi }}\exp {\left(\!\!{-}\displaystyle{\lpar{\rm \alpha} - {\rm \theta} \rpar^2 \over 2}\right)}\comma \right.\cr &\left. \quad \displaystyle{1 \over {\sqrt 2\rm \pi }}\left(1 - \exp {\displaystyle{\left(\!\!{-}{( {\rm \alpha} - {\rm \beta} ) ^2 \over 2}\right)}}\right)\right\}\comma}$$
$$\eqalign{bField_m \lpar \rm \alpha \rpar & = FRB_{FT} \lpar tField_m \comma \; B\rpar = \lcub \alpha \comma \; \,p_{\rm \alpha} \comma \; q_{\rm \alpha} \rcub \cr & = \!\left\{ {\rm \alpha} \comma \displaystyle{1 \over {\sqrt 2\pi }}\exp {\left(\!\!{-}\displaystyle{\lpar{\rm \alpha} - {\rm \theta} \rpar^2 \over 2}\right)}\comma \right.\cr &\left. \quad \displaystyle{1 \over {\sqrt 2\rm \pi }}\left(1 - \exp {\displaystyle{\left(\!\!{-}{( {\rm \alpha} - {\rm \beta} ) ^2 \over 2}\right)}}\right)\right\}\comma}$$where α is the direction for the next move, p α is the probability that direction α should be taken, and q α is the probability that direction α should be avoided.
Behavior selection and FBRBS
After the behavior field is established, an mCell needs a mechanism for behavior selection. In this case study, we define two types of behavior selection: “select the best” and “select any one good enough,” as indicated below.
In the following, we will show the usefulness of the behavior field and the effectiveness of applying different behavior selection strategies. Figure 3 shows the time sequence of screen dumps of one of the simulation runs, with time steps indicated at the bottom of each box. As shown in Figure 3, a single explorer mCell (white circle in the figure) can travel from a randomly assigned position on the lower-left corner to a given destination on the upper-right corner. Both the mCell's initial position and the positions of all obstacles are randomly generated for each simulation run.

Fig. 3. (Color online) Simulation results of a single mCell exploring in a random obstacle field.
In this case study, the mCell acts solely based on the task assignments (represented as FRs) and its sensory information without memory and planning. The FBR FT operator constantly transforms the perceived task field into a local behavior field, allowing the mCell to “know” what valid behaviors are possible that can be performed at each moment. Furthermore, the FBR BS operator converts behavior or action potential into specific actions. By splitting the process of FBR into two steps, a designer can make various combinations and find the good ones for his/her task domain.
As one may imagine, when the density of obstacles increases, the mCell may be trapped on its way and not be able to reach the destination. Our simulation results verified this situation. To investigate how different FBR strategies may influence the “success rate” of the simulation runs, we examined two “behavior selection” strategies, that is, FBR BS-B (select the best) and FBR BS-G (select from good enough, i.e., top 40%, randomly). We ran 500 test runs for each obstacle density for FBR BS-B and FBR BS-G, respectively, and calculated the success rate based on the 500 runs. Figure 4 shows the comparison result with 40 to 120 randomly assigned obstacles.

Fig. 4. (Color online) A comparison of “select the best” (FBR BS-B) and “select from top 40% randomly” (FBR BS-G).
Figure 4 shows that overall the “select a good enough randomly” works more favorably than “select the best” and that as the density of obstacles increases, the advantage of the former increases. From a CSO system development perspective, the result is interesting in two ways. First, it indicates that behavior regulation strategies have profound impact on individual mCell's performance, and second, the “random behavior” seems to bring “intelligence” into the system in uncertain and unpredictable situations.
With the “select the best” strategy, an mCell always targets one single best direction in deciding on its next move. When the obstacle density is low, this strategy can likely produce ideal performance in which both time and energy (i.e., steps traveled) can be saved. With a limited number of obstacles distributed sparsely, there is low likelihood that the mCell becomes trapped by its own “best” calculation. When the density of obstacles increases, however, much more likely the “traps” exist in the field, resulting in a lower success rate for this strategy.
The “select from top 40% randomly” strategy may not work perfectly in terms of saving time and energy. However, when the environment becomes more unpredictable and unfriendly, the mCell can robustly survive the environmental change and maintain its performance. Thanks to the randomness of behavior selection, the “traps” may be overcome by the mCell through internal variability. Only the intrinsic variety of the system (i.e., mCell in this case) can concur with the variety of the environment (Ashby, Reference Ashby1958).
6.2. Case study 2: CSO mover system
In the single mCell case study, we demonstrated how tField can be defined and how bField can be generated and behavior selection be carried out through FBR. To investigate how FBR may impact on the emergence when multiple mCells work together for a single task, we conducted the second case study. In Case Study 2, the task for multiple identical mCells is to move an object from a starting point to a destination point in a two-dimensional unknown environment with obstacles randomly distributed in the field in the same way as in Case Study 1. The mCells are limited in action: they only push the object from their center to the object's center. At a given time, an mCell must decide on which direction to push the object. The overall movement of the object will be the result of the emergent behavior of all the mCells pushing the object.
In this case study, all mCells can only push from their centers to the object's center with the same force, and the overall movement of the object is the emergence of all mCells' relative locations around the object. The behavior of each mCell is to choose a “right” location to push the object. The three functional requirements for this task are
• FR1 = “stay close to the object,”
• FR2 = “push object to destination,” and
• FR3 = “avoid obstacles.”
An mCell can choose a relative location to the object, so the three behaviors are
• b 1 = “move to locations as close as possible to the object,”
• b 2 = “push the object toward destination,” and
• b 3 = “push the object away from obstacles.”
In this case study, all the mCells have the same setup as the previous case study; they can sense the destination anywhere, and they can only sense the obstacles within a certain range.
6.2.1. Task field
Similar to the previous case study, we also use parameter θ to represent the attraction field and β the repelling field. In addition to those two parameters, this case study introduces a new attraction field d as the relative distance from mCell to the object. The related task field is shown in Figure 5. Besides mCell m there are mCells i, j, and k in dashed lines. By combining θ, β, and d, we have a task field for mCell m denoted as follows:
where n is the number of obstacles.

Fig. 5. The tasks field for mCell m.
6.2.2. Behavior regulation
The two-step behavior regulation described in the previous case study is still valid in this case study.
Behavior field and FBRFT
In this example, the bField or bProfile determines the likelihood for an mCell either to stay in the current location and push the object or to move to another location and push the object from there. The mCell may decide to move to another location if the distance to the object (i.e., the value of d) is too large or the pushing direction (i.e., the direction from the mCell's location to the object center) is not desirable. The relative location for the mCell is represented by α and d, as shown in Figure 5. For one destination and one obstacle, we introduce the following FBR FT:
 $$\eqalign{ bField_m \lpar {\rm \alpha} \comma \; d\rpar &= FRB_{FD} \lpar tField_m \comma \; B\rpar \cr & = \lcub {\rm \alpha} \comma \; d\comma \; p_d \comma \; p_{\rm \alpha} \comma \; q_{\rm \alpha} \rcub \cr {\rm } & = \left\{ {\rm \alpha} \comma \; d\comma \; \displaystyle{{\rm 1} \over {\sqrt {{\rm 2}{\rm \pi} } }}\ \exp {\left( \!\!{-} \displaystyle{{d^2 } \over 2}\right)} \comma \; \displaystyle{{\rm 1} \over {\sqrt {{\rm 2}{\rm \pi} } }}\ \exp {\left( \!\!{-} \displaystyle{{\lpar {\rm \theta} - {\rm \alpha} \rpar ^2 } \over 2}\right)} \comma\right. \cr &\qquad\!\! {\left.\displaystyle{{\rm 1} \over {\sqrt {{\rm 2}\pi } }}\left[{1 - \exp {\left( \!\!{-} \displaystyle{{\lpar {\rm \beta} - {\rm \alpha} \rpar ^2 } \over 2}\right)} } \right]\right\} }\comma \;}$$
$$\eqalign{ bField_m \lpar {\rm \alpha} \comma \; d\rpar &= FRB_{FD} \lpar tField_m \comma \; B\rpar \cr & = \lcub {\rm \alpha} \comma \; d\comma \; p_d \comma \; p_{\rm \alpha} \comma \; q_{\rm \alpha} \rcub \cr {\rm } & = \left\{ {\rm \alpha} \comma \; d\comma \; \displaystyle{{\rm 1} \over {\sqrt {{\rm 2}{\rm \pi} } }}\ \exp {\left( \!\!{-} \displaystyle{{d^2 } \over 2}\right)} \comma \; \displaystyle{{\rm 1} \over {\sqrt {{\rm 2}{\rm \pi} } }}\ \exp {\left( \!\!{-} \displaystyle{{\lpar {\rm \theta} - {\rm \alpha} \rpar ^2 } \over 2}\right)} \comma\right. \cr &\qquad\!\! {\left.\displaystyle{{\rm 1} \over {\sqrt {{\rm 2}\pi } }}\left[{1 - \exp {\left( \!\!{-} \displaystyle{{\lpar {\rm \beta} - {\rm \alpha} \rpar ^2 } \over 2}\right)} } \right]\right\} }\comma \;}$$where α is the angle corresponding to an arbitrary predefined coordinate, d the distance between the mCell and the object, p d is the probability that distance d should be taken, p α is the probability that pushing direction α should be taken, and q α is the probability that pushing direction α should be avoided.
Behavior selection and FBRBS
After the behavior field is established, an mCell needs a mechanism for behavior selection. In this case study, we assume that the mCell will change its location when the probability is below a threshold instead of choosing the “best” locations.
In this case study, we show how the above-mentioned behavior field can be useful and effective not only for a single mCell case but also for an emergent system of multiple mCells.
6.2.3. Simulation results
Figure 6 shows the time sequence of simulation screen dumps with time steps indicated at the bottom of each block. Each mCell chooses a location to push the blue square object. Each mCell attempts to choose a “highly” recommended zone (the green/light region in Fig. 7) and move into it when the zone of its current location has the probability below the threshold. There is no explicit communication between the mCells. However, the mCells interact indirectly by avoiding overlapping with each other. Our simulation results showed that in almost all simulated test runs, the mCells were successful in pushing the square object into its destination.

Fig. 6. (Color online) A simulation for Case Study 2, cellular self-organizing object mover.

Fig. 7. (Color online) An illustration of the dynamic bField of the cellular self-organizing mover in the simulated field of obstacles.
One advantage of this behavior-based design is that the shape of the object and therefore the shape of the overall system are not predefined and limited. The mCells observe the world and decide on their behavior locally, while the global behavior emerges. Based on the Kolmogorov complexity measure (Li & Vitanyi, Reference Li and Vitanyi2008), our CSO system of multiple mCells can be considered highly complex because the states of each mCell changes dynamically without certainty and it takes a rather long description to capture the whole system. However, using FBR makes it possible to regulate mCells' behaviors and to lead the emergence to a productive direction.
Figure 7 illustrates the dynamically changing behavior field (bField) and how mCells choose their behaviors (i.e., locations) through FBR. As shown in Figure 7, different situations introduce two different bFields. Depending on the relative locations of the destination, obstacles, and the object, the field changes, as shown as color changes in Figure 7. Different colors in Figure 7 correspond to different probabilities, as indicated in the figure. The mCells try to choose the “green” or “yellow” zone to occupy. Through the use of FBR, the system dynamically adapts to its new situations even with the simple mCells of limited capability (i.e., to simply push from its center to the object's center). The system can move the object in an unknown environment by mCells using the fields as their dynamic model of the world. It is conceivable that the bField and the FBR concepts can be applied to many task situations where physical fields or chemical fields can be applied.
In our simulation test runs, we also examined how the system might perform if some mCells become inactive. Figure 8 shows the resilience of the overall system when some of the mCells becomes “dead” during the simulation. There are four mCells that were deactivated at Step 400. Because the system is fully decentralized, deactivated mCells had little influence on the rest of the mCells in the system. This way, although the system losses its performance owing to the loss of mCells, it could still successfully accomplish the task of moving the object to its destination, showing the system resilience.

Fig. 8. (Color online) The resilience test by deactivating 4 of 12 mCells at Step 400.
Because CSO systems are decentralized and have redundancies maintained among their mCells, they are more resilient than the systems with specified local functional components. When one part of the system fails, other nearby mCells can modify their functionality and redistribute their functions. This way, the system can adapt to not only the environmental change but also the system change.
7. CONCLUDING REMARKS
In this paper an FBR approach to designing CSO systems is presented. The concept of CSO systems is developed based on several observations. First, the current engineered systems are inherently incapable of dealing with variable functional requirements, changing environment situations, and possible system failures; and second, natural systems including dynamical systems and biological systems are formed in a bottom-up fashion and inherently equipped with capabilities to deal with uncertainties and unknowns. By combining the current engineering concepts of functions with the mechanisms of stability (attractor), self-organization, and DNA, our CSO systems framework leads to an alternative bottom-up approach to developing engineered systems.
In CSO systems, self-organization is the key concept. To make mCells self-organize in a bottom-up way, a field concept is introduced that allows cells to sense both the task and environment, and formulate a task field as a model of the task world. By following the FBR mechanism that we devised, mCells can transform the sensed task field into their behavioral field in which their possible behaviors are profiled and ready to be selected. The final behavior selection is carried out by the FBR behavior selection operator. It is worth mentioning that our FBR framework is composed of distinguishable stages of cellular operations, including sensing, field formation, field transformation, and behavior selection. These operators together with their associated variables provide a rich design space for us to explore and design CSO systems. The case studies discussed in the paper demonstrate how different FBR behavior selection strategies may yield different performances, and how transformation from task field to behavioral field determines the system behavior and capabilities.
In addition to the box-pushing task described above, CSO systems can be used in many other application domains, such as search-and-rescue, robotic teams, deep sea and space exploration, adaptive and self-repair structures, and amorphous materials. It is expected that different domain tasks require different designs of FBR mechanisms. Future research is needed to classify the domain tasks and explore various possible FBR designs.
Our current work on this research includes expanding the case study into more sophisticated problem domains, examining trade-offs of having various combinations of mCells including heterogeneous ones, and extending the distributed mCells presented in this paper to physically connected mCells. One of our ongoing case studies explores how mCells can transmit the circular motions of one object into the linear motion of another through FBR-based self-organization. This task requires not only more sophisticated representation of task fields but also various interactions and physical connections between mCells.
ACKNOWLEDGMENTS
This paper is based on work that was partially supported by the National Science Foundation under Grants CMMI-0943997 and CMMI-1201107. Any opinions, findings, and conclusions or recommendations expressed in this article are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Yan Jin is a Professor of aerospace and mechanical engineering at the University of Southern California. He received his PhD in naval architecture and ocean engineering from the University of Tokyo. Prior to joining the University of Southern California faculty in 1996, he worked as a research scientist at Stanford University for 5 years. Dr. Jin is a recipient of the NSF CAREER Award (1998), the TRW Excellence in Teaching Award (2001), and the Xerox Best Paper Award (ASME Design Theory and Methodology Conference, 2002). He currently serves as Editor-in-Chief of AIEDAM and as a member of the editorial board of Advanced Engineering Informatics and the International Journal of Design Creativity and Innovation. His current research focuses on self-organizing systems and design creativity.
Chang Chen is a Financial Software Engineer at Bloomberg LP, where he leads software projects to develop financial software systems for equity indexing and equity research applications. Prior to joining Bloomberg, Dr. Chen performed his PhD study at the Department of Aerospace and Mechanical Engineering of the University of Southern California. His PhD research was related to distributed intelligence design theory, self-organizing systems, and field-based regulation for cellular self-organizing systems. With his years of industrial and academic experiences, Dr. Chen has accumulated extensive expertise in engineering design, distributed systems, and software engineering.