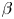Gyrokinetic analysis of an argon-seeded EDA H-mode in ASDEX Upgrade

Abstract

Understanding edge-localised-mode (ELM)-free high-confinement (H-)mode scenarios is vital for developing practical future demonstration reactor scenarios. An argon-seeded EDA H-mode discharge performed in ASDEX Upgrade is computationally studied in detail for the first time with the gyrokinetic GENE code using experimental profiles and magnetic equilibrium as direct code inputs. Linear scans outline dominant instabilities in the regime and reveal distinct ion- and electron-scale wavenumber growth-rate peaks for two local core and two local pedestal top scenarios. Linear ion-scale growth rates are found to be relatively insensitive to the addition of argon, and collisionality scans demonstrate increased sensitivity in the pedestal top. The addition of an argon impurity profile while keeping the input main ion temperature gradient (ITG) largely unchanged is found to reduce ITG-driven turbulence in the outer core. Nonlinear electromagnetic simulations reveal close agreement with experimentally predicted heat fluxes in the core, outline key sensitivities to electron $\beta$ and background $\boldsymbol{E\times B}$ shearing, and reveal gyrokinetic challenges in analysing the quasicoherent mode. Global electrostatic nonlinear simulations reduce local simulated heat transport overpredictions at the pedestal top. A quasilinear analysis finds that there is good core agreement but poor agreement in the pedestal between linear and nonlinear temperature and density fluctuation cross-phases. Local simulation limitations are elucidated and paths forward for future computation are suggested.

1. Introduction

Future magnetic confinement fusion devices seek to maximise the Lawson criteria (Lawson 1957) while avoiding large instabilities which can damage tokamak divertor and wall components. The high-confinement mode (H-mode) (Wagner et al. 1982) is characterised by an edge transport barrier (Wagner et al. 1984) linked to the radial electric field (Groebner, Burrell & Seraydarian 1990; Field, Fussmann & Hofmann 1992; Burrell et al. 1992) and subsequent turbulence-suppressing flow shears (Terry 2000) leading to the formation of a plasma pedestal with increased temperature and density profiles. However, the edge transport barrier of a standard H-mode is plagued by edge localised modes (ELMs) (Zohm 1996; Connor 1998) which can damage tokamak divertor and wall components in addition to degrading the plasma pedestal by transporting away particles and energy. It is increasingly clear that type-I ELMs will be unacceptable in ITER and DEMO (Eich et al. 2011; Wenninger et al. 2014) and future reactors will seek to avoid the occurrence of ELMs entirely (Sorbom et al. 2015), giving added urgency to the development of ELM-free scenarios.

The enhanced $D_\alpha$ (EDA) H-mode (Greenwald et al. 1999) is a stationary high- confinement ELM-free regime originally named for the high observed levels of Balmer series $D_\alpha$ radiation when compared with the non-stationary ELM-free H-mode. This regime was obtained first in Alcator C-Mod by applying ion cyclotron resonance heating (ICRH) after a fresh boronisation (Takase et al. 1997). It is notable for an edge fluctuation known as the quasicoherent mode (QCM) (Hubbard et al. 2001; Snipes et al. 2001; LaBombard et al. 2014) and stationary operation as long as the pressure gradient does not surpass the peeling–ballooning stability boundary due to excessive heating (Mossessian et al. 2002, 2003). The EDA H-mode has been researched extensively in C-Mod (Greenwald et al. 2007) and developed into a performant scenario with important accomplishments, such as the highest volume-averaged core plasma pressure ever achieved in a fusion device (Hughes et al. 2018).

More recently the EDA H-mode was also achieved at ASDEX Upgrade (Gil et al. 2020) and DIII-D (Paz-Soldan 2021) with electron cyclotron resonance heating (ECRH). Different measures have been taken to improve the performance of the EDA H-mode in AUG, which now features numerous desirable properties for future reactors (Gil et al. 2020). These include good energy confinement, high density, low impurity content, compatibility with tungsten walls, possibility of access at low input torque and power, with dominant electron heating, no need for a fresh boronisation and no impurity accumulation despite the absence of ELMs. Furthermore, argon seeding in EDA H-mode showed the compatibility of pedestal radiative cooling with no ELMs at high heating power (Kallenbach et al. 2021), including significant neutral beam injection (NBI).

Recent work has expanded upon the operational space of the EDA H-mode at AUG with different combinations of ECRH and NBI heating, impurity seeding, and deuterium fueling, resulting in a diverse dataset for investigating the physics of the regime. However, not all performed discharges had viable charge exchange recombination spectroscopy (CXRS) measurements of ion temperature and rotation profiles needed for more realistic gyrokinetic simulation. The argon-seeded EDA H-mode in AUG discharge 36330 outlined in Kallenbach et al. (2021) includes NBI heating and, therefore, has the benefit of CXRS measurements. In addition, the study of argon gas puffing in this discharge is of particular relevance to future reactors which seek to mitigate excessive divertor heat loads even in the absence of ELMs (Kallenbach et al. 2021).

This work provides the first ever detailed gyrokinetic exploration of an argon-seeded EDA H-mode in AUG, using experimental measurements from AUG discharge 36330 from 6.1 to 6.2 s as simulation inputs. During this phase the plasma is stationary with continuous NBI, allowing for suitable CXRS measurements (Viezzer et al. 2012; McDermott et al. 2017) in the absence of ELMs. The GENE code (Jenko et al. 2000; Görler et al. 2011) is used linearly and nonlinearly to simulate four radial positions locally with electromagnetic effects and is used nonlinearly to simulate the pedestal top globally using modified electrostatic parameters. The core and pedestal top of this scenario are characterised in a gyrokinetic context, comparisons are drawn between the experimentally measured and simulated heat fluxes using available simulations and, finally, current challenges and ideas for future work regarding this regime are elucidated.

This paper is organised as follows: in § 2 experimental measurements are presented which are used to create the inputs for the GENE simulations. Section 3 reviews the GENE code and the methodology of the numerical simulations carried out in this work. Section 4 includes all local linear simulation results, § 5 presents both local and global nonlinear GENE results and, finally, § 6 provides analysis together with a summary and context for future work.

2. Overview of argon-seeded EDA H-mode

ASDEX Upgrade discharge #36330 is an excellent candidate for gyrokinetic study, having well-diagnosed temperature and rotation profiles, and having previously been studied experimentally in Kallenbach et al. (2021). The discharge operates in a lower-single-null magnetic configuration with a toroidal magnetic field $B_T = -2.5\ {\rm T}$ on axis and a plasma current of 0.8 MA. The net power through the separatrix is feedback-controlled in real time via argon seeding, maintaining the absence of ELMs in EDA H-mode during auxiliary heating scans. The H-mode confinement phase is only lost upon the discontinuation of external heating. The stationary EDA H-mode period from 6.1–6.2 s with a constant and even mix of ECRH and NBI power totalling about 5 MW is chosen for the simulations. Furthermore, the QCM is experimentally present from around 20–40 kHz during this time phase in discharge 36330 (Kallenbach et al. 2021). The regime presented in this work has higher core temperature and pressure compared with lower-power unseeded EDA H-mode discharges in ASDEX Upgrade. However, the pedestal profiles remain low despite higher input power, offering an explanation for the absence of ELMs.

Figure 1 displays experimental radial profile measurements available for this discharge together with cubic spline fits used as simulation inputs shown by a solid line in each plot. The radial coordinate along the top axis of figure 1, $\rho _{\rm tor}= \sqrt {(\varPhi _{\rm tor}-\varPhi _{\rm a})/(\varPhi _{{\rm tor},{\rm sep}} - \varPhi _{a})}$ is used throughout this work, where $\varPhi _{\rm tor}$ is the toroidal magnetic flux, and the subscripts ‘${a}$’ and ‘${\rm {sep}}$’ refer to the magnetic axis and separatrix, respectively. The profiles are mapped to the outer midplane using the IDE equilibrium (Fischer et al. 2016) which considers the bootstrap current. The profiles are radially aligned, with shifts up to a few millimetres to account for certain equilibrium and measurement uncertainties, improving consistency between diagnostics.

Figure 1. Experimental radial profile measurements of ASDEX Upgrade discharge #36330 from 6.115–6.190 s, as a function of normalised poloidal (bottom) or toroidal (top) flux radius: (a) electron density from Thomson scattering, (b) electron and ion ($N^{7^{+}}$ impurity) temperature from Thomson scattering and CXRS, respectively, (c) impurity toroidal and poloidal rotation velocity from CXRS and (d) radial electric field from CXRS. Cubic spline fits used as GENE simulation inputs are shown as solid lines and local simulation locations are marked with dashed vertical lines. Spline knot locations in $\rho _{\rm {pol}}$ are: $a_{{\rm ne}}$, $[0.22,0.50,0.70,0.92,0.98,0.99,1.00,1.01,1.08]$; $b_{\rm Te}$, $[0.22,0.35,0.55,0.98,0.99,1.00,1.01,1.05]$; $b_{{\rm Ti}}$, $[0.00,0.50,0.70,0.98,0.99,1.01]$; $c_{{\rm vtor}}$, $[0.51,0.60,0.90,0.98,1.00]$; $c_{{\rm vpol}}$, $[0.93,0.97,0.99,1.00]$; and $d_{{\rm Er}}$, $[0.93,0.97,0.99,1.00]$.

Electron density and temperature are measured via Thomson scattering in the edge and core as shown in figures 1(a) and 1(b) and radially shifted in order for the separatrix temperature to be consistent with the two-point model of the divertor scrape-off layer (Stangeby 2000). The density profile is cross-validated by line-integrated interferometry measurements, also used to recalibrate the core Thomson scattering measurements by $-10\,\%$.

The regime outlined in this work includes heating from a continuous, full-power and full-voltage (60 kV) NBI source, allowing for CXRS-based $N^{7^{+}}$ temperature and rotation measurements in the core and pedestal, from $\rho _{\rm {tor}}= 0.35 \unicode{x2013}1$, as shown in figure 1. Poloidal and toroidal impurity rotation are also measured by CXRS, but only the edge system is capable of measuring the poloidal rotation, as shown in figure 1(c). Ion temperatures are taken from core and edge CXRS systems as shown in figure 1(b) and radially aligned for the position of maximum gradient (Viezzer et al. 2013) to match that of the electron temperature. The radial electric field, shown in figure 1(d), is computed from the radial force balance equation, $E_r = \boldsymbol {\nabla p_a} /( e Z_a n_a) - \boldsymbol{v_a \times B}$, where $\boldsymbol{p_a}$, $Z_a$, $n_a$ and $\boldsymbol{v_a}$ are the impurity pressure, charge number, density and velocity, respectively, $e$ is the elementary charge and $\boldsymbol{B}$ is the magnetic field. The impurity density profile of the fully stripped $N^{7+}$ population from CXRS measurements (McDermott et al. 2018) is included in the first term. The resulting ${\boldsymbol{E\times B}}$ shearing profile is used as input into the GENE simulations as discussed in detail in § 3, with the contribution from the poloidal velocity assumed to be negligible in the core.

Not included in figure 1 is a radially uniform effective ion charge estimate, $Z_{\rm {eff}}=2.05$, based on measurements of the background bremsstrahlung spectrum (Fischer et al. 2000; Rathgeber et al. 2010) and used throughout this work. The $Z_{\rm {eff}}$ parameter primarily influences collisionality in two species simulations while in three species simulations this parameter is discarded in favor of more realistic impurity profiles, the inclusion of which also affects density gradients and profiles in addition to collisionality.

Finally, an argon impurity density profile is reconstructed via modelling in a similar manner to argon analyses in Dux et al. (2020) and Kallenbach et al. (2021), using profiles from figure 1 as partial inputs to the impurity transport code STRAHL (Dux 2006). The argon density profile, labelled Ar profile 1 in figure 2(a), is derived in the core from the soft x-ray (SXR) diagnostic after tomographic inversion of measured line-of-sight integrals (Odstrčil et al. 2016). The contribution of tungsten and deuterium ions to the SXR emission is included in the calculation, being rather small when compared to the argon contribution in this discharge. In the pedestal where SXR emission is almost non-existent due to the lower temperature, the argon density is determined by fitting the modelled radiation, including charge exchange with neutral deuterium atoms, to spectral lines in the vacuum ultraviolet range measured by the SPRED spectrometer, and to the total radiated power measured by bolometry (David et al. 2021) and shown in figure 2(b). Previous analysis has clearly shown that argon seeding increases local radiation only slightly in the core, but significantly in the pedestal, contributing both to ELM avoidance and a colder divertor compared to an identical unseeded discharge.

Figure 2. (a) Two argon impurity profile fits used as GENE inputs plotted against $\rho _{\rm {tor}}$. Here $n_{\rm {Ar}}$ is the sum of the densities of all charged states of Ar. Profile 1 is derived from STRAHL modelling while profile 2 is based on a crude $Z_{\rm {eff}}$ estimate. (b) Experimental radiated, net, and total power flux integrated up to each flux surface.

A second crude argon profile estimate in figure 2(a), labelled Ar profile 2, is generated from assuming a uniform $Z_{\rm {eff}}=2.05$ and assuming argon as the only impurity while enforcing quasineutrality together with existing density profiles. This crude estimate is used as an alternate upper argon density estimate to further explore the effects of argon impurities. These argon profiles are used as impurity study inputs in §§ 4 and 5. GENE does not reproduce atomic radiation effects, however the net heat flux after excluding the experimentally measured radiated power, $P_{\rm {tot}} - P_{\rm {rad}}$, shown in figure 2(b), is used to compare simulated nonlinear heat fluxes with experimentally measured values in § 5. The total heat flux $P_{\rm {tot}}$ is computed with an interpretative TRANSP run (Pankin et al. 2004) that includes the local deposited heating power using the real geometry of the ECRH and NBI sources as well as profiles from figure 1 and argon profile 1.

3. Set-up of gyrokinetic modelling

Utilising the fits to the experimental data presented in figure 1, linear and nonlinear gyrokinetic computations are carried out locally at four radial positions and globally for one pedestal scenario using the GENE code. GENE employs a five-dimensional phase-space grid consisting of radial, binormal, field line following, parallel velocity (with respect to the magnetic field direction) and magnetic moment coordinates labelled as $x, y, z,v_{\parallel }$ and $\mu$, respectively. All simulations are local flux tube simulations self-consistently retaining $A_{||}$ and $B_{||}$ fluctuations, with the exception of the global gyrokinetic pedestal simulation, which is electrostatic due to computational limitations. Furthermore, all simulations use a realistic deuteron to electron mass ratio. All simulations use periodic boundary conditions, with the exception of the global simulations, which use Dirichlet boundary conditions with Krook-type (Görler et al. 2011) buffer zones in the outer $5\,\%$ of the simulation domain. All simulations are two species (deuteron and electron) with the exception of the linear impurity study in § 4 and the nonlinear case at $\rho _{\rm {tor}}=0.70$ in § 5.

Throughout this work the ‘Landau–Boltzmann’ collision operator is utilised (Doerk 2012) with the collisionality, $\nu _{{ei}}$, calculated (Neiser et al. 2019) from the other input parameters, and with finite Larmor radius (FLR) effects not included. Preliminary tests superfluous to this work reveal that using the ‘Sugama’ collision operator (Sugama, Watanabe & Nunami 2009) without FLR effects did not result in significant changes to linear growth-rates.

Linear growth rates are calculated for each wavenumber investigated, $k_y$, which is normalised by the respective gyroradius of the simulation $\rho _s = c_s/\varOmega _i$ with $c_s$ being the ion sound speed and $\varOmega _i$ being the ion cyclotron frequency. The gyroradius to tokamak minor radius is given as $\rho ^{*} = \rho _s/a$. Linear growth rates are normalised by $c_s/a$, where $c_s=\sqrt {T_e/m_{i}}$, $T_e$ is the electron temperature and $m_{i}$ is the ion mass. The total simulated heat flux for a given radial location is composed of contributions from two-species ion-scale, single-species electron-scale (adiabatic ions) and neoclassical estimates. Neoclassical calculations in GENE are based on a linearised solver described previously in Doerk (2012), Oberparleiter (2015) and Stimmel et al. (2019) and are here employing the Landau collision operator.

Important parameters used throughout this work which are taken from the experimental fits to the data are presented in table 1. Two core and two pedestal top positions are chosen for local simulations to allow for characterisation of core and pedestal top. Pedestal top and global simulation domain locations are limited radially by numerical prerequisites to ensure code stability (such as buffer zones) and experimental uncertainty. Ion and electron temperatures are presented in kiloelectronvolts, density $n_{\rm {ion}}$ is assumed to be equal to $n_e$ to enforce simulation quasineutrality in two species simulations, and all normalised logarithmic gradients are defined as $\omega _{{k}} = - ({1}/{k})({{\rm d}k}/{\rho _{\rm {tor}}})$ where $k$ represents the ion temperature $T_i$, electron temperature $T_e$ or the electron density $n_e$ in table 1.

Table 1. Nominal GENE input parameters taken from experimentally measured values from ASDEX Upgrade discharge #36330 from $t \sim 6.1 \unicode{x2013}6.2\ {\rm s}$ for four radial positions.

The thermal plasma pressure to magnetic pressure ratio is given as $\beta _e = {8 {\rm \pi}n_e T_e}/{B^{2}_{0}}$. The magnetic shear is defined as $\hat {s} = (\rho _{\rm {tor}}/q)({\rm d}q/{\rm d}\rho _{\rm {tor}})$ where $q$ is the tokamak plasma safety factor. The effective ion charge $Z_{\rm {eff}}$ is set to be 2.05 for all radial positions. In simulations where an impurity species profile is used, this parameter is ignored. The GENE ‘Landau–Boltzmann’ collision value, $\nu _{ei}$, is also listed in table 1 for reference.

Radial electric field shearing is included in nonlinear simulations by shifting the radial Fourier mode grid in time radially with aliasing compensation (Hammett et al. 2006; McMillan, Ball & Brunner 2019). The normalised local external shearing rate in GENE, $\gamma _{{E\times B}}$, is given as

(3.1)\begin{equation} \gamma_{{E\times B}} ={-}\sigma_{I_p} \sigma_{\omega} \sigma_{\partial_x |\omega|} \left| \frac{\rho_{\rm{tor,0}}}{q_0} \frac{\partial \omega_{\rm{tor}}}{\partial \rho_{\rm{tor}}} \right| \frac{a}{c_s}. \end{equation}

Here $\sigma _{I_p}$, $\sigma _{\varOmega }$ and $\sigma _{\partial _x |\varOmega |}$ are the sign of the plasma current, plasma rotation and radial derivative of the plasma rotation profile, respectively, with $+1/{-}1$ corresponding to clockwise/anticlockwise as seen from above. The reference flux surface, $\rho _{\rm {tor,0}}$, is taken at the simulation domain centre, $q_0$ is the safety factor at the simulation domain centre and $\omega _{\rm {tor}}$ is the toroidal angular velocity in radians per second taken from one of the two profiles displayed in figure 3.

Figure 3. Two background velocity profile fits used as GENE inputs for ASDEX Upgrade 36330. The blue $\omega _{\rm {tor}}$ fit represents the toroidal component of the total measured velocity. The dashed orange $\omega _{\rm {pseudo}}$ fit represents the $\boldsymbol{E\times B}$ velocity based on the radial electric field profile multiplied by the prefactor $|B_{\rm {Tot}}|/B_{\rm {pol}}$ for use via the Hammett–McMillan shearing mechanism in GENE.

Using the toroidal angular velocity profile to estimate the radial electric field is an appropriate estimate for core simulations. However, in the pedestal this assumption is no longer valid as the magnitude and sign of the $\boldsymbol{E\times B}$ velocity is no longer primarily represented by the toroidal component alone in the radial electric field force balance equation. The current implementation of $\boldsymbol{E\times B}$ shearing in the GENE code only considers a toroidal component, and so a pseudo-velocity, $\omega _{\rm {pseudo}}$, shown in figure 3, is used to replace $\omega _{\rm {tor}}$ in (3.1) as an ad-hoc representation for the full magnitude of the $\boldsymbol{E\times B}$ shearing in some nonlinear pedestal scenarios.

This pseudo-velocity is the full magnitude of the $\boldsymbol{E\times B}$ velocity calculated from the radial electric field shown in figure 1(d) (rather than just the toroidal component) multiplied by the prefactor $|B_{\rm {Tot}}|/B_{\rm {pol}}$ to seamlessly integrate with the toroidal $\boldsymbol{E\times B}$ shearing scheme already implemented in GENE. The resulting GENE $\gamma _{{E\times B}}$ shearing rates used in this work from both toroidal angular velocity profiles are listed in table 1. As is shown in detail in § 6, the utilisation of a pseudo-velocity to represent the full effect of the radial electric field shearing elucidates the importance of $\boldsymbol{E\times B}$ shearing in the tokamak pedestal, however it also demonstrates the limit of local GENE simulations to accurately represent shearing, and ultimately serves as a motivation for a more complete numerical methodology from the full radial electric field vector.

4. Linear instability study

Linear characterisation of the ELM-free regime presented in this paper reveals a core scenario similar to standard H-Mode, and a more complex picture of gyrokinetically modelled pedestal top turbulence. All linear simulations presented here are tested for numerical convergence by increasing spatial resolutions, box sizes and by varying the edge$\_$opt parameter, used to redistribute GENE parallel grid points to better adhere to tokamak magnetic geometry (Told 2012), until a growth-rate difference of less than 5 % or a difference of less than 0.01 $k_y\rho _s$ is achieved. Linear simulations utilised a resolution range of $N_x \times N_z \times N_{v\parallel } \times N_\mu = 31\unicode{x2013}127 \times 48\unicode{x2013}128 \times 32\unicode{x2013}48 \times 16$ where $N_x,N_z,N_{v\parallel }$ and $N_\mu$ are the number of radial, parallel coordinate, parallel velocity and magnetic moment grid points, respectively. Generally simulations with core parameters at ion scale $k_y\rho _s$ tend to require lower numeric resolutions while parameters at $k_y\rho _s < 0.2$ or at $k_y\rho _s > 10$ require additional resolution. Linear velocity and magnetic moment box size parameters of $L_v \times L_\mu = 3 \times 9 \unicode{x2013} 11$ are appropriate for all linear simulations. Values of ${\tt {edge\_opt}}= 1\unicode{x2013}2$ suffice for all simulations with the exception of $k_y\rho _s > 100$ calculations at $\rho _{\rm tor}= 0.95$ utilising ${\tt {edge\_opt}} = 4$. Linear simulations are carried out with deuteron and electron species unless noted otherwise and results shown are evaluated at a ballooning angle of zero.

A linear, local, initial-value scan across a wide range of $k_y \rho _s$ for four radial positions with two species gives a first characterisation of the regime as shown in figure 4.

Figure 4. Linear GENE growth rates ($\gamma$) and frequencies ($\omega$) for four radial positions across a range of $k_y\rho _s$. Negative frequencies in the GENE simulation co-moving frame correspond to the electron diamagnetic direction. A subplot shows ion-scale frequencies on a smaller scale for visibility. Frequencies from negative or zero growth rate $\gamma$ are omitted.

An ion-scale instability peak is present in all four cases at $k_y\rho _s < 1$ while an electron scale peak exists for core scenarios at $k_y\rho _s > 3$ and for pedestal top scenarios at $k_y\rho _s > 60$. When considering the heuristic rule (Görler & Jenko 2008a; Görler & Jenko 2008b; Jenko 2004) often applied to multiscale simulations of $\gamma _e/ \gamma _i \gg \sqrt {(m_i/m_e)} \sim 60$, the two core scenarios as well as the pedestal top scenario do not exceed $\gamma _e/ \gamma _i \gg \sim 60$ and, therefore, multiscale simulations are assumed to not be important. The $\rho _{\rm {tor}}=0.95$ case does exceed this value ($167 > 60$). However, all four scenarios do not meet the criteria for multiscale importance using ${\rm {max}}(\gamma _{\rm {ETG}}/k_y) \geqslant {\rm {max}}(\gamma _{\rm {ITG}}/k_y)$ from Staebler et al. (2017) and the ion and electron scale peaks are separated by more than two orders of magnitude; therefore, the assumption that these two peaks do not interact nonlinearly is made for this work.

Two intermediate range peaks from $k_y\rho _s=2\unicode{x2013}10$ with low growth rate relative to the respective ion-scale growth-rate peaks are also present for the two pedestal top scenarios. Gradient variation test scans (not shown) are performed for all four radial locations to help identify the dominant instability.

The two core scenarios are easily identifiable as ion temperature gradient (ITG) dominated at low $k_y\rho _s$ due to positive growth-rate frequencies and a sensitivity to varying $\omega _{{\rm Ti}}$ at low $k_y\rho _s$. The electron-scale core peaks are identified as electron temperature gradient (ETG) dominated due to negative growth-rate frequencies and a strong sensitivity to variations in $\omega _{{\rm Te}}$ at the upper $k_y\rho _s$ range.

Linear pedestal calculations present a more complex picture of the argon-seeded EDA H-mode. Negative-frequency instabilities sensitive to variation primarily in $\omega _{{\rm Te}}$ but also $\omega _{{\rm Ti}}$ and $\omega _{n}$ are found at ion-scale $k_y\rho _s$ for $\rho _{\rm tor}= 0.90$, with a positive frequency mode beginning to dominate at $k_y\rho _s = 1$, hinting at TEM transitioning to ITG as the dominant instabilities as $k_y\rho _s$ increases (Kotschenreuther et al. 2019). Although linear flux values are not meaningful on their own, by comparing the ratios of finite linear flux channels in converged linear simulations, it is possible to discern which flux channel is dominant to help identify an instability. These modes at $\rho _{\rm tor}= 0.90$ are dominated by electron electrostatic heat flux channel when considering the ratio of electrostatic to electromagnetic heat flux channel by species.

The ion-scale peak at $\rho _{\rm tor}= 0.95$ is characterised by negative frequencies and electron electrostatic dominated heat flux with the exception of the lowest positive growth rate at $k_y\rho _s = 0.1$ matching a microtearing mode (MTM) ballooning mode structure like in Hatch et al. (2015) for example, and electron electromagnetic-dominated heat flux.

Upon decreasing the density gradient, the growth rate increases by roughly a factor of two in the ion-scale and intermediate ranges. Finally, the electron scale peak at $\rho _{\rm tor}= 0.95$ is ETG-like, and is subject to an increased growth rate upon decreasing the density gradient as expected (Hatch et al. 2019; Parisi et al. 2020). While it has been previously demonstrated that ETG growth-rates in particular may peak at non-zero ballooning angles due to strong equilibrium shaping effects (Told et al. 2008), the focus in this section is limited to the growth rate at the outboard midplane for instability identification and comparison with nonlinear results; nonlinearly it is found throughout this work that heat flux spectra peak at or near the outboard midplane.

Additional scans over $\beta _e$ and collisionality are included for the two pedestal top scenarios and are displayed in figures 5 and 6, respectively.

Figure 5. GENE linear $\beta _e$ scan at (a) $\rho _{\rm {tor}}= 0.90$ and (b) $\rho _{\rm {tor}}= 0.95$. The black vertical line denotes the nominal $\beta _e$ value for each scenario.

Figure 6. GENE linear collisionality scan for two pedestal top positions at $\rho _{\rm {tor}} = 0.90$ and $0.95$. Three values of collisionality are tested for each $k_y\rho _s$.

Unlike some previous recent GENE pedestal studies (Bonanomi et al. 2019; Stimmel et al. 2019), scanning along increasing $\beta _e$ with fixed geometry does not reveal instabilities which are bordering a highly unstable kinetic ballooning mode (KBM)-like range at $\rho _{\rm tor}= 0.90$ as shown in figure 5. While a critical threshold is observed at higher $\beta _e$ at $\rho _{\rm tor}= 0.95$, the proximity of the nominal $\beta _e$ is at least a factor of two away from increased linear growth rates which are indicative of a KBM in both pedestal top scenarios in figure 5.

Collisionality scans at the ion-scale pedestal top scenario peaks with $50\,\%$ and $150\,\%$ the nominal collisionality value suggest again trapped modes which are sensitive to collisionality as shown in figure 6(a). Linear frequencies are plotted in figure 6(b) for reference, illustrating the effects of collisionality on linear frequencies. Together with the frequency of the ion-scale peaks in figure 4, one can deduce that at $\rho _{\rm {tor}} = 0.90$ the dominant instability transitions from TEM to ITG, while at $\rho _{\rm {tor}} = 0.95$ the ion-scale peak is TEM with a very weak MTM detected at the lowest positive growth rate $k_y\rho _s < 1$.

A scan across $k_y\rho _s$ performed with two different argon impurity profiles is shown in figure 7, together with a linear scan using only electrons with adiabatic ions. Introducing a third argon species into the linear core simulations is found to have only a minimal effect on dominant growth rates at ion-scale wavenumbers and decreases electron-scale growth-rate peaks significantly relative to two species linear calculations, thus rendering significant cross-scale coupling more unlikely. While the decrease in electron scale growth rate from the addition of argon agrees with expectations, the nonlinear electron-scale heat flux contribution is minimal as shown in § 5. The relatively small changes in ion-scale behaviour from the addition of argon weights the assumption of using two species for nonlinear simulations. Furthermore, it should be noted that using the artificially high Ar profile 2 is shown to have a relatively greater effect nonlinearly than linearly at $\rho _{\rm {tor}}=0.70$ as shown in § 5.

Figure 7. Linear GENE argon impurity study at four radial locations. (a)–(d) The converged linear growth ratesfor no impurity, impurity profile 1, impurity profile 2 and adiabatic ion linear scans for $\rho _{\rm {tor}}= 0.60,0.70,0.90$ and $0.95$, respectively.

In addition, linear scans at $\rho _{\rm {tor}}=0.70$ over $k_y\rho _s$ with the inclusion of argon profiles 1 and 2 are reproduced with a newly implemented dilution model in GENE. The new dilution model allows for the modification of density and gradient profiles without the direct introduction of a third species; the dilution model is used to linearly reproduce the density dilution and gradient modification introduced by the addition of argon profiles 1 and 2 as shown in figure 8.

Figure 8. Linear GENE growth rate comparison between three-species and dilution-model $k_y\rho _s$ scans. The default two-species linear scan is shown in black, scans with argon profiles 1 and 2 are shown in red and magenta, respectively, and the dilution model scans are shown in blue and green, respectively.

Figure 8 illustrates that at ion scales the linear growth rate peak and shape are closely reproduced by the dilution model for both argon profiles for ion scale at $\rho _{\rm {tor}}=0.70$, demonstrating the significance of gradient modification and density dilution from impurities. However, as shown in § 5, considering that the nonlinear heat flux shift is greater than the linear growth rate shift upon the addition of argon, one must not rule out the nonlinear role the addition of argon plays on turbulent heat transport.

In both cases linear simulations qualitatively predict the increased heat flux trend when comparing between two-species and three-species cases.

5. Nonlinear GENE simulations

Using linear analysis as an initial guide for the characterisation of the argon-seeded EDA H-mode, nonlinear gyrokinetic results are presented here. Nonlinear heat fluxes for various nonlinear simulations as well as neoclassical estimates are given in table 2 together with experimentally measured heat flux $P_{\rm {tot}} - P_{\rm {rad}}$ from figure 2(b).

Table 2. Simulated and experimental heat flux values in megawatts. From left to right the columns are radial position, optional modification to the ion-scale simulation, specification of either standard toroidal angular velocity or pseudo-angular velocity profile input used for determination of $\gamma _{E\times B}$, ion-scale heat flux subdivided into four channels (six with impurities), electron-scale heat flux sum where asterisks denote three-species simulations, neoclassical heat flux estimate, sum of total heat flux as an upper estimate with statistical error included and the net experimental heat flux value defined as $P_{\rm {tot}} - P_{\rm {rad}}$.

5.1. Simulation set-up

Nonlinear electromagnetic simulations are carried out at ion and electron-scale wavenumber ranges at four radial locations with periodic boundary conditions as well as radially global electrostatic ion-scale simulations from $\rho _{\rm {tor}} = 0.84 \unicode{x2013}0.96$ with Dirichlet boundary conditions. All periodic boundary simulations are tested for radial box size ($L_x$) and radial grid-point resolution ($n_{X_0}$) convergence and are tested to fully encapsulate the heat flux spectra peak in $k_y\rho _s$ space. The nonlinear resolution used for ion-scale simulations is $256 \leqslant N_x \leqslant 768 \times 48 \leqslant N_z \leqslant 50 \times N_{v_{||}} = 32 \times N_\mu = 16$ with the simulation box size varying from $117 \leqslant L_x \leqslant 230 \times 116 \leqslant L_y \leqslant 170$ $\rho _s$ and minimum toroidal mode number $4 \leqslant n_0 \leqslant 6$. The $k_y$ range in the simulations spans from $k_{y,{\rm min}}$ to $k_{y,{\rm min}} \times N_{ky}$ with $k_{y,{\rm min}} = [0.046, 0.054, 0.046, 0.03]$ and $N_{ky} = [24, 32, 32, 32]$ for $\rho _{\rm {tor}} = [0.60, 0.70 0.90, 0.95]$, respectively. Owing to the immense computational cost, global simulation resolution is based on successful local nonlinear simulations in the pedestal. Attempts to nonlinearly simulate beyond $\rho _{\rm {tor}}=0.96$ globally prove ineffectual due to numeric instability at the aforementioned resolution limit and due to increasing experimental uncertainty towards the separatrix. Similarly, nonlinear, local, pedestal scans are computationally limited as increasingly large $A_{||}$ structures demand larger radial box sizes and as higher radial resolution is required for steeper gradients toward the separatrix. Furthermore global simulations are electrostatic with $k_{y,{\rm min}} = 0.083$ and $N_{ky} = 26$ for numerical stability. Generally lower radial resolutions and box sizes suffice for core simulations while pedestal top simulations require large radial boxes and resolutions to fully capture large and distorted turbulent structures, even with the inclusion of $\boldsymbol{E \times B}$ shearing.

Differences in $\gamma _{E\times B}$ have a minimal effect on electron-scale simulations, but have a profound effect on ion-scale heat fluxes and resulting frequency spectra. The toroidal velocity profile used to determine the $\gamma _{E \times B}$ rate is specified as either toroidal velocity or pseudo-velocity in the third column of table 2.

Two species are used in all nonlinear ion-scale simulations unless specifically noted otherwise. The effective ion charge, $Z_{\rm {eff}}$, is used in two species simulations to account for the effect of impurities on collisions. Linear electron-scale simulations reveal that single-species electron (adiabatic ion) simulations reproduce three-species linear growth rates in the pedestal top scenarios, but not the core scenarios as shown in figure 7. Therefore, nonlinear electron-scale simulations are carried out with three species (electron, deuteron, argon) in the two core scenarios while kinetic electrons with adiabatic ions are used in pedestal top scenarios. Nonlinear electron-scale core simulations which use three species rather than kinetic electrons with adiabatic ions are denoted with an asterisk in table 2.

Nominal core electron-scale simulations therefore use $\times 14.53 \leqslant L_x \leqslant 14.83 \times 2.1 \leqslant L_y \leqslant 3.1$ $N_x = 256 \times N_z = 50 \times N_{v_{||}} = 32 \times N_{\mu } = 16$ $\rho _{s \mathrm {[ion]}}$ with $k_{y,\min [\rho _i]} = [2.00, 3.00]$ and $N_{ky} = [18, 16]$ at $\rho _{\rm {tor}} = [0.60, 0.70]$, respectively. Nominal pedestal top electron-scale simulations use $N_x = 512 \times N_z = 50 \times N_{v_{||}} = 32 \times N_{\mu } = 16 $  $\times 159.47 \leqslant L_x \leqslant 163.45 \times 62.8 \leqslant L_y \leqslant 156.9$ $\rho _{s \mathrm {[{e^{-}}]}}$ with $k_{y,\min [\rho _{e^{-}}]} = [0.04, 0.10]$ and $N_{ky} = [64, 64]$ at $\rho _{\rm {tor}} = [0.90, 0.95]$, respectively, with subscripts denoting reference to ion or electron gyroradius.

5.2. Overview and core analysis

Table 2 lists the various time-averaged quasistationary heat flux values for several scenarios and modified versions of each scenario. Contributions from ion-scale, electron-scale and neoclassical simulations are summed together as an upper estimate of simulated heat flux, noting that if cross-scale coupling were to be significant, the electron-scale heat flux may be smaller due to vortex shearing. This is presented together with the net experimental heat flux ($P_{\rm {tot}} - P_{\rm {rad}}$) calculated using TRANSP (Pankin et al. 2004) in the final two columns of table 2. It should be noted that measured radiative losses and ion–electron coupling are subject to experimental uncertainty, making reliable separation of experimental ion and electron channels in the pedestal and edge infeasible for the scenario at hand.

Analysis of modified scenarios allows for the characterisation of the argon-seeded EDA H-mode regime. Nonlinear simulations confirm initial linear findings in the core: sensitivity to $\omega _{{\rm Ti}}$ for both core scenarios together with heating flux primarily from the ion electrostatic channel suggests a familiar H-mode core characterisation where ITG turbulence dominates. Reduction of $\omega _{{\rm Ti}}$ by 15 %, considered reasonable based on a number of previous validation exercises (Holland et al. 2009; Told et al. 2013; Göler et al. 2014), allows for the outer core scenarios to approach the experimental heat flux value thus giving confidence to the diagnosis of ITG-type turbulence dominating the core. This is further enforced by the fact that all variants of nonlinear, local, ion-scale, core simulations are all ion-channel dominated, with ion to electron heat flux ratios of approximately 2.4 and 2.1 resembling the experimental TRANSP ion to electron heat flux ratios of 1.7 and 3.2 for $\rho _{\rm {tor}} = 0.60$ and 0.70, respectively.

5.3. Electron-gyroradius-scale contributions

Electron-scale turbulence only contributes a small fraction of the total heat flux in the four local scenarios while neoclassical calculations show moderate transport levels that increase with increasing radial position. Electron-scale turbulence is surprisingly low in pedestal top scenarios; destabilising $\omega _{n}$ and $\omega _{{\rm Te}}$ by 20 % in these scenarios increases the heat flux by roughly an order of magnitude in each case, however, this is still much less significant compared with ion-scale heat flux in each case. Using different values of $\gamma _{E\times B}$ calculated from $\omega _{\rm {tor}}$ or $\omega _{\rm {pseudo}}$ is found to have a negligible effect on electron-scale heat fluxes as expected.

5.4. Effect of impurity species

It has been suggested that the addition of argon may reduce ITG turbulence due to main ion density dilution (Ennever et al. 2015; Hatch et al. 2017; Kallenbach et al. 2021) in addition to profile (gradient) modification from radiation. Linearly it is found that introducing Ar profile 2 from figure 2 reduces ion-scale growth rates and suppresses ITG instabilities such that electron frequency dominated TEM-like instabilities are allowed to dominate at $\rho _{\rm {tor}}=0.70$.

To further investigate this effect, nonlinear ion-scale three-species simulations are carried out at $\rho _{\rm {tor}}=0.70$ using argon profiles 1 and 2. In these simulations, ion and electron temperatures are kept the same as in two-species simulations. It is found that the realistic argon profile 1 increases heat flux relative to the two-species simulation, while the near-flat argon profile 2 decreases heat flux. Including argon profile 1 inevitably steepens the ion density gradient relative to two species, which is the driver for the higher heat flux increasing 7 % from 6.26 to 6.75 MW. This qualitatively follows the slight 4 % linear increase in peak growth rate at $k_y\rho _s=0.70$ from 0.23 to 0.24 when comparing no argon and argon profile 1.

The addition of Ar profile 2 at $\rho _{\rm {tor}}=0.70$ reduces two-species ion-scale heat flux from 6.26 MW by 26 % to 4.61 MW which is larger than the small 9 % reduction in peak growth rates at $k_y\rho _s=0.70$ from 0.23 to 0.21, showing that linear simulations successfully predict a qualitative decrease in heat flux. Nonlinearly, however, using argon profile 2 it is not found that ITG turbulence is suppressed to such an extent that negative frequencies dominate the frequency spectrum; frequency spectra are qualitatively unchanged between two- and three-species nonlinear simulations. Finally, it is noteworthy that the addition of argon profile 2 here maintains almost exactly the same ion density gradient, demonstrating that the reduction in growth rate/heat flux is not necessarily from modifying the density gradient, but rather from a reduction in ion density and turbulent effects from the addition of the argon impurity.

It is important to consider that the introduction of argon does not only reduce heat flux because this effect is balanced by modifications to the density gradient. Furthermore, the linear change in growth rate is much smaller than the change in nonlinear heat flux; therefore, nonlinear extrapolation cannot be a straightforward procedure, but must rather consider a balance between profile modification and turbulent effects. Three-species pedestal simulations where argon seeding may have an important role in ELM suppression (Kallenbach et al. 2021) are of interest but are left to future work due to computational challenges.

5.5. Global pedestal simulations

Global effects are confirmed to be of importance in the pedestal regime as evidenced by two global, gradient-driven, electrostatic, ion-scale simulations Dirichlet boundary conditions that reduce local overpredictions of the experimental heat flux value at $\rho _{\rm tor}=0.90$, with the input $\gamma _{E\times B}$ profile proving crucial. Using past gyrokinetic findings such as those of Candy et al. (2009) and Görler et al. (2011), one might expect that $\rho ^{*} = 0.0018 < 0.002$ is satisfied at $\rho _{\rm {tor}}=0.90$ and that flux tube simulations would agree with global simulations. Considering that more recent findings show this scaling is not necessarily valid for medium-sized tokamaks, however (Navarro et al. 2016), and considering that the finite width of the steep gradient region is of greater importance than the overall system size (McMillan et al. 2010), it is not unexpected that global simulations correct a local overprediction at $\rho _{\rm {tor}}=0.90$.

Local simulations with electromagnetic effects offer additional insight to how the inclusion of realistic $\beta _e$ may affect the heat flux. Global investigation is motivated by the local ion-scale nonlinear simulation at $\rho _{\rm tor}=0.90$ which yields a heat flux more than an order of magnitude higher than the experimental value. Such an overprediction in the pedestal has previously been associated with proximity to a nonlinearly shifted critical $\beta _e$ KBM threshold; such cases typically demonstrate a clear increase in linear growth rates with increasing $\beta _e$ and a strong heat flux sensitivity to $\beta _e$ nonlinearly (Bonanomi et al. 2019; Stimmel et al. 2019). However, in this case even setting $\beta _e$ to zero together with a high estimate of $\gamma _{E\times B}$ does not recover the experimental heat flux, suggesting the strong relevance of finite-size effects.

To investigate this, two global, electrostatic, nonlinear simulations with two different toroidal velocity inputs used to calculate $\boldsymbol{E \times B}$ shearing are presented in table 2. Global electromagnetic GENE simulations, having recently been implemented, would be of high value but are left for future work due to the high computational cost.

The importance of the $\gamma _{E\times B}$ profile is explored globally and comparisons are drawn between local and global simulations. Using only the toroidal velocity component to calculate $\boldsymbol{E \times B}$ shear gives a total heat flux of about 3.7 MW, which is a slight overestimate of pedestal heat transport after factoring in radiative losses. On the other hand, the pseudo-velocity effectively damps all turbulence in the pedestal, not even reaching the experimental 2–3 MW range for the pedestal as shown in figure 9. Global effects are necessary to correct the local heat flux overprediction at $\rho _{\rm {tor}}=0.90$; compared with the 6.91 MW from the local electrostatic simulation at $\rho _{\rm {tor}}=0.90$, the global simulation using $\omega _{\rm {psu}}$ as GENE input yields less than 0.1 MW at a local slice around $\rho _{\rm {tor}}=0.90$, as shown in figure 9. Furthermore, the choice of input rotational velocity is shown to have a dramatic effect as shown in figure 9. While the heat flux is not perfectly recovered by global simulations, even these electrostatic cases demonstrate the importance of global effects in the pedestal. Based on the comparisons between nonlinear electrostatic and electromagnetic local simulations shown here alone, it is likely that more physical realism via inclusion of electromagnetic effects may help corroborate the underprediction of heat fluxes when using $\omega _{\rm {psu}}$ in a global pedestal simulation.

Figure 9. Global electrostatic GENE heat flux profiles for two simulations with different background $\gamma _{E\times B}$ profiles, and one electrostatic local simulation for comparison. Global Dirichlet boundary buffer zones are denoted with grey patches. The experimental net power flux is plotted as a dashed magenta line for reference.

Of key importance to the argon-seeded EDA H-mode on ASDEX Upgrade is understanding the QCM. Despite extensive efforts, notable challenges were encountered while attempting to elucidate more about the QCM. Previous work from LaBombard et al. (2014) shows the EDA H-mode spans the separatrix and into the steep gradient region of the pedestal; by considering this alone, the QCM would require a simulation which crosses the separatrix to fully capture the necessary physics. However, it is important to note that there is no evidence that the QCM does not exist further inside the pedestal top in ASDEX Upgrade ELM Free H-mode plasmas due to Doppler reflectometry limitations at higher densities inside the pedestal. Furthermore, evidence from Theiler et al. (2017) also suggests that the QCM resides inside the $\boldsymbol{E_r}$ well minimum rather than outside.

Assuming that the QCM could be found at the pedestal top, the biggest challenge in such an analysis is that the local pedestal top heat flux discrepancy between experiment and simulation may be too large to make any meaningful frequency comparison. Finally, even if there was no such discrepancy, analysis of the nonlinear local simulation frequencies using the more realistic $\omega _{{\rm psu}}$ at $\rho _{{\rm tor}}=0.90$ reveals that different velocity profiles simultaneously alter resulting shearing as well as the applied Doppler shift to the simulations, resulting in a wide range of outcomes from even small changes in the velocity profile. Using the more realistic, higher-valued $\omega _{{\rm psu}}$ velocity profile value in conjunction with higher gradient inputs at $\rho _{{\rm tor}}=0.95$ requires significantly more numerical resolution in the radial direction than using the $\omega _{{\rm tor}}$ profile for $\boldsymbol{E\times B}$ input, thus creating an impractical computational challenge. This stems from the current local implementation of $\boldsymbol{E\times B}$ shearing in GENE which requires very high radial resolution for intense shearing rates to prevent artificial discontinuities from forming.

Conjecture on nonlinear global electrostatic frequencies is omitted from the electrostatic global analysis so as to not misrepresent the electromagnetic QCM frequencies (LaBombard et al. 2014).

5.6. Quasilinearity analysis

When characterising such a multidimensional parameter space it useful to determine which linear features persist nonlinearly. Considering the four scenarios, there is fair quasilinear agreement at peak $k_y\rho _s$ for the two core scenarios while the linear and nonlinear pedestal cross-phases do not align. Figure 10 displays potential perpendicular temperature fluctuation and potential density fluctuation cross-phases using the same definition as in Told et al. (2013) at $\rho _{\rm {tor}}=0.95$. Linear cross-phase peaks denoted with crosses do not match the nonlinear cross-phase peaks denoted with small circles at peak heat flux $k_y\rho _s$ shown in orange, nor do secondary linear cross-phase peaks (not shown here) for either $\phi \times n$ or $\phi \times T_{\perp }$.

Figure 10. Local nonlinear (NL.) and linear (lin.) simulation maximum cross-phase (a) ion and (b) electron amplitudes for $\phi \times n$ and $\phi \times T_{\perp }$ at $\rho _{\rm {tor}}=0.95$ for AUG discharge #36330 from 6–6.2 s. Nonlinear data are shown as circles while linear data are displayed as crosses. Nonlinear time-averaged electrostatic (ES) and electromagnetic (EM) heat flux spectra are overlaid as solid and dashed orange lines, respectively, for reference.

Linear frequency computations at $\rho _{\rm {tor}}=0.90$ qualitatively predict TEM/ITG nonlinearly, yet nonlinear frequencies are generally sensitive to the input toroidal velocity profile. Both nonlinear scenarios at this radial position are identified as ITG/TEM from the electron to ion diffusivity ratios (Kotschenreuther et al. 2019) $\chi _e/ \chi _e \sim 1$ and $D_e/(\chi _i + \chi _e) \sim 0.16$ where $\chi _{i,e}$ is the ion or electron heat diffusivity and $D_e$ is the electron particle diffusivity. Using the stronger and more realistic $\omega _{\rm {psu}}$ profile as shearing input results in an increasingly negative-frequency (in the plasma frame) TEM-dominated frequency spectrum compared with $\omega _{\rm {tor}}$ at $\rho _{\rm {tor}}=0.90$.

Other recent research suggests that quasilinear agreement is attainable in lower-power scenarios (Bonanomi et al. 2019; Neiser et al. 2019; Stimmel et al. 2019) such as L- or I-mode, and even to some degree in an H-mode inter-ELM pedestal scenario (Hatch et al. 2015). However, these findings do not seem to translate to the pedestal top scenario here. Further considerations on quasilinear validity have previously been outlined in Casati (2012), and nonlinear effects for edge turbulence are detailed in Scott (2002).

6. Discussion and summary

The results presented here characterise the argon-seeded EDA H-mode microturbulence as ITG in the core and primarily TEM in the pedestal top at ion scales, demonstrate the limitations of quasilinear analysis and reveal challenges in attempting to gyrokinetically capture the QCM, thus further warranting global nonlinear electromagnetic simulations. Local core simulations reproduce experimentally measured heat transport by varying the $\gamma _{E \times B}$ shear and profiles within reasonable limits, however pedestal top scenarios require global effects and likely electromagnetic effects to closely approach experimental heat flux levels.

Experimental inner core heat fluxes are accurately reproduced within error bars, and outer core heat fluxes fall very close to the experimental values. The core is accurately modelled gyrokinetically with the combination of ion-scale, electron-scale and neoclassical simulations, and local simulations provide limited insight to the pedestal top. Nonlinear three-species core simulations reveal that argon is an important tool not only for shaping of profiles as expected experimentally and as shown with the introduction of argon profile 1, but can also have an effect on turbulent transport even when gradients are left unchanged.

The exploration of the argon-seeded EDA H-mode reveals a complex regime that is nonetheless an excellent candidate for further study both experimentally and computationally. The QCM is difficult to assess locally because the heat flux is overpredicted at $\rho _{\rm {tor}}=0.90$ and global simulations are missing full electromagnetic effects. This exploratory study warrants the use of global, electromagnetic, nonlinear gyrokinetic simulations which span deeper into the steep gradient region, as local simulations reach their limit and fail to capture the QCM as shown in this work.

Sensitivity to $\beta _e$ seems like a potential culprit for local overprediction at the pedestal top similar to nonlinear critical $\beta _e$ threshold shifts described in Bonanomi et al. (2019) and Stimmel et al. (2019). However, the local electrostatic simulation at $\rho _{\rm {tor}}=0.90$ still yields a heat flux higher than twice the experimental value, suggesting that this effect is not solely responsible for the large overprediction. Global simulations demonstrate the potential to correct such overpredictions; physically this is expected as streamers are sheared apart non-locally from turbulence and especially from radially varying $\boldsymbol{E\times B}$ rates. Future work may consider dedicated efforts to understanding how close to the marginal stability the pedestal scenarios are.

Radial electric field shearing is shown to have an important influence on ion-scale heat fluxes both locally and globally in the pedestal top. Differences in the toroidal velocity profile can lead to large changes in heat flux, frequency and applied Doppler shift, all influencing the perspective of the frequency composition and nature of the simulated turbulence. A more complete theoretical framework involving the background radial electric field and subsequent numerical implementation may be of future interest to further investigate radial electric field effects. Although many analogues may be drawn between the argon-seeded ECRH-NBI-heated EDA H-mode and the unseeded ECRH-only EDA H-mode, direct gyrokinetic extrapolation of microturbulent behaviour from one regime to another should still be done with caution as argon impurities and rotational effects from NBI heating can have a major effect, as is shown in this work.

Quasilinear comparisons demonstrate that some nonlinear pedestal top cross-phase features are not reproduced linearly, yet linear growth rates predict nonlinear heat flux trends relatively well, especially in the core.

In closing, the argon-seeded EDA H-mode provides an exciting path forward for higher-powered fusion plasmas while mitigating the risk of unacceptable divertor heat loads. This work presents the first steps to uncovering the remaining mysteries in the pedestal of this regime on ASDEX Upgrade, and demonstrates clear agreement in the core between experiment and simulation. This regime is an excellent candidate for continued study particularly to develop an understanding of the effect of argon seeding on the QCM and ELM suppression, and has the potential to be further exploited in the future.