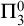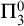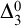1. Introduction
Reverse mathematics is a branch of mathematical logic. Its aim is to determine the strength of theorems which axioms are needed to prove these theorems. Among all axiom systems, reverse mathematics mainly focuses on five subsystems of second-order arithmetic, known as the Big Five:
The results of this paper are about
![]() $\textrm {ACA}_0$
, which is equivalent to say that the Turing jump exists for every set of natural numbers.
$\textrm {ACA}_0$
, which is equivalent to say that the Turing jump exists for every set of natural numbers.
One of the most important topics in reverse mathematics is Ramsey’s theorem and its variants. The version of Ramsey’s theorem studied in reverse mathematics is the infinite countable version of the finite Ramsey’s theorem from finite combinatorics. This theorem states that, for any finite coloring function c on
![]() $[\mathbb {N}]^n$
, there exists an infinite set H that
$[\mathbb {N}]^n$
, there exists an infinite set H that
![]() $[H]^n$
is monochromatic [Reference Jockusch12]. This infinite set is called a solution to c.
$[H]^n$
is monochromatic [Reference Jockusch12]. This infinite set is called a solution to c.
The strategy for analyzing these theorems is to study the computational complexity of their solutions. Jockusch proves that every recursive instance of
![]() $\mathrm {RT}^n_2$
(
$\mathrm {RT}^n_2$
(
![]() $n> 1$
) has a
$n> 1$
) has a
![]() $\Pi ^0_n$
solution and some recursive instance of
$\Pi ^0_n$
solution and some recursive instance of
![]() $\mathrm {RT}^3_2$
only has solutions computing the halting problem.
$\mathrm {RT}^3_2$
only has solutions computing the halting problem.
In this paper, we will discuss Hindman’s theorem. Hindman’s theorem is a Ramsey-type combinatorial theorem about finite sums:
Theorem 1.1 (Hindman [Reference Hindman9]).
For any coloring function
![]() $c:\mathbb {N}\rightarrow r$
, where
$c:\mathbb {N}\rightarrow r$
, where
![]() $r\geq 2$
is a natural number, there exists an infinite set
$r\geq 2$
is a natural number, there exists an infinite set
![]() $H\subset \mathbb {N}$
such that
$H\subset \mathbb {N}$
such that
![]() $FS(H)$
is monochromatic under c where
$FS(H)$
is monochromatic under c where
![]() $FS(H)$
is the set consisting of all finite sums of different numbers from H:
$FS(H)$
is the set consisting of all finite sums of different numbers from H:
 $$ \begin{align*} FS(H)=\left\{\sum_{x\in F}x:F\subset H, F\text{ is finite and nonempty}\right\}. \end{align*} $$
$$ \begin{align*} FS(H)=\left\{\sum_{x\in F}x:F\subset H, F\text{ is finite and nonempty}\right\}. \end{align*} $$
For convenience, we call such a set H in the above theorem a solution to c for Hindman’s theorem. In this paper, Hindman’s theorem will be abbreviated as
![]() $\textrm {HT}$
.
$\textrm {HT}$
.
The study of the reverse mathematics of Hindman’s theorem began with the paper by Blass, Hirst, and Simpson in 1987 [Reference Blass, Hirst and Simpson2]. They established some fundamental results about the complexity of solutions of Hindman’s theorem:
Theorem 1.2 (Blass, Hirst, and Simpson [Reference Blass, Hirst and Simpson2]).
1. For any coloring function
![]() $c:\mathbb {N}\rightarrow r$
, where
$c:\mathbb {N}\rightarrow r$
, where
![]() $r \geq 2$
is a natural number, there exists a solution to c for Hindman’s theorem that is recursive in
$r \geq 2$
is a natural number, there exists a solution to c for Hindman’s theorem that is recursive in
![]() $c^{(\omega +1)}$
, the
$c^{(\omega +1)}$
, the
![]() $(\omega +1)$
th Turing jump of c.
$(\omega +1)$
th Turing jump of c.
2. There exists a recursive coloring function c such that any solution to c can compute
![]() $c'$
, the Turing jump of c; this result can be relativized to any degree.
$c'$
, the Turing jump of c; this result can be relativized to any degree.
Based on these results about the complexity of solutions, they showed that the strength of Hindman’s theorem is between
![]() $\mathrm {ACA}_{0}$
and
$\mathrm {ACA}_{0}$
and
![]() $\mathrm {ACA}_{0}^{+}$
:
$\mathrm {ACA}_{0}^{+}$
:
![]() $\mathrm {ACA}_{0}$
is necessary and
$\mathrm {ACA}_{0}$
is necessary and
![]() $\mathrm {ACA}_{0}^{+}$
is sufficient. Simply speaking,
$\mathrm {ACA}_{0}^{+}$
is sufficient. Simply speaking,
![]() $\mathrm {ACA}_{0}^{+}$
is to say the
$\mathrm {ACA}_{0}^{+}$
is to say the
![]() $\omega $
th Turing jump of every set exists. However, this result has not been improved since 1987.
$\omega $
th Turing jump of every set exists. However, this result has not been improved since 1987.
In addition, before presenting their main results, Blass, Hirst, and Simpson provided another theorem as an example, which gives a lower bound on the complexity of a solution for Hindman’s theorem. That is the following:
Theorem 1.3 (Blass, Hirst, and Simpson [Reference Blass, Hirst and Simpson2]).
There exists a recursive coloring function c in two colors without any
![]() $\Delta ^0_2$
solutions for Hindman’s theorem.
$\Delta ^0_2$
solutions for Hindman’s theorem.
We may call Theorem 1.3 the
![]() $\Delta _2^0$
-unsolvability of Hindman’s theorem.
$\Delta _2^0$
-unsolvability of Hindman’s theorem.
For the meaning of Hindman’s theorem in reverse mathematics, see Montalbans’ paper [Reference Montalbán13]. For more information on reverse mathematics of Hindman’s theorem, see the references [Reference Dzhafarov and Mummert7, Reference Hirst11].
In this paper, we will prove the
![]() $\Pi _3^0$
-unsolvability of Hindman’s theorem:
$\Pi _3^0$
-unsolvability of Hindman’s theorem:
Theorem 1.4. There exists a recursive coloring function c in finitely many colors without any
![]() $\Pi _3^0$
solutions for Hindman’s theorem.
$\Pi _3^0$
solutions for Hindman’s theorem.
Restricted versions of Hindman’s theorem has received some attention in recent years. This idea comes from Blass’ paper [Reference Blass1]. The most common restricted Hindman’s theorem is the following theorem, denoted
![]() $\textrm {HT}^{\leq k}_r$
:
$\textrm {HT}^{\leq k}_r$
:
Theorem 1.5 (Restricted Hindman’s theorem
 $\textrm {HT}^{\leq k}_r$
for fixed numbers
$\textrm {HT}^{\leq k}_r$
for fixed numbers
 $r,k$
).
$r,k$
).
Suppose
![]() $r,k>0$
are two fixed natural numbers. For any coloring function
$r,k>0$
are two fixed natural numbers. For any coloring function
![]() $c:\mathbb {N}\rightarrow r$
, there exists an infinite set
$c:\mathbb {N}\rightarrow r$
, there exists an infinite set
![]() $H\subset \mathbb {N}$
such that
$H\subset \mathbb {N}$
such that
![]() $FS^{\leq k}(H)$
is monochromatic under c. Here,
$FS^{\leq k}(H)$
is monochromatic under c. Here,
![]() $FS^{\leq k}(H)$
is defined as follows:
$FS^{\leq k}(H)$
is defined as follows:
 $$ \begin{align*} FS^{\leq k}(H)=\left\{\sum_{x\in F}x:F\subset H, |F|\leq k\text{ is and nonempty}\right\}. \end{align*} $$
$$ \begin{align*} FS^{\leq k}(H)=\left\{\sum_{x\in F}x:F\subset H, |F|\leq k\text{ is and nonempty}\right\}. \end{align*} $$
We omit to mention colors when we are not interested in their number. There are plenty of results about the restricted Hindman’s theorems
![]() $\textrm {HT}^{\leq k}_r$
, see [Reference Carlucci3, Reference Carlucci4, Reference Dzhafarov, Jockusch, Solomon, Westrick, Day, Fellows, Greenberg, Khoussainov, Melnikov and Rosamond6]. However, even for such apparently weak theorems, we do not know much about their exact strength. For example, we do not know if
$\textrm {HT}^{\leq k}_r$
, see [Reference Carlucci3, Reference Carlucci4, Reference Dzhafarov, Jockusch, Solomon, Westrick, Day, Fellows, Greenberg, Khoussainov, Melnikov and Rosamond6]. However, even for such apparently weak theorems, we do not know much about their exact strength. For example, we do not know if
![]() $\mathrm {ACA}_{0}$
can prove any such restricted Hindman’s theorem, even the weakest
$\mathrm {ACA}_{0}$
can prove any such restricted Hindman’s theorem, even the weakest
![]() $\textrm {HT}^{\leq 2}_2$
. Meanwhile, the question of whether
$\textrm {HT}^{\leq 2}_2$
. Meanwhile, the question of whether
![]() $\textrm {HT}^{\leq 2}_2$
is provable in
$\textrm {HT}^{\leq 2}_2$
is provable in
![]() $\mathrm {ACA}_0$
, and whether it separates from
$\mathrm {ACA}_0$
, and whether it separates from
![]() $\mathrm {HT}$
is interestingly related to a combinatorial open question asked by Hindman, Leader, and Strauss in 2003 [Reference Hindman, Leader and Strauss10].
$\mathrm {HT}$
is interestingly related to a combinatorial open question asked by Hindman, Leader, and Strauss in 2003 [Reference Hindman, Leader and Strauss10].
In Section 2, we will prove the
![]() $\Delta _3^0$
-unsolvability for
$\Delta _3^0$
-unsolvability for
![]() $\textrm {HT}$
and
$\textrm {HT}$
and
![]() $\mathrm {HT}^{\leq 3}_2$
. In Section 3, we will prove the
$\mathrm {HT}^{\leq 3}_2$
. In Section 3, we will prove the
![]() $\Pi ^3_0$
-unsolvability for
$\Pi ^3_0$
-unsolvability for
![]() $\textrm {HT}$
with weak apartness (defined in Section 2). In Section 4, we will prove the
$\textrm {HT}$
with weak apartness (defined in Section 2). In Section 4, we will prove the
![]() $\Delta _3^0$
-unsolvability for
$\Delta _3^0$
-unsolvability for
![]() $\textrm {HT}^{\leq 3}$
and
$\textrm {HT}^{\leq 3}$
and
![]() $\Pi _3^0$
-unsolvability for
$\Pi _3^0$
-unsolvability for
![]() $\textrm {HT}$
without weak apartness. In Section 5, we will prove
$\textrm {HT}$
without weak apartness. In Section 5, we will prove
![]() $\Pi _3^0$
-unsolvability without weak apartness using only four colors.
$\Pi _3^0$
-unsolvability without weak apartness using only four colors.
2. Proof of
 $\Delta _3^0$
unsolvability
$\Delta _3^0$
unsolvability
In this section, we will construct a coloring function c in two colors such that any infinite
![]() $\Delta _3^0$
set is not a solution to c for
$\Delta _3^0$
set is not a solution to c for
![]() $\mathrm {HT}$
. First, we list some notations. Some of them are from Blass, Hirst, and Simpson’s paper [Reference Blass, Hirst and Simpson2], Hindman’s paper [Reference Hindman8, Reference Hindman9], and Carlucci’s paper [Reference Carlucci3].
$\mathrm {HT}$
. First, we list some notations. Some of them are from Blass, Hirst, and Simpson’s paper [Reference Blass, Hirst and Simpson2], Hindman’s paper [Reference Hindman8, Reference Hindman9], and Carlucci’s paper [Reference Carlucci3].
Definition 2.1.
-
1. We define two functions
 $\mu (x),\lambda (x)$
on
$\mu (x),\lambda (x)$
on
 $\mathbb {Z^+}$
as follows:
$\mathbb {Z^+}$
as follows:If
 $x=2^{n_0}+\dots +2^{n_k}\in \mathbb {Z^+}$
, where
$x=2^{n_0}+\dots +2^{n_k}\in \mathbb {Z^+}$
, where
 $n_0<\cdots <n_k\in \mathbb {N}$
, then
$n_0<\cdots <n_k\in \mathbb {N}$
, then
 $\mu (x)=n_k,\lambda (x)=n_0$
. If
$\mu (x)=n_k,\lambda (x)=n_0$
. If
 $x=2^{n_0}$
, then
$x=2^{n_0}$
, then
 $\mu (x)=\lambda (x)=n_0$
.
$\mu (x)=\lambda (x)=n_0$
. -
2. For two positive integers
 $x<y$
, we write that
$x<y$
, we write that
 $x\ll y$
or
$x\ll y$
or
 $y\gg x$
if
$y\gg x$
if
 $\mu (x)<\lambda (y)$
. A set A has apartness (or is with apartness; this concept origins from Hindman’s paper [Reference Hindman8], and this name apartness is from [Reference Carlucci3]) if for any
$\mu (x)<\lambda (y)$
. A set A has apartness (or is with apartness; this concept origins from Hindman’s paper [Reference Hindman8], and this name apartness is from [Reference Carlucci3]) if for any
 $x<y$
in A,
$x<y$
in A,
 $x\ll y$
. A number
$x\ll y$
. A number
 $x\gg Y$
for a set Y means that for any
$x\gg Y$
for a set Y means that for any
 $y\in Y$
,
$y\in Y$
,
 $x\gg y$
.
$x\gg y$
. -
3. For each natural number n, we define that
 $$ \begin{align*} B^n=\{x\in \mathbb{Z^+}:\mu(x)=n\}\text{ and }B^{\leq n}=\{x\in \mathbb{Z^+}: \mu(x)\leq n\}. \end{align*} $$
$$ \begin{align*} B^n=\{x\in \mathbb{Z^+}:\mu(x)=n\}\text{ and }B^{\leq n}=\{x\in \mathbb{Z^+}: \mu(x)\leq n\}. \end{align*} $$
-
4. A set A has weak apartness if: (1) For any natural number m,
 $B^m\cap A$
contains at most one element. (2) for any natural number l, there are at most two numbers x in A satisfying
$B^m\cap A$
contains at most one element. (2) for any natural number l, there are at most two numbers x in A satisfying
 $\lambda (x)=l$
; therefore, if a set A has weak apartness, then for any natural number L, there exists M such that for any
$\lambda (x)=l$
; therefore, if a set A has weak apartness, then for any natural number L, there exists M such that for any
 $x>M$
in A,
$x>M$
in A,
 $\lambda (x)>L$
.
$\lambda (x)>L$
.
In addition to the above definitions, for convenience, we also have some other conventions. 1. For a set A, we use
![]() $A(x)$
to denote its characteristic function. 2. We say that a coloring c or a construction of a coloring c kills a set A, or a set A is killed, if
$A(x)$
to denote its characteristic function. 2. We say that a coloring c or a construction of a coloring c kills a set A, or a set A is killed, if
![]() $FS(A)$
is not monochromatic (under c). 3. In this paper, all variables are natural numbers, any quantifier without specified range is over the set of natural numbers
$FS(A)$
is not monochromatic (under c). 3. In this paper, all variables are natural numbers, any quantifier without specified range is over the set of natural numbers
![]() $\mathbb {N}$
, and all intervals are intervals of natural numbers. For example,
$\mathbb {N}$
, and all intervals are intervals of natural numbers. For example,
![]() $\forall x \phi $
means that for any
$\forall x \phi $
means that for any
![]() $x\in \mathbb {N}$
,
$x\in \mathbb {N}$
,
![]() $\phi $
holds, and
$\phi $
holds, and
![]() $n\in (a,b),n\in (a,b],n\in [a,b)$
means that n is an integer between integers a and b. 4. Limit notations such as
$n\in (a,b),n\in (a,b],n\in [a,b)$
means that n is an integer between integers a and b. 4. Limit notations such as
![]() $\lim _x f(x)$
or
$\lim _x f(x)$
or
![]() $\lim \limits _{x}f(x)$
, mean:
$\lim \limits _{x}f(x)$
, mean:
![]() $\lim \limits _{x\rightarrow \infty }f(x)$
.
$\lim \limits _{x\rightarrow \infty }f(x)$
.
2.1. Strategy
A naive strategy is to set infinitely many requests
![]() $\langle x,y\rangle \in \mathbb {N}^2$
and each such request means that we let x be colored in one color, say Red, and let y be colored in another color, say Green. But this strategy does not succeed. Instead, we try a different approach using a new type of request. A request
$\langle x,y\rangle \in \mathbb {N}^2$
and each such request means that we let x be colored in one color, say Red, and let y be colored in another color, say Green. But this strategy does not succeed. Instead, we try a different approach using a new type of request. A request
![]() $\langle w,x\rangle $
means that
$\langle w,x\rangle $
means that
![]() $w+x$
and w need to have different colors. We must limit the number of requests we set. For example, if we set requests
$w+x$
and w need to have different colors. We must limit the number of requests we set. For example, if we set requests
![]() $\langle 4,2\rangle ,\langle 4,3\rangle $
, and
$\langle 4,2\rangle ,\langle 4,3\rangle $
, and
![]() $\langle 6,1\rangle $
, then because
$\langle 6,1\rangle $
, then because
![]() $4+2=6, 4+3=7,6+1=7$
, all three numbers
$4+2=6, 4+3=7,6+1=7$
, all three numbers
![]() $4,6,7$
need to have different colors, which contradicts the condition that c has only two colors.
$4,6,7$
need to have different colors, which contradicts the condition that c has only two colors.
Example 2.2. Consider a set of requests
![]() $\{\langle w,2^n\rangle :\lambda (w)>n\}$
. We want to find a coloring function
$\{\langle w,2^n\rangle :\lambda (w)>n\}$
. We want to find a coloring function
![]() $c:\mathbb {N}\rightarrow \{0,1\}$
such that for any two numbers w,n such that
$c:\mathbb {N}\rightarrow \{0,1\}$
such that for any two numbers w,n such that
![]() $\lambda (w)>n$
(i.e., w is divisible by
$\lambda (w)>n$
(i.e., w is divisible by
![]() $2^{n+1}$
), w and
$2^{n+1}$
), w and
![]() $w+2^n$
have different colors.
$w+2^n$
have different colors.
We can find a simple solution: let
![]() $c(w)$
be the number of digits
$c(w)$
be the number of digits
![]() $1$
mod 2 in the binary representation of w: for example,
$1$
mod 2 in the binary representation of w: for example,
![]() $c(2)=c(10_2)=1$
,
$c(2)=c(10_2)=1$
,
![]() $c(3)=c(11_2)=0$
,
$c(3)=c(11_2)=0$
,
![]() $c(4)=c(100_2)=1$
,
$c(4)=c(100_2)=1$
,
![]() $c(5)=c(101_2)=0$
and so on.
$c(5)=c(101_2)=0$
and so on.
We will construct a recursive function
![]() $R(n,w)$
from a recursive subset of
$R(n,w)$
from a recursive subset of
![]() $\mathbb {N}^2$
to
$\mathbb {N}^2$
to
![]() $\mathbb {N}$
to represent the desired request set: each pair
$\mathbb {N}$
to represent the desired request set: each pair
![]() $\langle w, R(n,w)\rangle $
will be a request. This function
$\langle w, R(n,w)\rangle $
will be a request. This function
![]() $R(n,w)$
will satisfy two conditions:
$R(n,w)$
will satisfy two conditions:
C1. There exists a recursive coloring function
![]() $c:\mathbb {N}\rightarrow \{0,1\}$
such that for any w and n, if
$c:\mathbb {N}\rightarrow \{0,1\}$
such that for any w and n, if
![]() $R(n,w)$
is defined, then
$R(n,w)$
is defined, then
![]() $c(w)\neq c(R(n,w)+w)$
.
$c(w)\neq c(R(n,w)+w)$
.
C2. For every infinite
![]() $\Delta _3^0$
set A with weak apartness, there exists
$\Delta _3^0$
set A with weak apartness, there exists
![]() $w\in FS(A)$
and n such that
$w\in FS(A)$
and n such that
![]() $R(n,w)$
is defined,
$R(n,w)$
is defined,
![]() $R(n,w)\in A$
and
$R(n,w)\in A$
and
![]() $R(n,w)+w\in FS(A)$
.
$R(n,w)+w\in FS(A)$
.
The following lemma provides a sufficient condition for
![]() $R(n,w)$
to satisfy C1.
$R(n,w)$
to satisfy C1.
Lemma 2.3. Let R be a function from a recursive subset of
![]() $\mathbb {N}^2$
to
$\mathbb {N}^2$
to
![]() $\mathbb {N}$
such that
$\mathbb {N}$
such that
![]() $R(n,w)\in B^n$
. There exists a coloring function
$R(n,w)\in B^n$
. There exists a coloring function
![]() $c:\mathbb {N}\rightarrow \{0,1\}$
recursive in R and its domain such that for any w and
$c:\mathbb {N}\rightarrow \{0,1\}$
recursive in R and its domain such that for any w and
![]() $n<\lambda (w)$
, if
$n<\lambda (w)$
, if
![]() $R(n,w)$
is defined, then
$R(n,w)$
is defined, then
Moreover, c is uniformly recursive in R and its domain: there exists a recursive functional
![]() $\Phi ^X$
such that
$\Phi ^X$
such that
![]() $\Phi ^{R\oplus \mathrm {dom}(R)}=c$
.
$\Phi ^{R\oplus \mathrm {dom}(R)}=c$
.
Proof Because the domain of
![]() $R(n,w)$
is recursive, first we extend R to the whole of
$R(n,w)$
is recursive, first we extend R to the whole of
![]() $\mathbb {N}^2$
: for
$\mathbb {N}^2$
: for
![]() $n,w$
,
$n,w$
,
![]() $R(n,w)$
has not been defined, let
$R(n,w)$
has not been defined, let
![]() $R(n,w)=2^n$
. The extended
$R(n,w)=2^n$
. The extended
![]() $R(n,w)$
is still a recursive function.
$R(n,w)$
is still a recursive function.
We construct the coloring function c stage by stage. At stage s, we color numbers in
![]() $B^s$
. For each s, we will create a graph with vertex set
$B^s$
. For each s, we will create a graph with vertex set
![]() $B^s$
and edges depending on the function
$B^s$
and edges depending on the function
![]() $R(n,w)$
so that this graph is a tree. So for any
$R(n,w)$
so that this graph is a tree. So for any
![]() $w_1,w_2\in B^s$
, there exists a unique path P from
$w_1,w_2\in B^s$
, there exists a unique path P from
![]() $w_1$
to
$w_1$
to
![]() $w_2$
.
$w_2$
.
Fix a stage s. For each
![]() $w\in B^s$
and
$w\in B^s$
and
![]() $n< \lambda (w)$
, We add one edge between
$n< \lambda (w)$
, We add one edge between
![]() $w+R(n,w)$
and w and call it
$w+R(n,w)$
and w and call it
![]() $e_{w,w+R(n,w)}$
. This graph does not contain any multiple edges or self-loops. We show that this graph is a tree by induction.
$e_{w,w+R(n,w)}$
. This graph does not contain any multiple edges or self-loops. We show that this graph is a tree by induction.
For every
![]() $w\in B^s$
and
$w\in B^s$
and
![]() $n<\lambda (w)$
, define the vertex set
$n<\lambda (w)$
, define the vertex set
and consider the corresponding induced subgraph. By definition,
![]() $T_{w_1,n_1}=T_{w_2,n_2}$
iff
$T_{w_1,n_1}=T_{w_2,n_2}$
iff
![]() $ \langle w_1,n_1\rangle =\langle w_2,n_2 \rangle $
; and if
$ \langle w_1,n_1\rangle =\langle w_2,n_2 \rangle $
; and if
![]() $n_1=n_2$
but
$n_1=n_2$
but
![]() $w_1\neq w_2$
, then
$w_1\neq w_2$
, then
![]() $T_{w_1,n_1},T_{w_2,n_2}$
are disjoint.
$T_{w_1,n_1},T_{w_2,n_2}$
are disjoint.
If we write integers in binary representation, then the vertex set
![]() $T_{w,n}$
looks like
$T_{w,n}$
looks like
where
![]() $w_sw_{s-1}\dots w_{n+1}$
is the highest
$w_sw_{s-1}\dots w_{n+1}$
is the highest
![]() $s-n$
many digits of w and it is the common part of all numbers in the vertex set
$s-n$
many digits of w and it is the common part of all numbers in the vertex set
![]() $T_{w,n}$
. All other digits of w are
$T_{w,n}$
. All other digits of w are
![]() $0$
. By definition, for
$0$
. By definition, for
![]() $n\geq 1$
,
$n\geq 1$
,
 $$ \begin{align*} T_{w,n}&=\{w+x:0\leq x<2^{n+1}\}\\ &=\{w+x:0\leq x<2^{n}\}\cup \{w+x:2^n\leq x<2^{n+1}\}\\ &=\{w+x:0\leq x<2^{n}\}\cup \{w+2^n+x:0\leq x<2^{n}\}\\ &=T_{w,n-1}\cup T_{w+2^n,n-1}. \end{align*} $$
$$ \begin{align*} T_{w,n}&=\{w+x:0\leq x<2^{n+1}\}\\ &=\{w+x:0\leq x<2^{n}\}\cup \{w+x:2^n\leq x<2^{n+1}\}\\ &=\{w+x:0\leq x<2^{n}\}\cup \{w+2^n+x:0\leq x<2^{n}\}\\ &=T_{w,n-1}\cup T_{w+2^n,n-1}. \end{align*} $$
The two sets
![]() $T_{w,n-1}$
and
$T_{w,n-1}$
and
![]() $T_{w+2^n,n-1}$
look like
$T_{w+2^n,n-1}$
look like
 $$ \begin{align*} T_{w,n-1}&=\{(w_sw_{s-1}\dots w_{n+1} 0 x_{n-1}\dots x_{0})_2:x_0,\dots,x_n\in\{0,1\}\}\\ T_{w+2^n,n-1}&=\{(w_sw_{s-1}\dots w_{n+1} 1 x_{n-1}\dots x_{0})_2:x_0,\dots,x_n\in\{0,1\}\}, \end{align*} $$
$$ \begin{align*} T_{w,n-1}&=\{(w_sw_{s-1}\dots w_{n+1} 0 x_{n-1}\dots x_{0})_2:x_0,\dots,x_n\in\{0,1\}\}\\ T_{w+2^n,n-1}&=\{(w_sw_{s-1}\dots w_{n+1} 1 x_{n-1}\dots x_{0})_2:x_0,\dots,x_n\in\{0,1\}\}, \end{align*} $$
where,
![]() $w_s,w_{s-1},\dots ,w_{n+1}$
are the first a few digits of w. They are disjoint. The induced subgraph of
$w_s,w_{s-1},\dots ,w_{n+1}$
are the first a few digits of w. They are disjoint. The induced subgraph of
![]() $T_{w,n}$
is equal to the union of the induced subgraphs of
$T_{w,n}$
is equal to the union of the induced subgraphs of
![]() $T_{w,n-1},T_{w+2^n,n-1}$
plus the edges between vertices in
$T_{w,n-1},T_{w+2^n,n-1}$
plus the edges between vertices in
![]() $T_{w,n-1}$
and vertices in
$T_{w,n-1}$
and vertices in
![]() $T_{w+2^n,n-1}$
. We claim that there exists exactly one edge between two vertex sets
$T_{w+2^n,n-1}$
. We claim that there exists exactly one edge between two vertex sets
![]() $T_{w,n-1},T_{w+2^n,n-1}$
.
$T_{w,n-1},T_{w+2^n,n-1}$
.
Suppose there is an edge
![]() $e'$
from
$e'$
from
![]() $w'\in T_{w,n-1}$
to
$w'\in T_{w,n-1}$
to
![]() $w'+R(n',w')\in T_{w+2^n,n-1}$
. Since
$w'+R(n',w')\in T_{w+2^n,n-1}$
. Since
![]() $\mu (R(n',w'))=n'<\lambda (w')$
by hypothesis on R and choice of n, if
$\mu (R(n',w'))=n'<\lambda (w')$
by hypothesis on R and choice of n, if
![]() $n'<n$
, then
$n'<n$
, then
![]() $w'+R(n',w')$
is still in
$w'+R(n',w')$
is still in
![]() $T_{w,n-1}$
; if
$T_{w,n-1}$
; if
![]() $n'>n$
, then
$n'>n$
, then
![]() $w'+R(n',w')$
is greater than all numbers in
$w'+R(n',w')$
is greater than all numbers in
![]() $T_{w+2^n,n-1}$
. Therefore,
$T_{w+2^n,n-1}$
. Therefore,
![]() $n'=n$
. Because
$n'=n$
. Because
![]() $n=n'<\lambda (w')$
,
$n=n'<\lambda (w')$
,
![]() $w'=w$
, otherwise
$w'=w$
, otherwise
![]() $w'$
is not in
$w'$
is not in
![]() $T_{w,n-1}$
. Therefore such edge is unique and the claim is true.
$T_{w,n-1}$
. Therefore such edge is unique and the claim is true.
We now show by induction on n that all induced graphs of
![]() $T_{w,n}$
are trees. For
$T_{w,n}$
are trees. For
![]() $n=0$
and any w such that
$n=0$
and any w such that
![]() $\lambda (w)>0$
,
$\lambda (w)>0$
,
![]() $T_{w,0}$
has a single vertex and the induced graph is a tree. For
$T_{w,0}$
has a single vertex and the induced graph is a tree. For
![]() $n>0$
, by the construction of edges, for any
$n>0$
, by the construction of edges, for any
![]() $w\in B^s$
that
$w\in B^s$
that
![]() $\lambda (w)>n$
, there is an edge
$\lambda (w)>n$
, there is an edge
![]() $w,w+R(n,w)$
between
$w,w+R(n,w)$
between
![]() $T_{w,n-1}$
and
$T_{w,n-1}$
and
![]() $T_{w+2^n,n-1}$
; because
$T_{w+2^n,n-1}$
; because
![]() $T_{w,n}$
is the union of two trees (induced graphs of
$T_{w,n}$
is the union of two trees (induced graphs of
![]() $T_{w,n-1}$
and
$T_{w,n-1}$
and
![]() $T_{w+2^n,n-1}$
) plus one edge between two trees, it is a tree. Finally, since
$T_{w+2^n,n-1}$
) plus one edge between two trees, it is a tree. Finally, since
![]() $B^s=T_{2^s,s-1}$
, the whole graph with
$B^s=T_{2^s,s-1}$
, the whole graph with
![]() $B^s$
as the vertex set is also a tree.
$B^s$
as the vertex set is also a tree.
We now define the coloring function c. Let
![]() $c(2^s)=0$
. For
$c(2^s)=0$
. For
![]() $w \in B^s$
other than
$w \in B^s$
other than
![]() $2^s$
, because the graph is a tree, we find the unique path P from
$2^s$
, because the graph is a tree, we find the unique path P from
![]() $2^{s}$
to w, and let
$2^{s}$
to w, and let
![]() $c(w)$
be the length of P mod 2. This definition is uniformly recursive in R.
$c(w)$
be the length of P mod 2. This definition is uniformly recursive in R.
Verification: Let
![]() $P_w$
be a path from
$P_w$
be a path from
![]() $2^s$
to w and
$2^s$
to w and
![]() $x=R(n,w)$
. If
$x=R(n,w)$
. If
![]() $w+x$
is a vertex in
$w+x$
is a vertex in
![]() $P_w$
, then it must be the vertex in
$P_w$
, then it must be the vertex in
![]() $P_w$
immediately preceding w, since otherwise there would be two paths from w to
$P_w$
immediately preceding w, since otherwise there would be two paths from w to
![]() $w+x$
. Then
$w+x$
. Then
![]() $c(w+x)\equiv |P_w|-1\ \mod 2$
which is not equal to
$c(w+x)\equiv |P_w|-1\ \mod 2$
which is not equal to
![]() $c(w)$
. If
$c(w)$
. If
![]() $w+x$
is not in the path, then the path
$w+x$
is not in the path, then the path
![]() $P_w$
plus
$P_w$
plus
![]() $e_{w,w+x}$
is a path from
$e_{w,w+x}$
is a path from
![]() $2^s$
to
$2^s$
to
![]() $w+x$
, and
$w+x$
, and
![]() $c(w+x)\equiv |P_w|+1\ \mod 2$
, which is not equal to
$c(w+x)\equiv |P_w|+1\ \mod 2$
, which is not equal to
![]() $c(w)$
. In both cases, we can see that
$c(w)$
. In both cases, we can see that
![]() $c(w) \neq c(w+x)$
, which completes the verification.
$c(w) \neq c(w+x)$
, which completes the verification.
Once we have Lemma 2.3, our task becomes to construct a function
![]() $R(n,w)$
defined on a recursive subset of
$R(n,w)$
defined on a recursive subset of
![]() $\{\langle n,w\rangle :n<\lambda (w)\}$
such that
$\{\langle n,w\rangle :n<\lambda (w)\}$
such that
![]() $R(n,w)\in B^n$
if defined, and satisfying the condition C2
$R(n,w)\in B^n$
if defined, and satisfying the condition C2
![]() $^*$
:
$^*$
:
C2
![]() $^*$
. For every infinite
$^*$
. For every infinite
![]() $\Delta _3^0$
set A with weak apartness, there exists
$\Delta _3^0$
set A with weak apartness, there exists
![]() $w\in FS(A)$
and
$w\in FS(A)$
and
![]() $n<\lambda (w)$
such that
$n<\lambda (w)$
such that
![]() $R(n,w)$
is defined and in A.
$R(n,w)$
is defined and in A.
The construction will use approximations of
![]() $\Delta _3^0$
sets. By recursion theory [Reference Soare14], a set A is
$\Delta _3^0$
sets. By recursion theory [Reference Soare14], a set A is
![]() $\Delta _3^0$
iff
$\Delta _3^0$
iff
![]() $A\leq _T \emptyset "$
, and
$A\leq _T \emptyset "$
, and
![]() $A\leq _T B'$
iff there exists a function
$A\leq _T B'$
iff there exists a function
![]() $\tilde {A}(x,k)\leq _T B$
such that
$\tilde {A}(x,k)\leq _T B$
such that
![]() $\lim _k \tilde {A}(x,k)=A$
. More precisely, we will use the following lemma.
$\lim _k \tilde {A}(x,k)=A$
. More precisely, we will use the following lemma.
Lemma 2.4. There exists a recursive list of total recursive functions
![]() $\{A_i(x,k,s)\}_{i\in \mathbb {N}}$
taking values in
$\{A_i(x,k,s)\}_{i\in \mathbb {N}}$
taking values in
![]() $\{0,1\}$
such that for any
$\{0,1\}$
such that for any
![]() $\Delta _3^0$
set A, there exists a function
$\Delta _3^0$
set A, there exists a function
![]() $A_i(x,k,s)$
in the list such that for any x,
$A_i(x,k,s)$
in the list such that for any x,
Proof If a set A is
![]() $\Delta _3^0$
, then
$\Delta _3^0$
, then
![]() $A\leq _T \emptyset "$
, and there exists a function
$A\leq _T \emptyset "$
, and there exists a function
![]() $\tilde {A}(x,k)\leq _T \emptyset '$
such that
$\tilde {A}(x,k)\leq _T \emptyset '$
such that
![]() $\lim _k \tilde {A}(x,k)=A(x)$
. Let
$\lim _k \tilde {A}(x,k)=A(x)$
. Let
![]() $\tilde {A}(x,k)=\Phi ^{\emptyset '}_i(x,k)$
, where
$\tilde {A}(x,k)=\Phi ^{\emptyset '}_i(x,k)$
, where
![]() $\Phi _i$
is the ith two variable recursive function with oracle. Consider
$\Phi _i$
is the ith two variable recursive function with oracle. Consider
![]() $\Phi _i^{\emptyset '[s]}(x,k)[s]$
. We will show that for every x,
$\Phi _i^{\emptyset '[s]}(x,k)[s]$
. We will show that for every x,
![]() $\lim _{k}\lim _s \Phi _i^{\emptyset '[s]}(x,k)[s]$
is defined and equal
$\lim _{k}\lim _s \Phi _i^{\emptyset '[s]}(x,k)[s]$
is defined and equal
![]() $A(x)$
.
$A(x)$
.
By definition, there exists
![]() $k_0$
such that for any
$k_0$
such that for any
![]() $k>k_0$
,
$k>k_0$
,
![]() $\tilde {A}(x,k)$
is defined and equal to
$\tilde {A}(x,k)$
is defined and equal to
![]() $A(x)$
, written as
$A(x)$
, written as
![]() $\tilde {A}(x,k)\downarrow =A(x)$
. Now for any number
$\tilde {A}(x,k)\downarrow =A(x)$
. Now for any number
![]() $k>k_0$
, we show that
$k>k_0$
, we show that
![]() $\lim _s\Phi _i^{\emptyset '[s]}(x,k)[s]=\tilde {A}(x,k)$
. Because
$\lim _s\Phi _i^{\emptyset '[s]}(x,k)[s]=\tilde {A}(x,k)$
. Because
![]() $\tilde {A}(x,k)=\Phi _i^{\emptyset '}(x,k)$
is defined, there exists s such that
$\tilde {A}(x,k)=\Phi _i^{\emptyset '}(x,k)$
is defined, there exists s such that
![]() $\Phi ^{\emptyset '[s]}(x,k)[s]\downarrow =\tilde {A}(x,k)$
and the use of
$\Phi ^{\emptyset '[s]}(x,k)[s]\downarrow =\tilde {A}(x,k)$
and the use of
![]() $\emptyset '$
in this computation will never change from stage s on. Hence for any
$\emptyset '$
in this computation will never change from stage s on. Hence for any
![]() $s'>s$
, this computation still holds and
$s'>s$
, this computation still holds and
![]() $\Phi ^{\emptyset '[s']}(x,k)[s']=\tilde {A}(x,k)$
. Therefore,
$\Phi ^{\emptyset '[s']}(x,k)[s']=\tilde {A}(x,k)$
. Therefore,
![]() $\lim _s\Phi ^{\emptyset '[s]}(x,k)[s]=\tilde {A}(x,k)$
and
$\lim _s\Phi ^{\emptyset '[s]}(x,k)[s]=\tilde {A}(x,k)$
and
![]() $\lim _{k}\lim _s \Phi _i^{\emptyset '[s]}(x,k)[s]=A(x)$
.
$\lim _{k}\lim _s \Phi _i^{\emptyset '[s]}(x,k)[s]=A(x)$
.
So we define the list as follows: for each number j, define the jth function in the list
if the value of right-hand side is
![]() $0$
or
$0$
or
![]() $1$
; otherwise
$1$
; otherwise
![]() $A_j(x,k,s)=0$
. This is a total recursive function and this list is also recursive.
$A_j(x,k,s)=0$
. This is a total recursive function and this list is also recursive.
Therefore, when discussing all
![]() $\Delta _3^0$
sets, we can focus on
$\Delta _3^0$
sets, we can focus on
![]() $\Delta _3^0$
sets in this list.
$\Delta _3^0$
sets in this list.
2.2. Strategy of killing one set
Assuming A is an infinite
![]() $\Delta _3^0$
set with weak apartness, we show how to kill A by constructing the function
$\Delta _3^0$
set with weak apartness, we show how to kill A by constructing the function
![]() $R(n,w)$
. If for this
$R(n,w)$
. If for this
![]() $R(n,w)$
, condition C2
$R(n,w)$
, condition C2
![]() $^*$
holds for set A, then, by Lemma 2.3, we can construct a coloring function c that kills the set A.
$^*$
holds for set A, then, by Lemma 2.3, we can construct a coloring function c that kills the set A.
Our strategy is to guess which number is in
![]() $A\cap B^n$
(by weak apartness,
$A\cap B^n$
(by weak apartness,
![]() $A\cap B^n$
contains at most one element) and let
$A\cap B^n$
contains at most one element) and let
![]() $R(n,w)$
be this element. We can use the approximation of A,
$R(n,w)$
be this element. We can use the approximation of A,
![]() $A(x,k,s)$
as a guessing function.
$A(x,k,s)$
as a guessing function.
We use a guessing function to construct the function
![]() $R(n,w)$
. For numbers
$R(n,w)$
. For numbers
![]() $n,w$
, we compute
$n,w$
, we compute
![]() $A(x,\lambda (w),\mu (w))$
for all
$A(x,\lambda (w),\mu (w))$
for all
![]() $x\in B^n$
and check if there exists any x in
$x\in B^n$
and check if there exists any x in
![]() $B^n$
such that
$B^n$
such that
which suggests that
![]() $x\in B^n\cap A$
; if such x exists, then we guess
$x\in B^n\cap A$
; if such x exists, then we guess
![]() $B^n\cap A\neq \emptyset $
and let
$B^n\cap A\neq \emptyset $
and let
![]() $R(n,w)$
be the minimal one among all such x; if such x does not exist, let
$R(n,w)$
be the minimal one among all such x; if such x does not exist, let
![]() $R(n,w)=2^{n+1}-1$
, i.e.:
$R(n,w)=2^{n+1}-1$
, i.e.:
We show that this construction kills set A. Because A is infinite, there exists n such that
![]() $B^n\cap A$
is nonempty. Let x be the unique element in
$B^n\cap A$
is nonempty. Let x be the unique element in
![]() $B^n\cap A$
. By Lemma 2.4, for any number y in
$B^n\cap A$
. By Lemma 2.4, for any number y in
![]() $B^n$
,
$B^n$
,
![]() $\lim _k\lim _s A(y,k,s)=A(y)$
. Because
$\lim _k\lim _s A(y,k,s)=A(y)$
. Because
![]() $B^n$
is finite,
$B^n$
is finite,
![]() $\lim _k\lim _s (A(\cdot ,k,s)\restriction B^n)=A(\cdot )\restriction B^n$
; for any natural numbers
$\lim _k\lim _s (A(\cdot ,k,s)\restriction B^n)=A(\cdot )\restriction B^n$
; for any natural numbers
![]() $k,s$
, if
$k,s$
, if
![]() $ A(\cdot ,k,s)\restriction B^n=A(\cdot )\restriction B^n$
, then
$ A(\cdot ,k,s)\restriction B^n=A(\cdot )\restriction B^n$
, then
![]() $A(x,k,s)=1$
and for any
$A(x,k,s)=1$
and for any
![]() $y\in B^n\setminus \{x\}$
,
$y\in B^n\setminus \{x\}$
,
![]() $A(y,k,s)=0$
.
$A(y,k,s)=0$
.
Now, look for a number K such that for any
![]() $k>K$
,
$k>K$
,
![]() $\lim _s (A(\cdot ,k,s)\restriction B^n)=A(\cdot )\restriction B^n$
, and choose a number
$\lim _s (A(\cdot ,k,s)\restriction B^n)=A(\cdot )\restriction B^n$
, and choose a number
![]() $w_1\in A$
such that
$w_1\in A$
such that
![]() $\lambda (w_1)$
is greater than K and n; let
$\lambda (w_1)$
is greater than K and n; let
![]() $k=\lambda (w_1)$
. Next, for the fixed number k, look for a number
$k=\lambda (w_1)$
. Next, for the fixed number k, look for a number
![]() $s_k$
such that for any
$s_k$
such that for any
![]() $s>s_k$
,
$s>s_k$
,
![]() $A(\cdot ,k,s)\restriction B^n=A(\cdot )\restriction B^n$
, and choose another number
$A(\cdot ,k,s)\restriction B^n=A(\cdot )\restriction B^n$
, and choose another number
![]() $w_2\gg w_1$
from A such that
$w_2\gg w_1$
from A such that
![]() $\mu (w_2)>s_k$
.
$\mu (w_2)>s_k$
.
Let
![]() $w=w_1+w_2$
, then
$w=w_1+w_2$
, then
![]() $\lambda (w)=\lambda (w_1)=k>K$
and
$\lambda (w)=\lambda (w_1)=k>K$
and
![]() $\mu (w)=\mu (w_2)>s_k$
. Combining all discussions above,
$\mu (w)=\mu (w_2)>s_k$
. Combining all discussions above,
![]() $A(\cdot ,\lambda (w),\mu (w))\restriction B^n=A(\cdot )\restriction B^n$
. This means
$A(\cdot ,\lambda (w),\mu (w))\restriction B^n=A(\cdot )\restriction B^n$
. This means
![]() $A(x,\lambda (w),\mu (w))=1$
while for any
$A(x,\lambda (w),\mu (w))=1$
while for any
![]() $y\in B^n\setminus \{x\}$
,
$y\in B^n\setminus \{x\}$
,
![]() $A(y,\lambda (w),\mu (w))=0$
. By the definition of function
$A(y,\lambda (w),\mu (w))=0$
. By the definition of function
![]() $R(n,w)$
,
$R(n,w)$
,
![]() $R(n,w_1+w_2)=x\in A$
. All three numbers
$R(n,w_1+w_2)=x\in A$
. All three numbers
![]() $x\ll w_1\ll w_2$
are in A. By Lemma 2.3, there exists a recursive function c such that
$x\ll w_1\ll w_2$
are in A. By Lemma 2.3, there exists a recursive function c such that
![]() $c(w_1+w_2)\neq c(x+w_1+w_2)$
where both
$c(w_1+w_2)\neq c(x+w_1+w_2)$
where both
![]() $w_1+w_2$
and
$w_1+w_2$
and
![]() $x+w_1+w_2$
are in
$x+w_1+w_2$
are in
![]() $FS(A)$
.
$FS(A)$
.
2.3. Strategy for killing infinitely many sets
The strategy of killing infinitely many sets is based on the strategy of killing a single set. Now, condition C2
![]() $^*$
, as defined earlier, becomes: for any
$^*$
, as defined earlier, becomes: for any
![]() $\Delta _3^0$
infinite set
$\Delta _3^0$
infinite set
![]() $A_i$
with weak apartness in the list of Lemma 2.4, there exist numbers
$A_i$
with weak apartness in the list of Lemma 2.4, there exist numbers
![]() $w\in FS(A_i)$
and
$w\in FS(A_i)$
and
![]() $n<\lambda (w)$
such that
$n<\lambda (w)$
such that
![]() $R(n,w)\in A_i$
. We will continue to use the construction of the previous subsection with one more step: first, we need to choose a set
$R(n,w)\in A_i$
. We will continue to use the construction of the previous subsection with one more step: first, we need to choose a set
![]() $A_i$
among all
$A_i$
among all
![]() $\Delta _3^0$
sets in the list of Lemma 2.4 by a priority argument, and then apply the construction introduced earlier. To do this, we first guess which
$\Delta _3^0$
sets in the list of Lemma 2.4 by a priority argument, and then apply the construction introduced earlier. To do this, we first guess which
![]() $A_i$
have nonempty intersection with
$A_i$
have nonempty intersection with
![]() $B^n$
, and then choose one such set among them. To use this argument, we need a function which guesses, for a number n and a set
$B^n$
, and then choose one such set among them. To use this argument, we need a function which guesses, for a number n and a set
![]() $A_i$
, whether
$A_i$
, whether
![]() $A_i\cap B^n$
is empty or not. For a set
$A_i\cap B^n$
is empty or not. For a set
![]() $A_i$
, a number w, and a number
$A_i$
, a number w, and a number
![]() $n<\lambda (w)$
, we check if there exists
$n<\lambda (w)$
, we check if there exists
![]() $x\in B^n$
such that
$x\in B^n$
such that
![]() $A_i(x,\lambda (w),\mu (w))=1$
and use a function
$A_i(x,\lambda (w),\mu (w))=1$
and use a function
![]() $a_i(n,k,s)$
to denote this check:
$a_i(n,k,s)$
to denote this check:
 $$ \begin{align*} a_i(n,k,s)=\max\{A_i(x,k,s):x\in B^n\}=\left\{\!\!\!\begin{array}{l} 1, \text{ if }\exists x\in B^n\ A_i(x,k,s)=1; \\ 0, \text{ otherwise.} \\ \end{array} \right. \end{align*} $$
$$ \begin{align*} a_i(n,k,s)=\max\{A_i(x,k,s):x\in B^n\}=\left\{\!\!\!\begin{array}{l} 1, \text{ if }\exists x\in B^n\ A_i(x,k,s)=1; \\ 0, \text{ otherwise.} \\ \end{array} \right. \end{align*} $$
Because
![]() $B^n=\{x:\mu (x)=n\}$
is finite, this function is also recursive and total. If
$B^n=\{x:\mu (x)=n\}$
is finite, this function is also recursive and total. If
![]() $a_i(n,\lambda (w),\mu (w))=1$
, which means that there exists a number
$a_i(n,\lambda (w),\mu (w))=1$
, which means that there exists a number
![]() $x\in B^n$
such that
$x\in B^n$
such that
![]() $A_i(x,\lambda (w),\mu (w))=1$
, then we guess
$A_i(x,\lambda (w),\mu (w))=1$
, then we guess
![]() $A_i\cap B^n$
is nonempty; otherwise, we guess
$A_i\cap B^n$
is nonempty; otherwise, we guess
![]() $A_i\cap B^n$
is empty.
$A_i\cap B^n$
is empty.
We cannot recursively list all infinite
![]() $\Delta _3^0$
sets, but by Proposition 2.4, we have a recursive list of some total recursive functions
$\Delta _3^0$
sets, but by Proposition 2.4, we have a recursive list of some total recursive functions
![]() $A_i(x,k,s)$
such that every
$A_i(x,k,s)$
such that every
![]() $\Delta _3^0$
set is represented in the list. This list contains approximations of all infinite
$\Delta _3^0$
set is represented in the list. This list contains approximations of all infinite
![]() $\Delta _3^0$
sets. However, some functions in the list may not correspond to an infinite
$\Delta _3^0$
sets. However, some functions in the list may not correspond to an infinite
![]() $\Delta _3^0$
set, a set with weak apartness or even a set.
$\Delta _3^0$
set, a set with weak apartness or even a set.
So we need to use some restrictions from Jockusch’s argument [Reference Jockusch12] for Ramsey’s theorem, which Blass, Hirst, and Simpson adapt to Hindman’s theorem [Reference Blass, Hirst and Simpson2]. During the construction, for any function
![]() $A_i(x,k,s)$
and any pair
$A_i(x,k,s)$
and any pair
![]() $k,s$
, we will choose at most
$k,s$
, we will choose at most
![]() $2^i$
many numbers
$2^i$
many numbers
![]() $n\in (i,s)$
and call them the candidates of
$n\in (i,s)$
and call them the candidates of
![]() $A_i$
for
$A_i$
for
![]() $k,s$
. For any
$k,s$
. For any
![]() $k,s$
, any set
$k,s$
, any set
![]() $A_i$
has at most
$A_i$
has at most
![]() $2^i$
many candidates. When defining
$2^i$
many candidates. When defining
![]() $R(n,w)$
, only if n is a candidate of
$R(n,w)$
, only if n is a candidate of
![]() $A_i$
for
$A_i$
for
![]() $k=\lambda (w),s=\mu (w)$
,
$k=\lambda (w),s=\mu (w)$
,
![]() $A_i$
may be chosen to apply the construction of killing one set.
$A_i$
may be chosen to apply the construction of killing one set.
2.4. Construction
We use the recursive list
![]() $\{A_i(x,k,s)\}_{i\in \mathbb {N}}$
from Lemma 2.4.
$\{A_i(x,k,s)\}_{i\in \mathbb {N}}$
from Lemma 2.4.
Part 1: For each
![]() $A_i(x,k,s)$
in the list, define
$A_i(x,k,s)$
in the list, define
![]() $a_i(n,k,s)=\max \{A_i(x,k,s):x\in B^n\}$
as mentioned earlier.
$a_i(n,k,s)=\max \{A_i(x,k,s):x\in B^n\}$
as mentioned earlier.
![]() $\langle a_i(n,k,s)\rangle _{i\in \mathbb {N}}$
is also a recursive list of total recursive functions. For each i and for each
$\langle a_i(n,k,s)\rangle _{i\in \mathbb {N}}$
is also a recursive list of total recursive functions. For each i and for each
![]() $k,s$
, define a candidate set
$k,s$
, define a candidate set
![]() $C_i(k,s)$
to be the set of first
$C_i(k,s)$
to be the set of first
![]() $2^i$
numbers
$2^i$
numbers
![]() $n\in (i,s)$
such that
$n\in (i,s)$
such that
![]() $a_i(n,k,s)=1$
. If there are not
$a_i(n,k,s)=1$
. If there are not
![]() $2^i$
many such numbers n, then let
$2^i$
many such numbers n, then let
![]() $C_i(k,s)$
be all
$C_i(k,s)$
be all
![]() $n\in (i,s)$
such that
$n\in (i,s)$
such that
![]() $a_i(n,k,s)=1$
. These sets
$a_i(n,k,s)=1$
. These sets
![]() $C_i(k,s)$
are uniformly recursive in
$C_i(k,s)$
are uniformly recursive in
![]() $i,k,s$
.
$i,k,s$
.
Part 2: For each
![]() $n,w$
such that
$n,w$
such that
![]() $n<\lambda (w)$
, compute the set
$n<\lambda (w)$
, compute the set
the index set of sets
![]() $A_i$
such that
$A_i$
such that
![]() $C_i(\lambda (w),\mu (w))$
contains n, which means that we guess
$C_i(\lambda (w),\mu (w))$
contains n, which means that we guess
![]() $A_i\cap B^n\neq \emptyset $
. Let
$A_i\cap B^n\neq \emptyset $
. Let
![]() $j=\min (\{i< n: n\in C_i(\lambda (w),\mu (w))\}\cup \{n\}))$
and
$j=\min (\{i< n: n\in C_i(\lambda (w),\mu (w))\}\cup \{n\}))$
and
as killing one set in previous subsection. This is the construction of function
![]() $R(n,w)$
.
$R(n,w)$
.
![]() $R(n,w)$
is a recursive function with recursive domain. By Lemma 2.3, we can construct a coloring function c uniformly recursive in
$R(n,w)$
is a recursive function with recursive domain. By Lemma 2.3, we can construct a coloring function c uniformly recursive in
![]() $R(n,w)$
that satisfies the condition C1: for any w and
$R(n,w)$
that satisfies the condition C1: for any w and
![]() $n<\lambda (w)$
,
$n<\lambda (w)$
,
![]() $c(w)\neq c(w+R(n,w))$
. The only remaining task is to verify condition C2
$c(w)\neq c(w+R(n,w))$
. The only remaining task is to verify condition C2
![]() $^*$
for
$^*$
for
![]() $R(n,w)$
.
$R(n,w)$
.
2.5. Verification
In this subsection, we show that the above construction satisfies condition C2
![]() $^*$
. By Proposition 2.4, every
$^*$
. By Proposition 2.4, every
![]() $\Delta _3^0$
set is contained in the list of Lemma 2.4, so we only need to consider sets in this list. We use
$\Delta _3^0$
set is contained in the list of Lemma 2.4, so we only need to consider sets in this list. We use
![]() $A_i$
to denote the set represented by
$A_i$
to denote the set represented by
![]() $A_i(x,k,s)$
if that set is defined. First, we have the following lemma.
$A_i(x,k,s)$
if that set is defined. First, we have the following lemma.
Lemma 2.5. Let
![]() $C_i(k,s)$
be the function in our construction. For any infinite
$C_i(k,s)$
be the function in our construction. For any infinite
![]() $\Delta _3^0$
set
$\Delta _3^0$
set
![]() $A_i$
with weak apartness, there exists a finite set
$A_i$
with weak apartness, there exists a finite set
![]() $C_i$
of size
$C_i$
of size
![]() $2^i$
such that
$2^i$
such that
![]() $\lim _k\lim _sC_i(k,s)\downarrow =C_i$
.
$\lim _k\lim _sC_i(k,s)\downarrow =C_i$
.
Proof Because
![]() $A_i$
is infinite and has weak apartness, there are infinitely many
$A_i$
is infinite and has weak apartness, there are infinitely many
![]() $n>i$
such that
$n>i$
such that
![]() $A_i\cap B^n$
is nonempty. Let N be the
$A_i\cap B^n$
is nonempty. Let N be the
![]() $2^i$
th such n.
$2^i$
th such n.
By definition, for any x in
![]() $B^{\leq N}$
,
$B^{\leq N}$
,
![]() $\lim _{k}\lim _s A_i(x,k,s)=A_i(x)$
. Because
$\lim _{k}\lim _s A_i(x,k,s)=A_i(x)$
. Because
![]() $B^{\leq N}$
is finite, by the properties of the limit operation, we also have
$B^{\leq N}$
is finite, by the properties of the limit operation, we also have
Hence for any sufficiently large k, there exists
![]() $s_k$
such that for any
$s_k$
such that for any
![]() $s>s_k$
and every
$s>s_k$
and every
![]() $n\leq N$
,
$n\leq N$
,
![]() $a_i(n,k,s)=\max \{A_i(x,k,s):x\in B^n\}=\max \{A(x):x\in B^n \}$
. This means that, for
$a_i(n,k,s)=\max \{A_i(x,k,s):x\in B^n\}=\max \{A(x):x\in B^n \}$
. This means that, for
![]() $n\leq N$
,
$n\leq N$
,
![]() $a_i(n,k,s)=1$
iff
$a_i(n,k,s)=1$
iff
![]() $B^n\cap A_i$
is nonempty. Because N is the
$B^n\cap A_i$
is nonempty. Because N is the
![]() $2^i$
th number
$2^i$
th number
![]() $n>i$
such that
$n>i$
such that
![]() $B^n\cap A_i$
is nonempty, there exists
$B^n\cap A_i$
is nonempty, there exists
![]() $2^i$
numbers
$2^i$
numbers
![]() $n\leq N$
greater than i such that
$n\leq N$
greater than i such that
![]() $B^n\cap A_i$
is nonempty and hence
$B^n\cap A_i$
is nonempty and hence
![]() $a_i(n,k,s)=1$
. By definition,
$a_i(n,k,s)=1$
. By definition,
![]() $C_i(k,s)$
is the set of first
$C_i(k,s)$
is the set of first
![]() $2^i$
elements
$2^i$
elements
![]() $n\in (i,s)$
such that
$n\in (i,s)$
such that
![]() $a_i(n,k,s)=1$
; hence for those k and s,
$a_i(n,k,s)=1$
; hence for those k and s,
![]() $C_i(k,s)$
is equal to the set of first
$C_i(k,s)$
is equal to the set of first
![]() $2^i$
number
$2^i$
number
![]() $n>i$
such that
$n>i$
such that
![]() $B^n\cap A_i\neq \emptyset $
.
$B^n\cap A_i\neq \emptyset $
.
So we can conclude that, for any sufficiently large k, there exists
![]() $s_k$
such that for any
$s_k$
such that for any
![]() $s>s_k$
,
$s>s_k$
,
![]() $C_i(k,s)$
exactly contains first
$C_i(k,s)$
exactly contains first
![]() $2^i$
number
$2^i$
number
![]() $n>i$
such that
$n>i$
such that
![]() $B^n\cap A_i\neq \emptyset $
. This means
$B^n\cap A_i\neq \emptyset $
. This means
![]() $\lim _{k}\lim _s C_i(k,s)\downarrow =C_i$
for a fixed set
$\lim _{k}\lim _s C_i(k,s)\downarrow =C_i$
for a fixed set
![]() $C_i$
.
$C_i$
.
Next, we have the following lemma:
Lemma 2.6. Let
![]() $R(n,k)$
be the function in our construction. For any
$R(n,k)$
be the function in our construction. For any
![]() $\Delta _3^0$
infinite set
$\Delta _3^0$
infinite set
![]() $A_i$
with weak apartness, there exists a finite set
$A_i$
with weak apartness, there exists a finite set
![]() $X_i\subset A_i$
such that
$X_i\subset A_i$
such that
Proof Consider limits
![]() $\lim _k\lim _sC_i(k,s)\downarrow =C_i$
and
$\lim _k\lim _sC_i(k,s)\downarrow =C_i$
and
![]() $\lim _{k}\lim _s A_i(\cdot ,k,s)\restriction B^{\leq N}=A_i(\cdot )\restriction B^{\leq N}$
in the proof of Lemma 2.5 and let
$\lim _{k}\lim _s A_i(\cdot ,k,s)\restriction B^{\leq N}=A_i(\cdot )\restriction B^{\leq N}$
in the proof of Lemma 2.5 and let
![]() $X_i=\cup _{n\in C_i}B^n\cap A_i$
. Using these two limits, there exists a number K such that for any
$X_i=\cup _{n\in C_i}B^n\cap A_i$
. Using these two limits, there exists a number K such that for any
![]() $k>K$
, there exists a number
$k>K$
, there exists a number
![]() $s_k$
such that for any
$s_k$
such that for any
![]() $s>s_k$
,
$s>s_k$
,
![]() $C_i(k,s)=C_i$
and
$C_i(k,s)=C_i$
and
![]() $A_i(\cdot ,k,s)\restriction B^{\leq N}=A_i(\cdot )\restriction B^{\leq N}$
. We show that if for numbers
$A_i(\cdot ,k,s)\restriction B^{\leq N}=A_i(\cdot )\restriction B^{\leq N}$
. We show that if for numbers
![]() $k,s$
, these two equations hold, then for any w such that
$k,s$
, these two equations hold, then for any w such that
![]() $k=\lambda (w),s=\mu (w)$
, there exists
$k=\lambda (w),s=\mu (w)$
, there exists
![]() $x\in X_i$
such that
$x\in X_i$
such that
![]() $R(\mu (x),w)=x$
and therefore this lemma is true.
$R(\mu (x),w)=x$
and therefore this lemma is true.
We claim that for these
![]() $k,s$
, for at least one
$k,s$
, for at least one
![]() $n\in C_i(k,s)=C_i$
,
$n\in C_i(k,s)=C_i$
,
By definition, for any
![]() $j<i$
,
$j<i$
,
![]() $|C_j(k,s)|\leq 2^j$
. So
$|C_j(k,s)|\leq 2^j$
. So
![]() $|\cup _{j<i}C_j(k,s)|<2^i$
. If this claim is not true, then for every
$|\cup _{j<i}C_j(k,s)|<2^i$
. If this claim is not true, then for every
![]() $n\in C_i(k,s)$
, there exists
$n\in C_i(k,s)$
, there exists
![]() $j<i$
such that
$j<i$
such that
![]() $n\in C_j(k,s)$
. This means that
$n\in C_j(k,s)$
. This means that
![]() $\cup _{j<i}C_j(k,s)\supseteq C_i(k,s)$
, which is impossible because
$\cup _{j<i}C_j(k,s)\supseteq C_i(k,s)$
, which is impossible because
![]() $|\cup _{j<i}C_j(k,s)|<2^i=|C_i(k,s)|$
. So the claim is true.
$|\cup _{j<i}C_j(k,s)|<2^i=|C_i(k,s)|$
. So the claim is true.
Let
![]() $n\in C_i$
be a number such that
$n\in C_i$
be a number such that
![]() $i=\min (\{j<n: n\in C_j(k,s)\}\cup \{n\})).$
For any w such that
$i=\min (\{j<n: n\in C_j(k,s)\}\cup \{n\})).$
For any w such that
![]() $\lambda (w)=k\wedge \mu (w)=s$
, by definition,
$\lambda (w)=k\wedge \mu (w)=s$
, by definition,
Because for
![]() $k,s$
,
$k,s$
,
![]() $A_i(x,k,s)=A_i(x)$
for all
$A_i(x,k,s)=A_i(x)$
for all
![]() $x\in B^n$
,
$x\in B^n$
,
![]() $\min \{x\in B^n: A_i(x,k,s)=1\}$
is defined and is just the unique element in
$\min \{x\in B^n: A_i(x,k,s)=1\}$
is defined and is just the unique element in
![]() $B^n\cap A_i$
. Hence
$B^n\cap A_i$
. Hence
![]() $R(n,w)$
is the unique element in
$R(n,w)$
is the unique element in
![]() $B^n\cap A_i$
and is in
$B^n\cap A_i$
and is in
![]() $X_i$
.
$X_i$
.
So for those
![]() $k,s$
such that
$k,s$
such that
![]() $C_i(k,s)=C_i$
and
$C_i(k,s)=C_i$
and
![]() $A_i(\cdot ,k,s)\restriction B^{\leq N}=A_i(\cdot )\restriction B^{\leq N}$
, for any w such that
$A_i(\cdot ,k,s)\restriction B^{\leq N}=A_i(\cdot )\restriction B^{\leq N}$
, for any w such that
![]() $\lambda (w)=k,\mu (w)=s$
, there exists
$\lambda (w)=k,\mu (w)=s$
, there exists
![]() $x\in X_i$
such that
$x\in X_i$
such that
![]() $R(\mu (x),w)=x$
. This finishes the proof.
$R(\mu (x),w)=x$
. This finishes the proof.
Now we can get the following result.
Theorem 2.7. There exists a recursive coloring function c such that for any infinite
![]() $\Delta _3^0$
set A with weak apartness, there exist
$\Delta _3^0$
set A with weak apartness, there exist
![]() $x\ll w_1\ll w_2$
in A such that
$x\ll w_1\ll w_2$
in A such that
Hence
![]() $FS^{\leq 3}(A)$
is not monochromatic under c.
$FS^{\leq 3}(A)$
is not monochromatic under c.
Proof Choose the coloring function c in our construction. For an infinite
![]() $\Delta _3^0$
set A with weak apartness, there exists a set
$\Delta _3^0$
set A with weak apartness, there exists a set
![]() $A_i$
in the list of Lemma 2.4 such that
$A_i$
in the list of Lemma 2.4 such that
![]() $A=A_i$
. We apply Lemma 2.6 to
$A=A_i$
. We apply Lemma 2.6 to
![]() $A_i$
and get
$A_i$
and get
![]() $X_i\subseteq A_i$
and K.
$X_i\subseteq A_i$
and K.
Choose a sufficiently large number
![]() $w_1\gg X_i$
in
$w_1\gg X_i$
in
![]() $A_i$
such that
$A_i$
such that
![]() $\lambda (w_1)>K$
; let
$\lambda (w_1)>K$
; let
![]() $k=\lambda (w_1)$
. For this fixed k, find
$k=\lambda (w_1)$
. For this fixed k, find
![]() $s_k$
by Lemma 2.6 and choose a sufficiently large
$s_k$
by Lemma 2.6 and choose a sufficiently large
![]() $w_2\gg w_1$
in
$w_2\gg w_1$
in
![]() $A_i$
such that
$A_i$
such that
![]() $\mu (w_2)>s_k$
; let
$\mu (w_2)>s_k$
; let
![]() $s=\mu (w_2)$
. Because
$s=\mu (w_2)$
. Because
![]() $w_2\gg w_1$
,
$w_2\gg w_1$
,
![]() $\lambda (w_1+w_2)=\lambda (w_1)=k,\mu (w_1+w_2)=\mu (w_2)=s$
. Hence by Lemma 2.6, there exists a number
$\lambda (w_1+w_2)=\lambda (w_1)=k,\mu (w_1+w_2)=\mu (w_2)=s$
. Hence by Lemma 2.6, there exists a number
![]() $x\in X_i$
such that
$x\in X_i$
such that
![]() $R(\mu (x),w_1+w_2)=x$
. By the construction and Lemma 2.3,
$R(\mu (x),w_1+w_2)=x$
. By the construction and Lemma 2.3,
![]() $c(w_1+w_2)\neq c(x+w_1+w_2)$
.
$c(w_1+w_2)\neq c(x+w_1+w_2)$
.
Theorem 2.7 shows that there exists a recursive coloring function c such that for any infinite
![]() $\Delta _3^0$
set A with weak apartness,
$\Delta _3^0$
set A with weak apartness,
![]() $FS^{\leq 3}(A)$
is not monochromatic. This theorem is close to our aim, except the requirement of weak apartness. We can use the following fact proved by Hindman:
$FS^{\leq 3}(A)$
is not monochromatic. This theorem is close to our aim, except the requirement of weak apartness. We can use the following fact proved by Hindman:
Lemma 2.8 [Reference Hindman9].
For any infinite set A, there exists an infinite set
![]() $B\leq _T A$
such that B has apartness and
$B\leq _T A$
such that B has apartness and
![]() $FS(B)\subseteq FS(A)$
.
$FS(B)\subseteq FS(A)$
.
So for the same coloring function c in Theorem 2.7, if it has any infinite
![]() $\Delta _3^0$
solution A, then A can compute an infinite solution B with apartness and hence weak apartness. Since A is
$\Delta _3^0$
solution A, then A can compute an infinite solution B with apartness and hence weak apartness. Since A is
![]() $\Delta _3^0$
and
$\Delta _3^0$
and
![]() $B\leq _T A$
, B is also
$B\leq _T A$
, B is also
![]() $\Delta _3^0$
. However, this is impossible. Now we have achieved our aim for this section:
$\Delta _3^0$
. However, this is impossible. Now we have achieved our aim for this section:
Theorem 2.9. There exists a recursive coloring function c without any
![]() $\Delta _3^0$
solution for Hindman’s theorem.
$\Delta _3^0$
solution for Hindman’s theorem.
Moreover, we can use Lemma 2.7 and nearby propositions from the paper of Carlucci et al. [Reference Carlucci, Kołodziejczyk, Lepore and Zdanowski5]. From these results, we know that for any n, for any recursive coloring function c of k many colors, there exists a recursive coloring function d of many
![]() $2k$
colors such that any solution B to d for
$2k$
colors such that any solution B to d for
![]() $\mathrm {HT}^{\leq n}$
can compute a solution A to c for
$\mathrm {HT}^{\leq n}$
can compute a solution A to c for
![]() $\mathrm {HT}^{\leq n}$
with apartness.
$\mathrm {HT}^{\leq n}$
with apartness.
Therefore, applying these results to our coloring function c, we get a coloring function d of four colors. Then if d has a
![]() $\Delta _3^0$
solution for
$\Delta _3^0$
solution for
![]() $\mathrm {HT}^{\leq 3}$
, c will also have a
$\mathrm {HT}^{\leq 3}$
, c will also have a
![]() $\Delta _3^0$
solution for
$\Delta _3^0$
solution for
![]() $\mathrm {HT}^{\leq 3}$
with apartness, which is impossible. Hence we can get the following theorem:
$\mathrm {HT}^{\leq 3}$
with apartness, which is impossible. Hence we can get the following theorem:
Theorem 2.10. There exists a recursive coloring function d of four colors without any
![]() $\Delta _3^0$
solution for
$\Delta _3^0$
solution for
![]() $\mathrm {HT}^{\leq 3}$
.
$\mathrm {HT}^{\leq 3}$
.
3. Proof of
 $\Pi _3^0$
unsolvability with weak apartness
$\Pi _3^0$
unsolvability with weak apartness
3.1. General preparation
To prove the
![]() $\Pi ^0_3$
case of unsolvability, we will use more than one function similar to
$\Pi ^0_3$
case of unsolvability, we will use more than one function similar to
![]() $R(n,w)$
, denoted as
$R(n,w)$
, denoted as
![]() $R,Q$
. In addition, we need to generalize Lemma 2.3:
$R,Q$
. In addition, we need to generalize Lemma 2.3:
Lemma 3.1. Let
![]() $r>1$
and
$r>1$
and
![]() $R(n,w)$
be a function with recursive domain such that
$R(n,w)$
be a function with recursive domain such that
![]() $R(n,w)\in B^n$
if it is defined. There exists a coloring function
$R(n,w)\in B^n$
if it is defined. There exists a coloring function
![]() $c:\mathbb {N}\rightarrow r$
uniformly recursive in R such that for any w and any
$c:\mathbb {N}\rightarrow r$
uniformly recursive in R such that for any w and any
![]() $n<\lambda (w)$
, if
$n<\lambda (w)$
, if
![]() $R(n,w)$
is defined, then
$R(n,w)$
is defined, then
Proof This proof is very similar to the proof of Lemma 2.3. Just like in Lemma 2.3, we start by extending the domain of function R to whole
![]() $\mathbb {N}^2$
.
$\mathbb {N}^2$
.
For each number s, we create a graph with vertex set
![]() $B^s$
as in Lemma 2.3. As shown in Lemma 2.3, this graph is a tree: there exists a unique path from one vertex to another.
$B^s$
as in Lemma 2.3. As shown in Lemma 2.3, this graph is a tree: there exists a unique path from one vertex to another.
Definition of the coloring: Let
![]() $c(2^s)=0$
. For another vertex w, since the graph is a tree, find the unique path P from
$c(2^s)=0$
. For another vertex w, since the graph is a tree, find the unique path P from
![]() $2^{s}$
to w. Even though the graph is undirected, we will still note the direction of this path, since it allows us to keep track of the order in which vertices are visited. An edge
$2^{s}$
to w. Even though the graph is undirected, we will still note the direction of this path, since it allows us to keep track of the order in which vertices are visited. An edge
![]() $e_{w',w'+R(n',w')}$
in the path is considered a positive edge if the direction from
$e_{w',w'+R(n',w')}$
in the path is considered a positive edge if the direction from
![]() $w'$
to
$w'$
to
![]() $w'+R(n',w')$
is the same as the direction from
$w'+R(n',w')$
is the same as the direction from
![]() $2^{s}$
to w, and negative otherwise. We count the number of positive edges as a and the numbers of negative edges as b. We then let the color of w be
$2^{s}$
to w, and negative otherwise. We count the number of positive edges as a and the numbers of negative edges as b. We then let the color of w be
![]() $a-b\ \mod r$
. This process is uniformly recursive in R.
$a-b\ \mod r$
. This process is uniformly recursive in R.
Verification: Similar to Lemma 2.3, let
![]() $P_w$
be the unique path from
$P_w$
be the unique path from
![]() $2^s$
to w, and
$2^s$
to w, and
![]() $x=R(n,w)$
. If
$x=R(n,w)$
. If
![]() $w+x$
is a vertex in
$w+x$
is a vertex in
![]() $P_w$
, then it must be the vertex in
$P_w$
, then it must be the vertex in
![]() $P_w$
immediately preceding w; and because the direction of edge
$P_w$
immediately preceding w; and because the direction of edge
![]() $e_{w,w+x}$
is from w to
$e_{w,w+x}$
is from w to
![]() $w+x$
,
$w+x$
,
![]() $P_w$
is
$P_w$
is
![]() $P_{w+x}$
plus a negative direction edge. So
$P_{w+x}$
plus a negative direction edge. So
![]() $c(w)\equiv c(x+w)-1\ \mod r$
. If
$c(w)\equiv c(x+w)-1\ \mod r$
. If
![]() $w+x$
is not in the path, then the path obtained by adding the edge
$w+x$
is not in the path, then the path obtained by adding the edge
![]() $e_{w,w+x}$
to
$e_{w,w+x}$
to
![]() $P_w$
is a path from
$P_w$
is a path from
![]() $2^s$
to
$2^s$
to
![]() $w+x$
; because the direction of edge
$w+x$
; because the direction of edge
![]() $e_{w,w+x}$
is from w to
$e_{w,w+x}$
is from w to
![]() $w+x$
,
$w+x$
,
![]() $P_{w+x}$
is
$P_{w+x}$
is
![]() $P_{w}$
plus a positive direction edge; so
$P_{w}$
plus a positive direction edge; so
![]() $c(w)+1\equiv c(x+w)\ \mod r$
. In either case, we have
$c(w)+1\equiv c(x+w)\ \mod r$
. In either case, we have
![]() $c(w)+1\equiv c(x+w)\ \mod r$
.
$c(w)+1\equiv c(x+w)\ \mod r$
.
We will use two special forms of this lemma. The first special form is when
![]() $r=2$
, it corresponds to Lemma 2.3. The second special form is when the function
$r=2$
, it corresponds to Lemma 2.3. The second special form is when the function
![]() $R(n,w)$
only depends on
$R(n,w)$
only depends on
![]() $\lambda (w)$
,
$\lambda (w)$
,
![]() $\mu (w)$
in addition to n: for example, the function in the last section,
$\mu (w)$
in addition to n: for example, the function in the last section,
For
![]() $w_1\neq w_2$
, if
$w_1\neq w_2$
, if
![]() $\lambda (w_1)=\lambda (w_2)$
and
$\lambda (w_1)=\lambda (w_2)$
and
![]() $\mu (w_1)=\mu (w_2)$
, then
$\mu (w_1)=\mu (w_2)$
, then
![]() $R(n,w_1)=R(n,w_2)$
. In this case, we treat these functions as three-variable functions like
$R(n,w_1)=R(n,w_2)$
. In this case, we treat these functions as three-variable functions like
![]() $R(n,k,s), Q(n,k,s):$
$R(n,k,s), Q(n,k,s):$
Corollary 1. Let
![]() $r>1$
and Q be a function from a recursive subset of
$r>1$
and Q be a function from a recursive subset of
![]() $\mathbb {N}^3$
to
$\mathbb {N}^3$
to
![]() $\mathbb {N}$
such that
$\mathbb {N}$
such that
![]() $Q(n,k,s)\in B^n$
. There exists a coloring function
$Q(n,k,s)\in B^n$
. There exists a coloring function
![]() $c:\mathbb {N}\rightarrow r$
uniformly recursive in Q such that for any w and
$c:\mathbb {N}\rightarrow r$
uniformly recursive in Q such that for any w and
![]() $n<\lambda (w)$
, if
$n<\lambda (w)$
, if
![]() $Q(n,\lambda (w),\mu (w))$
is defined, then:
$Q(n,\lambda (w),\mu (w))$
is defined, then:
![]() $\ c(w+Q(n,\lambda (w),\mu (w)))\equiv c(w)+1\ \mod r.$
$\ c(w+Q(n,\lambda (w),\mu (w)))\equiv c(w)+1\ \mod r.$
Similar to last section, we need to choose a list of approximation of
![]() $\Pi _3^0$
sets. By definition, every
$\Pi _3^0$
sets. By definition, every
![]() $\Pi _3^0$
set A can be represented as
$\Pi _3^0$
set A can be represented as
![]() $x\in A\leftrightarrow \forall y\ \Phi (x,y)$
by a
$x\in A\leftrightarrow \forall y\ \Phi (x,y)$
by a
![]() $\Sigma _2^0$
formula
$\Sigma _2^0$
formula
![]() $\Phi (x,y)$
. By recursion theory [Reference Soare14], there exists a total recursive function
$\Phi (x,y)$
. By recursion theory [Reference Soare14], there exists a total recursive function
![]() $g(i,x,y)$
such that if
$g(i,x,y)$
such that if
![]() $\Phi _i(x,y)$
is the ith
$\Phi _i(x,y)$
is the ith
![]() $\Sigma _2^0$
formula, then
$\Sigma _2^0$
formula, then
![]() $\Phi _i(x,y)$
holds iff
$\Phi _i(x,y)$
holds iff
![]() $W_{g(i,x,y)}$
, the
$W_{g(i,x,y)}$
, the
![]() $g(i,x,y)$
th r.e. set. And this is equivalent to the fact that
$g(i,x,y)$
th r.e. set. And this is equivalent to the fact that
![]() $\lim _{s} |W_{g(i,x,y),s}|$
is finite, where
$\lim _{s} |W_{g(i,x,y),s}|$
is finite, where
![]() $W_{g(i,x,y),s}$
is the sth stage of
$W_{g(i,x,y),s}$
is the sth stage of
![]() $W_{g(i,x,y)}$
and is a recursive finite set.
$W_{g(i,x,y)}$
and is a recursive finite set.
So we consider a function
the max value of sizes of
![]() $W_{g(i,x,y')}$
at stage s for all
$W_{g(i,x,y')}$
at stage s for all
![]() $y'\leq y$
. If
$y'\leq y$
. If
![]() $x\in A$
, then because for any y,
$x\in A$
, then because for any y,
![]() $W_{g(i,x,y)}$
is finite,
$W_{g(i,x,y)}$
is finite,
![]() $F(i,x,y,s)\leq \max _{y'\leq y} |W_{g(i,x,y'),s}|$
and hence
$F(i,x,y,s)\leq \max _{y'\leq y} |W_{g(i,x,y'),s}|$
and hence
![]() $\lim _s F(i,x,y,s)$
exists and is finite; if
$\lim _s F(i,x,y,s)$
exists and is finite; if
![]() $x\notin A$
, then there exists
$x\notin A$
, then there exists
![]() $y_0$
such that
$y_0$
such that
![]() $|W_{g(i,x,y_0)}|=\infty $
and
$|W_{g(i,x,y_0)}|=\infty $
and
![]() $\lim _s |W_{g(i,x,y_0),s}|=\infty $
, so for any
$\lim _s |W_{g(i,x,y_0),s}|=\infty $
, so for any
![]() $y\geq y_0$
,
$y\geq y_0$
,
![]() $\lim _s F(i,x,y,s)=\infty $
. We collect these observations in the following lemma:
$\lim _s F(i,x,y,s)=\infty $
. We collect these observations in the following lemma:
Lemma 3.2. There exists a total recursive function
![]() $F(i,x,y,s)$
such that:
$F(i,x,y,s)$
such that:
-
1. The function
 $F(i,x,y,s)$
is non-decreasing with respect to y and s separately. Therefore for any
$F(i,x,y,s)$
is non-decreasing with respect to y and s separately. Therefore for any
 $i,x$
and y, the limit
$i,x$
and y, the limit
 $\lim _s F(i,x,y,s)$
is defined
$\lim _s F(i,x,y,s)$
is defined
 $($
can be infinite
$($
can be infinite
 $)$
and this limit is non-decreasing with respect to y.
$)$
and this limit is non-decreasing with respect to y. -
2. For each i, let
 $A_i=\{x:\forall y\ \lim _s F(i,x,y,s)\text { is finite}\}$
. Then
$A_i=\{x:\forall y\ \lim _s F(i,x,y,s)\text { is finite}\}$
. Then
 $A_i$
is a
$A_i$
is a
 $\Pi _3^0$
set. Moreover,
$\Pi _3^0$
set. Moreover,
 $A_i^c=\{x:\exists y_0 \forall y>y_0\ \lim _s F(i,x,y,s)\text { is infinite}\}$
$A_i^c=\{x:\exists y_0 \forall y>y_0\ \lim _s F(i,x,y,s)\text { is infinite}\}$
-
3. For any
 $\Pi _3^0$
set A, there exists i such that
$\Pi _3^0$
set A, there exists i such that
 $A=A_i$
, where
$A=A_i$
, where
 $A_i$
is defined as in 2.
$A_i$
is defined as in 2.
Therefore, the function
![]() $F(i,x,y,s)$
defines a list
$F(i,x,y,s)$
defines a list
![]() $\langle A_i\rangle _{i\in \mathbb {N}}$
of
$\langle A_i\rangle _{i\in \mathbb {N}}$
of
![]() $\Pi ^0_3$
sets that includes all
$\Pi ^0_3$
sets that includes all
![]() $\Pi _3^0$
sets (finite and infinite, with apartness and without apartness).
$\Pi _3^0$
sets (finite and infinite, with apartness and without apartness).
3.2. Strategy
As in the
![]() $\Delta _3^0$
section, to define the recursive coloring function c, we will construct a recursive function
$\Delta _3^0$
section, to define the recursive coloring function c, we will construct a recursive function
![]() $R(n,w)$
and apply Lemma 3.1. Similar to the
$R(n,w)$
and apply Lemma 3.1. Similar to the
![]() $\Delta _3^0$
section, function
$\Delta _3^0$
section, function
![]() $R(n,w)$
must satisfy the condition that, for any infinite
$R(n,w)$
must satisfy the condition that, for any infinite
![]() $\Pi _3^0$
set
$\Pi _3^0$
set
![]() $A_i$
with weak apartness in the list, there exists
$A_i$
with weak apartness in the list, there exists
![]() $w\in FS(A_i)$
and
$w\in FS(A_i)$
and
![]() $n< \lambda (w)$
such that
$n< \lambda (w)$
such that
![]() $R(n,w)\in A_i$
. Constructing such a function
$R(n,w)\in A_i$
. Constructing such a function
![]() $R(n,w)$
is the key part of this strategy.
$R(n,w)$
is the key part of this strategy.
In the construction of the
![]() $\Delta _3^0$
section, for each n, we guess and choose a specific set
$\Delta _3^0$
section, for each n, we guess and choose a specific set
![]() $A_i$
such that
$A_i$
such that
![]() $A_i\cap B^n\neq \emptyset $
by a priority argument. We then try to construct a function
$A_i\cap B^n\neq \emptyset $
by a priority argument. We then try to construct a function
![]() $R(n,w)$
such that for sufficiently many w,
$R(n,w)$
such that for sufficiently many w,
![]() $R(n,w)$
is an element in
$R(n,w)$
is an element in
![]() $A_i$
.
$A_i$
.
In the
![]() $\Pi _3^0$
section, we will use a modified strategy. In this construction, for a fixed n, we guess and choose a specific set
$\Pi _3^0$
section, we will use a modified strategy. In this construction, for a fixed n, we guess and choose a specific set
![]() $A_i$
such that
$A_i$
such that
![]() $A_i\cap B^n\neq \emptyset $
by a priority argument, and aim to make it so that the value of
$A_i\cap B^n\neq \emptyset $
by a priority argument, and aim to make it so that the value of
![]() $R(n,w)$
can be any number in
$R(n,w)$
can be any number in
![]() $B^n$
when w goes through the set
$B^n$
when w goes through the set
![]() $FS(A_i)$
. If so, there exists a number
$FS(A_i)$
. If so, there exists a number
![]() $w\in FS(A_i)$
such that
$w\in FS(A_i)$
such that
![]() $R(n,w)\in A_i$
.
$R(n,w)\in A_i$
.
In other words, for a fixed n, we can regard
![]() $R(n,\cdot )$
as a coloring function sending
$R(n,\cdot )$
as a coloring function sending
![]() $w\in \mathbb {N}$
to a number
$w\in \mathbb {N}$
to a number
![]() $R(n,w)\in B^n$
, one of
$R(n,w)\in B^n$
, one of
![]() $|B^n|$
many colors. Our aim is to let
$|B^n|$
many colors. Our aim is to let
![]() $FS(A_i)$
includes all colors under the coloring function
$FS(A_i)$
includes all colors under the coloring function
![]() $R(n,\cdot )$
. We can use Corollary 1 to do this.
$R(n,\cdot )$
. We can use Corollary 1 to do this.
For each fixed n, to construct such a function
![]() $R(n,\cdot )$
, we construct a recursive function
$R(n,\cdot )$
, we construct a recursive function
![]() $Q_n(y,k,s):D\subseteq \mathbb {N}^3\rightarrow \mathbb {N}$
such that
$Q_n(y,k,s):D\subseteq \mathbb {N}^3\rightarrow \mathbb {N}$
such that
![]() $Q_n(y,k,s)\in B^y$
. Later we will apply Corollary 1 to
$Q_n(y,k,s)\in B^y$
. Later we will apply Corollary 1 to
![]() $Q_n(y,k,s)$
and
$Q_n(y,k,s)$
and
![]() $r=|B^n|$
to get our desired function
$r=|B^n|$
to get our desired function
![]() $R(n,\cdot )$
. The construction of
$R(n,\cdot )$
. The construction of
![]() $Q_n(y,k,s)$
depends on the choice of set
$Q_n(y,k,s)$
depends on the choice of set
![]() $A_i$
. If we choose a set
$A_i$
. If we choose a set
![]() $A_i$
, then our aim is ensure that for sufficiently many sufficiently large
$A_i$
, then our aim is ensure that for sufficiently many sufficiently large
![]() $y,k,s$
,
$y,k,s$
,
![]() $Q_n(y,k,s)$
is in
$Q_n(y,k,s)$
is in
![]() $A_i$
.
$A_i$
.
In this way, we can find sufficiently many sufficiently large
![]() $w\in A_i$
such that
$w\in A_i$
such that
![]() $w=Q_n(y,k,s)$
for some
$w=Q_n(y,k,s)$
for some
![]() $y,k,s$
. Moreover, we can find an arbitrarily long sequence of such w:
$y,k,s$
. Moreover, we can find an arbitrarily long sequence of such w:
all in
![]() $A_i$
and (because of Corollary 1) for any
$A_i$
and (because of Corollary 1) for any
![]() $1\leq k<L$
$1\leq k<L$
Therefore, for each k,
![]() $R(n,w_k+\dots +w_L)$
has a distinct value. If we choose
$R(n,w_k+\dots +w_L)$
has a distinct value. If we choose
![]() $L>r=|B^n|$
, then for every number
$L>r=|B^n|$
, then for every number
![]() $x\in B^n$
, we can find
$x\in B^n$
, we can find
![]() $k'$
such that
$k'$
such that
3.3. Preparation for the construction
We need to guess two things: whether
![]() $B^n\cap A_i$
is empty or not and if
$B^n\cap A_i$
is empty or not and if
![]() $B^n\cap A_i$
is nonempty, which element is in
$B^n\cap A_i$
is nonempty, which element is in
![]() $B^n\cap A_i$
.
$B^n\cap A_i$
.
First, we guess which element is in
![]() $B^n\cap A_i$
if assuming it is nonempty. If
$B^n\cap A_i$
if assuming it is nonempty. If
![]() $x\in B^n\cap A_i$
, then for any y,
$x\in B^n\cap A_i$
, then for any y,
![]() $\lim _s F(i,x,y,s)$
is finite, and if
$\lim _s F(i,x,y,s)$
is finite, and if
![]() $x\in B^n$
but
$x\in B^n$
but
![]() $x\notin A_i$
, then for almost all y,
$x\notin A_i$
, then for almost all y,
![]() $\lim _s F(i,x,y,s)$
is infinite. So we define the guessing function
$\lim _s F(i,x,y,s)$
is infinite. So we define the guessing function
![]() $x(i,n,y,s)$
to be the element
$x(i,n,y,s)$
to be the element
![]() $x\in B^n$
with minimal
$x\in B^n$
with minimal
![]() $F(i,x,y,s)$
value:
$F(i,x,y,s)$
value:
Here the
![]() $\min $
function means that if more than one element x in
$\min $
function means that if more than one element x in
![]() $B^n\cap A_i$
have the minimal
$B^n\cap A_i$
have the minimal
![]() $F(i,x,y,s)$
value, then we choose the least one. Because
$F(i,x,y,s)$
value, then we choose the least one. Because
![]() $F(i,x,y,s)$
is a total recursive function,
$F(i,x,y,s)$
is a total recursive function,
![]() $x(i,n,y,s)$
is also a total recursive function.
$x(i,n,y,s)$
is also a total recursive function.
Lemma 3.3 (Guessing a single set).
Let n be a natural number and
![]() $A_i$
be an infinite
$A_i$
be an infinite
![]() $\Pi _3^0$
set with weak apartness in the list of Lemma 3.2 such that
$\Pi _3^0$
set with weak apartness in the list of Lemma 3.2 such that
![]() $A_i\cap B^{n}$
is nonempty, then
$A_i\cap B^{n}$
is nonempty, then
![]() $\lim _{y}\lim _s x(i,n,y,s)$
exists and equals the unique element in
$\lim _{y}\lim _s x(i,n,y,s)$
exists and equals the unique element in
![]() $A_i\cap B^n$
.
$A_i\cap B^n$
.
Proof Since
![]() $A_i\cap B^n\neq \emptyset $
, we choose a number
$A_i\cap B^n\neq \emptyset $
, we choose a number
![]() $x_0\in A_i\cap B^n$
. Because
$x_0\in A_i\cap B^n$
. Because
![]() $A_i$
has weak apartness,
$A_i$
has weak apartness,
![]() $x_0$
is the unique element in
$x_0$
is the unique element in
![]() $B^n\cap A_i$
and
$B^n\cap A_i$
and
![]() $B^n\setminus A_i=B^n\setminus \{x_0\}$
. So for any
$B^n\setminus A_i=B^n\setminus \{x_0\}$
. So for any
![]() $x\in B^n\setminus \{x_0\}$
, there exists
$x\in B^n\setminus \{x_0\}$
, there exists
![]() $y_x$
such that
$y_x$
such that
![]() $\lim _s F(i,x,y,s)=\infty $
for any
$\lim _s F(i,x,y,s)=\infty $
for any
![]() $y>y_x$
. Let
$y>y_x$
. Let
![]() $y_0=\max \{y_x:x\in B^n\setminus \{x_0\}\}$
.
$y_0=\max \{y_x:x\in B^n\setminus \{x_0\}\}$
.
For any
![]() $y>y_0$
, there exists a number
$y>y_0$
, there exists a number
![]() $k_y$
such that
$k_y$
such that
![]() $\lim _s F(i,x_0,y,s)=k_y$
. And for each
$\lim _s F(i,x_0,y,s)=k_y$
. And for each
![]() $x\in B^n\setminus \{x_0\}$
,
$x\in B^n\setminus \{x_0\}$
,
![]() $ \lim _sF(i,x,y,s)$
is infinite. So for any
$ \lim _sF(i,x,y,s)$
is infinite. So for any
![]() $y>y_0$
, for any sufficiently large number s,
$y>y_0$
, for any sufficiently large number s,
![]() $x(i,n,y,s)=x_0$
.
$x(i,n,y,s)=x_0$
.
Next we define a function to guess whether
![]() $A_i\cap B^n$
is empty or not.
$A_i\cap B^n$
is empty or not.
Lemma 3.4. For every set
![]() $A_i$
in the list of Lemma 3.2, let
$A_i$
in the list of Lemma 3.2, let
Then if
![]() $A_i\cap B^n$
is nonempty, then
$A_i\cap B^n$
is nonempty, then
![]() $\forall y \lim _s B(i,n,y,s)<\infty $
; and if
$\forall y \lim _s B(i,n,y,s)<\infty $
; and if
![]() $A_i\cap B^n$
is empty, then
$A_i\cap B^n$
is empty, then
![]() $\exists y_0\forall y>y_0 \lim _s B(i,n,y,s)=\infty $
.
$\exists y_0\forall y>y_0 \lim _s B(i,n,y,s)=\infty $
.
Proof By Lemma 3.2 and property of limit.
We use the function
![]() $B(i,n,y,s)$
to guess whether
$B(i,n,y,s)$
to guess whether
![]() $A_i\cap B^n$
is empty or not. Specifically, for a given number k, if
$A_i\cap B^n$
is empty or not. Specifically, for a given number k, if
![]() $B(i,n,y,s)<k$
, we guess the
$B(i,n,y,s)<k$
, we guess the
![]() $A_i\cap B^n$
is nonempty at “stage” k and s.
$A_i\cap B^n$
is nonempty at “stage” k and s.
3.4. Construction
The construction consists of two parts:
Part 1: First, we define a function
![]() $I(n,y,k,s)$
which indicates the index of the choice
$I(n,y,k,s)$
which indicates the index of the choice
![]() $A_i$
as mentioned earlier and is a recursive function with recursive domain. For numbers
$A_i$
as mentioned earlier and is a recursive function with recursive domain. For numbers
![]() $n<y\leq k\leq s$
, if for all
$n<y\leq k\leq s$
, if for all
![]() $m<n$
,
$m<n$
,
![]() $I(m,y,k,s)$
is defined, then
$I(m,y,k,s)$
is defined, then
Part 2: Define
![]() $Q_n(y,k,s)$
: if
$Q_n(y,k,s)$
: if
![]() $I(n,y,k,s)\neq \infty $
, let
$I(n,y,k,s)\neq \infty $
, let
![]() $j=I(n,y,k,s)$
, and let
$j=I(n,y,k,s)$
, and let
otherwise let
![]() $Q_n(y,k,s)=2^{y}$
.
$Q_n(y,k,s)=2^{y}$
.
For each n, the function
![]() $Q_n(y,k,s)$
is recursive with a recursive domain. We can apply Corollary 1 to
$Q_n(y,k,s)$
is recursive with a recursive domain. We can apply Corollary 1 to
![]() $Q_n(y,k,s)$
and
$Q_n(y,k,s)$
and
![]() $r=|B^n|$
to obtain a function
$r=|B^n|$
to obtain a function
![]() $R_0(n,\cdot )$
with range
$R_0(n,\cdot )$
with range
![]() $\{0,\dots ,r-1\}$
. Because
$\{0,\dots ,r-1\}$
. Because
![]() $R(n,w)$
has a range
$R(n,w)$
has a range
![]() $B^n$
, we define
$B^n$
, we define
![]() $R(n,w)$
to be the
$R(n,w)$
to be the
![]() $R_0(n,w)$
th number in
$R_0(n,w)$
th number in
![]() $B^n$
.
$B^n$
.
The sequence
![]() $\langle Q_n(y,k,s)\rangle _{n\in \mathbb {N}}$
is a recursive sequence. Because the function in Corollary 1 is uniformly recursive in
$\langle Q_n(y,k,s)\rangle _{n\in \mathbb {N}}$
is a recursive sequence. Because the function in Corollary 1 is uniformly recursive in
![]() $Q_n(y,k,s)$
,
$Q_n(y,k,s)$
,
![]() $\langle R(n,\cdot )\rangle _{n\in \mathbb {N}}$
is a recursive sequence and the function
$\langle R(n,\cdot )\rangle _{n\in \mathbb {N}}$
is a recursive sequence and the function
![]() $R(n,w)$
is recursive.
$R(n,w)$
is recursive.
3.5. Verification, part 1
In this subsection, we will show that for any infinite
![]() $\Pi _3^0$
set
$\Pi _3^0$
set
![]() $A_i$
(with or without weak apartness) in the list of Lemma 3.2, there exists n such that
$A_i$
(with or without weak apartness) in the list of Lemma 3.2, there exists n such that
![]() $\lim _y\lim _k\lim _s I(n,y,k,s)=i$
.
$\lim _y\lim _k\lim _s I(n,y,k,s)=i$
.
Lemma 3.5. For any n,
![]() $\lim _y\lim _k\lim _s I(n,y,k,s)$
is defined. Moreover, if we let
$\lim _y\lim _k\lim _s I(n,y,k,s)$
is defined. Moreover, if we let
and
then for any n,
Proof We prove this lemma by induction on n. For a number n, we assume that for any
![]() $m<n$
,
$m<n$
,
![]() $I(m)$
is defined and
$I(m)$
is defined and
![]() $I(m)=\min (Z(m)\setminus H(m)\cup \{\infty \})$
.
$I(m)=\min (Z(m)\setminus H(m)\cup \{\infty \})$
.
By definition, for each
![]() $y,k,s$
,
$y,k,s$
,
Consider the following set in above definition:
which is the set
![]() $\{i<n:B(i,n,y,s)<k\}$
minus
$\{i<n:B(i,n,y,s)<k\}$
minus
![]() $\{i<n:\exists m<n\ I(m,y,k,s)=i\}$
. We claim that
$\{i<n:\exists m<n\ I(m,y,k,s)=i\}$
. We claim that
and
To prove equation (2.2.1), we use the definition of
![]() $Z(n)$
and
$Z(n)$
and
![]() $B(i,n,y,s)$
. By Lemma 3.4 and property of limit, there exists
$B(i,n,y,s)$
. By Lemma 3.4 and property of limit, there exists
![]() $y_1$
such that for any
$y_1$
such that for any
![]() $y>y_1$
and any k, there exists
$y>y_1$
and any k, there exists
![]() $s_{y,k}$
such that for any
$s_{y,k}$
such that for any
![]() $s>s_{y,k}$
and any
$s>s_{y,k}$
and any
![]() $i\in n\setminus Z(n)$
,
$i\in n\setminus Z(n)$
,
![]() $B(i,n,y,s)>k$
. Similarly, for any y there exists
$B(i,n,y,s)>k$
. Similarly, for any y there exists
![]() $k_y$
such that for any s and any
$k_y$
such that for any s and any
![]() $i\in Z(n)$
,
$i\in Z(n)$
,
![]() $B(i,n,y,s)<k_y$
. Hence:
$B(i,n,y,s)<k_y$
. Hence:
 $$ \begin{align*} \lim_y\lim_k\lim_s \{i<n:B(i,n,y,s)<k\}&\subseteq Z(n)\\ \lim_y\lim_k\lim_s \{i<n:B(i,n,y,s)<k\}&\supseteq Z(n). \end{align*} $$
$$ \begin{align*} \lim_y\lim_k\lim_s \{i<n:B(i,n,y,s)<k\}&\subseteq Z(n)\\ \lim_y\lim_k\lim_s \{i<n:B(i,n,y,s)<k\}&\supseteq Z(n). \end{align*} $$
Equation (2.2.1) is true.
We now prove equation (2.2.2). By the Induction Hypothesis, for any
![]() $m<n$
,
$m<n$
,
![]() $I(m)$
is defined. Using property of limit, we can find
$I(m)$
is defined. Using property of limit, we can find
![]() $y_0$
such that for any
$y_0$
such that for any
![]() $y>y_0$
, there exists
$y>y_0$
, there exists
![]() $k_y$
such that any
$k_y$
such that any
![]() $k>k_y$
, there exists
$k>k_y$
, there exists
![]() $s_{y,k}$
such that for any
$s_{y,k}$
such that for any
![]() $s>s_{y,k}$
and any
$s>s_{y,k}$
and any
![]() $m<n$
,
$m<n$
,
![]() $I(m,y,k,s)=I(m)$
. Thus, for those
$I(m,y,k,s)=I(m)$
. Thus, for those
![]() $y,k,s$
, we have that
$y,k,s$
, we have that
The right-hand side of this equation is equal to
![]() $H(n)$
. Therefore, we conclude that
$H(n)$
. Therefore, we conclude that
![]() $\lim _y\lim _k\lim _s \{i<n:\exists m<n,I(m,y,k,s)=i\}=H(n)$
.
$\lim _y\lim _k\lim _s \{i<n:\exists m<n,I(m,y,k,s)=i\}=H(n)$
.
Since equations (2.2.1) and (2.2.2) hold, by the properties of the limit operation,
 $$ \begin{align*} &I(n)=\lim_y\lim_k\lim_s\ I(n,y,k,s)\\ =&\lim_y\lim_k\lim_s\ \min(\{i<n:B(i,n,y,s)<k \wedge \forall m<n (I(m,y,k,s)\neq i)\}\cup\{\infty\})\\ =&\lim_y\lim_k\lim_s\ \min(\{i<n:B(i,n,y,s)<k\}\setminus\{i<n:\exists m<n(I(m,y,k,s)=i)\}\cup\{\infty\})\\ =&\min(Z(n)\setminus H(n)\cup\{\infty\}). \end{align*} $$
$$ \begin{align*} &I(n)=\lim_y\lim_k\lim_s\ I(n,y,k,s)\\ =&\lim_y\lim_k\lim_s\ \min(\{i<n:B(i,n,y,s)<k \wedge \forall m<n (I(m,y,k,s)\neq i)\}\cup\{\infty\})\\ =&\lim_y\lim_k\lim_s\ \min(\{i<n:B(i,n,y,s)<k\}\setminus\{i<n:\exists m<n(I(m,y,k,s)=i)\}\cup\{\infty\})\\ =&\min(Z(n)\setminus H(n)\cup\{\infty\}). \end{align*} $$
This concludes the proof.
Lemma 3.6. For any infinite
![]() $\Pi _3^0$
set
$\Pi _3^0$
set
![]() $A_i$
in the list of Lemma 3.2, there exists n such that
$A_i$
in the list of Lemma 3.2, there exists n such that
![]() $I(n)=i$
.
$I(n)=i$
.
Proof We prove this lemma by induction on i. For each i, if
![]() $A_i$
is infinite, there exist infinitely many n such that
$A_i$
is infinite, there exist infinitely many n such that
![]() $A_i\cap B^n\neq \emptyset $
. For any
$A_i\cap B^n\neq \emptyset $
. For any
![]() $j<i$
, if
$j<i$
, if
![]() $A_j$
is finite, there exists
$A_j$
is finite, there exists
![]() $n_j$
such that for any
$n_j$
such that for any
![]() $n>n_j$
,
$n>n_j$
,
![]() $A_j\cap B^n=\emptyset $
; and for any
$A_j\cap B^n=\emptyset $
; and for any
![]() $j<i$
, if
$j<i$
, if
![]() $A_j$
is infinite, by induction hypothesis, there exists
$A_j$
is infinite, by induction hypothesis, there exists
![]() $n_j$
such that
$n_j$
such that
![]() $I(n_j)=j$
. So we choose a number N sufficiently large such that
$I(n_j)=j$
. So we choose a number N sufficiently large such that
![]() $A_i\cap B^N$
is nonempty and for any
$A_i\cap B^N$
is nonempty and for any
![]() $j<i$
, either
$j<i$
, either
![]() $A_j\cap B^N=\emptyset $
or
$A_j\cap B^N=\emptyset $
or
![]() $\exists m<N, I(m)=j$
.
$\exists m<N, I(m)=j$
.
If there exists
![]() $n<N$
such that
$n<N$
such that
![]() $I(n)=i$
, the we are done. Otherwise by the definition of
$I(n)=i$
, the we are done. Otherwise by the definition of
![]() $H(N)$
, we have
$H(N)$
, we have
![]() $i\notin H(N)$
; since
$i\notin H(N)$
; since
![]() $B^n\cap A_i\neq \emptyset $
, we have
$B^n\cap A_i\neq \emptyset $
, we have
![]() $i\in Z(N)$
. Therefore
$i\in Z(N)$
. Therefore
![]() $i\in Z(N)\setminus H(N)$
. For any
$i\in Z(N)\setminus H(N)$
. For any
![]() $j<i$
, if
$j<i$
, if
![]() $A_j$
is finite, then
$A_j$
is finite, then
![]() $A_j\cap B^N=\emptyset $
, and
$A_j\cap B^N=\emptyset $
, and
![]() $j\notin Z(N)$
; if
$j\notin Z(N)$
; if
![]() $A_j$
is infinite, then
$A_j$
is infinite, then
![]() $\exists m<N, I(m)=j$
and hence
$\exists m<N, I(m)=j$
and hence
![]() $j\in H(N)$
. Thus for any
$j\in H(N)$
. Thus for any
![]() $j<i$
, we have
$j<i$
, we have
![]() $j\notin Z(N)\setminus H(N)$
. Therefore
$j\notin Z(N)\setminus H(N)$
. Therefore
![]() $i=\min (Z(N)\setminus H(N)\cup \{\infty \})$
and by Lemma 3.5,
$i=\min (Z(N)\setminus H(N)\cup \{\infty \})$
and by Lemma 3.5,
![]() $I(N)=i$
.
$I(N)=i$
.
Therefore, there exists
![]() $n\leq N$
such that
$n\leq N$
such that
![]() $I(n)=i$
.
$I(n)=i$
.
3.6. Verification: part 2
In this subsection, we will finish the verification.
Lemma 3.7. Let
![]() $A_i$
be an infinite
$A_i$
be an infinite
![]() $\Pi _3^0$
set with weak apartness and n be a number such that
$\Pi _3^0$
set with weak apartness and n be a number such that
![]() $I(n)=i$
. Then for any
$I(n)=i$
. Then for any
![]() $r>1$
and Y, there exists a sequence
$r>1$
and Y, there exists a sequence
all in
![]() $A_i$
such that:
$A_i$
such that:
(1)
![]() $\lambda (x_1)>Y$
.
$\lambda (x_1)>Y$
.
(2) For any
![]() $g\in (0,r)$
,
$g\in (0,r)$
,
![]() $\lim _sQ_n(\mu (x_{g}),\lambda (x_{g+1}),s)=x_{g}.$
$\lim _sQ_n(\mu (x_{g}),\lambda (x_{g+1}),s)=x_{g}.$
Proof Because
![]() $I(n)=i$
,
$I(n)=i$
,
![]() $\lim _y\lim _k\lim _s I(n,y,k,s)=i$
. We will prove this lemma by induction on r.
$\lim _y\lim _k\lim _s I(n,y,k,s)=i$
. We will prove this lemma by induction on r.
Because
![]() $I(n)=i$
and
$I(n)=i$
and
![]() $A_i$
has weak apartness, by Lemma 3.3, there exists
$A_i$
has weak apartness, by Lemma 3.3, there exists
![]() $Y_0$
such that for any
$Y_0$
such that for any
![]() $Y_1>Y_0$
,
$Y_1>Y_0$
,
![]() $\lim _k\lim _s I(n,Y_1,k,s)=i$
and if
$\lim _k\lim _s I(n,Y_1,k,s)=i$
and if
![]() $B^{Y_1}\cap A_i$
is nonempty, then
$B^{Y_1}\cap A_i$
is nonempty, then
![]() $B^{Y_1}\cap A_i$
contains exactly one element and
$B^{Y_1}\cap A_i$
contains exactly one element and
![]() $\lim _{k}\lim _s x(i,{Y_1},k,s)\in A_i$
. Because
$\lim _{k}\lim _s x(i,{Y_1},k,s)\in A_i$
. Because
![]() $\lim _k\lim _s I(n,Y_1,k,s)=i$
,
$\lim _k\lim _s I(n,Y_1,k,s)=i$
,
![]() $\lim _{k}\lim _s Q_n(Y_1,k,s)=\lim _{k}\lim _s x(i,Y_1,k,s)$
is defined and equal to the unique element
$\lim _{k}\lim _s Q_n(Y_1,k,s)=\lim _{k}\lim _s x(i,Y_1,k,s)$
is defined and equal to the unique element
![]() $x\in A_i\cap B^{Y_1}$
. Without loss of generality, we assume that
$x\in A_i\cap B^{Y_1}$
. Without loss of generality, we assume that
![]() $Y>Y_0$
.
$Y>Y_0$
.
For the case
![]() $r=2$
: in this case, g can only be
$r=2$
: in this case, g can only be
![]() $1$
. We choose
$1$
. We choose
![]() $x_1\in A_i$
such that
$x_1\in A_i$
such that
![]() $\lambda (x_1)>Y$
. Since
$\lambda (x_1)>Y$
. Since
![]() $ A_i\cap B^{\mu (x_1)}$
contains
$ A_i\cap B^{\mu (x_1)}$
contains
![]() $x_1$
, it is nonempty, and thus
$x_1$
, it is nonempty, and thus
Then we choose
![]() $k_0$
such that for any
$k_0$
such that for any
![]() $k>k_0$
,
$k>k_0$
,
![]() $\lim _s Q_n(\mu (x_1),k,s)=x_1$
, and choose a number
$\lim _s Q_n(\mu (x_1),k,s)=x_1$
, and choose a number
![]() $x_2\gg x_1$
in
$x_2\gg x_1$
in
![]() $A_i$
such that
$A_i$
such that
![]() $\lambda (x_2)>k_0$
. Then lims
Q
n
(μ(x
1), λ(x
2), s) = x
1. It follows that two numbers
$\lambda (x_2)>k_0$
. Then lims
Q
n
(μ(x
1), λ(x
2), s) = x
1. It follows that two numbers
![]() $x_2\gg x_1$
satisfy our requirements.
$x_2\gg x_1$
satisfy our requirements.
Suppose we have proved case
![]() $r\geq 2$
, by the Induction Hypothesis, for Y and r, there exists a sequence
$r\geq 2$
, by the Induction Hypothesis, for Y and r, there exists a sequence
![]() $x_1\ll \cdots \ll x_r$
that satisfies the lemma for
$x_1\ll \cdots \ll x_r$
that satisfies the lemma for
![]() $Y,r$
:
$Y,r$
:
and
![]() $\lambda (x_1)>Y$
. We need to find
$\lambda (x_1)>Y$
. We need to find
![]() $x_{r+1}$
such that
$x_{r+1}$
such that
![]() $\lim _s Q_n(\mu (x_r),\lambda (x_{r+1}),s)=x_r$
. Since
$\lim _s Q_n(\mu (x_r),\lambda (x_{r+1}),s)=x_r$
. Since
![]() $B^{\mu (x_r)}\cap A_i$
is nonempty,
$B^{\mu (x_r)}\cap A_i$
is nonempty,
![]() $\lim _{k}\lim _s Q_n(\mu (x_r),k,s)=x_r$
; therefore we only need to choose
$\lim _{k}\lim _s Q_n(\mu (x_r),k,s)=x_r$
; therefore we only need to choose
![]() $x_{r+1}$
such that
$x_{r+1}$
such that
![]() $\lambda (x_{r+1})$
is sufficiently large. Choose a sufficiently large
$\lambda (x_{r+1})$
is sufficiently large. Choose a sufficiently large
![]() $x_{r+1}\gg x_{r}$
in
$x_{r+1}\gg x_{r}$
in
![]() $A_i$
such that
$A_i$
such that
![]() $\lim _s Q_n(\mu (x_r),\lambda (x_{r+1}),s)=x_r$
. The sequence
$\lim _s Q_n(\mu (x_r),\lambda (x_{r+1}),s)=x_r$
. The sequence
![]() $x_1\ll x_2\cdots \ll x_{r+1}$
satisfies this lemma.
$x_1\ll x_2\cdots \ll x_{r+1}$
satisfies this lemma.
Lemma 3.8. Let
![]() $A_i$
be an infinite
$A_i$
be an infinite
![]() $\Pi _3^0$
set with weak apartness, n be a natural number such that
$\Pi _3^0$
set with weak apartness, n be a natural number such that
![]() $I(n)=i$
and
$I(n)=i$
and
![]() $R(n,w)$
be the function in our construction. For any
$R(n,w)$
be the function in our construction. For any
![]() $r>1$
, there exist r different numbers
$r>1$
, there exist r different numbers
![]() $w_h, 0< h\leq r$
in
$w_h, 0< h\leq r$
in
![]() $FS(A_i)$
such that:
$FS(A_i)$
such that:
(1) each
![]() $w_h$
is sum of finitely many numbers x in
$w_h$
is sum of finitely many numbers x in
![]() $A_i$
such that
$A_i$
such that
![]() $\lambda (x)>n$
;
$\lambda (x)>n$
;
(2) for any two different
![]() $w_{h_1}$
and
$w_{h_1}$
and
![]() $w_{h_2}$
,
$w_{h_2}$
,
![]() $R(n,w_{h_1})\neq R(n,w_{h_2})$
.
$R(n,w_{h_1})\neq R(n,w_{h_2})$
.
Proof By Lemma 3.7, there exists a sequence
![]() $x_1\ll x_2\ll \cdots \ll x_r$
such that
$x_1\ll x_2\ll \cdots \ll x_r$
such that
![]() $\lambda (x_1)>n$
and
$\lambda (x_1)>n$
and
Choose a sufficiently large
![]() $x_{r+1}\in A_i$
such that
$x_{r+1}\in A_i$
such that
![]() $x_{r+1}\gg x_r$
and
$x_{r+1}\gg x_r$
and
For
![]() $ h\in (0,r]$
, let
$ h\in (0,r]$
, let
![]() $w_h=\sum _{g=h}^{r+1}x_g$
. This is a sum of finitely many numbers
$w_h=\sum _{g=h}^{r+1}x_g$
. This is a sum of finitely many numbers
![]() $x_g$
in
$x_g$
in
![]() $A_i$
such that
$A_i$
such that
![]() $\lambda (x_g)>n$
. We show that for
$\lambda (x_g)>n$
. We show that for
![]() $0< h_2<h_1\leq r$
,
$0< h_2<h_1\leq r$
,
![]() $R(n,w_{h_1})\neq R(n,w_{h_2})$
. For each
$R(n,w_{h_1})\neq R(n,w_{h_2})$
. For each
![]() $w_h$
,
$w_h$
,
![]() $\mu (w_h)=\mu (x_{r+1})$
and
$\mu (w_h)=\mu (x_{r+1})$
and
![]() $\lambda (w_h)=\lambda (x_h)$
. So by Lemma 3.7 and our assumption,
$\lambda (w_h)=\lambda (x_h)$
. So by Lemma 3.7 and our assumption,
![]() $Q_n(\mu (x_{h}),\lambda (w_{h+1}),\mu (w_{h+1}))=x_{h}$
. Then by the construction and Corollary 1:
$Q_n(\mu (x_{h}),\lambda (w_{h+1}),\mu (w_{h+1}))=x_{h}$
. Then by the construction and Corollary 1:
 $$ \begin{align*} R_0(n,w_{h+1})+1&\equiv R_0(n,Q_n(\mu(x_{h}),\lambda(w_{h+1}),\mu(w_{h+1}))+w_{h+1})\quad \mod r\\ &\equiv R_0(n,x_{h}+w_{h+1})\quad \mod r\\ &\equiv R_0(n,w_{h})\quad \mod r. \end{align*} $$
$$ \begin{align*} R_0(n,w_{h+1})+1&\equiv R_0(n,Q_n(\mu(x_{h}),\lambda(w_{h+1}),\mu(w_{h+1}))+w_{h+1})\quad \mod r\\ &\equiv R_0(n,x_{h}+w_{h+1})\quad \mod r\\ &\equiv R_0(n,w_{h})\quad \mod r. \end{align*} $$
So,
![]() $R_0(n,w_{h_1})\equiv R_0(n,w_{h_2})-(h_1-h_2)\ \mod r$
and each
$R_0(n,w_{h_1})\equiv R_0(n,w_{h_2})-(h_1-h_2)\ \mod r$
and each
![]() $w_h$
has a distinct
$w_h$
has a distinct
![]() $R(n,w_h)$
value.
$R(n,w_h)$
value.
Lemma 3.9. Let
![]() $A_i$
be an infinite
$A_i$
be an infinite
![]() $\Pi _3^0$
set with weak apartness in the list of Lemma 3.2 and
$\Pi _3^0$
set with weak apartness in the list of Lemma 3.2 and
![]() $R(n,w)$
be the function in our construction. There exists n,
$R(n,w)$
be the function in our construction. There exists n,
![]() $x\in B^n\cap A_i$
and
$x\in B^n\cap A_i$
and
![]() $w\in FS(A_i)$
such that
$w\in FS(A_i)$
such that
![]() $\lambda (w)>n$
,
$\lambda (w)>n$
,
![]() $x+w\in FS(A_i)$
and
$x+w\in FS(A_i)$
and
Proof By Lemma 3.6, there exists n such that
![]() $I(n)=i$
and by Lemma 3.8, for
$I(n)=i$
and by Lemma 3.8, for
![]() $r=|B^n|$
, there exist numbers
$r=|B^n|$
, there exist numbers
![]() $w_h,1\leq h\leq r$
all in
$w_h,1\leq h\leq r$
all in
![]() $FS(A_i)$
such that each
$FS(A_i)$
such that each
![]() $w_h$
is a sum of finitely many numbers
$w_h$
is a sum of finitely many numbers
![]() $x'\in A_i$
such that
$x'\in A_i$
such that
![]() $\lambda (x')>n$
(hence
$\lambda (x')>n$
(hence
![]() $x+w_h\in FS(A_i)$
for any
$x+w_h\in FS(A_i)$
for any
![]() $x\in B^n$
), and each
$x\in B^n$
), and each
![]() $w_h$
has a distinct
$w_h$
has a distinct
![]() $R(n,w_h)$
value. Because
$R(n,w_h)$
value. Because
![]() $R(n,w_h)\in B^n$
for any such
$R(n,w_h)\in B^n$
for any such
![]() $w_h$
, for any
$w_h$
, for any
![]() $x\in B^n$
, there exists one
$x\in B^n$
, there exists one
![]() $w_h$
such that
$w_h$
such that
![]() $R(n,w_h)=x$
.
$R(n,w_h)=x$
.
By Lemma 3.5,
![]() $i=I(n)=\min \{Z(n)\setminus H(n)\cup \{\infty \}\}.$
Because i is a number rather than
$i=I(n)=\min \{Z(n)\setminus H(n)\cup \{\infty \}\}.$
Because i is a number rather than
![]() $\infty $
,
$\infty $
,
![]() $i\in Z(n)=\{i<n:A_i\cap B^n\neq \emptyset \}$
. Hence
$i\in Z(n)=\{i<n:A_i\cap B^n\neq \emptyset \}$
. Hence
![]() $A_i\cap B^n\neq \emptyset $
.
$A_i\cap B^n\neq \emptyset $
.
Therefore we can find
![]() $x\in B^n\cap A_i$
and
$x\in B^n\cap A_i$
and
![]() $w_h$
such that
$w_h$
such that
![]() $R(n,w_h)=x$
and these
$R(n,w_h)=x$
and these
![]() $n,w_h,x$
are what we need.
$n,w_h,x$
are what we need.
Theorem 3.10. There exists a recursive coloring function
![]() $c:\mathbb {N}\rightarrow 2$
such that for any infinite
$c:\mathbb {N}\rightarrow 2$
such that for any infinite
![]() $\Pi _3^0$
set A with weak apartness, there exist
$\Pi _3^0$
set A with weak apartness, there exist
![]() $w_1,w_2\in FS(A)$
such that
$w_1,w_2\in FS(A)$
such that
![]() $c(w_1)\neq c(w_2)$
.
$c(w_1)\neq c(w_2)$
.
Proof Use the function
![]() $R(n,w)$
in our construction and apply Corollary 1 to
$R(n,w)$
in our construction and apply Corollary 1 to
![]() $R(n,w)$
to get a coloring function c. We show that c is what we need.
$R(n,w)$
to get a coloring function c. We show that c is what we need.
Because any infinite
![]() $\Pi _3^0$
set A with weak apartness is equal to a set
$\Pi _3^0$
set A with weak apartness is equal to a set
![]() $A_i$
in the list of Lemma 3.2, by Lemma 3.9, there exists numbers
$A_i$
in the list of Lemma 3.2, by Lemma 3.9, there exists numbers
![]() $n,x,w$
such that
$n,x,w$
such that
![]() $x\in B^n\cap A_i$
,
$x\in B^n\cap A_i$
,
![]() $w\in FS(A_i)$
,
$w\in FS(A_i)$
,
![]() $\lambda (w)>n$
,
$\lambda (w)>n$
,
![]() $x+w\in FS(A_i)$
and
$x+w\in FS(A_i)$
and
![]() $R(n,w)=x$
. By Corollary 1,
$R(n,w)=x$
. By Corollary 1,
![]() $c(w)\neq c(w+R(n,w))$
if
$c(w)\neq c(w+R(n,w))$
if
![]() $n<\lambda (w)$
. So,
$n<\lambda (w)$
. So,
![]() $c(w)\neq c(w+x)$
. Because
$c(w)\neq c(w+x)$
. Because
![]() $\lambda (w)>n=\mu (x)$
, both w and
$\lambda (w)>n=\mu (x)$
, both w and
![]() $w+x$
are in
$w+x$
are in
![]() $FS(A_i)$
. Two numbers
$FS(A_i)$
. Two numbers
![]() $w,w+x$
are both in
$w,w+x$
are both in
![]() $FS(A_i)$
, and hence
$FS(A_i)$
, and hence
![]() $c(w)\neq c(w+x)$
. This concludes the proof.
$c(w)\neq c(w+x)$
. This concludes the proof.
4. Unsolvabilities without apartness
In this section, we will prove
![]() $\Pi _3^0$
unsolvability for
$\Pi _3^0$
unsolvability for
![]() $\mathrm {HT}$
without weak apartness. We use the idea of getting rid of apartness/weak apartness from paper by Dzhafarov et al. [Reference Dzhafarov, Jockusch, Solomon, Westrick, Day, Fellows, Greenberg, Khoussainov, Melnikov and Rosamond6], and also in Lemma 2.7 from the paper by Carlucci et al. [Reference Carlucci, Kołodziejczyk, Lepore and Zdanowski5]. While
$\mathrm {HT}$
without weak apartness. We use the idea of getting rid of apartness/weak apartness from paper by Dzhafarov et al. [Reference Dzhafarov, Jockusch, Solomon, Westrick, Day, Fellows, Greenberg, Khoussainov, Melnikov and Rosamond6], and also in Lemma 2.7 from the paper by Carlucci et al. [Reference Carlucci, Kołodziejczyk, Lepore and Zdanowski5]. While
![]() $\Delta _3^0$
unsolvability without apartness can be directly proved using results in the paper Carlucci et al. [Reference Carlucci, Kołodziejczyk, Lepore and Zdanowski5], for
$\Delta _3^0$
unsolvability without apartness can be directly proved using results in the paper Carlucci et al. [Reference Carlucci, Kołodziejczyk, Lepore and Zdanowski5], for
![]() $\Pi _3^0$
unsolvability, we need to write more details because
$\Pi _3^0$
unsolvability, we need to write more details because
![]() $A\leq _T B$
and B is
$A\leq _T B$
and B is
![]() $\Pi _3^0$
do not imply that A is also
$\Pi _3^0$
do not imply that A is also
![]() $\Pi _3^0$
.
$\Pi _3^0$
.
Lemma 4.1. There exists a recursive coloring function
![]() $c_0:\mathbb {N}\rightarrow \{0,1\}^2$
such that for any infinite set A, if it does not have weak apartness, then it is not a solution to c for
$c_0:\mathbb {N}\rightarrow \{0,1\}^2$
such that for any infinite set A, if it does not have weak apartness, then it is not a solution to c for
![]() $\mathrm {HT}^{\leq 2}$
.
$\mathrm {HT}^{\leq 2}$
.
Proof We define two coloring functions
![]() $c_1,c_2:\mathbb {N}\rightarrow \{0,1\}$
:
$c_1,c_2:\mathbb {N}\rightarrow \{0,1\}$
:
 $$ \begin{align*} c_1(x) \equiv \mu(x)\quad \mod 2;\\ c_2(x) \equiv \lambda(x)\quad \mod 2. \end{align*} $$
$$ \begin{align*} c_1(x) \equiv \mu(x)\quad \mod 2;\\ c_2(x) \equiv \lambda(x)\quad \mod 2. \end{align*} $$
We show that for
![]() $c_0=c_1\times c_2$
, if an infinite set A does not have weak apartness, then it is not monochromatic under
$c_0=c_1\times c_2$
, if an infinite set A does not have weak apartness, then it is not monochromatic under
![]() $c_0$
. If A has not weak apartness, there are two cases.
$c_0$
. If A has not weak apartness, there are two cases.
The first case is that, there are two numbers
![]() $x_1,x_2$
such that
$x_1,x_2$
such that
![]() $\mu (x_1)=\mu (x_2)=m$
. This means these two numbers are in the interval
$\mu (x_1)=\mu (x_2)=m$
. This means these two numbers are in the interval
![]() $[2^m,2^{m+1})$
. Thus
$[2^m,2^{m+1})$
. Thus
![]() $\mu (x_1+x_2)=m+1$
, and
$\mu (x_1+x_2)=m+1$
, and
![]() $c_1(x_1)\neq c_1(x_1+x_2)$
. Therefore,
$c_1(x_1)\neq c_1(x_1+x_2)$
. Therefore,
![]() $FS^{\leq 2}(A)$
is not monochromatic.
$FS^{\leq 2}(A)$
is not monochromatic.
The second case is that, there are three number
![]() $x_1,x_2,x_3$
such that
$x_1,x_2,x_3$
such that
![]() $\lambda (x_1)=\lambda (x_2)=\lambda (x_3)=l$
. In this case, all three numbers are divisible by
$\lambda (x_1)=\lambda (x_2)=\lambda (x_3)=l$
. In this case, all three numbers are divisible by
![]() $2^l$
and not by
$2^l$
and not by
![]() $2^{l+1}$
. So for any X among these three numbers,
$2^{l+1}$
. So for any X among these three numbers,
![]() $X\equiv 2^l \text { or }2^{l+1}+2^l\ \mod 2^{l+2}$
and there must be two number
$X\equiv 2^l \text { or }2^{l+1}+2^l\ \mod 2^{l+2}$
and there must be two number
![]() $X_1,X_2$
among
$X_1,X_2$
among
![]() $x_1,x_2,x_3$
such that
$x_1,x_2,x_3$
such that
![]() $X_1\equiv X_2\ \mod 2^{l+2}$
. Hence
$X_1\equiv X_2\ \mod 2^{l+2}$
. Hence
![]() $X_1+X_2$
is divisible by
$X_1+X_2$
is divisible by
![]() $2^{l+1}$
but not
$2^{l+1}$
but not
![]() $2^{l+2}$
and
$2^{l+2}$
and
![]() $\lambda (X_1+X_2)=l+1$
. Since
$\lambda (X_1+X_2)=l+1$
. Since
![]() $\lambda (x_1)=l$
,
$\lambda (x_1)=l$
,
![]() $c_2(X_1+X_2)\neq c_2(x_1)$
and
$c_2(X_1+X_2)\neq c_2(x_1)$
and
![]() $FS^{\leq 2}(A)$
is not monochromatic.
$FS^{\leq 2}(A)$
is not monochromatic.
In each case,
![]() $FS^{\leq 2}(A)$
is not monochromatic. Therefore, if A does not have weak apartness, then it is not a solution to
$FS^{\leq 2}(A)$
is not monochromatic. Therefore, if A does not have weak apartness, then it is not a solution to
![]() $c_0=c_1\times c_2$
.
$c_0=c_1\times c_2$
.
Using Lemma 4.1, we can prove our theorem.
Theorem 4.2. There exists a recursive coloring function
![]() $c:\mathbb {N}\rightarrow \{0,1\}^3$
such that any infinite
$c:\mathbb {N}\rightarrow \{0,1\}^3$
such that any infinite
![]() $\Pi _3^0$
set A is not a solution to c for
$\Pi _3^0$
set A is not a solution to c for
![]() $\mathrm {HT}$
.
$\mathrm {HT}$
.
Proof By Theorem 3.10, there exists a recursive coloring
![]() $c_2:\mathbb {N}\rightarrow \{0,1\}$
such that any infinite
$c_2:\mathbb {N}\rightarrow \{0,1\}$
such that any infinite
![]() $\Pi _3^0$
set with weak apartness is not a solution to
$\Pi _3^0$
set with weak apartness is not a solution to
![]() $c_2$
for
$c_2$
for
![]() $\mathrm {HT}$
.
$\mathrm {HT}$
.
Let
![]() $c=c_2\times c_0$
where
$c=c_2\times c_0$
where
![]() $c_0$
is the coloring function in Lemma 4.1. We claim that this coloring function is what we want.
$c_0$
is the coloring function in Lemma 4.1. We claim that this coloring function is what we want.
For any infinite
![]() $\Pi ^0_3$
set A, if it has weak apartness, then it is not a solution to
$\Pi ^0_3$
set A, if it has weak apartness, then it is not a solution to
![]() $c_2$
for
$c_2$
for
![]() $\mathrm {HT}$
; if it does not have weak apartness, then it is not a solution to
$\mathrm {HT}$
; if it does not have weak apartness, then it is not a solution to
![]() $c_0$
for
$c_0$
for
![]() $\mathrm {HT}^{\leq 2}$
(and hence
$\mathrm {HT}^{\leq 2}$
(and hence
![]() $\mathrm {HT}$
). So in either case, A is not a solution to
$\mathrm {HT}$
). So in either case, A is not a solution to
![]() $c=c_2\times c_0$
for
$c=c_2\times c_0$
for
![]() $\mathrm {HT}$
.
$\mathrm {HT}$
.
5.
 $\Pi _3^0$
-unsolvability with four colors
$\Pi _3^0$
-unsolvability with four colors
In this section, we will prove the
![]() $\Pi ^0_3$
-unsolvability with only four colors, i.e., the following theorem:
$\Pi ^0_3$
-unsolvability with only four colors, i.e., the following theorem:
Theorem 5.1. There exists a recursive coloring function
![]() $c:\mathbb {N}\rightarrow \{0,1\}^2$
such that any infinite
$c:\mathbb {N}\rightarrow \{0,1\}^2$
such that any infinite
![]() $\Pi _3^0$
set A is not a solution to c for
$\Pi _3^0$
set A is not a solution to c for
![]() $\mathrm {HT}$
.
$\mathrm {HT}$
.
This theorem is an improvement of 4.2 because the number of colors also matters in reverse mathematics investigations on Hindman’s theorem. For example,
![]() $\mathrm {HT}^{\leq 2}_4$
implies
$\mathrm {HT}^{\leq 2}_4$
implies
![]() $\mathrm {ACA}_0$
, but for
$\mathrm {ACA}_0$
, but for
![]() $\mathrm {HT}^{\leq 2}_2$
it is unknown, see [Reference Carlucci, Kołodziejczyk, Lepore and Zdanowski5].
$\mathrm {HT}^{\leq 2}_2$
it is unknown, see [Reference Carlucci, Kołodziejczyk, Lepore and Zdanowski5].
Recall that, the definition of weak apartness has two properties, and each one requires a
![]() $\times 2$
factor for the number of colors of the final coloring function. However, one property is not necessary to prove
$\times 2$
factor for the number of colors of the final coloring function. However, one property is not necessary to prove
![]() $\Pi ^0_3$
-unsolvability. We can use the following even weaker notion of apartness:
$\Pi ^0_3$
-unsolvability. We can use the following even weaker notion of apartness:
Definition 5.2. (1) An infinite set A has weak–weak-apartness if for any number L, there are only finitely many x such that
![]() $\lambda (x)\leq L$
.
$\lambda (x)\leq L$
.
(2) For an infinite set A with weak–weak-apartness, we define a function
![]() $p_A$
from
$p_A$
from
![]() $\mathbb {N}$
to
$\mathbb {N}$
to
![]() $\mathbb {N}$
:
$\mathbb {N}$
:
![]() $p_A(m)$
is the least value
$p_A(m)$
is the least value
![]() $\lambda (w)$
when
$\lambda (w)$
when
![]() $\mu (w)\geq m$
.
$\mu (w)\geq m$
.
Lemma 5.3. Let A be an infinite set with weak–weak-apartness, then:
(1) For any number L, there exists M such that for any
![]() $x>M$
in A,
$x>M$
in A,
![]() $\lambda (x)>L$
. And similarly, there exists M such that for any x, if
$\lambda (x)>L$
. And similarly, there exists M such that for any x, if
![]() $\mu (x)>M$
, then
$\mu (x)>M$
, then
![]() $\lambda (x)>L$
; then we define a function
$\lambda (x)>L$
; then we define a function
![]() $b_A(L)$
to be the least such M.
$b_A(L)$
to be the least such M.
(2)
![]() $p_A$
is well-defined and
$p_A$
is well-defined and
![]() $\lim _m p_A(m)=\infty $
.
$\lim _m p_A(m)=\infty $
.
Proof Both parts are quite obvious.
(1) By definition, there are only finitely many x in A that
![]() $\lambda (x)\leq L$
. If there does not exist such x, then let
$\lambda (x)\leq L$
. If there does not exist such x, then let
![]() $M=0$
and any x has that
$M=0$
and any x has that
![]() $\lambda (x)>L$
. If there exists at least one such x, we choose the largest number x and let
$\lambda (x)>L$
. If there exists at least one such x, we choose the largest number x and let
![]() $M=x$
, then for any
$M=x$
, then for any
![]() $x>M$
in A, not
$x>M$
in A, not
![]() $\lambda (x)\leq L$
and hence
$\lambda (x)\leq L$
and hence
![]() $\lambda (x)>L$
. Similarly, we choose the largest
$\lambda (x)>L$
. Similarly, we choose the largest
![]() $\mu (x)$
and let
$\mu (x)$
and let
![]() $M=\mu (x)$
, then for any x in A such that
$M=\mu (x)$
, then for any x in A such that
![]() $\mu (x)>M$
, we have
$\mu (x)>M$
, we have
![]() $\lambda (x)>L$
.
$\lambda (x)>L$
.
(2) The reason
![]() $p_A$
is well-defined is simply because A is infinite. This implies that for any m, there exists
$p_A$
is well-defined is simply because A is infinite. This implies that for any m, there exists
![]() $x\in A$
such that
$x\in A$
such that
![]() $\mu (x)\geq m$
. Thus, we can conclude that the least value of
$\mu (x)\geq m$
. Thus, we can conclude that the least value of
![]() $\lambda (w)$
exists.
$\lambda (w)$
exists.
![]() $\lim _m p_A(m)=\infty $
because for any L, by (1), there exists M such that for any
$\lim _m p_A(m)=\infty $
because for any L, by (1), there exists M such that for any
![]() $x>M$
in A,
$x>M$
in A,
![]() $\lambda (x)>L$
. So for any x in A, if
$\lambda (x)>L$
. So for any x in A, if
![]() $\mu (x)>M+1$
, because
$\mu (x)>M+1$
, because
![]() $\mu (x)\leq x-1$
, we have that
$\mu (x)\leq x-1$
, we have that
![]() $\lambda (x)>L$
and hence
$\lambda (x)>L$
and hence
![]() $p_A(M+1)>L$
. So
$p_A(M+1)>L$
. So
![]() $\lim _m p_A(m)=\infty $
.
$\lim _m p_A(m)=\infty $
.
We will show that the construction of Section 2.2 also kills all infinite
![]() $\Pi _3^0$
sets with weak–weak-apartness without any other modification. This is because the construction, definitions in verification part 1, and Lemma 3.6 all do not rely on apartness or weak-apartness. So we only need to modify and prove the conclusions in verification part 2 of Section 2.2.
$\Pi _3^0$
sets with weak–weak-apartness without any other modification. This is because the construction, definitions in verification part 1, and Lemma 3.6 all do not rely on apartness or weak-apartness. So we only need to modify and prove the conclusions in verification part 2 of Section 2.2.
For convenience, in this section, if
![]() $f(s)$
is a function with finite range and A is a set, then
$f(s)$
is a function with finite range and A is a set, then
![]() $\lim _s f(s)\in A$
means that there exists a number S such that for any
$\lim _s f(s)\in A$
means that there exists a number S such that for any
![]() $s>S$
,
$s>S$
,
![]() $f(s)\in A$
. We will use this expression frequently. In this case, it is possible that
$f(s)\in A$
. We will use this expression frequently. In this case, it is possible that
![]() $\lim _s f(s)$
does not exist. We introduce a generalization of Lemma 3.3.
$\lim _s f(s)$
does not exist. We introduce a generalization of Lemma 3.3.
Lemma 5.4 (Guessing a single set).
Let n be a natural number and
![]() $A_i$
be an infinite
$A_i$
be an infinite
![]() $\Pi _3^0$
set in the list of Lemma 3.2 such that
$\Pi _3^0$
set in the list of Lemma 3.2 such that
![]() $A_i\cap B^{n}$
is nonempty, then
$A_i\cap B^{n}$
is nonempty, then
![]() $\lim _{y}\lim _s x(i,n,y,s)\in A_i$
.
$\lim _{y}\lim _s x(i,n,y,s)\in A_i$
.
Proof Since
![]() $A_i\cap B^n\neq \emptyset $
, we choose a number
$A_i\cap B^n\neq \emptyset $
, we choose a number
![]() $x_0\in A_i\cap B^n$
. For any
$x_0\in A_i\cap B^n$
. For any
![]() $x\in B^n\setminus A_i$
, there exists
$x\in B^n\setminus A_i$
, there exists
![]() $y_x$
such that
$y_x$
such that
![]() $\lim _s F(i,x,y,s)=\infty $
for any
$\lim _s F(i,x,y,s)=\infty $
for any
![]() $y>y_x$
. Let
$y>y_x$
. Let
![]() $y_0=\max \{y_x:x\in B^n\setminus A_i\}$
.
$y_0=\max \{y_x:x\in B^n\setminus A_i\}$
.
For any
![]() $y>y_0$
, there exists a number
$y>y_0$
, there exists a number
![]() $k_y$
such that
$k_y$
such that
![]() $\lim _s F(i,x_0,y,s)=k_y$
. And for each
$\lim _s F(i,x_0,y,s)=k_y$
. And for each
![]() $x\in B^n\setminus A_i$
,
$x\in B^n\setminus A_i$
,
![]() $ \lim _sF(i,x,y,s)$
is infinite. So for any
$ \lim _sF(i,x,y,s)$
is infinite. So for any
![]() $y>y_0$
, for any sufficiently large number s,
$y>y_0$
, for any sufficiently large number s,
![]() $x(i,n,y,s)\in A_i$
.
$x(i,n,y,s)\in A_i$
.
Lemma 5.5. Let
![]() $A_i$
be an infinite
$A_i$
be an infinite
![]() $\Pi _3^0$
set in the list with weak–weak-apartness, and n be an number such that
$\Pi _3^0$
set in the list with weak–weak-apartness, and n be an number such that
![]() $I(n)=i$
. Then for any
$I(n)=i$
. Then for any
![]() $r>1$
and any Y, there exists a sequence
$r>1$
and any Y, there exists a sequence
![]() $m_1<\cdots <m_g\cdots <m_r$
such that:
$m_1<\cdots <m_g\cdots <m_r$
such that:
(1) For any
![]() $g\in (0,r]$
,
$g\in (0,r]$
,
![]() $B^{m_g}\cap A_i\neq \emptyset $
.
$B^{m_g}\cap A_i\neq \emptyset $
.
(2)
![]() $p_{A_i}(m_1)>Y$
and for any
$p_{A_i}(m_1)>Y$
and for any
![]() $g\in (0,r)$
,
$g\in (0,r)$
,
![]() $p_{A_{i}}(m_{g+1})>m_g$
.
$p_{A_{i}}(m_{g+1})>m_g$
.
(3) For any
![]() $g\in (0,r)$
and any
$g\in (0,r)$
and any
![]() $l\in [p_{A_i}(m_{g+1}),m_{g+1}]$
,
$l\in [p_{A_i}(m_{g+1}),m_{g+1}]$
,
Proof This proof is similar to Lemma 3.7 but more complex. By Lemma 5.4, for any sufficiently large M such that
![]() $B^M\cap A_i$
is nonempty,
$B^M\cap A_i$
is nonempty,
where the limit may not exist. And because
![]() $\lim _k\lim _s I(n,M,k,s)=i$
, we have that
$\lim _k\lim _s I(n,M,k,s)=i$
, we have that
for any sufficiently large M. Based on this, we prove the lemma by induction on r.
For
![]() $r=2$
: In this case, g can only be
$r=2$
: In this case, g can only be
![]() $1$
. Let Y be given, and without loss of generality, we assume that Y is sufficiently large:
$1$
. Let Y be given, and without loss of generality, we assume that Y is sufficiently large:
By Lemma 5.3, we choose a number
![]() $m_1$
such that
$m_1$
such that
![]() $p_{A_{i}}(m_1)>Y$
, and
$p_{A_{i}}(m_1)>Y$
, and
![]() $ A_i\cap B^{m_1}$
is nonempty. Hence
$ A_i\cap B^{m_1}$
is nonempty. Hence
Then we choose a number
![]() $k_0$
such that
$k_0$
such that
and a number
![]() $m_2$
such that
$m_2$
such that
![]() $ A_i\cap B^{m_2}$
is nonempty and
$ A_i\cap B^{m_2}$
is nonempty and
![]() $p_{A_{i}}(m_2)>m_1,k_0$
. Then lims
Q
n
(m
1, l, s) ∈ A
i
for any l in
$p_{A_{i}}(m_2)>m_1,k_0$
. Then lims
Q
n
(m
1, l, s) ∈ A
i
for any l in
![]() $[p_{A_i}(m_2),m_2]$
. This sequence
$[p_{A_i}(m_2),m_2]$
. This sequence
![]() $m_1<m_2$
satisfies our requirements.
$m_1<m_2$
satisfies our requirements.
For
![]() $r+1$
when
$r+1$
when
![]() $r\geq 2$
: Again, let Y be the given number that is sufficiently large. Applying the Induction Hypothesis for r and Y, there exists a sequence
$r\geq 2$
: Again, let Y be the given number that is sufficiently large. Applying the Induction Hypothesis for r and Y, there exists a sequence
![]() $m_1<\cdots <m_r$
such that:
$m_1<\cdots <m_r$
such that:
(1) for any
![]() $g\in (0,r]$
,
$g\in (0,r]$
,
![]() $B^{m_g}\cap A_i\neq \emptyset $
;
$B^{m_g}\cap A_i\neq \emptyset $
;
(2)
![]() $p_{A_i}(m_1)>Y$
and for any
$p_{A_i}(m_1)>Y$
and for any
![]() $g\in (0,r)$
,
$g\in (0,r)$
,
![]() $p_{A_{i}}(m_{g+1})>m_g$
;
$p_{A_{i}}(m_{g+1})>m_g$
;
(3) for any
![]() $g\in (0,r)$
and any
$g\in (0,r)$
and any
![]() $l\in [p_{A_i}(m_{g+1}),m_{g+1}]$
,
$l\in [p_{A_i}(m_{g+1}),m_{g+1}]$
,
Because
![]() $A_i\cap B^{m_r}\neq \emptyset $
,
$A_i\cap B^{m_r}\neq \emptyset $
,
![]() $m_r>Y$
and Y is sufficiently large,
$m_r>Y$
and Y is sufficiently large,
So we choose a number
![]() $k_0$
such that for any
$k_0$
such that for any
![]() $k>k_0, \lim _s Q_n(m_{r},k,s)\in A_i$
and choose a number
$k>k_0, \lim _s Q_n(m_{r},k,s)\in A_i$
and choose a number
![]() $m_{r+1}$
such that
$m_{r+1}$
such that
![]() $ A_i\cap B^{m_{r+1}}\neq \emptyset $
and
$ A_i\cap B^{m_{r+1}}\neq \emptyset $
and
![]() $p_{A_{i}}(m_{r+1})>m_r,k_0$
. Then for any
$p_{A_{i}}(m_{r+1})>m_r,k_0$
. Then for any
![]() $l\in [p_{A_{i}}(m_{r+1}),m_{r+1}]$
,
$l\in [p_{A_{i}}(m_{r+1}),m_{r+1}]$
,
We can see that this new the sequence
![]() $m_1<\cdots <m_r<m_{r+1}$
is what we want.
$m_1<\cdots <m_r<m_{r+1}$
is what we want.
Lemma 5.6. Let
![]() $A_i$
be a infinite
$A_i$
be a infinite
![]() $\Pi _3^0$
set with weak–weak-apartness, and n be a number such that
$\Pi _3^0$
set with weak–weak-apartness, and n be a number such that
![]() $I(n)=i$
. Then for any
$I(n)=i$
. Then for any
![]() $r>1$
and any number Y, there exists a sequence
$r>1$
and any number Y, there exists a sequence
![]() $x_1\ll x_2\ll \cdots \ll x_r\ll x_{r+1}$
all in
$x_1\ll x_2\ll \cdots \ll x_r\ll x_{r+1}$
all in
![]() $A_i$
such that
$A_i$
such that
![]() $\lambda (x_1)>Y$
and for any
$\lambda (x_1)>Y$
and for any
![]() $g\in (0,r)$
,
$g\in (0,r)$
,
Proof First of all, by Lemma 5.5, for r and Y, choose a sequence
![]() $\langle m_g\rangle , g\in [1,r]$
satisfying those properties, especially, for any
$\langle m_g\rangle , g\in [1,r]$
satisfying those properties, especially, for any
![]() $g\in [1,r-1]$
,
$g\in [1,r-1]$
,
So we choose a number
![]() $x_{r+1}\in A_i$
sufficiently large such that
$x_{r+1}\in A_i$
sufficiently large such that
![]() $\lambda (x_{r+1})>m_r$
and for any
$\lambda (x_{r+1})>m_r$
and for any
![]() $g\in [1,r-1]$
,
$g\in [1,r-1]$
,
Then we choose a number
![]() $x_r\in A_i$
such that
$x_r\in A_i$
such that
![]() $\mu (x_r)=m_r$
.
$\mu (x_r)=m_r$
.
Now we inductively construct the sequence
![]() $x_1\ll \cdots \ll x_r\ll x_{r+1}$
from
$x_1\ll \cdots \ll x_r\ll x_{r+1}$
from
![]() $x_r$
to
$x_r$
to
![]() $x_1$
satisfying the requirements of this lemma and
$x_1$
satisfying the requirements of this lemma and
![]() $\mu (x_h)=m_h$
for each
$\mu (x_h)=m_h$
for each
![]() $h\in [1,r]$
.
$h\in [1,r]$
.
Suppose for a number
![]() $h\in [2,r]$
, we have constructed a sequence
$h\in [2,r]$
, we have constructed a sequence
![]() $x_h\ll \cdots \ll x_r\ll x_{r+1}$
satisfying our requirements, then by the properties of the sequence
$x_h\ll \cdots \ll x_r\ll x_{r+1}$
satisfying our requirements, then by the properties of the sequence
![]() $\langle m_g\rangle _{g\in [1,r]}$
and because
$\langle m_g\rangle _{g\in [1,r]}$
and because
![]() $p_{A_i}(m_{h})\leq \lambda (x_{h})\leq m_h$
, we have that
$p_{A_i}(m_{h})\leq \lambda (x_{h})\leq m_h$
, we have that
So we can choose a number
![]() $x_{h-1}\in B^{m_{h-1}}\cap A_i$
such that
$x_{h-1}\in B^{m_{h-1}}\cap A_i$
such that
We add
![]() $x_{h-1}$
to the sequence. We can see this new sequence satisfies our requirements. This finishes the induction step. Finally, we show that
$x_{h-1}$
to the sequence. We can see this new sequence satisfies our requirements. This finishes the induction step. Finally, we show that
![]() $\lambda (x_1)>Y$
. This is simply because
$\lambda (x_1)>Y$
. This is simply because
![]() $p_{A_i}(m_1)>Y$
and
$p_{A_i}(m_1)>Y$
and
![]() $x_1\in B^{m_1}$
. This finishes the proof of this lemma.
$x_1\in B^{m_1}$
. This finishes the proof of this lemma.
Lemma 5.7. Let
![]() $R(n,w)$
be the function in previous construction,
$R(n,w)$
be the function in previous construction,
![]() $A_i$
be an infinite
$A_i$
be an infinite
![]() $\Pi _3^0$
set with weak–weak-apartness and n be a number such that
$\Pi _3^0$
set with weak–weak-apartness and n be a number such that
![]() $I(n)=i$
. Then, for
$I(n)=i$
. Then, for
![]() $r=|B^n|$
, there exist r many numbers
$r=|B^n|$
, there exist r many numbers
![]() $w_j\in FS(A_i)$
, with
$w_j\in FS(A_i)$
, with
![]() $j\in [1,r]$
, such that each
$j\in [1,r]$
, such that each
![]() $w_h$
is sum of finitely many numbers x in
$w_h$
is sum of finitely many numbers x in
![]() $A_i$
such that
$A_i$
such that
![]() $\lambda (x)>n$
and has a distinct
$\lambda (x)>n$
and has a distinct
![]() $R(n,w_j)$
value.
$R(n,w_j)$
value.
Proof This proof is almost the same as the proof of Lemma 3.8.
Apply Lemma 5.6 for
![]() $Y=n$
and r, there exists a sequence
$Y=n$
and r, there exists a sequence
![]() $\langle x_g\rangle $
with
$\langle x_g\rangle $
with
![]() $g\in [1,r+1]$
such that
$g\in [1,r+1]$
such that
![]() $\lambda (x_1)>n$
and for any
$\lambda (x_1)>n$
and for any
![]() $h\in [2,r]$
,
$h\in [2,r]$
,
Now for
![]() $ h\in [1,r]$
, let
$ h\in [1,r]$
, let
![]() $w_h=\sum _{g=h}^{r+1}x_g$
. It is obvious that
$w_h=\sum _{g=h}^{r+1}x_g$
. It is obvious that
![]() $\lambda (w_h)>n$
for any
$\lambda (w_h)>n$
for any
![]() $h\in [1,r]$
. We show that for
$h\in [1,r]$
. We show that for
![]() $1\leq h_2<h_1\leq r$
,
$1\leq h_2<h_1\leq r$
,
For each
![]() $w_h$
,
$w_h$
,
![]() $\mu (w_h)=\mu (x_{r+1})$
and
$\mu (w_h)=\mu (x_{r+1})$
and
![]() $\lambda (w_h)=\lambda (x_h)$
. So by our assumption, for
$\lambda (w_h)=\lambda (x_h)$
. So by our assumption, for
![]() $h\in [1,r]$
$h\in [1,r]$
Then by the construction and Corollary 1, for
![]() $h\in [2,r]$
$h\in [2,r]$
 $$ \begin{align*} R_0(n,w_{h})+1&\equiv R_0(n,Q_n(\mu(x_{h-1}),\lambda(w_{h}),\mu(w_{h}))+w_{h})\quad \mod r\\ &\equiv R_0(n,x_{h-1}+w_{h})\quad \mod r\\ &\equiv R_0(n,w_{h-1})\quad \mod r. \end{align*} $$
$$ \begin{align*} R_0(n,w_{h})+1&\equiv R_0(n,Q_n(\mu(x_{h-1}),\lambda(w_{h}),\mu(w_{h}))+w_{h})\quad \mod r\\ &\equiv R_0(n,x_{h-1}+w_{h})\quad \mod r\\ &\equiv R_0(n,w_{h-1})\quad \mod r. \end{align*} $$
So
![]() $R_0(n,w_{h_1})\equiv R_0(n,w_{h_2})-(h_1-h_2)\ \mod r$
and each
$R_0(n,w_{h_1})\equiv R_0(n,w_{h_2})-(h_1-h_2)\ \mod r$
and each
![]() $w_h$
has a distinct
$w_h$
has a distinct
![]() $R(n,w_h)$
value. This finishes the proof.
$R(n,w_h)$
value. This finishes the proof.
Lemma 5.8. Let
![]() $A_i$
be an infinite
$A_i$
be an infinite
![]() $\Pi _3^0$
set with weak–weak apartness in the list of Lemma 3.2 and
$\Pi _3^0$
set with weak–weak apartness in the list of Lemma 3.2 and
![]() $R(n,w)$
be the function in our construction. There exists n,
$R(n,w)$
be the function in our construction. There exists n,
![]() $x\in B^n\cap A_i$
and
$x\in B^n\cap A_i$
and
![]() $w\in FS(A_i)$
such that
$w\in FS(A_i)$
such that
![]() $x+w\in FS(A_i)n$
and
$x+w\in FS(A_i)n$
and
Proof This proof is very similar to the proof of Lemma 3.9.
By Lemma 3.6, there exists n such that
![]() $I(n)=i$
and by Lemma 5.7, for
$I(n)=i$
and by Lemma 5.7, for
![]() $r=|B^n|$
, there exist numbers
$r=|B^n|$
, there exist numbers
![]() $w_h,1\leq h\leq r$
all in
$w_h,1\leq h\leq r$
all in
![]() $FS(A_i)$
such that each
$FS(A_i)$
such that each
![]() $w_h$
is sum of finitely many numbers x in
$w_h$
is sum of finitely many numbers x in
![]() $A_i$
such that
$A_i$
such that
![]() $\lambda (x)>n$
, and each
$\lambda (x)>n$
, and each
![]() $w_h$
has a distinct
$w_h$
has a distinct
![]() $R(n,w_h)$
value. Because
$R(n,w_h)$
value. Because
![]() $R(n,w_h)\in B^n$
for any such
$R(n,w_h)\in B^n$
for any such
![]() $w_h$
, for any
$w_h$
, for any
![]() $x\in B^n$
, there exists one
$x\in B^n$
, there exists one
![]() $w_h$
such that
$w_h$
such that
![]() $R(n,w_h)=x$
.
$R(n,w_h)=x$
.
By Lemma 3.5,
![]() $i=I(n)=\min \{Z(n)\setminus H(n)\cup \{\infty \}\}.$
Because i is a number rather than
$i=I(n)=\min \{Z(n)\setminus H(n)\cup \{\infty \}\}.$
Because i is a number rather than
![]() $\infty $
,
$\infty $
,
![]() $i\in Z(n)=\{i<n:A_i\cap B^n\neq \emptyset \}$
. Hence
$i\in Z(n)=\{i<n:A_i\cap B^n\neq \emptyset \}$
. Hence
![]() $A_i\cap B^n\neq \emptyset $
.
$A_i\cap B^n\neq \emptyset $
.
Therefore we can find
![]() $x\in B^n\cap A_i$
and
$x\in B^n\cap A_i$
and
![]() $w_h$
such that
$w_h$
such that
![]() $R(n,w_h)=x$
and these
$R(n,w_h)=x$
and these
![]() $n,w_h,x$
are what we need.
$n,w_h,x$
are what we need.
Theorem 5.9. There exists a recursive coloring function
![]() $c:\mathbb {N}\rightarrow \{0,1\}$
such that any infinite
$c:\mathbb {N}\rightarrow \{0,1\}$
such that any infinite
![]() $\Pi _3^0$
set with weak–weak-apartness is not a solution of c for Hindman’s theorem.
$\Pi _3^0$
set with weak–weak-apartness is not a solution of c for Hindman’s theorem.
Proof We show that the coloring function c in Section 2.2, Theorem 3.10 is a witness for this theorem. This is almost the same as the proof of Theorem 3.10. Use the function
![]() $R(n,w)$
in our construction and apply Corollary 1 to
$R(n,w)$
in our construction and apply Corollary 1 to
![]() $R(n,w)$
to get a coloring function c. We show that c is what we need.
$R(n,w)$
to get a coloring function c. We show that c is what we need.
Because any infinite
![]() $\Pi _3^0$
set A is equal to a set
$\Pi _3^0$
set A is equal to a set
![]() $A_i$
in the list of Lemma 3.2, by Lemma 5.8, there exists numbers
$A_i$
in the list of Lemma 3.2, by Lemma 5.8, there exists numbers
![]() $n,x,w$
such that
$n,x,w$
such that
![]() $x\in B^n\cap A_i$
,
$x\in B^n\cap A_i$
,
![]() $w\in FS(A_i)$
,
$w\in FS(A_i)$
,
![]() $\lambda (w)>n$
,
$\lambda (w)>n$
,
![]() $x+w\in FS(A_i)$
and
$x+w\in FS(A_i)$
and
![]() $R(n,w)=x$
. By Corollary 1,
$R(n,w)=x$
. By Corollary 1,
![]() $c(w)\neq c(w+R(n,w))$
if
$c(w)\neq c(w+R(n,w))$
if
![]() $n<\lambda (w)$
. So
$n<\lambda (w)$
. So
![]() $c(w)\neq c(w+x)$
. Because
$c(w)\neq c(w+x)$
. Because
![]() $\lambda (w)>n=\mu (x)$
, both w and
$\lambda (w)>n=\mu (x)$
, both w and
![]() $w+x$
are in
$w+x$
are in
![]() $FS(A_i)$
. Two numbers
$FS(A_i)$
. Two numbers
![]() $w,w+x$
are both in
$w,w+x$
are both in
![]() $FS(A_i)$
and
$FS(A_i)$
and
![]() $c(w)\neq c(w+x)$
. This concludes the proof.
$c(w)\neq c(w+x)$
. This concludes the proof.
Lemma 5.10. There exists a recursive coloring function
![]() $c_0:\mathbb {N}\rightarrow \{0,1\}$
such that for any infinite set A, if it does not have weak–weak-apartness, then it is not a solution to c for
$c_0:\mathbb {N}\rightarrow \{0,1\}$
such that for any infinite set A, if it does not have weak–weak-apartness, then it is not a solution to c for
![]() $\mathrm {HT}^{\leq 2}$
.
$\mathrm {HT}^{\leq 2}$
.
Proof This proof is just a subset of the proof of Lemma 4.1.
We define a coloring function
![]() $c_0:\mathbb {N}\rightarrow \{0,1\}$
:
$c_0:\mathbb {N}\rightarrow \{0,1\}$
:
We show that if an infinite set A does not have weak–weak-apartness, then it is not monochromatic under
![]() $c_0$
. If A has not weak–weak-apartness, then there are three different numbers
$c_0$
. If A has not weak–weak-apartness, then there are three different numbers
![]() $x_1,x_2,x_3$
such that
$x_1,x_2,x_3$
such that
![]() $\lambda (x_1)=\lambda (x_2)=\lambda (x_3)=l$
; otherwise there are at most
$\lambda (x_1)=\lambda (x_2)=\lambda (x_3)=l$
; otherwise there are at most
![]() $2L$
numbers x that satisfies
$2L$
numbers x that satisfies
![]() $\lambda (x)\leq L$
, contradict to the assumption of weak–weak-apartness. All three numbers are divisible by
$\lambda (x)\leq L$
, contradict to the assumption of weak–weak-apartness. All three numbers are divisible by
![]() $2^l$
and not by
$2^l$
and not by
![]() $2^{l+1}$
. So for any X among these three numbers,
$2^{l+1}$
. So for any X among these three numbers,
![]() $X\equiv 2^l \text { or }2^{l+1}+2^l\ \mod 2^{l+2}$
and there must be two number
$X\equiv 2^l \text { or }2^{l+1}+2^l\ \mod 2^{l+2}$
and there must be two number
![]() $X_1,X_2$
among
$X_1,X_2$
among
![]() $x_1,x_2,x_3$
such that
$x_1,x_2,x_3$
such that
![]() $X_1\equiv X_2\ \mod 2^{l+2}$
. Hence
$X_1\equiv X_2\ \mod 2^{l+2}$
. Hence
![]() $X_1+X_2$
is divisible by
$X_1+X_2$
is divisible by
![]() $2^{l+1}$
but not
$2^{l+1}$
but not
![]() $2^{l+2}$
and
$2^{l+2}$
and
![]() $\lambda (X_1+X_2)=l+1$
. Since
$\lambda (X_1+X_2)=l+1$
. Since
![]() $\lambda (x_1)=l$
,
$\lambda (x_1)=l$
,
![]() $c_2(X_1+X_2)\neq c_2(x_1)$
and
$c_2(X_1+X_2)\neq c_2(x_1)$
and
![]() $FS^{\leq 2}(A)$
is not monochromatic.
$FS^{\leq 2}(A)$
is not monochromatic.
Therefore, if A does not have weak apartness, then it is not a solution to
![]() $c_0$
.
$c_0$
.
Now we can show the main theorem of this section.
Theorem 5.11. There exists a recursive coloring function
![]() $c:\mathbb {N}\rightarrow \{0,1\}^2$
such that any infinite
$c:\mathbb {N}\rightarrow \{0,1\}^2$
such that any infinite
![]() $\Pi _3^0$
set is not a solution of c for Hindman’s theorem.
$\Pi _3^0$
set is not a solution of c for Hindman’s theorem.
Proof From Lemmas 5.9 and 5.10, we can get recursive colorings
![]() $c_1,c_2$
such that any infinite
$c_1,c_2$
such that any infinite
![]() $\Pi ^0_3$
set with weak–weak-apartness is not monochromatic for
$\Pi ^0_3$
set with weak–weak-apartness is not monochromatic for
![]() $c_1$
, and any infinite
$c_1$
, and any infinite
![]() $\Pi ^0_3$
set without weak–weak-apartness is not monochromatic for
$\Pi ^0_3$
set without weak–weak-apartness is not monochromatic for
![]() $c_2$
.
$c_2$
.
Define the coloring
![]() $c=c_1\times c_2$
. We can easily see that any infinite
$c=c_1\times c_2$
. We can easily see that any infinite
![]() $\Pi ^0_3$
set is not monochromatic for c. Hence, any infinite
$\Pi ^0_3$
set is not monochromatic for c. Hence, any infinite
![]() $\Pi _3^0$
set is not a solution of c for Hindman’s theorem.
$\Pi _3^0$
set is not a solution of c for Hindman’s theorem.
6. Conclusion
We end with a few questions for further investigation. Some open questions are mentioned in [Reference Dzhafarov, Jockusch, Solomon, Westrick, Day, Fellows, Greenberg, Khoussainov, Melnikov and Rosamond6] or [Reference Carlucci4]. In this paper, we proved the
![]() $\Pi _3^0$
-unsolvability of
$\Pi _3^0$
-unsolvability of
![]() $\textrm {HT}$
. So the first question is about the
$\textrm {HT}$
. So the first question is about the
![]() $\Delta _4^0$
-unsolvability:
$\Delta _4^0$
-unsolvability:
Question 6.1. Is there any recursive coloring without any
![]() $\Delta _4^0$
solution for Hindman’s theorem?
$\Delta _4^0$
solution for Hindman’s theorem?
Similarly, in this paper, we proved the
![]() $\Delta _3^0$
-unsolvability of
$\Delta _3^0$
-unsolvability of
![]() $\textrm {HT}^{\leq 3}$
. However, we have not been able to prove the same theorem for the
$\textrm {HT}^{\leq 3}$
. However, we have not been able to prove the same theorem for the
![]() $\Pi _3^0$
case so far. Therefore, we pose the following question:
$\Pi _3^0$
case so far. Therefore, we pose the following question:
Question 6.2. Is there any recursive coloring such that any infinite
![]() $\Pi _3^0$
sets is not a solution for
$\Pi _3^0$
sets is not a solution for
![]() $\textrm {HT}^{\leq 3}$
?
$\textrm {HT}^{\leq 3}$
?
It is known from the literature that the weakest restriction of Hindman’s theorem that codes the jump (as the full version does) is
![]() $\mathrm {HT}^{\leq 2}_4$
, the restriction to sums of at most two numbers [Reference Carlucci, Kołodziejczyk, Lepore and Zdanowski5]. So, a natural question is whether our result is also true of the restriction to sums of at most 2.
$\mathrm {HT}^{\leq 2}_4$
, the restriction to sums of at most two numbers [Reference Carlucci, Kołodziejczyk, Lepore and Zdanowski5]. So, a natural question is whether our result is also true of the restriction to sums of at most 2.
Question 6.3. Is there any recursive coloring such that any infinite
![]() $\Delta _3^0$
sets is not a solution for
$\Delta _3^0$
sets is not a solution for
![]() $\textrm {HT}^{\leq 2}$
?
$\textrm {HT}^{\leq 2}$
?
And similarly, we can ask the following questions:
Question 6.4. Is there any recursive 2-coloring such that any infinite
![]() $\Delta _3^0$
sets is not a solution for
$\Delta _3^0$
sets is not a solution for
![]() $\textrm {HT}^{\leq 3}$
?
$\textrm {HT}^{\leq 3}$
?
Question 6.5. Is there any recursive 2-coloring such that any infinite
![]() $\Pi _3^0$
sets is not a solution for Hindman’s theorem?
$\Pi _3^0$
sets is not a solution for Hindman’s theorem?
An end to all these types of questions is to find a coloring without any arithmetic solution. However, there is currently no mainstream consensus on whether Hindman’s theorem has arithmetical solutions. It is even possible that every coloring function has a
![]() $\Delta _4^0$
solution.
$\Delta _4^0$
solution.
Acknowledgments
I wish to thank my supervisor, Yang Yue, for providing valuable comments and revision suggestions. This paper will be a chapter of my PhD thesis.
Funding
This research was partially supported by MOE2019-T2-2-121, R146-000-337-114 / A-0008494-00-00, and R252-000-C17-114 / A-0008454-00-00.