Background
There is interest in the flow properties of debris-laden ice because it is widespread near the base of ice sheets and glaciers. The deep cores extracted from near the bed in Greenland (Camp Century, Dye 3, GRIP and GISP2) and Antarctica (Byrd, Dome Summit South) all contain debris-laden ice up to many metres from the bottom. In ice sheets the basal layers generally have relatively high shear stress and temperature compared to the rest of the column, so the deformation and velocity profile through the ice sheet depends strongly on the flow properties of the basal ice. The flow properties of the basal ice become more important if the debris-laden ice flows much more readily than clean ice because the higher deformation rates would be significant for the movement of the ice mass and might be difficult to distinguish from high sliding rates (Reference Johnsen, Dansgaard and BroeckerJohnsen and Dansgaard, 1992; Reference DansgaardDansgaard and others, 1993; Reference CastelnauCastelnau and others, 1998). If, on the other hand, the flow rates are less than for clean ice, the dependence on the flow properties of basal ice will not be so severe and the flow profile will resemble a gradual approach to the zero deformation of the bed.
There are several previous works concerning the flow of debris-laden ice, some reporting enhanced flow. Some studies have reported on mechanical experiments (Reference Shoji and LangwayShoji and Langway, 1984; Reference LawsonLawson, 1996; Reference Fitzsimons, Mcmanus and LorrainFitzsimons and others, 1999). Others are based on structural properties of glacial ice, in which the impurity content is relatively low (Reference Holdsworth and BullHoldsworth and Bull, 1970; Reference AndertonAnderton, 1973; Reference Fisher and KoernerFisher and Koerner, 1986; Reference Echelmeyer and ZhongxiangEchelmeyer and Wang, 1987; Reference Tison, Petit, Barnola and MahaneyTison and others, 1993, Reference Tison, Thorsteinsson, Lorrain and Kipfstuhl1994; Reference Gow and MeeseGow and Meese, 1996). These reports have suggested that debris-laden ice exhibits enhanced flow (i.e. higher strain rates). For higher concentrations of impurities, lower strain rates are inferred by Reference Butkovich and LandauerButkovich and Landauer (1959) and Reference Nickling and BennettNickling and Bennett (1984). It should be noted that in these field situations it is not clear to what extent other factors such as the inhomogeneity of the stress field or the anisotropy of the debris-laden ice may also be relevant.
There are extensive results available on relative strengths of frozen soil (Reference VyalovVyalov and others, 1962; Reference Wijeweera and JoshiWijeweera and Joshi, 1993; Reference FishFish, 1994). However, there is much less material covering the steady-state creep of frozen soil or debris-laden ice with low impurity content at the low shear stresses which prevail in ice sheets. The basal shear stresses in glaciers and ice sheets are most commonly in the range 0.05–020 MPa. We are therefore particularly interested in the flow properties of debris-laden ice over this range. At these low stresses it takes considerable time for laboratory-made randomly oriented polycrystalline ice to reach minimum strain rate (at about 1% strain) and much longer to reach a steady-state tertiary strain rate (at 4 10% strain). In ice sheets and glaciers, large strains can be expected to prevail. We therefore need laboratory strain rates to also reach these large strains.
Other measurements of the creep-rate dependence of ice on debris content have not provided a clear relation between these two factors. Reference Hooke, Le, Dahlin and KauperHooke and others (1972) studied sand contents from 0% to ∼35% by volume under 0.56 MPa compression (0.26 MPa octahedral shear stress) at –9.1 °C. Considerable variation was found for concentrations less than 10% sand volume. For higher sand concentrations, a clear and strong decreasing trend in creep rate occurred to less than 10% of the clean-ice creep rate by 35% volume sand concentration.
Reference NayarNayar (1966) and Reference Nayar, Lenel and AnsellNayar and others (1971) studied ice with finely dispersed silica in the concentration range 0–1% by volume. The tests were in simple compression over the range 0.2–0.9 MPa octahedral at temperatures from –2° to –22°C. A strong decrease in creep rate with impurity concentration was obtained.
Reference Baker and GerberichBaker and Gerberich (1979) studied ice samples with sand volume concentrations of 0–6% in simple compression at ∼ 0.5 MPa (0.26 MPa octahedral) at various temperatures between –5° and –38°C. They also attempted to determine if the crystal size of the ice was relevant to the creep rate. For the present context, considering the dependence on sand concentration alone, they obtained little difference in creep rate relative to that of clean ice for low concentrations (up to 2% by volume). But they did find increased creep rates by a factor of about 1.8 for the range of concentrations 5–7% sand volume.
Reference Nickling and BennettNickling and Bennett (1984) performed shear experiments on two samples retrieved from rock glaciers in Grizzly Creek, Yukon Territory, Canada. Their shear experiments were run at –1°C, with sand contents ranging from 0% to near 100% volume and a constant loading rate of 9.63 6 10–4 cmmin–1. Results indicated that samples with higher sand content were subject to less interlocking than samples with lower sand content. The stress–strain curves for the 75% and 70% sand-content samples, though, resulted in more “regular” curves indicating that the particle interlocking of these samples was not as evident. Additionally, the sample shear strength increased as the sand content was increased.
Reference LawsonLawson (1996) conducted uniaxial compression tests on debris-laden field ice from Taylor Glacier, Antarctica, (5– 50% sand content) and on clean ice. The tests were performed at temperatures ranging from 0° to –25°C and with uniaxial compression strength of 1.1–7.6 MPa for debris-laden ice and 1.9–3.4 MPa for clean ice. The strain rates for the tests ranged from 10–2 to 10–3 s–1. Lawson observed that at high temperatures between 0° and –5°C, pressure melting was the dominant deformation mechanism in the debris-laden ice, while cracking was the dominant deformation mechanism in clean ice. But at temperatures of–25°C, the debris-laden ice reached higher strengths than the clean glacier ice, and cracking was the dominant deformation mechanism in both ice types.
Experimental Technique
Laboratory-prepared clean and sand-laden ice was prepared by a method similar to that proposed by Jack a and Lile (1984). Clean samples were included to provide control results against which results for sand-laden ice are compared. For the sand-laden samples, finely ground ice particles were mixed with cold mortar sand in approximately the required proportions before placing in a mould to which water at freezing point was added. The exact concentration of the sand was determined after each experiment, by weighing the residual sand after melting the sample. Mortar sand was used because it contains a range of particle sizes from typically coarse quartz sand (0.25–2.0mm diameter grains) to silty mud with particle sizes 50.05 mm. The sand particle-size distributions were strongly bimodal, centred around these two grades but with the coarse sand dominating. The concentration of silt to the total impurity amount was very variable but averaged about 15% for the sandy samples. This mix of sand and silt is not unlike the material found in the basal ice cores (Reference Holdsworth and BullHoldsworth and Bull, 1970; Reference AndertonAnderton, 1974; Reference Gow, Epstein and SheehyGow and others, 1979; Reference Herron and LangwayHerron and Langway 1979; Gunderstrup and Hansen, 1984; Reference Hammer, Clausen, Dansgaard, Neftel, Kristinsdottir, Johnson, Langway, Oeschger and DansgaardHammer and others, 1985).
In this paper, we present results of deformation tests in constant-load uniaxial compression (samples in group C1 and C2 of Table 1), constant-strain-rate uniaxial compression (samples in group C3 of Table 1) and constant-stress simple shear (group S1 of Table 1). Figure 1 shows creep curves for each test from groups C1, C2 and S1. The test samples for compression tests were cylinders of 25 mm (groups C1, C2) and 50 mm (group C3) diameter. Sample lengths were 60 mm (groups C1, C2) and -100 mm (group C3). Dimensions (length 6 width 6 height) of shear test samples (group S1) were 95 mm 6 15 mm 6 16 mm. At test commencement, shear samples had a 30° back cut so that at ∼1–10% strain, deformation of the sample was such that there was no vertical displacement, i.e. simple shear (Reference Li, Jacka and BuddLi and others, 2000).
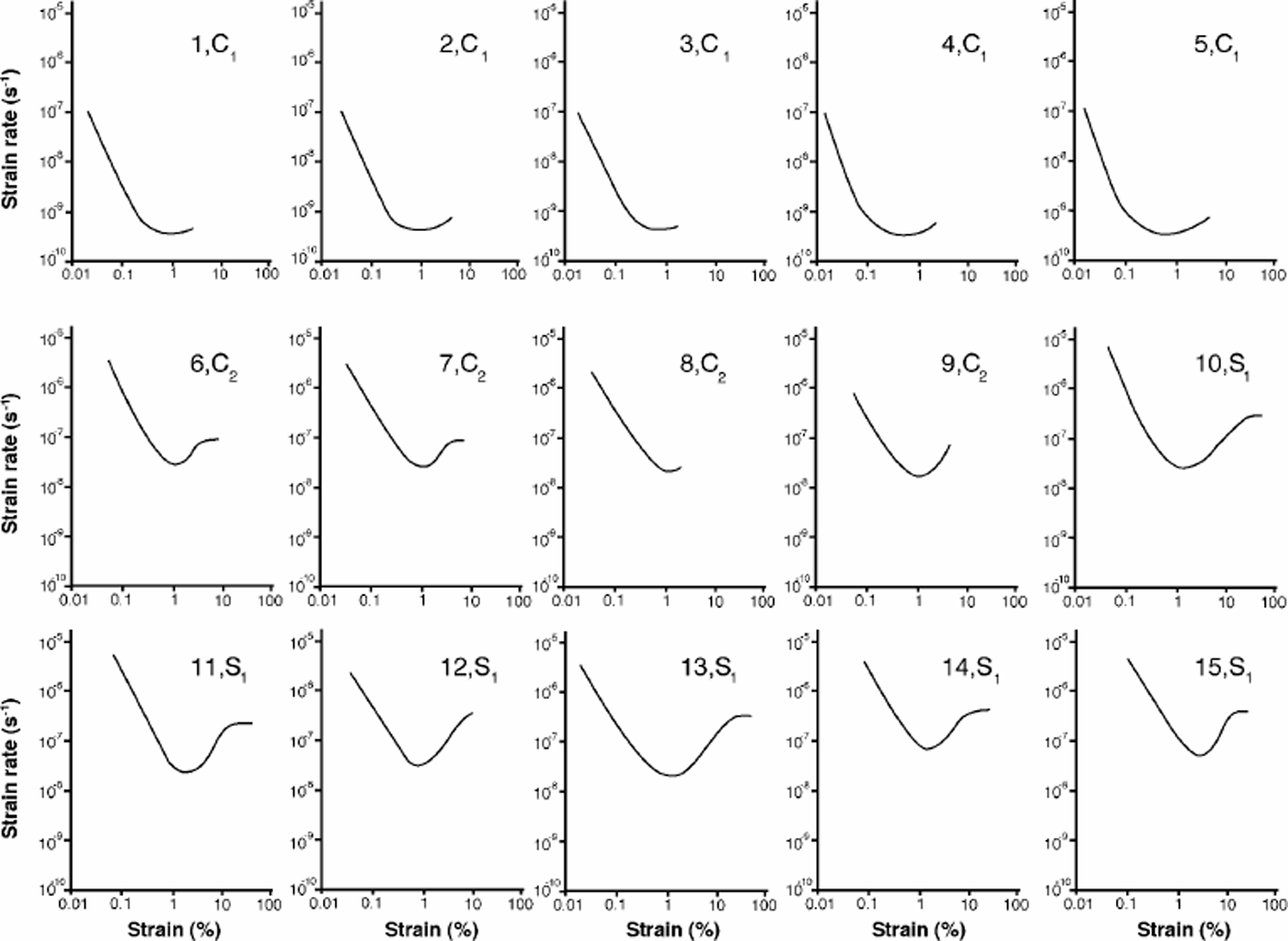
Fig. 1. Creep curves (plots of octahedral strain rate as a function of octahedral strain) for each of the tests in compression (labelled C1and C2) and shear (labelled S1) under constant load. Temperature, stress, debris content and other details are provided in Table1.
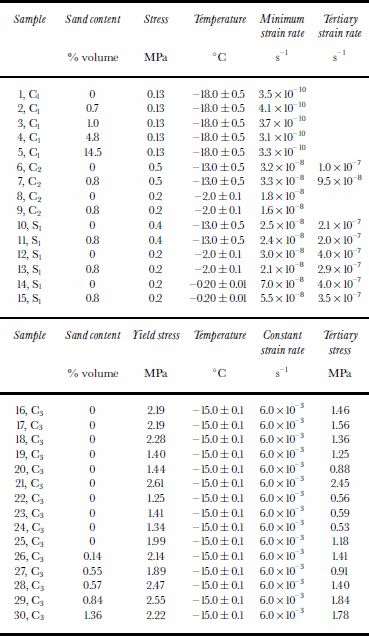
Table 1. Summary of test results in uniaxial compression (constant load), simple shear (constant stress) and uniaxial compression (constant strain rate), over the temperature range –0.20° to–18.0° C
The deformation apparatus for constant-load uniaxial compression tests has been described by Jack a and Lile (1984). The shear apparatus is described by Reference Li, Jacka and BuddLi and others (2000). The constant-strain-rate deformation apparatus is a Monsanto horizontal screw-driven universal testing machine that is able to apply a continually increasing load (maximum 20 kN) at fixed values of constant cross-head speed in the range 0.003–0.870mm s–1.
Stresses and strain rates used throughout this paper are octahedral (root mean square of the tensor deviators) values so that, at minimum strain rate (constant stress) or yield stress (constant strain rate), results in compression and shear are directly comparable (Reference Li, Jacka and BuddLi and others, 1996). Other properties of the tests are listed in Table 1.
Results
Group C1
In most of the laboratory tests of other workers so far carried out on debris-laden ice, there has been no clear evidence to show that similar creep curves or clear minimum creep rates were attained. Creep rates need to be compared at comparable total strains or at similar stages of the creep curves. The objective of the tests of group C1 was to examine the creep rate carefully through to comparable large strains for all tests. The stress chosen, 0.13 MPa octahedral in uniaxial compression, was meant to be realistic for comparison with the basal shear stresses typical of glaciers and ice sheets. The sand concentrations were selected to cover the lower end of the range up to 15% by volume. The temperature, –18°C, was the first in a series of tests aimed at covering a wide range of temperatures. These tests were run, typically to a strain of 4–6%, until a minimum flow rate had clearly been attained. Some of these tests took 4 1.8 years (4 16 000 hours) to attain this strain.
From Table 1, the close similarity in minimum strain rate between the five samples is remarkable (mean minimum strain rate is 3.54 6 10–10 s–1), and there is no relationship apparent between the very minor differences in minimum strain rate with sand content. There is little support here for any strong dependence of creep rate on debris content over this range of concentration (0–14.5% by volume). The measurements here are for a lower stress than previously reported results, but this lower stress is more relevant to the flow of polar ice masses.
Group C2
While these experiments include only 0.8% volume sand concentration, they have been continued to strains sufficient in some cases to attain tertiary strain rate. It is seen from Table 1 that the minimum strain rates for clean ice and sand-laden ice are close to identical. At 0.5 MPa and –13°C the tertiary creep rates are also very similar (samples 6 and 7).
Group S1
The sand content for the shear tests also is 0.8%. All shear tests were carried out at 0.2 MPa, while three different temperatures, –13°, –2.0° and– 0.20°C, were examined. For all three temperatures, even at –0.20°C, the minimum and tertiary creep rates appear unaffected (e.g. tertiary strain rates of 4.0 x 10–7 s–1 for clean ice compared with 3.5 x 10–7 s–1 for sand-laden ice) by 0.8% volume sand content.
As an aside, it is worth noting that the enhancement of tertiary flow rate over minimum flow rate for the compression tests (C2) above was ~3 and that for the shear tests (S1) it was ~9 for both the sand-laden samples and the clean samples. These values are similar to those found in the ice-mechanics literature for anisotropic ice in easy glide in compression and simple shear, respectively (e.g. Reference Li, Jacka and BuddLi and others, 1996).
Group C3
There appears to be a high degree of scatter in the constant-strain-rate results, and further, more careful examination may be required with the constant-strain-rate apparatus, in particular to examine the effect of debris on ice deformation at higher strain rates. The mean yield stress for the ten clean samples of group C3 (samples 16–25) is 1.81 ±0.49 MPa. The yield stresses for the five sand-laden samples (samples 26–30) are higher than this, but there is no clear trend of increasing yield stress with sand content. The tertiary stress values for the sand-laden samples are also higher than the mean value (1.18 ±0.59 MPa) for the ten clean samples. With one exception (sample 27), the tertiary stress also increases systematically with sand content. There is some evidence from these results, therefore, that at this strain rate (10–3 s–1) and at this temperature (–15°C) sand concentrations in the ice may tend to harden the ice, perhaps acting as a reinforcing agent within the ice. This result would seem to confirm Reference LawsonLawson’s (1996) result in the same strain-rate range as examined here, that at temperatures of–25°C the debris-laden ice reached higher strengths than the clean glacier ice.
Conclusions
Our laboratory results present evidence of no significant dependence of either minimum or tertiary flow rate on sand content (up to 15% volume) within ice under deformation in the stress range 0.13–0.5 MPa and temperature range –0.02 to –18.0°C. The laboratory tests have included both uniaxial compression and simple shear. These stress patterns and, importantly, the temperature and stress ranges we have examined are similar to those found at the base of the polar ice sheets.
This contrasts with some laboratory studies of other workers, generally at higher stresses, showing more variable results of both higher and lower strain rates compared with those for clean ice. Our results at higher stresses (and constant strain rate) also provided some indication that sand-laden ice is harder under these conditions, at least at –15°C. This result is of little relevance, however, to the flow of the polar ice sheets and mountain glaciers.
It is also important to examine the creep dependence on the type of solid impurity and whether inherent chemical effects with the impurities are also relevant. The change of the ice crystallographic properties through the course of the deformation for debris-laden ice should also be studied for comparison with the general results obtained for clean ice.
Caution is required in any assumptions about the flow rates of debris-laden ice in ice masses until a clearer understanding of the debris-laden ice-flow rates relative to those for clean ice has been obtained. To facilitate such an understanding, samples of debris-laden ice from field situations need to be studied in the laboratory under the same type of stress magnitude and configuration as exists in situ in field conditions. Comparisons need to be made with clean ice deformed to high strains under the same stress configuration, and adequate account then needs to be taken of other factors such as the crystallography and the development of anisotropy. This work is now in progress at the Antarctic CRC.




