AROUND THE NEARBY CYCLE FUNCTOR FOR ARITHMETIC $\mathscr{D}$-MODULES

Abstract

We will establish a nearby and vanishing cycle formalism for the arithmetic $\mathscr{D}$-module theory following Beilinson’s philosophy. As an application, we define smooth objects in the framework of arithmetic $\mathscr{D}$-modules whose category is equivalent to the category of overconvergent isocrystals.

Introduction

In this paper, we establish a theory of nearby/vanishing cycle functor in the framework of arithmetic $\mathscr{D}$ -modules and give some applications. Unipotent nearby/vanishing cycle formalism has already been established by the author together with Caro in [AC2] after the philosophy of Beilinson. Beilinson’s philosophy (cf. [Bei, Remark after Corollary 3.2]) also tells us how to go from unipotent nearby/vanishing cycle functors to the full ones, and in fact, this philosophy underlies the argument of [A2, Lemma 2.4.13]. The aim of this article is to carry this out more systematically so that the nearby/vanishing cycle formalism is also accessible in the $p$ -adic cohomology theory.

Now, let us clarify what properties make full nearby/vanishing cycle functors different from unipotent counterpart. Let $k$ be a perfect field of positive characteristic. Given a morphism of finite type $f:X\rightarrow \mathbb{A}_{k}^{1}$ , and a “ $p$ -adic coefficient object” $\mathscr{M}$ on $X$ , we have already defined unipotent nearby/vanishing cycles $\unicode[STIX]{x1D6F9}_{f}^{\text{un}}(\mathscr{M})$ and $\unicode[STIX]{x1D6F7}_{f}^{\text{un}}(\mathscr{M})$ as objects on $X_{0}:=X\times _{\mathbb{A}^{1}}\{0\}$ . These functors are compatible with pushforward by proper morphisms and pullback by smooth morphisms. An important property of full nearby cycle functor is that it computes the “cohomology of the generic fiber” when $f$ is proper. However, $\unicode[STIX]{x1D6F9}^{\text{un}}$ is not powerful enough to compute the cohomology. Let us explain what this means. Consider the simplest possible situation, namely $X=\mathbb{A}^{1}$ and $f=\text{id}$ . Consider the $p$ -adic coefficient $\mathscr{M}$ defined by the differential equation

$$\begin{eqnarray}x^{2}\unicode[STIX]{x2202}-\unicode[STIX]{x1D70B}=0.\end{eqnarray}$$

This differential equation has singularity at $0$ , and in fact, we may prove that the equation is trivialized by an Artin–Schreier type covering. The “cohomology” of $\mathscr{M}$ around the generic point of $\mathbb{A}^{1}$ is merely the “fiber” of $\mathscr{M}$ at the generic point because we are taking $f=\text{id}$ . Thus, this should be some vector space of dimension equal to the rank of $\mathscr{M}$ , which is $1$ in this situation. In particular, $\unicode[STIX]{x1D6F9}_{\text{id}}(\mathscr{M})$ should not be zero. However, we may compute that $\unicode[STIX]{x1D6F9}_{\text{id}}^{\text{un}}(\mathscr{M})=0$ . Thus, $\unicode[STIX]{x1D6F9}_{\text{id}}^{\text{un}}(\mathscr{M})$ does not meet our need. Beilinson suggests to consider $\bigoplus _{\mathscr{L}}\unicode[STIX]{x1D6F9}^{\text{un}}(\mathscr{M}\,\otimes \,\mathscr{L})$ where $\mathscr{L}$ runs over all the irreducible “local system on a disk”. In the situation above, $\mathscr{M}^{\vee }$ (where $(-)^{\vee }$ denotes the dual) should be considered as an irreducible local system on the disk around $0\in \mathbb{A}^{1}$ . Thus the contribution from $\unicode[STIX]{x1D6F9}^{\text{un}}(\mathscr{M}\,\otimes \,\mathscr{M}^{\vee })$ does not vanish, which gives us the correct computation of the cohomology of the generic fiber in terms of nearby cycle functor.

Even though it is straightforward what to do philosophically, some technical issues come in. First of all, the unipotent nearby/vanishing cycle functors we have already defined a priori depend on the choice of “parameter”, whereas it should not be ideally. This issue is treated in Section 1. Second, it is not clear from the definition that $\unicode[STIX]{x1D6F9}_{f}$ and $\unicode[STIX]{x1D6F7}_{f}$ have certain finiteness property. We argue as Deligne to show the finiteness in Section 2. After constructing nearby/vanishing cycle functors, we give small applications. In Section 3, we define the category of smooth objects intrinsically, and show that this category coincides with the category of overconvergent isocrystals. We also show that this category is stable under taking pushforward by proper and smooth morphism. In the final section, Section 4, we propose a category over a Henselian trait which is an analogue of that of $\ell$ -adic sheaves, and show that our nearby/vanishing cycle functors factor through this category.

Finally, it is my great pleasure to dedicate this article to Professor Shuji Saito, with deep respect to him and his mathematics, on the occasion of his 60th birthday. As a supervisor, Professor Saito taught me what it is to study mathematics. Even after I got Ph.D., he continuously encouraged me strongly in many occasions, advised me both on mathematics and on life. Without him, my life would not have been as rich.

1 Vanishing cycle functor

1.1

In the whole paper, we fix a (geometric) base tuple $(k,R,K,L)$ (cf. [A2, 1.4.10, 2.4.14]). This is a collection of data where $k$ is a perfect field of characteristic $p>0$ , $R$ is a discrete valuation ring whose residue field is $k$ such that some power of Frobenius automorphism on $k$ lifts to $R$ , $K:=\text{Frac}(R)$ , and $L$ is an algebraic extension of $K$ . Once we fix these data, we are able to define the $L$ -linear triangulated category $D(X)$ for a separated scheme $X$ of finite type over $k$ . This triangulated category is denoted by $D(X/L_{\emptyset })$ or $D(X/\mathfrak{T})$ where $\mathfrak{T}$ is the fixed base tuple to be more precise in [A2]. When $L=K$ and $X$ is quasi-projective (or more generally, realizable), we have a classical and more familiar description of $D(X)$ in terms of arithmetic $\mathscr{D}$ -modules of Berthelot: Take an embedding $X{\hookrightarrow}\mathscr{P}$ where $\mathscr{P}$ is a proper smooth formal scheme over $R$ . Then $D(X)$ is a full subcategory of $D_{\text{coh}}^{\text{b}}(\mathscr{D}_{\mathscr{P},\mathbb{Q}}^{\dagger })$ satisfying some finiteness condition called the overholonomicity and support condition. See [A2, 1.1.1] for more details.

The category $D(X)$ is equipped with a t-structure, called the holonomic t-structure, whose heart is denoted by $\text{Hol}(X)$ . Philosophically, this category corresponds to the category of perverse sheaves in the $\ell$ -adic theory. Furthermore, $D(X)$ is equipped with 6 functors. The category $D(X)$ is a closed monoidal category, so we have 2 functors $\otimes$ and ${\mathcal{H}}om$ . The unit object is denoted by $L_{X}$ . When $X$ is smooth quasi-projective and $L=K$ , $L_{X}$ is, in fact, represented by the structure sheaf up to some shift. Given a morphism $f:X\rightarrow Y$ between schemes of finite type, we have 4 more functors:

$$\begin{eqnarray}f_{\ast },f_{!}:D(X)\rightarrow D(Y),\qquad f^{\ast },f^{!}:D(Y)\rightarrow D(X).\end{eqnarray}$$

We denote by $f_{\ast }$ and $f^{\ast }$ for normal pushforward and pullback in accordance with the $\ell$ -adic theory, and not $f_{+}$ , $f^{+}$ as in [A2]. These functors enjoy a lot of standard properties. Some of the properties are summarized in [A2, 1.1.3], so we do not recall here. Finally, exclusively in Section 1.6, we consider Frobenius structure. In order to consider this extra structure, we remark that “arithmetic base tuple” (cf. [A2, 1.4.10, 2.4.14]) should be fixed, which contains some more information than geometric base tuple. We do not go into detail here.

Remark.

Since [A2, 1.1.3] is written only for realizable schemes, let us point out where in the paper the corresponding claim for separated schemes of finite type can be found. The functors $f_{\ast }$ , $f^{\ast }$ are defined in 2.3.7 and 2.3.10. The functor $\otimes$ is defined in 2.3.14, and Proposition 2.3.15 implies the existence of ${\mathcal{H}}om$ . The functor $f_{!}$ is defined in 2.3.21, and $f^{!}$ in 2.3.32. The coincidence of $f_{!}$ and $f_{\ast }$ when $f$ is proper follows by construction, and the base change is checked in 2.3.22. The projection formula is in 2.3.35, the Künneth formula is in 2.3.36, and the localization sequence is in 2.2.9. Duality results as well as trace formalism are also written in 2.3.

1.2

A projective system $\text{“}\varprojlim \text{”}_{i\in I}X_{i}$ , where $I$ is a filtered category which is said to be affine étale if all the morphisms $X_{i}\rightarrow X_{j}$ are affine and étale. By [EGA IV, 8.2.3] as well as [SGA 4, Exp. I, Proposition 8.1.6], the projective limit is representable in the category of schemes over $k$ . Let $\text{Sch}^{\text{ft}}(k)$ be the category of schemes separated of finite type over $k$ . We denote by $\text{Sch}(k)$ the full subcategory of noetherian schemes over $k$ which can be written as a projective limit of an affine étale inductive system in $\text{Sch}^{\text{ft}}(k)$ . From now on, we always mean an object of $\text{Sch}(k)$ by simply saying schemes. In particular, schemes are assumed noetherian.

Lemma 1.3.

1. (1) Any scheme in $\text{Sch}(k)$ is separated.

2. (2) Let $S\in \text{Sch}(k)$ , and $X\rightarrow S$ be a morphism of finite type. Then $X\in \text{Sch}(k)$ as well.

3. (3) The category $\text{Sch}(k)$ is closed under taking Henselization (resp. strict Henselization).

Proof. The first claim follows since, writing $X=\varprojlim \,X_{i}$ with $X_{i}\in \text{Sch}^{\text{ft}}(k)$ , $X_{i}$ is assumed separated and $X\rightarrow X_{i}$ is affine. The second claim is [EGA IV, 8.8.2]. For the last claim, we only need to check that the Henselization and the strict Henselization of a point of a noetherian scheme are noetherian, but these are [EGA IV, 18.6.6, 18.8.8].◻

1.4

Now, let us introduce the triangulated category of arithmetic $\mathscr{D}$ -modules for the schemes in $\text{Sch}(k)$ . Let $X\in \text{Sch}(k)$ . By definition, we may write $X\cong \mathop{\varprojlim }\nolimits_{i\in I}X_{i}$ where $X_{i}\in \text{Sch}^{\text{ft}}(k)$ and $\text{“}\varprojlim \text{”}_{i\in I}X_{i}$ is affine étale. Let $i\rightarrow j$ in $I$ . Since the induced morphism $\unicode[STIX]{x1D719}:X_{i}\rightarrow X_{j}$ is étale, we have the isomorphism between pullback functors $\unicode[STIX]{x1D719}^{\ast }\cong \unicode[STIX]{x1D719}^{!}:D(X_{j})\rightarrow D(X_{i})$ . We define

Since $\unicode[STIX]{x1D719}^{\ast }$ is t-exact with respect to the t-structure, $D(X)$ is also equipped with a t-structure, whose heart is still denoted by $\text{Hol}(X)$ . This category is independent of the choice of projective system up to canonical isomorphism, which justifies the notation $D(X)$ . Now, assume given any morphism $f:X\rightarrow Y$ in $\text{Sch}(k)$ . Then we can find a morphism of affine étale projective systems $\text{“}\varprojlim \text{”}_{i\in I}X_{i}\rightarrow \text{“}\varprojlim \text{”}_{j\in J}Y_{j}$ in $\text{Sch}^{\text{ft}}(k)$ which converges to $f$ . This presentation makes it possible to extend the pullback and extraordinary pullback functor on $\text{Sch}^{\text{ft}}(k)$ to

$$\begin{eqnarray}f^{\ast },f^{!}:D(Y)\rightarrow D(X).\end{eqnarray}$$

Independence of presentation follows easily. Assume further that $f$ is of finite type. Then [EGA IV, 8.8.2] implies that by changing the projective system $\text{“}\varprojlim \text{”}_{i\in I}X_{i}$ in $\text{Sch}^{\text{ft}}(k)$ if necessary, we may assume that $I=J$ and that for any $i\rightarrow j$ in $J$ the following diagram is cartesian:

Since $\unicode[STIX]{x1D719}_{Y}$ is étale, we have the canonical isomorphisms $\unicode[STIX]{x1D719}_{Y}^{\ast }\circ f_{j\ast }\cong f_{i\ast }\circ \unicode[STIX]{x1D719}_{X}^{\ast }$ , $f_{i!}\circ \unicode[STIX]{x1D719}_{X}^{\ast }\cong \unicode[STIX]{x1D719}_{Y}^{\ast }\circ f_{j!}$ by base change and $\unicode[STIX]{x1D719}_{\star }^{\ast }\cong \unicode[STIX]{x1D719}_{\star }^{!}$ . Thus, we have the pushforward and extraordinary pushforward functor

$$\begin{eqnarray}f_{\ast },f_{!}:D(X)\rightarrow D(Y).\end{eqnarray}$$

Lemma 1.5. For a scheme $X$ , $\text{Hol}(X)$ is a noetherian and artinian category.

Proof. Let $U$ be a scheme, and write $U\cong \varprojlim \,U_{i}$ where $U_{i}\in \text{Sch}^{\text{ft}}(k)$ . Assume $U_{i}$ is smooth. We say that $\mathscr{F}\in \text{Hol}(U)$ is smooth if there exists $i\in I$ and $\mathscr{F}^{\prime }\in \text{Hol}(U_{i})$ whose pullback is $\mathscr{F}$ such that $\mathscr{F}^{\prime }$ is smooth on $U_{i}$ in the sense of [A2, 1.3.1]. It is easy to check that any smooth object is of finite length, and for any $\mathscr{F}\in \text{Hol}(X)$ , there exists a smooth open dense subscheme $U\subset \text{Supp}(\mathscr{F})$ such that $\mathscr{F}|_{U}$ is smooth on $U$ . Now, let $j:V{\hookrightarrow}X$ be an open immersion. It suffices to check that for an irreducible object $\mathscr{F}_{V}\in \text{Hol}(V)$ , $j_{!\ast }(\mathscr{F}_{V})$ remains to be irreducible. The verification is standard (see, for example, [AC, Proposition 1.4.7]).◻

1.6

Exclusively in this paragraph, we consider Frobenius structure for the future reference. The reader who does not need to consider Frobenius structure may simply ignore Tate twists appearing in this paragraph.

Let $\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{A}_{k}^{1}$ be a morphism of finite type, and denote by $X_{0}$ the fiber over $0\in \mathbb{A}_{k}^{1}$ . Then the exact functors

$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}^{\text{un}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}^{\text{un}}:\text{Hol}(X)\rightarrow \text{Hol}(X_{0})\end{eqnarray}$$

are defined. ¹ Let us now recall the definition briefly. We put ${\mathcal{O}}_{\mathbb{G}_{\text{m}}}:={\mathcal{O}}_{\widehat{\mathbb{P}}_{R}^{1},\mathbb{Q}}(\text{}^{\dagger }\{0,\infty \})$ . We define ${\mathcal{L}}og^{n}$ for an integer $n\geqslant 0$ as follows:

$$\begin{eqnarray}{\mathcal{L}}og^{n}:=\bigoplus _{k=0}^{n-1}{\mathcal{O}}_{\mathbb{G}_{\text{m}}}\cdot \log _{t}^{[k]},\end{eqnarray}$$

the free ${\mathcal{O}}_{\mathbb{G}_{\text{m}}}$ -module of rank $n$ generated by the symbols $\log _{t}^{[k]}$ . For the later use, we denote $k!\cdot \log _{t}^{[k]}$ by $\log _{t}^{k}$ . There exists a unique $\mathscr{D}_{\widehat{\mathbb{P}}^{1},\mathbb{Q}}^{\dagger }$ -module structure on ${\mathcal{L}}og^{n}$ so that for $k\geqslant 0$ and $g\in {\mathcal{O}}_{\mathbb{G}_{\text{m}}}$ ,

$$\begin{eqnarray}\unicode[STIX]{x2202}_{t}(g\cdot \log _{t}^{[k]})=\unicode[STIX]{x2202}_{t}(g)\cdot \log _{t}^{[k]}+(g/t)\cdot \log _{t}^{[k-1]},\end{eqnarray}$$

where $\log _{t}^{[j]}:=0$ for $j<0$ . There is a canonical Frobenius structure on ${\mathcal{L}}og^{n}$ . This defines an object of $\text{Hol}(\mathbb{A}^{1})$ when $L=K$ . If $L\supsetneq K$ , we simply extend the scalar. We have the following exact sequence:

$$\begin{eqnarray}0\rightarrow {\mathcal{L}}og^{n}\rightarrow {\mathcal{L}}og^{n+m}\rightarrow {\mathcal{L}}og^{m}(-n)\rightarrow 0,\end{eqnarray}$$

where the first homomorphism sends $\log _{t}^{[i]}$ to $\log _{t}^{[i]}$ and the second sends $\log _{t}^{[i]}$ to $\log _{t}^{[i-n]}$ . We follow the easy-to-describe definitions of various functors of Beilinson (cf. [AC2, Remark 2.6 (i)]).

Recall we are given $\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{A}^{1}$ , and put $j:X\setminus X_{0}{\hookrightarrow}X$ , the open immersion, and $i:X_{0}{\hookrightarrow}X$ , the closed immersion. Now, we put ${\mathcal{L}}og_{\unicode[STIX]{x1D70B}}^{n}:=\unicode[STIX]{x1D70B}^{\ast }{\mathcal{L}}og^{n}$ . Using this we define for $\mathscr{F}\in \text{Hol}(X)$

and put $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}^{\text{un}}:=\unicode[STIX]{x1D6F1}_{!\ast }^{0,0}(1)$ , $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D70B}}:=\unicode[STIX]{x1D6F1}_{!\ast }^{0,1}$ . A key result of [AC2, Lemma 2.4] is that these limits are representable in $\text{Hol}(X)$ . We have the following complex in  $\text{Hol}(X)$ :

$$\begin{eqnarray}j_{!}\mathscr{F}\rightarrow \unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\oplus \mathscr{F}\rightarrow j_{\ast }\mathscr{F},\end{eqnarray}$$

and define $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}^{\text{un}}(\mathscr{F})$ to be the cohomology of this complex. Here, the homomorphism $j_{!}\mathscr{F}\rightarrow \unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D70B}}(\mathscr{F})$ is the obvious one, and $\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\rightarrow j_{\ast }\mathscr{F}$ is the inductive limit of the connecting homomorphism of the following diagram, recalling ${\mathcal{L}}og_{\unicode[STIX]{x1D70B}}^{1}\cong L_{X\setminus X_{0}}$ :

Moreover, this diagram induces the following exact sequence:

$$\begin{eqnarray}0\rightarrow \unicode[STIX]{x1D6F9}^{\text{un}}(\mathscr{F})\rightarrow \unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\rightarrow j_{\ast }(\mathscr{F})\rightarrow 0,\end{eqnarray}$$

where the surjectivity of the last homomorphism is also a part of the key result of [AC2]. This short exact sequence together with the definition of the vanishing cycle functor yield the following fundamental exact triangle:

(1.6.1) $$\begin{eqnarray}i^{\ast }[-1]\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}^{\text{un}}\rightarrow \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}^{\text{un}}\xrightarrow[{}]{+1}.\end{eqnarray}$$

Remark.

1. (1) In [AC2], the object ${\mathcal{I}}^{a,b}$ is used instead of ${\mathcal{L}}og^{n}$ . We may check easily that there exists an isomorphism ${\mathcal{I}}^{a,b}\xrightarrow[{}]{{\sim}}{\mathcal{L}}og^{b-a}$ where $s^{l}t^{s}$ , using the notation of [AC2, 2.3], is sent to $\log _{t}^{[l-a-1]}$ . The embedding ${\mathcal{L}}og_{t}^{n}{\hookrightarrow}{\mathcal{L}}og_{t}^{n+1}$ is compatible with the embedding ${\mathcal{I}}^{a,b}{\hookrightarrow}{\mathcal{I}}^{a,b+1}$ . The description using ${\mathcal{I}}^{a,b}$ is convenient to understand the relation with the dual functor, but in order to prove the theorem below, ${\mathcal{L}}og^{n}$ description reduces notation.

2. (2) We defined $\unicode[STIX]{x1D6F9}^{\text{un}}$ as $\unicode[STIX]{x1D6F1}_{!\ast }^{0,0}(1)$ , but in [AC2], following Beilinson, we did not put this Tate twist in the definition. This Tate twist is put in order that no Tate twist appears in (1.6.1). Since we do not consider Frobenius structure from the next paragraph, we may forget this confusing Tate twists.

1.7

Now, let $S$ be a scheme of finite type over $k$ , and $s\in S$ be a regular point of codimension $1$ . Let $\unicode[STIX]{x1D70B}:X\rightarrow S$ be a morphism of finite type. For a dominant morphism $h:S\rightarrow \mathbb{A}^{1}$ such that $h(s)=0$ , the functor $\unicode[STIX]{x1D6F9}_{h\circ \unicode[STIX]{x1D70B}}^{\text{un}}$ is defined. Note that such $h$ exists Zariski locally around $s$ . In this paper, for a morphism of schemes $f:X\rightarrow Y$ and a point $y\in Y$ , the fiber $X\otimes _{Y}k(y)$ is denoted by $X_{y}$ .

Theorem. The functors $\unicode[STIX]{x1D6F9}_{h\circ \unicode[STIX]{x1D70B}}^{\text{un}}|_{X_{s}}$ , $\unicode[STIX]{x1D6F7}_{h\circ \unicode[STIX]{x1D70B}}^{\text{un}}|_{X_{s}}$ does not depend on the choice of $h$ up to canonical equivalence. This justifies to denote these functors by $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B},s}^{\text{un}}$ and $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B},s}^{\text{un}}$ respectively.

Proof. Let $\mathbb{A}_{(x,y)}^{2}\rightarrow \mathbb{A}_{t}^{1}$ be the morphism sending $t$ to $xy$ . On $\mathbb{A}^{2}$ , we construct a homomorphism

$$\begin{eqnarray}\unicode[STIX]{x1D6FC}:{\mathcal{L}}og_{xy}^{n}\rightarrow {\mathcal{L}}og_{x}^{n}\,\otimes \,{\mathcal{L}}og_{y}^{n}.\end{eqnarray}$$

by sending $(\log xy)^{k}$ to $\sum _{i=0}^{k}\binom{k}{i}(\log x)^{i}\,\otimes \,(\log y)^{k-i}$ . It is easy to check that this defines a homomorphism of $\mathscr{D}^{\dagger }$ -modules. Now, shrink $S$ around $s$ , which is allowed since we only need the equivalence after $|_{X_{s}}$ , so that the closure of $s$ , is a smooth divisor denoted by $D$ . Let $u,v\in {\mathcal{O}}_{S}$ . These functions define a morphism $\unicode[STIX]{x1D70C}:S\rightarrow \mathbb{A}^{2}$ by sending $x$ , $y$ to $u$ , $v$ respectively. Then we get a homomorphism in $\text{Hol}(S)$

$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{u,v}:=\unicode[STIX]{x1D70C}^{\ast }(\unicode[STIX]{x1D6FC}):{\mathcal{L}}og_{uv}^{n}\rightarrow {\mathcal{L}}og_{u}^{n}\,\otimes \,{\mathcal{L}}og_{v}^{n}.\end{eqnarray}$$

Given $u,v,w\in {\mathcal{O}}_{S}$ , the following diagram is commutative:

(1.7.2)

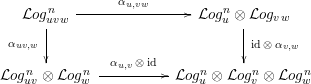
Now, for $h:S\rightarrow \mathbb{A}^{1}$ , we denote $\unicode[STIX]{x1D6F9}_{h\unicode[STIX]{x1D70B}}^{\text{un}}$ , $\unicode[STIX]{x1D6F7}_{h\unicode[STIX]{x1D70B}}^{\text{un}}$ , $\unicode[STIX]{x1D6EF}_{h\unicode[STIX]{x1D70B}}^{\text{un}}$ by $\unicode[STIX]{x1D6F9}_{h}$ , $\unicode[STIX]{x1D6F7}_{h}$ , $\unicode[STIX]{x1D6EF}_{h}$ respectively. Take another dominant morphism $h^{\prime }:S\rightarrow \mathbb{A}^{1}$ such that $h^{\prime }(s)=0$ . Possibly shrinking $S$ around $s$ , we may assume that there exists $u\in {\mathcal{O}}_{S}^{\times }$ such that $h^{\prime }=uh$ . Because the image of the associated morphism $u:S\rightarrow \mathbb{A}^{1}$ is contained in $\mathbb{G}_{\text{m}}$ , the object ${\mathcal{L}}og_{u}^{n}$ is an iterated extension of the trivial object $L_{S}$ . This implies that for $\star \in \{!,\ast \}$ ,

(1.7.3) $$\begin{eqnarray}j_{\star }(\mathscr{F}\,\otimes \,{\mathcal{L}}og_{u\unicode[STIX]{x1D70B}}^{n}\,\otimes \,{\mathcal{L}}og_{h\unicode[STIX]{x1D70B}}^{n})\cong j_{\star }(\mathscr{F}\,\otimes \,{\mathcal{L}}og_{h\unicode[STIX]{x1D70B}}^{n})\,\otimes \,{\mathcal{L}}og_{u\unicode[STIX]{x1D70B}}^{n},\end{eqnarray}$$

where $j:X\setminus (h\circ \unicode[STIX]{x1D70B})^{-1}(0){\hookrightarrow}X$ . Define

and put $\unicode[STIX]{x1D6F9}_{u,h}:=\unicode[STIX]{x1D6F1}_{(u,h)!\ast }^{0,0}$ , $\unicode[STIX]{x1D6EF}_{u,h}:=\unicode[STIX]{x1D6F1}_{(u,h)!\ast }^{0,1}$ as usual. Then (1.7.3) induces the canonical isomorphisms

as Ind objects. We have a homomorphism

$$\begin{eqnarray}{\mathcal{L}}og_{u}^{n}|_{D}\cong \bigoplus _{k=0}^{n-1}L_{D}\cdot \log _{u}^{[k]}\xrightarrow[{}]{\text{pr}_{0}}L_{D},\end{eqnarray}$$

where $\text{pr}_{0}$ denotes the projection by the factor indexed by $\log _{u}^{[0]}$ . By taking the limit, we have a homomorphism $\text{pr}_{0}:\mathop{\varinjlim }\nolimits_{n}{\mathcal{L}}og_{u}^{n}|_{D}\rightarrow L_{D}$ . Composing everything, we have

We may check easily that $\unicode[STIX]{x1D719}_{h,h}=\text{id}$ . Using (1.7.2), it is also an easy exercise to show that $\unicode[STIX]{x1D719}_{vuh,uh}\circ \unicode[STIX]{x1D719}_{uh,h}=\unicode[STIX]{x1D719}_{vuh,h}$ for $v\in {\mathcal{O}}_{S}^{\times }$ . Thus, $\unicode[STIX]{x1D719}_{uh,h}$ is an isomorphism for any $u\in {\mathcal{O}}_{S}^{\times }$ . In order to show the theorem for $\unicode[STIX]{x1D6F7}^{\text{un}}$ , we define $\unicode[STIX]{x1D6F7}_{u,h}$ by the cohomology of the following complex

and argue similarly.◻

1.8

Let $X\xrightarrow[{}]{\unicode[STIX]{x1D70B}}S\xrightarrow[{}]{h}S^{\prime }$ be morphisms of schemes of finite type over $k$ , $h$ is dominant, and $s\in S$ , $s^{\prime }\in S^{\prime }$ be codimension $1$ regular points such that $s$ is sent to $s^{\prime }$ . We have the canonical morphism $h^{\prime }:X_{s}\rightarrow X_{s^{\prime }}$ . Then by the construction of nearby/vanishing cycle functors, we have

(1.8.4) $$\begin{eqnarray}h^{\prime \ast }\unicode[STIX]{x1D6F9}_{h\circ \unicode[STIX]{x1D70B},s^{\prime }}^{\text{un}}\cong \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B},s}^{\text{un}},\qquad h^{\prime \ast }\unicode[STIX]{x1D6F7}_{h\circ \unicode[STIX]{x1D70B},s^{\prime }}^{\text{un}}\cong \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B},s}^{\text{un}}.\end{eqnarray}$$

By saying $(S,s,\unicode[STIX]{x1D702})$ is a Henselian trait, we mean $S$ is a scheme which is the spectrum of a Henselian discrete valuation ring with closed point $s$ and generic point $\unicode[STIX]{x1D702}$ , and a fixed separable closure $\overline{k(\unicode[STIX]{x1D702})}$ of $k(\unicode[STIX]{x1D702})$ often denoted by $\unicode[STIX]{x1D702}^{\text{sep}}$ . Let $(S,s,\unicode[STIX]{x1D702})$ be a Henselian trait. Assume given a morphism $\unicode[STIX]{x1D70B}:X\rightarrow S$ . Even if $X$ and $S$ are not of finite type over $k$ , we may define exact functors

$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}^{\text{un}},\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}^{\text{un}}:\text{Hol}(X)\rightarrow \text{Hol}(X_{s}).\end{eqnarray}$$

Indeed, we can find a diagram using [EGA IV, 8.8.2]

Here, $\widetilde{\unicode[STIX]{x1D70B}}$ is a morphism of schemes of finite type over $k$ , $\unicode[STIX]{x1D70C}(s)$ is a regular point $t\in {\mathcal{S}}$ of codimension $1$ , $\unicode[STIX]{x1D6FE}$ is the limit of a projective system of affine étale ${\mathcal{X}}\times _{{\mathcal{S}}}S$ -schemes. Let $\unicode[STIX]{x1D6FE}_{X}:X_{s}\rightarrow {\mathcal{X}}_{t}$ be the morphism induced by $\unicode[STIX]{x1D6FE}$ . Then we define $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}^{\text{un}}:=\unicode[STIX]{x1D6FE}_{X}^{\ast }\unicode[STIX]{x1D6F9}_{\widetilde{\unicode[STIX]{x1D70B}},t}^{\text{un}}$ , $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}^{\text{un}}:=\unicode[STIX]{x1D6FE}_{X}^{\ast }\unicode[STIX]{x1D6F7}_{\widetilde{\unicode[STIX]{x1D70B}},t}^{\text{un}}$ . We claim that these do not depend on the choice of the diagram. Indeed, assume we are given another morphism $\unicode[STIX]{x1D70C}^{\prime }:S\rightarrow {\mathcal{S}}^{\prime }$ such that $\unicode[STIX]{x1D70C}^{\prime }(s)$ is a regular point of codimension $1$ and also a morphism of finite type $\widetilde{\unicode[STIX]{x1D70B}}^{\prime }:{\mathcal{X}}_{{\mathcal{S}}^{\prime }}^{\prime }\rightarrow {\mathcal{S}}^{\prime }$ having analogous properties as $\widetilde{\unicode[STIX]{x1D70B}}$ . We need to show that the resulting $\unicode[STIX]{x1D6F9}^{\text{un}}$ and $\unicode[STIX]{x1D6F7}^{\text{un}}$ are canonically equivalent. By (1.8.4), we may change bases ${\mathcal{S}}$ , ${\mathcal{S}}^{\prime }$ , and assume that there is a morphism ${\mathcal{S}}\rightarrow {\mathcal{S}}^{\prime }$ , and we may even assume that ${\mathcal{S}}={\mathcal{S}}^{\prime }$ . Further changing the base, we may assume that there is a diagram of ${\mathcal{S}}$ -schemes

such that schemes on the 2nd row are of finite type over ${\mathcal{S}}$ and the vertical morphisms are étale. Since $\unicode[STIX]{x1D6F9}^{\text{un}}$ , $\unicode[STIX]{x1D6F7}^{\text{un}}$ are compatible with pullback by étale morphism, the independence follows.

1.9

Now, let $(S,s,\unicode[STIX]{x1D702})$ be a strict Henselian trait, and we define the category $\text{Hen}(S)$ to be the category of Henselian traits over $S$ which is generically étale, and the morphisms are morphisms of traits respecting the fixed separable closure. This is a filtered category. Morphisms are $S$ -morphisms. Given a morphism $h:S^{\prime }\rightarrow S$ in $\text{Hen}(S)$ , consider the following commutative diagram:

Now, assume given a morphism $f:X\rightarrow S$ . Let $f^{\prime }:X\times _{S}S^{\prime }\rightarrow S^{\prime }$ . By abuse of notation, we use the same symbols for the base change from $S$ to $X$ , for example $h\times \text{id}:X\times _{S}S^{\prime }\rightarrow X$ is denoted by $h$ . We have a canonical morphism

$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{f}^{\text{un}}\rightarrow \unicode[STIX]{x1D6F9}_{f}^{\text{un}}\circ h_{\ast }\circ h^{\ast }\cong h_{s,\ast }\circ \unicode[STIX]{x1D6F9}_{f^{\prime }}^{\text{un}}\circ h^{\ast },\end{eqnarray}$$

where the isomorphism follows since $h$ is proper and $s^{\prime }\rightarrow s\times _{S}S^{\prime }$ is a nilpotent immersion. Since $\unicode[STIX]{x1D6F9}_{f^{\prime }}^{\text{un}}\circ h^{\ast }\cong \unicode[STIX]{x1D6F9}_{f^{\prime }}^{\text{un}}\circ (j_{\ast }^{\prime }h_{\unicode[STIX]{x1D702}}^{\ast }j^{\ast })$ and the functor $j_{\ast }^{\prime }h_{\unicode[STIX]{x1D702}}^{\ast }j^{\ast }$ sends holonomic objects to holonomic objects, the exactness of $\unicode[STIX]{x1D6F9}^{\text{un}}$ implies that we have $\mathscr{H}^{i}(\unicode[STIX]{x1D6F9}_{f^{\prime }}^{\text{un}}\circ h^{\ast }(\mathscr{F}))=0$ for any $\mathscr{F}\in \text{Hol}(X)$ and $i\neq 0$ . Now, we have the following diagram of exact sequences by (1.6.1).

Here the middle homomorphism is an isomorphism since $h_{s}$ is an isomorphism, and the right vertical morphism is split injective since $j^{\ast }\mathscr{F}$ is a direct factor of $h_{\unicode[STIX]{x1D702}\ast }h_{\unicode[STIX]{x1D702}}^{\ast }j^{\ast }\mathscr{F}$ . This implies that $\mathscr{H}^{-1}(h_{s\ast }\unicode[STIX]{x1D6F7}_{f^{\prime }}^{\text{un}}(h^{\ast }\mathscr{F}))=0$ . Together with the other parts of the diagram of long exact sequences, we have $\mathscr{H}^{i}(h_{s\ast }\unicode[STIX]{x1D6F7}_{f^{\prime }}^{\text{un}}(h^{\ast }\mathscr{F}))=0$ for $i\neq 0$ and $\unicode[STIX]{x1D6F7}_{f}^{\text{un}}(\mathscr{F}){\hookrightarrow}h_{s\ast }\unicode[STIX]{x1D6F7}_{f^{\prime }}^{\text{un}}(h^{\ast }\mathscr{F})$ . This enables us to define exact functors $\text{Ind}\text{Hol}(X)\rightarrow \text{Ind}\text{Hol}(X_{s})$ as follows:

For Ind-categories, see [A2, 1.2.2]. These are endowed with an action of $I:=\text{Gal}(\unicode[STIX]{x1D702}^{\text{sep}}/\unicode[STIX]{x1D702})$ where $\unicode[STIX]{x1D702}^{\text{sep}}$ is the separable closure of $\unicode[STIX]{x1D702}$ . By construction, we have the homomorphism $c:\unicode[STIX]{x1D6F9}_{f}\rightarrow \unicode[STIX]{x1D6F7}_{f}$ compatible with the action of $I$ . Moreover, for $\unicode[STIX]{x1D70E}\in I$ , we have the variation homomorphism

$$\begin{eqnarray}v(\unicode[STIX]{x1D70E}):\unicode[STIX]{x1D6F7}_{f}(\mathscr{F})\rightarrow \unicode[STIX]{x1D6F9}_{f}(\mathscr{F})\end{eqnarray}$$

such that $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6F9}}=\text{id}+v(\unicode[STIX]{x1D70E})\circ c$ , $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6F7}}=\text{id}+c\circ v(\unicode[STIX]{x1D70E})$ where $\unicode[STIX]{x1D70E}_{-}$ is the action of $\unicode[STIX]{x1D70E}$ on $(-)$ . The variation homomorphism is defined as follows: Let $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}(\mathscr{F})$ . There exists $\unicode[STIX]{x1D6FC}^{\text{un}}\in \unicode[STIX]{x1D6F7}^{\text{un}}(\mathscr{F})\subset \unicode[STIX]{x1D6F7}(\mathscr{F})$ such that the images of $\unicode[STIX]{x1D6FC}$ and $\unicode[STIX]{x1D6FC}^{\text{un}}$ in $\mathscr{H}^{0}i^{\ast }(\mathscr{F})$ coincide. Then there exists $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6F9}(\mathscr{F})$ so that $c(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FC}^{\text{un}}$ . We define $v(\unicode[STIX]{x1D70E})(\unicode[STIX]{x1D6FC}):=\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6F9}}(\unicode[STIX]{x1D6FD})-\unicode[STIX]{x1D6FD}$ . We leave the reader to check that this is well-defined, and satisfies the desired properties.

Proposition 1.10. Let $(S,s,\unicode[STIX]{x1D702})$ , $(S^{\prime },s^{\prime },\unicode[STIX]{x1D702}^{\prime })$ be strict Henselian traits, and $\unicode[STIX]{x1D70B}:S^{\prime }\rightarrow S$ be a finite dominant morphism.

1. (1) For $\mathscr{F}\in \text{Hol}(\unicode[STIX]{x1D702}^{\prime })$ , the nearby cycles $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})$ are representable in $\text{Hol}(s^{\prime })$ .

2. (2) For $\mathscr{F}\in \text{Hol}(\unicode[STIX]{x1D702}^{\prime })$ , we have $\text{rk}(\mathscr{F})=\text{rk}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F}))$ .

3. (3) The morphism $\unicode[STIX]{x1D70B}_{s}^{\ast }\circ \unicode[STIX]{x1D6F9}_{\text{id}}\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6F9}_{\text{id}}\circ \unicode[STIX]{x1D70B}^{\ast }$ , where $\unicode[STIX]{x1D70B}_{s}:s^{\prime }\xrightarrow[{}]{{\sim}}s$ is the induced morphism, is isomorphic.

Proof. Let us check 3. Assume $\unicode[STIX]{x1D70B}$ is generically étale. Then $S^{\prime }\in \text{Hen}(S)$ . Thus we have the functor $\text{Hen}(S^{\prime })\rightarrow \text{Hen}(S)$ sending $S^{\prime \prime }\rightarrow S^{\prime }$ to $S^{\prime \prime }\rightarrow S^{\prime }\rightarrow S$ . This functor is cofinal, and since $\unicode[STIX]{x1D70B}_{s}$ is an isomorphism, we get the claim in this case. If $\unicode[STIX]{x1D70B}$ is not generically étale, the morphism $\unicode[STIX]{x1D702}^{\prime }\rightarrow \unicode[STIX]{x1D702}$ breaks up into $\unicode[STIX]{x1D702}^{\prime }\xrightarrow[{}]{a}\unicode[STIX]{x1D702}^{\text{sep}}\xrightarrow[{}]{b}\unicode[STIX]{x1D702}$ where $a$ is purely inseparable and $b$ is étale. By the generically étale case we have already treated, it suffices to check the claim for the case where $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D702}}$ is purely inseparable. In this case, $\unicode[STIX]{x1D70B}$ is universally homeomorphic, thus the functors do not see the difference between $S$ and $S^{\prime }$ (cf. [A2, Lemma 1.1.3]).

Let us check the other two claims. By 3, we may assume that $\unicode[STIX]{x1D70B}=\text{id}$ . Let $Y$ be a scheme and $y$ be a point such that $S$ is a strict Henselization of $Y$ at $y$ . By [EGA IV, 18.8.13], by replacing $Y$ by a neighborhood of $y$ , we may assume that $Y$ is smooth. Moreover, by [EGA IV, 18.8.12 (ii), 6.1.3], ${\mathcal{O}}_{Y,y}$ is of dimension $1$ . Thus, we may assume that $y$ is a generic point $\unicode[STIX]{x1D702}_{D}$ of a smooth divisor $D$ in $Y$ . By Kedlaya’s semistable reduction theorem [K2], at the cost of shrinking $Y$ further, there exists a surjective morphism $g:Y^{\prime }\rightarrow Y$ such that $Y^{\prime }$ is smooth, $g$ is étale outside of $D$ , and the pullback of $\mathscr{F}$ to $Y^{\prime }$ is log-extendable along the smooth irreducible divisor $D^{\prime }:=g^{-1}(D)$ with generic point $\unicode[STIX]{x1D702}_{D^{\prime }}$ . Replacing $Y$ by its étale neighborhood around $\unicode[STIX]{x1D702}_{D}$ , we may assume that $\unicode[STIX]{x1D702}_{D^{\prime }}\rightarrow \unicode[STIX]{x1D702}_{D}$ is an isomorphism. Take any function $h\in {\mathcal{O}}_{Y^{\prime }}$ such that the zero locus is equal to $D^{\prime }$ . In this situation, the computation of [AC2, Lemma 2.4] shows that $\unicode[STIX]{x1D6F9}_{h}^{\text{un}}(g^{\ast }\mathscr{F})$ is a smooth object on $D^{\prime }$ of rank equal to that of $\mathscr{F}$ . Now, take a finite morphism $\unicode[STIX]{x1D6FC}:Y^{\prime \prime }\rightarrow Y^{\prime }$ which is étale outside of $D^{\prime }$ . Then $g^{\ast }\mathscr{F}|_{Y^{\prime }\setminus D^{\prime }}$ is a direct factor of $\unicode[STIX]{x1D6FC}_{\ast }\unicode[STIX]{x1D6FC}^{\ast }g^{\ast }\mathscr{F}|_{Y^{\prime }\setminus D^{\prime }}$ , so we get that the canonical homomorphism

(1.10.5) $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{h}^{\text{un}}(g^{\ast }\mathscr{F})\rightarrow \unicode[STIX]{x1D6FC}_{\ast }\unicode[STIX]{x1D6F9}_{h\circ \unicode[STIX]{x1D6FC}}^{\text{un}}(\unicode[STIX]{x1D6FC}^{\ast }g^{\ast }\mathscr{F})\end{eqnarray}$$

is a split injective homomorphism. Since $\unicode[STIX]{x1D6FC}^{\ast }g^{\ast }\mathscr{F}$ is also log-extendable, the rank is the same as that of $\mathscr{F}$ . This implies that the canonical map (1.10.5) is an isomorphism. Thus, $\unicode[STIX]{x1D6F9}_{\text{id}}^{\text{un}}(\mathscr{F})$ is the same as the pullback of $g_{\ast }\unicode[STIX]{x1D6F9}_{h}^{\text{un}}(\mathscr{F})$ . ◻

2 Finiteness of nearby cycle

Throughout this section, we fix a strict Henselian trait $(S,s,\unicode[STIX]{x1D702})$ .

2.1

First, we need a preparation. Let $f:X\rightarrow Y$ be a morphism of finite type. We put $f_{\ast }^{i}:=\mathscr{H}^{i}f_{\ast }:\text{Hol}(X)\rightarrow \text{Hol}(Y)$ . This extends canonically to Ind-categories (cf. [A2, after (4) of 1.2.2]), and defines a functor $If_{\ast }^{i}:\text{Ind}\text{Hol}(X)\rightarrow \text{Ind}\text{Hol}(Y)$ , which we still denote by $f_{\ast }^{i}$ . If $f$ is smooth of codimension $d$ , we have the exact functor $f^{\ast }[d]:\text{Hol}(Y)\rightarrow \text{Hol}(X)$ . This functor also extends to Ind-categories, and is denoted by $f^{\circledast }$ .

Lemma. Let $S$ be a strict Henselian trait, and $f:X\rightarrow Y$ be a morphism of $S$ -schemes.

1. (1) If $f$ is proper, then there exists a canonical isomorphism $\unicode[STIX]{x1D6F9}\circ f_{\ast }^{i}\cong f_{\ast }^{i}\circ \unicode[STIX]{x1D6F9}$ in $\text{Ind}\text{Hol}(Y)$ for each $i$ .

2. (2) If $f$ is smooth, then there exists a canonical isomorphism $f^{\circledast }\circ \unicode[STIX]{x1D6F9}\cong \unicode[STIX]{x1D6F9}\circ f^{\circledast }$ in $\text{Ind}\text{Hol}(X)$ .

Proof. These are exercise of six-functor formalism, so we leave the verification to the reader.

Theorem 2.2. If $\unicode[STIX]{x1D70B}:X\rightarrow S$ is of finite type, the functors $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}$ and $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}$ define functors from $\text{Hol}(X)$ to $\text{Hol}(X_{s})$ .

By the fundamental exact triangle $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}^{\text{un}}\rightarrow \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}^{\text{un}}\rightarrow i^{\ast }\xrightarrow[{}]{+}$ , where $i:X_{s}\rightarrow X$ , it suffices to check the theorem just for $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}$ . The idea of the proof is essentially the same as [D, Théorème 3.2]. The proof is divided into several parts. We prove the theorem by induction on the dimension of $X_{\unicode[STIX]{x1D702}}$ . The case where $\dim (X_{\unicode[STIX]{x1D702}})=0$ has already been treated in Proposition 1.10. We assume that the theorem holds for $X$ such that $\dim (X_{\unicode[STIX]{x1D702}})<n$ . From now on, we assume that $\dim (X_{\unicode[STIX]{x1D702}})=n$ .

Lemma 2.3. [D, Lemme 3.5]

Let $K$ be a field containing $k$ . Let $X\subset \mathbb{A}_{K}^{n}$ be a closed subscheme, $\mathscr{F}\in \text{Ind}\text{Hol}(X)$ , and $\overline{\unicode[STIX]{x1D702}}$ be a geometric generic point of $\mathbb{A}_{K}^{1}$ . Let $X_{\overline{\unicode[STIX]{x1D702}},i}$ be the geometric generic fiber of the morphism $X\subset \mathbb{A}^{n}\xrightarrow[{}]{\text{pr}_{i}}\mathbb{A}^{1}$ , where $\text{pr}_{i}$ denotes the $i$ th projection, and $\mathscr{F}_{\overline{\unicode[STIX]{x1D702}},i}$ denotes the pullback of $\mathscr{F}$ to $X_{\overline{\unicode[STIX]{x1D702}},i}$ . Assume $\mathscr{F}_{\overline{\unicode[STIX]{x1D702}},i}\in \text{Hol}(X_{\overline{\unicode[STIX]{x1D702}},i})$ for all $i$ . Then there exists $\mathscr{F}^{\prime }\in \text{Hol}(X)$ contained in $\mathscr{F}$ such that the local sections of $\mathscr{F}/\mathscr{F}^{\prime }$ are supported on finitely many points, namely it is isomorphic to $\bigoplus _{x\in |\mathbb{A}^{n}|}\mathscr{G}_{x}$ where $\mathscr{G}_{x}$ is supported on $x$ .

Proof. Let $\unicode[STIX]{x1D70B}:\mathbb{A}^{n}\rightarrow \mathbb{A}^{1}$ be a projection. For each $x\in \mathbb{A}^{1}$ , denote by $i_{x}:\mathbb{A}_{x}:=\unicode[STIX]{x1D70B}^{-1}(x){\hookrightarrow}\mathbb{A}^{n}$ and by $\unicode[STIX]{x1D702}$ the generic point of $\mathbb{A}^{1}$ . Assume given $\mathscr{G}\in \text{Ind}\text{Hol}(\mathbb{A}^{n})$ such that the pullback to $\mathbb{A}_{\unicode[STIX]{x1D702}}$ is $0$ . Then

$$\begin{eqnarray}\mathscr{G}\cong \bigoplus _{x\in |\mathbb{A}^{1}|}i_{x,\ast }i_{x}^{\ast }\mathscr{G}.\end{eqnarray}$$

Indeed, since $\text{Hol}(\mathbb{A}^{n})$ is a noetherian category by Lemma 1.5, we may write $\mathscr{G}\cong \mathop{\varinjlim }\nolimits_{i}\mathscr{G}_{i}$ where $\mathscr{G}_{i}{\hookrightarrow}\mathscr{G}$ and $\mathscr{G}_{i}\in \text{Hol}(\mathbb{A}^{n})$ . Since the pullback by $\mathbb{A}_{\unicode[STIX]{x1D702}}\rightarrow \mathbb{A}^{n}$ is exact, by assumption, $\mathscr{G}_{i}$ becomes $0$ on $\mathbb{A}_{\unicode[STIX]{x1D702}}$ . This implies that $\mathscr{G}_{i}$ is supported on $\coprod _{i=1}^{n}\mathbb{A}_{x_{i}}$ where $x_{i}$ are closed points of $\mathbb{A}^{1}$ , and the claim follows.

Fix $i$ . There exists an étale neighborhood $U$ of $\overline{\unicode[STIX]{x1D702}}$ and $\mathscr{H}_{i}\in \text{Hol}(X_{U,i})$ , where $j_{i}:X_{U,i}:=X\times _{\text{pr}_{i},\mathbb{A}^{1}}U{\hookrightarrow}X$ , such that its pullback to $X_{\overline{\unicode[STIX]{x1D702}},i}$ is $\mathscr{F}_{\overline{\unicode[STIX]{x1D702}},i}$ . By shrinking $U$ if necessary, we may assume that the isomorphism $\mathscr{H}_{i,\overline{\unicode[STIX]{x1D702}},i}\xrightarrow[{}]{{\sim}}\mathscr{F}_{\overline{\unicode[STIX]{x1D702}},i}$ is induced by a homomorphism $\mathscr{H}_{i}\rightarrow \mathscr{F}_{U,i}$ where $\mathscr{F}_{U,i}$ denotes the pullback of $\mathscr{F}$ to $X_{U,i}$ . Now, put

$$\begin{eqnarray}\mathscr{F}^{\prime }:=\mathop{\sum }_{i=1}^{n}\text{Im}(j_{i!}\mathscr{H}_{i}\rightarrow \mathscr{F})\subset \mathscr{F}.\end{eqnarray}$$

By construction, $\mathscr{F}^{\prime }\in \text{Hol}(X)$ and $(\mathscr{F}/\mathscr{F}^{\prime })_{\overline{\unicode[STIX]{x1D702}},i}=0$ for any $n$ . Thus, using the observation above, any local section of $\mathscr{F}/\mathscr{F}^{\prime }$ is supported on finitely many points.◻

2.4

Let $s^{\prime }$ be the generic point of $\mathbb{A}_{s}^{1}$ , and let $(S^{\prime },s^{\prime },\unicode[STIX]{x1D702}^{\prime })$ be the strict Henselization of $\mathbb{A}_{S}^{1}$ at the generic point $s^{\prime }$ of the divisor $\mathbb{A}_{s}^{1}$ . Let $h:S^{\prime }\rightarrow S$ be the morphism. Deligne constructed the following diagram in the proof of [D, Lemme 3.3]:

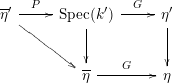
where horizontal maps are algebraic extensions of fields, and $P$ , $G$ denote the Galois groups of the extension. The group $P$ is a pro- $p$ -group. Now, let $\unicode[STIX]{x1D70B}^{\prime }:X^{\prime }\rightarrow S^{\prime }$ be a morphism, and let $\mathscr{F}\in \text{Hol}(X_{\unicode[STIX]{x1D702}^{\prime }}^{\prime })$ . Note that $X_{\unicode[STIX]{x1D702}}^{\prime }=X_{\unicode[STIX]{x1D702}^{\prime }}^{\prime }$ and $X_{s}^{\prime }=X_{s^{\prime }}^{\prime }$ . Then we have $\unicode[STIX]{x1D6F9}_{h\circ \unicode[STIX]{x1D70B}^{\prime }}(\mathscr{F})\cong \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}^{\prime }}(\mathscr{F})^{P}$ .

2.5 Proof of Theorem 2.2

Now, let $\unicode[STIX]{x1D70B}:X\rightarrow S$ be a morphism of finite type. We first assume $X$ affine, and take a closed immersion $X{\hookrightarrow}\mathbb{A}_{S}^{n}$ , and let $f:X\subset \mathbb{A}_{S}^{n}\rightarrow \mathbb{A}_{S}^{1}$ where the second morphism is a projection. Recall from the previous paragraph that $\unicode[STIX]{x1D706}:S^{\prime }{\hookrightarrow}\mathbb{A}_{S}^{1}$ is a strict Henselization of $\mathbb{A}_{S}^{1}$ . Consider the following diagram:

Let $\mathscr{F}^{\prime }$ be the pullback of $\mathscr{F}$ to $X^{\prime }$ . Then we have

$$\begin{eqnarray}\unicode[STIX]{x1D706}_{X}^{\circledast }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\cong \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D706}_{X}}(\mathscr{F})\cong \unicode[STIX]{x1D6F9}_{f^{\prime }}(\mathscr{F})^{P},\end{eqnarray}$$

where the first isomorphism follows by Lemma 2.1, and the second by 2.4. Now, the induction hypothesis tells us that $\unicode[STIX]{x1D6F9}_{f^{\prime }}(\mathscr{F})^{P}\in \text{Hol}(X_{s^{\prime }}^{\prime })$ , and by construction $X_{s^{\prime }}^{\prime }=X_{s}^{\prime }$ . This implies that $\unicode[STIX]{x1D706}_{X}^{\circledast }\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\in \text{Hol}(X_{s}^{\prime })$ . Lemma 2.3 ensures the existence of $\mathscr{G}\in \text{Hol}(X_{s})$ contained in $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})$ such that the local sections of $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})/\mathscr{G}$ are supported on finitely many points. Now, if $X$ is not affine, we take a finite affine open covering $\{U_{i}\}$ and we can get such $\mathscr{G}_{i}$ for each subscheme. Then $\mathscr{G}:=\text{Im}(\bigoplus \mathscr{H}^{0}\mathscr{G}_{i,!}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F}))$ , where $\mathscr{G}_{i,!}$ denotes the extension by zero of $\mathscr{G}_{i}$ to $X$ , is in $\text{Hol}(X_{s})$ and the local sections of $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})/\mathscr{G}$ are supported on finitely many points.

In order to show the finiteness of $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})$ , we may assume $X$ is proper over $S$ . Take $\mathscr{G}$ as above, and we may write $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})/\mathscr{G}\cong \bigoplus _{x\in |X_{s}|}\mathscr{G}_{x}$ where $\mathscr{G}_{x}$ is supported on $x$ . We have the following long exact sequence:

where the vertical isomorphism follows by Lemma 2.1. Since we already know that the objects with are in $\text{Hol}(s)$ , we have

$$\begin{eqnarray}\bigoplus _{x}\unicode[STIX]{x1D70B}_{s\ast }\mathscr{G}_{x}\cong \unicode[STIX]{x1D70B}_{s\ast }\biggl(\bigoplus _{x}\mathscr{G}_{x}\biggr)\in \text{Hol}(s).\end{eqnarray}$$

This implies that $\bigoplus _{x\in |X_{s}|}\mathscr{G}_{x}\in \text{Hol}(X_{s})$ , and thus $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\in \text{Hol}(X_{s})$ as required.◻

Corollary 2.6. Let $\unicode[STIX]{x1D70B}:X\rightarrow S$ be a morphism of finite type, and $f:X\rightarrow Y$ be a morphism of $S$ -schemes of finite type.

1. (1) If $f$ is proper, then there exists a canonical isomorphism $\unicode[STIX]{x1D6F9}\circ f_{\ast }\cong f_{\ast }\circ \unicode[STIX]{x1D6F9}$ in $D(Y)$ .

2. (2) If $f$ is smooth, then there exists a canonical isomorphism $f^{\ast }\circ \unicode[STIX]{x1D6F9}\cong \unicode[STIX]{x1D6F9}\circ f^{\ast }$ in $D(X)$ .

3. (3) We have the exact triangle of functors $i^{\ast }[-1]\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}\rightarrow \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70B}}\xrightarrow[{}]{+}$ .

Remark.

Let $R\unicode[STIX]{x1D713}$ and $R\unicode[STIX]{x1D719}$ be the nearby and vanishing cycle functors for $\ell$ -adic sheaves. The exact triangle for nearby/vanishing cycle functor usually goes $i^{\ast }\rightarrow R\unicode[STIX]{x1D713}\rightarrow R\unicode[STIX]{x1D719}\xrightarrow[{}]{+}$ . This difference arises because in the spirit of Riemann–Hilbert correspondence, $\unicode[STIX]{x1D6F9}=R\unicode[STIX]{x1D713}[-1]$ , $\unicode[STIX]{x1D6F7}=R\unicode[STIX]{x1D719}[-1]$ . We could have employed this normalization, but in order to be consistent with [AC2], we decided not to take the shift.

3 Smooth objects

3.1

Let $X$ be a scheme of finite type over $k$ . Then $D(X)$ is equipped with two t-structures; the holonomic t-structure whose heart is $\text{Hol}(X)$ , and the constructible t-structure defined in [A2, §1.3]. The heart of constructible t-structure is denoted by $\text{Con}(X)$ . Given a morphism of finite type $f:X\rightarrow Y$ , the pullback $f^{\ast }$ is exact with respect to constructible t-structure by [A2, 1.3.4]. Thus constructible t-structure extends to a t-structure on $D(X)$ for any scheme $X$ . The cohomology functor for holonomic t-structure is denoted by $\mathscr{H}^{\ast }$ , as we have already used several times, and the constructible t-structure by $\text{}^{\text{c}}\!\mathscr{H}^{\ast }$ .

Definition 3.2. Let $X$ be a scheme. Then $\mathscr{F}\in \text{Con}(X)$ is said to be smooth if for any morphism $\unicode[STIX]{x1D719}:S\rightarrow X$ from a strict Henselian trait, $\unicode[STIX]{x1D6F7}_{\text{id}}(\unicode[STIX]{x1D719}^{\ast }\mathscr{F})=0$ . The full subcategory of smooth objects in $\text{Con}(X)$ is denoted by $\text{Sm}(X)$ .

By Theorem 3.8, we can see that this definition is in fact a generalization of smoothness defined in [A2, 1.3.1]. To be more precise, when $X$ is a realizable scheme over $k$ such that $X_{\text{red}}$ is smooth, $\text{Sm}(X)$ is the same as the category introduced in [A2, 1.1.3 (12)].

Lemma 3.3. Let $f:Y\rightarrow X$ be a proper surjective morphism, and $\mathscr{F}\in \text{Con}(X)$ . If $f^{\ast }\mathscr{F}$ is smooth, then $\mathscr{F}$ is smooth.

Proof. Let $f:S^{\prime }\rightarrow S$ be a finite morphism between strict Henselian traits. In this case, we have an isomorphism $f_{s}^{\ast }\unicode[STIX]{x1D6F9}_{\text{id}}(\mathscr{F})\cong \unicode[STIX]{x1D6F9}_{\text{id}}(f^{\ast }\mathscr{F})$ by Proposition 1.10.3. Since $f_{s}^{\ast }$ is an isomorphism, the claim follows. Consider the general case. Given a morphism $\unicode[STIX]{x1D719}:S\rightarrow X$ from a strict Henselian trait, the fiber $Y\times _{X}\unicode[STIX]{x1D702}$ is nonempty since $f$ is assumed surjective. There exists a finite extension $\unicode[STIX]{x1D702}^{\prime }$ of $\unicode[STIX]{x1D702}$ and a morphism $\unicode[STIX]{x1D702}^{\prime }\rightarrow Y$ compatible with $\unicode[STIX]{x1D702}\rightarrow X$ , thus, by valuative criterion of properness, we have a commutative diagram

where $S^{\prime }$ is a strict Henselian trait, and $f^{\prime }$ is dominant. By the finite morphism case we have already treated, it suffices to check that $f^{\prime \ast }\unicode[STIX]{x1D719}^{\ast }\mathscr{F}$ is smooth, which follows by assumption.◻

3.4

Let us recall briefly some basics of the theory of descent. Let $\unicode[STIX]{x1D6E5}$ be the category of three objects $[0],[1],[2]$ where $[i]=\{0,\ldots ,i\}$ . The morphism $[i]\rightarrow [j]$ is a nondecreasing map. We denote by $\unicode[STIX]{x1D6FF}_{j}^{n}:[n-1]\rightarrow [n]$ the map skipping $j$ and $\unicode[STIX]{x1D70E}_{j}^{n}:[n+1]\rightarrow [n]$ be the map such that $(\unicode[STIX]{x1D70E}_{j}^{n})^{-1}(j)=\{j,j+1\}$ . A simplicial scheme $X_{\bullet }$ is a contravariant functor $\unicode[STIX]{x1D6E5}^{\circ }\rightarrow \text{Sch}(k)$ . Usually, this type of simplicial scheme is called $2$ -truncated simplicial scheme, but since we only use these, we abbreviate the word “ $2$ -truncated”. We put $X_{i}:=X_{\bullet }([i])$ , and $d_{j}^{n}:=X_{\bullet }(\unicode[STIX]{x1D6FF}_{j}^{n})$ and $s_{j}^{n}:=X_{\bullet }(\unicode[STIX]{x1D70E}_{j}^{n})$ . The category of descent data for $X_{\bullet }$ denoted by $\text{Con}(X_{\bullet })$ consists of the following data as objects:

• ∙ an object $\mathscr{F}\in \text{Con}(X_{0})$ ;

• ∙ an isomorphism $\unicode[STIX]{x1D719}:d_{0}^{1\ast }\mathscr{F}\xrightarrow[{}]{{\sim}}d_{1}^{1\ast }\mathscr{F}$ ;

which satisfies the cocycle condition $d_{2}^{2\ast }(\unicode[STIX]{x1D719})\circ d_{0}^{2\ast }(\unicode[STIX]{x1D719})=d_{1}^{2\ast }(\unicode[STIX]{x1D719})$ on $X_{2}$ and $s_{0}^{0\ast }\unicode[STIX]{x1D719}=\text{id}$ on $X_{0}$ . Given an augmentation $f:X_{\bullet }\rightarrow X$ , namely a morphism of simplicial schemes considering $X$ as the constant simplicial scheme, we say that $\text{Con}(X)$ satisfies the descent with respect to $f$ if the canonical functor $\text{Con}(X)\rightarrow \text{Con}(X_{\bullet })$ is an equivalence of categories. An augmentation $X_{\bullet }\rightarrow X$ is a proper hypercovering if the canonical morphisms $X_{0}\rightarrow X$ , $X_{0}\times _{X}X_{0}\rightarrow X_{1}$ , and $X_{2}\rightarrow \text{cosk}_{1}\text{sk}_{1}(X_{\bullet })_{2}$ are proper surjective. For the functors $\text{sk}_{1}$ and $\text{cosk}_{1}$ , one can refer, for example, to [St, Tag 0AMA].

Lemma 3.5. Let $f:Y\rightarrow X$ be a proper surjective morphism. Then the hypercovering $Y_{\bullet }:=\text{cosk}_{1}(Y\times _{X}Y\rightrightarrows Y)\rightarrow X$ satisfies the descent.

Proof. We have the natural functor $\unicode[STIX]{x1D6FC}:\text{Con}(X)\rightarrow \text{Con}(Y_{\bullet })$ , and we need to show that this is an equivalence. Let us construct the quasi-inverse. Let $(\mathscr{F},d_{0}^{1\ast }\mathscr{F}\cong d_{1}^{1\ast }\mathscr{F})$ where $\mathscr{F}\in \text{Con}(Y)$ is a descent data. This is sent to

$$\begin{eqnarray}\text{Ker}(f_{\ast }^{0}\mathscr{F}\rightrightarrows (f\circ d_{0}^{1})_{\ast }^{0}d_{0}^{1\ast }\mathscr{F}),\end{eqnarray}$$

where $g_{\ast }^{0}$ denotes $\text{}^{\text{c}}\!\mathscr{H}^{0}g_{\ast }$ for a morphism $g$ . This functor is denoted by $\unicode[STIX]{x1D6FD}$ . By adjunction, we have functors $\text{id}\rightarrow \unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}$ and $\unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D6FD}\rightarrow \text{id}$ , and it remains to check that these functors are equivalent. Since $f$ is assumed proper, by proper base change and [A2, 1.3.7 (i)], we may assume that $X$ is a point. Further, by replacing $X$ by its finite extension, we may assume that $f$ has a section $s:X\rightarrow Y$ . In this case, the argument is standard.◻

Corollary 3.6. Any proper hypercovering satisfies the descent.

Proof. Although the argument is very standard (for example, see [St, Tag 0D8D]), we give a proof for the convenience of the reader. Let $Y_{\bullet }\rightarrow X$ be a hypercovering of $X$ . If the hypercovering is $\text{cosk}_{1}(Y_{0}\times _{X}Y_{0}\rightrightarrows Y_{0})$ , then we already know the result by the lemma. The lemma also tells us that for a proper surjective morphism $W\rightarrow Z$ , the pullback $\text{Con}(Z)\rightarrow \text{Con}(W)$ is faithful. Thus, giving a descent data on $Y_{\bullet }$ is equivalent to giving a descent data on $\text{cosk}_{1}(Y_{1}\rightrightarrows Y_{0})$ . From now on, we assume that $Y_{\bullet }=\text{cosk}_{1}(Y_{1}\rightrightarrows Y_{0})$ .

Given a proper hypercovering $Y_{\bullet }$ , a descent data for $Y_{\bullet }$ is $\mathscr{F}\in \text{Con}(Y_{0})$ and an isomorphism $\unicode[STIX]{x1D719}:d_{0}^{1\ast }\mathscr{F}\cong d_{1}^{1\ast }\mathscr{F}$ satisfying some conditions. In order to define a descent data for $\text{cosk}_{1}(Y_{0}\times _{X}Y_{0}\rightrightarrows Y_{0})$ , we only need to descent $\unicode[STIX]{x1D719}$ to $Y_{0}\times _{X}Y_{0}$ . Now, we have the following morphism

$$\begin{eqnarray}\unicode[STIX]{x1D6FC}:=(\text{pr}_{1},\text{pr}_{2},s_{0}^{0}\circ d_{1}^{1}\circ \text{pr}_{1}):Y_{1}\times _{(Y_{0}\times _{X}Y_{0})}Y_{1}\rightarrow Y_{1}\times Y_{1}\times Y_{1}.\end{eqnarray}$$

This defines the following diagram of simplicial schemes:

where $d_{i}^{\prime 2}:=\text{pr}_{i}\circ \unicode[STIX]{x1D6FC}$ . By the universal property of $\text{cosk}$ , we have the dotted vertical arrow so that they form a morphism of simplicial schemes. The cocycle condition for $\unicode[STIX]{x1D719}$ on $Y_{2}$ pulled back to $Y_{1}\times _{(Y_{0}\times _{X}Y_{0})}Y_{1}$ by the dotted arrow gives us the following commutative diagram:

Thus, the isomorphism $\unicode[STIX]{x1D719}$ descends to $Y_{0}\times _{X}Y_{0}$ , and defines a descent data on $\text{cosk}_{1}(Y_{0}\times _{X}Y_{0}\rightrightarrows Y_{0})$ . Finally, use Lemma 3.5 to conclude.◻

Lemma 3.7. Let $X$ be a scheme, and $\mathscr{F}\in D^{{\leqslant}0}(X)$ . Then $\mathscr{H}^{0}(\mathscr{F})=0$ if and only if for any closed immersion $i:Z{\hookrightarrow}X$ , there exists a dense subscheme $U\subset Z$ such that $\mathscr{H}^{0}(i^{\ast }\mathscr{F})|_{U}=0$ .

Proof. Only if part follows since $i^{\ast }$ is right exact by [AC, Proposition 1.3.13]. Assume $\mathscr{H}^{0}\mathscr{F}$ is supported on a reduced scheme $Z$ . Consider the triangle

$$\begin{eqnarray}i_{Z}^{\ast }\unicode[STIX]{x1D70F}_{{<}0}\mathscr{F}\rightarrow i_{Z}^{\ast }\mathscr{F}\rightarrow i_{Z}^{\ast }\mathscr{H}^{0}(\mathscr{F})\xrightarrow[{}]{+}.\end{eqnarray}$$

Since $i^{\ast }$ is right exact, $\mathscr{H}^{i}i_{Z}^{\ast }\unicode[STIX]{x1D70F}_{{<}0}\mathscr{F}=0$ for $i\geqslant 0$ , which implies that $\mathscr{H}^{0}i_{Z}^{\ast }(\mathscr{F})\cong \mathscr{H}^{0}i_{Z}^{\ast }\mathscr{H}^{0}(\mathscr{F})$ . Since we assumed that $Z$ is the support of $\mathscr{H}^{0}\mathscr{F}$ , we have $i_{Z\ast }\mathscr{H}^{0}i_{Z}^{\ast }\mathscr{H}^{0}(\mathscr{F})\cong \mathscr{H}^{0}(\mathscr{F})$ . Combining these, we have $i_{Z\ast }\mathscr{H}^{0}i_{Z}^{\ast }(\mathscr{F})\cong \mathscr{H}^{0}(\mathscr{F})$ , and this vanishes generically on $Z$ by assumption. This can happen only when $Z=\emptyset$ .◻

3.8

Let us compare smooth objects with isocrystals. For a scheme $X$ of finite type over $k$ , we denote by $\text{Isoc}^{\dagger }(X)$ the subcategory of the category of overconvergent isocrystals on $X$ consisting of isocrystals whose constituents can be endowed with Frobenius structure (see right after [A2, 1.1.3 (11)]). Caution that $\text{Isoc}^{\dagger }(X)$ is slightly smaller than the category of overconvergent isocrystals on $X$ .

Theorem. Let $X$ be a scheme of finite type over $k$ . Then we have a canonical equivalence of categories $\text{Isoc}^{\dagger }(X)\xrightarrow[{}]{{\sim}}\text{Sm}(X)$ . This equivalence is compatible with pullback.

Proof. First, let us construct the functor in the case where $X$ is smooth. In this situation, Caro [C1] (cf. [A2, 2.4.15] for a summary) defines a fully faithful functor

$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{X}:\text{Isoc}^{\dagger }(X)\rightarrow D(X).\end{eqnarray}$$

Note that this functor is compatible with pullback. All we need to show is that the essential image of this functor is $\text{Sm}(X)$ . First, let us check this claim when $X$ is a curve. In this case, the inclusion $\text{Im}(\unicode[STIX]{x1D70C}_{X})\subset \text{Sm}(X)$ follows easily, and the other inclusion follows by [A2, Lemma 2.4.11]. We note that in [A2], $\mathscr{M}\in D(X)$ being smooth means $\mathscr{M}$ is in the essential image of $\unicode[STIX]{x1D70C}_{X}$ . Now assume $X$ is smooth but not necessarily a curve. We show by using the induction on the dimension of $X$ . We assume the equivalence is known for any smooth $X$ of dimension ${<}n$ . Assume $X$ is of dimension $n$ . Let $E\in \text{Isoc}^{\dagger }(X)$ , and let us check that $\unicode[STIX]{x1D70C}_{X}(E)$ is smooth. By definition and some limit argument, it suffices to check that for any morphism $c:C\rightarrow X$ from a smooth curve $C$ , $c^{\ast }\unicode[STIX]{x1D70C}_{X}(E)$ is smooth. However, since $c^{\ast }\unicode[STIX]{x1D70C}_{X}(E)\cong \unicode[STIX]{x1D70C}_{X}(c^{\ast }E)$ by the compatibility of pullback and we have already checked the claim for curves, $\unicode[STIX]{x1D70C}_{X}(c^{\ast }E)$ is smooth, thus $\unicode[STIX]{x1D70C}_{X}(E)\in \text{Sm}(X)$ . Let $\mathscr{L}\in \text{Sm}(X)$ , and let us show that $\mathscr{L}$ comes from an isocrystal. There exists an open dense subscheme $j:U\subset X$ such that $\mathscr{L}|_{U}\cong \unicode[STIX]{x1D70C}_{U}(E_{U})$ . We claim that $E_{U}$ extends to an isocrystal $E$ on $X$ . Indeed, let $c:C\rightarrow X$ be a morphism from a smooth curve $C$ . By the compatibility of pullback and the equivalence of $\unicode[STIX]{x1D70C}_{C}$ we have already checked, $c^{\ast }E_{U}$ does extend to an isocrystal on $C$ . Now, let $W\subset X$ be a closed subscheme of codimension ${\geqslant}2$ such that $(X\setminus U)\setminus W$ is smooth. By Shiho’s cut-by-curve theorem [S, Theorem 0.1] (see footnote of [A2, 2.4.13] when the base field $k$ is not uncountable for some explanation), $E_{U}$ extends to an isocrystal on $X\setminus W$ . Finally, by Kedlaya’s purity result [K1, Proposition 5.3.3], $E_{U}$ extends even to $X$ , and the claim follows. To conclude the proof, we need to show that the isomorphism $\mathscr{L}|_{U}\cong \unicode[STIX]{x1D70C}_{U}(E_{U})$ extends uniquely to an isomorphism $\mathscr{L}\cong \unicode[STIX]{x1D70C}_{X}(E)$ .

Let $i:Z\rightarrow X$ be the complement of $U$ . Let us show that $\mathscr{H}^{n}(i^{\ast }\mathscr{L})=0$ . In order to show this, it suffices to check that for any closed immersion $i_{W}:W{\hookrightarrow}Z$ , $\mathscr{H}^{n}(i_{W}^{\ast }i^{\ast }\mathscr{L})$ vanishes generically on $W$ by Lemma 3.7. Since the associated reduced scheme of $W$ is generically smooth, $i_{W}^{\ast }i^{\ast }\mathscr{L}$ is smooth on $W$ , and by induction hypothesis, $i_{W}^{\ast }i^{\ast }\mathscr{L}$ generically comes from an isocrystal. Since isocrystals concentrate on degree ${\leqslant}\dim (W)<n$ , we get the claim. Now, since $\mathscr{L}$ is constructible, $\mathscr{H}^{i}\mathscr{L}=0$ for $i>n$ . Considering the exact triangle $j_{!}\mathscr{L}\rightarrow \mathscr{L}\rightarrow i^{\ast }\mathscr{L}\xrightarrow[{}]{+}$ , the homomorphism $\mathscr{H}^{n}j_{!}\mathscr{L}\rightarrow \mathscr{H}^{n}\mathscr{L}$ is surjective because we have checked that $\mathscr{H}^{n}i^{\ast }\mathscr{L}=0$ . Thus, we have a canonical homomorphism $\mathscr{L}\rightarrow j_{!\ast }(\mathscr{L})$ . This induces $\mathscr{L}\rightarrow j_{!\ast }\mathscr{L}\cong j_{!\ast }\unicode[STIX]{x1D70C}_{U}(E_{U})\cong \unicode[STIX]{x1D70C}_{X}(E)$ whose restriction to $U$ is the given map. The compatibility of pullback and induction hypothesis implies that this is in fact an isomorphism and is a unique homomorphism extending the given $\mathscr{L}|_{U}\cong \unicode[STIX]{x1D70C}_{U}(E_{U})$ .

In the general case, by using de Jong’s alteration, we can take a proper hypercovering $Y_{\bullet }$ of $X$ such that $Y_{i}$ is smooth for any $i$ . By Corollary 3.6, proper descent of isocrystals [S, Proposition 7.3], and the compatibility of pullback, we have a functor $\text{Isoc}^{\dagger }(X)\rightarrow \text{Con}(X)$ . It is easy to check that this functor does not depend on the choice of $Y_{0}$ , $Y_{1}$ up to canonical isomorphism. The essential image coincides with $\text{Sm}(X)$ since smooth objects are preserved by pullback and Lemma 3.3.◻

Corollary 3.9. Let $X$ be a scheme, $j:U{\hookrightarrow}X$ an open immersion, and $\mathscr{L}\in \text{Sm}(X)$ . For any $\mathscr{G}\in D(X)$ , we have a canonical isomorphism

$$\begin{eqnarray}\mathscr{L}\,\otimes \,j_{\ast }(\mathscr{G})\xrightarrow[{}]{{\sim}}j_{\ast }(j^{\ast }\mathscr{L}\,\otimes \,\mathscr{G}).\end{eqnarray}$$

Proof. By limit argument, we may assume $X$ is of finite type over $k$ . The homomorphism is defined by adjunctions. Since it is an isomorphism on $U$ , it suffices to check that $i^{!}(\mathscr{L}\,\otimes \,j_{\ast }(\mathscr{G}))=0$ where $i:X\setminus U\rightarrow X$ . Let us show the claim using the induction on the dimension of the support of $\mathscr{G}$ . When the dimension is $0$ , there is nothing to show. Take an alteration $g:X^{\prime }\rightarrow X$ such that $X^{\prime }$ is smooth, and let $j_{UV}:V\subset U$ be an open dense subscheme such that $g_{V}:g^{-1}(V)\rightarrow V$ is finite étale. By induction hypothesis, we may assume that $\mathscr{G}=j_{UV\ast }\mathscr{G}_{V}$ for some $\mathscr{G}_{V}$ . Since $g_{V}$ is finite étale, $\mathscr{G}_{V}$ is a direct factor of $g_{V\ast }g_{V}^{\ast }\mathscr{G}_{V}$ . Consider the following diagram

Using the projection formula and the commutation of $g_{\ast }$ and $i^{!}$ , we have

$$\begin{eqnarray}\displaystyle i^{!}(\mathscr{L}\,\otimes \,j_{V\ast }g_{V\ast }g_{V}^{\ast }(\mathscr{G}_{V})) & \cong & \displaystyle i^{!}g_{\ast }(g^{\ast }\mathscr{L}\,\otimes \,j_{V\ast }^{\prime }g_{V}^{\ast }(\mathscr{G}_{V}))\nonumber\\ \displaystyle & \cong & \displaystyle g_{Z\ast }i^{\prime !}(g^{\ast }\mathscr{L}\,\otimes \,j_{V\ast }^{\prime }g_{V}^{\ast }(\mathscr{G}_{V})).\nonumber\end{eqnarray}$$

Thus, it suffices to check that $i^{\prime !}(g^{\ast }\mathscr{L}\,\otimes \,j_{V\ast }^{\prime }g_{V}^{\ast }(\mathscr{G}_{V}))=0$ , and may assume that $X$ is smooth. Then we use Theorem 3.8 and [A1, Proposition 5.8] to conclude.

Corollary 3.10. Let $(S,s,\unicode[STIX]{x1D702})$ be a Henselian trait. Let $\unicode[STIX]{x1D70B}:X\rightarrow S$ be a morphism of finite type and $\mathscr{L}\in \text{Sm}(X)$ . Then for any $\mathscr{G}\in \text{Hol}(X)$ , we have a canonical isomorphism

$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{L}\,\otimes \,\mathscr{G})\cong \mathscr{L}|_{X_{s}}\,\otimes \,\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{G}).\end{eqnarray}$$

Theorem 3.11. Let $f:X\rightarrow Y$ be a morphism of schemes.

1. (1) The functor $f^{\ast }$ preserves smooth objects. In particular, it induces a functor $f^{\ast }:\text{Sm}(Y)\rightarrow \text{Sm}(X)$ .

2. (2) Assume that $f$ is proper and smooth. Then $f_{\ast }$ preserves smooth objects.

Proof. The preservation under pullback follows directly by definition, and we write it just for the future reference. Let us check the second claim. Take a strict Henselian trait $S$ and a morphism $\unicode[STIX]{x1D719}:S\rightarrow Y$ . Using 1 and the commutation of $f_{\ast }$ and $\unicode[STIX]{x1D719}^{\ast }$ because $f$ is assumed proper, it suffices to check the claim when $Y$ is strict Henselian trait. Let $\mathscr{L}$ be a smooth object on $X$ . We have

$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\text{id}}f_{\ast }(\mathscr{L})\cong f_{\ast }\unicode[STIX]{x1D6F7}_{f}(\mathscr{L})\cong f_{\ast }(\unicode[STIX]{x1D6F7}_{f}(L_{X})\,\otimes \,\mathscr{L}|_{X_{s}}),\end{eqnarray}$$

where the first isomorphism follows by Corollary 2.6.1, and the second by Corollary 3.10. Finally, since $f$ is assumed smooth, we have  $\unicode[STIX]{x1D6F7}_{f}(L_{X})\cong f^{\ast }\unicode[STIX]{x1D6F7}_{\text{id}}(L_{Y})$ by Corollary 2.6.2. Since $Y$ is assumed strict Henselian trait, $\text{rk}(\unicode[STIX]{x1D6F9}_{\text{id}}(L_{Y}))=1$ by Proposition 1.10. Thus, the exact triangle 2.6.3 tells us that $\unicode[STIX]{x1D6F7}_{\text{id}}(L_{Y})=0$ , and the theorem follows.◻

Remark.

One can think part 2 of the theorem above as a $\mathscr{D}$ -module theoretic version of Berthelot’s conjecture [Ber, (4.3)]. This variant has already been considered by Caro in [C2, Théorème 4.4.2] when $X$ , $Y$ are realizable schemes. In that case, he proved without the existence of Frobenius structure, whereas we assume the existence implicitly in the construction of the category $\text{Hol}(X)$ . However, our theorem is stronger in the sense that the schemes need not be realizable. In order to deduce the original Berthelot’s conjecture from our result, one might need to compare our pushforward and relative rigid cohomology (cf. [A2, 2.4.16]). This will be addressed in future works.

Question 3.12. Assume $X$ is smooth. For any object $\mathscr{M}\in D(X)$ , the characteristic variety $\text{Car}(\mathscr{M})$ is defined as a closed subscheme of codimension $\dim (X)$ in $T^{\ast }X$ by Berthelot. We expect that this characteristic variety has the following characterization: for any $X\supset U\xrightarrow[{}]{f}\mathbb{A}^{1}$ such that $U$ is an open subscheme of $X$ and $df(U)\cap \text{Car}(\mathscr{M})=\emptyset$ we have $\unicode[STIX]{x1D6F7}_{f}(\mathscr{M})=0$ , and $\text{Car}(\mathscr{M})$ is the smallest closed subscheme of $T^{\ast }X$ having possessing such a property.

4 Toward a local theory

Definition 4.1.

1. (1) Let $S$ be a Henselian local scheme (i.e., it is a scheme which is the spectrum of a Henselian local ring), and let $i:s{\hookrightarrow}S$ be the closed immersion from the closed point. The category $\text{Loc}(S)$ is defined as follows: The object is the same as $\text{Hol}(S)$ . For $\mathscr{F}\in \text{Hol}(S)$ the corresponding object in $\text{Loc}(S)$ is denoted by $\mathscr{F}^{\text{loc}}$ . Then

   $$\begin{eqnarray}\text{Hom}_{\text{Loc}(S)}(\mathscr{F}^{\text{loc}},\mathscr{G}^{\text{loc}}):=H^{0}(s,i^{\ast }{\mathcal{H}}om_{S}(\mathscr{F},\mathscr{G})),\end{eqnarray}$$
   where $H^{i}(s,\mathscr{H}):=\text{Hom}_{D(s)}(L_{s},\mathscr{H}[i])$ . The object $L_{S}^{\text{loc}}$ is denoted by $L_{S}$ for simplicity.

2. (2) Let $S$ be a local Henselian scheme, and $f:X\rightarrow S$ be a morphism of finite type. Then $\text{Loc}(X/S)$ is defined as follows. The objects are the same as $\text{Hol}(X)$ . For $\mathscr{F},\mathscr{G}\in \text{Hol}(X)$ , we define

   $$\begin{eqnarray}\text{Hom}_{\text{Loc}(X/S)}(\mathscr{F},\mathscr{G}):=\text{Hom}_{\text{Loc}(S)}(L_{S},f_{\ast }{\mathcal{H}}om(\mathscr{F},\mathscr{G})).\end{eqnarray}$$

Remark 4.2.

1. (1) The category $\text{Loc}(X/S)$ is certainly an additive category. However, we do not know if this is abelian or not.

2. (2) We assume we are in the situation of 4.1.1. We remark that

   $$\begin{eqnarray}H^{i}(s,i^{\ast }{\mathcal{H}}om_{S}(\mathscr{F},\mathscr{G}))=0\end{eqnarray}$$
   for $i<0$ . Indeed, let us check first that for any scheme $X$ and $\mathscr{F},\mathscr{G}\in \text{Hol}(X)$ , $\text{}^{\text{c}}\!\mathscr{H}^{i}{\mathcal{H}}om_{X}(\mathscr{F},\mathscr{G})=0$ for $i<0$ . We may assume $X$ is smooth. For $\mathscr{F}\in D^{{\leqslant}0}(X)$ , $\mathscr{G}\in D^{{\geqslant}0}(X)$ , we may check as [BBD, 2.1.20] that ${\mathcal{H}}om(\mathscr{F},\mathscr{G})\in ^{\text{c}}D^{{\geqslant}0}(X)$ . Thus, $\text{}^{\text{c}}\!\mathscr{H}^{i}{\mathcal{H}}om(\mathscr{F},\mathscr{G})=0$ for $i<0$ . Since $i^{\ast }$ is c-t-exact and $L_{s}$ is constructible object, we get the claim.

3. (3) Ultimately, we expect a triangulated category $D_{\text{loc}}(X/S)$ with the following properties: First, we have a functor $\unicode[STIX]{x1D70C}:D(X)\rightarrow D_{\text{loc}}(X/S)$ . For $\mathscr{F},\mathscr{G}\in D(X)$ , we should have

   $$\begin{eqnarray}\text{Hom}_{D_{\text{loc}}(X/S)}(\unicode[STIX]{x1D70C}(\mathscr{F}),\unicode[STIX]{x1D70C}(\mathscr{G}))\cong \text{Hom}_{D(s)}(L_{s},i^{\ast }f_{\ast }{\mathcal{H}}om(\mathscr{F},\mathscr{G})).\end{eqnarray}$$
   Second, we have a t-structure on $D_{\text{loc}}(X/S)$ whose heart contains $\unicode[STIX]{x1D70C}(\text{Hol}(X))$ . The computation of part 2 above shows that the “higher homotopies” of $\unicode[STIX]{x1D70C}(\text{Hol}(X))$ vanish in the category $D_{\text{loc}}(X/S)$ . This gives us an evidence of the existence of such t-structure. The category $\text{Loc}(X/S)$ should be a full subcategory of this heart.

   This category should be an analogue of the derived category of constructible sheaves for $\ell$ -adic sheaves of a scheme of separated of finite type over a local Henselian scheme as in [E, Theorem 6.3]. The following Theorem 4.6 gives an evidence for this philosophy.

4.3

Let $S$ be a strict Henselian trait, and $\unicode[STIX]{x1D70B}:X\rightarrow S$ be a morphism of finite type. The nearby cycle formalism extends to that on $\text{Loc}(X)$ . For $\mathscr{F},\mathscr{G}\in D(X)$ , we have the canonical homomorphism

$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\,\otimes \,\mathscr{G}|_{X_{s}}\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F}\,\otimes \,\mathscr{G}).\end{eqnarray}$$

On the other hand, the adjunction induces a map

$$\begin{eqnarray}L_{X_{s}}\boxtimes H^{0}(X_{s},\mathscr{H})\rightarrow \mathscr{H}\end{eqnarray}$$

for any $\mathscr{H}\in D(X_{s})$ . Combining these, we obtain a homomorphism

$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F})\boxtimes \text{Hom}_{\text{Loc}(X)}(\mathscr{F}^{\text{loc}},\mathscr{G}^{\text{loc}})\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F}\,\otimes \,{\mathcal{H}}om(\mathscr{F},\mathscr{G}))\rightarrow \unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{G}).\end{eqnarray}$$

Thus, we have a homomorphism

$$\begin{eqnarray}\text{Hom}_{\text{Loc}(X)}(\mathscr{F}^{\text{loc}},\mathscr{G}^{\text{loc}})\rightarrow \text{Hom}_{\text{Hol}(X_{s})}(\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{F}),\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}(\mathscr{G})).\end{eqnarray}$$

If $\mathscr{F}=\mathscr{G}$ , then the identity is sent to the identity, and the map is compatible with the composition. Thus, $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70B}}$ is defined also on the level of the category $\text{Loc}(X)$ .

4.4

Let us describe the category $\text{Loc}(S)$ when $S$ is a Henselian trait in terms of the theory on a formal unit disk after Crew. Let $\mathscr{S}:=k[\![t]\!]$ , a formal disk. For this disk, he constructed the category $\text{Coh}^{\text{an}}({\mathcal{D}}^{\dagger })$ in [Cr1, 5.2]. Crew defined a category of holonomic objects in $\text{Coh}^{\text{an}}({\mathcal{D}}^{\dagger })$ with Frobenius structure, and denote it by $\text{Hol}^{\text{an}}(F{\mathcal{D}}^{\dagger })$ . As usual, we consider the full subcategory of $\text{Coh}^{\text{an}}({\mathcal{D}}^{\dagger })$ consisting of objects which are of finite length and whose constituent can be endowed with a Frobenius structure with which the constituent is in $\text{Hol}^{\text{an}}(F{\mathcal{D}}^{\dagger })$ . We denote this category by $\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$ , or $\text{Hol}^{\text{an}}({\mathcal{D}}_{\mathscr{S},\mathbb{Q}}^{\dagger })$ if we want to emphasize the formal disk. In this situation, the functors $j_{+}$ , $j^{+}$ $i_{+}$ , $i^{+}$ , $i^{!}$ are defined (cf. [Cr1, 5.2]). Even though the definition seems to be a bit involved, $\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$ is very close to the category which has already appeared in the theory of $p$ -adic differential equation. In fact, the category $\text{MLS}({\mathcal{R}},\mathbf{F},\mathbf{pot})$ appearing in [CM, Définition 6.0-19] is contained full faithfully in $\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$ , and it is easy to characterize this subcategory: it consists of the objects ${\mathcal{M}}\in \text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$ such that $i^{!}{\mathcal{M}}=0$ . The verification of this characterization is left to the reader.

4.5

Let $S$ be the Henselization of $\mathbb{A}_{k}^{1}$ at $0$ . Recall that Crew constructed a canonical functor $\text{An}:\text{Hol}(S)\rightarrow \text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$ sending an object $\mathscr{F}\in \text{Hol}(S)$ to $\mathscr{F}^{\text{an}}$ in [Cr1, (5.2.3)]. Since ${\mathcal{D}}^{\text{an}}$ is flat over ${\mathcal{D}}^{\dagger }$ , this functor extends to $\text{An}:D(S)\rightarrow D({\mathcal{D}}_{\mathscr{S},\mathbb{Q}}^{\text{an}})$ by simply considering ${\mathcal{D}}^{\text{an}}\otimes _{{\mathcal{D}}^{\dagger }}$ .

Lemma. For $\mathscr{F},\mathscr{G}\in \text{Hol}(S)$ , we define $\mathscr{F}\otimes ^{\text{an}}\mathscr{G}$ to be ${\mathcal{D}}^{\text{an}}\otimes _{{\mathcal{D}}^{\dagger }}(\mathscr{F}\otimes ^{\dagger }\mathscr{G})$ in $D^{\text{b}}({\mathcal{D}}^{\text{an}})$ . Then this functor factors through $\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$ .

Proof. Let $X$ be an étale neighborhood of $\mathbb{A}^{1}$ at $0$ so that $\mathscr{F}$ , $\mathscr{G}$ are defined in $\text{Hol}(X)$ . Let $\mathscr{X}$ be a smooth lifting of $X$ . We have the functor $\otimes ^{\dagger }:\underset{\longrightarrow }{LD}_{\mathbb{Q}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X}}^{(\bullet )})\,\otimes \,\underset{\longrightarrow }{LD}_{\mathbb{Q}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X}}^{(\bullet )})\rightarrow \underset{\longrightarrow }{LD}_{\mathbb{Q}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X}}^{(\bullet )})$ . This functor is isomorphic to $\unicode[STIX]{x1D6E5}^{!}(-\boxtimes ^{\dagger }-)$ up to some shift. Thus, by [C3, Theorem 3.4.9], $\otimes ^{\dagger }$ sends $\underset{\longrightarrow }{LD}_{\mathbb{Q},\text{coh}}^{\text{b}}\times \underset{\longrightarrow }{LD}_{\mathbb{Q},\text{coh}}^{\text{b}}$ to $\underset{\longrightarrow }{LD}_{\mathbb{Q},\text{coh}}^{\text{b}}$ . Let $\mathscr{F}=\mathscr{F}^{(\bullet )}$ , $\mathscr{G}=\mathscr{G}^{(\bullet )}$ in $\underset{\longrightarrow }{LD}_{\mathbb{Q},\text{coh}}^{\text{b}}$ . For $\mathscr{H}_{\mathbb{Q}}$ in $D_{\text{coh}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X},\mathbb{Q}}^{(m)})$ , we denote by $\mathscr{H}_{\mathbb{Q}}^{(m)\text{an}}$ the complex $R\,\mathop{\varprojlim }\nolimits_{r}(R\,\mathop{\varprojlim }\nolimits_{n}({\mathcal{O}}_{r,n}\otimes _{{\mathcal{O}}}^{L}\mathscr{H}))\,\otimes \,\mathbb{Q}$ where $\mathscr{H}$ is a complex in $D_{\text{coh}}^{\text{b}}(\widehat{\mathscr{D}}_{\mathscr{X}}^{(m)})$ such that $\mathscr{H}\,\otimes \,\mathbb{Q}\cong \mathscr{H}_{\mathbb{Q}}$ , using the notation appearing in [Cr1, (4.1.8)]. Then Caro’s finiteness above together with [Cr1, Theorem 4.1.1] implies that

This description implies that the functor factors through $\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$ .◻

For ${\mathcal{M}},{\mathcal{N}}\in \text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$ , we define ${\mathcal{H}}om({\mathcal{M}},{\mathcal{N}}):=(\mathbb{D}({\mathcal{M}})\otimes ^{\text{an}}{\mathcal{N}})[-1]$ . The definition of $\otimes ^{\text{an}}$ implies that for $\mathscr{F},\mathscr{G}$ in $\text{Hol}(S)$ , we have

$$\begin{eqnarray}{\mathcal{H}}om(\mathscr{F},\mathscr{G})^{\text{an}}\cong {\mathcal{H}}om(\mathscr{F}^{\text{an}},\mathscr{G}^{\text{an}}).\end{eqnarray}$$

This implies

(4.5.6) $$\begin{eqnarray}i^{\ast }{\mathcal{H}}om(\mathscr{F},\mathscr{G})\cong i^{+}{\mathcal{H}}om(\mathscr{F},\mathscr{G})^{\text{an}}\cong i^{+}{\mathcal{H}}om(\mathscr{F}^{\text{an}},\mathscr{G}^{\text{an}}).\end{eqnarray}$$

Theorem 4.6. Let $S$ be a Henselian trait such that the closed point is of finite type over $k$ . Let $\mathscr{S}$ be the formal completion of $S$ with respect to the closed point. Then we have the canonical equivalence of categories $\text{Loc}(S)\cong \text{Hol}^{\text{an}}({\mathcal{D}}_{\mathscr{S},\mathbb{Q}}^{\dagger })$ .

Proof. Let us show that the functor $\text{An}$ factors through $\text{Hol}(S)\rightarrow \text{Loc}(S)$ . Recall that we have the Crew–Matsuda canonical extension

$$\begin{eqnarray}\text{Can}:\text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })\rightarrow \text{Hol}(\mathbb{A}^{1})\end{eqnarray}$$

which is fully faithful and $\text{An}\circ \text{Can}\cong \text{id}$ (cf. [Cr1, Theorem 8.2.1]). Consider the canonical homomorphism $\text{Hom}(\mathscr{F},\mathscr{G})\rightarrow \mathscr{H}^{0}i^{\ast }{\mathcal{H}}om(\mathscr{F},\mathscr{G})$ for $\mathscr{F},\mathscr{G}\in D(\mathbb{A}^{1})$ . Let us show that this is an isomorphism if $\mathscr{F}$ and $\mathscr{G}$ are canonical extensions. Denote by $i:0{\hookrightarrow}\mathbb{A}^{1}$ the closed immersion and $j$ the complement. If $\mathscr{F}$ or $\mathscr{G}$ is of the form $i_{\ast }\mathscr{H}\cong i_{!}\mathscr{H}$ , then the claim follows by adjunction. Considering the localization sequence, this implies that we may assume that $\mathscr{G}=j_{\ast }j^{\ast }\mathscr{G}$ . In this case, we have ${\mathcal{H}}om(\mathscr{F},\mathscr{G})\cong j_{\ast }{\mathcal{H}}om(j^{\ast }\mathscr{F},j^{\ast }\mathscr{G})$ by adjunction. If $\mathscr{F}$ , $\mathscr{G}$ are canonical extensions, we get that ${\mathcal{H}}om(\mathscr{F},\mathscr{G})$ is a canonical extension as well. Thus, it remains to check that if $\mathscr{H}$ is a canonical extension and $\mathscr{H}\cong j_{\ast }j^{\ast }\mathscr{H}$ , then the restriction $H^{0}(\mathbb{A}^{1},\mathscr{H})\rightarrow \mathscr{H}^{0}i^{\ast }\mathscr{H}$ is an isomorphism. The source is isomorphic to $H^{0}(\mathscr{S},\mathscr{H}^{\text{an}})$ since the canonical extension is fully faithful, and the claim follows by the proof of [AM, Lemma 3.1.10] where we showed $H^{n}(\mathscr{S},\mathscr{H}^{\text{an}})\cong \mathscr{H}^{n}i^{+}\mathscr{H}^{\text{an}}$ . Now, we have

$$\begin{eqnarray}\displaystyle \text{Hom}(\mathscr{F}^{\text{loc}},\mathscr{G}^{\text{loc}}) & := & \displaystyle H^{0}(s,i^{\ast }{\mathcal{H}}om(\mathscr{F},\mathscr{G}))\nonumber\\ \displaystyle & \cong & \displaystyle H^{0}(s,i^{\ast }{\mathcal{H}}om(\text{Can}(\mathscr{F}^{\text{an}}),\text{Can}(\mathscr{G}^{\text{an}})))\nonumber\\ \displaystyle & \xleftarrow[{}]{{\sim}} & \displaystyle \text{Hom}(\text{Can}(\mathscr{F}^{\text{an}}),\text{Can}(\mathscr{G}^{\text{an}}))\cong \text{Hom}(\mathscr{F}^{\text{an}},\mathscr{G}^{\text{an}}),\nonumber\end{eqnarray}$$

where the 2nd isomorphism follows by (4.5.6) and the 3rd by the isomorphism we have just proven, and the last by full faithfulness of $\text{Can}$ . It is easy to check that this isomorphism is compatible with composition, and we have the desired functor $\text{Loc}(S)\rightarrow \text{Hol}^{\text{an}}({\mathcal{D}}^{\dagger })$ , which is moreover fully faithful. To check the equivalence, it remains to check that the functor is essentially surjective. This follows by Crew–Matsuda canonical extension. ◻

Remark 4.7.

1. (1) It might be possible to reprove [AM] without using microlocal technique by using the foundation of this paper instead.

2. (2) It would be interesting to compare the theory developed here and recent works of Lazda–Pal [LP], Caro–Vauclair [CV], or Crew [Cr2] on the theory of $p$ -adic cohomology theory for formal schemes or schemes over Laurent series field.