1. Introduction
The collaboration between CEMAGREF and the Centre d’Etudes de la Neige (CEN) of Météo-France aims to create a connected numerical drifting-snow model in order to forecast snow accumulation at the scale of an avalanche path. The output of the CEN modelling at large scale will be the input of the CEMAGREF modelling at small scale.
At present, both CEMAGREF and CEN are testing their own numerical modelling on a joint experimental site located at Lac Blanc Pass, with the logistic support of SATA (the Alpe d’Huez ski resort management company) and with the financial support of the Rhône-Alpes Region.
This site, which is located at 2700 m a.s.l. near the Alpe d’Huez ski resort (Reference Michaux, Naaim-Bouvet and NaaimMichaux and others, 2000), is a nearly flat area. It is a kind of natural cold wind tunnel with prevailing winds from north and south.
After describing the experimental site and the sensors used, we will present the processed data of winter 1998/99 used in the study of non-stationary phenomena of wind and drifting snow. The results of this study are the basis for some simplification of the numerical drifting-snow model, which will be presented in section 4 of the paper. The measurements are also used to validate this model.
2. Description of the Experimental Site
In order to follow the three-dimensional spatial distribution of snow during the winter and to determine where snow accumulates and settles for a given meteorological event, we set up two networks of metallic snow poles at Lac Blanc Pass (Reference CastelleCastelle, 1995). The results presented in this paper concern only one site, La Muzelle, which is located at the southern side of the pass. The prevailing winds at La Muzelle are from the north or south (Fig. 1). The high wind speeds and the snow cover are favourable to drifting snow. On this site, a square of 20 poles and a 200 m long profile of height poles have been set up (Fig. 2). This area is both an erosion zone (near the pass) and an accumulation zone. We climbed to this experimental site at least once a week, depending on snowdrift-event forecasts, in order to measure the snow depth at each snow pole. In addition, a stratigraphic profile of the snowpack and a ram test were carried out to collect data on the time progression of the snowpack and the depth of the snow. Automatically recorded meteorological data complete these measurements. A data logger recorded the following parameters every 15 min (with a scan rate of 1 s): average, maximum and minimum wind speed, direction, precipitation and temperature. Another weather station situated nearby has been equipped with an ultrasonic sensor which measures the snow depth.

Fig. 1. Distribution of winds on the La Muzelle site during winter 1998/99.

Fig. 2. The net of snow poles at Col du Lac Blanc, on the site of La Muzelle.
Nevertheless, all these meteorological data are not sufficient to test the numerical model; the snow mass flux and the threshold velocity are also necessary for these calculations. For that reason, CEMAGREF’s Erosion torrentielle, neige et avalanche (Etna) unit has developed an acoustic snowdrift sensor (Fig. 3) in collaboration with Hydroemac (Reference Font, Naaim-Bouvet and RousselFont and others, 1998). This is basically a miniature microphone located at the base of a 2 m long aluminium pole during snowdrift. The pole is exposed to the snow-particle flux, and part of the flux impacts on the pole during snowdrift. The sound produced by these impacts is recorded as an electrical signal. The lower- frequency signal produced by the wind and the higher- frequency signal, outside the audible range, are filtered out. The recorded output voltage indicates when snowdrift occurs. Six acoustic sensors were installed along the 200 m profile of the La Muzelle site. These sensors are located in the erosion area, in the transport zone and in the deposition zone. As mentioned above, the high wind speeds and the snow cover are favourable to drifting snow. Supposing that a 50 mV output signal (there is an offset of 45 mV) from the acoustic sensor indicates the beginning of a drifting-snow event (including snowfall with wind), 40% of February is subjected to drifting snow (Fig. 4).

Fig. 3. The acoustic snowdrift sensor.

Fig. 4. Occurrence of drifting-snow events.
3. Results Obtained During Winter 1998/99
3.1. The Acoustic Snowdrift Sensor
3.1.1. Relation between snow mass flux and data recorded by the acoustic sensor
The mass flux of drifting snow is one parameter in our numerical model. Up to now, the mass flux has been inferred from the wind speed by means of an empirical law (Reference Pomeroy and GrayPomeroy and Gray, 1990). In order to improve the model, however, we would like to obtain measurements of the flux. To this end, we plan to calibrate the acoustic sensor, in order to deduce the flux of drifting snow from the recorded signal. Therefore, we have performed experiments in which we compare the average mass flux during 15 min, and the average recorded signal.
The mass flux was determined using mechanical snow traps, called “butterfly nets”. These have a rectangular metal frame (15 cm × 2 cm) with an attached nylon bag. The traps, facing the prevailing wind direction, are fixed at different heights on a pole, next to the acoustic sensor. We obtain the drifting-snow flux by integrating the mass weight at each height. The collection efficiency of such mechanical traps depends on the wind speed and can be significantly below 100% (Reference FontFont, 1999). Lacking additional information, we applied no corrections.
The recorded signal is highly dependent on the snow depth. Therefore the acoustic sensor was fixed on a pole in a manner that allowed it to be raised during winter (Fig. 3). During the experiments for sensor calibration, the sensor was situated in an erosion zone with no snow on the ground. A plot of mass flux vs height with the output voltage as parameter is presented in Figure 5. The measurements correspond to two drifting-snow events (with and without snowfall). First of all, the data fit quite well with the values reported in Reference Mellor and FellersMellor and Fellers (1986) who did not distinguish the effect of snowfall in their experimental data processing (Reference Naaim-Bouvet, Naaim and MartinezNaaim-Bouvet and others, 1996). Here, however, the effect of snowfall is obvious: the mass flux above 1.3 m is constant and fairly substantial (8 gm–2 s-1).

Fig. 5. Relation between the snow mass flux and the data recordedby the acoustic sensor for different wind speeds (ms–1).
Moreover, we can compare the total measured mass flux (19–194 cm above the snow layer) and the sensor signal (Fig. 6). We notice a good correlation, but the low number of experiments prevents us from drawing final conclusions.

Fig. 6. Total measured mass flux (19–194 cm above the snow layer) vs the output voltage of the acoustic sensor.
3.1.2. Influence of snow-particle type on the acoustic sensor
Figures 7–9 illustrate the signal recorded by the acoustic snowdrift sensor (average signal over 15min vs the wind velocity) for various snowdrift episodes and thus for different snow types. In order to determine the snow type, we decided to rely on the SAFRAN (Reference Durand, Brun, Merindol, Guyomarc’h, Lesaffre and MartinDurand and others, 1993)/Crocus (Reference Brun, David, Sudul and BrunotBrun and others, 1992) model, for two reasons. Firstly, we were not always on our experimental site at the beginning of the drifting-snow event, so we have no other information about the snow type. Secondly, we are developing a connected model in which the output of SAFRAN/Crocus will be the input of our numerical drifting-snow model.

Fig. 7. Voltage (mean value over 15 min) from acoustic sensor No. 5 vs wind speed (mean value over 15min) for different drifting-snow events.

Fig. 8. Voltage (mean value over 15 min) from acoustic sensor No. 1 vs wind speed (mean value over 15 min).

Fig. 9. Evolution of snow depth near acoustic sensor No. 5 during winter 1998/99.
On 4 March 1998, we observed an episode with both snowfall and wind that appears as widely scattered data points in Figure 7. In this case, the mass flux was correlated with both the wind speed and the snowfall intensity, which was not constant. This scattering of data was always observed in episodes of snowdrift with snowfall during the winter (see Fig. 8).
The 8 March episode was characterized by drifting new snow, whereas the 17–20 March episode was characterized by rounded grains, and the episodes from 16–18 January and 3 March by faceted grains. The signal induced by rounded grains was higher than that generated by new-snow or faceted grains (see Fig. 7). However, we should keep in mind that this difference in signal might be caused by a shift of the signal due to the variation of the snow depth around the sensor during March. Figure 9 shows the evolution in time of the snow depth at sensor No. 5; the increase during March is caused by snowfall events without wind. The difference between signals for different types of grains was smaller for another sensor where the snow-depth variation was less (see Fig. 8). These observations confirm that a snow-depth sensor must accompany the acoustic sensor in an operational use. This will allow a correction of the data with regard to the ideal situation on which the sensor was calibrated (erosion area without snow).
As mentioned above, the 16–18 January and 3 March episodes were snowdrift events of faceted grains. These two graphs are relatively similar, with a recorded output voltage roughly proportional to the cube of the wind speed. Supposing that the mass flux is proportional to the cube of the wind speed, as predicted by some empirical formulations (Reference Dyunin and KotlyakovDyunin and Kotlyakov, 1980), led us to believe that the snowdrift flux might be proportional to the recorded signal on the acoustic sensor in these episodes. However, data on the calibration of the sensor are insufficient to confirm this hypothesis. On the other hand, preliminary laboratory studies on the acoustic sensor have shown that the signal generated by a quantity Q of sand falling from a height H was the double of the signal generated by a quantity Q/2 of sand falling from the same height within the same time (i.e. with the same speed).
3.2. Drifting snow: non-stationary phenomena
Early wind and snowdrift modelling used to take only average values into account. Therefore, focusing on the non-stationary aspect of these phenomena may provide useful information. For that reason, we studied the gust factor (for wind and drifting snow), defined as the ratio of the maximum and average data for a given period.
3.2.1. Wind-gustfactor
Data obtained at La Muzelle was processed in three steps. Firstly, we filtered out data with a mean wind speed of < 4 m s–1. For a wind speed weaker than 4 m s–1, we considered that there was no drifting snow, or very little. Furthermore, a low wind speed often generates a high gust factor, which is of no interest for the present purpose. A gust factor of 5 produced by a mean wind of 0.5 ms–1 and a gust of 2.5 ins”1 is very different from the same gust factor with a mean wind of 5 m s–1 and a gust of 25 m s–1.
Secondly, winds were separated into four classes: northerly, southerly, easterly and westerly. As can be seen in Figure 1, the experimental site is a kind of natural cold wind tunnel with a north-south axis. Therefore, a northerly and an easterly wind will probably have different effects.
Lastly, gust factors were calculated both for 15 min average winds and for hourly mean wind speeds, in order to compare our results with previous works.
The obtained gust factors range from 1.1 to 8.8. Sometimes these gust factors were higher than in other experiments (e.g. Reference DeavesDeaves (1993) reported values of <4). However, we found only a few strong gust factors during the winter, and our average gust factor remained around 1.8. It should be mentioned that gust factors have often been investigated near sea level (Reference Beranger and PagesBeranger and Pages, 1958; Reference DeavesDeaves, 1993), whereas the present data were collected in a high-mountain environment. In addition, we used Young anemometers which are very sensitive (response time of Is), whereas Reference DeavesDeaves (1993) used different anemometers. The value of our gust factor also depended strongly on the wind direction. For northerly and southerly winds, the probability P of having a gust factor of > 2 is on the order of 10%, whereas it is much higher for easterly and westerly winds (>40%) (Fig. 10). This large difference is probably caused by the geometry of the Lac Blanc Pass, but there are fewer data available for easterly winds (only 53 hourly data) compared to northerly winds (1139).

Fig. 10. Overstepping probability for northerly and easterly winds.
The probability of a gust factor exceeding a given value G is called the overstepping probability. It is often greater for hourly data than for data collected every 15 min, and it follows a Fisher-Tippet distribution law (Reference DeavesDeaves, 1993). This can be written as:
where a is a scattering parameter and G0 is a reference gust factor.
For most of our results (see Fig. 11), the data can be divided into two classes with different behaviours, i.e. data with gust factors < 5.5 and > 5.5. At 5.5 there is a kink in the data. Similar results were found by Reference DeavesDeaves (1993), even if the two classes of data were separated by a value of approximately 2.0 in his study.

Fig. 11. The Fisher- Tippet law, for a northerly gust factor at La Muzelle.
Studying events that generate high gust-factor values brings out two different types of events. The first type covers events with no variation in wind direction and a gust factor of 3–4. They reflect a decrease in the mean wind speed during an increase or a smaller decrease in the maximum wind speed. The second type corresponds to events with variation in the wind direction. These events are often characterized by high gust factors of 5.5–8.8. The highest gust factors are observed during wind-direction changes from southerly to northerly. These different types may explain the kink in the Fisher-Tippet law (Fig. 11).
3.2.2. Drifting-snow gust factor
As shown above, the wind-gust factor can provide information on the non-stationary aspects of the wind. Similarly, the gust factor relating to the signal of the acoustic snowdrift sensor, defined as the ratio Gs = maximum signal of the acoustic sensor/average signal, can provide information about the snowdrift.
For this purpose, data from acoustic sensor No. 5 at the La Muzelle site were used. We first removed the offset of the sensor (50 mV). Then we filtered out the average signal < 5mV, because lower values do not correspond to snowdrift. The gust factor was then calculated every 15 min for the whole winter (scan rate of 1 s). We found that the gust factor did not follow a Fisher-Tippet law, but rather a polynomial law (Fig. 12).
We determined two types of drifting-snow events:
A first type of periods of weak snowdrift.
A second type of periods of heavy snowdrift.

Fig. 12. Polynomial law for snowdrift gust factors, based on data from snowdrift acoustic sensor Mo. 5 at the La Muzelle site (p is the overstepping probability).
The first scenario corresponds to areas 1 and 3 in Figure 13, and areas A and B in Figure 14. In the first case (area 1 in Fig. 13, and A in Fig. 14), high wind-gust factors were found, indicating very gusty winds, but very low average snowdrift signals and snowdrift gust factors were observed. Thus, this scenario does not show significant erosion, snowdrift and deposition. The second case (area 3 in Fig. 13, and B in Fig. 14) is characterized by gusty snowdrift episodes with sporadic wind gusts generating moderate snowdrift.

Fig. 13. The average snowdrift signal on acoustic sensor Mo. 5 at La Muzelle.

Fig. 14. The snowdrift gust factor recorded by acoustic sensor Mo. 5 at La Muzelle.
The second scenario corresponds to area 2 of Figure 13 and area C of Figure 14. Due to the limited output voltage of 5000 mV for the acoustic sensor, the maximum snowdrift gust factor is 50 for average signals of > 100 mV, causing the cut-off in Figure 14. This type of snowdrift occurs during more regular wind episodes characterized by low wind-gust factors.
This study of the snowdrift gust factor demonstrates that snowdrift is more substantial/voluminous when it is generated by a regular, sufficiently strong wind than when it appears with sporadic wind gusts. This important result allows us to somewhat simplify the numerical model presented in the next section.
4. Numerical Model of Drifting Snow
4.1. Short description of the numerical model used
The numerical model used in this case is based on a physical model for each mechanism and an adequate mathematical formulation (Reference Naaim, Naaim-Bouvet and MartinezNaaim and others, 1998). The transport layer is decomposed into two zones: the suspension layer and the saltation layer. The suspension layer is described by mass- and momentum-conservation equations. These equations were formulated for both the solid and gaseous phases. The interaction between these two phases was taken into account by an equation based on the drag force of a particle in a turbulent flow. Turbulence was modelled by the k-e model, in which a reduction of the turbulence with the concentration was introduced (Reference Chen and WoodChen and Wood, 1985). The turbulent diffusion of the solid phase was considered higher than the turbulent diffusion of the gaseous phase. This was taken into account through a Schmidt number < 1, here set to 0.6 for snow particles (Reference Naaim and MartinezNaaim and Martinez, 1995). The saltation layer corresponds to the layer immediately in contact with the snow cover. In our model, it is described by its height, its concentration and two turbulent friction velocities, one for the solid phase and one for the gaseous phase. The expression of these two velocities takes into account the effect of the concentration. The saltation layer was considered the lower boundary of the suspension layer. The exchange between these two layers was determined from the balance between the sedimentation flux and the diffusion flux. The exchange between the saltation layer and the snow cover was described by an erosion and deposition model which takes into account the effects of the aerodynamic force as well as the effects of particle impact forces and of sedimentation. The equations of the global model thus constructed were solved by a finite-volume method. This model was tested by comparing leeward and windward drift equilibrium obtained in a wind tunnel near a small-scale snow fence. The numerical simulations were performed with all input parameters known (fall velocity, threshold shear velocity, shear velocity, mass concentration) which stayed constant throughout the experiment. The obtained results were quite satisfactory. The real case, however, is more complex.
4.2. Application to real snowdrift event
4.2.1. Description of the event
In contrast to wind-tunnel experiments, all input parameters change during a real dnfting-snow event. We selected five important drifting-snow events during winter 1998/99. The wind direction stayed more or less constant in only two episodes and there was snowfall during both. Nevertheless we tried to reproduce the snowdrift at the La Muzelle site for the period 26 January-1 February (Fig. 15). There was snowfall on 4 days (26–29 January), totalling 1.20 m. For this period a wide scattering of data points can be observed in Figure 16 because the snow mass flux is not simply correlated with wind speed during snowfall periods.

Fig. 15. Wind speed and drifting snow, 26 January-1 February.

Fig. 16. Signal (mean value over 15 min) from acoustic sensor No. 5 vs wind speed (mean value over 15min), 26–31 January.
4.2.2. Modifications of the numerical model
The simulation of a real drifting-snow event must take into account the modifications of input parameters as a function of time. Initially, we planned to introduce the measured mass flux in the numerical model, but at the present state of development (section 3.1) the acoustic sensor does not assess the mass flux. Nevertheless, it provides the real duration of the drifting-snow event, so we will use the wind measurements during this event and make several approximations.
The numerical simulation of this long period using the fully coupled wind and snowdrift model was beyond our computer capacity. We thus simplified the problem by simulating the snowdrift phenomenon using the fully coupled model during the first hour of the drifting-snow episode. We used the topography, the initial snow cover given by Crocus, an average precipitation rate, and a logarithmic velocity profile represented by the friction velocity u* (x = 0, t = 0) at the upstream boundary. The outputs of this first calculation at t = t0 are the turbulent friction velocity u* (x, t = t0) near the snow surface, the concentration field C(x,t = t0) near the snow surface, and the mass flux exchange with the snow cover, M(x, t = t0).
As the flow is turbulent with a fully developed turbulence, we assumed that if we changed the upstream friction velocity at the upstream boundary condition from u* (x = 0, t = 0) to u* (x = 0, t), the resulting friction velocity in each cell in contact with the snow cover, u* (x, t), may be determined by:
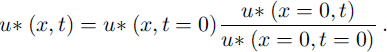
As presented in Reference Naaim, Naaim-Bouvet and MartinezNaaim and others (1998), the mass-exchange flux with the snow cover is a function of the concentration and the friction velocity near the ground.
According to Reference Pomeroy and GrayPomeroy and Gray (1990), the saltation mass flux is given by:
where u*t is the threshold friction velocity.
In each bottom cell, the reference saltation mass flux is:
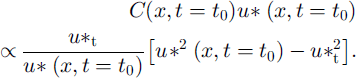
During the episode, in each bottom cell, the saltation mass flux is:
From the ratio between these two formulae, we deduce the concentration in each bottom cell:
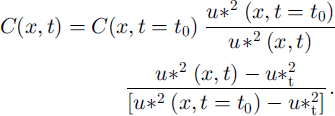
By introducing the in situ measured wind velocity (Fig. 15) at the upstream boundary of the simulation area during the storm, we applied the snow-erosion and -deposition model (Reference Naaim, Naaim-Bouvet and MartinezNaaim and others, 1998) to this episode.
The results are illustrated in Figure 17. On the left vertical axis the altitudes before and after the event are reported. On the right vertical axis the accumulation values obtained by the numerical simulation and by the in situ measurements are reported. If we compare the numerical model results with the measured data, we can assert that the numerical model correctly localizes the snowdrift accumulation. However, we notice an error in the accumulation that can reach 30%. The error may be related to the strong hypothesis we adopted. This work will be continued in the future using the fully coupled model on the whole episode and using calibrated data from the acoustic sensor in order to improve the model.

Fig. 17. Numerical simulation of drifting snow (snow poles 13–16).
5. Conclusions
Thanks to our high-altitude experimental site at Lac Blanc Pass, we have created a well-documented database, containing wind parameters, snowdrift episodes and snow-layer evolution. In particular, we found interesting results concerning wind-gust factors, which can attain greater values on our site than have been reported in earlier works. Furthermore, our acoustic snowdrift sensor revealed that episodes of strong snowdrift occur more often at relatively regular high wind speeds than with high wind gusts. Moreover, thanks to this database, we have tested the GEMAGREF numerical snowdrift model on in situ data.
To improve this model, we need to introduce the measured drifting-snow flux at the upstream boundary as an input of the model (until now it has been calculated from an empirical formula using measured wind speed and threshold wind speed). To this end, we need to calibrate our acoustic sensor in order to be able to correlate the recorded signal with the drifting-snow particle flux.



















