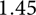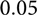Introduction
The Groningen reservoir in the Netherlands is the largest gas field in western Europe. Since 2014, annual production volumes from the Groningen gas field are rapidly declining. Although approximately one fifth of the initial
![]() $ \sim $
2900 billion
$ \sim $
2900 billion
![]() ${m^3}$
is still technically recoverable, the Dutch government has decided to cease production by 2023 or 2024 to ensure public safety and well-being. Induced earthquakes at the Groningen natural gas reservoir have put local communities at risk to a level that has led to societal and political upheaval (Vlek, Reference Vlek2019). The residential population living and working near the contours of the Groningen gas field is about half a million people. About 25,000 damage claims for masonry buildings have been filed in the past years of which a part can be associated to individual seismic events. Older homes and farms built with single brick walls are especially vulnerable; these are either taken down and rebuilt or structurally strengthened.
${m^3}$
is still technically recoverable, the Dutch government has decided to cease production by 2023 or 2024 to ensure public safety and well-being. Induced earthquakes at the Groningen natural gas reservoir have put local communities at risk to a level that has led to societal and political upheaval (Vlek, Reference Vlek2019). The residential population living and working near the contours of the Groningen gas field is about half a million people. About 25,000 damage claims for masonry buildings have been filed in the past years of which a part can be associated to individual seismic events. Older homes and farms built with single brick walls are especially vulnerable; these are either taken down and rebuilt or structurally strengthened.
The 100–300 m thick gas-bearing Rotliegend sandstone reservoir at 2.6–3.2 km deep is overlain by a 1 km thick Zechstein salt formation that acts as a seal (De Jager & Visser, Reference De Jager and Visser2017). Around 700 faults have been mapped in and below the reservoir (Kortekaas & Jaarsma, Reference Kortekaas and Jaarsma2017). The weight of the overburden causes compaction of the reservoir formation due to gas withdrawal. Differential compaction results in localized stress concentrations along existing faults resulting in ruptures and earthquakes (Van Thienen-Visser & Breunese, Reference Van Thienen-Visser and Breunese2015). Groningen-specific models describing this process are given by (Bourne et al., Reference Bourne, Oates, van Elk and Doornhof2014; Bourne & Oates, Reference Bourne and Oates2017; Candela et al., Reference Candela, Osinga, Ampuero, Wassing, Pluymaekers, Fokker and Muntendam-Bos2019; Bourne & Oates, Reference Bourne and Oates2020) and references therein.
The Gutenberg–Richter relation is a model for the magnitude distribution of earthquakes mostly characterized by its exponential coefficient, the b-value. Variations of the b-value express changes in the rate of occurrence of small earthquakes relative to large ones. Spatiotemporal b-value variations have been associated to various geophysical processes and circumstances for earthquake catalogues over natural tectonically active environments. Dependence of b-values on differential stress has been reported by Scholz (Reference Scholz1968) and Wyss (Reference Wyss1973). More specifically, spatial b-value variations have been related to variations in tectonic regimes: thrust faulting systems being associated with relatively low values, normal faulting systems with relatively high values and strike-slip systems in between (Gulia & Wiemer, Reference Gulia and Wiemer2010; Schorlemmer et al., Reference Schorlemmer, Wiemer and Wyss2005; Nakaya, Reference Nakaya2006). Also, the depth of occurrence of the events has been identified as a possible cause of b-value variations (Eaton et al. Reference Eaton, O’neill and Murdock1970; Wyss, Reference Wyss1973; Wiemer & Benoit, Reference Wiemer and Benoit1996; Mori & Abercrombie, Reference Mori and Abercrombie1997; Wyss et al., Reference Wyss, McNutt and Wyss1998; Spada et al., Reference Spada, Tormann, Wiemer and Enescu2013; Gerstenberger et al., Reference Gerstenberger, Wiemer and Giardini2001). Other possible factors that may be relevant to the Groningen situation include stress fluctuations or regimes (Wiemer & Wyss, Reference Wiemer and Wyss1997; Langenbruch & Shapiro, Reference Langenbruch and Shapiro2014; Scholz, Reference Scholz2015) and the (fractal) geometry of fault systems (Hirata, Reference Hirata1989; Rundle, Reference Rundle1989; Mandal & Rastogi, Reference Mandal and Rastogi2005).
In the context of induced seismicity, b-value variations have been attributed to several processes. These include: fluid-driven triggering mechanism possibly due to faults cutting into the reservoir and hydraulic connection between reservoir and basement at a CO2 injection site (Goertz-Allmann et al., Reference Goertz-Allmann, Gibbons, Oye, Bauer and Will2017); normalised shear stress instead of differential stress at the Basel Enhanced Geothermal System (Mukuhira et al., Reference Mukuhira, Fehler, Ito, Asanuma and Haring2021); loading rates in the Lacq gas field (Lahaie & Grasso, Reference Lahaie and Grasso1999) and at the The Geysers geothermal field (Henderson et al., Reference Henderson, Barton and Foulger1999); pore pressure, fluid content and injection activity at the Oklahoma oil field (Vorobieva et al., Reference Vorobieva, Shebalin and Narteau2020; Rajesh & Gupta, Reference Rajesh and Gupta2021).
Despite the large and increasing number of proposed b-value dependencies, the physical context is not always well understood. This especially holds for induced seismicity cases, where the number of studies is significantly lower (possibly due to the limited size of event catalogues). Considering the highly non-stationary characteristics of the anthropogenic activities, hazard and risk assessment models could benefit greatly from a better understanding of b-value variations. The current state-of-the-art seismological source models for the Groningen gas field (Bourne & Oates, Reference Bourne and Oates2017; Bourne & Oates, Reference Bourne and Oates2020) forecast spatiotemporal variations in both activity rate and magnitude distribution in terms of an induced stress metric. Bourne and Oates (Reference Bourne and Oates2020) provided an insightful separation of literature studies on stress dependent and not dependent b-value variations. The choice of induced stress as a predictor is based on a comparative analysis of a suite of possible predictors in Bourne and Oates (Reference Bourne and Oates2017) for seismic activity rate. However, it appears that the authors did not make a separate attempt to determine the most appropriate predictor for the magnitude frequency model. We consider it possible that the best predictor for activity rate may not automatically be the best predictor for the magnitude distribution.
In this paper, we perform statistical analyses on the spatiotemporal variations of the b-value in the Groningen gas field. We use a relatively small catalogue of 336 events with (local) magnitudes above the estimated completeness level of 1.45 over the entire observation time span from 1 January 1995 to 1 January 2022. We investigate the predictive capabilities of five physical quantities (covariates) that describe static or dynamic properties of the Groningen field. The general goal of the investigation is to steer the development of forecasting models that allow a more precise assessment of the seismic hazard and risk analysis through more precise forecasts on the magnitude distribution.
Data and methods
Earthquake catalogue
The first instrumentally recorded seismic event in the Groningen gas field was an earthquake with local magnitude 2.4 in 1991. When the event took place, the mean reservoir pressure had already decreased from the initial 350 bar to below 200 bar. With ongoing reservoir gas production the induced seismicity continued leading to the installation of a regional borehole seismic network by 1995 (Dost et al., Reference Dost, Ruigrok and Spetzler2017). In the following years, the annual number of recorded earthquakes fluctuated around ten to fifteen events per year until about 2003 when it started to increase, to nearly 120 in 2017. Figure 1(top) shows the annual number of event in different magnitude categories. The largest magnitude observed to date is the 3.6 event near Huizinge in 2012.

Fig. 1. Number of earthquakes in the Groningen field in different magnitude categories. This Figure is created by first rounding the magnitudes to 1 decimal place and subsequently assigning the earthquakes to their magnitude categories. Only events within the outline of the Groningen gas field are included (see also Fig. 2 ). Top view: all recorded events in said space/time window. Bottom view: the events above the minimum magnitude included in the current study (336 in total).
The sensitivity of the monitoring network has not been uniform in space and time. A relatively safe (conservative upper bound) estimate of the completeness level over the entire period and region is a magnitude of 1.5 (Dost et al., Reference Dost, Ruigrok and Spetzler2017). For the purpose of the current study we adopt this level as the minimum threshold
![]() ${m_{{\rm{min}}}}$
for earthquakes to be considered. In fact, since we use unrounded magnitude values we slightly relax the threshold to
${m_{{\rm{min}}}}$
for earthquakes to be considered. In fact, since we use unrounded magnitude values we slightly relax the threshold to
![]() ${m_{{\rm{min}}}} = 1.45$
, as the value 1.5 was specified for magnitude values rounded to one decimal place. Figure 1(bottom) shows the annual number of events in the curated catalogue.
${m_{{\rm{min}}}} = 1.45$
, as the value 1.5 was specified for magnitude values rounded to one decimal place. Figure 1(bottom) shows the annual number of events in the curated catalogue.
We note that the current study might, in principle, benefit from an enlarged data set by taking into account a time-dependent completeness level (Dost et al., Reference Dost, Ruigrok and Spetzler2017; Varty et al., Reference Varty, Tawn, Atkinson and Bierman2021). However, by taking a conservative assumption here, we largely steer clear of discussions on how the spatiotemporal completeness level should be estimated and to what extent imperfections would affect the results (e.g. Herrmann & Marzocchi, Reference Herrmann and Marzocchi2020). Also, since one of our objectives is to provide forecasting models for risks that occur only at magnitudes that are several units larger than the completeness magnitude (say, magnitude 4 and beyond), it is questionable whether we should go as low as we possibly can. After all, the lower we choose the range of input data for our model inference, the larger the distance we effectively have to extrapolate at a later stage.
We obtained the Groningen earthquake catalogue from the Seismological Service of the KNMI (KNMI, 2022b) through their FDSN Event Web Service (URL found in reference KNMI (2022a)), which provides origin times, locations in WSG-84 coordinates and unrounded local magnitudes. Epicentral coordinates have subsequently been transformed into the local Amersfoort/RD New coordinates system (epsg.io, 2022). The hypocenter depth is not used. We selected all earthquakes above
![]() ${m_{{\rm{min}}}} = 1.45$
, in the time window between 1 January 1995, T00:00 and 1 January 2022, T00:00. To avoid interference of earthquakes due to other exploration activities in the vicinity as much as possible, the spatial extent of the catalogue is limited to the Groningen gas field outline (NAM, 2021). The total number of events in the curated catalogue is 336. Figure 2 shows the catalogue of all earthquakes of the Groningen gas field.
${m_{{\rm{min}}}} = 1.45$
, in the time window between 1 January 1995, T00:00 and 1 January 2022, T00:00. To avoid interference of earthquakes due to other exploration activities in the vicinity as much as possible, the spatial extent of the catalogue is limited to the Groningen gas field outline (NAM, 2021). The total number of events in the curated catalogue is 336. Figure 2 shows the catalogue of all earthquakes of the Groningen gas field.

Fig. 2. Map view of the Groningen gas field and its location inset (in red at the top-left corner). Locations of all recorded induced earthquakes at any time in the vicinity are shown by grey dots. The colored dots represent the earthquakes included in the current study, that is, within the field outline and the time span from 1995-01-01 to 2022-01-01, and (1 decimal rounded) magnitudes of 1.5 and higher. The colors represent the magnitude categories, analogous to Fig. 1.
Gutenberg–Richter magnitude distribution
We employ the classical Gutenberg–Richter relation (Gutenberg & Richter, Reference Gutenberg and Richter1941, Reference Gutenberg and Richter1944), as a model for the magnitude distribution of induced earthquakes in the Groningen gas field. The survival function, or probability
![]() $P[Mm|M{m_{{\rm{min}}}}]$
of a random magnitude sample
$P[Mm|M{m_{{\rm{min}}}}]$
of a random magnitude sample
![]() $M$
exceeding
$M$
exceeding
![]() $m$
, under the condition that it exceeds
$m$
, under the condition that it exceeds
![]() ${m_{{\rm{min}}}}$
is given by:
${m_{{\rm{min}}}}$
is given by:
with
![]() $b$
the exponential parameter, or b-value, and its probability density function as:
$b$
the exponential parameter, or b-value, and its probability density function as:
where
![]() ${b^*} = b\log (10)$
.
${b^*} = b\log (10)$
.
Unlike previous authors (Bourne & Oates, Reference Bourne and Oates2020), we do not consider a dedicated prescription of the high-magnitude tail of the distribution such as a truncation or a taper. The focus of our efforts is to find evidence for any significant spatiotemporal variation of the magnitude distribution. However, as argued in Marzocchi et al. (Reference Marzocchi, Spassiani, Stallone and Taroni2019) and Bourne and Oates (Reference Bourne and Oates2020), among others, failure to recognize and accommodate a truncated or tapered tail may lead to artifacts appearing in b-value estimates, especially if the tail starts close to the
![]() ${m_{\min }}$
considered. However, we argue that if a tail effect is relevant, in the sense that it is somehow exposed in the data, then such artifacts may actually help to reveal any spatiotemporal variation of this effect through the analysis of the b-value. We only need to keep in mind that any significant spatiotemporal variation in the assessed b-value does not necessarily have to be caused by a variation in the exponential character of the distribution, but may also be caused by variations in the tail behaviour that we do not model explicitly.
${m_{\min }}$
considered. However, we argue that if a tail effect is relevant, in the sense that it is somehow exposed in the data, then such artifacts may actually help to reveal any spatiotemporal variation of this effect through the analysis of the b-value. We only need to keep in mind that any significant spatiotemporal variation in the assessed b-value does not necessarily have to be caused by a variation in the exponential character of the distribution, but may also be caused by variations in the tail behaviour that we do not model explicitly.
In this study we are interested in spatiotemporal variations of the b-value
![]() $b$
, so that we can express it as a function of time
$b$
, so that we can express it as a function of time
![]() $t$
and space coordinates
$t$
and space coordinates
![]() $x$
. More specifically, we test prospective predictors that may act as a spatiotemporal covariate
$x$
. More specifically, we test prospective predictors that may act as a spatiotemporal covariate
![]() $c(t,x)$
for the b-value:
$c(t,x)$
for the b-value:
where we use a generic functional form
![]() ${g_C}$
that depends on covariate
${g_C}$
that depends on covariate
![]() $c(t,x)$
and a, generally multivariate, parameter set
$c(t,x)$
and a, generally multivariate, parameter set
![]() $\theta $
, which represents, for example, the coefficients in functional form. We investigate a number of functional forms (i.e. models) with corresponding parameter sets, for which we infer information from the data.
$\theta $
, which represents, for example, the coefficients in functional form. We investigate a number of functional forms (i.e. models) with corresponding parameter sets, for which we infer information from the data.
The inference of model parameters starts with expressing the log-likelihood of the model, conditional on the data. The likelihood is defined as:
 $${\cal L}(\theta |\{ ({c_i},{m_i}),i = 1 \ldots N\} ) = \prod\limits_{i = 1}^N {f_M}({m_i}|{c_i},\theta ),$$
$${\cal L}(\theta |\{ ({c_i},{m_i}),i = 1 \ldots N\} ) = \prod\limits_{i = 1}^N {f_M}({m_i}|{c_i},\theta ),$$
with
![]() ${m_i}$
the magnitude, and
${m_i}$
the magnitude, and
![]() ${c_i} = c({t_i},{x_i})$
the covariate based on the time and location of each event
${c_i} = c({t_i},{x_i})$
the covariate based on the time and location of each event
![]() $i$
out of
$i$
out of
![]() $N$
events in the catalogue. Each event in the catalogue is associated to a specific b-value bi:
$N$
events in the catalogue. Each event in the catalogue is associated to a specific b-value bi:
such that the log-likelihood equals:
 $$\matrix{
{\log ({\cal L})(\theta |\{ ({c_i},{m_i}),i = 1 \ldots N\} ) = \sum\limits_{i = 1}^N {[\log (b_i^*)} } \hfill\cr
{\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - b_i^*({m_i} - {m_{\min }})].} \hfill\cr} $$
$$\matrix{
{\log ({\cal L})(\theta |\{ ({c_i},{m_i}),i = 1 \ldots N\} ) = \sum\limits_{i = 1}^N {[\log (b_i^*)} } \hfill\cr
{\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - b_i^*({m_i} - {m_{\min }})].} \hfill\cr} $$
Note that for a constant b-value a maximization of
![]() $\log ({\cal L})$
is achieved algebraically in closed form by the maximum likelihood estimate (MLE) b-value
$\log ({\cal L})$
is achieved algebraically in closed form by the maximum likelihood estimate (MLE) b-value
![]() ${b_{{\rm{MLE}}}}$
:
${b_{{\rm{MLE}}}}$
:
where
![]() $\bar m$
is the arithmetic mean of the magnitudes in the data set (Aki, Reference Aki1965). For non-constant models the maximum-likelihood parameters can be found by maximizing the log-likelihood for model parameter vector
$\bar m$
is the arithmetic mean of the magnitudes in the data set (Aki, Reference Aki1965). For non-constant models the maximum-likelihood parameters can be found by maximizing the log-likelihood for model parameter vector
![]() $\theta $
to find
$\theta $
to find
![]() ${\theta _{{\rm{MLE}}}}$
. This search can be done using a gradient ascent algorithm or an exhaustive grid search.
${\theta _{{\rm{MLE}}}}$
. This search can be done using a gradient ascent algorithm or an exhaustive grid search.
Assuming a constant b-value we have determined the MLE b-value for the entire catalogue:
![]() ${b_{{\rm{MLE}}}} = 0.96$
. The result is shown together with the empirical distribution in Fig. 3.
${b_{{\rm{MLE}}}} = 0.96$
. The result is shown together with the empirical distribution in Fig. 3.

Fig. 3. Empirical complementary cumulative distribution function (CCDF), or probability of exceedance per event. Also shown is the maximum-likelihood Gutenberg–Richter distribution under the assumption of a constant b-value. MLE for the constant b-value is 0.96.
Static and dynamic predictors
In Bourne and Oates (Reference Bourne and Oates2020), the authors propose two models for the spatiotemporal evolution of the magnitude distribution, that are both conditioned on the induced stress (“Coulomb stress”) predictor: one with a constant b-value and a stress-dependent high-magnitude taper, and one without a taper but with a stress-dependent b-value. On the basis of physical considerations and the result of some statistical tests the authors express a preference for the former model. As mentioned in sec:intro, they did not investigate or report alternative predictors for the magnitude distribution.
Similar to the approach of Bourne and Oates (Reference Bourne and Oates2017) for activity rate prediction, we investigate a range of physical reservoir properties as predictors for the b-value throughout the Groningen gas field. These prospective predictors are related to the geological layout of the gas reservoir, the gas depletion process itself, or a combination of both.
-
Reservoir thickness The reservoir thickness
 $h(x)$
is a 2-D spatial representation of the thickness of the Rotliegend reservoir formation, provided by the field operator (NAM, 2021) and is given in units of meters. The thickness is assumed to be static (time-invariant) and independent of the gas production. The (relatively small) compaction of the reservoir due to the gas extraction is considered as a separate prospective predictor below.
$h(x)$
is a 2-D spatial representation of the thickness of the Rotliegend reservoir formation, provided by the field operator (NAM, 2021) and is given in units of meters. The thickness is assumed to be static (time-invariant) and independent of the gas production. The (relatively small) compaction of the reservoir due to the gas extraction is considered as a separate prospective predictor below. -
Topographic gradient The topographic gradient Γ(x) is a spatially smoothed, 2-D, static measure of the roughness of the topography of the top of reservoir. This roughness is largely due to faults with varying offsets (Bourne & Oates, Reference Bourne and Oates2017). It is calculated based on the locations and offsets of the pre-existing faults in the reservoir, and is controlled by two parameters:
 ${r_{{\rm{max}}}}$
and
${r_{{\rm{max}}}}$
and
 $\sigma $
. The parameter
$\sigma $
. The parameter
 ${r_{{\rm{max}}}}$
describes an upper cut-off value for the local fault offset-to-thickness ratio. Faults with an offset-to-thickness ratio larger than
${r_{{\rm{max}}}}$
describes an upper cut-off value for the local fault offset-to-thickness ratio. Faults with an offset-to-thickness ratio larger than
 ${r_{{\rm{max}}}}$
are disregarded in the calculation. The final property is calculated by mapping the fault offsets that pass the
${r_{{\rm{max}}}}$
are disregarded in the calculation. The final property is calculated by mapping the fault offsets that pass the
 ${r_{{\rm{max}}}}$
filter onto a regular grid, which is subsequently smoothed by a Gaussian kernel with kernel size
${r_{{\rm{max}}}}$
filter onto a regular grid, which is subsequently smoothed by a Gaussian kernel with kernel size
 $\sigma $
. As a result, the property is roughly proportional to both fault offset and fault density. A ready-made topographic gradient grid with parameter values
$\sigma $
. As a result, the property is roughly proportional to both fault offset and fault density. A ready-made topographic gradient grid with parameter values
 ${r_{{\rm{max}}}} = 1.1$
and
${r_{{\rm{max}}}} = 1.1$
and
 $\sigma = 3500$
m is supplied by the operator (NAM, 2021; Bourne & Oates, Reference Bourne and Oates2020).
$\sigma = 3500$
m is supplied by the operator (NAM, 2021; Bourne & Oates, Reference Bourne and Oates2020). -
Pressure drop The pressure drop
 $\Delta P(t,x)$
is at any time
$\Delta P(t,x)$
is at any time
 $t$
a 2-D spatial representation of the vertically averaged pore pressure depletion in the reservoir with respect to the original (pre-production) gas pressure, provided by the operator (NAM, 2021). This property is dynamic (time-dependent) and naturally depends on the gas production.
$t$
a 2-D spatial representation of the vertically averaged pore pressure depletion in the reservoir with respect to the original (pre-production) gas pressure, provided by the operator (NAM, 2021). This property is dynamic (time-dependent) and naturally depends on the gas production. -
Reservoir compaction The reservoir compaction
 $\Delta h(t,x)$
is at any time
$\Delta h(t,x)$
is at any time
 $t$
a 2-D spatial representation of the change in reservoir thickness as a result of the gas pressure decline. This covariate is defined as:
$t$
a 2-D spatial representation of the change in reservoir thickness as a result of the gas pressure decline. This covariate is defined as:
where
![]() $\Delta P(t,x)$
is the dynamic pressure drop,
$\Delta P(t,x)$
is the dynamic pressure drop,
![]() ${c_m}$
is the poro-elastic coupling coefficient, and
${c_m}$
is the poro-elastic coupling coefficient, and
![]() $h(x)$
is the reservoir thickness. These are all provided by the operator (NAM, 2021). Reservoir compaction is a dynamic (time-dependent) property due to its dependence on the gas production.
$h(x)$
is the reservoir thickness. These are all provided by the operator (NAM, 2021). Reservoir compaction is a dynamic (time-dependent) property due to its dependence on the gas production.
-
Induced stress The induced stress at any time
 $t$
is a 2-D spatial property representing the (spatially smoothed) change in Coulomb stress on pre-existing faults according to the thin-sheet model. It is calculated in accordance with Bourne and Oates (Reference Bourne and Oates2017) as
Footnote 1
:
$t$
is a 2-D spatial property representing the (spatially smoothed) change in Coulomb stress on pre-existing faults according to the thin-sheet model. It is calculated in accordance with Bourne and Oates (Reference Bourne and Oates2017) as
Footnote 1
:
where Γ(x) is the topographic gradient, and
![]() ${H_s}$
is a stiffness parameter. Both Γ(x) and
${H_s}$
is a stiffness parameter. Both Γ(x) and
![]() ${H_s}={10^7}$
MPa are supplied by the operator (NAM, 2021). Induced stress is dynamic due to its dependence on the gas production. We note that the use of a spatial Gaussian smoothing kernel in the calculation of the topographic gradient makes it difficult to interpret the numerical values of this covariate field in terms of absolute stress changes. Rather, it is a metric that combines fault density of faults below a certain offset-to-thickness ratio and vertical compaction strain. In a stricter sense, it is perhaps best interpreted as a propensity-to-failure proxy, rather than Coulomb stress change.
${H_s}={10^7}$
MPa are supplied by the operator (NAM, 2021). Induced stress is dynamic due to its dependence on the gas production. We note that the use of a spatial Gaussian smoothing kernel in the calculation of the topographic gradient makes it difficult to interpret the numerical values of this covariate field in terms of absolute stress changes. Rather, it is a metric that combines fault density of faults below a certain offset-to-thickness ratio and vertical compaction strain. In a stricter sense, it is perhaps best interpreted as a propensity-to-failure proxy, rather than Coulomb stress change.
Along with the above five prospective predictors representing physical properties of the reservoir, we also take time as a possible predictor to complete a set of six predictors that we submit to the same sequence of statistical tests. Figure 4 illustrates the spatial variation patterns of the six predictors. The figures come without explicit legend, serving as a visual representation of the spatial patterns. For the dynamic predictors (pressure drop, reservoir compaction and induced stress), the situation at the end of the observation period (i.e. 2022-01-01) has been chosen. The numerical value ranges of the predictors are shown in Table 1.

Fig. 4. The six predictors for b-value variations investigated in this study represented as contour plots within the outline of the Groningen field. Each figure is individually scaled, where green colors correspond to the lowest, orange to the highest values. Representative values for the covariates are presented in Table 1 . For the dynamic predictors (pressure drop, reservoir compaction and induced stress), the state at the end of the observation period (i.e. 2022-01-01) is shown.
Table 1. Predictor value ranges as sampled by the catalogue.

In the statistical analysis that follows, earthquakes are associated, or ’labelled’, with the predictor values at the origin time and location of the earthquake according to the catalogue. For example, for the predictor reservoir thickness, we label each earthquake with the reservoir thickness at the location of the earthquake, while for the predictor induced stress, we label each earthquake with the induced stress at the location and the origin time of the earthquake. To facilitate the statistical analysis, after the earthquakes have been labelled, we perform a linear rescaling to the covariate values, such that the earthquake with the lowest covariate value receives a covariate value of 0 and the earthquake with the largest covariate value receives rescaled value of 1. In most figures, the minimum and maximum covariate values are simply labeled as ‘min’ and ‘max’ respectively.
The labelling of each event by the predictor values determines an ordering of observed magnitudes specific to that predictor. These predictor-specific orderings are displayed in Fig. 5. The corresponding value ranges are given in Table 1. If a reservoir property has a predictive capacity with regard to the magnitude distribution, then the ordering (and spacing) of the magnitudes may be distinguishable from random orderings. In that case, the property has the potential to be used as a predictor in a seismic hazard and risk forecasting. In the following section we use this concept of ordering to define a null hypothesis.

Fig. 5. For each of the six prospective predictors, the magnitudes of the earthquakes in the seismic catalogue are plotted against the predictor value. Each predictor provides it own specific ordering and spacing of the catalogue.
Statistical toolkit
Null hypothesis realization by random shuffling
If a predictor has predictive power for the magnitude distribution, then that implies that the ordering of magnitudes relative to that predictor may carry information on variations and trends. This also means that when the magnitudes of the events are randomly shuffled, that is, all magnitudes are reassigned in the catalogue randomly to the predictor labels, that information will be erased. As a result, such a random shuffling represents a realization of a magnitude distribution that carries no relation to the predictor. In other words, the magnitude distribution is constant relative to the predictor. Random shufflings may therefore be regarded as realizations of a constant distribution.
In the following we consistently make use of random shufflings as realizations of a constant null hypothesis. If we observe a certain quantitative features in the data we may judge the feature significance from the occurrence frequency in random shufflings.
An alternative approach to realize samples of the null hypothesis would be to generate (new) magnitude samples from a (constant) magnitude distribution based on the Gutenberg–Richter distribution. However, by applying the random shuffling technique we make sure that the generated statistics are not contaminated by any possible deviation of our observations from an idealized Gutenberg–Richter distribution. By exactly honouring the empirical magnitude distribution we can focus on the spatiotemporal variations.
Moving window analysis
To gain some first-order insight into the spatiotemporal variations in the magnitude distribution as characterized by the MLE b-value, we apply moving window analysis. We perform a 1-D analysis on the set of six predictors that includes time, and a 2-D analysis on the spatial coordinates.
We define an algorithm that works consistently for both 1-D and 2-D cases and automatically adapts the algorithm resolution to the available data. We associate to each event in the catalogue a “window” of the
![]() $N$
“nearest” neighbouring events. Then, for each window we determine the MLE b-value, under the assumption of a constant magnitude distribution, according to Equation 8. Note that we use the MLE b-value simply as a statistic on the data, without any reference to its uncertainty or evaluating the appropriateness of the Gutenberg–Richter model that it defines.
$N$
“nearest” neighbouring events. Then, for each window we determine the MLE b-value, under the assumption of a constant magnitude distribution, according to Equation 8. Note that we use the MLE b-value simply as a statistic on the data, without any reference to its uncertainty or evaluating the appropriateness of the Gutenberg–Richter model that it defines.
What remains is to define the concept of “nearest” that we apply. Although it is possible to use the Euclidean distance in terms of the covariate at hand (i.e. the difference in predictor values in 1-D, or the geometric distance in 2-D space), we have chosen instead to use the Euclidean distance in terms of the sequence number on each of the covariates. For space this means that we first define for each event a sequence number for both coordinates. This choice of nearest neighbourhood definition was made for a practical purpose. Using sequence numbers, the statistics of the null-hypothesis (i.e. constant magnitude distribution) are exactly the same for all 1-D analyses. Using the distance in terms of the covariate values, however, can lead to slightly different window configurations for each predictor and therefore slightly different statistics.
We use windows of
![]() $N = 51$
and
$N = 51$
and
![]() $N = 101$
events. These choices are to a large extent arbitrary, but naturally represent a sort of compromise between resolution and stability. Within the resolution limits imposed by the size of the windows, the moving window analysis is sensitive to any type of b-value variation in the 1-D or 2-D domain considered and therefore is suitable for exploratory research. However, for the benefit of model building for forecasting purposes and hazard and risk assessment, it is more practical to consider simpler models with a limited number of parameters. These are introduced in the next section.
$N = 101$
events. These choices are to a large extent arbitrary, but naturally represent a sort of compromise between resolution and stability. Within the resolution limits imposed by the size of the windows, the moving window analysis is sensitive to any type of b-value variation in the 1-D or 2-D domain considered and therefore is suitable for exploratory research. However, for the benefit of model building for forecasting purposes and hazard and risk assessment, it is more practical to consider simpler models with a limited number of parameters. These are introduced in the next section.
If there are spatiotemporal variations in the b-value, or if a prospective predictor does carry information on b-values variations, then we may expect the b-value variability among the collection of windows higher than if the b-value would actually be a constant. Like Schorlemmer et al. (Reference Schorlemmer, Neri, Wiemer and Mostaccio2003), we choose the difference between the maximum and the minimum b-value as a statistic representing these variations, and call it the min-max statistic. The min-max statistic obtained for the observed catalogue can be compared with the distribution of this statistic under the null hypothesis to determine its significance.
Functional forms and maximum-likelihood estimation
If we can establish that a certain reservoir property carries information on the magnitude distribution we may try to exploit the predictive power of such property for more precise forecasting. We apply a total of five functional forms for the scalar predictor/covariate
![]() $c \in [0,1]$
, with one, two or three free parameters (
$c \in [0,1]$
, with one, two or three free parameters (
![]() ${\theta _0},{\theta _1},{\theta _2}$
):
${\theta _0},{\theta _1},{\theta _2}$
):
-
constant:
 $b = {\theta _0}$
,
$b = {\theta _0}$
, -
linear:
 $b = {\theta _0} + ({\theta _1} - {\theta _0})c$
,
$b = {\theta _0} + ({\theta _1} - {\theta _0})c$
, -
quadratic:
 $b = {\theta _0} + ({\theta _1} - {\theta _0})c + {\theta _2}c(c - 1)$
,
$b = {\theta _0} + ({\theta _1} - {\theta _0})c + {\theta _2}c(c - 1)$
, -
step:
 $b = {\theta _0} + ({\theta _1} - {\theta _0})H(c - {\theta _2})$
, and
$b = {\theta _0} + ({\theta _1} - {\theta _0})H(c - {\theta _2})$
, and -
hyperbolic tangent:
 $b = {\theta _0} + {\theta _1}(1 - \tanh ({\theta _2} \times c))$
,
$b = {\theta _0} + {\theta _1}(1 - \tanh ({\theta _2} \times c))$
,
with
![]() $H(c)$
the Heaviside step function. For our statistical investigations the constant model represents the null hypothesis. In all cases we determine the maximum-likelihood parameter estimates on both the observed data and on the synthetic realizations (by random shuffling) of the null hypothesis. The linear and the step model are subjected to significance tests. In particular, we use both the parameter difference
$H(c)$
the Heaviside step function. For our statistical investigations the constant model represents the null hypothesis. In all cases we determine the maximum-likelihood parameter estimates on both the observed data and on the synthetic realizations (by random shuffling) of the null hypothesis. The linear and the step model are subjected to significance tests. In particular, we use both the parameter difference
![]() $({\theta _1} - {\theta _0})$
and the (maximum) likelihood as test statistics. The quadratic model is used in addition to compare the performance of the models in terms of their maximum-likelihood. We look at the added value of the extra quadratic term relative to the linear model and we compare the performance of the quadratic and step models in relation to their equal number of parameters.
$({\theta _1} - {\theta _0})$
and the (maximum) likelihood as test statistics. The quadratic model is used in addition to compare the performance of the models in terms of their maximum-likelihood. We look at the added value of the extra quadratic term relative to the linear model and we compare the performance of the quadratic and step models in relation to their equal number of parameters.
Finally, the hyperbolic tangent (tanh) model is used, albeit only for the induced stress predictor, as it is used in the Groningen source model of Bourne and Oates (Reference Bourne and Oates2020). We note that for the tanh model we apply a slightly different scaling for the covariate. To reproduce the model of Bourne and Oates (Reference Bourne and Oates2020) we need to associate
![]() $c = 0$
with the zero induced stress rather than with the lowest value of stress in the catalogue as shown in Fig. 5. The value
$c = 0$
with the zero induced stress rather than with the lowest value of stress in the catalogue as shown in Fig. 5. The value
![]() $c = 1$
is still associated with the maximum value of stress in the catalogue.
$c = 1$
is still associated with the maximum value of stress in the catalogue.
Cramér-von Mises test
The maximum-likelihood regression of the step model effectively leads to a partitioning (in two parts) of both the predictor range and the catalogue ordered according to this predictor, each with a constant b-value. The significance of this partition can be further studied by a two-sample goodness-of-fit test. Such a test attempts to reject the null hypothesis that the two samples are actually generated by the same distribution. Commonly applied tests include Kolmogorov-Smirnov, Anderson-Darling, and Cramér-von Mises (Stephens, Reference Stephens1970; Darling, Reference Darling1957). For our experiments we picked the Cramér-von Mises test as it turned out to be the most efficient in terms of computation time, while there was no particular reason to prefer one over the other.
Important to note, however, is that the p-value result from the goodness-of-fit test cannot be used without the following consideration. Due to the maximum-likelihood optimization of the step model, the two subsets are not completely independent anymore. In fact, the total likelihood of the step model benefits if both subsets are as dissimilar as possible. As a result, an overabundance of low p-values is to be expected even for the null hypothesis. Therefore, the Cramér-von Mises test needs to be recalibrated for this particular purpose. This is achieved by the experiment illustrated in Fig. 6. The yellow curve shows that the Cramér-von Mises test works as expected for random partitions of a Groningen-sized constant b-value catalogue. The blue curve shows that introducing the optimization step compromises the test results. However, a correction is obtained relatively easily by applying the inverse CDF of the p-value distribution (blue curve). The formal test result appears on the horizontal axis, while the corrected result appears on the vertical axis. A formal Cramèr-von Mises p-value of 0.05 should be corrected to a p-value of 0.36 for this experiment (as indicated by the grey crosshair).

Fig. 6. Results of applying the Cramér-von Mises test on two subsets of 10,000 randomly drawn catalogues (N = 336, b = 0.96). For each catalogue, a random split point is chosen in the catalogue, and an optimal split point is found by considering the step location of the maximum-likelihood step function. The Cramér-von Mises test is then applied, and a p-value is obtained for subsets created by the random split point and the optimal split point. The blue curve shows a CDF of p-values obtained over 10,000 catalogues for the optimal split point, while the yellow curve shows the CDF for the random split points. The Cramér-von Mises p-values for the yellow curve are distributed homogeneously between 0 and 1, while the blue curve shows an overabundance of low p-values. This indicates that the likelihood optimization corrupts the test, which should be corrected for. In fact, the blue curve provides the correction: the formal test result appears on the x-axis, while the corrected test result appears on the y-axis.
Likelihood ratio and the Akaike information criterion
As we investigate a total of six prospective predictors and five functional forms, we have quite a collection of statistical models for which we can assess the performance in terms of their maximum-likelihood with respect to the Groningen observations. At this point we immediately want to make the disclaimer that we do not intend to apply these maximum-likelihood models directly to hazard and risk assessments. For that purpose we prefer to apply the models in a Bayesian context, where we can take all uncertainties into account and make use of probability distributions of the model parameters rather than just the maximum-likelihood point estimates used in this study. Moreover, we would like to submit these models to pseudo-prospective testing and performance assessment before deciding on their use (e.g. Zechar et al., Reference Zechar, Gerstenberger and Rhoades2010; Bourne et al., Reference Bourne, Oates, van Elk and Doornhof2014).
That being said, model selection is commonly based on the likelihood-ratio test and information-theoretical extension such as the Akaike Information Criterion (e.g. Burnham et al., Reference Burnham, Anderson and Huyvaert2011; Lewis et al., Reference Lewis, Butler and Gilbert2011). These methods simply take maximum-likelihood results as an input.
The Akaike Information Criterion
![]() $AI{C_j}$
for model
$AI{C_j}$
for model
![]() $j$
is defined as:
$j$
is defined as:
where
![]() ${p_i}$
is the number of model parameters (or degrees of freedom therein). According to this definition, a lower AIC corresponds to a better performance. Two models that differ by
${p_i}$
is the number of model parameters (or degrees of freedom therein). According to this definition, a lower AIC corresponds to a better performance. Two models that differ by
![]() $\Delta p$
degrees of freedom are considered to have an equal performance if their likelihoods differ by a factor
$\Delta p$
degrees of freedom are considered to have an equal performance if their likelihoods differ by a factor
![]() ${e^{ - \Delta p}}$
. The inclusion of
${e^{ - \Delta p}}$
. The inclusion of
![]() ${p_i}$
in Equation 11 is basically a bias correction that compensates for the higher likelihood values expected for models with a higher number of parameters under the null hypothesis that these parameters are not required.
${p_i}$
in Equation 11 is basically a bias correction that compensates for the higher likelihood values expected for models with a higher number of parameters under the null hypothesis that these parameters are not required.
The Akaike likelihood ratio
![]() ${{\cal R}_{ij}}$
between models
${{\cal R}_{ij}}$
between models
![]() $i$
and
$i$
and
![]() $j$
is basically a bias corrected likelihood ratio:
$j$
is basically a bias corrected likelihood ratio:
We compute AIC-corrected likelihood ratio’s with respect to the constant b-value null hypothesis. This gives us relative measures of the model performance in terms of the relative likelihood. From an information-theory perspective these numbers indicate the relative probability that model
![]() $j$
(relative to model i) is able to minimize the information loss inherent to the abstraction of reality in terms of a (mathematical) model.
$j$
(relative to model i) is able to minimize the information loss inherent to the abstraction of reality in terms of a (mathematical) model.
We like to note that during the evaluation of the results of our analysis we found out that the Akaike formula (11) does adequately compensate the expected likelihood gain for the step model, as illustrated in Fig. 7. Although the constant model is a nested model, that is, special case of the step model, the likelihood ratio statistics are not chi-square distributed. It turns out that relative to the null hypothesis, the step model has an advantage that is higher than the number of its free parameters (3) would suggest. As a result, the AIC likelihood ratio’s for the step model relative to the other models are expected to be inflated, that is, biased by over-fitting. The performance results of the step models should therefore be interpreted with restraint. We speculate that the cause is related to the discontinuity of the model, and to the fact that the null hypothesis does not constrain the third parameter, that is, the location of the discontinuity. Exploration of this specific hypothesis is beyond the scope of this paper. We expect that in a pseudo-prospective model performance testing procedure (Zechar et al., Reference Zechar, Gerstenberger and Rhoades2010), that we anticipate any new model to be subjected to before application in hazard and risk assessment, this issue will be treated adequately.

Fig. 7. Likelihood ratio statistics for maximum-likelihood linear, quadratic and step b-value functions, relative to the maximum-likelihood constant b-value model. The statistics are obtained for 1000 random reassignments of the magnitudes to the catalogue’s reservoir thickness samples. Other predictors give comparable results. Both the linear and quadratic functions closely follow a maximum-likelihood chi-square distribution (dashed curves), with degrees of freedom very close to the theoretic values of 1 and 2, for functions with 1 and 2 degrees of freedom more, respectively, than the constant function. The step function, however, also has just two more parameters than the constant function, but apparently is expected to perform much better than the quadratic, and apparently is not chi-square distributed (the dashed curve is the maximum-likelihood chi-square fit to the data). As a result, the Akaike Information Criterion does not compensate adequately for the surplus degrees of freedom.
Results
The results of the analyses as described in Section 2 are shown in Figs. 8 to 13, and in Tables 2 and 3.

Fig. 8. B-values resulting from the spatial moving window analysis. Each earthquake is assigned the MLE b-value for the sub-catalogue consisting of the event itself and its 50 (left) or 100 (right) nearest neighbors. The legend applies to all corresponding figures.
Table 2. For each of the six prospective predictors for b-value variations in the Groningen field, a total of seven statistics are compared to the distribution of results generated for the null-hypothesis, in which the predictor does not carry any information on the b-value. Realizations of the null-hypothesis are generated by random shuffling of the observed magnitudes with respect to the predictor values. The exceedance probabilities, that is, p-values, indicate the probability that the observed statistics are the result of chance. Lower values give stronger stronger evidence for rejecting the null hypothesis that a b-value is constant. The column C-vM* refers to the corrected Cramér-von Mises test result.

Table 3. Relative likelihood of predictive models for b-value variations in the Groningen field consisting of simple functional forms conditioned on six possible predictor covariates. The likelihoods are calculated according to the Akaike Information Criterion and normalized relative to the likelihood of the constant model, or null hypothesis.

Figure 8 shows the result of the spatial moving window analysis. A NW-SE trend can be seen in both the 51-event and the 101-event windows. The 51-event window results in a wider spread of MLE b-values. We determine the difference min-max statistic for both window sizes and compare it with the null hypothesis distribution. This comparison is visualized for both the spatial and the temporal moving windows in Fig. 9. The Figure shows that the test statistic for temporal moving windows is not particularly special, as it is exceeded quite frequently in the null hypothesis distribution. As a result it cannot be used to reject the null hypothesis. The statistic for the spatial moving windows however is quite high and rarely exceeded for the null hypothesis. The corresponding p-values are 0.03 and 0.07 for the 51- and 101-event window sizes, respectively. The moving window analysis does not resolve any trend or variation in time, but it is unlikely that the magnitude distribution is constant in space.

Fig. 9. The graphs show empirical distributions (CCDF) for 1000 51-event (top) and 101-event (bottom) moving window analyses in both time and space on random realizations of the null-hypothesis obtained by magnitude shuffling. The test statistic is the difference between the maximum and the minimum MLE b-value estimate in the moving window collection. Vertical bars indicate the observed values for the Groningen catalogue. The corresponding values on the vertical axis indicate the p-value.
The moving window analyses for the other predictors follow the same procedure. The p-values are provided in Table 2, to be discussed below.
Figure 10 shows a visual summary of the moving window and maximum-likelihood analyses for all six considered covariates. The maximum-likelihood results are visualized in the spatial context in in Figs. 11 and 12. Note that due to the static, spatial nature of these figures, the trends for the covariates reservoir thickness and topographic gradient, which are static spatial covariates, are easier to discern than for the dynamic covariates. It is interesting to see the difference in the empirical and MLE magnitude distributions for the catalogue partitioning that the step model effectively creates. These results are on display in Fig. 13.

Fig. 10. For each predictor, five lines are shown. In silver (51-event) and black (101-event) the moving windows analyses (see section 2.4.2). We have chosen to plot the results for each window at the mean value of the contributing covariates. In blue, orange and green, the maximum-likelihood estimates of the constant, linear, and step models, respectively. Note that the moving-window results and the maximum-likelihood models are each independently generated from the magnitude data in Fig. 5 . In particular, the MLE functions are not intended to fit the moving window results.

Fig. 11. The MLE linear trend models for each predictor result in a b-value for each event in the catalogue. Here, we show the b-value assigned to each event in its spatial context. Yellow shades correspond to lower, blue shades to higher values of the covariate.

Fig. 12. The MLE step-function models for each predictor result in a b-value for each event in the catalogue. Here, we show the b-value assigned to each event in its spatial context. Yellow shades correspond to lower, blue shades to higher values of the covariate.

Fig. 13. The MLE step-function models effectively separate the catalogue into two sub-catalogues, each with their own b-value: one for the low covariate values, and one for the high covariate values. This Figure shows the resulting sub-catalogues with their b-values.
Table 2 summarizes the p-values of all statistical tests on the moving window and maximum-likelihood analyses. The table reveals that reservoir thickness as a predictor consistently scores lowest p-values, indicating a low probability that it does not carry any information on the magnitude distribution. To a lesser extent the same holds for topographic gradient on wide set of tests, and induced stress in particular for the linear trend model. In summary it appears that static factors are more informative than dynamic factors.
Finally, Table 3 shows the relative likelihood of the various combinations of predictor and functional form. In this table we also include the results for the quadratic function for which we do not provide visualizations. The Table shows that the extra degree of freedom for quadratic models relative to the linear models does not lead to better results. The Table also shows an (apparently) exceptional performance of the step function, which we discuss in Section “Likelihood ratio and the Akaike Information Criterion”, and accompany with a warning to interpret with restraint. Overall, the Table shows that the maximum-likelihood models for reservoir thickness provide the best performance relative to the other predictors.
Discussion
Previous analysis of variations of the magnitude distribution in the Groningen field focused on induced stress as the predicting covariate (Bourne & Oates, Reference Bourne and Oates2020). In this study, we have investigated the possibility of other covariates performing better as predictors of the observed earthquake magnitude distribution. Our exploratory moving window analysis indicated that while temporal variation in b-value appear to be statistically insignificant, there are significant spatial variations. In our subsequent search for a better b-value predictor, we tested a number of covariates, each of them with a distinct physical relation to the Groningen gas field. Reservoir thickness, a static property, unaffected by the gas production process, proves to be the statistically superior predictor of the b-value spatial variation.
In order to facilitate the comparison between different models, we have focused our attention on the relative performance of the MLE models. Although this provides a first-order indication of relative predictive performance, the performance assessment is not yet in line with the approach followed in seismic hazard and risk analysis. For future integration the models should be cast in a Bayesian framework, including the definition of a prior distribution for the model parameters and taking into account the full likelihood distribution of the model parameters conditional on the observation. In this framework a forecast is based on an integration of the posterior model parameter distribution. Therefore, ultimately, it is the performance of this integrated prediction that is of prime interest.
Nevertheless, our MLE based assessment provides valuable insights. Variations of b-value over the Groningen field seem to be predominantly controlled by static rather than dynamic factors, resulting in significant spatial variations, but (for the field as a whole) no significant changes in time. We find that the dynamic induced stress predictor does resolve a significant linear trend, albeit at lower significance level than reservoir thickness. Future work may investigate combinations of predictors to establish whether the static factors are sufficient predictors for b-value variations by itself, or that dynamic factors are able to contribute significantly.
Although our predictors were chosen because of their direct physical relation to the Groningen gas field, it should be noted that we are strictly looking at correlations. As such, the famous wisdom correlation does not imply causation also applies here. We do not propose a physical model that explains the observed effectiveness of the different predictors, nor do we claim that there necessarily is a direct causal relation between the more effective predictors (e.g. reservoir thickness) and the b-value. For reservoir thickness, we have shown that it is statistically very unlikely that the observed correlation is purely due to chance. However, it is possible (and perhaps even likely) that a confounding factor exists (i.e. that reservoir thickness itself is not the driving mechanism behind the b-value difference).
Conclusions
We have investigated spatiotemporal variations of magnitude distributions as characterized by the Gutenberg–Richter b-value in the Groningen gas field. We have found that spatial variations are more pronounced than variations in time. In addition we have investigated the predictability of observed variations in terms of a number of physical properties of the reservoir, including both static and dynamic properties, the latter being directly coupled to gas production.
We find evidence that observed variations are more likely to be controlled by static rather than by dynamic properties. Predictions in terms of the static properties topographic gradient and reservoir thickness lead to very low likelihood, around 2% and lower, of the null-hypothesis (i.e., no relation, or constant b-value) on a variety of statistical tests. Of the dynamic properties, induced stress is the most convincing predictor, still resolving a significant linear trend for the b-value.
In terms of relative likelihood, statistical models for b-values based on reservoir thickness outperform models based on the other predictor properties. An MLE linear model based on reservoir thickness outperforms the MLE linear model based on induced stress by a factor of 3. The hyperbolic tangent model based on induced stress, which is currently being applied in hazard and risk assessment models (Bourne & Oates, Reference Bourne and Oates2020), does not manage to improve on the linear trend with its extra parameter.
We find that step models, in general, reach higher likelihoods than linear and quadratic models, but we also note that these results may be inflated due to a level of over-fitting that is not adequately compensated for in the Akaike Information Criterion.
The main conclusion of this study is that reservoir thickness is a strong predictor for spatial b-value variations in the Groningen field. We propose to develop a forecasting model for Groningen magnitude distributions conditioned on reservoir thickness, to be used alongside, or as a replacement, for the current models conditioned on induced stress.
Acknowledgments
We thank the Groningen field operator NAM for providing the reservoir properties used as (input for) the prospective predictors investigated in this study. We thank KNMI for generating, maintaining and exposing the seismic monitoring database (KNMI, 2022a, 2022b), and the KEM subpanel (kemprogramma.nl) for several fruitful discussions about model performance and statistical methods. Most calculations and visualizations have been performed using Wolfram Mathematica (Wolfram Research, 2021). We thank Matteo Taroni and an anonymous reviewer for their constructive comments.