On the strength of the weakly nonlinear theory for surface gravity waves

Abstract

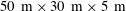Recently, Bonnefoy et al. (J. Fluid Mech., vol. 805, 2016, R3) studied the resonant interaction of oblique surface gravity waves in a large $50~\text{m}\times 30~\text{m}\times 5~\text{m}$ wave basin. Their experimental results are in excellent quantitative agreement with predictions of the weakly nonlinear wave theory, and provide additional evidence to the strength of this widely used mathematical formulation. In this article, the reader is introduced to the many facets of the weakly nonlinear theory for surface gravity waves, and to its current and possible future applications, deterministic as well as stochastic.

1 Introduction

A typical monochromatic wave on the surface of the ocean is $\unicode[STIX]{x1D706}_{O}=100~\text{m}$ long, $H_{O}=2~\text{m}$ high, has a period $T_{O}=(2\unicode[STIX]{x03C0}\unicode[STIX]{x1D706}/g)^{1/2}\approx 8~\text{s}$ and the idealised shape of a sine curve. Its laboratory representation can have $\unicode[STIX]{x1D706}_{L}=1~\text{m}$ , $H_{L}=2~\text{cm}$ and $T_{L}=0.8~\text{s}$ . Both of the above waves have the same steepness $\unicode[STIX]{x1D700}=\unicode[STIX]{x03C0}H_{O}/\unicode[STIX]{x1D706}_{O}=\unicode[STIX]{x03C0}H_{L}/\unicode[STIX]{x1D706}_{L}=0.063=o(1)$ . All progressive gravity waves have small steepnesses due to the fact that they tend to break when $\unicode[STIX]{x1D700}$ exceeds 0.2 (although the strict theoretical value is close to $\unicode[STIX]{x1D700}=0.4$ ).

Another crucial piece of knowledge is the fact that the flow associated with these waves is potential, and is governed by the Laplace equation, which is linear. However, the boundary condition at the water–air interface, which by itself is an unknown of the problem, has linear and nonlinear terms of order $\unicode[STIX]{x1D700},\unicode[STIX]{x1D700}^{2},\unicode[STIX]{x1D700}^{3},\ldots .$ For some engineering purposes, such as the diffraction of waves by structures, keeping only the linear terms of the boundary condition is good enough, and the whole mathematical problem becomes linear. For gravity waves, the inclusion of $\unicode[STIX]{x1D700}^{2}$ terms provides only a small correction to the linear result, as one would naturally expect. The discovery of the dominance of the linear theory has a crucial advantage, since linear waves do not interact with one another.

Thus, the quite often complex structure of the ocean surface can be represented by a collection of several (or many) sinusoidal waves, each with its own wavelength, propagation direction and wave height. Such a collection of waves is called a wave spectrum.

Quite surprisingly, adding terms of order $\unicode[STIX]{x1D700}^{3}$ seems to be a significant game changer. It is the gateway to the realm of weakly nonlinear wave theory, where waves slowly exchange energy with each other. At this point, it is only fair to mention that for some problems, i.e. steep waves breaking on a wall, one needs all the terms of the free-surface boundary condition. Such problems are referred to as strongly nonlinear.

The mathematical relation between the wavelength and the wave period is called the dispersion relation, and for linear gravity waves on deep water it has the simple structure $T^{2}=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D706}/g$ , which can also be written as $\unicode[STIX]{x1D714}^{2}=gk$ , where $\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}/T$ is the wave frequency and $k=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}$ is called the wavenumber. The energy exchange in the weakly nonlinear theory is enabled by the occurrence of resonating quartets of waves with vector wavenumbers $\boldsymbol{k}_{a},\boldsymbol{k}_{b},\boldsymbol{k}_{c}$ and $\boldsymbol{k}_{d}$ for which $\boldsymbol{k}_{a}+\boldsymbol{k}_{b}-\boldsymbol{k}_{c}-\boldsymbol{k}_{d}=0$ , and $\unicode[STIX]{x1D714}_{a}+\unicode[STIX]{x1D714}_{b}-\unicode[STIX]{x1D714}_{c}-\unicode[STIX]{x1D714}_{d}=O(\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D714}_{a})$ . When the right-hand side of this last equation is strictly zero, the quartet is said to be in exact resonance, otherwise it is in a near-resonant state. Quartets in exact/near-resonance conditions exchange energy on the slow time scale $T_{2}=\unicode[STIX]{x1D700}^{-2}T$ , where $T$ is the typical period of the waves.

2 Overview

The dynamics of weakly nonlinear gravity waves has many facets, but all of them can be derived from one mathematical model: the so-called Zakharov equation, see Zakharov (1968). The solutions of the Zakharov equation give the deterministic evolution of the amplitude of the $O(\unicode[STIX]{x1D700})$ linear waves due to energy exchanges amongst themselves, which are governed by third-order $O(\unicode[STIX]{x1D700}^{3})$ nonlinearities, i.e. by quartet resonance.

Note that the structure of the dispersion relation for surface gravity waves in deep water does not enable the existence of resonating triads. It does, however, allow for resonating quintets which also enable energy exchange, albeit on the slower time scale of $T_{3}=\unicode[STIX]{x1D700}^{-3}T$ .

The distribution of energy on the wavenumber plane, called the amplitude spectrum, can be either discrete or continuous, and additionally its footprint on this plane can be either narrow or broad (i.e. of radius $O(\unicode[STIX]{x1D700}\Vert \boldsymbol{k}_{0}\Vert )$ or $O(\Vert \boldsymbol{k}_{0}\Vert )$ , respectively, where $\boldsymbol{k}_{0}$ is inside the footprint).

Amplitude spectra, which are discrete, represent waves which cover the entire (infinite) free surface, whereas those which are continuous represent localized, bounded disturbances, such as the well-known solitons. The solitons were originally obtained as solutions of the nonlinear Schrödinger equation (NLS), which is an excellent mathematical model for weakly nonlinear gravity waves with narrow spectra, and is formulated in the physical plane, see Peregrine (1983). One can derive the NLS and the so-called modified NLS, as well as all the other equations which will be mentioned in this note, from the original Zakharov equation.

A simple and attractive discrete spectrum is that of a degenerated quartet, for which one of the waves is counted twice, so that $2\boldsymbol{k}_{a}=\boldsymbol{k}_{b}+\boldsymbol{k}_{c}$ and $2\unicode[STIX]{x1D714}_{a}=\unicode[STIX]{x1D714}_{b}+\unicode[STIX]{x1D714}_{c}$ . This is the example treated by Bonnefoy et al. (2016) in the recent article which motivated this Focus on Fluids note. In this case, the Zakharov equation predicts that if one initially introduces energy into $\boldsymbol{k}_{a}$ and $\boldsymbol{k}_{b}$ , but not into $\boldsymbol{k}_{c}$ , the latter wave will appear spontaneously, and in the initial stages of evolution will grow at a linear rate. While previous experiments have confirmed parts of this theory for two initially perpendicular waves, for the first time a comprehensive verification for a range of angles and steepnesses has been performed.

An interesting companion case to that studied by Bonnefoy et al. (2016) is the well-known Benjamin–Feir instability of a Stokes wave, where the interacting waves in a degenerate quartet are collinear. In this case, Benjamin & Feir (1967) have shown both theoretically and experimentally that a monochromatic Stokes wave (a sinusoidal wave $\boldsymbol{k}_{a}$ with somewhat larger steepness, say $\unicode[STIX]{x1D700}=0.1$ ) transfers energy to two initially very much smaller side bands (i.e. narrow spectrum) $\boldsymbol{k}_{b}$ and $\boldsymbol{k}_{c}$ . Applying linear stability analysis on the NLS or on the Zakharov equation one can discover the most unstable modes, and it is quite clear that it is enough to have some small background noise in order to start the instability of the Stokes wave. The fate of these instabilities at longer times can sometimes be recurrent (akin to the Fermi–Pasta–Ulam recurrence), rather complex or even chaotic.

Zakharov’s equation is usually solved by specifying an initial condition at a given time, whereas in the laboratory experiments, one specifies a boundary condition at the location of the wave makers. This non-trivial transformation is handled very elegantly by Bonnefoy et al. (2016).

A main target of the studies on weakly nonlinear gravity waves is the improvement of ocean wave-forecasting abilities. The evolution of oceanic wave fields depends on the generation of the waves by the wind, their mutual energy exchange, and their loss of energy due to breaking. It is generally accepted that the complex nature of the ocean surface structure, and our intrinsic inability to know and follow its various details, calls for a stochastic approach, in which at least the phase shifts of the sinusoidal spectral components are assumed to be random. In such an approach a continuous energy spectrum usually replaces the complex-valued, discrete, but deterministic amplitude spectrum, mentioned previously.

The evolution of the energy spectrum is governed by an energy-transfer equation known as the kinetic equation, which one can obtain from the Zakharov equation by making some appropriate statistical and asymptotic assumptions, see Mei, Stiassnie & Yue (2005). The kinetic equation was first derived by Hasselmann (1962) from the hydrodynamic equations. The time scale of this equation turns out to be $T_{4}=\unicode[STIX]{x1D700}^{-4}T$ , where, as before, $T$ is a typical wave period. Another dominant feature of the kinetic equation is the fact that all energy exchange occurs through exactly resonating quartets, as if all the interactions due to the much more plentiful near-resonating quartets had been averaged out.

3 Future

Taking typical values for the wave period $T=10~\text{s}$ , and for the steepness $\unicode[STIX]{x1D700}=0.1$ yields the slow time scales $T_{2}=10^{3}~\text{s}\approx 17~\text{min}$ , and $T_{4}=10^{5}~\text{s}\approx 27~\text{h}$ , for Zakharov’s and Hasselmann’s equations, respectively. The latter is so long that it must raise some doubts about the actual applicability of Hasselmann’s equation, simplifications of which are currently installed in almost any wave-forecasting software. Moreover, the kinetic equation is based on the dominance of the wave quartets in exact resonance over those in a near-resonance condition. However, one can argue that the sum $(\unicode[STIX]{x1D714}_{a}+\unicode[STIX]{x1D714}_{b}-\unicode[STIX]{x1D714}_{c}-\unicode[STIX]{x1D714}_{d})$ in the resonance condition should be replaced by $(\unicode[STIX]{x1D6FA}_{a}+\unicode[STIX]{x1D6FA}_{b}-\unicode[STIX]{x1D6FA}_{c}-\unicode[STIX]{x1D6FA}_{d})$ , where $\unicode[STIX]{x1D6FA}$ is the weakly nonlinear frequency, sometimes called the Stokes corrected frequency, for which $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D714}(1+O(\unicode[STIX]{x1D700}^{2}))$ , where the term of $O(\unicode[STIX]{x1D700}^{2})$ varies in time and has a known functional relation to the amplitudes of the wave field. Some initial efforts to overcome these difficulties, and obtain energy-transfer equations with the more sensible slow time $T_{2}$ and which include near-resonant terms, already appear in the scientific literature, and more are expected to follow.

These efforts concentrate on two fronts related to two possible but different stochastic approaches. The first approach treats the wave fields as statistically homogeneous processes, whereas the second one treats them as statistically inhomogeneous processes. To be a little more precise, the ensemble average of two complex amplitudes $a_{i}$ and $a_{j}$ , denoted $R_{ij}=\langle a_{i}a_{j}^{\ast }\rangle$ , (where the angular brackets denote the ensemble average and $^{\ast }$ a complex conjugate) exists for the inhomogeneous case, but does not exist for the homogeneous one unless $i=j$ . Some efforts towards progress on the homogeneous case include the works of Annenkov & Shrira (2006) and Gramstad & Stiassnie (2013). Those for the inhomogeneous wave fields have been, so far, limited to narrow spectra only, see Alber (1978) and Ribal et al. (2013). One advantage of the latter approach is that it has a good chance of predicting the probability of occurrence of extremely high waves, known as freak or rogue waves. The ultimate success will probably be a combination of both of the above approaches, including both $R^{2}$ and $R^{3}$ terms, representing the inhomogeneous and homogeneous dominant processes, respectively.

As a final remark, we note that the length scales compatible with the $T_{2}$ and $T_{4}$ values mentioned at the beginning of this section are $L_{2}=10~\text{km}$ and $L_{4}=1000~\text{km}$ . On a laboratory scale, this corresponds to $L_{2}=100~\text{m}$ and $L_{4}=10~\text{km}$ . Note that $L_{2}=100~\text{m}$ is indeed comparable to the size of the wave basin used by Bonnefoy et al. (2016), but $L_{4}=10~\text{km}$ is unreachable on any foreseeable laboratory scale. However Nazarenko et al. (2010) use a somewhat surprising approach, and seemingly overcome this experimental shortcoming.