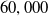Nomenclature
-

-
aspect ratio
-
 $b$
$b$
-
wingspan
-
 $\bar c$
$\bar c$
-
wing mean aerodynamic chord
-
 ${C_D}$
${C_D}$
-
drag coefficient
-
 ${C_{{D_0}}}$
${C_{{D_0}}}$
-
parasite drag coefficient
-
 ${C_L}$
${C_L}$
-
lift coefficient
-
 ${C_{{L_\alpha }}}$
${C_{{L_\alpha }}}$
-
lift curve slope
-
 ${C_R}$
${C_R}$
-
roll moment coefficient
-
 ${C_M}$
${C_M}$
-
pitch moment coefficient
-
 ${C_N}$
${C_N}$
-
yaw moment coefficient
-
 $CG$
$CG$
-
centre of gravity
-
 $D$
$D$
-
drag force
-
 $I$
$I$
-
inertia matrix
-
 $L$
$L$
-
lift force
-
 $R$
$R$
-
rotation matrix
-
 $\bar q$
$\bar q$
-
dynamic pressure
-
 $Re$
$Re$
-
reynolds number
-
 ${S_{REF}}$
${S_{REF}}$
-
wing reference area
-
 $u,v,w$
$u,v,w$
-
body fixed velocity components
-
 $V$
$V$
-
inertial velocity
-
 $x,y,z$
$x,y,z$
-
position components
-
 ${X_{np}}$
${X_{np}}$
-
neutral point
-
 ${e_0}$
${e_0}$
-
oswald efficiency factor
-
 ${C_{{n_\beta }}}$
${C_{{n_\beta }}}$
-
weather vane stability
-
 ${C_{{l_\beta }}}$
${C_{{l_\beta }}}$
-
roll stability
-
 $\forall $
$\forall $
-
volume
Greek symbol
-
 $\alpha $
$\alpha $
-
angle-of-attack
-
 $\beta $
$\beta $
-
sideslip angle
-
 $\delta_{e}$
$\delta_{e}$
-
elevator deflection
-
 $\phi, \theta, \psi $
$\phi, \theta, \psi $
-
roll, pitch and yaw angles
-
 $\omega $
$\omega $
-
angular velocity
-
 ${\omega _{n,ph}}$
${\omega _{n,ph}}$
-
phugoid natural frequency
1.0 Introduction
The aerodynamic behaviour of small unmanned aerial vehicles (sUAVs) differ from well-established theoretical principles and empirical findings derived from full-scale aircraft [Reference Pines and Bohorquez1–Reference Uhlig3], and can be primarily attributed to low Reynolds number effects. Delving into the intricacies of sUAV aerodynamics is essential for comprehending the complex interactions between the vehicle and its surrounding airflow so as to glean a thorough understanding of their performance, safety, efficiency and manoeuverability. By conducting systematic analyses, researchers and engineers can acquire valuable insights that facilitate the optimisation of design parameters and operational strategies, leading to improved overall performance and mission success. However, there remains a scarcity of aerodynamic data for sUAVs, which can be mainly attributed to the difficulties in measuring data at the low Reynolds number conditions in which sUAVs typically operate (below
![]() $60,000$
) and generating the correct atmospheric conditions sUAVs are subjected to in wind tunnel testing [Reference Uhlig3, Reference Mettler4]. The lack of data in turn restricts our understanding and ability to develop control systems for sUAVs to efficiently manoeuver and retain control in real flight conditions. Driven by recent advancements in motion tracking technologies for the estimation of aerodynamic parameters, the objective of the current study is two-fold: (i) to verify the efficacy of motion capture systems as a dependable instrument for flight testing, thereby facilitating the comprehensive characterisation of aerodynamic and stability parameters of sUAVs, and (ii) to analyse the impact of low Reynolds number effects on the aerodynamic behaviour of sUAVs.
$60,000$
) and generating the correct atmospheric conditions sUAVs are subjected to in wind tunnel testing [Reference Uhlig3, Reference Mettler4]. The lack of data in turn restricts our understanding and ability to develop control systems for sUAVs to efficiently manoeuver and retain control in real flight conditions. Driven by recent advancements in motion tracking technologies for the estimation of aerodynamic parameters, the objective of the current study is two-fold: (i) to verify the efficacy of motion capture systems as a dependable instrument for flight testing, thereby facilitating the comprehensive characterisation of aerodynamic and stability parameters of sUAVs, and (ii) to analyse the impact of low Reynolds number effects on the aerodynamic behaviour of sUAVs.
Currently, most of the aerodynamic data for sUAVs is obtained through wind tunnel testing. However, these methods can be costly and increase in complexity as the scale of the vehicle decreases [Reference Krashanitsa, Silin, Shkarayev and Abate5–Reference Ifju, Waszak and Jenkins8]. Moreover, the size and weight limitations of sUAVs impose significant constraints on traditional flight testing, making it challenging to accommodate on-board flight data instrumentation [Reference Johnson, Turbe, Wu, Kannan and Neidhoefer9]. Significant progress in camera technology and advanced software algorithms for data extraction have facilitated the utilisation of off-board motion tracking as an alternative approach to acquire aerodynamic data. This approach has been demonstrated to have numerous advantages over conventional wind and water tunnel testing including cost-effectiveness, simplicity and the ability to capture detailed flight data at higher frequencies across all flight conditions of sUAVs [Reference Uhlig3, Reference Mettler4, Reference Rhinehart and Mettler10]. The method involves attaching reflective markers to the sUAV and using a set of high-frequency cameras to capture and track the markers positions and attitudes through triangulation [Reference Uhlig and Selig11]. The marker(s) captured position in a three-dimensional space with respect to time can then be used to determine the aerodynamic forces and moments acting on the sUAV [Reference Uhlig3, Reference Mettler4, Reference Rhinehart and Mettler10–Reference Uhlig and Selig16]. Since the late 2000s, multiple researchers [Reference Mettler4, Reference Rhinehart and Mettler10, Reference Woollands15, Reference Cory and Tedrake17, Reference Cory18] have demonstrated the successful utilisation of in-flight trajectory sampling for extracting aerodynamic characteristics for fixed-wing micro air vehicles (MAVs). Extensive research utilising motion capture trajectory sampling was carried out by Uhlig et al. [Reference Uhlig3, Reference Uhlig and Selig11, Reference Uhlig and Selig14, Reference Uhlig, Sareen, Sukumar, Rao and Selig19] to comprehensively investigate a wide range of flight regimes on various sUAVs with wing aspect ratios ranging from
![]() $2.5$
to
$2.5$
to
![]() $12$
. Parallel research by Rao et al. [Reference Rao, Uhlig and Selig12] effectively employed a motion capture system to implement a thrust model for powered flight, yielding successful outcomes. Furthermore, Cory et al. [Reference Cory and Tedrake17, Reference Cory18], Paranjape et al. [Reference Paranjape, Kim, Gandhi and Jo Chung20] and Moore [Reference Moore21] successfully utilised motion capture systems for control modeling, showcasing their efficacy in capturing and analysing motion dynamics and highlighting the valuable role of motion capture systems in advancing control modeling techniques.
$12$
. Parallel research by Rao et al. [Reference Rao, Uhlig and Selig12] effectively employed a motion capture system to implement a thrust model for powered flight, yielding successful outcomes. Furthermore, Cory et al. [Reference Cory and Tedrake17, Reference Cory18], Paranjape et al. [Reference Paranjape, Kim, Gandhi and Jo Chung20] and Moore [Reference Moore21] successfully utilised motion capture systems for control modeling, showcasing their efficacy in capturing and analysing motion dynamics and highlighting the valuable role of motion capture systems in advancing control modeling techniques.
One of the notable observations regarding sUAV aerodynamics made by Uhlig et al. [Reference Uhlig and Selig11, Reference Uhlig, Sareen, Sukumar, Rao and Selig19] is the deviation of experimental forces and moments measurements from theoretical predictions and large-scale aircraft flight data for all sUAVs investigated in their studies. These deviations are primarily attributed to scaling and low Reynolds number effects, and are in line with deductions made by other researchers regarding low Reynolds number sUAV flight operations [Reference Pines and Bohorquez1, Reference Mueller2]. Therefore, attaining an in-depth understanding of low Reynolds number effects on sUAV flight dynamics is necessary to effectively advance the technology. While restrictive for full-configuration sUAVs, the existing body of experimental research provides a good understanding of the effects of low Reynolds number flows on aerofoil and wing aerodynamics [Reference Krashanitsa, Silin, Shkarayev and Abate5–Reference Pelletier and Mueller7, Reference Selig and Mcgranahan22–Reference Torres and Mueller28]. Particular to wing aerodynamics in low Reynolds number flows, Spedding and McArthur [Reference Spedding and McArthur23] conducted an exhaustive study on flow behaviour at said conditions and described the concept of a down-scaling factor to refine the prediction of aerodynamic characteristics for
![]() $Re \lt 100,000$
. Subsequent research by Ananda et al. [Reference Ananda, Sukumar and Selig27, Reference Ananda, Sukumar and Selig29], aimed at establishing a correlation between low Reynolds number effects and aspect ratio, showed a consistent decrease in the Oswald efficiency factor with increasing wing aspect ratio.
$Re \lt 100,000$
. Subsequent research by Ananda et al. [Reference Ananda, Sukumar and Selig27, Reference Ananda, Sukumar and Selig29], aimed at establishing a correlation between low Reynolds number effects and aspect ratio, showed a consistent decrease in the Oswald efficiency factor with increasing wing aspect ratio.
Building upon the existing state-of-the-art depicted in the literature, the present study seeks to establish the off-board capability of estimating aerodynamic parameters for sUAVs during glide flight for an existing motion-capture system. A comprehensive analysis is subsequently conducted on the aerodynamics of various full-scale sUAVs with wing aspect ratios ranging between
![]() $2.56$
and
$2.56$
and
![]() $6.32$
, with the aim of understanding the effects of low Reynolds number flows on sUAV aerodynamics and stability. The current work will serve as the first step to the future development of off-board aerodynamic estimation capabilities of sUAVs in powered level- and manoeuvering-flights in flow conditions typically encountered during real flight. The following section (Section 2) details the experimental data acquisition system. In Section 3, the data collection and processing techniques are discussed in detail. System uncertainity, flight repeatability tests and data filtering methods used in the current work are detailed in Section 4. Following this, the flight results for the baseline aircraft are analysed and compared against theory and existing literature in Section 5. Finally, Section 6 summarises the conclusions drawn from the results and provides future research directions.
$6.32$
, with the aim of understanding the effects of low Reynolds number flows on sUAV aerodynamics and stability. The current work will serve as the first step to the future development of off-board aerodynamic estimation capabilities of sUAVs in powered level- and manoeuvering-flights in flow conditions typically encountered during real flight. The following section (Section 2) details the experimental data acquisition system. In Section 3, the data collection and processing techniques are discussed in detail. System uncertainity, flight repeatability tests and data filtering methods used in the current work are detailed in Section 4. Following this, the flight results for the baseline aircraft are analysed and compared against theory and existing literature in Section 5. Finally, Section 6 summarises the conclusions drawn from the results and provides future research directions.
2.0 Experimental apparatus
2.1 Motion capture system
Experiments were conducted in the Autonomous Systems Research Laboratory (ASRL) located at the Raspet Flight Research Laboratory. The ASRL is equipped with an OptiTrack [30] system that is composed of a set of 12
![]() $Prim{e^x}41$
cameras placed at a height of 5.4864m, and covering a test area of 14.516m × 9.611m (Fig. 1). The cameras have a resolution of 4.1 megapixels and frame rates reaching 250Hz, and are equipped with a low distortion lenses called fast glass. The 12mm lens is treated with anti-reflective coating. Additionally, the cameras have a 10 bit grayscale depth leading to lower noise and highly improved precision. Data provided by the developers state that positional errors are less than
$Prim{e^x}41$
cameras placed at a height of 5.4864m, and covering a test area of 14.516m × 9.611m (Fig. 1). The cameras have a resolution of 4.1 megapixels and frame rates reaching 250Hz, and are equipped with a low distortion lenses called fast glass. The 12mm lens is treated with anti-reflective coating. Additionally, the cameras have a 10 bit grayscale depth leading to lower noise and highly improved precision. Data provided by the developers state that positional errors are less than
![]() $ \pm 0.10$
mm and rotational error are smaller 0.5 degrees for a reference (9m
$ \pm 0.10$
mm and rotational error are smaller 0.5 degrees for a reference (9m
![]() $ \times $
9m) tracking area. The system features integrated image processing allowing for precise marker centre detection. To triangulate an object, reflective markers (that come in different shapes and sizes) are placed on the object’s surface. The Motive Optical motion capture software is used to gather the motion capture data.
$ \times $
9m) tracking area. The system features integrated image processing allowing for precise marker centre detection. To triangulate an object, reflective markers (that come in different shapes and sizes) are placed on the object’s surface. The Motive Optical motion capture software is used to gather the motion capture data.

Figure 1. Optitrack system: (a) camera placement and field of view and (b) test area.
Prior to using the OptiTrack system, a calibration routine is carried out to get the best possible results and keep the residual values to a minimum. Several calibration methods were studied in order to get a consistent residual throughout testing. The final method used for calibration is the wanding technique where a wand containing three spherical marker is moved in the capture volume, after the control volume is prepared and optimised for calibration by masking any extraneous reflections and unnecessary markers. The wanding technique involves collecting a sufficient number of samples by waving the wand gently across the entire capture volume. For the current work, a calibration threshold was reached when each camera captured 12,000 points covering the majority of the capture volume. This translated to a residual range of 0.4–0.55mm which was considered exceptional by the software’s algorithm. Consistent residual is of high importance through testing, and for small dynamic testing times typically ranging from 1 to 2 seconds, very small variations were observed.
2.2 Rail system
A 1.2m linear rail launch system was designed to launch the aircraft. As shown in Fig. 2, the system is mounted on an adjustable angle bracket that allows launching slope angles ranging from 0 to 90 degrees. A release mechanism composed of an electromagnet, a stepper motor and an ultrasonic sensor was implemented to release the aircraft once a predefined travel distance threshold was reached.

Figure 2. Linear rail system with hinged F4U-Corsair.
2.3 Aircraft
A set of six aircraft, shown in Fig. 3, were used in the current study to validate the efficacy of the motion capture system in characterising sUAV flight dynamics and studying low Reynolds number effects on the aerodynamics. Square reflective markers were placed on the aircraft surface to allow the motion capture system triangulate the sUAV. The markers were placed in a manner that allowed for the least amount of standard deviation in the captured data. The only modifications to the out-of-the-box aircraft was the removal of the battery and the replacement of the propeller with a 3D-spherical marker to enhance aircraft’s detectability within the testing environment. As it was crucial to accurately establish the geometric constants of the sUAVs to ensure precise analysis and evaluation of their aerodynamic behaviour, geometric property estimation was carried out by digitising the surfaces of interest. Wing surface areas were determined using Green’s theorem. To determine the inertial moments of the aircraft, the pendulum swing measurement technique [Reference Wolowicz and Yancey31] was employed. Table 1 provides mass and geometric details for all six sUAVs used in the current study.

Figure 3. (a) UMX-Vapor (b) Micro Vintage Stick (c) Edge A-430 (d) S2-CUB (e) F4U-Corsair (f) TR-C285G.
Table 1. Aircraft properties

3.0 Data collection and processing
The Optitrack system creates a rigid frame by triangulating the earth-referenced position of markers placed on the aircraft and returns the positional ([
![]() ${x_e}$
${x_e}$
![]() ${y_e}$
${y_e}$
![]() ${z_e}$
]) and Euler angles (
${z_e}$
]) and Euler angles (
![]() $\phi $
$\phi $
![]() $\theta $
$\theta $
![]() $\psi $
]) data in the earth-referenced axis system. The data collected has to be filtered to account for noise. Based on multiple smoothing methods that were investigated by Uhlig [Reference Uhlig3], a third order linear regression filter implementing the Savitzky-Golay algorithm was used for position and attitude smoothing, as shown in Fig. 4. The
$\psi $
]) data in the earth-referenced axis system. The data collected has to be filtered to account for noise. Based on multiple smoothing methods that were investigated by Uhlig [Reference Uhlig3], a third order linear regression filter implementing the Savitzky-Golay algorithm was used for position and attitude smoothing, as shown in Fig. 4. The
![]() ${R^2}$
values observed for the third-order Savitzky-Golay filter applied to the raw data for each flight were above
${R^2}$
values observed for the third-order Savitzky-Golay filter applied to the raw data for each flight were above
![]() $0.985$
for all measured variables. In this instance,
$0.985$
for all measured variables. In this instance,
![]() ${R^2}$
values of
${R^2}$
values of
![]() $0.999,0.997,0.996$
were obtained for roll, yaw, and pitch fitted data, respectively.
$0.999,0.997,0.996$
were obtained for roll, yaw, and pitch fitted data, respectively.

Figure 4. Filter application on attitude data for the UMX-Vapor.
To transform the earth-referenced frame to the body-referenced frame (aligned such that the nose is along the positive x-axis and the right wing is along the positive y-axis), a rotation matrix is used [Reference Uhlig3, Reference Mettler4, Reference Uhlig and Selig11, Reference Uhlig and Selig14, Reference Uhlig, Sareen, Sukumar, Rao and Selig19].
 \begin{align}R = \left[ {\begin{array}{c@{\quad}c@{\quad}c}{{\rm{cos}}( \theta ){\rm{cos}}( \psi )} {}& {{\rm{cos}}( \theta ){\rm{cos}}( \psi )} & {}{ - {\rm{sin}}( \theta )}\\[3pt] { - {\rm{cos}}( \phi ){\rm{sin}}( \psi ) + {\rm{sin}}( \phi ){\rm{sin}}( \theta ){\rm{cos}}( \psi )} & {}{{\rm{cos}}( \phi ){\rm{cos}}( \psi ) + {\rm{sin}}( \phi ){\rm{sin}}( \theta ){\rm{sin}}( \psi )} {}& {{\rm{sin}}( \phi ){\rm{cos}}( \theta )}\\[3pt] {{\rm{sin}}( \phi ){\rm{sin}}( \psi ) + {\rm{cos}}( \phi ){\rm{sin}}( \theta ){\rm{cos}}( \psi )} & {}{ - {\rm{sin}}( \phi ){\rm{cos}}( \psi ) + {\rm{cos}}( \phi ){\rm{sin}}( \theta ){\rm{sin}}( \psi )} & {}{{\rm{cos}}( \phi ){\rm{cos}}( \theta )}\end{array}} \right]\end{align}
\begin{align}R = \left[ {\begin{array}{c@{\quad}c@{\quad}c}{{\rm{cos}}( \theta ){\rm{cos}}( \psi )} {}& {{\rm{cos}}( \theta ){\rm{cos}}( \psi )} & {}{ - {\rm{sin}}( \theta )}\\[3pt] { - {\rm{cos}}( \phi ){\rm{sin}}( \psi ) + {\rm{sin}}( \phi ){\rm{sin}}( \theta ){\rm{cos}}( \psi )} & {}{{\rm{cos}}( \phi ){\rm{cos}}( \psi ) + {\rm{sin}}( \phi ){\rm{sin}}( \theta ){\rm{sin}}( \psi )} {}& {{\rm{sin}}( \phi ){\rm{cos}}( \theta )}\\[3pt] {{\rm{sin}}( \phi ){\rm{sin}}( \psi ) + {\rm{cos}}( \phi ){\rm{sin}}( \theta ){\rm{cos}}( \psi )} & {}{ - {\rm{sin}}( \phi ){\rm{cos}}( \psi ) + {\rm{cos}}( \phi ){\rm{sin}}( \theta ){\rm{sin}}( \psi )} & {}{{\rm{cos}}( \phi ){\rm{cos}}( \theta )}\end{array}} \right]\end{align}
An off-set matrix and off-set vector are computed to translate the system captured centre of gravity (henceforth referred to as the centroid) to the actual aircraft CG. The Euler angles are then extracted from the new rotation matrix,
![]() ${R_{EB}}$
, given as,
${R_{EB}}$
, given as,
where
![]() ${R_{ET}}$
is the rotation from earth to centroid frame of reference and
${R_{ET}}$
is the rotation from earth to centroid frame of reference and
![]() ${R_{TB}}$
is the rotation from centroid to body/CG frame of reference. Angular velocity, angular acceleration, translational velocity and translational acceleration in the body frame are computed in a manner similar to that employed in Refs (Reference Uhlig3, Reference Mettler4). The body acceleration is then calculated using the equation,
${R_{TB}}$
is the rotation from centroid to body/CG frame of reference. Angular velocity, angular acceleration, translational velocity and translational acceleration in the body frame are computed in a manner similar to that employed in Refs (Reference Uhlig3, Reference Mettler4). The body acceleration is then calculated using the equation,
where
![]() $\vec r$
is the translation vector from the rigid body centroid to the UAV centre of gravity and
$\vec r$
is the translation vector from the rigid body centroid to the UAV centre of gravity and
![]() $\omega $
is the angular acceleration, whose components (
$\omega $
is the angular acceleration, whose components (
![]() $p,q,r$
) are calculated as,
$p,q,r$
) are calculated as,
 \begin{align}\left[ {\begin{array}{l} p\\[3pt] q\\[3pt] r\end{array}} \right] = \left[ {\begin{array}{l@{\quad}c@{\quad}c} 1 & {}0 & {}{ - {\rm{sin}}( \theta )}\\[3pt] 0 & {}{{\rm{cos}}( \phi )} {}& {{\rm{sin}}( \phi ){\rm{cos}}( \theta )}\\[3pt] 0 & {}{ - {\rm{sin}}( \phi )} {}& {{\rm{cos}}( \phi ){\rm{cos}}( \theta )}\end{array}} \right]\left[ {\begin{array}{l}{\dot \phi }\\[3pt] {\dot \theta }\\[3pt] {\dot \psi }\end{array}} \right]\end{align}
\begin{align}\left[ {\begin{array}{l} p\\[3pt] q\\[3pt] r\end{array}} \right] = \left[ {\begin{array}{l@{\quad}c@{\quad}c} 1 & {}0 & {}{ - {\rm{sin}}( \theta )}\\[3pt] 0 & {}{{\rm{cos}}( \phi )} {}& {{\rm{sin}}( \phi ){\rm{cos}}( \theta )}\\[3pt] 0 & {}{ - {\rm{sin}}( \phi )} {}& {{\rm{cos}}( \phi ){\rm{cos}}( \theta )}\end{array}} \right]\left[ {\begin{array}{l}{\dot \phi }\\[3pt] {\dot \theta }\\[3pt] {\dot \psi }\end{array}} \right]\end{align}
The body velocity components (
![]() $u,v,w$
) of the UAV are determined using equation,
$u,v,w$
) of the UAV are determined using equation,
Subsequently, the total velocity, angle-of-attack, and sideslip angle are using equations,
The aerodynamic forces and moments acting on the body are then calculated as,
Subsequently, the aerodynamic forces and moment coefficients and evaluated as,
4.0 Uncertainty analysis, flight repeatability, and data filtering
4.1 Uncertainty analysis
The uncertainty analysis of the motion capture system was done through a set of static and dynamic tests, detailed in the following subsections.
4.1.1 Static tests
The standard deviation in position and attitude measured by the motion capture system was investigated using the F4U-Corsair and UMX Vapor aircraft. Table 2 shows the standard deviation in positional and angular data at measurement frequencies ranging from 200 to 250Hz. It was observed that measuring at a higher frequency resulted in higher standard deviations. While the deviation in measured values could be attributed to vibrations occurring along a particular axis, they were still comparable to, and at most times lesser than the standard deviations of the motion-capture systems used by other researchers [Reference Uhlig3, Reference Mettler4]. Based on the current results and literature [Reference Uhlig3], a measuring frequency of 200Hz was used for the study.
Table 2. Standard deviations in position and attitude with respect to frequency

4.1.2 Dynamic tests
To demonstrate the accuracy of the motion capture system in measuring acceleration, the acceleration due to gravity of an object under free-fall conditions was measured. A 5.4kg shot-put ball with a smooth finish was equipped with nine reflective sticker markers and released from an initial height of 2.8m. However, data was only analysed between a height of 1.8 and 0.1m to remove the effects of release and impact (Fig. 5(a)). The mean acceleration due to gravity for four runs was measured to be 9.7978m/s
![]() ${{\rm{\;}}^2}$
, as seen in Fig. 5(b). On comparing the result to the local gravity value of 9.79535m/s
${{\rm{\;}}^2}$
, as seen in Fig. 5(b). On comparing the result to the local gravity value of 9.79535m/s
![]() ${{\rm{\;}}^2}$
(at Raspet II Laboratory, Starkville, MS) [32], we observed that the prediction error in acceleration by the system was
${{\rm{\;}}^2}$
(at Raspet II Laboratory, Starkville, MS) [32], we observed that the prediction error in acceleration by the system was
![]() $0.025{\rm{\% }}$
, which is within the acceptable error range.
$0.025{\rm{\% }}$
, which is within the acceptable error range.

Figure 5. Free-fall tests: (a) height versus time for different drop tests (b) mean acceleration due to gravity and resulting error.
To explore uncertainties in angular rotation, additional testing was conducted using a US-digital optical encoder connected to a dual shaft step-motor and a rotating bar. The motion capture system tracked the movement, measuring an error smaller than 0.28 degrees for a (14.5m × 9.6m) capture volume.
4.1.3 Uncertainty propagation
The root sum square (RSS) method was implemented to measure the uncertainty propagation from the Optitrack outputs (
![]() $x,y,z,\phi, \theta, \psi $
) to the aerodynamic parameters [Reference Barford33]. The standard deviation obtained is Section 4.1.1 are combined as shown in Equation (18), where
$x,y,z,\phi, \theta, \psi $
) to the aerodynamic parameters [Reference Barford33]. The standard deviation obtained is Section 4.1.1 are combined as shown in Equation (18), where
![]() $M$
denotes a general measurement function such that
$M$
denotes a general measurement function such that
![]() $M = f\left( {x,y,z,\phi, \theta, \psi } \right)$
referring to an aerodynamic parameter (
$M = f\left( {x,y,z,\phi, \theta, \psi } \right)$
referring to an aerodynamic parameter (
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
,…).
$\beta $
,…).
 \begin{align}{\sigma _{combined}} = \sqrt {{{\left(\frac{{\partial M}}{{\partial x}}{\sigma _x}\right)}^2} + {{\left(\frac{{\partial M}}{{\partial y}}{\sigma _z}\right)}^2} + {{\left(\frac{{\partial M}}{{\partial z}}{\sigma _z}\right)}^2} + {{\left(\frac{{\partial M}}{{\partial \theta }}{\sigma _\theta }\right)}^2} + {{\left(\frac{{\partial M}}{{\partial \phi }}{\sigma _\phi }\right)}^2} + {{\left(\frac{{\partial M}}{{\partial \psi }}{\sigma _\psi }\right)}^2}} \end{align}
\begin{align}{\sigma _{combined}} = \sqrt {{{\left(\frac{{\partial M}}{{\partial x}}{\sigma _x}\right)}^2} + {{\left(\frac{{\partial M}}{{\partial y}}{\sigma _z}\right)}^2} + {{\left(\frac{{\partial M}}{{\partial z}}{\sigma _z}\right)}^2} + {{\left(\frac{{\partial M}}{{\partial \theta }}{\sigma _\theta }\right)}^2} + {{\left(\frac{{\partial M}}{{\partial \phi }}{\sigma _\phi }\right)}^2} + {{\left(\frac{{\partial M}}{{\partial \psi }}{\sigma _\psi }\right)}^2}} \end{align}
The partial derivatives of the aerodynamic parameters listed in Section 3 were found and the respective propagated uncertainties are listed in Table 3.
Table 3. Aerodynamic parameter uncertainties

4.2 Flight repeatability
To deduce the consistency of the flight path obtained using the rail-launch system described in Section 2.2, the UMX Vapor aircraft was launched using the rail system at a set trim angle. Figures 6(a)–(c) shows the recorded positions for four flights of the UXM Vapor. The tests showed variation along the
![]() $y$
-axis, but little to no variance along the
$y$
-axis, but little to no variance along the
![]() $x$
and
$x$
and
![]() $z$
axes. Drift along the y-axis was attributed to the way the aircraft was hinged on the rail system. The lift and drag coefficients in glide flight were estimated by processing the position and attitude data, and truncating the time history to the area of interest of the flight (Fig. 6(d)–(e)). For the UMX Vapor in glide,
$z$
axes. Drift along the y-axis was attributed to the way the aircraft was hinged on the rail system. The lift and drag coefficients in glide flight were estimated by processing the position and attitude data, and truncating the time history to the area of interest of the flight (Fig. 6(d)–(e)). For the UMX Vapor in glide,
![]() ${C_L}$
ranged from 0.25 to approximately 0.3 and
${C_L}$
ranged from 0.25 to approximately 0.3 and
![]() ${C_D}$
fluctuated around a value of 0.1 in glide flight. While not plotted, similar fluctuations were observed for the other sUAVs as well. As the limits of the deviations in force coefficients during glide flight seen in the current tests were comparable to those observed by Uhlig [Reference Uhlig3], it was concluded that the rail system provided consistent launch characteristics. However, due to difficulties with resetting the rail system after every launch, hand-launched flight data was also used in combination to allow for a larger amount of data to be collected and analysed.
${C_D}$
fluctuated around a value of 0.1 in glide flight. While not plotted, similar fluctuations were observed for the other sUAVs as well. As the limits of the deviations in force coefficients during glide flight seen in the current tests were comparable to those observed by Uhlig [Reference Uhlig3], it was concluded that the rail system provided consistent launch characteristics. However, due to difficulties with resetting the rail system after every launch, hand-launched flight data was also used in combination to allow for a larger amount of data to be collected and analysed.

Figure 6. Flight repeatability tests for the UMX Vapor. Variation in (a)
![]() $x$
, (b)
$x$
, (b)
![]() $y$
, (c)
$y$
, (c)
![]() $z$
, (d)
$z$
, (d)
![]() ${C_L}$
and (e)
${C_L}$
and (e)
![]() ${C_D}$
with time.
${C_D}$
with time.
4.3 Quasi-steady data filtering
Achieving perfect glide flight (and therefore steady flight) for every launch (via the rail-system or hand-launch) can be a very time consuming and cumbersome process. Therefore, quasi-steady flight data was considered to study glide flight to enable larger data sets for analysis. Figure 7(a) shows the drag polars obtained for 24 flights of the UMX Vapor at different elevator deflections (in black), and therefore different trim angles. When considering the full flight trajectories, coefficients of lift and drag were observed to go as high as
![]() $2.5$
and
$2.5$
and
![]() $2$
respectively due to unsteady effects and aggressive stalls. In an effort to filter the data such that the unsteady effects are negligible, low angular rate (LAR) conditions were applied to the cumulative dataset. Based on the available literature [Reference Uhlig3, Reference Rao, Uhlig and Selig12, Reference Selig13], the conditions needed for LAR were
$2$
respectively due to unsteady effects and aggressive stalls. In an effort to filter the data such that the unsteady effects are negligible, low angular rate (LAR) conditions were applied to the cumulative dataset. Based on the available literature [Reference Uhlig3, Reference Rao, Uhlig and Selig12, Reference Selig13], the conditions needed for LAR were
![]() $\dot \alpha \lt 20$
deg/s and
$\dot \alpha \lt 20$
deg/s and
![]() $\dot \beta, p,q,r \lt 30$
deg/s. Additionally, the sampled data was restricted to lift coefficients values below stall. On applying the data filter based on LAR and
$\dot \beta, p,q,r \lt 30$
deg/s. Additionally, the sampled data was restricted to lift coefficients values below stall. On applying the data filter based on LAR and
![]() ${C_L}$
limits to the UMX Vapor data shown in Fig. 7(a), quasi-steady flight data was obtained (red markers). On evaluating the reduced frequency (
${C_L}$
limits to the UMX Vapor data shown in Fig. 7(a), quasi-steady flight data was obtained (red markers). On evaluating the reduced frequency (
![]() $k$
) for the quasi-steady data, we see that the filtered data was within (
$k$
) for the quasi-steady data, we see that the filtered data was within (
![]() $k$
) limits of
$k$
) limits of
![]() $ \pm 0.03$
. As quasi-steady flight can be considered as long as
$ \pm 0.03$
. As quasi-steady flight can be considered as long as
![]() $\left| k \right| \lt 0.05$
[Reference Uhlig and Selig14, Reference Cooper and Wright34], the above data filtering scheme has been used for the remainder of the analysis to study glide-flight aerodynamics of the sUAVs.
$\left| k \right| \lt 0.05$
[Reference Uhlig and Selig14, Reference Cooper and Wright34], the above data filtering scheme has been used for the remainder of the analysis to study glide-flight aerodynamics of the sUAVs.

Figure 7. (a) Full lift and drag data co-plotted with sampled LAR data (b) reduced frequency as a function of
![]() $\alpha $
.
$\alpha $
.
Figure 8 plots the experimentally measured lift coefficient,
![]() ${C_L}$
, for the entire sUAV alongside the augmented lift coefficient due to unsteady effects, represented by
${C_L}$
, for the entire sUAV alongside the augmented lift coefficient due to unsteady effects, represented by
![]() ${\rm{\Delta }}{C_{L,k}} = {C_{{L_\alpha }}}k\left( {\frac{1}{2} - a} \right)$
, where
${\rm{\Delta }}{C_{L,k}} = {C_{{L_\alpha }}}k\left( {\frac{1}{2} - a} \right)$
, where
![]() $a$
was assumed to be
$a$
was assumed to be
![]() $ - $
0.5 at the quarter chord. Observations show that the constraints on the angular rates eliminated unsteady flights and any possible uncertainties in the data due to un-modelled unsteady effects. The scatter observed in the data is expected and can be attributed to, but not solely limited to, time lag effects and laminar separation bubbles. However, despite this variability, linear stability derivatives such as
$ - $
0.5 at the quarter chord. Observations show that the constraints on the angular rates eliminated unsteady flights and any possible uncertainties in the data due to un-modelled unsteady effects. The scatter observed in the data is expected and can be attributed to, but not solely limited to, time lag effects and laminar separation bubbles. However, despite this variability, linear stability derivatives such as
![]() ${C_{{L_\alpha }}}$
exhibited consistent trends due to their inherent robustness, similar to observations made by Rinehart and Mettler [Reference Rhinehart and Mettler10]. These trends are further discussed in the following section.
${C_{{L_\alpha }}}$
exhibited consistent trends due to their inherent robustness, similar to observations made by Rinehart and Mettler [Reference Rhinehart and Mettler10]. These trends are further discussed in the following section.

Figure 8. Comparison between experimentally measured
![]() ${C_L}$
and augmented
${C_L}$
and augmented
![]() ${C_L}$
due to unsteady effects.
${C_L}$
due to unsteady effects.
5.0 Results and discussion
5.1 Flight data
The current section presents the flight data for the sUAVs tested. For the sake of brevity, detailed discussion is presented for three sUAVs: the F4U-Corsair, TR-C285G and UXM Vapor, as these were observed to best represent the corner cases. Flight data for the remainder three sUAVs have been presented in the Appendix.
5.1.1 F4U-Corsair
Flight data for the F4U-Corsair (
![]() $AR = 5.68$
) sUAV was collected over 192 flights, with each flight generating approximately 200 data points. Velocity data showed that the wing chord-based Reynolds number varied between 15,000–40,000. On applying the LAR and
$AR = 5.68$
) sUAV was collected over 192 flights, with each flight generating approximately 200 data points. Velocity data showed that the wing chord-based Reynolds number varied between 15,000–40,000. On applying the LAR and
![]() ${C_L}$
limit conditions, quasi-steady (a) drag polar, (b) lift curve, (c) drag curve and (d) pitching moment were measured and have been plotted in Fig. 9. The Oswald efficiency factor (
${C_L}$
limit conditions, quasi-steady (a) drag polar, (b) lift curve, (c) drag curve and (d) pitching moment were measured and have been plotted in Fig. 9. The Oswald efficiency factor (
![]() ${e_o}$
) for the F4U-Corsair was calculated to be
${e_o}$
) for the F4U-Corsair was calculated to be
![]() $0.31$
based on the the parabolic fit
$0.31$
based on the the parabolic fit
![]() ${C_D} = 0.073 + 0.18C_L^2$
(co-plotted in Fig. 9(a)). This
${C_D} = 0.073 + 0.18C_L^2$
(co-plotted in Fig. 9(a)). This
![]() ${e_0}$
value, while much lower than that for conventional aircraft (typically
${e_0}$
value, while much lower than that for conventional aircraft (typically
![]() $0.7 - 0.85$
), was comparable in magnitude to measurements made by Spedding and McArthur [Reference Spedding and McArthur23], who observed an
$0.7 - 0.85$
), was comparable in magnitude to measurements made by Spedding and McArthur [Reference Spedding and McArthur23], who observed an
![]() ${e_o}$
of
${e_o}$
of
![]() $0.53$
for an aspect ratio
$0.53$
for an aspect ratio
![]() $6$
wing with an Eppler 387 aerofoil section operating in a
$6$
wing with an Eppler 387 aerofoil section operating in a
![]() $Re = 20,000$
flow. Spedding and McArthur [Reference Spedding and McArthur23] attributed the reduced values of
$Re = 20,000$
flow. Spedding and McArthur [Reference Spedding and McArthur23] attributed the reduced values of
![]() ${e_o}$
to low Reynolds number effects.
${e_o}$
to low Reynolds number effects.

Figure 9. Flight data for the F4U-Corsair (![]()
![]() $= 5.68$
): (a) experimental drag polar with parabolic fit, (b) experimental lift curve with linear regression, (c) experimental drag curve with quadratic regression and (d) experimental pitching moment with linear regression.
$= 5.68$
): (a) experimental drag polar with parabolic fit, (b) experimental lift curve with linear regression, (c) experimental drag curve with quadratic regression and (d) experimental pitching moment with linear regression.
First order linear regression was applied to the
![]() ${C_L}$
vs.
${C_L}$
vs.
![]() $\alpha $
data to obtain the lift curve for the full aircraft (Fig. 9(b)). Additionally, the lift curves for the wing and tail surfaces were isolated by using equations,
$\alpha $
data to obtain the lift curve for the full aircraft (Fig. 9(b)). Additionally, the lift curves for the wing and tail surfaces were isolated by using equations,
and have been co-plotted in Fig. 9(b). While
![]() ${C_L}$
and
${C_L}$
and
![]() ${C_{{M_{cg}}}}$
were calculated using the position and attitude measurements from the motion capture system, the pitching moment coefficient,
${C_{{M_{cg}}}}$
were calculated using the position and attitude measurements from the motion capture system, the pitching moment coefficient,
![]() ${C_{{M_{ac,w}}}}$
, for the isolated wing was determined to be
${C_{{M_{ac,w}}}}$
, for the isolated wing was determined to be
![]() $ - $
0.17 using XFLR5. The values of
$ - $
0.17 using XFLR5. The values of
![]() ${C_{{M_{ac,w}}}}$
were observed to vary between
${C_{{M_{ac,w}}}}$
were observed to vary between
![]() $ - 0.04$
and
$ - 0.04$
and
![]() $ - 0.3$
throughout the Reynolds number flight envelope of the F4U-Corsair over an angle-of-attack range from -5 degrees to 20 degrees. The dynamic pressure ratio (
$ - 0.3$
throughout the Reynolds number flight envelope of the F4U-Corsair over an angle-of-attack range from -5 degrees to 20 degrees. The dynamic pressure ratio (
![]() ${\eta _h}$
) was assumed to be 0.9, based on Ref. (Reference Uhlig3). The aerodynamic chord of the wing and horizontal tail (
${\eta _h}$
) was assumed to be 0.9, based on Ref. (Reference Uhlig3). The aerodynamic chord of the wing and horizontal tail (
![]() ${\bar x_{ac,w}},{\bar x_{ac,h}}$
) were approximated to be
${\bar x_{ac,w}},{\bar x_{ac,h}}$
) were approximated to be
![]() $25{\rm{\% }}$
and the CG location was measured using a point balance. The lift curve slopes for the full aircraft as well as the isolated wing were determined to be
$25{\rm{\% }}$
and the CG location was measured using a point balance. The lift curve slopes for the full aircraft as well as the isolated wing were determined to be
![]() $2.88$
and
$2.88$
and
![]() $2.38/{\rm{rad}}$
, respectively. Lifting-line theory, on the other hand, predicted a lift-slope of
$2.38/{\rm{rad}}$
, respectively. Lifting-line theory, on the other hand, predicted a lift-slope of
![]() $4.64/{\rm{rad}}$
. This significant over prediction (
$4.64/{\rm{rad}}$
. This significant over prediction (
![]() $\sim 51.28{\rm{\% }}$
with respect to the isolated wing) in the lift curve slope by theory was not only attributed to low-
$\sim 51.28{\rm{\% }}$
with respect to the isolated wing) in the lift curve slope by theory was not only attributed to low-
![]() $Re$
effects but also the fact that the F4U-Corsair’s wing loading cannot be approximated by an ideal elliptical distribution due to its taper and dihedral. Furthermore, investigations by Uhlig [Reference Uhlig3] showed that, for a similar sUAV of equal wingspan and slightly lower
$Re$
effects but also the fact that the F4U-Corsair’s wing loading cannot be approximated by an ideal elliptical distribution due to its taper and dihedral. Furthermore, investigations by Uhlig [Reference Uhlig3] showed that, for a similar sUAV of equal wingspan and slightly lower ![]() of 5.12 in glide flight, a
of 5.12 in glide flight, a
![]() $27.27{\rm{\% }}$
over-prediction by theory was reported when compared to measurements, for an operating Reynolds number of
$27.27{\rm{\% }}$
over-prediction by theory was reported when compared to measurements, for an operating Reynolds number of
![]() $\sim 26,000$
.
$\sim 26,000$
.
In an attempt to further validate the measurements, the experimental
![]() ${C_L}$
vs.
${C_L}$
vs.
![]() $\alpha $
data was compared with viscous results from XFOIL using the aerofoil section of the F4U-Corsair. The assumptions made for this analysis were (i) all the lift is being generated by the wing and (ii) the wing is assumed to be rectangular with no taper or dihedral. The sectional wing coordinates were physically extracted from two different sections along the wing span – wing root (S1) and
$\alpha $
data was compared with viscous results from XFOIL using the aerofoil section of the F4U-Corsair. The assumptions made for this analysis were (i) all the lift is being generated by the wing and (ii) the wing is assumed to be rectangular with no taper or dihedral. The sectional wing coordinates were physically extracted from two different sections along the wing span – wing root (S1) and
![]() $75{\rm{\% }}$
span (S2), as shown in Fig. 10(a). Upon non-dimensionalising the coordinates, we concluded that the same aerofoil section was used for the entire wing section (Fig. 10(b)). A final, clean aerofoil profile was generated using the extracted sectional coordinates and analysed in XFOIL for a
$75{\rm{\% }}$
span (S2), as shown in Fig. 10(a). Upon non-dimensionalising the coordinates, we concluded that the same aerofoil section was used for the entire wing section (Fig. 10(b)). A final, clean aerofoil profile was generated using the extracted sectional coordinates and analysed in XFOIL for a
![]() $Re$
range of
$Re$
range of
![]() $15,000 - 40,000$
. The full aircraft
$15,000 - 40,000$
. The full aircraft
![]() ${C_L}$
versus
${C_L}$
versus
![]() $\alpha $
was then calculated by determining the glide angle-of-attack at the
$\alpha $
was then calculated by determining the glide angle-of-attack at the
![]() $Re\sqrt {{C_L}} $
value for the F4U-Corsair in glide (Fig. 10(c)), which equated to a value of
$Re\sqrt {{C_L}} $
value for the F4U-Corsair in glide (Fig. 10(c)), which equated to a value of
![]() $1.8 \times {10^4}$
. The glide
$1.8 \times {10^4}$
. The glide
![]() ${C_L}$
was then determined from XFOIL data for the corresponding
${C_L}$
was then determined from XFOIL data for the corresponding
![]() $Re - {\alpha _{glide}}$
combination. When co-plotted with the experimental results (Fig. 9(b)), we see that the first-order fit for the isolated wing obtained from the flight data compares well for angles of attack above 5 degrees. The mismatch at lower angles of attack can be attributed to the lack of sufficient flight data at said conditions. Overall, the XFOIL analysis helped ascertain that the lift measurements made by the motion capture system as well as the trends predicted were logical and in line with what should be expected.
$Re - {\alpha _{glide}}$
combination. When co-plotted with the experimental results (Fig. 9(b)), we see that the first-order fit for the isolated wing obtained from the flight data compares well for angles of attack above 5 degrees. The mismatch at lower angles of attack can be attributed to the lack of sufficient flight data at said conditions. Overall, the XFOIL analysis helped ascertain that the lift measurements made by the motion capture system as well as the trends predicted were logical and in line with what should be expected.

Figure 10. Wing sectional coordinates and XFOIL analysis: (a) extracted coordinates, (b) aerofoil generated for analysis and (c)
![]() $Re\sqrt {{C_L}} $
for the operating Reynolds number range.
$Re\sqrt {{C_L}} $
for the operating Reynolds number range.
Second-order quadratic and first-order linear regressions were applied to the drag (Fig. 9(c)) and the pitching-moment (Fig. 9(d)) data, respectively. Both metrics showed similar trends when compared to flight data for a comparable aircraft (SU-26XP, ![]()
![]() $ = 5.12$
) investigated by Uhlig [Reference Uhlig3].
$ = 5.12$
) investigated by Uhlig [Reference Uhlig3].
5.1.2 TR-C285G
To gain deeper insights into the impact of low Reynolds numbers and confirm the patterns observed for the F4U-Corsair (Section 5.1.1), the TR-C285G model was selected for analysis. This particular model features a simplified wing design, closely resembling a rectangular wing with no dihedral effects and a moderate taper ratio. Additionally, the TR-C285G has an aspect ratio of 6.05, which closely aligns with the aspect ratio of the F4U-Corsair (![]()
![]() $ = 5.68$
). Flight data was obtained across 70 flights and 14 trim angles. Velocity data showed the wing chord-based Reynolds number varying between 20,000–40,000. Figure 11 plots the (a) drag polar, (b) lift curve, (c) drag curve, and (d) pitching moment for the TR-C285G aircraft. Additionally, Fig. 11(a) plots the drag polar obtained for a second set of flight tests conducted independently of the initial flight tests in order to examine measurement repeatability. The resulting parabolic fits for both flight data sets were
$ = 5.68$
). Flight data was obtained across 70 flights and 14 trim angles. Velocity data showed the wing chord-based Reynolds number varying between 20,000–40,000. Figure 11 plots the (a) drag polar, (b) lift curve, (c) drag curve, and (d) pitching moment for the TR-C285G aircraft. Additionally, Fig. 11(a) plots the drag polar obtained for a second set of flight tests conducted independently of the initial flight tests in order to examine measurement repeatability. The resulting parabolic fits for both flight data sets were
![]() ${C_D} = 0.08 + 0.17C_L^2$
and and
${C_D} = 0.08 + 0.17C_L^2$
and and
![]() ${C_{{D_2}}} = 0.083 + 0.172C_L^2$
, respectively. The attendant Oswald efficiency factors for the two data sets were calculated to be
${C_{{D_2}}} = 0.083 + 0.172C_L^2$
, respectively. The attendant Oswald efficiency factors for the two data sets were calculated to be
![]() $0.309$
and
$0.309$
and
![]() $0.305$
, respectively, thereby showing that the motion capture system was capturing flight data across the full operating regime in a repeatable manner. The slight reduction in
$0.305$
, respectively, thereby showing that the motion capture system was capturing flight data across the full operating regime in a repeatable manner. The slight reduction in
![]() ${e_o}$
for the TR-C285G aircraft when compared to the F4-U Corsair’s 0.31 can be attributed to the marginally higher
${e_o}$
for the TR-C285G aircraft when compared to the F4-U Corsair’s 0.31 can be attributed to the marginally higher ![]() . This deduction was confirmed by conclusions made by Ananda et al. [Reference Ananda, Sukumar and Selig27] who, while conducting experiments on wings with different aspect ratios, observed a reduction in the Oswald efficiency factor with increasing
. This deduction was confirmed by conclusions made by Ananda et al. [Reference Ananda, Sukumar and Selig27] who, while conducting experiments on wings with different aspect ratios, observed a reduction in the Oswald efficiency factor with increasing ![]() at low Reynolds numbers. Analysis of the experimental lift curve of the TR-C285G also showed similar trends to those observed for the F4U-Corsair, with the slope from the first order regression of the isolated wing equating to
at low Reynolds numbers. Analysis of the experimental lift curve of the TR-C285G also showed similar trends to those observed for the F4U-Corsair, with the slope from the first order regression of the isolated wing equating to
![]() $2.2/{\rm{rad}}$
(compared to
$2.2/{\rm{rad}}$
(compared to
![]() $2.38/{\rm{rad}}$
for the F4U-Corsair). Additionally, similar to the F4U-Corsair, the lift curve slope was measured to be
$2.38/{\rm{rad}}$
for the F4U-Corsair). Additionally, similar to the F4U-Corsair, the lift curve slope was measured to be
![]() $\sim 46.61{\rm{\% }}$
lower than that predicted by lifting-line theory (
$\sim 46.61{\rm{\% }}$
lower than that predicted by lifting-line theory (
![]() ${C_{L\alpha }}$
, lifting-line =
${C_{L\alpha }}$
, lifting-line =
![]() $4.72/{\rm{rad}}$
), and could once again be attributed to low-
$4.72/{\rm{rad}}$
), and could once again be attributed to low-
![]() $Re$
effects. Overall, trends in the aerodynamic flight data for the TR-C285G matched well with that of the F4U-Corsair, thereby giving further credence to the ability of the motion capture system to effectively measure sUAV aerodynamics.
$Re$
effects. Overall, trends in the aerodynamic flight data for the TR-C285G matched well with that of the F4U-Corsair, thereby giving further credence to the ability of the motion capture system to effectively measure sUAV aerodynamics.

Figure 11. Flight data for the TR-C285G (![]()
![]() $ = 6.05$
): (a) experimental drag polar with parabolic fit, (b) experimental lift curve with linear regression, (c) experimental drag curve with quadratic regression and (d) experimental pitching moment with linear regression.
$ = 6.05$
): (a) experimental drag polar with parabolic fit, (b) experimental lift curve with linear regression, (c) experimental drag curve with quadratic regression and (d) experimental pitching moment with linear regression.
5.1.3 UMX Vapor
To test the quality of flight data measured and the low-
![]() $Re$
effects for low-
$Re$
effects for low- ![]() aircraft, the aerodynamic performance for the UMX Vapor (
aircraft, the aerodynamic performance for the UMX Vapor (![]()
![]() $ = 2.56$
) was investigated. Data across a total of 24 flights at different trim angles/elevator deflections was processed and filtered to obtain the force and moment coefficient characteristics of the UMX Vapor. Figure 12 shows the experimentally computed (a) drag polar, (b) lift curve, (c) drag curve and (d) pitching moment for the UMX Vapor based on the sampled LAR and the corresponding first/second order least square regression fits. An additional, independently measured flight data set was also analysed to ascertain measurement repeatability.
$ = 2.56$
) was investigated. Data across a total of 24 flights at different trim angles/elevator deflections was processed and filtered to obtain the force and moment coefficient characteristics of the UMX Vapor. Figure 12 shows the experimentally computed (a) drag polar, (b) lift curve, (c) drag curve and (d) pitching moment for the UMX Vapor based on the sampled LAR and the corresponding first/second order least square regression fits. An additional, independently measured flight data set was also analysed to ascertain measurement repeatability.

Figure 12. Flight data for the UXM Vapor (![]()
![]() $ = 2.56$
): (a) experimental drag polar with parabolic fit, (b) experimental lift curve with linear regression, (c) experimental drag curve with quadratic regression and (d) experimental pitching moment with linear regression.
$ = 2.56$
): (a) experimental drag polar with parabolic fit, (b) experimental lift curve with linear regression, (c) experimental drag curve with quadratic regression and (d) experimental pitching moment with linear regression.
The parabolic fits computed for the drag polars of the two flight data sets (Fig. 12(a)) yielded Oswald efficiency factors of
![]() $0.71$
and
$0.71$
and
![]() $0.72$
, respectively. While much higher than the values obtained for the higher
$0.72$
, respectively. While much higher than the values obtained for the higher ![]() sUAVs (
sUAVs (
![]() $0.3113$
for the F4U-Corsair and
$0.3113$
for the F4U-Corsair and
![]() $0.307$
for the TR-C285G aircraft), the magnitude of the measured
$0.307$
for the TR-C285G aircraft), the magnitude of the measured
![]() ${e_o}$
for the UMX Vapor are in line with observations made by Ananda et al. [Reference Ananda, Sukumar and Selig27], who reported an Oswald efficiency factor of
${e_o}$
for the UMX Vapor are in line with observations made by Ananda et al. [Reference Ananda, Sukumar and Selig27], who reported an Oswald efficiency factor of
![]() $\sim 0.81$
for an
$\sim 0.81$
for an ![]()
![]() $ = 2$
flat-plate wings at low Reynolds numbers (
$ = 2$
flat-plate wings at low Reynolds numbers (
![]() $60,000 \le Re \le 200,000$
). Calculation of the lift curve slope from the first-order regression curve yielded a value of
$60,000 \le Re \le 200,000$
). Calculation of the lift curve slope from the first-order regression curve yielded a value of
![]() $3.29/{\rm{rad}}$
, which compared very well with the lifting-line theory prediction of
$3.29/{\rm{rad}}$
, which compared very well with the lifting-line theory prediction of
![]() $3.53/{\rm{rad}}$
. This is in contrast to the observations made for the F4U-Corsair and TR-C285G aircraft, and could be attributed to the UMX Vapor’s flat-plate, elliptically loaded wing. A detailed analysis on the trends observed and the contrasting results between the sUAVs tested is presented in the following section (Section 5.2). However, it should be noted that the overall trends in the aerodynamic data obtained for the UMX Vapor are in close agreement with results obtained by Uhlig [Reference Uhlig3] for the exact aircraft with the only difference being in the wing camber (symmetric wing in the current study versus a cambered wing in Ref. (Reference Uhlig3)). Consequently, a difference of
$3.53/{\rm{rad}}$
. This is in contrast to the observations made for the F4U-Corsair and TR-C285G aircraft, and could be attributed to the UMX Vapor’s flat-plate, elliptically loaded wing. A detailed analysis on the trends observed and the contrasting results between the sUAVs tested is presented in the following section (Section 5.2). However, it should be noted that the overall trends in the aerodynamic data obtained for the UMX Vapor are in close agreement with results obtained by Uhlig [Reference Uhlig3] for the exact aircraft with the only difference being in the wing camber (symmetric wing in the current study versus a cambered wing in Ref. (Reference Uhlig3)). Consequently, a difference of
![]() $32.39{\rm{\% }}$
and
$32.39{\rm{\% }}$
and
![]() $36.39{\rm{\% }}$
in
$36.39{\rm{\% }}$
in
![]() ${e_o}$
and
${e_o}$
and
![]() ${C_{L\alpha }}$
were observed between the current measurements and Ref. (Reference Uhlig3).
${C_{L\alpha }}$
were observed between the current measurements and Ref. (Reference Uhlig3).
5.2 Efficiency analysis
To gain deeper insights into the effects of low Reynolds numbers on sUAV aerodynamics, trends in Oswald efficiency factors and lift-curve slopes with aspect ratio and Reynolds number for all six aircraft (
![]() $2.56 \le$
$2.56 \le$
![]()
![]() $ \le 6.30 $
) are plotted (in Fig. 13) and analysed.
$ \le 6.30 $
) are plotted (in Fig. 13) and analysed.

Figure 13. (a) Oswald efficiency
![]() ${e_0}$
factor with respect to aspect ratio
${e_0}$
factor with respect to aspect ratio ![]() compared to literature, (b) Oswald efficiency
compared to literature, (b) Oswald efficiency
![]() ${e_0}$
factor with respect Reynolds number
${e_0}$
factor with respect Reynolds number
![]() $Re$
compared to literature (c) Lift curve slope
$Re$
compared to literature (c) Lift curve slope
![]() ${C_{{L_\alpha }}}$
with respect to aspect ratio
${C_{{L_\alpha }}}$
with respect to aspect ratio ![]() compared to theory.
compared to theory.
Figure 13(a) plots the Oswald efficiency factor (
![]() ${e_0}$
) obtained from the drag polar for each sUAV with respect to
${e_0}$
) obtained from the drag polar for each sUAV with respect to ![]() and compares it with results obtained by Ananda et al. [Reference Ananda, Sukumar and Selig27] for flat-plate wings. It is noted that the reference data has been obtained at
and compares it with results obtained by Ananda et al. [Reference Ananda, Sukumar and Selig27] for flat-plate wings. It is noted that the reference data has been obtained at
![]() $Re = 60,000$
while the Reynolds number range for the aircraft tested is lower and varies between
$Re = 60,000$
while the Reynolds number range for the aircraft tested is lower and varies between
![]() $10,000$
to
$10,000$
to
![]() $50,000$
. However, both data sets are firmly in the low-
$50,000$
. However, both data sets are firmly in the low-
![]() $Re$
regime, therefore allowing us to verify the current measured trends and make appropriate deductions. Results obtained from the six sUAVs show that increasing the aspect ratio leads to a decrease in
$Re$
regime, therefore allowing us to verify the current measured trends and make appropriate deductions. Results obtained from the six sUAVs show that increasing the aspect ratio leads to a decrease in
![]() ${e_0}$
, therefore adhering to the trends observed by Ananda et al. [Reference Ananda, Sukumar and Selig27]. However, while the magnitude of
${e_0}$
, therefore adhering to the trends observed by Ananda et al. [Reference Ananda, Sukumar and Selig27]. However, while the magnitude of
![]() ${e_0}$
for the sUAVs with
${e_0}$
for the sUAVs with ![]()
![]() $\gt 4$
align with those measured by Ananda et al. [Reference Ananda, Sukumar and Selig27], it is over predicted for
$\gt 4$
align with those measured by Ananda et al. [Reference Ananda, Sukumar and Selig27], it is over predicted for ![]()
![]() $ \lt 4$
. This could be attributed to the much lower operating Reynolds number range of the Vapor and Stick aircraft (
$ \lt 4$
. This could be attributed to the much lower operating Reynolds number range of the Vapor and Stick aircraft (
![]() $10,000 \lt Re \lt 25,000$
). Next, we compare the variation of
$10,000 \lt Re \lt 25,000$
). Next, we compare the variation of
![]() ${e_0}$
with
${e_0}$
with
![]() $Re$
against experimental results for flat plates with
$Re$
against experimental results for flat plates with ![]() ranging from 2 to 5 [Reference Ananda, Sukumar and Selig27] and an Eppler 387 wing with
ranging from 2 to 5 [Reference Ananda, Sukumar and Selig27] and an Eppler 387 wing with ![]()
![]() $ = 6$
[Reference Spedding and McArthur23] in Fig. 13(b). Observations show that the
$ = 6$
[Reference Spedding and McArthur23] in Fig. 13(b). Observations show that the
![]() ${e_0}$
measured for all aircraft with
${e_0}$
measured for all aircraft with ![]()
![]() $ \gt 4$
and operating at
$ \gt 4$
and operating at
![]() $Re \gt 20,000$
matches well with Spedding and McArthur [Reference Spedding and McArthur23]. However, a sharp increase in
$Re \gt 20,000$
matches well with Spedding and McArthur [Reference Spedding and McArthur23]. However, a sharp increase in
![]() ${e_0}$
is observed for the Vapor and Stick aircraft (
${e_0}$
is observed for the Vapor and Stick aircraft (![]()
![]() $ \lt 4$
). Based on the above behaviour, it can be concluded that, while, in general, an increase in
$ \lt 4$
). Based on the above behaviour, it can be concluded that, while, in general, an increase in ![]() leads to a decrease in
leads to a decrease in
![]() ${e_0}$
during low-
${e_0}$
during low-
![]() $Re$
operations, the magnitude of the drop in
$Re$
operations, the magnitude of the drop in
![]() ${e_0}$
increases with decreasing
${e_0}$
increases with decreasing
![]() $Re$
.
$Re$
.
Lift-curve slope results show a decreasing trend with increasing ![]() (Fig. 13(c)). Additionally, on comparing the results with analytical predictions from lifting-line theory and Hembold equation, we observe that, barring the lift-curve slope of the Vapor, analytical methods overpredict
(Fig. 13(c)). Additionally, on comparing the results with analytical predictions from lifting-line theory and Hembold equation, we observe that, barring the lift-curve slope of the Vapor, analytical methods overpredict
![]() ${C_{{L_\alpha }}}$
for wings operating at low Reynolds numbers. To understand the reason as to why the analytical methods predict the
${C_{{L_\alpha }}}$
for wings operating at low Reynolds numbers. To understand the reason as to why the analytical methods predict the
![]() ${C_{{L_\alpha }}}$
with reasonable accuracy, despite the Vapor being affected by low-
${C_{{L_\alpha }}}$
with reasonable accuracy, despite the Vapor being affected by low-
![]() $Re$
effects, we refer to the experiments conducted by Torres et al. [Reference Torres and Mueller28] on flat plates with aspect ratios below 3. They observed a lift curve slope of 0.056 per degree at
$Re$
effects, we refer to the experiments conducted by Torres et al. [Reference Torres and Mueller28] on flat plates with aspect ratios below 3. They observed a lift curve slope of 0.056 per degree at ![]() for an elliptically loaded wing, which matches with the current data for the Vapor sUAV which has an elliptical flat wing with an aspect ratio of 2.56 and exhibits a lift curve slope of
for an elliptically loaded wing, which matches with the current data for the Vapor sUAV which has an elliptical flat wing with an aspect ratio of 2.56 and exhibits a lift curve slope of
![]() $0.0574$
per degree. Furthermore, Torres et al. [Reference Torres and Mueller28] concluded that, within the range of aspect ratios they tested, efficiency factors ranging from 0.5 to 0.8 were consistent with the expressions derived from lifting line theory for an elliptically loaded wing, thereby confirming the results observed in Fig. 13(a) for the Vapor. Similarly, in a study conducted by Okamoto and Azuma [Reference Okamoto and Azuma35], elliptical wings with aspect ratios ranging from 1 to 8 were investigated. Their study reported a lift curve slope of
$0.0574$
per degree. Furthermore, Torres et al. [Reference Torres and Mueller28] concluded that, within the range of aspect ratios they tested, efficiency factors ranging from 0.5 to 0.8 were consistent with the expressions derived from lifting line theory for an elliptically loaded wing, thereby confirming the results observed in Fig. 13(a) for the Vapor. Similarly, in a study conducted by Okamoto and Azuma [Reference Okamoto and Azuma35], elliptical wings with aspect ratios ranging from 1 to 8 were investigated. Their study reported a lift curve slope of
![]() $0.043$
per degree for a wing with an aspect ratio of
$0.043$
per degree for a wing with an aspect ratio of ![]() . For the other five sUAVs, which had non-elliptical wings, the deviation in
. For the other five sUAVs, which had non-elliptical wings, the deviation in
![]() ${C_{{L_\alpha }}}$
from analytical predictions were in line with observations made by Spedding and McArthur [Reference Spedding and McArthur23], who attributed the limitations of the analytical predictions to their inability to account for low-
${C_{{L_\alpha }}}$
from analytical predictions were in line with observations made by Spedding and McArthur [Reference Spedding and McArthur23], who attributed the limitations of the analytical predictions to their inability to account for low-
![]() $Re$
effects. While Spedding and McArthur [Reference Spedding and McArthur23] introduced a correction factor to the theory, a high-level of uncertainty in the applicability of said correction was acknowledged.
$Re$
effects. While Spedding and McArthur [Reference Spedding and McArthur23] introduced a correction factor to the theory, a high-level of uncertainty in the applicability of said correction was acknowledged.
5.3 Stability analysis
Understanding the factors that affect the stability of sUAVs holds immense value in their design and operation [Reference Uhlig3]. Stability refers to the ability of an sUAV to maintain a balanced and controlled flight, resisting deviations from its intended trajectory, and effectively countering external disturbances. The current analysis focuses on evaluating the longitudinal stability, lateral stability and phugoid mode characteristics of the sUAVs and the attendant ability of the motion capture system to provide insights into their inherent stability, dynamic response and oscillatory behaviour. While all six sUAVs are considered for the phugoid mode analysis, only the TR-C285G and F4U-Corsair aircraft are used for the lateral and longitudinal stability analysis due to the availability of their respective wing cross-sectional geometry and attendant aerodynamic forces and moments (using XFOIL).
5.3.1 Longitudinal stability
Longitudinal stability pertains to the capability of an aircraft to retain control over its pitch axis and regain its original trim angle-of-attack when subjected to disturbances. To achieve longitudinal stability, several factors come into play including the positioning and design of the aircraft’s wings, horizontal stabiliser and elevator. The wing generates lift while the horizontal stabiliser and elevator work together to create forces that counteract any deviations in pitch and restore stability. Additionally, longitudinal stability is intricately tied to the neutral point, which is fundamentally associated with the aircraft’s CG. The neutral point denotes a specific position on the aircraft’s longitudinal axis where alterations in lift forces exert minimal influence on the pitching moment experienced by the aircraft. When the CG is positioned ahead of the neutral point the aircraft typically exhibits longitudinal stability. In such a configuration, if the aircraft encounters a nose-up disturbance the increased lift generated by the wings creates a pitching moment that counteracts the disturbance, assisting the aircraft in returning to its original trim angle. Conversely, when the CG is located aft of the neutral point, the aircraft tends to be longitudinally unstable. In this scenario, a nose-up disturbance prompts the aircraft to generate a pitching moment that magnifies the disturbance, resulting in a greater deviation from the trim angle. When a precise angle,
![]() ${\delta _e}$
, is applied to the elevator deflection, it causes the aircraft to experience a shift in its pitch attitude, resulting in a noticeable pitch-up or pitch-down motion. This alteration in elevator deflection influences the distribution of lift across the wings, which in turn affects the overall pitching moment coefficient (
${\delta _e}$
, is applied to the elevator deflection, it causes the aircraft to experience a shift in its pitch attitude, resulting in a noticeable pitch-up or pitch-down motion. This alteration in elevator deflection influences the distribution of lift across the wings, which in turn affects the overall pitching moment coefficient (
![]() ${C_{{M_\alpha }}}$
) generated by the aircraft. Consequently, these changes in the pitching moment coefficient impact the position of the neutral point.
${C_{{M_\alpha }}}$
) generated by the aircraft. Consequently, these changes in the pitching moment coefficient impact the position of the neutral point.
The aircraft’s trim angle-of-attack can be determined through the analysis of the slope
![]() ${C_{{M_\alpha }}}$
, where
${C_{{M_\alpha }}}$
, where
![]() ${\alpha _{trim}}$
is the angle-of-attack corresponding to
${\alpha _{trim}}$
is the angle-of-attack corresponding to
![]() ${C_M} = 0$
for each individual elevator deflection angle. The neutral point is then calculated by,
${C_M} = 0$
for each individual elevator deflection angle. The neutral point is then calculated by,
 \begin{align}{X_{np}} = \frac{{{C_{{L_{\alpha, w}}}}{{\bar x}_{ac,w}} + {C_{{L_{\alpha, h}}}}{{\bar x}_{ac,h}}{\eta _h}\frac{{{S_h}}}{{{S_{ref}}}}\left( {1 - \frac{{\partial \varepsilon }}{{\partial \alpha }}} \right)}}{{{C_{{L_{\alpha, w}}}} + {C_{{L_{\alpha, h}}}}{\eta _h}\frac{{{S_h}}}{{{S_{ref}}}}\left( {1 - \frac{{\partial \varepsilon }}{{\partial \alpha }}} \right)}}\end{align}
\begin{align}{X_{np}} = \frac{{{C_{{L_{\alpha, w}}}}{{\bar x}_{ac,w}} + {C_{{L_{\alpha, h}}}}{{\bar x}_{ac,h}}{\eta _h}\frac{{{S_h}}}{{{S_{ref}}}}\left( {1 - \frac{{\partial \varepsilon }}{{\partial \alpha }}} \right)}}{{{C_{{L_{\alpha, w}}}} + {C_{{L_{\alpha, h}}}}{\eta _h}\frac{{{S_h}}}{{{S_{ref}}}}\left( {1 - \frac{{\partial \varepsilon }}{{\partial \alpha }}} \right)}}\end{align}
where the subscripts
![]() $w$
and
$w$
and
![]() $h$
represent wing and horizontal tail respectively.
$h$
represent wing and horizontal tail respectively.
![]() $\bar{x}_{ac}$
is the aerodynamic centre, and was assumed to be at 25% chord.
$\bar{x}_{ac}$
is the aerodynamic centre, and was assumed to be at 25% chord.
![]() ${S_{ref}}$
, and
${S_{ref}}$
, and
![]() ${S_h}$
represent the reference areas of the wing and horizontal tail. The downwash from the main wing
${S_h}$
represent the reference areas of the wing and horizontal tail. The downwash from the main wing
![]() $\frac{{\partial \varepsilon }}{{\partial \alpha }}$
was assumed to be 0.45, and the velocity deficit ratio
$\frac{{\partial \varepsilon }}{{\partial \alpha }}$
was assumed to be 0.45, and the velocity deficit ratio
![]() ${\eta _h}$
was set to be 0.8 from theoretical calculations [Reference Uhlig3]. Figure 14 shows the neutral point (
${\eta _h}$
was set to be 0.8 from theoretical calculations [Reference Uhlig3]. Figure 14 shows the neutral point (
![]() ${X_{np}}$
) with respect of trim angle-of-attack (
${X_{np}}$
) with respect of trim angle-of-attack (
![]() ${\alpha _{trim}}$
) and is compared to the CG location of both sUAVs. The measurements are made from the wing root leading edge and are non-dimensionalised with respect to the wing root chord. The results obtained for both aircraft indicate that the neutral point is in close proximity to the CG, thereby indicating that both sUAVs are longitudinally stable at the conditions tested (small-to-moderate elevator deflection inputs, typically ranging between -10 to 10 degrees). However, the TR-C285G displayed a rearward shift of its neutral point in relation to the CG at negative as well as angles of attack higher than 8 degrees, indicating an aftward shift of the neutral point with respect to the CG, and therefore imminent longitudinal instability.
${\alpha _{trim}}$
) and is compared to the CG location of both sUAVs. The measurements are made from the wing root leading edge and are non-dimensionalised with respect to the wing root chord. The results obtained for both aircraft indicate that the neutral point is in close proximity to the CG, thereby indicating that both sUAVs are longitudinally stable at the conditions tested (small-to-moderate elevator deflection inputs, typically ranging between -10 to 10 degrees). However, the TR-C285G displayed a rearward shift of its neutral point in relation to the CG at negative as well as angles of attack higher than 8 degrees, indicating an aftward shift of the neutral point with respect to the CG, and therefore imminent longitudinal instability.

Figure 14. Experimental neutral point and CG versus trim angle-of-attack.
5.3.2 Lateral stability
Lateral stability in the context of sUAVs pertains to the aircraft’s capacity to sustain stable flight in the lateral axis direction. It encompasses the inherent ability of the sUAV to counteract rolling movements and uphold a level attitude throughout the flight. In the current work, we focus on examining the experimental weather vane stability (
![]() ${C_{{n_\beta }}}$
) and roll stability (
${C_{{n_\beta }}}$
) and roll stability (
![]() ${C_{{l_\beta }}}$
). Weather vane stability measures the yawing response of an aircraft caused by a sideslip angle and is measured using the equation,
${C_{{l_\beta }}}$
). Weather vane stability measures the yawing response of an aircraft caused by a sideslip angle and is measured using the equation,
where
![]() ${\eta _v}$
is the vertical tail efficiency factor,
${\eta _v}$
is the vertical tail efficiency factor,
![]() ${a_v}$
is vertical tail angle-of-attack,
${a_v}$
is vertical tail angle-of-attack,
![]() ${\forall _v}$
is the tail volume ratio, and
${\forall _v}$
is the tail volume ratio, and
![]() $\forall $
is the volume of the equivalent fuselage. A positive weather vane stability coefficient indicates the aircraft’s inclination to align itself with the relative wind while a negative value suggests a propensity for the aircraft to deviate from its intended heading. Figure 15(a) plots the weather vane stability for the two sUAVs as a function of trim angle-of-attack. We observe that, at all trim angles, the TR-C285G consistently exhibited positive weather vane stability. In contrast, the F4U-Corsair displayed instability beyond an angle-of-attack of 15 degrees, at which point any sideslip was not being dampened out. Additionally, at an approximate trim angle-of-attack of
$\forall $
is the volume of the equivalent fuselage. A positive weather vane stability coefficient indicates the aircraft’s inclination to align itself with the relative wind while a negative value suggests a propensity for the aircraft to deviate from its intended heading. Figure 15(a) plots the weather vane stability for the two sUAVs as a function of trim angle-of-attack. We observe that, at all trim angles, the TR-C285G consistently exhibited positive weather vane stability. In contrast, the F4U-Corsair displayed instability beyond an angle-of-attack of 15 degrees, at which point any sideslip was not being dampened out. Additionally, at an approximate trim angle-of-attack of
![]() $\sim 10$
degrees, a slight negative value of
$\sim 10$
degrees, a slight negative value of
![]() ${C_{{n_\beta }}}$
was observed, indicating marginal instability of the aircraft.
${C_{{n_\beta }}}$
was observed, indicating marginal instability of the aircraft.
Roll stability (dihedral effect) is equated using the equation,
where
![]() ${a_w}$
is the wing angle-of-attack and
${a_w}$
is the wing angle-of-attack and
![]() ${\rm{\Gamma }}$
is the geometric angle of dihedral. Given that
${\rm{\Gamma }}$
is the geometric angle of dihedral. Given that
![]() ${C_{{l_\beta }}}$
is a function of dihedral, roll stability was only analysed for the F4U-Corsair aircraft as the TR-C285G does not have any dihedral. Negative values of roll stability indicate stable conditions where the aircraft has the ability to attenuate and stabilise against any disturbances or perturbations. Results for the F4U-Corsair, plotted in Fig. 15(b), show a negative
${C_{{l_\beta }}}$
is a function of dihedral, roll stability was only analysed for the F4U-Corsair aircraft as the TR-C285G does not have any dihedral. Negative values of roll stability indicate stable conditions where the aircraft has the ability to attenuate and stabilise against any disturbances or perturbations. Results for the F4U-Corsair, plotted in Fig. 15(b), show a negative
![]() ${C_{{l_\beta }}}$
at all trim angles of attack, indicating roll stability across the tested flight conditions.
${C_{{l_\beta }}}$
at all trim angles of attack, indicating roll stability across the tested flight conditions.
5.3.3 Dynamic stability
Dynamic stability of an aircraft can be determined by analysing its phugoid mode, characterised by a unique longitudinal oscillation pattern featuring extended durations of climbing and descending flight paths. During the phugoid mode, the aircraft continuously exchanges energy between potential and kinetic forms as it cyclically trades altitude for airspeed. The dynamic interplay between altitude and velocity helps maintain the stability and equilibrium of the aircraft during flight. By carefully monitoring the flight’s time history and analysing the variations in altitude, the phugoid half period can be identified. The method of extracting the phugoid half period is illustrated in Fig. 16(a) using data for a single flight of the TR-C285G aircraft. By co-plotting the time history of the altitude changes and corresponding airspeed, we observe that the TR-C285G demonstrates a half period of approximately 1 second for the given flight. Similar behaviour was observed across multiple flight instances of the aircraft as well. The process was repeated for multiple flight data sets for all six sUAVs to determine their respective phugoid periods. To verify the results, the measured phugoid period was compared with theoretical predictions. The natural frequency of the phugoid is mainly a function of gravitational acceleration (
![]() $g$
) and velocity (
$g$
) and velocity (
![]() $V$
) when neglecting compressibility effects [Reference Nelson36, Reference Bossert, Hallgren, Yechout and Morris37]. The linear longitudinal equation of motion can therefore be approximated to
$V$
) when neglecting compressibility effects [Reference Nelson36, Reference Bossert, Hallgren, Yechout and Morris37]. The linear longitudinal equation of motion can therefore be approximated to
![]() $\sqrt 2 \frac{g}{V}$
to evaluate the theoretical natural phugoid frequency (
$\sqrt 2 \frac{g}{V}$
to evaluate the theoretical natural phugoid frequency (
![]() ${\omega _{n,ph}}$
) and hence the phugoid period. Figure 16(b) shows the comparison between the theoretical phugoid period and the experimentally observed period. The sUAVs that were flown within specific speed regimes exhibited good agreement with theoretical predictions thereby confirming the capability of the motion capture system in effectively capturing the essential dynamics of the phugoid modes for sUAVs.
${\omega _{n,ph}}$
) and hence the phugoid period. Figure 16(b) shows the comparison between the theoretical phugoid period and the experimentally observed period. The sUAVs that were flown within specific speed regimes exhibited good agreement with theoretical predictions thereby confirming the capability of the motion capture system in effectively capturing the essential dynamics of the phugoid modes for sUAVs.

Figure 15. Experimental (a) weather vane stability and (b) roll stability.

Figure 16. Phugoid mode analysis: (a) time history of altitude and airspeed and (b) comparison between the experimental and theoretical phugoid period.
6.0 Conclusion
The objective of this study was to utilise an existing motion capture system to aerodynamically characterise sUAVs via off-board measurements and study the effects of low-
![]() $Re$
conditions on the aircraft aerodynamics. Initial efforts were centred around assessing system uncertainties through static tests to examine the standard deviation in position and attitude for a stationary aircraft and dynamic tests to ascertain the system’s accuracy in determining body acceleration by measuring the acceleration due to gravity during free fall. Subsequently, flight data for six sUAVs were successfully acquired, with the analysis primarily focused on quasi-steady flight conditions. To gain insights into the influence of low Reynolds number effects on the aerodynamic data, trends in the Oswald efficiency factor and lift curve-slope were investigated. Lastly, a comprehensive stability analysis was carried out to ascertain the effectiveness of the motion capture system in characterising flight stability.
$Re$
conditions on the aircraft aerodynamics. Initial efforts were centred around assessing system uncertainties through static tests to examine the standard deviation in position and attitude for a stationary aircraft and dynamic tests to ascertain the system’s accuracy in determining body acceleration by measuring the acceleration due to gravity during free fall. Subsequently, flight data for six sUAVs were successfully acquired, with the analysis primarily focused on quasi-steady flight conditions. To gain insights into the influence of low Reynolds number effects on the aerodynamic data, trends in the Oswald efficiency factor and lift curve-slope were investigated. Lastly, a comprehensive stability analysis was carried out to ascertain the effectiveness of the motion capture system in characterising flight stability.
Uncertainty analysis of the motion capture system showed that the standard deviation in position and attitude measurements were less than
![]() $0.05$
mm and
$0.05$
mm and
![]() $0.02$
degrees, respectively. Additionally, the free-fall tests demonstrated that the error in acceleration measured by the motion capture system was less than
$0.02$
degrees, respectively. Additionally, the free-fall tests demonstrated that the error in acceleration measured by the motion capture system was less than
![]() $0.025{\rm{\% }}$
. Analysis of the aerodynamic data measured for the six sUAVs with aspect ratios ranging from
$0.025{\rm{\% }}$
. Analysis of the aerodynamic data measured for the six sUAVs with aspect ratios ranging from
![]() $2$
to
$2$
to
![]() $6.3$
revealed trends in Oswald efficiency factors and lift-curve slope that clearly showed the effect of low Reynolds number on the flight aerodynamics. While low aspect ratio wings (
$6.3$
revealed trends in Oswald efficiency factors and lift-curve slope that clearly showed the effect of low Reynolds number on the flight aerodynamics. While low aspect ratio wings (![]()
![]() $ \lt 4$
) had Oswald efficiency factors above
$ \lt 4$
) had Oswald efficiency factors above
![]() $0.65$
and matched with theoretical predictions, increasing the aspect ratio led to a sharp drop in Oswald efficiency factors (
$0.65$
and matched with theoretical predictions, increasing the aspect ratio led to a sharp drop in Oswald efficiency factors (
![]() $ \lt 0.4$
). The above trends matched with low Reynolds number wing data from literature, with the sharp drop in
$ \lt 0.4$
). The above trends matched with low Reynolds number wing data from literature, with the sharp drop in
![]() ${e_0}$
being attributed to low Reynolds number effects. Lift curve slope measurements matched well with theory for aircraft with elliptical wings but were observed to be lower than theoretical predictions for non-elliptical wings, as expected. Additionally, the lift-curve slope was observed to decrease with increasing wing aspect ratio. Stability analysis of the captured flight data for the F4U-Corsair and the TR-C285G aircraft showed that the neutral point tended to cluster around the centre of gravity location across the range of trim angles tested, showing lateral stability. Both aircraft also showed positive weather vane stability across all trim angles. Additionally, the F4U-Corsair displayed roll stability across all trim angles tested. Dynamic stability analysis, determined by the phugoid mode, showed the measured phugoid period matching well with theoretical predictions.
${e_0}$
being attributed to low Reynolds number effects. Lift curve slope measurements matched well with theory for aircraft with elliptical wings but were observed to be lower than theoretical predictions for non-elliptical wings, as expected. Additionally, the lift-curve slope was observed to decrease with increasing wing aspect ratio. Stability analysis of the captured flight data for the F4U-Corsair and the TR-C285G aircraft showed that the neutral point tended to cluster around the centre of gravity location across the range of trim angles tested, showing lateral stability. Both aircraft also showed positive weather vane stability across all trim angles. Additionally, the F4U-Corsair displayed roll stability across all trim angles tested. Dynamic stability analysis, determined by the phugoid mode, showed the measured phugoid period matching well with theoretical predictions.
Overall, in addition to successfully demonstrating the capability of the motion capture method in characterising the aerodynamic and stability characteristics of sUAVs (via experimental and analytical validation), the current research adds new knowledge to existing literature by shedding light on the effects of low-
![]() $Re$
flows on the Oswald efficiency factors and lift-curve slopes for sUAVs with varying wing aspect ratios.
$Re$
flows on the Oswald efficiency factors and lift-curve slopes for sUAVs with varying wing aspect ratios.
Acknowledgements
The authors gratefully acknowledge the support of Dr. Jichul Kim and Raspet Flight Research Labs for providing access to and training on the motion capture system. The authors would also like to thank Mr. Calvin Walker (aerospace engineering, Mississippi State University) for his guidance on the subject matter and feedback on the manuscript.
Competing interests
The authors declare none.
Appendix
A. Appendix
Flight data for the Micro Stick Vintage, Edge A-340, and S2-CUB sUAVs have been provided in the current section.

Figure A1. Flight data for the Micro Stick Vintage (![]()
![]() $ = 3.8$
): (a) experimental drag polar with parabolic fit, (b) experimental lift curve with linear regression, (c) experimental drag curve with quadratic regression and (d) experimental pitching moment with linear regression.
$ = 3.8$
): (a) experimental drag polar with parabolic fit, (b) experimental lift curve with linear regression, (c) experimental drag curve with quadratic regression and (d) experimental pitching moment with linear regression.

Figure A2. Flight data for the Edge A-430 (![]()
![]() $ = 4.5$
): (a) experimental drag polar with parabolic fit, (b) experimental lift curve with linear regression, (c) experimental drag curve with quadratic regression and (d) experimental pitching moment with linear regression.
$ = 4.5$
): (a) experimental drag polar with parabolic fit, (b) experimental lift curve with linear regression, (c) experimental drag curve with quadratic regression and (d) experimental pitching moment with linear regression.

Figure A3. Flight data for the S2-CUB (![]()
![]() $ = 6.32$
): (a) experimental drag polar with parabolic fit, (b) experimental lift curve with linear regression, (c) experimental drag curve with quadratic regression and (d) experimental pitching moment with linear regression.
$ = 6.32$
): (a) experimental drag polar with parabolic fit, (b) experimental lift curve with linear regression, (c) experimental drag curve with quadratic regression and (d) experimental pitching moment with linear regression.