Deformational rigidity of integrable metrics on the torus

Abstract

It is conjectured that the only integrable metrics on the two-dimensional torus are Liouville metrics. In this paper, we study a deformative version of this conjecture: we consider integrable deformations of a non-flat Liouville metric in a conformal class and show that for a fairly large class of such deformations, the deformed metric is again Liouville. The principal idea of the argument is that the preservation of rational invariant tori in the foliation of the phase space forces a linear combination on the Fourier coefficients of the deformation to vanish. Showing that the resulting linear system is non-degenerate will then yield the claim. Since our method of proof immediately carries over to higher dimensional tori, we obtain analogous statements in this more general case. To put our results in perspective, we review existing results about integrable metrics on the torus.

1. Introduction

Let ${\mathbb {T}}^2 = \mathbb {R}^2 / \mathbb {Z}^2$ be the two-dimensional torus being equipped with a $C^2$ -smooth global Liouville metric g, that is, having line element

(1.1) $$ \begin{align} d s^2 = (f_1(x^1) + f_2(x^2)) ((d x^1)^2 + (d x^2)^2), \end{align} $$

where $(x^1,x^2) \in {\mathbb {T}}^2$ are the standard periodic coordinates and $f_1, f_2 \in C^2({\mathbb {T}})$ are positive Morse functions or positive constants and thus ‘non-degenerate’. (Recall that Morse functions on a manifold M are characterized by having no degenerate critical points. They form a dense and open set in $C^2(M)$ and are thus ‘generic’.) The corresponding geodesic flow (see §1.1) is well known to be integrable and a longstanding folklore conjecture says that Liouville metrics are the only integrable metrics on ${\mathbb {T}}^2$ . We emphasize that, in this context, integrability always allows for singularities in the foliation of the phase space of the naturally associated Hamiltonian system, which is made precise in Definition 1.2 below.

Although the validity of the folklore conjecture appeared conceivable for a long time, there is strong indication for it being false in its very general form, as shown in [35]: here, the authors constructed a Hamiltonian counterexample which is locally integrable in a p-cone in the cotangent bundle. This means that, on a fixed energy level, there exists an analytic change of variables, transforming the Hamiltonian with non-Liouville potential to the standard form $(p_1^2 + p_2^2)/2$ but only for $p_i$ in a certain cone in $\mathbb {R}^2$ (see also Theorem 3.8 below for a more precise statement). However, despite this delicate example, certain suitably weakened conjectures are still believed to be true, which is supported by a variety of partial results obtained in this direction, starting from classical ones by Dini [43], Darboux [37], and Birkhoff [22] and further developed in [11, 62, 64]. In particular, several works by Bialy, Mironov [13, 17–19], Denisova, Kozlov, Treshev [39–42, 70], Mironov [79], and others [2, 11, 64, 87] strongly indicate the validity of the following (yet unproven) conjecture: Every polynomially integrable metric g on ${\mathbb {T}}^2$ is of Liouville type. We refer to §3 for details. (See also [24, 31] for recent surveys on open problems and questions concerning geodesics and integrability of finite-dimensional systems.)

In this paper, we are concerned with a perturbative version of the folklore conjecture: Let $(g_\varepsilon )_{|\varepsilon | \le \varepsilon _0}$ for some small $\varepsilon _0> 0$ be a family of perturbations of $g \equiv g_0$ in the same conformal class (note that on the torus, there exist global isothermal coordinates [26, Ch. 11]) having line-element

(1.2) $$ \begin{align} d s^2_\varepsilon = (f_1(x^1) + f_2(x^2) + \varepsilon \unicode{x3bb}(x^1, x^2)) ((d x^1)^2 + (d x^2)^2), \end{align} $$

where $\unicode{x3bb} \in C^2({\mathbb {T}}^2)$ is assumed to be a Morse function (or constant) and have an absolutely convergent Fourier series. We will assume that the perturbed family $g_\varepsilon $ remains integrable, meaning that within the foliation of the phase space for the unperturbed Liouville metric in equation (1.1), the deformation in equation (1.2) preserves sufficiently many rational invariant tori (see Assumption (P) below for a precise formulation of our requirement on the preservation of these tori). Then we obtain that $\unicode{x3bb} $ is necessarily separable in a sum of two single-valued functions, that is,

for some $\unicode{x3bb} _1, \unicode{x3bb} _2 \in C^2({\mathbb {T}})$ . Therefore, our main results formulated (somewhat informally) below assert the following.

The class of Liouville metrics is deformationally rigid under a fairly wide class of integrable conformal perturbations.

To the best of our knowledge, this is the first instance of a rigidity result for (not necessarily analytically) integrable dynamical systems allowing for singularities in the invariant foliation of the unperturbed system. The precise statements of our main results are given in Theorems 2.2, 2.3, and 2.4 in §2.

Main Results. Let g be a non-degenerate Liouville metric on ${\mathbb {T}}^2$ as in equation (1.1) and assume that the family $(g_\varepsilon )_{|\varepsilon | \le \varepsilon _0}$ of perturbations defined in equation (1.2) remains integrable. Then we have the following.

1. (i) In the case where $f_1, f_2 \equiv \mathrm {const}.$ , then $\unicode{x3bb} $ is separable.

2. (ii) In the case where $f_1 \equiv \mathrm {const}.$ , $\unicode{x3bb} $ is a trigonometric polynomial in $x^2$ , and the relative difference $\mu _2$ between $f_2$ and its mean $\int _{\mathbb {T}} f_2$ , that is, $\mu _2 := \Vert f_2 - \int _{\mathbb {T}} f_2 \Vert _{C^0} / \int _{\mathbb {T}} f_2$ is small, then $\unicode{x3bb} $ is separable.

   If, additionally, $f_2$ is analytic, we have that $\unicode{x3bb} $ is separable, irrespective of the size $\mu _2$ of the fluctuations of $f_2$ (but only for $\mu _2$ outside of an exceptional (Lebesgue) null-set).

3. (iii) In general, if $\unicode{x3bb} $ is a trigonometric polynomial and the relative differences $\mu _i$ , $i=1,2$ , between the $f_i$ and their means $\int _{\mathbb {T}} f_i$ , that is, the $\mu _i := \Vert f_i - \int _{\mathbb {T}} f_i \Vert _{C^0} / \int _{\mathbb {T}} f_i$ are small, then $\unicode{x3bb} $ is separable.

   If, additionally, $f_i$ is analytic (for one or both $i = 1, 2$ ), we have that $\unicode{x3bb} $ is separable, irrespective of the size $\mu _i$ of the fluctuations of $f_i$ (outside of an exceptional null-set).

It is straightforward to generalize our results to higher dimensional tori ${\mathbb {T}}^d = \mathbb {R}^d / \mathbb {Z}^d$ . To ease notation and make the presentation clearer, we only mention it here and postpone a more detailed discussion to Appendix A.

Remark 1.1. (Generalization to higher dimensions)

Analogously to equation (1.1), let ${\mathbb {T}}^d$ be equipped with a $C^2$ -smooth global Liouville metric g having line element

(1.3) $$ \begin{align} d s^2 = (f_1(x^1) + \cdots + f_d(x^d)) ((d x^1)^2 + \cdots + (d x^d)^2), \end{align} $$

where $x = (x^1, \ldots , x^d) \in {\mathbb {T}}^d$ are standard periodic coordinates and $f_i \in C^2 ({\mathbb {T}})$ for $1 \le i \le d$ are positive Morse functions or constants. Again, it is easy to see that the geodesic flow is integrable. Just as in equation (1.2), we now perturb equation (1.3) in the same conformal class by some $\unicode{x3bb} \in C^2({\mathbb {T}}^d)$ having an absolutely convergent Fourier series.

Under the assumption that the family of perturbed metrics $(g_\varepsilon )_{|\varepsilon | \le \varepsilon _0}$ remains integrable, we have the following (somewhat informal) rigidity result.

Let $f_i \equiv \mathrm {const}.$ for the first $0 \le d_{\mathrm {flat}} \le d$ indices, and $f_j$ be analytic for the last $0 \le d_{\mathrm {anlyt}} \le d - d_{\mathrm {flat}}$ indices. Then, if $\unicode{x3bb} $ is a trigonometric polynomial in $x^k$ for $k \in \{d_{\mathrm {flat}} + 1, \ldots , d\}$ , and the relative differences between $f_{d_{\mathrm {flat}} + 1}, \ldots , f_{d - d_{\mathrm {anlyt}}}$ and their mean values are small, we have that $\unicode{x3bb} $ is separable, irrespective of size $\mu _j$ of the fluctuations of $f_j$ (outside of a null-set).

This result unifies and generalizes the three separate statements given above. A precise formulation is given in Theorem A.1 in Appendix A.

The present paper is not the first study on rigidity of important integrable systems. In [10, 60], Avila, de Simoi, Kaloshin and Kaloshin, Sorrentino recently solved both, a deformative and a perturbative version of the famous Birkhoff conjecture concerning integrable billiards in two dimensions. In a nutshell, their result says that a strictly convex domain with integrable billiard dynamics sufficiently close to an ellipse is necessarily an ellipse. This can be viewed as an analogue of the perturbative version of the folklore conjecture formulated above [61]. More precisely, our main results concerning general $f_i \in C^2({\mathbb {T}})$ are similar—in spirit—to the deformational rigidity for ellipses of small eccentricity (cf. $f_1,f_2$ in equation (1.1) having small fluctuations), which has been shown first in [10], later extended by Huang, Kaloshin, and Sorrentino [59] to a local notion of integrability, and finally significantly improved in [66]. The overall strategy pursued in [10, 59, 60] also inspired the arguments employed in the present paper.

In a more recent work, Arnaud, Massetti, and Sorrentino [4] (replacing the earlier preprint [74]) studied the rigidity of integrable symplectic twist maps on the $2d$ -dimensional annulus ${\mathbb {T}}^d \times \mathbb {R}^d$ . More precisely, they consider one-parameter families $(f_\varepsilon )_{\varepsilon \in \mathbb {R}}$ of symplectic twist maps $f_\varepsilon (x,p) = f_0(x , p + \varepsilon \nabla G(x))$ and prove two main rigidity results. First, in the analytic category for $f_0$ and the perturbation G, if a single rational invariant Lagrangian graph of $f_\varepsilon $ exists for infinitely many values of $\varepsilon $ (e.g., an interval around zero), then G must necessarily be constant. Second, if $f_0$ is analytic and completely integrable (that is, not plagued with singularities in the invariant foliation of the phase space, see [16, 86]), G is of class $C^2$ , and sufficiently (infinitely) many rational invariant Lagrangian graphs of $f_\varepsilon $ persist for small $\varepsilon \neq 0$ , then G must necessarily be constant. Note that in this second result, the entire phase space is foliated by invariant tori, and the perturbation solely depends on the angle variables of the dynamical system. In this sense, Theorem 2.2 can—morally—be viewed as a special case of the second result in [4] (see also [74, Theorem 2]), but Theorems 2.3 and 2.4 generalize this statement to more general functional dependencies of the perturbation. Apart from this, our general results (that is, those not concerning analytic functions $f_i$ ) do not require any regularity beyond the standard $C^2$ .

As mentioned above, by assuming that the family of metrics $(g_\varepsilon )_{|\varepsilon | \le \varepsilon _0}$ remains integrable, we mean that, in particular, sufficiently many rational invariant tori in an isoenergy manifold of the Hamiltonians associated to the metric by the Maupertuis principle (see §1.2) are preserved. This will be made precise in Assumption (P) below. As we will show, the preservation of an $(n,m)$ -rational invariant torus ‘annihilates’ the Fourier coefficients $\unicode{x3bb} _{k_1, k_2}$ with indices $(k_1, k_2) \in \{ (n,m)\}^{\perp }$ of

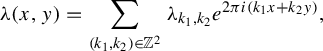
or of the corresponding perturbing mechanical potential, denoted by U later on. We already noted that, contrary to items (ii) and (iii), the unperturbed metric in our first result is guaranteed to be completely integrable. Moreover, the perturbation $\unicode{x3bb} $ depends solely on the angular but not the action coordinates of the unperturbed problem. Although the analog of this result for symplectic twist maps in this peculiar setting has already been shown in [4, 74] by methods similar to ours, we reprove it by pursuing an only slightly different but original strategy, which is suitable for certain inevitable modifications for the proofs of the more general statements under items (ii) and (iii). These two cases (corresponding to surfaces of revolution and general Liouville metrics, see §3) build on perturbative estimates for (possibly infinitely many) systems of linear equations for the Fourier coefficients. These are obtained from the first-order term of an expansion in $\varepsilon $ , somewhat similar to the (subharmonic) Melnikov potential in the Poincaré–Melnikov method [8, 55, 91]. Establishing this expansion as well as proving that the resulting systems of linear equations are of full rank requires perturbative estimates on action-angle coordinates and certain basic objects from weak KAM theory [85]. Finally, the extension of our results for analytic functions $f_i$ beyond the perturbative regime are proven by exploiting the analytic dependence of the linear system on the size $\mu _i$ of the fluctuations of $f_i$ (see Appendix C).

In the remainder of this introduction, we recall basic notions in geometry and dynamical systems, which are frequently used in this paper, and introduce the problem of classifying integrable metrics on Riemannian manifolds, in particular, the torus ${\mathbb {T}}^2$ , as formulated in Questions (Q1) and (Q2) below. In §2, we formulate our main results in Theorems 2.2, 2.3, and 2.4. In §3, we present related existing results and known partial answers on the classification problem for integrable metrics on the torus ${\mathbb {T}}^2$ (a few of which have already been mentioned above) to put our results into context. In §4, we give the proofs of our main results, and, finally, comment on possible generalizations, different approaches, and a list of open problems in §5. As already mentioned above, the precise formulation of our result for higher dimensions is given in Theorem A.1 in Appendix A. A fundamental perturbation theoretic lemma on action-angle coordinates, a concise study on important analyticity properties of these, and a brief overview of the relevant aspects of weak KAM theory are presented in three further appendices.

An extended version of this paper containing more details and background can be found at arXiv: 2210.02961.

1.1. Geodesic flow and integrability

Let $(M,g)$ be a (compact) $C^2$ -smooth n-dimensional connected Riemannian manifold without boundary equipped with the Riemannian metric $g = (g_{ij}(x))_{ij}$ . Geodesics of the given metric g are defined as smooth parameterized curves $\gamma (t) = (x^1(t), \ldots , x^n(t))$ that are solutions to the system of differential equations

(1.4) $$ \begin{align} \nabla_{\dot{\gamma}} \dot{\gamma} = 0, \end{align} $$

where $\dot {\gamma } = ({d \gamma }/{d t})$ denotes the velocity vector of the curve $\gamma $ , and $\nabla $ is the covariant derivative operator related to the Levi–Civita connection associated with the metric g.

It is well known that the geodesic equation in equation (1.4) can also be viewed as a Hamiltonian system on the cotangent bundle $T^*M$ , and the geodesics $\gamma $ themselves can be regarded as projections of trajectories of the Hamiltonian system onto M. Therefore, let x and p be natural coordinates on the cotangent bundle $T^*M$ and $\omega = d x \wedge d p$ denote the standard symplectic structure. Then, the Hamiltonian function $H \in C^2(T^*M)$ is defined as

(1.5) $$ \begin{align} H(x,p) = \frac{1}{2} \sum_{ij} g^{ij}(x)p_ip_j = \frac{1}{2} \vert p \vert_g^2. \end{align} $$

A trajectory $(x(t),p(t))$ is an integral curve for the Hamiltonian vector field if and only if the following Hamiltonian system of differential equations (written in local coordinates) is satisfied:

(1.6) $$ \begin{align} \begin{cases} \dot{p}_i =& - \dfrac{\partial H}{\partial x^i}, \\[5pt] \dot{x}^i =& \dfrac{\partial H}{\partial p_i}. \end{cases} \end{align} $$

In view of this connection to Hamiltonian dynamics, it is natural to ask for a classification of Riemannian manifolds $(M,g)$ , for which the geodesic equations in equation (1.4) can be solved explicitly. More precisely, we can formulate the following questions.

1. (Q1) On which manifolds do there exist Riemannian metrics whose (co-)geodesic flow is integrable?

2. (Q2) Given such a manifold, how does one characterize the class of metrics with integrable geodesic flow?

Clearly, the answers and their complexity hinge on the notion of integrability for the Hamiltonian system (see §3). In this paper, we will be concerned with the standard notion, that is, Liouville integrability, which we recall for the readers convenience.

Definition 1.2. The geodesic flow on $(M,g)$ is called Liouville integrable if there exist n functions $F_1,\ldots ,F_n \in C^2(T^*M)$ (called first integrals) that are:

1. (i) functionally independent on $T^{\kern-0.1pt*}M$ , that is, the vector fields $X_{F_1}\kern-0.3pt(x,\kern-0.3ptp)\kern-0.1pt, \ldots ,\kern-0.3pt X_{F_n}\kern-0.3pt(x\kern-0.3pt,\kern-0.3pt p\kern-0.5pt)$ are linear independent in $T_{(x,p)}(T^*M)$ for all $(x,p) \in \mathcal {M} \subset T^*M$ , where $\mathcal {M}$ is some open and everywhere dense set of full measure (cf. the restriction to Morse functions);

2. (ii) pairwise in involution, that is,

   $$ \begin{align*} \{F_k,F_l\} := \omega(X_{F_k},X_{F_l}) = \sum_{i} \bigg(\frac{\partial F_k}{\partial x^i} \frac{\partial F_l}{\partial p_i} - \frac{\partial F_k}{\partial p_i} \frac{\partial F_l}{\partial x^i}\bigg) = 0. \end{align*} $$

Whenever the geodesic flow on $(M,g)$ is Liouville integrable, we call g an integrable metric on M. Moreover, we call the Hamiltonian system in equation (1.6) (or the corresponding Hamiltonian in equation (1.5) itself) integrable, whenever the associated metric g is integrable on M.

Remark 1.3. Whenever the first integrals $F_1, \ldots , F_n$ can be chosen to be functions that are polynomially in the momentum variables, the metric is often called polynomially integrable or algebraically integrable. If we aim at indicating the order of the polynomial, we speak of linearly/quadratically/… integrable metrics.

Remark 1.4. Note that since one can always choose $H=F_1$ as a first integral for the geodesic flow, the question of integrability for one-dimensional manifolds is completely answered. Therefore, the simplest manifolds, for which the answers to Questions (Q1) and (Q2) are non-trivial, are two-dimensional.

In this work, we are mainly concerned with a characterization of integrable metrics in the sense of Question (Q2) for the two-dimensional torus ${\mathbb {T}}^2$ . In this case, the largest known class of such metrics g are so-called Liouville metrics, where the line element takes the form in equation (1.1) in appropriate global coordinates $(x^1, x^2)$ , and where $f_1$ and $f_2$ are sufficiently regular positive periodic functions. See §3.2 for more details.

1.2. Maupertuis principle

To approach Questions (Q1) and (Q2), we will use the Maupertuis principle (see, e.g., [28]): for a compact Riemannian manifold, $(M,g)$ , let

(1.7) $$ \begin{align} H(x,p) = \frac{1}{2}\sum_{ij} g^{ij}(x)p_ip_j - V(x) \end{align} $$

be a natural mechanical Hamiltonian function on $T^*M$ , where $V \in C^2(M)$ denotes some potential function. Moreover, let $T_h = \{ H(x,p) = h\}$ be an isoenergy submanifold for some $h> - \min _x V(x)$ and note that $T_h$ is also an isoenergy submanifold for another system with Hamiltonian function

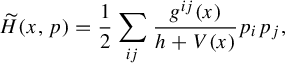$$ \begin{align*} \widetilde{H}(x,p) = \frac{1}{2}\sum_{ij} \frac{g^{ij}(x)}{h+V(x)}p_ip_j, \end{align*} $$

that is, $T_h = \{\widetilde {H}(x,p) = 1\}$ . Now, the Maupertuis principle states that the integral curves for the Hamiltonian vector fields $X_H$ and $X_{\widetilde {H}}$ on the fixed isoenergy submanifold $T_h$ coincide. Moreover, if there exists an additional first integral F for H on $T_h$ , then there also exists a first integral $\tilde {F}$ for $\widetilde {H}$ on the whole of $T^*M$ (except, potentially, at the zero section). Finally, note that the vector field $X_{\widetilde {H}}$ gives rise to the geodesic flow of the Riemannian metric $\widetilde {g}$ with

(1.8) $$ \begin{align} \widetilde{g}_{ij}(x) = (h+V(x))g_{ij}(x), \end{align} $$

which is the correspondence between Hamiltonian systems and geodesic flows we will use.

2. Main results

The main results of this paper are rigidity results in the sense of Question (Q2) for classes of integrable metrics on the two-torus $\mathbb {T}^2 = \mathbb {R}^2 /\Gamma $ , initially equipped with the flat metric, and hence obtained by a Hamiltonian defined on $T^*{\mathbb {T}}^2$ by means of the Maupertuis principle. In general, $\Gamma \subset \mathbb {R}^2$ is an arbitrary lattice, but we focus on the case $\Gamma = \mathbb {Z}^2$ here. We define the Hamiltonian function

(2.1) $$ \begin{align} H_0(x,p) = \frac{p_1^2}{2}+\frac{p_2^2}{2} - \mu_1\, V_1(x^1) - \mu_2 \, V_2(x^2) \end{align} $$

on $T^*\mathbb {T}^2$ , where $\mu _i \in [0,\infty )$ are parameters, and $V_i \in C^2(\mathbb {T})$ with $V_i \ge 0$ and $\Vert V_i \Vert _{C^0} \le \mathcal {C}_i$ are Morse functions (or constant). We may assume without loss of generality that $\min _{x^i} V_i(x^i) = 0$ . This includes, e.g., the situation of two pendulums, that is, $V_i(x^i) = 1- \cos (2\pi x^i)$ . The torus coordinates are denoted by $x = (x^1,x^2) \in \mathbb {T}^2$ and the conjugate coordinate pairs are $(x^1,p_1)$ and $(x^2,p_2)$ . By the Maupertuis principle, for fixed $e>0$ , the Hamiltonian flow on the isoenergy manifold $T_{e} = \{H_0 = e \}$ coincides with the geodesic flow on $\mathbb {T}^2$ with the Liouville metric $g_{e}$ (see equation (1.1) and §3.2 for more details) having line element

$$ \begin{align*} d s^2_e = (e+\mu_1 \, V_1(x^1) +\mu_2 \, V_2(x^2)) ((d x^1)^2 + (d x^2)^2). \end{align*} $$

The system with the Hamiltonian function in equation (2.1) is clearly integrable in the sense of Definition 1.2, since an additional conserved quantity can easily be found as

(2.2) $$ \begin{align} F_1(x,p) = \frac{p_1^2}{2} - \mu_1 \, V_1(x^1). \end{align} $$

The Liouville foliation of $T_{e}$ has the following qualitative structure that is similar to the phase portrait of the pendulum. The common level surface

$$ \begin{align*} T_{(e,f)} = \{ H_0 = e, \ F_1 = f \} \end{align*} $$

differs in shape, depending on the values of e and f. Recall that $e>0$ and $V_i \ge 0$ . If (i) $f\in (- \mu _1 \max _{x^1} V_1(x^1), 0)$ and $e-f> 0$ , $T_{(e,f)}$ is an annulus; if (ii) $f> 0$ and $e-f>0$ , $T_{(e,f)}$ is a torus; if (iii) $f> 0 $ and $e-f \in (- \mu _2 \max _{x^2} V_2(x^2), 0)$ , $T_{(e,f)}$ is an annulus. Therefore, if $V_1$ and $V_2$ are both non-constant, the foliation qualitatively exhibits a pendulum-like phase portrait (see Figure 1).

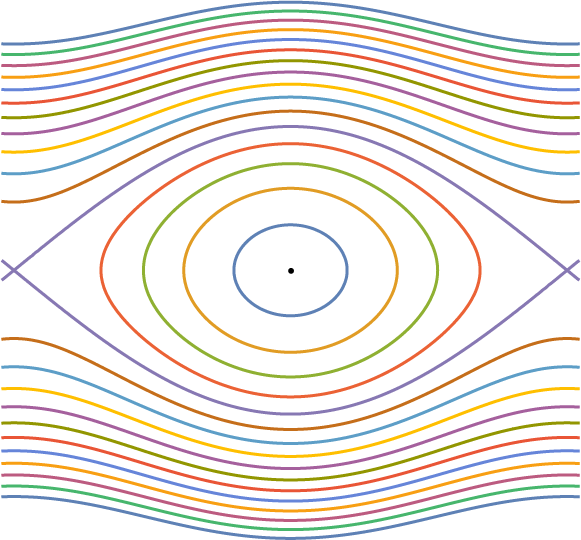
Figure 1 Schematic picture of the Liouville foliation of the phase space $T^{*}{\mathbb {T}} \cong {\mathbb {T}} \times \mathbb {R}$ for the classical one-dimensional pendulum system described by the Hamiltonian function $H(x,p) = {p^2}/{2} - ( 1- \cos (2 \pi x)).$ The horizontal direction covers slightly more than one period of length one.

2.1. Definitions and assumptions

Our main results concern perturbations of the Hamiltonian function in equation (2.1) in the class of mechanical systems as

(2.3) $$ \begin{align} H_\varepsilon(x,p) = H_0(x,p) + \varepsilon U(x), \end{align} $$

where $\varepsilon \in \mathbb {R}$ and $U \in C^2(\mathbb {T}^2)$ denotes a perturbing potential, which is assumed to be a Morse function (or a constant) and have an absolutely convergent Fourier series:

$$ \begin{align*} U(x) = \sum_{k_1 \in \mathbb{Z}} U_{k_1}(x^2) e^{i 2 \pi k_1 x^1 }= \sum_{(k_1,k_2) \in \mathbb{Z}^2} U_{k_1,k_2} e^{i 2\pi (k_1 x^1 + k_2 x^2)}. \end{align*} $$

(Note that in two dimensions, $C^2$ -regularity is not sufficient for ensuring an absolutely convergent Fourier series, although in one dimension it is). In the following, we introduce several subsets of $\mathbb {Z}^2$ in such a way that their definitions immediately carry over in arbitrary dimension $d \in \mathbb {N}$ (see Remark 1.1). First, we define the spectrum of U, that is, the set of non-vanishing Fourier coefficients, as

(2.4) $$ \begin{align} \mathcal{S}_U := \{ \boldsymbol{k} = (k_1, k_2) \in \mathbb{Z}^2 : U_{\boldsymbol{k}} \neq 0 \}, \end{align} $$

while the non-singular spectrum is denoted by

(2.5) $$ \begin{align} \mathcal{S}_{U,0} := \{ \boldsymbol{k} \in \mathcal{S}_U : \text{ there exists } i \neq j \ \text{such that}\ k_i \cdot k_j \neq 0 \}. \end{align} $$

Moreover, we define the coprime set of the orthogonal complement of $\mathcal {S}_U$ as well as its non-singular subset via

(2.6) $$ \begin{align} \mathcal{B}(\mathcal{S}_U^\perp) := \{ \boldsymbol{b} \in \mathcal{S}_U^\perp : \boldsymbol{b} \ \mathrm{coprime} \} \quad \text{and} \quad \mathcal{B}_0(\mathcal{S}^\perp_U) := \bigg\{ \boldsymbol{b} \in \mathcal{B}(\mathcal{S}^\perp_U) : \prod_i b_i \neq 0 \bigg\}, \end{align} $$

respectively. Note that the orthogonal complement is taken within $\mathbb {Z}^2$ . For the proofs in §4 and the generalization in Appendix A, it is important to observe that for every $\boldsymbol {k} \in \mathcal {S}_{U,0}$ exists some $\boldsymbol {b} \in \mathcal {B}_0(\mathcal {S}_U^\perp )$ such that $\boldsymbol {b} \cdot \boldsymbol {k} = 0$ .

Our main results will be formulated under the following assumptions.

Assumptions on the perturbed Hamiltonian function in equation (2.3)

Let $H_0 \in C^2(T^*{\mathbb {T}}^2)$ denote the Hamiltonian function from equation (2.1) with $\min V_i = 0$ , $\Vert V_i \Vert _{C^0} \le \mathcal {C}_i$ and $\mu _i \in [0,\tilde {\mu }_i]$ for some $\tilde {\mu _i} \in [0,\infty )$ , $i \in \{1,2\}$ , and U be a perturbing potential as in equation (2.3), which satisfies one of the following assumptions.

1. (A1) If $\tilde {\mu }_1 = \tilde {\mu }_2 = 0$ , we have $U \in C^2(\mathbb {T}^2)$ .

2. (A2) If, without loss of generality, $\tilde {\mu }_1 = 0$ and $\tilde {\mu }_2> 0$ , we have $U \in C^2(\mathbb {T}^2)$ and there exists $d^{(2)} \ge 0$ such that

   (2.7) $$ \begin{align} \mathcal{S}_U \subset \mathbb{Z} \times [-d^{(2)}, d^{(2)}] , \end{align} $$
   that is, U is a trigonometric polynomial in the second variable $x^2$ .

3. (A3) If $\tilde {\mu }_1, \tilde {\mu }_2> 0$ , we have $U \in C^2(\mathbb {T}^2)$ and there exist $d^{(1)}, d^{(2)}\ge 0$ such that

   (2.8) $$ \begin{align} \mathcal{S}_U \subset [- d^{(1)}, d^{(1)}] \times [- d^{(2)}, d^{(2)}], \end{align} $$
   that is, U is a trigonometric polynomial.

We denote the minimum over all $d^{(i)}$ such that equation (2.7) (respectively equation (2.8)) holds as $\deg _U^{(i)}$ and call it the i-degree of U. Whenever we refer to one of the Assumptions (A1), (A2), or (A3), we implicitly assume that $H_0 \in C^2(T^*{\mathbb {T}}^2)$ is of the form in equation (2.1).

Note that the assumption on the spectrum in equation (2.4) of U is more restrictive when we include more general potentials $\mu _1 V_1$ and $\mu _2 V_2$ in the unperturbed Hamiltonian $H_0$ in equation (2.1).

The following basic proposition is fundamental for the precise formulation of our assumptions concerning preservation of integrability. It rephrases certain aspects of the standard Liouville–Arnold theorem [7] in our concrete setting using standard notions from weak KAM theory (see Appendix D and its extension in the arXiv: 2210.02961 version of this article).

Proposition 2.1. (Liouville–Arnold theorem and weak KAM theory [85])

Let $H_0 \in C^2(T^*{\mathbb {T}}^2)$ be the Hamiltonian function from equation (2.1).

1. (a) In the region of phase space, where $f> 0$ as well as $e - f> 0$ , each of the two connected components of a Liouville torus $T_{(e, f)}$ (again denoted by $T_{(e, f)}$ ) is a Lipschitz (we will see in Appendix D that $u_{\boldsymbol {c}} \in C^3({\mathbb {T}}^2)$ , so the regularity of $T_{(e,f)}$ is in fact $C^2$ ) Lagrangian graph, that is,

   $$ \begin{align*} T_{(e, f)} = \{ (x, {\boldsymbol{c}} + \nabla_x u_{{\boldsymbol{c}}}) : x \in {\mathbb{T}}^2\} \end{align*} $$
   for a unique cohomology class ${\boldsymbol {c}} \in H^1({\mathbb {T}}^2, \mathbb {R}) \cong \mathbb {R}^2$ with $|c_i|> \sqrt {\mu _i} \mathfrak {c}(V_i)$ and $u_{\boldsymbol {c}} \in C^{1,1}({\mathbb {T}}^2)$ so we may equivalently write $T_{(e, f)} \equiv T_{\boldsymbol {c}}$ . Here, $\mathfrak {c}(V_i):= \int _{0}^{1}\!\! \sqrt {2 \, V_i(x^i)}\,d x^i$ (see Appendix D) and $C^{1,1}$ denotes the functions in $C^1$ with Lipschitz derivative. The function $u_{\boldsymbol {c}} \in C^{1,1}({\mathbb {T}}^2)$ is a classical solution of the Hamilton–Jacobi equation
   $$ \begin{align*} \alpha_{}({\boldsymbol{c}}) = H_0(x, {\boldsymbol{c}} + \nabla_x u_{ {\boldsymbol{c}}}(x)), \end{align*} $$
   where the left-hand side is Mather’s $\alpha $ -function (see Appendix D).

2. (b) The Hamiltonian flow on $T_{\boldsymbol {c}}$ is conjugated to a rotation on ${\mathbb {T}}^2$ , that is, there exists a diffeomorphism $\varphi : {\mathbb {T}}^2 \to T_{\boldsymbol {c}}$ such that $\varphi ^{-1}\circ \Phi _t^{X_H} \circ \varphi = R_t^{\boldsymbol {\omega }}\ \text {for all } t \in \mathbb {R}$ , where $R_t^{\boldsymbol {\omega }}: {\mathbb {T}}^2 \to {\mathbb {T}}^2, x \mapsto (x + \boldsymbol {\omega } t\ \mod \mathbb {Z}^2)$ for some rotation vector $\boldsymbol {\omega } \in \mathbb {R}^2$ .

An invariant Liouville torus $T_{\boldsymbol {c}}$ is called irrational or non-resonant if ${{\boldsymbol {k}}} \cdot \boldsymbol {\omega } \neq 0$ for all . If this is not the case, the invariant torus is rational or resonant. For two-dimensional manifolds (and if $\omega _2 \neq 0$ ), this can be phrased as a distinction between $\omega _1/\omega _2 \notin \mathbb {Q}$ and $\omega _1/\omega _2 \in \mathbb {Q}$ .

Assumptions on the preserved integrability of equation (2.3)

Let $H_0 \in C^2(T^*{\mathbb {T}}^2)$ denote the Hamiltonian function from equation (2.1) satisfying one of the Assumptions (A1)–(A3), and U a perturbing potential as in equation (2.3) such that the following statement concerning the perturbed Hamilton–Jacobi equation (HJE):

(2.9) $$ \begin{align} \alpha_{\varepsilon}({\boldsymbol{c}}) = H_\varepsilon(x, {\boldsymbol{c}} + \nabla_x u_{\varepsilon, {\boldsymbol{c}}}(x) ) \end{align} $$

as well as the preserved integrability of $H_\varepsilon $ is satisfied.

1. (P) There exists an energy $e>0$ such that for every $(n,m) \in \mathcal {B}_0(\mathcal {S}_U^\perp )$ (recall equation (2.6)) and $\mu _i \in [0,\tilde {\mu }_i]$ , $i \in \{1,2\}$ , there exists a sequence $(\varepsilon _k)_{k \in \mathbb {N}}$ with $\varepsilon _k \neq 0$ but $\varepsilon _k \to 0$ such that we have the following.

   1. (i) The resonant torus from Proposition 2.1, characterized by $\boldsymbol {c} \in H^1({\mathbb {T}}^2, \mathbb {R})$ with

      (2.10) $$ \begin{align} |c_i|> \sqrt{\mu_i}\, \mathfrak{c}(V_i) \end{align} $$
      in the isoenergy submanifold $T_e$ having rotation vector proportional to $(n,m)$ , is preserved under the sequence of deformations $(H_{\varepsilon _k})_{k \in \mathbb {N}}$ .

   2. (ii) For ${\boldsymbol {c}} \in H^1({\mathbb {T}}^2, \mathbb {R})$ satisfying equation (2.10), Mather’s $\alpha $ -function and a solution $u_{\varepsilon ,{\boldsymbol {c}}}:{\mathbb {T}}^2 \to \mathbb {R}$ of the HJE in equation (2.9) can be expanded to first order in $\varepsilon $ , that is,

      (2.11) $$ \begin{align} u_{\varepsilon, {\boldsymbol{c}}} = u_{{\boldsymbol{c}}}^{(0)} + \varepsilon u_{ {\boldsymbol{c}}}^{(1)} + \mathcal{O}_{\boldsymbol{c}}(\varepsilon^2)\quad \text{and} \quad \alpha_{\varepsilon} = \alpha^{(0)} + \varepsilon \alpha^{(1)} + \mathcal{O}(\varepsilon^2), \end{align} $$
      where $u_{{\boldsymbol {c}}}^{(0)} , u_{ {\boldsymbol {c}}}^{(1)} \in C^{1,1}({\mathbb {T}}^2)$ and $O_{\boldsymbol {c}}(\varepsilon ^2)$ is understood in $C^{1,1}$ -sense. (Having $C^1$ -regularity here would be sufficient for our proofs in §4. However, we chose $C^{1,1}$ -regularity for the formulation of Assumption (P) to be in agreement with the statement from Proposition 2.1(b). More precisely, $C^{1,1}$ -regularity is kind of a compromise between the true $C^3$ -regularity of $u_{\boldsymbol {c}}$ and the required $C^1$ -regularity of $u_{\varepsilon , {\boldsymbol {c}}}$ . In addition, $C^{1,1}$ is the optimal regularity for subsolutions of equation (2.9), which exist, even if the Hamiltonian $H_\varepsilon $ is not integrable (see [12, 46]).)

We comment on the validity of assuming Assumption (P) in Remark D.1 in Appendix D. Moreover, we shall also discuss an alternative to equation (2.11) in Remark D.3. Finally, one can easily see from the proofs given in §4 that the condition on a fixed isoenergy manifold $\{ H_\varepsilon = e\}$ can be relaxed to having preservation of invariant tori in isoenergy manifolds characterized by energies $e \ge e_0$ for some fixed $e_0> 0$ .

Note that the rational invariant tori are the most ‘fragile’ objects of an integrable system as the KAM theorem [5, 63, 80] predicts that general (non-integrable) perturbations preserve only ‘sufficiently irrational’ (Diophantine) invariant tori.

2.2. Results

As mentioned above, our main results in Theorems 2.2, 2.3, and 2.4 concern rigidity of certain deformations of integrable metrics (in the sense of Question (Q2)), which, by means of the Maupertuis principle, correspond to perturbations of the form in equation (2.3). More precisely, under the assumptions formulated above, our results show that the perturbed Hamiltonian function in equation (2.3) has to be of the same general form as the unperturbed Hamiltonian function in equation (2.1). This means that the potential U is separable, that is, there exist $U_1,U_2 \in C^2({\mathbb {T}}^2)$ such that

$$ \begin{align*} U(x) = U_1(x^1) + U_2(x^2). \end{align*} $$

Theorem 2.2. Let $H_\varepsilon $ from equation (2.3) satisfy Assumption (A1) and Assumption (P) for some energy $e> 0$ . Then U is separable in a sum of two single-valued functions.

Put briefly, in view of of the Maupertuis principle, this means that integrable deformations in the same conformal class of a flat metric are Liouville metrics. Now, Theorem 2.3 generalizes Theorem 2.2 to Hamiltonian functions which depend on one toral position variable via a mechanical potential.

Theorem 2.3. Let $H_\varepsilon $ from equation (2.3) satisfy Assumption (A2) and Assumption (P) for some energy $e> 0$ . Then the following hold.

1. (a) If $\tilde {\mu }_2 = \tilde {\mu }_2(\mathcal {C}_2, \deg _U^{(2)}, e)>0$ is small enough (see Lemma 4.2), we have that U is separable in a sum of two single-valued functions.

2. (b) If, additionally, $V_2$ is analytic, then U is separable, irrespective of $\tilde {\mu }_2> 0$ , but only for $\mu _2 \in [0,\tilde {\mu }_2]$ outside of an exceptional null-set.

Therefore, by means of the Maupertuis principle, we infer that integrable deformations in the same conformal class of metrics realizing surfaces of revolution (see §3.2) are Liouville metrics. Finally, Theorem 2.4 generalizes the above results to Hamiltonian functions, which correspond to arbitrary Liouville metrics by means of the Maupertuis principle.

Theorem 2.4. Let $H_\varepsilon $ from equation (2.3) satisfy Assumption (A3) and Assumption (P) for some energy $e> 0$ . Then the following hold.

1. (a) If $\tilde {\mu }_1 = \tilde {\mu }_1(\mathcal {C}_1, \deg _U^{(1)}, \deg _U^{(2)}, e)>0$ and $\tilde {\mu }_2 = \tilde {\mu }_2(\mathcal {C}_2, \deg _U^{(1)}, \deg _U^{(2)}, e)>0$ are small enough (see Lemma 4.3), we have that U is separable in a sum of two single-valued functions.

2. (b) If, additionally, $V_2$ is analytic and $\tilde {\mu }_1 = \tilde {\mu }_1(\mathcal {C}_2, \deg _U^{(1)}, \deg _U^{(2)},e)> 0$ is small enough, then U is separable, irrespective of $\tilde {\mu }_2> 0$ , but only for $\mu _2\in [0,\tilde {\mu }_2]$ outside of an exceptional one-dimensional null-set (depending on $\mu _1 \in [0,\tilde {\mu }_1]$ ).

3. (c) If both $V_i$ for $i = 1, 2$ are analytic, then U is separable, irrespective of $\tilde {\mu }_1, \tilde {\mu }_2> 0$ , but only for $(\mu _1, \mu _2)\in [0,\tilde {\mu }_1] \times [0,\tilde {\mu }_2]$ outside of an exceptional two-dimensional null-set.

Our results formulated in Theorems 2.2, 2.3, and 2.4 can each be viewed as a verification of a special case of the following conjecture, saying that ‘(nice) integrable deformations of Liouville metrics are Liouville metrics’.

Conjecture. (Deformational rigidity of Liouville metrics)

Let g be a Liouville metric on ${\mathbb {T}}^2$ and let $(g_t)_{t \in [0,1]}$ with $g_0 = g$ be a deformation that preserves all rational invariant tori (except finitely many). Then $g_t$ is a Liouville metric for all $t \in [0,1]$ .

This conjecture is in strong analogy to the perturbative Birkhoff conjecture for integrable billiards, which is discussed in §3.4 below.

3. Literature review: integrable metrics on the torus

As pointed out in §1.1, integrability of metrics on one-dimensional manifolds is not questionable and the first non-trivial examples occur whenever M has dimension two. Recall from Definition 1.2 that integrability of metrics on two-dimensional manifolds requires the existence of only one additional first integral (beside the Hamiltonian).

3.1. Topological obstructions

The following theorem due to Kozlov [68, 69] (see [15] for a strengthened version of this result) categorizes two-dimensional compact manifolds regarding the possibility to endow them with an integrable metric (see Question (Q1)).

Theorem 3.1. (Kozlov [68, 69])

Let M be a two-dimensional compact and real-analytic manifold that is endowed with a real-analytic Riemannian metric g. If the Euler characteristic $\chi _M$ of M is negative, then there exists no other non-trivial real-analytic first integral.

A result similar to Theorem 3.1 holds for polynomially integrable geodesic flows.

Theorem 3.2. (Kolokoltsov [64])

There exist no polynomially integrable geodesic flow on a closed two-dimensional Riemannian manifold M with negative Euler characteristic $\chi _M$ .

Recall that any two-dimensional compact manifold M can be represented either as the sphere with handles or the sphere with Möbius strips, in the orientable and non-orientable case, respectively. The Euler characteristic $\chi _M$ can be computed as

$$ \begin{align*} \chi_M = 2-2g \quad \text{respectively}\ \chi_M = 2-m, \end{align*} $$

where g is the number of handles (the genus) and m is the number of Möbius strips. To have integrability, the above theorem imposes the condition $\chi _M\ge 0$ on M and we thus know that the number of handles is at most $1$ and the number of Möbius strips is not greater than $2$ . Therefore, any real-analytic two-dimensional compact Riemannian manifold $(M,g)$ with real-analytic (or polynomial) additional integral is either the sphere $\mathbb {S}^2$ or the torus ${\mathbb {T}}^2$ (in the orientable case), or the projective plane $\mathbb {R}\mathbb {P}^2$ or the Klein bottle $\mathbb {K}^2$ (in the non-orientable case). In [29], Bolsinov and Taimanov give a striking example of a real-analytic Riemannian manifold of dimension three, whose geodesic flow has the peculiar property, and that it is smoothly (but not analytically) integrable although it has positive topological entropy [1]. The problem of proving (non-)existence of smoothly (but not analytically) integrable geodesic flows on compact surfaces of genus $g> 1$ is widely open (see [31]).

In this work, we focus on integrable metrics on the torus ${\mathbb {T}}^2$ and refer to works by Bolsinov, Fomenko, Matveev, Kolokoltsov, and others [27, 48, 64, 78, 81] for studies on integrable metrics on the sphere, the projective plane, and the Klein bottle. See [24, 31] for recent surveys on open problems, and questions concerning geodesics and integrability of finite-dimensional systems in general.

3.2. Linearly and quadratically integrable metrics

The first non-trivial class of integrable metrics on the torus ${\mathbb {T}}^2$ is surfaces of revolution. Consider a two-dimensional surface $M \subset \mathbb {R}^3$ given by the equation $r = r(z)$ in standard cylindrical coordinates $(r, \varphi , z) \in (0,\infty ) \times [0,2\pi ) \times \mathbb {R}$ . As local coordinates on M, we take z and $\varphi $ . In the case where $r(z)$ is L-periodic and we identify $0$ and L, then M is diffeomorphic to the torus ${\mathbb {T}}^2$ and the Riemannian metric induced on M by the Euclidean metric on $\mathbb {R}^3$ has line element

(3.1) $$ \begin{align} d s^2 = (1+r'(z)^2) d z^2 + r(z)^2 d \varphi^2. \end{align} $$

Since the corresponding Hamiltonian function in equation (1.5) is independent of $\varphi $ , its associated momentum variable $p_\varphi $ is an additional first integral and thus the metric in equation (3.1) is integrable. Note that the additional first integral is linear in the momentum variables.

As discussed earlier, a Riemannian metric g on ${\mathbb {T}}^2$ is called a Liouville metric, whenever its line element can be written in the form in equation (1.1) in appropriate global coordinates $(x^1, x^2)$ , and where $f_1$ and $f_2$ are smooth positive periodic functions. The corresponding Hamiltonian function in equation (1.5) is given by

$$ \begin{align*} H(x^1,x^2,p_1,p_2) = \frac{p_1^2 + p_1^2}{2 (f_1(x^1)+f_2(x^2))} \end{align*} $$

and an additional first integral can easily be obtained as

$$ \begin{align*} F(x^1,x^2,p_1,p_2) = p_1^2 - f_1(x^1) H(x^1,x^2,p_1,p_2). \end{align*} $$

Therefore, clearly, also Liouville metrics are integrable. Note that the additional first integral F is quadratic in the momentum variables. It is not hard to see that a surface of revolution is just a particular case of a Liouville metric, where one can choose, e.g., $f_2 \equiv 0$ , by employing a simple change of variables.

The following proposition also provides the converse to the observation that surfaces of revolution and Liouville metrics admit additional first integrals which are linear and quadratic in the momenta, respectively. It collects several statements that have been proven in early works by Dini [43], Darboux [37], and Birkhoff [22], and were further developed by Babenko and Nekhoroshev [11], Kiyohara [62], Kolokoltsov [64], and others.

Proposition 3.3. (Linear and quadratic first integrals [11, 22, 37, 43, 62, 64])

1. (a) Let the metric g on $\mathbb {T}^2$ possess an additional first integral F that is linear in the momenta. Then there exist global periodic coordinates $(x^1,x^2)$ on the torus such that the line element of g takes the form

   $$ \begin{align*} d s^2 = f(x^1) (a(d x^1)^2 + c \,d x^1\,d x^2 + b (d x^2)^2), \end{align*} $$
   where f is some positive periodic function and $a,b,c \in \mathbb {R}$ such that the quadratic form $a\, (d x^1)^2 + c \, d x^1\, d x^2 + b\,(d x^2)^2$ is positive definite.

   Conversely, any such metric on the torus ${\mathbb {T}}^2$ admits an additional first integral that is linear in the momentum variables.

   In case a linear in momenta F exists locally near a point $q \in {\mathbb {T}}^2$ , then there exists local coordinates $(x^1,x^2)$ near q such that the line element of g reads

   $$ \begin{align*} d s^2 = f(x^1) ((d x^1 )^2+(d x^2)^2). \end{align*} $$

2. (b) A metric g on ${\mathbb {T}}^2$ possess an additional first integral F that is quadratic in the momenta if and only if there exists a finite-sheeted covering $\pi :\widetilde {{\mathbb {T}}}^2\to {\mathbb {T}}^2$ by another torus, such that the lifted metric $\widetilde {g} = \pi ^* g$ is globally Liouville, that is, there exist global periodic coordinates $(x^1,x^2)$ on $\widetilde {{\mathbb {T}}}^2$ and smooth positive periodic functions $f_1$ and $f_2$ such that the line element of $\widetilde {g}$ takes the form in equation (1.1).

   There exist Riemannian metrics g on ${\mathbb {T}}^2$ which are not globally Liouville but have an additional first integral that is quadratic in the momentum variables.

   In case a quadratic in momenta F exists locally near a point $q \in {\mathbb {T}}^2$ , then there exist local coordinates $(x^1,x^2)$ near q such that the line element of g takes the form in equation (1.1).

This classical result completely characterizes the integrable metrics g on ${\mathbb {T}}^2$ that admit an additional first integral that is linear or quadratic in the momentum variables. Similar results hold for Riemannian metrics on general two-dimensional manifolds [27, 48, 64, 81].

3.3. Polynomially integrable metrics of higher degree

In the case of a sphere $\mathbb {S}^2$ , one can easily construct examples of metrics which admit an additional first integral that is cubic respectively quartic in the momentum variables. Using the Maupertuis principle, these can be obtained from the metrics constructed from Goryachev and Chaplygin [33, 54], and Kovaleskaya [67] in the situation of the dynamics of a rigid body. Therefore, let $h>1$ be large enough (cf. equation (1.8)) and define the metrics $g_3$ and $g_4$ on $\mathbb {R}^3$ via their respective line elements

$$ \begin{align*} d s^2_3 = \frac{h-x^1}{4} \, \frac{(d x^1)^2 + (d x^2)^2 + 4 (d x^3)^2}{(x^1)^2 + (x^2)^2 + (x^3)^2/4}, \quad d s^2_4 = \frac{h-x^1}{2} \, \frac{(d x^1)^2 + (d x^2)^2 + 2 (d x^3)^2}{(x^1)^2 + (x^2)^2 + (x^3)^2/2}. \end{align*} $$

By restriction of $g_3$ and $g_4$ to the unit sphere $\mathbb {S}^2 \subset \mathbb {R}^3$ , the resulting metrics admit an additional first integral that is cubic respectively quartic in the momentum variables. It was shown by Bolsinov, Fomenko, and Kozlov [25, 28] that these cannot be reduced to first integrals that are polynomially in the momentum variables of a lower degree, that is, they are not linearly or quadratically integrable. Since all attempts to construct such examples for the case of the torus have failed so far, the following folklore conjecture emerged.

Folklore Conjecture. Liouville metrics are the only integrable metrics on ${\mathbb {T}}^2$ .

In this general form, there is strong indication for the conjecture being false, as to be shown below (see Theorem 3.8). We will, however, provide existing results, which indicate that a certain weaker version of this conjecture, also formulated below, is indeed true.

It was proven by Korn and Lichtenstein [65, 71] that on every point on a two-dimensional Riemannian manifold $(M,g)$ , there exist locally isothermal coordinates, that is, locally, the line element takes the form

(3.2) $$ \begin{align} d s^2 = \unicode{x3bb}(x^1,x^2) ((d x^1)^2 + (d x^2)^2), \end{align} $$

where $\unicode{x3bb} $ is some smooth positive function. In the case of a torus, it can be shown (by virtue of the uniformization theorem) that there exist global isothermal coordinates (not necessarily periodic), so the metric g is conformal equivalent to the Euclidean metric $g_{\mathrm {eucl}}$ . In particular, assuming that $(x^1,x^2)$ are just the angular coordinates on the torus ${\mathbb {T}}^2$ and in the special case of $\unicode{x3bb} $ being a trigonometric polynomial (this means that the spectrum $\mathcal {S}_\unicode{x3bb} $ defined in equation (2.4) is bounded), we have the following result due to Denisova and Kozlov.

Theorem 3.4. (Denisova and Kozlov [39])

Let $\unicode{x3bb} $ from equation (3.2) be a trigonometric polynomial and assume that the geodesic flow on ${\mathbb {T}}^2$ is polynomially integrable. Then there exists an additional polynomial first integral of degree at most two.

Note that by Weierstrass’s theorem, any conformal factor $\unicode{x3bb} $ can be approximated as closely as required by a trigonometric polynomial. However, in the case of a general conformal factor $\unicode{x3bb} $ , there is the following theorem, again due to Denisova and Kozlov [40].

Theorem 3.5. (Denisova and Kozlov [40])

Assume that the geodesic flow on $({\mathbb {T}}^2, g)$ is polynomially integrable with first integral F of degree n such that:

1. (a) if n is even, then F is an even function of $p_1$ and $p_2$ ;

2. (b) if n is odd, then F is an even function of $p_1$ (or $p_2$ ) and an odd function of $p_2$ (or $p_1$ ).

Then there exists an polynomial first integral of degree at most two.

In the following theorem, we collect several results from Bialy [13], Denisova, Kozlov [41] and Treshchev [42], Agapov and Aleksandrov [2], and Mironov [79].

Theorem 3.6. Let H be a natural mechanical Hamiltonian (see equation (1.7)) on the torus ${\mathbb {T}}^2$ equipped with the flat metric $g_{\mathrm {eucl}}$ . Assume that H is polynomially integrable of degree n. If $n = 3,4$ , there exists another polynomial first integral of degree at most two. Whenever H is a real-analytic Hamiltonian, this is also true for $n=5$ .

Kozlov and Treshchev [70] considered the problem from yet another point of view. They investigated the case of a mechanical Hamiltonian

$$ \begin{align*} H = \frac{1}{2} \sum_{ij} a_{ij} p_i p_j + V(x^1, \ldots , x^n), \end{align*} $$

where $A = (a_{ij})_{ij}$ is a positive definite matrix and V is a trigonometric polynomial of $(x^1, \ldots , x^n) \in {\mathbb {T}}^n$ . On the one hand, they show that there exist n polynomial first integrals if and only if the spectrum $\mathcal {S}_V$ of V is contained in $m \le n$ mutually orthogonal lines meeting at the origin. On the other hand, they showed that whenever there exist n polynomial integrals with independent forms of highest degree, then there exist n independent involutive polynomial first integrals of degree at most two. In the case where $a_{ij} = \delta _{i,j}$ (which can be achieved by diagonalization and scaling), Combot [34] improved the first result from the assumption of polynomial integrability to rational integrability, that is, the additional first integrals being rational functions of $p_i$ and $e^{i 2 \pi x^i}$ . More recently [57, 83, 84], the problem was rephrased in the language of Killing tensor fields on ${\mathbb {T}}^2$ , where the order of an additional (polynomial) first integral is replaced by the rank of a Killing tensor field.

The results of Theorems 3.4, 3.5, and 3.6 support the validity of the following weaker version of the folklore conjecture formulated by Denisova and Kozlov [39].

Conjecture. [39]

If g is a metric on ${\mathbb {T}}^2$ that is polynomially integrable, then there exists an additional polynomial first integral of degree at most two.

By Proposition 3.3, this means that polynomially integrable metrics on ${\mathbb {T}}^2$ are Liouville metrics. However, beside the partial results given above, a proof of this conjecture is still open. The numerous attempts on proving it used methods of complex analysis [11, 22] and the theory of partial differential equations (PDEs) [17, 19]. More precisely, it is shown by Kolokoltsov [64] that there exists an additional first integral quadratic in the momenta if and only if there exists a holomorphic function $R(z) = R_1(z) +i R_2(z)$ , with real valued $R_1$ and $R_2$ , and $z = x^1+i x^2$ , which solves

(3.3) $$ \begin{align} R_2 (\partial_{x^2}^2 \unicode{x3bb} - \partial_{x^1}^2 \unicode{x3bb}) + R_1 (\partial_{x^1} \partial_{x^2} \unicode{x3bb}) - 3 (\partial_{x^1} R_2)( \partial_{x^1} \unicode{x3bb}) +3 (\partial_{x^2} R_2) (\partial_{x^2} \unicode{x3bb}) + 2 (\partial_{x^2}^2 R_2) \unicode{x3bb} = 0, \end{align} $$

where $\unicode{x3bb} $ denotes the conformal factor from equation (3.2). Note that the second term in equation (3.3) disappears whenever $\unicode{x3bb} $ is the conformal factor of a Liouville metric. In this situation, the linear PDE in equation (3.3) always has a holomorphic solution $R = R_1+i R_2$ . The existence of first integrals of higher degree turns out to be equivalent to delicate questions about nonlinear PDEs of hydrodynamic type [17–19]. The PDE approach has also successfully been applied to generate new examples of integrable magnetic geodesic flows as analytic deformations of Liouville metrics on ${\mathbb {T}}^2$ without magnetic field (see [3]). In fact, the examples from [3] disprove the folklore conjecture when understood in the larger class of magnetic geodesic flows.

However, even for the original folklore conjecture stated above, there is a result due to Corsi and Kaloshin [35], which indicates it being false in the following (considerably weaker) sense.

Theorem 3.8. (Corsi and Kaloshin [35])

There exists a real-analytic mechanical Hamiltonian

$$ \begin{align*} H_\varepsilon(x^1,x^2,p_1,p_2) = \frac{p_1^2 + p_2^2}{2} + U(x^1,x^2;\varepsilon) \end{align*} $$

with a non-separable potential U and an analytic change of variables $\Phi $ such that $H_\varepsilon \circ \Phi = (p_1^2 + p_2^2)/2$ on the energy surface $\{ H_\varepsilon = 1/2 \}$ and $p \in \mathcal {P}$ , where $\mathcal {P}$ denotes a certain cone in the action space. (The function U is called non-separable whenever it cannot be written as a sum of two single-valued functions.)

If one assumes that the whole phase space $T^*{\mathbb {T}}^2$ is foliated by two-dimensional invariant Liouville tori (which is often called $C^0$ -integrability or complete integrability), then it follows from Hopf conjecture [30, 58] that the associated metric must be flat. This notion of integrability is thus too strong for a meaningful characterization of integrable metrics on ${\mathbb {T}}^2$ . (Similar results have been shown for geodesic flows of more general Finsler metrics on ${\mathbb {T}}^2$ preserving a sufficiently regular foliation of the phase space [52, 53].)

3.4. Analogy to integrable billiards

The fundamental Question (Q2) of characterizing integrable metrics on the torus ${\mathbb {T}}^2$ can be thought of as an analogue of identifying the class of integrable billiards [61]. For billiards, integrability is understood in a similar way as for the geodesic flow (see Definition 1.2). More precisely, integrability is characterized either through the existence of an integral of motion (near the boundary of the billiard table) for the so-called billiard ball map, or the existence of a foliation of the phase space (globally or near the boundary), consisting of invariant curves. The classical Birkhoff conjecture [23, 82] states that the boundary of a strictly convex integrable billiard table is necessarily an ellipse. This corresponds to the folklore conjecture formulated above. Remarkably, while the Birkhoff conjecture is believed to be true, and there is strong evidence that this indeed the case [10, 20, 49, 60] (on the opposite side, Treshev constructed a non-elliptic billiard table which is formally integrable close to a two-periodic orbit [88–90]. This formal power series has recently been shown to be of Gervey class of order $\sigma> 9/4$ [93]), the folklore conjecture in its general form was shown to be false by Theorem 3.8.

However, recall that if one assumes $C^0$ -integrability of a metric on ${\mathbb {T}}^2$ , the metric is actually flat [30, 58]. This corresponds to the following result from Bialy in the case of billiards.

Theorem 3.9. (Bialy [14])

If the phase space of the billiard ball map is completely foliated by continuous invariant curves which are all not null-homotopic, then the boundary of the billiard table is a circle.

Following a similar strategy leading to Theorem 3.9, Bialy and Mironov [21] proved the Birkhoff conjecture for centrally symmetric billiards, assuming only local $C^0$ -integrability, that is, the foliation of a suitable open proper subset of the phase space. In addition to this, the weakened version of the folklore conjecture (polynomial integrals can be reduced to integrals of degree at most two) corresponds to the so-called algebraic Birkhoff conjecture, which has recently been proven [20, 49].

The main results of this paper in Theorems 2.2, 2.3, and 2.4 prove special cases of our conjecture that integrable deformations of Liouville metrics which preserve all (but finitely many) rational invariant tori are again Liouville metrics. This is related to the following conjecture in the case of billiards.

Perturbative Birkhoff Conjecture. [61]

A smooth strictly convex domain that is sufficiently close to an ellipse and whose corresponding billiard ball map is integrable is necessarily an ellipse.

A first result in this direction was obtained by Delshams and Ramírez-Ros [38]. More recently, Avila, De Simoi, and Kaloshin [10] proved the conjecture for domains which are sufficiently close to a circle. The complete proof for domains sufficiently close to an ellipse of any eccentricity is given by Kaloshin and Sorrentino in [60]. Both works require the preservation of rational caustics (a curve $\Gamma $ is a caustic for the billiard in the domain $\Omega $ if every time a trajectory is tangent to it, then it remains tangent after every reflection according to the billiard ball map), which can be thought of as an analogue for the preservation of rational invariant tori as a fundamental assumption of our main results from §2. The result in [10] was later extended by Huang, Kaloshin, and Sorrentino [59] to the case of local integrability close to the boundary and finally significantly improved by Koval [66].

Finally, as shown by Vedyushkina and Fomenko [92], linearly and quadratically integrable geodesic flows on orientable two-dimensional Riemannian manifolds are Liouville equivalent to topological billiards, glued from planar billiards bounded by concentric circles and arcs of confocal quadrics, respectively.

4. Proofs

In this section, we prove our main result as formulated in Theorems 2.2, 2.3, and 2.4. All proofs will, in general, follow the same three-step strategy.

1. (i) Transform the unperturbed system $H_0$ in action-angle coordinates.

2. (ii) Derive a first-order harmonic equation (that is, concerning the Fourier coefficients) for the perturbation by Assumption (P).

3. (iii) Annihilate sufficiently many Fourier coefficients of the perturbing potential by proving a certain full-rank condition for a naturally associated linear system for each of the three theorems separately (cf. Lemmas 4.1, 4.2, and 4.3). Finally, for analytic potentials $V_i$ , the extensions of our results beyond the perturbative regime are proven by exploiting the analytic dependence of the linear system on $\mu _i$ (see Appendix C).

4.1. Proof of Theorem 2.2

The argument is divided into three steps.

Step (i). Fix an energy $e> 0$ . Since the Hamiltonian is already in action-angle coordinates, we simply change notation and write $(x^i,p_i) = (\theta ^i,I_i)$ for $i = 1,2$ as well as $\theta = (\theta ^1, \theta ^2)$ and $I = (I_1,I_2)$ , such that the perturbed Hamiltonian function $H_\varepsilon $ takes the form

$$ \begin{align*} H_\varepsilon(\theta, I) = \frac{I_1^2}{2} + \frac{I_2^2}{2} + \varepsilon U(\theta). \end{align*} $$

Step (ii). By Assumption (P), for any $(n,m) \in \mathcal {B}_0(\mathcal {S}_U^\perp )$ (recall equation (2.6)), we can find (in the isoenergy manifold $T_{e_\varepsilon }$ with energy $e = e_\varepsilon $ and $\varepsilon = \varepsilon _k $ for some $k \in \mathbb {N}$ ) a rational invariant invariant Liouville torus with rotation vector ${\boldsymbol {\omega }} = (\omega _1, \omega _2)$ which satisfies

(4.1) $$ \begin{align} \frac{\omega_1}{\omega_2} = \frac{n}{m} \in \mathbb{Q}. \end{align} $$

Moreover, we fix ${\boldsymbol {c}} \in H^1({\mathbb {T}}^2, \mathbb {R}) \cong \mathbb {R}^2$ to be given by ${\boldsymbol {c}} = (\omega _1, \omega _2)$ . We make this choice to cancel the average over a trajectory in equation (4.3) of the first term on the right-hand side of equation (4.2) (cf. also equations (4.6)–(4.8) below).

Using Assumption (P) again, we can expand the Hamilton–Jacobi equation in equation (2.9) as

$$ \begin{align*} \alpha_\varepsilon({\boldsymbol{c}}) &= H_\varepsilon(\theta, {\boldsymbol{c}} + \nabla u_{\varepsilon, {\boldsymbol{c}}}(\theta)) \\ &= \frac{\vert \partial_{\theta^1} u_{\varepsilon, {\boldsymbol{c}}}(\theta) + c_1\vert^2}{2} + \frac{\vert \partial_{\theta^2} u_{\varepsilon, {\boldsymbol{c}}}(\theta) + c_2\vert^2}{2} + \varepsilon U(\theta) \\ &= \frac{c_1^2}{2} + \frac{c_2^2}{2} + \langle {\boldsymbol{c}}, \nabla u_{\varepsilon, {\boldsymbol{c}}}(\theta) \rangle + \varepsilon U(\theta) + \frac{(\partial_{\theta^1} u_{\varepsilon, {\boldsymbol{c}}}(\theta) )^2}{2} + \frac{(\partial_{\theta^2} u_{\varepsilon, {\boldsymbol{c}}}(\theta))^2}{2}, \end{align*} $$

and it holds that

$$ \begin{align*} u_{\varepsilon, {\boldsymbol{c}}} = u_{{\boldsymbol{c}}}^{(0)} + \varepsilon u_{{\boldsymbol{c}}}^{(1)} + \mathcal{O}_{\boldsymbol{c}}(\varepsilon^2) \end{align*} $$

with $u_{{\boldsymbol {c}}}^{(0)} = u_{0,{\boldsymbol {c}}}$ . Since $H_0(\theta ,I)$ is integrable (and written in action-angle coordinates), one can choose $u_{0,{\boldsymbol {c}}} \equiv 0$ . By equation (D.6) in Proposition D.2 (see also [50]), we have $\alpha ^{(1)}({\boldsymbol {c}}) = [U]_0$ , where

$$ \begin{align*} [U]_0 = \int_{{\mathbb{T}}^2} U(x^1, x^2)\,d x^1 \wedge dx^2. \end{align*} $$

Since the sequence $(\varepsilon _k)_{k \in \mathbb {N}}$ from Assumption (P) converges to zero, we compare coefficients and establish the first-order equation

(4.2)

Averaging equation (4.2) over the trajectory $\theta (t) = \theta _0 + {\boldsymbol {\omega }} t \in {\mathbb {T}}^2$ , with initial position $\theta _0 \in {\mathbb {T}}^2$ and where ${\boldsymbol {\omega }} = {\boldsymbol {c}}$ is chosen according to equation (4.1), such that the period $T_{{\boldsymbol {\omega }}}$ satisfies $T_{\boldsymbol {\omega }} \cdot {\boldsymbol {\omega }} = (n,m)$ , we get

(4.3) $$ \begin{align} [U]_0 = \frac{1}{T_{\boldsymbol{\omega}}} \int_{0}^{T_{\boldsymbol{\omega}}}\, \frac{d}{dt}u^{(1)}_{\varepsilon, {\boldsymbol{c}}}(\theta(t))\,dt + \frac{1}{T_{\boldsymbol{\omega}}} \int_{0}^{T_{\boldsymbol{\omega}}} U(\theta(t))\,dt. \end{align} $$

The first integral vanishes since $\theta (0) =\theta (T_{\boldsymbol {\omega }}) $ such that we are left with

(4.4) $$ \begin{align} \int_{0}^{1} (U(\theta_0^1 + n t,\theta_0^2 + m t) - [U]_0)\,dt = 0 \end{align} $$

for all $\theta _0 = (\theta _0^1, \theta _0^2) \in {\mathbb {T}}^2$ , which easily follows from equation (4.3) after a change of variables.

Before continuing with the third and final step, we have two important observations. First, by replacing $U \to U - [U]_0$ , we can assume without loss of generality that $[U]_0 = 0$ . Second, we define the separable part, $U_{\mathrm {sep}}$ , of U as

(4.5)

(recall the definition of the spectrum and the non-singular spectrum in equations (2.4) and (2.5)). Then, after a simple computation, we find that

$$ \begin{align*} \int_{0}^{1} U_{\mathrm{sep}}(\theta_0^1 + nt, \theta_0^2 + m t)\,dt = [U_{\mathrm{sep}}]_0 \quad \text{for all } (\theta_0^1, \theta_0^2) \in {\mathbb{T}}^2 \end{align*} $$

holds generally (that is, independent of the first-order relation in equation (4.2)) by means of equation (D.6) in Proposition D.2 (see also Remark D.1). We can thus split off the separable part and assume that $\mathcal {S}_U = \mathcal {S}_{U,0}$ in the following. Hence, the third step consists of showing that ${\mathcal {S}_U = \mathcal {S}_{U,0} = \emptyset }$ .

Step (iii). The goal of this final step is to establish the following lemma.

Lemma 4.1. Let $(n,m) \in \mathcal {B}_0(\mathcal {S}_U^\perp )$ as in equation (4.1) from Step (ii). Then $U_{jm, -jn} = 0$ for all .

Since $(n,m) \in \mathcal {B}_0(\mathcal {S}_U^\perp )$ were arbitrary, this proves that

$$ \begin{align*} \mathcal{S}_U \subset(\{ 0 \} \times \mathbb{Z}) \cup (\mathbb{Z} \times \{ 0 \}), \end{align*} $$

or equivalently $\mathcal {S}_{U,0} = \emptyset $ and we have shown Theorem 2.2. It remains to prove Lemma 4.1.

Proof of Lemma 4.1

Starting from equation (4.4), we perform a Fourier decomposition to infer

$$ \begin{align*} \sum_{ k_1, k_2 \neq 0} \bigg[U_{k_1, k_2} \int_{0}^{1} e^{i 2 \pi k_1 n t} e^{i 2 \pi k_2 m t}\,d t\bigg] {e}^{{i} 2 \pi k_1 \theta_0^1} {e}^{{i} 2 \pi k_1 \theta_0^2} = 0 \quad \text{for all } (\theta_0^1, \theta_0^2) \in {\mathbb{T}}^2, \end{align*} $$

which implies that

$$ \begin{align*} U_{k_1, k_2} \cdot \delta_{k_1n+ k_2m, \, 0} = 0.\\[-34pt] \end{align*} $$

Applying Lemma 4.1 for every $(n,m) \in \mathcal {B}_0(\mathcal {S}_U^\perp )$ , we find that $\mathcal {S}_{U,0} = \emptyset $ , which finishes the proof of Theorem 2.2.

4.2. Proof of Theorem 2.3

For notational simplicity, we write $\mu \equiv \mu _2> 0$ and $V \equiv V_2 \in C^2({\mathbb {T}})$ .

Step (i). We fix an energy $e>0$ and consider the region of the phase space, where the subsystem in the second pair of coordinates is rotating, that is,

$$ \begin{align*} \frac{p_2^2}{2} - \mu V(x^2) = e^{(2)}>0 \end{align*} $$

and for ${p_1^2}/{2} = e^{(1)}> 0$ , we have $e = e^{(1)} + e^{(2)}$ . In a neighborhood of each of the two Liouville tori characterized by $H_0 = e$ and ${p_1^2}/{2} = e^{(1)}$ , we can find a change of variables $(x^2,p_2) = \Phi ^{(2)}_\mu (\theta ^2,I_2)$ (and we denote $(x^1, p_1) = (\theta ^1, I_1)$ ) such that the Hamiltonian function $H_0$ gets transformed in action-angle coordinates, that is,

$$ \begin{align*} H_0(\theta^1, I_1, \Phi^{(2)}_\mu(\theta^2,I_2)) = \frac{I_1^2}{2} + h^{(2)}_\mu(I_2) \end{align*} $$

for some smooth function $h^{(2)}_\mu $ agreeing with Mather’s $\alpha $ -function for the one-dimensional subsystem described by the Hamiltonian ${p_2^2}/{2} - \mu V(x^2)$ (see Appendix D). The change in the order of the four arguments of $H_0$ should not lead to confusion. Now, the perturbed Hamiltonian takes the form

$$ \begin{align*} H_\varepsilon(\theta^1, I_1, \Phi^{(2)}_\mu(\theta^2,I_2)) = \frac{I_1^2}{2} + h^{(2)}_\mu(I_2) + \varepsilon U(\theta^1, x^2(\theta^2,I_2,\mu)), \end{align*} $$

where we write $x^2_\mu (\theta ^2,I_2)$ for the first component of $\Phi ^{(2)}_\mu (\theta ^2,I_2)$ .

Step (ii). Assume without loss of generality that the $2$ -degree ${\deg }^{(2)}_U$ of U is at least $1$ (recall equation (2.7)), as otherwise, we had $U(x) = U_1(x^1)$ and Theorem 2.3 was proven. Then, for any $(n,m) \in \mathcal {B}_0(\mathcal {S}_U^\perp )$ , in particular with $| n| \le {\deg }_U^{(2)}$ , we can find (in the isoenergy manifold $T_{e_\varepsilon }$ with energy $ e= e_\varepsilon $ and $\varepsilon = \varepsilon _k$ for some $k \in \mathbb {N}$ ) a rational invariant Liouville torus with rotation vector $\boldsymbol {\omega } = (\omega _1, \omega _2)$ , which satisfies

(4.6) $$ \begin{align} \frac{\omega_1}{\omega_2} = \frac{n}{m} \in \mathbb{Q} \quad \text{and} \quad \boldsymbol{\omega} = (c_1, \nabla h^{(2)}_\mu(c_2)) \end{align} $$

for some $\boldsymbol {c} \in H^1({\mathbb {T}}^2, \mathbb {R}) \cong \mathbb {R}^2$ with $c_1 = \omega _1$ (as around equation (4.1)) and $\vert c_2 \vert> \gamma + \sqrt {\mu } \mathfrak {c}(V)$ for some $\gamma = \gamma (e, {\deg }^{(2)}_U)> 0$ , which we fix now. This new parameter $\gamma $ quantifies a safe distance (depending on the total energy $e>0$ and the degree of the trigonometric polynomial) to the region, opposite to where (i) the change of variables $\Phi ^{(2)}_\mu $ has bounded derivative (cf. equation (4.7)) and (ii) the function $h_\mu ^{(2)}$ is bounded from below (cf. equation (4.12)). In §4.3, we will have two such parameters, $\gamma _1, \gamma _2$ , for both coordinates directions which get transformed by some $\Phi $ .

By Assumption (P), we have

$$ \begin{align*} u_{\varepsilon, {\boldsymbol{c}}} = u_{{\boldsymbol{c}}}^{(0)} + \varepsilon u_{{\boldsymbol{c}}}^{(1)} + \mathcal{O}_{\boldsymbol{c}}(\varepsilon^2) \end{align*} $$

with $u_{{\boldsymbol {c}}}^{(0)} = u_{0,{\boldsymbol {c}}}$ and since $H_0(\theta ,I)$ is integrable (and written in action-angle coordinates), one can choose $u_{0,{\boldsymbol {c}}} \equiv 0$ . Therefore, by Assumption (P) again, we expand the Hamilton Jacobi equation in equation (2.9) as

(4.7) $$ \begin{align} \alpha_{\varepsilon}({\boldsymbol{c}}) &= H_\varepsilon(\theta, {\boldsymbol{c}} + \nabla u_{\varepsilon, {\boldsymbol{c}}}(\theta))\nonumber \\ & \nonumber= \frac{\vert \partial_{\theta^1} u_{\varepsilon, {\boldsymbol{c}}}(\theta) + c_1\vert^2}{2} + h_\mu^{(2)}(\partial_{\theta^2} u_{\varepsilon, {\boldsymbol{c}}}(\theta) + c_2)+ \varepsilon U(\theta^1,x^2_\mu(\theta^2, \partial_{\theta^2} u_{\varepsilon, {\boldsymbol{c}}}(\theta) + c_2)) \\ & \nonumber= \frac{c_1^2}{2} + h_\mu^{(2)}( c_2) + \varepsilon\langle (c_1, \nabla h_\mu^{(2)}( c_2)), \nabla u_{\varepsilon, {\boldsymbol{c}}}^{(1)}(\theta) \rangle + \varepsilon U(\theta^1, x^2_\mu(\theta^2, c_2)) \\ & \quad + \mathcal{O}( \Vert (\nabla^2 h_\mu^{(2)})\vert_{\{ \vert c_2 \vert> \gamma + \sqrt{\mu} \mathfrak{c}(V) \}} \Vert_{C^0} \varepsilon^2) + \mathcal{O} ( \Vert (\partial_{I_2} \Phi_\mu^{(2)})\vert_{\{ \vert c_2 \vert > \gamma + \sqrt{\mu} \mathfrak{c}(V) \}} \Vert_{C^0} \varepsilon^2). \end{align} $$

Since $|c_2|> \gamma + \sqrt {\mu } \mathfrak {c}(V)$ , both error terms are of the order $\mathcal {O}_\gamma (\varepsilon ^2)$ .

Analogously to the proof of Theorem 2.2, we thus obtain the first-order equation

(4.8) $$ \begin{align} [U]_0 = \langle (c_1, \nabla h_\mu^{(2)}( c_2)), \nabla u_{\varepsilon, {\boldsymbol{c}}}^{(1)}(\theta) \rangle + U(\theta^1, x^2_\mu(\theta^2, c_2)), \end{align} $$

where the constant $\alpha ^{(1)} \equiv [U]_0$ is given in equation (D.6) in Proposition D.2 (see also [50]). Just as in the proof of Theorem 2.2, after averaging equation (4.8) over the trajectory $\theta (t) = \theta _0 + {\boldsymbol {\omega }} t \in {\mathbb {T}}^2$ , with initial position $\theta _0 \in {\mathbb {T}}^2$ and where ${\boldsymbol {\omega }}$ is chosen according to equation (4.6), such that the period $T_{{\boldsymbol {\omega }}}$ satisfies $T_{\boldsymbol {\omega }} \cdot {\boldsymbol {\omega }} = (n,m)$ , we find

(4.9) $$ \begin{align} \int_{0}^{1} (U(\theta_0^1 +n t, x^2_\mu(\theta_0^2 + m t,c_2)) - [U]_0)\,{d} t = 0 \end{align} $$

for all $\theta _0 = (\theta _0^1, \theta _0^2) \in {\mathbb {T}}^2$ .

Finally, analogously to §4.1, we may assume without loss of generality $[U]_0 = 0$ and observe that

$$ \begin{align*} \int_{0}^{1} U_{\mathrm{sep}}(\theta_0^1 + nt,x^2_\mu(\theta_0^2 + m t,c_2))\,dt = [U_{\mathrm{sep}}]_0 \quad \text{for all } (\theta_0^1, \theta_0^2) \in {\mathbb{T}}^2 \end{align*} $$

holds generally (that is, independent of the first-order relation in equation (4.8)) by a simple calculation based on equation (D.6) in Proposition D.2 (see also Remark D.1). We can thus split off the separable part $U_{\mathrm {sep}}$ of U defined in equation (4.5) and assume that $\mathcal {S}_U = \mathcal {S}_{U,0}$ in the following. Hence, the third step consists of showing that $\mathcal {S}_U = \mathcal {S}_{U,0} = \emptyset $ .

Step (iii). We begin this final step with performing a Fourier decomposition in equation (4.9) such that we obtain

$$ \begin{align*} \sum_{ k_1\neq 0}&\bigg[ \sum_{0 \neq |k_2| \le \deg_U^{(2)}} U_{k_1, k_2} \int_{0}^{1} {e}^{{i} 2 \pi k_1 n t} {e}^{{i} 2 \pi k_2 x_\mu^2(\theta_0^2 + mt, c_2)}\,d t \bigg] {e}^{{i} 2 \pi k_1 \theta_0^1} = 0\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \text{for all } (\theta_0^1, \theta_0^2) \in {\mathbb{T}}^2, \end{align*} $$

which implies that $[\cdots ] = 0$ for every and $\theta _0^2 \in {\mathbb {T}}$ .

After having eliminated $\theta _0^1 \in {\mathbb {T}}$ , we now fix some and consider the family of functions $(f^{(k_1, \mu )}_{k_2})_{0 \neq |k_2| \le \deg _U^{(2)}}$ in the Hilbert space $L^2({\mathbb {T}})$ , where

(4.10) $$ \begin{align} f_{k_2}^{(k_1, \mu)}: {\mathbb{T}} \to \mathbb{C}, \quad \theta_0^2 \mapsto \sum_{\substack{(n,m) \in \mathcal{B}_0(\mathcal{S}^\perp_U) \\ \exists 0 \neq |\tilde{k}_2| \le \deg_U^{(2)} : k_1n+\tilde{k}_2m = 0}}\! \int_{0}^{1} e^{i 2 \pi k_1 n t} e^{i 2 \pi k_2 x_\mu^2(\theta_0^2 + mt, c_2)}\,dt. \end{align} $$

Note that the sum in equation (4.10) is finite by Assumption (A2) (more precisely, it ranges over at most $2 \cdot \deg _U^{(2)}$ elements from $\mathcal {B}_0(\mathcal {S}_U^\perp )$ ) and we suppressed the dependence of $|c_2|> \gamma + \sqrt {\mu } \mathfrak {c}(V)$ on $(n,m) \in \mathcal {B}_0(\mathcal {S}_U^\perp )$ from the notation (recall equation (4.6)).

In this way, the problem of proving Theorem 2.3, that is, justifying $\mathcal {S}_{U,0} = \emptyset $ , reduces to a question about linear independence for the family of functions in equation (4.10) in the Hilbert space $L^2({\mathbb {T}})$ . Recall that the family $(f^{(k_1, \mu )}_{k_2})_{0 \neq |k_2| \le \deg _U^{(2)}}$ being linearly independent is equivalent to the Gram matrix

(4.11) $$ \begin{align} G^{(k_1, \mu)} = (G_{k_2, k^{\prime}_2}^{(k_1, \mu)})_{0 \neq |k_2|, |k^{\prime}_2| \le \deg_U^{(2)}} \quad \text{with } G_{k_2, k^{\prime}_2}^{(k_1, \mu)}:= \langle f_{k_2}^{(k_1, \mu)}, f_{k^{\prime}_2}^{(k_1, \mu)} \rangle_{L^2({\mathbb{T}})} \end{align} $$

being of full rank, where $\langle g,h\rangle _{L^2({\mathbb {T}})}$ denotes the standard inner product of $g,h \in L^2({\mathbb {T}})$ .

Lemma 4.2. There exists $\tilde {\mu } = \tilde {\mu }(\mathcal {C}_2, \deg _U^{(2)}, e)> 0$ such that for all $\mu \in [0, \tilde {\mu }]$ , the Gram matrix $G^{(k_1, \mu )}$ from equation (4.11) is of full rank.

Proof. Using the version of Lemma B.1 for the inverse function, we find that

(4.12) $$ \begin{align} \Vert e^{i 2 \pi k_2 x^2_{\mu}( \, \cdot ,c_2)} - e^{i 2 \pi k_2 \, \cdot} \Vert_{C^0} = \mathcal{O}\bigg(\deg^{(2)}_U\frac{\mu \Vert V \Vert_{C^0}}{h_{\mu}(\gamma + \sqrt{\mu} \mathfrak{c}(V))}\bigg) =: \mathcal{O}(\mu) \end{align} $$

uniformly in $|k_2| \le \deg _U^{(2)}$ and $(n,m) \in \mathcal {B}_0(\mathcal {S}_U^\perp )$ .

With a slight abuse of notation for the error term, the elements $G^{(k_1, \mu )}_{k_2, k^{\prime }_2}$ of the Gram matrix can thus be computed as

$$ \begin{align*} &\int_{0}^{1}\,d \theta_0^2 \bigg( \bigg[\sum_{(n,m)} \int_{0}^{1}\,dt \, e^{-i 2 \pi k_1 n t} ( e^{-i 2 \pi k_2 m t} + \mathcal{O}(\mu)) \bigg] e^{-i 2 \pi k_2 \theta_0^2} \bigg. \\ &\quad\bigg. \times \ e^{i 2 \pi k^{\prime}_2 \theta_0^2} \bigg[\sum_{(n',m')} \int_{0}^{1}\,d t'e^{i 2 \pi k_1 n' t'} ( e^{i 2 \pi k^{\prime}_2 m' t'} + \mathcal{O}(\mu) ) \bigg]\bigg), \end{align*} $$

where the summations over $(n,m)$ and $(n',m')$ are understood as in equation (4.10). Using that for every $(k_1, k_2) \in \mathcal {S}_{U,0}$ , there exist exactly two elements from $\mathcal {B}_0(\mathcal {S}_U^\perp )$ (differing by a sign), we can evaluate both brackets $[\cdots ]$ being equal to $2 + \mathcal {O}(\deg _U^{(2)} \mu )$ .

From this, we conclude that

$$ \begin{align*} G^{(k_1, \mu)}_{k_2, k^{\prime}_2}\!=\!\int_{0}^{1}\!\!\!\,d \theta_0^2 [2 + \mathcal{O}(\deg_U^{(2)} \mu)] e^{i 2 \pi (k^{\prime}_2-k_2) \theta_0^2} [2 + \mathcal{O}(\deg_U^{(2)} \mu)] = 4 \delta_{k_2, k^{\prime}_2} + \mathcal{O}(\deg_U^{(2)}\! \mu). \end{align*} $$

Therefore, going back to equation (4.12), we infer the existence of $\tilde {\mu } = \tilde {\mu }(\mathcal {C}_2, \deg _U^{(2)}, e)> 0$ such that for all $\mu \in [0, \tilde {\mu }]$ , the Gram matrix $G^{(k_1, \mu )}$ from equation (4.11) is of full rank.

Since was arbitrary and Lemma 4.2 is independent of $k_1$ , this concludes the proof of Theorem 2.3(a).

For part (b), we note that $e^{i 2 \pi k_2 x_\mu ^2(\theta _0^2 + mt, c_2)} $ from equation (4.10) depends analytically on $\mu $ (see Appendix C). Therefore, the function $ \mu \mapsto G^{(k_1, \mu )}$ mapping to the Gram matrix in equation (4.11), for every fixed , is also analytic. (Using joint continuity of $(u,\mu ) \mapsto e^{i 2 \pi k_2 x_\mu ^2(u, c_2)}$ , it is an elementary exercise to show that the integrals over t and $\theta _0^2$ do not disturb the analyticity in $\mu $ .) This in turn implies that $\det (G^{(k_1, \mu )})$ is analytic in $\mu $ and thus, since $\det (G^{(k_1, \mu )}) \neq 0$ for $\mu \in (0,\tilde {\mu })$ (see Lemma 4.2), we find that the zero set

$$ \begin{align*} \mathcal{E}_0^{(k_1)} := \{ \mu \in (0,\infty) \mid \det(G^{(k_1, \mu)}) = 0 \} \subset (\tilde{\mu}, \infty) \end{align*} $$

of $\mu \mapsto \det (G^{(k_1, \mu )})$ is at most countable (finite in every compact subset), that is, in particular, a set of zero measure. Finally, setting

we constructed the exceptional null set, for which the conclusion $\mathcal {S}_{U,0} = \emptyset $ is not valid.

This finishes the proof of Theorem 2.3(b).

4.3. Proof of Theorem 2.4

As above, the argument is divided into three steps.

Step (i). We fix an energy $e>0$ and consider the region of the phase space, where both one-dimensional subsystems are rotating, that is,

$$ \begin{align*} \frac{p_1^2}{2} - \mu_1 V_1(x^1) = e^{(1)}>0\quad \text{and} \quad \frac{p_2^2}{2} - \mu_2 V_2(x^2) = e^{(2)}>0, \end{align*} $$

such that we have $e = e^{(1)} + e^{(2)}$ . In a neighborhood of each of the two Liouville tori characterized by $H_0 = e$ and $({p_1^2}/{2}) - \mu _1 V_1(x^1)= e^{(1)}$ , we can find two changes of variables $(x^1,p_1) = \Phi ^{(1)}_{\mu _1}(\theta ^1,I_1)$ and $(x^2,p_2) = \Phi ^{(2)}_{\mu _2}(\theta ^2,I_2)$ such that the Hamiltonian function $H_0$ gets transformed in action-angle coordinates, that is,

$$ \begin{align*} H_0(\Phi^{(1)}_{\mu_1}(\theta^1,I_1), \Phi^{(2)}_{\mu_2}(\theta^2,I_2)) = h^{(1)}_{\mu_1}(I_1) + h^{(2)}_{\mu_2}(I_2) \end{align*} $$

for some smooth functions $h^{(1)}_{\mu _1}$ and $h^{(2)}_{\mu _2}$ , which agree with Mather’s $\alpha $ -functions for the one-dimensional subsystem described by the Hamiltonians $({p_1^2}/{2}) - \mu _1 V(x^1)$ , respectively $({p_2^2}/{2}) - \mu _2 V(x^2)$ (see Appendix D). As in the proof of Theorem 2.3, the change in the order of the four arguments of $H_0$ should not lead to confusion.

Now, the perturbed Hamiltonian takes the form

$$ \begin{align*} H_\varepsilon(\Phi^{(1)}_{\mu_1}(\theta^1,I_1), \Phi^{(2)}_{\mu_2}(\theta^2,I_2)) = h^{(1)}_{\mu_1}(I_1)+ h^{(2)}_{\mu_2}(I_2) + \varepsilon U(x^1_{\mu_1}(\theta^1,I_1), x^2_{\mu_2}(\theta^2,I_2)), \end{align*} $$

where we write $x^i_{\mu _i}(\theta ^i,I_i)$ for the first component of $\Phi ^{(i)}_{\mu _i}(\theta ^i,I_i)$ , $i \in \{1,2\}$ .

Step (ii). Analogously to the proof of Theorem 2.3, we assume without loss of generality that the $1$ - and $2$ -degree ${\deg }^{(1)}_U$ and ${\deg }^{(2)}_U$ of U are at least $1$ (recall equation (2.8)), as otherwise, we had $U(x) = U_2(x^2)$ or $U(x) = U_1(x^1)$ and Theorem 2.4 was proven. Then, for any $(n,m) \in \mathcal {B}_0(\mathcal {S}_U^\perp )$ , in particular with $|m| \le {\deg }_U^{(1)}$ and $|n| \le {\deg }_U^{(2)}$ , we can find (in the isoenergy manifold $T_{e_\varepsilon }$ with energy $ e= e_\varepsilon $ and $\varepsilon = \varepsilon _k$ for some $k \in \mathbb {N}$ ) a rational invariant Liouville torus with rotation vector $\boldsymbol {\omega } = (\omega _1, \omega _2)$ which satisfies

(4.13) $$ \begin{align} \frac{\omega_1}{\omega_2} = \frac{n}{m} \in \mathbb{Q} \quad \text{and} \quad \boldsymbol{\omega} = (\nabla h^{(1)}_{\mu_1}(c_1), \nabla h^{(2)}_{\mu_2}(c_2)) \end{align} $$

for some $\boldsymbol {c} \in H^1({\mathbb {T}}^2, \mathbb {R}) \cong \mathbb {R}^2$ with $\vert c_1 \vert> \gamma _1 + \sqrt {\mu _1} \mathfrak {c}(V_1)$ and $\vert c_2 \vert> \gamma _2 + \sqrt {\mu _2} \mathfrak {c}(V_2)$ for some $\gamma _1 = \gamma _1(e, {\deg }^{(1)}_U)> 0$ , respectively $\gamma _2 = \gamma _2(e, {\deg }^{(2)}_U)> 0$ , which we fix now (see the paragraph below equation (4.6) for a discussion of the $\gamma $ parameters).

By Assumption (P), we have

$$ \begin{align*} u_{\varepsilon, {\boldsymbol{c}}} = u_{{\boldsymbol{c}}}^{(0)} + \varepsilon u_{{\boldsymbol{c}}}^{(1)} + O_{\boldsymbol{c}}(\varepsilon^2) \end{align*} $$

with $u_{{\boldsymbol {c}}}^{(0)} = u_{0,{\boldsymbol {c}}}$ and since $H_0(\theta ,I)$ is integrable (and written in action-angle coordinates), one can choose $u_{0,{\boldsymbol {c}}} \equiv 0$ . Therefore, by Assumption (P) again, we expand the Hamilton Jacobi in equation (2.9) as

$$ \begin{align*} \alpha_{\varepsilon}({\boldsymbol{c}}) &= H_\varepsilon(\theta, {\boldsymbol{c}} + \nabla u_{\varepsilon, {\boldsymbol{c}}}(\theta) ) \\ &= h_{\mu_1}^{(1)}(\partial_{\theta^1} u_{\varepsilon, {\boldsymbol{c}}}(\theta) + c_1) + h_{\mu_2}^{(2)}(\partial_{\theta^2} u_{\varepsilon, {\boldsymbol{c}}}(\theta) + c_2) \\[1mm] & \quad + \varepsilon U(x^1_{\mu_1}(\theta^1, \partial_{\theta^1} u_{\varepsilon, {\boldsymbol{c}}}(\theta) + c_1),x^2_{\mu_2}(\theta^2, \partial_{\theta^2} u_{\varepsilon, {\boldsymbol{c}}}(\theta) + c_2)) \\[1mm] & =\! \sum_{i=1}^{2}h_{\mu_i}^{(i)}( c_i)\! +\! \varepsilon \langle (\nabla h_{\mu_1}^{(1)}( c_1), \nabla h_{\mu_2}^{(2)}( c_2)), \nabla u_{\varepsilon, {\boldsymbol{c}}}^{(1)}(\theta) \rangle + \varepsilon U(x^1_{\mu_1}(\theta^1, c_1), x^2_{\mu_2}(\theta^2, c_2)) \\ & \quad + \mathcal{O}\bigg( \sum_{i=1}^{2}(\Vert (\nabla^2 h_{\mu_i}^{(i)})\vert_{\{ \vert c_i \vert> \gamma_i + \sqrt{\mu_i} \mathfrak{c}(V_i) \}} \Vert_{C^0} + \Vert (\partial_{I_i} \Phi_{\mu_i}^{(i)})\vert_{\{ \vert c_i \vert > \gamma_i + \sqrt{\mu_i} \mathfrak{c}(V_i) \}} \Vert_{C^0} ) \varepsilon^2\bigg). \end{align*} $$

Since $|c_i|> \gamma _i + \sqrt {\mu _i} \mathfrak {c}(V_i)$ , the error term is of order $\mathcal {O}_{\gamma _i}(\varepsilon ^2)$ .

Analogously to the proofs of Theorems 2.2 and 2.3, we thus obtain the first-order equation

(4.14) $$ \begin{align} [U]_0 = \langle (\nabla h_{\mu_1}^{(1)}( c_1), \nabla h_{\mu_2}^{(2)}( c_2)), \nabla u_{\varepsilon, {\boldsymbol{c}}}^{(1)}(\theta) \rangle + U(x^1_{\mu_1}(\theta^1, c_1), x^2_{\mu_2}(\theta^2, c_2)), \end{align} $$

where the constant $\alpha ^{(1)} \equiv [U]_0$ is again given by equation (D.6) in Proposition D.2 (see also [50]). Just as in the proof of Theorems 2.2 and 2.3, after averaging equation (4.14) over the trajectory $\theta (t) = \theta _0 + {\boldsymbol {\omega }} t \in {\mathbb {T}}^2$ , with initial position $\theta _0 \in {\mathbb {T}}^2$ and where ${\boldsymbol {\omega }}$ is chosen according to equation (4.13) such that the period $T_{{\boldsymbol {\omega }}}$ satisfies $T_{\boldsymbol {\omega }} \cdot {\boldsymbol {\omega }} = (n,m)$ ,

(4.15) $$ \begin{align} \int_{0}^{1} (U(x^1_{\mu_1}(\theta_0^1 +n t, c_1), x^2_{\mu_2}(\theta_0^2 + m t,c_2)) - [U]_0)\,{d} t = 0 \end{align} $$

for all $\theta _0 = (\theta _0^1, \theta _0^2) \in {\mathbb {T}}^2$ .

Finally, analogously to §§4.1 and 4.2, we may assume without loss of generality $[U]_0 = 0$ and observe that

$$ \begin{align*} \int_{0}^{1} U_{\mathrm{sep}}(x^1_{\mu_1}(\theta_0^1 +n t, c_1),\ x^2_{\mu_2}(\theta_0^2 + m t,c_2))\,dt = [U_{\mathrm{sep}}]_0 \quad \text{for all } (\theta_0^1, \theta_0^2) \in {\mathbb{T}}^2 \end{align*} $$

holds generally (that is, independent of the first-order relation in equation (4.14)) by a simple calculation based on equation (D.6) in Proposition D.2 (see also Remark D.1). We can thus split off the separable part $U_{\mathrm {sep}}$ of U defined in equation (4.5) and assume that $\mathcal {S}_U = \mathcal {S}_{U,0}$ in the following. Hence, the third step consists of showing that $\mathcal {S}_U = \mathcal {S}_{U,0} = \emptyset $ .

Step (iii). We begin this final step with performing a Fourier decomposition in equation (4.15), such that we obtain

$$ \begin{align*} \sum_{\substack{ 0 \neq |k_1| \le \deg_U^{(1)} \\ 0 \neq |k_2| \le \deg_U^{(2)}}} U_{k_1, k_2}\! \int_{0}^{1} e^{i 2 \pi k_1 x_{\mu_1}^1(\theta_0^1 + nt, c_1)} e^{i 2 \pi k_2 x_{\mu_2}^2(\theta_0^2 + mt, c_2)}\,dt = 0 \quad \text{for all } (\theta_0^1, \theta_0^2) \in {\mathbb{T}}^2. \end{align*} $$

Analogously to the proof of Theorem 2.3, we now consider the family of functions

$$ \begin{align*} (f^{(\mu_1, \mu_2)}_{k_1, k_2})_{0 \neq |k_1| \le \deg_U^{(1)}, 0 \neq |k_2| \le \deg_U^{(2)}} \end{align*} $$

in the Hilbert space $L^2({\mathbb {T}}^2)$ , where

(4.16) $$ \begin{align} f_{k_1, k_2}^{(\mu_1, \mu_2)}: {\mathbb{T}}^2 \to \mathbb{C}, \quad (\theta_0^1, \theta_0^2) \mapsto \! \sum_{\substack{(n,m) \in \mathcal{B}_0(\mathcal{S}^\perp_U) }}\! \int_{0}^{1} e^{i 2 \pi k_1 x_{\mu_1}^1(\theta_0^1 + nt, c_1)} e^{i 2 \pi k_2 x_\mu^2(\theta_0^2 + mt, c_2)}\,dt. \end{align} $$

Note that the sum in equation (4.16) is finite by Assumption (A3) (more precisely, it ranges over the at most $(2 \deg _U^{(1)}) \cdot (2 \deg _U^{(2)}) $ elements from $\mathcal {B}_0(\mathcal {S}_U^\perp )$ ) and we suppressed the dependence of $|c_i|> \gamma _i + \sqrt {\mu _i} \mathfrak {c}(V_i)$ on $(n,m) \in \mathcal {B}_0(\mathcal {S}_U^\perp )$ from the notation (recall equation (4.13)).

In this way, the problem of proving Theorem 2.4, that is, justifying $\mathcal {S}_{U,0} = \emptyset $ , reduces to a question about linear independence for the family of functions in equation (4.16) in the Hilbert space $L^2({\mathbb {T}}^2)$ . Recall that the family $(f^{( \mu )}_{k_1, k_2})_{(k_1, k_2)}$ being linearly independent is equivalent to the Gram matrix $G^{( \mu )} $ with entries

(4.17) $$ \begin{align} G_{(k_1, k_2), (k^{\prime}_1, k^{\prime}_2)}^{(\mu_1, \mu_2)}:= \langle f_{k_1, k_2}^{( \mu_1, \mu_2)}, f_{k^{\prime}_1, k^{\prime}_2}^{(\mu_1, \mu_2)} \rangle_{L^2({\mathbb{T}}^2)} \quad \text{for } 0 \neq |k_i|, |k^{\prime}_i| \le \deg_U^{(i)}, \ i \in \{1,2\}, \end{align} $$

being of full rank, where $\langle g,h\rangle _{L^2({\mathbb {T}}^2)}$ denotes the standard inner product of $g,h \in L^2({\mathbb {T}}^2)$ .

Lemma 4.3. There exist $\tilde {\mu }_i = \tilde {\mu }(\mathcal {C}_i,\deg _U^{(1)}, \deg _U^{(2)}, e)> 0$ such that for all $\mu _i \in [0, \tilde {\mu }_i]$ , $i \in \{1,2\}$ , the Gram matrix $G^{(\mu _1, \mu _2)}$ from equation (4.17) is of full rank.

Proof. Using the version of Lemma B.1 for the inverse function, we find that

(4.18) $$ \begin{align} \Vert e^{i 2 \pi k_i x^i_{\mu_i}( \, \cdot ,c_i)} - e^{i 2 \pi k_i \, \cdot} \Vert_{C^0} = \mathcal{O}\bigg(\deg^{(i)}_U\frac{\mu_i \Vert V_i \Vert_{C^0}}{h_{\mu_i}^{(i)}(\gamma_i + \sqrt{\mu_i} \mathfrak{c}(V_i))}\bigg) =: \mathcal{O}(\mu_i) \end{align} $$

uniformly in $|k_i| \le \deg _U^{(i)}$ and $(n,m) \in \mathcal {B}_0(\mathcal {S}_U^\perp )$ .

Similarly to Lemma 4.2, with a slight abuse of notation for the error term, the elements $ G_{(k_1, k_2), (k^{\prime }_1, k^{\prime }_32)}^{(\mu _1, \mu _2)}$ of the Gram matrix can thus be computed as

$$ \begin{align*} &\int_{0}^{1}\,d \theta_0^1 \int_{0}^{1}\,d \theta_0^2 \bigg( \bigg[\sum_{(n,m)} \int_{0}^{1}\,dt ( e^{-i 2 \pi k_1 n t} + \mathcal{O}(\mu_1)) ( e^{-i 2 \pi k_2 m t} + \mathcal{O}(\mu_2) ) \bigg] e^{-i 2 \pi k_1 \theta_0^1}e^{-i 2 \pi k_2 \theta_0^2} \\ &\quad \times \ e^{i 2 \pi k^{\prime}_1 \theta_0^1}e^{i 2 \pi k^{\prime}_2 \theta_0^2} \bigg[\sum_{(n',m')} \int_{0}^{1}\,d t' ( e^{i 2 \pi k^{\prime}_1 n' t'} + \mathcal{O}(\mu_1)) ( e^{i 2 \pi k^{\prime}_2 m' t'} + \mathcal{O}(\mu_2) ) \bigg]\bigg), \end{align*} $$

where the summations over $(n,m)$ and $(n',m')$ are understood as in equation (4.16). Using that for every $(k_1, k_2) \in \mathcal {S}_{U,0}$ , there exist exactly two elements from $\mathcal {B}_0(\mathcal {S}_U^\perp )$ (differing by a sign), we can evaluate both brackets $[\cdots ]$ being given by

$$ \begin{align*} 2 + \mathcal{O}(\deg_U^{(1)} \deg_U^{(2)}\mu_1)+ \mathcal{O} (\deg_U^{(1)}\deg_U^{(2)} \mu_2) =: 2 + \mathcal{O}( \deg_U^{(1)} \deg_U^{(2)} (\mu_1 + \mu_2 )), \end{align*} $$

after absorption of the second-order error in the first-order ones.

From this, we conclude that

$$ \begin{align*} G_{(k_1, k_2), (k^{\prime}_1, k^{\prime}_2)}^{(\mu_1, \mu_2)} &= \int_{0}^{1}\,d \theta_0^1 \int_{0}^{1}\,d \theta_0^2 ( [ 2 + \mathcal{O}(\deg_U^{(1)} \deg_U^{(2)} (\mu_1 + \mu_2 ))] e^{i 2 \pi (k^{\prime}_1-k_1)\theta_0^1} \\ &\quad \times \, e^{i 2 \pi (k^{\prime}_2-k_2) \theta_0^2} [ 2 + \mathcal{O}( \deg_U^{(1)} \deg_U^{(2)} (\mu_1 + \mu_2 ) ) ] ) \\ &=4 \delta_{k_1, k^{\prime}_1} \delta_{k_2, k^{\prime}_2}+\mathcal{O} ( \deg_U^{(1)} \deg_U^{(2)} (\mu_1 + \mu_2 )). \end{align*} $$

Therefore, going back to equation (4.18), we infer the existence of $\tilde {\mu }_i = \tilde {\mu }(\mathcal {C}_i,\deg _U^{(1)}, \deg _U^{(2)}, e)> 0$ , $i \in \{1,2\}$ , such that for all $\mu _i \in [0, \tilde {\mu }_i]$ , the Gram matrix $G^{(\mu _1, \mu _2)}$ from equation (4.17) is of full rank.

This finishes the proof of Theorem 2.4(a). For part (b), similarly to the proof of Theorem 2.3(b), we observe that for every fixed $\mu _1 \in [0,\tilde {\mu }_1]$ , the function $\mu _2 \mapsto \det (G^{(\mu _1, \mu _2)})$ is analytic. Since $\det (G^{(\mu _1, \mu _2)}) \neq 0$ for $\mu _2 \in (0,\tilde {\mu }_2)$ (see Lemma 4.3), we find that the zero set

$$ \begin{align*} \mathcal{E}_0^{(\mu_1)} := \{ \mu_2 \in (0,\infty) \mid \det(G^{(\mu_1, \mu_2)}) = 0 \} \subset (\tilde{\mu}_2, \infty) \end{align*} $$

of $\mu _2 \mapsto \det (G^{(\mu _1, \mu _2)})$ is at most countable (finite in every compact subset), that is, in particular, a (one-dimensional) set of zero measure.

Finally, for part (c), we note that, similarly to the proof of Theorem 2.3(b) and by means of Hartogs’s theorem on separate analyticity [56] (a separately analytic function is jointly analytic), the function $(\mu _1, \mu _2) \mapsto \det (G^{(\mu _1, \mu _2)})$ is (jointly) analytic. Since $\det (G^{(\mu _1, \mu _2)}) \neq 0$ for $(\mu _1, \mu _2) \in (0,\tilde {\mu }_1) \times (0,\tilde {\mu }_2)$ (see Lemma 4.3), we find that the zero set

$$ \begin{align*} \mathcal{E}_0 := \{ (\mu_1, \mu_2) \in (0,\infty)\times (0,\infty) \mid \det(G^{(\mu_1, \mu_2)}) = 0 \} \subset (\tilde{\mu}_1, \infty) \times (\tilde{\mu}_2, \infty) \end{align*} $$

of $(\mu _1, \mu _2) \mapsto \det (G^{(\mu _1, \mu _2)})$ is a (two-dimensional) set of zero measure.

This concludes the proof of Theorem 2.4(c).

5. Concluding remarks and outlook

We have shown that integrable deformations of Liouville metrics on ${\mathbb {T}}^2$ are Liouville metrics—at least when more restrictive conditions on the unperturbed metric are balanced with more general conditions on the perturbation. Removing this balancing, that is, showing that arbitrary integrable deformations of arbitrary Liouville metrics remain of Liouville type, is an interesting problem for future investigations resolving the conjecture proposed at the end of §2. This would require stronger versions of Lemmas 4.2 and 4.3 in two senses.

1. (a) Allow for possibly infinitely many non-zero Fourier coefficients and refrain from restricting to trigonometric polynomials. A resolution of this issue has been found in the context of the perturbative Birkhoff conjecture [10, 60] concerning integrable billiards. Here, the authors studied the matrix of correlations between the standard basis $(e^{i 2 \pi k x})_{k \in \mathbb {Z}}$ of $L^2({\mathbb {T}})$ and certain deformed dynamical modes (given as some kind of Jacobi elliptic function, see Appendix C of the arXiv: 2210.02961 version of this article), corresponding to $e^{i 2 \pi k_i x^i_{\mu _i}( \, \cdot ,c_i)}$ in Lemmas 4.2 and 4.3. Exponential estimates for the entries of this matrix (obtained from considering the maximal width of a strip of analyticity around the real axis for the dynamical modes) allowed to prove a suitable full-rank lemma, also for infinitely many coefficients.

2. (b) Allow arbitrary $\tilde {\mu _i}> 0$ and refrain from restricting to small ones. Also for this issue, a potential resolution might be found by analytically extending action-angle coordinates to the complex plane and exploiting their singularities away from the real axis. However, this requires the potentials $V_i$ in the unperturbed Hamiltonian to be restrictions of holomorphic functions and, as such, way more special than generic $V_i \in C^2({\mathbb {T}})$ .

Moreover, we note that in [60], the authors also outlined a potential strategy for proving the classical (non-perturbative) Birkhoff conjecture, which might possibly be adapted for proving a suitably weakened version of the folklore conjecture given in §3.

We end this section with a brief list of open problems being related to the main results of the present paper.

1. (i) As described above, it is an natural follow-up problem to extend our results to the situation where arbitrary integrable deformations of arbitrary Liouville metrics remain of Liouville type, that is, remove the restricting assumptions from Assumptions (A1)–(A3) and prove the conjecture formulated at the end of §2.

2. (ii) In particular, starting with (the time-independent version of) Arnold’s example [6] for diffusion,

   $$ \begin{align*} H_0(x,p) = \frac{p_1^2}{2} + \frac{p_2^2}{2} - \mu (1 - \cos(2 \pi x^2)), \end{align*} $$
   is it possible to deduce rigidity, similarly to Theorem 2.3, but without restricting to the perturbation being a trigonometric polynomial in $x^2$ and any smallness condition on $\mu \in [0,1]$ ? In this case, the full rank lemma might be obtained by proving non-degeneracy of certain infinite-dimensional matrices, which have Fourier coefficients of powers of Jacobi elliptic functions (see Appendix C of the arXiv: 2210.02961 version of this article) as their entries.

3. (iii) In view of the non-trivial examples of magnetic geodesic flows found in [3] and the potential counterexample constructed in [35], it is a major task to completely settle the folklore conjecture mentioned in §§1 and 3, that is, clarify which part is only ‘folklore’ and which part is ‘real’.

4. (iv) In particular, the main result of [35], which we stated in Theorem 3.8, should be extended to show that the system is really integrable on an open set in the phase space and not only on an isoenergy manifold. Furthermore, it remains open, whether the PDEs underlying the examples in [3] can be solved with zero magnetic fields or not and thus potentially disproves the folklore conjecture.

5. (v) For our main results, we assumed the preservation of rational invariant tori ‘outside the eye of the pendulum’ (cf. Figure 1). Can one obtain the same result, if only tori ‘inside the eye’ are preserved?

6. (vi) An alternative approach to the one chosen here could be to study perturbations of the additional first integral in equation (2.2), that is, write $F_\varepsilon = F_0 + \varepsilon F_1 + \mathcal {O}(\varepsilon ^2)$ and use the vanishing of the Poisson bracket $\{H_\varepsilon , F_\varepsilon \} = 0$ with $H_\varepsilon = H_0 + \varepsilon U$ to obtain the first-order equation

   $$ \begin{align*} \{H_0, F_1\} + \{U, F_0\} = 0 \end{align*} $$
   for the perturbing potential U.

7. (vii) Does there exist a Riemannian metric g on ${\mathbb {T}}^2$ such that its geodesic flow admits hyperbolic periodic orbits of at least three different homotopy types? If yes, does there exist a Liouville metric with this property? (These questions were suggested by Vadim Kaloshin.)