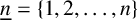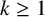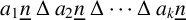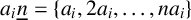1 Introduction
Although the conjecture mentioned in the title originated through its connections with coding theory (see [Reference Pilz4] regarding minimum distances of certain linear codes defined via polynomial near-rings), we intend to discuss it here from a more informal and general viewpoint, without its connections to coding theory.
Imagine three people with the numbers 1, 2 and 3 on their respective T-shirts entering an empty room. After a minute, three other people with the numbers 2, 4 and 6 on their T-shirts enter the room. There are now two people with the number 2, and these two decide to leave the room, leaving the four people with numbers 1, 3, 4 and 6 behind in the room. After another minute, three further people, with the numbers 3, 6 and 9 on their T-shirts enter the room, and the same procedure is followed: the two with number 3, as well as the two with number 6, leave the room, and the three without matching numbers (1, 4 and 9) stay in the room. Then three more people with the numbers 4, 8 and 12 enter the room, and so on. The conjecture is that there will always be at least three people left in the room. Note that we could reformulate this in terms of symmetric differences of sets, namely, the cardinality of
![]() $\{1,2,3\}\, {\mathbin {\Delta }}\, \{2,4,6\}\, {\mathbin {\Delta }}\cdots {\mathbin {\Delta }}\, \{k,2k,3k\}$
is at least 3 for any positive integer k. This result is fairly easy to prove. A slightly more general form of this conjecture is also not too difficult to establish: the cardinality of
$\{1,2,3\}\, {\mathbin {\Delta }}\, \{2,4,6\}\, {\mathbin {\Delta }}\cdots {\mathbin {\Delta }}\, \{k,2k,3k\}$
is at least 3 for any positive integer k. This result is fairly easy to prove. A slightly more general form of this conjecture is also not too difficult to establish: the cardinality of
is at least three for any sequence
![]() $a_{1}<a_{2}<\cdots <a_{k}$
of positive integers.
$a_{1}<a_{2}<\cdots <a_{k}$
of positive integers.
The most general form of the conjecture is the following assertion.
General Conjecture. For any positive integer n, the cardinality of the set
is at least n for any sequence
![]() $a_{1}<a_{2}<\cdots <a_{k}$
of positive integers.
$a_{1}<a_{2}<\cdots <a_{k}$
of positive integers.
Some partial results have been established. For example, the conjecture is known to be true when
![]() $\{a_{1},a_{2},\ldots ,a_{k}\}=\{1,2,\ldots ,k\}$
(see [Reference Huang, Ke and Pilz2, Reference Pach and Szabó3]). We note that the reviewer of the article [Reference Pach and Szabó3] (Mathematical Reviews, #MR2862558) wrote ‘
$\{a_{1},a_{2},\ldots ,a_{k}\}=\{1,2,\ldots ,k\}$
(see [Reference Huang, Ke and Pilz2, Reference Pach and Szabó3]). We note that the reviewer of the article [Reference Pach and Szabó3] (Mathematical Reviews, #MR2862558) wrote ‘
![]() $\ldots $
and therefore establishes the value of the distance of the aforementioned code’. This is not true as the minimal distance of the code is only determined when the general conjecture is proved. The general conjecture is also known to be true for all n with
$\ldots $
and therefore establishes the value of the distance of the aforementioned code’. This is not true as the minimal distance of the code is only determined when the general conjecture is proved. The general conjecture is also known to be true for all n with
![]() $1\le n\le 6$
(see [Reference Pilz4]). There are also combinatorial problems motivated by the conjecture (see [Reference Caicedo, Chartier and Pach1]).
$1\le n\le 6$
(see [Reference Pilz4]). There are also combinatorial problems motivated by the conjecture (see [Reference Caicedo, Chartier and Pach1]).
The aim of this paper is to show that the general conjecture is true for all positive integers n and for all
![]() $a_{1},a_{2},\ldots ,a_{k}$
, where
$a_{1},a_{2},\ldots ,a_{k}$
, where
![]() $1\le k\le 3$
.
$1\le k\le 3$
.
Although the general consensus is that the conjecture should be true, no proof is known. One easily senses that the cardinality of such symmetric differences can get as large as possible. In fact, this is true. As shown in [Reference Huang, Ke and Pilz2], when
![]() $\{a_{1},a_{2},\ldots ,a_{k}\}=\{1,2,\ldots ,k\}$
, the resulting cardinality of the symmetric difference is at least
$\{a_{1},a_{2},\ldots ,a_{k}\}=\{1,2,\ldots ,k\}$
, the resulting cardinality of the symmetric difference is at least
![]() $\max \{k,n\}$
. As an extreme case, when
$\max \{k,n\}$
. As an extreme case, when
![]() $\{a_{1},a_{2},\ldots ,a_{k}\}=\{1,n+1,\ldots ,kn+1\}$
, the cardinality of the symmetric difference is
$\{a_{1},a_{2},\ldots ,a_{k}\}=\{1,n+1,\ldots ,kn+1\}$
, the cardinality of the symmetric difference is
![]() $kn,$
since no cancellations occur. However, it is also true that for any fixed
$kn,$
since no cancellations occur. However, it is also true that for any fixed
![]() $n\geq 2$
and for any
$n\geq 2$
and for any
![]() $r\geq 0$
, one can choose
$r\geq 0$
, one can choose
![]() $a_{1}<a_{2}<\cdots <a_{k}$
, where
$a_{1}<a_{2}<\cdots <a_{k}$
, where
![]() $k>r$
, such that the cardinality of
$k>r$
, such that the cardinality of
is exactly n. A proof of this fact will be given in the last section. One realises from these facts that there can be no straightforward way to approach the problem. For example, induction may not work on the general situation. Some new ideas are needed.
We hope that the material presented here will spark interest in the problem so that more, if not all, cases will be proved.
2 Terminology
To begin with, we establish some notation and terminology. For any positive integer n, put
![]() $\underline {n}=\{1,2,\ldots ,n\}$
. For positive integers
$\underline {n}=\{1,2,\ldots ,n\}$
. For positive integers
![]() $a_{1}<a_{2}<\cdots <a_{k}$
, where
$a_{1}<a_{2}<\cdots <a_{k}$
, where
![]() $k\ge 1$
, we consider the symmetric difference of the sets
$k\ge 1$
, we consider the symmetric difference of the sets
![]() $a_{i}\underline {n}=\{a_{i},2a_{i},\ldots ,na_{i}\}$
,
$a_{i}\underline {n}=\{a_{i},2a_{i},\ldots ,na_{i}\}$
,
![]() $i=1,2,\ldots ,k$
, that is,
$i=1,2,\ldots ,k$
, that is,
![]() $\Delta _{i=1}^{k}a_{i}\underline {n}=a_{1}\underline {n}{\mathbin {\Delta }} a_{2}\underline {n}{\mathbin {\Delta }}\cdots {\mathbin {\Delta }} a_{k}\underline {n}$
. Throughout the article, the k integers
$\Delta _{i=1}^{k}a_{i}\underline {n}=a_{1}\underline {n}{\mathbin {\Delta }} a_{2}\underline {n}{\mathbin {\Delta }}\cdots {\mathbin {\Delta }} a_{k}\underline {n}$
. Throughout the article, the k integers
![]() $a_{1},a_{2},\ldots ,a_{k}$
will be referred to as the multipliers. By using standard counting techniques based on the inclusion–exclusion principle, it follows that the cardinality of
$a_{1},a_{2},\ldots ,a_{k}$
will be referred to as the multipliers. By using standard counting techniques based on the inclusion–exclusion principle, it follows that the cardinality of
![]() $\Delta _{i=1}^{k}a_{i}\underline {n}$
is given by
$\Delta _{i=1}^{k}a_{i}\underline {n}$
is given by
 $$ \begin{align} \xi_{n,k}(a_{1},a_{2},\ldots,a_{k})=\sum_{r=1}^{k}\sum_{1\le i_{1}<i_{2}<\cdots<i_{r}\le k}(-1)^{r-1}2^{r-1}\bigg\lfloor\frac{a_{i_{1}}\!\cdot{n}}{[a_{i_{1}},a_{i_{2}},\ldots,a_{i_{r}}]}\bigg\rfloor. \end{align} $$
$$ \begin{align} \xi_{n,k}(a_{1},a_{2},\ldots,a_{k})=\sum_{r=1}^{k}\sum_{1\le i_{1}<i_{2}<\cdots<i_{r}\le k}(-1)^{r-1}2^{r-1}\bigg\lfloor\frac{a_{i_{1}}\!\cdot{n}}{[a_{i_{1}},a_{i_{2}},\ldots,a_{i_{r}}]}\bigg\rfloor. \end{align} $$
Here, and throughout the rest of our discussion, we use
![]() $[x,y,z,\ldots ]$
for the least common multiple of the integers
$[x,y,z,\ldots ]$
for the least common multiple of the integers
![]() $x,y,z,\ldots .$
Likewise, we use
$x,y,z,\ldots .$
Likewise, we use
![]() $(x,y,z,\ldots )$
for the greatest common divisor of
$(x,y,z,\ldots )$
for the greatest common divisor of
![]() $x,y,z,\ldots .$
$x,y,z,\ldots .$
The conjecture asserts that
![]() $\xi _{n,k}(a_{1},a_{2},\ldots ,a_{k})\ge n$
for any
$\xi _{n,k}(a_{1},a_{2},\ldots ,a_{k})\ge n$
for any
![]() $n\ge 1$
and any sequence
$n\ge 1$
and any sequence
![]() $a_{1}<a_{2}<\cdots <a_{k}$
of k multipliers, for any
$a_{1}<a_{2}<\cdots <a_{k}$
of k multipliers, for any
![]() $k\ge 1$
. Our aim is to prove this conjecture for the cases
$k\ge 1$
. Our aim is to prove this conjecture for the cases
![]() $k=1,2,3$
.
$k=1,2,3$
.
3 The cases
 $k=1$
and
$k=1$
and
 $k=2$
$k=2$
The conjecture is trivially true when
![]() $k=1$
, since
$k=1$
, since
![]() $\xi _{n,1}(a_{1})=n$
, which is the cardinality of
$\xi _{n,1}(a_{1})=n$
, which is the cardinality of
![]() $a_{1}\underline {n}=\{a_{1},2a_{1},\ldots ,na_{1}\}$
.
$a_{1}\underline {n}=\{a_{1},2a_{1},\ldots ,na_{1}\}$
.
For
![]() $k=2$
, consider the multipliers
$k=2$
, consider the multipliers
![]() $a_{1}<a_{2}$
. Since
$a_{1}<a_{2}$
. Since
![]() $a_{1}<a_{2}\le [a_{1},a_{2}]$
, and since
$a_{1}<a_{2}\le [a_{1},a_{2}]$
, and since
![]() ${a_{1}\mid [a_{1},a_{2}]}$
, we have
${a_{1}\mid [a_{1},a_{2}]}$
, we have
![]() $[a_{1},a_{2}]\ge 2a_{1}$
. So,
$[a_{1},a_{2}]\ge 2a_{1}$
. So,
![]() ${a_{1} n}/{[a_{1},a_{2}]}\le {n}/{2}$
, from which it follows that
${a_{1} n}/{[a_{1},a_{2}]}\le {n}/{2}$
, from which it follows that
since
![]() $\lfloor {n}/{2}\rfloor \le {n}/{2}$
.
$\lfloor {n}/{2}\rfloor \le {n}/{2}$
.
4 The case
 $k=3$
$k=3$
The conjecture is known to be true for
![]() $1\le n\le 6$
[Reference Pilz4, Corollary 2]. Hence, for the remainder of this paper, we will assume that
$1\le n\le 6$
[Reference Pilz4, Corollary 2]. Hence, for the remainder of this paper, we will assume that
![]() $n\ge 7$
. To avoid unnecessary subscripts, we will simply denote the multipliers
$n\ge 7$
. To avoid unnecessary subscripts, we will simply denote the multipliers
![]() $a_{1}<a_{2}<a_{3}$
by
$a_{1}<a_{2}<a_{3}$
by
![]() $a<b<c$
in this section. Furthermore, since
$a<b<c$
in this section. Furthermore, since
![]() $a=1$
does not have any prime divisors, it turns out that we should treat this case separately.
$a=1$
does not have any prime divisors, it turns out that we should treat this case separately.
Hence, we will assume first that the multipliers are
![]() $1<b<c$
. Here we want to show that
$1<b<c$
. Here we want to show that
This will be investigated by considering two sub-cases.
(1) Assume
![]() $b\mid c$
, say
$b\mid c$
, say
![]() $c=tb,\ t\ge 2$
. Then,
$c=tb,\ t\ge 2$
. Then,
 $$ \begin{align*} n-\bigg(\bigg\lfloor\frac{n}{b}\bigg\rfloor+\bigg\lfloor\frac{n}{c}\bigg\rfloor+\bigg\lfloor\frac{bn}{[b,c]}\bigg\rfloor\bigg)+2\bigg\lfloor\frac{n}{[b,c]}\bigg\rfloor & =n-\bigg(\bigg\lfloor\frac{n}{b}\bigg\rfloor+\bigg\lfloor\frac{n}{c}\bigg\rfloor+\bigg\lfloor\frac{bn}{c}\bigg\rfloor\bigg)+2\bigg\lfloor\frac{n}{c}\bigg\rfloor\\ & =n-\bigg(\bigg\lfloor\frac{n}{b}\bigg\rfloor+\bigg\lfloor\frac{n}{tb}\bigg\rfloor+\bigg\lfloor\frac{n}{t}\bigg\rfloor\bigg)+2\bigg\lfloor\frac{n}{tb}\bigg\rfloor\\ & =n-\bigg(\bigg\lfloor\frac{n}{b}\bigg\rfloor+\bigg\lfloor\frac{n}{t}\bigg\rfloor\bigg)+\bigg\lfloor\frac{n}{tb}\bigg\rfloor\\& \ge n-2\bigg\lfloor\frac{n}{2}\bigg\rfloor+\bigg\lfloor\frac{n}{tb}\bigg\rfloor,\text{ since }b\ge2\text{ and } t \ge 2\\ & \ge \bigg\lfloor\frac{n}{tb}\bigg\rfloor\ge0. \end{align*} $$
$$ \begin{align*} n-\bigg(\bigg\lfloor\frac{n}{b}\bigg\rfloor+\bigg\lfloor\frac{n}{c}\bigg\rfloor+\bigg\lfloor\frac{bn}{[b,c]}\bigg\rfloor\bigg)+2\bigg\lfloor\frac{n}{[b,c]}\bigg\rfloor & =n-\bigg(\bigg\lfloor\frac{n}{b}\bigg\rfloor+\bigg\lfloor\frac{n}{c}\bigg\rfloor+\bigg\lfloor\frac{bn}{c}\bigg\rfloor\bigg)+2\bigg\lfloor\frac{n}{c}\bigg\rfloor\\ & =n-\bigg(\bigg\lfloor\frac{n}{b}\bigg\rfloor+\bigg\lfloor\frac{n}{tb}\bigg\rfloor+\bigg\lfloor\frac{n}{t}\bigg\rfloor\bigg)+2\bigg\lfloor\frac{n}{tb}\bigg\rfloor\\ & =n-\bigg(\bigg\lfloor\frac{n}{b}\bigg\rfloor+\bigg\lfloor\frac{n}{t}\bigg\rfloor\bigg)+\bigg\lfloor\frac{n}{tb}\bigg\rfloor\\& \ge n-2\bigg\lfloor\frac{n}{2}\bigg\rfloor+\bigg\lfloor\frac{n}{tb}\bigg\rfloor,\text{ since }b\ge2\text{ and } t \ge 2\\ & \ge \bigg\lfloor\frac{n}{tb}\bigg\rfloor\ge0. \end{align*} $$
So (4.1) holds in this case.
(2) Assume
![]() $b\nmid c$
. Before we proceed with this case, we first mention three results.
$b\nmid c$
. Before we proceed with this case, we first mention three results.
-
(a) For real numbers x and y, it is well known that
 $\lfloor x\rfloor +\lfloor y\rfloor \le \lfloor x+y\rfloor $
.
$\lfloor x\rfloor +\lfloor y\rfloor \le \lfloor x+y\rfloor $
. -
(b) For a real number x, we have
 $\lfloor -2x\rfloor =-2\lfloor x\rfloor +\delta $
, where
$\lfloor -2x\rfloor =-2\lfloor x\rfloor +\delta $
, where
 $\delta \in \{-2,-1,0\}$
.
$\delta \in \{-2,-1,0\}$
.Proof. Consider three cases.
-
(i)
 $x=m\in \mathbb {Z}$
. Then,
$x=m\in \mathbb {Z}$
. Then,
 $\lfloor -2x\rfloor =-2m=-2\lfloor m\rfloor =-2\lfloor x\rfloor $
, which gives
$\lfloor -2x\rfloor =-2m=-2\lfloor m\rfloor =-2\lfloor x\rfloor $
, which gives
 $\delta =0$
.
$\delta =0$
. -
(ii)
 $x=m+\epsilon $
, where
$x=m+\epsilon $
, where
 $m\in \mathbb {Z}$
and
$m\in \mathbb {Z}$
and
 $\epsilon \in \mathbb {R}$
with
$\epsilon \in \mathbb {R}$
with
 $0<\epsilon <\tfrac 12$
. Then,
$0<\epsilon <\tfrac 12$
. Then,
 $-2x=-2m-2\epsilon =-2m-1+(1-2\epsilon )$
with
$-2x=-2m-2\epsilon =-2m-1+(1-2\epsilon )$
with
 $0<1-2\epsilon <1$
. It follows that
$0<1-2\epsilon <1$
. It follows that
 $\lfloor -2x\rfloor =-2m-1=-2\lfloor x\rfloor -1\text {, giving }\delta =-1.$
$\lfloor -2x\rfloor =-2m-1=-2\lfloor x\rfloor -1\text {, giving }\delta =-1.$
-
(iii)
 $x=m+\epsilon $
, where
$x=m+\epsilon $
, where
 $m\in \mathbb {Z}$
and
$m\in \mathbb {Z}$
and
 $\epsilon \in \mathbb {R}$
with
$\epsilon \in \mathbb {R}$
with
 $\tfrac 12\le \epsilon <1$
. As in Case (ii), we see that
$\tfrac 12\le \epsilon <1$
. As in Case (ii), we see that
 $\lfloor -2x\rfloor =-2\lfloor x\rfloor -2$
, so that
$\lfloor -2x\rfloor =-2\lfloor x\rfloor -2$
, so that
 $\delta =-2$
.
$\delta =-2$
.
-
-
(c) Consider the function
 $f(x,y)={1}/{x}+{1}/{y}-{2}/{xy}$
, where x and y are real variables with
$f(x,y)={1}/{x}+{1}/{y}-{2}/{xy}$
, where x and y are real variables with
 $x\ge 2$
and
$x\ge 2$
and
 $y\ge 3$
. Then the maximum value of
$y\ge 3$
. Then the maximum value of
 $f(x,y)$
is given by
$f(x,y)$
is given by
 $f(2,y)={1}/{2}$
for any
$f(2,y)={1}/{2}$
for any
 $y\ge 3$
.
$y\ge 3$
.Proof.
 $f(x,y)=({1}/{x})(1-{2}/{y})+{1}/{y}$
, and since
$f(x,y)=({1}/{x})(1-{2}/{y})+{1}/{y}$
, and since
 $1-{2}/{y}>0$
,
$1-{2}/{y}>0$
,
 $f(x,y)$
achieves its maximum value when x is as small as possible, that is,
$f(x,y)$
achieves its maximum value when x is as small as possible, that is,
 $x=2$
. However, then
$x=2$
. However, then
 $f(2,y)={1}/{2}$
for any
$f(2,y)={1}/{2}$
for any
 $y\ge 3$
.
$y\ge 3$
.
We are now ready to proceed with Case (2), where
![]() $b\nmid c$
. We have
$b\nmid c$
. We have
![]() $b<c<[b,c]$
, and from
$b<c<[b,c]$
, and from
![]() $b\mid [b,c]$
and
$b\mid [b,c]$
and
![]() $c\mid [b,c]$
, we get
$c\mid [b,c]$
, we get
![]() $3b\le [b,c]$
. Hence,
$3b\le [b,c]$
. Hence,
![]() ${n}/{3}\ge {bn}/{[b,c]}$
, from which it follows that
${n}/{3}\ge {bn}/{[b,c]}$
, from which it follows that
![]() $-\lfloor {bn}/{[b,c]}\rfloor \ge -\lfloor {n}/{3}\rfloor $
. So we see that
$-\lfloor {bn}/{[b,c]}\rfloor \ge -\lfloor {n}/{3}\rfloor $
. So we see that
It therefore suffices to show that
From item (c),
using item (a). It follows that
by item (b). Since
![]() $[b,c]\le bc$
, this gives
$[b,c]\le bc$
, this gives
For
![]() $n\ge 12$
, it easily follows that
$n\ge 12$
, it easily follows that
![]() $n-2\ge {n}/{2}+{n}/{3}\ge \lfloor {n}/{2}\rfloor +\lfloor {n}/{3}\rfloor $
, that is,
$n-2\ge {n}/{2}+{n}/{3}\ge \lfloor {n}/{2}\rfloor +\lfloor {n}/{3}\rfloor $
, that is,
![]() $\lfloor {n}/{2}\rfloor +2\le n-\lfloor {n}/{3}\rfloor $
. Direct checking shows that this relation is also valid for
$\lfloor {n}/{2}\rfloor +2\le n-\lfloor {n}/{3}\rfloor $
. Direct checking shows that this relation is also valid for
![]() $7\le n\le 11$
. Indeed,
$7\le n\le 11$
. Indeed,
 $$ \begin{align*} n=7 & :\quad \lfloor\tfrac{7}{2}\rfloor+2=5 \le7-2=7-\lfloor\tfrac{7}{3}\rfloor,\\ n=8 & :\quad \lfloor\tfrac{8}{2}\rfloor+2=6 \le8-2=8-\lfloor\tfrac{8}{3}\rfloor,\\ n=9 & : \quad \lfloor\tfrac{9}{2}\rfloor+2=6 \le9-3=9-\lfloor\tfrac{9}{3}\rfloor,\\ n=10 & :\quad \lfloor\tfrac{10}{2}\rfloor+2=7 \le10-3=10-\lfloor\tfrac{10}{3}\rfloor,\\ n=11 & : \quad\lfloor\tfrac{11}{2}\rfloor+2=7 \le11-3=11-\lfloor\tfrac{11}{3}\rfloor. \end{align*} $$
$$ \begin{align*} n=7 & :\quad \lfloor\tfrac{7}{2}\rfloor+2=5 \le7-2=7-\lfloor\tfrac{7}{3}\rfloor,\\ n=8 & :\quad \lfloor\tfrac{8}{2}\rfloor+2=6 \le8-2=8-\lfloor\tfrac{8}{3}\rfloor,\\ n=9 & : \quad \lfloor\tfrac{9}{2}\rfloor+2=6 \le9-3=9-\lfloor\tfrac{9}{3}\rfloor,\\ n=10 & :\quad \lfloor\tfrac{10}{2}\rfloor+2=7 \le10-3=10-\lfloor\tfrac{10}{3}\rfloor,\\ n=11 & : \quad\lfloor\tfrac{11}{2}\rfloor+2=7 \le11-3=11-\lfloor\tfrac{11}{3}\rfloor. \end{align*} $$
Hence, for all
![]() $n\ge 7$
,
$n\ge 7$
,
that is, (4.2) holds. This completes the discussion for
![]() $a=1$
.
$a=1$
.
From here on, we assume that
![]() $2\le a<b<c$
. We may also assume that
$2\le a<b<c$
. We may also assume that
![]() $(a,b,c)=1$
(since each fraction
$(a,b,c)=1$
(since each fraction
![]() ${a_{i_{1}}}/{[a_{i_{1}},a_{i_{2}},\ldots ,a_{i_{r}}]}$
in (2.1) remains unchanged if we cancel out any common factor between
${a_{i_{1}}}/{[a_{i_{1}},a_{i_{2}},\ldots ,a_{i_{r}}]}$
in (2.1) remains unchanged if we cancel out any common factor between
![]() $a_{i_{1}}$
and
$a_{i_{1}}$
and
![]() $[a_{i_{1}},a_{i_{2}},\ldots ,a_{i_{r}}]$
.) We begin by investigating when
$[a_{i_{1}},a_{i_{2}},\ldots ,a_{i_{r}}]$
.) We begin by investigating when
Note that whenever (4.3) holds,
 $$ \begin{align*} \frac{\xi_{n,3}(a,b,c)-n}{2} & =n-\bigg(\bigg\lfloor\frac{a\cdot n}{[a,b]}\bigg\rfloor+\bigg\lfloor\frac{a\cdot n}{[a,c]}\bigg\rfloor+\bigg\lfloor\frac{b\cdot n}{[b,c]}\bigg\rfloor\bigg)+2\bigg\lfloor\frac{a\cdot n}{[a,b,c]}\bigg\rfloor\\ & \ge n-\bigg(\frac{a\cdot n}{[a,b]}+\frac{a\cdot n}{[a,c]}+\frac{b\cdot n}{[b,c]}\bigg)\quad\text{using Case~(2)(a)}\\ & =\big(1-g(a,b,c)\big)\cdot n \ge0, \end{align*} $$
$$ \begin{align*} \frac{\xi_{n,3}(a,b,c)-n}{2} & =n-\bigg(\bigg\lfloor\frac{a\cdot n}{[a,b]}\bigg\rfloor+\bigg\lfloor\frac{a\cdot n}{[a,c]}\bigg\rfloor+\bigg\lfloor\frac{b\cdot n}{[b,c]}\bigg\rfloor\bigg)+2\bigg\lfloor\frac{a\cdot n}{[a,b,c]}\bigg\rfloor\\ & \ge n-\bigg(\frac{a\cdot n}{[a,b]}+\frac{a\cdot n}{[a,c]}+\frac{b\cdot n}{[b,c]}\bigg)\quad\text{using Case~(2)(a)}\\ & =\big(1-g(a,b,c)\big)\cdot n \ge0, \end{align*} $$
from which it follows that
![]() $\xi _{n,3}(a,b,c)\ge n$
.
$\xi _{n,3}(a,b,c)\ge n$
.
Let
![]() $d_{1}=(a,b)$
,
$d_{1}=(a,b)$
,
![]() $d_{2}=(b,c)$
and
$d_{2}=(b,c)$
and
![]() $d_{3}=(a,c)$
. Then,
$d_{3}=(a,c)$
. Then,
![]() ${(d_{1},d_{2})=(d_{1},d_{3})=(d_{2},d_{3})=1}$
, because
${(d_{1},d_{2})=(d_{1},d_{3})=(d_{2},d_{3})=1}$
, because
![]() $(a,b,c)=1$
. So
$(a,b,c)=1$
. So
![]() $a=d_{1}d_{3}q_{1}$
,
$a=d_{1}d_{3}q_{1}$
,
![]() $b=d_{1}d_{2}q_{2}$
,
$b=d_{1}d_{2}q_{2}$
,
![]() $c=d_{2}d_{3}q_{3}$
for some mutually relatively prime positive integers
$c=d_{2}d_{3}q_{3}$
for some mutually relatively prime positive integers
![]() $q_{1},q_{2}$
and
$q_{1},q_{2}$
and
![]() $q_{3}$
. It follows that
$q_{3}$
. It follows that
and
 $$ \begin{align} g(a,b,c)=\frac{1}{d_{2}q_{2}}+\frac{1}{d_{2}q_{3}}+\frac{1}{d_{3}q_{3}}. \end{align} $$
$$ \begin{align} g(a,b,c)=\frac{1}{d_{2}q_{2}}+\frac{1}{d_{2}q_{3}}+\frac{1}{d_{3}q_{3}}. \end{align} $$
Furthermore, there exist positive integers
![]() $s_{1}$
,
$s_{1}$
,
![]() $s_{2}$
and
$s_{2}$
and
![]() $s_{3}$
such that
$s_{3}$
such that
![]() $b=a+s_{1}d_{1}$
,
$b=a+s_{1}d_{1}$
,
![]() $c=b+s_{2}d_{2}$
and
$c=b+s_{2}d_{2}$
and
![]() $c=a+s_{3}d_{3}$
.
$c=a+s_{3}d_{3}$
.
We now proceed by partitioning the possible values of the triples
![]() $(d_{1},d_{2},d_{3})$
into four different classes.
$(d_{1},d_{2},d_{3})$
into four different classes.
Class 1: triples
![]() $(d_{1},d_{2},d_{3})$
for which
$(d_{1},d_{2},d_{3})$
for which
![]() $d_{1}\ge 2$
. Here,
$d_{1}\ge 2$
. Here,
![]() $b=a+s_{1}d_{1}$
implies that
$b=a+s_{1}d_{1}$
implies that
![]() $d_{2}q_{2}=d_{3}q_{1}+s_{1}\ge 2$
. Similarly,
$d_{2}q_{2}=d_{3}q_{1}+s_{1}\ge 2$
. Similarly,
![]() $c=b+s_{2}d_{2}$
implies that
$c=b+s_{2}d_{2}$
implies that
![]() $d_{3}q_{3}=d_{1}q_{2}+s_{2}\ge 3$
, and also,
$d_{3}q_{3}=d_{1}q_{2}+s_{2}\ge 3$
, and also,
![]() $c=a+s_{3}d_{3}$
implies that
$c=a+s_{3}d_{3}$
implies that
![]() $d_{2}q_{3}=d_{1}q_{1}+s_{3}\ge 3$
. If each of these inequalities happens to be an equality, we obtain
$d_{2}q_{3}=d_{1}q_{1}+s_{3}\ge 3$
. If each of these inequalities happens to be an equality, we obtain
![]() $g(a,b,c)=\tfrac 12+\tfrac 13+\tfrac 13=\tfrac 76$
, which is greater than
$g(a,b,c)=\tfrac 12+\tfrac 13+\tfrac 13=\tfrac 76$
, which is greater than
![]() $1$
. However, if any one of these inequalities becomes strict, we see that
$1$
. However, if any one of these inequalities becomes strict, we see that
![]() $g(a,b,c)\le 1$
. In the special event of three equalities, we must have
$g(a,b,c)\le 1$
. In the special event of three equalities, we must have
![]() $d_{2}q_{2}=2$
,
$d_{2}q_{2}=2$
,
![]() $d_{3}q_{3}=3$
and
$d_{3}q_{3}=3$
and
![]() $d_{2}q_{3}=3$
. However, this can only happen if
$d_{2}q_{3}=3$
. However, this can only happen if
![]() $d_{2}=d_{3}=1$
,
$d_{2}=d_{3}=1$
,
![]() $q_{2}=2$
and
$q_{2}=2$
and
![]() $q_{3}=3$
, giving
$q_{3}=3$
, giving
![]() $c=d_{2}d_{3}q_{3}=3$
, which is not possible, since
$c=d_{2}d_{3}q_{3}=3$
, which is not possible, since
![]() $a\ge 2$
. Therefore,
$a\ge 2$
. Therefore,
![]() $g(a,b,c)\le 1$
for all triples
$g(a,b,c)\le 1$
for all triples
![]() $(a,b,c)$
for which
$(a,b,c)$
for which
![]() $d_{1}=(a,b)\ge 2$
.
$d_{1}=(a,b)\ge 2$
.
Class 2: triples
![]() $(d_{1},d_{2},d_{3})$
for which
$(d_{1},d_{2},d_{3})$
for which
![]() $d_{1}=1$
and
$d_{1}=1$
and
![]() $d_{2}\ge 2$
. Here,
$d_{2}\ge 2$
. Here,
![]() $b=d_{2}q_{2}=d_{3}q_{1}+s_{1}\ge 2$
,
$b=d_{2}q_{2}=d_{3}q_{1}+s_{1}\ge 2$
,
![]() $d_{3}q_{3}=q_{2}+s_{2}\ge 2$
and
$d_{3}q_{3}=q_{2}+s_{2}\ge 2$
and
![]() $d_{2}q_{3}=q_{1}+s_{3}\ge 2$
.
$d_{2}q_{3}=q_{1}+s_{3}\ge 2$
.
If
![]() $d_{2}=2$
, then, since
$d_{2}=2$
, then, since
![]() $a=d_{3}q_{1}\ge 2$
and
$a=d_{3}q_{1}\ge 2$
and
![]() $(a,b,c)=1$
, we must have either
$(a,b,c)=1$
, we must have either
![]() $d_{3}\ge 3$
or
$d_{3}\ge 3$
or
![]() $q_{1}\ge 3$
. If
$q_{1}\ge 3$
. If
![]() $d_{3}\ge 3$
, then, from the inequalities above,
$d_{3}\ge 3$
, then, from the inequalities above,
![]() $b=d_{2}q_{2}=d_{3}q_{1}+s_{1}\ge 4$
,
$b=d_{2}q_{2}=d_{3}q_{1}+s_{1}\ge 4$
,
![]() $d_{3}q_{3}=q_{2}+s_{2}\ge 3$
and
$d_{3}q_{3}=q_{2}+s_{2}\ge 3$
and
![]() $d_{2}q_{3}=q_{1}+s_{3}\ge 2$
, so that
$d_{2}q_{3}=q_{1}+s_{3}\ge 2$
, so that
![]() $g(a,b,c)\le \tfrac 14+\tfrac 13+\tfrac 12={13}/{12}$
. By checking the small cases, there is only one instance where
$g(a,b,c)\le \tfrac 14+\tfrac 13+\tfrac 12={13}/{12}$
. By checking the small cases, there is only one instance where
![]() $1<g(a,b,c)\le {13}/{12}$
, namely
$1<g(a,b,c)\le {13}/{12}$
, namely
![]() $g(3,4,6)={13}/{12}$
. In this case, referring to (4.1),
$g(3,4,6)={13}/{12}$
. In this case, referring to (4.1),
However, if
![]() $q_{1}\ge 3$
, then, as above,
$q_{1}\ge 3$
, then, as above,
![]() $b=d_{2}q_{2}=d_{3}q_{1}+s_{1}\ge 4$
,
$b=d_{2}q_{2}=d_{3}q_{1}+s_{1}\ge 4$
,
![]() $d_{3}q_{3}=q_{2}+s_{2}\ge 2$
and
$d_{3}q_{3}=q_{2}+s_{2}\ge 2$
and
![]() $d_{2}q_{3}=q_{1}+s_{3}\ge 4$
, implying that
$d_{2}q_{3}=q_{1}+s_{3}\ge 4$
, implying that
![]() $g(a,b,c)\le \tfrac 14+\tfrac 12+\tfrac 14=1$
.
$g(a,b,c)\le \tfrac 14+\tfrac 12+\tfrac 14=1$
.
Next, consider
![]() $d_{2}\ge 3$
. Using the same inequalities as above, we see that now
$d_{2}\ge 3$
. Using the same inequalities as above, we see that now
![]() $g(a,b,c)\le \tfrac 13+\tfrac 12+\tfrac 13=\tfrac 76$
. Again, checking small cases, there is only one instance here where
$g(a,b,c)\le \tfrac 13+\tfrac 12+\tfrac 13=\tfrac 76$
. Again, checking small cases, there is only one instance here where
![]() $1<g(a,b,c)\le \tfrac 76$
, namely
$1<g(a,b,c)\le \tfrac 76$
, namely
![]() $g(2,3,6)=\tfrac 76$
. In this case,
$g(2,3,6)=\tfrac 76$
. In this case,
We see that, apart from these two exceptional cases (which satisfy
![]() $\xi _{n,3}(a,b,c) \ge n$
by direct checking), all the other triples
$\xi _{n,3}(a,b,c) \ge n$
by direct checking), all the other triples
![]() $(a,b,c)$
in this class have
$(a,b,c)$
in this class have
![]() $g(a,b,c)\le 1$
, so that
$g(a,b,c)\le 1$
, so that
![]() $\tfrac 12{(\xi _{n,3}(a,b,c)-n)}\ge (1-g(a,b,c))n\ge 0$
.
$\tfrac 12{(\xi _{n,3}(a,b,c)-n)}\ge (1-g(a,b,c))n\ge 0$
.
Class 3: triples
![]() $(d_{1},d_{2},d_{3})$
for which
$(d_{1},d_{2},d_{3})$
for which
![]() $d_{1}=d_{2}=1$
and
$d_{1}=d_{2}=1$
and
![]() $d_{3}\ge 2$
. Now we have
$d_{3}\ge 2$
. Now we have
![]() $b=q_{2}=d_{3}q_{1}+s_{1}\ge 3$
,
$b=q_{2}=d_{3}q_{1}+s_{1}\ge 3$
,
![]() $c=d_{3}q_{3}=q_{2}+s_{2}\ge 2$
and
$c=d_{3}q_{3}=q_{2}+s_{2}\ge 2$
and
![]() $c=d_{3}q_{3}=d_{3}q_{1}+s_{3}d_{3}$
, giving
$c=d_{3}q_{3}=d_{3}q_{1}+s_{3}d_{3}$
, giving
![]() $q_{3}=q_{1}+s_{3}\ge 2$
. From
$q_{3}=q_{1}+s_{3}\ge 2$
. From
![]() $q_{3}\ge 2$
and
$q_{3}\ge 2$
and
![]() $d_{3}\ge 2$
, it follows that
$d_{3}\ge 2$
, it follows that
![]() $c=d_{3}q_{3}$
is actually greater than or equal to
$c=d_{3}q_{3}$
is actually greater than or equal to
![]() $4$
. For
$4$
. For
![]() $c=4$
, there is only one possible triple
$c=4$
, there is only one possible triple
![]() $(a,b,c)$
, namely
$(a,b,c)$
, namely
![]() $a=2$
,
$a=2$
,
![]() $b=3$
and
$b=3$
and
![]() $c=4$
, and we already know that
$c=4$
, and we already know that
![]() $\xi _{n,3}(2,3,4)\ge n$
. So we may assume that
$\xi _{n,3}(2,3,4)\ge n$
. So we may assume that
![]() $q_{3}\ge 3$
or
$q_{3}\ge 3$
or
![]() $d_{3}\ge 3$
. In the former case,
$d_{3}\ge 3$
. In the former case,
![]() $g(a,b,c)=g(d_{3}q_{1},q_{2},d_{3}q_{3})={1}/{q_{2}}+{1}/{q_{3}}+{1}/{d_{3}q_{3}}\le {1}/{3}+{1}/{3}+{1}/{6}={5}/{6}\le 1$
, and in the latter case,
$g(a,b,c)=g(d_{3}q_{1},q_{2},d_{3}q_{3})={1}/{q_{2}}+{1}/{q_{3}}+{1}/{d_{3}q_{3}}\le {1}/{3}+{1}/{3}+{1}/{6}={5}/{6}\le 1$
, and in the latter case,
![]() $g(a,b,c)={1}/{q_{2}}+{1}/{q_{3}}+{1}/{d_{3}q_{3}}\le {1}/{3}+{1}/{2}+{1}/{6}=1$
. As in the previous paragraphs, we conclude that
$g(a,b,c)={1}/{q_{2}}+{1}/{q_{3}}+{1}/{d_{3}q_{3}}\le {1}/{3}+{1}/{2}+{1}/{6}=1$
. As in the previous paragraphs, we conclude that
![]() $\xi _{n,3}(a,b,c)\ge n$
for all triples
$\xi _{n,3}(a,b,c)\ge n$
for all triples
![]() $(a,b,c)$
that belong to this class.
$(a,b,c)$
that belong to this class.
Class 4:
![]() $d_{1}=d_{2}=d_{3}=1$
. From (4.4),
$d_{1}=d_{2}=d_{3}=1$
. From (4.4),
![]() $2\le q_{1}<q_{2}<q_{3}$
. Then,
$2\le q_{1}<q_{2}<q_{3}$
. Then,
![]() $g(a,b,c)= g(q_{1},q_{2},q_{3}) \le \tfrac 13+\tfrac 15+\tfrac 15={11}/{15}<1$
, and we again have
$g(a,b,c)= g(q_{1},q_{2},q_{3}) \le \tfrac 13+\tfrac 15+\tfrac 15={11}/{15}<1$
, and we again have
![]() ${\xi _{n,3}(a,b,c)}\ge n$
.
${\xi _{n,3}(a,b,c)}\ge n$
.
5 Infinitely many cases where
 $\xi _{n,k}(a_{1},a_{2},\ldots ,a_{k})=n$
.
$\xi _{n,k}(a_{1},a_{2},\ldots ,a_{k})=n$
.
One should not be misled by thinking that
![]() $\xi _{n,k}(a_{1},a_{2},\ldots ,a_{k})$
would grow without bound as k gets bigger. In this section, we conclude our discussion by proving that
$\xi _{n,k}(a_{1},a_{2},\ldots ,a_{k})$
would grow without bound as k gets bigger. In this section, we conclude our discussion by proving that
![]() $\xi _{n,k}(a_{1},a_{2},\ldots ,a_{k})=n$
is possible for arbitrarily large k.
$\xi _{n,k}(a_{1},a_{2},\ldots ,a_{k})=n$
is possible for arbitrarily large k.
Theorem 5.1. Let
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $n\geq 2$
. For each
$n\geq 2$
. For each
![]() $r\geq 0$
, we can find multipliers
$r\geq 0$
, we can find multipliers
![]() $a_{1}<a_{2}<\dots <a_{k}$
, where
$a_{1}<a_{2}<\dots <a_{k}$
, where
![]() $k>r$
, such that
$k>r$
, such that
![]() $\Delta _{i=1}^{k}a_{i}\underline {n}=\{a_{1},\text { }2^{2^{r}}\!\cdot a_{1},\text { }3^{2^{r}}\!\cdot a_{1},\text { }\dots ,\text { }n^{2^{r}}\!\cdot a_{1}\}$
.
$\Delta _{i=1}^{k}a_{i}\underline {n}=\{a_{1},\text { }2^{2^{r}}\!\cdot a_{1},\text { }3^{2^{r}}\!\cdot a_{1},\text { }\dots ,\text { }n^{2^{r}}\!\cdot a_{1}\}$
.
Proof. For the sake of this theorem, we denote
The proof is by induction on r. For
![]() $r=0$
, take
$r=0$
, take
![]() $k=1\text { and }a_{1}=1$
so that
$k=1\text { and }a_{1}=1$
so that
Assume that the statement is true for some
![]() $r\geq 0$
, and
$r\geq 0$
, and
![]() $a_{1}<a_{2}<\dots <a_{k}$
, where
$a_{1}<a_{2}<\dots <a_{k}$
, where
![]() $k>r$
, are the multipliers used to produce the symmetric difference
$k>r$
, are the multipliers used to produce the symmetric difference
Then, for each m,
![]() $1\le m\le n$
,
$1\le m\le n$
,
 $$ \begin{align*} {\mathbin{\Delta}}_{j=1}^{k}(m^{2^{r}}a_{j}\cdot{\underline{n}}) & =m^{2^{r}}{\mathbin{\Delta}}_{j=1}^{k}(a_{j}\underline{n})\\ & =\{m^{2^{r}}\!\cdot a_{1},\text{ }m^{2^{r}}(2^{2^{r}}\!\cdot a_{1}),\text{ }m^{2^{r}}(3^{2^{r}}\!\cdot a_{1}),\text{ }\dots,\text{ }m^{2^{r}}(n^{2^{r}}\!\cdot a_{1})\}\\ & =m^{2^{r}}D_{n,k}^{r}(a_{1},a_{2},\ldots,a_{k}). \end{align*} $$
$$ \begin{align*} {\mathbin{\Delta}}_{j=1}^{k}(m^{2^{r}}a_{j}\cdot{\underline{n}}) & =m^{2^{r}}{\mathbin{\Delta}}_{j=1}^{k}(a_{j}\underline{n})\\ & =\{m^{2^{r}}\!\cdot a_{1},\text{ }m^{2^{r}}(2^{2^{r}}\!\cdot a_{1}),\text{ }m^{2^{r}}(3^{2^{r}}\!\cdot a_{1}),\text{ }\dots,\text{ }m^{2^{r}}(n^{2^{r}}\!\cdot a_{1})\}\\ & =m^{2^{r}}D_{n,k}^{r}(a_{1},a_{2},\ldots,a_{k}). \end{align*} $$
Now take the symmetric difference between the n sets:

Due to the symmetry of this ‘matrix’, the symmetric difference is the ‘diagonal’,
This symmetric difference uses the list of multipliers
There may be duplicates in this list. Since two identical entries will not have any effect on D, our final list of multipliers
![]() $a^{\prime }_{1}<a^{\prime }_{2}<\cdots <a^{\prime }_{k'}$
is given by
$a^{\prime }_{1}<a^{\prime }_{2}<\cdots <a^{\prime }_{k'}$
is given by
and
Since
![]() $n>1$
, there is a prime p with
$n>1$
, there is a prime p with
![]() ${n}/{2}<p\leq n$
. Then,
${n}/{2}<p\leq n$
. Then,
![]() $\{a_{1},p^{2^{r}}a_{1},p^{2^{r}}a_{2},\dots ,p^{2^{r}}a_{k}\}\subseteq A'$
, and so
$\{a_{1},p^{2^{r}}a_{1},p^{2^{r}}a_{2},\dots ,p^{2^{r}}a_{k}\}\subseteq A'$
, and so
![]() $r+1<k+1\leq k'$
. The induction is complete.
$r+1<k+1\leq k'$
. The induction is complete.
Acknowledgement
The second author would like to express his gratitude to Professor Ke and his family for their hospitality during his visit to Tainan, Taiwan.