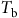Modeling weed seedling emergence for time-specific weed management: a systematic review

Abstract

Understanding the timing of weed emergence is crucial to effective management. Management practices implemented too early may fail to completely control late-emerging seedlings, whereas management practices implemented too late will suffer from low efficacy. Weed emergence times reflect biological factors, such as seed dormancy and germination requirements, as well as environmental conditions. We conducted a systematic review of studies that developed models to predict weed emergence temporal patterns. We screened 1,854 studies, 98 of which were included in the final dataset. Most of the studies included were conducted in North America (51%) or Europe (30%). A wide variety of weed species (102) and families (21) were included, and many studies modeled several weeds. Grass weeds (Poaceae) were modeled most frequently (83 instances). Most weeds (40%) had base temperature ${T_{\rm{b}}}$ values between 0 and 5 C, and 38% had base water potential ${{\rm{\psi }}_{\rm{b}}}$ ranging from −1.0 to −0.5 MPa. Most studies used empirical parametric models, such as Weibull (40%) or Gompertz (30%) models. Nonparametric and mechanistic models were also represented. Models varied in their biological and environmental data requirements. In general, empirical parametric models based on hydrothermal time (i.e., time above base temperature and water potential thresholds) represented a good balance between ease of use and prediction accuracy. Soft computing approaches such as artificial neural networks demonstrated substantial potential in situations with complex emergence patterns and limited data availability, although they (soft computing approaches) can be susceptible to overfitting. Our study also demonstrated variability in model performance and limited generalizability across species and regions. This finding underscores the need for context-specific and well-validated weed emergence models to inform management, especially in the context of climate change.

Introduction

Agricultural weed management is essential to crop productivity and environmental health. The timing of management operations is a key determinant of management efficacy (Mohler et al. 2021; Zimdahl 2018). Many control tactics, such as cultivation or herbicide applications, are most effective against newly germinated or young weeds. Delayed management typically results in inferior control, allowing more weeds to compete against crops for resources later in the season (Mohler et al. 2021; Zimdahl 2018). If management is delayed, resource-independent interference processes may also be set in motion by the time of management (Horvath et al. 2023). However, early management is challenging if field access is limited due to unforeseen environmental conditions. Another drawback of early management is that late-germinating weeds may remain as seeds in the soil seedbank, largely unaffected by control measures; these seeds are likely to survive, emerge, and cause problems later in the season. Thus, there is an optimal window of action during which weed control tactics are most likely to be effective (Reinhardt Piskackova et al. 2021). Defining this specific time frame is fundamental to the framework that we refer to as “Time-Specific Weed Management” (TSWM). In this framework, the decision on when to implement control measures is based on a quantitative analysis of the weed’s temporal dynamics, primarily seedling emergence, using a modeling approach (Figure 1). TSWM is consistent with the concept of a critical period for weed control (Knezevic et al. 2002; Nieto et al. 1968). Although weed control opportunities also occur at other times of the year, early-season control of young weeds may be critical to sustainable management (Storkey et al. 2021a).

Figure 1. Components of time-specific weed management tools may include models that predict temporal trends in weed seedling emergence, early weed growth, the relationship between weed size and weed control efficacy, crop injury risk, and crop yield loss as function of weed density and duration of competition.

A major challenge in scheduling weed management operations is that it is difficult to predict when weeds will emerge. Unlike crops, which have been under selection for uniform germination and are sown at a consistent depth, weeds have evolved myriad mechanisms to achieve variability in germination timing (Baskin and Baskin 2014). Weed emergence times reflect biotic factors, such as differences in seed dormancy and germination requirements, that vary between and within weed species (Baskin and Baskin 2014; Grundy 2003; Zimdahl 2018). Requirements for dormancy release and germination, although not necessarily the same, involve a wide range of environmental factors, including temperature, moisture, nitrate, oxygen, light, and the presence of inhibitors or stimulants (Figure 2). Environmental factors vary with climatic conditions across large geographic areas and with edaphic conditions or management practices at small scales. They also show significant interannual variability. Predicting weed emergence times represents a major technical challenge due to these factors, with potential solutions encompassing mathematical models of varying complexity (Brown et al. 2022; Ghersa and Holt 1995).

Figure 2. Seedling emergence is a multistage process involving dormancy release, germination, and preemergent growth. Abiotic and biotic factors, such as those shown, influence each stage of seedling emergence.

Models that predict the timing of weed emergence require different amounts of biological or environmental data and perform different operations on these data (Figure 3). Common types of biological data include threshold parameters such as base temperatures ( ${T_{\rm{b}}}$ ) and water potentials ( ${{\rm{\psi }}_{\rm{b}}}$ ) for germination or emergence. Germination and emergence do not occur at or below threshold values that are specific to each species (Bradford 2002) and can sometimes vary significantly between populations within a species (Bürger et al. 2020). However, efforts have been made to identify predictable patterns across species (e.g., Gardarin et al. 2010). Above the thresholds, increasing temperatures and water availability may accelerate germination and emergence to a certain limit. Other biological factors such as seed size (weight) and age affect the likelihood or timing of seedling emergence (Figure 2), but are less frequently included in weed emergence models. For example, larger and less light-sensitive seeds are more capable of emerging from greater burial depths than smaller light-sensitive seeds (Batlla and Benech-Arnold 2014; Juroszek and Gerhards 2004; Mohler et al. 2021), but only a few seedling emergence models have included seed size as a model input (Colbach et al. 2006; Vleeshouwers and Kropff 2000). Any abiotic influence on seed germination or emergence may interact with other abiotic factors or with seed age (Baskin and Baskin 2014; Martinkova et al. 2006).

Figure 3. Weed emergence models integrate environmental data with species-specific biological data to produce various outputs. From a management perspective, the crucial outputs are the timing and amount of seedling emergence. Modeling approaches may be characterized as empirical parametric, empirical nonparametric, or mechanistic (process based). RGR, Relative Growth Rate.

Modeling approaches can be classified as empirical parametric, empirical nonparametric, or mechanistic, that is, process based (Figure 3). The distinction between empirical and mechanistic modeling is better understood as a spectrum than a sharp division. At the empirical end of the spectrum, models link accessible data inputs with emergence outcomes but do not represent any underlying eco-physiological processes. Most empirical models are parametric and consist of a nonlinear S-shaped function, typically a logistic, Gompertz, or Weibull function, with up to four parameters (Gonzalez-Andujar et al. 2016a). Although empirical in nature, some parameters of these models may have direct biological relevance. For example, the lag parameter in the Weibull model (see “Results and Discussion”) measures the amount of time to the onset of emergence. The measure of time is most often a measure of thermal or hydrothermal time (Bradford 2002; Forcella et al. 2000), but other options are available.

Because emergence data do not always meet the assumptions of parametric models, semiparametric or nonparametric approaches have been proposed to increase flexibility (Cao et al. 2013; Chantre et al. 2014; Gonzalez-Andujar et al. 2016b). Examples of nonparametric approaches include established statistical methods as well as emerging soft computing techniques (Onofri et al. 2022; Royo-Esnal et al. 2020). While nonparametric models can fit complex patterns of emergence effectively, they are susceptible to overfitting. This tendency can limit their generalizability to different contexts, such as varying sites and years.

Contrasting with empirical models, mechanistic or process-based models may include several modules to represent stages of dormancy release, germination, and preemergent growth (Figure 3). Each module may require complex data inputs to characterize associated biotic and abiotic dynamics. Largely for this reason, mechanistic models are less common than empirical models and have been developed for fewer species (Gonzalez-Andujar et al. 2016a; Royo-Esnal et al. 2020). However, mechanistic models have the potential to generalize across diverse environmental and temporal conditions and produce deeper insights into weed ecology and management. For decades, researchers have noted the promise of mechanistic or semimechanistic approaches and called for further development of these approaches (Forcella et al. 2000; Vleeshouwers and Kropff 2000).

We performed a systematic review of the literature on weed emergence modeling. Other recent reviews of this topic have been narrative rather than systematic and focused on the technical details and statistical limitations of different modeling approaches (Gonzalez-Andujar et al. 2016a; Royo-Esnal et al. 2020). Our goal was to complement these existing reviews by providing a comprehensive and systematic survey of the literature with a focus on recent advances and their implications for management. In particular, we were interested in understanding the extent to which currently available tools can guide farmers’ decision making, and the practical steps necessary to develop useful guidance for more cropping systems. From this perspective, we note the advantages and disadvantages of current approaches and highlight areas for future research. Finally, we present a consolidated summary of all mathematical equations employed in prior studies, which can serve as a valuable reference for researchers engaged in modeling seedling emergence or other phenological stages of plants.

Materials and Methods

We performed a systematic literature review according to Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines (Page et al. 2021; Tricco et al. 2018), adapted as needed for the weed science context. On February 19, 2019, we searched for relevant peer-reviewed articles using the following search query in Scopus:

(TITLE (emerg*) OR TITLE (seedling) AND TITLE-ABS-KEY (weed)) AND (EXCLUDE (SUBJAREA, “IMMU”) OR EXCLUDE (SUBJAREA, “MEDI”) OR EXCLUDE (SUBJAREA, “PHAR”) OR EXCLUDE (SUBJAREA, “SOCI”)) AND (EXCLUDE (DOCTYPE, “cp”) OR EXCLUDE (DOCTYPE, “re”) OR EXCLUDE (DOCTYPE, “ch”) OR EXCLUDE (DOCTYPE, “no”)) AND (EXCLUDE (DOCTYPE, “bk”) OR EXCLUDE (DOCTYPE, “cr”) OR EXCLUDE (DOCTYPE, “er”) OR EXCLUDE (DOCTYPE, “le”))

This query is crafted to retrieve academic articles on topics related to seedling emergence and weeds. It searches for titles (‘TITLE’) with “emerg*” or “seedling”, and requires the presence of “weed” in the title, abstract, or keywords (‘TITLE-ABS-KEY’). The query specifically excludes publications from certain subject areas: immunology (IMMU), medicine (MEDI), pharmacology (PHAR), and social sciences (SOCI), using the parameters ‘EXCLUDE (SUBJAREA, “IMMU/MEDI/PHAR/SOCI”)’. Additionally, it filters out various document types like conference papers (cp), reports (re), book chapters (ch), notes (no), books (bk), conference reviews (cr), errata (er), and letters (le), indicated by ‘EXCLUDE (DOCTYPE, “cp/re/ch/no/bk/cr/er/le”)’. This focused strategy ensures that the search results are highly relevant to specific fields like plant science or agriculture, avoiding unrelated disciplines and document types. No geographic limitations were set. The resulting 1,854 papers were imported into Covidence (Melbourne, Australia), a standard systematic review platform for Cochrane reviews. Covidence was used to screen studies for eligibility according to the criteria outlined in Table 1. To summarize, the criteria for inclusion required that all studies present a model of weed emergence over time that must be calibrated or validated using field data. Consequently, studies conducted exclusively in greenhouses or controlled environments were excluded from consideration.

Table 1. Criteria used for title/abstract and full-text screening

Titles and abstracts were screened by two independent reviewers, and disagreements were resolved by a third reviewer. Of the 1,854 papers, 148 studies (8%) passed the initial title and abstract screening and subsequently underwent full-text review by two or three reviewers. A total of 98 studies were included in the final dataset (for a list of studies used and respective weed species, refer to Supplementary Table S1). For studies excluded at the full-text stage, the most common reasons were that the paper did not present emergence over time (e.g., only final emergence was reported) or did not present a model. Less common reasons were the absence of field data, emergence data, or peer review. For the studies that were included, we extracted data including, where available, the year and location of the study, weed species, soil texture, cropping system, type of seedbank (e.g., natural or seeded), experimental factors, the equations used along with their estimated parameters, model performance metrics (such as Root Mean Squared Error [RMSE]), and species-specific threshold parameters (like base temperature and base water potential).

Results and Discussion

Species and Geographic Distributions

Our dataset encompassed 102 plant species, although in some rare instances, studies identified weeds only at the genus level (such as Amaranthus spp., Echinochloa spp., and Bromus spp.) or referred to the entire weed community without providing species identification (Supplementary Table S1). The species whose emergence was modeled most frequently (13 instances) was common lambsquarters (Chenopodium album L.). However, the family that was modeled most frequently (83 instances) was Poaceae (grasses; Figure 4). Overall, monocot weeds comprised 36% of the species in the studies, while dicot weeds made up the remaining 64% (Supplementary Table S1). Nearly all studies measured the emergence of weed species. A small number of studies considered volunteer crops such as flax (Linum usitatissimum L.) and canola (Brassica napus L.) (Dexter et al. 2010; Lawson et al. 2006) or used a crop such as wheat (Triticum aestivum L.) as a surrogate weed (Bullied et al. 2012). Monitoring and modeling seedling emergence of crops along with weeds can be useful, because volunteer crops can be considered weeds in some crops. Further, understanding crop phenology aids in the implementation of time-specific weed management strategies, as illustrated in Figure 1. For example, quantifying the tolerance of crops to herbicides is crucial when deciding on the timing of application. Therefore, the timing of control measures is influenced not only by the temporal pattern of weed emergence but also by the phenology of the crops.

Figure 4. Distribution of weed families represented in the dataset collated from 98 seedling emergence modeling studies.

Most studies were conducted in either North America (51%) or Europe (30%), but some studies were conducted in South America, Asia, or Africa (Figure 5A). The climate in which each study site was located was described using the Köppen-Geiger climate classification system (Kottek et al. 2006). Some articles used data from multiple climatic zones. In these cases, each climate type was recorded once per publication. The two climate types that occurred most frequently were temperate (54%) and continental (26%) (Figure 5B).

Figure 5. Distribution of (A) continents and (B) Köppen-Geiger climate zones represented in the dataset collated from 98 seedling emergence modeling studies.

Existing models largely focus on the spring emergence of annual weeds in temperate areas of North America and Europe. Other patterns, for example, seedling emergence at the beginning of the rainy season in tropical areas, are not well characterized in the literature. Our analysis revealed clear geographic, climatic, and taxonomic biases that rendered the task of generalizing weed emergence models quite challenging.

Empirical Parametric Models

A comprehensive summary of almost all nonlinear models that we found in modeling weed seedling emergence is presented in Table 2. Most studies reported one or more empirical parametric models. Among studies that focused on a single model type, Weibull functions were the most common (40% studies), followed by Gompertz functions (30% studies) and logistic functions (17 studies). Many of these studies reported several models of the indicated type. For example, a single study might fit separate models for different weed species, sites, or management treatments. Some studies attempted to compare model parameter values using mixed-effects models, including studies of common sunflower (Helianthus annuus L.) and giant ragweed (Ambrosia trifida L.) emergence in relation to hydrothermal time across the midwestern United States (Clay et al. 2014; Davis et al. 2013).

Table 2. Major nonlinear model types used for modeling weed seedling emergence across 98 studies, with the recommended formulation of each model type highlighted in bold

The widespread use of Weibull, Gompertz, and logistic functions is primarily attributed to their ease of use and straightforward parameterization. Additionally, when data are transformed into a cumulative format, they often form an S-shaped curve, which fits well with these models. These three functions as well as sigmoidal functions are broadly suitable for predicting cumulative seedling emergence based on calendar days or thermal or hydrothermal time. However, notable differences exist between these models, each with various formulations. For instance, as detailed in Table 2, eight distinct versions of the Weibull model have been employed, each differing in versatility and parametric interpretation. One key difference, often causing confusion, lies in the interpretation of the inflection point. In logistic and sigmoid models, this represents the midpoint (e.g., time to 50% emergence). In contrast, for Gompertz and Weibull models, it indicates 36.78% [ ${\rm{exp}}\left( { - 1} \right)$ ] and 63.21% [ $1 - {\rm{exp}}\left( { - 1} \right)$ ] of the maximum emergence, respectively. Another critical consideration is that most S-shaped functions yield nonzero values at time zero ( $x = 0$ ), which is unrealistic. Weibull models are an exception, and even some of their formulations incorporate a lag parameter $l$ , determining the onset of emergence (Table 2). While other functions can be modified to ensure $y = 0$ at $x = 0$ or include a lag, such modifications are not inherent and require additional equation restructuring and coding. We also observed that the asymptote parameter $a$ , setting the maximum emergence value (Table 2), is sometimes incorrectly reported as exceeding 100% (or >1 for proportional data), which is not feasible and indicative of a modeling artifact. Researchers should ensure that this parameter does not surpass 100% (or 1), and if data are normalized, it is unnecessary to include parameter a in the model, instead fixing it at 100 (or 1).

As a general guideline, we recommend the Weibull model as the most suitable option for most modeling practices, especially the version that incorporates a lag parameter $l$ . While some variations of this model might appear complex (such as Equation 6 in Table 2), our experience indicates that these more complex formulations do not necessarily offer superior results compared with those with simpler parameterization (like Equation 1). Furthermore, complex models can pose challenges in estimating initial values for fitting, potentially leading to issues like convergence failure. Although the inflection point in the Weibull model is set at 63.21%, which might not align with the conventional preference for a 50% midpoint, this can be easily adjusted. By including ${\rm{ln}}\left( 2 \right)$ in the equation, as demonstrated in Equation 5 of Weibull in Table 2, the inflection point can be recalibrated to 50%. This modification provides flexibility for researchers accustomed to interpreting the midpoint as the time to 50% of an event. Ultimately, the Weibull model was found to be among the top-performing models along with Gompertz based on RMSE values (Figure 6), highlighting its suitability based on relevance to emergence biology but also its statistical robustness.

Figure 6. Comparison of five major model types used for modeling weed seedling emergence, based on their reported Root Mean Squared Error (RMSE) values. The box spans from the first to the third quartile, encompassing the interquartile range (IQR). Within each box, the solid line indicates the median, whereas the solid circle represents the mean. Whiskers extend to the smallest and largest values within 1.5 times the IQR. Empty circles represent individual RMSE values extracted from studies. For a detailed description of the model types, refer to Table 2.

Occasionally, to depict non-monotonic and potentially biphasic emergence patterns, two S-shaped functions are combined (see examples in Table 2). This approach is particularly relevant when the presence of subpopulations with distinct biological attributes results in multiple cohorts of emergence, a scenario that cannot be adequately captured by a single, unimodal model. A notable example of this is found in the study by Leon et al. (2015), in which the emergence of itchgrass [Rottboellia cochinchinensis (Lour.) W.D. Clayton] in Costa Rica exhibited a biphasic pattern. In this tropical environment, the standard models like Weibull, Gompertz, or logistic were insufficient for accurately modeling the observed emergence pattern of R. cochinchinensis. Composite (two-phase) models, while highly versatile in accommodating complex emergence patterns, tend to overfit, thereby reducing their generalizability. It is important to assess whether the additional complexity is statistically justified by comparing the error magnitude between simple and complex models. For example, in Argentina, junglerice [Echinochloa colona (L.) Link] emergence was suggested to be best explained by a double logistic model with two inflection points (Picapietra et al. 2021). However, the RMSE reported for the double-logistic model was only marginally smaller than that of the other best, simple model: 9.08 versus 9.8, a difference that may not be significant to justify the selection of more complex model. Additionally, the performance of these models should be evaluated using independent data to confirm their validity beyond the calibration dataset. Furthermore, interpreting parameters and their derivatives in these composite models becomes more complex. We observed that the three composite models outlined in Table 2 yield unrealistic values for time zero. This highlights the need for careful consideration and validation when employing these more intricate modeling approaches.

An alternative method to address multimodal emergence patterns involves using daily seedling density instead of modeling cumulative seedling emergence. Shem-Tov and Fennimore (2003) monitored annual bluegrass (Poa annua L.) continuously for 41 mo and used waveform sine regression to describe the seasonal (cyclical) patterns in seedling density. In a long-term study, A. trifida emergence was recorded in terms of growing seasons after burial (Harrison et al. 2007). Repeated-measures data from this experiment were analyzed by jointly fitting a binomial model (to account for the binary variable, emergence or not) and a geometric model (to account for the number of seasons before emergence).

Four studies focused on the use of shrub phenology to predict weed emergence. Two of these studies also reported new Gompertz models predicting weed emergence in terms of (hydro)thermal time (Masin et al. 2005; Otto et al. 2007). The other studies focused more on development of the phenological calendar but compared their results with those of existing models (Cardina et al. 2007, 2011). Phenological approaches are purely correlative and therefore may be limited in their precision or vulnerable to changes in the phenology of plants used as indicators. Nonetheless, weed emergence predictions based on phenological cues are widely accessible to farmers, unlike most of the tools discussed in this review, and therefore merit increased attention.

Sixteen studies compared multiple functions for use in empirical parametric models. Although this practice is likely common during exploratory stages of data analysis, many published papers focus on the best model rather than describing the results of all models. As model performance is context specific, it is best to avoid comparing the performance of different model types fit in different studies. Therefore, studies that report comparisons using a single dataset provide helpful insights into the relative performance of different functions.

Studies comparing multiple empirical parametric functions did not identify a clear front-runner. Dorado et al. (2009) used logistic, generalized logistic, Gompertz, and Weibull functions to predict emergence of 10 weed species in corn (Zea mays L.) in Spain and Portugal. The Gompertz function provided the best fit for the greatest number of species–site combinations, but each of the three other functions provided the best fit for at least one species–site combination. Gompertz and Weibull models predicted tall fescue [Schedonorus arundinaceus (Schreb.) Dumort; syn.: Festuca arundinacea Schreb.] and wheatgrass [Agropyron desertorum (Fisch. ex Link) Schult.] emergence timing more successfully than logistic, Verhulst, or Richards models (Behtari and Luis 2012). A study of sterile oat [Avena sterilis ssp. ludoviciana (Durieu) Gillet & Magne] found that a Weibull model outperformed Gompertz and log-logistic alternatives (Sousa-Ortega et al. 2021a). Based on a study of velvetleaf (Abutilon theophrasti Medik.) emergence across 11 site-years and two continents, Egea-Cobrero et al. (2020) concluded that the Weibull generally achieved greater prediction accuracy than the logistic model. This study also demonstrated the value of using multiple performance indicators rather than relying exclusively on the coefficient of determination (R²). The use of the R² for evaluating the performance of nonlinear models is strongly discouraged. This is because a model can achieve high R² values while its predictions still deviate significantly from the observed data. Instead, our preferred metric is the RMSE. RMSE is straightforward to calculate, with most software packages readily providing it, and it is not prone to the issues associated with R². RMSE offers a more reliable measure of model accuracy by quantifying the average magnitude of the prediction errors, thus providing a clearer indication of the model’s performance. Supplementary Figure S1, using hypothetical emergence data, illustrates that two models with starkly different performances can yield identical high R² values (in this case, 0.9946), despite the clear lack of fit in one. However, when comparing models based on RMSE, the less effective model registers an RMSE of 37.7%, whereas the more appropriate model has an RMSE of just 3.3%.

RMSE values compiled from various studies for five major model types revealed Gompertz and Weibull models as the top performers, followed by the sigmoid model, albeit with considerable variation within each model type (Figure 6). The average RMSE for Gompertz and Weibull models was around 13%, whereas it was approximately 15% for the sigmoid model. However, several challenges arise with the RMSE data reported here. First, not all studies used RMSE values; many provided R² or other metrics like Akaike information criterion (AIC) instead. Second, the RMSE data we present amalgamate values from both the model calibration and validation phases, as it was difficult to ascertain whether the reported values are from the calibration or validation phase in many cases. Third, some studies evaluate different models, model modifications, or methods for calculating thermal time, leading to the reporting of RMSEs for various combinations. This variety complicates the task of determining which RMSE or set of RMSEs most accurately represents the outcomes of a study. We attempted to compile all reported values despite these challenges.

Although model parameters are usually estimated using nonlinear regression, other approaches are possible. For example, genetic algorithms have been successfully used for parameter estimation in empirical models (Haj Seyed Hadi and Gonzalez-Andujar 2009) as well as more mechanistic models (Blanco et al. 2014). Although such approaches to model fitting are not always necessary and may be computationally intensive, they can be useful when regression techniques do not perform well.

Choices about model structure and parameter optimization are important, but it is also important to recognize that these choices cannot address drawbacks common to all empirical parametric models. These drawbacks have been well summarized elsewhere, especially by Cao et al. (2011) and Royo-Esnal et al. (2020). It is noteworthy that most of the statistical issues outlined by Onofri et al. (2018, 2022) in the context of germination modeling are also applicable to the analysis of emergence data. Briefly, the issues highlighted may encompass, but are not limited to, the non-independence of samplings and the challenge of not knowing the exact moment of emergence between samplings, leading to censored data. Additionally, the selection of poor initial parameters or suboptimal optimization algorithms can lead to inaccurate model solutions. There are also several biological problems. One biological problem is that weed emergence is not a single process but rather the result of multiple processes combined. These processes—dormancy release, germination, and preemergent growth—are influenced by environmental conditions in different ways. Another problem is that each stage of weed emergence is influenced by multiple interacting signals; most of this complexity is not captured by a simple thermal or hydrothermal time index. In addition, weeds exhibit intraspecific (interpopulation and even intrapopulation) variation that limits prediction accuracy.

Empirical Nonparametric Models

Our dataset contained seven studies presenting nonparametric or semiparametric models. Five of these studies also included parametric models fit with nonlinear regression for comparison.

Cao et al. (2011, 2013) largely pioneered the use of nonparametric modeling in this context, drawing on established nonparametric estimation techniques that had not previously been applied to weed emergence data. These studies predicted emergence of ripgut brome (Bromus diandrus Roth) by estimating the cumulative distribution function of cumulative hydrothermal time using nonparametric methods, without presupposing the shape of the distribution. A few subsequent studies built on this research. Gonzalez-Andujar et al. (2016b) modeled emergence of awned canary grass (Phalaris paradoxa L.) using similar methods in southern Spain. They found that a nonparametric estimator outperformed parametric models (logistic, Gompertz, or Weibull) in its ability to describe complex emergence patterns. However, both nonparametric and parametric methods showed a poor predictive ability when tested on independent data from different years, perhaps because factors other than cumulative hydrothermal time influenced emergence. Sousa-Ortega et al. (2021b) used nonparametric methods to predict emergence in three canarygrass species: short-spiked canarygrass (Phalaris brachystachys Link), little-seed canarygrass (Phalaris minor Retz.), and P. paradoxa. The performance of nonparametric models was similar to the performance of parametric Weibull models. Recently, Onofri et al. (2022) developed a new R package, drcte, which offers versatile options for fitting nonparametric models to germination and emergence data.

Artificial neural networks (ANNs) represent another alternative to conventional nonlinear regression techniques. In the context of weed emergence, ANNs were first used to model emergence of wild oat (Avena fatua L.) (Chantre et al. 2012). Temperature and moisture values were included as separate inputs to the ANNs, rather than being combined into a hydrothermal index as in typical nonlinear regressions. This bivariate structure enabled ANNs to provide better predictions than Weibull or logistic models on a test dataset (Chantre et al. 2012). In a later study, a bivariate ANN outperformed a Weibull model in terms of RMSE of the test set by more than 70% (Chantre et al. 2014). ANNs based directly on meteorological data—not soil conditions—have successfully described the irregular emergence of A. fatua, Italian ryegrass (Lolium multiflorum Lam.), and hairy vetch (Vicia villosa Roth) in the semiarid Pampean region of Argentina (Chantre et al. 2018).

The primary advantages of the approaches developed in these studies are increased flexibility and alleviation of statistical concerns. However, these approaches sometimes suffer from overfitting and are more difficult to implement than nonlinear regression, largely explaining why they remain uncommon in the literature (Chantre et al. 2018; Gonzalez-Andujar et al. 2016a). In addition, empirical models—parametric or not—do not represent underlying eco-physiological processes contributing to emergence. Representing these processes requires a more mechanistic approach.

Mechanistic Models

Only six studies were characterized as mechanistic, and these studies varied in their complexity. At the simpler end of the spectrum, some studies used parametric equations to create separate models of dormancy release, germination, and/or preemergent growth (Oryokot et al. 1997). For example, pigweed (Amaranthus spp.) emergence was modeled as the process of germination (dependent on temperature and moisture) followed by the process of preemergent shoot elongation (dependent on temperature; Oryokot et al. 1997). These modules were designed for incorporation into a crop growth model. Similarly, C. album germination was modeled as a function of hydrothermal time, then shoot elongation was modeled as a function of thermal time (Roman et al. 2000). Blanco et al. (2014) modeled A. fatua dormancy release in terms of afterripening thermal time and germination in terms of hydrothermal time. Logistic functions were used for both components, and a genetic algorithm was used for parameter estimation. The resulting model was more parsimonious than ANN or regression approaches for the same system (Blanco et al. 2014).

A more complex model of V. villosa emergence included four submodels: release of physical dormancy, release of physiological dormancy and germination thermal requirements, moisture requirements, and preemergent growth (Renzi et al. 2018). Environmental data requirements for this model were typical (i.e., soil temperature and moisture), but the model did require more biological data than empirical approaches, because cardinal temperatures were needed for each submodel (see following section). Other mechanistic models may require additional environmental data as well. A mechanistic model parameterized for C. album, ladysthumb (Polygonum persicaria L.; syn.: Persicaria maculosa Gray), and corn spurry (Spergula arvensis L.) required data on the date of soil cultivation, soil temperature, and soil penetration resistance (Vleeshouwers and Kropff 2000). One of the most complex weed emergence models is AlomySys, a model of blackgrass (Alopecurus myosuroides Huds.) emergence that includes submodels focused on the soil environment; seed distribution after tillage; seed survival, dormancy, and germination; and preemergent growth (Colbach et al. 2006). AlomySys demonstrates the potential of mechanistic approaches to provide detailed representations of weed biology and the effects of management on weed emergence. This model (as FlorSys) was later extended to other species using functional traits (Gardarin et al. 2012).

After more than 25 years of development, data requirements for parameterization and application remain a major limitation of mechanistic models. Advantages of these models include their potential for high accuracy and their capacity to yield insights into processes underlying weed emergence. Mechanistic models are often favored for their ability to predict the actual number of seedlings, rather than just a relative number, thus enabling applications such as forecasting the impact of weeds on crop yields. However, even with highly accurate emergence models, determining the absolute number of seedlings necessitates an accurate estimation of seedbank size, which is inherently variable across surface and with depth and time.

Species’ Threshold Parameters

Thermal and hydrothermal time are normally calculated according to the assumption that emergence does not occur below base temperature ${T_{\rm{b}}}$ or water potential ${{\rm{\psi }}_{\rm{b}}}$ values and occurs more rapidly with increasing temperature above ${T_{\rm{b}}}$ (see later discussion of why increase in rapidity does not apply to water potential value above $\;{{\rm{\psi }}_{\rm{b}}}$ ). The threshold values vary between weed species and may be determined in laboratory studies before model development (e.g., Dorado et al. 2009) or selected according to which values produce the best-fitting models of observed field emergence (e.g., Norsworthy and Oliveira 2007). Temperature and water potential requirements also vary at population and individual levels within weed species, but this intraspecific variation is not easily accounted for in models of seedling emergence. Some models account for inhibitory effects of high temperatures on germination, for example, by imposing a ceiling temperature, but most models do not. The importance of this parameter depends on climatic context.

We compiled ${T_{\rm{b}}}$ data for 100 species (as shown in Figure 7) and ${{\rm{\psi }}_{\rm{b}}}$ for 57 species (Figure 8). ${T_{\rm{b}}}$ values ranged from −3.1 C in smallseed falseflax (Camelina microcarpa Andrz. ex DC.) to 28.0 C in tropic ageratum (Ageratum conyzoides L.), with most weeds (40%) having ${T_{\rm{b}}}$ values between 0 and 5 C. Regarding ${{\rm{\psi }}_{\rm{b}}}$ , most species (38%) fell within the range of −1.0 to −0.5 MPa. However, ${{\rm{\psi }}_{\rm{b}}}$ estimates are less reliable, as evidenced by extreme values, such as −30 MPa in A. trifida or values close to zero (−0.008 MPa in wild radish [Raphanus raphanistrum L.]). Extremely negative ${{\rm{\psi }}_{\rm{b}}}$ values often arise when hydrothermal time is determined by adjusting ${{\rm{\psi }}_{\rm{b}}}$ to best fit field emergence data, potentially indicating that emergence is not highly sensitive to soil moisture and that a thermal time model might suffice. The most accurate estimates of ${{\rm{\psi }}_{\rm{b}}}$ are generally obtained through germination assays under varying water potential levels, followed by fitting hydrotime models (Bradford 1990). Seedling emergence models typically use a single ${{\rm{\psi }}_{\rm{b}}}$ value, while it is known this parameter varies from seed to seed and can be better described by statistical distributions (Bradford 2002; Mesgaran et al. 2013). Furthermore, water and temperature can interact to affect these threshold parameters (Mesgaran et al. 2017), but due to the high variability of field-collected seedling emergence data, these nuances are often negligible or difficult to discern. We also observed that for species with multiple estimates of ${T_{\rm{b}}}$ (Figure 7) or ${{\rm{\psi }}_{\rm{b}}}$ (Figure 8), there is considerable variability in these values. This variation can have biological origins, stemming from differences among populations, or it can be methodological, arising from variations in experimental conditions or the statistical models used.

Figure 7. Base temperature (T _b) of 100 weed species compiled from 98 seedling emergence modeling studies along with the histogram displaying the frequency distribution of this threshold parameter. Horizontal line on a data point (mean), if present, indicates the range of base temperature values found for the given species.

Figure 8. Base water potential (ψ_b) of 57 weed species compiled from 98 seedling emergence modeling studies along with the histogram displaying the frequency distribution of this threshold parameter. Horizontal line on a data point (mean), if present, indicates the range of base water potential values found for the given species.

Temperature and Moisture Data

Most models of weed emergence, including nearly all empirical parametric models, use thermal or hydrothermal time as the independent variable. Our dataset contained 37 studies that used thermal time, 27 studies that used hydrothermal time, 23 studies that compared multiple measures of time (e.g., thermal, hydrothermal, photo-hydrothermal, and/or chronological), 2 studies that compared hydrothermal time with bivariate hydrotime and thermal time inputs (the bivariate approaches involving ANNs), 5 studies that used only chronological time, and 4 studies with more complex data inputs. Hydrothermal times used in seedling emergence models are not calculated in the original manner devised for modeling seed germination responses to water (Bradford 2002; Mesgaran et al. 2017). They are more accurately described as moisture-constrained thermal times. The crucial difference lies in how these models treat the moisture variable, ${\rm{\psi }}$ . In seedling emergence models, ${\rm{\psi }}$ is converted into a binary variable HT (HT = 1, if ${\rm{\psi \;}} \gt \;{{\rm{\psi }}_{\rm{b}}}$ or HT =,0, if ${\rm{\psi \;}} \le {\rm{\;}}{{\rm{\psi }}_{\rm{b}}}$ ), and thermal time is accumulated only during periods when this variable takes the value 1. In contrast, true hydrothermal time models accumulate the magnitude of the difference ${\rm{\psi \;}} - {\rm{\;}}{{\rm{\psi }}_{\rm{b}}}$ (when ${\rm{\psi }} \gt \;{{\rm{\psi }}_{\rm{b}}}$ ) in a similar manner to thermal time models. This distinction may explain why some studies find little difference between thermal time and hydrothermal time models, as treating moisture as a binary variable might not significantly alter the accumulation of thermal time, whether or not moisture is included. Additionally, as mentioned earlier, unlike thermal time, which is calculated based on a single ${T_{\rm{b}}}$ , authentic hydrothermal time models developed for seed germination use a distribution of ${{\rm{\psi }}_{\rm{b}}}$ values rather than a single fixed value.

In general, our review supports the use of hydrothermal time but does not invalidate the use of thermal time. Models of both types tend to be successful in the context in which they were developed, but are difficult to extrapolate to other cropping systems or locations. Masin et al. (2010) modeled emergence of A. theophrasti and johnsongrass [Sorghum halepense (L.) Pers.] using thermal time with a predefined base temperature of 5 C, thermal time with base temperatures estimated by bootstrapping for each species and ecotype, or hydrothermal time with estimated base temperatures and base water potentials. All three models provided good predictions of emergence dynamics for both species. However, adding the soil moisture component did slightly improve model fit by predicting pauses in emergence caused by low soil moisture. In some cases, model accuracy might be further improved by the inclusion of photoperiod data (Royo-Esnal et al. 2015a, 2015b). However, the physiological mechanisms underlying the influence of photoperiod on seedling emergence require further investigation.

Including more data does not always improve performance. A study of American sicklepod [Senna obtusifolia (L.) Irwin & Barneby] evaluated cumulative seedling emergence as a function of chronological, thermal, or hydrothermal time (Reinhardt Piskackova et al. 2020b). Interestingly, the authors found that chronological data produced the most negative AIC, suggesting better model performance. This finding likely indicates that neither temperature nor moisture was strongly limiting during the period of emergence (Reinhardt Piskackova et al. 2020b; see also Leon et al. 2015). Sousa-Ortega et al. (2021a) evaluated A. sterilis ssp. ludoviciana emergence models based on thermal developed by Leguizamón et al. (2005) on a new test dataset. The authors also developed and tested new models based on hydrothermal time. Inclusion of soil moisture did not improve the performance of models from Leguizamón et al. (2005), but it did improve the accuracy of the newly developed model (Sousa-Ortega et al. 2021a).

Our review also highlights several key characteristics of temperature and moisture data used in weed emergence models. A more general source of variation stems from the fact that (hydro)thermal time is typically measured by calculating degree days. The degree-day concept does not fully capture plant responses to their environment, and the choice of calculation method can be important (Bonhomme 2000; Roltsch et al. 1999). For example, thermal time is frequently calculated by averaging the maximum and minimum daily temperatures, then comparing the result to a base temperature. This method can sometimes be misleading, for example, if the maximum daily temperature is above the base temperature but the calculated average is below the base temperature. Alternatives include triangulation and sine-wave methods or use of hourly data collected by soil temperature sensors. Additionally, while most weed seeds germinate in the top 5-cm layer of soil, accurately measuring soil moisture at this depth is challenging and perhaps not very accurate. Moreover, this layer is not the only soil stratum from which temperature and moisture data should be collected as some seeds can germinate from deeper layers. Determining the appropriate depth or depths for data collection is not always straightforward, adding to the complexity of accurately assessing the conditions affecting seed germination (Cao et al. 2011). Data on soil temperature and moisture are frequently measured in situ or estimated using software such as the Soil Temperature and Moisture Model (STM²; https://www.ars.usda.gov/research/software/download/?softwareid=209; Spokas and Forcella 2009). Neither method is infallible or highly accessible to farmers.

Part of the promise of machine learning approaches is that they might function using meteorological data (e.g., air temperature, precipitation) and without the need for users to input biological parameters like base temperatures (Chantre et al. 2018). However, there are limits to what can be achieved using meteorological data alone. Weed emergence is also responsive to site-specific factors such as landscape position and the presence of crop residue (Page et al. 2006). Therefore, information about the precise location of a field and its management may help maximize the accuracy of weed emergence predictions. Despite these caveats and sources of variation, models based on either thermal or hydrothermal time are generally robust.

Management Practices

Several of the studies included in our dataset measured the effects of weed management on emergence. For example, mechanical weed control practices (in-row cultivation and rotary hoeing) changed the parameters of a Gompertz equation for weed emergence in dry bean (Phaseolus vulgaris L.) (Amador-Ramirez et al. 2002). Some studies have found that tillage treatments influence weed emergence time (Bullied et al. 2003), whereas other studies have found no effect of tillage (Barnes et al. 2017). Some forms of tillage may complicate the prediction of weed emergence by increasing heterogeneity in the soil or weed seedbank distribution (Roman et al. 2000). Like tillage, application of preemergence herbicides can alter the timing of Palmer amaranth (Amaranthus palmeri S. Watson) emergence (Chahal et al. 2021). Preemergence herbicides may delay A. palmeri emergence through their residual activity, but farmers should be prepared to perform additional management if needed once the residual activity dissipates (Chahal et al. 2021). Cultural factors such as crop sowing time also affect weed emergence (Goulart et al. 2020; Shivrain et al. 2009). One study measured the effects of tillage, herbicide application, and soybean [Glycine max (L.) Merr.] seeding rate on common purslane (Portulaca oleracea L.) emergence (Khakzad et al. 2019). All three factors altered emergence dynamics, demonstrating the value of considering multiple management practices simultaneously. However, what may appear as direct causal relationships between cropping system management and weed emergence can sometimes be coincidental or mediated through other factors. For instance, the impact of tillage on seedling emergence might be attributed to its alteration of seed placement within the soil profile. This change in position can affect the hydrothermal conditions surrounding the seed, as well as the physical resistance the seedling encounters in reaching the soil surface.

Certainly, the idea that management practices within cropping systems can influence the timing of weed emergence is well established in both scientific research and among farmers.

Modeling efforts do have the potential to optimize management. This principle is especially true for tactics that rely on changing weed emergence times. Notably, false and stale seedbank tactics work by stimulating weed emergence and then killing the newly emerged, vulnerable weeds. Weed emergence models could be used to determine the ideal timing and probable efficacy of these tactics (Travlos et al. 2020). Similarly, models could help farmers determine whether a practice like delayed crop planting is worthwhile as a weed control measure (Schutte et al. 2008).

More generally, weed emergence models can identify the best timing for any mechanical or chemical weed control operation and thereby reduce the likelihood that a follow-up operation will be needed. Our review shows that a weed emergence model based solely on hydrothermal time can identify this timing with considerable accuracy in the cropping system and location for which it was parameterized. However, generalizing the models to a novel system may require more information, including information about the management practices recently applied in the novel system.

Future Directions

Anthropogenic trends such as climate change and cropping system intensification threaten to increase weed pressure in cropping systems worldwide (Storkey et al. 2021b). At the same time, weed control measures have environmental as well as economic costs, and indiscriminate application of these measures will reduce their efficacy. Addressing these overlapping challenges requires adoption of an integrated weed management paradigm grounded in weed ecology (MacLaren et al. 2020; Mortensen et al. 2012).

Weed emergence modeling is a good example of a method in which ecological data support more sustainable weed management. This systematic review demonstrates that the irregular patterns of weed emergence in the field reflect aspects of weed biology and environmental conditions. These relationships can be understood and predicted to a degree, enabling farmers to time their weed management operations for maximum efficacy and efficiency. Our review also demonstrated that, despite substantial progress in the field of weed emergence modeling, these models are not yet assisting most farmers. Three major barriers are that (1) weed emergence models are time-consuming to develop, (2) models are difficult to apply in new contexts, and (3) most models have not been translated into user-friendly decision support tools.

Both empirical and mechanistic models have traditionally been produced through time-intensive laboratory and field studies. It is difficult to perform these tasks (e.g., weekly counting of emerged seedlings) at a very large scale. Consequently, automating parts of data collection could accelerate model development. We recommend increased research on image analysis methods to rapidly produce data on emergence time (Reinhardt Piskackova et al. 2020a). Weed detection methods are advancing rapidly in support of site-specific weed management programs (Gerhards et al. 2022) and might be readily tailored to this use. Once data are collected, machine learning techniques such as ANNs also merit increased attention, given their flexibility and ability to handle multivariate inputs and outputs (Gonzalez-Andujar et al. 2016a).

Weed emergence models frequently only work well for the location, cropping system, and weed population used to train the model. For example, annual ryegrass (Lolium rigidum Gaudin) showed different emergence patterns in different regions of Spain, and no single Weibull model was appropriate for all sites (Sousa-Ortega et al. 2020). In addition to climatic variability, interpopulation variability can limit prediction accuracy (Loddo et al. 2019). Most weed emergence models have not been tested in many places or on many populations of the modeled weed species, so global analyses of their performance would be valuable (Egea-Cobrero et al. 2020). Developing a better understanding of when and how underperforming models might be adjusted in the field would be valuable. For example, many farmers perform some weed scouting. Studies on weed emergence tend to describe modeling as a way to reduce the need for scouting (Reinhardt Piskackova et al. 2020b), although not a replacement (Martinson et al. 2007). We propose that scouting data could instead be more actively integrated into model development or even used to make early-season corrections to model parameters.

A few online and software tools (e.g., WeedCast, AlertInf, WEPS-ANN) have made weed emergence predictions accessible to farmers and other stakeholders (Royo-Esnal et al. 2020; Šoštarčić et al. 2021). More such tools are needed. Although weed emergence models are useful on their own, they have even greater value as components of comprehensive models covering all stages of weed life cycles (Bagavathiannan et al. 2020; Molinari et al. 2020). Such comprehensive models provide decision support and demonstrate the long-term effects of integrative weed management. In this respect, they differ from most current emergence models, which are limited by their short-term focus (Royo-Esnal et al. 2020). As an alternative to this comprehensive vision, a more targeted decision support tool might include multiple components, including weed emergence models, that help farmers with time management operations such as herbicide applications (Figure 1). The need for time-specific weed management is both well recognized (Buhler 2002) and increasingly urgent, given worsening stressors, including climatic variability, species’ invasions, and herbicide resistance. Consequently, there is no better time to translate research on weed emergence into practice.